数字逻辑与数字系统 第四版 (白中英 著) 科学出版社 课后答案 chapter3 课后答案
数字逻辑与数字系统设计习题参考答案

(4)(0.785)10=(0.011110000101)8421BCD
1.9
(1)(106)10=(1101010)2原码=反码=补码=01101010
(2)(-98)10=(-1100010)2原码=11100010
不考虑无关项,化简后的表达式:
F=
按考虑无关项化简结果绘制的逻辑电路习题4.10图(a)所示:
习题4.10图(a)
按不考虑无关项化简结果绘制的逻辑电路如习题4.10图(b)所示
习题4.10图(b)
4.11解:这是一个优先编码器的问题,设特快为A,直快为B,慢车为C,没有开车要求,输出为0,若A要求开车则输出,1,B要求开车输出为2,C要求开车输出3,根据A-B-C的优先顺序列功能表如下:
4.6解:根据题意:F= ,所以,可绘制电路如习题4.6图所示
习题4.6图
4.7解:根据题意:F= ,所以,可绘制电路如习题4.7图所示
习题4.7图
4.8解:
习题4.8图
4.9解:根据题意,三个变量有两个为1的卡诺图如习题4.9图(a)所示:
习题4.9图(a)
由此可列出逻辑表达式为:F= ,根据逻辑表达式可绘制逻辑电路习题4.9图(b)所示:
输入
输出
A
B
C
T1
T0
0
0
0
0
0
0
0
1
1
1
0
1
0
1
0
0
1
1
1
0
1
0
0
0
1
1
0
数字逻辑与数字系统一二三章答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 6153 65127 177635 11737.493 111.1111 7.7479.43 . 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 1261 7592 1340.10011 0.59375 0.4647 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC 5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B )+AB(C+C ) =AB+AC =右边(3) E D C CD A C B A A )(++++=A+CD+E 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) =Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑(白中英)课后习题答案
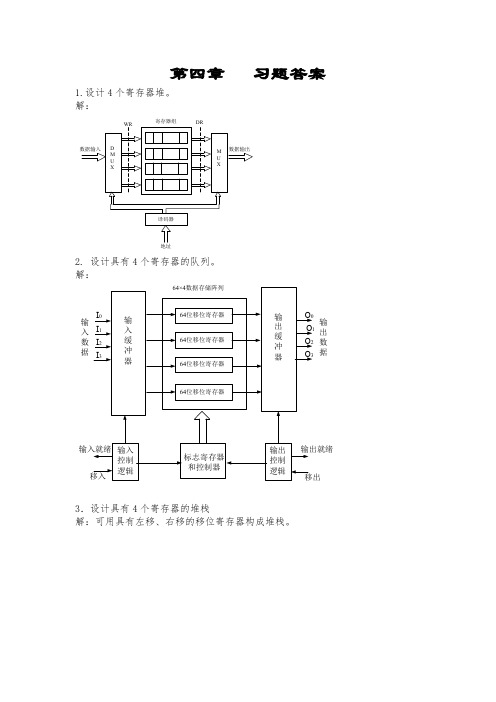
第四章习题答案1.设计4个寄存器堆。
解:寄存器组2. 设计具有4个寄存器的队列。
解:输入数据输出数据3.设计具有4个寄存器的堆栈解:可用具有左移、右移的移位寄存器构成堆栈。
栈顶SR 1SR 2SR 3输入数据输出数据压入弹出4.SRAM 、DRAM 的区别解:DRAM 表示动态随机存取存储器,其基本存储单元是一个晶体管和一个电容器,是一种以电荷形式进行存储的半导体存储器,充满电荷的电容器代表逻辑“1”,“空”的电容器代表逻辑“0”。
数据存储在电容器中,电容存储的电荷一般是会慢慢泄漏的,因此内存需要不时地刷新。
电容需要电流进行充电,而电流充电的过程也是需要一定时间的,一般是0.2-0.18微秒(由于内存工作环境所限制,不可能无限制的提高电流的强度),在这个充电的过程中内存是不能被访问的。
DRAM 拥有更高的密度,常常用于PC 中的主存储器。
SRAM 是静态的,存储单元由4个晶体管和两个电阻器构成,只要供电它就会保持一个值,没有刷新周期,因此SRAM 比DRAM 要快。
SRAM 常常用于高速缓冲存储器,因为它有更高的速率;5. 为什么DRAM 采用行选通和列选通解:DRAM 存储器读/写周期时,在行选通信号RAS 有效下输入行地址,在列选通信号CAS 有效下输入列地址。
如果是读周期,此位组内容被读出;如果是写周期,将总线上数据写入此位组。
由于DRAM 需要不断刷新,最常用的是“只有行地址有效”的方法,按照这种方法,刷新时,是在RAS 有效下输入刷新地址,存储体的列地址无效,一次选中存储体中的一行进行刷新。
每当一个行地址信号RAS 有效选中某一行时,该行的所有存储体单元进行刷新。
6. 用ROM 实现二进制码到余3码转换 解: 真值表如下:8421码 余三码B3B2 B1 B0G3G2 G1G00 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 10 1 1 01 0 0 01 0 1 01 1 0 01 1 1 10 0 0 10 0 1 10 1 0 10 1 1 110 0最小项表达式为:G 3=∑)9,8,7,6,5( G 2=∑)9,4,3,2,1( G 1=∑)8,7,4,3,0( G 0=∑)8,6,4,2,0( 阵列图为:G 3G 2G 1GB 3B 2B 1B B 07. 用ROM 实现8位二进制码到8421码转换解:输入为8位二进制数,输出为3位BCD 码,12位二进制数,所以,所需ROM 的容量为:28*12=30728.ROM、EPROM和EEPROM的区别解:ROM 指的是“只读存储器”,即Read-Only Memory。
数字逻辑第四版课后练习题含答案

数字逻辑第四版课后练习题含答案1. 第一章1.1 课后习题1. 将十进制数22转换为二进制数。
答:22 = 101102. 将二进制数1101.11转换为十进制数。
答:1101.11 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 1 x 2^(-1) + 1 x 2^(-2) = 13.753. 将二进制数1101.01101转换为十进制数。
答:1101.01101 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 0 x 2^(-1)+ 1 x 2^(-2) + 1 x 2^(-4) + 0 x 2^(-5) + 1 x 2^(-6) = 13.406251.2 实验习题1. 合成与门电路设计一个合成与门电路,使得它的输入A,B和C,只有当A=B=C=1时输出为1,其他情况输出为0。
答:下面是一个合成与门电路的示意图。
合成与门电路示意图其中,S1和S2是两个开关,当它们都被打开时,电路才会输出1。
2. 第二章2.1 课后习题1. 将十进制数168转换为八进制数和二进制数。
答:168 = 2 x 8^3 + 1 x 8^2 + 0 x 8^1 + 0 x 8^0 = 250(八进制)。
168 = 10101000(二进制)。
2. 将八进制数237转换为十进制数和二进制数。
答:237 = 2 x 8^2 + 3 x 8^1 + 7 x 8^0 = 159(十进制)。
237 = 010111111(二进制)。
2.2 实验习题1. 全加器电路设计一个全加器电路,它有三个输入A,B和C_in,两个输出S和C_out。
答:下面是一个全加器电路的示意图。
C_in|/ \\/ \\/ \\/ \\/ \\A|________ \\| | AND Gate______| |B|__| XOR |_| S\\\\ /\\ /\\ /\\ /| | OR Gate| ||_| C_out其中,AND Gate表示与门,XOR Gate表示异或门,OR Gate表示或门。
数字逻辑 习题与答案.(优选)

F0 0 000 0 110 1 0
1
0 1 1
1
1 0 0
1
1 0 1
1
1 1 0
1
1 1 1
0
(3)逻辑图(4)波形图
14输入信号A,B,C的波形如图P1.2所示,试画出电路输出F1、F2的波形图
解:
波形如下:
第2章习题P56
2.分析图P2.2所示逻辑电路,其中S3、S2、S1、S0为控制输入端,列出真值表,说明F与A,B的关系。
习题与答案
《数字逻辑与数字系统(第四版)》,白中英
第1章习题P30
7证明下列等式
(2)
证明:
8用布尔代数简化下列各逻辑函数表达式
(4)
解:
9将下列函数展开为最小项表达式
(1)
解:
10用卡诺图化简下列各式
(2)
解:
由卡诺图知,
(4)
解:
12逻辑函数 ,试用真值表、卡诺图、逻辑图、波形图表示该函数。
解:(1)真值表(2)卡诺图
解:(1)表达式:
(2)真值表
S1 S0
F
0 0
0 1
1 0
1 1
0
(3)说明F与A,B的关系
F与A,B的关系如真值所示。
4.图P2.4所示为数据总线上的一种判零电路,写出F的表达式,说明该电路的逻辑功能。
解:(1)表达式
(2)功能说明
当且仅当全部输入都为0时,输出F才为1。
6.图P2.6所示为两种十进制数代码转换器,输入为余3码,分析输出是什么码。
最新文件----------------仅供参考--------------------已改成-----------word文本---------------------方便更改
数字逻辑课本习题答案
习 题 五1. 简述时序逻辑电路与组合逻辑电路的主要区别。
解答组合逻辑电路:若逻辑电路在任何时刻产生的稳定输出值仅仅取决于该时刻各输入值的组合,而与过去的输入值无关,则称为组合逻辑电路。
组合电路具有如下特征:②信号是单向传输的,不存在任何反馈回路。
时序逻辑电路:若逻辑电路在任何时刻产生的稳定输出信号不仅与电路该时刻的输入信号有关,还与电路过去的输入信号有关,则称为时序逻辑电路。
时序逻辑○1○2 电路中包含反馈回路,通过反馈使电路功能与“时序”○3 电路的输出由电路当时的输入和状态(过去的输入)共同决定。
2. 作出与表1所示状态表对应的状态图。
表 1解答根据表1所示状态表可作出对应的状态图如图1所示。
图13.已知状态图如图2所示,输入序列为x=11010010,设初始状态为A,求状态和输出响应序列。
图 2解答状态响应序列:A A B C B B C B输出响应序列:0 0 0 0 1 0 0 14. 分析图3所示逻辑电路。
假定电路初始状态为“00”,说明该电路逻辑功能。
图 3 解答○1根据电路图可写出输出函数和激励函数表达式为 xK x,J ,x K ,xy J y xy Z 1111212=====○2 根据输出函数、激励函数表达式和JK 触发器功能表可作出状态表如表2所示,状态图如图4所示。
表2图4○3由状态图可知,该电路为“111…”序列检测器。
5. 分析图5所示同步时序逻辑电路,说明该电路功能。
图5解答○1根据电路图可写出输出函数和激励函数表达式为 )(D ,x y x D y y x Z 21112121212y x y y y y y x ⊕=+=+=○2 根据输出函数、激励函数表达式和D 触发器功能表可作出状态表如表3所示,状态图如图6所示。
表3图6○3由状态图可知,该电路是一个三进制可逆计数器(又称模3可逆计数器),当x=0时实现加1计数,当x=1时实现减1计数。
6.分析图7所示逻辑电路,说明该电路功能。
数字逻辑第四版华科出版1~7全答案

(1) 29 (2) 0.27 (3) 33.33
解答: (1) 29 = (11101)2=(65)8=(1D)16 (2) 0.27 = (0.0100)2=(0.21)8=(0.4 )16
(3)33.33 = (100001.0101)2 = (41.24)8= (41.2508)8= (41.2507)8 = (21.5)16 = (21.547B)16=(21.547A)16
ABCD
AB CD 00 01 11 10
00
1 11
01
1 11
11 1 1 1 1
所以,F(A,B,C,D) =m(3-15)
10
1 11
=M(0-2)
精选ppt
22
习题课
2.8 用卡诺图化简法求出下列逻辑函数的最简“与-或”表 达式和最简“或-与”表达式。
(1) F (A ,B ,C ,D ) A B A C D A C B C (2) F (A ,B ,C ,D ) B D C D (B C )A ( B D ) (3) F ( A ,B , C ,D ) M ( 2 , 4 , 6 , 1 , 1 , 1 0 , 1 1 , 1 2 , 1 3 ) 4 5 解答: (1) F (A ,B ,C ,D ) A B A C D A C B C
yzxyyzxz精选ppt191926用逻辑代数的公理定理和规则将下列逻辑函数化简为最简与或表达式精选ppt2020精选ppt212127将下列逻辑函数表示成最小项之和及最大项之积形式00011110abcd00011110所以m471215m03811精选ppt222200011110abcd00011110所以m315m02精选ppt232328用卡诺图化简法求出下列逻辑函数的最简与或表达式和最简或与表达式
数字逻辑第四版白中英第五章

第五章可编程逻辑5.1 PLD 的基本概念5.2 现场可编程门阵列FPGA5.3 在系统可编程ISP5.4 可编程逻辑的原理图方式设计5.5 可编程逻辑的VHDL文本方式设计返回目录5.1 PLD的基本概念5.1.1 可编程阵列5.1.2 PLD的类型5.1.1 可编程阵列1.与阵列图5.1 与阵列图5.2例1的与阵列编程2.或阵列或阵列如图5.3所示,可编程矩阵的输出连接到或门上。
图5.3 或阵列图5.4 例3的与-或阵列编程3.可编程连接技术图5.5 SRAM 为基的与阵列概念5.1.2 PLD的类型1.简单可编程逻辑器件SPLD图5.6SPLD内部结构框图2.复杂可编程逻辑器件CPLDCPLD本质上是:利用可编程的互连总线连接起来的多路SPLD。
图5.7 CPLD结构框图5.2 现场可编程门阵列FPGA5.2.1 FPGA的基本结构5.2.2 可组态逻辑块CLB5.2.3 SRAM为基础的FPGA5.2.1 FPGA的基本结构图5.8FPGA的基本结构框图5.2.2 可组态逻辑块CLB图5.9基本可组态CLB图5.10 FPGA中一个逻辑模块的框图图5.11 LUT编程后用作SOP表达式输出5.2.3 SRAM为基础的FPGA图5.12 可变FPGA配置的基本概念5.3 在系统可编程ISP5.3.1 ispLSI器件的体系结构5.3.2 在系统编程原理5.3.1 ispLSI器件的体系结构1.ispLSI 1032框图和巨块的组成图5.13 ispLSI 1032的体系结构框图和引脚图2.通用逻辑块GLB图5.14 GLB的结构框图图5.15 GLB的标准组态3.布线区图5.16 ORP逻辑图4.输入输出单元IOC图5.18 I/O单元工作组态图5.17 IOC的结构框图5.时钟分配网络图5.19 时钟设置网络6.ispMACH 4000系列器件图5.20 ispMACH 4000系列结构框图5.3.2 在系统编程原理1.在系统编程原理图5.21 ispLSI器件的编程结构转换示意图2.isp器件的编程方式图5.22典型ISP编程电路5.4 可编程逻辑的原理图方式设计5.4.1 编程环境和设计流程图5.4.2 设计输入5.4.3 功能模拟5.4.4 综合和实现(软件)5.4.5 时序模拟5.4.6 器件下载5.4.1 编程环境和设计流程图1.编程环境2.设计流程图图5.24 可编程逻辑设计流程5.4.2 设计输入图5.25原理图方式(a)和文本方式(b)设计同一逻辑电路图5.26 逻辑分段与结合的例子5.4.3 功能模拟图5.27功能模拟显示图5.4.4 综合和实现(软件)1.综合阶段图5.28综合阶段的优化例子2.实现阶段5.4.5 时序模拟图5.29时序模拟的假定例子5.4.6 器件下载图5.30下载一个设计到目标器件5.5 可编程逻辑的VHDL文本方式设计5.5.1 VHDL的基本概念5.5.2 VHDL的组合逻辑设计5.5.3 VHDL的时序逻辑设计5.5.1 VHDL的基本概念图5.315.5.2 VHDL的组合逻辑设计1.VHDL编程中的数据流描述方法图5.32 一个SOP形式逻辑电路2.VHDL编程中的结构描述方法图5.33 VHDL结构法与固定逻辑IC硬件实现法的比较图5.34 VHDL组件示例图5.35 例8的逻辑电路图3.VHDL编程中库元件调用法5.5.3 VHDL的时序逻辑设计图5.36 时钟边沿与属性描述图5.37 序列检测器有限状态机。
大学教材课后题答案网站

大学教材部分答案参考网站 (供大家学习)1、C 程序设计第三版 (谭浩强著) 清华大学出版社课后答案/bbs/viewthread.php?tid=80&fromuid=92、复变函数与积分变换第四版 (张元林西安交大著) 高等教育出版社课后答案/bbs/viewthread.php?tid=612&fromuid=9C 语言程序设计教程第三版(谭浩强张基温著) 高等教育出版社课后答案[khdaw_lxywyl]/bbs/viewthread.php?tid=79&fromuid=9C 语言程序设计教程第二版 (谭浩强张基温著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=256&fromuid=9离散数学(第三版)(耿素云屈婉玲张立昂著) 清华大学出版社课后答案【khdaw_ricardo】/bbs/viewthread.php?tid=293&fromuid=9耿国华数据结构课后答案/bbs/viewthread.php?tid=103&fromuid=9严蔚敏《数据结构(c 语言版)习题集》答案/bbs/viewthread.php?tid=102&fromuid=9谭浩强C++程序设计习题答案/bbs/viewthread.php?tid=420&fromuid=9《微机原理与接口技术》清华(冯博琴吴宁)版课后答案/bbs/viewthread.php?tid=707&fromuid=9数据库系统概论 (王珊萨师煊著) 清华大学出版社课后答案/bbs/viewthread.php?tid=991&fromuid=9C 程序设计第二版 (谭浩强著) 课后答案/bbs/viewthread.php?tid=47&fromuid=9清华大学《数据结构》习题+课后答案/bbs/viewthread.php?tid=249&fromuid=9《数学物理方法》(梁昆淼第二版)习题解答谢希仁版《计算机网络教程》课后答案/bbs/viewthread.php?tid=203&fromuid=9《计算机网络第四版》答案【khdaw】/bbs/viewthread.php?tid=340&fromuid=9数据结构习题集(C 版)答案/bbs/viewthread.php?tid=374&fromuid=9计算机操作系统 (汤子赢著) 西安电子科技大学课后答案/bbs/viewthread.php?tid=1083&fromuid=9离散数学 (左孝凌著) 上海科学技术文献出版社课后答案【khdaw】/bbs/viewthread.php?tid=466&fromuid=9近世代数基础 (刘绍学著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=177&fromuid=9计算机组成原理习题&答案唐朔飞高等教育出版社【khdaw】/bbs/viewthread.php?tid=984&fromuid=9计算机网络(第4 版)清华(Andrew S.Tanenbaum)版答案(中文版)【khdaw】/bbs/viewthread.php?tid=201&fromuid=9《常微分方程》王高雄高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=567&fromuid=9数学分析(陈传璋版)习题答案下载/bbs/viewthread.php?tid=714&fromuid=9计算机算法设计与分析(第 3 版) (王晓东著) 电子工业出版社课后答案【khdaw_ricardo】/bbs/viewthread.php?tid=3162&fromuid=9《计算机系统结构》清华第2 版习题解答(chm)【khdaw】/bbs/viewthread.php?tid=1303&fromuid=9《编译原理》课后习题答案/bbs/viewthread.php?tid=175&fromuid=9《计算机网络》(第三版) (Andrew S.Tanenbaum 著) 清华大学出版社课后答案《软件工程》课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=896&fromuid=9C++语言程序设计(第3 版) (郑莉著) 清华大学出版社课后答案/bbs/viewthread.php?tid=988&fromuid=9计算机操作系统第三版 (汤子瀛哲凤屏汤小丹著) 西安电子科技大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=691&fromuid=9微型计算机接口技术及应用【khdaw】/bbs/viewthread.php?tid=375&fromuid=9常微分方程 (王高雄)第三版高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=2563&fromuid=9编译原理第三版 (陈火旺著) 国防工业出版社课后答案/bbs/viewthread.php?tid=1476&fromuid=9《常微分方程》(王高雄版)习题答案/bbs/viewthread.php?tid=489&fromuid=9大学计算机基础教程答案/bbs/viewthread.php?tid=379&fromuid=980x86 汇编语言程序设计 (沈明美温冬禅著) 清华大学出版社课后答案/bbs/viewthread.php?tid=523&fromuid=9IBM-PC 汇编语言程序设计课后习题答案 (美明温冬婵著) 清华大学出版社课后答案/bbs/viewthread.php?tid=370&fromuid=9数学分析 (华东师范大学数学系著) 高等教育出版社课后答案/bbs/viewthread.php?tid=238&fromuid=9李春葆:数据结构习题与解析-C 语言版/bbs/viewthread.php?tid=1005&fromuid=9visual basic 示例程序、实验答案下载/bbs/viewthread.php?tid=508&fromuid=9汇编语言 (王爽著) 课后答案清华版《编译原理》课后答案/bbs/viewthread.php?tid=228&fromuid=9离散数学(高等教育出版社)耿素云屈婉玲【khdaw】/bbs/viewthread.php?tid=1224&fromuid=9离散数学及其应用 (傅彦顾小丰著) 电子工业出版社课后答案/bbs/viewthread.php?tid=233&fromuid=9《计算机网络》机械工业出版社(James F.Kurose, Keith W.Ross)答案【khdaw_cola】/bbs/viewthread.php?tid=730&fromuid=9计算机网络(第5 版)课后习题答案【khdaw】/bbs/viewthread.php?tid=2981&fromuid=9常微分方程课后习题答案(华东师范版)/bbs/viewthread.php?tid=172&fromuid=9《Visual FoxPro 程序设计教程》课后习题答案(刘卫国主编)/bbs/viewthread.php?tid=232&fromuid=9有关《计算机组成原理》相关课后答案发布/bbs/viewthread.php?tid=3565&fromuid=9《计算机组成原理》课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=505&fromuid=9C 程序设计第三版 (谭浩强著) 清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=3690&fromuid=9离散数学教程 (耿素云屈婉玲王捍贫著) 北京大学出版社课后答案/bbs/viewthread.php?tid=36&fromuid=9数据库系统概念答案【khdaw_cola】/bbs/viewthread.php?tid=759&fromuid=9数据库系统概论答案清华版【khdaw_cola】/bbs/viewthread.php?tid=337&fromuid=9所有有关《操作系统》的答案发布和一些版本的答案求助【khdaw】/bbs/viewthread.php?tid=3320&fromuid=9/bbs/viewthread.php?tid=2653&fromuid=9数据库系统概论(第四版)王珊、萨师煊【khdaw】/bbs/viewthread.php?tid=2291&fromuid=9数学分析答案复旦陈纪修【khdaw_cola】/bbs/viewthread.php?tid=328&fromuid=9《数据库系统概论》课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=219&fromuid=9数据库系统概论-第四版-高教版-王珊-封面看内图【khdaw_cola】/bbs/viewthread.php?tid=2344&fromuid=9计算机组成原理课后答案(白中英版)/bbs/viewthread.php?tid=173&fromuid=9所有《数据结构》版本课后答案发布/bbs/viewthread.php?tid=4310&fromuid=9《数值分析》(第4版)李庆扬编清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=3596&fromuid=9《数学分析》(第三版)华东师范大学高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=7192&fromuid=9数学分析复旦大学陈传章/bbs/viewthread.php?tid=448&fromuid=9近世代数基础 (张禾瑞著) 课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=269&fromuid=9《计算机组成与结构》王爱英(第四版)答案/bbs/viewthread.php?tid=4836&fromuid=9《软件工程导论》张海潘第五版清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=7159&fromuid=9所有有关《数据库系统概论》的答案发布和一些有关数据库版本的答案求助【khdaw】/bbs/viewthread.php?tid=3321&fromuid=9离散数学耿素云屈婉玲高等教育出版社课后习题参考答案【khdaw】C++语言程序设计(第3 版)(郑莉版)郑莉清华大学出版社【khdaw_lxywyl】/bbs/viewthread.php?tid=1106&fromuid=9目前最完整的数据结构1800 题包括完整答案(word 版本)/bbs/viewthread.php?tid=1244&fromuid=9《操作系统》(中国铁道出版社,刘振鹏,李亚平,王煜,张明)习题答案/bbs/viewthread.php?tid=348&fromuid=9机械工业版《c++程序设计语言》题解下载/bbs/viewthread.php?tid=254&fromuid=9《数字逻辑》(第二版)鲍家元毛文林高教出版课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1081&fromuid=9《Visual FoxPro 及其应用系统开发》(简明版)谭浩强清华大学出版【khdaw_cola】/bbs/viewthread.php?tid=1362&fromuid=9《数据结构题集》严蔚敏 (C 语言版)答案【khdaw】/bbs/viewthread.php?tid=3319&fromuid=9《计算机组成原理与汇编语言程序设计》教材答案【khdaw_cola】/bbs/viewthread.php?tid=1233&fromuid=9计算机网络第二版 (吴功宜著) 清华大学出版社课后答案/bbs/viewthread.php?tid=4403&fromuid=9计算机网络谢希仁第五版电子工业出版社课后参考答案【khdaw_cola】/bbs/viewthread.php?tid=6495&fromuid=9复变函数与积分变换第四版西安交大课后答案/bbs/viewthread.php?tid=2181&fromuid=9《数学物理方法》学习指导【khdaw_cola】/bbs/viewthread.php?tid=1142&fromuid=9数值分析【khdaw_cola】/bbs/viewthread.php?tid=1521&fromuid=9信息论与编码学习辅导及习题详解/bbs/viewthread.php?tid=1903&fromuid=9/bbs/viewthread.php?tid=3048&fromuid=9VB 高教版课后答案/bbs/viewthread.php?tid=250&fromuid=9实变函数与泛函分析课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1332&fromuid=9《微机系统原理与接口技术》课后答案【khdaw_cola】/bbs/viewthread.php?tid=1304&fromuid=9清华版编译原理课后答案(chm)【khdaw】/bbs/viewthread.php?tid=1302&fromuid=9计算机网络教程谢希仁版/bbs/viewthread.php?tid=1082&fromuid=9数值分析第四版 (李庆扬王能超易大义著) 清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=8086&fromuid=9耿国华数据结构---C 语言的描课后大部分习题答案西安电大学出版社【khdaw_cola】/bbs/viewthread.php?tid=2015&fromuid=9新版汇编语言程序设计 (钱晓捷著) 电子工业出版社课后答案/bbs/viewthread.php?tid=692&fromuid=9《计算机组成原理》唐朔飞第二版高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9774&fromuid=9计算机组成原理白中英第四版课后答案【khdaw_cola】/bbs/viewthread.php?tid=3419&fromuid=9IBM-PC 汇编语言程序设计(第2 版) (沈美明温冬婵编著著) 清华出版社课后答案/bbs/viewthread.php?tid=3497&fromuid=9初等数论答案严士健高教版【khdaw_cola】/bbs/viewthread.php?tid=2360&fromuid=9计算机组成原理唐朔飞版高等教育出版社(部分答案)【khdaw】/bbs/viewthread.php?tid=3422&fromuid=9西电汤操作系统第三版【khdaw_cola】计算机应用基础 (不详著) 不详课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=262&fromuid=9数学模型(第三版)习题参考解答/bbs/viewthread.php?tid=4879&fromuid=9微型计算机原理与接口技术 (冯博琴著) 清华出版课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=2617&fromuid=9离散答案(王元元张桂蕓编著)科学出版社【khdaw_cola】/bbs/viewthread.php?tid=1100&fromuid=9《C 程序设计》谭浩强(第三版)清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=2608&fromuid=9C++ 程序设计(第二版)高等教育出版课件例题源代码及习题答案/bbs/viewthread.php?tid=1751&fromuid=9计算机网络教程第五版 (谢希仁著) 电子工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=11354&fromuid=9计算机网络第4 版 (谢希仁著) 电子工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=225&fromuid=9软件工程导论第五版 (张海藩著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=7449&fromuid=9数据结构教程(第2 版)李春葆答案/bbs/viewthread.php?tid=3334&fromuid=9数值分析 (未知著) 华中科技大课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=3525&fromuid=9数据结构(C 语言版) (严蔚敏吴伟民米宁著) 清华大学出版社课后答案/bbs/viewthread.php?tid=2067&fromuid=9泛函分析讲义-习题解答张恭庆、林源渠北大版【khdaw_cola】/bbs/viewthread.php?tid=3139&fromuid=9近世代数基础 (张禾瑞著) 课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=3510&fromuid=9【khdaw_ricardo】/bbs/viewthread.php?tid=11229&fromuid=9白中英《计算机组成原理_试题、题解与题库》电子书(超星版)/bbs/viewthread.php?tid=1085&fromuid=9电子工业版《vb 语言程序设计》习题答案/bbs/viewthread.php?tid=107&fromuid=9C++ 程序设计教程(第二版) (钱能著) 清华大学出版课后答案/bbs/viewthread.php?tid=2503&fromuid=9计算机应用基础理论习题参考答案/bbs/viewthread.php?tid=116&fromuid=9数学模型第三版 (姜启源谢金星叶俊著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1972&fromuid=9Java 编程思想.第四版.课后练习答案/bbs/viewthread.php?tid=1846&fromuid=9《Java2 实用教程》(第三版)清华(耿祥义张跃平)版课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=6922&fromuid=9中文原版《编译原理》课后答案机械工业出版社李建中编/bbs/viewthread.php?tid=1847&fromuid=9计算机组成原理(教师用书)附带答案蒋本珊清华大学出版社【khdaw】/bbs/viewthread.php?tid=9254&fromuid=9《积分变换》张元林第四版东南大学答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5074&fromuid=9《马克思主义基本原理概论》课后答案(很全哦)(2008 年修订版)【khdaw_cola】/bbs/viewthread.php?tid=6053&fromuid=9<计算机操作系统教程>清华大学第二版/第三版张尧学课后习题答案【khdaw】/bbs/viewthread.php?tid=9091&fromuid=9<计算机网络教程> 谢希仁第二版人民邮电出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=4862&fromuid=9/bbs/viewthread.php?tid=7785&fromuid=9vfp 数据库课后题答案/bbs/viewthread.php?tid=231&fromuid=9单片机基础第3 版李广第朱月秀冷祖祁编著北京航空航天大学出版社【khdaw_cola】/bbs/viewthread.php?tid=4271&fromuid=9电工学第六版 (秦曾煌著) 高等教育出版社课后答案【khdaw_ricardo】/bbs/viewthread.php?tid=11241&fromuid=9《数据通信与计算机网络》高传善(第二版)高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=6610&fromuid=9《计算机组成原理》唐朔飞第4,5 章课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1144&fromuid=9软件工程导论第五版 (张海藩著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=13716&fromuid=9初等数论第三版 (闵嗣鹤著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1508&fromuid=9《数据库系统概论》王珊萨师煊(第四版)高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5249&fromuid=9计算机数值方法 (施吉林著) 高等教育出版社课后答案/bbs/viewthread.php?tid=3903&fromuid=9离散数学耿素云屈婉玲课后答案/bbs/viewthread.php?tid=7839&fromuid=9数据结构---C 语言描述答案(耿国华)高教版【khdaw_cola】/bbs/viewthread.php?tid=2094&fromuid=9软件工程导论课后答案/bbs/viewthread.php?tid=5172&fromuid=9数据结构(殷人昆主编)【khdaw】/bbs/viewthread.php?tid=3077&fromuid=9《c 程序设计语言》英文第2 版课后答案严蔚敏数据结构例题算法代码/bbs/viewthread.php?tid=1031&fromuid=9国防科学技术大学计算机学院离散数学课后习题答案/bbs/viewthread.php?tid=100&fromuid=9计算机网络-自顶向下方法与Internet 特色第三版英文课后答案【khdaw_cola】/bbs/viewthread.php?tid=2495&fromuid=9《计算机组成原理》白中英第三版课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=3423&fromuid=9数据结构(C++版)王红梅,胡明,王涛版课后答案【khdaw_cola】/bbs/viewthread.php?tid=4426&fromuid=9清华版编译原理【khdaw_cola】/bbs/viewthread.php?tid=1027&fromuid=9微机原理与接口技术-基于IA-32 处理器和32 为汇编语言 (钱晓捷著) 机械工业出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=5668&fromuid=9《离散数学》左孝凌,刘永才上海科学技术文献出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5236&fromuid=9网络操作系统课后答案/bbs/viewthread.php?tid=430&fromuid=9《点集拓扑讲义》高教(熊金城)版课后答案【khdaw_cola】/bbs/viewthread.php?tid=6441&fromuid=9数学分析第二版 (陈传章著) 高等教育出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=2442&fromuid=9软件工程【khdaw】/bbs/viewthread.php?tid=3072&fromuid=9操作系统教程第4 版 (张钟秀著) 高等教育出版社课后答案/bbs/viewthread.php?tid=7703&fromuid=9信息论与编码技术--冯桂林其伟陈东华--清华大学出版社【khdaw_cola】/bbs/viewthread.php?tid=3332&fromuid=9编译原理课程设计报告(词法,语法等)【khdaw_cola】/bbs/viewthread.php?tid=2514&fromuid=9微机原理与接口技术楼顺天,周佳社科学出版社【khdaw_cola】/bbs/viewthread.php?tid=5304&fromuid=9《单片机原理及接口技术》梅丽凤清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5538&fromuid=9数据库系统概论_王珊、萨师煊第四版(chm 格式)【khdaw】/bbs/viewthread.php?tid=6403&fromuid=9数字逻辑答案第三版(华中科大欧阳星明)/bbs/viewthread.php?tid=6833&fromuid=9算法导论(英文版)答案【khdaw_cola】/bbs/viewthread.php?tid=2792&fromuid=9数学物理方法第三版 (梁昆淼著) 高等教育出版社课后答案/bbs/viewthread.php?tid=2398&fromuid=9微型计算机原理与接口技术 (周荷琴吴秀清著) 课后答案/bbs/viewthread.php?tid=4086&fromuid=9《工程数学概率统计简明教程(同济大学应用数学系)》课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=7219&fromuid=9复变函数答案【khdaw_cola】/bbs/viewthread.php?tid=6557&fromuid=9复变函数与积分变换 (马柏林著) 复旦大学课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=14749&fromuid=9计算机操作系统教程(第二版)左万历周长林【khdaw_cola】/bbs/viewthread.php?tid=1690&fromuid=9计算机组成原理(唐朔飞)答案高等教育出版社【khdaw】/bbs/viewthread.php?tid=8804&fromuid=9信息论与编码陈运电子工业出版社【khdaw_cola】/bbs/viewthread.php?tid=2828&fromuid=9计算机网络英文原版(第4 版)【khdaw】/bbs/viewthread.php?tid=3239&fromuid=9《数据库系统概念》(第五版影印版)高级教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5283&fromuid=9离散数学 (王义和著) 哈尔滨工业大学出版社课后答案【khdaw_ricardo】/bbs/viewthread.php?tid=5724&fromuid=9IBM-PC 汇编语言程序设计(沈美明2 版)【khdaw_cola】/bbs/viewthread.php?tid=5203&fromuid=9《C 程序设计解题与上机指导》谭浩强第二版清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1551&fromuid=9《组合数学》第四版机械工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=4346&fromuid=9《计算机英语(第2 版)》参考译文与习题解答【khdaw】/bbs/viewthread.php?tid=2963&fromuid=9C 语言程序设计教程杨路明北京邮电大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10074&fromuid=9《数据库系统及应用》崔魏(第二版)高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=2482&fromuid=9编译原理第三板 (陈火旺刘春林著) 国防工业课后答案/bbs/viewthread.php?tid=7680&fromuid=9《SQL SERVER 2005 数据库开发与实现》微软公司课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=1335&fromuid=9信号与线性系统管致中第4 版答案/bbs/viewthread.php?tid=6729&fromuid=9《计算机算法基础》(第三版)华中科技大4、5、6、8 章课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=4348&fromuid=9计算机系统结构第二版清华大学出版社课后答案/bbs/viewthread.php?tid=5370&fromuid=9《visual basic》课后作业答案【khdaw_lxywyl】常微分方程(张禾瑞)第三版【khdaw_cola】/bbs/viewthread.php?tid=1654&fromuid=9《数学分析》陈传璋课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=2217&fromuid=9高等几何梅学明高教版【khdaw_cola】/bbs/viewthread.php?tid=5698&fromuid=9数学分析高教出版社第二版复旦数学系主编/bbs/viewthread.php?tid=3025&fromuid=9编译原理第三版西北工业大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5614&fromuid=9数值分析数值计算方法曾金平湖南大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=9628&fromuid=9C 语言程序设计 (何钦铭颜晖著) 浙江科学技术出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=14395&fromuid=9计算机网络第四版【khdaw_cola】/bbs/viewthread.php?tid=1084&fromuid=9数据结构课后答案(高等教育出版社唐策善版))【khdaw】/bbs/viewthread.php?tid=5994&fromuid=9微型计算机技术及应用答案/bbs/viewthread.php?tid=6013&fromuid=9实变函数论第三版(江泽坚吴智泉纪友清著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=11505&fromuid=9《微积分》人教版课后课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5190&fromuid=9严蔚敏《数据结构(c 语言版)习题集》答案/bbs/viewthread.php?tid=6170&fromuid=9微型计算机原理与接口技术 (邹逢兴著) 清华大学出版社课后答案【khdaw_cola】数据结构习题答案+耿国华主编【khdaw_cola】/bbs/viewthread.php?tid=7218&fromuid=9《数据库系统概论》王珊萨师煊(第四版)课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=6054&fromuid=9计算机组成与结构第四版 (王爱英著) 清华大学出版社课后答案【khdaw_ricardo】/bbs/viewthread.php?tid=11208&fromuid=9《数据结构习题集》答案严蔚敏【khdaw_cola】/bbs/viewthread.php?tid=6552&fromuid=9概率论与数理统计 (同济大学应用数学系著) 高等教育出版社课后答案/bbs/viewthread.php?tid=9101&fromuid=9立体几何大题30 题(有详细答案)[整理]人教版/bbs/viewthread.php?tid=333&fromuid=9计算机答案合集(组成原理,操作系统...)/bbs/viewthread.php?tid=5204&fromuid=9《应用概率统计》(张国权)版科学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=7334&fromuid=9《C 程序设计》谭浩强编习题答案【khdaw_cola】/bbs/viewthread.php?tid=7836&fromuid=9数据结构(C 语言版)习题答案/bbs/viewthread.php?tid=5200&fromuid=9编译原理 (陈火旺著) 国防工业出版社课后答案/bbs/viewthread.php?tid=2978&fromuid=9微机原理与接口技术第三章 (郭兰英赵祥模著) 清华出版社课后答案_khdaw/bbs/viewthread.php?tid=7347&fromuid=9计算机网络第二版) (冯博琴陈文革著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5989&fromuid=9《数据结构》清华大学答案+例程+ppt 课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9713&fromuid=9软件工程第二版 (张海藩著) 人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10940&fromuid=9计算机专业英语课后答案【khdaw_cola】/bbs/viewthread.php?tid=7258&fromuid=9数值计算课后答案曾喆昭文卉编著【khdaw_cola】/bbs/viewthread.php?tid=2538&fromuid=9计算机组成与结构(第4 版)习题解答(上)【khdaw_cola】/bbs/viewthread.php?tid=6286&fromuid=9数据结构(c 语言版)习题集答案/bbs/viewthread.php?tid=6096&fromuid=9vb 程序设计(第四版)课后习题答案【khdaw】/bbs/viewthread.php?tid=2994&fromuid=9汇编语言(清华大学出版社)【khdaw】/bbs/viewthread.php?tid=3421&fromuid=9离散数学答案修订版 (耿素云屈婉玲著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=15917&fromuid=9《编译原理》蒋立源课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=4518&fromuid=9《数字逻辑》(第二版)华中科技大学出版社(欧阳星明)版课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=7332&fromuid=9严蔚敏数据机构实习报告部分答案【khdaw_cola】/bbs/viewthread.php?tid=1036&fromuid=9数值分析部分答案/bbs/viewthread.php?tid=3523&fromuid=9《数字图像处理》(第二版)英文版习题答案(全)【khdaw_lxywyl】/bbs/viewthread.php?tid=5854&fromuid=9C 程序设计(第二版)谭浩强习题解答清华大学出版社课后答案【khdaw_cola】/bbs/viewthread.php?tid=5679&fromuid=9微分几何梅向明第三版黄敬之高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=9287&fromuid=9c++语言基础教程 (吕凤葛著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=14461&fromuid=9求《数值分析》第五版答案/bbs/viewthread.php?tid=6704&fromuid=9微分几何第三章、第四章 (梅向明著) 高等教育出版社课后答案/bbs/viewthread.php?tid=4721&fromuid=9《计算机组成原理》白中英(第四版•立体化教材)课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5281&fromuid=9数值分析/bbs/viewthread.php?tid=4245&fromuid=9c 程序设计 (谭浩强著) 清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=7611&fromuid=9《数据库原理》课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=4345&fromuid=9数据结构/bbs/viewthread.php?tid=1624&fromuid=9现代微机原理与接口技术 (杨全胜著) 电子工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=11531&fromuid=9《计算机系统组成与体系结构》人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=2852&fromuid=9求数值分析(第4版)李庆扬编/bbs/viewthread.php?tid=6580&fromuid=9java2 实用教程(第三版)【khdaw_cola】/bbs/viewthread.php?tid=7256&fromuid=9数据结构答案【khdaw】/bbs/viewthread.php?tid=2066&fromuid=9人工智能原理及其应用王万森电子工业出版社(2-7 章)【khdaw】/bbs/viewthread.php?tid=9145&fromuid=9JAVA 大学实用教程第二版 (耿祥义张跃平著) 电子工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=15805&fromuid=9Visual C++面向对象编程教程(第2 版) (王育坚著) 清华大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=14404&fromuid=9清华大学出版社计算机网络第4 版中文答案【khdaw_cola】/bbs/viewthread.php?tid=8080&fromuid=9计算机网络第四版 (潘爱民译著) 清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=15080&fromuid=9初等数学研究学习指导 (叶立军著) 华东师范大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=13939&fromuid=9《复变函数论》张锦豪邱维元版高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5919&fromuid=9算法导论原书第二版 (潘金贵顾铁成李成法著) 机械工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=12100&fromuid=9张禾瑞的<<近世代数基础>>的答案/bbs/viewthread.php?tid=1540&fromuid=9c++程序设计/bbs/viewthread.php?tid=5608&fromuid=9《概率论与统计学》浙大出版社(复习指南)课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=4871&fromuid=9计算机基础课后答案(浙江科学出版社)/bbs/viewthread.php?tid=2014&fromuid=9《C 语言程序设计》张世禄,潘大志,冯天敏电子工业出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=2568&fromuid=9C 语言程序设计(洪维恩)课后答案【khdaw】/bbs/viewthread.php?tid=1955&fromuid=9《计算机组成原理》白中英第四版科学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=6433&fromuid=9微机原理与接口技术第 4 版 (周荷琴,吴秀清著) 中国科学技术大学出版社课后答案【khdaw】/bbs/viewthread.php?tid=15151&fromuid=9数值计算课后答案(清华大学出版)/bbs/viewthread.php?tid=5246&fromuid=9java 程序设计【khdaw_cola】/bbs/viewthread.php?tid=7541&fromuid=9《高等数值分析》清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5692&fromuid=9数据与计算机通信(第七版) William Stallings 等【khdaw_cola】/bbs/viewthread.php?tid=5201&fromuid=9数值方法第二版 (金一庆陈越著) 机械工业出版社课后答案/bbs/viewthread.php?tid=11539&fromuid=9高等代数北师大高教第三版张和瑞【khdaw】/bbs/viewthread.php?tid=8607&fromuid=9微波技术与天线(第二版) 王新稳李萍李延平编电子工业出版社【khdaw_cola】/bbs/viewthread.php?tid=6534&fromuid=9数据结构(陈慧南编 C++描述)南京邮电大学课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9506&fromuid=9四川大学出版社编的离散数学教程答案【khdaw_cola】/bbs/viewthread.php?tid=7402&fromuid=9计算机组成原理(白中英版)【khdaw_cola】/bbs/viewthread.php?tid=3243&fromuid=9现代微型计算机与接口教程课后答案杨文显主编寿庆余副主编【khdaw_cola】/bbs/viewthread.php?tid=7964&fromuid=9C 语言程序设计 3-5 章部分程序题答案杨路明北京邮电大学出版社【khdaw】/bbs/viewthread.php?tid=8775&fromuid=9《操作系统》汤子赢西安电子科技大学答案【khdaw_lxywyl】/bbs/viewthread.php?tid=6055&fromuid=9数据库原理与应用教程第二版陈志泊人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=9933&fromuid=9数据结构与算法分析(C++ 第二版)Clifford A. Shaffer 电子工业出版社【khdaw】/bbs/viewthread.php?tid=9211&fromuid=9《程序设计基础》练习题及答案【khdaw_lxywyl】/bbs/viewthread.php?tid=2801&fromuid=9《多媒体技术基础(第2 版)》林福宗清华大学出版社课后参考答案【khdaw】/bbs/viewthread.php?tid=9299&fromuid=9计算机专业英语(含课文、译文、模拟试题、专业英语习题、答案)【khdaw】/bbs/viewthread.php?tid=9364&fromuid=908 版考研概率复习指南答案/bbs/viewthread.php?tid=509&fromuid=9计算机网络(第4 版) (Andrew S.Tanenbaum 著) 清华大学出版社课后答案/bbs/viewthread.php?tid=11361&fromuid=9计算机图形学王汝传 1-4 章人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10000&fromuid=9计算机网络教程(第3 版)习题答案【khdaw_cola】/bbs/viewthread.php?tid=7777&fromuid=9c++语言程序设计(实验部分)第 3 版(郑莉著) 清华大学出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=15124&fromuid=9数字信号处理学习指导与题解 (丁美玉高西全王军宁著) 电子工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=15168&fromuid=9计算机网络第五版 (谢希仁著) 电子工业出版社课后答案/bbs/viewthread.php?tid=16108&fromuid=9数学物理方程与特殊函数第三版完整 (东南大学数学系王元明著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=17311&fromuid=9《操作系统概念》英文版高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=3491&fromuid=9计算机网络第二版蔡开裕朱培栋徐明(国防科技大学版)【khdaw】/bbs/viewthread.php?tid=9239&fromuid=9《C++语言程序设计教程》吕凤翥人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=8119&fromuid=9电工学第七版下册 (秦曾黄著) 高等教育出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=19778&fromuid=9vfp 表修复工具/bbs/viewthread.php?tid=73&fromuid=9C++语言基础教程吕凤翥人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10016&fromuid=9数据库及其应用教材课后习题答案_【khdaw_lxywyl】/bbs/viewthread.php?tid=9530&fromuid=9Turbo C 错误信息表/bbs/viewthread.php?tid=70&fromuid=9《微机原理及汇编技术》课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=5684&fromuid=9复变函数答案第四版 (余家荣著) 高等教育出版社课后答案【khdaw】/bbs/viewthread.php?tid=17004&fromuid=9Java 程序设计(第二版) (朱喜福著) 人民邮电出版社课后答案【khdaw_lxywyl】/bbs/viewthread.php?tid=10576&fromuid=9计算机专业英语教程译文(第 4 版) (金志权等主编著) 电子工业出版社课后答案【khdaw】/bbs/viewthread.php?tid=14170&fromuid=9数据结构习题/bbs/viewthread.php?tid=4344&fromuid=9《计算机英语》第2版全书翻译及课后答案_【khdaw_lxywyl】。
数字逻辑与数字系统设计习题参考答案

input a,b,c,d;
output f;
reg f;
always @(a or b or c or d)
case({a,b,c,d})
4'b0011: f<=1'b1;
4'b0100: f<=1'b1;
4'b0101: f<=1'b1;
4'b1010: f<=1'b1;
W=∑m(5,6,7,8,9)+∑d(10,11,12,13,14,15)
X=∑m(1,2,3,4,9)+∑d(10,11,12,13,14,15)
Y=∑m(0,3,4,7,8)+∑d(10,11,12,13,14,15)
Z=∑m(0,2,4,6,8)+∑d(10,11,12,13,14,15)
用卡诺图化简得:
[104-97]补=01101000+10011111=00000111, 104-97=(00000111)2=7
(2)(-125)10=(-1111101)2[-1111101]补=10000011
(79)10=(01001111)2[01001111]补=01001111
[-125+79]补=10000011+01001111=11010010,-125+79=(-0101110)2=-46
(5)F=∑m(1,2,3,4,5,6)
(6)F=∑m(4,7,8,11)
2.9解:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
或=
数字逻辑与数字系统第四版课后答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC 5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B )+AB(C+C ) =AB+AC =右边(3) E D C CD A C B A A )(++++=A+CD+E 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) =Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++ (4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
《数字逻辑》第四版部分习题答案

www.khd课后a答w案.网com
从以上两个卡诺图可以看出,当 a =1 和 b =1 时, 能得到取简的“与-或”表达式。 2.11 用卡诺图化简包含无关取小项的函数和多输出函数。
⑴ F ( A, B,C , D ) = ∑m(0,2,7,13,15)+ ∑d(1,3,4,5,6,8,10)
∴ F ( A, B,C , D ) = A + BD
www.khd课后a答w案.网com
课后答案网
《数字逻辑》习题解答
习题二
2.1 分别指出变量(A,B,C,D)在何种取值组合时,下列函数值为 1。 ( 1 ) F = BD + ABC 如下真值表中共有 6 种 ( 2 ) F = ( A + B + AB )( A + B )AB + D = D 如下真值表中共有 8 种 ( 3 ) F = ( A + A⋅ C )D + ( A + B )CD = AB + C + D 如下真值表中除 0011、1011、1111 外共有 13
⑵ F ( A, B,C , D ) = A ⋅ B + A ⋅ CD + AC + BC = A ⋅ B + BC + AC 或= AB + A ⋅ C + BC = ( A + B + C )( A + B + C )
⑶ F ( A, B,C , D ) = BC + D + D( B + C )( AD + B ) = B+ D = (B+ D)
⑶ F = AB + AD + B ⋅ D + AC ⋅ D = A( B + D + C ⋅ D ) + B ⋅ D = A( B + D + C ) + B ⋅ D
数字逻辑与数字系统(第四版)课后答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC 5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B )+AB(C+C ) =AB+AC =右边(3) E D C CD A C B A A )(++++=A+CD+E 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) =Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++ (4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑与数字系统(第四版)课后答案

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC 5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B )+AB(C+C ) =AB+AC =右边(3) E D C CD A C B A A )(++++=A+CD+E 证明:左边=E D C CD A C B A A )(++++ =A+CD+A B C +CD E =A+CD+CD E =A+CD+E =右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) =Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++ (4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑与数字系统设计习题参考答案

2.3解:根据逻辑图可直接写出逻辑表达式:(a) F= ;(b) F=
解:设3个输入变量分别为A、B、C,输出为F,按题意,其中有奇数个为1,则输出F=1,因此可写出其逻辑表达式为F= 。根据逻辑表达式可绘制逻辑习题2.3图如下:
习题2.3图
2.4解:根据逻辑图可直接写出逻辑表达式:(a) F= ;(b) F=
2.5解:
(1)若A+B=A+C,则B=C
不正确。若A=1,B和C为不同值(如B=0,C=1或B=1,C=0),A+B=A+C仍然成立。
(2)若AB=BC,则A=C
不正确。若B=0,A和C为不同值,等式仍然成立。
(3)若1+A=B,则A+AB=B
1.6(1)(117)8=(1001111)2=(79)10
(2)(7456)8=(111100101110)2=(3886)10
(3)(23765.64)8=(10 0111 1111 0101.1101)2=(10229.8125)10
(4)(0.746)8=(0.11111)2=(0.96875)10
W=A+BD+BCX= Y= Z=
= = = =
根据化简并变换后的逻辑表达式可绘制逻辑习题4-12图所示下:
4.13解:
//4.6的VerilogHDL描述
module ex6(a,b,s,f);//
input a,b,s;
output f;
assign f=(s?b:a);
endmodule
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
G1 G2A G2B A2 A1 A0 G1
Y0
Q0
Y7 Y0
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10
译 码 器
0
G2A G2B A2
1 CP
ENP ENT
CO Q3 Q2 Q1 Q0
74LS163
D3 D2 D1 D0 1 1 1 1
n n
Y0 1 0 0 0 0
Y1 0 1 0 0 0
Y2 0 0 1 0 0
Y3 0 0 0 1 0
Y4 0 0 0 0 1
Φ
若用与非门实现,译码器输出端的逻辑函数为:
Y0 Q1 Q3 Y1 Q1 Q3 Y2 Q1Q2 Y3 Q1Q3 Y4 Q2 Q3
若用译码器 74LS138 实现,译码器输出端 的逻辑函数为:
1/0
H 偶数
I 奇数
22.简化下列完全定义时序电路状态表为最简状态表
B C D E F G H
A B C D E F G H I
23.对下面的时序电路状态表进行状态编码,作出编码后的状态转移表,并用 D 触发器和与非门加以实现
解:
B C D E F
× × × × ×
A
× × × ×
B
× × ×
C
Y0 Q1Q2 Q3 Y1 Q1 Q2 Q3 Y2 Q1Q2 Q3 Y3 Q1Q2 Q3 Y4 Q1 Q2 Q3
74LS138
G1 G2A G2B Q3 Q2 Q1 A0 A1 A2
Y0 Y0 Y3 Y1 Y4 Y7 Y2
14. 用 74LS290 构成模为 8 和 9 的计数器,各采用两种方案画出其接线图
QA QB QC QD
QA QB QC QD
(b) 模9计数器
74LS290 CP CP1 CP2 R01 R02 S91 S92
74LS290 CP CP1 CP2 R01 R02 S91 S92
QA QB QC QD
QA QB QC QD
(b) 模9计数器
15.若将下图接成 12 进制加法器,预置值应为多少?画出状态图及输出波形图。 解:预置值应 C=0,B=1,A=1。
A
s
A B C D E F G H I
x
0/0
1/0 1/0 1/0
0
B/0 D/0 E/0 F/0 G/0 H/0 I/0 A/0 A/1
1
C/0 E/0 D/0 G/0 F/0 I/0 H/0 A/1 A/0
B
0/0 0/0
C
0/0
D
0/0
1/0
1/0
E
0/0
0/1
1/1
F
0/0
1/0
1/0
G
0/0
n 1 Q2
Q1n 1
0 1 1 0 0 0
Q0n 1
1 1 1 1 0 0
N 0 0 0 0 0 1
0 0 0 1 1 1 化简得:
0 0 1 1 1 0
n Z Q2 Q0n n 1 n Q1n Q2 Q2 Q0n n Q1n 1 Q2 Q0n n Q0n 1 Q2 Q1n
Q1
n 1 n 1
Q1
n
n n n n n
Q2
( X Q1 )Q2 ( X Q1 )Q2
n
Z Q1 Q2
X=0 00/1 10/1 X=1 X=0 X=1 X=1 11/ 0 X=0 01/1 X=1 X=0
Q1n Q2n 0 0 1 1 0 1 0 1
Q1n+1 Q2n+1 / Z X =0 10 / 1 11 / 1 01 / 1 00 / 0 X =1 11 / 1 10 / 1 00 / 1 01 / 0
解:
74LS290 CP CP1 CP2 R01 R02 S91 S92 74LS290 CP CP1 CP2 R01 R02 S91 S92
QA QB QC QD
QA QB QC QD
(a) 模8计数器
74LS290 CP CP1 CP2 R01 R02 S91 S92
74LS290 CP CP1 CP2 R01 R02 S91 S92
电路图:
Q0
Q1
Q2
0
1
2
12. 用 D 触发器设计 3 位二进制加法计数器,并画出波形图。
解:
Q1n 0 0 0 0 1 1 1 1
Q2n 0 0 1 1 0 0 1 1
Q3 n 0 1 0 1 0 1 0 1
Q1n+1 Q2n+1 Q3n+1 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0
(1) 若采用 RS 触发器。有以下(a) 、 (b)两种方案:
Q2 R S R Q1 S R Q0 S
Q2 Q D 接收控制 Q1 Q D Q0 Q D
接收控制
D2
D1
D0
D2
D1
D0
(a)
(b)
8. 设计实现 8 位数据的串行→并行转换器。 SR G1 74LS299 QA A/QA C/QC D/QD E/QE F/QF , 1 S1 , 0 S2 , 1 S3 , 0 X =1 S3 , 1 S2 , 1 S0 , 0 S2 , 0
? ?
D
?
E
S0 S1 S2 S3
S0
0/1 1/1 0/0 1/0 1/0
S1
1/1
0/0
S3
S2
0/1
24. 某时序机状态图如下图所示。请用“一对一法”设计其电路
Q 1n+1 = Q 2 n Q 1 n + Q 3 n Q 1 n Q 2n+1 = Q 1 n Q 3n+1 = Q 2 n
000 100 110
111
101
010
001
011
10. 作出状态转移表和状态图,确定其输出序列。
解:
D1 = Q1n+1 = Q2n Q3n D2 =Q2n+1 = Q1n D3 =Q3n+1 = Q2n
k =0 k =0
1000
S0
k =1 k =0
k =1 k =0
k =1 k =0
0001
k =1 k =0
0100
S3
k =0
S1
k =1
k =0
0010
k =1 k =1
S2
k =1
D0 Q0n 1 Q0n K Q3n K D1 Q1n 1 Q0n K Q1n K
n 1 n D 2 Q2 Q2 K Q1n K n D3 Q3n 1 Q2 K Q3n K
LD CR
1
A1 A0 Y7 Y11
74LS138
17. 改用一片 74LS195 移位寄存器来代替上题中的 74LS163,完成同样的设计
解:
74LS138
1 Q3 Q2
Y0 Y1 ...... ...... Y11
G1 G2A G2B A2 A1 A0 G1
Y0
Q1 Q0
Y7 Y0
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10
S1 SL
M
0 3
R
C
D7 D6 D5 D4 D3 D2 D1 D0 EN1
2
QB
QE QG QH
C
D Q
9. 分析下图所示同步计数电路
解:先写出激励方程,然后求得状态方程
Q1n Q2n Q3n 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 Q1n+1 Q2n+1 Q3n+1 1 1 0 0 1 0 1 0 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1
Q1n+1 = Q1n + Q3n Q1n = Q1n + Q3n Q2n+1 = Q2n + Q1n Q2n = Q2n + Q1n Q3n+1 = Q1nQ3n + Q2nQ3n
译码器功能表
Q1 Q 2 Q3n 0 1 0 1 0 0 1 1 1 0 1 1 1 0 1 0 0 0 1 1 0 0 0 1
该电路是 Mealy 型电路。 当 X=0 时,电路为模 4 加法计数器;
当 X=1 时,电路为模 4 减法计数器 19. 分析下图所示同步时序逻辑电路,作出状态转移表和状态图, 说明这个电路能对何种 序列进行检测? 解:电路的状态方程和输出方程为:
0/0
X/Z
00
Q1n Q2n 0 0 1 1 0 1 0 1 Q1n+1 Q2n+1 X =0 00 / 0 01 / 1 11 / 0 11 / 1
D2 Q2 Q0 (Q2 Q1 )Q0 D1 Q1 Q0 D0 Q0
13. 用下图所示的电路结构构成五路脉冲分配器,试分别用简与非门电路及 74LS138 集成译码器构成这个译码器,并画出连线图。
解:先写出激励方程,然后求得状态方程
Q1n 0 0 0 0 1 1 1 1 Q2n 0 0 1 1 0 0 1 1 Q3n 0 1 0 1 0 1 0 1 Q1n+1 Q2n+1 Q3n+1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 1 0 1 0 1 1 1 0 1 1
输出序列:00011
101
000
100
110
010
001
011
