自动控制原理 第十二讲 状态反馈
现代控制理论 状态反馈与状态观测器

五、带观测器的状态反馈系统 • 在状态反馈中,不采样原系统的状态进行反 馈而采用状态观测器估计的状态进行反馈, 其结构图如下图所示.
• 状态估计器
x ( A GC ) x Bu Gy ˆ ˆ ˆ y Cx
• 原系统
x Ax Bu ˆ x Ax Bkx Bv y Cx ˆ x ( A Bk ) x Bk ( x x) Bv u v kx ˆ
• 传函不变,即
y C (sI A Bk ) B.v
1
• 显然系统的特性由矩阵的特征多项式
ˆ A Bk A 0 A GC Bk
决定.
• 由
ˆ det[ I A] det( I A Bk ) det( A GC ) 0
• 注意上述方法仅适用于SISO系统.
4.几点说明
(1).对SISO系统来说,状态反馈只改变极点位 臵,不影响零点. (2).由于改变了极点,因此可能出现零极点对 消,从而影响系统的可观性.
(3).从实现的角度,状态反馈比输出反馈 困难,复杂. (4)对SISO系统来说,极点配臵只改变了极 点在S平面上的位臵,显然不采用这种方法 难于达到系统动静性能的一致. (5).对MIMO来说,极点配臵的方法与SISO 方法是一致的,但SISO的k阵是唯一的,而 MIMO的k阵是非唯一的.
• 系统的状态估计器极点可任意配臵的充要 条件是:该系统的状态是可观的.
(3).状态估计器的设计方法. • 仿照状态反馈的极点配臵设计方法,只需先 进行可控性检验,改成可观性检查即可,其余 步骤相同.
四、降维观测器设计
• 一般情况下观测器是建立在对原系统模拟基 础上的,因而其维数和受控系统维数是相同 的,称为全维观测器(或估计器)。
自动控制原理简答题

概念:设动态系统为)()()(,)()()(t Du t Cx t y t Bu t Ax t x+=+= ,(1)若At e t =Φ)(,则)(t Φ称为(状态转移矩阵 )(2)若D B A sI C s G +-=-1)()(,则)(s G 称为( 传递函数矩阵 )(3)若],,,,[],[12B A B A AB B B A n c -=Γ ,则],[B A c Γ称为(能控性矩阵) (4)若Tn o CA CA CA C A C ],,,,[],[12-=Γ ,则],[A C o Γ称为(能观性矩阵) (5)若],,,,,[],,[12D B CA B CA CAB CB B A C n oc -=Γ ,则],,[B A C oc Γ称为(输出能控性矩阵) (6)李雅普诺夫方程Q PA P AT-=+,其中Q 为正定对称阵,当使方程成立的P 为( 正定对称阵 )时,系统为渐近稳定。
(7)设系统0)0(,0,)(=≥=f t x f x ,如果存在一个具有一阶导数的标量函数)(x V ,0)0(=V ,并且对于状态空间X 中的且非零点x 满足如下条件:)(x V 为(正定);)(x V 为(负定);当∞→x 时,∞→)(x V 。
则系统的原点平衡状态是(大范围渐近稳定的)。
(8)状态反馈不改变系统的(可控性)。
输出至状态微分反馈不改变系统的(可观测性)。
输出至参考输入反馈,不改变系统的(可控性和可观测性)。
状态反馈和输出反馈都能影响系统的(稳定性和动态性能)。
(9)状态反馈控制的极点任意配置条件是系统状态(完全可控)。
状态观测的极点任意配置条件是系统状态(完全可观)。
(10)系统线性变换Px x =时,变换矩阵P 必须是(非奇异的,或满秩)的。
二:已知系统传递函数 )2()1(5)(2++=s s s G ,试求约当型动态方程。
解:2515)1(5)2()1(5)(22+++-+=++=s s s s s s G 由上式,可得约当型动态方程[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321555110200010011x x x y u x x x x x x三:试求下列状态方程的解 x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=300020001 的解 解:由题意可得:⎪⎪⎩⎪⎪⎨⎧-=-==-=---011010)()()()(xA sI L t x x A sI x xx A sI Ax x0320111000000310002100011300020001)(x e e e x s s s L x s s s L t x t t t⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=------五:设系统状态方程为0111x x u a b ⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦,并设系统状态可控,试求,a b 。
自动控制原理线性定常系统的反馈结构及状态观测器教学PPT

状态反馈在形成最优控制、克服和抑制扰动作用、实现系统解耦 控制等方面具有很多的应用。
1、极点可配置的条件 1)利用状态反馈的极点可配置条件
定理5:用状态反馈任意配置闭环极点的充要条件:受控系统可控 证明: (1)充分性
u v Kx
通过反馈构成的闭环系统
x (A- BK)x Bv
是渐近稳定的,即(A-BK)的特征值均有负实部,则称系统 实现了状态反馈镇定。
定理4:当且仅当线性定常系统的不可控部分渐近稳定时,系统 是状态可镇定的。
定理4:当且仅当线性定常系统的不可控部分渐近稳定时,系统 是状态可镇定的。
证明:由于系统 {A, B} 不完全可控,则有可控性结构分解
vu
B
_
xI x S
A
F
y
C
x (A- BK)x Bv
如果 FC K 输出反馈等价于状态反馈
2、反馈结构对系统性能的影响
x (A- BK)x Bv
x (A- HC)x Bu
x (A- BFC)x Bv
状态反馈、输出反馈都会改变系统的系数矩阵,会影响系统的可 控性、可观测性、稳定性、响应特性等。
0 0 1 P 0 1 12
1 18 144
0 1 0 0
x 0 0
1
x
0u
0 72 18 1
0 0 0 1
x 1 6
0
x
0u
0 1 -12 0
系统的特征多项式 det[sI A] s3 18s2 72 s
希望特征多项式 a *(s) (s 1)(s 2 )(s 3 ) s3 4s2 6s 4
自动控制原理学生实验:线性系统的状态反馈及极点配置
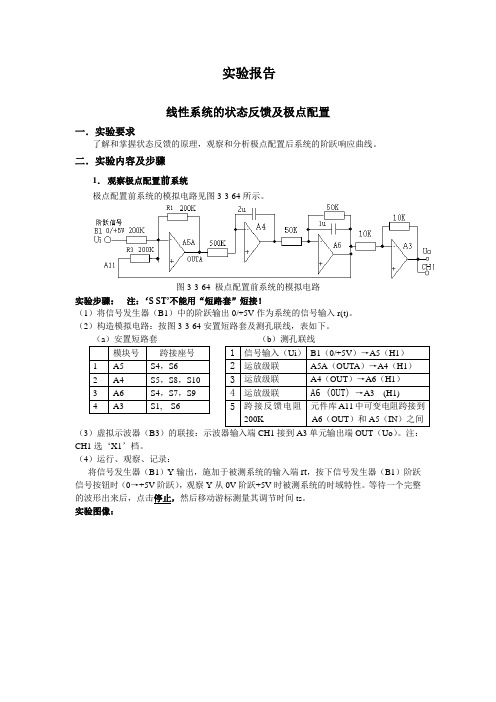
实验报告线性系统的状态反馈及极点配置一.实验要求了解和掌握状态反馈的原理,观察和分析极点配置后系统的阶跃响应曲线。
二.实验内容及步骤1.观察极点配置前系统极点配置前系统的模拟电路见图3-3-64所示。
图3-3-64 极点配置前系统的模拟电路实验步骤:注:‘S ST’不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入r(t)。
(2)构造模拟电路:按图3-3-64安置短路套及测孔联线,表如下。
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A3单元输出端OUT(Uo)。
注:CH1选‘X1’档。
(4)运行、观察、记录:将信号发生器(B1)Y输出,施加于被测系统的输入端rt,按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),观察Y从0V阶跃+5V时被测系统的时域特性。
等待一个完整的波形出来后,点击停止,然后移动游标测量其调节时间ts。
实验图像:由图得ts=3.880s 2.观察极点配置后系统 极点的计算:受控系统如图所示,若受控系统完全可控,则通过状态反馈可以任意配置极点。
受控系统设期望性能指标为:超调量M P ≤5%;峰值时间t P ≤0.5秒。
由1095.01t 707.0%5eM n n 2n p 1/p 2=≥⇒≤-==⇒≤=--ωωζωπζζζπ取因此,根据性能指标确定系统希望极点为:⎪⎩⎪⎨⎧--=+-=07.707.707.707.7*2*1j j λλ受控系统的状态方程和输出方程为:⎪⎩⎪⎨⎧=+=-----⋅-xC y b x A x μ式中][01,10,020120,21=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=----C b A x x x系统的传递函数为:202020a S a S βS β)(2012010++=+++=S S S G受控制系统的可控规范形为:[][]020T C C b T b a a T A T A X T X X C Y U b X A X K K i o K K KK k K K K ===⎥⎦⎤⎢⎣⎡==⎥⎦⎤-⎢⎣⎡-=⎥⎦⎤-⎢⎣⎡-===⎩⎨⎧=+=---10111,1020120010T ββ为变换阵),(式中当引入状态反馈阵K K =[K 0K 1]后,闭环系统()K K K K K C b K b A ,,-的传递函数为:()()()01201120120)20(20)(K S K S K a S K a S S S G o ++++=+++++=ββ而希望的闭环系统特征多项为:1001.14))(()(2*2*1**12*++=--=++=S S S S a S a S S f oλλ 令G K (S)的分母等于F #(S),则得到K K 为:[][]9.58010-==K K K k最后确定原受控系统的状态反馈阵K :由于 1-=T K K k求得和===---111,T C b T b T A T A K k K求得 ⎥⎥⎦⎤⎢⎢⎣⎡-=-1102011T所以状态反馈阵为: [][]9.59.91102019.580-=⎥⎥⎦⎤⎢⎢⎣⎡--=K极点配置系统如图所示:极点配置后系统根据极点配置后系统设计的模拟电路见下图所示。
(完整版)自动控制原理简答题

47、传递函数:传递函数是指在零初始条件下,系统输出量的拉式变换与系统输入量的拉式变换之比。
48、系统校正:为了使系统达到我们的要求,给系统加入特定的环节,使系统达到我们的要求,这个过程叫系统校正。
49、主导极点:如果系统闭环极点中有一个极点或一对复数极点据虚轴最近且附近没有其他闭环零点,则它在响应中起主导作用称为主导极点。
51、状态转移矩阵:()Att e φ=,描述系统从某一初始时刻向任一时刻的转移。
52、峰值时间:系统输出超过稳态值达到第一个峰值所需的时间为峰值时间。
53、动态结构图:把系统中所有环节或元件的传递函数填在系统原理方块图的方块中,并把相应的输入输出信号分别以拉氏变换来表示从而得到的传递函数方块图就称为动态结构图。
54、根轨迹的渐近线:当开环极点数 n 大于开环零点数 m 时,系统有n-m 条根轨迹终止于 S 平面的无穷远处,且它们交于实轴上的一点,这 n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近线。
55、脉冲传递函数:零初始条件下,输出离散时间信号的z 变换()C z 与输入离散信号的变换()R z 之比,即()()()C z G z R z =。
56、Nyquist 判据(或奈氏判据):当ω由-∞变化到+∞时, Nyquist 曲线(极坐标图)逆时针包围(-1,j0)点的圈数N ,等于系统G(s)H(s)位于s 右半平面的极点数P ,即N=P ,则闭环系统稳定;否则(N ≠P )闭环系统不稳定,且闭环系统位于s 右半平面的极点数Z 为:Z=∣P-N ∣57、程序控制系统: 输入信号是一个已知的函数,系统的控制过程按预定的程序进行,要求被控量能迅速准确地复现输入,这样的自动控制系统称为程序控制系统。
58、稳态误差:对单位负反馈系统,当时间t 趋于无穷大时,系统对输入信号响应的实际值与期望值(即输入量)之差的极限值,称为稳态误差,它反映系统复现输入信号的(稳态)精度。
59、尼柯尔斯图(Nichocls 图):将对数幅频特性和对数相频特性画在一个图上,即以(度)为线性分度的横轴,以 l(ω)=20lgA(ω)(db )为线性分度的纵轴,以ω为参变量绘制的φ(ω) 曲线,称为对数幅相频率特性,或称作尼柯尔斯图(Nichols 图)60、零阶保持器:零阶保持器是将离散信号恢复到相应的连续信号的环节,它把采样时刻的采样值恒定不变地保持(或外推)到下一采样时刻。
(完整版)状态反馈控制器的设计
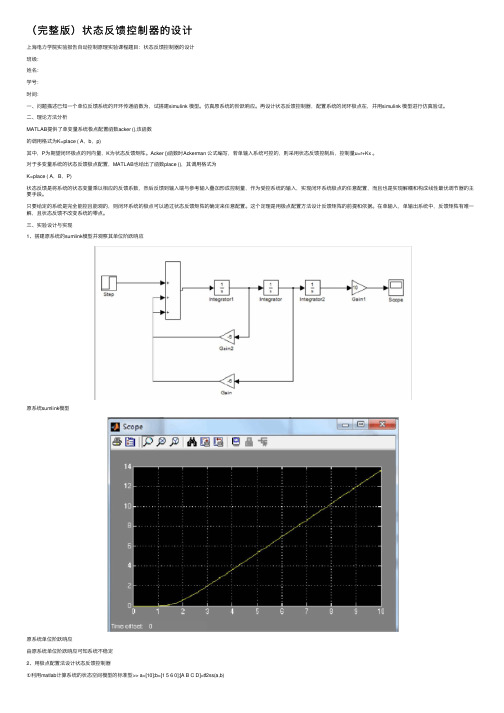
(完整版)状态反馈控制器的设计上海电⼒学院实验报告⾃动控制原理实验课程题⽬:状态反馈控制器的设计班级:姓名:学号:时间:⼀、问题描述已知⼀个单位反馈系统的开环传递函数为,试搭建simulink 模型。
仿真原系统的阶跃响应。
再设计状态反馈控制器,配置系统的闭环极点在,并⽤simulink 模型进⾏仿真验证。
⼆、理论⽅法分析MATLAB提供了单变量系统极点配置函数acker (),该函数的调⽤格式为K=place ( A,b,p)其中,P为期望闭环极点的列向量,K为状态反馈矩阵。
Acker ()函数时Ackerman 公式编写,若单输⼊系统可控的,则采⽤状态反馈控制后,控制量u=r+Kx 。
对于多变量系统的状态反馈极点配置,MATLAB也给出了函数place (),其调⽤格式为K=place ( A,B,P)状态反馈是将系统的状态变量乘以相应的反馈系数,然后反馈到输⼊端与参考输⼊叠加形成控制量,作为受控系统的输⼊,实现闭环系统极点的任意配置,⽽且也是实现解耦和构成线性最优调节器的主要⼿段。
只要给定的系统是完全能控且能观的,则闭环系统的极点可以通过状态反馈矩阵的确定来任意配置。
这个定理是⽤极点配置⽅法设计反馈矩阵的前提和依据。
在单输⼊,单输出系统中,反馈矩阵有唯⼀解,且状态反馈不改变系统的零点。
三、实验设计与实现1、搭建原系统的sumlink模型并观察其单位阶跃响应原系统sumlink模型原系统单位阶跃响应由原系统单位阶跃响应可知系统不稳定2、⽤极点配置法设计状态反馈控制器①利⽤matlab计算系统的状态空间模型的标准型>> a=[10];b=[1 5 6 0];[A B C D]=tf2ss(a,b)A = -5 -6 01 0 00 1 0B = 1C = 0 0 10③系统能控性矩阵>> uc=ctrb(A,B)uc = 1 -5 190 1 -50 0 1 >> rank(uc) ans = 3 所以系统完全能控③系统能观型矩阵>> vo=obsv(A,C) vo = 0 0 100 10 010 0 0 >> rank(vo) ans = 3 所以系统完全能观所以可以⽤极点配置法设计状态反馈控制器④求解系统反馈矩阵>> p=[-3 -0.5+j -0.5-j];k=acker(A,B,p)k = -1.0000 -1.7500 3.7500 加⼊反馈后的系统闭环极点为:>>sysnew=ss(A-B*k,B,C,D);pole(sysnew)ans = -3.0000-0.5000 + 1.0000i-0.5000 - 1.0000i⑤搭建加⼊反馈控制器后系统的sumlink模型⑥观察新系统的单位阶跃响应四、实验结果分析加⼊反馈控制器后系统的闭环极点在,符合题⽬要求。
系统的能控性与能观性分析及状态反馈极点配置要点

实 验 报 告课程 自动控制原理 实验日期 12 月26 日 专业班级 姓名 学号实验名称 系统的能控性与能观性分析及状态反馈极点配置 评分批阅教师签字一、实验目的加深理解能观测性、能控性、稳定性、最小实现等观念,掌握状态反馈极点配置方法,掌握如何使用MATLAB 进行以下分析和实现。
1、系统的能观测性、能控性分析;2、系统的最小实现;3、进行状态反馈系统的极点配置;4、研究不同配置对系统动态特性的影响。
二、实验内容1.能控性、能观测性及系统实现(a )了解以下命令的功能;自选对象模型,进行运算,并写出结果。
gram, ctrb, obsv, lyap, ctrbf, obsvf, mineral ; (b )已知连续系统的传递函数模型,182710)(23++++=s s s as s G ,当a 分别取-1,0,1时,判别系统的能控性与能观测性;(c )已知系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=2101013333.06667.10666.6A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110B ,[]201=C ,判别系统的能控性与能观测性;(d )求系统1827101)(23++++=s s s s s G 的最小实现。
2.实验内容原系统如图1-2所示。
图中,X 1和X 2是可以测量的状态变量。
图1-2 系统结构图试设计状态反馈矩阵,使系统加入状态反馈后其动态性能指标满足给定的要求:(1) 已知:K=10,T=1秒,要求加入状态反馈后系统的动态性能指标为:σ%≤20%,ts≤1秒。
(2) 已知:K=1,T=0.05秒,要求加入状态反馈后系统的动态性能指标为:σ%≤5%,ts≤0.5秒。
状态反馈后的系统,如图1-3所示:图1-3 状态反馈后系统结构图分别观测状态反馈前后两个系统的阶跃响应曲线,并检验系统的动态性能指标是否满足设计要求。
三、实验环境 1、计算机1台;2、MATLAB6.5软件1套。
四、实验原理(或程序框图)及步骤 1、系统能控性、能观性分析设系统的状态空间表达式如下:p m n R y R u R x Du Cx y Bu Ax x∈∈∈⎩⎨⎧+=+=(1-1)其中A 为n ×n 维状态矩阵;B 为n ×m 维输入矩阵;C 为p ×n 维输出矩阵;D 为p ×m 维传递矩阵,一般情况下为0。
极点配置法设计状态反馈控制器——自动控制原理

这两个多项式的系数相等,可得出:
0 0
1
1
n n1
i中含F阵系数fij
当F阵为1 n时
n个方程可解n个系数 fi
(i 1,2,...,n)
设计算法--适用于用能控标准形表示的SI系统的算法
设系统期望的闭环极点为s1、s2、sn ,则其
闭环特征式为s s1 s s2 s s3 s sn
SI系统,所以设 F f1 f2 fn
ห้องสมุดไป่ตู้
设计算法--适用于用能控标准形表示的SI系统的算法
s
1
0
0
0
0
s
1
0
0
0
0
0
s
1
a0 f1 a1 f2 a2 f3 an2 fn1 an1 fn s
sn (an1 fn )sn1 a1 f2 s a0 f1
设计算法--适用于用能控标准形表示的SI系统的算法
解:
系统能控。
举例----求解过程
期望闭环系统特征多项式为:
设: F f1 f2
F 7 1
w
u+
x2 ∫
--
++ -5
x2 x1
∫ x1
-
F 7 1
1
+
2
+
y
-6 1
7
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
试求:(1)求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
自动控制原理部分简答题

一.名词解释1、传递函数:传递函数是指在零初始条件下,系统输出量的拉式变换与系统输入量的拉式变换之比。
2、系统校正:为了使系统达到我们的要求,给系统加入特定的环节,使系统达到我们的要求,这个过程叫系统校正。
3、主导极点:如果系统闭环极点中有一个极点或一对复数极点据虚轴最近且附近没有其他闭环零点,则它在响应中起主导作用称为主导极点。
4、香农定理:要求离散频谱各分量不出现重叠,即要求采样角频率满足如下关系: ωs ≥2ωmax 。
5、状态转移矩阵:()At t e φ=,描述系统从某一初始时刻向任一时刻的转移。
6、峰值时间:系统输出超过稳态值达到第一个峰值所需的时间为峰值时间。
7、动态结构图:把系统中所有环节或元件的传递函数填在系统原理方块图的方块中,并把相应的输入、输出信号分别以拉氏变换来表示,从而得到的传递函数方块图就称为动态结构图。
8、根轨迹的渐近线:当开环极点数 n 大于开环零点数 m 时,系统有n-m 条根轨迹终止于 S 平面的无穷远处,且它们交于实轴上的一点,这 n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近线。
9、脉冲传递函数:零初始条件下,输出离散时间信号的z 变换()C z 与输入离散信号的z 变换()R z 之比,即()()()C z G z R z =。
10、Nyquist 判据(或奈氏判据):当ω由-∞变化到+∞时, Nyquist 曲线(极坐标图)逆时针包围(-1,j0)点的圈数N ,等于系统G(s)H(s)位于s 右半平面的极点数P ,即N=P ,则闭环系统稳定;否则(N ≠P )闭环系统不稳定,且闭环系统位于s 右半平面的极点数Z 为:Z=∣P-N ∣11、程序控制系统: 输入信号是一个已知的函数,系统的控制过程按预定的程序进行,要求被控量能迅速准确地复现输入,这样的自动控制系统称为程序控制系统12、稳态误差:对单位负反馈系统,当时间t 趋于无穷大时,系统对输入信号响应的实际值与期望值(即输入量)之差的极限值,称为稳态误差,它反映系统复现输入信号的(稳态)精度。
现代控制理论 状态反馈与状态观测器

• 所谓状态观测器是物理上可以实现的动力 学系统,它在被观测系统输入量和输出量的 激励下,产生一组逼近于被观测系统的状态 变量的输出.
• 这组输出的状态变量便可作为被观测系统 状态变量的估计值.
2.极点配置条件
• 若被控系统0(A, B) 是状态完全能控的,那么 反馈系统的极点必是可以任意配置的,或者 说,能使闭环系统极点任意配置的条件是被 控系统完全可控.
• 注意:
(1).对不可控的系统则不可能采用状态反馈 方法重新配置所有极点. (2).状态反馈可改变系统的极点,但不改变零 点.
• 以上是状态观测器的整个设计思想和目的.
• 估计的模型
xˆAxˆBuG(yCxˆ) (2) (AGC)xˆBuGy
(1).G的选择原则.
由(1)和(2)建立误差方程 定义 exxˆ 则 exxˆ(AG C)e显然误差e的特性是由
(A-GC)的特征值决定,显然G选择的原则是使 e tt1 0,t1 足够地小,从而G的选择也是使 A-GC的特征根按要求放在合适的位置上.
自动控制原理Ⅱ
第六章 状态反馈与状 态观测器
主要讲述:
1).状态反馈. 2).极点配置. 3).状态观测器.
一.系统的状态反馈
• 对于方程
x Ax Bu
y
Cx
• 系统的性质完全是由A决定的,因此要改变 系统的性质,只需改变A的形式.
• 从数学上来讲,即构造u,从而导致下列方程 成立
四、降维观测器设计
x Ax Br
y
Cx
• A 是满足要求的方阵
自动控制原理反馈控制的概念

自动控制原理反馈控制的概念自动控制原理中的反馈控制,这个听起来很高大上的概念,其实在我们日常生活中随处可见,想想看,开车的时候你是不是会根据车速和路况调整油门?那就是反馈控制在起作用。
别看这玩意儿听上去复杂,其实就是一个不断调整、适应的过程。
就像我们打游戏一样,遇到困难就会调整策略,最后打出高分,这不就是反馈控制的精髓吗?想象一下你在厨房里做饭,哎呀,盐放多了怎么办?这时候你就得尝一口,发现味道不对,于是决定加点水,哇,瞬间就变得可口了。
这就是反馈控制!你的味觉就像是系统的传感器,反馈给你真实的情况,然后你做出调整。
这种“试错”的过程,不就是反馈控制的真实写照吗?生活中的每一次选择、每一次调整,都是在告诉我们,反馈控制其实就是适应环境的一种智慧。
反馈控制就像是你和朋友之间的默契。
当你跟朋友一起聊天,发现他有点不高兴,你就会试着换个话题或者讲个笑话,看看能不能让气氛活跃起来。
这种灵活调整的能力,恰恰是反馈控制的关键所在。
你能想到的,生活中的小细节,都在用着这个原理呢!这就是为什么反馈控制在工程领域那么重要,简单的一句话,反馈控制就是“听话”与“调整”的艺术。
再来聊聊自动驾驶汽车,它的运作就离不开反馈控制。
汽车上的各种传感器不断监测速度、距离、路况等等,然后根据这些信息不断调整行驶状态,保持安全和顺畅。
想象一下,开车时前方突然出现障碍物,车子立马做出反应,刹车、转向,哇,简直像是在玩“速度与激情”!这些动作背后,正是反馈控制在悄悄发力,让驾驶体验安全又刺激。
反馈控制还涉及到一个重要的概念,那就是“目标”。
你要清楚自己想要什么,才能有效调整。
就像你想减肥,就得关注每天的饮食和运动量。
每当体重变化,你就会做出相应的调整。
这种不断循环的过程,其实就是反馈控制在工作。
目标明确,反馈及时,才会事半功倍。
不过,有时候反馈控制也会遇到“误差”。
比如说,温度控制器,设定温度是22度,可是有时候它会波动。
你可能会觉得很烦,哎呀,这个系统怎么总是不稳定?这也是反馈控制的一部分。
北京科技大学《自动控制原理》课件-状态反馈 (1)

, Bi
Bi1 Bi 2
i 1
, Jij
i
J ii
i i
Bii
i p
0 0 1 9
4 0 0 2
1
i
4
x
0
0
4
0
x
1
u
若U
c不满秩,则U
行线性相关,即存在
c
n维非零列向量,使得:
T
tf 0
eAt BBT eATt dt
TWc (t f
)
0
Wc (t f )奇异 矛盾
此式对t微分有:
0 TUc T [B, AB,, An1B] 2RankUc n ( A, B)能控(反证法)
上司的判断和决策在很大程度上是根据秘书的汇报作出来的汇报的内容是否真实汇报的数据是否准确汇报的用语是否恰当目录content112233线性系统的结构特性线性系统的结构特性状态观测器状态观测器4455本章小结本章小结状态反馈与输出反馈状态反馈与输出反馈上司的判断和决策在很大程度上是根据秘书的汇报作出来的汇报的内容是否真实汇报的数据是否准确汇报的用语是否恰当8181上司的判断和决策在很大程度上是根据秘书的汇报作出来的汇报的内容是否真实汇报的数据是否准确汇报的用语是否恰当输入量状态变量输出量输入量输出量状态方程输出方程古典控制一问题的提出dtdtdtdudtdtdt求系统的状态空间表达式上司的判断和决策在很大程度上是根据秘书的汇报作出来的汇报的内容是否真实汇报的数据是否准确汇报的用语是否恰当durcdurcdtdurcdurcdtdurcdtdurctitaxtexbudeud求x00时的状态方程的解
自动控制原理反馈的原理

自动控制原理反馈的原理
自动控制原理中的反馈原理是指将系统的输出作为输入的一部分,通过对输出进行测量和比较,然后根据比较结果对系统的输入进行调整以达到所需的输出。
反馈原理的基本思想是在系统中引入一个反馈回路,通过比较系统的输出与期望输出,计算得到误差信号,再根据该误差信号对系统的控制输入进行修正,以使系统输出逐渐接近期望输出,并实现系统的自动调节。
反馈原理的主要作用是提供系统的稳定性和鲁棒性,使系统具有抗干扰能力、自适应能力和优化特性。
通过反馈原理,系统可以根据实际输出来不断修正输入,使系统的动态性能更好、稳定性更强,能够适应环境变化和干扰的影响。
在控制系统中,反馈原理常常用于实现闭环控制,通过不断地测量输出、计算误差并调整控制输入,使系统的输出逐渐稳定在期望值附近。
同时,反馈原理也可以用于系统故障检测和故障处理,通过对输出的监测和比较,及时发现系统性能下降或出现异常状况,并采取相应的措施进行处理。
总之,反馈原理在自动控制原理中起着重要的作用,通过对系统输出进行测量和比较,根据比较结果对系统的输入进行修正,使系统的输出逐渐接近期望值,从而实现系统的自动调节和优化。
状态反馈与闭环极点配置条件-自动控制原理

A
BK HC
BK
x xˆ
BB r
y C
0
x xˆ
引入线性变换
x xe
In I n
0 x In xˆ
得
x x e
A
BK 0
A
BK HC
x xe
B 0
r
y C
0
x xe
35
极点配置的分离性原理
带状态观测器的状态反馈系统的特征多项式为
det sI
s 0 0 1 1 0 1
det 0
s
0 1
1
0
0
k1
k2
k3
0 0 s 0 1 3 0
s3 ( k1 3 )s2 ( k2 2k1 2 )s ( k3 3k2 3k1 6 )
而系统希望的特征多项式为
f * ( s ) ( s 1 )( s 2 )( s 3 ) s3 5s2 17 s 13 令 f * ( s ) f ( s ) 得 k1 8, k2 35, k3 136
1 2 3 1
15
解: 状态反馈系统的特征多项式为
f ( s ) det[ sI A BK ] s3 ( k1 3 )s2 ( k2 2k1 2 )s ( k3 3k2 3k1 6 ) 而系统希望的特征多项式为 f * ( s ) ( s 1 )3 s3 3s2 3s 1
1
( s 3 )( s 1.414 )( s 1.414 )
有反馈时 x ( A BK )x Br , X ( s ) G f ( s )U ( s ),
Gf
(
s
)
(
sI
A
BK
)1 B
1
(
技术讲座论文-状态反馈控制概念特性及一阶倒立摆状态反馈控制系统的应用状态反馈

课程名称:新技术讲座学生姓名:张敏学号:1123160151日期:2014年12月状态反馈控制概念特性及一阶倒立摆状态反馈控制系统的应用状态反馈1、状态反馈的概念状态反馈就是将系统的每一个状态变量乘以相应的反馈系数反馈到输入端与参考输入相加,其和作为受控系统的输入。
设SISO系统的状态空间表达式为:•x=Ax+bu,y=cx状态反馈矩阵为K,则状态反馈系统动态方程为:•x=Ax+b(v-Kx)=(A-bK)x+bvy=cx式中:K为1×n矩阵,即K=[k0 k1… k n-1],称为状态反馈增益矩阵。
(A-bK)称为闭环系统矩阵。
闭环特征多项式为|λI-(A-bK)|可见,阴郁状态反馈后,只改变了系统矩阵及其特征值,b、c阵均无变化。
2、状态反馈系统的可控性和可观性2.1 状态反馈系统的可控性定理:多变量线性系统(定常的或时变的)∑0}CB,A,{,在任何形如u(t)=r(t)+K(t)x(t)的状态反馈下,状态反馈闭环系统∑+K}CB, BK,A{完全可控的充要条件是被控对象∑0}CB,A,{完全可控。
证明:充分性证明,即若∑0可控,则∑K就可控。
令x0和x1是状态空间中的任意两个状态,据∑0可控的假定,必存在能将x0在有限时间内转移到x1的输入u。
现在对于∑K,若选r=u+Kx,则输入r也能将x0转移到x1,因此断定∑K也可控。
充分性得证。
必要性证明,即若∑0不可控,则∑K也不可控。
由结构图一可见,输入r不直接控制x,而必须通过产生控制信号u来控制x,因此,如u不可控制x,则r也不能控制x,换言之,若∑0不可控,则∑K也不可控。
必要性得证。
注意到上述证明过程没有哟感到单变量和定常的条件,所以,上述定理对于多变量时变系统也是合适的。
2.2状态反馈系统的可观性虽然状态反馈保持了动态方程的可控性,但总可以选择某一状态反馈阵K,破坏动态方程的可观性。
用一个特例就可以证明。
例2.1 设对象的动态方程为因为所以,该系统是完全可控的,但不是完全客观的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K. J. Åström 1. Introduction 2. An Example 3. The General Case 4. Integral Action 5. Summary
Theme: Using the state for control.
Closed loop system
−a12 a11
−a21
dx = dt
0
1
− l1
− l2
x+
0 lr
2 Choosing lr = ω 0 gives the correct steady state value.
Characteristic polynomial det (sI − A)
det
0 0 1 0 0
A Special Case
−a1 −a2 . . . an−1 −an 1 1 0 0 0 0 dz 0 1 0 0 0 = z + u dt . . . . . .
State Feedback
Assume that the process is described by
dx = Ax + Bu dt y = Cx
The Mathematical Tool - Matrices
Please refresh your knowledge of matrices. • What is a matrix • Matrix algebra: addition, multiplication, notice AB = B A (a very useful property), transpose • Matlab • Linear equations and inverses Ax = B , x = A−1 B • Eigenvalues and eigenvectors
0 0 1 0 0
The feedback u = −l1 z1 − l2 z2 − . . . − ln zn + lr r gives −a1 − l1 −a2 − l2 . . . −an − ln lr 1 0 0 0 dz 0 1 0 0 = z + r dt . . . . . .
0 0 0 0
The feedback
u = −l1 z1 − l2 z2 − . . . − ln z n + lr r l1 = p1 − a1 , l2 = p2 − a2 , . . . , ln = pn − an
gives the characteristic polynomial
sn + p1 sn−1 + p2 sn−2 + . . . + pn
Simple Examples
Consider the following matrices and their transpose
A=
a11 a21 a12 a22
Example - The Car
Process model
c12 c22 c13 c23
dx = dt 0 0 1 0 x+ 0)x 0 1 u
The closed loop system has the characteristic equation
det(sI − A + B L) = 0
Can we choose L so that this equation has specified poles?
c K. J. Åström August, 2001 1
s ( s + l1 ) = s 2 + l1 s = 0
This implies
t 0
e− As Bu(s)ds = −a + be− At
We cannot obtain a desired characteristic polynomial. Why? The control signal does not influence the second state! Some conditions are required!
0 0 1 0 0
The Characteristic Equation
The system −a1 −a2 . . . −an−1 −an 1 1 0 0 0 0 dz 0 1 0 0 0 = z + u dt . . . . . .
c K. J. Åström August, 2001 2
Controllability ...
t 0
Examples
dx = dt
0 0 1 0
e− As Bu(s)ds = −a + be− At
x+
0 1
u
It follows from Cayley-Hamiltons theorem (a matrix satisfies it own characteristic equation) that
Control law
u = −l1 x1 − l2 x2 + lr r
gives the characteristic polyno2 mial s2 + 2ζ ω 0 s + ω 0 . The closed loop system is
Y ( s) = r lr R( s ) 2 s2 + 2ζ ω 0 s + ω 0
Try to do same thing for
dx = dt 0 0 1 0 x+ 0) x 1 0 u
Controllability
dx = Ax + Bu dt Find control signal that moves the system from x(0) = a to x(t) = b. Hence
t lr 0
y = Cx = ( 1
Control law u = −l1 x1 − l2 x2 + lr r. Closed loop system
dx = dt
− l1
0 1 − l2 0
x+
b = x(t) = e a +
At 0
eA(t−s) Bu(s)ds
r
Characteristic equation
Introduction
• The simple design method becomes very cumbersome for systems of high order • The PID controller predicts based on linear extrapolation • Can we do something better • Where to look for inspiration? • State a number of variables that summarizes the past that is useful for prediction • The future behavior can be predicted from the state • Can we find a general controller? • The state is an ideal basis for control • We will focus on the predictive part, reference values and integral action will be dealt with later
Ae = λ e ( A − λ I)e = 0 det A − λ I = 0
The general linear controller is: u = − Lx + lr r The closed loop system then becomes
dx = Ax + Bu = Ax + B (− Lx + lr r) = ( A − B L) x + Blr r dt
Choosing
2 l1 = 2ζ ω 0, l2 = ω 0
,
B=
b11 b21
b12 b22
,
C=
c11 c21
y = Cx = ( 1
• Which matrices can be added? • Which matrices can be multiplied?
det A = a11 a22 − a12 a21 A−1 = 1 det A a22
Wc = ( B AB . . . An−1 B )
B . Equation
we have
Wc = ( B , AB ) =
1 0 0 0
Not Controllable!
can be inverted. Controllability!
A Special Case
The system −a1 −a2 . . . an−1 −an 1 1 0 0 0 0 dz 0 1 0 0 0 = z + u dt . . . . . .
The General Casal case. Can we transform a given system to this case? Start with
