有理数的加法的应用题
有理数的加法的应用题

有理数的加法的应用题 Ting Bao was revised on January 6, 20021有理数的加法的应用题某商场老板对今年上半年每月的利润作了如下记录:1、2、5、6月盈利分别是13万元、12万元、12.5万元、10万元,3、4月亏损分别是0.7万元和0.8万元。
试用正、负数表示各月的利润,并算出该商场上半年的总利润额。
某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负,某天自O地出发到收工时所走路线(单位:千米)为:+10、-3、+4、+2、-8、+13、-2、+12、+8、+5(1)问收工时距O地多远?(2)若每千米耗油0.2升,从O地出发到收工时共耗油多少升?北京时间8月13日,2008年北京奥运会射击项目继续在北京射击馆进行,在女子25米运动手枪的资格赛中,中国名将陈颖以585环的成绩名列第三,落后第一名蒙古选手贡德格玛5环。
在决赛中,陈颖凭借稳定的发挥,反超贡德格玛,最后获得该项目金牌。
在决赛的20发中,如果统计(3)陈颖最后以多少环的成绩获得冠军家饭店,地面上18层,地下1层,地面上1楼为接待处,顶楼为公共设施处,其余16层为客房;地面下1楼为停车场。
(1)客房7楼与停车场相差几层楼(2)某会议接待员把汽车停在停车场,进入该层电梯,往上14层,又下5层,再下3层,最后上6层,你知道他最后在哪里(3)某日,电梯检修,一服务生在停车场停好汽车后,只能走楼梯,他先去客房,依次到了8楼、接待处、4楼,又回接待处,最后回到停车场,他共走了几层楼梯先阅读下面的问题:例如:某校初一级篮球队12名同学的身高(厘米)分别如下:171,168,170,173,165,178,166,161,176,172,176,176求全队同学的平均身高?解:分别将各数减去170,得1,,0,3,,8,-4,,6,2,,6这组新数的平均数为:(1-2+0+3-5+8-4-9+6+2+6+6)÷12=。
有理数加减法练习题难点

一、有理数加法1. 计算:2 + 32. 计算:5 + (8)3. 计算:7 + (4)4. 计算:6 + 5 + 25. 计算:3 + 2 + (1) + 46. 计算:7 + (2) + 5 + (3)7. 计算:4 + (1) + 3 + (6)8. 计算:2 + 5 + (3) + 49. 计算:6 + (4) + 2 + (1)10. 计算:3 + 2 + (5) + 4二、有理数减法1. 计算:5 32. 计算:8 (2)3. 计算:7 (4)4. 计算:6 55. 计算:3 2 16. 计算:7 (2) 57. 计算:4 1 + 38. 计算:2 + 5 39. 计算:6 4 + 210. 计算:3 2 + 5三、有理数加减混合运算1. 计算:2 + 3 52. 计算:5 8 + 23. 计算:7 (4) + 14. 计算:6 + 5 25. 计算:3 + 2 1 + 46. 计算:7 (2) + 5 37. 计算:4 1 + 3 68. 计算:2 + 5 3 + 49. 计算:6 4 + 2 110. 计算:3 2 + 5 4四、有理数加减法应用题1. 甲数比乙数大5,乙数比丙数大3,求甲数比丙数大多少?2. 一支铅笔比一支钢笔贵1元,一支钢笔比一支圆珠笔贵2元,一支圆珠笔比一支水笔贵3元,求一支铅笔比一支水笔贵多少元?3. 一个班级有男生40人,女生比男生少10人,求这个班级女生有多少人?4. 一辆汽车行驶了300千米,比原计划少行驶了20千米,求原计划行驶的千米数。
5. 一本书原价100元,打八折后售价为80元,求这本书的折扣率。
五、有理数加减法综合题1. 计算:3 + 4 2 + 5 12. 计算:7 (3) + 2 5 + 63. 计算:8 + (4) 3 + 2 (1)4. 计算:5 (2) + 3 4 + (1)5. 计算:6 + 7 3 + 4 (2)6. 计算:5 (3) + 2 1 + 57. 计算:4 + 6 (2) + 3 48. 计算:2 5 + 4 (3) + 19. 计算:7 + 3 (2) + 5 610. 计算:6 (4) + 2 3 + 1六、有理数加减法应用题1. 一辆自行车以每小时15千米的速度行驶,行驶了3小时后,又以每小时10千米的速度行驶了2小时,求这辆自行车总共行驶了多少千米?2. 一个长方形的长是10厘米,宽是6厘米,求这个长方形的面积。
初中数学 有理数的加法和减法运算的解题应用题是什么

初中数学有理数的加法和减法运算的解题应用题是什么解题应用题1:题目:小明去超市买东西,他花费了50元。
如果他支付了30元,还欠15元,那么他以多少元的有理数借了钱?解题步骤:1. 设小明借的钱为x元。
2. 根据题意,我们可以写出方程:30 + x = 50 - 15。
3. 化简方程:x = 50 - 15 - 30。
4. 计算:x = 5元。
答案:小明以5元的有理数借了钱。
解题应用题2:题目:在一场比赛中,小红的得分是-15,小明的得分是10。
他们的总得分是多少?解题步骤:1. 小红的得分是-15,小明的得分是10。
2. 计算总得分:-15 + 10 = -5。
答案:他们的总得分是-5。
解题应用题3:题目:小明家的温度计显示-8摄氏度,他把温度计放在阳台上,经过一段时间后,温度显示变为了3摄氏度。
温度的变化是多少摄氏度?解题步骤:1. 温度计的初始温度是-8摄氏度,变化后的温度是3摄氏度。
2. 计算温度的变化:3 - (-8) = 3 + 8 = 11摄氏度。
答案:温度的变化是11摄氏度。
解题应用题4:题目:小明在一家书店买了一本书,原价是50元,打折后的价格是-40元。
小明支付了-30元,他实际上还要支付多少钱?解题步骤:1. 书的原价是50元,打折后的价格是-40元。
2. 计算小明还要支付的钱:-40 - (-30) = -40 + 30 = -10元。
答案:小明还要支付-10元。
解题应用题5:题目:小明的银行账户里有100元,他取出了-50元,还款给朋友借的钱。
他账户里还剩下多少钱?解题步骤:1. 小明的账户里有100元,取出了-50元。
2. 计算账户剩下的钱:100 + (-50) = 100 - 50 = 50元。
答案:小明账户里还剩下50元。
通过这些解题应用题,我们可以更好地理解有理数的加法和减法运算在实际生活中的应用。
这些应用题能够帮助我们将数学的知识与实际问题相结合,提高解决实际问题的能力。
(完整版)有理数加法应用题
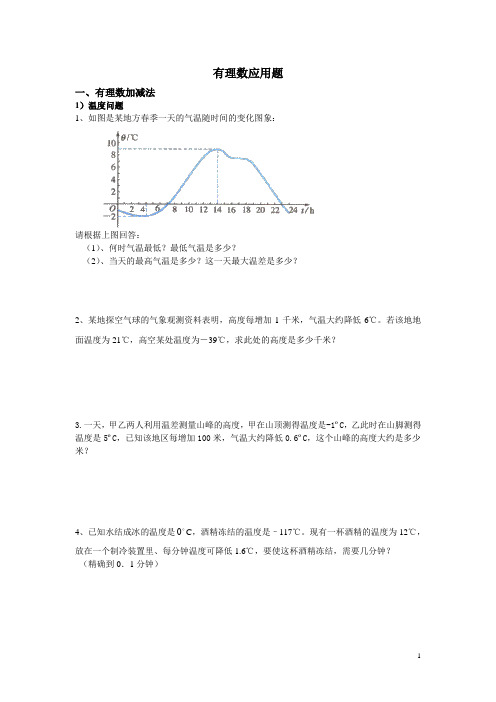
有理数应用题一、有理数加减法1)温度问题1、如图是某地方春季一天的气温随时间的变化图象:请根据上图回答:(1)、何时气温最低?最低气温是多少?(2)、当天的最高气温是多少?这一天最大温差是多少?2、某地探空气球的气象观测资料表明,高度每增加1千米,气温大约降低6℃。
若该地地面温度为21℃,高空某处温度为-39℃,求此处的高度是多少千米?3.一天,甲乙两人利用温差测量山峰的高度,甲在山顶测得温度是-1ºC,乙此时在山脚测得温度是5ºC,已知该地区每增加100米,气温大约降低0.6ºC,这个山峰的高度大约是多少米?4、已知水结成冰的温度是 0C,酒精冻结的温度是–117℃。
现有一杯酒精的温度为12℃,放在一个制冷装置里、每分钟温度可降低1.6℃,要使这杯酒精冻结,需要几分钟?(精确到0.1分钟)2)时差问题1.下表列出了国外几个大城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数)(1)如果现在是北京时间上午8:00,那么东京时间是多少?(2)如果小强在北京时间下午15:00打电话给远在纽约的姑姑,你认为合适吗?试说明你的理由。
3)路程问题1.柳州出租车司机小李,一天下午以白沙客站为出发点,在南北走向的跃进路上营运,如果规定向北为正,向南为负,他这天下午行车里程(单位:千米)如下:+15,-2,+5,-13, +10,-7,-8,+12,+4,-5,+6(1)将最后一名乘客送到目的地时,小李距下午出车时的出发白沙客站多远? 在白沙客站的什么方向?(2)若每千米的价格为3.5元,这天下午小李的营业额是多少?2. 某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、-3、-5、+4、-8、+6、-3、-6、-4、+10。
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?3.李老师在学校西面的南北路上从某点A出发来回检查学生的植树情况,设定向南的路程记为正数.向北的路程记为负数,那么李老师所行路程依次为(单位:百米):+12,-l0,+10,-8,-6,-5,-3.(1)求李老师最后是否回到出发点A?(2)李老师离开出发点A最远时有多少千米? (3)李老师共走了多少千米?4.在一条东西走向的马路旁,有青少年宫、党校、商场、医院四家公共场所.已知青少年宫在学校东300m处,商场在学校西200m处,医院在学校东500m处,若将马路近似地看作一条直线,以学校为原点,向东为正方向,用1个单位长度表示100m.(1)在数轴上表示四家公共场所的位置.(2)列式计算青少年宫与商场之间的距离.5.检修组乘汽车,沿公路检修线路,约定向东为正.向西为负,某天自A出发,到收工时,行走记录为(单位:千米):+8、-9、+4、+7、-2、-10、+18、-3、+7、+5 回答下列问题:(1)收工时在A地的哪边?距A地多少千米?(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?6. 某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行-+-++--驶为负,一天中七次行驶纪录如下。
有理数加减法计算题练习题及答案

有理数加减法计算题练习题及答案一、基础练习1. 计算:(-3) + 5答案:22. 计算:16 - (-4)答案:203. 计算:(-9) + (-6)答案:-154. 计算:9 - 12答案:-35. 计算:(-5) + 0答案:-56. 计算:0 - 8答案:-87. 计算:(-11) + 11答案:08. 计算:(-4) - 13答案:-179. 计算:7 + (-7)答案:010. 计算:3 - (-9)答案:12二、应用题1. 阿明每天存钱,存入正数,取出则为负数。
星期一他存了20元,星期二他取了10元,星期三他又存了15元,星期四他取了5元。
请计算他的余额。
答案:20 - 10 + 15 - 5 = 20元2. 琳琳和小明比赛做数学题,她们答对的题数分别是15和12。
请计算琳琳和小明答题的总共题数差。
答案:15 - 12 = 3题3. 一个海拔为负数表示海平面以下。
某城市的海拔是-80米,另一个城市的海拔是-20米,哪个城市的海拔更高?答案:-20 > -80,所以第二个城市的海拔更高。
4. 温度计上的零度表示摄氏温度下的冰点,而摄氏温度下的沸点为100度。
某天的温度是5度,另一天的温度是-10度,哪一天的温度更低?答案:-10 < 5,所以第二天的温度更低。
5. 一根铁棒原长为30厘米,被切了两刀,分成了三段,第一段长为5厘米,第二段长为10厘米,剩下的一段铁棒长多少厘米?答案:30 - 5 - 10 = 15厘米三、挑战题1. 计算:(4 + 5) - (-3)答案:122. 计算:(-3) - (7 + 4)答案:-143. 计算:12 - 4 - (-8)答案:164. 计算:(-5) + (-3) + 2 - (-7)答案:15. 计算:(7 - 3) + (10 - (-2))答案:22四、综合应用题1. 一家商店的收入情况如下:星期一赚了80元,星期二亏了50元,星期三又赚了40元,星期四赚了90元。
七年级数学有理数加减混合运算应用题

七年级数学有理数加减混合运算应用题
以下是一些七年级数学有理数加减混合运算应用题的例子:
1.小明从A地出发,向北走20米到达B地,然后向东走30米到达C地,最
后再向南走40米到达D地。
请问他最终离出发点A地有多远?
解答:小明从A地出发,先向北走20米到B地,再向东走30米到C地,最后向南走40米到D地。
因为北和南是相反的方向,所以20米和40米会相互抵消,只剩下向东的30米。
因此,他最终离A地30米。
2.一个书架上有10本图书,第一天借出了4本,第二天归还了2本。
请问两
天后书架上还剩多少本书?
解答:开始时有10本书,第一天借出了4本,所以剩下10 - 4 = 6本。
第二天归还了2本,所以6 + 2 = 8本。
因此,两天后书架上还剩8本书。
3.小华和小明一起从学校出发去图书馆。
小华先走了20分钟,然后小明开始
追赶他。
如果小明的速度是每小时6公里,而小华的速度是每小时4公里,请问小明需要多长时间才能追上小华?
解答:因为小华先走了20分钟,所以他已经走了4×20/60 = 1.33公里。
小明每小时比小华快6 - 4 = 2公里,所以他需要追赶1.33公里。
因此,所需时间为1.33/2 = 0.665小时,也就是40分钟。
初中数学 有理数的加法和减法运算的应用题是什么

初中数学有理数的加法和减法运算的应用题是什么以下是一些初中数学中关于有理数加法和减法运算的应用题:1. 问题解决:a) 一个温度计上的温度为-5摄氏度,经过3小时后温度上升了7摄氏度,求现在的温度是多少摄氏度?b) 一辆汽车从一个城市出发,行驶了120公里后向左转行驶了80公里,最后又向右转行驶了100公里,求汽车最后所在的位置离出发点的距离是多少公里?2. 债务问题:a) 小明向小红借了20元钱,小红又向小明借了15元钱,最后小明又向小红借了8元钱,求小明最后欠小红多少元钱?b) 爸爸从银行取了200元钱,妈妈又从银行取了150元钱,然后他们一起去商场购物,最后付款时他们还剩下350元钱,求他们在商场上花了多少钱?3. 海拔问题:a) 一个城市的海拔为-100米,另一个城市的海拔为150米,求这两个城市的海拔差是多少米?b) 一个滑雪场的海拔为2400米,一个登山基地的海拔为3800米,求这两个地点的海拔差是多少米?4. 温度变化问题:a) 早晨气温为-3摄氏度,中午气温上升了8摄氏度,晚上气温下降了5摄氏度,求晚上的气温是多少摄氏度?b) 一天中的最高气温为30摄氏度,最低气温为15摄氏度,求一天的温差是多少摄氏度?5. 账户余额问题:a) 小明的银行账户里有300元钱,他向账户存入了120元钱,然后又从账户取出了80元钱,最后账户里还剩多少钱?b) 爸爸的信用卡欠款为-500元钱,他向信用卡还款了200元钱,然后又向信用卡借款了100元钱,最后信用卡欠款是多少元钱?这些应用题涉及到有理数加法和减法在实际问题中的应用。
通过解决这些问题,学生可以将数学知识与现实生活相结合,提高解决实际问题的能力。
建议学生在解决问题时,先分析问题,提取关键信息,然后应用有理数加法和减法的规则进行计算。
希望这些应用题能够帮助学生更好地理解有理数运算的实际应用,并提高数学解题的能力。
有理数加法的50道题目

有理数加法的50道题目1. 将 -3/4 和 1/2 相加。
2. 计算 -5/8 加上 3/4 的结果。
3. 把 2/3 和 -1/3 加在一起。
4. 计算 -7/6 加上 2/3 的值。
5. 把 -4/5 和 -2/5 相加。
6. 将 1/6 和 -1/2 加在一起。
7. 计算 -3/7 加上 -1/7 的结果。
8. 把 -2/9 和 1/3 相加。
9. 将 5/6 和 1/6 加在一起。
10. 计算 -1/2 加上 -3/4 的值。
11. 把 -2/3 和 1/4 相加。
12. 计算 -5/6 加上 2/5 的结果。
13. 把 1/2 和 -1/3 加在一起。
14. 计算 -7/8 加上 2/3 的值。
15. 把 -3/4 和 -1/2 相加。
16. 将 1/3 和 -1/6 加在一起。
17. 计算 -1/7 加上 -3/7 的结果。
18. 把 -1/3 和 2/9 相加。
19. 将 1/6 和 5/6 加在一起。
20. 计算 -3/4 加上 -1/2 的值。
21. 把 1/4 和 -2/3 相加。
22. 计算 -2/5 加上 5/6 的结果。
23. 把 -1/3 和 1/2 加在一起。
24. 计算 -2/3 加上 7/8 的值。
25. 把 -1/2 和 -3/4 相加。
26. 将 -1/6 和 1/3 加在一起。
27. 计算 -3/7 加上 -1/7 的结果。
28. 把 1/3 和 -2/9 相加。
29. 将 5/6 和 1/6 加在一起。
30. 计算 -1/2 加上 -5/8 的值。
31. 把 -2/3 和 1/4 相加。
32. 计算 -5/6 加上 3/4 的结果。
33. 把 1/2 和 -1/3 加在一起。
34. 计算 -2/3 加上 7/8 的值。
35. 把 -1/2 和 -3/4 相加。
36. 将 1/6 和 -1/3 加在一起。
37. 计算 -3/7 加上 -1/7 的结果。
38. 把 -2/9 和 1/3 相加。
有理数加减混合运算应用题

有理数加减混合运算应用题
哎呀,前几天我去超市购物,可真是经历了一场“有理数加减混合运算大冒险”!
那天我兴高采烈地走进超市,准备大采购一番。
一进去,就被琳琅满目的商品迷花了眼。
我先拿了一袋薯片,标价 5 块 5。
接着又看到了巧克力,8 块 9 一盒,毫不犹豫地放进了购物篮。
走到水果区,红彤彤的苹果吸引了我。
苹果 3 块一斤,我挑了两斤。
然后又看到了香蕉,2 块 5 一斤,称了三斤。
这时候,我遇到了我的好朋友小李。
她笑着跟我说:“你买这么多,小心超预算啦!”我自信地回答:“没事,我心里有数!”
接着我来到了饮料区,拿了一瓶可乐,4 块 8。
还选了一瓶果汁,6 块 2。
当我推着满满当当的购物车去结账时,心里开始默默计算起来。
薯片 5.5 元,巧克力 8.9 元,苹果 3×2 = 6 元,香蕉 2.5×3 = 7.5 元,可乐 4.8 元,果汁 6.2 元。
我在心里嘀咕着:“5.5 8.9 6 7.5 4.8 6.2,哎呀,这可怎么算呀!”收银员小姐姐迅速地操作着收银机,一边扫码一边说:“一共 38.9 元。
”
我掏出 50 块递给她,心里想着:“50 - 38.9 = 11.1 元,应该找我 11.1 元。
”果然,小姐姐很快就找给了我 11 块 1 毛。
拎着购物袋走出超市,我得意地跟小李说:“看,我算得准吧!”小李冲我竖起大拇指:“厉害啦!”
这次超市购物,让我深深感受到了有理数加减混合运算在生活中的大用处,真是有趣又实用呢!。
六年级数学上册2.4.2有理数加法运算律的应用题组训练(含解析)鲁教版五四制

有理数加法运算律的应用1.下列变形,运用有理数的加法运算律正确的是( )A.3+(-2)=2+3B.4+(-6)+3=(-6)+4+3C.[5+(-2)]+4=[5+(-4)]+2D.+(-1)+=+(+1)【变式训练】7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是应用了( )A.加法交换律B.加法结合律C.符号化简D.加法交换律与结合律2.下列运算中正确的是( )A.8+[14+(-9)]=15B.(-2.5)+[5+(-2.5)]=5C.+(-2)=-2D.3.14+[(-8)+3.14]=-83.计算(-4)+(-3)+(-4)+3的结果是.4.计算++2+的结果是.5.绝对值小于π的所有整数的和是.【互动探究】绝对值小于100的所有整数的和是.6.计算:(1)(-32)+(-27)+(-15).(2)(+29)+(-11)+(+32).(3)(+7.8)+(-3.5)+(+2.7).(4)(-13.2)+++.有理数加法运算律的实际应用1.某天早晨气温是-3℃,到中午升高了5℃,晚上又降低了3℃,到午夜又降低了4℃,午夜时气温为( )A.5℃B.15℃C.-5℃D. -1℃2.一升降机,第一次上升5m,第二次又上升6m,第三次下降4m,第四次又下降9m.这时升降机在原始位置的( )A.上方24mB.下方24mC.上方2mD.下方2m3.某商店去年四个季度盈亏情况如下(盈余为正):+128.5万元,-140万元,-95.5万元,280万元,这个商店去年的总盈利情况是( )A.盈余644万元B.亏本173万元C.盈余173万元D.亏本64万元4.某天股票A开盘价12元,上午11:40跌1.0元,下午收盘时又涨了0.2元,则股票A这天收盘价为( )A.0.2元B.9.8元C.11.2元D.12元5.某人用320元购买了8套儿童服装,准备以一定价格出售,如果每套儿童服装以55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,-3,+2,+1,-1,-2,0,-2,当卖完这8套儿童服装后是盈利还是亏损?盈利(亏损)多少钱?6.有一批味精,标准质量为每袋100g,现抽取10袋样品进行检测,其结果是:99,102,101,101,98,99,100,97,99,103(单位:g),用简便方法求这10袋味精的总质量是多少?【错在哪?】作业错例课堂实拍计算:3++5+.(1)找错:从第____步开始出现错误.(2)纠错:_____________________________________.提技能·题组训练有理数加法运算律的应用1.下列变形,运用有理数的加法运算律正确的是( )A.3+(-2)=2+3B.4+(-6)+3=(-6)+4+3C.[5+(-2)]+4=[5+(-4)]+2D.+(-1)+=+(+1)【解析】选B.选项A,C,D在运用加法交换律时符号有错误.【变式训练】7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是应用了( )A.加法交换律B.加法结合律C.符号化简D.加法交换律与结合律【解析】选D.观察所给式子可知,在运算过程中应用了加法交换律与结合律.2.下列运算中正确的是( )A.8+[14+(-9)]=15B.(-2.5)+[5+(-2.5)]=5C.+(-2)=-2D.3.14+[(-8)+3.14]=-8【解析】选C.选项A的结果是13,选项B的结果是0,选项D的结果是-1.72.3.计算(-4)+(-3)+(-4)+3的结果是.【解析】(-4)+(-3)+(-4)+3=[(-4)+(-4)]+[(-3)+3]=-8+0=-8.答案:-8【易错提醒】题中的-3与3是互为相反数,而其他两个数相等,解答时不要把两个-4错认为是互为相反数.4.计算++2+的结果是.【解析】++2+=+=3+=.答案:5.绝对值小于π的所有整数的和是.【解析】因为绝对值小于π的所有整数有:-3,-2,-1,0,1,2,3;所以-3+(-2)+(-1)+0+1+2+3=(-3+3)+(-2+2)+(-1+1)+0=0.答案:0【互动探究】绝对值小于100的所有整数的和是.【解析】因为绝对值小于100的整数有0,±1,±2,±3,…,±99,所以0+[1+(-1)]+[2+(-2)]+…+[99+(-99)]=0.答案:06.计算:(1)(-32)+(-27)+(-15).(2)(+29)+(-11)+(+32).(3)(+7.8)+(-3.5)+(+2.7).(4)(-13.2)+++.【解析】(1)原式=-(32+27+15)=-74.(2)原式=[(+29)+(+32)]+(-11)=61+(-11)=50.(3)原式=[(+7.8)+(+2.7)]+(-3.5)=10.5+(-3.5)=7.(4)原式=+=(-9)+0=-9.有理数加法运算律的实际应用1.某天早晨气温是-3℃,到中午升高了5℃,晚上又降低了3℃,到午夜又降低了4℃,午夜时气温为( )A.5℃B.15℃C.-5℃D. -1℃【解析】选C.由题意得,午夜时气温为:(-3)+(+5)+(-3)+(-4)=[(-3)+(-3)+(-4)]+(+5)=-5(℃).2.一升降机,第一次上升5m,第二次又上升6m,第三次下降4m,第四次又下降9m.这时升降机在原始位置的( )A.上方24mB.下方24mC.上方2mD.下方2m【解题指南】解答本题的三个关键1.规定上升为正,下降为负.2.计算4个数的和.3.根据结果的正负判断方向.【解析】选D.若规定上升为正,下降为负,则5+6+(-4)+(-9)=(5+6)+[(-4)+(-9)]=11+(-13)=-2.因为-2是负数,所以升降机在原始位置的下方2m.3.某商店去年四个季度盈亏情况如下(盈余为正):+128.5万元,-140万元,-95.5万元,280万元,这个商店去年的总盈利情况是( )A.盈余644万元B.亏本173万元C.盈余173万元D.亏本64万元【解析】选C.(+128.5)+(-140)+(-95.5)+280=(128.5+280)+[(-140)+(-95.5)]=408.5+(-235.5)=408.5-235.5=173.4.某天股票A开盘价12元,上午11:40跌1.0元,下午收盘时又涨了0.2元,则股票A这天收盘价为( )A.0.2元B.9.8元C.11.2元D.12元【解析】选C.由题意得12+(-1.0)+(+0.2)=11.2.5.某人用320元购买了8套儿童服装,准备以一定价格出售,如果每套儿童服装以55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,-3,+2,+1,-1,-2,0,-2,当卖完这8套儿童服装后是盈利还是亏损?盈利(亏损)多少钱?【解析】因为2+(-3)+2+1+(-1)+(-2)+0+(-2)=[2+(-2)]+[2+(-2)]+[1+(-1)]+(-3)+0=0+0+0+(-3)+0=-3,所以共卖55×8+(-3)=437(元),437-320=117(元),所以卖完这8套儿童服装后盈利117元.【易错提醒】题中+2,-3,+2,+1,-1,-2,0,-2的和表示与8件以55元为标准的差值,不要以这8个数的和的正负判断亏损或盈利.6.有一批味精,标准质量为每袋100g,现抽取10袋样品进行检测,其结果是:99,102,101,101,98,99,100,97,99,103(单位:g),用简便方法求这10袋味精的总质量是多少?【解析】规定超过100g的记为正,不足的记为负.则这10袋味精与标准的差累计是:(-1)+(+2)+(+1)+(+1)+(-2)+(-1)+0+(-3)+(-1)+(+3)=[(-1)+(+1)+(+2)+(-2)+(+1)+(-1)+(-3)+(+3)]+[0+(-1)]=0+(-1)=-1(g).所以100×10+(-1)=999(g).答:这10袋味精的总质量是999g.【错在哪?】作业错例课堂实拍计算:3++5+.(1)找错:从第____步开始出现错误.(2)纠错:_____________________________________.答案: (1)① (2)=+++--1323原式(35)[(2)(8)]4455=9+(-11)=-2。
有理数的加减应用题正版式1

(绝对值的和即算术和)
(3)若汽车行驶每千米耗油0.3升,求该天共耗油多少升? (4)在8次记录中,哪一次离A点最近?哪一次离A点最远?
(分析)将行驶记录相加,若结果为正,则在原出发地 A地的正东方向;若结果为负,则在原出发地A地的 正西方向。汽车耗油跟方向无关,只跟行驶的总路程 有关。而每段路程即记录的绝对值,总路程即每段路 程绝对值的和。 解:(1):(+18)+(-9)+(-7)+(-14)+(-6) +(+13)+(-6)+(-8)=-19(千米) 所以,B地在A地的西方,距A地19千米处。 (2):|+18|+|-9|+|-7|+|-14|+|-6|+|+13|+|-6|+|-8|=81 (千米) 81X 0.3=24.3(升) 答:B地在A地的西方,距A地5千米, 该天共耗油24.3升。
三
-0.35
四
+0.03
五 六
+0.28 -0.36
日
-0.01
水位变化 (米)
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?哪一天最低?它们 位于警戒水位之上还是之下?与警戒水位的距离分 别为多少米? (2)与上周日相比,本周日河流的水位是上升了还 是下降了?
• 例1:动物园在检测成年麦哲伦企鹅的身体 状况时,最重要一项就是称体重。已知某 动物园对6只成年麦哲伦企鹅进行称重检测, 以4kg为标准,超过或不足的千克数分别用 正数、负数表示,称重记录如下表所示, 求这6只企鹅的总体重。
七年级上册有理数应用题

七年级上册有理数应用题
一、有理数加减法应用题
1. 题目
某冷库的温度是零下10℃,下降 -3℃后又下降5℃,两次变化后冷库的温度是多少?
解析
零下10℃记为 10℃。
下降 -3℃,这里的“下降 -3℃”实际是温度上升3℃,此时温度变为 -10+3 = -7℃。
然后又下降5℃,那么最终温度为 -7 5=-12℃。
2. 题目
小明在一条东西向的跑道上,先走了20米,又走了 -30米,此时他在原来位置的哪个方向,距离原来位置多少米?
解析
把向东走记为正方向。
先走了20米,即 +20米。
又走了 -30米,这里的“ -30米”表示向西走30米。
那么小明的位置变化为 +20+( -30)=20 30=-10米。
所以小明在原来位置的西方,距离原来位置10米。
二、有理数乘除法应用题
1. 题目
某商场去年亏损10万元,今年盈利12万元,若盈利记为正,亏损记为负,该商场这两年的盈亏情况如何表示?这两年总的盈亏是多少万元?
解析
去年亏损10万元,记为 -10万元。
今年盈利12万元,记为+12万元。
这两年总的盈亏情况为(-10)+12 = 2万元。
所以这两年总的是盈利2万元。
2. 题目
已知一个数的倒数是 -2,另一个数是公式,求这两个数的商。
解析
因为一个数的倒数是 -2,那么这个数是公式。
求公式与公式的商,即公式。
完整版)初一有理数加减法应用题训练

完整版)初一有理数加减法应用题训练初一有理数加减法应用题训练解下列各题。
1、已知12箱苹果,以每箱10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,称重记录如下:0.2,—0.2,+0.7,—0.3,—0.4,+0.6,—0.1,—0.6,+0.5,—0.2,—0.5.1) 求12箱苹果的总重量;2) 若每箱苹果的重量标准为10±0.5(千克),则这12箱有几箱不合乎标准的?解答:1) 12箱苹果的总重量为:10×(0.2-0.2+0.7-0.3-0.4+0.6-0.1-0.6+0.5-0.2-0.5)=12千克。
2) 在10±0.5(千克)的标准范围内,每箱苹果的重量应该在9.5千克至10.5千克之间。
根据记录可知,有4箱不合乎标准。
2.柳州出租车司机XXX,一天下午以白沙客站为出发点,在南北走向的跃进路上营运,如果规定向北为正,向南为负,他这天下午行车里程(单位:千米)如下:15,-2,+5,-13.+10,-7,-8,+12,+4,-5,+61) 将最后一名乘客送到目的地时,XXX距下午出车时的出发白沙客站多远?在白沙客站的什么方向?2) 若每千米的价格为3.5元,这天下午XXX的营业额是多少?解答:1) XXX最后一次行驶的距离为6千米,向北行驶了21千米,向南行驶了15千米,因此距离出发点的距离为6千米,向北方向。
2) XXX这天下午的总行驶里程为45千米,营业额为45×3.5=157.5元。
3、某国股民XXX上星期六买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况:(单位:元)星期:一二三四五六每股涨跌:+4 +4.5 -1 -2.5 -6 +21) 星期三收盘时,每股是多少元?2) 本周内最高价是每股多少元?最低价是每股多少元?3) 已知XXX买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果XXX在星期六收盘前将全部股票卖出,他的收益情况如何?解答:1) 星期三收盘时,每股为27-1=26元。
有理数加法应用题

1. 某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负,某天自A 地出发到收工时所走路线
(单位:千米)为:+10、-3、+4、+2、-8、+13、-2、+12、+8、+5
(1)问收工时距A 地多远?(2)若每千米耗油0.2升,从O 地出发到收工时共耗油多少升?
2、 某人用400元购买了8套儿童服装,准备以一定的价格出售,如果以每套55元的价格为标准,超出的记为正数,不足的记为负数,记录如下:(单位:元)+2,-3,+2,-1,-2,+1,-2,0
(1)当他卖完这8套服装后的总收入是多少? (2)盈利(或亏损)了多少元?
3、8筐苹果,以每筐30千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重的记录如下:505315110523....,,,,,,---。
(1)总计超过或不足多少千克?(2)问这8筐苹果的总重量是多少?
4、下列是我校七年级5名学生的体重情况,
5. 某摩托车厂本周内计划每日生产300辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实
(2) 本周总生产量与计划生产量相比,是增加还是减少?
(3) 产量最多的一天比产量最少的一天多生产了多少辆?
6).
(1)
(2) 小兵现在想给远在巴黎的爸爸打电话,你认为合适吗?
7.阅读下列材料:
因为111122=-⨯,1112323=-⨯,…,11119201920
=-⨯ 所以111223++⨯⨯...111111920223+=-+-+⨯ (11119119202020)
+-=-= 请模仿上面的方法计算:
111233420092010
++⋅⋅⋅+⨯⨯⨯.。
有理数加减法应用题

有理数加减法应用题一、有理数加减法应用题(一)温度相关1. 某天早晨的气温是5℃,中午上升了8℃,中午的气温是多少摄氏度?解析:5 + 8 = 3(℃),中午的气温是3℃。
2. 某天的最高气温是10℃,最低气温是3℃,这一天的温差是多少?解析:10 (3) = 10 + 3 = 13(℃),这一天的温差是13℃。
(二)盈利亏损3. 某商店上月盈利 2500 元,本月亏损 500 元,该商店两个月总的盈利或亏损情况如何?解析:2500 + (500) = 2000(元),两个月总的盈利 2000 元。
4. 某公司第一季度盈利 15 万元,第二季度亏损 8 万元,第三季度亏损 3 万元,该公司前三季度总的盈利情况如何?解析:15 + (8) + (3) = 15 8 3 = 4(万元),前三季度总的盈利 4 万元。
(三)海拔高度5. 甲地海拔为 100 米,乙地比甲地高 50 米,乙地的海拔是多少米?解析:100 + 50 = 50(米),乙地的海拔是 50 米。
6. 某山峰比海平面高 1536 米,记作 +1536 米,某盆地比海平面低 100 米,记作 100 米,山峰比盆地高多少米?解析:1536 (100) = 1536 + 100 = 1636(米),山峰比盆地高1636 米。
(四)行程问题7. 小明从家出发,先走了 3 千米,又后退了 2 千米,此时小明离家多远?解析:3 + (2) = 1(千米),此时小明离家 1 千米。
8. 一辆汽车从 A 地出发,先向东行驶 15 千米,再向西行驶 25 千米,此时汽车在 A 地的什么方向,距离 A 地多远?解析:15 + (25) = 10(千米),此时汽车在 A 地的西方,距离A 地 10 千米。
(五)库存变化9. 仓库里原有货物 50 吨,运出 18 吨,又运进 12 吨,现在仓库里有货物多少吨?解析:50 18 + 12 = 44(吨),现在仓库里有货物 44 吨。
七年级有理数加减法应用题

七年级有理数加减法应用题《有理数加减法的奇妙冒险》哎呀呀,同学们,你们知道吗?有理数加减法可真是一场奇妙的冒险!就好像我们在一个充满数字小精灵的神秘世界里探索一样。
有一天,老师在课堂上出了一道题:小明有10 元钱,买文具花了-5 元(这里的负5 元表示支出),后来又收到妈妈给的8 元,那小明现在一共有多少钱?这可难不倒我!我心里想:“小明一开始有10 元,花了-5 元,那不就是10 + (-5) = 5 元嘛。
然后妈妈又给了8 元,那就是5 + 8 = 13 元啦!”我赶紧举手回答,老师笑着点了点头,说:“答对啦,真聪明!”我心里那叫一个美呀,就像吃了蜜一样甜。
还有一次,我们小组一起讨论有理数加减法的问题。
小李说:“这有理数加减法,就跟咱们玩跳棋似的,正数向前跳,负数向后跳。
”小王接着说:“对呀对呀,跳来跳去的,可有意思啦!”我也忍不住插话:“那要是正数负数一起跳,不就更热闹啦?”大家都哈哈大笑起来。
记得有一次数学考试,有道题是这样的:仓库里第一天运进300 千克大米,第二天运出-150 千克大米,第三天又运进200 千克大米,问仓库里这三天一共运进了多少千克大米?我当时心里一紧,哎呀,这可怎么算呀?不过我深吸一口气,告诉自己别慌,冷静思考。
我先算出第一天和第三天一共运进了300 + 200 = 500 千克大米,第二天运出-150 千克,那不就是500 + (-150) = 350 千克大米嘛。
做完这道题,我长舒了一口气,心里的大石头总算落了地。
有理数加减法,有时候就像一场刺激的拔河比赛。
正数和负数分别在两边用力,看最后哪边的力量大,结果是正还是负。
比如说 5 + (-3) ,就好像 5 个大力士在这边,3 个大力士在那边,最后还是这边的力量大,结果就是2 啦。
在学习有理数加减法的过程中,我也遇到过困难,有时候会算错,会烦恼,会觉得自己怎么这么笨呀?可是,我从来没有放弃过。
我就像一个勇敢的战士,一次又一次地挑战这些难题。
有理数和整式的加减应用题

七年级有理数和整式的加减应用题1. 有20筐白菜,以每筐15千克为标准,超过或不足的千克数分别用正负数来表示, 记录如下:(1)这20筐白菜中,最重的一筐比最轻的筐重多少千克?(2)与标准重量比较, 20筐白菜总计超过或不足多少千克?(3)若白菜每千克售价3.99元,则出售这20筐白菜可卖多少元? (结果精确到0.1).2. 如图为北京市地铁1号线地图的一部分,某天,小王参加志愿者服务活动,从西单站出发,到从A 站出站时,本次志愿者服务活动结束,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站):4+,3-,6+,-8,9+,2-,7-,1+.(1)请通过计算说明A 站是哪一站?(2)若相邻两站之间的平均距离为1.2千米,求这次小王志愿服务期间乘坐地铁行进的总路程约是多少千米?3. 出租车司机小王某天下午的营运全是在东西走向的某条大街上进行的.如果规定向东为正,向西为负,他这天下午的行车里程(单位:km )如下:16+,2-,5+,1-,12+,3-,4-,10+,3+,5-,6+ (1)将最后一名乘客送往目的地时,小王距离下午出车时的出发点 km .(2)若汽车耗油量为a L/km ,这天下午小王的车共耗油 L (用含a 的式子表示).(3)小王所开的出租车按物价部门规定,起步价(不超过3km 时)车费5元,超过3km 时,每千米车费加价1元,小王这天下午总共收入多少元?4. 国庆小长假后,高速公路养护小组乘车沿南北向公路巡视维护,如果约定向北为正,向南为负,当天的行驶记录如下:(单位;千米)12+、9-、16-、7+、6-、11+、8-、5+.(1)养护小组最后到达的地方在出发点的哪个方向?距出发点多远?(2)若他们所乘车辆的耗油量为0.08升/千米,则这次养护共耗油多少升?5. 有一根弹簧原长10厘米,挂重物后(不超过50克),它的长度会改变,请根据下面表格中的一些数据回答下列问题:(1)要想使弹簧伸长5厘米,应挂重物多少克?(2)当所挂重物为x 克时,用代数式表示此时弹簧的总长度.(3)当x =30克时,求此时弹簧的总长度.6. 两个文具商店销售同一种笔记本,在甲商店购买的售价为2.3元/本,在乙商店购买不超过100本的售价为2.5元/本,超过100本的部分售价为2.1元/本,设购买x 本()100x ≥.(1)乙商店购买x 本需要________元(用含x 的代数式表示);(2)购买150本时,选择________商店便宜(在横线上直接填甲或乙);(3)如果购买总金额为460元时,在甲,乙两商店购买的本数是否相同,说明理由.7. 某文具店在某一时段的销售情况如下,请分别完成下列问题:(1)受疫情影响,该文具店在一周销售中,盈亏情况如表(盈余为正,亏损为负,单位:元). 表中星期四的盈亏被墨水涂污了,请你算出星期四的盈亏数,并说明星期四是盈还是亏?盈亏是多少?(2)该文具店去年12~月平均每月盈利0.2万元, 36~月平均每月亏损0.25万元,79~月平均每月盈利0.4万元,1012~月平均每月亏损0.3万元,则该文具店去年总的盈亏情况如何?8. 随着出行方式的多样化,某市三类打车方式的收费标准如下:已知三种打车的平均车速均为40千米/小时.如:乘坐8千米,耗时8406012÷⨯=分钟.出租车收费为:()10 2.48322+⨯-=(元);滴滴快车的收费为:8 1.2120.616.8⨯+⨯=(元);T3出行的收费为:8 1.6120.417.6⨯+⨯=(元).(1)如果乘车路程20千米,使用T3出行,需支付的费用是______元;(2)如果乘车路程()3x x >千米,使用出租车出行,需支付的费用是______元;使用滴滴快车出行,需支付的费用是______元;(3)T3出行和滴滴快车为了竞争客户,分别推出了优惠方式:滴滴快车对于乘车路程在6千米以上(含6千米)的客户每次收费减免11元;T3出行车费半价优惠.若乘车路程()6m m >千米,使用T3出行比使用滴滴快车出行省20元,直接写出含未知数m 的符合题意的方程.的的9. “双十一”即将来临,某超市规定消费不超过200元按原价,对消费超过200元以上的顾客的实行如下优惠:(1)小博妈妈一次性购物x 元(200600x <≤),她实际付款____________元.(用含x 的式子表示)(2)小西妈妈一次性购物x 元(200x <),小博妈妈一次性购物()300x +元,结账时小博妈妈比小西妈妈多付250元,求x 的值.(3)小博和妈妈一起在超市购买了如下标价的物品:一个电饭煲445元,五斤排骨(38元/斤),两提牛奶(75元/提),两板鸡蛋(35元/板),一提卷简纸27元,一个文具袋6元,妈妈正准备一次性付款,小博说他有更省钱的方法.你知道他的方法吗,请问小博能为妈妈节省多少钱?10. 如图,在长方形休闲广场的一组对角设计两块半径相同的四分之一圆形花坛,另一组对角设计两个大小一样的三角形草坪,圆形的半径、三角形与广场边重合的边长都为m r ,广场长为m a ,宽为m b .(1)列式表示广场空地的面积(结果保留π)(2)若100,60,5a b r ===,现在广场中央修建一个周长为32m 且长宽比例与广场相同的长方形水池,求广场空地的面积(π取3.14,结果取整)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理数的加法的应用题
某商场老板对今年上半年每月的利润作了如下记录:1、2、5、6月盈利分别是13万元、12万元、12.5万元、10万元,3、4月亏损分别是0.7万元和0.8万元。
试用正、负数表示各月的利润,并算出该商场上半年的总利润额。
某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负,某天自O地出发到收工时所走路线(单位:千米)为:+10、-3、+4、+2、-8、+13、-2、+12、+8、+5(1)问收工时距O地多远?(2)若每千米耗油0.2升,从O地出发到收工时共耗油多少升?
北京时间8月13日,2008年北京奥运会射击项目继续在北京射击馆进行,在女子25米运动手枪的资格赛中,中国名将陈颖以585环的成绩名列第三,落后第一名蒙古选手贡德格玛5环。
在决赛中,陈颖凭借稳定的发挥,反超贡德格玛,最后获得该项目金牌。
在决赛的20发中,如果统计时以10环为标准,超过部分记为正,不足部分记为负,记录如下:
请问:(1)在决赛中陈颖打出的最好成绩是多少环?(2)在决赛的20发中实际平均每发打出几环?(3)陈颖最后以多少环的成绩获得冠军?
家饭店,地面上18层,地下1层,地面上1楼为接待处,顶楼为公共设施处,其余16层为客房;地面下1楼为停车场。
(1)客房7楼与停车场相差几层楼?(2)某会议接待员把汽车停在停车场,进入该层电梯,往上14层,又下5层,再下3层,最后上6层,你知道他最后在哪里?(3)某日,电梯检修,一服务生在停车场停好汽车后,只能走楼梯,他先去客房,依次到了8楼、接待处、4楼,又回接待处,最后回到停车场,他共走了几层楼梯?
先阅读下面的问题:例如:某校初一级篮球队12名同学的身高(厘米)分别如下:171,168,170,173,165,178,166,161,176,172,176,176求全队同学的平均身高?
解:分别将各数减去170,得1,,0,3,,8 ,-4,,6, 2,,6
这组新数的平均数为:(1-2+0+3-5+8-4-9+6+2+6+6)÷12=。
则已知数据的平均数为:170+ = 答:全队同学的平均身高为厘米。
通过阅读上面解决问题的方法,请利用它解决下面的问题:(1)10 筐苹果称重(千克)如下:32, 26, 32.5, 33, 29.5, 31.5, 33, 29, 30, 27.5问这10筐苹果的平均重量是多少?
小东的爸爸是出租车司机,为了计算汽车每千米的耗油量,某天上午,他在沿着南北方向营运是详细记录了行车情况,他规定向南为正,向北为负,下面是他这天上午行驶记录:(单
位:千米) 21
16+-,,+4,-5.2,-3.8,+15,-6,-9已知该出租车这天上午共耗油9.6升,你知道小东爸爸的出租车每千米的耗油量是多少吗?
下表列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京的时间早的时数)。
现在的北京时间是上午8∶00 (1)求现在纽约时间是多少?
(2。
