信号与系统习题答案 第三章
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统 梁风梅主编 电子工业出版社 ppt第三章答案

习题三3.1考虑一个连续时间LTI 系统,满足初始松弛条件,其输入)(t x 与输出)(t y 的关系由下列微分方程描述:d ()4()()d y t y t x t t+= (1)若输入(13)()()j t x t e u t -+=,求输出)(t y 。
(2)若输入()e cos(3)()t x t t u t -=,求输出)(t y 。
解:此系统的特征方程为40s += 所以4()t h y t Ae -= (1)(13)()()j tx t eu t -+=设(13)()e j t p y t Y -+= 则(13)(13)(13)(13j)e 4e e ,0j tj t j t Y Y t -+-+-+-++=>解得11336jY j -==+ 所以4(13)1()()()e e ()6t j t h p j y t y t y t A u t --+-⎛⎫=+=+ ⎪⎝⎭又因为初始松弛,所以106jA -+= 即16j A -=所以4(13)11()()()()()66t j th p j j y t y t y t e e u t --+--=+=+ (2)()cos(3)()t x t e t u t -=是(1)中(13)()()j tx t eu t -+=的实部,用2()x t 表示cos(3)()t e t u t -,用1()x t 表示(13)()j t e u t -+观察得{}21()Re ()x t x t =所以{}421111()Re ()cos(3)sin(3)()666t t t y t y t e e t e t u t ---⎛⎫==-++ ⎪⎝⎭3.2若离散时间LTI 系统的输入[]x n 与输出][n y 的关系由下述差分方程给出:][]1[25.0][n x n y n y =--求系统的单位冲激响应][n h 。
解:[]0.25[1][]h n h n n δ=-+因为该系统是因果的,所以0n <时,[]0h n =2231[0]0.25[1][0]01111[1]0.25[0][1]1044111[2]0.25[1][2]0444111[3]0.25[2][3]0444 (111)[]0.25[1][]0444n nh h h h h h h h h n h n n δδδδδ-=-+=+==+=⨯+==+=⨯+==+=⨯+==-+=⨯+=综上,1[][]4n h n u n = 3.3系统S 为两个系统1S 与2S 的级联:S1:因果LTI 系统,[]0.5[1][]w n w n x n =-+; S2: 因果LTI 系统,[][1][]y n ay n bw n =-+][n x 与][n y 的关系由下列差分方程给出:[]0.125[2]0.75[1][]y n y n y n x n +---=(1) 确定a 与b 。
信号与系统王明泉第三章习题解答

(4)频域分析法分析系统;
(5)系统的无失真传输;
(6)理想低通滤波器;
(7)系统的物理可实现性;
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零,即:
如果 和 为相互正交的单位矢量,则 和 就构成了一个二维矢量集,而且是二维空间的完备正交矢量集。也就是说,再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示,有
条件1:在一周期内,如果有间断点存在,则间断点的数目应是有限个。
条件2:在一周期内,极大值和极小值的数目应是有限个。
条件3:在一周期内,信号绝对可积,即
(5)周期信号频谱的特点
第一:离散性,此频谱由不连续的谱线组成,每一条谱线代表一个正弦分量,所以此谱称为不连续谱或离散谱。
第二:谐波性,此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱; (b)周期、离散频谱;
(c)连续、非周期频谱; (d)离散、非周期频谱。
答案:(d)
题7、 的傅里叶变换为
答案:
分析:该题为典型信号的调制形式
题8、 的傅里叶变换为
答案:
分析:根据时移和频移性质即可获得
题9、已知信号 如图所示,且其傅里叶变换为
试确定:
(1)
(2)
(3)
解:
(1)将 向左平移一个单位得到
对于奇谐函数,满足 ,当 为偶数时, , ;当 为奇数时, , ,即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
(4)周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说,任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中,经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差,即 。式中, , 。研究表明, 越大, 越小,当 时, 。
第三章作业答案_1-7

a2 N =
1 1 T 1 T − j (4 N π / T ) t 2 x t e dt = x(t )e− j (4 Nπ / T )t dt + ∫T x(t )e− j (4 Nπ / T )t dt ( ) ∫ ∫ T T T 0 T 2 =
T 1 T T ( ∫ 2 x(t )e − j (4 Nπ / T )t dt + ∫T − x(t − )e− j (4 Nπ / T )t dt ) T 0 2 2 T 1 T ( ∫ 2 x(t )e − j (4 Nπ / T ) t dt + ∫ 2 − x(t )e− j (4 Nπ / T )t dt ) = 0 0 T 0
+∞
e − j 2ω (答案) 2 + jω
+∞ +∞ −∞
X ( jϖ ) = ∫ x(t )e − jωt dt = ∫ e −2 ( t − 2) u (t − 2)e − jωt dt = ∫ e −2 ( t − 2) e − jωt dt
−∞ 2
= ∫ e −( 2+ jω )t + 4 dt =
jkπt
,由已知条件 k ≤ 4 时,H(jw)不为零,而 k ≥ 5 ,H(jw)=0
jkπt
故响应为: y k (t ) = H ( jkπ ) a k e 当 k > 5 时,激励 x k (t ) = a k e 此有 y (t ) =
= (1 −
k 5
)a k e jkπt , k ≤ 4
(2) 由于系统的单位冲激响应 h(t)已知,可以据此而求出其频谱。因为 h(t)是方波脉冲,直 接由典型信号的频谱得:
FT h(t ) ←→ H ( jω ) =
信号与系统课后习题与解答第三章
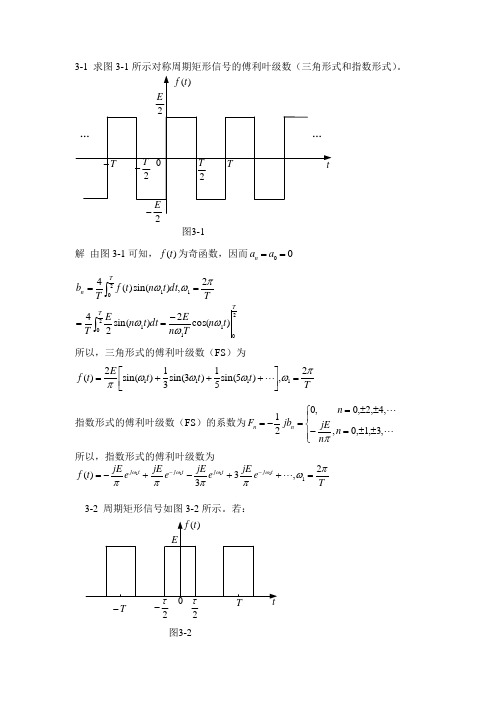
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统第三章习题部分参考答案

(7) (1 − t) f (1 − t) ;
(2) [1 + m f (t)]cosω0 t
(4) (t + 2) f (t); ( ) (6) e− jω0 t df t
dt
(8) f (t)∗ f (t − 3);
t
(9) ∫τ f (τ )dτ −∞
1−t / 2
(11) ∫ f (τ )dτ −∞
2π (sin π t )2 ↔ 2π (1− ⎜w⎜)[ε(w + 2π ) − ε(w − 2π )]
πt
2π
即 (sin π t )2 ↔ (1− ⎜w⎜)[ε(ω + 2π ) − ε(w − 2π )]
πt
2π
(3)双边指数信号
∵ e−a⎜t⎜
↔
2a a2 + w2
(−∞
<
t
<
+∞)
∴ 2a a2 + w2
(13) f (t)∗ Sa(2t) (15) t df (1 − t)
dt
t+5
(10) ∫ f (τ )dτ −∞
(12) df (t) + f (3t ) − 2 e− jt ;
dt
(14) f (t) u(t)
(16) (t − 2) f (t)e j2(t−3)
解:(1) f 2 (t) + f (t) = f (t). f (t) + f (t) ↔ 1 [F (w}* F (w)] + F (w)
又 f (t) = 2 + cos⎜⎛ 2πt ⎟⎞ + 4sin⎜⎛ 5πt ⎟⎞
⎝3⎠
《信号与系统(第四版)》习题详解图文

故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组{ξ1(t),ξ2(t),ξ3(t),ξ4(t)}在(0,4)区间上是否 为正交函数组,是否为归一化正交函数组,是否为完备正交函 数组,并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到:
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=-f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω),且 试在K≥ωm条件下化简下式:
72
第3章 连续信号与系统的频域分析 73
107
信号与系统课后答案第三章作业答案

初始为 0, C2 -4
y f (t) -4e3tu(t) 4e2tu(t)
全响应= yx (t)+y f (t) 4e2tu(t)-2e3tu(t)
3-2 描述某 LTI 系统的微分方程为
d2 y(t) dt 2
3dy(t) dt来自2y(t)
df (t) dt
6
1
1
(2e1 e1 et ) u(t)
e1(2 et ) u(t)
(2)
f
(t)
a[u(t
s) 2
u(t
2)]
h(t) b[u(t 2) u(t 3)]
f
(t)
h(t)
ab[(t
1 2
)
u(t
1 2
)
(t
1 2
)
u(t
1) 2
tu(t)
1 4
(et
e3t
)u(t)
1 2
t
e3tu(t)
[
1 4
et
(
1 2
t
1 4
)e3t
]u
(t)
3-19 一 个 LTI 系 统 , 初 始 状 态 不 祥 。 当 激 励 为 f (t) 时 其 全 响 应 为
(2e3t sin 2t)u(t) ;当激励为 2 f (t) 时其全响应为 (e3t 2sin 2t)u(t) 。求
(1) 初始状态不变,当激励为 f (t 1) 时的全响应,并求出零输入相应、
零状态响应; (2) 初始状态是原来的两倍、激励为 2 f (t) 时系统的全响应。
信号与系统第三章习题答案

d (t - 1) « e- jw
\ e-2( t -1)d (t - 1) « e- jw
(8) U (t ) - U (t - 3) Q 根据傅里叶变换的线性性质可得: 1 U (t ) « p d (w ) + jw 1 U (t - 3) « e - j 3w (p d (w ) + ) jw \ U (t ) - U (t - 3) « ( 1- e - j 3w )(p d (w ) + 1 ) jw
U (t - 1) « e - jw (pd (w ) +
t 1 U ( - 1) « 2e - j 2w (pd (2w ) + ) 2 j 2w Q d (aw ) = 1 d (w ) a
\ 2e- j 2wpd (2w ) = 2pd (2w )w =0 = pd (w ) \ 2e - j 2w (pd (2w ) +
e - jtd (t - 2 ) « e - j 2(w +1)
(6) e -2( t -1)d (t - 1) Q 根据傅里叶变换的性质 f (t ± t0 ) « e ± jwt0 F ( jw ) 可得: e -2( t -1)d (t - 1) = d (t - 1) d (t ) « 1 (t = 1)
d F ( jw ) - 2 F ( jw ) dw
y ''(t ) + 4 y '(t ) + 3 y (t ) = f (t ) y ''(t ) + 5 y '(t ) + 6 y (t ) = f '(t ) + f (t )
(1) 求系统的频率响应 H(jw)和冲激响应 h(t) ; (2) 若激励 f (t ) = e-2tU (t ) ,求系统的零状态响应 y f (t ) 。 解: 方程 1:
信号与系统王明泉科学出版社第三章习题解答

左右对t求导,得:
显然, 的指数傅里叶级数为 (式中 )
3.9求题图3.9所示各信号的傅里叶变换。
题图3.9
解:根据定义
3.10计算下列每个信号的傅里叶变换。
(1) ;(2) ;
(3) ;(4)
(5) ;(6)
解: (1)
(2)
(3)由于
根据卷积乘积性质,得
(4)由于
所以
(5) ,设
第3章傅里叶变换与连续系统的频域分析
3.6本章习题全解
3.1证明函数集 在区间 内是正交函数集。
证明:对任意的自然数n,m (n m),有
=0
证毕
3.2一个由正弦信号合成的信号由下面的等式给出:
(1)画出这个信号的频谱图,表明每个频率成分的复数值。对于每个频率的复振幅,将其实部和虚部分开或者将其幅度和相位分开来画。
图3-19-3
3.21用傅里叶变换法求题图3.21所示周期信号 的傅里叶级数。
题图3.21
解:对x(t)一个周期信号x0(t)的傅里叶变换为
X0(j )=
=
傅里叶级数
3.22求题图3.22所示周期性冲激信号的频谱函数。
题图321-1
3.23已知 的幅频与相频特性如题图3.23所示,求其傅里叶逆变换 。
(a)(b)
题图3.12
解:令傅里叶变换对 ,
(1)根据已知图形可知:
,
已知有
所以
根据傅里叶变换的微积分性质
所以
即
(2) ,
根据(1)的结论得
根据傅里叶变换的微积分性质
所以
即
3.13利用傅里叶变换的对称性求下列信号的频谱函数。
(1) ;(2) ;
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集? 解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
北邮信号与系统课后答案第3章部分1
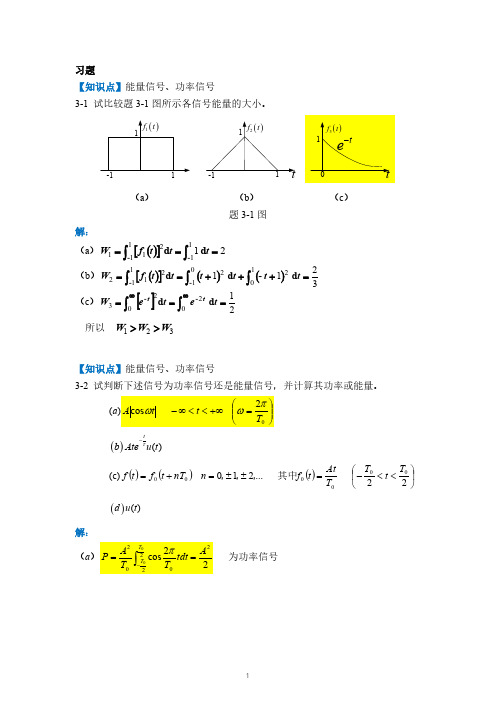
为功率信号
(d) P lim 1 T0 u t 2 dt lim 1 T0 1dt 1
T0
2T0 T0
T0 2T0 0
2
为功率信号。
【知识点】能量信号、功率信号 3-3 对信号 f (t) 在数值和时间两方面进行运算变成 af (bt)
(1)如果在全部时间
t
内, f (t) 是具有能量为 W 的能量信号,
f1 t 1
f2 t 1
0
1
2
3t
0
1
2
3t
锯齿形脉冲
正弦脉冲
题 3-6 图
解:
3
0 f1 t f2 t d t
31 t sin
tdt
- t cos
t - 3 sin
3
t
03 3
3
2 30
3
3
sin
2
tdt
31 1 - cos 2 t d t 3
03
02
3
2
C12 2
t2
fe t
- sin t
3
3
3 t - 2 sin t sin tdt
sin 2
1t
4
3 cos 2 1 t 4
15 cos 4 1 t 4
...
2
A 1 T A
sin 2
1t
2
2A 3 cos 2 1t
2A 15 cos 4 1t 2 ...
AA
2A
2A
cos 2
1t
3 cos 2 1t
15 cos 4 1t
...
9
随着T , C12 ,当T
时使得 C12 0 。
信号系统习题解答3版-第三章-推荐下载
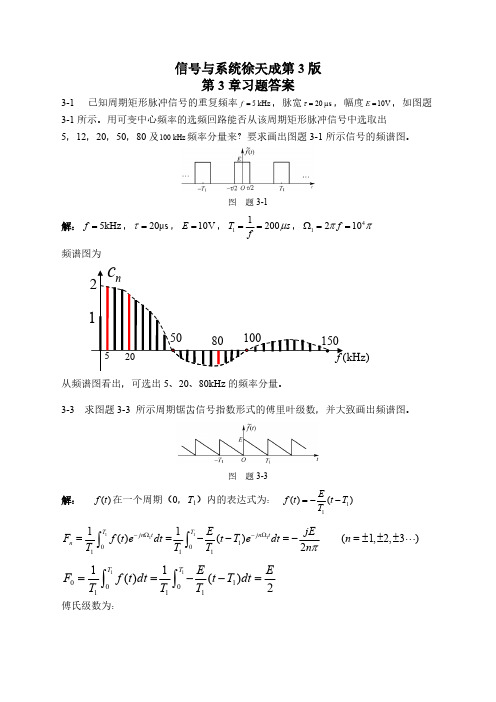
信号与系统徐天成第3版第3章习题答案3-1 已知周期矩形脉冲信号的重复频率,脉宽,幅度,如图题5 kHz f=20 s τ=μ10V E =3-1所示。
用可变中心频率的选频回路能否从该周期矩形脉冲信号中选取出5,12,20,50,80及频率分量来?要求画出图题3-1所示信号的频谱图。
100 kHz 图 题3-1解:,,,,5kHz f =20μs τ=10V E =11200T s fμ==41210f ππΩ==频谱图为从频谱图看出,可选出5、20、80kHz 的频率分量。
3-3 求图题3-3所示周期锯齿信号指数形式的傅里叶级数,并大致画出频谱图。
图 题3-3解: 在一个周期(0,T 1)内的表达式为: ()f t 11()()Ef t t T T =--111110011111()()(1,2,3)2T T jn tjn t n E jE F f t e dt t T e dt n T T T n π-Ω-Ω==--=-=±±±⎰⎰ 11010011111()()2T T E E F f t dt t T dt T T T ==--=⎰⎰傅氏级数为:111122()22244j t j t j t j tE jE jE jE jE f t e e e e ππππΩ-ΩΩ-Ω=-+-+-(1,2,3)2n E F n n π==±±± (0)2(0)2n n n πϕπ⎧->⎪⎪=⎨⎪<⎪⎩3-4 求图题3-4 所示半波余弦信号的傅里叶级数,若, ,大致画出幅10 V E =10 kHz f =度谱。
图 题3-4解:由于是偶函数,所以展开式中只有余弦分量,故傅氏级数中,另由图()f t 0n b =可知有直流分量, 在一个周期(,)内的表达式为:()f t ()f t 2T -2T其中:111cos 4()04T E t t f t T t ⎧Ω<⎪⎪=⎨⎪>⎪⎩112T πΩ=11112401112411()cos T T T T E a f t dt E tdt T T π--==Ω=⎰⎰111111241112422()cos T T jn t jn t T T n n a c f t e dt E t e dt T T -Ω-Ω--===Ω⋅⎰⎰211sin sin 2122cos 3,5,71112n n E E n n n n n πππππ+-⎡⎤⎢⎥=+=-=⎢⎥+--⎢⎥⎣⎦111211122()2T j t T E a c f t e dt T -Ω-===⎰所以,的三角形式的傅里叶级数为:()f t 11122()cos cos 2cos 42315E E E Ef t t t t πππ=+Ω+Ω-Ω+ 3-6 利用信号的对称性,定性判断图题3-6中各周期信号的傅里叶级数中所含有()f t的频率分量。
信号与系统第3章习题和重点

ZB
3-26
已知 f (t) = f1(t) + f2(t)的频谱密度函数 F(ω) = 4Sa(ω) − j
4
ω
,
为偶函数, 为奇函数, 且 f1(t)为偶函数, f2(t)为奇函数,试求 f1(t)和 f2(t) 。 解:由题意知
f1(t) ↔4Sa(ω) = AτSa( 2 ∴f1(t) = 2g2(t)
F = n 1 T 1 T
∫ ∫
3T 4 T 4
f (t)e− jnω0tdt
L − 2 L 2 2 2 −2T −T 0 T 2T t
() 1
− jnω0 T 2 ) = 1 (1−e− jnπ )
−
=
T 1 δ (t) −δ (t − )e− jnω0tdt = (1−e T 2 T − 4
0
T
ZB
3-4 已知周期信号 f (t)的前四分之一周期的波形如图所 且其余每一段四分之一周期的波形要与之相同, 示,且其余每一段四分之一周期的波形要与之相同,试 整个周期的波形。 就下列情况分别画出 f (t)整个周期的波形。 为偶函数, 解:(1) f (t)为偶函数,且只含偶次谐波
f (t)
∞
F(ω) =
∫ = e e ∫
=
−∞ 0 2t − jωt
e2tε(−t)e− jωtdt dt
−∞ (2− jω)t 0 e
2 − jω −∞
ZB
1 = 2 − jω 《信号与系统》SIGNALS AND SYSTEMS
3-19 设 f (t) ↔F(ω) ,试证: 试证: (1) ∫ ∞ f (t)dt = F(0) ) −
解: (2) 为非周期信号 T →∞
信号与系统-第三章习题讲解

E
[Sa2 (
0
)e
j
( 0 2
)
Sa2 (
0
)e
j
( 0 2
)
]
4
4
4
3 39决 定 下 列 信 号 的 最 低 抽 样 频 率 与 奈 奎 斯 特 间 隔 : (1) : S a (1 0 0 t ); ( 2 ) : S a 2 (1 0 0 t ); (3 ) : S a (1 0 0 t ) S a (5 0 t ); ( 4 ) : S a (1 0 0 t ) S a 2 (6 0 t )
故 f ( t ) 2 E 1 s i n ( n t ) 2 E 1 s i n ( n 2 t )
n n 1 . 3 . 5 . . .
n n 1 . 3 . 5 . . .
T
= 2 E [sin ( t) 1 sin (3 t) 1 sin (5 t) ...]
1 2
[ (
0 ) (
0 )]* [
1 j
( )]
11
[
2 j( 0 )
j(
1
] 0)
2
[
(
0)
(
0 )]
j
2 0
2
2
[
(
0)
(
0 )]
单边正弦函数的傅立叶变换为:
F [sin( 0t)u (t)]
1 2
F T [sin( 0t)]* F T [u (t)]
1 2
0
b n
2 T1
T1 0
f
(t ) s in ( n 1t ) d t
2[
T 2
E
sin (n t)d t
南邮信号与系统课后答案第三章

3-14
如题图 3 14 所示信号 f t F ,在不求出 前提下,求
1
F 的
f t
(1) F 0 F 0
-1
0
1
t
解: F 0 F 0
f t e
j t
dt
0
f t dt
f 1 t
1
(a)
2 5
0
-1
2 5
t
2 2 解: f 1 t cos 10 t u t u t cos 10 tg 4 t 5 5 5 2 f t g 4 t Sa F 5 5 5 4 f 1 t 1 2
y 1 t
H 2
cos 2 t
4 5
sin 2 t cos 2 t 127
4 5 Ae
j
另解:
1 j2 1 j2
j
e
j 127
y t A cos 2 t cos 2 t 127
1 10
g 10 t Sa 5 1 10 5
1 10 , A 10
Sa 5 t 2
g 10
对称性
u 5 u 5
g 10
5
3-8
已知 f t F ,求下列函数的傅里叶
2 j
F e
2 j
t ( 6 ) t 2 f 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)由 的波形可知, 为奇谐函数,即
则有
即 的傅里叶级数中只含有奇次谐波,包括正弦波和余弦波。
3.9如图的周期性方波电压作用于 电路,试求电流 的前五次谐波。
解:由 的波形图可知周期 ,则有
由此可得傅立叶级数的系数
因 为偶数,则
则电路激励 的前五次谐波为
解:(1)由 的波形可得其闭合表达式为
由此可得
又有
可得
则有
当 时上式值为0,则有
由 的波形可得其闭合表达式为
由此可得
又有
可得
则有
当 时,上式为0,则有
3.17已知 ,试求下列函数的频谱:
解: 根据频域微分特性可知
则有
根据尺度变换特性可得
则可得
根据频域微分特性可得
则有
由傅立叶变换的线性性质可得
由时域微分特性可得
3.18求下列函数的傅立叶逆变换
解: 傅立叶逆变换为
由于1
由频移特性可得
则有
的傅立叶逆变换为
由于 1,得 ,则有
的傅立叶逆变换为
由于 ,则由时移特性可知
, ,
则 的傅立叶逆变换为
3.19用傅里叶变换性质,求如图所示函数的傅里叶逆变换。
(a) 的幅频图和相频图可得
由 ,将 代入,得
由傅里叶变换对称性可得
信号与系统习题答案 第三章
第三章习题
基础题
3.1证明 , ,…, (n为正整数),在区间 的正交集。它是否是完备集
解: (积分???)此含数集在 为正交集。又有 不属于此含数集 ,对于所有的m和n。由完备正交函数定义所以此函数集不完备。
3.2上题的含数集在 是否为正交集?
解:
由此可知此含数集在区间 内是正交的。
则由傅立叶变换的性质可知, 的傅立叶变换为
(d)令 ,由前题可知其傅立叶变换为
由 的波形可知
由傅立叶变换的性质可知,
(e)由 的波形图可知
则 的傅立叶变换为
(f)由 的波形图可知
则 的傅立叶变换为
3.12若 为虚函数,且 ,试证
解:令 , 为t的实函数,则有
式中频谱函数的实部和虚部为
则有
即
由上面结果可知
3.3实周期信号 在区间 内的能量定义为 。如有和信号 若 与 在区间 内相互正交,证明和信号的总能量等于各信号的能量之和;
若 与 不是相互正交的,求和信号的总能量。
解: 和信号f(t)的能量为
(少乘以2)
由 与 在区间内正交可得
则有
即此时和信号的总能量等于各信号的能量之和。
和信号的能量为
(少乘以2吧?)
(2)由 的波形求得 的波形
则奇分量的波形为 = 偶分量的波形为 =
3.8利用奇偶性判断图示各周期信号的傅里叶级数中所含有的频率分量。
解:
(1)由 的波形可知
= =
则有
则 的傅里叶级数中含有的频率分量为奇次余弦波。
(2)由 的波形可知
则有
则 的傅里叶级数中含有的频率分量为正弦波。
(3)由 的波形可知 则有
整理得
由时移特性可得
则 的傅里叶逆变换为
(b)由 的幅频图和相频图可得
由 ,将 代入,得
由傅里叶变换对称性可得
整理得
由频移特性得
又由于
则 的傅里叶逆变换为
3.20试用下列方法求图示信号的频谱函数
利用延时和线性性质(门函数的频谱可利用已知结果);
利用时域积分定理;
由电路得系统微分方程为
欲求电流 的前五次谐波,即求此微分方程激励的前五次谐波的特解。
设
代入上面微分方程比较两边系数可得
则电流 的前五次谐波为
3.10求图示各信号的傅立叶变换。
解:(a)由 的波形可知
则 的傅立叶变换为
(b)由 的波形可知
则 的傅立叶变换为
(c)由 的波形可知
则 的傅立叶变换为
(d)由 的波形可知
利用以上结果求图(d)的信号 的傅里叶级数;
解:
由 的波形可知
令 ,则有
则 的傅里叶级数为
由 和 的波形图可知
或
则 的傅里叶数为
由 的波形可知
则 的傅里叶级数为
有 的波形可知
则 的傅里叶级数为
3.7试画出图示信号的奇分量和偶分量
解:
(1)由 的波形求得 的波形
则奇分量的波形为 = 偶分量的波形为 =
3.13若 为复函数,可表示为
且 的频谱函数为 。式中 、 均为实函数,证明:
解:
而 ,则有
由 , ,可知
由 ,利用傅立叶变换的线性性质可得
3.14据傅立叶变换对称性求下列函数的傅立叶变换
解: 由于宽度为 ,幅度为1的门函数 的频谱函数为 ,即
取 幅度为 ,根据傅立叶变换的线性性质有
即
注意到 是偶函数,根据对称性可得
根据时移性和尺度变换可知
由 ,可知
由于
可知
即 的傅立叶变换为
由于
根据对称性可知
根据频域卷积性质,可得
又有
3.15求下列信号的傅立叶变换
解: 已知
由时移性质可得
再由频移性质可得 的傅立叶变换
又 由时移特性可知 的傅立叶变换为
又
则有
由
利用时移特性可得
再由尺度变换特性可得
即 的傅立叶变换为
3.16试用时域微积分性质,求图示信号的频谱。
则 的傅立叶变换为
3.11根据上题(a)(b)的结果,利用傅立叶变换的性质,求下图所示各信号的傅立叶变换。
解:(a)令 ,由上题可知其傅立叶变换为
由 的波形可知
由傅立叶变换的性质可知 的傅立叶变换为
(b)令 ,由上题可知其傅立叶变换为
由 的波形可知
则由傅立叶变换的性质可知, 的傅立叶变换为
(c)由 的波形可知
解: 周期 ,则有
(k是整数;怎么求的边界条件?)
由此可得
(X?)
周期T=2, ,则有
由此可得: (积分?
3.6如图所示是4个周期相同的信号
用直接求傅里叶系数的方法求图(a)所示信号的傅里叶级数(三角形式);
将图(a)的函数 左(或右)移,就得图(b)的函数 ,利用 的结果求 的傅里叶级数;
利用以上结果求图(c)的函数 的傅里叶级数;
由 与 在区间 内不正交可得
则有
即此时和信号的总能量不等于各信号的能量之和。
3.4求下列周期信号的基波角频率 和周期T。
(1) (2)
(3) (4)
(5) (6)
解: 角频率为 = ,周期
角频率为 ,周期
角频率为 ,周期 (先求T,后求omg吧?)
角频率为 ,周期
角频率为 ,周期
角频率为 ,周期
3.5用直接计算傅里叶系数的方法,求图示周期函数的傅里叶系数(三角形式或指数形式)。
又由频域微分特性可得
则有
由反转特性可得
又由时移特性可得
即
由频域微分特性可得
由反转特性可得
又由时移性质可得到
即
由时移性质可得
又由尺度变换特性可得
由尺度变换特性可得
又由时移性质可得
则有
当 时,上式为 ,又有
则利用时域积分性质可得
由尺度变换特性可得
由时移特性可得
又由频移特性可得
由时域微分特性可得
又有
则由时域卷积定理可得
