(完整版)控制系统的极点配置设计法
rst结构控制器极点配置方法

一、简介在控制系统设计中,rst结构控制器是一种常用的控制器结构,其极点配置是控制系统设计中重要的一环。
极点配置方法可以有效地影响控制系统的性能指标,如稳定性、快速响应性等。
本文将介绍rst结构控制器的极点配置方法,帮助读者更好地理解和应用该方法。
二、rst结构控制器的基本原理1. rst结构控制器概述rst结构控制器是由一个比例环节、一个复式滤波器和一个时延环节组成的控制器结构。
其闭环传递函数可以表示为:G(s) = K * (1 + Ts) / (1 + Ts + Td*s)其中,K为比例增益,T为复式滤波器的时间常数,Td为时延环节的时间常数。
rst结构控制器既可以用于离散系统,也可以用于连续系统。
2. rst结构控制器的特点- rst结构控制器可以在保证系统稳定性的前提下,实现对系统性能的灵活调节。
- 通过合理配置比例环节、复式滤波器和时延环节的参数,可以使系统在满足动态响应指标的前提下,获得较好的抗干扰性能和鲁棒性能。
三、rst结构控制器极点配置方法1. 极点配置的基本原理极点配置方法是一种通过选取控制系统闭环传递函数的极点来调节系统的性能指标的方法。
rst结构控制器的极点配置方法主要包括两种:位置型极点配置和动态可调型极点配置。
2. 位置型极点配置方法- 位置型极点配置方法是指通过直接选取所需的闭环极点位置来调节系统的性能指标。
这种方法需要事先确定所需的阶跃响应特性,并根据特性要求来确定控制系统的极点位置,然后通过计算得到对应的rst结构控制器参数。
- 位置型极点配置方法适用于要求系统快速响应和较好抗干扰性能的场合,但对稳定性的要求不是很高。
3. 动态可调型极点配置方法- 动态可调型极点配置方法是指在闭环极点位置一定的情况下,通过调节rst结构控制器的参数来实现对系统性能指标的调节。
这种方法通常需要通过迭代计算或数值优化方法来确定合适的参数值。
- 动态可调型极点配置方法适用于对系统性能指标要求较为严格的场合,需要兼顾稳定性、快速响应性、抗干扰性等多个方面。
实验八控制系统极点的任意配置综合性设计性实验

实验八控制系统极点的任意配置(综合性设计性实验)
一、实验目的
1. 掌握用全状态反馈的设计方法实现控制系统极点的任意配置;
2. 用电路模拟的方法,研究参数的变化对系统性能的影响。
二、实验设备
同实验一。
三、实验内容
1. 用全状态反馈实现二阶系统极点的任意配置,并用电路模拟的方法予以实现;
2. 用全状态反馈实现三阶系统极点的任意配置,并通过电路模拟的方法予以实现。
四、实验原理(略)
五、实验步骤
请自行提出实验步骤,选择实验台上的通用电路单元设计并组建相应的模拟电路。
(K 值可参考取5,12,20等)。
完成实验报告,结合实验提出相应思考题。
控制系统的极点配置设计法
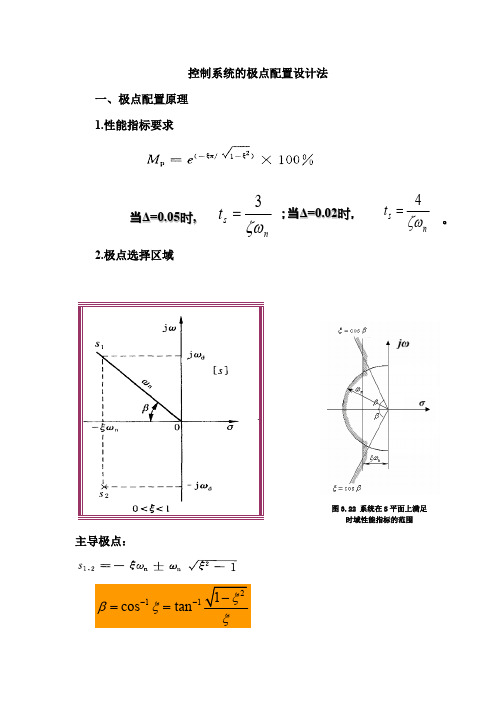
控制系统的极点配置设计法一、极点配置原理1.性能指标要求n s t ζω4=;当Δ=0.02时,。
ns t ζω3= 当Δ=0.05时,2.极点选择区域主导极点:2111cos tan ξβξξ---==3.其它极点配置原则系统传递函数极点在s 平面上的分布如图(a )所示。
极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍,即(此处,对应于极点s 1、s 2);同时,极点n s s ξω5Re 5Re 13=≥ξn ωs 1、s 2的附近不存在系统的零点。
由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω式中是极点s 1、s 2所对应过渡过程的调整时间。
1s tn x o (t)(a )(b系统极点的位置与阶跃响应的关系图(b )表示图(a )所示的单位阶跃响应函数的分量。
由图可知,由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用,即主导极点。
因为它衰减得最慢。
其它远离虚轴的极点s 3、s 4、s 5所对应的单位阶跃响应衰减较快,它们仅在极短时间内产生一定的影响。
因此,对系统过渡过程进行近似分析时。
可以忽略这些分量对系统过渡过程的影响。
二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。
主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。
设电磁铁绕组上的电流为I0,它对转子产生的吸力F和转子的重力mg相平衡,转子处于悬浮的平衡位置,这个位置称为参考位置。
(a)(b)图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上,转子受到一个向下的扰动,转子就会偏离其参考位置向下运动,此时传感器检测出转子偏离其参考位置的位移,控制器将这一位移信号变换成控制信号,功率放大器又将该控制信号变换成控制电流I0+i,控制电流由I0增加到I0+i,因此,电磁铁的吸力变大了,从而驱动转子返回到原来的平衡位置。
5第五节极点配置

K = [− 9.4 − 79.1 − 170.8]
以上述状态阵K反馈后的状态方程为:
1 0 0 0 ɺ X = ( A + B K ) X + Bv = 0 0 1 X + 0 v − 172.8 − 82.1 − 14.4 1 y 输出方程为: = x1 = [1 0 0]X
Saturday, June 25,1]一个三阶系统的微分方程为:ɺ(t ) + 5 ɺɺ(t ) + 3 y (t ) + 2 y (t ) = u (t ) y 希望该系统有小的超调量,调整时间小于1秒。试确定状态反馈 阵K,以满足上述要求。
选择希望的特征方程为: * (λ ) = (λ2 + 2ζλ + ω n 2 )(λ + ζω n ) = 0 f 因为要求小的超调量,所以可以取ζ = 0.8,那么调整时间为:
Saturday, June 25, 2011
11
Saturday, June 25, 2011
9
u K 状态反馈阵K是: = [k1 k 2 k3 ] 。取控制量为: = K X ɺ 则:X = A X + B K X = ( A + B K ) X 1 0 0 0 1 其中:A + B K = 0 − 2 + k1 − 3 + k 2 − 5 + k3 特征方程为: f (λ ) = det[λI − ( A + B K )] = λ3 + (5 − k3 )λ2 + (3 − k 2 )λ + (2 − k1 )
u
B
图a
ɺ x
+
控制器极点配置方法

控制器极点配置方法如果已知系统的模型或传递函数,通过引入某种控制器,使得闭环系统的极点可以移动到指定的位置,从而使系统的动态性能得到改善。
这种方法称为极点配置法。
例6-12 有一控制系统如图6-38,其中,要求设计一个控制器,使系统稳定。
图6-38解:(1)校正前,闭环系统的极点:> 0因而控制系统不稳定。
(2)在控制对象前串联一个一阶惯性环节,c>0,则闭环系统极点:显然,当,时,系统可以稳定。
但此对参数c 的选择依赖于 a 、b 。
因而,可选择控制器,c 、d ,则有特征方程:当,时,系统稳定。
本例由于原开环系统不稳定,因而不能通过简单的零极点相消方式进行控制器的设计,其原因在于控制器的参数在具体实现中无法那么准确,从而可能导致校正后的系统仍不稳定。
例6-13 已知一单位反馈控制系统的开环传递函数:要求设计一串联校正装置Gc(s) ,使校正后系统的静态速度误差系统,闭环主导极点在处。
解:首先,通过校正前系统的根轨迹可以发现,如图6-39所示,其主导极点为:。
图6-39为使主导极点向左偏移,宜采用超前校正装置。
(2)令超前校正装置,可采用待定系数法确定相关参数:又其中、、、为待定系数。
进一步可得:即将代入式子可以得到:,,,。
进一步可得超前校正装置的传递函数:校正后系统的根轨迹如图6-39所示。
该校正装置与例6-7中由超前装置获取的校正装置结果基本相同,说明结果是正确的。
在matlab中,亦有相应的命令可进行极点配置,主要有三个算法可实现极点配置算法:Bass-Gura算法、Ackermann 算法和鲁棒极点配置算法。
这些算法均以状态空间进行表征,通过设定期望极点位置,获取状态反馈矩阵K。
下面通过示例介绍其中的一种算法。
例6-14 考虑给定的系统,其状态方程模型如下:,期望的闭环系统配置在,,,试设计其控制器。
解:可以使用下面的MATLAB语句来实现极点的配置:A=[0,1,0,0;0,0,-1,0;0,0,0,1;0,0,11,0]; B=[0;1;0;-1];eig(A)'ans =0 0 3.3166 -3.3166P=[-1;-2;-1+sqrt(-1);-1-sqrt(-1)];K=place(A,B,P)place: ndigits= 15Warning: Pole locations are more than 10% in error.K =-0.4000 -1.0000 -21.4000 -6.0000eig(A-B*K)'ans =-1.0000 - 1.0000i -1.0000 + 1.0000i -2.0000 -1.0000。
极点配置法设计状态反馈控制器——自动控制原理理论篇

设计算法--适用于用能控标准形表示的SI系统的算法
a0 f1 0 a1 f 2 1
an1 f n n1
f1 0 a0 f2 1 a1
fn n1 an1
举例
例8-21 设系统的状态空间描述为
x(t)
0 6
1 0 5x(t) 1u(t)
y(t) 2 1x(t)
试求:(1)求状态反馈矩阵F使闭环系统有期望 极点s1,2=-3±2j; (2)绘制带有状态反馈控制器的状态变量图
举例----求解过程
解: 0
B 1
0 1 0 1 AB 6 51 5
rankS
rankB
AB
0 1
1 5
2
系统能控。
举例----求解过程
期望闭环系统特征多项式为:
(s s1)(s s2 ) (s 3 2 j)(s 3 2 j) s2 6s 13
设: F f1 f2
s sI A BF
6 f1
SI系统,所以设 F f1 f2 fn
| sI A BF |
0 1
0 0
s 0
0
s
s
0
a0
0 a1
1
0
1
0
f1
f
2
f
n
an1 1
极点配置法设计状态反馈控制器
——《自动控制原理-理论篇》第8.8节
极点配置设计与间接自校正控制方法

极点配置设计与间接自校正控制方法极点配置(Pole Placement )设计是控制系统中一种常用的设计方法,它能适应逆不稳(Inverse instability )系统和开环不稳定的情况,并且有设计方法直观、动态性能好、系统稳定的特点。
设已知被控对象或过程可用下列方程描述:()()()11()()d k k k A z y z B z u v ---=+ (3-1)式中,y(k)、u(k)、v(k)分别为系统的输出、控制和干扰,d 为纯延时。
111112012()1()aa bb n n n n A z a z a z B z b b z b z b z -------=+++=++++我们打算设计的控制器是()()()111()()()k r k k F z u R z y G z y ---=- (3-2)其中1()F z -、1()R z -、1()G z -为待定多项式,()r k y 为参考输入。
于是,极点配置系统控制的方框图如下图3-2所示:图3-2 极点配置系统控制方框图该系统的输出表达式为(r k y )()k v()()()11111111111()()()()()()()()()()()d k r k d k d z B z R z y y A z F z z B z G z F z v A z F z z B z G z --------------=+++闭环特征多项式为11111()()()()()d c A z F z z B z G z A z ------+= (3-3) 极点配置的设计任务就是要根据系统的固有性质和设计要求决定期望的闭环特征多项式1()c A z -,通过式(3-3)确定出1()F z -和1()G z -来加以实现。
该式称为Diophantine 方程式。
设期望的输入输出表达式为(不考虑干扰)()()11()()d m m m k r k A z y z B z y ---=式中,1()m A z -为期望的传递函数分母多项式;1()m B z -为期望的传递函数分子多项式,并且两多项式互质。
连续时间系统极点配置设计

连续时间系统极点配置设计连续时间系统极点配置设计是一种重要的控制系统设计方法,通过调整系统的极点位置来实现对系统动态响应的控制。
在控制系统设计中,合理配置系统的极点可以有效地改善系统的稳定性、快速性和精确性等性能指标。
一、连续时间系统极点配置设计概述连续时间系统极点配置设计是指根据控制要求和系统特性,通过选择合适的控制器参数或调整反馈环节来改变系统的极点位置。
根据所需的动态响应特性,可以将极点配置为稳定、快速或者抑制干扰等不同目标。
二、连续时间系统极点配置设计方法1. 极点分布法:该方法根据所需的动态响应特性,将所有极点分布在复平面上合适的位置。
常见的分布方式有根轨迹法、频率域法等。
通过选择不同的分布方式和调整参数,可以实现不同目标下的极点配置。
2. 极点追踪法:该方法通过观察被控对象输出信号与期望信号之间的差异,并根据差异调整控制器参数,使得被控对象输出信号能够尽可能地接近期望信号。
通过迭代调整控制器参数,最终实现期望的极点配置。
3. 极点映射法:该方法通过将所需的极点位置映射到单位圆上,并根据映射关系选择合适的控制器参数。
通过调整参数,可以实现所需的极点配置。
三、连续时间系统极点配置设计步骤1. 确定系统要求:根据控制对象和控制要求,明确系统的性能指标和动态响应特性要求。
2. 分析系统特性:对被控对象进行建模和分析,得到系统的传递函数或状态空间模型。
3. 选择设计方法:根据系统特性和要求,选择合适的极点配置设计方法。
4. 进行极点配置设计:根据选定的设计方法,进行具体的极点配置设计。
可以借助计算机辅助工具进行仿真与优化。
5. 调试与验证:将设计好的控制器应用于实际系统中,并进行调试与验证。
根据实际效果对设计进行修正和优化。
四、连续时间系统极点配置设计案例假设有一个二阶惯性环节控制系统,传递函数为G(s) = K / (s^2 + 2ξω_ns + ω_n^2),其中K为增益,ξ为阻尼比,ω_n为自然频率。
自控原理实验极点配置

实验3 控制系统极点的任意配置一、实验目的1. 掌握用全状态反馈的设计方法实现控制系统极点的任意配置2. 用电路模拟的方法,研究参数的变化对系统性能的影响二、实验设备1.THSSC-4型信号与系统·控制理论·计算机控制技术实验箱2.PC机一台(含上位机软件)、USB数据采集卡、37针通信线1根、16芯数据排线、USB接口线三、实验内容1. 用全状态反馈实现二阶系统极点的任意配置,并用电路模拟的方法予以实现2. 用全状态反馈实现三阶系统极点的任意配置,并通过电路模拟的方法予以实现四、实验原理由于控制系统的动态性能主要取决于它的闭环极点在S平面上的位置,因而人们常把对系统动态性能的要求转化为一组希望的闭环极点。
一个单输入单输出的N阶系统,如果仅靠系统的输出量进行反馈,显然不能使系统的n个极点位于所希望的位置。
基于一个N阶系统有N个状态变量,如果把它们作为系统的反馈信号,则在满足一定的条件下就能实现对系统极点任意配置,这个条件就是系统能控。
理论证明,通过状态反馈的系统,其动态性能一定会优于只有输出反馈的系统。
设系统受控系统的动态方程为=Axbux+y=cx图3-1为其状态变量图。
图3-1 状态变量图令Kx r u -=,其中]...[21n k k k K =,r 为系统的给定量,x 为1⨯n 系统状态变量,u 为1×1控制量。
则引入状态反馈后系统的状态方程变为bu x bK A x+-=)( 相应的特征多项式为)](det[bK A SI --,调节状态反馈阵K 的元素]...[21n k k k ,就能实现闭环系统极点的任意配置。
图3-2为引入状态反馈后系统的方框图。
图3-2 引入状态变量后系统的方框图1. 典型二阶系统全状态反馈的极点配置二阶系统方框图如3-3所示。
图3-3 二阶系统的方框图1.1 由图得)15.0(10)(+=S S S G ,然后求得:223.0=ξ,%48≈p δ同时由框图可得:2115.01)(X S X R =+- ,2110X X = 所以:R X X X 222212+--= R X X ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=2022100[]X X y 011==1.2 系统能控性[]242200=⎥⎦⎤⎢⎣⎡-=rank Ab b rank 所以系统完全能控,即能实现极点任意配置。
第4章 极点配置设计

Φn1Γ a1Φn2 Γ an-1Γ ) (4.15)
极点配置设计问题容易得到显式解。值得注意的是能 达性是解决此问题的充要条件。
实际中为了应用极点配置设计方法,就必须了解闭环 系统极点和采样周期这类设计参数是怎样影响闭环系 统的特性的。
在以前针对开环系统的采样周期的选择的讨论中。 建议可以这样选择采样周期:
(4.24)
y(k) CΦn1x(k-n 1) CΦn2u(k-n 1)
引入向量Uk-1和Yk:
0
Uk 1
u(k
n
1)
u(k 1)
CΓu(k 1)
y(k n 1)
Yk
y(k
n 2)
y(k)
典型的例子是阶跃,斜坡和正弦信号。
过程的不确定性
用状态空间描述可以处理矩阵A和B中各元素的不确定性, 但是状态空间描述不便于处理其他形式的未建模动力学特 性。因此,当建立更合适的工具之后,我们再来讨论过程 的不确定性。
性能准则
调节问题 受扰之后,其性能准则是力图使状态归零。 在极点配置表达中,这种状态衰减速率是通过规定闭
过程模型:假设可以用模型为:
dx Ax(t) Bu(t)
(4.1)
dt
其中,u表示控制变量,x表示状态向量。A和B是定常矩阵。
系统(4.1)采用零阶保持采样后,得离散时间系统为:
x(k 1) Φx(k) Γu(k)
(4.2)
注意: ① 信号的自变量不是实际时间,而是采样间隔数 。
u(k) Lx(k) (4.3)
4 举例
例4.1 双重积分器对象的极点配置
控制系统的极点配置设计法
3其它极点配置原则
系统传递函数极点在s平面上的分布如图(a)所示。极点S3距
虚轴距离不小于共轭复数极点Si、S2距虚轴距离的5倍,即
Res^| 5Resi5n(此处,n对应于极点Si、S2);同时,极点Si、
S2的附近不存在系统的零点。由以上条件可算出与极点S3所对应的过
渡过程分量的调整时间为
°N2A I
式中,o为真空磁导率,N为线圈匝数,A为铁心与气隙的横截面面 积,I为电流,x为气隙大小.
设转子处于平衡位置时的气隙为go,当转子离开平衡位置向电磁 铁方向产生偏移量x,则通过减小流进绕组的电流i来调节使转子回 复到平衡位置,把电流表示成I 10i。在转子位移变化很小(xvvg。) 时,将其线性化得
FxKxx Kii(2)
3222
式中,Kx0A'1。为位移刚度系数;KiOAN2I0为电流刚度系数。
2g°2g°
其拉普拉斯变换为:
Fx(s) KxX(s) Kil(s)
2.电磁绕组端电压方程
由于常导电磁轴承的转子位移变化时,其自感系数也要变化,即
常导电磁轴承的线圈的电感系数是转子位移x的函数,因此其端电压
、极点配置原理
控制系统的极点配置设计法
1•性能指标要求
Mp=占七x100%
当2 0.05时,ts
;当A=0.02时,tsFra bibliotek2.极点选择区域
K
_!VX
L
—gs0
J
1
1
1
1
1
J”
MM,
^2
0<f< L
* Jwd
主导极点:
s=coa
= lasjd
图3.22系统在S平面上满足
网络控制系统的增广状态极点配置设计法

网络控制系统的增广状态极点配置设计法网络控制系统的增广状态极点配置设计方法是一种针对网络控制系统稳定性和性能优化的设计方法。
该方法通过优化极点的位置来改变系统的特性,从而实现系统的稳定性和响应性能的优化。
这种方法可以用于解决一般的网络控制系统设计中遇到的性能问题,如抖动、不稳定等。
在网络控制系统中,增广状态极点通常是指将控制器引入系统后,系统的特征方程中新增的极点。
这些极点可以通过调整控制器参数来改变,从而实现对系统的优化。
增广状态极点配置设计方法的目标是将新增的极点配置到合适的位置,使得系统的稳定性和响应性能达到最佳状态。
增广状态极点配置设计方法通常分为两个步骤:极点配置和参数优化。
首先,进行极点配置。
极点配置的目标是将控制器引入系统后的增广状态极点配置到合适的位置。
一般来说,对于网络控制系统,我们希望系统的极点分布在左半平面,这样系统就能保持稳定。
同时,我们还可以根据系统的响应速度要求,将极点配置在合适的位置,从而获得更好的响应性能。
常用的极点配置方法有根轨迹法、随机法、模拟退火法等。
其次,进行参数优化。
参数优化的目标是确定控制器的参数,使得系统的增广状态极点配置到合适的位置。
参数优化可以使用各种优化算法,如遗传算法、粒子群算法、模拟退火算法等。
通过优化算法最优参数,使得控制器的增广状态极点配置到合适的位置,并且使得系统的指标函数最小化。
在进行增广状态极点配置设计时,需要考虑一些因素。
首先是系统的稳定性,即极点的位置应该在左半平面,以保持系统的稳定。
其次是系统的性能要求,即我们希望系统的响应速度和稳态误差达到一定的要求。
另外,还需要考虑控制器的结构和计算复杂度,以及系统的可行性和可实现性。
总结起来,增广状态极点配置设计方法是一种针对网络控制系统稳定性和性能优化的设计方法。
通过优化控制器的参数和极点位置,可以实现系统的稳定性和响应性能的优化。
该方法可以应用于一般的网络控制系统设计中,提供一种解决性能问题的有效方法。
极点配置控制器的设计法则(97)980707

報告人:郭洲成 日 期:1998/7/7
報告內容:
第一部份
極點配置控制器的介紹
V
強健性的設計:
觀念:系統對任何的步階干擾輸入的響應都能
消為零,則系統有抗步階干擾的能力。 lim y p t 0 設計 A 0 0
t
Ps Y p s
H s
Y p s H s Ps
N s As a D p s X s s
T
-1
k k
simplify
k 1 k K k 1 y k 1 - x T k 1 k
How to choose the initial values
Take the first k data points and solve k and p k directly Set 0 arbitrarily and p0 I where
How to choose
X s
依據系統抗干擾能力及 系統的強健性來做判斷
自由參數的選擇:
• 我們必頇知道: X s 的選擇(1)並不影響系統的輸出
(2)也不影響系統驅動信號的大小
P
+
Vref
Ls
+
A -1s
+
Cout
Gs
V
第五章 计算机实时控制系统的设计4(极点配置)

于是,闭环系统特征方程式经过P阵变换后, 能够写成
| P 1 | | zI G HK || P | | zI P 1GP P 1 HKP | ˆ ˆ~ | zI G HK |
将方程式(5.87),(5.89)和(5.90)代入上式,
得
ˆ ˆ~ | zI G HK | I q 0 G11 G12 H11 z 0 0 [ K11 K 12 ] G22 0 I n q z I q G11 H11 K11 G12 H11 K12 0 z I n q G22
11 11 11
下面来导出充足条件。如果系统的状态是完全可控的,存 在着一个矩阵 K 能使 G-HK 的特征值有任意的期望值, 或配置闭环极点在任意期望的位置上。 假设的期望特征值为 , , … , ;系统的期望特征 2 n 1 方程式为
( z 1 )( z 2 ) ( z n ) z n 1 z n1 2 z n2 n1 z n 0
(5.256)
将(5.256)式的等号两边左乘W阵,得
1 0 0 0 a 3 0 1 0 a 2 W W 0 0 1 0 1 a1 a3 a 2 a1
(5.257)
(5.257)式左边为
0 0 a3 a 2 a1 1 a3 0 0 1 0 a 2 a1 1 0 0 a1 1 0 1 a1 1 0 0 0 1 0
a1 1 1 0 0 0 0 0 n 2
an
则
ˆ ( MW )1G ( MW ) W 1 M 1GMW T GT G
极点配置

得出detQ = -1。因此,rankQ = 3。因而该系统是状态完全可控的, 可任意配置极点。 下面用两种方法求解。
方法1:利用刚才介绍的求解步骤,计算系统矩阵A的特征多 项式,求特征值。
s | sI A | 0 1 s 3 6s 2 1 s 5 5s 1 0 1 s 6
a1 1 a1
a2 2 a2
an n an
求解上述方程组,得到 i 的 值,则 K KP 1 [ n n 1 1 ]P 1
1 [ an an a n a a a a a ] P 1 n 1 2 2 1 1
可配置条件_极点配置定理
考虑线性定常系统 Ax Bu x 假设控制输入u的幅值是无约束的。如果选取控制规律为
u r Kx
式中K为线性状态反馈矩阵。
定理 (极点配置定理) 线性定常系统可通过线性状态反馈任 意地配置其全部极点的充要条件是,此被控系统状态完全 可控。 该定理对多变量系统也成立。 证明 (对单输入单输出系统) 1、充分性 2、必要性
上式为可控标准形。选取一组期望的特征值
为
u1 , u2 ,, un
,则期望的特征方程为
n * n1 1 * *
( s 1 )(s 2 )( s n ) s a s a n1s a n 0
设
x 由于 u r Kx r KPx r K,此时该系统的状态方程为
式中ai为特征多项式的系数: sI A s n a1s n1 an1s an
x Px 定义一个新的状态向量 如果可控性矩阵Q的秩为n(即系统是状态完全可控的), 则矩阵Q的逆存在,并且可将原线性系统 Ax Bu x Ac x Bcu 改写为 x
极点配置状态反馈控制器设计方法

极点配置状态反馈控制器设计方法
嘿,朋友们!今天咱来聊聊极点配置状态反馈控制器设计方法。
这玩意儿啊,就像是给一个系统装上了精准的导航仪,能让它乖乖地按照咱的想法走。
你看啊,一个系统就好比是一辆汽车,而极点配置状态反馈控制器就是那个掌握方向盘的司机。
咱得通过巧妙的设计,让这个司机能精准地操控汽车,该加速的时候加速,该转弯的时候转弯,不能有一点儿含糊。
设计这个控制器就像是搭积木,一块一块地拼凑起来。
咱得先了解系统的特性,就像了解汽车的性能一样。
然后呢,根据这些特性来选择合适的参数,这可不能马虎,得仔细琢磨。
比如说,要是参数没选好,那可就糟糕啦!就像司机开车老是开歪一样,系统也会变得不稳定,那可不行!咱得让系统稳稳当当的,该干啥干啥。
这其中的学问可大着呢!就好像做菜一样,各种调料得搭配得恰到好处,才能做出美味的菜肴。
极点配置状态反馈控制器的设计也是如此,每个环节都得精心处理。
而且哦,这个设计方法可不是一成不变的。
不同的系统就像不同口味的人,得用不同的方法去对待。
有时候得灵活一点,不能太死板啦。
想想看,如果所有系统都用一种方法去设计控制器,那多无趣啊!就像所有人都穿一样的衣服,那还有啥意思呢?咱得根据实际情况来调整,找到最适合的方案。
在实际应用中,这可真是帮了大忙啦!它能让那些复杂的系统乖乖听话,按照我们的要求运行。
这多厉害呀!难道不是吗?
所以啊,极点配置状态反馈控制器设计方法可真是个宝贝!咱可得好好研究,好好利用。
让它为我们的各种系统服务,让它们变得更智能、更高效。
怎么样,是不是觉得很有意思呢?别犹豫啦,赶紧去试试吧!。
控制系统极点的任意配置

检查能控性 0 2500 =2 50 −2500 所以系统完全能控,即具备极点任意配置的条件。 rank b Ab = rank λ I−A = 可知,原系统中 ζω n = 25 若要极点配置后系统的响应时间是原系统的5,且为临界阻尼则 ζω n = 125 ζ = 1,ω n = 125 希望的闭环特征多项式为: s 2 + 250s + 15625 引入状态反馈后系统的特征方程式为 s −50 sI − (A − bk) = 50 + 50k1 s + 50 + 50k 2 = s 2 + (50k 2 + 50)s + 2500k1 + 2500 = s2 + 250s + 15625 解得: k1 = 5.25,k 2 = 4 R1 = 3.81kΩ ,R 2 = 5kΩ 引入状态反馈后的方框图为
15625引入状态反馈后系统的特征方程式为si505050k250s156255k引入状态反馈后的方框图为系统框图可简化为62515625250s15625250015625625系统存在稳态误差需要在通过一个增益进行补偿可以通过反馈环路外的反相放大器来实现这样就不会改系统的性能
实验十六 控制系统极点的任意配置
实验步骤
1、 按照系统模拟电路图搭建原系统的模型 2、 运放电压为±15V,输入正负方波的幅值为 0.5V,频率为 1Hz,测量输入 和输出波形,观察输出对输入的跟踪情况,以及系统的阶跃响应。 3、 按照系统模拟电路图搭建控制器的模型,加入到原系统中。 4、 同样的输入下测量输出波形,并与校正前的系统比较,看是否满足题目 要求,是否与仿真结果相同。 5、 如果与仿真结果有差异,分析差异产生的原因,并作出调整。
一种设计控制系统的极点配置法

一种设计控制系统的极点配置法
陈伦铭
【期刊名称】《四川建材学院学报》
【年(卷),期】1990(005)001
【摘要】本文对线性系统极点配置问题进行了探索。
基于采用一个被定义的串接设计比例阵,即串接比例调节器,得出一种新的极点配置法。
运用这个方法,导出对系统任意配置极点的充分必要条件。
【总页数】8页(P27-34)
【作者】陈伦铭
【作者单位】无
【正文语种】中文
【中图分类】O231
【相关文献】
1.一类线性控制系统的快速极点配置法 [J], 胡金莲;熊金志
2.线性控制系统的推广极点配置法 [J], 胡金莲
3.基于极点配置法的香蕉索道防摇控制器设计 [J], 李伟;杨洲;李君;孙振刚
4.基于极点配置法的倒立摆系统控制器设计 [J], 李洁;李世煜
5.基于极点配置法的倒立摆系统控制器设计 [J], 李洁; 李世煜
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制系统的极点配置设计法一、极点配置原理1.性能指标要求2.极点选择区域主导极点:2111cos tanξβξξ---==图3.22 系统在S平面上满足时域性能指标的范围nstζω4=;当Δ=0.02时,。
nstζω3=当Δ=0.05时,3.其它极点配置原则系统传递函数极点在s 平面上的分布如图(a )所示。
极点s 3距虚轴距离不小于共轭复数极点s 1、s 2距虚轴距离的5倍,即n s s ξω5Re 5Re 13=≥(此处ξ,n ω对应于极点s 1、s 2);同时,极点s 1、s 2的附近不存在系统的零点。
由以上条件可算出与极点s 3所对应的过渡过程分量的调整时间为1351451s n s t t =⨯≤ξω 式中1s t 是极点s 1、s 2所对应过渡过程的调整时间。
图(b )表示图(a )所示的单位阶跃响应函数的分量。
由图可知,由共轭复数极点s 1、s 2确定的分量在该系统的单位阶跃响应函数中起主导作用,即主导极点。
因为它衰减得最慢。
其它远离虚轴的极点s 3、s 4、s 5 所对应的单位阶跃响应衰减较快,它们仅在极短时间内产生一定的影响。
因此,对系统过渡过程进行近似分析时。
可以忽略这些分量对系统过渡过程的影响。
n x o (t)(a )(b )系统极点的位置与阶跃响应的关系二、极点配置实例磁悬浮轴承控制系统设计1.1磁悬浮轴承系统工作原理图1是一个主动控制的磁悬浮轴承系统原理图。
主要由被悬浮转子、传感器、控制器和执行器(包括电磁铁和功率放大器)四大部分组成。
设电磁铁绕组上的电流为I0,它对转子产生的吸力F和转子的重力mg相平衡,转子处于悬浮的平衡位置,这个位置称为参考位置。
(a)(b)图1 磁悬浮轴承系统的工作原理Fig.1 The magnetic suspension bearing system principledrawing假设在参考位置上,转子受到一个向下的扰动,转子就会偏离其参考位置向下运动,此时传感器检测出转子偏离其参考位置的位移,控制器将这一位移信号变换成控制信号,功率放大器又将该控制信号变换成控制电流I0+i,控制电流由I0增加到I0+i,因此,电磁铁的吸力变大了,从而驱动转子返回到原来的平衡位置。
反之,当转子受到一个向上的扰动并向上运动,此时控制器使得功率放大器的输出电流由I0,减小到I0-i,电磁铁的吸力变小了,转子也能返回到原来的平衡位置。
因此,不论转子受到向上或向下的扰动,都能回到平衡状态。
这就是主动磁轴承系统的工作原理。
即传感器检测出转子偏移参考点的位移,作为控制器的微处理器将检测到的位移信号变换成控制信号,然后功率放大器将这一控制信号转换成控制电流,控制电流在执行磁铁中产生磁力从而使转子维持其悬浮位置不变。
悬浮系统的刚度、阻尼及稳定性主要是由控制规律决定。
实际的磁悬浮轴承系统中,在某个坐标方向上,通常是对称于转子布置两个结构及参数完全相同而作用相反的电磁铁,由这两个电磁铁共同作用产生磁悬浮力将转子悬浮在平衡位置,如图1(b )所示。
2.磁悬浮轴承的开环控制模型 2.1磁悬浮轴承的控制模型 1.磁悬浮力方程由图1(b )求磁悬浮轴承的单边子系统电磁铁对转子产生的磁悬浮力,可根据法拉第电磁力公式近似表示为2204x N A I F x μ⎛⎫=⎪⎝⎭(1)式中,0μ为真空磁导率,N 为线圈匝数,A 为铁心与气隙的横截面面积,I 为电流,x 为气隙大小.设转子处于平衡位置时的气隙为0g ,当转子离开平衡位置向电磁铁方向产生偏移量x ,则通过减小流进绕组的电流i 来调节使转子回复到平衡位置,把电流表示成0I I i =-。
在转子位移变化很小(x<<g o )时,将其线性化得x x i F K x K i =⋅+⋅ (2)式中,32200302x AN I K g μ=为位移刚度系数;20202o i AN I K g μ=为电流刚度系数。
其拉普拉斯变换为:()()()x x i F s K X s K I s =⋅+⋅ (3)2.电磁绕组端电压方程由于常导电磁轴承的转子位移变化时,其自感系数也要变化,即常导电磁轴承的线圈的电感系数是转子位移x 的函数,因此其端电压(或电流)也是转子位移x 的函数。
对于图2的转子上、下电磁铁绕组,由于x 为一微小量,故其自感系数分别近似为2200100022002000(1)2()2(1)2()2SN SN xL g x g g SN SN x L g x g g μμμμ⎧=≈+⎪-⎪⎨⎪=≈-⎪+⎩(4) 绕组端电压分别为0010000200()(1)22()(1)22L L i x di dxu t Ri g dt g dt L L i x di dx u t Ri g dt g dt⎧=+++⎪⎪⎨⎪=--+⎪⎩(5)式中,R 为各电磁铁绕组电阻,2000SN L g μ=为转子处于平衡位置时上下常导绕组的电感值。
由式(9)的第一式加上第二式可得整个串联线圈绕组的端电压为120()()()()2di t u t u t u t L Ri dt=+=+ (6) 其拉氏变换为:()0()2()U s L s R I s =+ (7)式中,2002o AN L g μ=为转子在平衡位置时绕组的电感。
3.转子运动方程根据牛顿第二定律得球形转子沿x 方向运动的运动方程为22x d d xF F m dt+= (8)式中,m 为球形转子的质量;d F 为电磁悬浮力以外的扰动作用。
将上式进行拉普拉斯变换得:)()()(2s F s F s X ms d x += (9)式(3)、式(7)以及式(9)即为描述通风机磁悬浮轴承系统动力学特性的数学模型。
不考虑干扰情况下,由它们得输入绕组电压信号到输出转子径向位移信号的开环系统传递函数为:()()20()()2i x K X s U s L s R ms K =+- (10) 由上式可知,开环系统存在S 复平面上的右极点,故系统不可能稳定。
要使其稳定,必须采用反馈控制对系统进行闭环控制。
3.磁悬浮轴承的闭环控制 1.系统控制策略及闭环传递函数 1)控制框图及闭环传递函数由(10)式可知,要使系统稳定,必须对系统进行综合校正。
本文采用PD 控制策略对系统进行串联校正,图2为PD 控制风机磁悬浮系统框图。
图2磁悬浮轴承系统的PID 控制系统框图()0320000()()()22id p i p x i d x X s s v s K T s K L mK K RK K T L K R s s s L L m L mΦ=⋅+=--+++(11)由上式得系统的特征方程为320000220i p x i d xK K RK K T L K R s s s L L m L m--+++= (12) 欲使系统满足稳定性要求,由特征方程解出来的特征根必须具有负实部。
2)使系统响应速度为最快的极点配置本设计对系统采用极点配置方法来确定有关控制参数。
为了提高系统的响应速度,并减小稳态误差,应尽可能使系统PD 控制器的系数p K 和d T 增大。
为了确定控制器的参数,可对系统配置3个位于根平面(S 复平面)左侧的闭环极点,并设其中2个极点相等即,12(0)s s r r ==->,3(0)s p p =->,于是系统的特征方程应表述为2()()0s r s p ++=3222(2)(2)0s r p s r pr s pr +++++= (13)对比式(14)与式(15)得020*******i d xi p x Rr p L K T L K r pr L m K K RK r pL m ⎧=+⎪⎪⎪-⎪=+⎨⎪⎪-⎪=⎪⎩(14) 由上式可知,要改善系统的快速响应速度、提高控制精度以及加强系统的稳定性,必须使第2式~第3式中的系数p K 和d T 的值尽可能大。
解式(14)得020002300243222x di x piR p r L R r r L m L K L T K R r r L m RK L K K ⎧⎛⎫=-⎪ ⎪⎝⎭⎪⎪⎛⎫⎪-+ ⎪⎪⎝⎭=⎨⎪⎪⎛⎫⎪-+ ⎪⎪⎝⎭=⎪⎩(15) 为使p K 和d T 为最大值,应满足00200460460d i p i R r L m L dT drK R r r L m dK L drK ⎧⎛⎫-⎪ ⎪⎝⎭⎪==⎪⎪⎨⎛⎫⎪- ⎪⎪⎝⎭⎪==⎪⎩ (16) 求解上式得023Rr L =,将其代入式()并把系统所有相应的结构参数代入得各控制参数为15.72531013212.640172510003.49978d pr p T K ⎧==⎪=⎨⎪=⎩ 于是系统的闭环传递函数为()321111.11212.640172510003.49978()47.1759304741.85613623888.639272s s s s s ⨯+Φ=+++ (17) 仿真结果 仿真程序:mun=1111.11*[0 0 212.6401725 10003.49978]; den=[1 47.1759304 741.86561362 3888.639272]; t=0:0.01:1;step(mun,den,t); 仿真结果图:00.10.20.30.40.50.60.70.80.910.20.40.60.811.21.4Step ResponseTime (sec)A m p l i t u d e2)使系统满足性能指标要求配置极点 性能指标为005e σ-=≤ (18)40.1s nt s ξω≈≤ (19)式中ξ,和ωn 为系统的阻尼比和无阻尼自然振荡角频率。
按照系统的性能指标要求,可取阻尼比ξ=1,则ωn =40,于是主导极点可配置为:1,240n s ξω=-±=± (20)另一极点取:s 3=-400。
则系统的期望闭环特征方程为2(40)(400)s s ++32480336006400000s s s =+++=(22)将上式与式(12)对比得02480RL = 0033600i d x K T L K L m -= 02640000i p x K K RK L m-= 则结构参数为()321111.11242.212502102322.8()48033600640000s s s s s ⨯+Φ=+++ (23)仿真程序:mun=1111.11/178*[0 0 242.212502 102322.8]; den=[1 480 33600 640000]; t=0:0.01:1; step(mun,den,t); 仿真图:00.10.20.30.40.50.60.70.80.910.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e。
