matlab实验7 无约束优化
数学实验——无约束优化
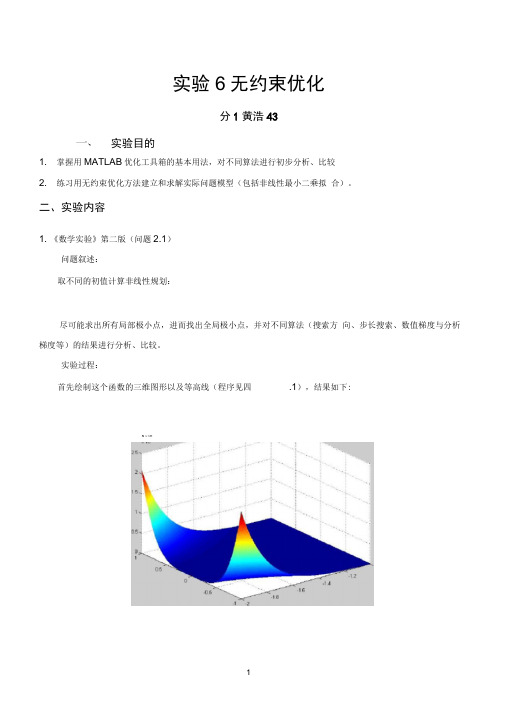
实验6无约束优化分1黄浩43实验目的1. 掌握用MATLAB优化工具箱的基本用法,对不同算法进行初步分析、比较2. 练习用无约束优化方法建立和求解实际问题模型(包括非线性最小二乘拟合)。
二、实验内容1. 《数学实验》第二版(问题2.1)问题叙述:取不同的初值计算非线性规划:尽可能求出所有局部极小点,进而找出全局极小点,并对不同算法(搜索方向、步长搜索、数值梯度与分析梯度等)的结果进行分析、比较。
实验过程:首先绘制这个函数的三维图形以及等高线(程序见四.1),结果如下:s M tn0-”19 A8 A1G \ 5 -14 -13 \ 2 A1通过观察这两幅图,可以得到,x2确定时,x1越负,函数值越大,x1确定时,x2绝对值越大,函数值越大。
但对于x1正向偏离0的情况,并没有很好的反映,于是扩大绘图范围,做出下图(程序见四.2):-1 -10由上面两幅图可见,方程像是一个四角被捏起的花布,而且z的最小值为0< 因此只要求解该方程的零点,即得到了方程的局部极小点,且若将原方程变形为:我们容易发现,该方程的零点为:x2=0或x1=0或x1=1或在求解零点之前,先针对一个零点,不妨用x1=1, x2=1,分析不同算法的优劣。
在matlab的无约束优化中,可以使用fminumc和fminsearch两种函数,搜索方向的算法有BFGS 公式、DFP公式和最速下降法三种(书中还提到的Gill-Murray 公式在matlab中已经不再使用),步长的一维搜索有混合二次三次多项式插值和三次多项式插值两种方法,另外,在求解函数梯度是也有数值方法和分析方法两种。
在对上述四类算法因素进行分析时,我们采用控制变量法,每次只保持一种或两种算法因素改变,分析它的精度及效率。
(一)分析fminumc与fminsearch两种方法的精度及效率选择初值为x1=0.8,x2=0.8,使用fminunc和fminsearch的默认算法及控制参数,输出结果如下(程序见四.3、四.4):因为精确解为x1=1, z=0,我们便可以比较出不同算法的精度。
第7章无约束优化问题

Matlab设计与优化
注意:
1.对于求解平方和的问题,fminunc函数 不是最好的选择,用lsqnonlin函数效果更 佳。
2.使用大型方法时,必须通过将options. GradObj设置为'on'来提供梯度信息,否 则将给出警告信息。
唯一极小 (全局极小)
f 0.298
f 0
f (x1 x2 ) 2x12 2x1x2 x22 3x1 x2
多局部极小
f 0.298
搜索过程 minMaft(laxb1 设x计2 )与优10化0 (x2 x12 )2 (1 x1)2
x1 x2 f
-1 1 4.00 -0.79 0.58 3.39 -0.53 0.23 2.60 -0.18 0.00 1.50 0.09 -0.03 0.98 0.37 0.11 0.47 0.59 0.33 0.20 0.80 0.63 0.05 0.95 0.90 0.003 0.99 0.99 1E-4 0.999 0.998 1E-5
第7章 无约束优化问题
最优化数学模型的不带约束条件形式;
优化问题一般指:寻找 x* (x1*, x2*, , xn* )T D
使 z f (x1*, x2*, , xn*)为目标函数f在可行域上的
最小值(或最大值).
称为最优解, x*
f (x1*, x2*, , xn* )
称为最优值.
Matlab设计与优化
Matlab设计与优化
关于fminbnd函数
算法: fminbnd是一个M文件。其算法基于黄金分割法和二次插值 法。 局限性: 1.目标函数必须是连续的。 2.fminbnd函数可能只给出局部最优解。 3.当问题的解位于区间边界上时,fminbnd函数的收敛速度 常常很慢。此时,fmincon函数的计算速度更快,计算精度 更高。 4.fminbnd函数只用于实数变量。 参见:
用MATLAB求解无约束优化问题-电子科技大学

-218.0000
注:有些实际问题可能会有一个约束条件:决策变量
只能取整数,如x1、x2取整数。这类问题实际上是整数线 性规划问题。如果把它当成一个线性规划来解,求得其最 优解刚好是整数时,故它就是该整数规划的最优解。若用 线性规划解法求得的最优解不是整数,将其取整后不一定 是相应整数规划的最优解,这样的整数规划应用专门的方 法求解(如割平面法、分支定界法)。
S.t.
0.4 0
1.1 0
1 0
0 0.5
0 1.2
10.3X 890000
x1
1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 400 0X 600 1 500
x2
,X
x3
最速下降法是一种最基本的算法,它在最优化方法中占有重要地位.最
速下降法的优点是工作量小,存储变量较少,初始点要求不高;缺点是收敛
慢,最速下降法适用于寻优过程的前期迭代或作为间插步骤,当接近极值
点时,宜选用别种收敛快的算法.
2.牛顿法算法步骤:
(1) 选定初始点 X 0 E n ,给定允许误差 0 ,令 k=0;
s.t. AX b
命令:x=linprog(c,A,b)
2、模型:min z=cX
s.t. AX b Aeq X beq
命令:x=linprog(c,A,b,Aeq,beq)
注意:若没有不等式:AX b 存在,则令A=[ ],b=[ ].
3、模型:min z=cX
s.t. AX b Aeq X beq
x1 0, x2 0
解: 编写M文件如下:
实验7 无约束优化

在第一幅图中,最大的函数值的数量级已到 107,说明画图范围取得过大,函数值为 0 的,点在该图中均呈现一平面, 故需要缩小自变量的范围再绘图。 修改程序 guancha1.m 如下。
[x,y]=meshgrid(-0.1:0.01:1.1,-0.1:0.01:1.1);%选定x,y范围均为[-0.1,1.1] z=((x.*y).^2).*((1-x).^2).*((1-x-y.*((1-x).^5)).^2); mesh(x,y,z);%画三维图像 title('图2.1 三维图像'); pause contour(x,y,z,200) %画等高线 title('图2.2 等高线 ')
2.2 matlab 求解 2.2.1 输出三维图像和等高线,直观观察最优解所在位置 首先,先让 MATLAB 输出的三维图像,直观地观察最优解的大致范围。程序 guancha.m 如下。
[x,y]=meshgrid(-2:0.01:2,-2:0.01:2);%选定x,y范围均为[-2,2] z=((x.*y).^2).*((1-x).^2).*((1-x-y.*((1-x).^5)).^2); mesh(x,y,z);%画三维图像 title('图2.1 三维图像'); pause contour(x,y,z,30) %画等高线 title('图2.2 等高线 ')
3.42E-08 3.41E-08 2.21E-05 3.42E-08 3.41E-08 2.21E-05
2.42E-17 2.40E-17 1.00E-11 2.42E-17 2.40E-17 1.00E-11
18 18 99 18 18 99
2.比较分析梯度与数值梯度对结果的影响 首先计算 f(x)的梯度
实验7 无约束优化

数学实验作业(第八周)郭明钊 2012011880 化21一、原子位置问题1、 问题分析:题目中给出了各个原子之间的距离关系,所要求的就是每个原子在平面直角坐标系之中的具体位置。
则可以假设第i 个原子的坐标为(,)i i x y ,且假设第一个原子的位置为坐标原点,即(0,0),则问题所求就转化为了使得2222[()()]i ji j ij ij x x y y d -+--∑达到最小值时的解。
这样问题就转化为了无约束优化:2222min [()()]i j i j ij ij x x y y d -+--∑,在这里,建立数组x ,其中有50个数,()i x i 为奇数为第i 个原子的横坐标,()i x i 为偶数为第i 个原子的纵坐标。
2、 使用matlab 中的lsqnonlin 函数实现:首先建立函数m 文件function y=distance(x,d)y(1)=(x(2*4-1))^2+(x(2*4))^2-d(1)^2;y(2)=(x(2*12-1))^2+(x(2*12))^2-d(2)^2;y(3)=(x(2*13-1))^2+(x(2*13))^2-d(3)^2;y(4)=(x(2*17-1))^2+(x(2*17))^2-d(4)^2;y(5)=(x(2*21-1))^2+(x(2*21))^2-d(5)^2;y(6)=(x(2*5-1)-x(2*2-1))^2+(x(2*5)-x(2*2))^2-d(6)^2;y(7)=(x(2*16-1)-x(2*2-1))^2+(x(2*16)-x(2*2))^2-d(7)^2;y(8)=(x(2*17-1)-x(2*2-1))^2+(x(2*17)-x(2*2))^2-d(8)^2;y(9)=(x(2*25-1)-x(2*2-1))^2+(x(2*25)-x(2*2))^2-d(9)^2;y(10)=(x(2*5-1)-x(2*3-1))^2+(x(2*5)-x(2*3))^2-d(10)^2;y(11)=(x(2*20-1)-x(2*3-1))^2+(x(2*20)-x(2*3))^2-d(11)^2;y(12)=(x(2*21-1)-x(2*3-1))^2+(x(2*21)-x(2*3))^2-d(12)^2;y(13)=(x(2*24-1)-x(2*3-1))^2+(x(2*24)-x(2*3))^2-d(13)^2;y(14)=(x(2*5-1)-x(2*4-1))^2+(x(2*5)-x(2*4))^2-d(14)^2;y(15)=(x(2*12-1)-x(2*4-1))^2+(x(2*12)-x(2*4))^2-d(15)^2;y(16)=(x(2*24-1)-x(2*4-1))^2+(x(2*24)-x(2*4))^2-d(16)^2;y(17)=(x(2*8-1)-x(2*6-1))^2+(x(2*8)-x(2*6))^2-d(17)^2;y(18)=(x(2*13-1)-x(2*6-1))^2+(x(2*13)-x(2*6))^2-d(18)^2;y(19)=(x(2*19-1)-x(2*6-1))^2+(x(2*19)-x(2*6))^2-d(19)^2;y(20)=(x(2*25-1)-x(2*6-1))^2+(x(2*25)-x(2*6))^2-d(20)^2;y(21)=(x(2*8-1)-x(2*7-1))^2+(x(2*8)-x(2*7))^2-d(21)^2;y(22)=(x(2*14-1)-x(2*7-1))^2+(x(2*14)-x(2*7))^2-d(22)^2;y(23)=(x(2*16-1)-x(2*7-1))^2+(x(2*16)-x(2*7))^2-d(23)^2;y(24)=(x(2*20-1)-x(2*7-1))^2+(x(2*20)-x(2*7))^2-d(24)^2;y(25)=(x(2*21-1)-x(2*7-1))^2+(x(2*21)-x(2*7))^2-d(25)^2;y(26)=(x(2*14-1)-x(2*8-1))^2+(x(2*14)-x(2*8))^2-d(26)^2;y(27)=(x(2*18-1)-x(2*8-1))^2+(x(2*18)-x(2*8))^2-d(27)^2;y(28)=(x(2*13-1)-x(2*9-1))^2+(x(2*13)-x(2*9))^2-d(28)^2;y(29)=(x(2*15-1)-x(2*9-1))^2+(x(2*15)-x(2*9))^2-d(29)^2;y(30)=(x(2*22-1)-x(2*9-1))^2+(x(2*22)-x(2*9))^2-d(30)^2;y(31)=(x(2*11-1)-x(2*10-1))^2+(x(2*11)-x(2*10))^2-d(31)^2;y(32)=(x(2*13-1)-x(2*10-1))^2+(x(2*13)-x(2*10))^2-d(32)^2;y(33)=(x(2*19-1)-x(2*10-1))^2+(x(2*19)-x(2*10))^2-d(33)^2;y(34)=(x(2*20-1)-x(2*10-1))^2+(x(2*20)-x(2*10))^2-d(34)^2;y(35)=(x(2*22-1)-x(2*10-1))^2+(x(2*22)-x(2*10))^2-d(35)^2;y(36)=(x(2*18-1)-x(2*11-1))^2+(x(2*18)-x(2*11))^2-d(36)^2;y(37)=(x(2*25-1)-x(2*11-1))^2+(x(2*25)-x(2*11))^2-d(37)^2;y(38)=(x(2*15-1)-x(2*12-1))^2+(x(2*15)-x(2*12))^2-d(38)^2;y(39)=(x(2*17-1)-x(2*12-1))^2+(x(2*17)-x(2*12))^2-d(39)^2;y(40)=(x(2*15-1)-x(2*13-1))^2+(x(2*15)-x(2*13))^2-d(40)^2;y(41)=(x(2*19-1)-x(2*13-1))^2+(x(2*19)-x(2*13))^2-d(41)^2;y(42)=(x(2*15-1)-x(2*14-1))^2+(x(2*15)-x(2*14))^2-d(42)^2;y(43)=(x(2*16-1)-x(2*14-1))^2+(x(2*16)-x(2*14))^2-d(43)^2;y(44)=(x(2*20-1)-x(2*16-1))^2+(x(2*20)-x(2*16))^2-d(44)^2;y(45)=(x(2*23-1)-x(2*16-1))^2+(x(2*23)-x(2*16))^2-d(45)^2;y(46)=(x(2*18-1)-x(2*17-1))^2+(x(2*18)-x(2*17))^2-d(46)^2;y(47)=(x(2*19-1)-x(2*17-1))^2+(x(2*19)-x(2*17))^2-d(47)^2;y(48)=(x(2*20-1)-x(2*19-1))^2+(x(2*20)-x(2*19))^2-d(48)^2;y(49)=(x(2*23-1)-x(2*19-1))^2+(x(2*23)-x(2*19))^2-d(49)^2;y(50)=(x(2*24-1)-x(2*19-1))^2+(x(2*24)-x(2*19))^2-d(50)^2;y(51)=(x(2*23-1)-x(2*21-1))^2+(x(2*23)-x(2*21))^2-d(51)^2;y(52)=(x(2*23-1)-x(2*22-1))^2+(x(2*23)-x(2*22))^2-d(52)^2;运行实现d=[0.9607 0.4399 0.8143 1.3765 1.2722 0.5294 0.6144 0.3766 0.6893 0.9488...0.8000 1.1090 1.1432 0.4758 1.3402 0.7006 0.4945 1.0559 0.6810 0.3587...0.3351 0.2878 1.3746 0.3870 0.7511 0.4439 0.8363 0.3208 0.1574 1.2736...0.5781 0.9254 0.6401 0.2467 0.4727 1.3840 0.4366 1.0307 1.3904 0.5725...0.7660 0.4394 1.0952 1.0422 1.8255 1.4325 1.0851 0.4995 1.2277 1.1271...0.7060 0.8052]';x0=[zeros(1,3),ones(1,47)]; %设初值[x,norms,res]=lsqnonlin(@distance,x0,[],[],[],d)a=reshape(x,2,25)'b=a(:,1)';c=a(:,2)';plot(b,c,'*') %在坐标系中显示出各个原子的位置3、结果如下:误差平方和:norms = 0.1625误差向量res =8.4224e-002 -5.6716e-002 5.4597e-0025.6860e-003 -1.1847e-001 5.8619e-0023.8879e-002 1.1819e-001 2.2805e-0023.8320e-002 -3.4772e-003 -3.9762e-0021.1452e-002 5.3897e-002 -4.3139e-0022.1071e-002 -4.4450e-002 9.6968e-003-5.6455e-002 4.0990e-002 2.7157e-0021.4843e-001 1.5864e-002 -3.7006e-003-1.3585e-001 2.6711e-002 -3.8390e-0039.0472e-003 2.9573e-002 -4.3175e-003-2.5224e-003 -4.7600e-004 1.2934e-002-2.4690e-002 7.6172e-003 2.5536e-003-5.2482e-003 7.3814e-002 -3.1225e-003-6.2153e-002 4.1666e-002 1.3685e-0016.4955e-002 2.3253e-003 -6.2132e-002-1.5985e-003 -5.7399e-002 -1.5199e-0021.3400e-002 -1.8521e-002 1.2003e-0013.1653e-003各个原子的坐标数值(第一列为横坐标,第二列为纵坐标)ans =0 00.2496 1.37301.6630 1.60100.7720 0.64120.7953 1.17011.2807 0.94921.4662 0.83651.2996 0.50230.3616 0.50871.1538 0.82271.1655 1.3985-0.3685 -0.03120.2287 0.81570.9857 0.85610.5856 0.44400.6025 1.9132-0.2599 1.35380.5372 0.16430.7983 1.36701.1261 1.01080.8162 0.91311.6189 0.70121.0248 0.15481.4666 0.46970.8870 1.0702 显示在坐标系中:当改变初值时x0=[zeros(1,2),ones(1,48)]; %设初值得norms =0.2298ans =0 00.7773 1.54251.2131 1.73990.8442 0.52390.6526 0.98631.4017 1.14390.7255 0.70991.0215 0.8220-0.0902 0.93201.2946 1.03960.7993 1.3167-0.4498 0.26080.4560 0.67820.6244 1.06130.1326 1.11251.2374 1.98050.5434 1.25021.2808 0.02161.3079 0.47031.0750 0.94510.2150 1.25031.0575 0.51940.1391 0.52860.3273 1.01521.0902 0.9464当换成其他初值时,答案也会明显不同。
Mtlab 无约束最优化问题

第16章 无约束最优化问题单变量最小化基本数学原理本节讨论只有一个变量时的最小化问题,即一维搜索问题。
该问题在某些情况下可以直接用于求解实际问题 ,但大多数情况下它是作为多变量最优化方法的基础,因为进行多变量最优化要用到一维搜索算法。
该问题的数学模型为:返回标量为函数为标量式中,)(,,,)(min 2121x f x x x x x x x f << 该问题的搜索过程可用下式表达:..,,,* 1次迭代的条件次迭代的信息来构造下用本所以一维搜索就是要利数为搜索方向上的步长参为搜索方向为本次迭代的值式中ααd x d x x k k k +=+ 求解单变量最优化问题的方法有很多种。
根据目标函数是否需要求导,可以分为两类,即直接法和间接法。
直接法不需要目标函数的导数,而间接法则需要用到目标函数的导数。
1. 直接法常用的一维直接法主要有消去法和近似法两种。
(1)消去法。
该法利用单峰函数具有的消去性质进行反复迭代,逐渐消去不包含极小 *点的区间,缩小搜索区间,直到搜索区间缩小到给定的允许精度为止。
一种典型的消去法为黄金分割搜索法(GoIden Section Search )。
黄金分割搜索法的基本思想是在单峰区间内适当插入两点,将区间分为3段,然后通过比较这两点函数值的大小来确定是删去最左段还是删去最右段,或是同时删去左、右两段保留中间段。
重复该过程使区间无限缩小。
插入点的位置放在区间的黄金分割点及其对称点上,所以该法称为黄金分割搜索法。
该法的优点是算法简单,效率较高,稳定性好。
(2)多项式近似法。
该法用于目标函数比较复杂的情况。
此时寻找一个与它近似的函 数来代替目标函数,并用近似函数的极小点作为原函数极小点的近似。
常用的近似函数为二次和三次多项式。
二次内插涉及到形如下式的二次函数数据拟合问题:c b a m q ++=ααα2)(其中步长极值为 .2*ab -=α 然后只要利用3个梯度或函数方程组就可以确定系数a 和b,从而可以确定*。
matlab实验7 无约束优化
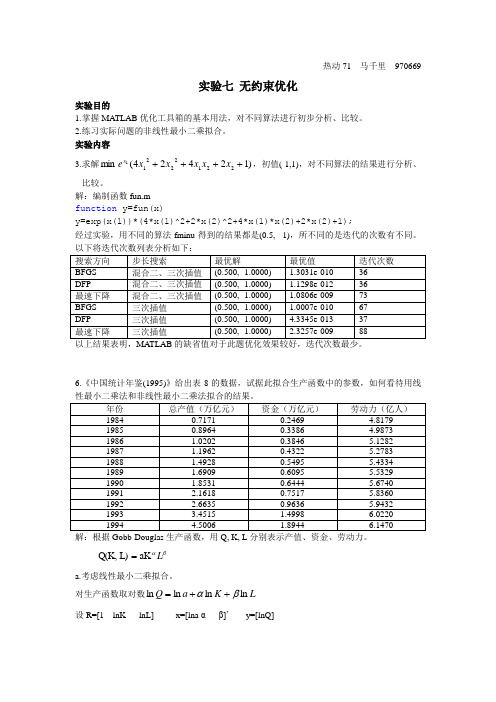
热动71 马千里 970669实验七 无约束优化实验目的1. 掌握MATLAB 优化工具箱的基本用法,对不同算法进行初步分析、比较。
2. 练习实际问题的非线性最小二乘拟合。
实验内容3. 求解)12424(min 22122211++++x x x x x e x ,初值(-1,1),对不同算法的结果进行分析、比较。
解:编制函数fun.mfunction y=fun(x)y=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);经过实验,用不同的算法fminu 得到的结果都是(0.5, -1),所不同的是迭代的次数有不同。
以上结果表明,MA TLAB 的缺省值对于此题优化效果较好,迭代次数最少。
6.《中国统计年鉴(1995)》给出表8的数据,试据此拟合生产函数中的参数,如何看待用线性最小二乘法和非线性最小二乘法拟合的结果。
解:根据Gobb-Douglas 生产函数,用Q, K, L 分别表示产值、资金、劳动力。
βαL aK L)Q(K,=a. 考虑线性最小二乘拟合。
对生产函数取对数L K a Q ln ln ln ln βα++=设R=[1 lnK lnL] x=[lna α β]’ y=[lnQ]R=1.0000 -1.3988 1.57231.0000 -1.0829 1.60691.0000 -0.9556 1.63481.0000 -0.8389 1.66361.0000 -0.5987 1.69261.0000 -0.4951 1.71071.0000 -0.4394 1.73591.0000 -0.2854 1.76401.0000 -0.0371 1.78221.0000 0.4053 1.7954 1.0000 0.6389 1.8160则Rx=y 代表一组超定方程组。
在MATLAB 下用x=R\y 得到最小二乘意义下的解 x=-3.23600.62082.3728即a=exp(-3.2360)=0.0393 α=0.6208 β=2.3728b.非线性模型function f=pp1(c)Q=[0.7171 0.8964 1.0202 1.1962 1.4928 1.6909 1.8531 2.1618 2.6635 3.45154.5006];K=[0.2469 0.3386 0.3846 0.4322 0.5495 0.6095 0.6444 0.7517 0.9636 1.49981.8944];L=[4.8179 4.9873 5.1282 5.2783 5.4334 5.5329 5.6740 5.8360 5.9432 6.02206.1470];f=Q-c(1)*k.^c(2).*L.^c(3);c0=[1 1 1]c=leastsq(‘pp1’, c0)y=sum(pp1(c).*pp1(c)) 计算误差平方和得到c= 0.0357 0.6300 2.4290y= 0.0394即a=0.0357 α=0.6300 β=2.4290再对线性模型计算误差平方和以做比较y=sum(pp1([0.0393 0.6208 2.3728]).* pp1([0.0393 0.6208 2.3728]))得到y=0.0441将以上结果列表如下是在不同意义下的最小二乘解。
无约束优化

数学实验七无约束优化化21 张冶5.某分子由25个原子组成,并且已经通过实验测量得到了其中某些原子对之间的距离(假设在平面结构上讨论),确定每个原子的位置关系。
解:由已知得,找到25个原子的相对坐标,使其满足题中所给数据,使其误差最小。
令第一个点的坐标为(0,0),其余点的坐标为(x i,y j), 则只需找出余下24个点的坐标使∑[(x i−x j)2+(y i−y j)2−d ij2]2i,j最小即可。
设x=[x2 y2 x3 y3 x4 y4 ······x12 y12······x24 y24]编写M文件如下:function y=yuanzi(x,d)y(1)=(x(2*4-3))^2+(x(2*4-2))^2-d(1)^2;y(2)=(x(2*12-3))^2+(x(2*12-2))^2-d(2)^2;y(3)=(x(2*13-3))^2+(x(2*13-2))^2-d(3)^2;y(4)=(x(2*17-3))^2+(x(2*17-2))^2-d(4)^2;y(5)=(x(2*21-3))^2+(x(2*21-2))^2-d(5)^2;y(6)=(x(2*5-3)-x(2*2-3))^2+(x(2*5-2)-x(2*2-2))^2-d(6)^2;y(7)=(x(2*16-3)-x(2*2-3))^2+(x(2*16-2)-x(2*2-2))^2-d(7)^2;y(8)=(x(2*17-3)-x(2*2-3))^2+(x(2*17-2)-x(2*2-2))^2-d(8)^2;y(9)=(x(2*25-3)-x(2*2-3))^2+(x(2*25-2)-x(2*2-2))^2-d(9)^2;y(10)=(x(2*5-3)-x(2*3-3))^2+(x(2*5-2)-x(2*3-2))^2-d(10)^2;y(11)=(x(2*20-3)-x(2*3-3))^2+(x(2*20-2)-x(2*3-2))^2-d(11)^2;y(12)=(x(2*21-3)-x(2*3-3))^2+(x(2*21-2)-x(2*3-2))^2-d(12)^2;y(13)=(x(2*24-3)-x(2*3-3))^2+(x(2*24-2)-x(2*3-2))^2-d(13)^2;y(14)=(x(2*5-3)-x(2*4-3))^2+(x(2*5-2)-x(2*4-2))^2-d(14)^2;y(15)=(x(2*12-3)-x(2*4-3))^2+(x(2*12-2)-x(2*4-2))^2-d(15)^2;y(16)=(x(2*24-3)-x(2*4-3))^2+(x(2*24-2)-x(2*4-2))^2-d(16)^2;y(17)=(x(2*8-3)-x(2*6-3))^2+(x(2*8-2)-x(2*6-2))^2-d(17)^2;y(18)=(x(2*13-3)-x(2*6-3))^2+(x(2*13-2)-x(2*6-2))^2-d(18)^2;y(19)=(x(2*19-3)-x(2*6-3))^2+(x(2*19-2)-x(2*6-2))^2-d(19)^2;y(20)=(x(2*25-3)-x(2*6-3))^2+(x(2*25-2)-x(2*6-2))^2-d(20)^2;y(21)=(x(2*8-3)-x(2*7-3))^2+(x(2*8-2)-x(2*7-2))^2-d(21)^2;y(22)=(x(2*14-3)-x(2*7-3))^2+(x(2*14-2)-x(2*7-2))^2-d(22)^2;y(23)=(x(2*16-3)-x(2*7-3))^2+(x(2*16-2)-x(2*7-2))^2-d(23)^2;y(24)=(x(2*20-3)-x(2*7-3))^2+(x(2*20-2)-x(2*7-2))^2-d(24)^2;y(25)=(x(2*21-3)-x(2*7-3))^2+(x(2*21-2)-x(2*7-2))^2-d(25)^2;y(26)=(x(2*14-3)-x(2*8-3))^2+(x(2*14-2)-x(2*8-2))^2-d(26)^2;y(27)=(x(2*18-3)-x(2*8-3))^2+(x(2*18-2)-x(2*8-2))^2-d(27)^2;y(28)=(x(2*13-3)-x(2*9-3))^2+(x(2*13-2)-x(2*9-2))^2-d(28)^2;y(29)=(x(2*15-3)-x(2*9-3))^2+(x(2*15-2)-x(2*9-2))^2-d(29)^2;y(30)=(x(2*22-3)-x(2*9-3))^2+(x(2*22-2)-x(2*9-2))^2-d(30)^2;y(31)=(x(2*11-3)-x(2*10-3))^2+(x(2*11-2)-x(2*10-2))^2-d(31)^2;y(32)=(x(2*13-3)-x(2*10-3))^2+(x(2*13-2)-x(2*10-2))^2-d(32)^2;y(33)=(x(2*19-3)-x(2*10-3))^2+(x(2*19-2)-x(2*10-2))^2-d(33)^2;y(34)=(x(2*20-3)-x(2*10-3))^2+(x(2*20-2)-x(2*10-2))^2-d(34)^2;y(35)=(x(2*22-3)-x(2*10-3))^2+(x(2*22-2)-x(2*10-2))^2-d(35)^2;y(36)=(x(2*18-3)-x(2*11-3))^2+(x(2*18-2)-x(2*11-2))^2-d(36)^2;y(37)=(x(2*25-3)-x(2*11-3))^2+(x(2*25-2)-x(2*11-2))^2-d(37)^2;y(38)=(x(2*15-3)-x(2*12-3))^2+(x(2*15-2)-x(2*12-2))^2-d(38)^2;y(39)=(x(2*17-3)-x(2*12-3))^2+(x(2*17-2)-x(2*12-2))^2-d(39)^2;y(40)=(x(2*15-3)-x(2*13-3))^2+(x(2*15-2)-x(2*13-2))^2-d(40)^2;y(41)=(x(2*19-3)-x(2*13-3))^2+(x(2*19-2)-x(2*13-2))^2-d(41)^2;y(42)=(x(2*15-3)-x(2*14-3))^2+(x(2*15-2)-x(2*14-2))^2-d(42)^2;y(43)=(x(2*16-3)-x(2*14-3))^2+(x(2*16-2)-x(2*14-2))^2-d(43)^2;y(44)=(x(2*20-3)-x(2*16-3))^2+(x(2*20-2)-x(2*16-2))^2-d(44)^2;y(45)=(x(2*23-3)-x(2*16-3))^2+(x(2*23-2)-x(2*16-2))^2-d(45)^2;y(46)=(x(2*18-3)-x(2*17-3))^2+(x(2*18-2)-x(2*17-2))^2-d(46)^2;y(47)=(x(2*19-3)-x(2*17-3))^2+(x(2*19-2)-x(2*17-2))^2-d(47)^2;y(48)=(x(2*20-3)-x(2*19-3))^2+(x(2*20-2)-x(2*19-2))^2-d(48)^2;y(49)=(x(2*23-3)-x(2*19-3))^2+(x(2*23-2)-x(2*19-2))^2-d(49)^2;y(50)=(x(2*24-3)-x(2*19-3))^2+(x(2*24-2)-x(2*19-2))^2-d(50)^2;y(51)=(x(2*23-3)-x(2*21-3))^2+(x(2*23-2)-x(2*21-2))^2-d(51)^2;y(52)=(x(2*23-3)-x(2*22-3))^2+(x(2*23-2)-x(2*22-2))^2-d(52)^2;运行程序如下:d=[0.9607 0.4399 0.8143 1.3765 1.2722 0.5294 0.6144 0.3766 0.6893 0.9488 0.8000 1.1090 1.1432 0.4758 1.3402 0.7006 0.4945 1.0559 0.6810 0.3587 0.3351 0.2878 1.1346 0.3870 0.75110.4439 0.8363 0.3208 0.1574 1.2736 0.5781 0.9254 0.6401 0.2467 0.4727 1.3840 0.4366 1.03071.3904 0.5725 0.7660 0.4394 1.0952 1.0422 1.8255 1.4325 1.0851 0.4995 1.2277 1.1271 0.70600.8052];x0=ones(1,48);[x,norms]=lsqnonlin(@yuanzi,x0,[],[],[],d); x=[0,0,x] ;D=reshape(x,2,25)'normsfor i=1:25plot(D(i,1),D(i,2),'*')hold on;end得到如下结果:D =0 01.7141 -0.04411.8719 -1.06420.8171 -0.55351.2606 -0.33781.5533 -0.56431.0677 -0.34581.0960 -0.73060.1433 -0.25541.4056 -0.53960.8949 -0.23200.0899 0.55620.5029 -0.70131.1012 -0.28760.5994 -0.29362.1994 -0.41771.3519 -0.07831.4262 -1.50811.2498 -1.17381.1860 -0.67640.7593 -1.02011.1465 -0.92950.3792 -0.40761.3248 -0.05561.2114 -0.5142norms =0.3008画出分布图:并且经过检验,发现当初值x0不同时,可能得到不同的结果。
无约束优化

1. 用黑塞矩阵判断驻点的性质 X 已知函数f(X)的驻点 ,可以利用驻点处的黑塞矩阵来 判断驻点的性质: (1)若 2 f ( X ) 是正定的,则驻点 X 是极小点; 2 (2)若 f ( X ) 是负定的,则驻点 X 是极大点; (3)若 2 f ( X ) 是不定的,则驻点 X 不是极值点; 2 (4)若 f ( X ) 是半定的,则驻点 X 可能是极值点; 也可能不是极值点,视高阶导数情况而定.
4 1 3 2 2 3 2 1 2
2 3
2 4 x13 2 x1 x2 x3 2 2 f ( X ) 6 x2 x1 4 x3 6 x3 4 x2 2 x1 x3
12 x12 2 x2 2 x1 2 x3 2 f ( X ) 2 x1 12 x2 4 2 x3 4 6 2 x 1
无约束优化
标准形式:
其中
X R
min f X n
X R
f : R n R1
X R
max f X = min [ f X ] n n
数学预备知识
1 梯度
定义1 设f(X)是定义在n维欧氏空间的
R n 上的
可微函数,我们称
(
为函数 f(X)在点X处的梯度,记为▽ f(X). 1,梯度方向是函数在点X处增长最快的方向, 负梯度方向是函数在点X处下降最快的方向. 2,梯度的模是函数沿这一方向的变化率.
2 极值点的必要条件和充分条件
n X R 定义1 对于问题(1),设 是任一给定点,P是
是非零向量,若存在一个数 0,使得对于任意 (0, ) 都有 f ( X P) f ( X ) ,则称P是f(X)在 X 处的下降方向.
matlab 牛顿法 多维无约束最优化

matlab 牛顿法多维无约束最优化在MATLAB中,你可以使用内置的优化工具箱函数来使用牛顿法进行多维无约束最优化。
具体来说,你可以使用fminunc函数,该函数使用一种基于牛顿法的优化算法。
以下是一个示例:
MATLABfunction [x,fval,exitflag,output] = multidimensional_unconstrained_optimization()
% 定义目标函数
fun = @(x) x(1)^2 + x(2)^2 - 4*cos(x(1)) - 2*cos(x(2));
% 定义初始点
x0 = [0.5,0.5];
% 调用fminunc函数
options = optimoptions('fminunc','Algorithm','quasi-newton');
[x,fval,exitflag,output] = fminunc(fun,x0,options);
end在这个例子中,我们定义了一个目标函数fun,它是一个多维函数,然后我们定义了一个初始点x0。
然后我们调用fminunc函数,并指定我们想要使用的算法为quasi-newton(一种牛顿法)。
最后,我们得到了优化问题的解x,以及目标函数在最优解处的值fval。
注意:这个例子中的目标函数是一个简单的二次函数,其最小值在原点。
因此,对于更复杂的目标函数,你可能需要更精细地调整初始点或选项。
数学实验 7:无约束优化

实验 7:无约束优化习题2:取不同的初值计算下列非线性规划,尽可能求出所有局部极小点,进而找出全局极小点,并对不同算法的结果进行分析比较:c a a c a a x x x x z T T 222111)()(1)()(1min +---+---=,2R ∈x其中)73.0,7.0(),(21=c c ,T a )4,4(1=,Ta )8.3,5.2(2=。
1. 程序设计1)构建题目中的方程function [f,g]=func(x) a1=[4,4]'; a2=[2.5,3.8]'; c=[0.7,0.73];f=-1/((x-a1)'*(x-a1)+c(1))-1/((x-a2)'*(x-a2)+c(2));%自定义目标函数的梯度函数 if nargout>1g(1)=2*(x(1)-a1(1))/((x(1)-a1(1))^2+(x(2)-a1(2))^2+c(1))^2+2*(x(1)-a2(1))/((x(1)-a2(1))^2+(x(2)-a2(2))^2+c(2))^2g(2)=2*(x(2)-a1(2))/((x(1)-a1(1))^2+(x(2)-a1(2))^2+c(1))^2+2*(x(2)-a2(2))/((x(1)-a2(1))^2+(x(2)-a2(2))^2+c(2))^2 end2)进行非线性规划并比较不同算法的不同opt1=optimset('LargeScale','off','MaxFunEvals',1000,'TolFun',1e-8,'To lX',1e-8,’GradObj ’,’off ’);%关闭大规模算法,规定最大调用次数,以及计算精度,拟牛顿法DFGS 公式,是否采用自设梯度%函数可调opt2=optimset(opt1,'HessUpdate','dfp');%拟牛顿法BFP 公式 opt3=optimset(opt1,'HessUpdate','gillmurray'); %拟牛顿法GM 公式 opt4=optimset(opt1,'HessUpdate','steepdesc'); %最速下降法opt5=optimset(opt1,'lineSearchType',' cubicpoly');%采用三次多项式插值 opt6=optimset(opt5,'HessUpdate','dfp'); opt7=optimset(opt5,'HessUpdate','gillmurray'); opt8=optimset(opt5,'HessUpdate','steepdesc');x0=[3,3]';%设置不同初值,比较结果[x1,v1,exit1,out1]=fminunc(@func,x0,opt1) %进行非线性规划[x2,v2,exit2,out2]=fminunc(@func,x0,opt2)[x3,v3,exit3,out3]=fminunc(@func,x0,opt3)[x4,v4,exit4,out4]=fminunc(@func,x0,opt4)[x5,v5,exit5,out5]=fminunc(@func,x0,opt5)[x6,v6,exit6,out6]=fminunc(@func,x0,opt6)[x7,v7,exit7,out7]=fminunc(@func,x0,opt7)[x8,v8,exit8,out8]=fminunc(@func,x0,opt8)3)绘制原函数的三维图形,找到全局极小点n1=2;n2=5; %绘图范围m=300; %取点个数x1=linspace(n1,n2,m);x2=linspace(n1,n2,m);[X,Y]=meshgrid(x1,x2);F=0;for i=1:mfor j=1:mF(i,j)=func([x1(i),x2(j)]');endendmesh(X,Y,F)xlabel('X1');ylabel('X2');zlabel('Func');pause;contour(x1,x2,F,50); %绘制等高线50条xlabel('X1');ylabel('X2');2.运行结果及分析可以看到采用BFGS与GM算法的结果完全相同,事实上,在运行时MatLab会输出警告,GM方法采用的应该还是默认的BFGS算法。
无约束优化方法与MATLAB实现

例4-1 MA TLAB实现,用M函数文件形式求解:syms s t;f=s^2+3*t^2-2*t*s+4*t+3*s;[x,minf]=minZBLH(f,[-2 6],[0.2 0.2],1.5,[t s],0.0001,0.0001) 坐标轮换minZBLH函数文件如下:function [x,minf] = minconPS2(f,x0,delta,u,var,eps1,eps2)%目标函数:f;%初始点:x0;%收缩系数:u;%自变量向量:var;%步长精度:eps1;%自变量精度:eps2;if nargin == 7eps2 = 1.0e-6;endn = length(var);y = x0;bmainCon = 1;while bmainConyf = subs(f,var,y);yk_1 = y;for i=1:ntmpy = zeros(size(y));tmpy(i) = delta(i);tmpf = subs(f, var,y+tmpy);if tmpf < yfbcon = 1;while bcontmpy(i) = 2*tmpy(i);tmpf_i = subs(f, var,y+tmpy);if tmpf_i <yfy_res = y + tmpy;elsebcon = 0;endendelsetmpy(i) = delta(i);tmpf = subs(f, var,y-tmpy);if tmpf < yfbcon = 1;while bcontmpy(i) = 2*tmpy(i);tmpf_i = subs(f, var,y-tmpy);if tmpf_i <yfy_res = y - tmpy;elsebcon = 0;endendelsey_res = y ;delta = delta/u;endendy = y_res;endif norm(y - yk_1) <= eps2if max(abs(delta)) <= eps1x = y;bmainCon = 0;elsedelta = delta / u;endendendminf =subs(f,var,x);M函数文件的运行结果如下:x = -1.7499-3.2499minf = -8.3750======================================================= 例4-2 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2+s^2-t*s-10*t-4*s+60;[x,mf]=minFD(f,[0 0],[t s])梯度法函数文件minFD如下:function [x,minf] = minFD(f,x0,var,eps)%目标函数:f;%初始点:x0;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量值:x;%目标函数的最小值:minfformat long;if nargin == 3eps = 1.0e-6;endsyms l;tol = 1;gradf = - jacobian(f,var);while tol>epsv = subs(gradf,var,x0);tol = norm(v);y = x0 + l*v;yf = subs(f,var,y);[a,b] = minJT(yf,0,0.1);xm = minHJ(yf,a,b); %用黄金分割法进行一维搜索x1 = x0 + xm*v;x0 = x1;endx = x1;minf = subs(subs(f,x(1)),x(2));format short;M函数文件的运行结果如下:x = 8.0000 6.0000mf =8.0000======================================================================= 例4-3 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2-4*s^2;[x,mf]=minNT(f,[1 1],[t s])牛顿法函数文件minNT如下function [x,minf] = minNT(f,x0,var,eps)%目标函数:f;%初始点:x0;%自变量向量var;%精度:eps;%目标函数取最小时的自变量值:x;%目标函数最小值:minf;format long;if nargin == 3eps = 1.0e-6;endtol = 1;x0 = transpose(x0);gradf = jacobian(f,var); %梯度方向jacf = jacobian(gradf,var); %雅克比矩阵while tol>epsv = subs(gradf,var,x0);tol = norm(v);pv = subs(jacf,var,x0);p = -inv(pv)*transpose(v); %搜索方向p = double(p);x1 = x0 + p;x0 = x1;endx = x1;minf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 0mf = 0============================================================================ 例4-4 MA TLAB实现,用M函数文件形式求解:syms t s z;f=(t-s+z)^2+(-t+s+z)^2+(t+s+z)^2[x,mf]=minMNT(f,[0.5 1 0.5],[t s z])阻尼牛顿法函数文件minNT如下function [x,minf] = minMNT(f,x0,var,eps)format long;if nargin == 3eps = 1.0e-6;endtol = 1;x0 = transpose(x0);syms l;gradf = jacobian(f,var);jacf = jacobian(gradf,var);while tol>epsv = subs(gradf,var,x0);tol = norm(v);pv = subs(jacf,var,x0);p = -inv(pv)*transpose(v);y = x0 + l*p;[a,b] = minJT(yf,0,0.1); %进退法求单峰区间xm = minHJ(yf,a,b); %黄金分割法进行一维搜素x1 = x0 + xm*p;x0 = x1;endx = x1;minf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 1.0e-015 *-0.3468-0.6936-0.3468mf =2.4053e-030=================================================================== 例4-5 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2+4*s^2;[x,mf]=minGETD(f,[1 1],[t s])共轭梯度法函数文件minGETD如下x0 = transpose(x0);n = length(var);syms l;gradf = jacobian(f,var);v0 = subs(gradf,var,x0);p = -transpose(v0);k = 0;while 1v = subs(gradf,var,x0);tol = norm(v);if tol<=epsx = x0;break;endy = x0 + l*p;yf = subs(f,var,y);[a,b] = minJT(yf,0,0.1); %进退法确定单峰区间xm = minPWX(yf,a,b); %二次插值一维搜素x1 = x0 + xm*p;vk = subs(gradf,var,x1);if tol<=epsx = x1;break;endif k+1==nx0 = x1;continue;elselamda = dot(vk,vk)/dot(v,v);p = -transpose(vk) + lamda*p;k = k+1;x0 = x1;endendminf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 1.0e-015 *0.33310.0971mf = 1.4868e-031=================================================================== 例4-6 MA TLAB实现,用M函数文件形式求解:syms t s;f=4*(t-5)^2+(s-6)^2;X=[8 10 11;9 11 11];[x,mf]=minSimpSearch(f,X,1.2,0.5,2.0,0.3,[t s])单纯形法函数文件minGETD如下function [x,minf] = minSimpSearch(f,X,alpha,sita,gama,beta,var,eps)%:f;%反射系数:alpha;%紧缩系数:sita;%扩展系数:gama;%收缩系数:beta;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量值:x;%目标函数最小值:minf;format long;if nargin == 7eps = 1.0e-6;endN = size(X);n = N(2);FX = zeros(1,n);while 1for i=1:nFX(i) = subs(f,var,X(:,i));end[XS,IX] = sort(FX); %将单纯形的顶点按目标函数值的大小重新编号Xsorted = X(:,IX); %排序后的编号px = sum(Xsorted(:,1:(n-1)),2)/(n-1); %单纯形的中心Fpx = subs(f,var,px);SumF = 0;for i=1:nSumF = SumF + (FX(IX(i)) - Fpx)^2;endSumF = sqrt(SumF/n);if SumF <= epsx = Xsorted(:,1);break;elsex2 = px + alpha*(px - Xsorted(:,n)); %将中心点向单纯形外反射fx2 = subs(f,var,x2);if fx2 < XS(1)x3 = px + gama*(x2 - px); %中心点的扩展fx3 = subs(f,var,x3);if fx3 < XS(1)Xsorted(:,n) = x3;X = Xsorted;continue;elseXsorted(:,n) = x2;X = Xsorted;continue;endelseif fx2 < XS(n-1)Xsorted(:,n) = x2;X = Xsorted;continue;elseif fx2 < XS(n)Xsorted(:,n) = x2;endx4 = px + beta*(Xsorted(:,n) - px); %中心点压缩fx4 = subs(f,var,x4);FNnew = subs(f,var,Xsorted(:,n));if fx4 < FNnewXsorted(:,n) = x4;X = Xsorted;continue;elsex0 = Xsorted(:,1);for i=1:nXsorted(:,j) = x0 + sita*(Xsorted(:,j) - x0);endendendendendX = Xsorted;endminf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 5.00025.9999mf =1.8370e-007================================================================= 例4-7 MA TLAB实现,用M函数文件形式求解:syms t s;f=t^2+2*s^2-4*t-2*t*s;p=[-1 0; 0 1];[x,mf]=minPowell(f,[1 1],p,[t s])Powell法函数文件minPowell如下function [x,minf] = minPowell(f,x0,P,var,eps)%目标函数:f;%初始搜索点:x0;%线性无关的初始向量组:p;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量:x;%目标函数的最小值:minf:format long;if nargin == 4eps = 1.0e-6;endn = length(var)+1;syms l;while 1y = zeros(size(P));y(:,1) = x0;for i=1:n-1 %在每个搜索方向上进行一维搜索yv = y(:,i) + l*P(:,i);fy = subs(f, var,yv);[a,b] = minJT(fy,0,0.1);tl = minPWX(fy,a,b);y(:,i+1) = y(:,i) + tl*P(:,i);endP(:,n) = y(:,n) - y(:,1);if norm(P(:,n)) <= eps %精度判断x = y(:,n);break;elsefor j=1:nFY(j) = subs(f, var,y(:,j));endmaxDF = -inf;m = 0;for j=1:n-1 %求出算法中对应的m df = FY(j) - FY(j+1);if df > maxDFmaxDF = df;m = j+1;endendtmpF = subs(f, var,2*y(:,n)-y(:,1));fl = FY(1) - 2*FY(n) + tmpF;if fl<2*maxDFyv = y(:,n) + l*P(:,n);fy = subs(f, var,yv);[a,b] = minJT(fy,0,0.1);tl = minPWX(fy,a,b);x0 = y(:,n) + tl*P(:,n);P(:,m:(n-1)) = P(:,(m+1):n); %重新设置搜索方向elsex0 = y(:,n);endendendminf = subs(f,var,x);format short;M函数文件的运行结果如下:x = 4.00002.0000mf = -8.0000====================================================================== 例4-8 MA TLAB实现,用M函数文件形式求解:syms x1 x2f=x1^2+4*x2^2;[x,mf]=minDFP(f,[1 1],[x1 x2])DF P法函数文件minDFP如下function [x,minf] = minDFP(f,x0,var,eps)%目标函数:f:%初始点:x0;%自变量向量:var;%精度:eps;%目标函数取最小值时的自变量:x;%目标函数的最小值:minf;format long;if nargin == 3eps = 1.0e-6;endx0 = transpose(x0);n = length(var);syms l;H = eye(n,n);gradf = jacobian(f,var);v0 = subs(gradf,var,x0);p = -H*transpose(v0);k = 0;while 1v = subs(gradf,var,x0);tol = norm(v);if tol<=epsx = x0;break;endy = x0 + l*p;yf = subs(f,var,y);[a,b] = minJT(yf,0,0.1);xm = minPWX(yf,a,b); %用抛物线法进行一维搜索 x1 = x0 + xm*p;vk = subs(gradf,var,x1);tol = norm(vk);if tol<=epsx = x1;break;endif k+1==n %重新迭代x0 = x1;continue;elsedx = x1 - x0;dgf = vk - v;dgf = transpose(dgf);dxT = transpose(dx);dgfT = transpose(dgf);mdx = dx*dxT;mdgf = dgf*dgfT;fz = H*(dgf*(dgfT*H));H = H + mdx/(dxT*dgf)-inv(dgfT*(H*dgf))*fz; %校正公式 p = -H*transpose(vk);k = k+1;x0 = x1;endendminf = subs(f,var,x);format short;M 函数文件的运行结果如下:x = 1.0e-015 *⎪⎪⎭⎫ ⎝⎛-0555.01110.0 mf = 2.4652e-032==============================例4-10 用fminsearch 函数求解函数5)1(213)2(1)(2221-+-+--=x x X f 的极值。
实验七(无约束优化)

一、实验目的1、掌握MATLAB优化工具箱的基本用法,对不同算法进行初步分析、比较。
2、练习用无约束优化方法建立和求解实际问题的模型(包括最小二乘拟合)。
二、实验容项目一:某分子由25个原子组成,并且已经通过实验测量得到了其中某些原子队之间的距离(假设在平面结构上讨论),如表所示。
请你确定每个原子的位置关系。
原子对距离原子对距离原子对距离原子对距离(4,1) 0.9607 (5,4) 0.4758 (18,8) 0.8363 (15,13) 0.5725 (12,1) 0.4399 (12,4) 1.3402 (13,9) 0.3208 (19,13) 0.7660 (13,1) 0.8143 (24,4) 0.7006 (15,9) 0.1574 (15,14) 0.4394 (17,1) 1.3765 (8,6) 0.4945 (22,9) 1.2736 (16,14) 1.0952 (21,1) 1.2722 (13,6) 1.0559 (11,10) 0.5781 (20,16) 1.0422(5,2) 0.5294 (19,6) 0.6810 (13,10) 0.9254 (23,16) 1.8255 (16,2) 0.6144 (25,6) 0.3587 (19,10) 0.6401 (18,17) 1.4325 (17,2) 0.3766 (8,7) 0.3351 (20,10) 0.2467 (19,17) 1.0851 (25,2) 0.6893 (14,7) 0.2878 (22,10) 0.4727 (20,19) 0.4995(5,3) 0.9488 (16,7) 1.1346 (18,11) 1.3840 (23,19) 1.2277 (20,3) 0.8000 (20,7) 0.3870 (25,11) 0.4366 (24,19) 1.1271(21,3) 1.1090 (21,7) 0.7511 (15,12) 1.0307 (23,21) 0.7060 (24,3) 1.1432 (14,8) 0.4439 (17,12) 1.3904 (23,22) 0.8025问题分析:每个原子的位置都是未知的,在坐标系中只有相对的位置参数,不妨固定原子1的坐标为(0,0)。
利用MATLAB求解无约束优化问题 ppt课件

[3] fminunc为中型优化算法的步长一维搜索提供了两种算法,
由options中参数LineSearchType控制:
LineSearchType=’quadcubic’(缺省值),
混合的二次和三次多项式插值;
LineSearchType=’cubicpoly’,三次多项式插值
利用MATLAB求解无约束
优化问题
3
例1 min f(x)=(4x12+2x22+4x1x2+2x2+1)*ex1
1、编写M-文件 fun.m: function f = fun (x) f = exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
2、输入M文件wliti.m如下: x0 = [-1, 1]; x=fminunc(‘fun’,x0); y=fun(x)
[2] fminunc为中型优化算法的搜索方向提供了3种算法,
由 options中的参数HessUpdate控制: HessUpdate=’bfgs’(默认值),拟牛顿法的BFGS公式; HessUpdate=’dfp’,拟牛顿法的DFP公式; HessUpdate=’steepdesc’,最速下降法
利用MATLAB求解无约束优化问题
matlab解多元函数无约束优化问题
标准型为:min F(X)
命令格式为: [x,fval,exitflag,output]= fminunc(fun, x0 ,options);
或 [x,fval,exitflag,output]= fminsearch(fun, x0 ,options);
(3)比较各种算法主程序compare.m
matlab无约束最优化实验

班级: 学号: 姓名: 实验日期:2015年9月26日
● 实验名称:无约束优化问题
● 实验目的:
1.
了解Matlab 软件的基本操作 2.
学会使用Matlab 求解一元函数无约束优化问题 3.
学会使用Matlab 求解多元函数无约束优化问题 4. 掌握使用Matlab 解无约束优化问题的基本方法与步骤
● 实验内容:
1.求函数y =2x 3+3x 2-12x +14在区间[-3,4]上的最小值。
2.求x = 2e sin x x 在0<x <8中的最小值与最大值.
3.有边长为3m 的正方形铁板,在四个角剪去相等的正方形以制成方形无盖水槽,问如何剪法使水槽的容积最大?
设剪去的正方形的边长为x ,则水槽的容积为:
x x 2)23(- 建立无约束优化模型为:min y =-
x x 2)23(-, 0<x <1.5
即剪掉的正方形的边长为0.5m时水槽的容积最大,最大容积为2m^3
4. 用fminsearch函数求解'100*(x(2)-x(1)^2)^2+(1-x(1))^2
实验总结:
通过这次实验,我对Matlab这款软件有了一个基本的了解,认识到了它在数据处理中的重要作用。
同时,也学会了使用Matlab软件来解决求一元函数和多元函数在给定区间内的最大值、最小值的问题。
其中,求解f(x)的最大值时,通常转化为求- f(x)的最小值,然后使用fminbnd()函数来求解。
用Matlab解无约束优化问题
返回
用Matlab解无约束优化问题
1. 一元函数无约束优化问题:
min f(x)
x1 ≤ x ≤ x 2
常用格式如下: (1)x= fminbnd (fun,x1,x2) (2)x= fminbnd (fun,x1,x2 ,options) (3)[x,fval]= fminbnd(...) (4)[x,fval,exitflag]= fminbnd(...) (5)[x,fval,exitflag,output]= fminbnd(...) 其中(3)、(4)、(5)的等式右边可选用(1)或 (2)的等式右边。 函数fminbnd的算法基于黄金分割法和二次插值法,它 要求目标函数必须是连续函数,并可能只给出局部最优 解。
fval
exitflag
output
所
Options中常用的几个参数的名称、含义、取值如下:
(1) Display: 显示水平.取值为’off’时,不显示输出; 取值为’iter’时,显示每次迭代的信息;取值为’final’时, 显示最终结果.默认值为’final’. (2) MaxFunEvals: 允许进行函数评价的最大次数,取 值为正整数. (3) MaxIter: 允许进行迭代的最大次数,取值为正整数.
3. 优化函数的输出变量下表:
变量 x 描 述 由优化函数求得的值.若exitflag>0,则x 为解;否则,x不是最终解,它只是迭代制止 时优化过程的值 解x处的目标函数值 描述退出条件: exitflag>0,表目标函数收敛于解x处 exitflag=0,表已达到函数评价或迭代 的最大次数 exitflag<0,表目标函数不收敛 包含优化结果信息的输出结构. Iterations:迭代次数 Algorithm:所采用的算法 FuncCount:函数评价次数 调用函数 所有优化函数 linprog,quadprog,fgoalattain, fmincon,fminimax,lsqcurvefit, lsqnonlin, fminbnd
工程计算MATLAB_优化设计_方法函数无约束最优化

(2)梯度法 在函数的导数可求的情况下,梯度法是一种更 优的方法。 常见的梯度法有最速下降法、Newton法、 Marquart法、共轭梯度法和拟牛顿法(QuasiNewton method)等。 在所有这些方法中,用的最多的是拟牛顿法
33/45
5.2 无约束最优化问题
5.2 无约束最优化问题
5.2.2 单变量最小化问题 2. 相关函数
(1)fminbnd 功能:找到固定区间内单变量函数的最小值。 语法: [x,fval] = fminbnd(...) 返回解x处目标函数的值。 [x,fval,exitflag] = fminbnd(...) 返回exitflag值描述fminbnd函数的退出条件。 [x,fval,exitflag,output] = fminbnd(...) 返回包含优化信息的结构输出。
13/45
5.1 优化函数
5.1.3 @(函数句柄)函数
>> x=0:0.001:1; >> y=humps(x); >> plot(x,y); >> .1.3 @(函数句柄)函数
>> x=fminbnd(@humps,0.3,1) x= 0.6370
15/45
28/45
2. 相关函数
5.2 无约束最优化问题
5.2.2 单变量最小化问题 2. 相关函数
(2)实例 例1:在区间(0,2π)上求函数sin(x)的最小值
>> x=fminbnd(@sin,0,2*pi)
x= 4.7124 >> y=sin(x) y= -1.0000
29/45
5.2 无约束最优化问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热动71 马千里 970669
实验七 无约束优化
实验目的
1. 掌握MATLAB 优化工具箱的基本用法,对不同算法进行初步分析、比较。
2. 练习实际问题的非线性最小二乘拟合。
实验内容
3. 求解)12424(min 2212
2211++++x x x x x e x ,初值(-1,1),对不同算法的结果进行分析、比较。
解:编制函数fun.m
function y=fun(x)
y=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
经过实验,用不同的算法fminu 得到的结果都是(0.5, -1),所不同的是迭代的次数有不同。
以上结果表明,MA TLAB 的缺省值对于此题优化效果较好,迭代次数最少。
6.《中国统计年鉴(1995)》给出表8的数据,试据此拟合生产函数中的参数,如何看待用线性最小二乘法和非线性最小二乘法拟合的结果。
解:根据Gobb-Douglas 生产函数,用Q, K, L 分别表示产值、资金、劳动力。
βαL aK L)Q(K,=
a. 考虑线性最小二乘拟合。
对生产函数取对数L K a Q ln ln ln ln βα++=
设R=[1 lnK lnL] x=[lna α β]’ y=[lnQ]
R=
1.0000 -1.3988 1.5723
1.0000 -1.0829 1.6069
1.0000 -0.9556 1.6348
1.0000 -0.8389 1.6636
1.0000 -0.5987 1.6926
1.0000 -0.4951 1.7107
1.0000 -0.4394 1.7359
1.0000 -0.2854 1.7640
1.0000 -0.0371 1.7822
1.0000 0.4053 1.7954 1.0000 0.6389 1.8160
则Rx=y 代表一组超定方程组。
在MATLAB 下用x=R\y 得到最小二乘意义下的解 x=
-3.2360
0.6208
2.3728
即a=exp(-3.2360)=0.0393 α=0.6208 β=2.3728
b.非线性模型
function f=pp1(c)
Q=[0.7171 0.8964 1.0202 1.1962 1.4928 1.6909 1.8531 2.1618 2.6635 3.4515
4.5006];
K=[0.2469 0.3386 0.3846 0.4322 0.5495 0.6095 0.6444 0.7517 0.9636 1.4998
1.8944];
L=[4.8179 4.9873 5.1282 5.2783 5.4334 5.5329 5.6740 5.8360 5.9432 6.0220
6.1470];
f=Q-c(1)*k.^c(2).*L.^c(3);
c0=[1 1 1]
c=leastsq(‘pp1’, c0)
y=sum(pp1(c).*pp1(c)) 计算误差平方和
得到
c= 0.0357 0.6300 2.4290
y= 0.0394
即a=0.0357 α=0.6300 β=2.4290
再对线性模型计算误差平方和以做比较
y=sum(pp1([0.0393 0.6208 2.3728]).* pp1([0.0393 0.6208 2.3728]))
得到y=0.0441
将以上结果列表如下
是在不同意义下的最小二乘解。
y = -0.3325 -0.1094 0.0200 0.1791 0.4007 0.5253 0.6169 0.7709 0.9796 1.2388 1.5042。
