《长方体、正方体的认识》PPT课件
合集下载
《长方体的认识》长方体和正方体PPT

ppt素材: . /sucai/
ppt背景: . /beijing/
ppt图表: . /tubiao/
ppt下载: . /xiazai/
ppt教程: . /powerpoint/
资料下载: . /ziliao/
范文下载: . /fanwen/
试卷下载: . /shiti/
教案下载: . /jiaoan/
解:设这个长方体的高是 x厘米,则宽为 1.5x厘米, 长为 2×1.5x厘米。
(2×1.5x+1.5x+x)×4=110 5.5x×4=110 22x=110 x=5
1.5×5=7.5(厘米) 2×1.5×5=15(厘米)
答:这个长方体的长是15厘米,宽是7.5厘米,高是5厘米。
一级标题
你有什么收获?
长 相交于一个顶点的三条棱,分别叫做长方体 的长、宽、高。
练习 一 级 标 题
1.看图说出下面每个长方体的长、宽、 高各是多少?
长:( 4cm ) 宽:( 3cm) 高:( 9cm)
长:( 2cm) 宽:( 5cm) 高:( 4cm)
长:( 5cm ) 宽:( 1cm ) 高:( 5cm)
练习 一 级 标 题
化学课件: . /kejian/huaxue/ 生物课件: . /kejian/shengwu/
地理课件: . /kejian/dili/
历史课件: . /kejian/lishi/
长方形
正方形 三角形
圆形 梯形 平行四边形
生活中的这些物体都是什么形状呢?
周围很多物体的形状都是长方体 或正方体(正方体也叫立方体)。
从顶点这个方面有序观察,有什么发现。
一共有8个顶点。
梳理归纳一,揭级示标概念题
3.1《长方体和正方体的认识》课件

4 厘 米 5厘米
6厘米
长方 ____ 6 厘米,宽_____ 5 厘米。
上图是一个_______体,它的上面是_______形,长
长方
1、看图说出每个长方体的长、宽、高各是多少。
3cm
7cm
长:7cm 宽:4cm 高:3cm
4dm
长:4dm 宽:6dm 高:5m
8mm
长:8mm 宽:20mm 高:8mm
认识长方体
长方体有多少条棱?
认识长方体
长方体有多少条棱?
认识长方体
长方体有多少条棱?
认识长方体
长方体有多少条棱?
认识长方体
长方体有多少条棱?
相对的棱长度相等.
12条棱长度的和叫做棱长总和。
认识长方体
顶点.
三条棱相交的点叫做顶点.
长方体一共有8个 顶点.
相交于同一个顶点的三条棱分别叫做长方体的 长、宽、高。
8mm
5dm
想一想:
1、用铁丝焊成一个长20厘米,宽15厘米, 高10厘米的长方体框架,至少需要铁丝多 少厘米?
本节课到此结束! 谢谢同学们的倾听!
再见!
新庄赵小学 党丛丛
分一分,按一定标准分为两类
1 2 3 4 5
6
7
8
9
平面图形:2、3、5、7、9 立体图形:1、4面是什么 形状?
上面 上面 后面 左面
下面(底面)
前面
下面(底面)
右面
认识长方体
相对的面有什么特点?
相对的面完全相同.
认识长方体
棱lé ng 两个面 相交的 边叫做 棱.
高
宽 长 实际上长方体的长、宽、高的位置不是固定不变的。 一般情况把底面中较长的一条棱叫做长,较短的一 条棱叫做宽,垂直于底面的棱叫做高。
长方体和正方体的认识完美PPT幻灯片.ppt

2、 判断。正确的在括号里画“√”,错 误的在括号里画“×”。
(1)长方体中可能有4个正方形的面。 ( ×)
(2)长方体有6个面,每个面有4条棱,共四六二
十四条棱。
()
×
(3)一个长方体,它有两个面是正方形,那么
有四个面面积相等。
() √
(4)长方体是特殊的正方体。
( )×
20
思考题:
1.用一根长36厘米的铁丝,围成一个 正方体,那么每条棱长为多少厘米?
长方体和正方体都有6个面,12条棱和8个顶点
8
观察长方体的物品,思考下面的问题:
4、每个面是长方形(特殊情况
4、长方体的有六两个个面相对是的什面么是形正状方的形?)。 5、哪些面是5完、全相对相的同面的是?完全相同的。 6、长方体的61、2互条相棱平中行,的哪棱些长棱度相的等长,分 度相等?可分成成3组几。组?
1
2
长方体
正方体(立方体)
3
观察长方体的物品,思考下面的问题:
1、长方体有几个面? 2、长方体有几条棱? 3、长方体有几个顶点?
4
1、长方体有6个面。 2、长方体有12条棱。 3、长方体有8个顶点。
那正方体呢?
5
1、正方体有6个面。 2、正方体有12条棱。 3、正方体有8个顶点。
6
1、长方体有6个面。 2、长方体有12条棱。 3、长方体有8个顶点。
9
总结:
1长方体是由六个长方形的面围成的立体图形。 2在一个长方体中,相对的面完全相同,互相平 行的棱长度相等。
10
高
长
宽
长 方 体 的 12 条 棱可以分成3组。
相交于一个顶点的三条棱的长度分别叫 做长方体的长、宽、高。
长方体和正方体的认识及展开图(课件)六年级上册数学苏教版

课堂检测
【答案】 (1)
(2)3,2,4
课堂检测
4.用铁丝焊一个长是20厘米,宽是10厘米,高是8厘米的长方体框 架,至少需要多少的铁丝?
课堂检测
4.用铁丝焊一个长是20厘米,宽是10厘米,高是8厘米的长方体框 架,至少需要多少的铁丝?
【答案】 (20+10+8)×4=152(厘米) 答:至少需要152厘米的铁丝。
知识小结
长方体是由6个长方形围成的立体图形,共有6个面, 12条棱和8个顶点;在同一个长方体中,相对的面完全 相等,相对的棱长度相等。
பைடு நூலகம்方体
我们知道了长方体的特征,那么正方体呢?它 有几个面、几条棱和几个顶点?它的面和棱各 有什么特点?
正方体
下图中,哪个是正方体,哪个是长方体?正方体的棱长是多 少?有几个面完全相同?
知识讲解
长方体
长方体有几个面?从不同的角度观察一个长方体,最多能同时 看到几个面?
长方体
观察长方体物体和长方体的直观图,都可以 发现,从不同角度观察同一个长方体,最多 同时只能看到3个面
长方体
围成长方体的每一个长方形叫作长方体的面,两个面相 交的线叫作长方体的棱,3条棱相交的点叫作长方体的 顶点。那么,长方体有几个面、几条棱和几个顶点呢?
实战演练
课堂检测
1.看图填空。
(1)这是一个(
)体。
(2)它的棱长是( )厘米。
(3)由一个顶点引出的三条棱的长度和是(
(4)它的棱长总和是( )厘米。
)厘米。
课堂检测
【答案】 (1) 正方 (2) 5 (3) 15 (4) 60
课堂检测
2.选择题
(1)做一个长方体的框架,求用多少铁丝,是求长方体的( )。
长方体和正方体的认识课件

关知识。
引入先进技术: 利用现代科技手 段,如虚拟现实、 增强现实等技术, 让学生更加直观 地了解长方体和 正方体的形态和
特点。
多元化教学方式: 未来教学将采用 多种教学方式, 如小组合作、探 究式学习等,以 激发学生的学习 兴趣和主动性。
培养学生的创新 思维:未来教学 将注重培养学生 的创新思维和解 决问题的能力, 让学生能够更好 地应对各种挑战。
长方体和正方体在数学中的应用
空间观念的培养:长方体和正方 体作为三维图形,在数学中可以 帮助学生建立空间观念,理解三 维空间中的点、线、面关系。
空间想象能力的提升:通过长方 体和正方体的组合、拼接等操作, 可以培养学生的空间想象能力和 创造力。
添加标题
添加标题
添加标题
添加标题
几何图形的计算:长方体和正方 体的体积、表面积等计算,可以 锻炼学生的计算能力和空间思维 能力。
01
添加章节标题
02
引言
课程背景
课程目标:介绍本节课的学习目标,包括掌握长方体和正方体的基本概念、特征和性质等。
知识储备:回顾学生已经学过的与长方体和正方体相关的知识,如平面几何中的点、线、面等概 念。
现实应用:介绍长方体和正方体在现实生活中的应用,如建筑、家具等,激发学生学习兴趣。
课程意义:阐述学习长方体和正方体的重要性和意义,如培养学生的空间想象能力和几何思维能 力等。
分类:长方体可以分为三类,分别是长方体、正方体和斜方体。其中,正方体是 特殊的长方体,它的六个面都是正方形。
体积:长方体的体积可以通过其底面积和高来计算,公式为:体积 = 底面积 × 高。
表面积:长方体的表面积可以通过其六个面的面积之和来计算,公式为:表面积 = 2 × (底面积 + 侧面积 + 前后面积)。
引入先进技术: 利用现代科技手 段,如虚拟现实、 增强现实等技术, 让学生更加直观 地了解长方体和 正方体的形态和
特点。
多元化教学方式: 未来教学将采用 多种教学方式, 如小组合作、探 究式学习等,以 激发学生的学习 兴趣和主动性。
培养学生的创新 思维:未来教学 将注重培养学生 的创新思维和解 决问题的能力, 让学生能够更好 地应对各种挑战。
长方体和正方体在数学中的应用
空间观念的培养:长方体和正方 体作为三维图形,在数学中可以 帮助学生建立空间观念,理解三 维空间中的点、线、面关系。
空间想象能力的提升:通过长方 体和正方体的组合、拼接等操作, 可以培养学生的空间想象能力和 创造力。
添加标题
添加标题
添加标题
添加标题
几何图形的计算:长方体和正方 体的体积、表面积等计算,可以 锻炼学生的计算能力和空间思维 能力。
01
添加章节标题
02
引言
课程背景
课程目标:介绍本节课的学习目标,包括掌握长方体和正方体的基本概念、特征和性质等。
知识储备:回顾学生已经学过的与长方体和正方体相关的知识,如平面几何中的点、线、面等概 念。
现实应用:介绍长方体和正方体在现实生活中的应用,如建筑、家具等,激发学生学习兴趣。
课程意义:阐述学习长方体和正方体的重要性和意义,如培养学生的空间想象能力和几何思维能 力等。
分类:长方体可以分为三类,分别是长方体、正方体和斜方体。其中,正方体是 特殊的长方体,它的六个面都是正方形。
体积:长方体的体积可以通过其底面积和高来计算,公式为:体积 = 底面积 × 高。
表面积:长方体的表面积可以通过其六个面的面积之和来计算,公式为:表面积 = 2 × (底面积 + 侧面积 + 前后面积)。
1《长方体和正方体的认识》课件

高
长
宽
实际上长方体的长宽高不是固定不变的。 一般情况把底面较长的一条棱叫做长, 较短的棱叫做宽,垂直于底面的棱叫做高。 绿色圃中小学教育网
说说下面各个长方体的长、宽、高。
( ) ( )
( )
说说下面各个长方体的长、宽、高。
(高 ) (长 ) (宽 )
( )
长方体有6个面,通常情况每个面都是长方形。
长方体有6个面,按刚才的数法可以将它们分成几组呢?
上下、
前后、
左右
三组相对的面
认识长方体
这些面有什么特点?
每组相对的两个面完全相等。
认识长方体
lé ng
两个面相交的线
叫做棱 。
认识长方体
长方体有多少条棱? 棱的长度有什么特点?
相对的棱长度相等,
认识长方体
2厘米 6分米
6分米
思考:长方体的12条棱长的总和应该怎样算呢?
长方体棱长总和=长X4+宽X4+高X4 长方体棱长总和=(长+宽+高)X4
思考:正方体的12条棱长的总和应该怎样算呢?
正方体棱长总和=棱长X12
面 名 称 数量 长 方 体 正 方 体 形状
棱
顶点
哪些面完 哪些棱长 数量 数量 全相同 度相等
12条
相对的棱的长 度相等
长方形 6个 (特殊情况有 相对面完全相 两个相对的面 同 是正方形)
8个
6个
正方形
每个面都完全 相同
12条
所有的棱的长 度都相等
8个
(棱长)
(
)
长方体和正方体的相同点和不同点
形 体
长 方 体
相同点
面 棱 顶点
五年级下册数学课件 - 长方体和正方体的认识 人教版(共38张PPT)

8x12=96(厘米)
3、有一根150cm的铁丝,用这根铁丝焊接成一个正方 体框150-6)÷12 =144÷12 =12(厘米)
4、小明用一根铁丝围成一个长30厘米、宽20厘米、高 10厘米的长方体框架。如果把它改围成一个正方体框架, 这个正方体框架的棱长是多少厘米? (30+20+10)x4
=(长+宽+高)X 4
随堂练习
1、长方体有( 6 )个面,它们一般都是( 长方形 ), 也有可能有( 2 )个相对的面是正方形。 2、长方体的上面和下面、前面和后面、左面和右面都 叫做( 相对面),他们相对的面积( 相等 )。 3、长方体有( 12)条棱,每相对的( 4 )条棱算作一 组,可以分成( 3 )组。
正方体棱长=棱长总和÷12
例3 用一根铁丝围成一个长方体,它的长是12分米,
宽是8分米,高是4分米。如果把这根铁丝改围成一个
正方体,这个正方体的棱长是多少?
(12+8+4)x4 =24x4 =96(分米) 96÷12=8(分米)
随堂练习
一个棱长6分米的正方体框架,若把它改成一个长10分
米,宽5分米的长方体框架,这个长方体的高是多少分
100÷4-(8+12) =25-20 =5(厘米) 12x5=60(平方厘米)
例3 有一个礼盒需要用彩带捆扎,捆扎效果如图,打结 部分需要10厘米彩带,一共需要多长的彩带?
(30+20)x2+20x4 =100+80 =180(厘米) 180+10=190(厘米)
例4 用一根长28厘米的铁丝做一个棱长是整厘米数的 长方体框架,这个长方体框架的长、宽、高可能是多少 厘米?想一想,填一填。
4、相较于一个顶点的三条棱的长度,叫做长方体的 ( 长)、( 宽)、( 高)。
3、有一根150cm的铁丝,用这根铁丝焊接成一个正方 体框150-6)÷12 =144÷12 =12(厘米)
4、小明用一根铁丝围成一个长30厘米、宽20厘米、高 10厘米的长方体框架。如果把它改围成一个正方体框架, 这个正方体框架的棱长是多少厘米? (30+20+10)x4
=(长+宽+高)X 4
随堂练习
1、长方体有( 6 )个面,它们一般都是( 长方形 ), 也有可能有( 2 )个相对的面是正方形。 2、长方体的上面和下面、前面和后面、左面和右面都 叫做( 相对面),他们相对的面积( 相等 )。 3、长方体有( 12)条棱,每相对的( 4 )条棱算作一 组,可以分成( 3 )组。
正方体棱长=棱长总和÷12
例3 用一根铁丝围成一个长方体,它的长是12分米,
宽是8分米,高是4分米。如果把这根铁丝改围成一个
正方体,这个正方体的棱长是多少?
(12+8+4)x4 =24x4 =96(分米) 96÷12=8(分米)
随堂练习
一个棱长6分米的正方体框架,若把它改成一个长10分
米,宽5分米的长方体框架,这个长方体的高是多少分
100÷4-(8+12) =25-20 =5(厘米) 12x5=60(平方厘米)
例3 有一个礼盒需要用彩带捆扎,捆扎效果如图,打结 部分需要10厘米彩带,一共需要多长的彩带?
(30+20)x2+20x4 =100+80 =180(厘米) 180+10=190(厘米)
例4 用一根长28厘米的铁丝做一个棱长是整厘米数的 长方体框架,这个长方体框架的长、宽、高可能是多少 厘米?想一想,填一填。
4、相较于一个顶点的三条棱的长度,叫做长方体的 ( 长)、( 宽)、( 高)。
北师大五年级下册数学课件《长方体和正方体的认识》
都二
能分
运浇
用灌
好,
“八
二分
八等
定待
律;
”二
,分
我管
们教
一,
起八
,分
静放
待手
花;
开二
。分
成
➢ Pure of heart, life is full of sweet and joy!
绩 ,
八
分
方
法
。
愿
全
天
下
所
有
长方体
正方体
长方体
正方体
6个面都是长方 面 形,相对的面形
状相同,面积相 等。
6个面都是正 方形,6个面 的面积相等。
12条棱,相对 12条棱的长度相 棱 的棱长度相等 等。
顶 8个
8个
点
努 力 吧 !
判断下面哪几个图形是长方体?
√
×
×
√
填一填
(1)长方体有( 6 )个面,( 12)条棱, ( 8)个顶点。
8个
4 厘 米 5厘米
7厘米
4 厘 米
6厘米
5厘米
4 厘 米
5厘米
5厘米
4 厘 米
4厘米
5厘米
1、正方体和长方体有什么相同的地方?
4 厘 米
4厘米
2、又有什么区别呢?
4厘米
正方体有什么特征呢
面: 有6个面,完全相同,都是正方形。 棱: 有12条棱,长度都相等。 顶点: 有8个顶点。
长方体和正方体有什么关系呢 正方体是长、宽、高都相等的长方体, 它是一种特殊的长方体。
认识长方体
长方体的12条棱可以怎样分组? 分成几组?
认识长方体
长方体正方体的认识课件ppt课件

物流运输 在物流运输中,长方体和正方体常被用作货物的装载单元, 通过合理的空间利用和堆放方式,提高运输效率和降低成 本。
艺术设计
长方体和正方体也是艺术设计中常用的元素之一,通过对 其进行变形、组合、叠加等操作,可以创造出丰富多样的 艺术效果和视觉冲击力。
06
练习题与课堂互动环节
判断题练习
正方体的六个面都是正 方形。
THANK YOU
感谢聆听
建筑结构
在建筑结构中,长方体和正方 体常被用作承重结构的基本单 元,如梁、柱、楼板等,其坚 固耐用的特性保证了建筑物的 安全性。
建筑装饰
长方体和正方体也被广泛应用 于建筑装饰中,如门窗、隔断、 装饰画等,通过不同的材质和 颜色搭配,营造出丰富多彩的 室内环境。
包装设计领域应用实例分析
包装容器
长方体和正方体是包装设计中常 用的容器形状,如纸箱、木箱、 塑料盒等,其规整的形态便于堆 放和运输,同时也方便消费者携
长方体与正方体关系
长方体与正方体都属于六面体 的范畴。
正方体是长方体的一种特殊情 况,当长方体的长、宽、高都 相等时,就变成了正方体。
长方体和正方体在几何性质上 有很多相似之处,如都有6个面、 12条棱、8个顶点等。但在一些 特定的性质上,如面的形状和 大小、棱的长度等,两者又有 所不同。
02
长方体与正方体性质探究
计算长方体水池的容积、长方体木块的体积等。
正方体体积公式推导及应用
1 2
正方体体积公式 V = a^3
公式推导 正方体每个面都是正方形,面积相等,因此体积 等于一个面的面积乘以高(即边长)。
3
应用举例 计算正方体骰子的体积、正方体砖块的体积等。
复杂组合图形体积计算方法
艺术设计
长方体和正方体也是艺术设计中常用的元素之一,通过对 其进行变形、组合、叠加等操作,可以创造出丰富多样的 艺术效果和视觉冲击力。
06
练习题与课堂互动环节
判断题练习
正方体的六个面都是正 方形。
THANK YOU
感谢聆听
建筑结构
在建筑结构中,长方体和正方 体常被用作承重结构的基本单 元,如梁、柱、楼板等,其坚 固耐用的特性保证了建筑物的 安全性。
建筑装饰
长方体和正方体也被广泛应用 于建筑装饰中,如门窗、隔断、 装饰画等,通过不同的材质和 颜色搭配,营造出丰富多彩的 室内环境。
包装设计领域应用实例分析
包装容器
长方体和正方体是包装设计中常 用的容器形状,如纸箱、木箱、 塑料盒等,其规整的形态便于堆 放和运输,同时也方便消费者携
长方体与正方体关系
长方体与正方体都属于六面体 的范畴。
正方体是长方体的一种特殊情 况,当长方体的长、宽、高都 相等时,就变成了正方体。
长方体和正方体在几何性质上 有很多相似之处,如都有6个面、 12条棱、8个顶点等。但在一些 特定的性质上,如面的形状和 大小、棱的长度等,两者又有 所不同。
02
长方体与正方体性质探究
计算长方体水池的容积、长方体木块的体积等。
正方体体积公式推导及应用
1 2
正方体体积公式 V = a^3
公式推导 正方体每个面都是正方形,面积相等,因此体积 等于一个面的面积乘以高(即边长)。
3
应用举例 计算正方体骰子的体积、正方体砖块的体积等。
复杂组合图形体积计算方法
《长方体和正方体的认识》PPT课件

包装设计应用
包装容器
长方体和正方体是常见的 包装容器形状,如纸箱、 木箱等,用于装载和保护 物品。
节约空间
在物流运输和仓储过程中 ,使用长方体和正方体形 状的包装可以更有效地利 用空间,降低成本。
美观实用
长方体和正方体的包装设 计可以实现美观与实用的 平衡,提升产品的整体形 象和市场竞争力。
其他领域应用
02
长方体和正方体性质探究
长方体性质
01
长方体有6个面,每个面 都是矩形,相对的两个 面完全相同。
02
长方体有12条棱,其中 4条长、4条宽、4条高 ,分别对应三组相对的 面。
03
长方体有8个顶点,每个 顶点由3条棱相交而成。
04
长方体的对角线相等, 且互相平分。
正方体性质
01
02
03
04
正方体是特殊的长方体,它的 6个面都是正方形,且每个面
正方体表面积公式推导
正方体表面积 = 6 × 边长^2
公式推导:正方体有6个面,每个面的面积都是边长×边长。因为正方体所有面都 相等,所以表面积计算公式为上述公式。
实例分析与计算
实例1
一个长方体的长、宽、高分别为5cm、 3cm、2cm,求其表面积。
实例2
一个正方体的边长为4cm,求其表面积。
计算
根据长方体表面积公式,表面积 = 2 × (5cm × 3cm + 5cm × 2cm + 3cm × 2cm) = 2 × (15cm^2 + 10cm^2 + 6cm^2) = 2 × 31cm^2 = 62cm^2。
计算
根据正方体表面积公式,表面积 = 6 × 4cm^2 = 96cm^2。
《长方体和正方体的认识》PPT课件

正方体性质
正方体具有长方体的所有性质;此外, 正方体的每个面都是中心对称和轴对 称的图形;正方体的体对角线长度等 于棱长的根号3倍。
03
长方体和正方体表面积计算
表面积概念引入
表面积定义
长方体或正方体六个面的面积之和。
与体积的区别
表面积是物体外部的大小,体积是物 体内部空间的大小。
为什么要学习表面积
空间想象力培养方法
观察实物模型
通过观察实物模型,了解几何体的形状、结构 和空间位置关系。
绘制三视图
通过绘制几何体的三视图(主视图、俯视图、 左视图),培养空间想象力和图形表达能力。
制作几何体模型
通过动手制作几何体模型,加深对几何体形状 和结构的理解。
实际应用场景举例
机械制造领域
在机械制造中,需要运用几何体 知识来设计和制造各种零部件和 机器设备,如发动机、齿轮等。
正方体体积计算公式推导
引导学生理解正方体的特点,即长、 宽、高都相等。
让学生通过具体计算,掌握正方体体 积的计算方法。
通过实例演示,推导出正方体体积的 计算公式:体积 = 边长 × 边长 × 边 长。
空间观念培养方法
通过观察实物和图形,培养学生的空间想象力。 引导学生通过动手操作,理解物体的空间位置和关系。
长方体与正方体的关系
01
正方体是长方体的特例,当长方体的长、宽、高都相等时,就
变成了正方体。
相似性质
02
长方体和正方体都有六个面、十二条棱和八个顶点;它们的对
面都是平行且相等的;它们的角都是直角。
不同之处
03
长方体的长、宽、高可以不相等,而正方体的长、宽、高必须
相等。
其他相似几何体介绍
正方体具有长方体的所有性质;此外, 正方体的每个面都是中心对称和轴对 称的图形;正方体的体对角线长度等 于棱长的根号3倍。
03
长方体和正方体表面积计算
表面积概念引入
表面积定义
长方体或正方体六个面的面积之和。
与体积的区别
表面积是物体外部的大小,体积是物 体内部空间的大小。
为什么要学习表面积
空间想象力培养方法
观察实物模型
通过观察实物模型,了解几何体的形状、结构 和空间位置关系。
绘制三视图
通过绘制几何体的三视图(主视图、俯视图、 左视图),培养空间想象力和图形表达能力。
制作几何体模型
通过动手制作几何体模型,加深对几何体形状 和结构的理解。
实际应用场景举例
机械制造领域
在机械制造中,需要运用几何体 知识来设计和制造各种零部件和 机器设备,如发动机、齿轮等。
正方体体积计算公式推导
引导学生理解正方体的特点,即长、 宽、高都相等。
让学生通过具体计算,掌握正方体体 积的计算方法。
通过实例演示,推导出正方体体积的 计算公式:体积 = 边长 × 边长 × 边 长。
空间观念培养方法
通过观察实物和图形,培养学生的空间想象力。 引导学生通过动手操作,理解物体的空间位置和关系。
长方体与正方体的关系
01
正方体是长方体的特例,当长方体的长、宽、高都相等时,就
变成了正方体。
相似性质
02
长方体和正方体都有六个面、十二条棱和八个顶点;它们的对
面都是平行且相等的;它们的角都是直角。
不同之处
03
长方体的长、宽、高可以不相等,而正方体的长、宽、高必须
相等。
其他相似几何体介绍
长方体和正方体单元整理复习ppt课件.ppt

12dm
8dm 6dm
底面积 =长x宽 长方体的体积=长x宽x高
=底面积 x高
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
正方体的体积=棱长x棱长x棱长
=底面积 X高
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
是不是所有的物体都有容积呢? 结论:
只有容器才能有容积,如果是实心 的木块等,是不会有容积的。
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
前
左
上
后
右
下
正方体的表面积=棱长×棱长×6
2
或者:正方体的表面积=棱长 ×6
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
分析在计算下列物体面积时,应考虑几 个面的面积。 1、制作一个无盖的铁皮桶的用料。 五个面
2、火柴盒的外壳用料。 五个面 3、火柴盒的内壳用料。 四个面
体
体的表面 2、表面积的计算
和
积
正方体:S=棱长X棱长X6
正
方
3、无盖,无底
体
1、体积和体积单位 体积的定义
体积单位
3、长 方体和 正方体
2、体积计算公式
长方体 V=abh 正方体 V=a3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX 时 间:XX年XX月XX日
1.掌握长方体和正方体的特征,认识 它们之间的关系。 2.培养同学们动手操作、观察、抽象 概括的能力和初步的空间观念。 3.渗透事物是相互联系,发展变化的 辩证唯物主义观点。
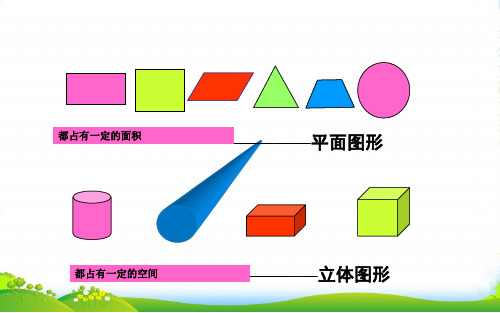
平面图形
立体图形
长方体
正方体
面
长方体 正方体
数量 6个面 6个面
特点 相对的两个面完全相同
6个面完全相同
棱
长方体 正方体
特点
高 宽
长
棱长 棱长
棱长
长方体
正方体
课堂活动
1.
1
7
2
4
5
3
6
8 9
平面图形有( 1 5 6 7 9 )
立体图形有( 2 3 4 8
)
2. 我指你说。
3.看图说出下面每个长方体的长、宽、高 各是多少?
2厘米
8厘米
3厘一个小和尚从长方体顶点A出发,沿着棱长 走向另一个顶点B(每次只能经过三条棱)。 经过的路线一共有几条?
数量 12条棱 12条棱
特点 相对的4条棱一样长 12条棱一样长
顶点
数量 长方体 8个顶点 正方体 8个顶点
特点
面
长方体 正方体
数量 6个面 6个面
特点 相对的两个面完全相同
6个面完全相同
棱
长方体 正方体
数量 12条棱 12条棱
特点 相对的4条棱一样长 12条棱一样长
顶点
数量 长方体 8个顶点 正方体 8个顶点
B
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX 时 间:XX年XX月XX日
1.掌握长方体和正方体的特征,认识 它们之间的关系。 2.培养同学们动手操作、观察、抽象 概括的能力和初步的空间观念。 3.渗透事物是相互联系,发展变化的 辩证唯物主义观点。
平面图形
立体图形
长方体
正方体
面
长方体 正方体
数量 6个面 6个面
特点 相对的两个面完全相同
6个面完全相同
棱
长方体 正方体
特点
高 宽
长
棱长 棱长
棱长
长方体
正方体
课堂活动
1.
1
7
2
4
5
3
6
8 9
平面图形有( 1 5 6 7 9 )
立体图形有( 2 3 4 8
)
2. 我指你说。
3.看图说出下面每个长方体的长、宽、高 各是多少?
2厘米
8厘米
3厘一个小和尚从长方体顶点A出发,沿着棱长 走向另一个顶点B(每次只能经过三条棱)。 经过的路线一共有几条?
数量 12条棱 12条棱
特点 相对的4条棱一样长 12条棱一样长
顶点
数量 长方体 8个顶点 正方体 8个顶点
特点
面
长方体 正方体
数量 6个面 6个面
特点 相对的两个面完全相同
6个面完全相同
棱
长方体 正方体
数量 12条棱 12条棱
特点 相对的4条棱一样长 12条棱一样长
顶点
数量 长方体 8个顶点 正方体 8个顶点
