实验三、控制系统的分析(报告完整版)
控制系统时间响应分析”实验报告

实验一、“控制系统时间响应分析”实验报告一、 实验类型验证性实验二、 实验目的1、 求系统在时间常数 T 不同取值时的单位脉冲、单位阶跃响应和任意输入响应,熟悉系统 时间响应的定义和图形曲线2、 求系统的上升时间、峰值时间、最大超调量和调整时间等性能指标,熟悉系统瞬态性 能指标的定义。
三、 实验仪器与设备(或工具软件)计算机,MATLAB 软件四、 实验内容、实验方法与步骤已知系统传递函数1、 求系统在时间常数 T 不同取值时的单位脉冲、单位阶跃响应和任意输入响应。
应用impulse 函数,可以得到T 0 , T =0.0125、T =0.025 时系统单位脉冲响应;应用 step 函数,同样可以得到 T =0 , T 0.0125、T =0.025时系统单位阶跃响应。
2、 求系统的瞬态性能指标五、实验结果1、系统在时间常数 T 不同取值时的单位脉冲、单位阶跃响应和任意输入响t=[0:0.01:0.8];% 仿真时间区段n G=[50];tao=0; dG=[0.05 1+50*tao 50]; G1=tf(nG,dG);tao=0.0125; dG=[0.051+50*tao 50]; G2=tf(nG,dG); tao=0.025;dG=[0.05 1+50*tao 50]; G3=tf(nG,dG);% 三种 T 值下,系统的传递函数模 型[y1,T]=impulse(G1,t);[y1a,T]=step(G1,t);[y2,T]=impulse(G2,t);[y2a,T]=step(G2,t);[y3,T]=impulse(G3,t);[y3a,T]=step(G3,t);% 系统响应 subplot(131),plot(T,y1,'--',T,y2,'-.',T,y3,'-') lege nd('tao=0','tao=0.0125','tao=0.025') xlabel('t(sec)'),ylabel('x(t)');grid on; subplot(132),plot(T,y1a,'--',T,y2a,'-.',T,y3a,'-')lege nd('tao=0','tao=0.0125','tao=0.025')grid on;xlabel('t(sec)'),ylabel('x(t)');% 产生图形t=[0:0.01:1];u=si n(2*pi*t);% 仿真时间区段和输入 G(s) 50 ______ 0.05s 2 (1 )s 50Tao=0.025;nG=[50]; dG=[0.05 1+50*tao 50]; G=tf(nG,dG);% 系统传递函数模型y=lsim(G,u,t); %求系统响应plot(t,u,'--',t,y,'-',t,u'-y,'-.','l in ewidth',1)lege nd('u(t)','xo(t)','e(t)')grid; xlabel('t(sec)'),ylabel('x(t)');% 产生图形t=[0:0.01:1];u=si n(2*pi*t);tao=0.025;1+50*tao 50];G=tf( nG,dG);n G=[50];dG=[0.05y=lsim(G,u,t);subplot(133),plot(t,u,'--',t,y,'-',t,u-y','-.','li newidth',1) lege nd('u(t)','xo(t)','e(t)') gridon;xlabel('t(sec)'),ylabel('x(t)');系统在时间常数T不同取值时的单位脉冲、单位阶跃响应和任意输入响应匍启• ........ 4- -------------------------------- kOil CL4 QS I Q32、系统的瞬态性能指标t=0:0.001:1; % 设定仿真时间区段和误差限yss=1;dta=0.02;tao=0; dG=[0.05 1+50*tao 50]; G1=tf(nG,dG);tao=0.0125; dG=[0.05 1+50*tao 50]; G2=tf(nG,dG);tao=0.025; dG=[0.05 1+50*tao 50]; G3=tf(nG,dG); % 三种T值下,系统的传递函数模型y1=step(G1,t);y2=step(G2,t);y3=step(G3,t); %三种T值下,系统的单位阶跃响应r=1;while y1(r)<yss;r=r+1;endtr1=(r-1)*0.001; % T=0时的上升时间[ymax,tp]=max(y1);tp1=(tp-1)*0.001;% 峰值时间mp1=(ymax-yss)/yss;% 最大超调量s=1001;while y1(s)>1-dta&y1(s)<1+dta;s=s-1;endts1=(s-1)*0.001;% 调整时间r=1;while y2(r)<yss;r=r+1;end tr2=(r-1)*0.001;[ymax,tp]=max(y2);tp2=(tp-1)*0.001;mp2=(ymax-yss)/yss;s=1001;while y2(s)>1-dta&y2(s)<1+dta;s=s-1;endts2=(s-1)*0.001;% 7=0.0125 的性能指标r=1;while y3(r)<yss;r=r+1;end tr3=(r-1)*0.001;[ymax,tp]=max(y3);tp3=(tp-1)*0.001;mp3=(ymax-yss)/yss;s=1001;while y3(s)>1-dta&y3(s)<1+dta;s=s-1;endts3=(s-1)*0.001;% 7=0.025 的性能指标[tr1 tp1 mp1 ts1;tr2 tp2 mp2 ts2;tr3 tp3 mp3 ts3]% 显示ans =0.0640 0.1050 0.3509 0.35300.0780 0.1160 0.1523 0.25000.1070 0.1410 0.0415 0.1880实验二“控制系统频率特性分析”实验报告一、实验类型验证性实验二、实验目的1利用MATLAB 绘制Nyquist图2、利用MATLAB 绘制Bode图3、利用MATLAB求系统的频域特征量三、实验仪器与设备(或工具软件)计算机,MATLAB软件四、实验内容、实验方法与步骤已知系统传递函数〜、24(0.25s 0.5)G(s)(2.5s 1)(0.025s 1)1利用MATLAB 绘制Nyquist图2、利用MATLAB 绘制Bode图3、利用MATLAB求系统的频域特征量五、实验结果(1)k=24, numG 仁k*[0.25 0.5];denG仁conv([5 2],[0.05 2]); % 系统的传递函数%[re,im]=nyquist( nu mG1,de nG1); % 求时频特性和虚频特性% plot(re,im);grid % 生成Nyquist 图利用MATLAB绘制Nyquist图:(2)k=24,numG1= k*[0.25 0.5];denG 仁conv([5 2],[0.05 2]);% 系统的传递函数 % w=logspace(-2,3,100); % 产生介于 10-2(0.01)和 103(1000)之间的 100 个频率点 %bode(numG1,denG1,w);grid %绘制 Bode 图 利用MATLAB 绘制Bode 图% : Fr 舒朋riGf (3 )禾9用MATLAB 求系统的频域特征量k =24Mr =9.5398Wr =0.0100M0 =9.5398Wb =3.3516mp)IJpnII&lelAIio'2 1C -1 10°10 1O 2 10i -ir r r«i r -------------- R — t - - lr r mT T —i —■— r T■上4一实验三、“控制系统的稳定性分析”实验报告一、实验类型验证性实验二、实验目的1利用MATLAB求系统的特征根。
大工14秋《控制系统实验》实验报告

大工14秋《控制系统实验》实验报告
实验目标
本实验旨在帮助学生掌握控制系统的基本原理和实验方法,通
过实际操作和数据分析来加深对控制系统的理解。
实验步骤
1. 实验准备:确认实验所需设备和材料是否齐全,并检查实验
装置是否正常运行。
2. 实验设置:根据实验要求,调整实验装置的参数和初始条件。
3. 数据记录:在实验过程中,记录所测得的各项数据,包括输
入信号、输出信号和系统参数。
4. 数据分析:对实验所得数据进行分析,利用控制系统原理和
方法来验证实验结果的正确性。
5. 实验总结:根据实验过程和结果,总结实验所得的经验和教训,并提出改进控制系统的建议。
实验结果
根据实验数据和分析结果,我们得出以下结论:
1. 控制系统在给定输入下能够达到稳定状态,并且输出与预期
值吻合。
2. 调整系统参数能够改变系统的动态响应特性,如稳定时间、
超调量等。
3. 控制系统的性能指标可以通过合适的控制策略得到改善。
实验总结
通过本次实验,我们对控制系统的基本原理和实验方法有了更
深入的了解。
同时,我们也意识到控制系统设计的重要性和挑战性。
在今后的研究和工作中,我们将继续深化对控制系统的研究和应用。
参考文献
- 控制系统实验教程
- 控制系统原理与设计,第四版
- 控制系统实验报告范例。
计算机控制实验报告初稿

G(s)=Gc(s)·Gp2(s)
=K(Tis+1)/s·1/s(0.1s+1)
为使用环系统稳定,应满足Ti>0.1,即K1<10
7.PID递推算法如果PID调节器输入信号为e(t),其输送信号为u(t),则离散的递推算法如下:
Gs=tf([5],[1,1,0]);
Gz=c2d(Gs,0.1,'zoh');//求解广义对象的脉冲传递函数
Transfer function:
0.02419 z + 0.02339
----------------------
z^2 - 1.905 z + 0.9048
Sampling time: 0.1
G=c2d(G1,0.01,'zoh');//求系统脉冲传递函数
rlocus(G);//绘制系统根轨迹
将图片放大得到
Z平面的临界放大系数由根轨迹与单位圆的交点求得。
放大图片分析:
[k,poles]=rlocfind(G)
Select a point in the graphics window
selected_point =
0.9905 + 0.1385i
k =
193.6417
poles =
0.9902 + 0.1385i
0.9902 - 0.1385i
得到0<K<193
(2)假设不考虑采样开关和零阶保持器的影响,即看作一连续系统,讨论令系统稳定的 的取值范围;
解:
G1=tf([1],[1 1 0]);
实验三、控制系统的稳定性分析
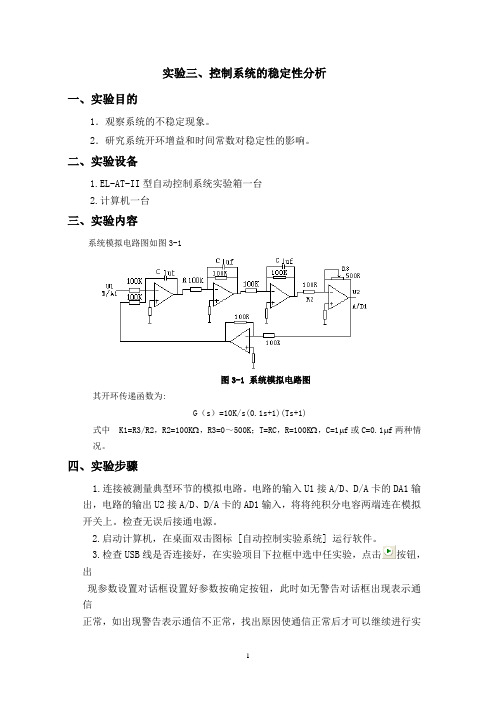
实验三、控制系统的稳定性分析一、实验目的1.观察系统的不稳定现象。
2.研究系统开环增益和时间常数对稳定性的影响。
二、实验设备1.EL-AT-II型自动控制系统实验箱一台2.计算机一台三、实验内容系统模拟电路图如图3-1图3-1 系统模拟电路图其开环传递函数为:G(s)=10K/s(0.1s+1)(Ts+1)式中 K1=R3/R2,R2=100KΩ,R3=0~500K;T=RC,R=100KΩ,C=1μf或C=0.1μf两种情况。
四、实验步骤1.连接被测量典型环节的模拟电路。
电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入,将将纯积分电容两端连在模拟开关上。
检查无误后接通电源。
2.启动计算机,在桌面双击图标 [自动控制实验系统] 运行软件。
3.检查USB线是否连接好,在实验项目下拉框中选中任实验,点击按钮,出现参数设置对话框设置好参数按确定按钮,此时如无警告对话框出现表示通信正常,如出现警告表示通信不正常,找出原因使通信正常后才可以继续进行实验。
4.在实验项目的下拉列表中选择实验三[控制系统的稳定性分析], 鼠标单击按钮,弹出实验课题参数设置对话框。
在参数设置对话框中设置目的电压U1=1000mV鼠标单击确认等待屏幕的显示区显示实验结果。
5.取R3的值为50KΩ,100KΩ,200KΩ,此时相应的K=10K1=5,10,20。
观察不同R3值时显示区内的输出波形(既U2的波形),找到系统输出产生增幅振荡时相应的R3及K值。
再把电阻R3由大至小变化,即R3=200kΩ,100kΩ,50kΩ,观察不同R3值时显示区内的输出波形, 找出系统输出产生等幅振荡变化的R3及K值,并观察U2的输出波形。
6.在步骤5条件下,使系统工作在不稳定状态,即工作在等幅振荡情况。
改变电路中的电容C由1μf变成0.1μf,重复实验步骤4观察系统稳定性的变化。
7.将实验结果添入下表中:五、实验结果12(1)C=1uf R3=50K K=2(2)R3=100K C=1uf K=10(3)R3=200K C=1uf K=20(4) C=0.1uf R3=50K K=5(5) R3=100K C=0.1uf K=10(6) R3=200K C=0.1uf K=20六、实验总结通过这次实验,我观察了系统的不稳定现象,并了解了系统开环增益和时间常数对稳定性的影响。
控制系统的稳定性分析实验报告范文

控制系统的稳定性分析实验报告范文下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!控制系统的稳定性分析实验报告1. 引言控制系统的稳定性分析是控制工程领域的重要研究方向之一。
数字pid控制实验报告doc

数字pid控制实验报告doc数字pid控制实验报告篇一:实验三数字PID控制实验三数字PID控制一、实验目的1.研究PID控制器的参数对系统稳定性及过渡过程的影响。
2.研究采样周期T对系统特性的影响。
3.研究I型系统及系统的稳定误差。
二、实验仪器1.EL-AT-III型计算机控制系统实验箱一台2.PC计算机一台三、实验内容1.系统结构图如3-1图。
图3-1 系统结构图图中 Gc(s)=Kp(1+Ki/s+Kds)Gh(s)=(1-e-TS)/sGp1(s)=5/((0.5s+1)(0.1s+1))Gp2(s)=1/(s(0.1s+1))2.开环系统(被控制对象)的模拟电路图如图3-2和图3-3,其中图3-2对应GP1(s),图3-3对应Gp2(s)。
图3-2 开环系统结构图1 图3-3开环系统结构图23.被控对象GP1(s)为“0型”系统,采用PI控制或PID控制,可系统变为“I型”系统,被控对象Gp2(s)为“I型”系统,采用PI控制或PID控制可使系统变成“II 型”系统。
4.当r(t)=1(t)时(实际是方波),研究其过渡过程。
5.PI调节器及PID调节器的增益Gc(s)=Kp(1+K1/s)=KpK1((1/k1)s+1) /s=K(Tis+1)/s式中 K=KpKi ,Ti=(1/K1)不难看出PI调节器的增益K=KpKi,因此在改变Ki时,同时改变了闭环增益K,如果不想改变K,则应相应改变Kp。
采用PID调节器相同。
6.“II型”系统要注意稳定性。
对于Gp2(s),若采用PI调节器控制,其开环传递函数为G(s)=Gc(s)·Gp2(s)=K(Tis+1)/s·(本文来自:/doc/a1e402b1c081e53a580216fc700abb 68a882ad33.html 小草范文网:数字pid控制实验报告)1/s(0.1s+1)为使用环系统稳定,应满足Ti>0.1,即K1 7.PID 递推算法如果PID 调节器输入信号为e(t),其输送信号为u(t),则离散的递推算法如下:u(k)=u(k-1)+q0e(k)+q1e(k-1)+q2e(k-2)其中 q0=Kp(1+KiT+(Kd/T))q1=-Kp(1+(2Kd/T))q2=Kp(Kd/T)T--采样周期四、实验步骤1.连接被测量典型环节的模拟电路(图3-2)。
计算机控制系统实验报告

《计算机控制系统》实验报告学校:上海海事大学学院:物流工程学院专业:电气工程及其自动化姓名:***学号:************一、实验课程教学目的与任务通过实验设计或计算机仿真设计,使学生了解和掌握数字PID控制算法的特点、了解系统PID参数整定和数字控制系统的直接设计的基本方法,了解不同的控制算法对被控对象的控制特性,加深对计算机控制系统理论的认识,掌握计算机控制系统的整定技术,对系统整体设计有一个初步的了解。
根据各个实验项目,完成实验报告(用实验报告专用纸)。
二、实验要求学生在熟悉PC机的基础上,熟悉MATLAB软件的操作,熟悉Simulink工具箱的软件编程。
通过编程完成系统的设计与仿真实验,逐步学习控制系统的设计,学习控制系统方案的评估与系统指标评估的方法。
计算机控制系统主要技术指标和要求:根据被控对象的特性,从自动控制系统的静态和动态质量指标要求出发对调节器进行系统设计,整体上要求系统必须有良好的稳定性、准确性和快速性。
一般要求系统在振荡2~3次左右进入稳定;系统静差小于3%~5%的稳定值(或系统的静态误差足够小);系统超调量小于30%~50%的稳定值;动态过渡过程时间在3~5倍的被控对象时间常数值。
系统整定的一般原则:将比例度置于较大值,使系统稳定运行。
根据要求,逐渐减小比例度,使系统的衰减比趋向于4:1或10:1。
若要改善系统的静态特性,要使系统的静差为零,加入积分环节,积分时间由大向小进行调节。
若要改善系统的动态特性,增加系统的灵敏度,克服被控对象的惯性,可以加入微分环节,微分时间由小到大进行调节。
PID控制的三个特性参数在调节时会产生相互的影响,整定时必需综合考虑。
系统的整定过程是一个反复进行的过程,需反复进行。
实验一、数字PID 参数的整定一、 实验目的1)、了解数字PID 控制回路的结构。
2)、掌握数字PID 控制算法的控制原理。
3)、掌握数字PID 控制算法的整定原理。
控制系统实训实验报告

一、实验目的1. 了解控制系统的基本组成和原理。
2. 掌握控制系统调试和性能测试方法。
3. 培养动手能力和团队协作精神。
4. 熟悉相关实验设备和软件的使用。
二、实验原理控制系统是指通过某种方式对某个系统进行控制,使其按照预定的要求进行运行。
控制系统主要由控制器、被控对象和反馈环节组成。
控制器根据被控对象的输出信号,通过调节输入信号,实现对被控对象的控制。
本实验主要研究PID控制系统的原理和应用。
三、实验仪器与设备1. 实验箱:用于搭建控制系统实验电路。
2. 数据采集卡:用于采集实验数据。
3. 计算机:用于运行实验软件和数据处理。
4. 实验软件:用于控制系统仿真和调试。
四、实验内容1. 控制系统搭建:根据实验要求,搭建PID控制系统实验电路,包括控制器、被控对象和反馈环节。
2. 控制系统调试:对搭建好的控制系统进行调试,包括控制器参数的整定、系统稳定性和响应速度的调整等。
3. 控制系统性能测试:对调试好的控制系统进行性能测试,包括系统稳定性、响应速度、超调量等指标。
4. 控制系统仿真:利用实验软件对控制系统进行仿真,分析系统在不同参数下的性能。
五、实验步骤1. 控制系统搭建:按照实验要求,连接控制器、被控对象和反馈环节,搭建PID控制系统实验电路。
2. 控制系统调试:根据实验要求,调整控制器参数,使系统达到预定的性能指标。
3. 控制系统性能测试:对调试好的控制系统进行性能测试,记录测试数据。
4. 控制系统仿真:利用实验软件对控制系统进行仿真,分析系统在不同参数下的性能。
六、实验结果与分析1. 控制系统搭建:成功搭建了PID控制系统实验电路。
2. 控制系统调试:通过调整控制器参数,使系统达到预定的性能指标。
3. 控制系统性能测试:系统稳定性、响应速度、超调量等指标均达到预期效果。
4. 控制系统仿真:仿真结果表明,系统在不同参数下具有良好的性能。
七、实验总结1. 通过本次实验,了解了控制系统的基本组成和原理。
系统控制实验报告(3篇)

第1篇一、实验目的1. 掌握系统控制的基本原理和方法。
2. 熟悉最少拍控制系统的分析方法。
3. 了解输入信号对最小拍控制系统的影响及其改进措施。
4. 培养实验操作能力和数据分析能力。
二、实验原理最少拍控制系统是一种直接数字设计方法,其目的是使闭环系统对于某种特定的输入在最少个采样周期内达到无静差的稳态,使系统输出值尽快地跟踪期望值的变化。
其闭环传递函数具有形式:\[ G(s) = \frac{1}{(z-1)^N} \]其中,N是可能情况下的最小正整数。
这一传递形式表明闭环系统的脉冲响应在N个采样周期后变为零,从而意味着系统在N拍之内到达稳态。
三、实验设备1. 硬件环境:- 微型计算机一台,Pentium 4以上各类微机2. 软件平台:- 操作系统:Windows 2000- 仿真软件:MATLAB6.0四、实验内容与步骤1. 计算控制器:- 按照系统要求计算最少拍有纹波控制器。
2. 构造系统结构图模型:- 在Simulink下构造系统结构图模型。
- 取输入信号为单位阶跃信号和单位速度信号。
3. 设计控制器:- 设计控制器,观察输入输出波型,标明参数,打印结果。
4. 观察系统输出波形:- 观察系统输出波形在采样点以外的波形。
五、实验结果与分析1. 单位阶跃输入下的最少拍有纹波控制系统:- 通过仿真,可以得到单位阶跃输入下的最少拍有纹波控制系统的输出波形,如图1-2所示。
- 从图中可以看出,系统在3个采样周期内达到稳态,且稳态误差较小。
2. 单位速度输入下的最少拍有纹波控制系统:- 通过仿真,可以得到单位速度输入下的最少拍有纹波控制系统的输出波形。
- 从图中可以看出,系统在3个采样周期内达到稳态,且稳态误差较小。
3. 输入信号对系统的影响:- 通过改变输入信号,可以观察到输入信号对系统输出波形的影响。
- 例如,当输入信号为单位阶跃信号时,系统输出波形呈现出明显的纹波现象;而当输入信号为单位速度信号时,系统输出波形则较为平滑。
电气控制系统工程实习报告

电气控制系统工程实习报告一、实习单位简介在XX公司进行了为期8周的电气控制系统工程实习。
该公司是一家专注于电力工程设计与施工的企业,承接了大量的电力工程项目,包括变电站、配电线路、发电厂等等。
实习期间,我主要参与了一个变电站的电气控制系统设计与调试工作。
二、实习目标与任务1.实习目标:通过实习,加深对电气控制系统的理解与认识,了解实践中的问题与挑战,提高工程实践能力。
2.实习任务:参与变电站电气控制系统的设计与调试工作,包括了解设计要求、制定方案、安装调试等。
三、实习过程1.学习与了解:首先,我对电气控制系统进行了深入学习与了解,包括控制系统的组成、原理、常见的控制方式等。
通过阅读相关资料与参观实际工程现场,对电气控制系统的实践应用进行了初步了解。
2.制定方案:在了解了工程项目的具体要求后,我参与了电气控制系统的方案制定。
通过与其他团队成员的讨论与交流,我们确定了最佳的方案,并开始进行设计。
3.设计与制作:在设计过程中,我主要负责电气控制系统中的开关控制电路与电气接口设计。
通过使用CAD软件进行布线设计与绘制,我成功完成了相关设计的任务。
4.安装调试:随后,我参与了电气控制系统的安装与调试工作。
这包括了对电气控制设备的安装、接线与连接的工作,以及联调与调试的过程。
5.质量检验与维护:最后,我参与了对已安装调试的电气控制系统的质量检验与维护工作。
通过对系统各个部分的检查与测试,确保系统运行良好,符合设计要求。
四、实习收获与体会1.知识应用:通过实习,我将学习到的电气控制系统理论知识应用到了实际工程中,提高了自己的工程实践能力。
2.团队合作:在与团队成员的合作中,我了解到了团队协作的重要性。
只有相互配合、共同努力,才能顺利完成工程任务。
3.问题解决:在实习过程中,我遇到了一些问题与挑战,包括设备故障、接线错误等。
通过仔细分析与解决,我成功解决了这些问题,提升了自己的问题解决能力。
4.工程实践:实习期间,我真实地体验了电气控制系统工程的实践过程,对工程管理、施工流程等方面有了更深入的了解。
控制系统设计实验报告

控制系统设计实验报告本实验旨在设计并验证一个基本控制系统,通过对系统的各种参数进行调整,以实现对被控对象的控制。
在本实验中,我们将尝试使用PID控制器来控制一个由电机驱动的转动物体的角度。
通过调整PID控制器的参数,我们将研究不同参数对系统性能的影响,以及如何优化控制系统以实现更精确的控制。
1. 实验设备与原理我们使用的控制系统由以下几个部分组成:电机驱动的转动物体、编码器、PID控制器、电机驱动器以及PC这几个基础模块。
电机驱动的转动物体作为被控对象,编码器用于检测物体的实际角度,PID控制器根据检测到的角度与期望角度之间的误差来调整控制信号,电机驱动器根据PID控制器输出的信号驱动电机进行运动,PC用于设置期望角度、监控系统运行情况以及调整PID控制器的参数。
2. 实验步骤首先,我们需要连接各个模块,确保他们能够正常工作。
然后,在PC上设置期望角度,并将PID控制器初始参数设为0,0,0。
启动系统后,我们可以观察到被控对象的实际角度逐渐接近期望角度。
接下来,我们开始调整PID控制器的参数,首先逐步增大比例系数Kp,观察系统响应速度以及超调量的变化。
然后,我们继续增大积分系数Ki,观察系统的稳定性和静差的变化。
最后,我们调整微分系数Kd,观察系统对干扰的抑制能力。
通过这一系列操作,我们可以找到最佳的PID控制器参数组合,使系统表现出最优的性能。
3. 实验结果与分析经过多次实验,我们得到了一组最佳的PID控制器参数:Kp=1.2,Ki=0.5,Kd=0.1。
使用这组参数,系统能够在较短的时间内将被控对象的实际角度调整到期望角度,且幅度较小的超调量。
同时,系统对干扰的抑制也表现出较好的效果,能够快速回到期望角度。
4. 结论与展望通过本实验,我们成功设计并验证了一个基本的控制系统,并找到了最佳的PID控制器参数组合。
在今后的研究中,我们可以进一步优化控制系统,尝试其他类型的控制器,如模糊控制器、神经网络控制器等,以实现更加精确和高效的控制。
控制实验完整版

2
0.5S 3 +S 2 +0.5S+2
3.
主导极点的作用: 将高阶系统的主导极点分析出来, 可以用主导极点来评估高阶系统的性能 指标,利用主导极点来分析系统,相当于降低了系统的阶数,给分析带来方便。
实验二:根轨迹绘制与分析
传递函数 根轨迹图形
Kg 0.2s + 1 (2s + 1)
Kg(0.1S + 1) 0.2s + 1 (2s + 1)
Kg 0.2s + 1 2s + 1 (S + 1)
Kg(S + 1) 0.2s + 1 (2s + 1)
Kg(0.01S + 1) 0.2s + 1 (2s + 1)
Kg 0.2s + 1 2s + 1 (0.1S + 1)
Kg 0.2s + 1 2s + 1 (10S + 1)
附加零极点对根轨迹的影响: (1)增加零极点会改变渐近线的条数;(2)增加零点,根轨迹 向左弯曲或者移动,增加了系统的稳定性,且越靠近原点,系统的稳定性越强; (3)增加极 点,根轨迹向右弯曲或者移动,降低了系统的稳定性,且越靠近原点,系统的稳定性越差。
;阻尼比:ζ =2
1
T0 K1T1
T1
?
n ?
实验图象
1.2
0.2
������ ������ ������������
������
1.414
0.707
������ ������
������
1
1
������ ������
1
三阶系统: 1.系统的开环传函为:G(S) H(S)=T0T1T2S 3 +T0 2.(1).系统稳定 K 值的范围:T0>
控制系统的稳定性分析实验报告

控制系统的稳定性分析实验报告引言控制系统的稳定性是指系统在扰动作用下,能否保持稳定运行的能力。
在实际应用中,对于控制系统的稳定性分析具有重要的意义。
本实验旨在通过实际实验,分析控制系统的稳定性,并对结果进行报告。
实验设备和方法设备本实验使用的设备如下:1.一台控制系统稳定性分析实验设备2.一台电脑方法1.将实验设备接通电源,等待设备启动完毕。
2.打开电脑,运行实验软件。
3.在实验软件中设置实验参数,包括控制系统的传递函数、采样时间等。
4.开始实验,并记录实验过程中的数据。
5.分析实验结果,得出控制系统的稳定性结论。
6.撰写实验报告。
实验结果与分析在本次实验中,我们选择了一个二阶惯性系统作为被控对象,传递函数为$G(s)=\\frac{1}{(s+1)(s+2)}$。
我们使用了PID控制器进行控制,并设置了合适的参数。
实验过程中,我们输入了一个单位阶跃信号,观察系统的响应。
通过记录实验数据并进行分析,我们得到了以下实验结果:1.系统的超调量为5%;2.系统的稳态误差为0.1;3.系统的调节时间为2秒。
根据实验结果,我们可以得出以下结论:1.系统的超调量很小,说明系统具有较好的动态性能;2.系统的稳态误差较小,说明系统具有较好的稳定性;3.系统的调节时间较短,说明系统的响应速度较快。
综上所述,实验结果表明控制系统具有较好的稳定性。
结论通过本次实验,我们通过实际实验和数据分析,得出了控制系统的稳定性结论。
实验结果表明控制系统具有较好的稳定性。
控制系统的稳定性是保证系统正常运行的重要指标,对于工程应用具有重要的意义。
参考文献无。
自动控制原理实验报告(实验一,二,三)分析

自动控制原理实验报告实验名称:线性系统的时域分析线性系统的频域分析线性系统的校正与状态反馈班级:学号:姓名:指导老师:2013 年12 月15日典型环节的模拟研究一. 实验目的1.了解和掌握各典型环节模拟电路的构成方法、传递函数表达式及输出时域函数表达式2.观察和分析各典型环节的阶跃响应曲线,了解各项电路参数对典型环节动态特性的影响二.实验内容及步骤观察和分析各典型环节的阶跃响应曲线,了解各项电路参数对典型环节动态特性的影响.。
改变被测环节的各项电路参数,画出模拟电路图,阶跃响应曲线,观测结果,填入实验报告运行LABACT 程序,选择自动控制菜单下的线性系统的时域分析下的典型环节的模拟研究中的相应实验项目,就会弹出虚拟示波器的界面,点击开始即可使用本实验机配套的虚拟示波器(B3)单元的CH1测孔测量波形。
具体用法参见用户手册中的示波器部分1).观察比例环节的阶跃响应曲线典型比例环节模拟电路如图3-1-1所示。
图3-1-1 典型比例环节模拟电路传递函数:01(S)(S)(S)R R K KU U G i O === ; 单位阶跃响应: K )t (U = 实验步骤:注:‘S ST ’用短路套短接!(1)将函数发生器(B5)所产生的周期性矩形波信号(OUT ),作为系统的信号输入(Ui );该信号为零输出时,将自动对模拟电路锁零。
① 在显示与功能选择(D1)单元中,通过波形选择按键选中矩形波’(矩形波指示灯亮)。
② 量程选择开关S2置下档,调节“设定电位器1”,使之矩形波宽度>1秒(D1单元左显示)。
③ 调节B5单元的“矩形波调幅”电位器使矩形波输出电压= 4V (D1单元‘右显示)。
(2)构造模拟电路:按图3-1-1安置短路套及测孔联线,表如下。
(a )安置短路套 (b )测孔联线(3)运行、观察、记录:打开虚拟示波器的界面,点击开始,按下信号发生器(B1)阶跃信号按钮(0→+4V 阶跃),观测A5B 输出端(Uo )的实际响应曲线。
控制系统实验报告(2013-1-18)

控制系统实验报告(2013-1-18)电⽓学科⼤类2010 级《信号与控制综合实验》课程实验报告(基本实验⼀:⾃动控制理论基本实验)姓名学号专业班号同组者1 学号专业班号同组者2 学号专业班号指导教师⽇期实验成绩评阅⼈实验评分表⽬录实验⼗⼀、⼆阶系统的模拟与动态性能的研究 (3)⼀、实验⽬的 (3)⼆、实验原理 (3)三、⽅案实现过程 (3)四、实验结果 (3)五、实验结果分析 (4)六、思考题 (4)实验⼗⼆、⼆阶系统的模拟与动态性能的研究 (4)⼀、实验⽬的 (4)⼆、实验原理 (5)三、⽅案实现过程 (5)四、实验结果 (5)五、实验结果分析 (5)六、思考题 (5)实验⼗四、线性控制系统的设计与校正 (6)⼀、实验⽬的 (6)⼆、实验原理 (6)三、⽅案实现过程 (6)四、实验结果 (8)五、实验结果分析 (9)六、思考题 (9)实验⼗六、控制系统状态反馈控制器设计 (9)⼀、实验⽬的 (10)⼆、实验原理 (10)三、⽅案实现过程 (10)四、实验结果 (11)五、实验结果分析 (12)六、思考题 (12)实验⼗七、基于内模原理的状态反馈控制 (13)⼀、实验⽬的 (13)⼆、实验原理 (13)三、⽅案实现过程 (13)四、实验结果 (14)五、实验结果分析 (15)六、思考题 (16)参考⽂献 (16)感想 (16)实验⼗⼀、⼆阶系统的模拟与动态性能的研究⼀、实验⽬的1.学会各个环节的模拟电路的实现⽅法,并学会构建⼆阶系统模型;2.理解电路参数对⼆阶系统参数的影响并掌握其设计⽅法。
3.设计时利⽤速度反馈使阻尼⽐和⽆阻尼⾃然频率相互独⽴。
⼆、实验原理由实验电路图可推知,只改变可变电阻的⼤⼩可以只改变⼆阶系统的阻尼⽐,只改变电容的⼤⼩则只改变⽆阻尼⾃然频率。
这是因为引⼊了速度反馈。
三、⽅案实现过程1.按电路图搭建好⼆阶系统,调节函数信号发⽣器,使其输出峰峰值为1V ,频率为10Hz 的⽅波,将其作为⼆阶系统的输⼊,并将⽰波器的CH1接⼆阶系统的输⼊,CH2接⼆阶系统的输出。
电机控制实验报告分析(3篇)

第1篇一、实验背景电机控制技术在现代工业和日常生活中扮演着重要角色,其性能直接影响着设备的运行效率和稳定性。
为了更好地理解和掌握电机控制技术,我们进行了一系列电机控制实验。
本报告将对实验过程、结果及分析进行详细阐述。
二、实验目的1. 熟悉电机控制系统的基本组成和原理;2. 掌握电机控制实验的操作步骤和注意事项;3. 分析实验数据,验证电机控制理论;4. 提高实际操作能力和故障排除能力。
三、实验内容1. 电机控制实验平台搭建实验平台主要包括电机、控制器、传感器、电源等设备。
实验过程中,我们需要根据实验要求,正确连接各设备,确保实验顺利进行。
2. 电机调速实验通过调整PWM信号的占空比,实现对电机转速的调节。
实验中,我们测试了不同占空比下电机的转速,并记录实验数据。
3. 电机转向控制实验通过改变PWM信号的极性,实现对电机转向的控制。
实验中,我们测试了不同极性下电机的转向,并记录实验数据。
4. 电机制动实验通过调整PWM信号的占空比和极性,实现对电机制动的控制。
实验中,我们测试了不同制动条件下电机的制动效果,并记录实验数据。
四、实验结果与分析1. 电机调速实验结果分析实验结果显示,随着PWM占空比的增大,电机转速逐渐提高。
当占空比为100%时,电机达到最大转速。
实验数据与理论分析基本一致。
2. 电机转向控制实验结果分析实验结果显示,通过改变PWM信号的极性,可以实现对电机转向的控制。
当PWM信号极性为正时,电机正转;当PWM信号极性为负时,电机反转。
实验数据与理论分析相符。
3. 电机制动实验结果分析实验结果显示,通过调整PWM信号的占空比和极性,可以实现对电机制动的控制。
当PWM信号占空比为0时,电机完全制动;当占空比逐渐增大时,电机制动效果逐渐减弱。
实验数据与理论分析基本一致。
五、实验结论1. 电机控制实验平台搭建成功,能够满足实验要求;2. 电机调速、转向和制动实验均取得了良好的效果,验证了电机控制理论;3. 通过实验,提高了实际操作能力和故障排除能力。
计算机控制系统实验报告DOC

计算机控制系统实验报告实验一 :D/A 数模转换实验实验报告:1、数字量与模拟量的对应曲线:2、理论值与实测值对比:数字量模拟量 理论值实测值1004756 4722 200 4512 4412 300 4268 4325 400 4023 4078 500 3780 3664 600353536313、分析产生误差的原因:答:a)外界干扰会对实验造成误差;b)系仪器本身误差;c)仪器元件不够精确,导致试验产生误差。
这是本实验的最主要的误差来源。
4、总结:本次试验需要进行的连电路、实验软件操作都比较简单,但对于实验原理我们应有更加深刻的理解,对于实验箱内部的D/A转换原理要有所思考,不能只满足与简单的实验表象,而应思考更深层次的问题。
实验二 :A/D 模数转换实验实验报告:1、模拟量与数字量的对应曲线:2、理论值与实测值对比:3、分析产生误差的原因:答:a)系仪器误差、实验软件的精度误差;b)外界干扰会对实验造成误差;模拟量数字量理论值实测值 500 439 461 1000 409 410 2000 292 307 4000 97 103 -1000 586 614 -4000879921c)仪器元件不够精确,导致试验产生误差。
这是本实验的最主要的误差来源。
4、总结:书本上学习的模数转换都是理论知识,过程相对比较复杂,本次试验需要进行的连电路、实验软件操作都比较简单,但对于实验原理我们应有更加深刻的理解,对于实验箱内部的A/D转换原理要有所思考,不能只满足与简单的实验表象,而应思考更深层次的问题。
实验三:数字PID控制实验报告:1、画出所做实验的模拟电路图:2、当被控对象为Gpl(s时)取过渡过程为最满意时Kp,Ki,Kd,画出校正后的Bode图,查出相对裕量γ和穿越频率Wc:跃响应曲线及时域性能指标,记入表中:0型系统:实验结果参数δ% Ts(ms)阶跃响应曲线Kp Ki Kd1 0.02 1 11.9% 720 见图3—11 0.05 1 32.5% 800 见图3--25 0.02 1 44.4% 1050 见图3--35 0.05 1 46.1% 1900 见图3--4I型系统:实验结果参数δ% Ts(ms)阶跃响应曲线Kp Ki Kd1 0.02 1 16.0% 420 见图3—51 0.02 2 36.4% 606 见图3--63 0.02 1 49.4% 500 见图3--73 0.1 1 56.4% 1050 见图3--8下面是根据上表中数据,所得到的相应曲线:图3-1 Kp=1 Ki=0.02 Kd=1 Gp1最满意的曲线图其中,相对稳定裕量γ= 82°穿越频率ωc=230rad/s图3-2 Kp=1 Ki=0.05 Kd=1图3-3 Kp=5 Ki=0.02 Kd=1图3-4 Kp=5 Ki=0.05 Kd=1图3-5 Kp=1 Ki=0.02 Kd=1图3-6 Kp=3 Ki=0.02 Kd=1图3-7 Kp=1 Ki=0.02 Kd=2图3-8 Kp=3 Ki=0.01 Kd=13、总结一种有效的选择Kp,Ki,Kd方法,以最快的速度获得满意的参数:答:参数整定找最佳,从小到大顺序查,先是比例后积分,最后再把微分加,曲线振荡很频繁,比例度盘要放大,曲线漂浮绕大湾,比例度盘往小扳,曲线偏离回复慢,积分时间往下降,曲线波动周期长,积分时间再加长,曲线振荡频率快,先把微分降下来,动差大来波动慢,微分时间应加长,理想曲线两个波,前高后低4比1。
实验三 控制系统的稳定性分析
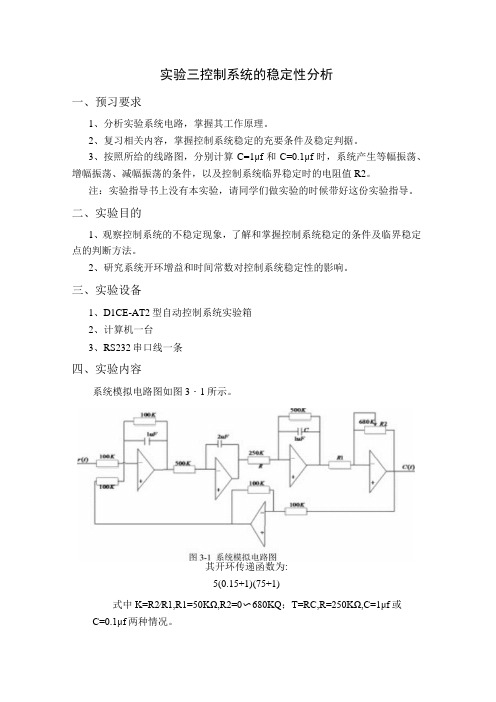
实验三控制系统的稳定性分析一、预习要求1、分析实验系统电路,掌握其工作原理。
2、复习相关内容,掌握控制系统稳定的充要条件及稳定判据。
3、按照所给的线路图,分别计算C=1μf和C=0.1μf时,系统产生等幅振荡、增幅振荡、减幅振荡的条件,以及控制系统临界稳定时的电阻值R2。
注:实验指导书上没有本实验,请同学们做实验的时候带好这份实验指导。
二、实验目的1、观察控制系统的不稳定现象,了解和掌握控制系统稳定的条件及临界稳定点的判断方法。
2、研究系统开环增益和时间常数对控制系统稳定性的影响。
三、实验设备1、D1CE-AT2型自动控制系统实验箱2、计算机一台3、RS232串口线一条四、实验内容系统模拟电路图如图3・1所示。
其开环传递函数为:5(0.15+1)(75+1)式中K=R2∕R1,R1=50KΩ,R2=0〜680KQ;T=RC,R=250KΩ,C=1μf或C=0.1μf两种情况。
1.按系统模拟电路图连接电路(依次使用运放单元U3,U6,U4,U5,U8和U23构建),电路的输入为阶跃信号。
启动计算机运行D1CE计算机控制实现软件,打开实验箱电源。
2.分别取R2的值为IOOKd200KΩ,250KΩ,500KΩ,此时相应的K=2,4,5,IOo 观察不同R2值时示波器窗口内的输出波形(既UO的波形),找到系统输出产生增幅振荡时相应的R2及K值;再把电阻R2由大至小变化,即R2=500KΩ,250KΩ,200KΩ,100KΩ,观察不同R2值时显示区内的输出波形,找出系统输出产生等幅振荡变化的R2及K值,并观察Uo的输出波形。
3.在步骤2条件下,使系统工作在不稳定状态,即工作在等幅振荡情况。
改变电路中的电容C由1μf变成0.1μf,分别取R2的值为500KΩ,680KΩ,750KΩ,950KQ(此时相应的K=IO,13.6,15,19)。
观察不同R2值时示波器窗口内的输出波形(既UO的波形),找到系统输出产生增幅振荡时相应的R2及K值;再把电阻R2由大至小变化,WR2=950KΩ,750KΩ,680KΩ,500KΩ,观察系统稳定性的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名:
一、 实验目的
熟悉 MATLAB 对控制系统的建模以及时域和频域的分析函数。模型,并转化成其他的数学模型
实验代码及执行结果:
1-(1)实验代码及执行结果:
%1-(1)传递函数 G1 ( s)
4( s 2)( s 2 6s 6)2 s( s 1)3 ( s3 3s 2 2s 5)
实验代码:
% stepchar.m子函数 function [pos,tr,ts,tp]=stepchar(g0,delta) [y,t]=step(g0); [mp,ind]=max(y); dimt=length(t); yss=y(dimt); pos=100*(mp-yss)/yss; tp=t(ind); for i=1:dimt if y(i)>=yss tr=t(i);
相角裕度: =42.6 在命令窗口输入命令:[Gm,Pm,Wcm,Wcp]=margin(G) 可以求出幅值裕度:Gm= 5.4038
3.
已知系统传递函数为:
(1)绘出系统在阶跃信号为0.11(t)时的响应曲线,并求系统性能指标:峰值时间、 上升时间、调节时间(要求时间的搜索方向为逆方向,即从 t=->0 方向)、 超调量。 (2)绘出离散化系统在阶跃信号为0.11(t)时的响应曲线,采样周期为T=0.3S.
-1.0000
1.0000 0 B3 = 1 0 C3 = 0 0.5000 D3 = 0 G3zpk = 0.5 ------------(s+2) (s+0.5)
1-(4)实验代码及执行结果:
x1 0 1 x1 0 u -1 -2 x2 1 x % 1-(4)状态方程组 2 x y 0 1 1 x2
2.
一个系统的结构框图如下所示
R(s)
1.5
+ -
s 0.5 s 0.1
20 s ( s 2)( s 10)
Y(s)
(1)试绘出系统闭环的根轨迹图;并确定使系统的阶跃响应为非周期运动模态和 使系统稳定的增益K范围; (2)试绘出系统的bode图,并计算系统的幅值裕量和相角裕量。
(1)与(2)程序代码:
[A2 B2 C2 D2]=tf2ss(num2,den2) [z,p,k]=tf2zp(num2,den2); G2zpk=zpk(z,p,k)
执行结果: A2 = 0 -2 1 0 0 1 B2 = 1 0 0 C2 = 0 4 D2 = 0 G2zpk =
-5 0 0
-2
4 (s-0.5) -------------------------------(s+1.328) (s^2 - 1.328s + 3.764)
超调量 2.5945
上升时间 4.5988
调节时间 6.7396
峰值时间 5.7881
绘出离散化系统在阶跃信号为 0.11(t)时的响应曲线,采样周期为 T=0.3S
实验代码: 在前面的基础上在命令窗口输入命令: step(g0,'r-',sysd,'b-') 绘制图像如下:
4.
已知系统的方框图如下图所示。其中 R1 1, R2 2,C1 3,C2 4, 计算系统的
[z,p,k]=tf2zp(num1,den1); G1zpk=zpk(z,p,k)
%由传递函数形式得到Z、P、K参数 %由上面得到Z、P、K参数转换为零极点形 %式输出到命令窗口
执行结果: G1 = 4 s^5 + 56 s^4 + 288 s^3 + 672 s^2 + 720 s + 288 ----------------------------------------------------s^7 + 6 s^6 + 14 s^5 + 21 s^4 + 24 s^3 + 17 s^2 + 5 s Continuous-time transfer function. A1 = -6 -14 -21 -24 -17 -5 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 B1 = 1 0 0 0 0 0 0 C1 = 0 4 56 288 672 720 288 D1 = 0 G1zpk = 4 (s+4.732)^2 (s+2) (s+1.268)^2 -------------------------------------------s (s+2.904) (s+1)^3 (s^2 + 0.09584s + 1.722)
Gk=tf([1 0.5],[1 0.1])*tf(20,conv([1 2 0],[1 10]));%开环传函 G=1.5*feedback(Gk,1) subplot(2,2,1) step(G) subplot(2,2,2) rlocus(Gk*1.5) subplot(2,2,3) bode(G) 执行结果: %闭环传函并在命令窗口显示 %在同一个图形串口显示多个图像 %绘制闭环传函的阶跃响应曲线 %绘制系统根轨迹图 %绘制系统伯德图
num1=conv(conv([4 8],[1 6 6]),[1 6 6]); %1-(1)分子多项式 den1=conv(conv(conv([1 3 2 5 0],[1 1]),[1 1]),[1 1]); %1-(1) %母子多项式 G1=tf(num1,den1) %1-(1)传递函数 [A1 B1 C1 D1]=tf2ss(num1,den1)%由传递函数转换为状态空间矩阵并输出
break; end end; for i=length(y):-1:1 if y(i)<=(1-delta)*yss||y(i)>=(1+delta)*yss ts=t(i); break; end end %绘系统在阶跃信号为0.11(t)时响应曲线,求系统性能指标:峰值时间、上升时 间、调节时间(要求时间的搜索方向为逆方向,即从t=->0 方向)、超调量。 num=[20]; den=[1 8 36 40 20]; g0=tf(0.1*num,den); delta=0.02; [pos,tr,ts,tp]=stepchar(g0,delta); %调子函数 disp(' 超调量 上升时间 调节时间 ·峰值时间') disp([pos,tr,ts,tp]) sysd=c2d(g0,0.3); step(g0,'r-',sysd,'b-') 执行结果: 系统在阶跃信号为0.11(t)时的响应曲线如下图所示:
(s)=
C (s) 。 R( s )
实验代码:
% 已 知系统的方框图如下图所示。其中 R1 1, R2 2,C1 3,C2 4 , 计算系统的
C (s ) (s ) = 。 R( s )
sys1=tf(1,1);
sys2=tf(1/3,[1 0]); sys3=tf(1/2,1); sys4=tf(1/4,[1 0]); sys5=tf(1,1); sys6=tf(1,1); sys7=tf(1,1); sys=append(sys1,sys2,sys3,sys4,sys5,sys6,sys7); Q=[1,-6,0;2,1,-7;3,2,-5;4,3,0;5,4,0;6,2,0;7,3,0]; outputs=5; inputs=1; sysc=connect(sys,Q,inputs,outputs) 执行结果: sysc = 0.04167 ----------------------s^2 + 0.625 s + 0.04167
系统的阶跃响应为非周期运动模态和使系统稳定的增益 K 范围:
对根轨迹图放大(如下图所示)可以求出非周期运动模态增益 K 范围为: 0<K<0.0036
对根轨迹图放大(如下图所示)可以求出使系统稳定的增益 K 范围:
0 K 5.59
由 bode 图(放大图如下图所示)可知,系统的相角裕量:
1-(2)实验代码及执行结果:
% 1-(2)传递函数 G2 ( s) num2=[4 -2];
4s 2 s 2s 5 %1-(2)分子多项式
3
den2=[1 0 2 5]; G2=tf(num2,den2);
%1-(2)分母多项式 %1-(2)传递函数 %由传递函数形式转换为状态空间 %矩阵输出 %由传递函数形式得到Z、P、K参数 %由上面得到Z、P、K参数转换为零 %极点形式输出到命令窗口
A4=[0 1;-1 -2]; %状态矩阵 B4=[0;1]; C4=[0 1]; D4=0; [z p k]=ss2zp(A4,B4,C4,D4,1);
%状态矩阵转换为Z、P、K参数
G4zpk=zpk(z,p,k) %由Z、P、K参数得到零极点模型 [num4,den4]=ss2tf(A4,B4,C4,D4,1); %状态模型转换为传递函数模型 G4=tf(num4,den4) 执行结果: G4zpk = s ------(s+1)^2 Continuous-time zero/pole/gain model. G4 = s - 2.22e-16 ------------s^2 + 2 s + 1
1-(3)实验代码及执行结果:
% 1-(3)传递函数 G3 ( s)
1 (2s 1)( s 2)
num3=1; den3=conv([2 1],[1 2]); G3=tf(num3,den3); [A3 B3 C3 D3]=tf2ss(num3,den3) [z,p,k]=tf2zp(num3,den3); G3zpk=zpk(z,p,k) 执行结果: A3 = -2.5000
