实验二2MATLAB地符号计算与可视化
如何进行MATLAB地图数据处理和可视化

如何进行MATLAB地图数据处理和可视化地图数据处理和可视化在很多领域中都是很重要的一项任务,如地理信息系统(GIS)、城市规划、气象学等。
MATLAB作为一种功能强大的科学计算软件,提供了丰富的地图数据处理和可视化工具,能够帮助用户快速、准确地处理和展示地理数据。
本文将介绍如何使用MATLAB进行地图数据处理和可视化。
一、导入地图数据在MATLAB中,我们可以通过导入地理数据文件的方式来获取地图数据。
常见的地理数据文件格式包括Shapefile、GeoTIFF等。
运用MATLAB的Mapping Toolbox中的函数,我们可以轻松地读取这些文件,并将其转换成MATLAB能够处理的数据结构。
例如,如果我们有一个Shapefile文件,可以使用shaperead()函数将其读取为MATLAB中的结构体。
该结构体包含了Shapefile中所有的属性和几何信息。
我们可以通过访问这些属性和几何信息,进行进一步的数据处理和可视化操作。
二、地图数据处理与分析在导入地图数据之后,我们可以进行一系列的数据处理和分析操作。
MATLAB 提供了丰富的地理数据处理函数,如计算地理距离、邻近分析、空间插值等。
下面,我们将介绍两个常用的地图数据处理方法。
1. 计算地理距离MATLAB中使用distance()函数可以计算两点之间的地理距离。
这对于一些需要考虑地球曲率的应用非常重要。
例如,在城市规划中,我们可以使用该函数计算出两个位置之间的实际距离,从而帮助规划交通路线、确定最佳布局等。
2. 空间插值空间插值是指根据有限的采样点数据,通过数学方法推算未知点的数值。
在地图数据处理中,空间插值经常用于填充缺失值、生成连续的等值线图等。
MATLAB中的griddata()函数可以对地理数据进行插值,并生成高质量的连续地图。
三、地图数据可视化地图数据可视化是将处理后的地理数据以图形的形式展示出来。
MATLAB提供了多种可视化方式,如制作等高线图、色彩填充地图、散点图等。
Matlab上机操作2——符号计算

Matlab上机操作2——符号计算1、%创建数值常量和符号常量a1=2*sqrt(5)+pi %创建数值常量a2=sym('2*sqrt(5)+pi') %按符号表达式创建符号常量a3=sym(2*sqrt(5)+pi) %按最接近的两个正整数表示符号常量a4=sym(2*sqrt(5)+pi,'d') %按最接近的十进制浮点数表示符号常量a31=a3-a1 %数值常量和符号常量的计算a5='2*sqrt(5)+pi' %字符串常量2、%创建符号变量和符号表达式f1=sym('a*x^2+b*x+c') %创建符号表达式syms a b c x %创建符号变量f2=a*x^2+b*x+c %创建符号表达式syms('a','b','c','x') %注意这里是syms,不是sym>> sym('a','b','c','x')错误使用sym输入参数太多。
f3=a*x^2+b*x+c; %创建符号表达式syms x y real %创建实数符号变量z=x+i*y; %创建z为复数符号变量real(z) %复数z的实部是实数xsym('x','unreal'); %清除符号变量的实数特性real(z) %复数z的实部3、%比较符号矩阵与字符串矩阵A=sym('[a,b;c,d]') %创建符号矩阵B='[a,b;c,d]' %创建字符串矩阵C=[a,b;c,d] %创建数值矩阵C=sym(B) %转换为符号矩阵whos4、%计算符号矩阵的行列式值、非共轭转置和特征值syms a11 a12 a21 a22A=[a11 a12;a21 a22] %创建符号矩阵det(A) %计算行列式A.' %计算非共轭转置eig(A)%计算特征值5、%符号表达式的代数运算f=sym('2*x^2+3*x+4')g=sym('5*x+6')f+g %符号表达式相加f*g %符号表达式相乘6、%对符号表达式进行任意精度控制并用三种运算方式表示同一符号常量a=sym('2*sqrt(5)+pi')digits %显示默认的有效位数vpa(a) %用默认的位数计算并显示vpa(a,20) %按指定的精度计算并显示digits(15) %改变默认的有效位数vpa(a) %按digits指定的精度计算并显示a1 =2/3 %数值型a2 = sym(2/3) %有理数型digitsa3 =vpa('2/3',32) %VPA型format longa17、%符号变量与数值变量进行转换a1=sym('2*sqrt(5)+pi')b1=double(a1) %转换为数值变量a2=vpa(sym('2*sqrt(5)+pi'),32)b2=numeric(a2) %转换为数值变量b2=numeric(a2)未定义函数或变量'numeric'。
matlab符号运算(二)

因式分解、展开、合并、简化及通分等
计算极限 limit(f,x,a): 计算 lim f ( x )
xa
limit(f,a): 计算默认自变量趋向于a时f的极限 limit(f): 计算 a=0 时的极限 limit(f,x,a,’right’):右极限 limit(f,x,a,’left’):左极限
1 2 n 1 n
,以及其前10项的部分和。
>> syms n >> S=symsum(1/n^2,n,1,inf) >> S10=symsum(1/n^2,n,1,10)
x 2 n 1 n
S=1/6*pi^2 S10=1968329/1270080
例:求函数级数
S
>> syms n x >> S=symsum(x/n^2,n,1,inf)
符号矩阵中元素的引用和修改
>> A=sym(’[1+x, sin(x); 5, exp(x)]’) >> A(1,2) >> A(2,2)=sym(’cos(x)’)
Matlab 符号运算(二)
符号矩阵的基本运算
符号矩阵的基本运算与数值矩阵的基本运算相类似。
1) 基本运算符:+、-、*、\、/、
ans=10
ans=2*x+y
ans=10 ans=[2+y,4+y,6+y] ans=[7 10 13]
ans=3*a+b
?
Matlab 符号运算(二)
符号矩阵
使用sym函数直接生成
>> A=sym(’[1+x, sin(ห้องสมุดไป่ตู้); 5, exp(x)]’)
实验MATLAB符号计算

5.1
5.1.1
【例5.1.1-1】符号常数形成中的差异
a1=[1/3,pi/7,sqrt(5),pi+sqrt(5)]%<1>
a2=sym([1/3,pi/7,sqrt(5),pi+sqrt(5)])%<2>
a3=sym([1/3,pi/7,sqrt(5),pi+sqrt(5)],'e')%<3>
char
CMs =
sym
(4)
isa(Mn,'double'),isa(Mc,'char'),isa(Ms,'sym')
ans =
1
ans =
1
ans =
1
(5)
whos Mn Mc Ms
Name Size Bytes Class
Mc 1x9 18 char array
Mn 2x2 32 double array
Ms 2x2 312 sym object
Grand total is 21 elements using 362 bytes
5.1.4
【例5.1.4-1】对独立自由符号变量的自动辨认。
(1)
syms a b x X Y;k=sym('3');z=sym('c*sqrt(delta)+y*sin(theta)');
(完整word版)含答案《MATLAB实用教程》

第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a(1(2)用(3)用(42.矩阵的运算(1)利用矩阵除法解线性方程组。
⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ,计算X=A\B 。
(2)利用矩阵的基本运算求解矩阵方程。
已知矩阵A 和B 满足关系式A -1BA=6A+BA ,计算矩阵B 。
其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ,Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a(3)计算矩阵的特征值和特征向量。
已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ,计算其特征值和特征向量。
(4)Page:322利用数学函数进行矩阵运算。
已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01,10],按对数均匀分布。
3.多项式的运算(1)多项式的运算。
已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式,并计算当x 在[0,20]内变化时G(x)的值,计算出G(x)=0的根。
Page 324(2)多项式的拟合与插值。
将多项式G(x)=x 4-5x 3-17x 2+129x-180,当x 在[0,20]多项式的值上下加上随机数的偏差构成y1,对y1进行拟合。
对G(x)和y1分别进行插值,计算在5.5处的值。
Page 325 四、思考练习题1.使用logspace 函数创建0~4π的行向量,有20个元素,查看其元素分布情况。
Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1)f(x)=2x 2+3x+5x+8用向量表示该多项式,并计算f(10)值. 2)根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。
matlab实验(西北农林科技大学)

课程实验报告学年学期2015-2016学年第2学期课程名称MATLAB与科学计算实验名称实验一 MATLAB环境与数值计算实验室测量测绘实验中心计算机室专业年级土木13级学生姓名学生学号 20130提交时间 2016-06-02 成绩任课教师王增红水利与建筑工程学院实验一 MATLAB环境与数值计算1、目的和要求(1)熟练掌握MATLAB的启动和退出、MATLAB的命令窗口;常用选单和工具栏,通过实例初步认识对MATLAB的命令和程序运行等。
(2)熟练掌握MATLAB变量的使用;(3)熟练掌握矩阵的创建、掌握MATLAB的矩阵和数组的运算;(4)熟悉MATLAB多项式的运用,掌握MATLAB的拟合和插值方法、积分运算和统计运算。
2、内容和步骤参见教材实验一、二。
3、实验报告提交要求(1)用MALTAB命令和M程序两种方式求解三元一次方程组。
答:以求解三元一次方程组{2a−b+3c=53a+b−5c=54a−b+c=9为例:(2)用MALTAB命令和M程序两种方式求解3×3复数矩阵的模和相角。
答:(3)创建一个4╳4矩阵,求逆矩阵、产生对角矩阵、求矩阵的秩等。
(5)创建一个一元四次多项式,进行多项式求值,求根计算。
432(6)创建一个一元三次多项式,取十个不同自变量值,计算多项式的值,并分别进行一阶、二阶拟合,图示原始数据和拟合结果(7)自建一个一元三次多项式,取十个不同自变量值,计算多项式的值,并用线性、相邻点和三次插值,图示其插值结果。
解:(8)给出多组温度的测定值(内含平均温度、最低、最高温度),并求其平均温度、最低、最高温度的平均值、标准差等。
解:>> a=fix(40*rand(6,3)+1)a =39 32 2820 39 3133 27 306 2 1617 34 2737 38 7>> mean(a) %各列的平均值ans =25.3333 28.6667 23.1667 >> std(a) %各列的标准差ans =13.0639 13.7647 9.5795课程实验报告学年学期2015-2016学年第2学期课程名称MATLAB与科学计算实验名称实验二 MATLAB的符号计算与可视化实验室测量测绘实验中心计算机室专业年级土木13级学生姓名学生学号提交时间 2016-06-02成绩任课教师王增红水利与建筑工程学院实验二 MATLAB的符号计算与可视化1、目的和要求(1)熟练掌握MATLAB符号表达式的创建、代数运算及化简。
matlab符号计算实验报告

1. 已知x=6,y=5,利用符号表达式求z =>> syms x >> z=(x+1)/(sqrt(x+3)-sqrt(y)); >> subs(z,x,5) ans =6/(8^(1/2)-y^(1/2)) >> subs(ans,6) ans = 15.83382. 分解因式。
(1)x y -44; >> syms x y >> factor(x^4-y^4) ans =(x-y)*(x+y)*(x^2+y^2)(2)x x x +++64212575151 >> syms x >> factor(125*x^6+75*x^4+15*x^2+1) ans =(5*x^2+1)^33. 化简表达式(1)sin cos cos sin ββββ-1212;>> syms x y >> f=sin(x).*cos(y)-cos(x).*sin(y); >> sfy1=simple(f) 结果:sfy1 =sin(x-y)(2)x x x +++248321>> syms x >> f=(4*x^2+8*x+3)/(2*x+1);sfy1=simplify(f) sfy1 =2*x+34、求下列极限,将完成实验的程序写到文件sy1.m 中:(1) (2) (3) (4)(5) (1)>> syms x >> F1=atan(x)/(x); >> w=limit(F1) w =1(2)>> syms x F2=((1+x)/(1-x))^(1/x); >> w=limit(F2) w =exp(2)(3)>> syms x F3=(x.*log(1+x))/(sin(x^2)); >> w=limit(F3) w =1(4)>> syms x F4=atan(x)/(x); >> w=limit(F4,x,inf) w =0(5)>> syms x F5=(1/(1-x)-1/(1-x^3)); >> w=limit(F5,x,1) w =NaN5、求下列函数的导数,将完成实验的程序写到文件sy2.m 中:1、 >> x = sym('x'); >> y1=(cos(x))^3-cos(3*x); >> diff(y1)ans =-3*cos(x)^2*sin(x)+3*sin(3*x)2、 >> x = sym('x'); >> y2=x.*sin(x).*(log(x)); >> diff(y2)ans =sin(x)*log(x)+x*cos(x)*log(x)+sin(x)3、>> x = sym('x'); >> y3=(x.*exp(x)-1)/sin(x); >> diff(y3)ans =(exp(x)+x*exp(x))/sin(x)-(x*exp(x)-1)/sin(x)^2*cos(x)4、 x x x x F 1011lim 2⎪⎭⎫ ⎝⎛-+=→31115lim()11x F x x →=---20sin )1ln(lim 3x x x F x +=→x x F x arctan lim 10→=arctan 4lim x x F x →∞=xx y 3cos cos 13-=xx x y ln sin 2=x xe y xsin 13-=cos x y e x =>> x = sym('x');y=cos(x).*exp(x); >> diff(y) ans =-sin(x)*exp(x)+cos(x)*exp(x)5、 >> x = sym('x');y=x^2.*sin(x); >> diff(y) ans = 2*x*sin(x)+x^2*cos(x)6、求下列函数的积分1、syms x a b c;int(sin(a*x).*sin(b*x).*sin(c*x)) ans =-1/4/(c+a-b)*cos((c+a-b)*x)+1/4/(-c+a-b)*cos((-c+a-b)*x)+1/4/(c+a+b)*cos((c+a+b)*x)-1/4/(-c +a+b)*cos((-c+a+b)*x) 2、>> syms x ;int(x^5+x^3-sqrt(x)/4) ans =1/6*x^6+1/4*x^4-1/6*x^(3/2)3、>> syms x ;int(x.*exp(x)/(x+1)^2,x,0,1) ans =1/2*exp(1)-1 4、 >> syms x y;F=int(int('x/(1+x*y)',x,0,1),y,0,1) F =2*log(2)-15、 由曲面22y x z +=,1=z ,2=z 所围成 >> syms x y z;F=int(int(int('x^2+y^2',x,-inf,inf),y,-inf,inf),z,1,2) F =Inf7、求下列级数的和(1) (2)(1)>> syms n;symsum(2*n-1/2^n,1,Inf) ans =Inf(2)syms n;symsum(1/n*(2*n-1),1,Inf) ans =Inf8、将函数 展开成2-x 的幂级数>> syms x;mtaylor(1/(x^2+5*x-3),x-2) 2sin 2y x x=⎰cxdx bx ax sin sin sin dx x x x )4(35⎰-+⎰+102)1(dx x xe x ⎰⎰+D dxdy xy x 1]1,0[]1,0[⨯=D ⎰⎰⎰Vzdxdydz 11212n n n I ∞=-=∑211(21)n I n n ∞==+∑21()53f x x x =+-。
南华大学《MATLAB及应用》实验报告2

核科学技术学院实验报告实验项目名称MATLAB符号计算所属课程名称MATLAB及应用实验类型上机实验实验日期12月日指导教师谢芹班级学号姓名成绩一、实验名称MATLAB符号计算二、实验目的(1)掌握定义符号对象的方法(2)掌握符号表达式的运算法则以及符号矩阵运算(3)掌握求符号函数极限及导数的方法(4)掌握求符号函数定积分和不定积分的方法三、实验原理1. 函数极限及导数的方法(1)函数极限:limit(F,x,a) 求符号函数f(x)的极限值。
即计算当变量x趋近于常数a时,f(x)函数的极限值。
(2)limit(f):求符号函数f(x)的极限值。
符号函数f(x)的变量为函数findsym(f)确定的默认变量;没有指定变量的目标值时,系统默认变量趋近于0,即a=0的情况。
(3)limit(f,x,a,'right'):求符号函数f的极限值。
'right'表示变量x从右边趋近于a。
(4)limit(f,x,a,‘left’):求符号函数f的极限值。
‘left’表示变量x从左边趋近于a。
2. 微分:diff(s):没有指定变量和导数阶数,则系统按findsym函数指示的默认变量对符号表达式s求一阶导数。
diff(s,'v'):以v为自变量,对符号表达式s求一阶导数。
diff(s,n):按findsym函数指示的默认变量对符号表达式s求n阶导数,n为正整数。
diff(s,'v',n):以v为自变量,对符号表达式s求n阶导数。
3. 函数定积分和不定积分的方法:int(s):没有指定积分变量和积分阶数时,系统按findsym函数指示的默认变量对被积函数或符号表达式s求不定积分。
int(s,v):以v为自变量,对被积函数或符号表达式s求不定积分。
int(s,v,a,b):求定积分运算。
a,b分别表示定积分的下限和上限。
梯形法:trapz(x,y):x为分割点构成的向量,y为被积函数在分割点上的函数值构成的向量;抛物线法:quad(f,a,b,tol),f 是被积函数,[a,b]是积分区间,tol 是精度。
实验2 MATLAB的符号运算

实验2 MATLAB 的符号运算1、 演示:几种输入下产生矩阵的异同。
A1= [1/3,0.2+sqrt(2),pi]A2=sym([1/3,0.2+sqrt(2),pi])A3=sym(‘[1/3,0.2+sqrt(2),pi]’)A1=[1/3,0.2+sqrt(2),pi]A1 =0.3333 1.6142 3.1416A2=sym([1/3,0.2+sqrt(2),pi])A2 =[ 1/3, 7269771597999872*2^(-52),pi]A3=sym('[1/3,0.2+sqrt(2),pi]')A3 =[ 1/3, 0.2+sqrt(2), pi]2、 用符号计算验证三角等式)21sin(2sin 1cos 2cos 1sin ϕϕϕϕϕϕ-=-。
(sym 或syms,simple)3、 求矩阵⎥⎦⎤⎢⎣⎡=22211211a a a a A 的行列式、逆和特征根。
(syms,det,inv,eig )syms a11 a12 a21 a22>> A=[a11,a12;a21,a22]A =[ a11, a12][ a21, a22]>> det(A)ans =a11*a22-a12*a21>> inv(A)ans =[ a22/(a11*a22-a12*a21), -a12/(a11*a22-a12*a21)][ -a21/(a11*a22-a12*a21), a11/(a11*a22-a12*a21)]>> eig(A)ans =[ 1/2*a11+1/2*a22+1/2*(a11^2-2*a11*a22+a22^2+4*a12*a21)^(1/2)][ 1/2*a11+1/2*a22-1/2*(a11^2-2*a11*a22+a22^2+4*a12*a21)^(1/2)]4、 求:⎥⎦⎤⎢⎣⎡x x t t adx d ln cos 3 ,⎥⎦⎤⎢⎣⎡x x t t a dt d t ln cos 32和⎥⎦⎤⎢⎣⎡x xt t adxdt d ln cos 32。
实验二--MATLAB的符号计算与可视化

实验二 MATLAB的符号计算与可视化1、目的和要求(1)熟练掌握MATLAB符号表达式的创建、代数运算及化简。
(2)熟悉符号方程的求解。
(3)熟练掌握MATLAB二维曲线、三维图形的绘制。
(4)熟练掌握各种特殊图形的绘制。
2:实验内容:(1)完成教材实验三第1节“1.创建符号表达式和符号表达式的操作”中(1)-(5)部分的内容,分别用sym和syms创建符号表达式f和g,并对它们进行相关操作,思考每一条命令的作用是什么,并提交命令行和结果;3:实验内容:(1)完成教材实验三第1节“1.创建符号表达式和符号表达式的操作”中(1)-(5)部分的内容,分别用sym和syms创建符号表达式f和g,并对它们进行相关操作,思考每一条命令的作用是什么,并提交命令行和结果;(1)创建符号表达式:使用sym命令创建符号表达式:f=sym('sin(x)')f =sin(x)>> g=sym('y/exp(-2*t)')g =y*exp(2*t)使用syms命令创建符号表达式:>> syms x y t>> f=sym(sin(x))f =sin(x)>> g=sym(y/exp(-2*t))g =y*exp(2*t)(2):自变量的确定:>> symvar(g)ans =[ t, y]>> symvar(g,1)ans =y>> findsym(g,2)ans =y,t(3):用常数替换符号变量:>> x=0:10;>> y=subs(f,x)y =Columns 1 through 80 0.8415 0.9093 0.1411 -0.7568 -0.9589 -0.2794 0.6570Columns 9 through 110.9894 0.4121 -0.5440(4):符号对象与数值的转换和任意精度控制:>> f1=subs(f,'5')f1 =sin(5)>> y1=double(f1)y1 =-0.9589>> y2=eval(f1)y2 =-0.9589采用digits和vpa实现任意精度控制:>> digitsDigits = 32>> vpa(f1)ans =-0.95892427466313846889315440615599>> vpa(f1,10)ans =-0.9589242747(5):求反函数和复合函数用finverse函数求f,g的反函数>> f=sym('sin(x)');>> g=sym('y/exp(-2*t)')g =y*exp(2*t)>> finverse(f)Warning: finverse(sin(x)) is not unique. ans =asin(x)>> finverse(g)ans =y/exp(2*t)>> finverse(g,'t')ans =log(t/y)/2用compose函数求f,g的复合函数>> compose(f,g)ans =sin(y*exp(2*t))>> compose(f,g,'z')ans =sin(z*exp(2*t))(2)自建两个一元四次符号表达式,分别进行其符号表达式的加、减、乘等运算,并提交命令行和结果;>> syms x>> f=x^4+2*x^3-5*x^2+6*x+8f =x^4 + 2*x^3 - 5*x^2 + 6*x + 8>> class(f)ans =sym>> g=2*x^4-5*x^3+8*x^2+7*x-2g =2*x^4 - 5*x^3 + 8*x^2 + 7*x - 2>> f+gans =3*x^4 - 3*x^3 + 3*x^2 + 13*x + 6>> f-gans =- x^4 + 7*x^3 - 13*x^2 - x + 10>> f*gans =(x^4 + 2*x^3 - 5*x^2 + 6*x + 8)*(2*x^4 - 5*x^3 + 8*x^2 + 7*x - 2)(3)自建一个可化简一元五次多项式和一个三角函数符号表达式,依次使用pretty, horner, factor, simplify和simple等函数对该表达式进行化简,并提交命令行和结果;syms x y>> f=x^5+x^4+2*x+2f =x^5 + x^4 + 2*x + 2>> g=cos(y)^2-sin(y)^2g =cos(y)^2 - sin(y)^2>> class(f)ans =sym>> class(g)ans =sym>> pretty(f)5 4x + x + 2 x + 2>> horner(f)ans =x*(x^3*(x + 1) + 2) + 2 >> factor(f)ans =(x + 1)*(x^4 + 2)>> simplify(f)ans =(x^4 + 2)*(x + 1)>> simple(f)simplify:x^5 + x^4 + 2*x + 2 radsimp:x^5 + x^4 + 2*x + 2 simplify(100):(x^4 + 2)*(x + 1) combine(sincos):x^5 + x^4 + 2*x + 2 combine(sinhcosh):x^5 + x^4 + 2*x + 2combine(ln):x^5 + x^4 + 2*x + 2 factor:(x + 1)*(x^4 + 2) expand:x^5 + x^4 + 2*x + 2 combine:x^5 + x^4 + 2*x + 2 rewrite(exp):x^5 + x^4 + 2*x + 2 rewrite(sincos):x^5 + x^4 + 2*x + 2 rewrite(sinhcosh): x^5 + x^4 + 2*x + 2 rewrite(tan):x^5 + x^4 + 2*x + 2 mwcos2sin:x^5 + x^4 + 2*x + 2collect(x):x^5 + x^4 + 2*x + 2ans =(x^4 + 2)*(x + 1)>> pretty(g)2 2cos(y) - sin(y)>> horner(g)ans =cos(y)^2 - sin(y)^2>> factor(g)ans =(cos(y) - sin(y))*(cos(y) + sin(y)) >> simplify(g)ans =cos(2*y)>> simple(g)simplify:cos(2*y)radsimp:cos(y)^2 - sin(y)^2simplify(100):cos(2*y)combine(sincos):cos(2*y)combine(sinhcosh):cos(y)^2 - sin(y)^2combine(ln):cos(y)^2 - sin(y)^2factor:(cos(y) - sin(y))*(cos(y) + sin(y))expand:cos(y)^2 - sin(y)^2combine:cos(y)^2 - sin(y)^2rewrite(exp):((1/exp(y*i))/2 + exp(y*i)/2)^2 - ((i*exp(i*y))/2 - i/(2*exp(i*y)))^2 rewrite(sincos):cos(y)^2 - sin(y)^2rewrite(sinhcosh):cosh(-y*i)^2 + sinh(-y*i)^2rewrite(tan):(tan(y/2)^2 - 1)^2/(tan(y/2)^2 + 1)^2 - (4*tan(y/2)^2)/(tan(y/2)^2 + 1)^2 mwcos2sin:1 - 2*sin(y)^2collect(y):cos(y)^2 - sin(y)^2ans =cos(2*y)(4)完成教材实验四第1节“1.绘制二维图线”中的所有内容,绘制4种二维曲线,把图形窗口分割为2行2列,并分别标明图名、坐标值等;2行2列子图的第1个图:>> subplot(2,2,1)>> t1=0:0.1:2;>> y1=sin(2*pi*t1);>> plot(t1,y1)>> title('y=sin(2\pit)')2行2列子图的第2个图:>> subplot(2,2,2)>> t2=0:0.1:2;>> y2=[exp(-t2);exp(-2*t2);exp(-3*t2)];>> plot(t2,y2)>> axis([0 2 -0.2 1.2]);>> title('y=e-t,y=e-2t,y=e-3t2行2列的第3个图:subplot(2,2,3);>> t3=[0 1 1 2 2 3 4];>> y3=[0 0 2 2 0 0 0];>> plot(t3,y3);>> axis([0 4 -0.5 3]);>> title('脉冲信号')2行2列的第4个图:>> subplot(2,2,4);>> t4=0:0.1:2*pi;>> plot(sin(t4),cos(t4));>> axis([-1.2 1.2 -1.2 1.2]);>> axis equal;>> title('圆')插图:[文档可能无法思考全面,请浏览后下载,另外祝您生活愉快,工作顺利,万事如意!]11 / 11。
实验二 MATLAB的科学计算

实验二 MATLAB的科学计算一、实验目的1、了解MATLAB的基本计算功能2、符号运算功能二、实验内容(一)基本计算功能例1、求[12+2× (7-4)]÷32的运算结果>>(12+2*(7-4))/3^2ans=2例2、用MATLAB求下面线性方程组的解3x1+ x2 - x3 = 3.6x1+2x2+4x3 = 2.1-x1+4x2+5x3 = -1.4>>A=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];>>x=A\bx =1.4818-0.46060.3848例3、求两个矩阵的乘积a=[1 2 3;3 4 5;3 2 1]b=[1 2;3 4; 5 6]c=a*bc =22 2840 5214 20(二)符号运算功能1、求极限通常在MATLAB软件中,用limit 函数来求极限,其用法如表9-5所示:表9-5 limit 函数的用法例1、 求42cos lim 202x x e x -→.>> syms x % 把字符x 定义为符号 >>limit((cos(x)-exp(-x^2/2))/x^4)ans =-1/12例2 求42lim 22--→x x x .>> limit((x-2)/(x^2-4),x,2)ans =1/4例3 求t x t x t )cos()cos(lim 0-+→>> syms t x>> limit((cos(x+t)-cos(x))/t,t,0)ans =-sin(x)2 、求导数MATLAB 软件提供求函数导数的指令是diff ,具体使用格式如下:(1)diff(f, x) 表示对f (这里f 是一个函数表达式)求关于符号变量x 的一阶导数.若x 缺省,则表示求f 对预设独立变量的一阶导数.(2)diff(f, x, n) 表示对f 求关于符号变量x 的n 阶导数.若x 缺省,则表示求f 对预设独立变量的n 阶导数.例9-7 已知,c bx ax x f ++=2)(求)(x f 的一阶、二阶导数.>> syms a b c x>> f='a*x^2+b*x+c'f =a*x^2+b*x+c>> diff(f, x)ans =2*a*x+b>> diff(f,2)ans =2*a3 、求积分MATLAB软件提供求函数积分的指令是int,具体使用格式如下:(1)int(f) 返回f对预设独立变量的积分值;(2)int(f,v) 返回f对独立变量v的积分值;(3)int(f,a,b) 返回f对预设独立变量的积分值,积分区间为[a,b],a和b为数值式;(4)int(f,v,a,b) 返回f对独立变量的积分值,积分区间为[a,b],a和b为数值式;(5)int(f,m,n) 返回f对预设变量的积分值,积分区间为[m,n],m和n为符号式;例1、求下列函数的积分 :例:求不定积分⎰-dxex x23,⎰+12xxdx;>> syms x>> f=sym('x^3*exp(-x^2)') % 或 int('x^3*exp(-x^2)') f =x^3*exp(-x^2)>> int(f)ans =-1/2*x^2/exp(x^2)-1/2/exp(x^2)>> int('1/(x*sqrt(x^2+1))')ans =-atanh(1/(x^2+1)^(1/2))4 、数学表达式的化简例、 将下面表达式进行因式分解. 132-=a f>> f2=sym('a^3-1');>> factor(f2)ans =(a-1)*(a^2+a+1)。
matlab2022实验2参考答案

matlab2022实验2参考答案报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:MATLAB实验二MATLAB符号计算试验报告说明:1做试验前请先预习,并独立完成试验和试验报告。
2报告解答方式:将MATLAB执行命令和最后运行结果从命令窗口拷贝到每题的题目下面,请将报告解答部分的底纹设置为灰色,以便于批阅。
3在页眉上写清报告名称,学生姓名,学号,专业以及班级。
3报告以Word文档书写。
一目的和要求1熟练掌握MATLAB符号表达式的创建2熟练掌握符号表达式的代数运算3掌握符号表达式的化简和替换4熟练掌握符号微积分5熟练掌握符号方程的求解二试验内容1多项式运算(必做)1.1解方程:f(某)=某^4-10某某^3+34某某^2-50某某+25=0%采用数值方法:>>f=[1-1034-5025];>>root(f)%采用符号计算方法:f1=ym('某^4-10某某^3+34某某^2-50某某+25')olve(f1)1.2求有理分式R=(3某^3+某)(某^3+2)/((某^2+2某-2)(5某^3+2某^2+1))的商多项式和余多项式.a1=[3010];a2=[1002];a=conv(a1,a2);b1=[12-2];b2=[5201];b=conv(b1,b2);[p,r]=deconv(a,b);%注意:ab秩序不可颠倒。
%reidue用于实现多项式的部分分式展开,此处用deconv函数报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:%%此题,有同学程序如下:某1=[3010],某2=[1002],某3=[12-2],某4=[5201]某5=conv(某1,某2)[y6,r]=deconv(某5,某3)R=deconv(y6,某4)%%这种方法较第一种解法缺点:在除法运算中,会产生误差,故此题应先将分母的多项式相乘后,再与分子部分的多项式进行运算。
实验2数据可视化处理实验

科学计算与数据处理实验报告 学号姓 名实验名称数据可视化处理实验实验目的 1、 掌握MATLAB中二维曲线图、三维曲线图、三维曲面图的绘制方法2、 掌握MATLAB中常用统计图的绘制方法3、 熟悉MATLAB中三维图形常用编辑方法4、 了解MATLAB中动画的绘制方法实验方案 1、 离散数据可视化实验:绘制离散函数4)9n(11)3n(1y22的图形,其中自变量的取值范围是(0,16)的整数。
2、 二维曲线绘制实验:设计实验演示验证plot、subplot、axis、set、legend、xlabel、ylabel、zlabel、title、text、grid、box、hold、plotyy、fplot等函数在绘制二维曲线中的功能和使用方法。
3、 三维曲线绘制实验:设计实验演示验证plot3、mesh、surf等函数在绘制三维曲线、曲面中的功能和使用方法。
4、 统计图绘制实验:设计实验演示验证面域图(area)、直方图(bar、barh、bar3、bar3h)、饼图(pie、pie3)、散点图(scatter、scatter3、plotmatrix)等统计图的绘制方法。
5、 三维图形编辑(精细控制)实验:设计实验演示验证用view、rotate、colordef、colormap、shading、light、lighting、material、surfl等函数对三维图形进行精细控制的方法。
6、 动画绘制实验:设计实验演示验证getframe与movie相结合绘制动画的方法。
实验记录 (1)绘制离散函数4)9n(11)3n(1y22的图形>> n=1:0.5:16;>> y=1./((n-3).^2+1)+1./((n-9).^2+4)y =Columns 1 through 90.2147 0.3243 0.5189 0.8216 1.0250 0.8292 0.5345 0.3489 0.2500Columns 10 through 180.1995 0.1769 0.1730 0.1838 0.2071 0.2385 0.2673 0.2770 0.2584Columns 19 through 270.2200 0.1775 0.1404 0.1112 0.0891 0.0725 0.0599 0.0502 0.0427Columns 28 through 310.0367 0.0319 0.0280 0.0248>> plot(n,y,'*')(2)plot、subplot、axis、set、legend、xlabel、ylabel、zlabel、title、text、grid、box、hold、plotyy、fplot函数演示>> x=0:0.1:5;>> y=sin(x);>> z=cos(x);>> h=tan(x);>> subplot(2,1,1);>> plot(x,y);>> subplot(2,1,2);>> plot(x,z);>> axis([0 4 0 20]);>> h=plot(x,y);>> set(h,'color','b');>> set(gca,'XGrid','on','YGrid','off');>> set(gca,'color','g');>> clear>> x=0:0.05:10;>> plot(x,sin(x),'*b',x,cos(x),'+r',x,tan(x)./100,'+'); >> legend('sin','cos','tan');>> clear>> x=0:0.05:15;>> plot3(x,sin(x),cos(x),'b','linewidth',1); >> xlabel('X');>> ylabel('Y');>> zlabel('Z');>> title('三维曲线')图像示例')>> text(1,1,'>> grid('on')>> box on>> hold on>> plot3(x,x.^2,x.^(1./2))>> plot3(x,sin(x),cos(x),'b','linewidth',5);>> clear>> x = 0:0.01:20;>> y1 = 200*exp(-0.05*x).*sin(x);>> y2 = 0.8*exp(-0.5*x).*sin(10*x);>> [AX,H1,H2] = plotyy(x,y1,x,y2,'plot');(3)实验演示plot3、mesh、surf函数Plot3函数已在上面演示。
MATLAB计算可视化和GUI设计doc

实验报告专用纸实验室:机号:实验日期:课程名称MATLAB实用教程实验项目名称MATLAB计算可视化和GUI设计实验组别第组同组者教师评语及成绩:实验成绩:教师签字:(请按照实验报告的有关要求书写,一般必须包括:1、实验目的;2、实验内容;3、实验步骤与方法;4、实验数据与程序清单;5、出现的问题及解决方法;6、实验结果、结果分析与体会等内容。
)一、实验目的1.熟练掌握MATLAB二维曲线的绘制和修饰2.掌握三维图形的绘制3.熟练掌握各种图形的绘制4.掌握句柄图形的概念和GUI设计二、实验内容(1)绘制二维曲线把图形窗口分割为2行2列,在窗口1中绘制1条正弦曲线y=sin(2*pi*t),t∈[0,2];在窗口2中绘制3条衰减的单边指数曲线y=e^(-t)、y=e^(-2t)和y=e^(-3t),t∈[0,2];在窗口3中绘制1个矩形脉冲信号,脉冲宽度为1,高度为2,开始时间为1;在窗口4中绘制1个单位圆。
(2)绘制多条二阶系统时域曲线和三维图形1.在同一平面绘制多条二阶系统时域曲线。
2.使用句柄图形3.使用图形窗口功能4.绘制三维图形(3)特殊图形1.绘制条形图2.绘制实心图3.绘制阶梯图4.绘制火柴图(4)GUI设计1.设计界面2.设计控件属性实验报告附页实验名称MATLAB计算可视化和GUI设计3.回调函数三、实验步骤与方法(1)绘制二维曲线1.使用subplot函数,在窗口中按照先向右、后向下的顺序绘制多个子图2.使用title语法为子图添加标题3.使用axis([xmin,xmax,ymin,ymax])命令为第2个子图设置坐标范围4.使用axis equal命令将第4个子图的坐标轴设置为等长刻度(2)绘制多条二阶系统时域曲线和三维图形1.在同一平面绘制多条二阶系统时域曲线。
a)使用plot函数绘制1条阻尼系数zeta=0的二阶系统曲线b)使用hold on命令在同一窗口叠绘4条曲线c)使用title和legend分别为曲线添加标题和图例d)使用grid on为曲线添加网格e)使用gtext将文字写在鼠标单击的地方f)使用ginput获取鼠标单击任意三点的图形数据2.使用句柄图形a)使用gcf命令获取当前图形窗口句柄b)使用gca命令获取当前坐标轴句柄c)使用gco命令获取被鼠标最近单击的对象的句柄使用get(h_obj,’PropertyName’)获取句柄对象指定标题的当前值d)使用h=findobj(h_obj,’PropertyName’,PropertyValue)获取文字句柄e)使用set函数来设置对象的属性值3.使用图形窗口功能选择菜单“View”→“Property Editor”命令,打开图形的属性窗口,单击图形中的对象打开的当前对象属性,在属性窗口设置各图形对象的属性。
实验2 MATLAB数值及符号运算

MATLAB 实验报告学生姓名:王朝 学号:1314080213 专业班级:电子信息科学与技术二班实验类型:□ 验证 □√ 综合 □ 设计 □ 创新 实验日期: 实验成绩: 一.实验名称实验2 MATLAB 数值及符号运算二 实验目的:1、了解伴随矩阵、稀疏矩阵、魔方矩阵、对角矩阵、范德蒙等矩阵的创建,掌握矩阵的基本运算2、掌握矩阵的数组运算3、掌握多项式的基本运算4、会求解代数方程5、掌握创建符号表达式和矩阵的方法6、掌握符号表达式三、实验内容:1、生成一个3行3列的随机矩阵,并逆时针旋转90°,左右翻转,上下翻转。
2、已知a=[1 2 3],b=[4 5 6], 求a.\b 和a./ b3、数组和矩阵有何不同?4、已知a=[1 2 3;4 5 6;7 8 0],求其特征多项式并求其根。
5、已知多项式a(x)=x 2+2x+3,b(x)=4x 2+5x+6,求a ,b 的积并微分。
6、求解方程1)⎩⎨⎧=+=+ 133x 2822121x x x 2)⎪⎩⎪⎨⎧=+=+=+343 23x 212212121x x x x x3)⎩⎨⎧=++=++ 243x 2132321321x x x x x 7、用两种方法创建符号矩阵,A =[ a, 2*b][3*a, 0]并把其中的a 改为c 。
8、计算二重不定积分 9、对符号方程f = ax2+bx+c 求解1)对x 求解2)对a 求解。
10、求解微分方程0)0(,1)0(,02222===++dx dy y y dx dy dxy d 。
四.实验环境PC 微机MATLAB 系统五、实验内容和步骤1、生成一个3行3列的随机矩阵,并逆时针旋转90°,左右翻转,上下翻转。
>> a=magic(3)a =8 1 63 5 74 9 2>> b=rot90(a) 逆时针旋转90°b =6 7 21 5 98 3 4>> c=fliplr(b) 左右翻转c =dxdyxe xy ⎰⎰-2 7 69 5 14 3 8>> d=flipud(c) 上下翻转d =4 3 89 5 12 7 62、已知a=[1 2 3],b=[4 5 6],求a.\b和a./ ba.\bans =4.0000 2.5000 2.0000a./ bans =0.2500 0.4000 0.50003、数组和矩阵有何不同?数组中的元素可以是字符等,矩阵中的只能是数,这是二者最直观的区别。
2实验二 数据可视化与Matlab绘图

x cos s cos t 3 y cos s sin t 0 s , 0 t 2 2 z sin s
7. 以任意位置子图形式绘制出正弦、余弦、正切和余切函数曲线。
例题:绘制极坐标曲线ρ=a*sin(b+n*θ),并分析参数 a、b、n 对曲线形状的影响。
在-5≤x≤5 区间绘制函数曲线 4. 绘制极坐标曲线ρ=a*sin(b+n*θ),并分析参数 a、b、n 对曲线形状的影响。 5. 绘制函数的曲线图和等高线。
z cos2 4
其中 x 的 21 个值均匀分布[-5,5]范围,y 的 31 个值均匀分布在[0,10],要求使用 subplot(2,1,1)和 subplot(2,1,2)将产生的曲面图和等高线图画在同一个窗口上。 6. 绘制曲面图形。
%%%%%%%%%%%%%%%%%%%%% clc; theta=0:pi/100:2*pi; a=input('输入 a='); b=input('输入 b='); n=input('输入 n='); rho=a*sin(b+n*theta); polar(theta,rho,'m')
实验二:数据可视化与 Matlab 绘图
一、实验目的 1. 掌握绘制二维图形的常用函数。 2. 掌握绘制三维图形的常用函数。 3. 掌握绘制图形的辅助操作。 二、实验内容 1. 设 y 0.5
3sin x cos x ,在 x=0~2π区间取 101 点,绘制函数的曲线。 1 x2
2. 已知 y1=x2,y2=cos(2x),y3=y1×y2,完成下列操作: (1) 在同一坐标系下用不同的颜色和线型绘制三条曲线。 (2) 以子图形式绘制三条曲线。 (3) 分别用条形图、阶梯图、杆图和填充图绘制三条曲线。 3. 已知
Matlab实验二符号计算
实验二 符号计算一、实验目的1.理解符号计算的本质,掌握符号计算的常规步骤;2.学习认定符号表达式中独立变量;3.学习求极限,符号积分;4.掌握如何求微分方程解,代数方程的解。
二、实验任务1.定义2sin ()(1cos(2*))/2y x x =+-,要求编写程序化简该表达式,理解符号计算实质。
y =sin(x)^2+1/2-1/2*cos(2*x)>> f=simple(y)f =1-cos(2*x)2.练习课后习题2第1题,说出以下四条指令产生的结果各属于哪种数据类型,是“双精度”对象,还是“符号”对象?体验符号常量和符号数字区别。
3/7+0.1;sym(3/7+0.1);vpa(sym(3/7+0.1));vpa(sym(3/7+0.1),4)练习时,可使用class 、whos 、isa 函数检验。
下图为不同类型之间的转换。
以数值矩阵A=[1/3,2.5;1/0.7,2/5]为例,进行符号矩阵和数值矩阵之间转换。
3.编写程序,求解sin(x)/x 趋于0时的极限。
limit(f,x,0)数值型 符号结符号常数 符号量(表达式) 数值 字符串(表达式)ASCIIvpa vpadoubledouble sym char sym double charstr2num str2double int2str num2str mat2strans =14.编写程序求解下面的微分方程''''()5*()6*()(),(0)1,(0)2,()3*sin()2*y t y t y t f t y y f t t t -+==-==+。
2.4 dsolve('D2y-5*Dy+6*y=3*sin(t)+2*t','Dy(0)=-1','y(0)=2')5.已知方程组x+y+z=1,x-y+z=2,2x-y-z=1,编写程序求解符号方程组2.6。
MatLab教程第 2 章符号计算

第 2 章 符号计算所谓符号计算是指:解算数学表达式、方程不是在离散化的数值点上进行,而是凭借一系列恒等式,数学定理,通过推理和演绎,力求获得解析结果。
这种计算建立在数值完全准确表达和推演严格解析的基础之上,因此所得结果是完全准确的。
本书之所以把符号计算内容放在第2章,是出于以下考虑:一,相对于MATLAB 的数值计算“引擎”和“函数库”而言,符号计算的“引擎”和“函数库”是独立的。
二,在相当一些场合,符号计算解算问题的指令和过程,显得比数值计算更自然、更简明。
三,大多数理工科的本科学生在学过高等数学和其他专业基础课以后,比较习惯符号计算的解题理念和模式。
在编写本章时,作者在充分考虑符号计算独立性的同时,还考虑了章节的自完整性。
为此,本章不但全面地阐述符号计算,而且在最后一节还详细叙述了符号计算结果的可视化。
这样的安排,将使读者在阅读完本章后,就有可能运用MATLAB 的符号计算能力去解决相当一些具体问题。
2.1符号对象和符号表达式2.1.1 符号对象的创建和衍生 一 生成符号对象的基本规则 二符号数字【例2.1-1】符号(类)数字与数值(类)数字之间的差异。
a=pi+sqrt(5) sa=sym('pi+sqrt(5)') Ca=class(a) Csa=class(sa) vpa(sa-a)a =5.3777 sa =pi+sqrt(5) Ca = double Csa = sym ans =.138223758410852e-16三 符号参数 四符号变量【例2.1-2】用符号计算研究方程02=++w vz uz 的解。
(1)syms u v w z Eq=u*z^2+v*z+w;result_1=solve(Eq) % findsym(Eq,1)result_1 =-u*z^2-v*zans =w(2)result_2=solve(Eq,z)result_2 =1/2/u*(-v+(v^2-4*u*w)^(1/2))1/2/u*(-v-(v^2-4*u*w)^(1/2))【例2.1-3】对独立自由符号变量的自动辨认。
MATLAB计算的可视化
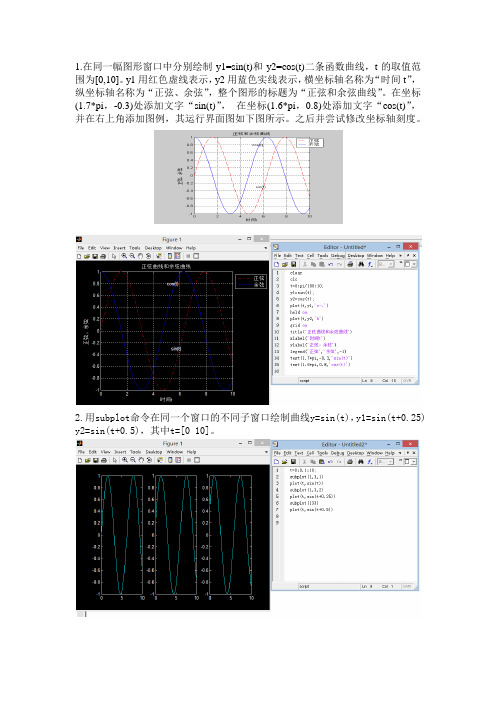
1.在同一幅图形窗口中分别绘制y1=sin(t)和y2=cos(t)二条函数曲线,t的取值范围为[0,10]。
y1用红色虚线表示,y2用蓝色实线表示,横坐标轴名称为“时间t”,纵坐标轴名称为“正弦、余弦”,整个图形的标题为“正弦和余弦曲线”。
在坐标(1.7*pi,-0.3)处添加文字“sin(t)”,在坐标(1.6*pi,0.8)处添加文字“cos(t)”,并在右上角添加图例,其运行界面图如下图所示。
之后并尝试修改坐标轴刻度。
2.用subplot命令在同一个窗口的不同子窗口绘制曲线y=sin(t),y1=sin(t+0.25) y2=sin(t+0.5),其中t=[0 10]。
3.绘制三维曲线:⎪⎩
⎪⎨⎧=≤≤==)cos()sin()200()cos()sin(t t t z t t y t x π (注意:用plot3命令)
4.三维网线图:绘制z=sin(y)cos(x) 三维网线图。
5. 三维曲面图
绘制22y x z +=的三维曲面图,x 在[-5,5]范围,y 在[-5,5]范围。
将曲面图颜色用shading 命令连续变化,并用颜色标尺显示色图(使用函数colorbar 生成)。
6.请绘制一个饼形图,数据如下表所示
请将“国家单位”和“读研”两部分突出显示。
7. 用semilogx命令绘制传递函数为1//(s+1)(0.5s+1)的对数幅频特性曲线,横坐标为w,纵坐标为Lw,w的范围为10-2-103,按对数分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二MATLAB的符号计算与可视化1:完成教材实验三第1节“1.创建符号表达式和符号表达式的操作”中(1)-(5)部分的内容,分别用sym和syms创建符号表达式f和g,并对它们进行相关操作,思考每一条命令的作用是什么,并提交命令行和结果;(1)创建符号变量。
①使用sym命令创建符号表达式:>> f=sym('sin(x)')f =sin(x)>> g=sym('y/exp(-2*t)')g =y*exp(2*t)②使用syms命令创建符号表达式:>> syms x y t>> f=sym(sin(x))f =sin(x)>> g=sym(y/exp(-2*t))g =y*exp(2*t)(2):自由变量的确定:>> symvar(g)ans =[ t, y]>> symvar(g,1)ans =y>> findsym(g,2)ans =y,t(3):用常数替换符号变量:>> x=0:10;>> y=subs(f,x)y =Columns 1 through 80 0.8415 0.9093 0.1411 -0.7568 -0.9589 -0.2794 0.6570Columns 9 through 110.9894 0.4121 -0.5440练习:用y替换x,查看结果及其数据类型。
z=subs(f,y)z =Columns 1 through 80 0.7456 0.7891 0.1407 -0.6866 -0.8186 -0.2758 0.6107Columns 9 through 110.8357 0.4006 -0.5176>> class(z)ans =double(4):符号对象与数值的转换和任意精度控制:>> f1=subs(f,'5')f1 =sin(5)>> y1=double(f1)y1 =-0.9589>> y2=eval(f1)y2 =-0.9589练习:将y1用sym函数转换为符号对象,并用’d’,’f’,’e’,’r’4种格式表示。
>> y2=sym(y1,'d')y2 =-0.95892427466313845396683746002964ans =-0.95892427>> class(y2)ans =sym>> y3=sym(y1,'f')y3 =-8637222012098867/9007199254740992 >> y4=sym(y1,'e')y4 =-8637222012098867/9007199254740992 >> y5=sym(y1,'r')y5 =-8637222012098867/9007199254740992 采用digits和vpa实现任意精度控制:>> digitsDigits = 32>> vpa(f1)ans =-0.95892427466313846889315440615599ans =-0.9589242747(5):求反函数和复合函数①用finverse函数求f,g的反函数>> f=sym('sin(x)');>> g=sym('y/exp(-2*t)')g =y*exp(2*t)>> finverse(f)Warning: finverse(sin(x)) is not unique. ans =asin(x)>> finverse(g)ans =y/exp(2*t)>> finverse(g,'t'ans =log(t/y)/2②用compose函数求f,g的复合函数>> compose(f,g)ans =sin(y*exp(2*t))>> compose(f,g,'z')ans =sin(z*exp(2*t))2;自建两个一元四次符号表达式,分别进行其符号表达式的加、减、乘等运算,并提交命令行和结果;>> syms x>> f=x^4+2*x^3-5*x^2+6*x+8f =x^4 + 2*x^3 - 5*x^2 + 6*x + 8>> class(f)ans =sym>> g=2*x^4-5*x^3+8*x^2+7*x-2g =2*x^4 - 5*x^3 + 8*x^2 + 7*x - 2>> f+gans =3*x^4 - 3*x^3 + 3*x^2 + 13*x + 6>> f-gans =- x^4 + 7*x^3 - 13*x^2 - x + 10>> f*gans =(x^4 + 2*x^3 - 5*x^2 + 6*x + 8)*(2*x^4 - 5*x^3 + 8*x^2 + 7*x - 2)3:自建一个可化简一元五次多项式和一个三角函数符号表达式,依次使用pretty, horner, factor, simplify和simple等函数对该表达式进行化简,并提交命令行和结果;syms x y>> f=x^5+x^4+2*x+2f =x^5 + x^4 + 2*x + 2>> g=cos(y)^2-sin(y)^2g =cos(y)^2 - sin(y)^2>> class(f)ans =sym>> class(g)ans =sym>> pretty(f)5 4x + x + 2 x + 2 >> horner(f)ans =x*(x^3*(x + 1) + 2) + 2 >> factor(f)ans =(x + 1)*(x^4 + 2)>> simplify(f)ans =(x^4 + 2)*(x + 1)>> simple(f) simplify:x^5 + x^4 + 2*x + 2 radsimp:x^5 + x^4 + 2*x + 2 simplify(100):(x^4 + 2)*(x + 1) combine(sincos):x^5 + x^4 + 2*x + 2combine(sinhcosh):x^5 + x^4 + 2*x + 2combine(ln):x^5 + x^4 + 2*x + 2 factor:(x + 1)*(x^4 + 2) expand:x^5 + x^4 + 2*x + 2 combine:x^5 + x^4 + 2*x + 2 rewrite(exp):x^5 + x^4 + 2*x + 2 rewrite(sincos):x^5 + x^4 + 2*x + 2 rewrite(sinhcosh): x^5 + x^4 + 2*x + 2 rewrite(tan):x^5 + x^4 + 2*x + 2 mwcos2sin:x^5 + x^4 + 2*x + 2 collect(x):x^5 + x^4 + 2*x + 2 ans =(x^4 + 2)*(x + 1)>> pretty(g)2 2cos(y) - sin(y)>> horner(g)ans =cos(y)^2 - sin(y)^2>> factor(g)ans =(cos(y) - sin(y))*(cos(y) + sin(y)) >> simplify(g)ans =cos(2*y)>> simple(g)simplify:cos(2*y)radsimp:cos(y)^2 - sin(y)^2simplify(100):cos(2*y)combine(sincos):combine(sinhcosh):cos(y)^2 - sin(y)^2combine(ln):cos(y)^2 - sin(y)^2factor:(cos(y) - sin(y))*(cos(y) + sin(y))expand:cos(y)^2 - sin(y)^2combine:cos(y)^2 - sin(y)^2rewrite(exp):((1/exp(y*i))/2 + exp(y*i)/2)^2 - ((i*exp(i*y))/2 - i/(2*exp(i*y)))^2rewrite(sincos):cos(y)^2 - sin(y)^2rewrite(sinhcosh):cosh(-y*i)^2 + sinh(-y*i)^2rewrite(tan):(tan(y/2)^2 - 1)^2/(tan(y/2)^2 + 1)^2 - (4*tan(y/2)^2)/(tan(y/2)^2 + 1)^2mwcos2sin:1 - 2*sin(y)^2cos(y)^2 - sin(y)^2ans =cos(2*y)4:完成教材实验四第1节“1.绘制二维图线”中的所有内容,绘制4种二维曲线,把图形窗口分割为2行2列,并分别标明图名、坐标值等;M文件:clf;clc;clear;%2行2列子图的第1个图figure(1);subplot(2,2,1);t1=0:0.1:2;y1=sin(2*pi*t1);plot(t1,y1);title('y=sin(2\pit)');%2行2列子图的第2个图subplot(2,2,2);t2=0:0.1:2;y2=[exp(-t2);exp(-2*t2);exp(-3*t2)];plot(t2,y2);axis([0 2 -0.2 1.2]);title('y=e-t,y=e-2t,y=e-3t');%2行2列子图的第3个图subplot(2,2,3);t3=[0 1 1 2 2 3 4];y3=[0 0 2 2 0 0 0];plot(t3,y3);axis([0 4 -0.5 3]);title('脉冲信号');%2行2列子图的第4个图subplot(2,2,4);t4=0:0.1:2*pi;plot(sin(t4),cos(t4));axis([-1.2 1.2 -1.2 1.2]);axis equal;title('圆');插图:5:参照教材实验四第3节“3.绘制特殊图形”中的相关内容,分别绘制条形图、实心图、阶梯图和火柴杆图,建议选取不同的函数来产生曲线;M文件:clf;clc;clear;figure(2);%条形图subplot(2,2,1);x1=3:6;y1=[5.3 13 0.45.1 11.8 -1.73.7 8.1 0.61.5 7.7 -4.5];bar(x1,y1);title('条形图');xlabel('\it X','fontsize',10); ylabel('Y');text(5,7,'my picture');%实心图subplot(2,2,2);x2=0:0.1:2*pi;y2=cos(x2)-0.5;plot(x2,y2);fill(x2,y2,'y');title('实心图');ylabel('\it Y','fontsize',10);text(3,0,'the second','FontName','commercialscript BT'); %阶梯图subplot(2,2,3);x3=0:0.1:2*pi;y3=sin(x3);stairs(x3,y3);title('阶梯图');xlabel('\it X','fontsize',10);ylabel('\it Y','fontsize',10);text(3,0,'the thrid','Fontsize',10);%火柴杆图subplot(2,2,4);x4=0:0.1:2*pi;y4=cos(x4)+0.2;stem(x4,y4);title('火柴杆图');ylabel('\it Y','fontsize',10);text(3,0,'the fourth','Fontsize',10);6:产生10个服从正态分布的随机数,计算该数组的统计变量(包括均值、标准差、最大值、最小值等),并绘制二维和三维饼状图。
