应用回归分析_第2章答案

合集下载

《应用回归分析》部分课后习题答案-何晓群版

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么？答：变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系，而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。

1.2 回归分析与相关分析的联系与区别是什么？答：联系有回归分析和相关分析都是研究变量间关系的统计学课题。

区别有 a.在回归分析中，变量y称为因变量，处在被解释的特殊地位。

在相关分析中，变量x和变量y处于平等的地位，即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。

b.相关分析中所涉及的变量y与变量x全是随机变量。

而在回归分析中，因变量y是随机变量，自变量x可以是随机变量也可以是非随机的确定变量。

C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。

而回归分析不仅可以揭示变量x对变量y的影响大小，还可以由回归方程进行预测和控制。

1.3 回归模型中随机误差项ε的意义是什么？答：ε为随机误差项，正是由于随机误差项的引入，才将变量间的关系描述为一个随机方程，使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系，由于客观经济现象是错综复杂的，一种经济现象很难用有限个因素来准确说明，随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。

1.4 线性回归模型的基本假设是什么？答：线性回归模型的基本假设有：1.解释变量x1.x2….xp是非随机的，观测值xi1.xi2…..xip是常数。

2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)=｛σ^23.正态分布的假定条件为相互独立。

4.样本容量的个数要多于解释变量的个数，即n>p.1.5 回归变量的设置理论根据是什么？在回归变量设置时应注意哪些问题？答：理论判断某个变量应该作为解释变量，即便是不显著的，如果理论上无法判断那么可以采用统计方法来判断，解释变量和被解释变量存在统计关系。

应用回归分析-第2章课后习题参考答案

第二章一元線性回歸分析思考與練習參考答案2.1 一元線性回歸有哪些基本假定?答：假設1、解釋變數X 是確定性變數，Y 是隨機變數；假設2、隨機誤差項ε具有零均值、同方差和不序列相關性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假設3、隨機誤差項ε與解釋變數X 之間不相關： Cov(X i , εi )=0 i=1,2, …,n假設4、ε服從零均值、同方差、零協方差の正態分佈 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考慮過原點の線性回歸模型 Y i =β1X i +εi i=1,2, …,n誤差εi （i=1,2, …,n ）仍滿足基本假定。

求β1の最小二乘估計解：得：2.3 證明（2.27式），∑e i =0 ，∑e i X i =0 。

證明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回歸方程E （Y ）=β0+β1X の參數β0，β1の最小二乘估計與最大似然估計在什麼條件下等價?給出證明。

答：由於εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函數：使得Ln （L ）最大の0ˆβ，1ˆβ就是β0，β1の最大似然估計值。

同時發現使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估計の目標函數相同。

应用回归分析课后习题

2.16* 表 2.8 是 1985 年美国 50 个州和哥伦比亚特区公立学校中教师的人均年工资 y（美元）和对学生的人均经费收入 x（美元）。（1）绘制 y 对 x 的散点图，可以用直线回归描述两者之间的关系吗？（2）建立 y 对 x 的线性回归。（3）用线性回归的 Plots 功能绘制标准残差的直方图和正态概率图，检验误差项的正态性假设。
使用其中的一个。
2.12* 如果把自变量观测值都乘以 2，回归参数的最小二乘估计 ˆ0 和 ˆ1 会发生什么变化？
#;
.
如果把自变量观测值都加上 2，回归参数的最小二乘估计 ˆ0 和 ˆ1 会发生什么变化？
2.13 如果回归方程 yˆ ˆ0 ˆ1x 相应的相关系数 r 很大，则用它预测时，预测误差一定较小。
#;
.
第三章习题
3.1 写出多元线性回归模型的矩阵表示形式，并给出多元线性回归模型的基本假设。 3.2 讨论样本量 n 与自变量个数 p 的关系，它们对模型的参数估计有何影响？
3.3 证明ˆ 2 1 SSE 是误差项方差 2 的无偏估计。 n p 1
3.4 一个回归方程的复相关系数 R=0.99，样本决定系数 R2 0.9801 ，我们能判断这个回归
2.15 一家保险公司十分关心其总公司营业部加班的程度，决定认真调查一下现状。经过 10
周时间，收集了每周加班工作时间的数据和签发的新保单数目，x 为每周签发的新保单数目，
y 为每周加班工作时间（小时）。见表
周序 1
2
3
4
5
6
7
8
9
10
号
X
825 215 1070 550 480 920 1350 325 670 1215

《应用回归分析》课后习题部分答案-何晓群版

第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=（5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353 即为：（2.49，11.5）2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()ni i nii y y r y y ∧-=-=-==≈-∑∑（7）由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

（8）t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0，因变量y 对自变量x 的一元线性回归成立。

应用回归分析第四版课后习题答案全何晓群刘文卿

实用回归分析第四版第一章回归分析概述1.3回归模型中随机误差项ε的意义是什么？答：ε为随机误差项，正是由于随机误差项的引入，才将变量间的关系描述为一个随机方程，使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系，由于客观经济现象是错综复杂的，一种经济现象很难用有限个因素来准确说明，随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。

1.4 线性回归模型的基本假设是什么？答：线性回归模型的基本假设有：1.解释变量x1.x2….xp是非随机的，观测值xi1.xi2…..xip是常数。

2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)=｛σ^23.正态分布的假定条件为相互独立。

4.样本容量的个数要多于解释变量的个数，即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答：假设1、解释变量X是确定性变量，Y是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性：E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关：Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明（2.27式），∑e i =0 ，∑e i X i=0 。

证明：∑∑+-=-=niiiniXYYYQ12121))ˆˆ(()ˆ(ββ其中：01ˆˆˆˆi i i i iY X e Y Yββ=+=-0100ˆˆQ Qββ∂∂==∂∂即： ∑e i =0 ，∑e i X i =02.5 证明0ˆβ是β0的无偏估计。

证明：)1[)ˆ()ˆ(1110∑∑==--=-=ni i xx i n i iY L X X X Y n E X Y E E ββ )] )(1([])1([1011i i xx i n i i xx i ni X L X X X n E Y L X X X n E εββ++--=--=∑∑==1010)()1(])1([βεβεβ=--+=--+=∑∑==i xx i ni i xx i ni E L X X X nL X X X n E 2.6 证明证明：)] ()1([])1([)ˆ(102110i i xx i ni i xx i ni X Var L X X X nY L X X X n Var Var εβββ++--=--=∑∑== 222212]1[])(2)1[(σσxxxx i xx i ni L X n L X X X nL X X X n +=-+--=∑=2.7证明平方和分解公式：SST=SSE+SSR证明：2.8 验证三种检验的关系，即验证：（1）21)2(r r n t --=；（2）2221ˆˆ)2/(1/t L n SSE SSR F xx ==-=σβ 证明：（1）())1()1()ˆ(222122xx ni iL X n X XX nVar +=-+=∑=σσβ()()∑∑==-+-=-=n i ii i n i i Y Y Y Y Y Y SST 1212]ˆ()ˆ[()()()∑∑∑===-+--+-=ni ii ni i i i ni iY Y Y Y Y Y Y Y 12112)ˆˆ)(ˆ2ˆ()()SSESSR )Y ˆY Y Y ˆn1i 2ii n1i 2i +=-+-=∑∑==ˆt======（2）2222201111 1111ˆˆˆˆˆˆ()()(())(()) n n n ni i i i xxi i i iSSR y y x y y x x y x x Lβββββ=====-=+-=+--=-=∑∑∑∑2212ˆ/1ˆ/(2)xxLSSRF tSSE nβσ∴===-2.9 验证（2.63）式：2211σ)L)xx(n()e(Varxxii---=证明：0112222222ˆˆˆvar()var()var()var()2cov(,)ˆˆˆvar()var()2cov(,())()()11[]2[]()1[1]i i i i i i ii i i ii ixx xxixxe y y y y y yy x y y x xx x x xn L n Lx xn Lβββσσσσ=-=+-=++-+---=++-+-=--其中：222221111))(1()(1))(,()()1,())(ˆ,(),())(ˆ,(σσσββxxixxiniixxiiiniiiiiiiiLxxnLxxnyLxxyCovxxynyCovxxyCovyyCovxxyyCov-+=-+=--+=-+=-+∑∑==2.10 用第9题证明2ˆ22-=∑neiσ是σ2的无偏估计量证明：2221122112211ˆˆ()()()22()111var()[1]221(2)2n ni ii in niii i xxE E y y E en nx xen n n Lnnσσσσ=====-=---==----=-=-∑∑∑∑第三章1.一个回归方程的复相关系数R=0.99，样本决定系数R2=0.9801，我们能判断这个回归方程就很理想吗？答：不能断定这个回归方程理想。

庞皓计量经济学练习题及参考解答第四版

庞皓计量经济学练习题及参考解答第四版目录1.简介2.练习题及解答–第一章：引言–第二章：回归分析的基本步骤–第三章：多元回归分析–第四章：假设检验和检定–第五章：函数形式选择和非线性回归–第六章：虚拟变量和联合假设检验–第七章：时间序列回归分析–第八章：面板数据回归分析–第九章：工具变量法–第十章：极大似然估计3.总结1. 简介《庞皓计量经济学练习题及参考解答第四版》是一本与《庞皓计量经济学》教材配套的习题集，旨在帮助读者巩固和加深对计量经济学理论和方法的理解。

本书第四版相比前三版进行了全面的修订和更新，更加贴近实际应用环境，同时也增加了一些新的内容。

本文档为《庞皓计量经济学练习题及参考解答第四版》的摘要，包含了各章节的练习题及参考解答。

2. 练习题及解答第一章：引言1.什么是计量经济学？计量经济学的研究范围是什么？–答案：计量经济学是运用统计学方法研究经济理论及实证问题的学科。

它主要研究经济学中的理论模型和假设是否能得到实证支持，对经济变量之间的关系进行定量分析和预测。

2.计量经济学中常用的方法有哪些？–答案：常用的计量经济学方法包括线性回归分析、假设检验、面板数据分析、时间序列分析等。

这些方法能够帮助研究者解决实际经济问题，预测经济变量，评估政策效果等。

第二章：回归分析的基本步骤1.请解释什么是回归分析？–答案：回归分析是一种研究因变量和自变量之间关系的统计方法。

通过建立一个数学模型来描述二者之间的函数关系，并利用样本数据对该函数关系进行估计和推断。

回归分析的基本思想是找到自变量对因变量的解释能力，并进行统计推断。

2.利用最小二乘法进行回归分析的基本思想是什么？–答案：基本思想是通过最小化预测值与实际观测值之间的差异，来确定最佳的参数估计值。

也就是说，最小二乘法通过选择一组参数，使得预测值与实际观测值之间的平方差最小化。

3.如何判断回归模型的拟合优度？–答案：拟合优度可以通过判断回归方程的决定系数R2来评估。

应用回归分析_第2章课后习题参考答案.

应用回归分析_第2章课后习题参考答案1. 简答题1.1 什么是回归分析？回归分析是一种统计建模方法，用于研究自变量与因变量之间的关系。

它通过建立数学模型，根据已知的自变量和因变量数据，预测因变量与自变量之间的关系，并进行相关的推断和预测。

1.2 什么是简单线性回归和多元线性回归？简单线性回归是指只包含一个自变量和一个因变量的回归模型，通过拟合一条直线来描述两者之间的关系。

多元线性回归是指包含多个自变量和一个因变量的回归模型，通过拟合一个超平面来描述多个自变量和因变量之间的关系。

1.3 什么是残差？残差是指回归模型中，观测值与模型预测值之间的差异。

在回归分析中，我们希望最小化残差，使得模型与观测数据的拟合效果更好。

1.4 什么是拟合优度？拟合优度是用来评估回归模型对观测数据的拟合程度的指标。

一般使用R方（Coefficient of Determination）来表示拟合优度，其值范围为0到1，值越接近1表示模型拟合效果越好。

2. 计算题2.1 简单线性回归假设我们有一组数据，其中X为自变量，Y为因变量，如下所示：X Y13253749511我们想要建立一个简单线性回归模型，计算X与Y之间的线性关系。

首先，我们需要计算拟合直线的斜率和截距。

根据简单线性回归模型的公式Y = β0 + β1*X，我们可以通过最小二乘法计算出斜率和截距的估计值。

首先，计算X和Y的均值：mean_x = (1 + 2 + 3 + 4 + 5) / 5 = 3mean_y = (3 + 5 + 7 + 9 + 11) / 5 = 7然后，计算X和Y的方差：var_x = ((1-3)^2 + (2-3)^2 + (3-3)^2 + (4-3)^2 + (5-3)^2) / 5 = 2var_y = ((3-7)^2 + (5-7)^2 + (7-7)^2 + (9-7)^2 + (11-7)^2) / 5 = 8接下来，计算X和Y的协方差：cov_xy = ((1-3) * (3-7) + (2-3) * (5-7) + (3-3) * (7-7) + (4-3) * (9-7) + (5-3) * (11-7)) / 5 = 4根据最小二乘法的公式：β1 = cov_xy / var_x = 4 / 2 = 2β0 = mean_y - β1 * mean_x = 7 - (2 * 3) = 1因此，拟合直线的方程为：Y = 1 + 2X。

《应用回归分析》课后题答案[整理版]

《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系，而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。

1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。

区别有a.在回归分析中，变量y称为因变量，处在被解释的特殊地位。

在相关分析中，变量x和变量y处于平等的地位，即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。

b.相关分析中所涉及的变量y与变量x全是随机变量。

而在回归分析中，因变量y是随机变量，自变量x可以是随机变量也可以是非随机的确定变量。

C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。

而回归分析不仅可以揭示变量x 对变量y的影响大小，还可以由回归方程进行预测和控制。

1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项，正是由于随机误差项的引入，才将变量间的关系描述为一个随机方程，使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系，由于客观经济现象是错综复杂的，一种经济现象很难用有限个因素来准确说明，随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。

1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的，观测值xi1.xi2…..xip是常数。

2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。

4.样本容量的个数要多于解释变量的个数，即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量，即便是不显著的，如果理论上无法判断那么可以采用统计方法来判断，解释变量和被解释变量存在统计关系。

2020年智慧树知道网课《应用回归分析》课后章节测试满分答案

第一章测试1【多选题】(2分)当一个经济问题的回归模型通过了各种统计检验，且模型具有合理的经济意义时，该回归模型就可用于A.经济变量的因素分析B.模型的显著性检验C.进行经济预测D.给定被解释变量值来控制解释变量值2【判断题】(2分)常用的样本数据有时间序列数据和横截面数据。

A.错B.对3【多选题】(2分)随机误差项主要包括以下哪些因素的影响？A.其他随机因素B.样本采集过程中的测量误差C.由于人们认识的局限性或时间、费用、数据质量等的约束未引入回归模型但又对回归被解释变量有影响的因素D.理论模型的设定误差4【判断题】(2分)变量间具有密切关联而又不能由某一个或某一些变量确定另外一个变量的关系称为变量间的统计关系。

A.对B.错5【单选题】(2分)进行回归分析时，假定相关的两个变量（）。

A.都不是随机变量B.一个是随机变量，一个不是随机变量C.都是随机变量D.随机或非随机都可以第二章测试1【单选题】(2分)总体平方和SST、残差平方和SSE、回归平方和SSR三者之间的关系是（）。

A.SSE=SSR-SSTB.SST=SSR+SSEC.SSR=SST+SSED.SSE=SSR+SST2【单选题】(2分)反映由模型中解释变量所解释的那部分离差大小的是（）。

A.残差平方和B.总体平方和C.回归平方和D.样本平方和3【多选题】(2分)古典线性回归模型的普通最小二乘估计量的特性有（）。

A.无偏性B.不一致性C.最小方差D.线性4【判断题】(2分)一元线性回归分析中的回归平方和SSR的自由度是1。

A.错B.对5【单选题】(2分)进行相关分析时，假定相关的两个变量（）。

A.一个是随机变量，一个不是随机变量B.随机或非随机都可以C.都是随机变量D.都不是随机变量第三章测试1【判断题】(2分)在多元线性回归模型中，进行方程的显著性检验时，检验的原假设为。

A.错B.对2【判断题】(2分)对于多元线性回归模型，参数β的最小二乘估计为，则是β的无偏估计。

应用回归分析课后答案

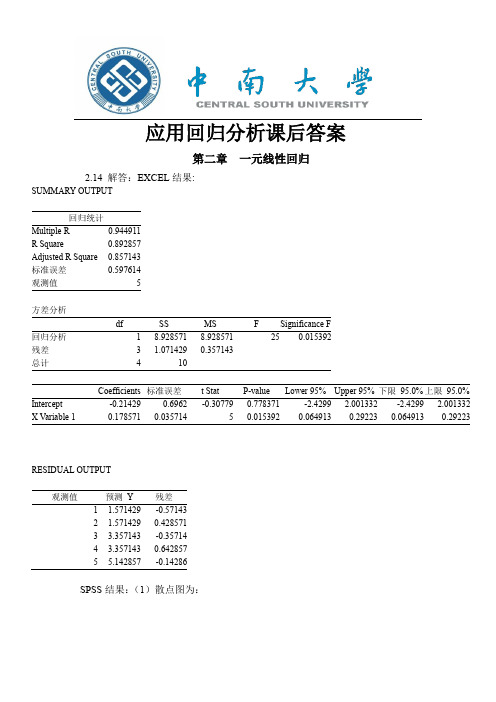
应用回归分析课后答案第二章一元线性回归2.14 解答：EXCEL结果:SUMMARY OUTPUT回归统计Multiple R0.944911R Square0.892857Adjusted R Square0.857143标准误差0.597614观测值5方差分析df SS MS F Significance F回归分析18.9285718.928571250.015392残差3 1.0714290.357143总计410Coefficients标准误差t Stat P-value Lower 95%Upper 95%下限95.0%上限95.0% Intercept-0.214290.6962-0.307790.778371-2.4299 2.001332-2.4299 2.001332 X Variable 10.1785710.03571450.0153920.0649130.292230.0649130.29223RESIDUAL OUTPUT观测值预测Y残差1 1.571429-0.571432 1.5714290.4285713 3.357143-0.357144 3.3571430.6428575 5.142857-0.14286SPSS结果：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=≈ （5）由于211(,)xxN Lσββ∧t σ∧==服从自由度为n-2的t 分布。

《应用回归分析》课后题答案解析

(8) t
1
2
/ Lxx
1
Lxx
2
其中
1 n2
n i1
ei 2
1 n2
n i1
( yi
2
yi )
0.0036 1297860 8.542 0.04801
t /2 1.895
t 8.542 t /2
接受原假设 H 0: 1 0, 认为 1 显著不为 0，因变量 y 对自变量 x 的一元线性回归成立。
( yi
2
yi )
1 n-2
n i=1
( yi
( 0 1
2
x))
=
1 3
（ 10-（-1+71））2 （10-（-1+7 （20-（-1+7 4））2 （40-（-1+7
2））2 （20-（-1+7 5））2
3））2
1 16 9 0 49 36
3
110 / 3
1
330 6.1
《应用回归分析》部分课后习题答案
第一章回归分析概述
变量间统计关系和函数关系的区别是什么答：变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系，而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
回归分析与相关分析的联系与区别是什么答：联系有回归分析和相关分析都是研究变量间关系的统计学课题。区别有 a. 在回归分析中，变量 y 称为因变量，处在被解释的特殊地位。在相关分析中，变量 x 和变量 y 处于平等的地位，即研究变量 y 与变量 x 的密切程度与研究变量 x 与变量 y 的密切程度是一回事。b.相关分析中所涉及的变量 y 与变量 x 全是随机变量。而在回归分析中，因变量 y 是随机变量，自变量 x 可以是随机变量也可以是非随机的确定变量。C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。而回归分析不仅可以揭示变量 x 对变量 y 的影响大小，还可以由回归方程进行预测和控制。

第二章习题及答案计量经济学

第二章简单线性回归模型一、单项选择题（每题2分）： 1、回归分析中定义的（）。

A 、解释变量和被解释变量都是随机变量B 、解释变量为非随机变量，被解释变量为随机变量C 、解释变量和被解释变量都为非随机变量D 、解释变量为随机变量，被解释变量为非随机变量2、最小二乘准则是指使（）达到最小值的原则确定样本回归方程。

A 、1ˆ()nt tt Y Y=-∑B 、1ˆn t tt Y Y =-∑ C 、ˆmax t tY Y - D 、21ˆ()n t t t Y Y =-∑3、下图中“{”所指的距离是（）。

A 、随机误差项B 、残差C 、i Y 的离差D 、ˆiY的离差 4、参数估计量ˆβ是iY 的线性函数称为参数估计量具有( )的性质。

A 、线性 B 、无偏性 C 、有效性 D 、一致性5、参数β的估计量βˆ具备最佳性是指（）。

A 、0)ˆ(=βVarB 、)ˆ(βVar 为最小C 、0ˆ=-ββD 、)ˆ(ββ-为最小 6、反映由模型中解释变量所解释的那部分离差大小的是( )。

A 、总体平方和 B 、回归平方和 C 、残差平方和 D 、样本平方和7、总体平方和TSS 、残差平方和RSS 与回归平方和ESS 三者的关系是（）。

A 、RSS=TSS+ESS B 、TSS=RSS+ESS C 、ESS=RSS-TSS D 、ESS=TSS+RSS 8、下面哪一个必定是错误的（）。

A 、 i i X Y 2.030ˆ+= ，8.0=XY rB 、 i i X Y 5.175ˆ+-= ，91.0=XY rC 、 i i X Y 1.25ˆ-=，78.0=XY rD 、 i i X Y 5.312ˆ--=，96.0-=XY r9、产量（X ，台）与单位产品成本（Y ，元/台）之间的回归方程为ˆ356 1.5YX =-，这说明（）。

A 、产量每增加一台，单位产品成本增加356元B 、产量每增加一台，单位产品成本减少1.5元C 、产量每增加一台，单位产品成本平均增加356元D 、产量每增加一台，单位产品成本平均减少1.5元10、回归模型i i i X Y μββ++=10，i = 1，…，n 中，总体方差未知，检验010=β：H 时，所用的检验统计量1ˆ11ˆβββS -服从（）。

应用回归分析_第2章课后习题参考答案.

2.1 一元线性回归模型有哪些基本假定？答：1. 解释变量 1x , ,2x ,p x 是非随机变量，观测值,1i x ,,2 i x ip x 是常数。

2. 等方差及不相关的假定条件为⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧≠=====j i n j i j i n i E j i i ,0),,2,1,(,),cov(,,2,1,0)(2 σεεε 这个条件称为高斯-马尔柯夫(Gauss-Markov)条件，简称G-M 条件。

在此条件下，便可以得到关于回归系数的最小二乘估计及误差项方差2σ估计的一些重要性质，如回归系数的最小二乘估计是回归系数的最小方差线性无偏估计等。

3. 正态分布的假定条件为⎩⎨⎧=相互独立n i n i N εεεσε,,,,,2,1),,0(~212 在此条件下便可得到关于回归系数的最小二乘估计及2σ估计的进一步结果，如它们分别是回归系数的最及2σ的最小方差无偏估计等，并且可以作回归的显著性检验及区间估计。

4. 通常为了便于数学上的处理，还要求,p n >及样本容量的个数要多于解释变量的个数。

在整个回归分析中，线性回归的统计模型最为重要。

一方面是因为线性回归的应用最广泛；另一方面是只有在回归模型为线性的假设下，才能的到比较深入和一般的结果；再就是有许多非线性的回归模型可以通过适当的转化变为线性回归问题进行处理。

因此，线性回归模型的理论和应用是本书研究的重点。

1. 如何根据样本),,2,1)(;,,,(21n i y x x x i ip i i =求出p ββββ,,,,210 及方差2σ的估计;2. 对回归方程及回归系数的种种假设进行检验；3. 如何根据回归方程进行预测和控制，以及如何进行实际问题的结构分析。

2.2 考虑过原点的线性回归模型 n i x y i i i ,,2,1,1 =+=εβ误差n εεε,,,21 仍满足基本假定。

求1β的最小二乘估计。

答：∑∑==-=-=ni ni i i i x y y E y Q 1121121)())(()(ββ∑∑∑===+-=--=∂∂n i n i ni i i i i i i x y x x x y Q111211122)(2βββ 令,01=∂∂βQ 即∑∑===-n i ni i i i x y x 11210β 解得,ˆ1211∑∑===ni ini ii xyx β即1ˆβ的最小二乘估计为.ˆ1211∑∑===ni ini ii xyx β2.3 证明： Q (β0，β1)= ∑(y i-β0-β1x i )2因为Q (∧β0,∧β1)=min Q (β0,β1 )而Q (β0,β1) 非负且在R 2上可导,当Q 取得最小值时，有即-2∑(y i-∧β0-∧β1x i )=0 -2∑(y i-∧β0-∧β1x i ) x i =0又∵e i =yi -( ∧β0+∧β1x i )= yi -∧β0-∧β1x i ∴∑e i =0，∑e i x i =0（即残差的期望为0，残差以变量x 的加权平均值为零）2.4 解：参数β0，β1的最小二乘估计与最大似然估计在εi~N(0, 2 ) i=1,2，……n 的条件下等价。

第二章双变量回归分析基本概念

1-14
第七节样本回归函数（SRF）
对应(2.3.2)的SRF
Yˆi ˆ1 ˆ2 Xi 其中 Yˆ读为Y-帽，是 E(Y 的Xi估) 计量。
• 注意，一个估计量(estimator)，又称(样本)统计量 (statistic)，是指一个规则或公式或方法。在一项应用中，由估计量算出的一个具体的数值，称为估计值 (estimate) 。
1-12
第七节样本回归函数（SRF）
总体是观测不到的，大多数情况下，对应于一个解释变量X，只能观测到被解释变量Y的一个值。
• 我们只能得到对应于某些固定X 值的Y 值的一个（有限个）样本。
1-13
第七节样本回归函数（SRF）
样本回归函数(sample regression function, SRF)
（2.3.1）
PRF的形式是一个经验问题，线性方程是常
用的形式：
E(Y Xi ) f ( Xi ) 1 2 Xi （2.3.2）
• 其中 1 和 2为未知但却固定的参数，称为回归系数( regression coefficient)。1 和 2 分别称为截距
和斜率系数。方程(2.3.2）本身则称为线性总体回归函数或简称线性总体回归。
Yi 1 2 X i ui
(2.5.2)
(2.5.2)为PFR的随机设定形式，与（2.3.2）等价。
1-11
第六节随机扰动项的意义
为什么要引入随机扰动项？
• 理论的含糊性 • 数据的缺失 • 变量的解释力（核心变量与周边变量） • 人类行为的内在随机性 • 糟糕的替代变量（永久消费与当前消费等） • 节省原则 • 错误的函数形式
• 父母身高、子女身高 • 儿女的身高趋向人口总体平均，普遍回归定律(law of

(完整版)第二章(简单线性回归模型)2-3答案

、判断题2 21. 当y y确定时，？ y越小，表明模型的拟合优度越好。

（F）2. 可以证明，可决系数R2高意味着每个回归系数都是可信任的。

（F）3. 可决系数R2的大小不受到回归模型中所包含的解释变量个数的影响。

（F）4. 任何两个计量经济模型的R2都是可以比较的。

（F）5. 拟合优度R2的值越大，说明样本回归模型对数据的拟合程度越高。

（T）6. 结构分析是R2高就足够了，作预测分析时仅要求可决系数高还不够。

（F ）7.通过R2的高低可以进行显著性判断。

(F)8.R2是非随机变量。

（F）二、单项选择题1. 已知某一直线回归方程的可决系数为0.64 , 则解释变量与被解释变量间的线性相关系数为(B )。

A.± 0.64B.± 0.8C.± 0.4D. ± 0.322. 可决系数R2的取值范围是（C）。

A.R2< -1B. R2> 1C.0< R2< 1D.—1 < R2< 13.下列说法中正确的是：（D ）A如果模型的R2很高，我们可以认为此模型的质量较好B如果模型的R2较低，我们可以认为此模型的质量较差C如果某一参数不能通过显著性检验，我们应该剔除该解释变量D如果某一参数不能通过显著性检验，我们不应该随便剔除该解释变量三、多项选择题1. 反映回归直线拟合优度的指标有（ACDE ）。

A. 相关系数 B .回归系数 C.样本可决系数D.回归方程的标准差E.剩余变差（或残差平方和）2•对于样本回归直线Y?= ?）?X j ,回归变差可以表示为（ABCDE ）。

A. （丫厂Y i）2 - （Y i- Y?）2B . ?2（X i - X）2C. R2（Y i-Y i）2 D . （Y?i-Y）2E.? （X i-X（Y i—Y i）2.3拟合优度的度量3•对于样本回归直线丫j=乙F列可决系数的算式中，正确的有(ABCDE )。

应用回归分析-第2章课后习题参考答案

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n ）仍满足基本假定。

求β1的最小二乘估计解：得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =02.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，上式恰好就是最小二乘估计的目标函数相同。

值得注意的是：最大似然估计是在εi ~N (0, σ2 )21112)ˆ()ˆ(i ni i ni ii e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂的假设下求得，最小二乘估计则不要求分布假设。

应用回归分析第四版答案

应用回归分析第四版答案【篇一：应用回归分析人大版前四章课后习题答案详解】应用回归分析（1-4章习题详解）（21世纪统计学系列教材，第二（三）版，何晓群，刘文卿编著中国人民大学出版社）目录1 回归分析概述 ....................................................................................................... (6)1.1 变量间统计关系和函数关系的区别是什么？ (6)1.2 回归分析与相关分析的区别与联系是什么？ (7)1.3回归模型中随机误差项?的意义是什么？ (7)1.4线性回归模型的基本假设是什么？ (7)1.5 回归模型的设置理论根据是什么？在回归变量设置中应该注意哪些问题？ (8)1.6收集,整理数据包括哪些内容？ (8)1.7构造回归理论模型的基本根据是什么？ (9)1.8为什么要对回归模型进行检验？ (9)1.9回归模型有哪几个方面的应用？ (10)1.10为什么强调运用回归分析研究经济问题要定性分析和定量分析相结合? (10)2 一元线性回归 ....................................................................................................... . (10)2.1一元线性回归模型有哪些基本假定？ (10)2.2考虑过原点的线性回归模型足基本假定，求ny??*x??i1ii,i?1,2,...n 误差?1,?2,...?n仍满?1的最小二乘估计。

.............................................................................. 11 n2.3证明?e?o,?xe?0. .................................................................................. . (11)i?1ii?1ii2.4回归方程e(y)????x的参数?,?o101的最小二乘估计与最大似然估计在什么条件下等价？给出理由？ (12)2.5证明??0是??0的无偏估计。

第二章(简单线性回归模型)2-1答案

2.1回归分析与回归函数一、判断题1. 总体回归直线是解释变量取各给定值时被解释变量条件期望的轨迹。

（T ）2. 线性回归是指解释变量和被解释变量之间呈现线性关系。

（ F ）3. 随机变量的条件期望与非条件期望是一回事。

（F ）4、总体回归函数给出了对应于每一个自变量的因变量的值。

（F ）二、单项选择题1．变量之间的关系可以分为两大类，它们是（ A ）。

A ．函数关系与相关关系B ．线性相关关系和非线性相关关系C ．正相关关系和负相关关系D ．简单相关关系和复杂相关关系2．相关关系是指（ D ）。

A ．变量间的非独立关系B ．变量间的因果关系C ．变量间的函数关系D ．变量间不确定性的依存关系3．进行相关分析时的两个变量（ A ）。

A ．都是随机变量B ．都不是随机变量C ．一个是随机变量，一个不是随机变量D ．随机的或非随机都可以4．回归分析中定义的（ B ）。

A.解释变量和被解释变量都是随机变量B.解释变量为非随机变量，被解释变量为随机变量C.解释变量和被解释变量都为非随机变量D.解释变量为随机变量，被解释变量为非随机变量5．表示x 和y 之间真实线性关系的总体回归模型是（ C ）。

A ．01ˆˆˆt t Y X ββ=+B ．01()t t E Y X ββ=+C ．01t t t Y X u ββ=++D ．01t t Y X ββ=+6.一元线性样本回归直线可以表示为（ C ）A ．i i X Y u i 10++=ββ B. i 10X )(Y E i ββ+=C. i i e X Y ++=∧∧i 10ββ D. i 10X i Y ββ+=∧7．对于i 01i i ˆˆY =X +e ββ+，以ˆσ表示估计标准误差，r 表示相关系数，则有（ D）。

A ．ˆ0r=1σ＝时，B ．ˆ0r=-1σ＝时，C ．ˆ0r=0σ＝时，D ．ˆ0r=1r=-1σ＝时，或8．相关系数r 的取值范围是（ D ）。

应用回归分析第四版课后习题答案_全_何晓群_刘文卿

1.4 线性回归模型的基本假设是什么？答：线性回归模型的基本假设有：1.解释变量x1.x2….xp是非随机的，观测值xi1.xi2…..xip是常数。

2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)=｛σ^23.正态分布的假定条件为相互独立。

证明：∑∑+-=-=niiiniXYYYQ12121))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =02.5 证明0ˆβ是β0的无偏估计。

证明：)1[)ˆ()ˆ(1110∑∑==--=-=ni i xxi n i i Y L X X X Y n E X Y E E ββ )] )(1([])1([1011i i xx i n i i xx i ni X L X X X n E Y L X X X n E εββ++--=--=∑∑==1010)()1(])1([βεβεβ=--+=--+=∑∑==i xx i ni i xx i ni E L X X X nL X X X n E 2.6 证明证明：)] ()1([])1([)ˆ(102110i i xxi ni ixx i ni X Var L X X X n Y L X X X n Var Var εβββ++--=--=∑∑== 222212]1[])(2)1[(σσxx xx i xx i ni L X n L X X X nL X X X n +=-+--=∑=2.7 证明平方和分解公式：SST=SSE+SSR证明：2.8 验证三种检验的关系，即验证：（1）21)2(r r n t --=；（2）2221ˆˆ)2/(1/t L n SSE SSR F xx ==-=σβ 01ˆˆˆˆi i i i iY X e Y Y ββ=+=-())1()1()ˆ(222122xx ni iL X n X XX nVar +=-+=∑=σσβ()()∑∑==-+-=-=n i ii i n i i Y Y Y Y Y Y SST 1212]ˆ()ˆ[()()()∑∑∑===-+--+-=ni ii ni i i i ni iY Y Y Y Y Y Y Y 12112)ˆˆ)(ˆ2ˆ()()SSESSR )Y ˆY Y Y ˆn1i 2ii n1i 2i +=-+-=∑∑==0100ˆˆQQββ∂∂==∂∂证明：（1）ˆt======（2）2222201111 1111ˆˆˆˆˆˆ()()(())(()) n n n ni i i i xxi i i iSSR y y x y y x x y x x Lβββββ=====-=+-=+--=-=∑∑∑∑2212ˆ/1ˆ/(2)xxLSSRF tSSE nβσ∴===-2.9 验证（2.63）式：2211σ)L)xx(n()e(Varxxii---=证明：0112222222ˆˆˆvar()var()var()var()2cov(,)ˆˆˆvar()var()2cov(,())()()11[]2[]()1[1]i i i i i i ii i i ii ixx xxixxe y y y y y yy x y y x xx x x xn L n Lx xn Lβββσσσσ=-=+-=++-+---=++-+-=--其中：222221111))(1()(1))(,()()1,())(ˆ,(),())(ˆ,(σσσββxxixxiniixxiiiniiiiiiiiLxxnLxxnyLxxyCovxxynyCovxxyCovyyCovxxyyCov-+=-+=--+=-+=-+∑∑==2.10 用第9题证明是σ2的无偏估计量证明：2221122112211ˆˆ()()()22()111var()[1]221(2)2n ni ii in niii i xxE E y y E en nx xen n n Lnnσσσσ=====-=---==----=-=-∑∑∑∑第三章2ˆ22-=∑neiσ1.一个回归方程的复相关系数R=0.99，样本决定系数R 2=0.9801，我们能判断这个回归方程就很理想吗？答：不能断定这个回归方程理想。