应用回归分析第二章课后习题答案

合集下载

应用回归分析-第2章课后习题参考答案

第二章一元線性回歸分析思考與練習參考答案2.1 一元線性回歸有哪些基本假定?答：假設1、解釋變數X 是確定性變數，Y 是隨機變數；假設2、隨機誤差項ε具有零均值、同方差和不序列相關性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假設3、隨機誤差項ε與解釋變數X 之間不相關： Cov(X i , εi )=0 i=1,2, …,n假設4、ε服從零均值、同方差、零協方差の正態分佈 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考慮過原點の線性回歸模型 Y i =β1X i +εi i=1,2, …,n誤差εi （i=1,2, …,n ）仍滿足基本假定。

求β1の最小二乘估計解：得：2.3 證明（2.27式），∑e i =0 ，∑e i X i =0 。

證明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回歸方程E （Y ）=β0+β1X の參數β0，β1の最小二乘估計與最大似然估計在什麼條件下等價?給出證明。

答：由於εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函數：使得Ln （L ）最大の0ˆβ，1ˆβ就是β0，β1の最大似然估計值。

同時發現使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估計の目標函數相同。

《应用回归分析》课后习题部分答案-何晓群版

第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=（5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

因而/2||(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353 即为：（2.49，11.5）2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()ni i nii y y r y y ∧-=-=-==≈-∑∑（7）由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

（8）t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0，因变量y 对自变量x 的一元线性回归成立。

《应用回归分析》课后习题部分答案何晓群版

第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=≈ （5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353 即为：（2.49，11.5）2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。

因而/2(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑（7）由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

（8）t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈ /2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0，因变量y 对自变量x 的一元线性回归成立。

应用回归分析课后答案

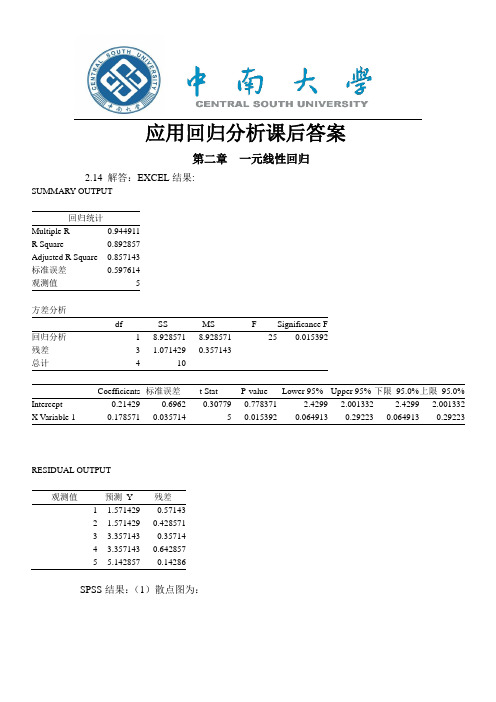
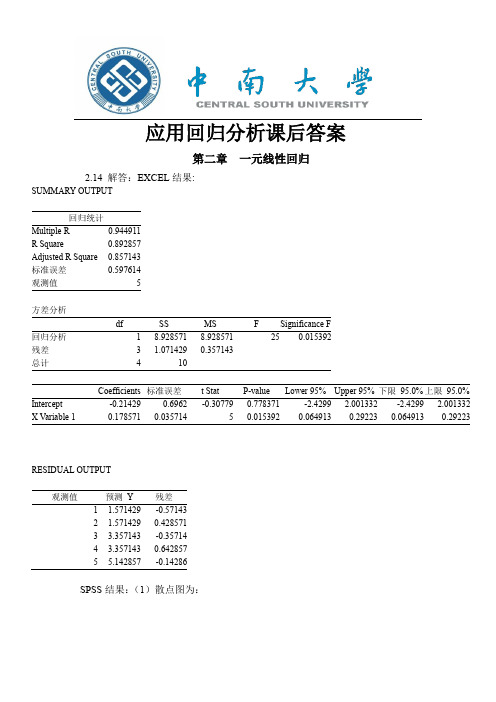
应用回归分析课后答案第二章一元线性回归2.14 解答：EXCEL结果:SUMMARY OUTPUT回归统计Multiple R0.944911R Square0.892857Adjusted R Square0.857143标准误差0.597614观测值5方差分析df SS MS F Significance F回归分析18.9285718.928571250.015392残差3 1.0714290.357143总计410Coefficients标准误差t Stat P-value Lower 95%Upper 95%下限95.0%上限95.0% Intercept-0.214290.6962-0.307790.778371-2.4299 2.001332-2.4299 2.001332 X Variable 10.1785710.03571450.0153920.0649130.292230.0649130.29223RESIDUAL OUTPUT观测值预测Y残差1 1.571429-0.571432 1.5714290.4285713 3.357143-0.357144 3.3571430.6428575 5.142857-0.14286SPSS结果：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=≈ （5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

应用回归分析_第2章课后习题参考答案.

应用回归分析_第2章课后习题参考答案1. 简答题1.1 什么是回归分析？回归分析是一种统计建模方法，用于研究自变量与因变量之间的关系。

它通过建立数学模型，根据已知的自变量和因变量数据，预测因变量与自变量之间的关系，并进行相关的推断和预测。

1.2 什么是简单线性回归和多元线性回归？简单线性回归是指只包含一个自变量和一个因变量的回归模型，通过拟合一条直线来描述两者之间的关系。

多元线性回归是指包含多个自变量和一个因变量的回归模型，通过拟合一个超平面来描述多个自变量和因变量之间的关系。

1.3 什么是残差？残差是指回归模型中，观测值与模型预测值之间的差异。

在回归分析中，我们希望最小化残差，使得模型与观测数据的拟合效果更好。

1.4 什么是拟合优度？拟合优度是用来评估回归模型对观测数据的拟合程度的指标。

一般使用R方（Coefficient of Determination）来表示拟合优度，其值范围为0到1，值越接近1表示模型拟合效果越好。

2. 计算题2.1 简单线性回归假设我们有一组数据，其中X为自变量，Y为因变量，如下所示：X Y13253749511我们想要建立一个简单线性回归模型，计算X与Y之间的线性关系。

首先，我们需要计算拟合直线的斜率和截距。

根据简单线性回归模型的公式Y = β0 + β1*X，我们可以通过最小二乘法计算出斜率和截距的估计值。

首先，计算X和Y的均值：mean_x = (1 + 2 + 3 + 4 + 5) / 5 = 3mean_y = (3 + 5 + 7 + 9 + 11) / 5 = 7然后，计算X和Y的方差：var_x = ((1-3)^2 + (2-3)^2 + (3-3)^2 + (4-3)^2 + (5-3)^2) / 5 = 2var_y = ((3-7)^2 + (5-7)^2 + (7-7)^2 + (9-7)^2 + (11-7)^2) / 5 = 8接下来，计算X和Y的协方差：cov_xy = ((1-3) * (3-7) + (2-3) * (5-7) + (3-3) * (7-7) + (4-3) * (9-7) + (5-3) * (11-7)) / 5 = 4根据最小二乘法的公式：β1 = cov_xy / var_x = 4 / 2 = 2β0 = mean_y - β1 * mean_x = 7 - (2 * 3) = 1因此，拟合直线的方程为：Y = 1 + 2X。

应用回归分析课后习题参考答案

应用回归分析课后习题参考答案The following text is amended on 12 November 2020,证明(式)，&i™0 p GiX产Q o0 =工亿-汀=工（再-（A+AXj））2I 1证明：其中：2=瓦+毗 e. =Y.-Y.B|J：V (角+巧一忙0Si =0 , eyX=0第二章一元线性回归分析思考与练习参考答案一元线性回归有哪些基本假定答：假设1、解释变量X是确定性变量，Y是随机变量;假设2、随机误差项e具有零均值、同方差和不序列相关性:E(£j=Oi=l, 2,…,nCov( J. 6)=0 iHj i打=1, 2,…小假设3、随机误差项£与解释变量X之间不相关:CoV (Xif £ i)二0假设4、£服从零均值、同方差、零协方差的正态分布i=l, 2,…,n考虑过原点的线性回归模型E"北# J 21, 2,…,n误差5 （212…"丿仍满足基本假定。

求伏的最小一乘估计（■I1-1解:得: dO " -^ = -2y(r,-Ax,)x,=odp,台Z(3)B\ = ---------饷2)回归方程E <n "gx 的参数 5 已的最小二乘佔计与最大似然估计在什么条件下等价给出证明。

答：山于e fN(O, 2)所以乙=0o+ 0/+ E i~NW&BK , 2最大似然函数：E （0»Q,b2） = nUa2（2耐2 严 2t 相 _斗£ y-（0o+Q0°,Xf）］2} 2b i>>I «22b j.i使得Ln (L)最大的, B\就是％伙的最大似然估计值。

同时发现使得Ln (L)最大就是使得下式最小，/J” A八Q 二工厲-£)2=工(乙一(0°+AXi))2i I上式恰好就是最小二乘估讣的u 标函数相同。

《应用回归分析》课后习题部分答案-何晓群版

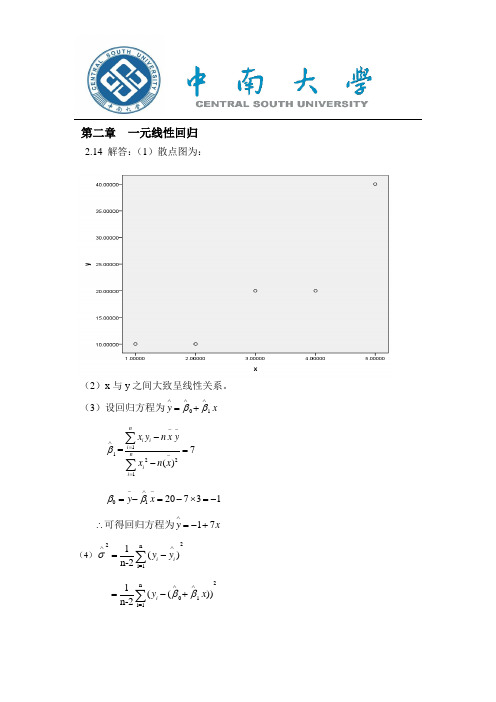
第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑2n01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=≈ （5）由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353 即为：（2.49，11.5）22001()(,())xxx N n L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。

因而/2|(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

（8）t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 3.66==≈/2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0，因变量y 对自变量x 的一元线性回归成立。

应用回归分析(第三版)何晓群_刘文卿_课后习题答案_完整版

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n）仍满足基本假定。

求β1的最小二乘估计解：21112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =02.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：)()(ˆ1211∑∑===ni ini ii XY X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估计的目标函数相同。

应用回归分析_第2章答案

应⽤回归分析_第2章答案第⼆章⼀元线性回归分析思考与练习参考答案2.1 ⼀元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同⽅差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同⽅差、零协⽅差的正态分布εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n ）仍满⾜基本假定。

求β1的最⼩⼆乘估计解：得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：∑∑+-=-=nii i ni X Y Y Y Q 121021))??(()?(ββ其中：即： ∑e i =0 ，∑e i X i =021112)?()?(ini i ni i i e X Y Y Y Q β∑∑==-=-=01i ii i iY X e Y Y ββ=+=-0100??QQββ==2.4回归⽅程E （Y ）=β0+β1X 的参数β0，β1的最⼩⼆乘估计与最⼤似然估计在什么条件下等价?给出证明。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最⼤似然函数：使得Ln （L ）最⼤的0β，1?β就是β0，β1的最⼤似然估计值。

同时发现使得Ln （L ）最⼤就是使得下式最⼩，∑∑+-=-=nii i n i X Y Y Y Q 121021))??(()?(ββ上式恰好就是最⼩⼆乘估计的⽬标函数相同。

应用回归分析-课后习题答案-何晓群

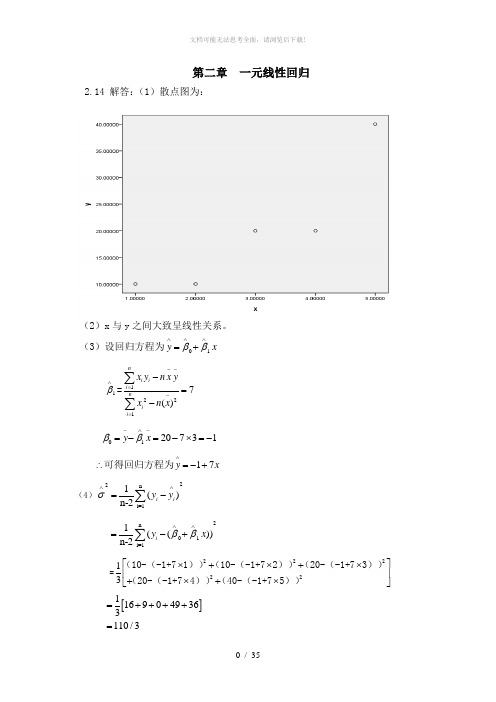
第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑2n01i=11(())n-2i y x ββ∧∧=-+∑ =2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=≈（5）由于2 11(,)xxNLσββ∧tσ∧==服从自由度为n-2的t分布。

因而/2||(2)1P t nαασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(p t tααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为（7-2.3537+2.353即为：（2.49，11.5）22001()(,())xxxNn Lββσ-∧+t∧∧==服从自由度为n-2的t分布。

因而/2||(2)1P t nαα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1pβσββσα∧∧∧∧-<<+=-可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x与y的决定系数22121()490/6000.817()niiniiy yry y∧-=-=-==≈-∑∑（7）ANOVAx平方和 df均方 F显著性组间（组合） 9.000 2 4.500 9.000 .100线性项加权的 8.167 1 8.167 16.333 .056偏差.833 1 .833 1.667.326组内 1.0002 .500总数10.0004由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

应用回归分析-课后习题答案-何晓群.doc

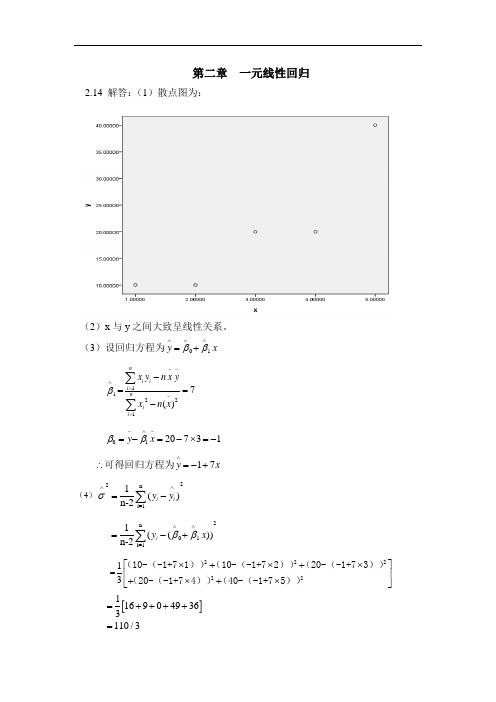
第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与y 之间大致呈线性关系。

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=1330 6.13σ∧=≈ （5）由于211(,)xxN L σββ∧1112()/xxxxL t L ββσσ∧∧-==服从自由度为n-2的t 分布。

因而1/2()|(2)1xx L P t n αββασ∧⎡⎤-⎢⎥<-=-⎢⎥⎣⎦也即：1/211/2(xxxxp t t L L ααβββ∧∧∧∧-<<+=1α-可得11195%333333β∧的置信度为的置信区间为（7-2.353，7+2.353）即为：（2.49，11.5）2201()(,())xxx N n L ββσ-∧+00002221()1()()xxxxt x x n L n L σσ∧∧--∧∧==++服从自由度为n-2的t 分布。

因而00/22(2)11()xx P t n x n L αασ∧-∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥+⎢⎥⎣⎦即220/200/21()1()()1xxxxx x p t t n L n L βσββσα--∧∧∧∧-+<<++=- 可得195%7.77,5.77β∧-的置信度为的置信区间为（）（6）x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑（7）ANOV Ax平方和df均方 F 显著性组间（组合） 9.000 2 4.500 9.000 .100 线性项加权的 8.167 1 8.167 16.333 .056 偏差.833 1 .833 1.667.326组内 1.000 2 .500总数10.0004由于(1,3)F F α>,拒绝0H ,说明回归方程显著，x 与y 有显著的线性关系。

应用回归分析+第2章详细答案

2.3由⎪⎪⎩⎪⎪⎨⎧=β-β-=β∂∂=β-β-=β∂∂∑∑=β=β=β=βn1i i i 10i ˆ1n 1i i 10i ˆ00x )x ˆˆy (Q 0)x ˆˆy (Q 1100得⎪⎪⎩⎪⎪⎨⎧==-==-∑∑∑∑====n 1i n 1i i i i i i n 1i n1i i i i 0x e x )y ˆy (0e )y ˆy (2.4在),0(N ~2i σε的正态分布假定下，10,ββ的最小二乘估计与最大似然估计等价，求对数似然函数的极大值等价于对∑=β+β-n1i 2i 10i )]x (y [求极小值，至此与最小二乘估计原理完全相同2.52.62n1i 2i212210])x x()x (n 1[)ˆvar()x (n 1)x ˆy var()ˆvar(σ-+=β+σ=β-=β∑=2.7SSR SSE )y y ˆ)(y ˆy (2)y y ˆ()y ˆy ()y y ˆyˆy ()y y (SST n1i i i i n 1i 2i n 1i 2i i n 1i 2i i i n 1i 2i +=--+-+-=-+-=-=∑∑∑∑∑=====2.8（1）22i2i 2i2i 2i2i2i i2i i xx1xx 1r 12n r )y y ()y y ˆ(12n r )y y ()y yˆ()y y (2n r )y y ()yˆy (2n r )y ˆy (2n L ˆˆL ˆt --=----=-----=---=--β=σβ=∑∑∑∑∑∑∑∑（2）F )2n /(SSE 1/SSR SSE SSR )2n (SSTSSR 1SST SSR)2n (r 1r )2n (t 222=-=-=--=--= 2.92xxi 2i10L )x x (n 1)x ˆˆvar(σ-+σ=β+β xx2i 2xx i 2i i 2xx i i i i 2i 1i L )x x (n 1)L y )x x (,y cov(n 1)L y )x x ()x x (,y cov(n 1))x x (ˆy ,y cov(-+σ=-+σ=--+σ=-β+∑2xx 2i 22i1i i 10i i i i n11[L )x x (n 1))x x (ˆy ,y cov(2)x ˆˆvar()y var()y y var()e var(--=σ--σ-σ=-β+-β+β+=-=2.1022xx2i i 2i 2i 2i i 2)L )x x (1n (2n 1))e (E )e (var(2n 1)e (E 2n 1))y ˆy (2n 1(E )ˆ(E σ=σ----=--=-=--=σ∑∑2.112n F F )2n /(SSE SSE SSR )2n /(SSE SSR )2n /(SSE SST )2n /(SSE SSR SSTSSR r 2-+=-+-=--==如果一个线性回归方程通过F 检验，只能说明x 与y 之间的线性关系是显著的，不能说明数据拟合得很好，决定系数r 2是一个回归直线与样本观测值拟合优度的相对指标。

应用回归分析-第2章课后习题参考答案

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n）仍满足基本假定。

求β1的最小二乘估计解：得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

21112)ˆ()ˆ(ini i n i i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi i i i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，上式恰好就是最小二乘估计的目标函数相同。

值得注意的是：最大似然估计是在εi ~N (0, σ2 )的假设下求得，最小二乘估计则不要求分布假设。

应用回归分析_整理课后习题答案

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答：假设1、解释变量X 是确定性变量，Y 是随机变量；假设2、随机误差项ε具有零均值、同方差和不序列相关性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关： Cov(X i , εi )=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考虑过原点的线性回归模型 Y i =β1X i +εi i=1,2, …,n误差εi （i=1,2, …,n ）仍满足基本假定。

求β1的最小二乘估计解：得：2.3 证明（2.27式），∑e i =0 ，∑e i X i =0 。

证明：其中：即： ∑e i =0 ，∑e i X i =0∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ21112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=0)ˆ(2ˆ111=--=∂∂∑=ii ni i eX X Y Q ββ)()(ˆ1211∑∑===ni i ni ii X Y X β01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回归方程E （Y ）=β0+β1X 的参数β0，β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。

答：由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函数：使得Ln （L ）最大的0ˆβ，1ˆβ就是β0，β1的最大似然估计值。

同时发现使得Ln （L ）最大就是使得下式最小，上式恰好就是最小二乘估计的目标函数相同。

(完整word版)应用回归分析,第2章课后习题参考答案汇总(word文档良心出品)

第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定？答：假设1解释变量X是确定性变量，丫是随机变量;假设2、随机误差项&具有零均值、同方差和不序列相关性:E( i)=0 i=1,2,…,n2Var (i)=, i=1,2, …,nCov( E £)=0 i 工j i,j= 1,2, …,nCov(X i, i )=0 i=1,2, …,n假设4、&服从零均值、同方差、零协方差的正态分布2i~N(0, ~)i=1,2,…,n2.2考虑过原点的线性回归模型Y i= 0X i+ i i=1,2,…,nn nQ e 八(Y i -Y?)2八(Y i -?i X i)2i』i=1得: f?=M羊Xi)X^0n' (X i Y i)i dn' (X i2)i =1i d2.3 证明(2.27 式)，工e i =0 ，工eXi=0。

n nQ=S：(丫-Y?)2=迟(Y i —(f?°+f?X i))2 证明： 1 1其中：丫?=児+叹e=Y-丫？即: I ^(A+AA；-l；) = 0|V^o+/?rVj-T；)A；= 0^e =0 ，乞eX i=0假设3、随机误差项&与解释变量X之间不相关:误差 $ (i=1,2,解：…)n仍满足基本假定。

求仪的最小二乘估计2.4回归方程E (Y ) = 00+ 3X 的参数①，妆的最小二乘估计与最大似然估计在什么条件下等价？给出证明。

答：由于 £ 厂N(0, ~2)i=1,2,…,n所以 Y i =场 + 0X + £~N ( [3D + [3iX i , o 2) 最大似然函数：1 nL( 0, i ,；「2)=二爲 f i (Y i ) =(2=2)』/2exp{——2、 [Y i -( o i o ,X i )]2}2 ynLn{L( o , i ,二2)}= -：帕(2二2)-2、 M -( o i o ,X i )]222<r y使得Ln (L )最大的况,瞬就是肉，0的最大似然估计值。

应用回归分析课后答案

（3）设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为（4）22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦（10-（-1+71））（10-（-1+72））（20-（-1+73））（20-（-1+74））（40-（-1+75）） []1169049363110/3=++++=6.1σ∧=≈ （5）由于211(,)xxN Lσββ∧t σ∧==服从自由度为n-2的t 分布。