中考数学压轴专题最值问题系列
专题09 几何中最小值计算压轴真题训练(解析版)

挑战2023年中考数学选择、填空压轴真题汇编专题09 几何中最小值计算压轴真题训练一.轴对称-最短路线问题1.(2022•眉山)如图,点P为矩形ABCD的对角线AC上一动点,点E为BC 的中点,连接PE,PB,若AB=4,BC=4,则PE+PB的最小值为 .【答案】6【解答】解:如图,作点B关于AC的对称点B',交AC于点F,连接B′E 交AC于点P,则PE+PB的最小值为B′E的长度,∵四边形ABCD为矩形,∴AB=CD=4,∠ABC=90°,在Rt△ABC中,AB=4,BC=4,∴tan∠ACB==,∴∠ACB=30°,由对称的性质可知,B'B=2BF,B'B⊥AC,∴BF=BC=2,∠CBF=60°,∴B′B=2BF=4,∵BE=BF,∠CBF=60°,∴△BEF是等边三角形,∴BE=BF=B'F,∴△BEB'是直角三角形,∴B′E===6,∴PE+PB的最小值为6,故答案为:6.2.(2022•自贡)如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 .【答案】3 【解答】解:解法一:如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,∵CH=EF=1,CH∥EF,∴四边形EFCH是平行四边形,∴EH=CF,∴G'H=EG'+EH=EG+CF,∵AB=4,BC=AD=2,G为边AD的中点,∴DG'=AD+AG'=2+1=3,DH=4﹣1=3,由勾股定理得:HG'==3,即GE+CF的最小值为3.解法二:∵AG=AD=1,设AE=x,则BF=AB﹣EF﹣AE=4﹣x﹣1=3﹣x,由勾股定理得:EG+CF=+,如图,矩形EFGH中,EH=3,GH=2,GQ=1,P为FG上一动点,设PG=x,则FP=3﹣x,∴EP+PQ=+,当E,P,Q三点共线时,EP+PQ最小,最小值是3,即EG+CF的最小值是3.故答案为:3.3.(2022•鄂州)如图,定直线MN∥PQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AE∥BC∥DF,AE=4,DF=8,AD=24,当线段BC在平移过程中,AB+CD的最小值为( )A.24B.24C.12D.12【答案】C【解答】解:如图,作DL⊥PQ于L,过点A作PQ的垂线,过点D作PQ的平行线,它们交于点R,延长DF至T,使DT=BC=12,连接AT,AT交MN于B′,作B′C′∥BC,交PQ于C′,则当BC在B′C′时,AB+CD 最小,最小值为AT的长,可得AK=AE•sin60°==2,DL==4,=6,∴AR=2+6+4=12,∵AD=24,∴sin∠ADR==,∴∠ADR=30°,∵∠PFD9=60°,∴∠ADT=90°,∴AT===12,故答案为:C.4.(2022•贺州)如图,在矩形ABCD中,AB=8,BC=6,E,F分别是AD,AB的中点,∠ADC的平分线交AB于点G,点P是线段DG上的一个动点,则△PEF的周长最小值为 .【答案】5+ 【解答】解:如图,在DC上截取DT,使得DT=DE,连接FT,过点T作TH ⊥AB于点H.∵四边形ABCD是矩形,∴∠A=∠ADT=90°,∵∠AHT=90°,∴四边形AHTD是矩形,∵AE=DE=AD=3.AF=FB=AB=4,∴AH=DT=3,HF=AF﹣AH=4﹣3=1,HT=AD=6,∴FT===,∵DG平分∠ADC,DE=DT,∴E、T关于DG对称,∴PE=PT,∴PE+PF=PF+PT≥FT=,∵EF===5,∴△EFP的周长的最小值为5+,故答案为:5+.5.(2022•滨州)如图,在矩形ABCD中,AB=5,AD=10.若点E是边AD 上的一个动点,过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F,则在点E移动的过程中,AF+FE+EC的最小值为 .【答案】+【解答】解:如图,过点E作EH⊥BC于点H.∵四边形ABCD是矩形,∴∠B=∠BAD=∠BHE=90°,∴四边形ABHE是矩形,∴EH=AB=5,∵BC=AD=10,∴AC===5,∵EF⊥AC,∴∠COF=90°,∴∠EFH+∠ACB=90°,∵∠BAC+∠ACB=90°,∴∠EFH=∠BAC,∴△EHF∽△CBA,∴==,∴==,∴FH=,EF=,设BF=x,则DE=10﹣x﹣=﹣x,∵EF是定值,∴AF+CE的值最小时,AF+EF+CE的值最小,∵AF+CE=+,∴欲求AF+CE的最小值相当于在x轴上找一点P(x,0),使得P到A(0,5),B(,5)的距离和最小,如图1中,作点A关于x轴的对称点A′,连接BA′交xz轴于点P,连接AP,此时PA+PB 的值最小,最小值为线段A′B的长,∵A′(0,﹣5),B(,5),∴A′B==,∴AF+CE的最小值为,∴AF+EF+CE的最小值为+.解法二:过点C作CC′∥EF,使得CC′=EF,连接C′F.∵EF=CC′,EF∥CC′,∴四边形EFC′C是平行四边形,∴EC=FC′,∵EF⊥AC,∴AC⊥CC′,∴∠ACC=90°,∵AC′===,∴AF+EC=AF+FC′≥AC′=,∴AF+EF+CE的最小值为+.故答案为:+二.胡不归问题6.(2022•鄂尔多斯)如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .【答案】4【解答】解:如图,在∠BAC的外部作∠CAE=15°,作BF⊥AE于F,交AD于P,此时PA+2PB最小,∴∠AFB=90°∵AB=AC,AD⊥BC,∴∠CAD=∠BAD=,∴∠EAD=∠CAE+∠CAD=30°,∴PF=,∴PA+2PB=2()=2(PF+PB)=2BF,在Rt△ABF中,AB=4,∠BAF=∠BAC+∠CAE=45°,∴BF=AB•sin45°=4×=2,∴(PA+2PB)=2BF=4,最小故答案为:4.三.旋转的性质7.(2022•黄石)如图,等边△ABC中,AB=10,点E为高AD上的一动点,以BE为边作等边△BEF,连接DF,CF,则∠BCF= ,FB+FD的最小值为 .【答案】30°5 【解答】解:如图,∵△ABC是等边三角形,AD⊥CB,∴∠BAE=∠BAC=30°,∵△BEF是等边三角形,∴∠EBF=∠ABC=60°,BE=BF,∴∠ABE=∠CBF,在△BAE和△BCF中,,∴△BAE≌△BCF(SAS),∴∠BAE=∠BCF=30°,作点D关于CF的对称点G,连接CG,DG,BG,BG交CF的延长线于点F′,连接DF′,此时BF′+DF′的值最小,最小值=线段BG的长.∵∠DCF=∠FCG=30°,∴∠DCG=60°,∵CD=CG=5,∴△CDG是等边三角形,∴DB=DC=DG,∴∠CGB=90°,∴BG===5,∴BF+DF的最小值为5,故答案为:30°,5.8.(2022•柳州)如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为 .【答案】2﹣2【解答】解:连接DG,将DG绕点D逆时针旋转90°得DM,连接MG,CM,MF,作MH⊥CD于H,∵∠EDF=∠GDM,∴∠EDG=∠FDM,∵DE=DF,DG=DM,∴△EDG≌△MDF(SAS),∴MF=EG=2,∵∠GDC=∠DMH,∠DCG=∠DHM,DG=DM,∴△DGC≌△MDH(AAS),∴CG=DH=2,MH=CD=4,∴CM==2,∵CF≥CM﹣MF,∴CF的最小值为2﹣2,故答案为:2﹣2.9.(2022•广州)如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP′,连接PP′,CP′.当点P′落在边BC上时,∠PP′C的度数为 ;当线段CP′的长度最小时,∠PP′C的度数为 .【答案】120°,75°【解答】解:如图,以AB为边向右作等边△ABE,连接EP′.∵△BPP′是等边三角形,∴∠ABE=∠PBP′=60°,BP=BP′,BA=BE,∴∠ABP=∠EBP′,在△ABP和△EBP′中,,∴△ABP≌△EBP′(SAS),∴∠BAP=∠BEP′=90°,∴点P′在射线EP′上运动,如图1中,设EP′交BC于点O,当点P′落在BC上时,点P′与O重合,此时∠PP′C=180°﹣60°=120°,当CP′⊥EP′时,CP′的长最小,此时∠EBO=∠OCP′=30°,∴EO=OB,OP′=OC,∴EP′=EO+OP′=OB+OC=BC,∵BC=2AB,∴EP′=AB=EB,∴∠EBP′=∠EP′B=45°,∴∠BP′C=45°+90°=135°,∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣60°=75°.故答案为:120°,75°.10.(2022•无锡)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF= °;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是 .【答案】80,4﹣.【解答】解:∵△ACB,△DEC都是等边三角形,∴AC=CB,DC=EC,∠ACB=∠DCE=60°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴∠DBC=∠EAC=20°,∵∠BAC=60°,∴∠BAF=∠BAC+∠CAE=80°.如图1中,设BF交AC于点T.同法可证△BCD≌△ACE,∴∠CBD=∠CAF,∵∠BTC=∠ATF,∴∠BCT=∠AFT=60°,∴点F在△ABC的外接圆上运动,当∠ABF最小时,AF的值最小,此时CD⊥BD,∴BD===4,∴AE=BD=4,∠BDC=∠AEC=90°,∵CD=CE,CF=CF,∴Rt△CFD≌Rt△CFE(HL),∴∠DCF=∠ECF=30°,∴EF=CE•tan30°=,∴AF的最小值=AE﹣EF=4﹣,故答案为:80,4﹣.四.折叠有关最值问题11.(2022•青岛)如图,已知△ABC,AB=AC,BC=16,AD⊥BC,∠ABC的平分线交AD于点E,且DE=4.将∠C沿GM折叠使点C与点E恰好重合.下列结论正确的有: .(填写序号)①BD=8②点E到AC的距离为3③EM=④EM∥AC【答案】①④【解答】解:在△ABC中,AB=AC,BC=16,AD⊥BC,∴BD=DC=BC=8,故①正确;如图,过点E作EF⊥AB于点F,EH⊥AC于点H,∵AD⊥BC,AB=AC,∴AE平分∠BAC,∴EH=EF,∵BE是∠ABD的角平分线,∵ED⊥BC,EF⊥AB,∴EF=ED,∴EH=ED=4,故②错误;由折叠性质可得:EM=MC,DM+MC=DM+EM=CD=8,设DM=x,则EM=8﹣x,Rt△EDM中,EM2=DM2+DE2,∴(8﹣x)2=42+x2,解得:x=3,∴EM=MC=5,故③错误;设AE=a,则AD=AE+ED=4+a,BD=8,∴AB2=(4+a)2+82,∵=,∴,∴,∴AB=2a,∴(4+a)2+82=(2a)2,解得:a=或a=﹣4(舍去),∴tan C==,又∵tan∠EMD=,∴∠C=∠EMD,∴EM∥AC,故④正确,故答案为:①④.12.(2022•铜仁市)如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE 上的动点,过点N作NP∥EM交MC于点P,则MN+NP的最小值为 .【答案】【解答】解:作点P关于CE的对称点P′,由折叠的性质知CE是∠DCM的平分线,∴点P′在CD上,过点M作MF⊥CD于F,交CE于点G,∵MN+NP=MN+NP′≥MF,∴MN+NP的最小值为MF的长,连接DG,DM,由折叠的性质知CE为线段DM的垂直平分线,∵AD=CD=2,DE=1,∴CE==,∵CE×DO=CD×DE,∴DO=,∴EO=,∵MF⊥CD,∠EDC=90°,∴DE∥MF,∴∠EDO=∠GMO,∵CE为线段DM的垂直平分线,∴DO=OM,∠DOE=∠MOG=90°,∴△DOE≌△MOG,∴DE=GM,∴四边形DEMG为平行四边形,∵∠MOG=90°,∴四边形DEMG为菱形,∴EG=2OE=,GM=DE=1,∴CG=,∵DE∥MF,即DE∥GF,∴△CFG∽△CDE,∴,即,∴FG=,∴MF=1+=,∴MN+NP的最小值为;方法二:同理方法一得出MN+NP的最小值为MF的长,DO=,∴OC==,DM=2DO=,=DM•OC=CD•MF,∵S△CDM即×=2×MF,∴MF=,∴MN+NP的最小值为;故答案为:.13.(2022•辽宁)如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,当GF最小时,AE的长是 .【答案】5﹣5 【解答】解:∵将△ABE沿BE翻折得到△FBE,∴BF=BA=10,∴点F在以B为圆心,10为半径的圆上运动,∴当点G、F、B三点共线时,GF最小,连接EG,设AE=x,由勾股定理得,BG=5,∵S梯形ABGD =S△EDG+S△ABE+S△EBG,∴(5+10)×10=++,解得x=5﹣5,∴AE=5﹣5,故答案为:5﹣5.14.(2022•台州)如图,在菱形ABCD中,∠A=60°,AB=6.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M 与点B重合时,EF的长为 ;当点M的位置变化时,DF长的最大值为 .【答案】3,6﹣3.【解答】解:如图1中,∵四边形ABCD是菱形,∴AD=AB=BC=CD,∠A=∠C=60°,∴△ADB,△BDC都是等边三角形,当点M与B重合时,EF是等边△ADB的高,EF=AD•sin60°=6×=3.如图2中,连接AM交EF于点O,过点O作OK⊥AD于点K,交BC于点T,过点A作AG⊥CB交CB的延长线于点G,取AF的中点R,连接OR.∵AD∥CG,OK⊥AD,∴OK⊥CG,∴∠G=∠AKT=∠GTK=90°,∴四边形AGTK是矩形,∴AG=TK=AB•sin60°=3,∵OA=OM,∠AOK=∠MOT,∠AKO=∠MTO=90°,∴△AOK≌△MOT(AAS),∴OK=OT=,∵OK⊥AD,∴OR≥OK=,∵∠AOF=90°,AR=RF,∴AF=2OR≥3,∴AF的最小值为3,∴DF的最大值为6﹣3.解法二:如图,过点D作DT⊥CB于点T.∵DF=AD﹣AF,∴当AF最小时,DF的值最大,∵AF=FM≥DT=3,∴AF的最小值为3,∴DF的最大值为6﹣3.故答案为:3,6﹣3.五.与圆有关最值计算15.(2022•泸州)如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,半径为1的⊙O在Rt△ABC内平移(⊙O可以与该三角形的边相切),则点A 到⊙O上的点的距离的最大值为 .【答案】2+1【解答】解:当⊙O与BC、BA都相切时,连接AO并延长交⊙O于点D,则AD为点A到⊙O上的点的距离的最大值,设⊙O与BC、BA的切点分别为E、F,连接OE、OF,则OE⊥BC,OF⊥AB,∵AC=6,BC=2,∴tan∠ABC==,AB==4,∴∠ABC=60°,∴∠OBF=30°,∴BF==,∴AF=AB﹣BF=3,∴OA==2,∴AD=2+1,故答案为:2+1.37.(2022•桂林)如图,某雕塑MN位于河段OA上,游客P在步道上由点O 出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN 最大时,游客P行走的距离OP是 米.【答案】20 【解答】解:如图,取MN的中点F,过点F作FE⊥OB于E,以直径MN作⊙F,∵MN=2OM=40m,点F是MN的中点,∴MF=FN=20m,OF=40m,∵∠AOB=30°,EF⊥OB,∴EF=20m,OE=EF=20m,∴EF=MF,又∵EF⊥OB,∴OB是⊙F的切线,切点为E,∴当点P与点E重合时,观景视角∠MPN最大,此时OP=20m,故答案为:20.。
2023年中考数学压轴题专题11 二次函数与单线段最值问题【含答案】

专题11二次函数与单线段最值问题【例1】(2022•襄阳)在平面直角坐标系中,直线y=mx﹣2m与x轴,y轴分别交于A,B两点,顶点为D 的抛物线y=﹣x2+2mx﹣m2+2与y轴交于点C.(1)如图,当m=2时,点P是抛物线CD段上的一个动点.①求A,B,C,D四点的坐标;②当△PAB面积最大时,求点P的坐标;(2)在y轴上有一点M(0,m),当点C在线段MB上时,①求m的取值范围;②求线段BC长度的最大值.【例2】(2022•湖州)如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C分别在x轴的正半轴和y轴的正半轴上.抛物线y=﹣x2+bx+c经过A,C两点,与x轴交于另一个点D.(1)①求点A,B,C的坐标;②求b,c的值.(2)若点P是边BC上的一个动点,连结AP,过点P作PM⊥AP,交y轴于点M(如图2所示).当点P 在BC上运动时,点M也随之运动.设BP=m,CM=n,试用含m的代数式表示n,并求出n的最大值.【例3】(2021•青海)如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A,B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A,B,C.(1)求抛物线的解析式;(2)根据图象写出不等式ax2+(b﹣1)x+c>2的解集;(3)点P是抛物线上的一动点,过点P作直线AB的垂线段,垂足为Q点.当PQ=时,求P点的坐标.【例4】(2022•雅安)已知二次函数y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),且与y轴交于点C (0,﹣3).(1)求此二次函数的表达式及图象顶点D的坐标;(2)在此抛物线的对称轴上是否存在点E,使△ACE为Rt△,若存在,试求点E的坐标,若不存在,请说明理由;(3)在平面直角坐标系中,存在点P,满足PA⊥PD,求线段PB的最小值.1.(2020•河北模拟)已知抛物线C:y=ax2+bx+c(a>0,c<0)的对称轴为x=4,C为顶点,且A(2,0),C(4,﹣2)【问题背景】求出抛物线C的解析式.【尝试探索】如图2,作点C关于x轴的对称点C′,连接BC′,作直线x=k交BC′于点M,交抛物线C于点N.①连接ND,若四边形MNDC′是平行四边形,求出k的值.②当线段MN在抛物线C与直线BC′围成的封闭图形内部或边界上时,请直接写出线段MN的长度的最大值.【拓展延伸】如图4,作矩形HGOE,且E(﹣3,0),H(﹣3,4),现将其沿x轴以1个单位每秒的速度向右平移,设运动时间为t,得到矩形H′G′O′E′,连接AC′,若矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分,请求出t的取值范围.2.(2018秋•宁城县期末)已知,如图,抛物线与x轴交点坐标为A(1,0),C(﹣3,0),(1)如图1,已知顶点坐标D为(﹣1,4)或B点(0,3),选择适当方法求抛物线的解析式;(2)如图2,在抛物线的对称轴DH上求作一点M,使△ABM的周长最小,并求出点M的坐标;(3)如图3,将图2中的对称轴向左移动,交x轴于点P(m,0)(﹣3<m<﹣1),与抛物线,线段BC的交点分别为点E、F,用含m的代数式表示线段EF的长度,并求出当m为何值时,线段EF最长.3.(2021•桥西区模拟)如图1,抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,且CO=BO,连接BC.(1)求抛物线的解析式;(2)如图2,抛物线的顶点为D,其对称轴与线段BC交于点E,求线段DE的长度;(3)如图3,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,连接CP,CD,抛物线上是否存在点P,使△CDE∽△PCF,如果存在,求出点P的坐标,如果不存在,请说明理由.4.(2022•和平区二模)如图,在平面直角坐标系中,已知抛物线顶点A的坐标为(﹣2,4),且经过坐标原点,与x轴负半轴交于点B.(1)求抛物线的函数表达式并直接写出点B的坐标;(2)过点A作AC⊥x轴于点C,若点D是y轴左侧的抛物线上一个动点(点D与点A不重合),过点D 作DE⊥x轴于点E,连接AO,DO,当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,求点D的坐标;(3)在(2)的条件下,当点D在第二象限时,在平面内存在一条直线,这条直线与抛物线在第二象限交于点F,在第三象限交于点G,且点A,点B,点D,到直线FG的距离都相等,请直接写出线段FG的长.5.(2022•鹿城区校级二模)如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(5,0),与y轴交于点C.(1)求抛物线的解析式和顶点D的坐标.(2)连结AD,点E是对称轴与x轴的交点,过E作EF∥AD交抛物线于点F(F在E的右侧),过点F作FG∥x轴交ED于点H,交AD于点G,求HF的长.6.(2021•南岗区模拟)如图,抛物线y=ax2+bx﹣4交x轴于点A(﹣3,0),B(4,0),交y轴于点C.(1)求抛物线的解析式;(2)点P为第一象限抛物线上一点,过点P作x轴的平行线,与抛物线的另一个交点为点G,连接CG交x轴于点N,设点P的横坐标为t,ON的长为d,求d与t之间的函数解析式(不要求写出自变量t的取值范围);(3)在(2)的条件下,连接PB,将线段PB绕着点P顺时针旋转90°得到线段PD,点D恰好落在y轴上,点E在线段OB上,连接PE,点Q在EB的延长线上,且EQ=PE,连接DQ交PE于点F,若PE=3PF,求QN的长.7.(2021•凉山州模拟)如图1,在平面直角坐标系中,已知B点坐标为(1,0),且OA=OC=3OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点,其中D点是该抛物线的顶点.(1)求抛物线的解析式;(2)判断△ADC的形状并且求△ADC的面积;(3)如图2,点P是该抛物线第三象限部分上的一个动点,过P点作PE⊥AC于E点,当PE的值最大时,求此时P点的坐标及PE的最大值.8.(2022•无锡二模)已知抛物线y=mx2﹣2mx+3(m<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.(1)求抛物线的函数表达式;(2)若M、N是第一象限的抛物线上不同的两点,且△BCN的面积总小于△BCM的面积,求点M的坐标;(3)若D为抛物线的顶点,P为第二象限的抛物线上的一点,连接BP、DP,分别交y轴于点E、F,若EF=OC,求点P的坐标.9.(2021•乳源县三模)如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0,).(1)求抛物线的解析式;(2)若点M是抛物线的顶点,连接AM,CM,求△AMC的面积;(3)若点P是抛物线上的一个动点,过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点P的坐标.10.(2021•河池)在平面直角坐标系中,抛物线y=﹣(x﹣1)2+4与x轴交于A,B两点(A在B的右侧),与y轴交于点C.(1)求直线CA的解析式;(2)如图,直线x=m与抛物线在第一象限交于点D,交CA于点E,交x轴于点F,DG⊥CA于点G,若E为GA的中点,求m的值.(3)直线y=nx+n与抛物线交于M(x1,y1),N(x2,y2)两点,其中x1<x2.若x2﹣x1>3且y2﹣y1>0,结合函数图象,探究n的取值范围.11.(2021•桂林)如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m),与x轴的正半轴交于点C.(1)求a,m的值和点C的坐标;(2)若点P是x轴上的点,连接PB,PA,当=时,求点P的坐标;(3)在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横坐标;若不存在,请说明理由.12.(2021•吉林)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象经过点A(0,﹣),点B(1,).(1)求此二次函数的解析式;(2)当﹣2≤x≤2时,求二次函数y=x2+bx+c的最大值和最小值;(3)点P为此函数图象上任意一点,其横坐标为m,过点P作PQ∥x轴,点Q的横坐标为﹣2m+1.已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.①求m的取值范围;②当PQ≤7时,直接写出线段PQ与二次函数y=x2+bx+c(﹣2≤x<)的图象交点个数及对应的m的取值范围.13.(2020•武汉模拟)已知:在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a交x轴于A、B两点(点A在点B的左边),交y轴负半轴于点C.(1)则点A的坐标为,点B的坐标为.(2)如图1,过点A的直线y=ax+a交y轴正半轴于点F,交抛物线于点D,过点B作BE∥y轴交AD于E,求证:AF=DE.(3)如图2,直线DE:y=kx+b与抛物线只有一个交点D,与对称轴交于点E,对称轴上存在点F,满足DF=FE.若a=1,求点F坐标.14.(2020•哈尔滨模拟)如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tan C=,5OA=3OB.(1)求抛物线的解析式;(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.15.(2019•衡阳)如图,二次函数y=x2+bx+c的图象与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点N,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接CP,过点P作CP的垂线与y 轴交于点E.(1)求该抛物线的函数关系表达式;(2)当点P在线段OB(点P不与O、B重合)上运动至何处时,线段OE的长有最大值?并求出这个最大值;(3)在第四象限的抛物线上任取一点M,连接MN、MB.请问:△MBN的面积是否存在最大值?若存在,求出此时点M的坐标;若不存在,请说明理由.16.(2020•天津)已知点A(1,0)是抛物线y=ax2+bx+m(a,b,m为常数,a≠0,m<0)与x轴的一个交点.(Ⅰ)当a=1,m=﹣3时,求该抛物线的顶点坐标;(Ⅱ)若抛物线与x轴的另一个交点为M(m,0),与y轴的交点为C,过点C作直线l平行于x轴,E是直线l上的动点,F是y轴上的动点,EF=2.①当点E落在抛物线上(不与点C重合),且AE=EF时,求点F的坐标;②取EF的中点N,当m为何值时,MN的最小值是?17.(2020•凉山州)如图,二次函数y=ax2+bx+c的图象过O(0,0)、A(1,0)、B(,)三点.(1)求二次函数的解析式;(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ 的长最大时,求点P的坐标.18.(2020•滨州)如图,抛物线的顶点为A(h,﹣1),与y轴交于点B(0,﹣),点F(2,1)为其对称轴上的一个定点.(1)求这条抛物线的函数解析式;(2)已知直线l是过点C(0,﹣3)且垂直于y轴的定直线,若抛物线上的任意一点P(m,n)到直线l 的距离为d,求证:PF=d;(3)已知坐标平面内的点D(4,3),请在抛物线上找一点Q,使△DFQ的周长最小,并求此时△DFQ周长的最小值及点Q的坐标.19.(2016•巴彦淖尔)如图所示,抛物线y=ax2﹣x+c经过原点O与点A(6,0)两点,过点A作AC⊥x 轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.(1)求抛物线的解析式,并求出点C和点D的坐标;(2)求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;(3)点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.20.(2018•葫芦岛)如图,抛物线y=ax2+4x+c(a≠0)经过点A(﹣1,0),点E(4,5),与y轴交于点B,连接AB.(1)求该抛物线的解析式;(2)将△ABO绕点O旋转,点B的对应点为点F.①当点F落在直线AE上时,求点F的坐标和△ABF的面积;②当点F到直线AE的距离为时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.【例1】(2022•襄阳)在平面直角坐标系中,直线y=mx﹣2m与x轴,y轴分别交于A,B两点,顶点为D 的抛物线y=﹣x2+2mx﹣m2+2与y轴交于点C.(1)如图,当m=2时,点P是抛物线CD段上的一个动点.①求A,B,C,D四点的坐标;②当△PAB面积最大时,求点P的坐标;(2)在y轴上有一点M(0,m),当点C在线段MB上时,①求m的取值范围;②求线段BC长度的最大值.【分析】(1)根据函数上点的坐标特点可分别得出A,B,C,D的坐标;①当m=2时,代入上述坐标即可得出结论;②过点P作PE∥y轴交直线AB于点E,设点P的横坐标为t,所以P(t,﹣t2+4t﹣2),E(t,2t﹣4).根据三角形的面积公式可得△PAB的面积,再利用二次函数的性质可得出结论;(2)由(1)可知,B(0,﹣2m),C(0,﹣m2+2),①y轴上有一点M(0,m),点C在线段MB上,需要分两种情况:当点M的坐标大于点B的坐标时;当点M的坐标小于点B的坐标时,分别得出m的取值范围即可;②根据①中的条件可知,分两种情况,分别得出BC的长度,利用二次函数的性质可得出结论.【解答】解:(1)∵直线y=mx﹣2m与x轴,y轴分别交于A,B两点,∴A(2,0),B(0,﹣2m);∵y=﹣(x﹣m)2+2,∴抛物线的顶点为D(m,2),令x=0,则y=﹣m2+2,∴C(0,﹣m2+2).①当m=2时,﹣2m=﹣4,﹣m2+2=﹣2,∴B(0,﹣4),C(0,﹣2),D(2,2).②由上可知,直线AB的解析式为:y=2x﹣4,抛物线的解析式为:y=﹣x2+4x﹣2.如图,过点P作PE∥y轴交直线AB于点E,设点P的横坐标为t,∴P(t,﹣t2+4t﹣2),E(t,2t﹣4).∴PE=﹣t2+4t﹣2﹣(2t﹣4)=﹣t2+2t+2,∴△PAB的面积为:×(2﹣0)×(﹣t2+2t+2)=﹣(t﹣1)2+3,∵﹣1<0,∴当t=1时,△PAB的面积的最大值为3.此时P(1,1).(2)由(1)可知,B(0,﹣2m),C(0,﹣m2+2),①∵y轴上有一点M(0,m),点C在线段MB上,∴需要分两种情况:当m≥﹣m2+2≥﹣2m时,可得≤m≤1+,当m≤﹣m2+2≤﹣2m时,可得﹣3≤m≤1﹣,∴m的取值范围为:≤m≤1+或﹣3≤m≤1﹣.②当≤m≤1+时,∵BC=﹣m2+2﹣(﹣2m)=﹣m2+2m+2=﹣(m﹣1)2+3,∴当m=1时,BC的最大值为3;当m≤﹣m2+2≤﹣2m时,即﹣3≤m≤1﹣,∴BC=﹣2m﹣(﹣m2+2)=m2﹣2m﹣2=(m﹣1)2﹣3,当m=﹣3时,点M与点C重合,BC的最大值为13.∴当m=1时,BC的最大值为3;当m=﹣3时,BC的最大值为13.【例2】(2022•湖州)如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C分别在x轴的正半轴和y轴的正半轴上.抛物线y=﹣x2+bx+c经过A,C两点,与x轴交于另一个点D.(1)①求点A,B,C的坐标;②求b,c的值.(2)若点P是边BC上的一个动点,连结AP,过点P作PM⊥AP,交y轴于点M(如图2所示).当点P 在BC上运动时,点M也随之运动.设BP=m,CM=n,试用含m的代数式表示n,并求出n的最大值.【分析】(1)①根据正方形的性质得出点A,B,C的坐标;②利用待定系数法求函数解析式解答;(2)根据两角相等证明△MCP∽△PBA,列比例式可得n与m的关系式,配方后可得结论.【解答】解:(1)①四边形OABC是边长为3的正方形,∴A(3,0),B(3,3),C(0,3);②把A(3,0),C(0,3)代入抛物线y=﹣x2+bx+c中得:,解得:;(2)∵AP⊥PM,∴∠APM=90°,∴∠APB+∠CPM=90°,∵∠B=∠APB+∠BAP=90°,∴∠BAP=∠CPM,∵∠B=∠PCM=90°,∴△MCP∽△PBA,∴=,即=,∴3n=m(3﹣m),∴n=﹣m2+m=﹣(m﹣)2+(0≤m≤3),∵﹣<0,∴当m=时,n的值最大,最大值是.【例3】(2021•青海)如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A,B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A,B,C.(1)求抛物线的解析式;(2)根据图象写出不等式ax2+(b﹣1)x+c>2的解集;(3)点P是抛物线上的一动点,过点P作直线AB的垂线段,垂足为Q点.当PQ=时,求P点的坐标.【分析】(1)根据题意得出A、B点的坐标,然后利用待定系数法求出二次函数的解析式;(2)根据(1)的解析式由图象判断即可;(3)作PE⊥x轴于点E,交AB于点D,根据函数图象点P的位置分三种情况分别计算出P点的坐标即可.【解答】解:(1)当x=0,y=0+2=2,当y=0时,x+2=0,解得x=﹣2,∴A(﹣2,0),B(0,2),把A(﹣2,0),C(1,0),B(0,2)代入抛物线解析式,得,解得,∴该抛物线的解析式为:y=﹣x2﹣x+2;(2)方法一:ax2+(b﹣1)x+c>2,即﹣x2﹣2x+2>2,当函数y=﹣x2﹣2x+2=2时,解得x=0或x=﹣2,由图象知,当﹣2<x<0时函数值大于2,∴不等式ax2+(b﹣1)x+c>2的解集为:﹣2<x<0;方法二:ax2+(b﹣1)x+c>2,即﹣x2﹣x+2>x+2,观察函数图象可知当﹣2<x<0时y=﹣x2﹣x+2的函数值大于y=x+2的函数值,∴不等式ax2+(b﹣1)x+c>2的解集为:﹣2<x<0;(3)作PE⊥x轴于点E,交AB于点D,作PQ⊥AB于Q,①如图1,当P在AB上方时,在Rt△OAB中,∵OA=OB=2,∴∠OAB=45°,∴∠PDQ=∠ADE=45°,在Rt△PDQ中,∠DPQ=∠PDQ=45°,∴PQ=DQ=,∴PD==1,设点P(x,﹣x2﹣x+2),则点D(x,x+2),∴PD=﹣x2﹣x+2﹣(x+2)=﹣x2﹣2x,即﹣x2﹣2x=1,解得x=﹣1,∴此时P点的坐标为(﹣1,2),②如图2,当P点在A点左侧时,同理①可得PD=1,设点P(x,﹣x2﹣x+2),则点D(x,x+2),∴PD=(x+2)﹣(﹣x2﹣x+2)=x2+2x,即x2+2x=1,解得x=±﹣1,由图象知此时P点在第三象限,∴x=﹣﹣1,∴此时P点的坐标为(﹣﹣1,﹣),③如图3,当P点在B点右侧时,在Rt△OAB中,∵OA=OB=2,∴∠OAB=45°,∴∠PDQ=∠DPQ=45°,在Rt△PDQ中,∠DPQ=∠PDQ=45°,∴PQ=DQ=,∴PD==1,设点P(x,﹣x2﹣x+2),则点D(x,x+2),∴PD=(x+2)﹣(﹣x2﹣x+2)=x2+2x,即x2+2x=1,解得x=±﹣1,由图象知此时P点在第一象限,∴x=﹣1,∴此时P点的坐标为(﹣1,),综上,P点的坐标为(﹣1,2)或(﹣﹣1,﹣)或(﹣1,).【例4】(2022•雅安)已知二次函数y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),且与y轴交于点C (0,﹣3).(1)求此二次函数的表达式及图象顶点D的坐标;(2)在此抛物线的对称轴上是否存在点E,使△ACE为Rt△,若存在,试求点E的坐标,若不存在,请说明理由;(3)在平面直角坐标系中,存在点P,满足PA⊥PD,求线段PB的最小值.【分析】(1)设二次函数的表达式为交点式,将点C坐标代入,进而求得结果;(2)先把AC,CE,AE的平方求出或表示出来,然后分为∠CAE=90°,∠ACE=90°及∠AEC=90°,然后根据勾股定理逆定理列出方程,解方程,进而求得结果;(3)根据∠APD=90°确定点P在以AD的中点为圆心,为半径的圆上,进一步求得结果.【解答】解:(1)由题意设二次函数表达式为:y=a(x+1)•(x﹣3),∴a•(﹣3)=﹣3,∴a=1,∴y=(x+1)•(x﹣3)=x2﹣2x﹣3=(x﹣1)2﹣4,∴D(1,﹣4);(2)存在点E,使△ACE是直角三角形,过程如下:设点E(1,m),∵A(﹣1,0),C(0,﹣3),∴AC2=10,AE2=4+m2,CE2=1+(m+3)2,当∠EAC=90°时,AE2+AC2=CE2,∴14+m2=1+(m+3)2,∴m=,∴E1(1,),当∠ACE=90°时,AC2+CE2=AE2,∴11+(m+3)2=4+m2,∴m=﹣,∴E2(1,﹣),当∠AEC=90°时,AE2+CE2=AC2,∴5+m2+(m+3)2=10,∴m=﹣1或﹣2,∴E3(1,﹣1),E4(1,﹣2),综上所述:点E(1,)或(1,﹣)或(1,﹣1)或(1,﹣2);(3)设AD的中点为I,∵A(﹣1,0),D(1,﹣4),∴AD==2,I(0,﹣2),∴PA⊥PD,∴∠ADP=90°,∴点P在以AD的中点I为圆心,为半径的圆上,∵BI==,=﹣.∴PB最小1.(2020•河北模拟)已知抛物线C:y=ax2+bx+c(a>0,c<0)的对称轴为x=4,C为顶点,且A(2,0),C(4,﹣2)【问题背景】求出抛物线C的解析式.【尝试探索】如图2,作点C关于x轴的对称点C′,连接BC′,作直线x=k交BC′于点M,交抛物线C于点N.①连接ND,若四边形MNDC′是平行四边形,求出k的值.②当线段MN在抛物线C与直线BC′围成的封闭图形内部或边界上时,请直接写出线段MN的长度的最大值.【拓展延伸】如图4,作矩形HGOE,且E(﹣3,0),H(﹣3,4),现将其沿x轴以1个单位每秒的速度向右平移,设运动时间为t,得到矩形H′G′O′E′,连接AC′,若矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分,请求出t的取值范围.【分析】【问题背景】A(2,0),对称轴为x=4,则点B(6,0),则抛物线的表达式为:y=a(x﹣2)(x ﹣6),将点C的坐标代入上式即可求解;【尝试探索】①四边形MNDC′是平行四边形,则MN=DC′=2,即|k2﹣4k+6﹣(﹣k+6)|=2,解得:k=3或3,②MN=(﹣k+6)﹣(k2﹣4k+6)=﹣k2+3k,即可求解;【拓展延伸】(Ⅰ)当t=2时,矩形过点A,此时矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分;(Ⅱ)当H′E′与对称轴右侧抛物线有交点时,此时y=H′E′=4,即x2﹣4x+6=4,解得:x=4(舍去4﹣2),即可求解.【解答】解:【问题背景】A(2,0),对称轴为x=4,则点B(6,0),则抛物线的表达式为:y=a(x﹣2)(x﹣6),将点C的坐标代入上式得:﹣2=a(4﹣2)•(4﹣6),解得:a=,故抛物线的表达式为:…①;【尝试探索】①点C′(4,2),由点B、C′的坐标可得,直线BC′的表达式为:y=﹣x+6…②,四边形MNDC′是平行四边形,则MN=DC′=2,设点N的坐标为:(x,k2﹣4k+6),则点M(k,﹣k+6),即|k2﹣4k+6﹣(﹣k+6)|=2,解得:k=3或3,故k的值为:;②联立①②并解得:x=0或6,故抛物线C与直线BC′围成的封闭图形对应的k值取值范围为:0≤k≤6,MN=(﹣k+6)﹣(k2﹣4k+6)=﹣k2+3k,∵0,故MN有最大值,最大值为;【拓展延伸】由点A、C′的坐标得,直线AC′表达式为:y=x﹣2…③,联立①③并解得:x=2或8,即封闭区间对应的x取值范围为:2≤x≤8,(Ⅰ)当t=2时,矩形过点A,此时矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分,(Ⅱ)当H′E′与对称轴右侧抛物线有交点时,此时y=H′E′=4,即x2﹣4x+6=4,解得:x=4(舍去4﹣2),即x=4+2,则t=3+4+2=7+2,故t的取值范围为:2≤t≤.2.(2018秋•宁城县期末)已知,如图,抛物线与x轴交点坐标为A(1,0),C(﹣3,0),(1)如图1,已知顶点坐标D为(﹣1,4)或B点(0,3),选择适当方法求抛物线的解析式;(2)如图2,在抛物线的对称轴DH上求作一点M,使△ABM的周长最小,并求出点M的坐标;(3)如图3,将图2中的对称轴向左移动,交x轴于点P(m,0)(﹣3<m<﹣1),与抛物线,线段BC的交点分别为点E、F,用含m的代数式表示线段EF的长度,并求出当m为何值时,线段EF最长.【分析】(1)根据顶点D坐标设其顶点式,再将点C(2)连接BC,交DH于点M,使△ABM周长最小,即AM+BM最小,先求出BC直线解析式,再令x=﹣1,求得M(﹣1,2);(3)由题意得出E(m,﹣m2﹣2m+3),F(m,m+3),据此可知EF=EP﹣FP=﹣m2﹣2m+3﹣(m+3),再根据二次函数的性质可得答案.【解答】解:(1)由抛物线的顶点D的坐标(﹣1,4)可设其解析式为y=a(x+1)2+4,将点C(﹣3,0)代入,得:4a+4=0,解得a=﹣1,则抛物线解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3;(2)连接BC,交DH于点M,此时△ABM的周长最小,当y=0时,﹣(x+1)2+4=0,解得x=﹣3或x=1,则A(1,0),C(﹣3,0),当x=0时,y=3,则B(0,3),设直线BC的解析式为y=kx+b,将B(0,3),C(﹣3,0)代入得,解得:,∴直线BC解析式为y=x+3,当x=﹣1时,y=﹣1+3=2,所以点M坐标为(﹣1,2);(3)由题意知E(m,﹣m2﹣2m+3),F(m,m+3),则EF=EP﹣FP=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m=﹣(m+)2+,∴当m=﹣时,线段EF最长.3.(2021•桥西区模拟)如图1,抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,且CO=BO,连接BC.(1)求抛物线的解析式;(2)如图2,抛物线的顶点为D,其对称轴与线段BC交于点E,求线段DE的长度;(3)如图3,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,连接CP,CD,抛物线上是否存在点P,使△CDE∽△PCF,如果存在,求出点P的坐标,如果不存在,请说明理由.【分析】(1)根据题意可求得点C,B的坐标,将A,B坐标代入抛物线解析式求出a,b的值,即可得到抛物线解析式;(2)设直线BC的解析式为y=kx+b,将点C,B的坐标代入求得k,b的值,即可求得直线BC的解析式,再求DE即可;(3)根据△CDE∽△PCF,DE∥PF,可得:=,设点P坐标为(t,﹣t2+2t+3),点F坐标为(t,﹣t+3),建立关于t的方程求解即可.【解答】解:(1)在抛物线y=ax2+bx+3中,令x=0,得y=3,∴C(0,3),∴CO=3,∵CO=BO,∴BO=3,∴B(3,0),∵A(﹣1,0),∴,解得:,∴抛物线的解析式为:y=﹣x2+2x+3;(2)设直线BC的解析式为y=kx+b,∵B(3,0),C(0,3),∴,解得:,∴直线BC的解析式为y=﹣x+3,∵抛物线y=﹣x2+2x+3的顶点D坐标为(1,4),∴当x=1时,y=﹣1+3=2,∴E(1,2),∴DE=2;(3)∵PF∥DE,∴∠CED=∠CFP,当=时,△PCF∽△CDE,由D(1,4),C(0,3),E(1,2),利用勾股定理,可得CE==,DE=4﹣2=2,设点P坐标为(t,﹣t2+2t+3),点F坐标为(t,﹣t+3),∴PF=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,CF==t,∴=,∵t≠0,∴t=2,当t=2时,﹣t2+2t+3=﹣22+2×2+3=3,∴点P坐标为(2,3).4.(2022•和平区二模)如图,在平面直角坐标系中,已知抛物线顶点A的坐标为(﹣2,4),且经过坐标原点,与x轴负半轴交于点B.(1)求抛物线的函数表达式并直接写出点B的坐标;(2)过点A作AC⊥x轴于点C,若点D是y轴左侧的抛物线上一个动点(点D与点A不重合),过点D 作DE⊥x轴于点E,连接AO,DO,当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,求点D的坐标;(3)在(2)的条件下,当点D在第二象限时,在平面内存在一条直线,这条直线与抛物线在第二象限交于点F,在第三象限交于点G,且点A,点B,点D,到直线FG的距离都相等,请直接写出线段FG的长.【分析】(1)设该抛物线解析式为y=a(x+2)2+4(a≠0),把点(0,0)代入,即可求解;(2)根据题意得OC=2,AC=4,设点D(x,﹣x2﹣4x),则DE=|﹣x2﹣4x|,OE=﹣x,根据∠ACO=∠DEO=90°,可得当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,∠AOC=∠ODE 或∠AOC=∠DOE,分两种讨论,即可求解;(3)求出直线BD的解析式y=x+14,直线BD与y轴交于(0,14),可得过点A平行于BD的直线AM的解析式为y=x+11,交y轴于(0,11),可得直线FG的的解析式为y=x+,联立方程组,得到点F.G的坐标,即可求解.【解答】解:(1)∵抛物线顶点的坐标为(﹣2,4),∴设抛物线解析式为y=a(x+2)2+4(a≠0),把点(0,0)代入得:0=a(x+2)2+4.解得:a=﹣1,∴抛物线解析式为y=﹣(x+2)2+4=﹣x2﹣4x.令y﹣0,则﹣x2﹣4x=0,解得:x1=﹣4,x2=0,∴点B(﹣4,0),∴抛物线解析式为y=﹣x2﹣4x.点B(﹣4,0);(2)∵AC⊥x轴,点A(﹣2,4),∴点C(﹣2,0),∴OC=2,AC=4,∵∠ACO=∠DEO=90°,∴当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,∠AOC=∠ODE或∠AOC=∠DOE,设D(x,﹣x2﹣4x),①当∠AOC=∠ODE时,△AOC∽△ODE,如图:∵∠AOC=∠ODE,∴tan∠AOC=tan∠ODE,∴==2,∴=2,∴﹣x=2(x2+4x)或﹣x=﹣2(x2+4x),∴x1=0(舍去),x2=﹣或x3=0(舍去),x4=﹣,∴点D的坐标为(﹣,﹣)或(﹣,);②当∠AOC=∠DOE时,△AOC∽△DOE,如图:∵∠AOC=∠DOE,∴tan∠AOC=tan∠DOE,∴==2,∴=2,∴﹣2x=x2+4x或2x=x2+4x,∴x1=0(舍去),x2=﹣6或x3=0(舍去),x4=﹣2(舍去),∴点D的坐标为(﹣6,﹣12);点D(﹣6,﹣12);综上所述,当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,点D的坐标为(﹣6,﹣12)或(﹣,﹣)或(﹣,);(3)∵在(2)的条件下,点D在第二象限,∴点D的坐标为(﹣,),直线BD的解析式y=kx+m,∴,解得,∴直线BD的解析式y=x+14,直线BD与y轴交于(0,14),∴过点A平行于BD的直线AM的解析式为y=x+11,交y轴于(0,11),∵点A,点B,点D,到直线FG的距离都相等,∴直线FG的的解析式为y=x+,联立得,解得,,∴F(﹣,),G(﹣5,﹣5),∴FG==.5.(2022•鹿城区校级二模)如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(5,0),与y轴交于点C.(1)求抛物线的解析式和顶点D的坐标.(2)连结AD,点E是对称轴与x轴的交点,过E作EF∥AD交抛物线于点F(F在E的右侧),过点F作FG∥x轴交ED于点H,交AD于点G,求HF的长.【分析】(1)把点A(﹣1,0),B(5,0)代入抛物线解析式即可求解;(2)延长FG交y轴于点I,根据A,E,D坐标求出AE=3,DE=9,在Rt△EAD中,tan∠EAD=3,再根据四边形AGFE是平行四边形,得出tan∠EFH=tan∠EAD=3,设HF=m,EH=3m,易证四边形OIHE是矩形,把点F(m+2,﹣3m)代入y=x2﹣4x﹣5,求出m即可.【解答】解:(1)把点A(﹣1,0),B(5,0)代入抛物线解析式,得:,解得:,∴y=x2﹣4x﹣5=(x﹣2)2﹣9,∴抛物线解析式为y=x2﹣4x﹣5,顶点D坐标为(2,﹣9);(2)延长FG交y轴于点I,∵A(﹣1,0),E(2,0),D(2,﹣9),∴AE=3,DE=9,∴在Rt△EAD中,,∵EF∥AD,FG∥x轴,∴四边形AGFE是平行四边形,∴tan∠EFH=tan∠EAD=3,∴在Rt△EHF中,EH=3HF,设HF=m,EH=3m,易证四边形OIHE是矩形,把点F(m+2,﹣3m)代入y=x2﹣4x﹣5,得,﹣3m=(m+2)2﹣4(m+2)﹣5,解得:或m=(舍去),∴.6.(2021•南岗区模拟)如图,抛物线y=ax2+bx﹣4交x轴于点A(﹣3,0),B(4,0),交y轴于点C.(1)求抛物线的解析式;(2)点P为第一象限抛物线上一点,过点P作x轴的平行线,与抛物线的另一个交点为点G,连接CG交x轴于点N,设点P的横坐标为t,ON的长为d,求d与t之间的函数解析式(不要求写出自变量t的取值范围);(3)在(2)的条件下,连接PB,将线段PB绕着点P顺时针旋转90°得到线段PD,点D恰好落在y轴上,点E在线段OB上,连接PE,点Q在EB的延长线上,且EQ=PE,连接DQ交PE于点F,若PE=3PF,求QN的长.【分析】(1)运用待定系数法即可得出答案;(2)设P(t,t2﹣t﹣4),则G(1﹣t,t2﹣t﹣4),利用tan∠GCH==,求出CN,即可得出答案;(3)过点P作PT⊥x轴于点T,可证得△PDH≌△PBT(AAS),过点F作x轴的垂线,垂足为K,过点D 作KF的垂线,垂足为R,KR与PH交于点M,再证得△DRF≌△QKF(ASA),过点Q作QW∥PD,可证得△DPF≌△QWF(AAS),过点Q作QZ⊥PE于点Z,再证明△EQZ≌△EPT(AAS),再利用HL证明Rt △QWZ≌Rt△PBT,设EB=m,运用勾股定理建立方程求解即可.【解答】解:(1)∵抛物线y=ax2+bx﹣4交x轴于点A(﹣3,0),B(4,0),∴,解得:,∴抛物线的解析式为;(2)如图1,设P(t,t2﹣t﹣4),∵抛物线的对称轴为直线,PG∥x轴,∴点G与点P是抛物线上的一对对称点,∴G(1﹣t,t2﹣t﹣4),设PG与y轴交于点H,则H(0,t2﹣t﹣4),在抛物线中,令x=0,得y=﹣4,∴C(0,﹣4),∴OC=4,又CH=t2﹣t﹣4﹣(﹣4)=t2﹣t,GH=t﹣1,∵tan∠GCH==,∴,解得:,∴d与t之间的函数解析式为d=;(3)如图2,过点P作PT⊥x轴于点T,∵∠DPB=∠PHO=∠HOB=∠PTO=∠PHD=90°,∴四边形PHOT为矩形,∴∠HPT=90°,∴∠DPH=∠BPT,∵PD=PB,∴△PDH≌△PBT(AAS),∴DH=BT,PH=PT,∴,解得:t1=6,t2=﹣2(舍),∴P(6,6),∴T(6,0),∴DH=BT=2,ON=d=2,过点F作x轴的垂线,垂足为K,过点D作KF的垂线,垂足为R,KR与PH交于点M,∵PE=3PF,∴EF=2PF,∵cos∠PFM=cos∠EFK,∴,∴FK=2FM,∵∠MPT=∠PTK=∠TKM=90°,∴四边形PMKT为矩形,∴MK=PT=6,∴FM=2,FK=4,同理四边形DHMR为矩形,∴DH=RM=2,RF=FK=4,∠R=∠FKQ=90°,∵∠DFR=∠KFQ,∴△DRF≌△QKF(ASA),∴DF=QF,过点Q作QW∥PD,∴∠DPF=∠QWF∵∠DFP=∠WFQ,DF=FQ,∴△DPF≌△QWF(AAS),∴DP=QW=PB,PF=WF,∴,过点Q作QZ⊥PE于点Z,∴∠EZQ=∠PTE=90°,∵∠PET=∠QEZ,EP=EQ,∴△EQZ≌△EPT(AAS),∴PT=QZ,EZ=ET,∵QW=PB,∴Rt△QWZ≌Rt△PBT(HL),∴WZ=BT,∴EW=EB.设EB=m,则EW=WF=FP=m,∴EP=3m,∵BT=2,∴ET=m+2,PT=6,在Rt△EPT中,∵PE2=ET2+PT2,∴(3m)2=(m+2)2+62,解得:,m2=﹣2(舍),∴,∴BQ=2BE=5,∵OB=4,∴OQ=9,∵ON=2,∴QN=OQ+ON=11.7.(2021•凉山州模拟)如图1,在平面直角坐标系中,已知B点坐标为(1,0),且OA=OC=3OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点,其中D点是该抛物线的顶点.(1)求抛物线的解析式;(2)判断△ADC的形状并且求△ADC的面积;(3)如图2,点P是该抛物线第三象限部分上的一个动点,过P点作PE⊥AC于E点,当PE的值最大时,求此时P点的坐标及PE的最大值.【分析】(1)根据B点坐标为(1,0),且OA=OC=3OB,得出B,C点的坐标,用待定系数法求解析式即可;(2)根据坐标求出三角形各边的长,利用勾股定理判断其为直角三角形,再用三角形面积公式求面积即可;(3)求出直线AC的解析式,过点P作PH∥y轴交AC于H,设出P点和H点坐标,用含x的代数式求出PE的值,根据二次函数性质求最值即可.【解答】解:(1)∵B点坐标为(1,0),∴OB=1,又∵OA=OC=3OB,∴OA=OC=3,∴A(﹣3,0),C(0,﹣3),将A,B,C三点代入解析式得,,解得,∴抛物线的解析式为:y=x2+2x﹣3;(2)由(1)知抛物线的解析式为y=x2+2x﹣3,∴对称轴为直线x=﹣=﹣1,当x=﹣1时,y=(﹣1)2+2×(﹣1)﹣3=﹣4,∴D点的坐标为(﹣1,﹣4),∴|AD|==2,|AC|==3,|CD|==,∵|AD|2=|AC|2+|CD|2,∴△ACD是直角三角形,S△ABC=|AC|•|CD|=×=3;(3)设直线AC的解析式为y=sx+t,代入A,C点坐标,得,解得,∴直线AC的解析式为y=﹣x﹣3,如右图,过点P作y轴的平行线交AC于点H,∵OA=OC,∴∠OAC=∠OCA=45°,∵PH∥y轴,∴∠PHE=∠OCA=45°,设点P(x,x2+2x﹣3),则点H(x,﹣x﹣3),∴PH=﹣x﹣3﹣(x2+2x﹣3)=﹣x2﹣3x,∴PE=PH•sin∠PHE=(﹣x2﹣3x)×=﹣(x+)2+,∴当x=﹣时,PE有最大值为,此时P点的坐标为(﹣,﹣).8.(2022•无锡二模)已知抛物线y=mx2﹣2mx+3(m<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.(1)求抛物线的函数表达式;(2)若M、N是第一象限的抛物线上不同的两点,且△BCN的面积总小于△BCM的面积,求点M的坐标;(3)若D为抛物线的顶点,P为第二象限的抛物线上的一点,连接BP、DP,分别交y轴于点E、F,若EF=OC,求点P的坐标.【分析】(1)设A(x1,0),B(x2,0),因为OB=3OA,所以x2=﹣3x1,又由于x1,x2是方程mx2﹣2mx+3=0的两根,所以x1+x2=2,从而求出x1的值,得到A点坐标,代入到解析式中,求出m,即可解决问题;(2)由题意可得,只要求得第一象限内M点,使△BCM面积最大,过M作y轴平行线交BC于G点,设M(a,﹣a2+2a+3),先求出直线BC的解析式,可以得到G(a,﹣a+3),从而得的MG=﹣a2+3a,利用S=S△MGC+S△MGB,得到S△MBC=,当a=时,△MBC面积最大,从而求得M点坐△MBC标;。
初中数学动点最值问题19大模型+例题详解,彻底解决压轴难题

动点最值问题永远都是中考最难的压轴类题目,很多同学都反应不知道该怎么下手寻找思路。
其实这类题目的题型有限,全部总结归纳就是这19种,希望同学们对每一种都能掌握技巧,再遇见类似的就能及时找到思路。
PS:可下载电子版打印高清版本,链接文末获取!
1、将军饮马模型(对称点模型)
2、利用三角形两边差求最值
3、手拉手全等取最值
4、手拉手相似取最值
5、平移构造平行四边形求最小
6、两点对称勺子型连接两端求最小
7、两点对称折线连两端求最小
8、时钟模型,中点两定边求最小值
9、时钟模型,相似两定边求最小值
10、转化构造两定边求最值
11、面积转化法求最值
12、相似转化法求最值
13、相似系数化一法求最值
14、三角函数化一求最值
15、轨迹最值
16、三动点的垂直三角形
17、旋转最值
18、隐圆最值-定角动弦
19、隐圆最值-动角定弦。
2017-中考数学-压轴专题-最值问题系列(一)

专题最值问题—— 1(几何模型)一、归于几何模型,这类模型又分为以下情况:1. 归于“两点之间的连线中,线段最短”。
凡属于求“变动的两线段之和的最小值”时,大都应用这一模型。
2.归于“三角形两边之差小于第三边”。
凡属于求“变动的两线段之差的最大值”时,大都应用这一模型。
3.利用轴对称知识(结合平移)。
4. 应用“点到直线的距离,垂线段最短。
”性质。
5. 定圆中的所有弦中,直径最长;以及直线与圆相切的临界位置等等。
二、基础知识模型(一)“将军饮马”问题1.如图1,将军骑马从A出发,先到河边a喝水,再回驻地B,问将军怎样走路程最短?2.如图,一位将军骑马从驻地M出发,先牵马去草地OA吃草,再牵马去河边OB喝水,最后回到驻地M,问:这位将军怎样走路程最短?图1 图23. 如图,A为马厩,B为帐篷,将军某一天要从马厩牵马,先到草地一处牧马,再到河边饮马,然后回到帐篷,请你帮助确定这一天的最短路线。
(二)“造桥选址”问题(选自人教版七年级下册)1. 如图1,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河两岸1l、l2平行,桥MN 与河岸垂直)练习:1. 如图,在边长为2㎝的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为____________㎝(结果不取近似值).1题图2题图2.已知点A是半圆上的一个三等分点,点B是弧AN的中点,点P是半径ON上的动点,若⊙O的半径长为1,则AP+BP的最小值为__________.3.如图3,已知点A的坐标为(-4,8),点B的坐标为(2,2),请在x轴上找到一点P,使PA+PB最小,并求出此时P点的坐标和PA+PB的最小值。
变式1:如图,已知点A 的坐标为(-4,8),点B 的坐标为(2,2),点C 的坐标为(-2,0).把点A 和点B 向左平移 m 个单位,得到点A '和点B ',使C B C A '+'最短,求m 的值.变式2:如图,已知点A 的坐标为(-4,8),点B 的坐标为(2,2),点C 的坐标为(-2,0),点D 的坐标为(-4,0). 把点A 和点B 向左或向右平移m 个单位,得到点A '和点B ',使四边形A 'B 'CD 的周长最短,求m 的值.中考真题练习2.如图(1),抛物线3518532+-=x x y 和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长。
中考数学压轴题专题-二次函数与线段最值定值及数量关系问题

专题10二次函数与线段最值定值及数量关系问题图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用.一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【例1】(2021•沈阳)如图,平面直角坐标系中,O是坐标原点,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点B坐标是(3,0).抛物线与y轴交于点C(0,3),点P是抛物线的顶点,连接PC.(1)求抛物线的函数表达式并直接写出顶点P的坐标.(2)直线BC与抛物线对称轴交于点D,点Q为直线BC上一动点.①当△QAB的面积等于△PCD面积的2倍时,求点Q的坐标;②在①的条件下,当点Q在x轴上方时,过点Q作直线l垂直于AQ,直线y=x﹣交直线l于点F,点G在直线y=x﹣上,且AG=AQ时,请直接写出GF的长.【例2】(2021•滨州)如下列图形所示,在平面直角坐标系中,一个三角板的直角顶点与原点O重合,在其绕原点O旋转的过程中,两直角边所在直线分别与抛物线y=x2相交于点A、B(点A在点B的左侧).(1)如图1,若点A、B的横坐标分别为﹣3、,求线段AB中点P的坐标;(2)如图2,若点B的横坐标为4,求线段AB中点P的坐标;(3)如图3,若线段AB中点P的坐标为(x,y),求y关于x的函数解析式;(4)若线段AB中点P的纵坐标为6,求线段AB的长.【例3】(2021•盘锦)如图,抛物线y=﹣x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C,直线y=x﹣2与y轴交于点D,与x轴交于点E,与直线BC交于点F.(1)点F的坐标为;(2)如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q,PM⊥BC于点M,QN⊥BC于点N,若=,求点P的坐标;(3)如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出发,沿射线DE方向以每秒4个单位长度的速度运动,当SE=SG,且tan∠SEG=时,求点G的运动时间t.【例4】(2021•巴中)已知抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C (0,﹣3).(1)求抛物线的表达式;(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当最大时,求点P的坐标及的最大值;(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使△BCD是直角三角形,若存在,请直接写出点D的坐标;若不存在,请说明理由.【例5】(2020•孝感)在平面直角坐标系中,已知抛物线y=ax2+4ax+4a﹣6(a>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.(1)当a=6时,直接写出点A,B,C,D的坐标:A,B,C,D;(2)如图1,直线DC交x轴于点E,若tan∠AED=43,求a的值和CE的长;(3)如图2,在(2)的条件下,若点N为OC的中点,动点P在第三象限的抛物线上,过点P作x 轴的垂线,垂足为Q,交AN于点F;过点F作FH⊥DE,垂足为H.设点P的横坐标为t,记f=FP+FH.①用含t的代数式表示f;②设﹣5<t≤m(m<0),求f的最大值.【例6】(2020•恩施州)如图1,抛物线y=−14x2+bx+c经过点C(6,0),顶点为B,对称轴x=2与x轴相交于点A,D为线段BC的中点.(1)求抛物线的解析式;(2)P为线段BC上任意一点,M为x轴上一动点,连接MP,以点M为中心,将△MPC逆时针旋转90°,记点P的对应点为E,点C的对应点为F.当直线EF与抛物线y=−14x2+bx+c只有一个交点时,求点M的坐标.(3)△MPC在(2)的旋转变换下,若PC=2(如图2).①求证:EA=ED.②当点E在(1)所求的抛物线上时,求线段CM的长.【题组一】1.(2021•青山区模拟)已知抛物线y=ax2﹣4ax﹣12a与x轴相交于A,B两点,与y轴交于C点,且OC =OA.设抛物线的顶点为M,对称轴交x轴于点N.(1)求抛物线的解析式;(2)如图1,点E(m,n)为抛物线上的一点,且0<m<6,连接AE,交对称轴于点P.点F为线段BC上一动点,连接EF,当PA=2PE时,求EF+BF的最小值.(3)如图2,过点M作MQ⊥CM,交x轴于点Q,将线段CQ向上平移t个单位长度,使得线段CQ 与抛物线有两个交点,求t的取值范围.2.(2021•赣州模拟)已知抛物线C1:y=x2﹣4x+3m和C2:y=mx2﹣4mx+3m,其中m≠0且m≠1.(1)抛物线C1的对称轴是,抛物线C2的对称轴是;(2)这两条抛物线相交于点E,F(点E在点F的左侧),求E、F两点的坐标(用含m的代数式表示)并直接写出直线EF与x轴的位置关系;(3)设抛物线C1的顶点为M,C2的顶点为N;①当m为何值时,点M与点N关于直线EF对称?②是否存在实数m,使得MN=2EF?若存在,直接写出实数m的值,若不存在,请说明理由.3.(2021•桓台县二模)在平面直角坐标系中,抛物线y=x2+bx+c交x轴于A,B两点,点A,B的坐标分别为(﹣1,0),(3,0),点M为顶点.(1)求抛物线的解析式;(2)过点M作y轴的垂线,垂足为C,过点B作y轴的平行线,交CM于点D,点H为OC上的任一点,将线段HB绕点H逆时针旋转90°到HP.求∠PCD的度数;(3)在(2)的条件下,将点H改为y轴上的一动点,连接OP,BP,求OP+BP的最小值.4.(2021•成都模拟)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)求抛物线的解析式.(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G,H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°,求m的值.【题组二】5.(2021•攸县模拟)材料:对抛物线,定义:点叫做该抛物线的焦点,直线叫做该抛物线的准线,且该抛物线上任意一点到焦点的距离与它到准线的距离相等.运用上述材料解决如下问题:如图所示,已知抛物线C:y=ax2﹣4ax的图象与x轴交于O、A两点,且过点.(1)求抛物线C的解析式和点A的坐标;(2)若将抛物线C的图象先向左平移2个单位,再向上平移1个单位得到抛物线C'的图象.①求抛物线C'的焦点坐标和准线方程.②设M为抛物线C'位于第一象限内图象上的任意一点,MN⊥x轴于点N,求MN+MA的最小值,并求出取得这个最小值时点M的坐标.6.(2021•南沙区一模)已知,抛物线y=mx2+x﹣4m与x轴交于点A(﹣4,0)和点B,与y轴交于点C.点D(n,0)为x轴上一动点,且有﹣4<n<0,过点D作直线l⊥x轴,且与直线AC交于点M,与抛物线交于点N,过点N作NP⊥AC于点P.点E在第三象限内,且有OE=OD.(1)求m的值和直线AC的解析式.(2)若点D在运动过程中,AD+CD取得最小值时,求此时n的值.(3)若△ADM的周长与△MNP的周长的比为5:6时,求AE+CE的最小值.7.(2021•宝安区模拟)(1)已知二次函数经过点A(﹣3,0)、B(1,0)、C(0,3),请求该抛物线解析式;(2)点M为抛物线上第二象限内一动点,BM交y轴于点N,当BM将四边形ABCM的面积分为1:2两部分时,求点M的坐标;(3)点P为对称轴上D点下方一动点,点Q为直线y=x第一象限上的动点,且DP=OQ,求BP+BQ 的最小值并求此时点P的坐标.8.(2021•茶陵县模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,点P是直线BC上方抛物线上的动点.(1)求抛物线的解析式;(2)如图①,连接BC与OP,交于点D,求当的值最大时点P的坐标;(3)如图②,过点P作PD∥AC交x轴于点D,交BC于点E,求BE的最大值及点P的坐标.【题组三】9.(2021•东莞市校级一模)如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.(1)求抛物线的函数解析式;(2)设点P是直线l上的一个动点,当PA+PC的值最小时,求PA+PC长;(3)已知点N(0,﹣1),在y轴上是否存在点Q,使以M、N、Q为顶点的三角形与△BCM相似?若存在,请求出点Q的坐标;若不存在,请说明理由.10.(2021•怀化模拟)如图,已知抛物线y=ax2+bx+3的对称轴是直线x=1,与x轴交于点A、B,与y 轴交于点C,其中点A的坐标是(﹣1,0).(1)直接写出点B的坐标并求出抛物线的解析式;(2)点P是抛物线上的一个动点.①当∠PCB=∠OCB时,求点P的坐标;②当点P在B、C两点之间运动时,连接AP,交BC于点Q,设t=,求当t值最大时点P的坐标.11.(2021•罗湖区三模)如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.(1)直接写出抛物线的解析式:;(2)点D为第一象限内抛物线上的一动点,作DE⊥x轴于点E,交BC于点F,过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H,设点D的横坐标为m.①求DF+HF的最大值;②连接EG,若∠GEH=45°时,求m的值.12.(2021•南海区二模)如图1,抛物线y=x2+bx+c与x轴交于A、B两点,点A、B分别位于原点左、右两侧,且AO=2BO=4,过A点的直线y=kx+c交y轴于点C.(1)求k、b、c的值;(2)在抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由;(3)如图2,点M为线段AC上一点,连接OM,求AM+OM的最小值.【题组四】13.(2020•西宁二模)如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0,52).(1)求抛物线的解析式;(2)若点M是抛物线的顶点,连接AM,CM,求△AMC的面积;(3)若点P是抛物线上的一个动点,过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x 轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点P的坐标.14.(2020•涡阳县一模)如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式.(2)点P是直线上方的抛物线上的一个动点,求△ABP的面积最大时的P点坐标.(3)若点P是抛物线上的一个动点(不与点A点B重合),过点P作直线PD⊥x轴于点D,交直线AB 于点E.当PE=2ED时,求P点坐标;(4)设抛物线与y轴交于点F,在抛物线的第一象限内,是否存在一点M,使得AM被FC平分?若存在,请求出点M的坐标;若不存在,说明理由.15.(2020•哈尔滨模拟)如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tan C=355OA=3OB.(1)求抛物线的解析式;(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.16.(2020•皇姑区校级一模)如图,在平面直角坐标系中,抛物线y=−12x2+bx+c与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).(1)求抛物线y=−122+bx+c和直线BC的函数表达式;(2)点P是直线BC上方的抛物线上一个动点,当点P到直线BC的距离最大时,求点P的坐标;(3)连接点O与(2)中求出的点P,交直线BC于点D,点N是直线BC上的一个动点,连接ON,作DF⊥ON于点F,点F在线段ON上,当OD=5DF时,请直接写出点N的坐标.【题组五】17.(2020•岳阳二模)如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y 轴相交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)若点E在x轴上,且∠ECB=∠CBD,求点E的坐标.(3)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M.①求线段PM长度的最大值.②在①的条件下,若F为y轴上一动点,求PH+HF的最小值.18.(2020•白云区模拟)如图,抛物线y=x2+bx+c交x轴于点A,B两点,OA=1,与y轴交于点C,连接AC,tan∠OAC=3,抛物线的对称轴与x轴交于点D.(1)求点A,C的坐标;(2)若点P在抛物线上,且满足∠PAB=2∠ACO,求直线PA在与y轴交点的坐标;(3)点Q在抛物线上,且在x轴下方,直线AQ,BQ分别交抛物线的对称轴于点M、N.求证:DM+DN 为定值,并求出这个定值.19.(2020•福安市校级模拟)已知,抛物线y=ax2,其中a>0.(1)如图1,若点A、B是此抛物线上两点,且分属于y轴两侧,连接AB与y轴相交于点C,且∠AOB =90°.求证:CO=1;(2)如图2,若点A是此抛物线上一点,过点A的直线恰好与此抛物线仅有一个交点,且与y轴交于点B,与x轴相交于点C.求证:AC=BC.20.(2020•德城区一模)已知,在以O为原点的直角坐标系中,抛物线的顶点为A(﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.(1)求直线OB以及该抛物线相应的函数表达式;(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB 交于点N,求MN的最大值;(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.【题组六】21.(2020•青山区模拟)如图,在平面直角坐标系xOy中,一次函数y=54x+m(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B(1)求m的值及抛物线的函数表达式;(2)是否存在抛物线上一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若存在,请说明理由;(3)若P是抛物线对称轴上一动点,且使△ACP周长最小,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问1δ212是否为定值,如果是,请求出结果,如果不是请说明理由.(参考公式:在平面直角坐标系中,若A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=(1−2)2+(1−2)2)22.(2020•新都区模拟)已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.(1)如图1,求抛物线的解析式;(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB ﹣TS=23,求点R的坐标.23.(2020•自贡)在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣3,0)、B(1,0),交y 轴于点N,点M为抛物线的顶点,对称轴与x轴交于点C.(1)求抛物线的解析式;(2)如图1,连接AM,点E是线段AM上方抛物线上一动点,EF⊥AM于点F,过点E作EH⊥x轴于点H,交AM于点D.点P是y轴上一动点,当EF取最大值时:①求PD+PC的最小值;②如图2,Q点为y轴上一动点,请直接写出DQ+14OQ的最小值.24.(2020•凉山州)如图,二次函数y=ax2+bx+c的图象过O(0,0)、A(1,0)、B(32,32)三点.(1)求二次函数的解析式;(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.。
2022年中考数学压轴题讲义 利用代数求解最值问题
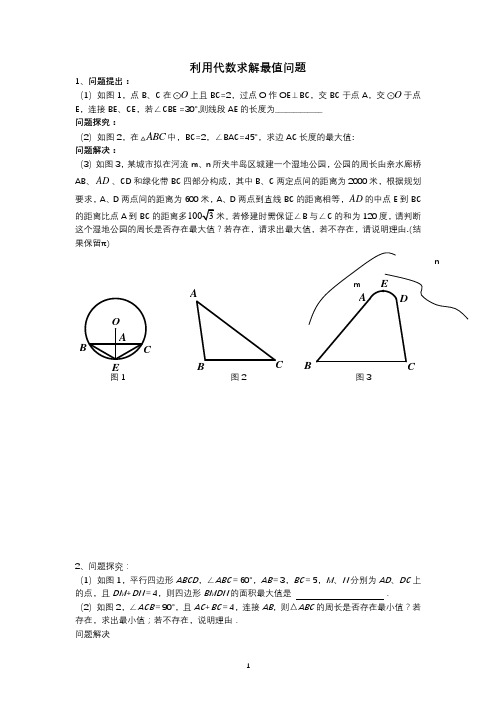
利用代数求解最值问题1、问题提出:(1)如图1,点B 、C 在O 上且BC=2,过点O 作OE ⊥BC ,交BC 于点A ,交O 于点E ,连接BE 、CE ,若∠CBE =30°,则线段AE 的长度为_____________问题探究:(2)如图2,在ABC 中,BC=2,∠BAC=45°,求边AC 长度的最大值: 问题解决:(3)如图3,某城市拟在河流m 、n 所夹半岛区城建一个湿地公园,公园的周长由亲水廊桥AB 、AD 、CD 和绿化带BC 四部分构成,其中B 、C 两定点间的距离为2000米,根据规划要求,A 、D 两点间的距离为600米,A 、D 两点到直线BC 的距离相等,AD 的中点E 到BC 的距离比点A 到BC 的距离多1003米。
若修建时需保证∠B 与∠C 的和为120度,请判断这个湿地公园的周长是否存在最大值?若存在,请求出最大值,若不存在,请说明理由. (结果保留π)图1 图2 图32、问题探究:(1)如图1,平行四边形ABCD ,∠ABC =60°,AB =3,BC =5,M 、N 分别为AD 、DC 上的点,且DM +DN =4,则四边形BMDN 的面积最大值是 . (2)如图2,∠ACB =90°,且AC +BC =4,连接AB ,则△ABC 的周长是否存在最小值?若存在,求出最小值;若不存在,说明理由. 问题解决EDC AO E C BBAB Cmn(3)如图3,在四边形ABCD中,AD∥BC,对角线AC交BD于O,已知∠AOB=120°,且AC+BD=10,则△AOD与△BOC的周长之和是否为定值?若是,求出定值;若不是,求出最小值.3、如图,四边形ABCD中,∠ABC=90°,AB∥CD.AB=5,AD=6,∠A=60°,在AD边上确定一点E,使得∠BEC=60°,则AE=()A.4−√6B.6﹣2√3C.5−√13D.3√324、【问题提出】(1)如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,若AP=2,PC=2DP,则BC=____________(2)如图2,在四边形ABCD中,∠A=∠B=90°,AB=10,AD=13,点E在线段BC上且BE=6,连接DE,作DE⊥EF,交AB于点F,则四边形ADEF的面积为___________【问题解决】(3)某精密仪器厂接到生产一种特殊四边形金属部件的任务,部件要求:如图3,四边形ABCD中,AB=4厘米,点C到AB的距离为5厘米,∠C=90°,且BC=2CD,在满足要求和保证质量的前提下,仪器厂希望造价最低,已知这种金属材料每平方厘米造价50元,请问一个这种四边形金属部件的造价最低是多少元?图1 图2 图35、如图,已知30MAN ∠=,点P 为MAN ∠内部一点,PEF 为等边三角形,点F 落在AM 上,点E 落在AN 上,过点P 做PC AN ⊥于点C ,PD AM ⊥于点D ,设PC 的长为x ,PEF 的面积为y ,若43AC =y 与x 之间的函数关系式;6、如图,等腰Rt △DEF 的三个顶点分别在等边△ABC 的三条边上,∠EDF=90°,已知AB=3√3+3,则△DEF 面积的最小值是_____________C DCB A D CFM NAP EFCABED7、问题提出(1)如图1,已知三角形ABC ,请在BC 边上确定一点D ,使得AD 的值最小. 问题探究(2)如图2,在等腰△ABC 中,AB =AC ,点P 是AC 边上一动点,分别过点A ,点C 作线段BP 所在直线的垂线,垂足为点D ,E ,若AB =5,BC =6,求线段BP 的取值范围,并求AD +CE 的最大值.问题解决(3)如图3,正方形ABCD 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点A 处和BC 边的两个三等分点E 、F 之间的某点P 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为BB ′、CC ′、DD ′.若你是此次项目设计的负责人,要使三条运输轨道的距离之和(BB ′+CC ′+DD ′)最小,你能不能按照要求进行规划,请通过计算说明.8、(1)问题初探:在直角三角形中,两直角边的长度之和是10,当两直角边分别是_____,_______时,直角三角形的面积最大;(2)问题解决:如图,在一个t R EFG 的内部作一个矩形ABCD ,其中点A 和点D 分别在两直角边上,BC 在斜边上,EF=30cm ,FG=40cm ,矩形面积最大是多少?(3)问题拓展:如图,矩形ABCD 中,AB=20cm ,BC=30cm ,点E 是AD 边上的动点(点E 与A,D 两点不重合),连接BE 、CE ,点F 是BC 边上的动点,过F 作FG ∥CE 交BE 于点G ,求三角形EFG 面积的最大值。
2024年中考数学高频压轴题训练——二次函数与最值(含答案)

2024年中考数学高频压轴题训练——二次函数与最值(1)求一次函数和反比例函数的表达式;(2)求面积的最大值.3.如图,有长为的篱笆,一面利用墙(墙的最大可利用长度为),围成中间隔有一道篱笆的长方形花圃,设花圃的宽为,面积为.(1)求S 与x 的函数关系式;(2)如果要围成面积为的花圃,的长是多少m ;(3)当的长是多少m 时,S 取得最大值,最大值是多少?DPQ V 24m 10m AB m x 2m S 245m AB AB(1)不论取何值,直线必经过定点,直接写出点(2)如图,已知、两点关于抛物线的对称轴对称.①求证:直线必经过一定点;②当时,的最大值与最小值的差为2,求的值.①当时,求的值;②当取最大值时,求的值.k 23y kx k =-+P B C AC 1m x m +≤≤y m 42S =x S x8.如图(1),一块钢板余料截面的两边为线段,,另一边曲线为抛物线的一部分,其中点为抛物线的顶点,于,以边所在直线为轴,边所在直线为轴,建立平面直角坐标系,规定一个单位代表1米.已知米,米,米.(1)求曲线所在抛物线的函数表达式;(2)若在该钢板余料中截取一个一边长为3米的矩形,设该矩形的另一边长为米,求的取值范围;(3)如图(2),若在该钢板余料中截取一个,其中点在抛物线上,记的面积为,求的最大值.9.公司电商平台准备在2022年十一长假期间销售某种儿童玩具,市场调查反映:当它的售价为每件80元时,每天可卖出100件;售价每增加1元,每天销售量会减少2件.(售价不能超过每件100元),已知玩具的进价为60元.设售价增加x 元,每天售OA OB ACB C CD OA ⊥D OA x OB y xOy 1OD =2DA =4CD =ACB h h PBD △P ACB PBD △S S(1)求该二次函数的表达式;(2)当x 取何值时,该二次函数取得最大值?最大值是多少?(3)当时,请写出x 3y >(1)求的值和反比例函数的表达式;(2)观察图象,直接写出当(3)直线沿轴方向平移,当m 0x >y n =y(1)求抛物线的解析式.(2)当时,求二次函数的最大值和最小值.(3)点P 是抛物线上一点,其横坐标为m ,过点P 作,已知点P 与点Q 不重合,且线段的长度随①求m 的取值范围.②当时,在线段的右边作正方形,直接写出正方形函数的图象交点的个数及对应的m 的取值范围.22x -≤≤PQ 1m --PQ 12m -<<PQ PQRT ²y x bx c =++(1)求抛物线的解析式;(2)若,求点P 的坐标;(3)如图2,过点P 作,求的最大值.6AOP BOC S S =V V PD AC ⊥PD参考答案:。
二次函数与线段最值定值问题(八大类型)-2023年中考数学压轴题专项训练(学生版)

二次函数与线段最值定值问题(八大类型)考向分析题型一二次函数与单线段最值问题1.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(-1,0)两点,与.y轴交于点C0,52(1)求抛物线的解析式;(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.题型二二次函数与将军饮马型问题2.如图1,抛物线y=ax2+2x+c与x轴交于A(-4,0),B(1,0)两点,过点B的直线y=kx+23分别与y轴及抛物线交于点C,D.(1)求直线和抛物线的表达式;(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t 秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.题型三二次函数与胡不归型线段最值问题3.已知抛物线y=-1x2+bx+c(b,c为常数)的图象与x轴交于A(1,0),B两点(点A在点B左2侧).与y轴相交于点C,顶点为D.(Ⅰ)当b=2时,求抛物线的顶点坐标;(Ⅱ)若点P是y轴上一点,连接BP,当PB=PC,OP=2时,求b的值;(Ⅲ)若抛物线与x轴另一个交点B的坐标为(4,0),对称轴交x轴于点E,点Q是线段DE上一点,点NQ的最小值.N为线段AB上一点,且AN=2BN,连接NQ,求DQ+54二次函数与三线段和最值问题4.如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c 过A、B两点,且与x轴交于另一点C.(1)求b、c的值;(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR①求证:PG=RQ;②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.二次函数与线段倍分关系最值问题5.抛物线y=-x2+4ax+b(a>0)与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.(1)a=32时,求抛物线的解析式和BC的长;(2)如图a>1时,若AP⊥PC,求a的值;(3)是否存在实数a,使APPN =12若存在,求出a的值,如不存在,请说明理由.题型六二次函数与线段乘积问题6.已知直线y=12x+2分别交x轴、y轴于A、B两点,抛物线y=12x2+mx-2经过点A,和x轴的另一个交点为C.(1)求抛物线的解析式;(2)如图1,点D是抛物线上的动点,且在第三象限,求△ABD面积的最大值;(3)如图2,经过点M(-4,1)的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求OE•OF的值.备注:抛物线顶点坐标公式-b2a,4ac-b24a7.抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上一点,且位于x轴下方.(1)如图1,若P(1,-3),B(4,0).①求该抛物线的解析式;②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时,OE+OFOC是否为定值?若是,试求出该定值;若不是,请说明理由.8.如图,已知抛物线y=ax2+bx+c与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C,且OB=OC.(1)求抛物线的函数表达式;(2)如图1,点D是抛物线顶点,点P(m,n)是在第二象限抛物线上的一点,分别连接BD、BC、BP,若∠CBD=∠ABP,求m的值;(3)如图1,过B、C、O三点的圆上有一点Q,并且点Q在第四象限,连接QO、QB、QC,试猜想线段QO、QB、QC之间的数量关系,并证明你的猜想;(4)如图2,若∠BAC的角平分线交y轴于点G,过点G的直线分别交射线AB、AC于点E、F(不与点A重合),则1AE+1AF的值是否变化?若变化,请说明理由;若不变,请求出它的值.压轴题速练一、解答题1.如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为(5,0),点D的坐标为(1,3).(1)求该二次函数的表达式;(2)试问在该二次函数图象上是否存在点G,使得△ADG的面积是△BDG的面积的35若存在,求出点G的坐标;若不存在,请说明理由.2.在平面直角坐标系中,抛物线y=-x2-4x+c与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为(-5,0).(1)求点C的坐标;(2)如图1,若点P是第二象限内抛物线上一动点,求点P到直线AC距离的最大值;(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.3.如图,已知抛物线y=ax2-32x+c与x轴交于点点A(-4,0),B(1,0),与y轴交于点C.(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在点Q使QB+QC最小?若存在,请求出Q点坐标;若不存在,请说明理由;(3)点P为AC上方抛物线上的动点,过点P作PD⊥AC,垂足为点D,连接PC,当△PCD与△ACO相似时,求点P的坐标.4.如图,抛物线y=-12x2+bx+c过点A3,2,且与直线y=-x+72交于B、C两点,点B的坐标为4,m.(1)求抛物线的解析式;(2)点D为抛物线上位于直线BC上方的一点,过点D作DE⊥x轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求PD+PA的最小值.5.抛物线y=ax2+bx-3(a,b为常数,a≠0)交x轴于A-3,0两点.,B4,0(1)求该抛物线的解析式;(2)点C0,4,D是线段AC上的动点(点D不与点A,C重合).①点D关于x轴的对称点为D ,当点D 在该抛物线上时,求点D的坐标;②E是线段AB上的动点(点E不与点A,B重合),且CD=AE,连接CE,BD,当CE+BD取得最小值时,求点D的坐标.6.如图,在平面直角坐标系中,已知抛物线y =ax 2+bx +2a ≠0 与x 轴交于A -1,0 ,B 3,0 两点,与y 轴交于点C ,连接BC .(1)求该抛物线的解析式;(2)点P 为直线BC 上方的抛物线上一点,过点P 作y 轴的垂线交线段BC 于M ,过点P 作x 轴的垂线交线段BC 于N ,求△PMN 的周长的最大值.(3)若点N 为抛物线对称轴上一点,抛物线上是否存在点M ,使得以B ,C ,M ,N 为顶点的四边形是平行四边形?若存在,请求出所有满足条件的点M 的坐标;若不存在,请说明理由.7.如图,二次函数y=-14x2+12m-1x+m(m是常数,且m>0)的图象与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,动点P在对称轴l上,连接AC、BC、PA、PC.(1)求点A、B、C的坐标(用数字或含m的式子表示);(2)当PA+PC的最小值等于45时,求m的值及此时点P的坐标;(3)当m取(2)中的值时,若∠APC=2∠ABC,请直接写出点P的坐标.8.已知抛物线y=x+1(m为常数,m>1)的顶点为P.x-m(1)当m=5时,求该抛物线顶点P的坐标;(2)若该抛物线与x轴交于点A,C(点A在点C左侧),与y轴交于点B.①点Q是该抛物线对称轴上一个动点,当AQ+BQ的最小值为22时,求该抛物线的解析式和点Q 的坐标.②连接BC,与抛物线的对称轴交于点H,过点P作PD⊥BC,垂足为D,若BC=8PD,求该抛物线的解析式.9.已知抛物线y=ax2+bx+c(a、b、c是常数,a>0)的顶点为P,与x轴相交于点A-1,0和点B.(1)若b=-2,c=-3,①求点P的坐标;②直线x=m(m是常数,1<m<3)与抛物线相交于点M,与BP相交于点G,当MG取得最大值时,求点M,G的坐标;(2)若3b=2c,直线x=2与抛物线相交于点N,E是x轴的正半轴上的动点,F是y轴的负半轴上的动点,当PF+FE+EN的最小值为5时,直接写出顶点P的坐标.10.如图,抛物线y=-x2+bx+c交x轴于A、B两点(点A在点B的左侧)坐标分别为-2,0,4,0,交y轴于点C.(1)求出抛物线解析式:5时,请求(2)如图1,过y轴上点D做BC的垂线,交线段BC于点E,交抛物线于点F,当EF=35出点F的坐标;(3)如图2,点H的坐标是0,2在抛物线上,把△PHQ沿HQ翻折,,点Q为x轴上一动点,点P2,8使点P刚好落在x轴上,请直接写出点Q的坐标.11.抛物线y =ax 2+bx +c 与坐标轴交于A -1,0 、B 4,0 、C 0,2 三点.点P 为抛物线上位于BC 上方的一动点.(1)求抛物线的解析式;(2)如图,过点P 作PF ⊥x 轴于点F ,交BC 于点E ,连结CP 、CF .当S ΔPCE =2S ΔCEF 时,求点P 的坐标;(3)过点P 作PG ⊥BC 于点G ,是否存在点P ,使线段PG 、CG 的长度是2倍关系?若存在,求出点P 的坐标;若不存在,请说明理由.12.已知抛物线y=ax2+bx+c经过点A-4,0.、B1,0、C0,4(1)求抛物线解析式和直线AC的解析式;(2)如图(1),若点P是第四象限抛物线上的一点,若S△PAC=20,求点P的坐标;(3)如图(2),点M是直线AC上方抛物线上的一个动点(不与A、C重合),过点M作MH垂直AC于点H,求MH的最大值.13.如图,已知抛物线y=-x2+bx+c与一直线相交于A-1,0两点,与y轴交于点N,其顶,C2,3点为D.(1)求抛物线及直线AC的解析式.(2)设点M3,m,求使MN+MD的值最小时m的值.(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求出点E,F的坐标;若不能,请说明理由.14.已知抛物线y=ax2+bx+c(a≠0)与x轴有且只有一个交点A2,0,且与y轴于交于点B.(1)求a与c的关系式;(2)若a=1时,点P2,1c在抛物线的对称轴上;①若过B点的直线l:y=kx+m(k≠0)与抛物线只有一个交点;证明:直线l平分∠OBP;②设过P点的直线与抛物线交于M,N点,则1PM+1PN是否为定值,若为定值请求出定值,若不是定值请说明理由.15.如图1,抛物线y=ax2+2x+c,交x轴于A、B两点,交y轴于点C,F为抛物线顶点,直线EF垂直于x轴于点E,当y≥0时,-1≤x≤3.(1)求抛物线的表达式;(2)点P是线段BE上的动点(除B、E外),过点P作x轴的垂线交抛物线于点D.①当点P的横坐标为2时,求四边形ACFD的面积;②如图2,直线AD,BD分别与抛物线对称轴交于M、N两点.试问,EM+EN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.16.已知抛物线y=-x2+2kx-k2+4的顶点为H,与y轴交点为A,点P a,b是抛物线上异于点H的一个动点.(1)若抛物线的对称轴为直线x=1,请用含a的式子表示b;(2)若a=1,作直线HP交y轴于点B,当点A在x轴上方且在线段OB上时,直接写出k的取值范围;(3)在(1)的条件下,记抛物线与x轴的右交点为C,OA的中点为D,作直线CD,过点P作PF⊥CD 于点E并交x轴于点F,若a<3,PE=3EF,求a的值.17.已知抛物线y=ax2+bx+c(a≠0)与x轴只有一个公共点A2,0.且经过点3,1(1)求抛物线的函数解析式;(2)直线l:y=-x+m与抛物线y=ax2+bx+c相交于B、C两点(C点在B点的左侧),与对称轴相交于点P,且B、C分布在对称轴的两侧.若B点到抛物线对称轴的距离为n,且CP=t·BP(2≤t≤3).①试探求n与t的数量关系;②求线段BC的最大值,以及当BC取得最大值时对应m的值.18.如图1,二次函数y =ax 2+bx +3的图像与x 轴交于点A -1,0 ,B 3,0 ,与y 轴交于点C .(1)求二次函数的解析式;(2)点P 为抛物线上一动点.①如图2,过点C 作x 轴的平行线与抛物线交于另一点D ,连接BC ,BD .当S △PBC =2S △DBC 时,求点P 的坐标;②如图3,若点P 在直线BC 上方的抛物线上,连接OP 与BC 交于点E ,求PE OE的最大值.19.抛物线y=ax2-4经过A、B两点,且OA=OB,直线EC过点E4,-1,点D是线段,C0,-3OA(不含端点)上的动点,过D作PD⊥x轴交抛物线于点P,连接PC、PE.(1)求抛物线与直线CE的解析式;(2)求证:PC+PD为定值;(3)在第四象限内是否存在一点Q,使得以C、P、E、Q为顶点的平行四边形面积最大,若存在,求出Q点坐标;若不存在,请说明理由.20.如图1.在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A-2,0,,点B4,0与y轴交于点C0,2.(1)求抛物线的解析式;(2)点P是第一象限内的抛物线上一点.过点P作PH⊥x轴于点H,交直线BC于点Q,求PQ+5CQ的最大值,并求出此时点P的坐标;5(3)如图2.将地物线沿射线BC的方向平移5个单位长度.得到新抛物线y1=a1x2+b1x+c1a1≠0,新抛物线与原抛物线交于点G,点M是x轴上一点,点N是新抛物线上一点,若以点C、G、M、N为顶点的四边形是平行四边形时,请直接写出点N的坐标.。
几何最值问题-2023年中考数学压轴题专项训练(全国通用)(解析版)

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图,在矩形ABCD 中,AB =8,AD =4,点E 是矩形ABCD 内部一动点,且∠BEC =90°,点P 是AB 边上一动点,连接PD 、PE ,则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹,利用“将军饮马”模型将PE 进行转化即可求解.【详解】解:如图,设点O 为BC 的中点,由题意可知,点E 在以BC 为直径的半圆O 上运动,作半圆O 关于AB 的对称图形(半圆O '),点E 的对称点为E 1,连接O 'E 1,则PE =PE 1,∴当点D 、P 、E 1、O '共线时,PD +PE 的值最小,最小值为DE 1的长,如图所示,在Rt △DCO '中,CD =8,CO '=6,∴DO '=82+62=10,又∵O 'E 1=2,∴DE 1=DO '-O 'E 1=8,即PD +PE 的最小值为8,故选:A .【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理,利用“将军饮马”模型将PE 进行转化时解题的关键.2(2023·安徽黄山·校考模拟预测)如图,在平面直角坐标系中,二次函数y =32x 2-32x -3的图象与x 轴交于点A ,C 两点,与y 轴交于点B ,对称轴与x 轴交于点D ,若P 为y 轴上的一个动点,连接PD ,则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,可求得∠ABO =30°,从而得出PE =12PB ,进而得出PD +12PB =PD +EP ,进一步得出结果.【详解】解:如图,作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,抛物线的对称轴为直线x =--322×32=12,∴OD =12,当x =0时,y =-3,∴OB =3,当y =0时,32x 2-32x -3=0,∴x 1=-1,x 2=2,∴A (-1,0),∴OA =1,∵tan ∠ABO =OA OB =13=33,∴∠ABO =30°,∴PE =12PB ,∴12PB +PD =PD +PE ≥DF ,当点P 在P 时,PD +PE 最小,最大值等于DF ,在Rt △ADF 中,∠DAF =90°-∠ABO =60°,AD =OD +PA =12+1=32,∴DF =AD ⋅sin ∠DAE =32×32-334,∴12PB +PD 最小=DF =334,故选:A .【点睛】本题以二次函数为背景,考查了二次函数与一元二次方程之间的关系,解直角三角形等知识,解决问题的关键是用三角函数构造12PB .3(2023秋·浙江金华·九年级统考期末)如图,正方形ABCD 的边长为4,点E 是正方形ABCD 内的动点,点P 是BC 边上的动点,且∠EAB =∠EBC .连结AE ,BE ,PD ,PE ,则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°,即可得点E 在以AB 为直径的半圆上移动,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,问题随之得解.【详解】解:∵四边形ABCD 是正方形,∴∠ABC =90°,∴∠ABE +∠EBC =90°,∵∠EAB =∠EBC ,∴∠EAB +∠EBA =90°,∴∠AEB =90°,∴点E 在以AB 为直径的半圆上移动,如图,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,E∵∠G =90°,FG =BG =AB =4,∴OG =6,OA =OB =OE =2,∴OF =FG 2+OG 2=213,∴EF =OF -OE =213-2,故PE +PD 的长度最小值为213-2,故选:A .【点睛】本题考查了轴对称-最短路线问题,正方形的性质,勾股定理,正确的作出辅助线,得出点E 的运动路线是解题的关键.4(2022秋·安徽池州·九年级统考期末)如图,Rt △ABC 中,∠C =90°,AC =4,BC =3,点P 为AC 边上的动点,过点P 作PD ⊥AB 于点D ,则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,点P 即为所求作的点,此时PB +PD 有最小值,连接AB ,根据对称性的性质,可知:BP =B P ,△ABC ≅△AB C ,根据S △ABB =S △ABC +S △AB C =2S △ABC ,即可求出PB +PD 的最小值.【详解】解:如下图,作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,连接AB ,点P 即为所求作的点,此时PB +PD 有最小值,根据对称性的性质,可知:BP =B P ,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,∴AB =AC 2+BC 2=5,根据对称性的性质,可知:△ABC ≅△AB C ,∴S △ABB =S △ABC +S △ABC =2S △ABC ,即12×AB ⋅B D =2×12BC ⋅AC ,∴5B D =24,∴B D =245,故选:B .【点睛】本题考查了轴对称一最短路线问题,解题的关键是掌握轴对称的性质.5(2023秋·甘肃定西·八年级校考期末)如图所示,在△ABC 中,∠ABC =68°,BD 平分∠ABC ,P 为线段BD 上一动点,Q 为 边AB 上一动点,当AP +PQ 的值最小时,∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ,连接PE ,证明△PBQ ≌△PBE SAS ,得出PE =PQ ,说明AP +PQ =AP +PE ,找出当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ 最小,过点A 作AE ⊥BC 于点E ,交BD 于点P ,根据三角形外角的性质可得答案.【详解】解:在BC 上截取BE =BQ ,连接PE ,如图:∵BD 平分∠ABC ,∠ABC =68°,∴∠ABD =∠CBD =12∠ABC =34°,∵BP =BP ,∴△PBQ ≌△PBE SAS ,∴PE =PQ ,∴AP +PQ =AP +PE ,∴当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ最小,过点A作AE ⊥BC 于点E ,交BD 于点P ,如图:∵∠AEB =90°,∠CBD =34°,∴∠APB =∠AEB +∠CBD =124°.故选:D .5【点睛】本题主要考查了角平分线的定义,三角形全等的判定和性质,垂线段最短,三角形内角和定理与三角形的外角的性质,解题的关键是找出使AP +PQ 最小时点P 的位置.6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图,E 为正方形ABCD 边AD 上一点,AE =1,DE =3,P 为对角线BD 上一个动点,则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点,根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长,求出EC 的长即可.【详解】连接EC ,交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长.∵AE =1,DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选:A【点睛】本题主要考查了正方形的性质和两点之间线段最短,这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图,正方形ABCD 的边长为4,点M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称,连接BM 交AC 于N ′,N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可.【详解】∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,6连接BD ,BM 交AC 于N ′,连接DN ′,∴当B 、N 、M 共线时,DN +MN 有最小值,则BM 的长即为DN +MN 的最小值,∴AC 是线段BD 的垂直平分线,又∵CD =4,DM =1∴CM =CD -DM =4-1=3,在Rt △BCM 中,BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5.故选:D .【点睛】本题考查的是轴对称-最短路线问题及正方形的性质,先作出D 关于直线AC 的对称点,由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键.8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图,在平面直角坐标系中,二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点,与x 轴交于点C (3,0),若P 是x 轴上一动点,点D 的坐标为(0,-1),连接PD ,则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H ,根据2PD +PC =2PD +22PC =2PD +PJ ,求出DP +PJ 的最小值即可解决问题.【详解】解:连接BC ,过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H .∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0),∴b =2,∴二次函数的解析式为y =-x 2+2x +3,令y =0,-x 2+2x +3=0,解得x =-1或3,∴A (-1,0),令x =0,y =3,∴B (0,3),∴OB =OC =3,∵∠BOC =90°,∴∠OBC =∠OCB =45°,∵D(0,-1),∴OD =1,BD =4,∵DH ⊥BC ,∴∠DHB =90°,设DH =x ,则BH =x ,∵DH 2+BH 2=BD 2,7∴x =22,∴DH =22,∵PJ ⊥CB ,∴∠PJC =90°,∴PJ =22PC ,∴2PD +PC =2PD +22PC =2PD +PJ ,∵DP +PJ ≥DH ,∴DP +PJ ≥22,∴DP +PJ 的最小值为22,∴2PD +PC 的最小值为4.故选:A .【点睛】本题考查了二次函数的相关性质,以及等腰直角三角形的判定和性质,垂线段最短等知识,得到∠OBC =∠OCB =45°,PJ =22PC 是解题的关键.9(2022·山东泰安·统考中考真题)如图,四边形ABCD 为矩形,AB =3,BC =4.点P 是线段BC 上一动点,点M 为线段AP 上一点.∠ADM =∠BAP ,则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°,得出点M 在O 点为圆心,以AO 为半径的圆上,从而计算出答案.【详解】设AD 的中点为O ,以O 点为圆心,AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心,以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时,BM 最短∵BO 2=AB 2+AO 2,AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选:D .【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.810(2022·河南·校联考三模)如图1,正方形ABCD 中,点E 是BC 的中点,点P 是对角线AC 上的一个动点,设AP =x ,PB +PE =y ,当点P 从A 向点C 运动时,y 与x 的函数关系如图2所示,其中点M 是函数图象的最低点,则点M 的坐标是()A.42,35B.22,35C.35,22D.35,42【答案】A【分析】根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,从而确定正方形的边长为6,根据将军饮马河原理,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,利用相似三角形,计算AG 的长即为横坐标.【详解】如图,根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,∵点E 是BC 的中点,∴BC =6,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,∵四边形ABCD 是正方形,AB =6,∴CE ∥AD ,AC =62+62=62,DE =62+32=35,∴△CGE ∽△AGD ,∴CG AG =CE AD =12,∴AC AG=32,∴AG =42,故点M 的坐标为(42,35),故A 正确.故选:A .【点睛】本题考查了正方形的性质,三角形相似的判定和性质,函数图像信息的获取,将军饮马河原理,熟练掌握正方形的性质,灵活运用三角形相似,构造将军饮马河模型求解是解题的关键.2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图,矩形ABCD ,AB =4,BC =8,E 为AB 中点,F 为直线BC 上动点,B 、G 关于EF 对称,连接AG ,点P 为平面上的动点,满足∠APB =12∠AGB ,则DP 的最小值.【答案】210-22【分析】由题意可知,∠AGB =90°,可得∠APB =12∠AGB =45°,可知点P 在以AB 为弦,圆周角∠APB =45°的9圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧),设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,可知△AOB 为等腰直角三角形,求得OA =22AB =22=OP ,AQ =OQ =22OA =2,QD =AD -AQ =6,OD =OQ 2+QD 2=210,再由三角形三边关系可得:DP ≥OD -OP =210-22,当点P 在线段OD 上时去等号,即可求得DP 的最小值.【详解】解:∵B 、G 关于EF 对称,∴BH =GH ,且EF ⊥BG∵E 为AB 中点,则EH 为△ABG 的中位线,∴EH ∥AG ,∴∠AGB =90°,∵∠APB =12∠AGB ,即∠APB =12∠AGB =45°,∴点P 在以AB 为弦,圆周角∠APB =45°的圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧)设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,则OA =OB =OP ,∵∠APB =45°,∴∠AOB =90°,则△AOB 为等腰直角三角形,∴OA =22AB =22=OP ,又∵E 为AB 中点,∴OE ⊥AB ,OE =12AB =AE =BE ,又∵四边形ABCD 是矩形,∴∠BAD =90°,AD =BC =8,∴四边形AEOQ 是正方形,∴AQ =OQ =22OA =2,QD =AD -AQ =6,∴OD =OQ 2+QD 2=210,由三角形三边关系可得:DP ≥OD-OP =210-22,当点P 在线段OD 上时去等号,∴DP 的最小值为210-22,故答案为:210-22.【点睛】本题考查轴对称的性质,矩形的性质,隐形圆,三角形三边关系,正方形的判定及性质,等腰直角三角形的判定及性质,根据∠APB =12∠AGB =45°得知点P 在以AB 为弦,圆周角∠APB =45°的圆上是解决问题的关键.12(2023春·江苏连云港·八年级期中)如图,在边长为8的正方形ABCD 中,点G 是BC 边的中点,E 、F 分别是AD 和CD 边上的点,则四边形BEFG 周长的最小值为.【答案】2410【分析】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G ,根据两点之间线段最短即可解决问题.【详解】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G∵EB =EB ,FG =FG ,∴BE +EF +FG +BG =B E +EF +FG +BG ,∵EB +EF +FG ≥B G ,∴四边形BEFG 的周长的最小值=BG +B G ,∵正方形ABCD 的边长为8∴BG =4,BB =16,BG =12,∴B G =162+122=20,∴四边形BEFG 的周长的最小值为=4+20=24.故答案为:24.【点睛】本题考查轴对称求线段和的最短问题,正方形的性质,勾股定理,解题的关键是学会利用轴对称解决最短问题.13(2022·湖南湘潭·校考模拟预测)如图,菱形草地ABCD 中,沿对角线修建60米和80米两条道路AC <BD ,M 、N 分别是草地边BC 、CD 的中点,在线段BD 上有一个流动饮水点P ,若要使PM +PN 的距离最短,则最短距离是米.【答案】50【分析】作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,根据菱形的性质和勾股定理求出BC 长,即可得出答案.【详解】解:作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,∵四边形ABCD 是菱形,∴AC ⊥BD ,∠QBP =∠MBP ,即Q 在AB 上,∵MQ ⊥BD ,∴AC ∥MQ ,∴M 为BC 中点,∴Q 为AB 中点,∵N 为CD 中点,四边形ABCD 是菱形,∴BQ ∥CD ,BQ =CN ,∴四边形BQNC 是平行四边形,∴NQ =BC ,设AC 与BD 的交点为点O ,∵四边形ABCD 是菱形,∴AC ⊥BD,OC =12AC =30米,OB =12BD =40米,∴BC =OB 2+OC 2=50米,∴PM +PN 的最小值是50米.故答案为:50.11【点睛】本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P 的位置.14(2023春·江苏·九年级校考阶段练习)如图,正方形ABCD 的边长为4,⊙B 的半径为2,P 为⊙B 上的动点,则2PC -PD 的最大值是.【答案】2【分析】解法1,如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,连接PM 、DM ,推得2PC -PD=2PC -22PD =2PC -PM ,因为PC -PM ≤MC ,求出MC 即可求出答案.解法2:如图:连接BD 、BP 、PC ,在BD 上做点M ,使BM BP =24,连接MP ,证明△BMP ∼△BPD ,在BC 上做点N ,使BN BP=12,连接NP ,证明△BNP ∼△BPC ,接着推导出2PC -PD =22MN ,最后证明△BMN ∼△BCD ,即可求解.【详解】解法1如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,∴∠PDM =45,DM =PM =22PD ,∵四边形ABCD 正方形∴∠BDC =45°,DB DC=2又∵∠PDM =∠PDB +MDB ,∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ,DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为:2.解法2如图:连接BD 、BP 、PC根据题意正方形ABCD 的边长为4,⊙B 的半径为2∴BP =2,BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ,使BM BP=24,则BM =22,连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ,BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24,则PD =22PM ∵BP BC =24=12在BC 上做点N ,使BN BP=12,则BN =1,连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ,BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12,则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ,BM BC =224=28,BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为:2.【点睛】本题考查正方形的性质,相似三角形,勾股定理等知识,难度较大,熟悉以上知识点运用是解题关键.15(2023秋·广东广州·九年级统考期末)如图,四边形ABCD 中,AB ∥CD ,AC ⊥BC ,∠DAB =60°,AD =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则△MBC 面积的最小值为.【答案】63-4【分析】取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则OM +ME ≥OF ,通过计算得出当O ,M ,E 三点共线时,ME 有最小值,求出最小值即可.【详解】解:如图,取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则13OM +ME ≥OF ,∵AB ∥CD ,∠DAB =60°,AD =CD =4,∴∠ADC =120°,∵AD =CD ,∴∠DAC =30°,∴∠CAB =30°,∵AC ⊥BC ,∴∠ACB =90°∴∠B =90°-30°=60°,∴∠B =∠DAB ,∴四边形ABCD 为等腰梯形,∴BC =AD =4,∵∠AMD =90°,AD =4,OA =OD ,∴OM =12AD =2,∴点M 在以点O 为圆心,2为半径的圆上,∵AB ∥CD ,∴∠GCF =∠B =60°,∴∠DGO =∠CGF =30°,∵OF ⊥BC ,AC ⊥BC ,∴∠DOG =∠DAC =30°=∠DGO ,∴DG =DO =2,∴OG =2OD ⋅cos30°=23,GF =3,OF =33,∴ME ≥OF -OM =33-2,∴当O ,M ,E 三点共线时,ME 有最小值33-2,∴△MBC 面积的最小值为=12×4×33-2 =63-4.【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点,点M 位置的确定是解题关键.16(2023春·全国·八年级专题练习)如图,在等边△ABC 中,BD ⊥AC 于D ,AD =3cm .点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ,点M 为线段BD 上一动点,连接PM ,QM ,则PM +QM 的最小值为cm .【答案】5【分析】如图所示,作点P 关于BD 的对称点P ,且点P 在BC 上,则PM +QM =P M+QM ,当P ,M ,Q 在同一条直线上时,有最小值,证明四边形PP QA 是平行四边形,P Q =AP =AB -BP ,由此即可求解.【详解】解:如图所示,作点P 关于BD 的对称点P ,∵△ABC 是等边三角形,BD ⊥AC ,∴∠ABD =∠DBC =12∠ABC =12×60°=30°,14∴点P 在BC 上,∴P M =PM ,则PM +QM =P M +QM ,当P ,M ,Q 在同一条直线上时,有最小值,∵点P 关于BD 的对称点P ,∠ABD =∠DBC =30°,∴PP ⊥BM ,BP =BP =1cm ,∴∠BP P =60°,∴△BPP 是等边三角形,即∠BP P =∠C =60°,∴PP ∥AC ,且PP =AQ =1cm ,∴四边形PP QA 是平行四边形,∴P Q =AP =AB -BP ,在Rt △ABD 中,∠ABD =30°,AD =3,∴AB =2AD =2×3=6,∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5,故答案为:5.【点睛】本题主要考查动点与等边三角形,对称-最短路径,平行四边形的判定和性质的综合,理解并掌握等边三角形得性质,对称-最短路径的计算方法,平行四边形的判定和性质是解题的关键.17(2022秋·山东菏泽·九年级校考阶段练习)如图,在周长为12的菱形ABCD 中,DE =1,DF =2,若P 为对角线AC 上一动点,则EP +FP 的最小值为.【答案】3【分析】作F 点关于BD 的对称点F ,连接EF 交BD 于点P ,则PF =PF ,由两点之间线段最短可知当E 、P 、F 在一条直线上时,EP +FP 有最小值,然后求得EF 的长度即可.【详解】解:作F 点关于BD 的对称点F ,则PF =PF ,连接EF '交BD 于点P .∴EP +FP =EP +F P .由两点之间线段最短可知:当E 、P 、F '在一条直线上时,EP +FP 的值最小,此时EP +FP =EP +F P =EF .∵四边形ABCD 为菱形,周长为12,∴AB =BC =CD =DA =3,AB ∥CD ,∵AF =2,AE =1,∴DF =AE =1,∴四边形AEF D 是平行四边形,∴EF =AD =3.∴EP +FP 的最小值为3.故答案为:3.【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题,明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键.18(2023春·上海·八年级专题练习)如图,直线y =x +4与x 轴,y 轴分别交于A和B ,点C 、D 分别为线段AB 、OB 的中点,P 为OA 上一动点,当PC +PD 的值最小时,点P 的坐标为.15【答案】(-1,0)【分析】直线y =x +4与x 轴,y 轴分别交于A 和B ,可求出点A ,B 的坐标,点C 、D 分别为线段AB 、OB 的中点,可求出点C 、D 的坐标,作点C 关于x 轴的对称点C ,连接C D 与x 轴的交点就是所求点P 的坐标.【详解】解:直线y =x +4与x 轴,y 轴分别交于A 和B ,∴当y =0,x =-4,即A (-4,0);当x =0,y =4,即B (0,4),∵点C 、D 分别为线段AB 、OB 的中点,∴C (-2,2),D (0,2),如图所示,过点C 关于x 轴的对称点C,∴C (-2,-2),∴直线C D 的解析式为:y =2x +2,当y =0,x =-1,即P (-1,0),故答案为:(-1,0).【点睛】本题主要考查一次函数与最短线段的综合,掌握对称中最短线段的解题方法是解题的关键.19(2023秋·黑龙江鸡西·九年级统考期末)如图,抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,在其对称轴上有一动点M ,连接MA ,MC ,AC ,则△MAC 周长的最小值是.【答案】32+10【分析】根据“将军饮马”模型,先求出A 1,0 ,B 3,0 ,C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,从而C △MAC =CA +CM +MA =CA +CM +MB ,AC =OA 2+OC 2=10,则△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,从而得到CB =OC 2+OB 2=32,即可得到答案.【详解】解:∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,16∴当y =0时,0=x 2-4x +3解得x =1或x =3,即A 1,0 ,B 3,0 ;当x =0时,y =3,即C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,即MA =MB ,∴C △MAC =CA +CM +MA =CA +CM +MB ,∵AC =OA 2+OC 2=10,∴△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,∵CB =OC 2+OB 2=32,∴△MAC 周长的最小值为CA +CB =32+10,故答案为:32+10.【点睛】本题考查动点最值问题与二次函数综合,涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识,熟练掌握动点最值的常见模型是解决问题的关键.20(2023秋·浙江温州·九年级校考期末)如图所示,∠ACB =60°,半径为2的圆O 内切于∠ACB.P 为圆O 上一动点,过点P 作PM 、PN 分别垂直于∠ACB 的两边,垂足为M 、N ,则PM +2PN 的取值范围为.【答案】6-23≤PM +2PN ≤6+23【分析】根据题意,本题属于动点最值问题-“阿氏圆”模型,首先作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示,通过代换,将PM +2PN 转化为PN +12PM =PN +HP =NH ,得到当MP 与⊙O 相切时,MF 取得最大值和最小值,分两种情况,作出图形,数形结合解直角三角形即可得到相应最值,进而得到取值范围.【详解】解:作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示:∵PM ⊥AC ,PN ⊥CB ,∴∠PMC =∠PNC =90°,∴∠MPN =360°-∠PMC -∠PNC -∠C =120°,∴∠MPH =180°-∠MPN =60°,∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ,∴PN +12PM =PN +HP =NH ,∵MF =NH ,∴当MP 与⊙O 相切时,MF 取得最大和最小,①连接OP ,OG ,OC ,如图1所示:可得:四边形OPMG 是正方形,∴MG =OP =2,在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG +GM =2+23,在Rt △CMF 中,MF =CM ⋅sin60°=3+3,∴HN =MF =3+3,即PM +2PN =212PM +PN =2HN =6+23;②连接OP ,OG ,OC ,如图2所示:可得:四边形OPMG 是正方形,17∴MG =OP =2,由上同理可知:在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG -GM =23-2,在Rt △CMF 中,MF =CM ⋅sin60°=3-3,∴HN =MF =3-3,即PM +2PN =212PM +PN =2HN =6-23,∴6-23≤PM +2PN ≤6+23.故答案为:6-23≤PM +2PN ≤6+23.【点睛】本题考查动点最值模型-“阿氏圆”,难度较大,掌握解决动点最值问题的方法,熟记相关几何知识,尤其是圆的相关知识是解决问题的关键.3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图,已知抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,交y 轴于点C .(1)求抛物线的解析式,连接BC ,并求出直线BC 的解析式;(2)请在抛物线的对称轴上找一点P ,使AP +PC 的值最小,此时点P 的坐标是;(3)点Q 在第一象限的抛物线上,连接CQ ,BQ ,求出△BCQ 面积的最大值.【答案】(1)y =-x 2+3x +4;y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ,B 4,0 两点,代入抛物线解析式,可得到抛物线解析式,从而得到C 0,4 ,再设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入,即可求解;(2)连接BC ,PB ,根据题意可得A 、B 关于抛物线的对称轴直线x =32对称,从而得到当P 在直线AB 上三点共线时,AP +CP 的值最小,把x =32代入直线BC 的解析式,即可求解;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,可得QD =-d 2+4d ,从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8,即可求解;【详解】(1)解:(1)∵抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,∴a -b +4=016a +4b +4=0,解得:a =-1b =3 ,18∴抛物线的解析式为y =-x 2+3x +4;∵抛物线与y 轴的交点为C ,∴C 0,4 ,设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入得:4k +b =0b =4 ,解得:k =-1b =4 ,∴直线BC 的解析式为y =-x +4;(2)如图,连接BC ,PB ,∵y =-x 2+3x +4=-x -32 2+74,∴抛物线的对称轴为直线x =32,根据题意得:A 、B 关于抛物线的对称轴直线x =32对称,∴AP =BP ,∴AP +CP =BP +CP ≥BC ,即当P 在直线AB 上时,AP +CP 的值最小,∴当x =32时,y =-32+4=52,∴P 32,52 ,故答案是:32,52 ;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,∴QD =-d 2+3d +4 --d +4 =-d 2+4d ,∵B 4,0 ,∴OB =4,∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8,当d =2时,S ΔBCQ 取最大值,最大值为8,∴△BCQ 的最大面积为8;【点睛】本题主要考查了二次函数的图像和性质,利用数形结合思想和分类讨论思想是解题的关键.22(2023秋·江苏淮安·八年级统考期末)如图1,直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,过点B 的直线交x 轴负半轴于点C -3,0 .(1)请直接写出直线BC 的关系式:(2)在直线BC 上是否存在点D,使得S △ABD =S △AOD 若存在,求出点D 坐标:若不存请说明理由;(3)如图2,D 11,0 ,P 为x 轴正半轴上的一动点,以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ,连接QA ,QD .请直接写出QB -QD 的最大值:.19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时,S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点,可求出点B 的坐标,再用待定系数法即可求解;(2)设D (a ,2a +6),分别用含a 的式子表示出出S △AOD ,S △ABD ,由此即可求解;(3)△BPQ 是等腰直角三角形,设P (m ,0)(m >0),可表示出QB ,再证Rt △BOP ≌Rt △PTQ (AAS ),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值,可求得点R 的坐标,根据勾股定理即可求解.【详解】(1)解:∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,令x =0,则y =6,∴B (0,6),且C -3,0 ,设直线BC 的解析式为y =kx +b ,∴b =6-3k +b =0,解得,k =2b =6 ,∴直线BC 的解析式为y =2x +6,故答案为:y =2x +6.(2)解:由(1)可知直线BC 的解析式为y =2x +6,直线AB 的解析式为y =-x +6,∴A (6,0),B (0,6),C (-3,0),∴OA =6,BO =6,OC =3,如图所示,点D 在直线BC 上,过点D 作DE ⊥x 轴于E ,∴设D (a ,2a +6),E (a ,0),∴S △ABC =12AC ·OB =12×(6+3)×6=27,S △ADC =12AC ·DE =12×(6+3)×a =92a ,S △AOD =12OA ·DE =12×6×a =3a ,∴S △ABD =S △ABC -S △ADC =27-92a ,若S △ABD =S △AOD ,则27-92a =3a ,当a >0时,27-92a =3a ,解得,a =185,即D 185,665 ;当a <0时,27+92a =-3a ,解得,a =-185,即D -185,-65 ;综上所述,当D 185,665 或D -185,-65时,S △ABD =S △AOD .(3)解:已知A (6,0),B (0,6),D (11,0),设P (m ,0)(m >0),∴在Rt △BOP 中,OB =6,OP =m ,∵△BPQ 是等腰直角三角形,∠BPQ =90°,∴BP =QP ;如图所示,过点Q 作QT ⊥x 轴于T ,20在Rt △BOP ,Rt △PTQ 中,∠BOP =∠PTQ =90°,∠BPO +∠QPA =∠QPA +∠PQT =90°,∴∠BPO =∠PQT ,∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP,∴Rt △BOP ≌Rt △PTQ (AAS ),∴OP =TQ =m ,OB =PT =6,∴AT =OP +PT -OA =m +6-6=m ,∴AT =QT ,且QT ⊥x 轴,∴△ATQ 是等腰直角三角形,∠QAT =45°,则点Q 的轨迹在射线AQ 上,如图所示,作点D 关于直线AQ 的对称点R,连接QR ,BR ,AR ,A (6,0),B (0,6),D (11,0),∵△ATQ 是等腰直角三角形,即∠QAT =45°,根据对称性质,∴∠QAR =45°,∴RA ⊥x 轴,且△DQA ≌△RQA ,∴AR =AD =11-6=5,则R (6,5),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值;∴由勾股定理得:BR =62+(6-5)2=37,故答案为:37.【点睛】本题主要考查一次函数,几何的综合,掌握待定系数法求解析式,将军饮马问题,等腰直角三角形的性质,勾股定理是解题的关键.23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中,∠B =60°.(1)如图1,若AC >BC ,CD 平分∠ACB 交AB 于点D ,且AD =3BD .证明:∠A =30°;(2)如图2,若AC <BC ,取AC 中点E ,将CE 绕点C 逆时针旋转60°至CF ,连接BF 并延长至G ,使BF =FG ,猜想线段AB 、BC 、CG 之间存在的数量关系,并证明你的猜想;(3)如图3,若AC =BC ,P 为平面内一点,将△ABP 沿直线AB 翻折至△ABQ ,当3AQ +2BQ +13CQ 取得最小值时,直接写出BPCQ的值.【答案】(1)见解析(2)BC =AB +CG ,理由见解析(3)213+33913【分析】(1)过点D 分别作BC ,AC 的垂线,垂足为E ,F ,易得DE =DF ,由∠B =60°,可得DE =DF =32BD ,由AD =3BD ,求得sin A =DE AD=12,可证得∠A =30°;(2)延长BA ,使得BH =BC ,连接EH ,CH ,易证△BCH 为等边三角形,进而可证△BCF ≌△HCE SAS ,可得BF =HE ,∠BFC =∠HEC ,可知∠AEH =∠CFG ,易证得△AEH ≌△CFG SAS ,可得AH =CG ,由BC =BH =AB +AH =AB +CG 可得结论;(3)由题意可知△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,可得CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,可知△ACQ ∽△MCN ,可得MN =32AQ ,由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ,N 都在线段BM 上时,3AQ +2BQ+13CQ 有最小值,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,可得CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,可证△CBR ∽△MBT ,得BR CR =BT MT ,设BC =a 由等边三角形的性质,可得CM =32a ,进而可得CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,结合BR CR=BTMT 可得:BQ +213CQ 313CQ =a +334a 34a ,可得BQ CQ =213+33913,由翻折可知,BP =BQ ,可求得BP CQ的值.【详解】(1)证明:过点D 分别作BC ,AC 的垂线,垂足为E ,F ,∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,∴DE =DF ,又∵∠B =60°,∴DE =BD ⋅sin60°=32BD ,则DE =DF =32BD ,又∵AD =3BD ,∴sin A =DE AD =32BD3BD=12,∴∠A =30°;(2)BC =AB +CG ,理由如下:延长BA ,使得BH =BC ,连接EH ,CH ,∵∠ABC =60°,BH =BC ,∴△BCH 为等边三角形,∴CB =CH ,∠BCH =60°,∵CE 绕点C 逆时针旋转60°至CF ,∴CE =CF ,∠ECF =60°,则∠BCH -∠ACB =∠ECF -∠ACB ,∴∠ECH =∠FCB ,∴△BCF ≌△HCE SAS ,∴BF =HE ,∠BFC =∠HEC ,则∠AEH =∠CFG ,∵BF =FG ,∴BF =HE =FG ,又∵E 为AC 中点,∴AE =CE =CF ,∴△AEH ≌△CFG SAS ,∴AH =CG ,∴BC =BH =AB +AH =AB +CG ;(3)∵∠ABC =60°,AC =BC ,∴△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,则CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,∴sin ∠CQN =CN QN =313,cos ∠CQN =CQ QN =213,则∠ACM =∠QCN =90°,∴∠ACM -∠ACN =∠QCN -∠ACN ,则∠ACQ =∠MCN∴△ACQ ∽△MCN ,∴MN AQ =CM CA=32,即:MN =32AQ ,∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即:点Q ,N 都在线段BM 上时,3AQ +2BQ +13CQ 有最小值,如下图,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,则∠BRC =∠BTM =90°,CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,又∵∠CBR =∠MBT ,∴△CBR ∽△MBT ,∴BR CR=BT MT ,∵△ABC 是等边三角形,设BC =a ∴∠ACB =60°,AC =BC =a ,则CM =32a ,∵∠ACM =90°,∴∠MCT =30°,则CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,则由BR CR=BT MT 可得:BQ +213CQ 313CQ =a +334a34a ,整理得:133BQ CQ +23=4+333,得BQ CQ=213+33913,由翻折可知,BP =BQ ,∴BP CQ =BQ CQ=213+33913.【点睛】本题属于几何综合,考查了解直角三角形,等边三角形的判定及性质,全等三角形的判定及性质,相似三角形的判定及性质,旋转的性质以及费马点问题,掌握费马点问题的解决方法,添加辅助线构造全等三角形和相似三角形是解决问题的关键.24(2023春·江苏·八年级专题练习)定义:既相等又垂直的两条线段称为“等垂线段”,如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D 、E 分别在边AB 、AC 上,AD =AE ,连接DE 、DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点,且连接PM 、PN .(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”.(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置,连接BD ,CE ,试判断PM 与PN 是否为“等垂线段”,并说明理由.(3)拓展延伸把△ADE 绕点A 在平面内自由旋转,若DE =2,BC =4,请直接写出PM 与PN 的积的最大值.。
2024年中考数学压轴题型(广东专用)专题04特殊平行四边形中全等相似与最值问题(学生版)

专题04特殊平行四边形中全等相似与最值问题通用的解题思路:一、四边形与全等相似1.三角形与全等之六大全等模型:(1)一线三等角模型锐角一线三等角(2)手拉手模型(3)半角模型(4)倍长中线模型模型(6)雨伞等模型(5)平行线中等模型2.三角形与相似之四大相似模型:(1)A字模型(3)手拉手模型(2)8字模型(4)一线三等角模型B 二、四边形线段最值问题囹 1 C B D 02B (1)将军饮马模型两定一动模型一定两动模型两线段相减的最大值模型(三点共线)• B(2)费马点模型:将边以A 为顶点逆时针旋转60。
,得到AQE,连接P0则^APQ 为等边三角形,PA=PQ O1. (2023-r 东深圳•中考真题)(1)如图,在矩形ABCD 中,E 为AD 边上一点,连接BE,①若= 过C 作CFLBE 交BE 于点、F ,求证:AABE^AFCB ;②若S 矩形倔8 = 2。
时,则BECF=(2)如图,在菱形ABCD 中,cosA = |,过。
作CE1AB 交A8的延长线于点E,过E 作EF _LAD 交AD 于点、F ,若S 菱形*d =24时,求EF BC 的值.(3)如图,在平行四边形ABCD 中,匕4 = 60。
,AB = 6, AD=5,点E 在CD 上,且CE = 2,点F 为BC 上一点,连接时,过E 作EGLEF 交平行四边形ABCD 的边于点G,若EF ・EG = 70时,请直接写出AG 的长.D,E E a C C A B AB备用图2.(2022广东广州•中考真题)如图,在菱形ABCQ中,0BAD=120°,AB=6,连接8Q.⑴求BQ的长;⑵点E为线段BQ上一动点(不与点B,。
重合),点E在边AQ上,且BE二也DF,①当CE±AB时,求四边形的面积;②当四边形的面积取得最小值时,CE+右CT的值是否也最小?如果是,求CE+也CF的最小值;如果不是,请说明理由.题型一特殊平行四边形中全等相似计算1.(2024-P东汕头•一模)(1)如图1,在矩形ABCD中,E为AD边上一点,连接8E,①若BE=BC,过。
精编中考数学压轴题动点产生的定值与最值问题8个专题讲解

中考数学压轴题动点产生的定值与最值问题8个专题讲解目录第 1 讲角为定值的常规解法第 2 讲角为定值的高级解法第3讲边为定值的动点问题第4讲线段的和或差为定值的动点问题第5讲比值为定值的动点问题第6讲乘积为定值的动点问题第7讲面积为定值的动点问题第8讲动点产生的几何最值问题第1讲角为定值的常规解法【几何法证明角为定值】(1)三角形内角和定理(2)三角形外角定理(3)等腰三角形底角相等(4)直角三角形两锐角互余(5)平行线的同位角相等、内错角相等、同旁内角互补(6)平行四边形的对角相等、邻角互补(7)等腰梯形底角相等(8)圆所涉及的角的关系:圆心角、圆周角、弦切角定理等【例】如图,平面内两条互相垂直的直线相交于点O,∠MON=90°,点A、B分别在射线O M、ON 上移动,AC是△BAO的角平分线,BD为∠ABN的角平分线,AC与B D的反向延长线交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB 的度数;若发生变化,求出变化范围。
、【例】如图所示,O的直径A B=4,点P是A B延长线上的一点,过P点作O的切线,切点为C,连接AC.(1)若∠CPA=30°,求P C的长;(2)若点P在A B的延长线上运动,∠CPA的平分线交A C于点M,你认为∠CMP 的大小是否发生变化?若变化,请说明理由;若不变化,求出∠CMP 的大小。
【代数法求角为定值】一般在直角坐标系中,可以用坐标的方法表示出边或角,从而求解具体角为定值的问题。
【例】如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以毎秒1个单位长的速度运动t 秒(t>0),抛物线y = ax2 + bx + c 经过点O和点P,已知矩形A BCD的三个顶点为A(1,0),B(1,−5),D(4,0).(1)求c,b (用含t的代数式表示):(2)当4<t<5时,设抛物线分别与线段A B,CD交于点M,N.①在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP 的值;②求△MPN的面积S与t的函数关系式,并求t为何值时,S=218;(3)在矩形A BCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”。
中考压轴题突破:几何最值问题大全(将军饮马、造桥选址、胡不归、阿波罗尼斯圆等)

中考压轴题突破:几何最值问题大全(将军饮马、造桥选址、胡不归、阿波罗尼斯圆等)一、基本图形所有问题的老祖宗只有两个:①[定点到定点]:两点之间,线段最短;②[定点到定线]:点线之间,垂线段最短。
由此派生:③[定点到定点]:三角形两边之和大于第三边;④[定线到定线]:平行线之间,垂线段最短;⑤[定点到定圆]:点圆之间,点心线截距最短(长);⑥[定线到定圆]:线圆之间,心垂线截距最短;⑦[定圆到定圆]:圆圆之间,连心线截距最短(长)。
余不赘述,下面仅举一例证明:[定点到定圆]:点圆之间,点心线截距最短(长)。
已知⊙O半径为r,AO=d,P是⊙O上一点,求AP的最大值和最小值。
证明:由“两点之间,线段最短”得AP≤AO+PO,AO≤AP+PO,得d-r≤AP≤d+r,AP最小时点P在B处,最大时点P在C处。
即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。
(可用“三角形两边之和大于第三边”,其实质也是由“两点之间,线段最短”推得)。
上面几种是解决相关问题的基本图形,所有的几何最值问题都是转化成上述基本图形解决的。
二、考试中出现的问题都是在基本图形的基础上进行变式,如圆与线这些图形不是直接给出,而是以符合一定条件的动点的形式确定的;再如过定点的直线与动点所在路径不相交而需要进行变换的。
类型分三种情况:(1)直接包含基本图形;(2)动点路径待确定;(3)动线(定点)位置需变换。
(一)直接包含基本图形例 1.在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是。
(二)动点路径待确定例2.,如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B 重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是。
(三)动线(定点)位置需变换线段变换的方法:(1)等值变换:翻折、平移;(2)比例变换:三角、相似。
压轴题12关于二次函数性质与最值的推理计算综合问题-2023年中考数学压轴题专项训练(全国

2023年中考数学压轴题专项训练压轴题12关于二次函数性质与最值的推理计算综合问题例1.(2023•海曙区一模)对于抛物线y=ax2﹣4x+3(a>0).(1)若抛物线过点(4,3).①求顶点坐标;②当0≤x≤6时,直接写出y的取值范围为;(2)已知当0≤x≤m时,1≤y≤9,求a和m的值.例2.(2023春•上城区校级月考)设二次函数y=ax2+4ax+4a+1,a为常数,且a<0.(1)写出该函数的对称轴和顶点坐标.(2)若该函数图象经过点P(n,y1),Q(n+1,y2),当n≥1时,试比较y1和y2的大小关系.(3)若该函数图象经过点P(x1,y1),Q(x2,y2),设n≤x1≤n+1,当x2≥3时均有y1≥y2,请求出实数n的取值范围.例3.(2023春•顺义区校级月考)在平面直角坐标系xOy中,点A(x1,y1)、点B(x2,y2)为抛物线y=ax2﹣2ax+a(a≠0)上的两点.(1)求抛物线的对称轴;(2)当﹣2<x1<﹣1且1<x2<2时,试判断y1与y2的大小关系并说明理由;(3)若当t﹣1<x1<t且t+1<x2<t+2时,存在y1=y2,求t的取值范围.例4.(2023春•柯桥区月考)如图,已知二次函数y=x2+ax+a+1的图象经过点P(﹣2,3).(1)求a的值和图象的顶点坐标.(2)点Q(m,n)在该二次函数图象上.①当m=2时,求n的值.②当m≤x≤m+3时,该二次函数有最小值11,请根据图象直接写出m的值.1.(2023•深圳模拟)对于“已知x+y=1,求xy的最大值”这个问题,小明是这样求解的:∵x+y=1,∴y=1﹣x,∴xy=x(1−x)=x−x2=−(x−12)2+14;∴xy≤14,所以xy的最大值为14.请你按照这种方法计算:当2n+m=4(m>0,n>0)时,2m +1n的最小值.2.(2022秋•诸暨市期末)已知函数y=x2+bx+c(b,c为常数)的图象经过点(0,3),(6,3).(1)求b,c的值;(2)当0≤x≤4时,求y的最大值与最小值之差;(3)当k﹣4≤x≤k时,若y的最大值与最小值之差为8,求k的值.3.(2022秋•漳州期末)已知二次函数y=x2+bx+c(b、c为常数)的图象经过点(0,3)、(1,﹣2).(1)求b、c的值;(2)当3≤x≤m时,若y的最大值与最小值之和为1,求m的值.4.(2023•来安县一模)已知关于x的二次函数y1=(x+2a)(x﹣2b)(其中a,b为常数).(1)若a=1,该二次函数的图象经过点(﹣1,3),求b;(2)若a=b﹣2.①若(﹣1,m)和(3,n)是该二次函数图象上的点,比较m和n的大小;②设一次函数y2=﹣x+2b,当函数y=y1+y2的图象经过点(c,0)时,探索b与c之间的数量关系,并加以推理.5.(2023•北仑区一模)抛物线y=(x+1)(x﹣t)(t为常数)经过点A(4,5),B(m,n).(1)求t的值;(2)若n<5,求m的取值范围.6.(2023•秦皇岛一模)已知y =ax 2+bx +c 过点A (2,0),B (3n ﹣4,y 1),C (5n +6,y 2)三点,对称轴是直线x =1,关于x 的方程ax 2+bx +c =x 有两个相等的实数根.(1)求抛物线的解析式;(2)若B 点在直线x =1的左侧,C 点在直线x =1的右侧,且y 1>y 2,求n 的取值范围;(3)若n <﹣5,试比较y 1与y 2的大小.7.(2022•无为市三模)已知抛物线y =a (x ﹣h )2+k 经过点A (1,y 1),B (2,y 2),C (3,y 3),连接AB 、BC ,令AB BC =λ.(1)若a >0,h =2,求λ的值;(2)若h =1,λ=√55,求a 的值.8.(2022•平谷区二模)在平面直角坐标系xOy 中,点(﹣1,y 1)、(1,y 2)、(3,y 3)是抛物线y =x 2+bx +1上三个点.(1)直接写出抛物线与y 轴的交点坐标;(2)当y 1=y 3时,求b 的值;(3)当y 3>y 1>1>y 2时,求b 的取值范围.9.(2023•西城区校级模拟)在平面直角坐标系xOy中,已知抛物线y=x2﹣2ax﹣3.(1)求该抛物线的对称轴(用含a的式子表示);(2)A(x1,y1),B(x2,y2)为该抛物线上的两点,若x1=1﹣2a,x2=a+1,且y1>y2,求a的取值范围.10.(2022•海淀区校级模拟)二次函数y=ax2﹣2atx+c(a≠0)的图象经过A(﹣4,y1),B(﹣2,y2),C (1,y3),D(3,y4)四点.(1)求二次函数的对称轴(用含的代数式表示);(2)已知t=﹣1,若y2y3<0,请直接判断y1y4的正负性,即y1y40(填“>”或“<”);(3)若y3>y2>y4,求t的取值范围并判断y1,y2的大小关系.11.(2021•西湖区校级二模)已知:二次函数y=x2+bx﹣3的图象经过点P(﹣2,5).(1)求b的值;(2)设P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)均在该函数图象上,①当m=4时,y1、y2、y3能否作为同一个三角形三边的长?请说明理由;②当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长,请说明理由.12.(2021•安徽二模)二次函数y=ax2+bx+3(a≠0)的图象经过A(﹣1,0),B(3,0)两点,交y轴于点C.(1)求a,b的值;(2)点P为二次函数y=ax2+bx+3(a≠0)的图象上一动点,且位于第一象限,设△ABP的面积为S1,△CBP的面积为S2,记w=S1﹣2S2+1,求w的最小值.13.(2023•龙湾区一模)如图,已知点C为二次函数y=x2﹣4x+1的顶点,点P(0,n)为y轴正半轴上一点,过点P作y轴的垂线交函数图象于点A,B(点A在点B的左侧).点M在射线PB上,且满足PM =1+n.过点M作MN⊥AB交抛物线于点N,记点N的纵坐标为y N.(1)求顶点C的坐标.(2)①若n=3,求MB的值.②当0<n≤4时,求y N的取值范围.14.(2022•香洲区校级三模)直线y=−12x+1与x,y轴分别交于点A,B,抛物线的解析式为y=2x2﹣4ax+2a2+a.(1)求出点A,B的坐标,用a表示抛物线的对称轴;(2)若函数y=2x2﹣4ax+2a2+a在3≤x≤4时有最大值为a+2,求a的值;(3)取a=﹣1,将线段AB平移得到线段A'B',若抛物线y=2x2﹣4ax+2a2+a与线段A'B'有两个交点,求直线A'B'与y轴交点的纵坐标的取值范围.<0)上.(1)若m=4,n=﹣12,求抛物线的对称轴和顶点坐标;(2)已知点A(1,y1),B(4,y2)在该抛物线上,且mn=0.①比较y1,y2,0的大小,并说明理由;②将线段AB沿水平方向平移得到线段A'B',若线段A'B'与抛物线有交点,直接写出点A'的横坐标x的取值范围.16.(2022•博望区校级一模)已知二次函数y=ax2﹣2ax﹣3的图象经过点A(﹣1,0).(1)求a的值;(2)若点B(m,n)与点C(m+1,n+1)都在抛物线y=x2﹣2ax﹣3上,求m+n的值;(3)若一次函数y=(k+1)x+k+1的图象与二次函数y=ax2﹣2ax﹣3的图象的交点坐标是(x1,y1),(x2,y2)且x1<0<x2时,求函数w=y1+y2的最小值.17.(2022•海淀区校级模拟)在平面直角坐标系中,设二次函数y=(x+a)(x﹣a﹣1)(a>0),(1)求二次函数对称轴;(2)若当﹣1≤x≤3时,函数的最大值为4,求此二次函数的顶点坐标.(3)抛物线上两点M(x1,y1),N(x2,y2)若对于t<x1<t+1,t+2<x2<t+3都有y1≠y2,求t的取值范围.﹣2ax+a(a≠0)上的两点.(1)求抛物线的对称轴;(2)当﹣2<x1<﹣1且1<x2<2时,试判断y1与y2的大小关系并说明理由;(3)若当t<x1<t+1且t+2<x2<t+3时,存在y1=y2,求t的取值范围.19.(2022•萧山区二模)在平面直角坐标系中,已知二次函数y=ax2+(a﹣1)x﹣1.(1)若该函数的图象经过点(1,2),求该二次函数图象的顶点坐标.(2)若(x1,y1),(x2,y2)为此函数图象上两个不同点,当x1+x2=﹣2时,恒有y1=y2,试求此函数的最值.(3)当a<0且a≠﹣1时,判断该二次函数图象的顶点所在象限,并说明理由.20.(2022•盈江县模拟)抛物线C1:y=x2+bx+c的对称轴为x=1,且与y轴交点的纵坐标为﹣3.(1)求b,c的值;(2)抛物线C2:y=﹣x2+mx+n经过抛物线C1的顶点P.①求证:抛物线C2的顶点Q也在抛物线C1上;②若m=8,点E是在点P和点Q之间抛物线C1上的一点,过点E作x轴的垂线交抛物线C2于点F,求EF长度的最大值.。
二次函数与面积最值定值问题(六大类型)-2023年中考数学压轴题(解析版)

二次函数与面积最值定值问题(六大类型)1.考向分析题型一:二次函数与三角形面积最值问题1如图,已知抛物线y =12x 2+bx 过点A (-4,0)、顶点为B ,一次函数y =12x +2的图象交y 轴于M ,对称轴与x 轴交于点H .(1)求抛物线的表达式;(2)已知P 是抛物线上一动点,点M 关于AP 的对称点为N .①若点N 恰好落在抛物线的对称轴上,求点N 的坐标;②请直接写出△MHN 面积的最大值.【解析】解:(1)∵抛物线y =12x 2+bx 过点A (-4,0),∴12×(-4)2-4b =0,解得:b =2,∴该抛物线的表达式为y =12x 2+2x ;(2)①∵y =12x 2+2x ,∴抛物线对称轴为直线x =-22×12=-2,∵对称轴与x 轴交于点H ,∴H (-2,0),∵A (-4,0),∴AH =2,∵直线y =12x +2交y 轴于M ,∴M (0,2),∴AM 2=OA 2+OM 2=42+22=20,设N (-2,n ),则NH =|n |,如图1、图2,∵M 、N 关于直线AP 对称,∴AN =AM ,即AN 2=AM 2,∴22+n 2=20,∴n =±4,∴点N 的坐标为(-2,-4)或(-2,4);②如图,连接MH ,以点A 为圆心,AM 为半径作⊙A ,过点A 作AN ⊥MH 于点F ,交⊙A 于点N ,则AN =AM ,在Rt △AMO 中,OM =2,OA =4,∴AM =OA 2+OM 2=42+22=25,∴AN =25,∵OH =OM =2,∠HOM =90°,∴△HOM 是等腰直角三角形,∠MHO =45°,MH =22,∴∠AHF =∠MHO =45°,在Rt △AFH 中,AH =OA -OH =4-2=2,∴AF =AH ×sin45°=2×22=2,∴NF =AN +AF =25+2,∴S △MHN =12MH •NF =12×22×(25+2)=210+2,故△MHN 面积的最大值为210+2.题型二:二次函数与三角形面积等积问题2如图,等腰直角三角形OAB 的直角顶点O 在坐标原点,直角边OA ,OB 分别在y 轴和x 轴上,点C 的坐标为(3,4),且AC 平行于x 轴.(1)求直线AB 的解析式;(2)求过B ,C 两点的抛物线y =-x 2+bx +c 的解析式;(3)抛物线y =-x 2+bx +c 与x 轴的另一个交点为D ,试判定OC 与BD 的大小关系;(4)若点M 是抛物线上的动点,当△ABM 的面积与△ABC 的面积相等时,求点M 的坐标.【解析】解:(1)∵点C 的坐标为(3,4),且AC 平行于x 轴,∴点A 的坐标为(0,4)且OA =4,∵△OAB 是等腰直角三角形,∠AOB =90°,∴OB =OA =4,∵点B 的坐标为(4,0),设直线AB的解析式为:y=mx+n,由题意得4m+n=0n=4,解得:m=-1n=4,∴直线AB的解析式为:y=-x+4;(2)∵抛物线y=-x2+bx+c过B,C两点,∴-16+4b+c=0-9+3b+c=4,解得:b=3c=4,∴抛物线的解析式为:y=-x2+3x+4;(3)BD=OC;理由:∵抛物线的解析式为y=-x2+3x+4=-x-322+52,∴抛物线的对称轴直线为x=32,∵点B的坐标为(4,0),点B与点D关于对称轴对称,∴点D的坐标为(-1,0),∴BD=4-(-1)=5,∵点C的坐标为(3,4),∴OC=32+42=5,∴BD=OC;(4)∵点C的坐标为(3,4),且AC平行于x轴,∴AC=3,∴S△ABC=12AC•y C=12×3×4=6,当点M在直线AB的上方时,如图所示,过点M作MN∥y轴,交直线AB于点N,设M的坐标为(t,-t2+3t+4),则N的坐标为(t,-t+4),∴MN=-t2+3t+4-(-t+4)=-t2+4t,∴S△AMB=12MN•x B=12×(-t2+4t)×4=-2t2+8t,∵△ABM的面积与△ABC的面积相等,∴-2t2+8t=6,解得:t=1或t=3(舍,该点为点C),此时M的坐标为(1,6)或(3,4);当点M在直线AB的下方时,如图所示,过点M作MN∥x轴,交直线AB于点N,设M的坐标为(t,-t2+3t+4),则N的坐标为(t2-3t,-t2+3t+4),∴MN=t2-3t-t=t2-4t,∴S△ABM=12MN•y A=12×(t2-4t)×4=2t2-8t,∵△ABM的面积与△ABC的面积相等,∴2t2-8t=6,解得:t=2±7,此时M的坐标为(2+7,-1-7)或(2-7,7-1);综上可得,M的坐标为(2+7,-1-7)或(2-7,7-1)或(1,6).题型三:二次函数与四边形面积最值问题3如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C.已知A(3,0),该抛物线的对称轴为直线x=1.(1)求该抛物线的函数表达式;(2)求点B、C的坐标;(3)将线段BC平移,使得平移后线段的一个端点在这条抛物线上,另一个端点在x轴上,若将点B、C平移后的对应点分别记为点D、E,求以B、C、D、E为顶点的四边形面积的最大值.【解析】解:(1)∵抛物线对称轴为直线x=-b-2=1,∴b=2,∴y=-x2+2x+c,将(3,0)代入y=-x2+2x+c得0=-9+6+c,解得c=3,∴y=-x2+2x+3.(2)∵抛物线对称轴为直线x=1,点A坐标为(3,0),∴由抛物线对称性可得点B坐标为(-1,0),将x=0代入y=-x2+2x+3得y=3,∴点C坐标为(0,3).(3)如图,可得图2中四边形面积最大,∵BC∥DE且BC=DE,图1图2图3∵y C-y B=y E-y D,∴y D=-3,将y=-3代入y=-x2+2x+3得-3=-x2+2x+3,解得x1=1-7(舍),x2=1+7,∴点E横坐标为1+7+1=2+7,∴BE=2+7+1=3+7,∴S四边形BDEC =12BE•y C+12BE•|y D|=12×(3+7)×3+12×(3+7)×3=9+37.题型四:二次函数与面积分割问题4已知抛物线y=x2+4mx+4m2-4m-3的顶点C在定直线l上.(1)求C点的坐标(用含m的式子表示);(2)求证:不论m为何值,抛物线与定直线l的两交点间的距离d恒为定值;(3)当抛物线的顶点C在y轴上,且与x轴交于A,B两点(点A在点B的左侧)时,是否存在直线n满足以下三个条件:①n与抛物线相交于点M,N(点M在点N的左侧),且与线段AC交于点P;②∠APN=2∠ACO;③n将△ABC的面积分成1:2的两部分.若存在,求出直线n的解析式;若不存在,请说明理由.【解析】(1)解:∵y=x2+4mx+4m2-4m-3=(x+2m)2-4m-3,∴顶点C(-2m,-4m-3);(2)证明:∵C(-2m,-4m-3),∴C点在直线y=2x-3上,∴定直线l为y=2x-3,联立方程组y=2x-3y=x2+4mx+4m2-4m-3 ,解得x=-2my=-4m-3或x=2-2my=-4m+1,∴两个交点分别为(-2m,-4m-3),(2-2m,-4m+1),∴d=(2-2m+2m)2+(-4m+1+4m+3)2=25,∴抛物线与定直线l的两交点间的距离d恒为定值;(3)解:存在直线n,理由如下:∵顶点C在y轴上,∴m=0,∴y=x2-3,令y=0,则x2-3=0,解得x=3或x=-3,∴A(-3,0),B(3,0),∴AB=23,∵抛物线关于y轴对称,∴∠ACO=∠BCO,∵∠APN=2∠ACO,∴∠APN=∠ACB,∴MN ∥BC ,设直线BC 的解析式为y =kx +b ,∴b =-33k +b =0 ,解得k =3b =-3 ,∴y =3x -3,设直线MN 的解析式为y =3x +t ,直线MN 与x 轴的交点为H ,∵直线MN 将△ABC 的面积分成1:2,∴S △PAH =13S △ACB 或S △PAH =23S △ACB ,∴AH AB2=13或AH AB 2=23,∴AH 23=33或AH 23=63,解得AH =2或AH =22,∴H (2-3,0)或(22-3,0),∴直线MN 的解析式为y =3x +3-23或y =3x +3-26.题型五:二次函数与面积比问题5如图,在平面直角坐标系xOy 中,二次函数y =23x 2+bx -2的图象与x 轴交于点A (3,0),B (点B 在点A 左侧),与y 轴交于点C ,点D 与点C 关于x 轴对称,作直线AD .(1)填空:b = -43 ;(2)将△AOC 平移到△EFG (点E ,F ,G 依次与A ,O ,C 对应),若点E 落在抛物线上且点G 落在直线AD 上,求点E 的坐标;(3)设点P 是第四象限抛物线上一点,过点P 作x 轴的垂线,垂足为H ,交AC 于点T .若∠CPT +∠DAC =180°,求△AHT 与△CPT 的面积之比.【解析】解:(1)把A (3,0)代入y =23x 2+bx -2,得23×9+3b -2=0,解得b =-43;故答案为:-43;(2)如图所示:由(1)得y =23x 2-43x -2,令x =0,y =-2,∴C (0,-2),∵点D 与点C 关于x 轴对称,∴D (0,2),设直线AD :y =kx +2,把A (3,0)代入y =kx +2,得3k +2=0,解得k =-23,∴直线AD 解析式:y =-23x +2,∵将△AOC 平移到△EFG ,∴OA =EF =3,FG =OC =2,设E m ,23m 2-43m -2 ,则G m -3,-23(m -3)+2 ,F m -3,-23(m -3)+4 ,∵EF ∥x 轴,∴23m 2-43m -2=-23(m -3)2+4,解得m =-3或m =4,∴E (-3,8)或4,103;(3)如图所示:过C 作CK ⊥AD ,CQ ⊥HP ,∵OD =2,OA =3∴AD =13,∵CK ⊥AD∴CD •AO =AD •CK ,∴CK =121313,DK =81313,AK =51313,∴tan ∠CAK =CK AK=125,∵CQ ⊥HP ,∴∠CPQ +∠CPT =180°,∵∠CPT +∠DAC =180°,∴∠CPQ =∠CAK ,∴tan ∠CPQ =tan ∠CAK =125,∴CQ PQ =125,设P n ,23n 2-43n -2 ,∴PQ =23n 2-43n ,CQ =n ,∴n 23n 2-43n =125,解得n =218,∴P 218,-2932,∴CQ =218,AH =3-218=38,∵tan ∠OAC =TH AH =OC OA =23,∴TH =23AH =23×38=14,∴TP =2132,∴S △ATH S △CPT =12×AH ×TH 12×TP ×CQ =8147,即△AHT 与△CPT 的面积之比为8:147.题型六:函数关系与面积问题6平面直角坐标系中,已知抛物线y =-x 2+(1+m )x -m (m 为常数,m ≠±1)与轴交于定点A 及另一点B ,与y 轴交于点C .(1)当点(2,2)在抛物线上时,求抛物线解析式及点A ,B ,C 的坐标;(2)如图1,在(1)的条件下,D 为抛物线x 轴上方一点,连接BD ,若∠DBA +∠ACB =90°,求点D 的坐标;(3)若点P 是抛物线的顶点,令△ACP 的面积为S ,①直接写出S 关于m 的解析式及m 的取值范围;②当58≤S ≤158时,直接写出m 的取值范围.【解析】(1)将点(2,2)代入y =-x 2+(1+m )x -m ,求出m 即可确定函数的解析式;(2)过D 点作DE ⊥x 轴交于E ,过A 点作AF ⊥BC 交于F ,由题意可知∠ACB =∠BDE ,求出tan ∠ACF =tan ∠BDE =BE DE=35,设D (t ,-t 2+5t -4)(0<t <4),求出t 的值即可求D 点坐标;(3)①求出P 1+m 2,(1-m )24,C (0,-m ),定点A (1,0),B (m ,0),AC 的解析式为y =kx +b ,y =mx -m ,再画出函数图象结合函数图象分类讨即可;②对①中求出的解析式分别进行求解即可.【解答】解:(1)将点(2,2)代入y =-x 2+(1+m )x -m ,∴m =4,∴y =-x 2+5x -4,令x =0,则y =-4,∴C (0,-4),令y =0,则-x 2+5x -4=0,∴x =1或x =4,∴A (1,0),B (4,0);(2)如图1,过D 点作DE ⊥x 轴交于E ,过A 点作AF ⊥BC 交于F ,∵∠DBA +∠ACB =90°,∠DBA +∠BDE =90°,∴∠ACB =∠BDE ,∵B (4,0),C (0,-4),∴OB =OC =4,∴∠OBC =45°,∵BA =3,∴AF =322,∵A (1,0),∴AC =17,∴CF =522,∴tan ∠ACF =AF CF =35,∴tan ∠BDE =BE DE=35,设D (t ,-t 2+5t -4)(0<t <4),∴4-t -t 2+5t -4=35,解得x =4(舍)或x =83,∴D 83,209;(3)①∵y =-x 2+(1+m )x -m =-x -1+m 2 2+(1-m )24,∴P 1+m 2,(1-m )24,令x =0,则y =-m ,∴C (0,-m ),令y =0,则-x 2+(1+m )x -m =0,解得x =1或x =m ,∴定点A (1,0),B (m ,0),设AC 的解析式为y =kx +b ,∴k +b =0b =-m,解得k =m b =-m ,∴y =mx -m ,如图2,当m <-1时,S =S 梯形PNOC +S △OCA -S △PAN =12×(1-m )24-m×1+m 2+12×1×(-m )-12×1-1+m 2 ×(1-m )24=18m 2-18;如图3,当-1<m <0时,S =S 梯形PNOC +S △PNA -S △AOC =12×(1-m )24-m ×1+m 2+12×1-1+m 2 ×(1-m )24-12×1×(-m )=-18m 2+18;如图4,当0≤m <1时,设对称轴与直线AC 交于点M ,∴M 1+m 2,m 2-m 2,∴PM =-14m 2+14,∴S =12×-14m 2+14 ×1=-18m 2+18;如图5,当m >1时,过点C 作CM ⊥PN 交于点M ,∴M 1+m 2,-m ,∴S =S 矩形OCMN +S △APN -S △OCA -S △CMP =1+m 2×m +12×1+m 2-1 ×(1-m )24-12×1×m -12×1+m 2×(1-m )24+m =18m 2-18;综上所述:当m <-1时,S =18m 2-18;当-1<m <1,S =-18m 2+18;当m >1时,S =18m 2-18;②当m <-1时,58≤18m 2-18≤158,解得-4≤m ≤-6;当-1<m <0,58≤-18m 2+18≤158,此时m 无解;当0≤m <1时,58≤-18m 2+18≤158,此时m 无解;当m >1时,58≤18m 2-18≤158,解得6≤m ≤4;综上所述:当58≤S ≤158时,-4≤m ≤-6或6≤m ≤4.2.压轴题速练1一、解答题1(2023春·全国·九年级专题练习)已知:如图,抛物线y =ax 2+bx +c (a ≠0)与坐标轴分别交于点A (0,6),B (6,0),C (-2,0),点P 是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P 运动到什么位置时,△PAB 的面积有最大值,面积最大值是多少?【答案】(1)y =-12x 2+2x +6(2)当P 3,152 时,△PAB 的面积有最大值,最大值是272.【解析】(1)由题意得:36a +6b +c =04a -2b +c =0c =6,解得:a =-12b =2c =6,∴抛物线的表达式为:y =-12x 2+2x +6;(2)∵A (0,6)∴直线AB 的表达式为:y =kx +6,将点B 的坐标代入上式得:0=6k +6,解得:k =-1,∴直线AB 的表达式为:y =-x +6,点P 的横坐标为m ,则P m ,-12m 2+2m +6 ,过点P 作x 轴的垂线,交线段AB 于点D ,则D (m ,-m +6),∴S =12×OB ×PD =12×6×-12m 2+2m +6+m -6 =-32(m -3)2+272,∴当m =3时,S 的值取最大,此时P 3,152;2(2023春·全国·九年级专题练习)如图,抛物线y =ax 2+bx +6(a ≠0)与x 轴交于A (-1,0),B (6,0),与y 轴交于点C ,点P 为第一象限内抛物线上一动点,过点P 作x 轴的垂线,交直线BC 于点D ,交x 轴于点E ,连接 PB .(1)求该抛物线的解析式;(2)当△PBD 与△BDE 的面积之比为1:2时,求点P 的坐标;【答案】【答案】(1)y =-x 2+5x +6(2)P 12,334【解析】(1)∵抛物线y =ax 2+bx +6(a ≠0)与x 轴交于A -1,0 ,B 6,0∴a -b +6=036a +6b +6=0,∴a =-1b =5 ,∴抛物线的解析式为y =-x 2+5x +6;(2)∵抛物线y =-x 2+5x +6过点C ,∴C (0,6),设直线BC 的解析式为 y =kx +n ,∴6k +n =0n =6,∴k =-1n =6 ,∴直线BC 的解析式为y =-x +6,设P m ,-m 2+5m +6 ,则D m ,-m +6 ,∴PE =-m 2+5m +6,DE =-m +6,∵△PBD 与△BDE 的面积之比为1:2,∴PD :DE =1:2,∴PE :DE =3:2,∴3-m +6 =2-m 2+5m +6 ,解得m 1=12,m 2=6(舍去),∴P 12,334;3(2023春·全国·九年级专题练习)如图,抛物线y =-x 2+bx +c 过点A 、B ,抛物线的对称轴交x 轴于点D ,直线y =-x +3与x 轴交于点B ,与y 轴交于点C ,且OA =13OB .(1)求抛物线的解析式;(2)点M t ,0 是x 轴上的一个动点,点N 是抛物线对称轴上的一个动点,当DN =2t ,△MNB 的面积为154时,求出点M 与点N 的坐标;【答案】【答案】(1)y =-x 2+2x +3(2)3+262,0 ,1,3+26 【解析】(1)解:对于直线y =-x +3,令y =0,即-x +3=0,解得:x =3,令x =0,得y =3,∴B 3,0 ,C 0,3 ,∵A 为x 轴负半轴上一点,且OA =13OB ,∴A -1,0 .将点A 、B 的坐标分别代入y =-x 2+bx +c 中,得-1-b +c =0-9+3b +c =0 ,解得b =2c =3 ,∴抛物线的解析式为y =-x 2+2x +3;(2)解:由(1)知:A -1,0 ,B 3,0 ,抛物线解析式为y =-x 2+2x +3,∴对称轴x =-b 2a =-22×-1=1,∴D 点坐标为D 1,0 ,∵M t ,0∴BM =3-t ,∵S △MNB =12×BM ×DN =154,即12×3-t ×2t =154,当t <3时,12×3-t ×2t =154,化简得:4t 2-12t +15=0,∵Δ=b 2-4ac <0,∴方程无解;当t >3时,12×t -3 ×2t =154,解得t1=3+262,t2=3-262(舍),∴DN=2t=3+26,∴点M的坐标为3+262,0,点N的坐标为1,3+262;4(2023·广西贵港·统考一模)在平面直角坐标系中,已知抛物线y=ax2+bx经过A(4,0),B(1,3)两点.P是抛物线上一点,且在直线AB的上方.(1)求抛物线的表达式;(2)若△OAB面积是△PAB面积的2倍,求点P的坐标;(3)如图,OP交AB于点C,PD∥BO交AB于点D.记△CPB,△BCO的面积分别为S1,S2,判断S1S2是否存在最大值.若存在,求出最大值;若不存在,请说明理由.【答案】【答案】(1)y=-x2+4x(2)P(2,4)或(3,3)(3)见解析【解析】(1)解:将A(4,0),B(1,3)代入y=ax2+bx得16a+4b=0a+b=3,解得:a=-1b=4,∴抛物线的解析式为:y=-x2+4x;(2)解:设直线AB的解析式为:y=kx+t,将A4,0,B1,3代入y=kx+t得4k+t=0 k+t=3 ,解得:k=-1 t=4,∴直线AB的解析式为:y=-x+4,∵A4,0,B1,3,∴S△OAB=12×4×3=6,∴S△OAB=2S△PAB=6,即S△PAB=3,过点P作PM⊥x轴于点M,PM与AB交于点N,过点B作BE⊥PM于点E,如图,∴S△PAB=S△PNB+S△PNA=12PN×BE+12PN×AM=32PN=3,∴PN=2,设点P 的横坐标为m ,∴P (m ,-m 2+4m )(1<m <4),N (m ,-m +4),∴PN =-m 2+4m -(-m +4)=2,解得:m =2或m =3;∴P (2,4)或(3,3);(3)解:S 1S 2存在最大值.理由如下:∵PD ∥OB ,∴∠DPC =∠BOC ,∠PDC =∠OBC ,∴△DPC ∽△BOC ,∴CP :CO =CD :CB =PD :OB ,∵S 1S 2=CD CB =PD OB,设直线AB 交y 轴于点F ,则F (0,4),过点P 作PH ⊥x 轴,垂足为H ,PH 交AB 于点G ,如图,∵∠PDC =∠OBC ,∴∠PDG =∠OBF ,∵PG ∥OF ,∴∠PGD =∠OFB ,∴PD :OB =PG :OF ,∴△PDG ∽△OBF ,∴PD :OB =PG :OF ,设P (n ,-n 2+4n )1<n <4 由(2)可知,PG =-n 2+4n --n +4 =-n 2+5n -4,∴S 1S 2=PD BO =PG OF=14PG =-14n -52 2+916,∵1<n <4,∴当n =52时,S 1S 2的最大值为916.5(2023·新疆克孜勒苏·统考一模)如图所示,抛物线y =-x 2+2x +3的图像与x 轴交于A ,B 两点,与y 轴交于点C ,连结BC .(1)求抛物线顶点D 的坐标;(2)在直线BC 上方的抛物线上有一点M ,使得四边形ABMC 的面积最大,求点M 的坐标及四边形ABMC 面积的最大值;(3)点E 在抛物线上,当∠EBC =∠ACO 时,直接写出点E 的坐标.【答案】【答案】(1)(1,4)(2)当点M 32,154 时,四边形ABMC 面积最大,最大值为758(3)(1,4)或-12,74【解析】(1)∵y =-x 2+2x +3=-x -1 2+4.∴抛物线顶点D 的坐标为(1,4);(2)令y =0,则x 2-2x -3=0,解得x 1=-1,x 2=3,∴点A -1,0 ,B 3,0 ,令x =0,则y =-3,∴点C 的坐标为(0,3)∴AB =3--1 =4,OC =3,∴S ΔABC =12AB ⋅OC =6∴△BCM 的面积最大时四边形ABMC 面积最大.设直线BC 的解析式为y =kx +b ,则3k +b =0b =3,∴b =3k =-1 ,∴y =-x +3.设过点M 与y 轴平行的直线交BC 于点N ,M x ,-x 2+2x +3 ,N x ,-x +3 ,则MN =-x 2+2x +3 --x +3 =-x 2+3x ,S △BCM =12-x 2+3x ×3=-12x -32 2+278,∴当x =32时,△BCM 的面积最大,最大值为278,此时,y =-32 2+2×32+3=154,所以,当点M 32,154 时,四边形ABMC 面积最大,最大值为6+278=758(3)①连接CD ,BD ,作DM ⊥OC 于点M .∵C (0,3),D (1,4),∴CM =DM =1,∴△CDM 是等腰直角三角形,∴∠DCE =45°.∵B (3,0),C (0,3),∴△BOC 是等腰直角三角形,∴∠BCO =45°,∴∠BCD =90°,∵BC =32+32=32,CD =12+(-3+4)2=2,∴.tan ∠CBD =232=13,∴∠DBC =∠ACO ,∴点E 与点D 重合,∴点E 的坐标为(1,-4),②作点D 关于BC 的对称点D ,作DN ⊥OC 于点N ,∵∠DMC =∠D NC =90°,∠DCM =D CN ,DC =D C ,∴△DCM ≌△D CN ,∴D N =DM =1,CM =CN =1,∴ON =3-1=2,∴D (-1,2),设直线BD 的解析式为y =mx +n ,,则3m +n =0-m +n =2,解得m =-12n =32,所以,直线BD ′的解析式为y =-12x +32,联立y =-x 2+2x +3y =-12x +32,解得x 1=3y 1=0 (为点B 坐标,舍去),x 2=-12y 2=74,所以,点H 的坐标为-12,74 ,综上所述,点E 的坐标为1,4 或-12,74时,∠EBC =∠ACO .6(2023·广东珠海·统考一模)如图,抛物线与x 轴交于点A -1,0 、B 4,0 ,与y 轴交于点C 0,2 .点D 为抛物线第四象限一动点,连接AC 、BC 、BD 、AD .(1)求抛物线的解析式;(2)当S △BCD =S △ABC 时,求此时点D 的坐标;(3)在第(2)问的条件下,延长线段AC 、DB 交于点E .请判断△ADE 的形状,并说明理由.【答案】(1)y =-x 2+32x +2(2)D 5,-3(3)△ADE 是等腰直角三角形,理由见详解【解析】(1)设抛物线的解析式为y =ax 2+bx +c ,∵抛物线与x 轴交于点A -1,0 、B 4,0 ,与y 轴交于点C 0,2 ,∴a -b +c =016a +4b +c =0c =2,解得:a =-12b =32c =2 ,∴抛物线的解析式为y =-x 2+32x +2;(2)连接OD ,,∵A -1,0 ,B 4,0 ,C 0,2 ,∴AB =5,OC =2,∴S △ABC =12AB ⋅OC =5,设D m ,-12m 2+32m +2 m >4 ,∵S △BCD =S △OBD +S △OBC -S △OCD =S △ABC ,∴12×4×12m 2-32m -2 +12×4×2-12×2×m =5,整理,得m 2-4m -5=0,解得:m 1=5,m 2=-1(舍去),∴D 5,-3 ;(3)△ADE 是等腰直角三角形,理由如下:设直线AC 的解析式为y =k 1x +b 1,把A -1,0 ,C 0,2 代入,得-k 1+b 1=0b 1=2 ,解得:k 1=2b 1=2∴y =2x +2,设直线BD 的解析式为y =k 2x +b 2,把B 4,0 ,D 5,-3 代入,得4k 2+b 2=05k 2+b 2=-3 ,解得:k 2=-3b 2=12∴y =-3x +12,联立y =2x +2和y =-3x +12得,y =2x +2y =-3x +12 ,解得:x =2y =6 ,∴E 2,6 ,又∵A -1,0 ,D 5,-3 ,∴AE =-1-2 2+0-6 2=35,AD =-1-5 2+0+3 2=35,DE =5-2 2+-3-6 2=310,∴AE =AD ,AE 2+AD 2=DE 2,∴△ADE 是等腰直角三角形.7(2023春·上海·八年级专题练习)在边长为4的正方形ABCD 中,点O 是对角线AC 的中点,P 是对角线AC 上一动点,过点P 作PF ⊥CD 于点F ,作PE ⊥PB 交直线CD 于点E ,设PA =x ,S △PCE =y .(1)求证:DF =EF ;(2)当点P 在线段AO 上时,求y 关于x 的函数关系式及自变量x 的取值范围;(3)点P 在运动过程中能否使△PEC 为等腰三角形?如果能,请直接写出PA 的长;如果不能,请简单说明理由.【答案】(1)证明见解析(2)y =12x 2-32x +8,0≤x ≤22 (3)能使△PEC 为等腰三角形,PA =0或PA =4【解析】(1)证明:延长FP 交AB 于点G ,∵正方形ABCD 中,PF ⊥CD 于点F ,∴四边形AGFD 是矩形,∴DF =AG ,∠AGF =90°,∵正方形ABCD ,∴∠BAC =45°,∵∠AGF =90°,∴AG =GP ,∴DF =GP ,同理可得:CF =PF =BG ,∵PE ⊥PB ,∠AGF =90°,∴∠GBP +∠GPB =∠FPE +∠GPB =90°,∴∠GBP =∠FPE ,在△GBP 和△FPE 中,∵∠GBP =∠FPEPF =BG ∠BGP =∠PFE,∴△GBP ≌△FPE (ASA ),∴GP =EF ,∵DF =GP ,∴DF =EF ;(2)∵PA =x ,∴AG =GP =22x ,DF =EF =22x ,则DE =2x ,∴CE =4-2x ,∵PF =4-22x ,∴y =124-2x 4-22x =12x 2-32x +80≤x ≤22 ;(3)点P 在运动过程中能使△PEC 为等腰三角形;当点E 在CD 边上时,∵∠CEP ≥90°,若△PEC 为等腰三角形,只能是∠CPE =∠ECP =45°,则PE ⊥CE ,∵PE ⊥PB ,∴PB ∥CD ,∴PB ∥AB ,于是点P 在AB 上,又∵点P 在AC 上,∴A 与P 重合,此时PA =0;当点E 在DC 延长线上时,如图,若△PEC 为等腰三角形,只能是PC =CE ,设PA =x ,则PC =42-x ,EF =DF =AG =GP =22x ,PF =CF =BG =4-22x ,∴CE =EF -CF =22x -4-22x=2x -4,∵PC =CE ,∴42-x =2x -4,∴x =4,∴即PA =4;综上所述,当PA =0或PA =4时,△PEC 为等腰三角形.【点睛】本题主要考查正方形的性质的综合运用,等腰三角形的性质和判定,全等三角形的判定和性质,三角形的面积等知识,综合运用这些性质进行推理,同时注意对等腰的分类讨论是解题的关键.8(2023春·江苏无锡·九年级统考期中)在平面直角坐标系中xOy 中,二次函数y =ax 2+bx +2a <0 的图像与x 轴交于点A (-1,0)、B (2,0),与y 轴交于点C .(1)求二次函数的表达式;(2)若点P 是二次函数图像上位于线段BC 上方的一个动点.①如图,连接AC ,CP ,AP ,AP 交BC 于点E ,过点P 作AC 的平行线交BC 于点Q ,将△PEQ 与△PCE的面积比S △PEQ S △PCE 记为a ,将△PCE 与△ACE 的面积比S △PCE S △ACE记为b ,当a +22b 有最大值时,求点P 的坐标;②已知点N 是y 轴上一点,若点N 、P 关于直线AC 对称,求CN 的长.【答案】(1)y =-x 2+x +2(2)①当点P 的坐标为1,1 时,a +22b 有最大值;②CN =516【解析】(1)解:将A (-1,0)、B (2,0),代入y =ax 2+bx +2中可得:a -b +2=04a +2b +2=0 ,解得:a =-1b =1 ,∴二次函数的表达式为:y =-x 2+x +2;(2)①当x =0时,y =2,则C 0,2 ,设BC 的解析式为:y =kx +b ,将B (2,0),C 0,2 ,代入可得:2k +b =0b =2 ,解得:k =-1b =2 ,∴BC 的解析式为:y =-x +2,由题意可知,OB =OC =2,则△BOC 是等腰直角三角形,∴∠BCO =45°,∵A (-1,0),则OA =1,∴AC =OA 2+OC 2=5,∴sin ∠ACO =55,cos ∠ACO =255,过点P 作PN ∥y 轴,QM ⊥PN ,设AP 与y 轴交于点D ,则∠ADO =∠APN ,∠QNM =∠BCO =45°,即:△MQN 为等腰直角三角形,∴QM =MN ,∵AC ∥PQ ,∴∠CAP =∠APQ ,△AEC ∽△PEQ ,则EQ CE =EP AE =PQ AC,又∵∠ADO =∠ACP +∠ACO ,∠APN =∠APQ +∠QPM ,∴∠ACO =∠QPM ,则:PM =PQ ⋅cos ∠QPN =PQ ⋅cos ∠ACO =255PQ ,QM =MN =PQ ⋅sin ∠QPN =PQ ⋅sin ∠ACO =55PQ ,则PN =PM +MN =355PQ ,即:PQ =53PN ,∵S △PEQ S △PCE =EQ CE ,S △PCE S △ACE =EP AE ,EQ CE =EP AE =PQ AC,∴a =b =EQ CE =EP AE =PQ AC =PQ 5=13PN ,∴a +22b =1+22 ×13PN ,则当PN 取最大值时,a +22b 有最大值,设P t ,-t 2+t +2 ,0<t <2,则N t ,-t +2 ,∴PN =-t 2+t +2 --t +2 =-t 2+2t =-t -1 2+1,即:当t =1时,PN 取最大值,此时点P 的纵坐标为1,即:当点P 的坐标为1,1 时,a +22b 有最大值;②由题意可知,点N 在点C 下方时,点N 关于直线AC 的对称点在AC 的左侧,不符合题意,点N 在点C 上方时,连接PN ,交AC 于H ,作PF ⊥y 轴,由对称可知,NH =PH =12PN ,CH ⊥PN ,则∠NHC =∠PFN =90°,∴∠NCH +∠CNP =∠CNP +∠FPN ,∴∠NCH =∠FPN∵∠ACO =∠NCH ,sin ∠ACO =55,cos ∠ACO =255,∴∠ACO =∠NCH =∠FPN ,设CN =m ,则NH =CN ⋅sin ∠NCH =55m ,∴PN =2NH =255m ,则PF =PN ⋅cos ∠FPN =45m ,NF =PN ⋅sin ∠FPN =25m ∴CF =CN -NF =35m ,则OF =OC +CF =2+35m ,∴点P 的坐标为:45m ,2+35m ,0<45m <2,即0<m <52,∵点P 在二次函数图象上,∴-45m 2+45m +2=2+35m ,解得:m 1=0(舍去),m 2=516,∴CN =516.9(2023·黑龙江哈尔滨·统考一模)如图,在平面直角坐标系中,直线BC 的解析式为y =-x +6,直线BC 交x 轴和y 轴分别于点B 和点C ,抛物线y =-29x 2+bx +c 交x 轴于点A 和点B ,交y 轴于点C .(1)求抛物线的解析式;(2)点P 是第二象限抛物线上的点,连接PB 、PC ,设点P 的横坐标为t ,△PBC 的面积为S .求S 与t 的函数关系式(不要求写出t 的取值范围);(3)在(2)的条件下,点D 在线段OB 上,连接PD 、CD ,∠PDC =45°,点F 在线段BC 上,EF ⊥BC ,FE 的延长线交x 轴于点G ,交PD 于点E ,连接CE ,若∠GED +∠DCE =180°,DC >DE ,S △CDE =15,求点P 的横出标.【答案】(1)y =-29x 2+13x +6(2)S =23t 2-4t (3)3-3112【解析】(1)解:直线y=-x+6交x轴和y轴于点B和点C 令x=0时,y=6,即C0,6,令y=0时,x=6,即B6,0,∵点B、C在抛物线上,∴代入解析式可得:c=6-29×62+13×6+6=0,解得:c=6b=-13,∴解析式为y=-29x2+13x+6;(2)过点P作x轴的垂线交BC延长线于点M,交x轴于点N,过点C作CR⊥MN于R ∵P在抛物线上,P横坐标为t∴P t,-29t2+13t+6,∵M在直线BC上,∴M t,-t+6,∴MP=-t+6--29t2+13t+6=29t2-43t,S△PBC=S△MPB-S△MPC=12MP⋅OB=1229t2-43t×6=23t2-4t,即S=23t2-4t;(3)由(1)得,OB=OC=6,∴∠OBC=∠OCB=45°又EF⊥BC交x轴于点G,∴∠GFB=90°∴∠FGB=90°-∠FBG=45°即∠FGB=∠FBG=45°∴FG=FB又∠PDC=45°设∠PDA=α,∴∠CDA=45°+α=∠CBD+∠BCD=45°+∠BCD∴∠BCD=α=∠PDA又∠GED+∠DCE=180°(已知)∠GED+∠FED=180°(平角定义)∴∠DCE=∠FED,又∠FED=∠FGE+∠PDG=45°+a∴∠FED=∠CDA,∴∠DCE=∠CDA,过点D作DR⊥CE于R,如图所示∴在Rt△CRD中,∠CDR=90°-∠RCD=45°-α,∴∠RDE=∠CDE-∠CDR=α,,∴∠RDE=∠EDA=α,∵∠CRD=∠DOC=90°,∠DCE=∠CDA,CD=CD,∴△RCD≌△ODC(AAS),∴RD=CO=6,CR=OD,∠CDR=∠DCO,又∵S△DCE=15,∴12CE×DR=15∴CE=5作EM⊥x轴于M,CN⊥EM于N,DT⊥CN于T,如图所示∵∠RDE=∠EDA,∠ERD=∠EMD=90°,DE=DE,∴△RED ≌△MED (AAS ),∴RE =EM ,RD =MD ,∵EM ⊥x ,CN ⊥EM ,DT ⊥CN ,∴四边形NTDM 为矩形,∴∠MDT =90°,∴∠CDT =∠MDT -∠CDE -∠EDA =45°-α=∠CDR ,∴△DCR ≌△DCT (AAS ),∴DR =DT ,∴DM =DT ,∴四边形NMDT 是正方形∴DM =MN =NT =DT =OC =6,设EM =ER =m ,则CR =5-m =CT ,如图所示:∴NE =6-m ,NC =NT -TC =m +1在Rt △NEC 中,6-m 2+m +1 2=52解得:m 1=2,m 2=3,∵CD >DE ,∴m <5-m ,即m <2.5,∴m =3不符合题意,应舍去;当m =2时,CT =OD =3=MO ,∴E -3,2 ,又点D 3,0 ,设直线ED 的解析式为y =kx +b ,则-3k +b =23k +b =0 ,解得:k =-13b =1 ,∴直线ED 的解析式为:y =-13x +1,y =-13x +1y =-29x 2+13x +6 ,∴x =3-3112或3+3112(舍),∴P 的横坐标是3-311210(2023春·江苏宿迁·九年级统考阶段练习)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c a <0 与x 轴交于A -2,0 、B 4,0 两点,与y 轴交于点C ,且OC =2OA .(1)试求抛物线的解析式;(2)直线y =kx +1k >0 与y 轴交于点D ,与抛物线在第一象限交于点P ,与直线BC 交于点M ,记m =S △CPM S △CDM,试求m 的最大值及此时点P 的坐标;(3)在(2)的条件下,m 取最大值时,点Q 是x 轴上的一个动点,点N 是坐标平面内的一点,是否存在这样的点Q 、N ,使得以P 、D 、Q 、N 四点组成的四边形是矩形?请直接写出满足条件的N 点的坐标.【答案】(1)y =-12x 2+x +4(2)m 取得最大值23,此时点P 的坐标为2,4 (3)存在,满足条件的N 的坐标为72,3 或6,-3 【解析】(1)解:∵A -2,0 ,∴OA =2,∵OC =2OA ,∴OC =4,∴C 0,4 ,∵抛物线y =ax 2+bx +c 经过点A -2,0 ,B 4,0 ,C 0,4 ,∴4a -2b +c =016a +4b +c =0c =4,解得:a =-12b =1c =4,∴该抛物线的解析式为y =-12x 2+x +4;(2)解:如图1,过点P 作PE ∥y 轴交直线BC 于E ,连接CP ,设直线BC 的解析式为y =kx +d ,∵B 4,0 ,C 0,4 ,∴4k +d =0d =4 ,解得:k =-1d =4 ,∴直线BC 的解析式为y =-x +4,设P t ,-12t 2+t +4 ,则E t ,-t +4 ,∴PE =-12t 2+t +4-(-t +4)=-12t 2+2t ,∵直线y =kx +1k >0 与y 轴交于点D ,∴D 0,1 ,∴CD =4-1=3,∵PE ∥y 轴,即PE ∥CD ,∴△EMP ∽△CMD ,∴PM DM =PE CD =-12t 2+2t 3=-16t 2+23t ,∵m =S △CPM S △CDM =PM DM,∴m =-16t 2+23t =-16t -2 2+23,∵-16<0,∴当t =2时,m 取得最大值23,此时点P 的坐标为2,4 ;(3)解:存在这样的点Q 、N ,使得以P 、D 、Q 、N 四点组成的四边形是矩形.①当DP 是矩形的边时,有两种情形,a 、如图2-1中,四边形DQNP 是矩形时,由(2)可知P 2,4 ,代入y =kx +1中,得到k =32,∴直线DP 的解析式为y =32x +1,可得D 0,1 ,E -23,0 ,由△DOE ∽△QOD 可得OD OQ =OE OD,∴OD 2=OE ⋅OQ ,∴1=23⋅OQ ,∴OQ =32,∴Q 32,0 .根据矩形的性质,将点P 向右平移32个单位,向下平移1个单位得到点N ,∴N 2+32,4-1 ,即N 72,3 ,b 、如图2-2中,四边形PDNQ 是矩形时,∵直线PD 的解析式为y =32x +1,PQ ⊥PD ,∴直线PQ 的解析式为y =-23x +163,∴Q 8,0 ,根据矩形的性质可知,将点D 向右平移6个单位,向下平移4个单位得到点N ,∴N 0+6,1-4 ,即N 6,-3 .②当DP 是对角线时,设Q x ,0 ,则QD 2=x 2+1,QP 2=x -2 2+42,PD 2=13,∵Q 是直角顶点,∴QD 2+QP 2=PD 2,∴x 2+1+x -2 2+42=13,整理得x 2-2x +4=0,方程无解,此种情形不存在,综上所述,满足条件的N 的坐标为72,3 或6,-3 .11(2023·山东济宁·统考一模)如图,抛物线y =ax 2+bx +3与坐标轴分别交于A ,B ,C 三点,其中A (-4,0)、B (1,0),M 是第二象限内抛物线上的一动点且横坐标为m ,(1)求抛物线的解析式;(2)连接BM ,交线段AC 于点D ,求S ΔADM S ΔADB的最大值(其中符号S 表示面积);(3)连接CM ,是否存在点M ,使得∠ACO +2∠ACM =90°,若存在,求m 的值,若不存在,请说明理由.【答案】(1)y =-34x 2-94x +3(2)S ΔADM S ΔADB 的最大值为45(3)存在,m =-319【解析】(1)解:(1)分别代入A (-4,0)、B (1,0)到抛物线解析式,解得:y =-34x 2-94x +3;故答案为:y =-34x 2-94x +3.(2)设直线AC 的解析式为y =kx +b ,将点A (-4,0)和点C (0,3)代入y =kx +b 中,-4k +b =0b =3 ,解得:k =34b =3,∴直线AC 的解析式为y =34x +3,如图所示,过点M 作MG ∥x 轴交于AC 于点G ,过点A 作AF ⊥MB 交MB 与点F ,∴G 点的纵坐标与M 点的纵坐标相同,∵M 为抛物线y =-34x 2-94x +3上的一点,设M m ,-34m 2-94m +3 ,又∵G 点在直线AC 上,直线AC 的解析式为y =34x +3,∴G -m 2-3m ,-34m 2-94m +3 ,∴MG =-m 2-4m ,又∵MG ∥AB ,∴MD DB =MG AB =-m 2-4m 5,∵S ΔADM =12MD ⋅AF ,S ΔADB =12DB ⋅AF ,∴S ΔADM S ΔADB =DM DB,∴S ΔADB S ΔADB =DM DB =MG AB=-m 2-4m 5=-m 2+4m 5=-15m +2 2+45,∴S ΔADM S ΔADB 的最大值为45.故答案为:45.(3)过点C 作CP ∥x 轴,延长CM 交x 轴于点T .∴∠MCO =90°,∠MCP =∠MTA ,∵∠ACO +2∠ACM =90°∠ACO +∠PCM +∠MCA =90°,∴∠MCP =∠MCA ,∴∠MCA =∠MTA ,∴△ACT 为等腰三角形,∴AC =AT .在Rt △ACO 中,AC =AO 2+OC 2=42+32=5,∴AC =AT =5,∴OT =AT +OA =5+4=9,∴T (-9,0),设直线CT 的解析式为y =kx +b ,将点T (-9,0)和点C (0,3)代入y =kx +b 中,解得:k =13b =3 ,∴直线CT 的解析式为y =13x +3,∵M 是直线CT 和抛物线y =-34x 2-94x +3的交点,-4<m <0,∴令-34m 2-94m +3=13m +3,∴9m 2+27m +4m =0,∴9m 2+31m =0,∴m 9m +31 =0,解得m =0(舍去)或m =-319故答案为:m =-319.12(2023·海南海口·海口市第九中学校考二模)如图①,已知抛物线L :y =x 2+bx +c 的图象经过点A 0,3 ,B 1,0 .过点A 作AC ∥x 轴交抛物线于点C ,∠AOB 的平分线交线段AC 于点E ,连结OE .(1)求抛物线的关系式并写出点E的坐标;(2)若动点P在x轴下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出此时P点横坐标;(3)若将抛物线向上平移h个单位,且其顶点始终落在△OAE的内部或边上,写出h的取值范围;(4)如图②,F是抛物线的对称轴上l的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【答案】(1)y=x2-4x+3;E(3,3)(2)P的横坐标为52;(3)3≤h≤4;(4)存在,点P的坐标是:5-52,1-52或3-52,5+12或3+52,1-52或5+5 2,5+12【解析】(1)解:∵抛物线L:y=x2+bx+c的图象经过点A(0,3),B(1,0),∴1+b+c=0c=3,解得b=-4c=3,∴抛物线的解析式为:y=x2-4x+3;∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3),(2)如图1,过P作PG∥y轴,交OE于点G,设P(m,m2-4m+3),设直线OE的解析式为y=kx,把点E(3,3)代入得,3=3k,解得k=1,∴直线OE的解析式为:y=x,∴G(m,m),∴PG=m-(m2-4m+3)=-m2+5m-3,∴S△OPE=S△OPG+S△EPG=12PG×AE=12×3×(-m 2+5m -3)=-32(m 2-5m +3)=-32m -52 2+398,∵-32<0,∴当m =52时,△OPE 面积最大,∴P 的横坐标为52(3)由y =x 2-4x +3=(x -2)2-1,得抛物线l 的对称轴为直线x =2,顶点为(2,-1),抛物线L 向上平移h 个单位长度后顶点为F (2,-1+h ).设直线x =2交OE 于点M ,交AE 于点N ,则N (2,3),如图2,∵直线OE 的解析式为:y =x ,∴M (2,2),∵点F 在△OAE 内(包括△OAE 的边界),∴2≤-1+h ≤3,解得3≤h ≤4;(4)设P (m ,m 2-4m +3),分四种情况:①当P 在对称轴的左边,且在x 轴下方时,如图3,过P 作MN ⊥y 轴,交y轴于M ,交l 于N ,∴∠OMP =∠PNF =90°,∵△OPF 是等腰直角三角形,∴OP =PF ,∠OPF =90°,∴∠OPM +∠NPF =∠PFN +∠NPF =90°,∴∠OPM =∠PFN ,∴△OMP ≌△PNF (AAS ),∴OM =PN ,∵P (m ,m 2-4m +3),则-m 2+4m -3=2-m ,解得:m =5+52或5-52,∵m =5+52>2,不合题意,舍去,∴m =5-52,此时m 2-4m +3=1-52,∴P 的坐标为5-52,1-52;②当P 在对称轴的左边,且在x 轴上方时,同理得:2-m =m 2-4m +3,解得:m 1=3+52或m 2=3-52,∵3+52>2,不合题意,舍去,∴m =3-52,此时m 2-4m +3=5+12,∴P 的坐标为3-52,5+12;③当P 在对称轴的右边,且在x 轴下方时,如图4,过P 作MN ⊥x 轴于N ,过F 作FM ⊥MN 于M ,同理得△ONP ≌△PMF ,∴PN =FM ,则-m 2+4m -3=m -2,解得:m 1=3+52或m 2=3-52,∵3-52<2,不合题意,舍去,∴m =3+52,此时m 2-4m +3=1-52,P 的坐标为3+52,1-52;④当P 在对称轴的右边,且在x 轴上方时,如图5,同理得m 2-4m +3=m -2,解得:m =5+52或5-52(舍),P 的坐标为:5+52,5+12;综上所述,点P 的坐标是:5-52,1-52 或3-52,5+12或3+52,1-52 或5+52,5+12.13(2023·广东珠海·校考一模)如图,在平面直角坐标系中,抛物线y =-12x 2+bx +c 与x 轴交于点A ,B ,其中点B 的坐标为(4,0),与y 轴交于点C (0,2).(1)求抛物线y =-12x 2+bx +c 和直线BC 的函数表达式;(2)点P 是直线BC 上方的抛物线上一个动点,当△PBC 面积最大时,求点P 的坐标;(3)连接B 和(2)中求出点P ,点Q 为抛物线上的一点,直线BP 下方是否存在点Q 使得∠PBQ =45°?若存在,求出点Q 的坐标.【答案】(1)y =-12x 2+32x +2,y =-12x +2(2)(2,3)(3)存在,-35,2325【解析】(1)把B (4,0),C (0,2)代入y =-12x 2+bx +c 得:-8+4b +c =0c =2 ,解得b =32c =2,∴抛物线的函数表达式为y =-12x 2+32x +2;设直线BC 的函数表达式为y =mx +2,把B (4,0)代入得:4m +2=0,解得m =-12,∴直线BC 的函数表达式为y =-12x +2;(2)过P 作PH ∥y 轴交BC 于H ,如图:设P t ,-12t 2+32t +2 ,则H t ,-12t +2 ,∴PH =-12t 2+32t +2--12t +2 =-12t 2+2t ,∴S ΔPBC =12PH ⋅OB =12×-12t 2+2t ×4=-t 2+4t =-(t -2)2+4,∵-1<0,∴当t =2时,S ΔPBC 取最大值4,此时P 的坐标为(2,3);(3)直线BP 下方存在点Q ,使得∠PBQ =45°,理由如下:过P 作PM ⊥PB 交BQ 的延长线于M ,过P 作TK ∥x 轴,过B 作BK ⊥TK 于K ,过M 作MT ⊥TK 于T ,如图:由(2)知P (2,3),∵B (4,0),∴PK =2,BK =3,∵∠PBQ =45°,∴ΔPBM 是等腰直角三角形,∴∠MPB =90°,PB =PM ,∴∠KPB =90°-∠TPM =∠TMP ,∵∠K =∠T =90°,∴ΔBPK ≅ΔPMT (AAS ),∴PK =MT =2,BK =PT =3,∴M (-1,1),由M (-1,1),B (4,0)得直线BM 函数表达式为y =-15x +45,联立y =-15x +45y =-12x 2+32x +2 ,解得x =4y =0 或x =-35y =2325,∴Q 的坐标为-35,2325 .14(2023·广西梧州·统考一模)如图1,在平面直角坐标系中,△ABC 的顶点A -6,0 ,B 0,8 ,C 8,0,点P 为线段AC 上的一动点(点P 与点A ,C 不重合),过点P 作PQ ∥BC 交AB 于点Q ,将△APQ 沿PQ 翻折,点A 的对应点为点D ,连接PD ,QD ,BD .设点P 的坐标为t ,0(1)当点D 恰好落在BC 上时,求点P 的坐标;(2)若△PDQ 与△ABC 重叠部分面积S 与点P 横坐标t 之间的函数解析式为S =a (t +6)2(-6<t ≤1)-67t 2+bt +647(1<t <8) ,其图象如图2所示,求a 、b 的值;(3)是否存在点P ,使得∠BDQ 为直角?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】(1)1,0(2)a =27,b =247(3)67,0【解析】(1)解:∵A -6,0 ,B 0,8 ,C 8,0 ,∴OB =OC =8,∴∠C =45°.∵PQ ∥BC ,∴∠APQ =∠C =45°.由折叠的性质可得AP =PD ,∠APQ =∠DPQ =45°,∴∠DPA =90°.∵B 0,8 ,C 8,0 ,∴直线BC 的解析式为y =-x +8,∵P t ,0 ,∴PA =t --6 =t +6.∵点D 恰好落在BC 上,∴D (t ,-t +8),∴PD =-t +8,∴t +6=-t +8,解得:t =1,∴点P 的坐标为1,0 ;(2)解:∵PQ ∥BC ,∴可设直线PQ 的解析式为y =-x +m ,∴0=-t +m ,解得:t =m ,直线PQ 的解析式为y =-x +t .∵A -6,0 ,B 0,8 ,∴直线AB 的解析式为:y =43x +8. 联立y =-x +t y =43x +8 ,解得:x =3t -247y =4t +247,∴Q 3t -247,4t +247.当-6<t ≤1时,点D 在△ABC 内部,此时重叠部分面积为△PDQ 的面积,由折叠可知S △PDQ =S △APQ =12AP ⋅y Q =12×t +6 ×4t +247=27t +6 2,∴a =27;当1<t <8时,点D 在△ABC 外部,由图象可得当t =4时,S =1287,∴-67×42+4b +647=1287,解得:b =247;(3)解:如图,过点Q 和点B 分别作PD 的垂线,交PD 于点M 和PD 延长线于点N ,∵∠BDQ 为直角,∴∠BDN +∠MDQ =90°∵∠BDN +∠DBN =90°,∴∠MDQ =∠DBN ,∴tan ∠MDQ =tan ∠DBN ,即QM DM =DN BN .∵Q 3t -247,4t +247 ,M t ,4t +247,D t ,t +6 ,N t ,8 ,B 0,8 ,∴QM =t -3t -247=4t +247,DM =t +6-4t +247=3t +187,DN =8-(t +6)=2-t ,BN =t ,∴4t +2473t +187=2-t t,解得:t 1=67,t 2=-6(舍).∴存在,点P 的坐标为67,0 .15(2023·吉林长春·统考一模)在平面直角坐标系中,抛物线y =-x 2+ax +1(a 为常数),经过点P 2,-7 ,点Q 在抛物线上,其横坐标为m ,将此抛物线上P 、Q 两点间的部分(包括P 、Q 两点)记为图像G .。
2023年中考数学真题汇编几何综合压轴问题专项练习(共40题)(解析版)

几何综合压轴问题专项练习答案(40题)(1)将CDE 绕顶点C 旋转一周,请直接写出点M ,N 距离的最大值和最小值;(2)将CDE 绕顶点C 逆时针旋转120︒(如图2),求MN 【答案】(1)最大值为3,最小值为1(2)7【分析】(1)根据直角三角形斜边上的中线,得出,CM CN 解;(2)过点N 作NP MC ⊥,交MC 的延长线于点P ,根据旋转的性质求得进而可得1CP =,勾股定理解Rt ,Rt NCP MCP ,即可求解.【详解】(1)解:依题意,112CM DE ==,12CN AB =当M 在NC 的延长线上时,,M N 的距离最大,最大值为(2)解:如图所示,过点N 作NP MC ⊥,交MC 的延长线于点∵CDE 绕顶点C 逆时针旋转∴120BCE ∠=︒,∵45BCN ECM ∠=∠=︒,∴MCN BCM ECM ∠=∠-∠=∴60NCP ∠=︒,∴30CNP ∠=︒,∴112CP CN ==,在Rt CNP 中,2NP NC =-在Rt MNP △中,MP MC CP =+∴2234MN NP MP =+=+【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,勾股定理,旋转的性质,含(1)如图1,求证:DE BF =;(2)如图2,若2AD BF =,的延长线恰好经过DE 的中点【答案】(1)见解析(2)22BE =+△∵点G 是DE 的中点,∴GH 是FCD 的中位线,∴11122GH CD AD ===,设BE a =,则CH EH ==(1)如图1,求AB边上的高CH的长.''.(2)P是边AB上的一动点,点,C D同时绕点P按逆时针方向旋转90︒得点,C D①如图2,当点C'落在射线CA上时,求BP的长.△是直角三角形时,求BP的长.②当AC D''∴90C PQ PC Q '∠+∠='︒∵90C PQ CPH ∠+∠='︒∴PC Q CPH ∠=∠'.由旋转知PC PC '=,设C D ''与射线BA 的交点为作CH AB ⊥于点H .∵PC PC ⊥',∴90CPH TPC ∠'+∠=︒,∵C D AT ''⊥,∴90PC T TPC ∠'+∠='︒,【答案】(1)①见解析;②AD DF BD =+,理由见解析;【分析】(1)①证明:ABE CBD ∠=∠,再证明ABE ≅△可得DF DC =.证明AE DF =,从而可得结论;(2)如图,过点B 作BE AD ⊥于点E ,得90BED ∠=︒,证明2DE BD =,证明2AB BC =,ABE CBD ∠=∠,可得②AD DF BD=+.理由如下:∵DF和DC关于AD对称,=.∴DF DC=,∵AE CD∴AE DF=.∴AD AE DE DF BD=+=+∵DF 和DC 关于AD 对称,∴DF DC =,ADF ADC ∠=∠.∵CD BD ⊥,∴45ADF ADC ∠=∠=︒,∴45EBD ∠=︒.∴2DE BD =.∵AB AC AF ==,∴()11222HF BF BD DF ==-=,222262210BC BD CD =+=+=∴2221022AF AC BC ===⨯=25HF (2)知识应用:如图2Y是菱形;①求证:ABCD②延长BC至点E,连接OE交【答案】(1)见解析5∴1BG BO GC OD==,∴115222CG BC AD ===,∴552OF GC .处从由60PC P C PCP ''=∠=︒,,可知PCP '△为①三角形,故PP PC '=,又P A PA ''=,故PA PB PC PA PB PP A B '''++=++≥,由②可知,当B ,P ,P ',A 在同一条直线上时,PA PB PC ++取最小值,如图2,最小值为(3)如图5,设村庄A ,B ,C 的连线构成一个三角形,且已知4km 23km AC BC ==,,建一中转站P 沿直线向A ,B ,C 三个村庄铺设电缆,已知由中转站P 到村庄A ,B ,C 元/km ,a 元/km ,2a 元/km ,选取合适的P 的位置,可以使总的铺设成本最低为___________用含的式子表示)∵ACP A CP ''∠=∠,∴ACP BCP A CP BCP ∠+∠=∠+∠''又∵60PCP '∠=︒过点A '作A H BC '⊥,垂足为H ,∵60ACB ∠=︒,90ACA '∠=︒,∴30A CH '∠=︒,1猜想证明:(1)如图2,试判断四边形AEDG的形状,并说明理由.问题解决;(2)如图3,将图2中左侧折叠的三角形展开后,重新沿MN折叠,使得顶点B与点∵1122 CHGS CH HG=⋅=∴154302CG HE⋅=⨯=,①求证:PD PB =;②将线段DP 绕点P 逆时针旋转,化时,DPQ ∠的大小是否发生变化?请说明理由;③探究AQ 与OP 的数量关系,并说明理由.【答案】(1)①见解析;②不变化,(2)AQ CP =,理由见解析【分析】(1)①根据正方形的性质证明②作,PM AB PN AD ⊥⊥,垂足分别为点∵四边形ABCD 是正方形,∴45DAC BAC ∠=∠=︒,∴四边形AMPN 是矩形,∴90MPN ∠=︒,∵四边形ABCD 是正方形,∴45BAC ∠=︒,90AOB ∠=∴45AEP ∠=︒,四边形OPEF=作PM AB⊥于点M,则QM MB=,∴QA BE=.∴AQ CP(1)求BCF ∠的度数;(2)求CD 的长.深入探究:(3)若90BAC ∠<︒,将BMN 绕点B 顺时针旋转α,得到BEF △,连接AE ,CF 满足0360α︒<<︒,点,,C E F 在同一直线上时,利用所提供的备用图探究BAE ∠与ABF ∠的数量关系,并说明理由.【答案】初步尝试:(1)1MN AC =;MN AC ∥;(2)特例研讨:(1)30BCF ∠=︒;(2)CD∵MN 是BAC 的中位线,∴MN AC ∥,∴90BMN BAC ∠=∠=︒∵将BMN 绕点B 顺时针旋转α∴,BE BM BF BN ==;BEF ∠=∵点,,A E F 在同一直线上时,2∵,ADN BDE ANB BED ∠=∠∠=∠∴ADN BDE ∽,∴2222DN AN DE BE ===,设DE x =,则2DN x =,在Rt ABE △中,2,2BE AE ==在Rt ADN △中,22AD DN AN =+∵AB AC =,∴A ABC CB =∠∠,设ABC ACB θ∠=∠=,则1802BAC θ∠=︒-,∵MN 是ABC 的中位线,∴MN AC∥∴MNB MBN θ∠=∠=,∵将BMN 绕点B 顺时针旋转α,得到BEF △,∴EBF MBN ≌,MBE NBF α∠=∠=,∴EBF EFB θ∠=∠=∴1802BEF θ∠=︒-,∵点,,C E F 在同一直线上,∴2BEC θ∠=∴180BEC BAC ∠+∠=︒,∴,,,A B E C 在同一个圆上,∴EAC EBC αθ∠=∠=-∴()()1802BAE BAC EAC θαθ∠=∠-∠=︒---180αθ=︒--∵ABF αθ∠=+,∴180BAE ABF ∠∠=+︒;如图所示,当F 在EC 上时,∵,BEF BAC BC BC∠=∠=∴,,,A B E C 在同一个圆上,设ABC ACB θ∠=∠=,则1802BAC BEF θ∠=∠=︒-,将BMN 绕点B 顺时针旋转α,得到BEF △,设NBF β∠=,则EBM β∠=,则360αβ+=︒,∴ABF θβ∠=-,∵BFE EBF θ∠=∠=,EFB FBC FCB∠=∠+∠∴ECB FCB EFB FBC θβ∠=∠=∠-∠=-,∵ EBEB =∴EAB ECB θβ∠=∠=-∴BAE ∠ABF=∠综上所述,BAE ABF ∠=∠或180BAE ABF ∠∠=+︒【点睛】本题考查了圆周角定理,圆内接四边形对角互补,相似三角形的性质与判定,旋转的性质,中位线的性质与判定,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质,勾股定理,熟练掌握以上知识是解题的关键.10.(2023·湖北黄冈·统考中考真题)【问题呈现】CAB △和CDE 都是直角三角形,90,,ACB DCE CB mCA CE mCD ∠=∠=︒==,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当1m =时,直接写出AD ,BE 的位置关系:____________;(2)如图2,当1m ≠时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当3,47,4m AB DE ===时,将CDE 绕点C 旋转,使,,A D E 三点恰好在同一直线上,求(2)解:成立;理由如下:∵90DCE ACB ∠=∠=︒,∴DCA ACE ACE ∠+∠=∠+(3)解:当点E 在线段AD设AD y =,则AE AD DE =+根据解析(2)可知,DCA △∴3BE BC m AD AC===,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.(1)若点P 在AB 上,求证:A P AP '=;(2)如图2.连接BD .①求CBD ∠的度数,并直接写出当180n =时,x 的值;②若点P 到BD 的距离为2,求tan A MP '∠的值;∵PM 平分A MA '∠∴90PMA ∠=︒∴PM AB∥∴DNM DBA V V ∽∴DN DM MN DB DA BA ==∵8,6,90AB DA A ==∠=︒,∴2226BD AB AD =+=+∴2103sin 3BQ BP DBA ===∠,∵90PQB CBD DAB ∠=∠=∠=︒,∴90QPB PBQ DBA ∠=︒-∠=∠,∵A MP AMP ' ≌,∴90PA M A '∠=∠=︒,(2)如图②,在矩形ABCD 的BC 边上取一点E ,将四边形ABED 沿DE 翻折,使点B '处,若24,6BC CE AB ⋅==,求BE 的值;(3)如图③,在ABC 中,45,BAC AD BC ∠=︒⊥,垂足为点,10,D AD AE ==于点F ,连接DF ,且满足2DFE DAC ∠=∠,直接写出53BD EF +的值.∵EF BC ∥,∴2CDF DFE ∠=∠=∴CDH FDH ∠=∠,又∵DH DH =,CHD ∠∴(ASA CHD FHD ≌【点睛】本题考查矩形的性质、翻折性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、锐角三角函数等知识,综合性强,较难,属于中考压轴题,熟练掌握相关知识的联系与运用,添加辅助线求解是解答的关键.13.(2023·湖南郴州·=,连接点E,使CE AD(1)如图1,当点D在线段AB上时,猜测线段CF与BD的数量关系并说明理由;(2)如图2,当点D在线段AB的延长线上时,①线段CF与BD的数量关系是否仍然成立?请说明理由;②如图3,连接AE.设4AB=,若AEB DEB∠=∠,求四边形BDFC的面积.【答案】(1)1CF BD=,理由见解析∴60,ADG ABC AGD ∠=∠=︒∠=∠∴ADG △为等边三角形,∴AD AG DG ==,∵AD CE =,AD AB AG AC -=-∴DG CE =,BD CG =,于点由①知:ADG △为等边三角形,∵ABC 为等边三角形,∴4,AB AC BC BH CH =====∴2223AH AB BH =-=,(1)若正方形ABCD 的边长为2,E 是AD 的中点.①如图1,当90FEC ∠=︒时,求证:AEF DCE ∽△△;②如图2,当2tan 3FCE ∠=时,求AF 的长;(2)如图3,延长CF ,DA 交于点G ,当1,sin 3GE DE FCE =∠=时,求证:,可得结论;正方形ABCD 中,①ADC BAD ∠=∠ ∴AEF CED ∠+∠=AEF ECD ∴∠=∠,延长DA ,CF 交于点G ,作GH CE ⊥,垂足为H ,90EDC EHG ∠=∠=︒ 且∠问题探究:(1)先将问题特殊化,如图(2),当90α=︒时,直接写出GCF ∠的大小;(2)再探究一般情形,如图(1),求GCF ∠与α的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120α=︒时,若12DG CG =,求BE CE 的值.故答案为:45︒.(2)解:在AB上截取ANABC BAE AEB∠+∠+∠=∠=∠,ABC AEF22⎝⎭(3)解:过点A作CD的垂线交CD的延长线于点【点睛】此题考查菱形性质、三角形全等、三角形相似,解题的关键是熟悉菱形性质、三角形全等、三角形相似.16.(2023·山西·统考中考真题)问题情境:“综合与实践沿对角线剪开,得到两个全等的三角形纸片,表示为∠=∠=︒∠=∠.将ABCACB DEF A D90,和DFE△(1)数学思考:谈你解答老师提出的问题;(2)深入探究:老师将图2中的DBE绕点B逆时针方向旋转,使点问题.∠①“善思小组”提出问题:如图3,当ABE②“智慧小组”提出问题:如图AH的长.请你思考此问题,直接写出结果.【答案】(1)正方形,见解析(2)①AM BE=,见解析;【分析】(1)先证明四边形形;∠(2)①由已知ABE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、正方形的判定与性质、相似三角形的判定与性质、三角函数、勾股定理等知识点,适当添加的辅助线、构造相似三角形是解题的关键.17.(2023·湖北十堰·统考中考真题)过正方形E ,连接AE ,直线AE 交直线(1)如图1,若25CDP ∠=︒,则DAF ∠=___________(2)如图1,请探究线段CD ,EF ,AF 之间的数量关系,并证明你的结论;(3)在DP 绕点D 转动的过程中,设AF a =,EF 【答案】(1)20︒。
中考数学题型三 选择压轴题之几何最值问题

类型 2 利用“轴对称”求最值
高分技法
“将军饮马”问题是中考的热点问题之一,解决这类问题的方法 是找出两定点中任一点关于动点所在直线的对称点,再将另一点 与对称点相连,连线与直线的交点即为所求的点.通常情况下,求 三角形或四边形的周长的最小值时,往往也是利用轴对称进行解 题(详细讲解见“高分突破·微专项 利用对称解决与线段长有 关的最值问题”).
类型 3 利用“隐形圆”求最值
高分技法
利用“到定点的距离等于定长的点位于同一个圆上”或“90°的 圆周角所对的弦是直径”等可以确定某些动点的运动轨迹是圆 (或圆弧).当圆外一定点与圆上一动点位于圆心同侧,且三点共线 时,该动点到圆外定点的距离最短; 当圆外一定点与圆上一动点 位于圆心异侧,且三点共线时,该动点到圆外定点的距离最长.
题型帮
题型三 选择压轴题之几何最值问题
目录
考法帮
• 类型1 利用“垂线段最短”求最值 • 类型2 利用“轴对称”求最值 • 类型3 利用“隐形圆”求最值 • 类型4 利用“旋转”求最值 • 类型5 利用二次函数的性质求最值
考法帮
类型 1 利用“垂线段最短”求最值
例1 如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB
类型 4 利用“旋转”求最值 例4 [2021山东淄博中考改编]两张宽为3的纸条交叉重叠成四边形 ABCD,如图所示.若α=30°,则对角线BD上的动点P到A,B,C三点距 离之和的最小值是 ( )B
A.3 B.6 2C.2 5D.5
类型 5 利用二次函数的性质求最值
例5 如图,在△ABC中,AB=AC=5,BC=4 5,D为边AB上一动点(不与B 点重合),以CD为一边作正方形CDEF,连接BE,则△BDE的面积的最大 值为 8 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题最值问题—— 1(几何模型)一、归于几何模型,这类模型又分为以下情况:1. 归于“两点之间的连线中,线段最短”。
凡属于求“变动的两线段之和的最小值”时,大都应用这一模型。
2.归于“三角形两边之差小于第三边”。
凡属于求“变动的两线段之差的最大值”时,大都应用这一模型。
3.利用轴对称知识(结合平移)。
4. 应用“点到直线的距离,垂线段最短。
”性质。
5. 定圆中的所有弦中,直径最长;以及直线及圆相切的临界位置等等。
二、基础知识模型(一)“将军饮马”问题1.如图1,将军骑马从A出发,先到河边a喝水,再回驻地B,问将军怎样走路程最短?2.如图,一位将军骑马从驻地M出发,先牵马去草地OA吃草,再牵马去河边OB喝水,最后回到驻地M,问:这位将军怎样走路程最短?图1 图23. 如图,A为马厩,B为帐篷,将军某一天要从马厩牵马,先到草地一处牧马,再到河边饮马,然后回到帐篷,请你帮助确定这一天的最短路线。
(二)“造桥选址”问题(选自人教版七年级下册)1. 如图1,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河两岸1l、l2平行,桥MN 及河岸垂直)练习:1. 如图,在边长为2㎝的正方形ABCD中,点Q为BC边的中点,点P为对角线AC 上一动点,连接PB、PQ,则△PBQ周长的最小值为____________㎝(结果不取近似值).1题图 2题图2.已知点A是半圆上的一个三等分点,点B是弧AN的中点,点P是半径ON上的动点,若⊙O的半径长为1,则AP+BP的最小值为__________.3.如图3,已知点A的坐标为(-4,8),点B的坐标为(2,2),请在x轴上找到一点P,使PA+PB最小,并求出此时P点的坐标和PA+PB的最小值。
变式1:如图,已知点A的坐标为(-4,8),点B的坐标为(2,2),点C的坐标为(-2,0).把点A和点B向左平移m个单位,得到点A'和点B',使C'最短,求m的值.+BCA'变式2:如图,已知点A的坐标为(-4,8),点B的坐标为(2,2),点C的坐标为(-2,0),点D的坐标为(-4,0).把点A和点B向左或向右平移m个单位,得到点A'和点B',使四边形A'B'CD的周长最短,求m的值.中考真题练习2.如图(1),抛物线3518532+-=x x y 和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长。
1.3.4.(广州 2014 24题)已知平面直角坐标系中两定点A (﹣1,0)、B (4,0),抛物线y=ax 2+bx ﹣2(a ≠0)过点A ,B ,顶点为C ,点P (m ,n )(n <0)为抛物线上一点.(1)求抛物线的解析式和顶点C 的坐标;(2)当∠APB 为钝角时,求m 的取值范围;(3)若m >23,当∠APB 为直角时,将该抛物线向左或向右平移t (0<t <25)个单位,点C 、P 平移后对应的点分别记为C ′、P ′,是否存在t ,使得首位依次连接A 、B 、P ′、C ′所构成的多边形的周长最短?若存在,求t 的值并说明抛物线平移的方向;若不存在,请说明理由.(三)垂线段最短问题1.如图,点A的坐标为(-1,0),点B在直线y x上运动,当线段AB最短时,点B 的坐标为( )A.(0,0)B.(21-,21-)C.(22,22-) D.(22-,22-)变式1. 已知点A 的坐标为(-4,8),点B 的坐标为(2,2),在y 轴上找一点M ,使点M 到点C (-2,0)的距离和到直线AB 的距离之和最小,请求出最小值。
2. 已知点A 的坐标为(-4,8),点B 的坐标为(2,2)已知点C '的坐标为(2,0),在y 轴上找一点N ,使点N 到点C '的距离和到直线AB 的距离之和最小,请求出最小值.中考真题训练1. 如图,已知点A(-4,8)和点B(2,n)在抛物线y=ax 2上,点C 坐标为(-2,0).(1) 求a 的值;(2) 在x 轴上找一点Q ,使得△QAB 的周长最小,求出点Q 的坐标;(3) 已知点D 的坐标为(2,0),在y 轴上找一点Q ,使点Q 到点D 的距离和到直线AB 的距离之和最小,请求出最小值.2.对于平面直角坐标系x0y 中的点平P (a ,b ),点P '的坐标为⎪⎭⎫⎝⎛++b ka kba ,(其中k 为常数,且k ≠0),则称点P '为点P 的“k 属派生点”.例如:P (1,4)的“2属派生点”P '为(1+24,2×1+4),即P '(3,6). (1)①点P (-1,-2)的“2属派生点” P '的坐标为 ____________;②若点P 的“k 属派生点”P '的坐标为(3,3),请写出一个符合条件的点P 的坐标____________;(2)若点P在x轴的正半轴上,点P的“k属派生点”为P'点,且△OP P'为等腰直角三角形,则k的值为________;(3)如图, 点Q的坐标为(0,34),点A 在函数()034<xxy-=的图象上,且点A是点B的“3-属派生点”,当线段B Q最短时,求B点坐标.(四)“三角形两边之差小于第三边” (线段差最大问题)1.已知点A的坐标为(-4,8),点B的坐标为(2,2),(1)如图(1)请在x轴上找到一点P,使PBPA-最大,并求出此时P点的坐标。
(2)如图(2)请在y轴上找到一点P,使PBPA-最大,并求出此时P点的坐标。
图1 图2中考真题练习1.(2014年广东深圳)如图,在平面直角坐标系中,⊙M过原点O,及x轴交于A(4,0),及y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.(1)求⊙M的半径;(2)证明:BD为⊙M的切线;(3)在直线MC上找一点P,使|DP﹣AP|最大.(五)及圆有关的最值问题(1)利用“相切”解决最值问题(2)利用“直径是最长的弦”求最值(3)利用“对角互补存隐圆”、“定弦定角存隐圆”、“定点定长存隐圆”求最值1.(2013•枣庄)如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是()A.90°B.60°C.45° D.30°1题图 2题图 3题图2.(2016 广州天河一模)如图,AB为⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°,若点M,N分别是AB,BC的中点,则线段MN长的最大值是 .3.(2014•武汉模拟)如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP、AO分别及⊙O交于B、C两点.若⊙O的半径长为3,OP=,则弦BC的最大值为()A.2 B.3 C. D.34. (2014春•兴化市月考)在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C为第一象限内一点,且AC=2,设tan∠BOC=m,则m的取值范围是()A.m≥0 B. C. D.4题图 5题图 6题图5.(2015 花都一模)如图,E ,F 是正方形ABCD 的边AD 上两个动点,满足AE=DF .连接CF 交BD 于点G ,连接BE 交AG 于点H .若正方形的边长为2,则线段DH 长度的最小值是 .6.(2013•内江)在平面直角坐标系xOy 中,以原点O 为圆心的圆过点A (13,0),直线y=kx ﹣3k+4及⊙O 交于B 、C 两点,则弦BC 的长的最小值为 .7.(2015•泰兴市二模)如图,定长弦CD 在以AB 为直径的⊙O 上滑动(点C 、D 及点A 、B 不重合),M 是CD 的中点,过点C 作CP ⊥AB 于点P ,若CD=3,AB=8,PM=l ,则l 的最大值是 .GCDE7题图 8题图 9题图8.如图,在Rt △ABC 中,∠ACB=90°,AC=4,BC=3,点D 是平面内的一个动点,且AD=2,M 为BD 的中点,在D 点运动过程中,线段CM 长度的取值范围是 . 9. 正方形ABCD 中,BC=4,E ,F 分别为射线BC ,CD 上两个动点,且满足BE=CF ,设AE ,BF 交于G ,则DG 的最小值为 .10.如图, 边长为3的等边△ABC , D 、E 分别为边BC 、AC 上的点, 且BD =CE , AD 、BE 交于P 点, 则CP 的最小值为 .10题图11.(2015•安徽)在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q 在⊙O上,且OP⊥PQ.(1)如图1,当PQ∥AB时,求PQ的长度;(2)如图2,当点P在BC上移动时,求PQ长的最大值.12.(2016 合肥模拟)如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不及A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD也经过点B,BA,PC相交于点E.BE的值;(1)当BA平分∠PBC时,求CD(2)已知:AC=1,BC=2,求△PCD面积的最大值。
13.在平面直角坐标系中,O为原点,点A (-2,0),点B (0,2),点E ,点F 分别为OA ,OB 的中点.若正方形OEDF 绕点O 顺时针旋转,得正方形OE’D’F’,若直线AE’及直线BF’相交于点P.(1)求∠PAO 的最大值; (2)点P 运动的路径长.xy PF'D'DEGAoF E'巩固练习1.如图1,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是m.(结果不取近似值)1题图 2题图 3题图2.如图2,有一圆柱体高为10cm,底面圆的半径为4cm, AA1、BB1为相对的两条母线。
在AA1上有一个蜘蛛Q,QA=3cm;在BB1上有一只苍蝇P,PB1=2cm。
蜘蛛沿圆柱体侧面爬到P点吃苍蝇,最短的路径是 cm.(结果用带π和根号的式子表示)3.(深圳福田模拟)如图,∠MON=20°,A为射线OM上一点,OA=4,D为射线ON 上一点,OD=8,C为射线AM上任意一点,B是线段OD上任意一点,那么折线ABCD 的长AB+BC+CD的最小值是 ______.4. (2010•苏州)如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙C上的一个动点,线段DA及y轴交于点E,则△ABE面积的最小值是()A.2 B.1 C . D .4题图 5题图 6题图5.(2014春•兴化市校级月考)如图所示,已知A(1,y1),B(2,y2)为反比例函数y=图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP及线段BP之差达到最大时,点P 的坐标是.6. (2013•武汉模拟)如图∠BAC=60°,半径长1的⊙O及∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为()A.3 B.6 C. D.7.(2015年武汉中考)如图,△ABC、△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是 .8.(2013•日照)问题背景:MFEGD CA如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC及BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接AB′及直线l交于点C,则点C即为所求.(1)实践运用:如图(b),已知,⊙O的直径CD为4,点A在⊙O上,∠ACD=30°,B为弧AD的中点,P为直径CD上一动点,则BP+AP的最小值为.(2)知识拓展:如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.9. 如图,已知点A(-4,8)和点B(2,n)在抛物线y=ax2上.(1)求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB 最短,求出点Q的坐标;(2)平移抛物线y=ax2,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.①当抛物线向左平移到某个位置时,A′C+CB′最短,求此时抛物线的函数解析式;②当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.备用图10. 已知:如图,AB是⊙O的直径,在AB的两侧有定点C和动点P,AB=5,AC=3.点P在上运动(点P不及A,B重合),CP交AB于点D,过点C作CP的垂线,及PB 的延长线交于点Q.(1)求∠P的正切值;(2)当CP⊥AB时,求CD和CQ的长;(3)当点P运动到什么位置时,CQ取到最大值?求此时CQ的长.11.先阅读材料,再解答问题:小明同学在学习及圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图,点A、B、C、D均为⊙O上的点,则有∠C=∠D.小明还发现,若点E在⊙O外,且及点D在直线AB同侧,则有∠D>∠E.请你参考小明得出的结论,解答下列问题:(1) 如图1,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0) .①在图1中作出△ABC的外接圆(保留必要的作图痕迹,不写作法);②若在x轴的正半轴上有一点D,且∠ACB=∠ADB,则点D的坐标为;(2) 如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为x轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标.12. (8分)(2016•北京)在平面直角坐标系xOy 中,点P 的坐标为 ()11,y x ,点Q 的坐标为 ()22,y x ,且 2121,y y x x ≠≠,若P ,Q 为某个矩形的两个顶点,且该矩形的边均及某条坐标轴垂直,则称该矩形为点P ,Q 的“相关矩形”,如图为点P ,Q 的“相关矩形”示意图.(1)已知点A 的坐标为(1,0),①若点B 的坐标为(3,1),求点A ,B 的“相关矩形”的面积;②点C 在直线x=3上,若点A ,C 的“相关矩形”为正方形,求直线AC 的表达式;(2)⊙O 的半径为2,点M 的坐标为(m ,3),若在⊙O 上存在一点N ,使得点M ,N 的“相关矩形”为正方形,求m 的取值范围.。
