维纳滤波与卡尔曼滤波
[PPT课件]现代信号处理-维纳和卡尔曼滤波
![[PPT课件]现代信号处理-维纳和卡尔曼滤波](https://img.taocdn.com/s3/m/ee37c56427d3240c8447ef41.png)
2.2 维纳滤波器的离散形式——时域解
2.2.2 维纳—霍夫方程
把k的取值代入(2.2.9)式, 得到:
当k=0时,h1rxx(0)+h2rxx(1)+…+hMrxx(M-1)=rxd(0) k=1时, h1rxx(1)+ h2rxx(0)+…+ hMrxx(M-2)= rxd(+1)
k=M-1时, h1rxx(M-1)+ h2rxx (M-2)+…+hMrxx(0)= rxd(M-1)
(2.2.10)
…
2.2 维纳滤波器的离散形式——时域解
2.2.2 维纳—霍夫方程 定义 T T h h1, h2 ,, hM , Rxd rxd (0), rxd (1),, rxd (M 1),
rxx (0) rxx (0) Rxx r ( M 1) xx
2.1 引 言
为了得到不含噪声的信号 s(n) ,也称为期望信号, 系统的期望输出用 yd(n)表示,yd(n)应等于信号的真值
若滤波系统的单位脉冲响应为 h(n) (如图 2.1.2 所示), s(n);系统的实际输出用y(n)表示,y(n)是s(n)的逼近或
估计,用公式表示为yd(n)=s(n), y(n) =
因此,维纳滤波器的传输函数H(z)的求解转化为 G(z)的求解。
x(n)
1 B( z)
(n )
G(z)
^ y(n)= s (n)
图 2.3.3 维纳滤波解题思路
2.3 离散维纳滤波器的Z域解
2.3.1 非因果维纳滤波器的求解
假设待求维纳滤波器的单位脉冲响应为 ω(n),期 望信号 d(n)=s(n) ,系统的输出信号 y(n)=s(n) , g(n) 是 G(z)的逆Z变换, 如图2.3.3所示。
讲维纳和卡尔曼滤波 kay的统计信号处理基础

讲维纳和卡尔曼滤波 kay的统计信号处理基础维纳和卡尔曼滤波是两种常用的统计信号处理方法。
维纳滤波是一种线性滤波方法,用于信号的恢复和优化,而卡尔曼滤波则是一种递推滤波方法,用于动态系统状态估计和预测。
它们在信号处理、控制系统、雷达等多个领域都有广泛的应用。
维纳滤波(Wiener Filter)是由美国工程师诺尔伯特·维纳在上世纪四十年代提出的。
它的基本思想是通过最小化估计值与实际值之间的平方误差,来优化信号的恢复。
维纳滤波器是一个线性时不变系统,通过对输入信号进行加权平均来恢复原始信号。
维纳滤波器的权重函数是通过信号的功率谱密度和叠加信号的互功率谱密度来计算的。
当信号和噪声的功率谱密度已知时,维纳滤波器可以恢复出信号的最佳估计。
维纳滤波的数学模型可以表示为:\[ Y(k) = \sum_{n=0}^{N-1}h(n)X(k-n) + V(k) \]其中,Y(k)是输出信号,X(k)是输入信号,h(n)是维纳滤波器的冲激响应,V(k)是噪声。
维纳滤波器的关键是计算出冲激响应h(n),一般通过信号和噪声的功率谱密度来求解。
维纳滤波器的优点是简单易实现,计算量小,且可以通过对输入信号进行适当的加权平均来降低噪声。
但是,维纳滤波器对噪声和信号的功率谱密度的估计要求较高,对于非线性系统和非高斯噪声的处理效果较差。
相对于维纳滤波器,卡尔曼滤波(Kalman Filter)是一种更为复杂和高级的滤波方法,它由美国数学家鲁道夫·卡尔曼在上世纪五十年代提出,并在航天和导航领域得到了广泛应用。
卡尔曼滤波器是一种递推滤波方法,适用于状态变量随时间演化的动态系统。
卡尔曼滤波的基本思想是通过对系统状态进行递推估计,同时考虑系统的测量值和预测值,并根据它们的权重对估计值进行修正。
卡尔曼滤波器使用线性动力学模型来描述系统的状态变化,并基于高斯分布的统计特性来推导出滤波器的数学公式。
卡尔曼滤波器的数学模型可以表示为:\[ X_{k+1} = AX_k +Bu_k + w_k \]和\[ Z_k = HX_k + v_k \]其中,X_k是系统的状态向量,A是状态转移矩阵,B是输入控制向量,u_k是输入信号,w_k是过程噪声,Z_k是系统的观测向量,H是观测转移矩阵,v_k是观测噪声。
维纳滤波器和卡尔曼滤波器

Rxx
(N
1)
Rxx (N 2)
Rxx (0) h(N 1)
Rxs
(N
1)
……………(7-16)
第16页,此课件共105页哦
简化形式:
RxxH=Rxs
(7-17)
式中,H=[h(0) h(1) …h(N-1)]′,是待求的单位脉冲响应;
Rxs= Rxs (0), Rxs (1),Rxs (N 1)′,是互相关序列;
…………………..(7-14)
N 1
Rxs ( j) hopt (m)Rxx ( j m) m0
j 0,1,2,, N 1
(7-15)
第15页,此课件共105页哦
于是得到N个线性方程:
j0
j 1
j N 1
Rxs (0) h(0)Rxx (0) h(1)Rxx (1) h(N 1)Rxx (N 1) Rxs (1) h(0)Rxx (1) h(1)Rxx (0) h(N 1)Rxx (N 2)
E
e2 (n)
m in
E
(Байду номын сангаас(n)
N 1 m0
hopt
(m)
x(n
m))
2
N 1
N 1 N 1
E[s 2 (n) 2s(n) h(m)x(n m)
hopt (m)x(n m)hopt (r)x(n r)]
m0
m0 r0
N1
N 1
N 1
Rss (0) 2 hopt (m)Rxs (m) hopt (m) hopt (r)Rxx (m r)
若要进一步减小误差可以适当增加维纳滤波的阶数,但相应的计算量也会增加。
第22页,此课件共105页哦
维纳滤波和卡尔曼滤波

维纳滤波和卡尔曼滤波
哇塞!同学们,你们听说过维纳滤波和卡尔曼滤波吗?反正一开始我是完全不知道这俩是啥玩意儿。
就好像在一个神秘的科学王国里,突然冒出来两个奇怪的名字。
维纳滤波,这名字听起来是不是有点像某个超级英雄的技能?可它不是用来拯救世界的,而是在信号处理的世界里大展身手呢!
有一次上科学课,老师讲起维纳滤波,我那叫一个懵啊!老师说它就像是一个超级聪明的小助手,能把那些乱糟糟的信号变得整整齐齐。
我就想,这难道是有魔法吗?比如说,我们听到的广播里有时候会有沙沙的杂音,维纳滤波就能把这些杂音去掉,让声音变得清晰又好听。
这难道不神奇吗?
再说卡尔曼滤波,它就像是一个预测大师。
比如说,我们预测明天会不会下雨,可能不太准。
但卡尔曼滤波就能根据一堆的数据和信息,更准确地预测出一些变化。
我问同桌:“你能明白这俩滤波是咋回事不?”同桌摇摇头说:“我也迷糊着呢!”
后来老师又举了个例子,说维纳滤波好比是个精心整理房间的小管家,把房间里乱七八糟的东西归置得井井有条;卡尔曼滤波呢,就像是个能提前知道你需要什么东西的小精灵,早早地就给你准备好。
哎呀,虽然听了老师这么多例子,我还是觉得这俩滤波有点难理解。
不过我想,只要我努力学习,总有一天能搞清楚它们的!
同学们,你们是不是也和我一样,对维纳滤波和卡尔曼滤波充满了好奇和探索的欲望呢?反正我是下定决心要把它们弄明白啦!。
第七章 维纳滤波和卡尔曼滤

输入该滤波器时,在输出端能将信号尽可能精确地 表现出来。维纳滤波和卡尔曼滤波就是用来解决这 样一类问题的方法:从噪声中提取出有用的信号。 实际上,这种线性滤波方法也被看成是一种估计问 题或者线性预测问题。
设有一个线性系统,它的单位脉冲响应是,当输入一 个观测到的随机信号,简称观测值,且该信号包含噪 声和有用信号,简称信号,也即
]
= E[ s (n) − 2 s (n) ∑ h(m) x(n − m) + ∑∑ hopt (m) x(n − m)hopt (r ) x(n − r )]
m =0 m =0 r =0
N −1 = Rss (0) − 2∑ hopt (m) R xs (m) + ∑ hopt (m) ∑ hopt (r ) R xx (m − r ) m=0 m =0 r =0
N −1
N −1
由式(7 15)进一步化简得 由式(7-15)进一步化简得:
E[e ( n)] min = Rss (0) − ∑ hopt ( m) R xs (m)
2 m =0 N −1
(7-19)
用有限长的 h(n) 来实现维纳滤波时,当 已知观测值的自相关和观测值与信号的互 相关时就可以按照式(7-15)在时域里求解 hopt (n) 但是当N比较大时,计算量很大,并 且涉及到求自相关矩阵的逆矩阵问题。
……………(7-16)
简化形式:
RxxH=Rxs (7-17)
式中,H=[h(0) h(1) …h(N-1)]′,是待求的单位脉冲 响应;
Rxs= Rxx= =
[R xs (0), R xs (1),⋯ R xs ( N − 1)] ′,是互相关序列;
R xx (1) R xx (0) R (1) R xx (0) xx ⋮ ⋮ R xx ( N − 1) R xx ( N − 2) ⋯ R xx ( N − 1) ⋯ R xx ( N − 2) ,是自相关矩阵 ⋯ ⋮ ⋯ R xx (0)
第2章 维纳滤波和卡尔曼滤波

维纳 滤波器
相关函数
H(z)或h(n)
平稳
解析形式
卡尔曼 滤波器
前一个估 计值和最 近的观察
状态方程 量测方程
状态变量 估计值
平稳或 递推算法 非平稳
60 年代
2018年10月9日星期二
15:38:36
4
153
2.2 维纳滤波器的离散形式—时域解
§2.2 维纳滤波器的离散形式—时域解 2.2.1 维纳滤波器时域求解的方法 考虑到系统的因果性,即h(n)=0,n<0 (2.2.2) 设期望信号为d(n),计算误差和均方误差为 e(n)=d(n) -y(n)=s(n) -y(n) (2.2.3) (2.2.4)
15:38:36
24
153
2.2 维纳滤波器的离散形式—时域解
v2(n)是一个零均值的白噪声,它的自相关函数矩阵呈对角形,
且
2 rv2v2 (, 0) 2
因此,输出信号的自相关Ryy为
2018年10月9日星期二
15:38:36
25
153
2.2 维纳滤波器的离散形式—时域解
(3) 计算输出信号与期望信号的互相关函数矩阵。 由于两个信 号都是实信号,故 ryd(m)=E[y(n)d(n-m)]=E[y(n)x1(n-m)] =E[(x(n)+v2(n))x1(n-m)]=E[x(n)x1(n-m)] m=0, 1 根据图2.2.2系统H2(z)的输入与输出的关系, 有 x1(n)-b1x(n-1)=x(n) 这样 x1(n)=x(n)+b1x(n-1)
2018年10月9日星期二 15:38:的离散形式—时域解
% 滤波 y = filter(Wopt, 1, x); % 误差 En = d - y'; % 结果 figure, plot(n, d, 'r:', n, y, 'b-'); legend('维纳滤波信号真值','维纳滤波估计值'); title('期望信号 与滤波结果对比'); xlabel('观测点数');ylabel('信号幅度');figure, plot(n , En); title('维纳滤波误差曲线'); xlabel('观测点数');ylabel('误差幅度'); toc
第二章—维纳滤波和卡尔曼滤波

H
c
(z)
2
1 B(
z)
[
Ssx (z) B(z 1 )
]
• 计算步骤如下:
•
(1)对
S xx
(z)
进行谱分解(因式分解)
S
x
x
(
z)
2
B(
z)
B(
z
1
)
• (2)对 Ssx (z)
进行因果和逆因果分解
B(z 1 )
Ssx (z) B(z 1 )
[
Ssx (z B(z 1
) )
]
[
Ssx (z B(z 1
N
• 称y(n) 是 sˆ(n)的估计值。 h(n) 为估计器。这种滤波器
称为最佳滤波器。
• 如果:s(n) 和 v(n) 的谱在频域上是分离的,容易设计一个
线性滤波器抑制噪声并提取信号。这是本科中经典数字信号 处理理论中详细讨论过的数字滤波器的设计问题。但是
• s(n) 和 v(n) 的谱有一部分相互重叠,则问题就要复杂的
E[e(n) x(n j)] 0
• 上式称为正交方程。(这是讲当用两个矢量正交时它们的 点乘等于零的关系,正交性原理可借用几何图形表示)
• 可见,满足正交性原理与满足最小均方误差的条件是等价
的。由图知,sˆ(n) 最满足最小均方误差的估计值。
• 正交方程表明,任何时刻的估计误差与用于估计的所有数 据(即滤波器的输入)正交。
• (2)
Ssx (z) B( z 1 )
[
Ssx (z B( z 1
) )
]
[
Ssx (z B( z 1
) )
]
0.36
(1 0.8z 1 )(1 0.8z)
维纳滤波与卡尔曼滤波

第二章 维纳滤波与卡尔曼滤波§2.1 引言信号处理的实际问题,常常是要解决在噪声中提取信号的问题,因此,我们需要寻找一种所谓有最佳线性过滤特性的滤波器。
这种滤波器当信号与噪声同时输入时,在输出端能将信号尽可能精确地重现出来,而噪声却受到最大抑制。
维纳(Wiener)滤波与卡尔曼(Kalman)滤波就是用来解决这样一类从噪声中提取信号问题的一种过滤(或滤波)方法。
实际上这种线性滤波问题,可以看成是一种估计问题或一种线性估计问题。
一个线性系统,如果它的单位样本响应为h (n ),当输入一个随机信号x (n ),且)()()(n n s n x υ+=(2.1)其中s (n )表示信号,)(n υ表示噪声,则输出y (n )为∑-=mm n x m h n y )()()((2.2)我们希望x (n )通过线性系统h (n )后得到的y (n )尽量接近于s (n ),因此称y (n )为s (n )的估计值,用)(ˆn s表示,即)(ˆ)(n sn y = (2.3)图2.1 维纳滤波器的输入—输出关系如图2.1所示。
这个线性系统)(⋅h 称为对于s (n )的一种估计器。
实际上,式(2.2)的卷积形式可以理解为从当前和过去的观察值x (n ),x (n -1),x (n -2)…x (n -m ),…来估计信号的当前值)(ˆn s。
因此,用)(⋅h 进行过滤的问题可以看成是一个估计问题。
由于我们现在涉及的信号是随机信号,所以这样一种过滤问题实际上是一种统计估计问题。
一般,从当前的和过去的观察值x (n ),x (n -1),x (n -2),…估计当前的信号值)(ˆ)(n s n y =称为过滤或滤波;从过去的观察值,估计当前的或将来的信号值)0)((ˆ)(≥+=N N n sn y 称为预测或外推;从过去的观察值,估计过去的信号值)1)((ˆ)(>-=N N n sn y 称为平滑或插。
维纳滤波与卡尔曼滤波

FIR : IIR :
0 ~ M 1 ~ (非因果); 0 ~ (因果)
11
定义
第 四 章 维 纳 滤 波 和 卡 尔 曼 滤 波
h1 h2 h hM rxx (0) rxx (0) Rxx r ( M 1) xx
8
4.2 维纳滤波器的离散形式—时域解
第 四 章 维 纳 滤 波 和 卡 尔 曼 滤 波
x ( n) s ( n) v ( n)
i
(加性干扰)
ˆ(n) h(i ) x(n i ) x(n) h(n) y ( n) s ˆ( n ) ] 均方误差: (n) E[e (n)] E[ s (n) s
第 四 章 维 纳 滤 波 和 卡 尔 曼 滤 波
例
设y(n)=x(n)+v2(n),v2(n)是一白噪声,方差
σ22=0.1 。期望信号 x1(n) 的信号模型如图 (a) 所示, 其中白噪声 v1(n) 的方差 σ21=0.27 ,且 b0=0.8458 。
x(n)的信号模型如图(b)所示,b1=0.9458。假定
rxd (0) rxd (1) Rxd rxd ( M 1) rxx ( M 1) rxx (0) rxx ( M 2) rxx ( M 2) rxx (0) rxx (1)
12
第 四 章 维 纳 滤 波 和 卡 尔 曼 滤 波
* 2 * T h ( k ) r ( k ) ( h ) Rxd xd d
1 d2 ( Rdx )H Rxx Rdx
可以看出,均方误差与滤波器的单位脉冲响应是一个 二次函数关系。由于单位脉冲响应h(n) 为M维向量, 因此均方误差是一个超椭圆抛物形曲面,该曲面有极 小点存在。当滤波器工作于最佳状态时,均方误差取 得最小值。 16
维纳滤波和卡尔曼滤波
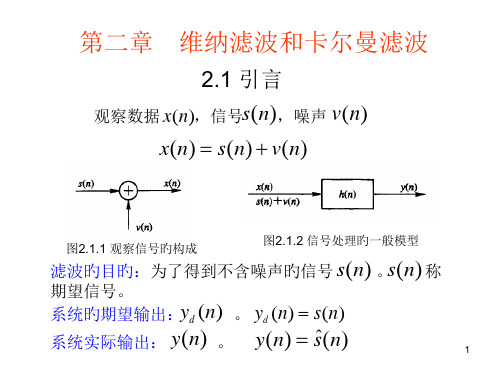
2.2 维纳滤波器旳离散形式--时域解
维纳滤波器设计旳任务就是选择 h(n),使其输出信号 y(n) 与期望信号 d (n)误差旳均方值最小,实质是解维纳-霍夫方程。
2.2.1维纳滤波器时域求解旳措施
假设滤波系统 h(n)是一种线性时不变系统,它旳h(n)和输 入信号都是复函数,设
h(n) a(n) jb(n)
系统实际输出: y(n) 。 y(n) sˆ(n) 1
预测:已知过去旳观察值 x(n 1), x(n 2), , x(n m),估计 目前及后来时刻旳信号值 sˆ(n N ) , N 0 。 滤波:已知目前和过去旳观察值 x(n), x(n 1), , x(n m) ,
估计目前旳信号sˆ(n) 。
卡尔曼滤波是20世纪60年代由卡尔曼提出旳。
2
维纳滤波和卡尔曼滤波比较:
共同点:都处理最佳线性滤波和预测问题,都以均方误差最 小为最优准则,平稳条件下它们得到旳稳态成果一致。 不同点: (1)维纳滤波根据 x(n), x(n 1), , x(n m) 估计信号旳目前值,
它旳解以系统旳系统函数H (z)或单位脉冲响应h(n)形式给出。
M 1
i0
h(i)x(n
i)
17
E
e(n)
2
E
d
(n)
2
M 1
k 0
h
(k
)E
x
(n
k)d
(n)
M 1
M 1 M 1
h(i)E x(n i)d (n) h(k)h(i)E[x*(n k)x(n i)]
i0
k0 i0
M 1
M 1(k
19
2.3离散维纳滤波旳Z域解
时域求解Wiener滤波器很困难,用Z域求解。又因为实际旳系统是因果旳,
卡尔曼滤波与维纳滤波在信号处理中的应用研究

卡尔曼滤波与维纳滤波在信号处理中的应用研究
卡尔曼滤波是一种线性的、递归的滤波算法,它能够对信号的状态进行估计和预测。
卡尔曼滤波是基于贝叶斯估计理论的一种优化方法,它不仅可以有效地消除噪声和偏差,还可以根据已有的历史数据对信号进行预测。
卡尔曼滤波广泛应用于航空航天、控制理论、信号处理等领域,是一种非常有效的信号处理算法。
维纳滤波是一种信号处理中最常用的滤波算法之一,它能够根据现有数据对信号进行优化处理,消除噪声和干扰,实现信号的恢复和重建。
维纳滤波利用了信号和噪声的统计特性,根据信号的功率谱和噪声的功率谱来进行滤波处理。
维纳滤波不仅可以用于图像处理、语音处理等多种信号处理领域,还可以应用于雷达信号处理、无线通信等工程实践中。
在实际应用中,卡尔曼滤波和维纳滤波通常结合使用,以获得更为准确和可靠的信号处理效果。
如在雷达信号处理中,利用卡尔曼滤波进行预测和估计,再经过维纳滤波进行优化处理,可以有效地消除噪声和干扰,获得高质量的信号信息。
在图像处理中,卡尔曼滤波和维纳滤波也可以结合使用,以实现图像的优化重建和增强。
总的来说,卡尔曼滤波和维纳滤波在信号处理中的应用非常广泛,可以有效地消除噪声和干扰,提高信号和数据的质量和可靠性,对于工程实践和科学研究都具有重要意义。
维纳滤波和卡尔曼滤波的联系与区别

随机信号或随机过程(random process)是普遍存在的。
一方面,任何确定性信号经过测量后往往就会引入随机性误差而使该信号随机化;另一方面,任何信号本身都存在随机干扰,通常把对信号或系统功能起干扰作用的随机信号称之为噪声。
噪声按功率谱密度划分可以分为白噪声(white noise )和色噪声(color noise ),我们把均值为0的白噪声叫纯随机信号(pure random signal )。
因此,任何其它随机信号都可看成是纯随机信号与确定性信号并存的混合随机信号或简称为随机信号。
要区别干扰(interference )和噪声( noise)两种事实和两个概念。
非目标信号(nonobjective signal )都可叫干扰。
干扰可以是确定信号,如国内的50Hz 工频干扰。
干扰也可以是噪声,纯随机信号(白噪声)加上一个直流成分(确定性信号),就成了最简单的混合随机信号。
医学数字信号处理的目的是要提取包含在随机信号中的确定成分,并探求它与生理、病理过程的关系,为医学决策提供一定的依据。
例如从自发脑电中提取诱发脑电信号,就是把自发脑电看成是干扰信号,从中提取出需要的信息成分。
因此我们需要寻找一种最佳线性滤波器,当信号和干扰以及随机噪声同时输入该滤波器时,在输出端能将信号尽可能精确地表现出来。
维纳滤波和卡尔曼滤波就是用来解决这样一类问题的方法:从噪声中提取出有用的信号。
实际上,这种线性滤波方法也被看成是一种估计问题或者线性预测问题。
由当前时刻的观测值和过去时刻的观测值、、…的估计值。
用当前的和过去的观测值来估计当前的信号称为滤波;用过去的观测值来估计当前的或将来的信号,N ,称为预测;用过去的观测值来估计过去的信号,N ,称为平滑或者内插。
本章将讨论滤波和预测问题。
维纳滤波和卡尔曼滤波都是解决线性滤波和预测问题的方法,并且都是以均方误差最小为准则的,在平稳条件下两者的稳态结果是一致的。
但是它们解决问题的方法有很大区别。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 维纳滤波与卡尔曼滤波§ 引言信号处理的实际问题,常常是要解决在噪声中提取信号的问题,因此,我们需要寻找一种所谓有最佳线性过滤特性的滤波器。
这种滤波器当信号与噪声同时输入时,在输出端能将信号尽可能精确地重现出来,而噪声却受到最大抑制。
维纳(Wiener)滤波与卡尔曼(Kalman)滤波就是用来解决这样一类从噪声中提取信号问题的一种过滤(或滤波)方法。
实际上这种线性滤波问题,可以看成是一种估计问题或一种线性估计问题。
一个线性系统,如果它的单位样本响应为h (n ),当输入一个随机信号x (n ),且)()()(n n s n x υ+=其中s (n )表示信号,)(n υ表示噪声,则输出y (n )为∑-=mm n x m h n y )()()(我们希望x (n )通过线性系统h (n )后得到的y (n )尽量接近于s (n ),因此称y (n )为s (n )的估计值,用)(ˆn s表示,即)(ˆ)(n sn y =图 维纳滤波器的输入—输出关系如图所示。
这个线性系统)(⋅h 称为对于s (n )的一种估计器。
实际上,式的卷积形式可以理解为从当前和过去的观察值x (n ),x (n -1),x (n -2)…x (n -m ),…来估计信号的当前值)(ˆn s。
因此,用)(⋅h 进行过滤的问题可以看成是一个估计问题。
由于我们现在涉及的信号是随机信号,所以这样一种过滤问题实际上是一种统计估计问题。
一般,从当前的和过去的观察值x (n ),x (n -1),x (n -2),…估计当前的信号值)(ˆ)(n s n y =称为过滤或滤波;从过去的观察值,估计当前的或将来的信号值)0)((ˆ)(≥+=N N n sn y 称为预测或外推;从过去的观察值,估计过去的信号值)1)((ˆ)(>-=N N n sn y 称为平滑或内插。
因此维纳过滤与卡尔曼过滤又常常被称为最佳线性过滤与预测或线性最优估计。
这里所谓“最佳”与“最优”是以最小均方误差为准则的。
本章仅讨论过滤与预测问题。
如果我们以ss ˆ与分别表示信号的真值与估计值,而用e (n )表示它们之间的误差,即)(ˆ)()(n sn s n e -=显然,e (n )可能是正的,也可能是负的,并且它是一个随机变量。
因此,用它的均方值来表达误差是合理的,所谓均方误差最小即它的平方的统计平均值最小:[][]22)ˆ()(ss E n e E -= 最小采用最小均方误差准则作为最佳过滤准则的原因还在于它的理论分析比较简单,不要求对概率的描述。
并且在这种准则下导出的最佳线性系统对其它很广泛一类准则而言也是最佳的。
维纳过滤与卡尔曼过滤都是解决最佳线性过滤和预测问题,并且都是以均方误差最小为准则的。
因此在平稳条件下,它们所得到的稳态结果是一致的。
然而,它们解决的方法有很大区别。
维纳过滤是根据全部过去的和当前的观察数据 ),2( ),1( ),(--n x n x n x 来估计信号的当前值,它的解是以均方误差最小条件下所得到的系统的传递函数H (z )或单位样本响应h (n )的形式给出的,因此更常称这种系统为最佳线性过滤器或滤波器。
而卡尔曼过滤是用前一个估计值和最近一个观察数据(它不需要全部过去的观察数据)来估计信号的当前值,它是用状态方程和递推的方法进行估计的,它的解是以估计值(常常是状态变量值)形式给出的。
因此更常称这种系统为线性最优估计器或滤波器。
维纳滤波器只适用于平稳随机过程,而卡尔曼滤波器却没有这个限制。
维纳过滤中信号和噪声是用相关函数表示的,因此设计维纳滤波器要求已知信号和噪声的相关函数。
卡尔曼过滤中信号和噪声是状态方程和量测方程表示的,因此设计卡尔曼滤波器要求已知状态方程和量测方程(当然,相关函数与状态方程和量测方程之间会存在一定的关系,见图及例3)。
卡尔曼过滤方法看来似乎比维纳过滤方法优越,它用递推法计算,不需要知道全部过去的数据,从而运用计算机计算方便,而且它可用于平稳和不平稳的随机过程(信号),非时变和时变的系统。
但从发展历史上来看维纳过滤的思想是40年代初提出来的,1949年正式以书[1]的形式出版。
卡尔曼过滤到60年代初才提出来[2],它是在维纳过滤的基础上发展起来的,虽然如上所述它比维纳过滤方法有不少优越的地方,但是最佳线性过滤问题是由维纳过滤首先解决的,维纳过滤的物理概念比较清楚,也可以认为卡尔曼滤波仅仅是对最佳线性过滤问题提出的一种新的算法。
§ 维纳滤波器的离散形式(I) —— 时域解维纳过滤最初是对连续信号用模拟滤波器的形式出现的,而后才有离散形式。
我们这里仅讨论维纳滤波的离散形式。
设计维纳滤波器的过程就是寻求在最小均方误差下滤波器的单位样本响应h (n )或传递函数H (z )的表达式,其实质是解维纳-霍夫(Wiener-Hopf)方程。
在要求满足因果性即物理可实现性的条件下,求解维纳-霍夫方程是一个典型的难题。
本节我们在时域求最小均方误差下的h (n ),并用)(n h opt 表示。
按图及式、、有∑-==mm n x m h n sn y )()()(ˆ)( 一个物理可实现的h (n ),必须是一个因果序列,即h (n )=0 当n <0因此上式的求和上下限应从0到∞,即∑∞=-==0)()()(ˆ)(m m n x m h n sn y上式可看成输出等于现在和过去各输入的加权之和。
为了讨论方便,上式可写成下列形式:∑∞==1)(ˆi i i x h n s式与式有如下关系:⎪⎭⎪⎬⎫-=+-==-=-=+=)()1()()1(11m n x i n x x m h i h h i m m i i i 或于是[]⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=∑∞=212)()(i i i x h n s E n e E现在的问题是需要求得使()[]2ˆss E -最小的i h ,为此,将上式对各h i 求偏导,并令其结果等于0,得)112()0 102()010i i i i j i i i i j E s n h x x j E ex E s n h x x j E ex ∞=∞=⎫⎡⎤⎛-=⎪⎢⎥ ⎝≥⎣⎦⎬⎪⎡⎤=⎣⎦⎭⎫⎡⎤⎛⎫-=⎪⎢⎥ ⎪⎝⎭≥⎣⎦⎬⎪⎡⎤=⎣⎦⎭∑∑式(2-10)称为正交性原理,这是借用当二个矢量正交时它们的点乘等于零的关系。
正交性原理也可以借用几何图形表示,如图所示。
正交性原理容易用i 的求和项数为2的特殊情况予以推广来理解。
在此情况下,21ˆx x s和必在共有的平面中,而e 则垂直于此平面,于是,21 ,x e x e ⊥⊥同时,此时e 的长度最短。
1z即图 用几何图形理解正交性原理由式可见,满足正交性原理与满足最小均方误差的条件是等价的。
由图所得到的sˆ即是满足最小均方误差的估计值。
因而我们可以从式中解得opt h 。
如果令[][]j j i sx j x x j i sx E x x E φφ∆∆及分别为x 的自相关函数和x 与s 的互相关函数,代入式得正交性原理的另一表达形式是∑∞=≥=11 ,i x x i s x j h ij jφφ如果我们将式的关系代回式及式,则式及式分别成为0 0)()()()(0≥=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡--∑∞=k k n x m n x m h n s E m opt及0k ,)()()(0≥-=∑∞=m k m h k xx m opt xs φφ式与式称为维纳-霍夫方程(离散形式)。
从维纳-霍夫方程式中解出h ,它就是在最小均方误差下的最佳)(opt h h =。
注意式(或式)有一个约束条件)1(0≥≥j k 或,因此,虽然在式中的h (k )与)(k xs φ有卷积的形式,但是我们不能简单地将式应用卷积定理变换到z 域求H (z ),然后从H (z )的反z 变换求得h (k )。
有了0≥k 这个约束条件,要从维纳-霍夫方程求解最佳h (k )就变得困难。
式中0≥k 的约束条件是来源于我们假设了h (n )是一个物理可实现的因果序列。
如果不加物理可实现的约束,式中的0≥k 的约束条件也将不复存在。
因此非因果的维纳-霍夫方程为∑∞-∞=-=m xx optxs m k m hk )()()(φφ它没有约束条件,我们容易把它变换到z 域得 )()()(z z H z xx opt xs φφ=()()()xs opt xx z H z z φφ=或[]⎥⎦⎤⎢⎣⎡==--)()(Ζ)(Ζ)(11z z z H n h xx xs opt opt φφ从式来看,0≥k 的约束就是只能取过去和当前的)(⋅x 的读数。
如果从{})()(n s n x 求的估计值,并不要求在当时立即得到,而许可在将来(经过等待或滞后)得到,那么式的求和下限就不限制在m =0而可以允许m <0,此时,就没有h (m <0)=0的约束,对于方程,相应地也就没有k >0的约束了。
但是,如果我们不容许上述等待或滞后,那就必须考虑因果性约束,此时可以用下列方法来逼近,从而得到方程的解。
设h (n )是一个因果序列可以用有限长(长度为N )的序列去逼近它,此时式,,,,分别成为⎪⎪⎭⎪⎪⎬⎫=-==∑∑=-=Ni i i N m x h n sm n x m h n sn y 11)(ˆ)()()(ˆ)([]⎪⎭⎪⎬⎫===⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-∑=0 , ,2 ,1 ,01j i N i i i ex E N j x x h s E⎪⎪⎭⎪⎪⎬⎫-=-===∑∑-==1011 , ,1 ,0k ),()()( , ,2 ,1 ,N m xx xs Ni x x i s x N m k m h k Nj h ij j φφφφ于是我们可以将式的维纳-霍夫方程写成矩阵形式。
为此先将式中j =1, 2, …, N 分别代入,写成N 个线性方程:⎪⎪⎭⎪⎪⎬⎫=+++==+++==+++=s x x x N x x x x s x x x N x x x x sx x x N x x x x N N N N N N N h h h N j h h h j h h h j φφφφφφφφφφφφ 21222212112111212121 2 1于是,它的矩阵形式为[][][]xx xs h φφ=式为维纳-霍夫方程的矩阵形式,其中[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=N h h h h 21式中h 1, h 2, …, h N 为h (n )序列在n =0, 1, …, N -1时的值。
[]⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=N N N N N N x x x x x x x x x x x x x x x x x x xx φφφφφφφφφφ 212221212111称为x 的自相关矩阵。
