沪教版初三上册396660《相似三角形》全章复习与巩固(基础) 知识讲解
最新沪科版九年级相似三角形知识点汇总讲义

相似三角形·基本知识讲义知识点一:放缩与相似1.图形的放大或缩小,称为图形的放缩运动。
2.把形状相同的两个图形说成是相似的图形,或者就说是相似性。
注意:⑴相似图形强调图形形状相同,与它们的位置、颜色、大小无关。
⑵相似图形不仅仅指平面图形,也包括立体图形相似的情况。
⑶我们可以这样理解相似形:两个图形相似,其中一个图形可以看作是由另一个图形放大或缩小得到的.⑷若两个图形形状与大小都相同,这时是相似图形的一种特例——全等形.3.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例。
注意:当两个相似的多边形是全等形时,他们的对应边的长度的比值是1. 知识点二:比例线段有关概念及性质(1)有关概念1.比:选用同一长度单位量得两条线段。
a 、b 的长度分别是m 、n ,那么就说这两条线段的比是a :b =m :n (或nm b a =) 2.比的前项,比的后项:两条线段的比a :b 中。
a 叫做比的前项,b 叫做比的后项。
说明:求两条线段的比时,对这两条线段要用同一单位长度。
3.比例:两个比相等的式子叫做比例,如d c b a = 4.比例外项:在比例dc b a =(或a :b =c :d )中a 、d 叫做比例外项。
5.比例内项:在比例dc b a =(或a :b =c :d )中b 、c 叫做比例内项。
6.第四比例项:在比例dc b a =(或a :b =c :d )中,d 叫a 、b 、c 的第四比例项。
7.比例中项:如果比例中两个比例内项相等,即比例为ab b a =(或a:b =b:c 时,我们把b 叫做a 和d 的比例中项。
8.比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即dc b a =(或a :b=c :d ),那么,这四条线段叫做成比例线段,简称比例线段。
(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位)(2)比例性质1.基本性质:bc ad d c b a =⇔= (两外项的积等于两内项积) 2.反比性质: cd a b d c b a =⇒= (把比的前项、后项交换) 3.更比性质(交换比例的内项或外项):()()()a b c d a c d c b d ba dbc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项4.合比性质:d d c b b a d c b a ±=±⇒=(分子加(减)分母,分母不变). 注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.5.等比性质:(分子分母分别相加,比值不变.) 如果)0(≠++++====n f d b nm f e d c b a ,那么b a n f d b m e c a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种方法.(2)应用等比性质时,要考虑到分母是否为零.(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.知识点三:黄金分割1)定义:在线段AB 上,点C 把线段AB 分成两条线段AC 和BC (AC >BC ),如果AC BC AB AC =即AC 2=AB ×BC ,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比。
沪科版九上数学相似三角形知识点总结 (2)

沪科版九上数学图形的相似 知识点总结知识点一1.相似图形:把具有相同形状的图形称为相似图形。
2.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边成比例。
知识点二:比例线段1.比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即dc b a =(或a :b=c :d ),那么,这四条线段叫做成比例线段,简称比例线段。
(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位)2.比例性质的基本性质: bc ad d c b a =⇔= (两外项的积等于两内项积)3.更比性质(交换比例的内项或外项):()()()a b c d a c d c b d b ad b c a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项4.合比性质:dd c b b a d c b a ±=±⇒=(分子加(减)分母,分母不变) 5.等比性质:(分子分母分别相加,比值不变.) 如果)0(≠++++====n f d b n m fe d c b a ,那么ba n f db m ec a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法.(2)应用等比性质时,要考虑到分母是否为零.知识点三:黄金分割1. 定义:在线段AB 上,点C 把线段AB 分成两条线段AC 和BC (AC >BC ),如果AC BC AB AC =,即AC 2=AB×BC ,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比。
其中AB AC 215-=≈0.618AB 。
知识点四:相似三角形1.相似三角形:两个三角形中,如果三角对应相等,三边对应成比例,那么这两个三角形叫做相似三角形。
如△ABC 与△DEF 相似,记作△ABC ∽△DEF 。
沪教版 九年级(上)数学 秋季课程 第2讲 相似三角形(解析版)
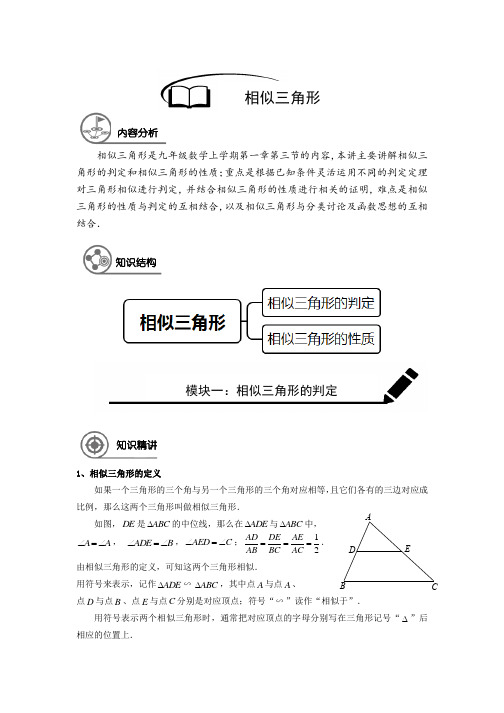
DABCE相似三角形是九年级数学上学期第一章第三节的内容,本讲主要讲解相似三角形的判定和相似三角形的性质;重点是根据已知条件灵活运用不同的判定定理对三角形相似进行判定,并结合相似三角形的性质进行相关的证明,难点是相似三角形的性质与判定的互相结合,以及相似三角形与分类讨论及函数思想的互相结合.1、相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等,且它们各有的三边对应成比例,那么这两个三角形叫做相似三角形.如图,DE 是ABC ∆的中位线,那么在ADE ∆与ABC ∆中,A A ∠=∠, ADEB ∠=∠,AEDC ∠=∠;12AD DE AE AB BC AC ===. 由相似三角形的定义,可知这两个三角形相似.用符号来表示,记作ADE ∆∽ABC ∆,其中点A 与点A 、点D 与点B 、点E 与点C 分别是对应顶点;符号“∽”读作“相似于”.用符号表示两个相似三角形时,通常把对应顶点的字母分别写在三角形记号“∆”后相应的位置上.相似三角形内容分析知识结构模块一:相似三角形的判定知识精讲2 / 31ABCA 1B 1C 1根据相似三角形的定义,可以得出:(1)相似三角形的对应角相等,对应边成比例;两个相似三角形的对应边的比,叫做这两个三角形的相似比(或相似系数).(2)如果两个三角形分别与同一个三角形相似,那么这两个三角形也相似. 2、相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似. 如图,已知直线l 与ABC ∆的两边AB 、AC 所在直线分别交于点D 和点E ,则ADE ∆∽ABC ∆.3、相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等,那么这两个三角形相似. 可简述为:两角对应相等,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果1A A ∠=∠、1B B ∠=∠,那么ABC ∆∽111A B C ∆.常见模型如下:A BCDEABCDEABCDEABCA 1B 1C 1ABCA 1B 1C 14、相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.可简述为:两边对应成比例且夹角相等,两个三角形相似.如图,在ABC ∆与111A B C ∆中,1A A ∠=∠,1111AB ACA B AC =,那么ABC ∆∽111A B C ∆.5、相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.可简述为:三边对应成比例,两个三角形相似. 如图,在ABC ∆与111A B C ∆中,如果111111AB BC CAA B B C C A ==,那么ABC ∆∽111A B C ∆.6、直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例,那么这两个直角三角形相似.可简述为:斜边和直角边对应成比例,两个直角三角形相似.如图,在Rt ABC ∆和111Rt A B C ∆中,如果190C C ∠=∠=︒,1111AB BCA B B C =,那么ABC ∆∽111A B C ∆.ABCA 1B 1C 14 / 31【例1】如图,已知点P 是ABC ∆中边AC 上一点,联结BP ,要使ABP ∆∽ACB ∆,那么应 添加的一个条件为____________,或____________,或____________.【答案】C ABP ∠=∠,ABC APB ∠=∠,AB APAC AB=. 【解析】根据相似三角形的判定定理1和判定定理2,题 目中有公共角,只需要加上一个等角或夹这个角的两边对应成比例的条件即可.【总结】考查相似三角形判定定理的应用,注意对定理内容的把握,判定定理2一定是夹等角的两条边对应成比例.【例2】下列命题正确的是( ) A .有一个角是40°的两个等腰三角形相似 B .有一个角是106°的两个等腰三角形相似 C .面积相等的两个直角三角形相似D .两边之比为3 : 5的两个直角三角形相似【答案】B【解析】有一个角是40°的等腰三角形,不能确定这个角是顶角还是底角,即不能确定三 角形形状,A 错误;有一个角是106°的等腰三角形,可以确定这个角一定是等腰三角 形的顶角,则底角大小也必相同,根据相似三角形判定定理1,B 正确;面积相等的直 角三角形,底边长和高长都不能确定,形状不确定,C 错误;两边之比为3:5,不能确 定这两条边是否同为两直角边或者一斜边一直角边,即不能确定直角三角形形状相同,D 错误.【总结】考查相似三角形判定定理的应用,注意一定要对题目提供的条件进行分析的基础上再确定是否能用判定定理证明相似.【例3】下列4⨯4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则例题解析ABCPAB C与ABC ∆相似的三角形所在的网格图形是( )A .B .C .D .【答案】C【解析】根据已知ABC ∆,得对应两直角边之比2ABBC=,三角形与ABC ∆相似,则两条直角边之比也为2,只有C 选项满足.【总结】相似三角形判定定理2可转化为一个三角形中的夹等角的两条边对应成比例.【例4】如图,ABC ∆中,AE 交BC 于点D ,C E ∠=∠,:3:5AD DE =,AE = 8,BD = 4,则DC 的长等于( )A .415B .125C .174D .154【答案】D【解析】由:3:5AD DE =,AE = 8,可得3AD =,5DE =, 由C E ∠=∠,结合一对对顶角BDE ADC ∠=∠,可得BDE ∆∽ADC ∆,由此则有BD DE AD CD =,代入即为453CD =,即得:154CD =,故选D . 【总结】考查相似三角形的判定和性质的综合应用,注意题目中相似图形的对应关系,对应成比例的线段和点一定要准确.【例5】在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似;A BCDE6 / 31乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.对于两人的观点,下列说法正确的是( ) A .两人多对 B .两人都不对C .甲对乙不对D .甲不对,乙对【答案】C【解析】直角三角形扩张以后得到的三角形三边分别与原三角形平行,得到两三角形三个内 角都相等,根据相似三角形判定定理1,可知相似,甲对;乙向外扩张后,矩形两邻边分别变为5和7,3557≠,两矩形的边不对应成比例,可知两矩形不相似,乙不对,故选C .【总结】对于三角形来讲,三角形个内角相等则各对应边比例相等,可以得到两三角形相似,对于其它的多边形来说,角相等不能保证相似,必须再确定两图形的对应边对应成比例才能判定相似,注意相似成立的条件.【例6】如图,ABC ∆中,AB = AC = 5,BC = 6,点M 为BC 中点,MN ⊥AC 于点N ,则 MN =______.【答案】125. 【解析】连结AM .由AB = AC = 5,M 为BC 中点, 可知AM BC ⊥,3BM CM ==,由勾股定理可得:224AM AC CM =-=.由面积法,可得:AM MC MN AC ⋅=⋅,即得431255AM MC MN AC ⋅⨯===. 【总结】考查图形性质的综合应用,本题中也可用“子母三角形”通过相似解题.【例7】如图,在平行四边形ABCD 中,F 是BC 上的一点,直线DF 与AB 的延长线相交于点E ,BP // DF ,且与AD 相交于点P ,则图中有______对相似的三角形.【答案】6.【解析】////AB CD AD BC ,,结合BP // DF ,由相图1图2 11 1 1111 ABCD EFPABCNMABCDEF似三角形预备定理,知CDF ∆、BEF ∆、ABP ∆、AED ∆四三角形两两相似,即共有6对相似三角形.【总结】考查相似三角形的预备定理,由平行可证相似,同时考查相似三角形的传递性.【例8】如图,在直角梯形ABCD 中,AD // BC ,90ABC ∠=︒,AB = 8,AD = 3,BC = 4, 点P 为AB 边上一动点,若PAD ∆与PBC ∆是相似三角形,则满足条件的点P 的个数是( ). A .1个B .2个C .3个D .4个【答案】C【解析】与是相似三角形,根据相似三角形判定定理2,首先易得 90A B ∠=∠=︒,则只需要两三角形夹直角的两边对应成比例即可,分成两种情况讨论,即AD AP BP BC =或AD APBC BP=,可分别得到2AP =或6AP =或247AP =,即满足条件的P 点有3个,故选C . 【总结】考查相似三角形判定定理2的应用,注意进行分类讨论,要经过准确计算,不能直接分两种情况得出两种结果.【例9】如图,在Rt ABC ∆中,90ACB ∠=︒,BC = 3,AC = 4,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( )A .32B .76C .256D .2【答案】B【解析】根据勾股定理,可得225AB BC AC =+=,则有 1522BD AB ==,由90BDE ACB ∠=∠=︒,A ∠为公共角, 根据相似三角形判定定理1,可证ABC ∆∽EBD ∆,则有AB BD BE BC =,代入线段可求得256BE =,则76CE BE BC =-=. 【总结】考查相似三角形判定定理和性质的综合应用,先判定再应用性质.【例10】如图,在平行四边形ABCD 中,过点A 作AE ⊥BC ,垂足为E ,连接DE ,F 为线 段DE 上一点,且AFE B ∠=∠. (1)求证:ADF ∆∽DEC ∆;(2)若AB = 8,AD =63,AF =43,求AE 的长.【答案】(1)略;(2)6ABCD PABCDE8 / 31AB CDEF【解析】(1)证明:四边形ABCD 是平行四边形,////AB CD AD BC ∴,.180ADF DEC B C ∴∠=∠∠+∠=︒,. 180AFE AFD AFE B ∠+∠=︒∠=∠,, AFD C ∴∠=∠,∴ADF ∆∽DEC ∆.(2)解:由(1)ADF ∆∽DEC ∆,∴AF AD CD DE=, 即43638DE=,解得:12DE =. AE BC ⊥,∴90EAD ∠=︒,根据勾股定理,即得:226AE DE AD =-=.【总结】考查相似三角形判定定理1,和相似三角形的相关性质的结合应用,先判定再应用性质,过程中注意对相关图形及性质的应用.【例11】如图,梯形ABCD 中,AD // BC ,AB = DC ,对角线AC 、BD 相交于点F ,点E 是 边BC 延长线上一点,且CDE ABD ∠=∠. (1)求证:四边形ACED 是平行四边形;(2)联结AE ,交BD 于点G ,求证:DG DFGB DB=. 【答案】略.【解析】证明:(1)AD // BC ,AB = DC ,GBAD CDA∴∠=∠.AB DC AD AD==,,ABD DCA∴∆≅∆.ACD ABD∴∠=∠.CDE ABD∠=∠,ACD CDE∴∠=∠.//AC DE∴.AD // BC,∴四边形ACED是平行四边形.(2)//AD BC,∴AD DFBC FB=.AD DFBC AD DF FB∴=++.四边形ACED是平行四边形,∴AD CE=,∴AD DFBC CE DF FB=++,即AD DFBE DB=.//AD BE,∴DG ADGB BE=,∴DG DFGB DB=.【总结】考查相似中有平行线的情况,即可直接利用图形中的“A”字型和“8”字型等基本图形进行等比例转化.【例12】如图,在ABC∆中,AB = AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF 与CE相交于点F,AF的延长线与BD相交于点G.(1)求证:2AD DG BD=;(2)联结CG,求证:ECB DCG∠=∠.【答案】略【解析】证明:(1)1122AB AC AE AB AD AC===,,,AD AE∴=.AB CDEFG10 / 31BAD CAE ∠=∠, BAD CAE ∴∆≅∆, ABD ACE ∴∠=∠.AD CD DF AC =⊥,, AF CF ∴=. GAC ACE ∴∠=∠.ABD GAD ∴∠=∠. ADB GDA ∠=∠, ADG ∴∆∽BDA ∆.AD DGBD AD∴=,即证2AD DG BD =. (2)AD CD =,2AD DG BD =,2CD DG GB ∴=⋅. 即CD GB DG CD=. GDC BDC ∠=∠, GDC ∴∆∽CDB ∆. DBC DCG ∴∠=∠. AB AC =,同(1)易证ECB DBC ∠=∠,ECB DCG ∴∠=∠.【总结】本题综合性较强,一方面考查了等腰三角形的性质以及线段垂直平分线的性质,另一方面考查了相似三角形的判定及性质,解题时注意对条件认真分析以及灵活运用.【例13】在ABC ∆中,AB = 40,AC = 24,BC = 32,点D 是射线BC 上的一点(不与端点重合),联结AD ,如果ACD ∆与ABC ∆相似,求BD 的值.【答案】14或50或64.【解析】由AB = 40,AC = 24,BC = 32,三角形三边满足222AC BC AB +=,即ABC ∆为直 角三角形,其中90ACB ∠=︒,D 在射线BC 上,相似三角形对应关系不确定,可知存 在以下几种情形:(1)D 在线段BC 上,此时ADC ∆∽BAC ∆,则有AC DCBC AC=,可得18DC =,则321814BD BC DC =-=-=;(2)D 在线段BC 延长线上,ADC ∆∽BAC ∆时,同(1)可得50BD BC DC =+=; (3)D 在线段BC 延长线上,DAC ∆∽BAC ∆时,则有DAC ∆≌BAC ∆,264BD BC ==.【总结】相似三角形的存在性问题,题目未给明对应关系,一定要注意进行分类讨论,本题中的点在射线上则更需要注意在线段延长线上时的情况.【例14】正方形ABCD 的边长为1,M 、N 分别是BC 、CD 上的两个动点,且始终保持AM ⊥MN ,求当BM 为多少时,四边形ABCN 的面积最大,最大面积为多少?【答案】12BM =时四边形ABCN 有最大面积58. 【解析】由90B ∠=︒,则有90BAM AMB ∠+∠=︒,AM ⊥MN ,则90NMC AMB ∠+∠=︒,NMC BAM ∠=∠,由90B C ∠=∠=︒,可证ABM ∆∽MCN ∆.则AB BMMC CN =,设BM x =,则1MC x =-,2CN x x =-, 则有()()2211115122228ABCNS CN AB BC x x x ⎛⎫=+⋅=-++=--+ ⎪⎝⎭. 由此可知当12x =,即12BM =时,四边形ABCN 有面积最大值58.【总结】考查“一线三直角”得到相似的基本模型,综合二次函数的最值问题.【例15】如图,将边长为6 cm 的正方形ABCD 折叠,使点D 落在AB 边的中点E 处,折痕为FH ,点C 落在Q 处,EQ 与BC 交于点G ,则EBG ∆的周长为______cm .【答案】12.【解析】设DF x =,根据翻折的性质,则有EF x =, 6AF x =-,在Rt AEF ∆中,用勾股定理,则有222AE AF EF +=,即()22236x x +-=,解得154x =, 则94AF =,由90A ∠=︒,则有90AFE AEF ∠+∠=︒, 同时90FEG D ∠=∠=︒,则90AEF EBG ∠+∠=︒,ABCDE FGH QA BCDNM12 / 31K MNHG FEDC BA得:AFE BEG ∠=∠,由90A B ∠=∠=︒,可证AEF ∆∽BGE ∆.则AE AF EFBG BE GE==,即9153443BG GE ==,解得4BG =,5EG =,故12EBG C cm ∆=. 【总结】考查“一线三直角”得到相似的基本模型.【例16】如图,Rt ABC ∆中,90ACB ∠=︒,AC = 4 cm ,BC = 2 cm ,D 为BC 的中点,若动 点E 以1 cm /s 的速度从A 点出发,沿着A B A →→的方向运动,设点E 的运动时间为t 秒,联结DE ,当t 为何值时,BDE ∆是直角三角形?【答案】955t =或5t =或35t =或1155t =. 【解析】根据勾股定理,可得2225AB AC BC =+=,点E 沿 A B A →→运动时,B ∠大小固定不变,可能存在90DEB ∠=︒和 90EDB ∠=︒两种情形:(1)当90DEB ∠=︒时,由B B ∠=∠,90DEB C ∠=∠=︒,得DEB ∆∽ACB ∆,则有DB EBAB BC =,即1225EB =,得55EB =,此时存在两种情形,即955t =或1155t =; (2)当90EDB ∠=︒时,由B B ∠=∠,90EDB C ∠=∠=︒,得EDB ∆∽ACB ∆,则有EB DBAB BC =,即1225EB =,得5EB =,此时存在两种情形,即5t =或35t =. 【总结】本题主要考查动点的分类讨论问题,注意运动过程中的不变量.【例17】如图,ABC ∆中,4AB = 5AC ,AD 为ABC ∆的角平分线,点E 在BC 的延长线上, EF ⊥AD 于点F ,点G 在AF 上,FG = FD ,联结EG 交AC 于点H ,若点H 是AC 的中点,求AGFD的值.【答案】43. 【解析】延长AC 到M ,使AM AB =,连结DM ,过点M 作//MN AD 交GE 于点N ,交BE 于K .∵AD 为ABC ∆的角平分线, ∴点D 到AB 、AC 的距离相等. 则54ABD ACD S BD AB CD S AC ∆∆===.ABCDEAB AM BAD MAD AD AD =∠=∠=,,,BAD MAD∴∆≅∆,54DM BD DC∴==.//MN AD,4DC ACCK CM∴==.54DK DC DM∴==,即M DK∆是等腰三角形.EF AD FG FD⊥=,,DEG∴∆是等腰三角形.∵//MN AD,GDE DKM∴∠=∠.∵DK DM DE GE==,,KDM DEG∴∠=∠.//GE DM∴.∴四边形DMNG是平行四边形.2MN GD FD∴==,又H是AC中点,22AG AG AHFD MN HM∴==.∵12211342ACAHHM AC AC==+,∴43AGFD=.【总结】考查角平分线,等腰三角形,全等,相似,平行四边形知识的综合应用,难度大,主要在于添加正确的辅助线.1、相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.2、相似三角形性质定理2相似三角形周长的比等于相似比.模块二:相似三角形的性质知识精讲14 / 313、相似三角形性质定理3相似三角形的面积的比等于相似比的平方.【例18】如果两个相似三角形的面积之比是9 : 25,其中小三角形一边上的中线长是12 cm ,那么大三角形对应边上的中线长是______cm .【答案】20【解析】根据相似三角形面积比等于相似比平方,可知两三角形相似比3:5k =,两三角形对应中线长之比也等于3:5k =,即得大三角形对应边上中线长为312205cm ÷=.【总结】考查相似三角形的面积比和对应中线比与相似比的关系.【例19】在ABC ∆中,DE // BC ,且D 在AB 边上,E 在AC 边上,若:1:4ADE BCED S S ∆=,则:ADE ABC C C ∆∆=______,:AD DB =______.【答案】5:5,()51:4+【解析】:1:4ADE BCED S S ∆=,得:1:5ADE ABC S S ∆∆=,可得相应相似比1:55:5k ==,则:5:5ADE ABC C C k ∆∆==,:5:5AD AB k ==,()():5:5551:4AD DB =-=+.【总结】考查相似三角形的面积比和对应边长比和周长比与相似比的关系.【例20】如图,梯形ABCD 中,AD // BC ,90B ACD ∠=∠=︒,AB = 2,DC = 3,则ABC ∆ 与DCA ∆的面积比为( )A .2 : 3B .2 : 5C .4 : 9D .2:3【答案】C【解析】由AD // BC ,可得BCA CAD ∠=∠,结合 90B ACD ∠=∠=︒,可证ABC ∆∽DCA ∆,则有23AB k DC ==,则222439ABC DCA S k S ∆∆⎛⎫=== ⎪⎝⎭,故选C .【总结】考查相似三角形的面积比与相似比的关系.例题解析ABCDAB CDE 【例21】如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长 分别是3、4及x ,那么x 的值为( )A .只有1个B .可以有2个C .可以有3个D .有无数个【答案】B 【解析】由6834=,可知这两条边分别为对应边,相似比2k =,第一个直角三角形中第三 边长有两种情况,即226810+=或228627-=,由此得102x=或272x =,解得5x =或7x =,故选B .【总结】考虑相似三角形的相似比,一定要确立好对应关系.【例22】如图,D 、E 分别在ABC ∆的边AB 、AC 上,23AD AE DE AB AC BC ===,且ABC ∆与ADE ∆的周长之差为15 cm ,求ABC ∆与ADE ∆的周长.【答案】45ABC C cm ∆=,30ADE C cm ∆=. 【解析】23AD AE DE AB AC BC ===,可知ADE ∆∽ABC ∆,其相似比23k =,则23ADE ABC C k C ∆∆==,又15ABC ADE C C ∆∆-=,可得:45ABC C cm ∆=,30ADE C cm ∆=.【总结】考查相似三角形的判定和性质的结合应用.【例23】如图,在ABC ∆中,D 、E 分别是AB 、BC 上的点,且DE // AC ,若:1:4BDE CDE S S ∆∆=,则:BDE ACD S S ∆∆=______.【答案】1:20.【解析】由:1:4BDE CDE S S ∆∆=,即得:1:4BE CE =,由DE // AC ,即得:14BD BE AD CE ==,可得:14BCD ACD S BD S AD ∆∆==,则有120BDE ACD S S ∆∆=. 【总结】等高三角形面积比等于底边长之比,结合三角形的相似性质即可.AB CD E16 / 31MNDCBA【例24】如图,在ABC ∆中,90C ∠=︒,将ABC ∆沿直线MN 翻折后,顶点C 恰好落在AB边上的点D 处,已知MN // AB ,MC = 6,23NC =,那么四边形MABN 的面积是______. 【答案】183.【解析】连结CD ,即得MN 垂直平分CD ,由MN // AB , 即得M 是AC 的中点,CMN ∆∽CAB ∆,则221124CMN CAB S CM S AC ∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,由此可得:133362318322MABN CMN S S MC NC ∆==⨯⋅=⨯⨯=.【总结】考查翻折与相似性质的结合应用.【例25】如图,在平行四边形ABCD 中,AB = 6,AD = 9,BAD ∠的平分线交BC 于E ,交DC 的延长线与F ,BG AE ⊥于G ,42BG =,则EFC ∆的周长为______.【答案】8.【解析】由//AD BC ,得DAE AEB ∠=∠,由AE平分BAD ∠,得BAE DAE AEB ∠=∠=∠, 可得6AB BE ==,由BG AE ⊥,42BG =, 根据勾股定理可得222GE BE BG =-=,则有24AE GE ==,3EC BC BE =-=,由//AB CF ,得EAB ∆∽EFC ∆,由此即得623ABE EFC C BE C EC ∆∆===,由16ABE C AB BE EC ∆=++=,得8EFC C ∆=.【总结】考查相似三角形结合平行四边形特殊图形性质,构造“A ”“8”字型等相关基本图形的应用,本题中注意运用“角平分线与平行线相结合得到等腰”的基本模型.【例26】如图,在ABC ∆中,BE 平分ABC ∠交AC 于点E ,ABC DEFGABCDE过点E 作ED // BC 交AB 于点 D . (1)求证:AE BC BD AC =;(2)如果3ADE S ∆=,2BDE S ∆=,DE = 6,求BC 的长.【答案】(1)略;(2)10. 【解析】(1)证明://ED BCDE AEDEB EBC BC AC∴∠=∠=, DBE EBC ∠=∠ DEB DBE ∴∠=∠ DE BD ∴= BD AEBC AC∴=即证AE BC BD AC = (2)解:由3ADE S ∆=,2BDE S ∆=,即得32ADE BDE S AD BD S ∆∆==,则有35AD AB =,由ED // BC ,可得:35DE AD BC AB ==,代入求得10BC =. 【总结】考查相似三角形面积比与等高三角形面积比的结合应用以及“角平分线与平行线相结合得到等腰”的基本模型的应用.【例27】如图,直角三角形ABC 中,90ACB ∠=︒,AB = 10,BC = 6,在线段AB 上取一点 D ,作DF AB ⊥交AC 于点F ,现将ADF ∆沿DF 折叠,使点A 落在线段DB 上,对应点记为1A ,AD 的中点E 的对应点记为1E ,若11E FA ∆∽1E BF ∆,则AD =______.【答案】165. 【解析】由90ACB ∠=︒,AB = 10,BC = 6,根据勾股定理得 228AC AB BC =-=,由90C EDA ∠=∠=︒,A A ∠=∠,可证ADE ∆∽ACB ∆,则有AF AD DFAB AC BC ==,可设3DE a =,则45AD a AE a ==,,122DE AD a ==,则13EF a =,根据翻折性质,得111213A E AE a E F EF a ====,, 1106BE a =-,11E FA ∆∽1E BF ∆,则有11111E F E AE B EF =,即13210613a a a a=-,解得45a =,由此即得1645AD a ==. 【总结】考查翻折的性质与相似结合,可以把对应边之比转化为同一个三角形的边长之比.【例28】如图,在Rt ABC ∆中,90C ∠=︒,AB = 5,BC = 3,点D 、E 分别在BC 、AC 上,且BD = CE ,设点C 关于DE 的对称点为F ,若DF // AB ,则BD 的长为______.ABCD E F A 1E 118 / 31MFEDCBA【答案】1.【解析】延长DF 交AC 于M , 由勾股定理,可得224AC AB BC =-=,90DFE C DMC A ∠=∠=︒∠=∠,,EFM ∴∆∽DCM ∆∽BCA ∆.3345EF DC BC EF BC EM MC AC EM AB ∴=====,. 设BD x =,则有CE EF x ==,53EM x =,3DC x =-,83MC x =,即有33843x x -=,解得:1x =,即1BD =. 【总结】相似三角形的性质可将两个相似三角形对应边之比转化为一个三角形中对应边长之比,便于计算.【例29】如图,在Rt ABC ∆中,90ACB ∠=︒,AC = 8,BC = 6,CD AB ⊥于点D .点P 从 点D 出发,沿线段CD 向点C 运动,点Q 从点C 出发,沿线段CA 向点A 运动,两点 同时出发,速度都为每秒1个单位长度,当点P 运动到点C 时,两点都停止.设运动 时间为t 秒.(1)求线段CD 的长;(2)设CPQ ∆的面积为S ,求S 与t 之间的关系式,并确定运动过程中是否存在某一时 刻t ,使得:9:100CPQ ABC S S ∆∆=?若存在,求出t 的值;若不存在,请说明理由;(3)当t 为何值时,CPQ ∆为等腰三角形?【答案】(1)245;(2)2248525S t t =-+, 1.8t =或3t =时,:9:100CPQ ABC S S ∆∆=;(3)125t =或14455t =或2411t =. 【解析】(1)根据勾股定理,可得2210AB AC BC =+=, 由直角三角形面积法,则有CD AB AC BC ⋅=⋅,解得:245CD =;(2)过点P 作PH AC ⊥交AC 于H , 90PHC ACB ∠=∠=︒,CPH A ∠=∠, PHC ∴∆∽ACB ∆,PH PCAC AB∴=. ABCDPQH依题意可得CQ PD t ==,则245CP t =-, 代入即为:245810tPH -=, 解得:42449655525PH t t ⎛⎫=-=-+ ⎪⎝⎭.21149624822525525S QC PH t t t t ⎛⎫∴=⋅=-+=-+ ⎪⎝⎭,其中2405t ≤≤; 若存在某一时刻,使得:9:100CPQ ABC S S ∆∆=,则有224891685251002S t t =-+=⨯⨯⨯,整理得:2524270t t -+=,解得:12935t t ==,,均符合题意;(3)分类讨论:①CQ CP =,即245t t =-,解得:125t =; ②PQ CP =,根据等腰三角形的性质可得625QC CH CP ==,即得62455t t =-,解得:14455t =; ③CQ PQ =,同理②,可得52465t t =-, 解得:2411t =. 综上:当CPQ ∆为等腰三角形时,t 的值为125或14455或2411. 【总结】本题综合性较强,考查的知识点比较多,特别是由动点引起的等腰三角形的问题要注意分类讨论,解题方法比较多样,主要是抓住题目中的条件认真分析.20 / 31A B C【习题1】如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中ABC ∆ 相似的是( )A .B .C .D . 【难度】★ 【答案】B【解析】由已知ABC ∆,可得一钝角135ABC ∠=︒,夹这个钝角两边之比22AB BC =,三角形与ABC ∆相似,则必有一角135︒,且夹这个角两边长之比为22,只有B 选项满足. 【总结】相似三角形判定定理2可转化为一个三角形中的夹等角的两条边对应成比例.【习题2】如图,D 是ABC ∆的边AC 上一点,CBD ∠的平分线交AC 于点E ,AE = AB ,则长度为线段AD 、AC 长度比例中项的线段是______.【答案】AE 和AB .【解析】AE = AB ,得ABE AEB ∠=∠,AEB C EBC ∠=∠+∠, 即得ABD DBE C EBC ∠+∠=∠+∠,BE 平分CBD ∠,即为DBE EBC ∠=∠,由此可得ABD C ∠=∠,又A A ∠=∠,即证ABD ∆∽ACB ∆,则有AD ABAB AC=,又AE = AB ,即得. 【总结】考查相似三角形的判定和性质的综合应用,先判定相似再应用性质,注意题目中一个条件的多种用途.【习题3】如图,在ABC ∆中,D 、F 是AB 的三等分点,DE // FG // BC ,分别交AC 于E 、随堂检测ABCDEG .记ADE ∆、四边形DFGE 、四边形FBCG 的面积分别为1S 、2S 、3S ,则123::S S S =______.【答案】1:3:5.【解析】D 、F 是AB 的三等分点,即::1:2:3AD AF AB =, 由DE // FG // BC ,即可得222::1:2:3ADE AFG ABC S S S ∆∆∆=, 即()()112123::1:4:9S S S S S S +++=,得123::1:3:5S S S =. 【总结】考查相似三角形的面积比等于相似比的平方,再进行比例转化即可.【习题4】如图,D 是ABC ∆的边BC 上一点,已知AB = 4,AD = 2,DAC B ∠=∠,若ABD ∆的面积为a ,则ACD ∆的面积为______.【答案】13a .【解析】由DAC B ∠=∠,C C ∠=∠,可得:BAC ∆∽ADC ∆,其相似比422AB k AD ===,由此可得:24BAC ADC S k S ∆∆==,则有3ABD ACD S S ∆∆=,即得:3ACD aS ∆=.【总结】考查相似三角形的面积比等于相似比的平方,再进行比例转化即可.【习题5】如图,矩形ABCD 中,AB = 3,BC = 4,动点P 从A 点出发,按A B C →→的方向在AB 和BC 上移动,记P A = x ,点D 到直线P A 的距离为y ,则y 关于x 的函数图像ABCDA BCD E FG22 / 31xy xy xy xy OOOO3 4 5 3 4 5 3 4 5 3 45 MEDC BA大致是( )A .B .C .D .【答案】B【解析】由运动轨迹可知,动点从A B →的过程中,D 到直线P A 的距离即为AD ,是一条与x 轴平行的直线,D 错误;动点从B C →的过程中,162APD ABCD S S ∆==矩形,即得162xy =,由此可得12y x=,D 直线的距离P A 函数是一段双曲线,可知正确答案是B .【总结】动点问题,进行准确分段分解,化作一段线段上的运动情况即可.【习题6】如图,已知点D 是等腰直角三角形ABC 斜边BC 上的一点,BC = 3BD ,CE ⊥AD , 则AECE=______.【答案】12.【解析】过点D 作DM AC ⊥交AC 于点M , 则有//DM AB ,则CMD ∆为等腰直角三角形, 由CE AC ⊥,可得:ADM ∆∽ACE ∆.12AE AM AM BD CE DM CM CD ∴====. 【总结】考查相似三角形性质的应用,构造平行线即可得到相似.【习题7】在同一时刻,两根木竿在太阳光下的影子如图所示,其中木竿AB = 2 m ,它的影 子BC = 1.6 m ,木竿PQ 的影子有一部分落在了墙上,PM = 1.2 m ,MN = 0.8 m ,则木竿PQ 的长度为______m .【答案】2.3.A B CDPx yAB CPN MQHMNH G FED C BA【解析】如图有 1.2HN PM ==, 0.8PH MN ==,同一时刻影子与木杆长度所成比例相同,则有AB QHBC HN=,得: 1.5QH =,则 2.3PQ QH HP m =+=.【总结】影长问题转化为相似,同一时刻下相似比相同.【习题8】如图,点E 是矩形ABCD 的边BC 上一点,EF ⊥AE ,EF 分别交AC 、CD 于点M 、 F ,BG ⊥AC ,垂足为点G ,BG 交AE 于点H . (1)求证:ABE ∆∽ECF ∆;(2)找出与ABH ∆相似的三角形,并证明;(3)若E 是BC 的中点,BC = 2AB ,AB = 2,求EM 的长.【答案】(1)略;(2)ECM ∆;(3)223. 【解析】(1)证明:EF AE ⊥,90AEB FEC ∴∠+∠=︒.90ABC ∠=︒ 90AEB BAE ∴∠+∠=︒ BAE FEC ∴∠=∠90ABE ECF ∠=∠=︒ ∴ABE ∆∽ECF ∆(2)由(1)BAE FEC ∠=∠,又90ABG GBC GBC BCG ∠+∠=∠+∠=︒ABG ECM ∴∠=∠ ∴ABH ∆∽ECM ∆(3)作MN BC ⊥交BC 于点N , 则有//MN AB ,由BC = 2AB ,得2CN MN =,2BC AB BE CE ==,45AB BE AEB FEC ∴=∠=∠=︒,12EN MN CN ∴==,得1233EN EC ==,则2223EM EN ==. 【总结】考查“子母三角形”中相似的应用.【习题9】如图,在矩形ABCD 中,AB = 2,BC = 3,点E 、F 、G 、H 分别在矩形ABCD 的各边上,EF // AC // HG ,EH // BD // FG ,求四边形EFGH 的周长.【答案】213.【解析】由EF // AC // HG ,EH // BD // FG ,可知四边形EFGH 是平行四边形,且EH AHBD AD=,ABCDEFGH24 / 31HG DH AC AD =,即得:1EH HGBD AC+=,由四边形是矩形,根据勾股定理可得2213AC BD AB BC ==+=,即有113EH HG+=,由此可得:13EH HG +=,故()2213EFGH C EH HG =+=.【总结】考查图形中的“A ”字型等基本图形的叠合应用,可进行比例转化得到一些特定的等量关系即可进行计算.【习题10】如图,在ABC ∆中,AB = AC ,AD ⊥BC 于点D ,BC = 10 cm ,AD = 8 cm .点P 从点B 出发,在线段BC 上以每秒3 cm 的速度向点C 匀速运动,与此同时,垂直于AD 的直线m 从底边BC 出发,以每秒2 cm 的速度沿DA 方向匀速平移,分别交AB 、AC 、 AD 于E 、F 、H ,当点P 到达点C 时,点P 与直线m 同时停止运动,设运动时间为t 秒(t > 0).(1)当t = 2时,连接DE 、DF ,求证:四边形AEDF 为菱形;(2)在整个运动过程中,所形成的PEF ∆的面积存在最大值,当PEF ∆的面积最大时, 求线段BP 的长;(3)是否存在某一时刻t ,使PEF ∆为直角三角形?若存在,请求出此时刻t 的值;若不存在,请说明理由.【答案】(1)略;(2)6;(3)280183t =或4017t =.【解析】(1)证明:当2t =时,24DH t AH ===.AB AC AD BC =⊥,, BD CD ∴=. //EF BC ,EH FH ∴=,∴四边形AEDF 是平行四边形,∵AD EF ⊥,∴四边形AEDF 是菱形. (2)//EF BC ,EF AE AHBC AB AD∴==. 由题意,可得:2DH t =,则有82AH t =-,即得:82108EF t-=. 5102EF t ∴=-+1003t ⎛⎫<≤ ⎪⎝⎭.()22115551021021022222PEF S EF DH t t t t t ∆⎛⎫∴=⋅=-+⋅=-+=--+ ⎪⎝⎭. A BCDEFmH由此可知2t =时,PEF ∆的面积有最大值,此时36BP t ==; (3)①90EPF ∠=︒,分别通过E 、F 向BC 作高,易得两个三角形相似,即有5324521034t tt t t t -=--,解得:280183t =; ②90EFP ∠=︒,过点F 向BC 作高,则有281035t t =-,解得:4017t =; ③90PEF ∠=︒,过点E 向BC 作高, 则有2835t t =,此时不存在;综上所述,280183t =或4017t =时,PEF ∆是直角三角形.【总结】本题是一道考查动点问题的综合题,难度较大,第(2)问中求面积最大值时,要运用配方的思想,第(3)问的直角三角形问题要注意分类讨论,求解时通过作高即可转化为“一线三直角”的基本模型进行求解.26 / 31ABCDE【作业1】如图,在ABC ∆中,DE // BC ,12AD DB =,则下列结论正确的是( ) A .12AE AC =B .12DE BC =C .13ADE ABC ∆=∆的周长的周长D .13ADE ABC ∆=∆的面积的面积【答案】C【解析】12AD DB =,DE // BC ,可得两三角形相似,相似比13AD k AC ==,则其对应边、对应周长之比应为13,对应面积比为21139⎛⎫= ⎪⎝⎭,故选C .【总结】考查相似图形的性质,各个量之比与相似比的关系.【作业2】如图,在ABC ∆中,点D 和点E 分别在边AB 、AC 上,下列条件不能判定ABC ∆ ∽AED ∆的是( ) A .AED B ∠=∠ B .ADE C ∠=∠C .AD AC AE AB=D .AD AE AB AC=【答案】D【解析】根据相似三角形判定定理1和判定定理2,可知ABC 都正确,故选D . 【总结】考查相似三角形判定定理的应用,可将相似比转化为一个图形中对应边之比.【作业3】一副三角尺按如图所示的方式叠放,则AOB ∆与DOC ∆的面积之比课后作业A BCDEABCDO为____________.【答案】13.【解析】由90ABC BCD ∠=∠=︒,可得//AB DC ,则有AOB ∆∽COD ∆,由30D ∠=︒,可得3DC BC =,由AB BC =,可得:1333AB k BC ===,则有213AOB COD S k S ∆∆==. 【总结】考查特殊的直角三角形中的边角关系的转化.【作业4】如图,点D 、E 分别在ABC ∆两边AB 、AC 上,且AD = 31,DB = 29,AE = 30, EC = 32.若50A ∠=︒,则关系式“1ADE B ∠>∠;2AED C ∠=∠;3ADE C ∠>∠;4AED B ∠=∠”中正确的有( )A .1个B .2个C .3个D .4个【答案】A【解析】由AD = 31,DB = 29,可得60AB AD DB =+=,由AE = 30,EC = 32,可得62AC AE EC =+=,则有AE ADAB AC =,又A A ∠=∠, 即得ADE ∆∽ACB ∆,则有ADE C ∠=∠,AED B ∠=∠,可知②③错误,④正确,同时根据“大边对大角”,可知ADE AED ∠<∠,可知①错误,即正确的只有④,故选A .【总结】考查相似三角形的判定定理2和相关相似性质的结合应用,先判定再应用性质,结合“大边对大角”性质即可解决问题.【作业5】在ABC ∆中,P 是AB 上的动点(P 异于A 、B ),过点P 的一条直线截ABC ∆,使截得的三角形与ABC ∆相似,我们不妨称这种直线为过点P 的相似线.ABCDE。
沪教版九年级上册数学(全册知识点考点梳理、重点题型分类巩固练习)(基础版)(家教、补习、复习用)

沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习相似形及比例线段(基础)知识讲解【学习目标】1、能通过生活中的实例认识图形的相似,能通过观察直观地判断两个图形是否相似;2、了解比例线段的概念及有关性质;3、探索相似图形的性质,知道两相似多边形的主要特征,并根据相似多边形的特征识别两个多边形是否相似,并会运用性质进行相关的计算,提高推理能力.【要点梳理】要点一、相似图形在数学上,我们把形状相同的图形称为相似图形或相似形.要点诠释:(1) 相似图形就是指形状相同,但大小不一定相同的图形;(2) “全等”是“相似”的一种特殊情况,即当“形状相同”且“大小相同”时,两个图形全等;要点二、相似多边形【:图形的相似二、图形的相似 2】相似多边形的概念:如果两个多边形的对应角相等,对应边的长度成比例,我们就说它们是相似多边形.要点诠释:(1)相似多边形的定义既是判定方法,又是它的性质.(2)相似多边形对应边的比称为相似比.要点三、比例线段【:图形的相似预备知识】1.成比例线段:对于四条线段a、b、c、d,如果其中两条线段的比与另两条线段的比相等,如a:b=c:d,我们就说这四条线段是成比例线段,简称比例线段.2.比例的性质:(1)基本性质:若a:b=c:d,则ad=bc;(2)合比性质:如果如果(3)等比性质:如果(4)比例中项:若a:b=b:c,则=ac,b称为a、c的比例中项.要点诠释:通常四条线段a,b,c,d的单位应该一致,但有时为了计算方便,a,b的单位一致,c,d的单位一致也可以。
要点四、黄金分割如果点P把线段AB分割成AP和PB,(AP>PB)两段,其中AP是AB和PB的比例中项,那么就称这种分割为黄金分割,点P是线段AB的黄金分割点.≈0.618AB(叫做黄金分割值).要点诠释:线段的黄金分割点有两个.【典型例题】类型一、相似图形1. 下面给出了一些关于相似的命题,其中真命题有()(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.A.1个B.2个C.3个D.4个【答案】C.【解析】解:(1)所有菱形的对应角不一定相等,故菱形不一定都相似;(2)等腰直角三角形都相似,正确;(3)正方形都相似,正确;(4)矩形对应边比值不一定相等,不矩形不一定都相似;(5)正六边形都相似,正确,故符合题意的有3个.故选:C.【总结升华】此题主要考查了相似图形,应注意:①相似图形的形状必须完全相同;②相似图形的大小不一定相同;③两个物体形状相同、大小相同时它们是全等的,全等是相似的一种特殊情况.举一反三:【变式】如图,左边是一个横放的长方形,右边的图形是把左边的长方形各边放大两倍,并竖立起来以后得到的,这两个图形是相似的吗?【答案】这两个图形是相似的,这两个图形形状是一样,对应线段的比都是1:2,虽然它们的摆放方法、位置不一样,但这并不会影响到它们的相似性.类型二、相似多边形2. 如图,已知四边形相似于四边形,求四边形的周长.【答案与解析】∵四边形相似于四边形∴,即∴∴四边形的周长.【总结升华】先根据相似多边形的对应边的比相等,求出四边形的未知边的长,然后即可求出该四边形的周长举一反三:【变式】如图所示的相似四边形中,求未知边x、y的长度和角的大小.【答案】根据题意,两个四边形是相似形,得,解得.3. 如图,在矩形ABCD中,AB=2AD,线段EF=10,在EF上取一点M,分别以EM、MF为一边作矩形EMNH、MFGN,使矩形MFGN与矩形ABCD相似.令MN=x,当x为何值时,矩形EMNH的面积S有最大值?最大值是多少?【答案与解析】解:∵矩形MFGN与矩形ABCD相似,当时,S有最大值,为.【总结升华】借助相似,把最值问题转移到函数问题上,是解决这类题型最好方法之一.类型三、比例线段4.(2016•兰州模拟)若a:b=2:3,则下列各式中正确的式子是()A.2a=3b B.3a=2b C.D.【思路点拨】根据比例的性质,对选项一一分析,选择正确答案.【答案】B.【解析】A、2a=3b⇒a:b=3:2,故选项错误;B、3a=2b⇒a:b=2:3,故选项正确;C、=⇒b:a=2:3,故选项错误;D、=⇒a:b=3:2,故选项错误.故选B.【总结升华】考查了比例的性质.在比例里,两个外项的乘积等于两个内项的乘积.举一反三:【变式】判断下列线段a、b、c、d是否是成比例线段:(1)a=4,b=6,c=5,d=10;(2)a=2,b=,c=,d=.【答案】(1) ∵,,∴,∴线段a、b、c、d不是成比例线段.(2) ∵,,∴,∴线段a、b、c、d是成比例线段.5. 主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是()①AB:AC=AC:BC;②AC≈6.18米;③;④.A. ①②③④B. ①②③C. ①③D. ④【答案】D.【解析】解:AB的黄金分割点为点C处,若AC>BC,则AB:AC=AC:BC,所以①不一定正确;AC≈0.618AB≈12.36或AC≈20﹣12.36=7.64,所以②错误;若AC为较长线段时,AC=AB=10(﹣1),BC=10(3﹣);若BC为较长线段时,BC=AB=10(﹣1),AC=10(3﹣),所以③不一定正确,④正确.故选D.【总结升华】黄金分割知识的理解和运用要结合生活实践.沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习相似形及比例线段(基础)巩固练习【巩固练习】一.选择题1. 在比例尺为1︰1 000 000的地图上,相距3 cm的两地,它们的实际距离为()A.3 kmB.30 kmC.300 kmD.3 000 km2. (2016•滨江区模拟)由5a=6b(a≠0),可得比例式()A.B.C.D.3.如图,用放大镜将图形放大,这种图形的改变是()A.相似B.平移 C.轴对称D.旋转4. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是相似图形,如图所示,则小鱼上的点(a,b)对应大鱼上的点( )A.(-2a,-2b) B.(-a,-2b) C.(-2b,-2a) D.(-2a,-b)5. 一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则此三角形其它两边的和是()A.19 B.17 C.24 D.216. .△ABC与△A1B1C1相似且相似比为,△A1B1C1与△A2B2C2相似且相似比为,则△ABC与△A2B2C2的相似比为 ( )A.B.C.或D.二. 填空题7. 两地实际距离为1 500 m,图上距离为5 cm,这张图的比例尺为_______.8. (2016•浦东新区一模)已知,那么= .9.判定两个多边形相似的方法是:当两个多边形的对应边_______,对应角_______时,两个多边形相似.10.已知则11.两个三角形相似,其中一个三角形两个内角分别是40°,60°,则另一个三角形的最大角为______,最小角为____________.12. (2015春·庆阳校级月考)要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一条最短边长为2,则另外一个三角形的周长为 .三综合题13. 已知,求的值.14. (1)已知a、b、c、d是成比例线段,其中a=3dcm,b=2cm,c=6cm,求线段d的长;(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项,求线段c的长.15. 市场上供应的某种纸有如下特征:每次对折后,所得的长方形均和原长方形相似,则纸张(矩形)的长与宽应满足什么条件?【答案与解析】一、选择题1.【答案】B.【解析】图上距离︰实际距离=比例尺.2.【答案】D.【解析】A、⇒ab=30,故选项错误;B、⇒ab=30,故选项错误;C、⇒6a=5b,故选项错误;D、⇒5(a﹣b)=b,即5a=6b,故选项正确.故选D.3.【答案】A【解析】根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选A.4.【答案】 A【解析】由图可知,小鱼和大鱼的相似比为1:2,若将小鱼放大1倍,则小鱼和大鱼关于原点对称.5.【答案】C【解析】相似三角形对应边的比相等6.【答案】A【解析】相似比AB︰A1B1=,A1B1︰A2B2=,计算出AB︰A2B2.二、填空题7.【答案】.1:30 000【解析】比例尺=图上距离︰实际距离.8.【答案】.【解析】∵的两个内项是y、1,两个外项是x、3,∴,根据合比定理,知==4;又∵上式的两个内项是x和4,两个外项是x+y和1,∴.9.【答案】成比例;相等.10.【答案】【解析】提示:设11.【答案】80°,40°.12.【答案】7.5.【解析】设另一个三角形周长是x.∵一个三角形的三边长是4,5,6,∴这个三角形的周长为:4+5+6=15.∵与它相似的另一个三角形最短的一边长是2,∴,解得:x=7.5.∴另一个三角形的周长是7.5.三、解答题13.【解析】设=k则∴==14.【解析】解:(1)∵a、b、c、d是成比例线段,∴a:b=c:d,∵a=3cm,b=2cm,c=6cm,∴d=4cm;(2)∵线段c是线段a和b的比例中项,a=4cm,b=9cm.∴c2=ab=36,解得:c=±6,又∵线段是正数,∴c=6cm.15.【解析】如图,为了方便分析可先画出草图,根据题意知两个矩形的长边之比应等于短边之比.设矩形的长为,宽为,由相似多边形的特征得,即纸张的长与宽之比为.沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习三角形一边的平行线知识讲解【学习目标】1、掌握三角形一边的平行线性质定理及推论;判定定理及推论;以及平行线分线段成比例定理的推导与应用;2、了解三角形的重心的意义和性质并能应用它解题;3、经历运用分类思想针对图形运动的不同位置分别探究的过程,初步领略运用运动观点、化归和分类讨论等思想进行数学思考的策略.【要点梳理】要点一、三角形一边的平行线性质定理及推论1.性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.2.推论:平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.要点诠释:(1)主要的基本图形:分A型和X型;A型 X型(2)常用的比例式:3.三角形的重心:三角形三条中线的交点叫做三角形的重心.要点诠释:(1)重心的性质:三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的二倍.(2)重心的画法:两条中线的交点.要点二、三角形一边的平行线判定定理及推论1.判定定理:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.2.推论:如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.要点诠释:判断平行线的条件中,只能是被截的两条直线的对应线段成比例(被判断的平行线本身不能参与作比例).要点三、平行线分线段成比例定理1.性质定理:两条直线被三条平行的直线所截,截得的对应线段成比例.2.平行线等分线段定理:两条直线被三条平行的直线所截,如果在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.要点诠释:(1)平行线等分线段定理是平行线分线段成比例定理的特例;(2)平行线分线段成比例没有逆定理;(3) 由于平行线分线段成比例定理中,平行线本身没有参与作比例,因此,有关平行线段的计算问题通常转化到“A”、“X”型中.【典型例题】类型一、三角形一边的平行线性质定理1. 如图已知直线截△ABC三边所在的直线分别于E、F、D三点且AD=BE.求证:EF:FD=CA:CB.【答案与解析】过D作DK∥AB交EC于K点.则,,即又∵AD=BE,∴.【总结升华】运用三角形一边的平行线性质定理,即只要有平行线就可推出对应线段成比例.举一反三【变式】如图,在⊿ABC, DG∥EC, EG∥BC,求证:【答案】∵DG∥EC,∴,∵EG∥BC,∴,∴,即.2.已知,△ABC中,G是三角形的重心, AG⊥GC,AG=3,GC=4,求BG的长.【答案与解析】延长BG交AC于点D,∵G是三角形的重心,∴点D是线段AC的中点,又∵AG⊥GC,AG=3,GC=4,∴AC=5,即DG=2.5,∵BG:GD=2:1.∴BG=5.【总结升华】三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的二倍.类型二、三角形一边的平行线判定定理3. 如图,AM是△ABC的中线,P是AM上任意一点,BP、CP的延长线分别交AC、AB于E、D两点.求证:DE∥BC.【答案与解析】延长AM到H,使HM=MP,连接BH、CH∵BM=MC∴四边形BPCH是平行四边形∵BH∥CD,CH∥BE在△ABH和△ACH中,有,∴DE∥BC【总结升华】平行线所截得的对应线段成比例,而两条平行线中的线段与所截得的线段不成比例.举一反三【变式】如图,在△ABC(AB>AC)的边AB上取一点D,在边AC 上取一点E,使AD=AE,直线DE和BC的延长线交于点P,求证:.【答案】过点C作CF∥AB交DP于点F,∵CF∥AB,∴∠ADE=∠EFC∵AD=AE,∴∠ADE=∠AED=∠FEC∴∠EFC=∠FEC∴CF=CE∵CF∥AB∴,即.类型三、平行线分线段成比例定理4. (2016•兰州)如图,在△ABC中,DE∥BC,若=,则=()A.B.C.D.【思路点拨】直接利用平行线分线段成比例定理写出答案即可.【答案】C.【解析】解:∵DE∥BC,∴==,故选C.【总结升华】本题考查了平行线分线段成比例定理,了解定理的内容是解答本题的关键,属于基础定义或定理,难度不大.举一反三【变式】(2015•舟山)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC 与DF相交于点G,且AG=2,GB=1,BC=5,则的值为()A. B. 2 C. D.【答案】D提示:∵AG=2,GB=1,∴AB=AG+BG=3,∵直线l1∥l2∥l3,∴=,沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习三角形一边的平行线【巩固练习】一.选择题1.(2016•杭州)如图,已知直线a∥b∥c,直线m交直线a,b,c 于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=()A.B.C.D.12. 如图,在△ABC中,DE∥BC,则下列比例式成立的是( )A.B. C.D.3. 在△ABC中,点D在AB上,点E在AC上,且DE∥BC,,则等于( )A.B.C. D.4. 如图,△ABC中,DE∥AC交AB、BC于D、E,如果AB=7cm,AC=5cm,AD=3cm,则DE=( )A.B. C.D.5. 如图,在△ABC中,如果DE∥BC,DF∥AC,则下列比例式中不正确的是( )A.B.C. D.6. 如图,△ABC中,G是BC中点,E是AG中点,CE的延长线交AB于D,则EC:DE的值为( )A.2 B.3 C.D.二. 填空题7. (2016•无锡一模)如图,直线AD∥BE∥CF,BC=AC,DE=4,那么EF的值是.8. 如图,DE∥BC,BF:EF=4:3,则AC:AE=____________.9.已知点G是△ABC的重心,AD是BC边上的中线,如果GD=2cm,那么AD=______.10. 如图,△PMN,点A,B分别在MP,NP的延长线上,,则________.11. 如图,四边形ABCD中,AC、BD相交于点P,若AP=8,CP=12,BC=15.则AD=_________.12.(2015•香坊区三模)如图,△ABC中,D、F在AB边上,E、G 在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC 的长为 .三.综合题13. 如图,已知,AB∥CD∥EF,OA=14,AC=16,CE=8,BD=12,求OB、DF的长.14.已知:如图,在△ABC中,AB=AC,且,EG∥CD.证明:AE=AF.15. 如图,△ABC中,AD是中线,点F在AD上,且AF:FD=1:2,BF的延长线交AC于E,求AE:EC=?【答案与解析】一、选择题1.【答案】B.【解析】∵a∥b∥c,∴==.故选B.2.【答案】 D.3.【答案】 C.【解析】∵DE∥BC,∴,又∵,∴,即=.4.【答案】D.【解析】∵DE∥AC,∴,又∵AB=7cm,AC=5cm,AD=3cm,∴BD=4,即DE=.5.【答案】C.【解析】提示:∵ DE∥BC,DF∥AC,∴DE=CF, DF=CE.6.【答案】B.【解析】作GM∥CD交AB于点M,∵E是AG中点,∴MG=2DE,又∵G是BC中点,∴CD=2MG=4DE∴EC=3DG,即EC:DE=3:1.二、填空题7.【答案】2.【解析】∵BC=AC,∴=,∵AD∥BE∥CF,∴=,∵DE=4,∴=2,∴EF=2.8.【答案】4:3.【解析】∵DE∥BC, BF:EF=4:3,∴9.【答案】6cm.【解析】∵点G是重心,∴AG:GD=2:1,又∵GD=2,∴AG=4,即AD=6cm.10.【答案】3:2.【解析】∵,∴.11.【答案】10.12.【答案】9.【解析】∵DE∥FG∥BC,∴=,而AD:DF:FB=3:2:1,∴=,∴=,∴EC=9.三、解答题13. 【解析】∵AB∥CD∥EF,∴,又∵OA=14,AC=16,BD=12,∴OB=.同理,CE=8,∴DF=6.14.【解析】证明:∵EG∥CD,∴=,且,∴=,∴=,即=,∵AB=AC,∴AE=AF.15.【解析】作DG∥BE,∵AD是中线,∴EG=GC,又∵AF:FD=1:2,∴EG=2AE,即EC=4AE,∴AE:EC=1:4.沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习相似三角形的判定--知识讲解(基础)【学习目标】1、了解相似三角形的概念,掌握相似三角形的表示方法及判定方法;2、进一步探索相似三角形的判定及其应用,提高运用“类比”思想的自觉性,提高推理能力.【要点梳理】要点一、相似三角形在和中,如果我们就说与相似,记作∽.k就是它们的相似比,“∽”读作“相似于”.要点诠释:(1)书写两个三角形相似时,要注意对应点的位置要一致,即∽,则说明点A的对应点是A′,点B的对应点是B′,点C的对应点是C′;(2)对于相似比,要注意顺序和对应的问题,如果两个三角形相似,那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时,两个三角形全等.要点二、相似三角形的判定定理【高清课程名称:相似三角形的判定(1)高清:394497:相似三角形的判定】1.判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.2.判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.3.判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.要点诠释:此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必需是两边的夹角,否则,判断的结果可能是错误的.4.判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.要点诠释:要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.要点三、相似三角形的常见图形及其变换:【典型例题】类型一、相似三角形1. 下列能够相似的一组三角形为( ).A.所有的直角三角形B.所有的等腰三角形C.所有的等腰直角三角形D.所有的一边和这边上的高相等的三角形【答案】C【解析】A中只有一组直角相等,其他的角是否对应相等不可知;B中什么条件都不满足;D中只有一条对应边的比相等;C中所有三角形都是由90°、45°、45°角组成的三角形,且对应边的比也相等.答案选C.【总结升华】根据相似三角形的概念,判定三角形是否相似,一定要满足三个角对应相等,三条对应边的比相等.举一反三:【变式】给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有(填序号).【答案】①②④⑤.类型二、相似三角形的判定2. 如图所示,已知中,E为AB延长线上的一点,AB=3BE,DE与BC相交于F,请找出图中各对相似三角形,并求出相应的相似比.【思路点拨】充分利用平行寻找等角,以确定相似三角形的个数. 【答案与解析】∵四边形ABCD是平行四边形,∴ AB∥CD,AD∥BC,∴△BEF∽△CDF,△BEF∽△AED.∴△BEF∽△CDF∽△AED.∴当△BEF∽△CDF时,相似比;当△BEF∽△AED时,相似比;当△CDF∽△AED时,相似比.【总结升华】此题考查了相似三角形的判定(有两角对应相等的两三角形相似)与性质(相似三角形的对应边成比例).解题的关键是要仔细识图,灵活应用数形结合思想.举一反三:【高清课程名称:相似三角形的判定(2)高清:394499:例4及变式应用】【变式】如图,AD、CE是△ABC的高,AD和CE相交于点F,求证:AF·FD=CF·FE.【答案】∵ AD、CE是△ABC的高,∴∠AEF=∠CDF=90°,又∵∠AFE=∠CFE,∴△AEF∽△CDF.∴, 即AF·FD=CF·FE.3. (2016•福州)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与AC•CD的大小关系;(2)求∠ABD的度数.【思路点拨】(1)先求得AD、CD的长,然后再计算出AD2与AC•CD的值,从而可得到AD2与AC•CD的关系;(2)由(1)可得到BD2=AC•CD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.【答案与解析】解:(1)∵AD=BC=1,BC=,∴AD=,DC=1﹣=.∴AD2==,AC•CD=1×=.∴AD2=AC•CD.(2)∵AD=BC,AD2=AC•CD,∴BC2=AC•CD,即.又∵∠C=∠C,∴△BCD∽△ACB.∴,∠DBC=∠A.∴DB=CB=AD.∴∠A=∠ABD,∠C=∠BDC.设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°.解得:x=36°.∴∠ABD=36°.【总结升华】本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角形内角和定理的应用,证得△BCD∽△ABC是解题的关键.4. 已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.【思路点拨】从求证可以判断是运用相似,再根据BP2=PE·PF,可以判定所给的线段不能组成相似三角形,这就需要考虑线段的等量转移了.【答案与解析】连接,,,是的中垂线,,,,.,.又,∽,,.【总结升华】根据求证确定相似三角形,是解决此类题型的捷径.举一反三:【变式】如图,F是△ABC的AC边上一点,D为CB延长线一点,且AF=BD,连接DF, 交AB于E. 求证:.【答案】过点F作FG∥BC,交AB于G.则△DBE∽△FGE△AGF∽△ABC∵,又∵AF=BD,∴∵△AGF∽△ABC∴,即.沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习相似三角形的判定--巩固练习(基础)【巩固练习】一、选择题1. 下列判断中正确的是( ).A.全等三角形不一定是相似三角形B.不全等的三角形一定不是相似三角形C.不相似的三角形一定不全等D.相似三角形一定不是全等三角形2.已知△ABC的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′ 相似, 那么△A′B′C′ 的第三边长应该是 ( ).A. B. C. D.3.(2015•大庆校级模拟)如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是()A.B.C.D.4. (2016•盐城)如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有()A.0个B.1个C.2个D.3个5.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有().A.ΔADE∽ΔAEF B.ΔECF∽ΔAEF C.ΔADE ∽ΔECF D.ΔAEF∽ΔABF6. 如图所示在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( ).A. B.8 C.10 D.16二、填空题7. (2016•娄底)如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是.(只需写一个条件,不添加辅助线和字母)8如图所示,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=________.9.如图所示,在直角坐标系中有两点A(4,0),B(0,2),如果点C 在x轴上(C与A不重合),当点C的坐标为________或________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).10.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.11.如图,CD∥AB,AC、BD相交于点O,点E、F分别在AC、BD上,且EF∥AB,则图中与△OEF相似的三角形为_________.12.如图,点E是平行四边形ABCD的边BC延长线上一点,连接AE 交CD于点F,则图中相似三角形共有_________对.三.解答题13. 如图,在△ABC中,DE∥BC,AD=3,AE=2,BD=4,求的值及AC、EC的长度.14. 如图在梯形ABCD中,AD∥BC,∠A=90°,且,求证:BD⊥CD.15.如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,(1)求证:AC2=CE•CF;(2)若∠B=38°,求∠CFD的度数.【答案与解析】一.选择题1.【答案】C.2.【答案】A.【解析】根据三边对应成比例,可以确定,所以第三边是3.【答案】B.【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、只有选项B的各边为1、、与它的各边对应成比例.故选B.4.【答案】C.【解析】∵四边形ABCD是平行四边形,∴AD∥BC,AB∥DC,∴△AEF∽△CBF,△AEF∽△DEC,∴与△AEF相似的三角形有2个.5.【答案】C.【解析】∵∠AEF=90°, ∴∠1+∠2=90°,又∵∠D=∠C=90°,∴∠3+∠2=90°,即∠1=∠3,∴△ADE∽△ECF.6.【答案】C.【解析】∵ EF∥AB,∴,∵,∴,,∴ CD=10,故选C.二. 填空题7.【答案】AB∥DE.【解析】∵∠A=∠D,∴当∠B=∠DEF时,△ABC∽△DEF,∵AB∥DE时,∠B=∠DEF,∴添加AB∥DE时,使△ABC∽△DEF.8.【答案】 3 .【解析】∵∠C=∠E,∠CAB=∠EAD,∴△ACB∽△AED,∴,BC=4,在Rt△ABC中,.9.【答案】;.10.【答案】4.【解析】∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,又∵AC⊥CE,∴∠BCA+∠DCE=90°,∴∠BCA=∠E,∴△ABC∽△CDE.∵C是线段BD的中点,ED=1,BD=4∴BC=CD=2∴,即AB=4.11.【答案】△OAB,△OCD.12.【答案】3.【解析】∵平行四边形ABCD,∴AD∥BE.AB∥CD∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.三综合题13.【解析】∵DE∥BC,∴△ADE∽△ABC,∵,,∴,∴AC=,∴EC=AC-AE=.14.【解析】∵AD∥BC,∴∠ADB=∠DBC,又∵,∴△ABD∽△DCB,∴∠A=∠BDC,∵∠A=90°,∴∠BDC=90°,∴BD⊥CD .15.【解析】解:(1)∵AD⊥BC,∴∠CFA=90°,∵∠BAC=90°,∴∠C FA=∠BAC,∵∠ACF=∠FCA,∴△CAF∽△CEA,∴=,∴CA2=CE•CF;(2)∵∠CAB=∠CDA,∠ACD=∠BCA,∴△CAD∽△CB A,∴=,∴C A2=CB×CD,同理可得:CA2=CF×CE,∴CD•BC=CF•CE,∴=,∵∠DCF=∠ECB,∴△CDF∽△CEB,∴∠CFD=∠B,∵∠B=38°,∴∠CFD=38°.沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习相似三角形的性质及应用--知识讲解(基础)【学习目标】1、探索相似三角形的性质,能运用性质进行有关计算;2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题). 【要点梳理】要点一、相似三角形的性质【高清课程名称:相似三角形的性质及应用高清:394500:相似形的性质】1.相似三角形的对应角相等,对应边的比相等.2. 相似三角形中的重要线段的比等于相似比.相似三角形对应高,对应中线,对应角平分线的比都等于相似比.要点诠释:要特别注意“对应”两个字,在应用时,要注意找准对应线段.3. 相似三角形周长的比等于相似比∽,则由比例性质可得:4. 相似三角形面积的比等于相似比的平方∽,则分别作出与的高和,则要点诠释:相似三角形的性质是通过比例线段的性质推证出来的.要点二、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.【高清课程名称:相似三角形的性质及应用高清:394500:应用举例及总结】要点诠释:测量旗杆的高度的几种方法:平面镜测量法影子测量法手臂测量法标杆测量法2.测量距离测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。
沪教版(上海)初中数学九年级第一学期 本章小结 相似三角形的复习 教案

相似三角形复习(2)教学内容:相似三角形复习课第二节(相似三角形判定定理)教学目标: 1、进一步理解和掌握相似三角形的判定定理、灵活应用这些定理去探索问题和解决问题。
2、培养在基本图形中运用知识的能力。
体会在发现中学习,在学习中发现。
发展学生的数学思维能力。
渗透图形运动、类比、分类讨论等数学思想。
3、提倡学生主动学习、积极参与教学,用所学的知识解决问题,提高学数学的热情。
在师生互动过程中,培养团结协作的精神。
教学重点:相似三角形判定定理的应用。
教学难点:能在复杂图形背景下、识别和判定三角形的相似,并正确推理论证,关注数学的严密性。
设计思想:本节课是在学习了相似三角形判定定理后的一节复习课。
一方面,抓住基本图形的特征,将基本图形通过平移、旋转、翻折、分解、组合成各种图形。
鼓励学生联想,培养学生创新意识。
另一方面,让学生进一步形成学习的主体意识、探究意识和合作意识。
教学过程:教师活动 学生活动 教学设计意图 我们已经认识了相似三角形,学习了相似三角形的判定,这节课我们要巩固我们所学的知识,并把所学的有关判定定理应用到实际的例题中,去探索和解决一些问题。
一;相似三角形基本图形以及判定定理的回顾。
问1: 若DE//BC ,则可以判定哪两个个三角形形相似?用哪条判定定理? 预备定理:如果一条直线平行于三角形的一条边,且这条直线与原三角形的两边(或其延长线)分别相交,那么所构成的三角形与原三角形相似。
这类基本图形我们称为平行线型生:△ADE ∽△ABC ,用预备定理生:△ADC ∽△ACB通过回忆使学生掌握相似三角形的所有的判定方法.1A BCD E 1AECBD三边对应成比例,两三角形相似。
这类网格型的题目还可以用那种判定方法。
通常网格类的相似,还可以用哪个判定定理? 最后,我们来回顾一下直角三角形相似的判定方法:问5:若BDACBE AB =,∠C=∠D=90°则可 以判定哪两个三角形形相似?用哪条判定定理 直角三角形相似的判定定理: 斜边和一条直角边对应成比例,则这两个直角三角形相似 上面我们回顾了相似三角形判定定理及重要 的基本图形,下面我们要应用这些定理来 解决一些几何问题。
沪教版初三上册39944相似三角形的判定--知识讲解(基础)

沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习相似三角形的判定--知识讲解(基础)【学习目标】1、了解相似三角形的概念,掌握相似三角形的表示方法及判定方法;2、进一步探索相似三角形的判定及其应用,提高运用“类比”思想的自觉性,提高推理能力.【要点梳理】要点一、相似三角形在和中,如果我们就说与相似,记作∽.k就是它们的相似比,“∽”读作“相似于”.要点诠释:(1)书写两个三角形相似时,要注意对应点的位置要一致,即∽,则说明点A的对应点是A′,点B的对应点是B′,点C的对应点是C′;(2)对于相似比,要注意顺序和对应的问题,如果两个三角形相似,那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时,两个三角形全等.要点二、相似三角形的判定定理【高清课程名称:相似三角形的判定(1)高清ID号:394497关联的位置名称:相似三角形的判定】1.判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.2.判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似. 3.判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.要点诠释:此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必需是两边的夹角,否则,判断的结果可能是错误的.4.判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.要点诠释:要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.要点三、相似三角形的常见图形及其变换:【典型例题】类型一、相似三角形1. 下列能够相似的一组三角形为( ).A.所有的直角三角形B.所有的等腰三角形C.所有的等腰直角三角形D.所有的一边和这边上的高相等的三角形【答案】C【解析】A中只有一组直角相等,其他的角是否对应相等不可知;B中什么条件都不满足;D中只有一条对应边的比相等;C中所有三角形都是由90°、45°、45°角组成的三角形,且对应边的比也相等.答案选C.【总结升华】根据相似三角形的概念,判定三角形是否相似,一定要满足三个角对应相等,三条对应边的比相等.举一反三:【变式】给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有(填序号).【答案】①②④⑤.类型二、相似三角形的判定2. 如图所示,已知中,E为AB延长线上的一点,AB=3BE,DE与BC相交于F,请找出图中各对相似三角形,并求出相应的相似比.【思路点拨】充分利用平行寻找等角,以确定相似三角形的个数.【答案与解析】∵四边形ABCD是平行四边形,∴ AB∥CD,AD∥BC,∴△BEF∽△CDF,△BEF∽△AED.∴△BEF∽△CDF∽△AED.∴当△BEF∽△CDF时,相似比;当△BEF∽△AED时,相似比;当△CDF∽△AED时,相似比.【总结升华】此题考查了相似三角形的判定(有两角对应相等的两三角形相似)与性质(相似三角形的对应边成比例).解题的关键是要仔细识图,灵活应用数形结合思想.举一反三:【高清课程名称:相似三角形的判定(2)高清ID号:394499关联的位置名称(播放点名称):例4及变式应用】【变式】如图,AD、CE是△ABC的高,AD和CE相交于点F,求证:AF·FD=CF·FE.【答案】∵ AD、CE是△ABC的高,∴∠AEF=∠CDF=90°,又∵∠AFE=∠CFE,∴△AEF∽△CDF.∴, 即AF·FD=CF·FE.3.(2016•福州)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与AC•CD的大小关系;(2)求∠ABD的度数.【思路点拨】(1)先求得AD、CD的长,然后再计算出AD2与AC•CD的值,从而可得到AD2与AC•CD的关系;(2)由(1)可得到BD2=AC•CD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.【答案与解析】解:(1)∵AD=BC=1,BC=,∴AD=,DC=1﹣=.∴AD2==,AC•CD=1×=.∴AD2=AC•CD.(2)∵AD=BC,AD2=AC•CD,∴BC2=AC•CD,即.又∵∠C=∠C,∴△BCD∽△ACB.∴,∠DBC=∠A.∴DB=CB=AD.∴∠A=∠ABD,∠C=∠BDC.设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.∵∠A+∠ABC+∠C=180°,∴x+2x+2x=180°.解得:x=36°.∴∠ABD=36°.【总结升华】本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角形内角和定理的应用,证得△BCD∽△ABC是解题的关键.4. 已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.【思路点拨】从求证可以判断是运用相似,再根据BP2=PE·PF,可以判定所给的线段不能组成相似三角形,这就需要考虑线段的等量转移了.【答案与解析】连接,,,是的中垂线,,,,.,.又,∽,,.【总结升华】根据求证确定相似三角形,是解决此类题型的捷径.举一反三:【变式】如图,F是△ABC的AC边上一点,D为CB延长线一点,且AF=BD,连接DF,交AB于E. 求证:.【答案】过点F作FG∥BC,交AB于G.则△DBE∽△FGE△AGF∽△ABC∵,又∵AF=BD,∴∵△AGF∽△ABC∴,即.。
沪教版(上海)初中数学九年级第一学期2相似三角形的判定课件

课堂练习:
1、如图:E是平行四边形ABCD的边BA 延长线上的一点,CE交AD于点F.图中 有那几对类似三角形?
E
E
E
A
F
D
A
F
F
A
D
B
C
B
C
C
∵AD∥BC
∵AB∥CD
∴△AFE∽△BCE
∴△AFE∽△DFC
由类似传递性可得:△DFC∽△BCE
课堂练习:
2、如图: △ABC∽△AED,AG=3,AD=6,AF=2,EF=6, 则△AFG与△ABC类似吗? 为什么?
∵ DE∥BC
ADE ∽ ABC
布置作业:练习册24.4(1)
A1B1 A1C1 B1C1
A1B1 A1C1 B1C1
A2 B2 A2C2 B2C2
A A1, B B1, C C1
类似三角形的定义
A1 A2 , B1 B2 , C1 C2
等量代换得
AB AC BC A2 B2 A2C2 B2C2
A A2 , B B2 , C C2
×可得: △ABC∽△A B C AB A1B1 AC A1C1 BC B1C1
A1B1 A2B2 A1C1 A2C22 B21C1 2 B2C2
类似三角形具有传递性(判定方法)
如果两个三角形分别与同一个三角形类似, 那么这两个三角形也类似. 符号语言:
∵ ABC ∽ A1B1C1 , A1B1C1 ∽ A2 B2C2 ∴ ABC ∽ A2B2C2 (类似三角形的传递性)
探究3 如图,点D、E分别在直线AB和AC 上,且DE∥BC ,那么△ADE 与
课堂小结: 本节课主要学习了什么,有何收获?
1、类似三角形的定义. 2、类似三角形的性质.
上海初三相似三角形总结

相似三角形知识点1 相似图形形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形. 知识点2 比例线段的相关概念如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=. 注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位.在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注意:(1)当两个比例式的每一项都对应相同,两个比例式才是同一比例式.(2)比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:adc b =.知识点3 比例的性质基本性质:(1)bc ad d c b a =⇔=::;(2)b a c b c c a ⋅=⇔=2::. 注意:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除 了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.更比性质(交换比例的内项或外项):()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 反比性质(把比的前项、后项交换):cd a b d c b a =⇒=. 合比性质:dd c b b a d c b a ±=±⇒=. 注意:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a 等等.等比性质:如果)0(≠++++====n f d b nmf e d c b a ,那么b a n f d b m ec a =++++++++ . 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法. (2)应用等比性质时,要考虑到分母是否为零.(3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . 知识点4 比例线段的有关定理平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 推论:(1)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. (2)平行于三角形一边并且和其它两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例.定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形第三边. 知识点5 黄金分割把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB . 知识点6 相似三角形的概念对应角相等,对应边成比例的三角形,叫做相似三角形. 相似用符号“∽”表示,读作“相似于” .相似三角形对应边的比叫做相似比(或相似系数). 相似三角形对应角相等,对应边成比例. 注意:①对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易找到相似三角形的对应角和对应边. ②顺序性:相似三角形的相似比是有顺序的. ③两个三角形形状一样,但大小不一定一样.④全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对应边成比例.知识点7 相似三角形的基本定理定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原 三角形相似. 定理的基本图形:用数学语言表述是: BC DE // ,ADE ∆∴∽ABC ∆.知识点8 相似三角形的等价关系(1)反身性:对于任一ABC ∆有ABC ∆∽ABC ∆.(2)对称性:若ABC ∆∽'''C B A ∆,则'''C B A ∆∽ABC ∆.(3)传递性:若ABC ∆∽C B A '∆'',且C B A '∆''∽C B A ''''''∆,则ABC ∆∽C B A ''''''∆. 知识点9 三角形相似的判定方法1、定义法:对应角相等,对应边成比例的两个三角形相似.2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角 形与原三角形相似.3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两 个三角形相似.简述为:两角对应相等,两三角形相似.4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹 角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似.6、判定直角三角形相似的方法: (1)以上各种判定均适用.(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
沪教版初三C专题(中考冲刺:因动点产生的相似三角形问题3星)巩固基础
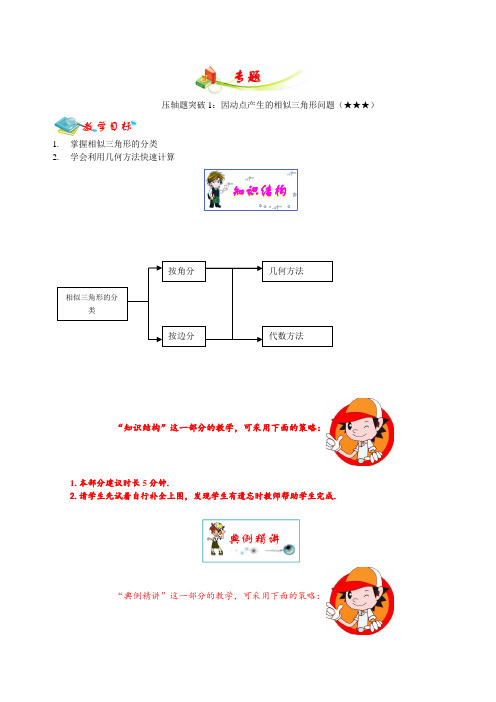
-------------压轴题突破1:因动点产生的相似三角形问题(★★★)1. 掌握相似三角形的分类2. 学会利用几何方法快速计算知识结构1.本部分建议时长5分钟.2.请学生先试着自行补全上图,发现学生有遗忘时教师帮助学生完成.“知识结构”这一部分的教学,可采用下面的策略:“典例精讲”这一部分的教学,可采用下面的策略:相似三角形的分类按角分按边分 几何方法代数方法1.本部分建议时长20分钟.2.进行例题讲解时,教师宜先请学生试着自行解答.若学生能正确解答,则不必做过多的讲解;若学生不能正确解答,教师应对相关概念、公式进行进一步辨析后再讲解例题.3.在每一道例题之后设置了变式训练题,应在例题讲解后鼓励学生独立完成,以判断学生是否真正掌握了相关考点和题型.4.教师应正确处理好例题与变式训练题之间的关系,宜采用讲练结合的方式,切不可将所有例题都讲完后再让学生做变式训练题.如图1,已知抛物线211(1)444by x b x =-++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C .(1)点B 的坐标为______,点C 的坐标为__________(用含b 的代数式表示);(2)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.(★★★)图1答案:(1)B 的坐标为(b, 0),点C 的坐标为(0, 4b).(2)由2111(1)(1)()4444b y x b x x x b =-++=--,得A(1, 0),OA =1.①如图4,以OA 、OC 为邻边构造矩形OAQC ,那么△OQC ≌△QOA .当BA QAQA OA =,即2QA BA OA =⋅时,△BQA ∽△QOA .所以2()14bb =-.解得843b =±.所以符合题意的点Q 为(1,23+). ②如图5,以OC 为直径的圆与直线x =1交于点Q ,那么∠OQC =90°。
沪科版九年级数学上册 相似三角形 知识点大总结

沪科版九年级数学上册 相似三角形 知识点大总结知识点1 有关相似形的概念(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形.相似多边形对应边长度的比叫做相似比(相似系数).知识点2 比例线段的相关概念(1)如果选用同一单位量得两条线段的长度分别为,那么就说这两条线段的比是,或写b a ,n m ,nmb a =成.注:在求线段比时,线段单位要统一。
n m b a ::=(2)在四条线段中,如果的比等于的比,那么这四条线段叫做成比例线段,d c b a ,,,b a 和d c 和d c b a ,,,简称比例线段.注:①比例线段是有顺序的,如果说是的第四比例项,那么应得比例式为:a d cb ,,.②a 、d 叫比例外项,b 、c 叫比例内项, a 、c 叫比例前项,a d cb =()ac a b cd b d==在比例式::中,b 、d 叫比例后项,d 叫第四比例项,如果b=c ,即 那么b 叫做a 、d 的比例中项, 此时有a b b d =::。
2b ad =(3)黄金分割:把线段分成两条线段,且使是的比例中项,即AB )(,BC AC BC AC >AC BC AB 和,叫做把线段黄金分割,点叫做线段的黄金分割点,其中2AC AB BC =⋅AB C AB ≈0.618.即简记为:AB AC 215-=AB AC BC AB AC ==长短==全长注:黄金三角形:顶角是360的等腰三角形。
黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质(注意性质立的条件:分母不能为0)(1) 基本性质:①;②.bc ad d c b a =⇔=::2::a b b c b a c =⇔=⋅注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如,除bc ad =了可化为,还可化为,d c b a ::=d b c a ::=,,,,,.b a dc ::=c ad b ::=c d a b ::=b d a c ::=a b c d ::=a c b d ::=(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb db a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项(3)反比性质(把比的前项、后项交换):.a cb d b da c=⇔=(4)合、分比性质:.a c a b c d b d b d±±=⇔=注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:等等.⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=d c d c b a b a ccd a a b d c b a(5)等比性质:如果,那么.)0(≠++++====n f d b n m f e d c b a ba n f db m ec a =++++++++ 注:①此性质的证明运用了“设法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例k 计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:;其中.baf d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322032≠+-f d b 知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或注:①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例.②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.已知AD∥BE∥CF,可得等. AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
沪科版九上数学相似三角形知识点总结

沪科版九上数学《相似三角形》知识点总结 姓名:_______1.相似三角形定义:对应角相等,对应边成比例的三角形,叫做相似三角形。
2.相似三角形的表示方法:用符号“∽”表示,读作“相似于”。
3.相似三角形的相似比:相似三角形的对应边的比叫做相似比。
4. 平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例. 已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等相似三角形的预备定理:平行于三角形一边的直线和其他两边(或两边的延长线) 相交,所截成的三角形与原三角形相似。
由DE ∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或5.相似三角形的判定定理:三角形相似的判定方法与全等的判定方法的联系列表如下: 6.直角三角形相似:(1)(2)应成比例,那么这两个直角三角形相似。
7.相似三角形的性质定理:(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
8. 相似三角形的传递性(3)BB如果△ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,那么△ABC∽A2B2C29.相似三角形的几种基本图形:①平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。
这个定理确定了相似三角形的两个基本图形“A”型和“ 8 ”型。
若DE∥BC(A型和X型)则△ADE∽△ABC②如图:其中∠1=∠2,则△ADE∽△ABC称为“斜交型”的相似三角形。
(有“反A共角型”、“反A共角共边型”、“蝶型”)③满足1、AC2=AD·AB,2、∠ACD=∠B,3、∠ACB=∠ADC,都可判定△ADC∽△ACB.④当AD AEAC AB或AD·AB=AC·AE时,都可判定△ADE∽△ACB.⑤)”“三垂直型”)⑥如图:∠1=∠2,∠B=∠D,则△ADE∽△ABC,称为“旋转型”的相似三角形。
沪科版九年级数学 22.2 相似三角形的判定(学习、上课课件)

感悟新知
解:∵四边形ABCD是平行四边形,
知2-练
∴ AB∥CD,AD∥BC,AB=CD.
∴△BEF ∽△CDF,△BEF ∽△AED.∴△CDF ∽△AED.
∵ AB=3BE,∴△BEF与△CDF的相似比k1=CBDE=BAEB=
1 3
;
△
BEF
与
△
AED
的
相
似
比
k2
=
BE AE
=
1 4
;
△
CDF
知1-练
感悟新知
知识点 2 平行线截三角形相似的定理
知2-讲
1. 定理 平行于三角形一边的直线与其他两边(或两边的
延长线)相交,截得的三角形与原三示,
∵ DE∥BC,
∴△ABC∽△ADE.
书写两个三角形相似时,要把表示对应顶 点的大写字母写在对应的位置上.
感悟新知
知2-练
解题秘方:判断是用“平行线截线段成比例”,还是用 “平行线截三角形相似的对应边成比例”解 题是关键.
解:由题意知BD⊥AB,AC⊥AB,∴ BD∥AC. ∴△ACE∽△BDE. ∴ BADC=ABEE,即A1C=1.60-.20.2 . ∴ AC=7 米.
感悟新知
知2-练
3-1.
感悟新知
知2-讲
2. 作用 本定理是相似三角形判定定理的预备定理, 它通过平行证三角形相似,再由相似证对应角相 等、对应边成比例.
感悟新知
特别提醒
知2-讲
根据定理得到的相似三角形的三个基本图形中都有
BC∥DE,图22.2-4 ①②很像大写字母A,故我们称之为
“A”型相似;图22.2-4 ③
很像大写字母X,故我们
沪教版(上海)初中数学九年级第一学期2相似三角形的判定课件

B1C1,垂足分别为点D,D1,且
AB A1B1
AD A1D1
求证:△A B C ∽△A1B1C1
课堂小结
直角三角形类似的判定方法:
预备定理
(判定定理1)两角对应相等
有一锐角相等的两Rt△类似
(判定定理2)两边对应成比例且夹角相等 (判定定理3)三边对应成比例 (特殊)斜边和直角边对应成比例
布置作业
HL
斜边和一条直角边对应相等, 两直角三角形全等
猜想:斜边和一条直角边对应成比例, 两直角三角形类似
已 知 : 如 图 , 在Rt△ABC与Rt△A1B1C1中 ,C C1 90 AB AC A1B1 A1C1
求 证 :Rt△ABC ∽ Rt△A1B1C1
A
A1
C
B
C1
B1
直角三角形类似判定方法
如果一个直角三角形的斜边和一条直角边与 另一个直角三角形的斜边和一条直角边对应成比 例,那么这两个直角三形类似。
简单地说: 斜边和直角边对应成比例,两直角三角形类似。
看一看
在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列两个直 角三角形是否类似?
(1)
D
A
45
12
15
C
B
F
E
(2)
A
5
C
( 2 ) AC=3,BC=4,A'C'=6,B'C'=8
两边对应成比例且夹角相等,两三角形类似
AC BC C C △ABC ∽△ABC AC BC
( 3 ) AC=3,AB=5,A'C'=6,A'B'=10
△ABC ∽△ABC
你的判定根据是?
沪教版九年级上学期-相似三角形讲义(含解析) (1)
一、比和比例一般来说,两个数或两个同类的量a与b相除,叫做a与b的比,记作:a b(或表示为ab );如果::a b c d=(或a cb d=),那么就说a、b、c、d成比例.二、比例的性质(1)基本性质:如果a cb d=,那么ad bc=;相似三角形知识结构模块一:比例线段知识精讲2 / 34如果a cb d =,那么b d ac =,a b cd =,c d a b=. (2) 合比性质: 如果a cb d =,那么a bc db d++=; 如果a cb d =,那么a bc db d--=. (3) 等比性质: 如果a c kb d ==,那么ac a c k bd b d+===+.三、比例线段的概念对于四条线段a 、b 、c 、d ,如果::a b c d =(或表示为a cb d=),那么a 、b 、c 、d 叫做成比例线段,简称比例线段. 四、黄金分割如果点P 把线段AB 分割成AP 和PB (AP PB >)两段(如下图),其中AP 是AB 和PB 的比例中项,那么称这种分割为黄金分割,点P 称为线段AB 的黄金分割点.其中,510.6182AP AB -=≈,称为黄金分割数,简称黄金数.五、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例. 如图,已知ABC ∆,直线l // BC ,且与AB 、AC 所在直线交于点D 和点E ,那么AD AEDB EC=.APBlAB CDEAB C DEAB CDE ll六、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.如图,点D 、E 分别在ABC ∆的边AB 、AC 上, 如果DE // BC ,那么DE AD AE BC AB AC==. 七、三角形的重心定义:三角形三条中线交于一点,三条中线交点叫三角形的重心.性质:三角形重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍. 八、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.九、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.如图,在ABC ∆中,直线l 与AB 、AC 所在直线交于点D 和点E ,如果ADAEDB EC=,那么l //BC .ABCD EA BCDEAB CDEABCD E4 / 34十、平行线分线段成比例定理两条直线被三条平行的直线所截,截得的对应线段成比例. 如图,直线1l //2l //3l ,直线m 与直线n 被直线1l 、2l 、3l所截,那么DF EGFB GC=.十一、平行线等分线段定理两条直线被三条平行的直线所截,如果一条直线上截得的线段相等,那么另一条直线上 截得的线段也相等.【例1】 如图,点D 、E 分别在ABC ∆的边AB 和BC 上.下列所给的四个条件中,不一定能得到DE // AC 的条件是( ) A .BE BCBD BA =B .CE ADBE BD =C .BD DEBA AC=D .BC CEAB AD=【难度】★ 【答案】C .例题解析A BCDEF BC D E F G【解析】如图,作DF DE =,则DF DE AC AC =,∴BD DEBA AC=不能判定DE // AC ,故选C . 【总结】本题考查了平行线分线段成比例定理,找准对应关系,避免错选.【例2】 在比例尺为1 : 40000的一张地图上,量得A 、B 两地的距离是37 cm ,那么A 、B两地的实际距离是______km .【难度】★ 【答案】14.8.【解析】设A 、B 两地的实际距离是x km ,则51371040000x -⨯=,解得:14.8x =. 【总结】本题考查了比例尺的有关计算,注意单位的换算.【例3】 如图,已知1l //2l //3l ,DE = 4,DF = 6,那么下列结论正确的是( )A .BC : EF = 1 : 1B .BC : AB = 1 : 2 C .AD : EF = 2 : 3 D .BE : CF = 2 : 3 【难度】★ 【答案】B .【解析】::1:2BC AB EF DE ==,故B 正确. 【总结】本题考查了平行线分线段成比例定理的运用.【例4】 如果线段a = 4 cm ,b = 9 cm ,那么它们的比例中项是______cm . 【难度】★ 【答案】6.【解析】设它们的比例中项是x cm ,则由题意得249x =⨯,解得:6x =. 【总结】本题考查了比例中项的概念及计算.6 / 34BC DE FGA【例5】 四边形ABCD 是平行四边形,点E 在边BA 的延长线上,CE 交边AD 于点F ,交对角线BD 于点G .求证:CG 是EG 与FG 的比例中项. 【难度】★ 【答案】详见解析.【解析】∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,∴CG BG FG GD =,EG BGCG GD=, ∴CG EGFG CG=, ∴CG 是EG 与FG 的比例中项. 【总结】本题考查了平行线分线段成比例定理的运用.【例6】 已知线段AB = 10,P 是线段AB 的黄金分割点(AP > PB ),则AP =______. 【难度】★ 【答案】555.【解析】由题意得51AP AB -=555AP =. 【总结】本题考查了黄金分割的有关计算.【例7】 已知23a c eb d f ===,18ac e =--,0bd f ++≠,求b d f ++的值. 【难度】★★ 【答案】27.【解析】∵23a c eb d f ===,0b d f ++≠,∴23a c e b d f ++=++, ∵18a c e =--,∴18a c e ++=,∴27b d f ++=.【总结】本题考查了等比性质的应用.【例8】 如果直角三角形的斜边长为18,那么这个三角形的重心到直角顶点的距离为______.【难度】★★ 【答案】6.【解析】如图,易得192CD AB ==,∴263CG CD ==. 【总结】本题考查了重心的性质及直角三角形斜边上的中线等于斜边的一半.【例9】 如图,已知AD // EF // BC ,AE = 3BE ,AD = 2,EF = 5,那么BC =______.【难度】★★ 【答案】6.【解析】作AN ∥DC 分别交EF 、BC 于点M 、N ,由题意得2NC MF AD ===,EM AEBN AB=, 即334BN =,∴4BN =,∴6AB =. 【总结】本题考查了平行线分线段成比例定理的运用.【例10】 如图,点E 、F 分别在正方形ABCD 的边AB 、BC 上,EF 与对角线BD 交于点G ,如果BE = 5,BF = 3,那么FG : EF 的比值是_______.【难度】★★A BCDEF M NA BCDEFGH【答案】38.【解析】作GH AB⊥于点H,易得GH BH=,∵GH EHBF EB=,535GH GH-=,解得:158GH=,∴38 FG BHEF BE==.【总结】本题考查了平行线分线段成比例定理的运用,注意比和比值的区别.【例11】如图,BD是ABC∆的角平分线,点E、F分别在BC、AB上,且DE // AB,DEF A∠=∠.(1)求证:BE = AF;(2)设BD与EF交于点M,联结AE,交BD于点N,求证:BN MD BD ND=.【难度】★★【答案】详见解析.【解析】(1)∵DE // AB,DEF A∠=∠,∴AD∥EF,∴四边形AFED是平行四边形,∴AF DE=,ABD EDB∠=∠,∵BD是ABC∆的角平分线,∴ABD EBD∠=∠,∴EDB EBD∠=∠,∴BE DE=,∴BE AF=;(2)∵DE // AB,∴BN AB ND ED=,∵AD∥EF,∴BD ABMD AF=,MAFB E CDN8/ 34ABCDEFM∵ED AF =,∴BD AB MD ED =,∴BN BDND MD=, ∴BN MD BD ND ⋅=⋅.【总结】本题考查了平行四边形的判定及平行线分线段成比例定理.【例12】 如图,在直角梯形ABCD 中,AD // BC ,90DAB ABC ∠=∠=︒,E 为CD 的中点,联结AE 并延长交BC 的延长线于F ; (1)联结BE ,求证:BE = EF .(2)联结BD 交AE 于M ,当AD = 1,AB =2,AM = EM 时,求CD 的长. 【难度】★★【答案】(1)详见解析;(2)5CD =.【解析】(1)∵AD // BC ,DE EC =,易得ADE ∆≌FCE ∆, ∴E 为AF 的中点,∵90DAB ABC ∠=∠=︒, ∴BE EF =;(2)∵AM EM =,∴13AM MF =,∴13AD BF =, ∵1AD CF ==,∴3BF =,2BC =,∵2AB =,∴()225DC BC AD AB -+.【总结】本题考查了直角三角形的性质、平行线分线段成比例定理及勾股定理等.10 / 34一、 相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等,且它们各有的三边对应成比例,那么这两个三角形叫做相似三角形.如图,DE 是ABC ∆的中位线,那么在ADE ∆与ABC ∆中, A A ∠=∠, ADE B ∠=∠,AED C ∠=∠;12AD DE AE AB BC AC ===.由相似三角形的定义,可知这两个三角形相似.用符号来表示,记作ADE ∆∽ABC ∆,其中点A 与点A 、点D 与点B 、点E 与点C 分别是对应顶点;符号“∽”读作“相似于”.用符号表示两个相似三角形时,通常把对应顶点的字母分别写在三角形记号“∆”后相应的位置上.根据相似三角形的定义,可以得出:(1)相似三角形的对应角相等,对应边成比例;两个相似三角形的对应边的比,叫做这两个三角形的相似比(或相似系数).(2)如果两个三角形分别与同一个三角形相似,那么这两个三角形也相似. 二、 相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似.模块二:相似三角形DABCE知识精讲AB C A 1B 1C 1如图,已知直线l 与ABC ∆的两边AB、AC 所在直线分别交于点D 和点E , 则ADE ∆∽ABC ∆.三、 相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等,那么这两个三角形相似. 可简述为:两角对应相等,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果1A A ∠=∠、1B B ∠=∠,那么ABC ∆∽111A B C ∆.常见模型如下:ABCDEAB C DEAB CDE12 / 34AB C AB CABC A 1B 1C 1四、 相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.可简述为:两边对应成比例且夹角相等,两个三角形相似. 如图,在ABC ∆与111A B C ∆中,1A A ∠=∠,1111AB ACA B AC =,那么ABC ∆∽111A B C ∆.五、 相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似. 可简述为:三边对应成比例,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果111111AB BC CAA B B C C A ==,那么ABC ∆∽111A B C ∆.六、 直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例,那么这两个直角三角形相似.可简述为:斜边和直角边对应成比例,两个直角三角形相似. 如图,在Rt ABC ∆和111Rt A B C ∆中,如果190C C ∠=∠=︒,1111AB BCA B B C =, 那么ABC ∆∽111A B C ∆.七、 相似三角形性质定理相似三角形性质定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都 等于相似比.相似三角形性质定理2:相似三角形周长的比等于相似比. 相似三角形性质定理3:相似三角形的面积的比等于相似比的平方.例题解析ABCA 1B 1C 114/ 34AB CDEF【例13】在下列44⨯的正方形网格图中,每个小正方形的边长都是1,三角形的顶点都在格点上,那么与图1中ABC∆相似的三角形所在的网格图是()A.B.C.D.【难度】★【答案】B.【解析】由图易得ABC∆为直角三角形,且:1:2BC AB=,故选B.【总结】本题考查了相似三角形的判定.【例14】已知ABC∆∽DEF∆,且相似比为3 : 4,2ABCS∆=cm2,则DEFS∆=______ cm2.【难度】★【答案】329.【解析】由题意得234ABCDEFSS∆∆⎛⎫= ⎪⎝⎭,∴329DEFS∆=cm2.【总结】本题考查了相似三角形的性质.【例15】如图,已知点D是ABC∆中的边BC上的一点,BAD C∠=∠,ABC∠的平分线交边AC于点E,交AD于F,那么下列结论中错误的是()A.BAC∆∽BDA∆B.BFA∆∽BEC∆图1ABCDABCD EF C .BDF ∆∽BEC ∆ D .BDF ∆∽BAE ∆【难度】★ 【答案】C .【解析】∵BAD C ∠=∠,ABD CBA ∠=∠,∴BAC ∆∽BDA ∆; ∵BAD C ∠=∠,ABF CBF ∠=∠,∴BFA ∆∽BEC ∆;∵BAE BDF ∠=∠,ABF CBF ∠=∠,∴BDF ∆∽BAE ∆;故C 错误.【总结】本题考查了相似三角形的判定.【例16】 如图,已知点D 在ABC ∆的边AB 上,且ACD B ∠=∠,:1:3ACD DBC S S ∆∆=.求AC AB的值. 【难度】★【答案】12.【解析】∵ACD B ∠=∠,CAD BAC ∠=∠,∴CAD BAC ∆∆,∴22::CAD BAC S S AC AB ∆∆=,∵:1:3ACD DBC S S ∆∆=,∴:1:4CAD BAC S S ∆∆=,∴12AC AB =. 【总结】本题考查了相似三角形的判定及性质.【例17】 如图,已知点E 、F 分别在矩形ABCD 的边BC 和CD 上,EF AE ⊥,BE = 3 cm ,AB = 6 cm ,矩形ABCD 的周长为28 cm ,求CF 的长.【难度】★16 / 34ABCDEAMG【答案】52CF =cm . 【解析】∵AB = 6 cm ,矩形ABCD 的周长为28 cm , ∴8BC =cm ,∴5EC =cm ,∵EF AE ⊥, 易证ABE ∆∽ECF ∆,∴AB BE EC CF =,即635CF =,解得:52CF =cm . 【总结】本题考查了一线三等角基本模型的运用.【例18】 如图,已知点D 、E 分别在ABC ∆边AB 、AC 上,DE // BC ,BD = 2AD ,那么:DEB EBC S S ∆∆等于( )A .1 : 2B .1 : 3C .1 : 4D .2 : 3【难度】★★ 【答案】B .【解析】∵BD = 2AD ,∴2BDE ADE S S ∆=,∵DE // BC ,∴9ABC ADE S S ∆∆=,∴6EBC ADE S S ∆∆=,∴:DEB EBC S S ∆∆1:3=.【总结】本题考查了相似三角形的性质及同底等高模型的综合运用.【例19】 如图,ABC ∆中,如果AB = AC ,AD ⊥BC 于点D ,M 为AC 中点,AD 与BM 交于点G ,那么:GDM GAB S S ∆∆的值为_______.【难度】★★ABCDEF【答案】14. 【解析】∵AB = AC ,AD ⊥BC , ∴BAD CAD ∠=∠,BD DC =, ∵M 为AC 中点,∴DM AM =,∴BAD MDA ∠=∠, ∴GDM ∆∽GAB ∆,∵点G 为ABC ∆的重心,∴214GDM GAB S GD S GA ∆∆⎛⎫== ⎪⎝⎭. 【总结】本题考查了相似三角形的判定及性质,同时考查了重心的性质.【例20】 如图,已知ABC ∆中,AB = AC ,CD 是边AB 上的高,且CD = 2,AD = 1,四边形BDEF 是正方形.CEF ∆和BDC ∆相似吗?试证明你的结论.【难度】★★【答案】相似,详见解析.【解析】由题意,可得:5AC AB =∴51BD DE EF ===,∴35CE =∴51BD DC -=355151CE EF --==-,∴BD CEDC EF=,∵BDC CEF∠=∠,∴CEF∆∽BDC∆.【总结】本题考查了相似三角形的判定.【例21】已知:如图,点E是四边形ABCD的对角线BD上一点,且BAC BDC DAE∠=∠=∠.(1)求证:ABE∆∽ACD∆;(2)求证:BC AD DE AC=.【难度】★★【答案】详见解析.【解析】(1)∵BAC BDC DAE∠=∠=∠,∴BAE CAD∠=∠,∵BEA EDA DAE∠=∠+∠,CDA EDA BDC∠=∠+∠,∴BEA CDA∠=∠,∴ABE∆∽ACD∆;(2)由(1)知AB AEAC AD=,∴AB ACAE AD=,又∵BAC EAD∠=∠,∴ABC∆∽AED∆,∴BC ACED AD=,∴BC AD DE AC=.【总结】本题考查了相似三角形的判定及性质的综合运用.EDCBA18/ 34ABCD EFGHA BCD EF 【例22】 如图,已知:四边形ABCD 是平行四边形,点E 在边BA 的延长线上,CE 交AD于点F ,ECA D ∠=∠. (1)求证:ECA ∆∽ECB ∆; (2)若DF = AF ,求AC : BC 的值. 【难度】★★【答案】(1)详见解析;(22. 【解析】(1)∵四边形ABCD 是平行四边形, ∴B D ∠=∠,∵ECA D ∠=∠,∴ECA B ∠=∠, 又∵E E ∠=∠, ∴ECA ∆∽ECB ∆; (2)∵DF AF =,易证DC AE AB ==,∴2EB EA =,由(1)得AC EC EA BC EB EC ==,即2EC EAEA EC=,∴2EC EA =, ∴22AC EA BC EC ==. 【总结】本题考查了相似三角形的判定及性质的应用.【例23】 如图,BD 是平行四边形ABCD 的对角线,若45DBC ∠=︒,DE BC ⊥于E ,BF CD ⊥于F ,DE 与BF 相交于H ,BF 与AD 的延长线相交于G .求证:(1)CD = BH ; (2)AB 是AG 和HE 的比例中项. 【难度】★★ 【答案】详见解析.【解析】(1)∵45DBC ∠=︒,DE BC ⊥, ∴ED EB =,∵BF CD ⊥,∴EBH CDE ∠=∠,∴EDC ∆≌EBH ∆,20 / 34∴CD BH =;(2)∵四边形ABCD 是平行四边形,∴C A ∠=∠,∴BHE A ∠=∠,∵EBH BGA ∠=∠,∴EBH ∆∽BGA ∆,∴AG ABHB HE=, ∵HB CD AB ==,∴AG ABAB HE=,∴AB 是AG 和HE 的比例中项. 【总结】本题考查了全等及相似三角形的判定.【例24】 如图,已知等腰ABC ∆中,AB = AC ,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E .(1)求证:CAD ECB ∠=∠;(2)点F 是AC 的中点,联结DF ,求证:2BD FC BE =.【难度】★★ 【答案】详见解析.【解析】(1)∵AD ⊥BC ,CE ⊥AB , ∴BAD ECB ∠=∠, ∵AB = AC ,∴BAD CAD ∠=∠, ∴CAD ECB ∠=∠; (2)由题意得12ED BC BD ==,∴DBE DEB ∠=∠, ∵点F 是AC 的中点,∴12DF AC FC ==,∴DCF FDC ∠=∠, ∵DBE DCF ∠=∠,∴CDF ∆∽BED ∆, ∴CD FC BE BD =,∵CD BD =,∴BD FCBE BD=, ∴2BD FC BE =.CBADEFABC D E F G【总结】本题考查了直角三角形的性质及相似三角形的判定.【例25】 如图,已知在梯形ABCD 中,AD // BC ,90A ∠=︒,AB = AD .点E 在边AB 上,且DE CD ⊥,DF 平分EDC ∠,交BC 于点F ,联结CE 、EF . (1)求证:DE = DC ;(2)如果2BE BF BC =,求证:BEF CEF ∠=∠. 【难度】★★ 【答案】详见解析.【解析】(1)作CH AD ⊥的延长线于点H , ∵AD // BC ,90A ∠=︒,AB = AD ,∴CH AD =,∵DE CD ⊥,∴ADE HCD ∠=∠, ∴ADE ∆≌HCD ∆,∴DE DC =;(2)∵2BE BF BC =,B B ∠=∠,∴BEF ∆∽BCE ∆,∴BEF BCE ∠=∠, ∵DF 平分EDC ∠,DE DC =,∴DEF ∆≌DCF ∆,∴DEF DCF ∠=∠,∵DEC DCE ∠=∠,∴CEF BCE ∠=∠,∴BEF CEF ∠=∠.【总结】本题考查了一线三直角模型及相似和全等三角形的综合应用.【例26】 已知:如图,在ABC ∆中,AB = AC ,点D 、E 分别是边AC 、AB 的中点,DF ⊥AC ,DF 与CE 相交于点F ,AF 的延长线与BD 相交于点G .(1)求证:2AD DG BD =;(2)联结CG ,求证:ECB DCG ∠=∠. 【难度】★★ 【答案】详见解析.【解析】(1)∵AB = AC ,点D 、E 分别是边AC 、AB 的中点,A BCDEFH∴ACE∆≌ABD∆,∴ABD ACE∠=∠,∵DF⊥AC,∴FAD FCD∠=∠,∴ABD FAD∠=∠,∴DAG∆∽DBA∆,∴AD DG BD AD=,∴2AD DG BD=;(2)∵AD DC=,∴DC DG BD DC=,∵CDG BDC∠=∠,∴CDG∆∽BDC∆,∴DBC DCG∠=∠,∵ABC ACB∠=∠,∴ABD GCB∠=∠,∴ACE GCB∠=∠,∴ECB DCG∠=∠.【总结】本题考查了相似三角形的判定及性质.ABCD EFG【例27】 如图,直角梯形ABCD 中,90B ∠=︒,AD // BC ,BC = 2AD ,点E 为边BC 的中点.(1)求证:四边形AECD 为平行四边形;(2)在CD 边上取一点F ,联结AF 、AC 、EF ,设AC 与EF 交于点G ,且EAF CAD ∠=∠.求证:AEC ∆∽ADF ∆;(3)在(2)的条件下,当45ECA ∠=︒时,求:FG : EG 的比值. 【难度】★★【答案】(1)详见解析;(2)详见解析;(3)45.【解析】(1)∵BC = 2AD ,点E 为边BC 的中点, ∴AD EC =,∵AD // BC ,∴四边形AECD 为平行四边形;(2)∵EAF CAD ∠=∠,∴EAC DAF ∠=∠, ∵四边形AECD 为平行四边形,∴AEC D ∠=∠, ∴AEC ∆∽ADF ∆;(3)∵45ECA ∠=︒,∴AB BC =,设1AD =,则1BE EC ==,2AB =,∴5AE =∵AEC ∆∽ADF ∆,∴AD DFAE EC=,解得5DF =,∴45FC , ∴45FG FC EG AE ==.24 / 34【总结】本题考查了平行四边形的判定、勾股定理、相似三角形的判定及性质的综合运用,综合性较强,解题时注意进行分析.【例28】 如图,已知在ABC ∆中,P 是边BC 上的一个动点,PQ // AC ,PQ 与边AB 相交于点Q ,AB = AC = 10,BC = 16,BP = x ,APQ ∆的面积为y . (1)求y 关于x 的函数解析式;(2)试探索:APQ ∆与ABP ∆能否相似?如果能相似,请求出x 的值,如果不能相似,请说明理由.【难度】★★★【答案】(1)()23301616y x x x =-<<;(2)能相似,394x =. 【解析】(1)作AH BC ⊥于点H ,ABCPQ H∵AB = AC = 10,BC = 16,∴6AH =,∴1482ABC S BC AH ∆=⋅⋅=,132ABP S BP AH x ∆=⋅⋅=, ∵PQ // AC ,∴BPQ ∆∽BCA ∆,∴22256BPQ BCAS BP x S BC ∆∆⎛⎫== ⎪⎝⎭,∴2316BPQ x S ∆=,∴23316APQ ABP BPQ S S S x x ∆∆∆=-=-,即()23301616y x x x =-<<; (2)能相似,此时394x =,详解如下: ∵BPQ ∆∽BCA ∆,∴BQ BP BA BC =,∴58BQ x =,∵AQP B ∠>∠,∴AQP APB ∠=∠,∴APQ ∆∽ABP ∆,∴AP PQ AB BP =,即5810xAP x =,解得:254AP =,∵AQ PQ AP BP =,即551088254x xx -=,解得:394x =, 综上,APQ ∆与ABP ∆能相似,此时394x =. 【总结】本题考查了相似三角形的性质及相似三角形的存在性问题.26 / 34ABCMN【习题1】 如果两个相似三角形的面积的比为4 : 9,那么它们对应的角平分线的比是______. 【难度】★ 【答案】2:3.【解析】相似三角形面积比等于相似比的平方. 【总结】本题考查了相似三角形的性质.【习题2】 如图,ABC ∆和AMN ∆都是等边三角形,点M 是ABC ∆的重心,那么AMNABCS S ∆∆的值为( ) A .23B .13C .14D .49【难度】★★ 【答案】B .【解析】∵点M 是ABC ∆的重心,设2AM =,则可得23AB =,∴AMN ABC S S ∆∆213AM AB ⎛⎫== ⎪⎝⎭,故选B . 【总结】本题考查了相似三角形及重心的性质的综合运用.【习题3】 如图,AB // DC ,DE = 2AE ,CF = 2BF ,且DC = 5,AB = 8,则EF =______. 【难度】★★随堂检测CDMABCDEF O P【答案】7.【解析】延长AD 、BC 交于点M ,∵AB // DC ,∴MD MCDA CB=, ∵DE = 2AE ,CF = 2BF ,∴MD MCDE CF=,∴EF // DC , 过点D 作DH ∥CB ,易求7EF =.【总结】本题考查了本题考查了平行线分线段成比例定理的运用.【习题4】 已知,如图,D 、E 、F 分别是ABC ∆的边BC 、AB 、AC 的中点,AD 与EF 相交于点O ,线段CO 的延长线交AB 于点P ,求证:AB = 3AP .【难度】★★【答案】详见解析.【解析】∵D 、E 、F 分别是ABC ∆的边BC 、AB 、AC 的中点, ∴EF ∥BC ,22BD CD OE OF ===,设PE k =,则14PE OE PB BC ==,∴4PB k =,3BE k =,∴3AE k =, ∴2AP k =,6AB k =,∴3AB AP =.【总结】本题考查了三角形一边平行线的性质定理及中位线性质定理的运用.【习题5】 如图,在平行四边形ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F .(1)求证:CD DF BC BE =;(2)若M 、N 分别是AB 、AD 中点,且60B ∠=︒,求证:EM // FN .ABCDEFMNG28 / 34ABCDEF【难度】★★ 【答案】详见解析.【解析】(1)∵四边形ABCD 是平行四边形, ∴B D ∠=∠, ∵AE ⊥BC ,AF ⊥CD ,∴ABE ∆∽ADF ∆,∴AB BEAD DF=,∵AB CD =,AD BC =, ∴CD DF BC BE =;(2)延长EM 、DA 交于点G ,∵M 、N 分别是AB 、AD 中点,AE ⊥BC ,AF ⊥CD ,∴EM BM =,FN ND =, ∵60B ∠=︒,∴BME ∆、DFN ∆为等边三角形, ∴60BEM DNF ∠=∠=︒,∵G BEM ∠=∠,∴G DNF ∠=∠,∴EM // FN .【总结】本题考查了相似三角形的判定及直角三角形的有关性质.【习题6】 如图,Rt ABC ∆中,90ACB ∠=︒,D 是边BC 上一点,点E 、F 分别是线段AB 、AD 中点,联结CE 、CF 、EF . (1)求证:CEF ∆≌AEF ∆;(2)联结DE ,当BD = 2CD 时,求证:DE = AF .【难度】★★【答案】详见解析.【解析】(1)∵90ACB∠=︒,点E、F分别是线段AB、AD中点,∴12CF AD AF==,12CE AB AE==,∵EF EF=,∴CEF∆≌AEF∆;(2)∵点E、F分别是线段AB、AD中点,∴EF∥BD,12EF BD=,∵BD = 2CD,∴EF CD=,∴四边形CFED是平行四边形,∴DE CF=,∵CF AF=,∴DE AF=.【总结】本题考查了直角三角形的性质、三角形全等及平行四边形的判定和性质的综合运用.【习题7】已知正方形ABCD的对角线相交于点O,CAB∠的平分线分别交BD、BC于点E、F,作BH AF⊥,垂足为H ,BH的延长线分别交AC、CD于点G、P.(1)求证:AE = BG;(2)求证:GO AG CG AO=.【难度】★★【答案】详见解析.【解析】(1)∵ABCD为正方形,∴OA OB=,AC BD⊥,∵BH AF⊥,∴BGO BEH∠=∠,∵AEO BEH∠=∠,∴BGO AEO∠=∠,∴AEO∆≌BGO∆,∴AE BG=;(2)∵AF为CAB∠的平分线,∴OAE BAF∠=∠,∵CBP BAF∠=∠,∴OAE∆∽CBP∆,∴OE PCAO BC=,∵AB BC=,GO OE=,∴GO PCAO AB=,A BCD PGOFHE30 / 34ABCDE F∵PC ∥AB ,∴CG PCAG AB=, ∴GO CGAO AG=,∴GO AG CG AO =. 【总结】本题考查了正方形的性质及相似三角形的判定.【作业1】 若ABC ∆∽111A B C ∆(其中点A 和1A 、B 和1B 、C 和1C 分别对应),且AB = 4,11A B= 6,则ABC ∆的周长和111A B C ∆的周长之比是( )A .9 : 4B .4 : 9C .2 : 3D .3 : 2【难度】★ 【答案】C .【解析】相似三角形的周长比等于相似比. 【总结】本题考查了相似三角形的性质.【作业2】 已知,如图,在Rt ABC ∆中,90ACB ∠=︒,点D 为AB 的中点,BE CD ⊥,垂足为点F ,BE 交AC 于点E ,CE = 1cm ,AE = 3 cm . 求证:(1)ECB ∆∽BCA ∆;(2)求斜边AB 的长.课后作业【难度】★【答案】详见解析.【解析】(1)∵BE CD⊥,90ACB∠=︒,∴ACD CBE∠=∠,∵点D为AB的中点,∴CD AD=,∴ACD DAC∠=∠,∴CBE A∠=∠,∴ECB∆∽BCA∆;(2)由(1)得CB CECA CB=,解得:2CB =cm,∴2225AB AC BC=+=cm.【总结】本题考查了相似三角形的判定及性质,注意观察母子形.【作业3】已知:如图,线段AB // CD,AC CD⊥,AC、BD相交于点P,E、F分别是线段BP和DP的中点.(1)求证:AE // CF;(2)如果AE和DC的延长线相交于点Q,M、N分别是线段AP和DQ的中点,求证:MN = CE.【难度】★★【答案】详见解析.【解析】(1)∵AB // CD,∴AP BP PC PD=,∵E、F分别是线段BP和DP的中点,A BCDEFPQNM32 / 34∴22AP PE PEPC PF PF==, ∴AE // CF ;(2)∵AC CD ⊥,E 、F 分别是线段BP 和DP 的中点,∴AE EP EB ==,∵EA EBEQ ED=,∴ED EQ =, ∵M 、N 分别是线段AP 和DQ 的中点,∴EM AC ⊥,EN DQ ⊥,∴四边形MNCE 是矩形,∴MN CE =.【总结】本题考查了平行线分线段成比例定理和矩形的判定及性质.【作业4】 如图,已知在四边形ABCD 中,AD // BC ,对角线AC 、BD 相交于点O ,BD 平分ABC ∠,过点D 作DF // AB ,分别交AC 、BC 于点E 、F . (1)求证:四边形ABFD 是菱形;(2)设AC AB ⊥,求证:AC OE AB EF =. 【难度】★★ 【答案】详见解析.【解析】(1)∵AD // BC ,DF // AB ,∴四边形ABFD 是平行四边形, ∵BD 平分ABC ∠,∴ABD DBC ∠=∠,∵ADB DBC ∠=∠, ∴ABD ADB ∠=∠,∴AB AD =,∴四边形ABFD 是菱形; (2)连接OF ,易证AOB ∆≌FOB ∆,∵AC AB ⊥,∴OF BC ⊥,∵DF // AB ,∴EF OC ⊥,∴CEF ∆∽FEO ∆,∴EF CEEO EF=, ∵CE EF AC AB =,即CE AC EF AB =,∴EF ACEO AB=,∴AC OE AB EF =. 【总结】本题考查了菱形的判定及相似三角形的判定及性质的综合运用.ABC DEFO【作业5】 已知:如图,四边形ABCD 是菱形,点E 在边CD 上,点F 在BC 的延长线上,CF = DE ,AE 的延长线与DF 相交于点G . (1)求证:CDF DAE ∠=∠;(2)如果DE = CE ,求证:AE = 3EG .【难度】★★ 【答案】详见解析.【解析】(1)∵四边形ABCD 是菱形,∴AD DC =,ADE DCF ∠=∠,∵CF = DE ,∴ADE ∆≌DCF ∆,∴CDF DAE ∠=∠;(2)延长AG 、BF 交于点M , ∵DE = CE ,易证ADE ∆≌MCE ∆,∴AE EM =,AD CM =, 设1DE =,则2AD DC CM ===,1CF FM ==,∴12MG MF AG AD ==,设MG k =,则2AG k =,1322AE AM k ==,∴12EG k =,∴3AE EG =.【总结】本题考查了全等三角形的判定及相似三角形的性质.【作业6】 已知:如图,在正方形ABCD 中,点E 是边AD 的中点,联结BE ,过点A 作AF BE ⊥,分别交BE 、CD 于点H 、F ,联结BF . (1)求证:BE = BF ;(2)联结BD ,交AF 于点O ,联结OE .求证:AEB DEO ∠=∠. 【难度】★★ 【答案】详见解析.EDCG FABMAB CDEFHO【解析】(1)∵四边形ABCD 是正方形,AF BE ⊥, ∴AB AD =,DAF ABE ∠=∠,∴DAF ∆≌ABE ∆,∴AE DF =,∴点F 为DC 中点,∴CBF ∆≌ABE ∆,∴BE BF =;(2)∵DE DF =,EDO FDO ∠=∠,DO DO =, ∴EDO ∆≌FDO ∆,∴DEO DFO ∠=∠,由(1)得AEB DFO ∠=∠,∴AEB DEO ∠=∠.【总结】本题考查了全等三角形的判定及正方形的性质的综合运用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习《相似三角形》全章复习与巩固(基础)知识讲解【学习目标】(1)了解比例的基本性质,了解线段的比、成比例线段的概念;(2)通过具体实例认识图形的相似,探索相似图形的性质,知道相似多边形的对应角相等,对应边成比例,周长的比等于对应边的比,面积的比等于对应边比的平方;(3)了解两个三角形相似的概念,探索两个三角形相似的条件;(4)通过典型实例观察和认识现实生活中物体的相似,利用图形的相似解决一些实际问题( 如利用相似测量旗杆的高度);(5)理解实数与向量相乘的定义及向量数乘的运算律.【知识网络】【要点梳理】要点一、比例线段及比例的性质1.比例线段:(1)线段的比:如果选用同一长度单位量得两条线段a,b的长度分别是m,n,那么就说这两条线段的比是a:b=m:n,或写成,其中a叫做比的前项;b叫做比的后项.(2)成比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.(3)比例的项:已知四条线段a,b,c,d,如果,那么a,b,c,d,叫做组成比例的项,线段a,d叫做比例外项,线段b,c叫做比例内项,线段d还叫做a,b,c的第四比例项.(4)比例中项:如果作为比例线段的内项是两条相同的线段,即a:b=b:c或,那么线段b叫做线段a和c的比例中项.要点诠释:通常四条线段a,b,c,d的单位应该一致,但有时为了计算方便,a,b的单位一致,c,d的单位一致也可以.2.比例的性质(1)比例的基本性质:(2)反比性质:(3)更比性质:或(4)合比性质:(5)等比性质:且3.平行线分线段成比例定理(1)三角形一边的平行线性质定理: 平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.(2)三角形一边的平行线性质定理推论:平行于三角形一边并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边的对应成比例.(3)三角形一边的平行线判定定理:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.(4)三角形一边的平行线判定定理推论:如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.(5)平行线分线段成比例定理:两条直线被三条平行的直线所截,截得的对应线段成比例.(6)平行线等分线段定理:两条直线被三条平行的直线所截,如果在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.这几个定理主要提出由平行线可得到比例式;反之,有比例可得到平行线.首先要弄清三个基本图形:这三个基本图形的用途是:1.由平行线产生比例式基本图形(1): 若l1//l2//l3,则或或或基本图形(2): 若DE//BC,则或或或基本图形(3): 若AC//BD,则或或或在这里必须注意正确找出对应线段,不要弄错位置.2.由比例式产生平行线段基本图形(2):若, , , , ,之一成立,则DE//BC.基本图形(3):若, , , , ,之一成立,则AC//DB.要点诠释:(1)平行线等分线段定理是平行线分线段成比例定理的特例;(2)平行线分线段成比例没有逆定理;(3)由于平行线分线段成比例定理中,平行线本身没有参与作比例,因此,有关平行线段的计算问题通常转化到“A”、“X”型中.A型 X型常用的比例式:.(4)判断平行线的条件中,只能是被截的两条直线的对应线段成比例(被判断的平行线本身不能参与作比例).4.三角形的重心三角形三条中线的交点叫做三角形的重心.要点诠释:(1)重心的性质:三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的二倍;(2)重心的画法:两条中线的交点.要点二、黄金分割1.黄金分割是指把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB)与较小线段(BC)的比例中项(AC2=AB·BC),C点为黄金分割点.2.黄金分割的求法①代数求法:已知:线段AB ,求作:线段AB的黄金分割点C.分析:设C点为所求作的黄金分割点,则AC2=AB·CB,设AB=,AC=x,那么CB=-x,由AC2=AB·CB,得:x2=·(-x)整理后,得:x2+x-=0,根据求根公式,得:x=∴ (不合题意,舍去)即AC=AB≈0.618AB,则C点可作.②黄金分割的几何求法(尺规法):已知:线段AB,求作:线段AB的黄金分割点C.作法:如图:(1)过B点作BD⊥AB,使BD=AB.(2)连结AD,在AD上截取DE=DB.(3)在AB上截取AC=AE.则点C就是所求的黄金分割点.证明:∵AC=AE=AD-AB而AD=∴AC=∴C点是线段AB的黄金分割点.要点诠释:①一条线段有两个黄金分割点.②这种分割之所以被人们称为黄金分割,是因为黄金分割存在美学规律和具有实用价值.德国著名天文学家开普勒 (Kepler,1571—1630)把这种分割称为“神圣的比例”,说它是几何中的瑰宝,大家也可以看一下课外的阅读材料,体会一下黄金分割中所蕴含的美学.要点三、相似三角形1.相似多边形(1)相似多边形的特征:相似多边形的对应角相等,对应边的比相等.(2)相似多边形的识别:如果两个多边形的对应角相等,对应边的比相等,那么这两个多边形相似.(3)相似比:我们把相似多边形对应边的比称为相似比.(4)相似多边形的性质①相似多边形的对应角相等,对应边的比相等.②相似多边形的周长比等于相似比.③相似多边形的面积比等于相似比的平方.2.相似三角形(1)相似三角形的定义:形状相同的三角形是相似三角形.(2)相似三角形的表示方法:用“∽”表示,读作相似于.如:△ABC和△DEF相似,可以写成△ABC∽△DEF,也可以写成△DEF ∽△ABC,读作△ABC相似于△DEF.(3)相似三角形的性质:①相似三角形的对应角相等,对应边的比相等.②相似三角形对应边上的高的比相等,对应边上的中线的比相等,对应角的角平分线的比相等,都等于相似比.③相似三角形的周长的比等于相似比,面积的比等于相似比的平方.要点诠释:相似三角形的性质是通过比例线段的性质推证出来的.(4)相似三角形的判定:①平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似;②如果两个三角形的三组对应边的比相等,那么这两个三角形相似;③如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;④如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.⑤如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边的比对应相等,那么这两个直角三角形相似.(5)相似三角形应用举例相似三角形的知识在实际生产和生活中有着广泛的应用,可以解决一些不能直接测量的物体的长度问题,加深学生对相似三角形的理解和认识.要点诠释:要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.要点四、实数与向量相乘1.实数与向量相乘的意义一般的,设为正整数,为向量,我们用表示个相加;用表示个相加.又当为正整数时,表示与同向且长度为的向量.要点诠释:设P为一个正数,P就是将的长度进行放缩,而方向保持不变;—P也就是将的长度进行放缩,但方向相反.2.向量数乘的定义一般地,实数与向量的相乘所得的积是一个向量,记作,它的长度与方向规定如下:(1)如果时,则:①的长度:;②的方向:当时,与同方向;当时,与反方向;(2)如果时,则:,的方向任意.实数与向量相乘,叫做向量的数乘.要点诠释:(1)向量数乘结果是一个与已知向量平行(或共线)的向量;(2)实数与向量不能进行加减运算;(3)表示向量的数乘运算,书写时应把实数写在向量前面且省略乘号,注意不要将表示向量的箭头写在数字上面;(4)向量的数乘体现几何图形中的位置关系和数量关系.3.实数与向量相乘的运算律设为实数,则:(1)(结合律);(2)(向量的数乘对于实数加法的分配律);(3)(向量的数乘对于向量加法的分配律)4.平行向量定理(1)单位向量:长度为1的向量叫做单位向量.要点诠释:任意非零向量与它同方向的单位向量的关系:,.(2)平行向量定理:如果向量与非零向量平行,那么存在唯一的实数,使.要点诠释:(1)定理中,,的符号由与同向还是反向来确定.(2)定理中的“”不能去掉,因为若,必有,此时可以取任意实数,使得成立.(3)向量平行的判定定理:是一个非零向量,若存在一个实数,使,则向量与非零向量平行.(4)向量平行的性质定理:若向量与非零向量平行,则存在一个实数,使.(5)A、B、C三点的共线若存在实数λ,使.要点五、向量的线性运算1.向量的线性运算定义向量的加法、减法、实数与向量相乘以及它们的混合运算叫做向量的线性运算.要点诠释:(1)如果没有括号,那么运算的顺序是先将实数与向量相乘,再进行向量的加减.(2)如果有括号,则先做括号内的运算,按小括号、中括号、大括号依次进行.2.向量的分解平面向量基本定理:如果是同一平面内两个不共线(或不平行)的向量,那么对于这一平面内的任一向量,有且只有一对实数,使得.要点诠释:(1)同一平面内两个不共线(或不平行)向量叫做这一平面内所有向量的一组基底.一组基底中,必不含有零向量.(2) 一个平面向量用一组基底表示为形式,叫做向量的分解,当相互垂直时,就称为向量的正分解.(3) 以平面内任意两个不共线的向量为一组基底,该平面内的任意一个向量都可表示成这组基底的线性组合,基底不同,表示也不同.3.用向量方法解决平面几何问题(1)利用已知向量表示未知向量用已知向量来表示另外一些向量,除利用向量的加、减、数乘运算外,还应充分利用平面几何的一些定理,因此在求向量时要尽可能转化到平行四边形或三角形中,利用三角形中位线、相似三角形对应边成比例等平面几何的性质,把未知向量转化为与已知向量有直接关系的向量来求解.(2)用向量方法研究平面几何的问题的“三步曲”:①建立平面几何与向量的联系,将平面几何问题转化为向量问题.②通过向量运算,研究几何元素的关系.③把运算结果“翻译”成几何关系.【典型例题】类型一、比例线段1.已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.(1)求a、b、c的值;(2)若线段x是线段a、b的比例中项,求x的值.【答案与解析】解:(1)∵a:b:c=3:2:6,∴设a=3k,b=2k,c=6k,又∵a+2b+c=26,∴3k+2×2k+6k=26,解得k=2,∴a=6,b=4,c=12;(2)∵x是a、b的比例中项,∴x2=ab,∴x2=4×6,∴x=2或x=﹣2(舍去),即x的值为.【总结升华】题目中已知三个量a,b,c的比例关系和有关a,b,c的等式,我们可以利用这个等量关系,通过设参数k, 转化成关于k的一元方程,求出k后,问题得解.举一反三:【变式】已知:,求的值.【答案】根据等比性质:由得.2.如图,在□ABCD中,E为AB中点, ,EF,AC相交于G,求.【答案与解析】分别延长FE,CB相交于H,(构造出了基本图形)在□ABCD中,ADBC,∵E为AB中点,∴AE=BE,∵AD//BC,∴∠AFE=∠H.在△AEF和△BEH中:∴△AEF≌△BEH(AAS)∴AF=BH,∵,设AF=k, 则FD=3k,AD=4k,BH=AF=k,BC=AD=4K,CH=5K,∵AD//BC,即AF//HC.∴∴【总结升华】欲求,就需要有平行线,并使已知条件得以利用,虽然题目中有平行线,但无基本图形,不能使已知条件发挥作用,需通过添加辅助线来寻找解题途径,构造基本图形.此题还有其他辅助线的作法,例如分别延长EF,CD相交于M.或取AC中点N,连结EN.请同学们思考,这两种方法构造了哪些基本图形,如何求出.举一反三:【变式】如图,在是两条中线,则()A.1∶2 B.2∶3C.1∶3 D.1∶4【答案】由题意可知,为的中位线,则△CED∽△CAB,∴,故选D.类型二、相似三角形3.(2016•南平)如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.【思路点拨】根据相似三角形的判定与性质,可得答案.【答案与解析】解:∵DE⊥AB,∴∠BED=90°,又∠C=90°,∴∠BED=∠C.又∠B=∠B,∴△BED∽△BCA,∴=,∴DE===4【总结升华】本题考查了相似三角形的判定与性质,利用相似三角形的性质得出=是解题关键.举一反三:【变式】如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若AB=2,BC=3,则△FC与△DG 的面积之比为()A.9:4B.3:2C.4:3D.16:9【答案】D.设CF=x,则BF=3-x,由折叠得F=BF=3-x,在Rt△FC中,由由勾股定理得CF2+C2=F2,x2+12=(3-x)2,解得x=,由已知可证Rt△FC∽Rt△DG,所以S△FC与S△DG的面积比为(:1)2=.类型三、实数与向量相乘4.已知下列命题:①;②;③;④其中正确命题序号是___________.【答案】②、④.【解析】掌握平面向量数量积的含义,平面数量积的运算律不同于实数的运算律.【总结升华】应用向量的运算性质.类型四、向量的线性运算5.如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,EG∥AC.(1)求证:FG∥AB;(2)设=,=,请用向量、表示.【答案与解析】(1)证明:∵AD=DE=EB,∴==,∵DF∥BC,EG∥AC,∴==,,∴,∴FG∥AB;(2)解:∵DF∥BC,FG∥AB,∴,,∴FG=AB,∵与同向,∴=,∵=,=,∴=﹣,∴=.【总结升华】此题考查了平面向量的知识以及平行线分线段成比例定理.解题时注意掌握数形结合思想的应用.类型五、相似与其它知识综合问题6.如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a、AC=b、AB=c.(1)求线段BG的长;(2)求证:DG平分∠EDF;(3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.【答案与解析】(1)∵D、C、F分别是△ABC三边中点,∴DE∥AB,DF∥AC,又∵△BDG与四边形ACDG周长相等,即BD+DG+BG=AC+CD+DG+AG.∴BG=AC+AG,∵BG=AB-AG,∴BG==,(2)证明:BG=,FG=BG-BF=-,∴FG=DF,∴∠FDG=∠FGD,又∵DE∥AB,∴∠EDG=∠FGD,∠FDG=∠EDG,∴DG平分∠EDF ,(3)在△DFG中,∠FDG=∠FGD, △DFG是等腰三角形,∵△BDG与△DFG相似,∴△BDG是等腰三角形,∴∠B=∠BGD,∴BD=DG,则CD= BD=DG,∴B、CG、三点共圆,∴∠BGC=90°,∴BG⊥CG.【总结升华】这是一道几何综合题,在计算证明时,根据题中已知条件,结合图形性质来完成.后面的问题可以结合前面问题来做.已知三角形三边中点连线,利用三角形中位线性质计算证明.(1)已知△ABC的边长,由三角形中位线性质知,根据△BDG与四边形ACDG周长相等,可得.(2)由(1)的结论,利用等腰三角形性质和平行线性质可证. (3)利用两个三角形相似,对应角相等,从而等角对等边,BD=DG=CD,即可证明.举一反三:【变式】如图,在口ABCD中,的平分线分别与、交于点、.(1)求证:;(2)当时,求的值.【答案】(1)如图,在口ABCD中,,∴.∵是的平分线,∴.∴.∴.(2)∴△∽△,∴,∴.。
