高中数学平面向量专题共26页
高中数学必修四《平面向量》PPT

B、e1和3e2 D、e1和e1 e2
2、指出下列两个向量的夹角。
120
0
1200
600
思维拓展
1、如图所示,在平行四边形ABCD中,
AD =a,AB=b,E、M分别是AD、DC的中
点,点F在BC上,且BC=3BF,以a,b为
基底分别表示向量 AM
B
和
F
EF
.
C
M
A ED
思维拓展 2、如图在平行四边形ABCD中, AC =a,BD =b,以a,b为基底分别表示 向量 AB 和 BC 。
AB 1 a- 1 b 22
BC 1 a+ 1 b 22
DF
C
M
AEB
思维拓展
3、设 e1, e2 是平面 的一组基底,如果 AB 3e1 2e2, BC 4e1 e2,CD=8e1 9e2 求证:A、B、D 三点共线.
2.3.1 平面向量基本定理
复习回顾
1.两向量的加法和减法有哪些几何法 则?
2.怎样理解向量的数乘运算 a?
(1)|λa|=|λ||a|;
(2)λ>0时,λa与 a方向相同;
λ<0时,λa与 a方向相反; λ=0时,λa=0.
3.平面向量共线定理是什么?
b与非零a共线
存在唯一实数λ,使b=λa.
思维引领
问题1:给定平面内任意两个向量e1,e2, 如何求作向量3e1+2e2和e1-2e2?
e1-2e2
B
e2
2e2
C
e1
O e1 D
3e1 A
3e1+2e2
思维引领
问题2:已知 e1 :
e2 :
分别用 e1,e2 表示下列向量:
高中数学必修四《平面向量的基本定理》PPT

第二章 平面向量
想一想 1.判断两个向量能否作为基底的关键是什么? 提示:判断两个向量能否作为基底的关键是看它们是否共 线,若共线,则不能作为基底,否则可以作为基底.
栏目 导引
第二章 平面向量
2.两向量的夹角与垂直
(1)夹角:已知两个__非__零__向__量___a 和 b,作O→A=a,O→B =b,则∠__A_O__B__=θ 叫做向量 a 与 b 的夹角.
【答案】 30° 60°
栏目 导引
第二章 平面向量
【名师点评】 两向量夹角的实质和求解 (1)明确两向量夹角的定义,实质是从同一起点出发的两 个非零向量构成的不大于平角的角,结合平面几何知识 加以解决. (2)求两个向量的夹角关键是利用平移的方法使两个向量 起点重合,作出两个向量的夹角,按照“一作二证三 算”的步骤求出.
栏目 导引
第二章 平面向量
跟踪训练
2.如图所示,已知等边三角形 ABC. (1)求向量A→B与向量B→C的夹角; (2)若 E 为 BC 的中点,求向量A→E与E→C的夹角.
栏目 导引
第二章 平面向量
解:(1)∵△ABC 为正三角形, ∴∠ABC=60°.延长 AB 至点 D,使|A→B|=|B→D|, ∴A→B=B→D, ∴∠DBC 为向量A→B与B→C的夹角,且∠DBC=120°. (2)∵E 为 BC 的中点,∴AE⊥BC, ∴A→E与E→C的夹角为 90°.
已知向量 a 与 b 的夹角为 60°,则向量-3a 和-12b 的夹 角为________.
答案:60°
栏目 导引
第二章 平面向量
典题例证技法归纳
题型探究
题型一 对基底概念的理解 例1 设e1,e2是不共线的两个向量,给出下列四组向量:
高中数学-平面向量专题.doc

v1.0可编辑可修改第一部分:平面向量的概念及线性运算一. 基础知识 自主学习1.向量的有关概念名称定义既有又有的量;向量的大小叫做向量向量的()或称 零向量长度为 的向量;其方向是任意的长度等于的单位向量向量平行向量 方向或 的非零向量共线向量的非零向量又叫做共线向量相等向量 长度 且方向 的向量相反向量长度 且方向 的向量2. 向量的线性运算法则 ( 或几何向量运算定义意义 )加法求两个向量和的运算备注平面向量是自由向量记作 0a非零向量 a 的单位向量为± |a |0 与任一向量 或共线两向量只有相等或不等, 不能比较大小0 的相反向量为 0运算律(1) 交换律:a +b = b +a .(2) 结合律:( a + b ) +c = a + ( b + c ) .求 a 与 b 的相反向量- b 减法的和的运算叫做 a 与 ba -b = a +( - b )的差法则(1)| λ aλ||aλ μa) = λμ a;| = ||.(求实数 λ 与向量 a 的积λaaaλa数乘(2) 当 λ >0 时,的方向与的方(λ +) = + ;的运算μ μa向;λ( a +b ) = λa + λb .v1.0 可编辑可修改当 λ<0 时, λ a 的方向与 a 的方向 ;当 λ= 0 时, λa = 0.3. 共线向量定理向量 ( a ≠0) 与 b 共线的条件是存在唯一一个实数λ ,使得 =.ab λ a二. 难点正本疑点清源1.向量的两要素向量具有大小和方向两个要素.用有向线段表示向量时, 与有向线段起点的位置没有关系. 同向且等长的有向线段都表示同一向量.或者说长度相等、方向相同的向量是相等的.向量只有相等或不等,而没有谁大谁小之说,即向量不能比较大小.2.向量平行与直线平行的区别向量平行包括向量共线( 或重合 ) 的情况,而直线平行不包括共线的情况. 因而要利用向量平行证明向量所在直线平行,必须说明这两条直线不重合.三.基础自测→ → → →1.化简 OP - QP + MS - MQ 的结果等于 ________ .2.下列命题:①平行向量一定相等;②不相等的向量一定不平行;③平行于同一个向量的两个向量是共线向量;④相等向量一定共线.其中不正确命题的序号是_______.→ → → → →3.在△ ABC 中, AB = c ,AC = b . 若点 D 满足 BD = 2DC ,则 AD = ________( 用 b 、c 表示 ) .4.如图,向量 a - b 等于 ()A .- 4e 1- 2e 2B .- 2e 1- 4e 2C . e 1- 3e 2D.3e 1- e 2→ →→5.已知向量a , ,且=+2,=-5a +6 , = 7 - 2 ,则一定共线的三点是()bAB a b BCb CD a bA .A 、B 、DB .A 、B 、C C .B 、C 、DD.A 、C 、 Dv1.0可编辑可修改四.题型分类深度剖析题型一平面向量的有关概念例 1给出下列命题:→ →①若 | a | = | b | ,则 a = b ;②若 A , B , C , D 是不共线的四点,则 AB =DC 是四边形 A BCD 为平行四边形的充要条件;③若 = ,= ,则 a = ;④ = b 的充要条件是 | a | = | | 且 ∥ ;⑤若 a ∥ , ∥ ,则 a ∥ . 其中正确的序号是 ________.a b b cc a b a b b b cc变式训练 1判断下列命题是否正确,不正确的请说明理由.(1) 若向量 a 与 b 同向,且 | a | = | b | ,则 a>b ;(2) 若 | a | =| b | ,则 a 与 b 的长度相等且方向相同或相反;(3) 若 | a | =| b | ,且 a 与 b 方向相同,则a =b ;(4) 由于零向量的方向不确定,故零向量不与任意向量平行; (5) 若向量 a 与向量 b 平行,则向量 a 与 b 的方向相同或相反;→→(6) 若向量 AB 与向量 CD 是共线向量,则 A , B , C ,D 四点在一条直线上; (7) 起点不同,但方向相同且模相等的几个向量是相等向量;(8) 任一向量与它的相反向量不相等题型二 平面向量的线性运算→→→1→→1→→ → → 例 2 如图,以向量 OA =a , OB = b 为边作 ? OADB , BM = 3BC , CN =3CD ,用 a 、b 表示 OM 、 ON 、 MN .→2→→ →变式训练 2 △ABC 中, AD = 3AB , DE ∥ BC 交 AC 于 E , BC 边上的中线AM 交 DE 于 N . 设AB = a ,AC = b ,用 a 、b 表示向→ → → → → →量 AE 、BC 、 DE 、DN 、 AM 、 AN .题型三平面向量的共线问题3- 3→→→例 3设e1,e2是两个不共线向量,已知AB=2e1-8e2, CB=e1+3e2, CD=2e1- e2.(1)求证: A、 B、 D三点共线;→(2)若 BF=3e1- ke2,且 B、 D、 F 三点共线,求 k 的值.变式训练3设两个非零向量 a 与 b 不共线,→→→(1)若 AB=a+ b, BC=2a+8b, CD=3( a- b).求证: A、 B、 D三点共线;(2)试确定实数 k,使 ka+b 和 a+ kb 共线.五.思想与方法5.用方程思想解决平面向量的线性运算问题试题:如图所示,在△中,→ =1→,→ =1→,与相交于点,设→ =,→=. 试用a和b表示向量ABO OC 4OA OD 2OB AD BC M OA a OB b →OM.六.思想方法感悟提高方法与技巧1.将向量用其它向量( 特别是基向量 ) 线性表示,是十分重要的技能,也是向量坐标形式的基础.2.可以运用向量共线证明线段平行或三点共线问题.如→ →→ →AB∥ CD且 AB与 CD不共线,则AB∥ CD;若 AB∥ BC,则 A、 B、C三点共线.失误与防范1.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.要特别注意零向量的特殊性.2.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.七.课后练习1.给出下列命题:①两个具有公共终点的向量,一定是共线向量;②两个向量不能比较大小,但它们的模能比较大小;③λa=0 (λ 为实数),则λ 必为零;④λ,μ 为实数,若λa=μb,则a与b共线.其中错误命题的个数为 ()A. 1 B. 2 C . 3 D.42.若A、B、C、D是平面内任意四点,给出下列式子:→→→→AB +CD=BC+DA;②AC+BD=BC AD ;③ AC -BD=→)DC+AB.其中正确的有(A.0 个 B .1个C.2个D . 3 个3. 已知 O、 A、B 是平面上的三个点,直线AB上有一点 C,满足2AC CB =0,则 OC 等于( )A. 2OA→B.→- OB OA +2OB2 1→D. 1OA +2→C. OA -3OB3 3OB31→→ →→4. 如图所示,在△ABC中,BD=2DC,AE= 3ED,若AB= a,AC= b,则BE等于( )1 1 1a+3b B .-2a+4b1 1 1a+ b D .- a+ b4 3 35.→) 在四边形 ABCD中,AB=a+2b,BC=-4a-b, CD=-5a-3b,则四边形 ABCD的形状是(A.矩形 B .平行四边形C.梯形 D .以上都不对6.AB =8, AC =5,则 BC 的取值范围是__________.7.给出下列命题:→→①向量 AB 的长度与向量BA的长度与向量BA的长度相等;②向量 a 与 b 平行,则 a 与 b 的方向相同或相反;③两个有共同起点而且相等的向量,其终点必相同;5- 5v1.0 可编辑可修改→→⑤向量 AB 与向量CD与向量CD是共线向量,则点A、B、C、D必在同一条直线上.其中不正确的个数为____________ .8. 如图,在△ABC中,点O是BC的中点 . 过点O的直线分别交直线AB、AC于不同的两点M、N.→若 AB =mAM,→,则 m+ n 的值为________.AC =nAN9.设 a 与 b 是两个不共线向量,且向量a+λ b 与- (b - 2a) 共线,则λ= ________.10. 在正六边形 ABCDEF中,AB a →AC, AD →b .=,AF=,求, AE11. 如图所示,△ABC中,点M是BC的中点,点N在边 AC上,且 AN=2NC, AM与 BN相交于点 P,求 AP∶PM的值.12. 已知点G是△ABO的重心,M是AB边的中点 .→ →( 1)求GA+GB+GO;(2) 若PQ过△ABO的重心 G,且AO=a, →→→ 1 1 = 3.OB=b,OP= m a,OQ= n b,求证:+m n第二部分:平面向量的基本定理及坐标表示一.基础知识自主学习1.两个向量的夹角定义范围6- 6v1.0 可编辑可修改→→已知两个 向量 a ,b ,作 OA = a ,OB = b ,则∠ AOB =,向量夹角 θ 的范围是 θ 叫做向量 a 与 b 的夹角 ( 如图 )时 , 两向量共线,当 θ=当 θ= 时,两向量垂直, 记作 a ⊥ b .2. 平面向量基本定理及坐标表示(1) 平面向量基本定理如果 e 1,e 2 是同一平面内的两个向量,那么对于这一平面内的任意向量 a , 一对实数 λ1,λ 2,使 a =. 其中,不共线的向量 e 1, e 2 叫做表示这一平面内所有向量的一组.(2) 平面向量的正交分解及坐标表示把一个向量分解为两个的向量,叫做把向量正交分解.(3) 平面向量的坐标表示①在平面直角坐标系中, 分别取与x 轴、 y 轴方向相同的两个单位向量 , 作为基底, 对于平面内的一个向量 a ,i j由平面向量基本定理可知,有且只有一对实数 x , ,使 = xi + yj ,这样,平面内的任一向量a 都可由 x ,y 唯一确y a定,把有序数对 叫做向量 a 的坐标,记作=,其中叫做 a 在 x 轴上的坐标, 叫做 a 在y 轴上的坐a标.→→→②设 OA = xi + yj ,则向量 OA 的坐标 ( x ,y ) 就是的坐标,即若 OA = ( x ,y ) ,则 A 点坐标为,反之亦成立. ( O 是坐标原点 )3.平面向量坐标运算(1) 向量加法、减法、数乘向量及向量的模设 a = ( x 1,y 1) , b = ( x 2,y 2) ,则a +b =,a - b =,λa =,| a | =.(2) 向量坐标的求法①若向量的起点是坐标原点,则终点坐标即为向量的坐标.→→ .②设 A ( x 1,y 1) , B ( x 2, y 2) ,则 AB =,| AB | =4.平面向量共线的坐标表示 :设 a = ( x ,y ) , b = ( x , y ) ,其中 b ≠∥ b ?.1122二.难点正本疑点清源1.基底的不唯一性只要两个向量不共线, 就可以作为平面的一组基底,对基底的选取不唯一, 平面内任意向量 a 都可被这个平面的一组基底e1, e2线性表示,且在基底确定后,这样的表示是唯一的.2.向量坐标与点的坐标的区别→在平面直角坐标系中,以原点为起点的向量OA=a,点 A 的位置被向量 a 唯一确定,此时点 A 的坐标与 a 的坐标→统一为 ( x,y) ,但应注意其表示形式的区别,如点A( x, y),向量 a= OA=( x, y).→→→→→当平面向量 OA平行移动到 O1A1时,向量不变即O1A1= OA=( x, y),但 O1A1的起点 O1和终点 A1的坐标都发生了变化.三.基础自测1.已知向量a=(2,-1), b=(-1, m), c=(-1,2),若( a+ b)∥ c,则 m=________.2.已知向量a=(1,2),b=(-3,2),若ka+b与b平行,则k=________.3.设向量a=(1,-3),b=(-2,4), c=(-1,-2).若表示向量4a、 4b-2c、 2( a-c) 、d的有向线段首尾相接能构成四边形,则向量d=____________.→→4.已知四边形ABCD的三个顶点 A(0,2),B(-1,-2),C(3,1),且BC=2AD,则顶点D的坐标为() C. (3,2)D. (1,3)5.已知平面向量a=( x, 1), b=(- x, x2),则向量 a+ b()A.平行于y 轴B.平行于第一、三象限的角平分线C.平行于x 轴D.平行于第二、四象限的角平分线四.题型分类深度剖析题型一平面向量基本定理的应用例 1→→→ →如图,在平行四边形 ABCD中, M, N分别为 DC, BC的中点,已知 AM= c,AN= d,试用 c, d 表示 AB,AD.1 如图,P→→+ 3→Q AB→变式训练是△内一点,且满足条件+ 2 = 0,设为的延长线与的交点,令=,试ABC AP BP CP CP CP p→用 p 表示 CQ.题型二向量坐标的基本运算→→→→→例 2已知A(-2,4),B(3,-1),C(-3,-4).设AB=a,BC=b,CA=c,且CM=3c,CN=-2b,→(1)求 3a+b- 3c; (2) 求满足a=mb+nc的实数m,n; (3) 求M、N的坐标及向量MN的坐标.→→1→变式训练 2 (1)已知点A、B、C的坐标分别为A(2,-4)、 B(0,6)、C(-8,10),求向量 AB+2BC-2AC的坐标;(2)已知 a=(2,1),b=(-3,4),求:①3 a+4b;② a-3b;③1a-1b.24题型三平行向量的坐标运算例 3平面内给定三个向量a=(3,2), b=(-1,2), c=(4,1),请解答下列问题:(1)求满足 a= mb+ nc 的实数 m, n;(2)若( a+kc)∥(2 b- a),求实数 k;(3) 若d满足 ( d-c) ∥(a+b) ,且 | d-c| =5,求d.变式训练3已知a=(1,0),b=(2,1).(1) 求 | a+3b| ; (2) 当k为何实数时,ka-b与a+ 3b平行,平行时它们是同向还是反向v1.0可编辑可修改五.易错警示8.忽视平行四边形的多样性致误试题:已知平行四边形三个顶点的坐标分别为( -1,0) , (3,0) , (1 ,- 5) ,求第四个顶点的坐标.六.思想方法感悟提高方法与技巧1.平面向量基本定理的本质是运用向量加法的平行四边形法则,将向量进行分解.2.向量的坐标表示的本质是向量的代数表示,其中坐标运算法则是运算的关键,通过坐标运算可将一些几何问题转化为代数问题处理,从而向量可以解决平面解析几何中的许多相关问题.3.在向量的运算中要注意待定系数法、方程思想和数形结合思想的运用.失误与防范1.要区分点的坐标与向量坐标的不同,尽管在形式上它们完全一样,但意义完全不同,向量坐标中既有方向也有大小的信息.2.若a= ( x1,y1) ,b= ( x2,y2) ,则a∥b的充要条件不能表示成x1 y10,所以应表示为x1y2 x=,因为 x2,y2有可能等于2y2- 2 1=0.同时,的充要条件也不能错记为12-12=0,1 1- 2 2=0等.x y a∥b x x y y x y x y 七.课后练习1.已知向量a= (1 ,- 2) , b= (1 +m,1-m) ,若 a∥b,则实数m的值为() A.3 B .-3C.2 D .-22.已知平面向量a= (1,2) , b=( - 2,m) ,且 a∥b,则 2a+ 3b 等于 () A.( -2,- 4)B.( -3,- 6)C.( -4,- 8)D.( -5,- 10)3. 设向量 a= (3 ,3) , b 为单位向量,且a∥b,则 b 等于 ()v1.0可编辑可修改3 1或-2,231或-2,-224. 已知向量 a =(1 ,- m ) , b = ( m ,m ) ,则向量 a + b 所在的直线可能为 ()A . x 轴B .第一、三象限的角平分线C . y 轴D.第二、四象限的角平分线5.已知 A(7,1) 、 B(1,4), 直线 y1 ax 与线段 AB 交于 C 且→ACCB ,则实数 a 等于 ()2,2A . 2B . 11 16.若三点 A (2,2) , B ( a, 0) , C (0 , b ) ( ab ≠0) 共线,则 a + b 的值等于 ________.7.已知向量 a = (1,2) ,b = ( x, 1) , u = a + 2b , v =2a - b ,且 u ∥ v ,则实数 x 的值为 ________.8.若向量 a(x 3, x 23x 4) 与 AB 相等,其中 A (1,2) , B (3 ,2) ,则 x = ________.9.若平面向量 a , b 满足 |a + b| = 1, a +b 平行于 y 轴, a =(2 ,- 1) ,则 b =______________. 10. a = (1,2) , b = ( -3,2) ,当 k 为何值时, ka +b 与 a - 3b 平行平行时它们是同向还是反向11.三角形的三内角, , 所对边的长分别为 , , ,设向量 m =(3 c - , - ) , n = (3 + 3 , ) , m n.A B C a b cb a ba b c∥(1) 求 cos A 的值; (2) 求 sin( A +30°) 的值.12.在△ ABC 中, a 、 b 、c 分别是角 A 、 B 、 C 的对边,已知向量m = ( a ,b ) ,向量 n = (cos A , cos B ) , 向量 = 2 2sinB +CA ,若 ∥ ,2为等边三角形., 2sinp = ,求证:△p 2m n9ABCv1.0可编辑可修改第三部分:平面向量的数量积一.基础知识自主学习1.平面向量的数量积已知两个非零向量 a 和 b,它们的夹角为θ,则数量_______叫做a和b的数量积(或内积),记作________________.规定:零向量与任一向量的数量积为____.两个非零向量 a 与 b 垂直的充要条件是,两个非零向量 a 与 b 平行的充要条件是.2.平面向量数量积的几何意义数量积 a·b 等于 a 的长度 |a| 与 b 在 a 的方向上的投影_________的乘积.3.平面向量数量积的重要性质(1)e · a= a·e=;(2) 非零向量 a, b,a⊥b? ;(3) 当 a 与 b 同向时, a·b=;当 a 与 b 反向时, a·b=,a·a= a2,|a| =a·a;(4)cosa·bθ=|a||b| ;(5)|a ·b|____|a|| b| . 4.平面向量数量积满足的运算律(1)a·b=(交换律);(2)( ) ·==(λ为实数 );λa b(3)( a+ b)·c=.5.平面向量数量积有关性质的坐标表示设向量 a=( x1,y1), b=( x2, y2),则 a·b=,由此得到(1) 若 a=( x, y),则| a| 2=或 | a| =.(2) 设 A( x1, y1), B( x2,y 2),则A、B两点间的距离|AB|= AB =.(3) 设两个非零向量 a,b, a=( x1,y1), b=( x2, y2),则 a⊥ b? .二.难点正本疑点清源1.向量的数量积是一个实数两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角的余弦值有关,在运用向量的数量积解题时,一定要注意两向量夹角的范围.2 .数量积的运算只适合交换律、加乘分配律及数乘结合律,但不满足向量间的结合律,即(a ·b)c不一定等于v1.0 可编辑可修改a(b ·c) .这是由于 (a ·b)c 表示一个与 c 共线的向量,而 a(b ·c) 表示一个与 a 共线的向量,而 c 与 a 不一定共线.三.基础自测1.已知向量 a 和向量 b 的夹角为 30°, |a| = 2, |b| = 3,则向量 a 和向量 b 的数量积 a ·b = ________.2. 在△ ABC 中, AB =3, AC =2, BC =10, 则 AB AC · = ______.3.已知 a = (2,3) , b = ( - 4,7) ,则 a 在 b 方向上的投影为______.4.已知 |a| = 6, |b| = 3,a ·b =- 12,则向量 a 在向量 b 方向上的投影是( )A .-4B .4C .-2D .25.已知向量 a = (1 ,- 1) , b = (1,2) ,向量 c 满足 (c +b) ⊥a , (c -a) ∥b ,则 c 等于 ()A . (2,1)B . (1,0)D.(0,- 1)四.题型分类深度剖析题型一求两向量的数量积例 1 (1) 在 Rt △ ABC 中,∠ C =90°, AB = 5, AC =4,求 AB ·BC ;(2) 若 a = (3 ,- 4) , b =(2,1) ,试求 (a -2b) ·(2a + 3b) .变式训练 1 (1) 若向量 a 的方向是正南方向, 向量 b 的方向是正东方向, 且 |a| = |b| = 1,则 ( -3a) ·(a + b) = ______.(2)如图,在△ ABC 中, AD ⊥ AB , BC = →3 BD ,| AD | =1,则 AC ·AD 等于 ()A .2 3题型二 求向量的模例 2已知向量 a 与 b 的夹角为 120°,且 |a| = 4, |b| = 2,求: (1)|a + b| ; (2)|3a- 4b| ; (3)(a-2b) ·(a + b) .v1.0可编辑可修改π变式训练 2 设向量 a, b 满足 |a -b|= 2, |a| = 2,且 a- b 与 a 的夹角为 3 ,则|b|=________.题型三利用向量的数量积解决夹角问题例 3已知a与b是两个非零向量,且|a| =|b| = |a - b| ,求 a 与 a+ b 的夹角.变式训练 3 设 n 和 m是两个单位向量,其夹角是60°,求向量a= 2m+ n 与 b= 2n- 3m的夹角.题型四平面向量的垂直问题例 4 已知 a= (cosα,sinα),b=(cosβ,sinβ)(0<α<β<π).(1)求证: a+ b 与 a- b 互相垂直;(2) 若k a+ b 与 a-k b 的模相等,求β -α.(其中k为非零实数)4 已知平面内A、B、C三点在同一条直线上,→→ →变式训练OA =(-2,m),OB=(n,1),OC=(5 ,- 1) ,且OA⊥OB,求实数 m, n 的值.五.答题规范v1.0可编辑可修改5.思维要严谨,解答要规范试题:设两向量e1、 e2满足 |e 1| = 2, |e 2| =1, e1、 e2的夹角为 60°,若向量2t e1+ 7e2与向量 e1+t e2的夹角为钝角,求实数t 的取值范围.六.思想方法感悟提高方法与技巧1.向量的数量积的运算法则不具备结合律,但运算律和实数运算律类似.如(a + b) 2=a2+2a·b+ b2;( λa+μb) ·(s a+t b) =λs a2+ ( λt+μs)a ·b+μt b2( λ,μ,s,t∈R).2.求向量模的常用方法:利用公式|a| 2= a2,将模的运算转化为向量的数量积的运算.3.利用向量垂直或平行的条件构造方程或函数是求参数或最值问题常用的方法技巧.失误与防范1. (1)0 与实数 0 的区别: 0a=0≠0, a+ ( - a) =0≠0,a·0=0≠0;(2)0的方向是任意的,并非没有方向,0 与任何向量平行,我们只定义了非零向量的垂直关系.2.a·b= 0 不能推出a=0 或 b=0,因为 a·b= 0 时,有可能a⊥b.3.一般地, (a ·b)c ≠(b ·c)a即乘法的结合律不成立.因a·b是一个数量,所以(a·b)c表示一个与 c 共线的向量,同理右边 (b ·c)a 表示一个与 a 共线的向量,而 a 与 c 不一定共线,故一般情况下 (a ·b)c ≠(b ·c)a.4.a·b=a·c(a ≠0) 不能推出 b= c.即消去律不成立.5.向量夹角的概念要领会,比如正三角形ABC中,〈 AB, BC 〉应为120°,而不是60°.七.课后练习1. 设向量 a= (1,0) , b=( 1 1, ) ,则下列结论中正确的是 () 2 2A.| |=| | B.=2ab a·b 2C.a∥b D.a-b与b垂直2. 若向量 a=(1,1) , b=(2,5) ,c=(3, x),满足条件 ( 8a-b) · c=30,则 x 等于() A.6 B. 5 C. 4 D. 3v1.0 可编辑可修改3. 已知向量 a,b 的夹角为60°,且 | a| = 2, | b| = 1,则向量a与a+ 2b的夹角等于 ()A.150° B .90°C.60°D.30°4. 平行四边形ABCD中, AC为一条对角线,若AB =(2,4),AC=(1,3),则AD BD等于( )A.6 B. 8 C.- 8 D.- 65. 若 e1、 e2是夹角为πa=2e1+ e2,向量 b=-3e1+2e2,则 a·b等于( ) 的单位向量,且向量3A.1 B.- 4 C.-726.若向量a, b 满足| a|=1,| b|=2且 a 与 b 的夹角为π,则| a+ b|=________. 37.已知向量a,b 满足| a|=3,| b|=2,a 与 b 的夹角为60°,则 a·b=________,若( a- mb)⊥ a,则实数 m=________. 8.设a、b、c是单位向量,且a+ b= c,则 a·c的值为________.9. ( O是平面上一点,A、B、C是平面上不共线的三点. 平面内的动点P 满足OP OA( AB AC),1若λ=2时,PA ( PB PC )的值为______.10.不共线向量a, b 的夹角为小于120°的角,且 | a| = 1,| b| = 2,已知向量c= a+2b,求| c|的取值范围.11.已知平面向量a=(1, x), b=(2 x+3,- x),x∈R.(1)若 a⊥ b,求 x 的值;(2)若 a∥ b,求| a- b|.12.向量a=(cos 23 °, cos 67 °) ,向量b=(cos 68°,cos 22°).(1) 求a·b; (2) 若向量b与向量m共线,u=a+m,求u的模的最小值.v1.0 可编辑可修改第四部分:平面向量应用举例一.基础知识自主学习1.向量在平面几何中的应用平面向量在平面几何中的应用主要是用向量的线性运算及数量积解决平面几何中的平行、垂直、平移、全等、相似、长度、夹角等问题.(1) 证明线段平行或点共线问题, 包括相似问题, 常用共线向量定理: a ∥b ??.(2) 证明垂直问题,常用数量积的运算性质a ⊥b??.a ·bx x +y y 2(3) 求夹角问题,利用夹角公式cos θ==1 21| a || b|22 2 2 ( θ 为 a 与 b 的夹角 ) .x 1+1x 2+ 2y y2.平面向量在物理中的应用(1) 由于物理学中的力、速度、位移都是 ,它们的分解与合成与向量的 相似,可以用向量的知识来解决.(2) 物理学中的功是一个标量,这是力F 与位移 s 的数量积.即 W = F ·s = |F || s|cos θ ( θ 为 F 与 s 的夹角 ) .3.平面向量与其他数学知识的交汇平面向量作为一种运算工具,经常与函数、不等式、三角函数、数列、解析几何等知识结合,当平面向量给出的形式中含有未知数时, 由向量平行或垂直的充要条件可以得到关于该未知数的关系式.在此基础上, 可以求解有关函数、不等式、三角函数、数列的综合问题.此类问题的解题思路是转化为代数运算,其转化途径主要有两种:一是利用平面向量平行或垂直的充要条件;二是利用向量数量积的公式和性质.二.难点正本疑点清源1.向量兼具代数的抽象与严谨和几何的直观,向量本身是一个数形结合的产物.在利用向量解决问题时,要注意数与形的结合、代数与几何的结合、形象思维与逻辑思维的结合.2.要注意变换思维方式,能从不同角度看问题,要善于应用向量的有关性质解题.三.基础自测1.在平面直角坐标系xOy 中,四边形 ABCD 的边 AB ∥ DC , AD ∥BC . 已知 A ( - 2,0) , B (6,8) , C (8,6) .则 D 点的坐标为 ________.2.已知平面向量α、β,|α |=1,|β|=2,α⊥(α-2β),则|2α+β |的值是________.y3.平面上有三个点A(-2, y),B 0,2, C( x, y),若AB⊥BC,则动点 C的轨迹方程为_______________.4.已知A、B是以C为圆心,半径为5的圆上两点,且| AB | =5,AC·CB等于()5A.-2C.05.某人先位移向量a:“向东走 3 km”,接着再位移向量b:“向北走 3 km”,则 a+b 表示( ) A.向东南走 3 2 km B .向东北走 3 2 kmC.向东南走 3 3 km D .向东北走 3 3 km四.题型分类深度剖析题型一向量在平面几何中的应用例 1 如图,在等腰直角三角形ABC中,∠ACB=90°,CA=CB,D为BC的中点,E是AB上的一点,且AE= 2EB. 求证:AD⊥ CE.变式训练1在平面直角坐标系xOy中,已知点A(-1,-2), B(2,3), C(-2,-1).(1) 求以线段AB、 AC为邻边的平行四边形的两条对角线的长;(2) 设实数t→→→t满足( -) ·=0,求的值.AB tOC OC题型二平面向量在解析几何中的应用→3→例 2 已知点P(0, -3 ),点A在x轴上,点M满足PA AM =0,AM=-2MQ,当点A在x轴上移动时,求动点M 的轨迹方程.变式训练 2 已知圆 C : ( x -3) 2+( y -3)2及点 A ( 1,1 ), M 是圆上的任意一点,点 N 在线段 MA 的延长线上,=4→且 MA = 2AN ,求点 N 的轨迹方程.题型三平面向量与三角函数例 3已知向量 a = (sin x , cos x ) , b = (sin x , sin x ) ,c = ( - 1,0) .π(1) 若 x = 3 ,求向量 a 与 c 的夹角;3ππ(2) 若 x ∈ - 8 , 4 ,求函数 f ( x ) = a ·b 的最值;2(3) 函数 f ( x ) 的图象可以由函数 y = 2 sin 2 x ( x ∈R)的图象经过怎样的变换得到变式训练 3 已知 (3,0) , (0,3) , (cosα , sinα ) .ABCα+ π若| OA +OC→(1) 若AC ·BC =- 1,求 sin的值; (2) | = 13,且 α∈(0 ,π ) ,求与 OC 的夹角.4OB五.易错警示9.忽视对直角位置的讨论致误试题:已知平面上三点A 、B 、C ,向量 BC = (2 -k, 3) , AC = (2,4) .(1) 若三点 A 、 B 、C 不能构成三角形,求实数k 应满足的条件; (2) 若△ ABC 为直角三角形,求 k 的值.v1.0可编辑可修改六.思想方法感悟提高方法与技巧1.向量的坐标运算将向量与代数有机结合起来,这就为向量和函数的结合提供了前提,运用向量的有关知识可以解决某些函数问题.2.以向量为载体,求相关变量的取值范围,是向量与函数、不等式、三角函数等相结合的一类综合问题.通过向量的坐标运算,将问题转化为解不等式或求函数值域,是解决这类问题的一般方法.3.有关线段的长度或相等,可以用向量的线性运算与向量的模.4.用向量方法解决平面几何问题的步骤(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;(2)通过向量运算,研究几何元素之间的关系;(3)把运算结果“翻译”成几何关系.5.向量的坐标表示,使向量成为解决解析几何问题的有力工具,在证明垂直、求夹角、写直线方程时显示出了它的优越性,在处理解析几何问题时,需要将向量用点的坐标表示,利用向量的有关法则、性质列出方程,从而使问题解决.失误与防范→1.向量关系与几何关系并不完全相同,要注意区别.例如:向量AB ∥CD并不能说明AB∥CD.2.加强平面向量的应用意识,自觉地用向量的思想和方法去思考问题.七.课后练习1.已知△ABC,AB AC ,则一定有()A.AB⊥AC B.AB=ACC.( AB + AC) ⊥(AB - AC)D.AB+AC=AB-AC2.点P在平面上做匀速直线运动,速度向量v=(4,-3)(即点 P 的运动方向与v 相同,且每秒移动的距离为| v| 个v1.0可编辑可修改单位 ) .设开始时点 P 的坐标为 ( - 10,10) ,则 5 秒后质点 P 的坐标为 ( )A . ( - 2,4)B . ( - 30,25)C . (10 ,- 5)D . (5 ,- 10)3. 平面上有四个互异点、、、,已知 (DB DC 2DA) ( AB AC) 0 ,则△ 的形状是 ()ABCD ABC A .直角三角形 B .等腰三角形C .等腰直角三角形D .等边三角形4. 如图,△ ABCO , AB =2, AC =3, BC = 7 , 则 AO BC 等于 ( )的外接圆的圆心为C .2D .35.平面上 、 、B 三点不共线,设 OA a,OB b ,则△ 的面积等于 ()O AOAB| a | 2| b | 2 -( a · b ) 2| a | 2| b | 2+ ( a · b ) 26.已知 |a| = 3, |b| = 2,〈 a , b 〉= 60°,则 |2a +b| = ________. 7.河水的流速为 2 m/s ,一艘小船想以垂直于河岸方向10 m/s 的速度驶向对岸,则小船的静水速度大小为________.8. 已知△ ABO 三顶点的坐标为 A (1,0), B (0,2), O (0,0), P ( x,y ) 是坐标平面内一点,且满足→→ →AP · OA ≤0, BP ·OB ≥0,则→OP · AB 的最小值为 ________.9.在△ ABC 中,角 A 、 B 、 C 所对的边分别为a 、b 、c ,若 AB · AC = BA BC1,那么 c =________.10. 如右图,在 Rt △ ABC 中,已知 BC =a, 若长为 2a 的线段 PQ 以点 A 为中心,问 →→PQ 与 BC 的夹角 θ 取何值时BP · CQ的值最大并求出这个最大值.11.已知向量 a = (sin θ, cos θ- 2sinθ) , b = (1,2) .(1) 若 a ∥ b ,求 tan θ 的值; (2) 若 | a | = | b |,0< θ<π,求 θ 的值.12.在△ ABC 中,角 A 、B 、 C 的对边分别为 a 、 b 、 c ,若 AB ·AC BA ·BC = k ( k ∈R).(1) 判断△ ABC 的形状; (2) 若 c =2,求 k 的值.v1.0可编辑可修改。
高一数学平面向量 PPT课件 图文

a-3b=(1, 2)-3(-3, 2)= (10, -4)
(ka+b)∥(a-3b)
-4(k-3)-10(2k+2)=0
K=- 1
3
∵
ka+b=
10 3
,
4 3
=-
1 3
(a-3b)
∴它们反向
例2
思考:
此题还有没有其它解法?
分析 要证A、B、D三点共线,可证 AB=λBD关键是找到λ
解: ∵BD=BC+CD= 2a + 8b+ 3(a b)=a+5b
∴AB=2 BD
AB∥ BD
且AB与BD有公共点B
∴ A、B、D 三点共线
例3
知识结构
平面向量小 复习
知识要点 例题解析 巩固练习
课外作业
练习5 已知a=(1,0),b=(1,1),c =(-1,0) 求λ和μ,使 c =λa +μb.
新课标人教版课件系列
《高中数学》
必修4
2.6《平面向量-复习》
平面向量复习
知识结构 要点复习 例题解析
巩固练习
制作:曾毅 审校:王伟
知识结构
平面向量 复习
知识要点 例题解析 巩固练习
课外作业
表示 向量的三种表示
平
三角形法则
面
向量加法与减法
向
平行四边形法则
量
向量平行的充要条件
运算 实数与向量的积
知识Байду номын сангаас点 例题解析 巩固练习
课外作业
高中数学人教A版必修4 平面向量专题复习PPT全文课件

途径二:“形”“数”相守 找坐标
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
y A
B (O) C 2
x
图13
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
练习1、【2017课标3,理12】在矩形ABCD中,AB=1
AD=2,
APABAD
动点P在以点C为圆心且与BD相切的圆上.若
(五)等与不等寻定值
极化恒等式
2
2
4a b a b a b
绝对值三角不等式
因对任意实数 m,n,恒有 m n m n 成立
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
(五)等与不等寻定值
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
(五)等与不等寻定值
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
高中数学【人教A版必修】4 平面向量专题复习PPT全文课件【完 美课件 】
数缺形时少直观, 形少数时难入微; 数形结合百般好, 隔离分家万事休.
(2013 年浙江省数学竞赛)已知直线 AB 与抛物线 y2 4x 交于 A, B 两点, M 为 AB的
中点, C 为抛物线上一个动点,若C0 满足 C0AC0B min CACB ,则下列一定成立的是
()
A. C0M AB C. C0 A C0B
纵观近五年的高考试题,平面向量的考查主要体现在2 个方面:
平面向量实用PPT课件PPT课件

AQ
4 3
13
9
9 第26页/共63页
例4:已知点M(-1,0),N(1,0),且点P使 MP MN, PM PN, NM PN成公差小于零的等差数列。
(1)求点P的横坐标所满足的方程。 (2)若 为 PM与 PN的夹角,求 的取值范围。
MP MN x 1, y 2,0 2x 2 PM PN x 1,y1 x,y x2 y2 1 NM NP 2,0 x 1, y 2x 2
a
B
③几何图形:用有箭头的线段来表示; A
3.向量的模:向量的大小叫作向量的模,记作
|
a |或
AB
4.零向量:规定模为零的向量叫作零向量;记作 0
零向量的方向是不确定的!
第1页/共63页
5.向量相等:
如果向量 a和
相等的向量,
记b 的作模a 相 b等 且方向相同,那a么这两个向量叫作
规定:零向量都是相等的。
AB 4,8, AC 6,4
直线AB的方程:y=2(x-1)
1
点P(4,6) Qx, y
cosBAC
65
直线AC的方程:y=-2/3(x-1)
SABC
1 2
AB
AC sinBAC
32
Q x, 2 x 1
3
SAPQ
x
1 2
SABC
12
16
4 x
1
AP
2
12
16
AQ 13
s
inBAC x 5,3
则平行四边形的对角线所表示的向量 OC c
就叫做向量 a 和 b 的和,记作 c a b
求向量和的运算,叫做向量的加法.
第4页/共63页
高一数学必修课件第二章平面向量

共线向量与共面向量
共线向量
方向相同或相反的非零向量叫做共线 向量。任意两个共线向量都可以表示 为$lambdavec{a}$($lambda in R$)的形式,其中$vec{a}$为非零 向量。
共面向量
平行于同一平面的两个或多个向量叫 做共面向量。在平面直角坐标系中, 任意两个向量都可以看作是共面向量 。
05 平面向量在解析 几何中的应用
直线的倾斜角和斜率关系
倾斜角定义
直线与x轴正方向之间的夹角,取 值范围为[0,π)。
斜率定义
直线上任意两点的纵坐标差与横坐 标差之商,即k=(y2-y1)/(x2-x1) 。
倾斜角与斜率关系
当倾斜角不为90°时,斜率k=tanα (α为倾斜角);当倾斜角为90°时 ,斜率不存在。
向量的共线与垂直
两个向量共线的充要条件是它们的坐 标成比例。两个向量垂直的充要条件 是它们的数量积为零。
向量的线性运算
包括向量的加法、减法和数乘。向量 的加法满足交换律和结合律,向量的 减法可以转化为加法进行运算。数乘 向量满足分配律和结合律。
平面向量的基本定理
平面内任意两个不平行的向量都可以 作为基底,平面内的任意一个向量都 可以由这两个基底唯一线性表示。
向量定义
向量是既有大小又有方向的量,通常用有向线段表示,有向 线段的长度表示向量的大小,箭头所指的方向表示向量的方 向。
向量表示方法
向量可以用小写字母$vec{a}$、$vec{b}$、$vec{c}$等表示 ,也可以用表示它的有向线段的起点和终点字母表示,如 $vec{AB}$。
零向量、单位向量与相等向量
两条直线平行或垂直条件
平行条件
两条直线的斜率相等,即k1=k2 。
(完整版)高中数学-平面向量专题
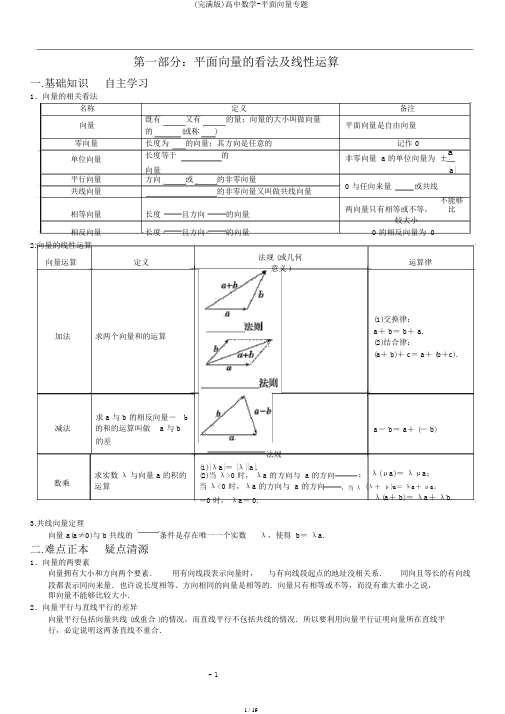
第一部分:平面向量的看法及线性运算一.基础知识自主学习1.向量的相关看法名称定义备注向量既有又有的量;向量的大小叫做向量平面向量是自由向量的(或称)零向量长度为的向量;其方向是任意的记作 0单位向量长度等于的非零向量 a 的单位向量为±a 向量|a|平行向量方向或的非零向量0 与任向来量或共线共线向量的非零向量又叫做共线向量相等向量长度且方向的向量两向量只有相等或不等,不能够比较大小相反向量长度且方向的向量0 的相反向量为 0 2.向量的线性运算向量运算定义法规 (或几何运算律意义 )加法求两个向量和的运算求 a 与 b 的相反向量-b 减法的和的运算叫做 a 与 b的差(1)交换律:a+ b= b+ a.(2)结合律:(a+ b)+ c= a+ (b+c).a- b= a+ (- b)法规求实数λ与向量 a 的积的(1)|λa|= |λ||a|.;λ(μa)=λμa;数乘(2)当λ>0 时,λa 的方向与 a 的方向运算当λ<0 时,λa 的方向与 a 的方向;当λ (λ+μ)a=λa+μa;=0 时,λa= 0.λ(a+ b)=λa+λb.3.共线向量定理向量 a(a≠0)与 b 共线的条件是存在唯一一个实数λ,使得 b=λa.二.难点正本疑点清源1.向量的两要素向量拥有大小和方向两个要素.用有向线段表示向量时,与有向线段起点的地址没相关系.同向且等长的有向线段都表示同向来量.也许说长度相等、方向相同的向量是相等的.向量只有相等或不等,而没有谁大谁小之说,即向量不能够比较大小.2.向量平行与直线平行的差异向量平行包括向量共线 (或重合 )的情况,而直线平行不包括共线的情况.所以要利用向量平行证明向量所在直线平行,必定说明这两条直线不重合.三.基础自测→→→→1.化简 OP- QP+ MS-MQ 的结果等于 ________.2.以下命题:①平行向量必然相等;②不相等的向量必然不平行;③平行于同一个向量的两个向量是共线向量;④相等向量必然共线.其中不正确命题的序号是_______.→→→→→3.在△ ABC 中, AB= c, AC= b.若点 D 满足 BD= 2DC ,则 AD = ________(用 b、 c 表示 ).4.如图,向量a- b 等于 ()A .- 4e1- 2e2B .- 2e1-4e2C. e1- 3e2 D . 3e1- e2→→→() 5.已知向量 a, b,且 AB= a+ 2b, BC=- 5a+ 6b,CD = 7a- 2b,则必然共线的三点是A . A、 B、DB .A、 B、CC. B、 C、D D .A、 C、 D四.题型分类深度剖析题型一平面向量的相关看法例 1给出以下命题:→→①若 |a|= |b|,则 a= b;②若 A,B,C,D 是不共线的四点,则AB= DC是四边形ABCD 为平行四边形的充要条件;③若 a= b,b= c,则 a= c;④ a= b 的充要条件是|a|= |b|且a∥ b;⑤若 a∥ b,b∥c,则 a∥ c.其中正确的序号是________.变式训练1判断以下命题可否正确,不正确的请说明原由.(1)若向量 a 与 b 同向,且 |a|= |b|,则 a>b ;(2)若 |a|= |b|,则 a 与 b 的长度相等且方向相同或相反;(3)若 |a|= |b|,且 a 与 b 方向相同,则 a= b;(4)由于零向量的方向不确定,故零向量不与任意向量平行;(5)若向量 a 与向量 b 平行,则向量 a 与 b 的方向相同或相反;→→(6)若向量 AB与向量 CD是共线向量,则 A, B, C, D 四点在一条直线上;(7)起点不相同,但方向相同且模相等的几个向量是相等向量;(8)任向来量与它的相反向量不相等题型二平面向量的线性运算例 2→→→ 1→→ 1→如图,以向量 OA= a, OB= b 为边作 ?OADB , BM=BC, CN=CD,用33→→→a、 b 表示 OM 、 ON、 MN.变式训练→ 2→→→2 △ABC 中, AD= AB,DE ∥BC 交 AC 于 E, BC 边上的中线 AM 交 DE 于 N.设 AB= a,AC= b,用 a、b3→ → → →→→表示向量 AE、 BC、 DE 、 DN、 AM、 AN.题型三平面向量的共线问题例 3设 e1 2→= 2e1→= e12→= 2e1是两个不共线向量,已知 AB2, CD2, e- 8e, CB+ 3e-e .(1)求证: A、B、 D 三点共线;→(2)若 BF = 3e1- ke2,且 B、D 、 F 三点共线,求 k 的值.变式训练3设两个非零向量 a 与 b 不共线,→→→(1)若 AB= a+ b, BC= 2a+8b, CD = 3(a-b).求证: A、 B、D 三点共线;(2)试确定实数 k,使 ka+b 和 a+ kb 共线.五.思想与方法5.用方程思想解决平面向量的线性运算问题试题:以下列图,在△→ 1→→ 1→→→ABO 中, OC= OA, OD = OB, AD 与 BC 订交于点 M,设 OA= a,OB= b.试用 a 和 b 42→表示向量 OM .六.思想方法感悟提高方法与技巧1.将向量用其他向量(特别是基向量)线性表示,是十分重要的技术,也是向量坐标形式的基础.→→→→2.能够运用向量共线证明线段平行或三点共线问题.如 AB∥ CD且 AB 与 CD 不共线,则 AB ∥CD ;若 AB∥ BC,则 A、B、C 三点共线.失误与防范1.解决向量的看法问题要注意两点:一是不但要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量可否也满足条件.要特别注意零向量的特别性.2.在利用向量减法时,易弄错两向量的序次,从而求得所求向量的相反向量,以致错误.七.课后练习1.给出以下命题:①两个拥有公共终点的向量,必然是共线向量;②两个向量不能够比较大小,但它们的模能比较大小;③ λa = 0 (λ为实数 ),则 λ必为零;④ λ, μ为实数,若 λa = μb ,则 a 与 b 共线.其中错误命题的个数为 ()A . 1B . 2C .3D .42.若 A 、B 、C 、D 是平面内任意四点,给出以下式子: → → →AD ;③ AC -AB + CD = BC + DA ;② AC + BD = BC→ → ) BD = DC + AB .其中正确的有 (A . 0 个B . 1 个C .2 个D . 3 个3. 已知 O 、 A 、 B 是平面上的三个点,直线AB 上有一点 C ,满足 2 AC CB =0,则 OC 等于 ()A. 2OA → →- OB B. OA + 2OB2 OA - 1 → D. 1 2 →C. 3OB 3OA + 3OB31→→→→4.以下列图, 在△ ABC 中, BD =DC ,AE = 3ED ,若 AB = a , AC =b ,则 BE 等于 ()21 11 1A. 3a +3bB .- 2a + 4b1 11 1 C.2a + 4b D .- 3a + 3b→,则四边形 ABCD 的形状是 (5. 在四边形 ABCD 中, AB =a + 2b, BC =- 4a -b , CD =- 5a - 3b A .矩形 B .平行四边形 C .梯形 uuur D .以上都不对uuur uuur6. AB =8, AC = 5,则 BC 的取值范围是 __________.7.给出以下命题:①向量 AB 的长度与向量 →→BA 的长度与向量 BA 的长度相等; ②向量 a 与 b 平行,则 a 与 b 的方向相同或相反; ③两个有共同起点而且相等的向量,其终点必相同;④两个有公共终点的向量,必然是共线向量;→ → ⑤向量 AB 与向量 CD 与向量 CD 是共线向量,则点 A 、 B 、 C 、 D 必在同一条直线上.其中不正确的个数为 ____________ .8.如图,在△ ABC 中,点 O 是 BC 的中点 .过点 O 的直线分别交直线AB 、AC 于不相同的两点 M 、→AB = mAM ,→AC = nAN ,则 m + n 的值为 ________. 9.设 a 与 b 是两个不共线向量,且向量 a +λb 与- (b -2a)共线,则 λ= ________.→ →10.在正六边形 ABCDEF 中, AB = a , AF = b ,求 AC, AD ,AE.11.以下列图,△ ABC 中,点 M 是 BC 的中点,点 N 在边 AC 上,且 AN =2NC , AM 与 BN 订交于点的值.12.已知点 G 是△ ABO 的重心, M 是 AB 边的中点 .→ →( 1)求 GA +GB +GO ;→→→ 11)N. 若P ,求 AP ∶ PM第二部分:平面向量的基本定理及坐标表示一.基础知识自主学习1.两个向量的夹角定义→→已知两个向量 a,b,作 OA= a,OB =b,则∠ AOB =θ叫做向量 a 与 b 的夹角 (如图 )范围向量夹角θ的范围是,当θ=时,两向量共线,当θ=时,两向量垂直,记作a⊥b.2.平面向量基本定理及坐标表示(1)平面向量基本定理若是 e1,e2是同一平面内的两个向量,那么关于这一平面内的任意向量a,一对实数λ1,λ2,使 a=.其中,不共线的向量e1, e2叫做表示这一平面内所有向量的一组.(2)平面向量的正交分解及坐标表示把一个向量分解为两个的向量,叫做把向量正交分解.(3)平面向量的坐标表示①在平面直角坐标系中,分别取与x 轴、 y 轴方向相同的两个单位向量i,j 作为基底,关于平面内的一个向量a,由平面向量基本定理可知,有且只有一对实数x,y,使 a=xi + yj,这样,平面内的任向来量 a 都可由 x,y 唯一确定,把有序数对叫做向量 a 的坐标,记作a=,其中叫做a在x轴上的坐标,叫做a在y轴上的坐标.→→→②设 OA= xi +yj,则向量 OA的坐标 (x, y)就是的坐标,即若OA=(x,y),则A点坐标为,反之亦成立. (O 是坐标原点 )3.平面向量坐标运算(1)向量加法、减法、数乘向量及向量的模设 a= (x1, y1) ,b= (x2, y2),则a+ b=,a-b=,λa=,|a|=.(2)向量坐标的求法①若向量的起点是坐标原点,则终点坐标即为向量的坐标.②设 A(x1 1→→22=, |AB., y ), B(x, y),则 AB|=4.平面向量共线的坐标表示:设 a= (x1, y1), b= (x2, y2),其中 b≠ 0a.∥ b?.二.难点正本疑点清源1.基底的不唯一性只要两个向量不共线,就可以作为平面的一组基底,对基底的采用不唯一,平面内任意向量 a 都可被这个平面的一组基底 e1,e2线性表示,且在基底确定后,这样的表示是唯一的.2.向量坐标与点的坐标的差异→a 唯一确定,此时点 A 的坐标与 a 的坐在平面直角坐标系中,以原点为起点的向量OA= a,点 A 的地址被向量标一致为 (x,y),但应注意其表示形式的差异,如点→A(x, y),向量 a=OA= (x, y).→→→→→当平面向量 OA平行搬动到 O11时,向量不变即O1A 1=OA=(x,y),但O11的起点O1和终点1的坐标都发生了变A A A 化.三.基础自测1.已知向量a= (2,- 1), b=(- 1, m),c= (- 1,2),若 (a+b) ∥c,则 m= ________.2.已知向量a= (1,2), b= (- 3,2),若 ka+ b 与 b 平行,则k= ________.3.设向量 a= (1,- 3), b= (- 2,4), c=(- 1,- 2).若表示向量4a、 4b-2c、 2(a- c)、 d 的有向线段首尾相接能构成四边形,则向量 d= ____________.→→4.已知四边形 ABCD 的三个极点 A(0,2), B(- 1,- 2), C(3,1) ,且 BC= 2AD ,则极点 D 的坐标为()A. 2,7B. 2,-1 22C. (3,2)D. (1,3)5.已知平面向量 a= (x,1), b=(- x, x2) ,则向量 a+ b()A .平行于 y 轴B .平行于第一、三象限的角均分线C.平行于 x 轴 D .平行于第二、四象限的角均分线四.题型分类深度剖析题型一平面向量基本定理的应用例 1→→→ →如图,在平行四边形ABCD 中, M, N 分别为 DC,BC 的中点,已知 AM= c, AN= d,试用 c,d 表示 AB, AD.→→→→变式训练 1 如图, P 是△ ABC 内一点,且满足条件 AP+ 2BP+ 3CP= 0,设 Q 为 CP 的延长线与AB 的交点,令CP= p,→试用 p 表示 CQ.题型二向量坐标的基本运算→→→→→例2 已知 A(-2,4), B(3,- 1), C(- 3,- 4).设 AB= a,BC= b, CA= c,且 CM = 3c,CN=- 2b,→(1) 求 3a+ b- 3c;(2) 求满足 a= mb+ nc 的实数 m, n; (3) 求 M、 N 的坐标及向量 MN 的坐标.变式训练 2(1) 已知点 A、B、 C 的坐标分别为→→ 1→A(2,- 4)、 B(0,6) 、 C(- 8,10),求向量 AB+ 2BC- AC的坐标;211(2) 已知 a= (2,1) , b= (- 3,4),求:① 3a+4b;② a- 3b;③2a-4b.题型三平行向量的坐标运算例 3平面内给定三个向量a= (3,2), b=(-1,2), c= (4,1),请解答以下问题:(1) 求满足 a= mb+ nc 的实数 m, n; (2)若 (a+ kc)∥ (2b-a) ,求实数k;(3) 若 d 满足 (d- c)∥ (a+ b),且 |d- c|= 5,求 d.变式训练3已知a=(1,0),b=(2,1).(1)求 |a+ 3b|; (2)当 k 为何实数时, ka- b 与 a+ 3b 平行,平行时它们是同向还是反向?五.易错警示8.忽视平行四边形的多样性致误试题:已知平行四边形三个极点的坐标分别为(- 1,0),(3,0) ,(1,- 5),求第四个极点的坐标.六.思想方法感悟提高方法与技巧1.平面向量基本定理的实质是运用向量加法的平行四边形法规,将向量进行分解.2.向量的坐标表示的实质是向量的代数表示,其中坐标运算法规是运算的要点,经过坐标运算可将一些几何问题转变成代数问题办理,从而向量能够解决平面剖析几何中的好多相关问题.3.在向量的运算中要注意待定系数法、方程思想和数形结合思想的运用.失误与防范1.要区分点的坐标与向量坐标的不相同,尽管在形式上它们完满相同,但意义完满不相同,向量坐标中既有方向也有大小的信息.1122),则 a∥ b 的充要条件不能够表示成x1=y1,由于 x22有可能等于0,所以应表示为 1 22.若 a=( x,y ),b= (x ,y x2y2,y x y y = 0.同时, a∥ b 的充要条件也不能够错记为x x - y y = 0, x y- x y = 0 等.- x2 1 1 21 2 1 1 2 2七.课后练习1.已知向量 a =(1,- 2), b =(1+ m,1- m),若 a ∥ b ,则实数 m 的值为 ( )A .3B .- 3C . 2D .- 2 2.已知平面向量 a = (1,2), b =(- 2, m) ,且 a ∥ b ,则 2a + 3b 等于 ( )A .( -2,- 4)B . (- 3,- 6)C .(- 4,- 8)D . (- 5,- 10)3.设向量 a = (3, 3), b 为单位向量,且 a ∥ b ,则 b 等于 ( )3 1 3 1 3 1A.2 ,- 2 或 - 2 , 2B.2 , 2313 13 1C. - 2 ,- 2D. 2 , 2或- 2 ,- 24.已知向量 a = (1,- m),b = (m 2, m),则向量 a + b 所在的直线可能为 ()A . x 轴B .第一、三象限的角均分线C . y 轴D .第二、四象限的角均分线5.已知 A(7,1) 、B(1,4), 直线 y1 →ax 与线段 AB 交于 C,且 AC2CB ,则实数 a 等于 ()245A . 2B . 1C. 5D.31+ 1的值等于 ________.6.若三点 A(2,2) ,B(a,0), C(0, b) (ab ≠ 0)共线,则 ab7.已知向量 a =(1,2) ,b = (x,1), u = a +2b , v = 2a - b ,且 u ∥ v ,则实数 x 的值为 ________. 8.若向量 a ( x 3, x 2 3 x 4) 与 AB 相等,其中 A(1,2) , B(3 , 2) ,则 =x ________.9.若平面向量 a , b 满足 |a + b|= 1, a + b 平行于 y 轴, a = (2,- 1),则 b = ______________. 10. a = (1,2), b = (- 3,2),当 k 为何值时, ka +b 与 a - 3b 平行?平行时它们是同向还是反向?11.三角形的三内角 A , B , C 所对边的长分别为 a , b , c ,设向量 m = (3c - b , a - b), n = (3a + 3b , c), m ∥n.(1) 求 cos A 的值; (2) 求 sin(A +30°)的值.12.在△ ABC 中, a 、 b 、c 分别是角 A 、 B 、 C 的对边,已知向量 m = (a , b),向量 n =(cos A , cos B),向量 p = 2 2sinB +C , 2sin A ,若 m ∥ n , p 2= 9,求证:△ ABC 为等边三角形. 2第三部分:平面向量的数量积一.基础知识 自主学习1.平面向量的数量积已知两个非零向量a 和b ,它们的夹角为 θ,则数量 _______叫做 a 和 b 的数量积 (或内积 ),记作 ________________.规定:零向量与任向来量的数量积为____.两个非零向量 a 与 b 垂直的充要条件是,两个非零向量 a 与 b 平行的充要条件是.2.平面向量数量积的几何意义数量积 a ·b 等于 a 的长度 |a|与 b 在 a 的方向上的投影 _________的乘积.3.平面向量数量积的重要性质(1)e ·a = a ·e =;(2) 非零向量 a , b ,a ⊥ b? ;(3) 当 a 与 b 同向时, a ·b =;当 a 与 b 反向时, a ·b =, a ·a = a 2,|a|=a ·a;a ·b (4)cos θ=;|a||b|(5)|a ·b|____|a|| b|.4.平面向量数量积满足的运算律(1) a ·b=(交换律 );(2)( λa )·b = =(λ为实数 );(3)( a + b) ·c =.5.平面向量数量积相关性质的坐标表示设向量 a = (x 1, y 1), b = (x 2 , y 2),则 a ·b=,由此获取(1) 若 a = (x , y),则 |a|2=或|a|=.(2) 设 A (x 1uuur.,y 1) ,B(x 2,y 2),则 A 、 B 两点间的距离 |AB|= AB =(3) 设两个非零向量 a , b , a = ( x , y ), b = (x , y ),则 a ⊥b?.1122二.难点正本 疑点清源1.向量的数量积是一个实数两个向量的数量积是一个数量, 这个数量的大小与两个向量的长度及其夹角的余弦值相关, 在运用向量的数量积解题时,必然要注意两向量夹角的范围.2.数量积的运算只适合交换律、 加乘分配律及数乘结合律, 但不满足向量间的结合律, 即 (a ·b)c 不用然等于a(b ·c).这是由于 (a ·b)c 表示一个与 c 共线的向量,而 a(b ·c)表示一个与 a 共线的向量,而 c 与 a 不用然共线.三.基础自测1.已知向量 a 和向量 b 的夹角为 30°, |a|= 2, |b|= 3,则向量 a 和向量 b 的数量积 a ·b=________.2.在△ ABC 中, AB =3, AC=2, BC=10 ,则 AB ·AC = ______.- 94.已知 |a|= 6, |b|=3, a·b=- 12,则向量 a 在向量 b 方向上的投影是()A .- 4B. 4C.- 2 D .25.已知向量a=(1,- 1), b=(1,2) ,向量 c 满足 (c+ b)⊥ a, (c- a)∥ b,则 c 等于()A . (2,1)B .(1,0)31C. 2,2D. (0,- 1)四.题型分类深度剖析题型一求两向量的数量积例1 (1) 在 Rt△ ABC 中,∠ C= 90°, AB= 5, AC=4,求AB·BC;(2)若 a= (3,- 4) ,b= (2,1),试求 (a-2b) · (2a+3b).变式训练 1 (1)若向量 a 的方向是正南方向,向量 b 的方向是正东方向,且|a|= |b|= 1,则 (- 3a) ·(a+ b)=______.uuur→ uuur(2) 如图,在△ ABC 中, AD ⊥ AB,BC= 3 BD, | AD |= 1,则AC·AD等于 ()33A . 2 3B. 2 C. 3 D.3题型二求向量的模例2 已知向量 a 与 b 的夹角为 120°,且 |a|= 4, |b|= 2,求: (1)|a+ b|; (2)|3a- 4b|; (3)(a- 2b) ·(a+b).π变式训练 2 设向量 a, b 满足 |a- b|= 2,|a|= 2,且 a- b 与 a 的夹角为3,则 |b|= ________.题型三利用向量的数量积解决夹角问题例 3已知a与b是两个非零向量,且|a|= |b|= |a- b|,求 a 与 a+ b 的夹角.变式训练 3 设 n 和 m 是两个单位向量,其夹角是60°,求向量a= 2m+ n 与 b= 2n-3m 的夹角.题型四平面向量的垂直问题例 4 已知 a= (cos α, sin α), b= (cos β, sin β)(0< α<β<π).(1)求证: a+ b 与 a- b 互相垂直;(2) 若 ka+ b 与 a- kb 的模相等,求β-α.(其中k为非零实数)uuur→uuur→→变式训练 4 已知平面内A、B、C 三点在同一条直线上,OA =(-2,m),OB=(n,1),OC=(5,-1),且OA⊥OB,求实数 m, n 的值.五.答题规范5.思想要慎重,解答要规范试题:设两向量 e1、e2满足 |e1 |= 2,|e2|= 1,e1、e2的夹角为60°,若向量 2te1+7e2与向量 e1+te2的夹角为钝角,求实数 t 的取值范围.六.思想方法感悟提高方法与技巧1.向量的数量积的运算法规不具备结合律,但运算律和实数运算律近似.如(a+ b)2=a2+2a·b+b2;22(λa+μb) ·(sa+ tb)=λs a+(λt+μs)a·b+μt b(λ,μ, s, t∈ R).2.求向量模的常用方法:利用公式|a|2= a2,将模的运算转变成向量的数量积的运算.3.利用向量垂直或平行的条件构造方程或函数是求参数或最值问题常用的方法技巧.失误与防范1. (1)0 与实数 0 的差异: 0a=0≠0, a+( -a)=0≠0,a·0=0≠0;(2)0 的方向是任意的,其实不是没有方向,0 与任何向量平行,我们只定义了非零向量的垂直关系.2. a·b=0 不能够推出 a= 0 或 b= 0,由于 a·b=0 时,有可能 a⊥ b.3.一般地, (a · b)c ≠ (b即·乘c)a法的结合律不行立.因a·b是一个数量,所以(a · b)c表示一个与 c 共线的向量,同理右边 (b ·c)a表示一个与 a 共线的向量,而 a 与 c 不用然共线,故一般情况下(a ·b)c ≠(b ·c)a. 4. a·b=a· c(a ≠不0)能推出 b= c.即消去律不行立.uuur uuur5.向量夹角的看法要意会,比方正三角形ABC 中,〈AB,BC〉应为 120°,而不是 60°.- 11七.课后练习1 1()1.设向量 a = (1,0), b =( , ),则以下结论中正确的选项是22A . |a|= |b|B . a ·b= 22 C . a ∥ b D .a - b 与 b 垂直 2.若向量 a = (1,1), b = (2,5), c = (3, x),满足条件 (8a - b)·c = 30,则 x 等于 ( )A . 6B .5C . 4D . 33.已知向量 a ,b 的夹角为 60°,且 |a|=2, |b|= 1,则向量 a 与 a + 2b 的夹角等于 ()A . 150 °B . 90°C . 60°D . 30°uuur uuur4.平行四边形 ABCD 中, AC 为一条对角线,若 AB = (2,4), AC = (1,3),则 AD BD 等于 ()A . 6B .8C .- 8D .- 6πa = 2e 1)1 2的单位向量,且向量2 1 25.若 e 、e 是夹角为 3+ e ,向量 b =- 3e +2e ,则 a ·b等于 (7 7A . 1B .- 4C .- 2D.2π6.若向量 a , b 满足 |a|=1 ,|b|= 2 且 a 与 b 的夹角为 3,则 |a + b|= ________.7.已知向量 a ,b 满足 |a|= 3,|b|= 2, a 与 b 的夹角为 60°,则 a ·b=________,若 (a -mb)⊥ a ,则实数 m = ________. 8.设 a 、 b 、 c 是单位向量,且 a + b = c ,则 a ·c 的值为 ________. 9.(O 是平面上一点, A 、 B 、C 是平面上不共线的三点 .平面内的动点 P 满足 OPOA (AB AC),uuuruuur uuur若 λ=1时, PA (PBPC ) 的值为 ______.210.不共线向量 a , b 的夹角为小于 120 °的角,且 |a|= 1, |b|=2,已知向量 c = a + 2b ,求 |c|的取值范围.11.已知平面向量 a = (1, x), b = (2x +3,- x), x ∈ R.(1) 若 a ⊥ b ,求 x 的值; (2)若 a ∥b ,求 |a -b|.12.向量 a = (cos 23 ,°cos 67 °),向量 b = (cos 68 ,°cos 22 °).(1) 求 a ·b;(2)若向量 b 与向量 m 共线, u = a +m ,求 u 的模的最小值.第四部分:平面向量应用举例一.基础知识自主学习1.向量在平面几何中的应用平面向量在平面几何中的应用主若是用向量的线性运算及数量积解决平面几何中的平行、垂直、平移、全等、相似、长度、夹角等问题.(1)证明线段平行或点共线问题,包括相似问题,常用共线向量定理:a∥ b??.(2)证明垂直问题,常用数量积的运算性质a⊥ b??.(3)求夹角问题,利用夹角公式cos θ=a·b =x1 x2+ y1y222 2 2 (θ为 a 与 b 的夹角 ).|a||b|x1+ y1x2+ y22.平面向量在物理中的应用(1)由于物理学中的力、速度、位移都是,它们的分解与合成与向量的相似,能够用向量的知识来解决.(2)物理学中的功是一个标量,这是力 F 与位移 s 的数量积.即W = F·s=|F|| s|cos θ(θ为 F 与 s 的夹角 ).3.平面向量与其他数学知识的交汇平面向量作为一种运算工具,经常与函数、不等式、三角函数、数列、剖析几何等知识结合,当平面向量给出的形式中含有未知数时,由向量平行或垂直的充要条件能够获取关于该未知数的关系式.在此基础上,能够求解相关函数、不等式、三角函数、数列的综合问题.此类问题的解题思路是转变成代数运算,其转变路子主要有两种:一是利用平面向量平行或垂直的充要条件;二是利用向量数量积的公式和性质.二.难点正本疑点清源1.向量兼具代数的抽象与慎重和几何的直观,向量自己是一个数形结合的产物.在利用向量解决问题时,要注意数与形的结合、代数与几何的结合、形象思想与逻辑思想的结合.2.要注意变换思想方式,能从不相同角度看问题,要善于应用向量的相关性质解题.三.基础自测1.在平面直角坐标系xOy 中,四边形ABCD 的边 AB∥ DC , AD∥ BC.已知 A(- 2,0),B(6,8), C(8,6).则D 点的坐标为 ________.2.已知平面向量α、β,|α|=1,|β|=2,α⊥ (α-2β),则|2α+β|的值是________.y uuur 3.平面上有三个点A( - 2, y), B 0,2, C( x, y),若ABuuur⊥ BC ,则动点C的轨迹方程为_______________.uuur5,AC·CB等于 () 4.已知 A、 B 是以 C 为圆心,半径为5的圆上两点,且 | AB |=5553A .-2 B.2C. 0D.25.某人先位移向量a : “向东走 3 km ”,接着再位移向量b : “向北走 3 km ”,则 a +b 表示()A .向东南走 3 2 kmB .向东北走 3 2 kmC .向东南走 33 kmD .向东北走 3 3 km四.题型分类 深度剖析题型一 向量在平面几何中的应用 例 1 如图,在等腰直角三角形 ABC 中,∠ ACB =90°, CA = CB , D 为 BC 的中点, E 是 AB 上的一点,且 AE = 2EB.求证: AD ⊥ CE.变式训练 1在平面直角坐标系 xOy 中,已知点 A(- 1,- 2),B(2,3), C(- 2,- 1).(1) 求以线段 AB 、 AC 为邻边的平行四边形的两条对角线的长;(2) →→ →设实数 t 满足 (AB - tOC) ·OC = 0,求 t 的值.题型二平面向量在剖析几何中的应用uuuuruuur →3 →例 2 已知点 P ( 0,-3),点 A 在 x 轴上,点 M 满足 PA AM =0 ,AM =-MQ ,当点 A 在 x 轴上搬动时,求动点 M2的轨迹方程.变式训练 2 已知圆 C : (x-3) 2+(y-3)2N 在线段 MA 的延长线上,=4 及点 A ( 1,1), M 是圆上的任意一点,点 uuur →且 MA = 2AN ,求点 N 的轨迹方程.题型三 平面向量与三角函数 例 3 已知向量 a = (sin x , cos x), b = (sin x , sin x) ,c = (- 1,0).π(1)若 x = 3,求向量 a 与 c 的夹角;3π π(2)若 x ∈ - 8 , 4 ,求函数 f(x) =a ·b 的最值;2 (3) 函数 f(x)的图象能够由函数y = 2 sin 2x (x ∈ R)的图象经过怎样的变换获取?变式训练 3已知 A(3,0) , B(0,3) , C(cos α, sin α).若 uuur uuur =- 1,求 sin α+ π的值; (2) uuur uuur = ,且 α∈ , π),求 → uuur (1) AC ·若 | OA+ OC | 13 OB 与 OC 的夹角.BC 4(0五.易错警示9.忽视对直角地址的谈论致误uuur uuur试题:已知平面上三点A 、B 、C ,向量 BC = (2- k,3), AC = (2,4).(1) 若三点 A 、B 、 C 不能够构成三角形,求实数 k 应满足的条件; (2)若△ ABC 为直角三角形,求k 的值.六.思想方法 感悟提高方法与技巧1. 向量的坐标运算将向量与代数有机结合起来,这就为向量和函数的结合供应了前提,运用向量的相关知识能够解决某些函数问题.2. 以向量为载体,求相关变量的取值范围,是向量与函数、不等式、三角函数等相结合的一类综合问题.经过向量的坐标运算,将问题转变成解不等式或求函数值域,是解决这类问题的一般方法.3. 相关线段的长度或相等,能够用向量的线性运算与向量的模.4.用向量方法解决平面几何问题的步骤(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转变成向量问题;(2)经过向量运算,研究几何元素之间的关系;(3) 把运算结果 “翻译 ”成几何关系.5.向量的坐标表示,使向量成为解决剖析几何问题的有力工具,在证明垂直、求夹角、写直线方程时显示出了它的优越性,在办理剖析几何问题时,需要将向量用点的坐标表示,利用向量的相关法规、性质列出方程,从而使问 题解决.失误与防范1.向量关系与几何关系其实不完满相同,要注意差异.比方:向量2.加强平面向量的应企图识,自觉地用向量的思想和方法去思虑问题.uuurAB→∥ CD 其实不能够说明AB ∥CD .七.课后练习1.已知△ ABC ,AB AC ,则必然有()A .AB⊥ACB .AB = ACC. ( AB + AC)⊥ ( AB - AC)D.AB + AC= AB - AC2.点 P 在平面上做匀速直线运动,速度向量v= (4,- 3)( 即点 P 的运动方向与v 相同,且每秒搬动的距离为|v|个单位 ) .设开始时点 P 的坐标为 ( - 10,10),则 5 秒后质点 P 的坐标为 ()A . (- 2,4)B .( -30,25)C. (10,- 5)D. (5,- 10)uuur uuur uuur uuur uuur3.平面上有四个互异点)A、 B、 C、D ,已知 (DB DC2DA) (AB AC) 0 ,则△ ABC 的形状是 (A .直角三角形B .等腰三角形C.等腰直角三角形D.等边三角形uuur uuur4.如图,△ ABC 的外接圆的圆心为 O,AB=2,AC=3,BC=7 ,则AO BC等于()35A. 2B.2C. 2D. 35.平面上 O、 A、 B 三点不共线,设OA a,OB,则△ OAB 的面积等于 ()bA.|a|2|b|2- (a·b)2B.|a|2 |b|2+ (a·b)2122- (a·b)21 2 2+ (a·b)2C.2D.2|a| |b||a| |b|6.已知 |a|= 3, |b|=2,〈 a, b〉= 60°,则 |2a+ b|= ________.7.河水的流速为 2 m/s,一艘小船想以垂直于河岸方向10 m/s 的速度驶向对岸,则小船的静水速度大小为________.→→ →→8.已知△ ABO 三极点的坐标为A(1,0), B(0,2), O(0,0),P(x,y)是坐标平面内一点,且满足 AP·OA≤0,BP·OB≥0,则 OP·AB的最小值为 ________.uuur uuur 9.在△ ABC 中,角 A、B、 C 所对的边分别为a、 b、 c,若AB·AC=BA BC 10.如右图,在Rt△ABC 中,已知 BC=a,若长为 2a 的线段 PQ 以点 A 为中心,问的值最大?并求出这个最大值.1,那么c=________.→→PQ 与BC的夹角θ取何值时BP·CQ11.已知向量a= (sin θ, cos θ- 2sin θ), b= (1,2).(1)若 a∥ b,求 tan θ的值; (2) 若 |a|= |b|,0<θ<π,求θ的值.12.在△ ABC 中,角 A、B、 C 的对边分别为a、 b、 c,若AB·AC BA·BC =k (k∈R).(1) 判断△ ABC 的形状; (2)若 c=2,求 k 的值.- 16。
高中数学课件-平面向量

)
A.
B.-
C.
D.-
→
→
解析:(1)因为 D 在线段 BC 上,且=2,
ቤተ መጻሕፍቲ ባይዱ
所以 S△ACD=S△ABD,又 E 为线段 AD 上一点,且△ABE 与△ACD 的面积相等,
所以 S△ABE= S△ABD,所以 E 为 AD 的中点.
如图建立平面直角坐标系,则 B(0,0),A( ,
→
→
在以 B 为圆心,1 为半径的圆上,则·的最大值为(
A.
+
B.5+
C.
D.
)
解析:(1)以点 B 为原点,直线 AB 为 x 轴建立平面直角坐标系,如图,
→
则 A(-2,0),C(-2,1),设 P(cos α,sin α),α∈[0,2π),因此,=(-2-cos α,-sin α),
→
所以=(,
答案:(1)D
→
),=(,-
→
→
),D(2,0),C(3,0),E( ,
),所以·=×-
×
),
=-.故选 D.
(2)(2022·全国甲卷)设向量 a,b 的夹角的余弦值为,且|a|=1,|b|=3,则
由<a,b>∈[0,π],所以 a 与 b 的夹角为.故选 B.
(2)(2022·湖南模拟联考)在一个边长为 2 的等边三角形 ABC 中,若点 P 是平面
高一数学平面向量26

第二十六教时教材:复习五——平面向量的数量积的坐标表示、平移目的:让学生对平面向量的数量积的理解更深刻,尤其在两个非零向量垂直与平行的充要条件的平行上更熟练。
过程:一、复习:设向量a = (x 1,y 1),b = (x 2,y 2),1.数量积的坐标表示:a •b = x 1x 2 + y 1y 22.关于距离公式3.二、 例题: 1.已知|a | = 3,b = (1,2),且a ∥b ,求a 的坐标。
解:设a = (x ,y ) ∵|a | = 3 ∴322=+y x …①又:∵a ∥b ∴1•y - 2•x = 0 …② 解之:⎪⎪⎩⎪⎪⎨⎧==556553y x 或⎪⎪⎩⎪⎪⎨⎧-=-=556553y x 即:a = (556,553) 或a = (556,553--) 2.设p = (2,7),q = (x ,-3),求x 的取值范围使得:①p 与q 的夹角为钝角 ②p 与q 的夹角为锐角。
解:①p 与q 的夹角为钝角⇔ p •q <0⇔2x -21<0⇔221<x 即x ∈(-∞,221) ②p 与q 的夹角为锐角⇔ p •q >021213.求证:菱形的对角线互相垂直。
证:设B (b 1,0),D (d 1,d 2),则= (b 1,0), = (d 1,d 2)于是=+= (b 112112=-= (d 1 -b 1,d 2)∵AC •BD = (b 1+d 1)(d 1 -b 1) + d 2d 2 = (d 12 + d 22)- b 12= ||2 - b 12 = ||2 - b 12 = b 12 - b 12 = 01a ⊥ba ∥b a •b = 0 ⇔ x 1x 2 + y 1y 2 = 0 存在唯一λ∈ R ⇔ x 1x 2 + y 1y 2 = 0 使a =λb 成立C∴⊥4.如图:ABCD 是正方形,M 是BC 的中点,将正方形折起使点A 与M 重合,设折痕为EF ,若正方形面积为64,求△AEM 的面积。
高考数学(理) A版:专题 5 平面向量(共118张PPT)

例 1[陕西西安中学 2018 届期中]给出下列四个命题: ①若|a|=|b|,则 a=b; → =DC → ”是 ②若 A,B,C,D 是不共线的四点,则“AB “四边形 ABCD 为平行四边形”的充要条件; ③若 a=b,b=c,则 a=c; ④“a=b”的充要条件是“|a|=|b|,且 a∥b”. 其中正确命题的序号是( A.①② )
例 2[江西抚州临川一中 2018 高三月考]已知 O 是△ABC → +(m-1)OC →- 所在平面内一点,若对∀m∈R,恒有|OA → |≥|OB → -OA → |,则△ABC 一定是( mOB A.锐角三角形 C.钝角三角形 )
B.直角三角形 D.不确定
【答案】B
→ +(m-1)OC → -mOB → |≥|OB → -OA →| 【解析】由|OA → +mBC → |≥|BA → |, 整理得到|CA → =mBC → ,则CA → +mBC → =DA →, 如图,设DC → |≥|BA → |恒成立,所以 AB⊥BC. 即|DA
数乘
3.向量共线的判定定理和性质定理 (1)判定定理:a是一个非零向量,若存在一个实 数λ ,使得b=λ a,则向量b与a共线. (2)性质定理:若向量b与非零向量a共线,则存在 唯一一个实数λ ,使得b=λ a. 运用向量的方法证明三点共线时,可以用两个向 量共线的充要条件去证,若点O不在直线AB上,则 A,B,P三点共线的充要条件是:存在一对实数λ , μ ,使得OP→=λ OA→+μ OB→,且λ +μ =1.
B.②③ C.③④ D.②④
【答案】B
→ =DC → 【解析】 ②若 A,B,C,D 是不共线的四点,则AB 能推出 AB 与 CD 平行,且 AB=CD,所以四边形 ABCD 为平行四边形,反之也成立,故②正确; ③若 a=b,则 a,b 大小相等,方向相同,若 b=c,则 b, c 大小相等,方向相同,则 a,c 大小相等,方向相同, 则 a=c,故③正确; 故正确命题的序号是②③.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16、人民应该为法律而战斗,就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为加以指责 ,并非 因为他 们愿意 做出这 种行为 ,而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令,就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律,其真实含 义是财 富。— —爱献 生
谢谢!
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
