控制工程基础实验报告
控制工程基础仿真实验报告

本科生课程论文控制工程基础仿真实验报告实验一一阶系统的单位阶跃响应一、实验目的1、学会使用ATLABM编程绘制控制系统的单位阶跃响应曲线;2、掌握准确读取动态特征指标的方法;3、研究时间常数T对系统性能的影响;4、掌握一阶系统11Ts+时间响应分析的一般方法;5、通过仿真实验,直观了解各典型环节的时间响应和频率响应,巩固课程中所学的基本概念和基本原理;二、实验要求1、输入3个不同的时间常数T,观察一阶系统11Ts+的单位阶跃响应曲线的变化,绘制响应曲线图,并分析时间常数T对系统性能的影响。
2、若通过实验已测得一阶系统11Ts+的单位阶跃响应曲线,试说明如何通过该曲线确定系统的时间常数T。
三、实验内容(一)实验设备计算机;WINDOWS操作系统,并安装Matlab语言编程环境。
(二)实验原理通过对各种典型环节的仿真实验,可以直观的看到各种环节的时间响应和频率响应的图像。
通过对所得图像的分析可以得出各种参数如何影响系统的性能。
四、实验过程在Matlab平台对一阶系统11Ts+的单位阶跃响应进行仿真。
(1)输入3个不同的时间常数T,观察一阶系统单位阶跃响应曲线的变化,绘制响应曲线图,并分析时间常数T对系统性能的影响。
在Matlab中进行操作,其代码如下:1.num=1;2.den=[11];3.g=tf(num,den)4.5.g =6.7.18. -----9. s + 110.11.Continuous-time transfer function.12.13.>> step(g)14.hold on15.>> step(tf(1,[21]))16.>> step(tf(1,[41]))17.>> legend('T=1','T=2','T=4');(2)对于已测得的一阶系统的单位阶跃响应曲线,分析通过该曲线确定系统的时间常数T的方法。
南京理工大学控制工程基础实验报告

《控制工程基础》实验报告姓名欧宇涵 914000720206周竹青 914000720215 学院教育实验学院指导老师蔡晨晓南京理工大学自动化学院2017年1月实验1:典型环节的模拟研究一、实验目的与要求:1、学习构建典型环节的模拟电路;2、研究阻、容参数对典型环节阶跃响应的影响;3、学习典型环节阶跃响应的测量方法,并计算其典型环节的传递函数。
二、实验内容:完成比例环节、积分环节、比例积分环节、惯性环节的电路模拟实验,并研究参数变化对其阶跃响应特性的影响。
三、实验步骤与方法(1)比例环节图1-1 比例环节模拟电路图比例环节的传递函数为:K s U s U i O =)()(,其中12R RK =,参数取R 2=200K ,R 1=100K 。
步骤: 1、连接好实验台,按上图接好线。
2、调节阶跃信号幅值(用万用表测),此处以1V 为例。
调节完成后恢复初始。
3、Ui 接阶跃信号、Uo 接IN 采集信号。
4、打开上端软件,设置采集速率为“1800uS”,取消“自动采集”选项。
5、点击上端软件“开始”按键,随后向上拨动阶跃信号开关,采集数据如下图。
图1-2 比例环节阶跃响应(2)积分环节图1-3 积分环节模拟电路图积分环节的传递函数为:ST V V I I O 1-=,其中T I =RC ,参数取R=100K ,C=0.1µf 。
步骤:同比例环节,采集数据如下图。
图1-4 积分环节阶跃响应(3)微分环节图1-5 微分环节模拟电路图200KRV IVoC2CR 1V IVo200K微分环节的传递函数为:K S T S T V V D D I O +-=1,其中 T D =R 1C 、K=12R R。
参数取:R 1=100K ,R 2=200K ,C=1µf 。
步骤:同比例环节,采集数据如下图。
图1-6 微分环节阶跃响应(4)惯性环节图1-7 惯性环节模拟电路图惯性环节的传递函数为:1+-=TS K V V I O ,其中2T R C =,21RK R =-。
南理工控制工程基础实验报告

南理工控制工程基础实验报告成绩:《控制工程基础》课程实验报告班级:学号:姓名:南京理工大学2015年12月《控制工程基础》课程仿真实验一、已知某单位负反馈系统的开环传递函数如下G(s)?10 s2?5s?25借助MATLAB和Simulink完成以下要求:(1) 把G(s)转换成零极点形式的传递函数,判断开环系统稳定性。
>> num1=[10]; >> den1=[1 5 25]; >> sys1=tf(num1,den1) 零极点形式的传递函数:于极点都在左半平面,所以开环系统稳定。
(2) 计算闭环特征根并判别系统的稳定性,并求出闭环系统在0~10秒内的脉冲响应和单位阶跃响应,分别绘出响应曲线。
>> num=[10];den=[1,5,35]; >>sys=tf(num,den); >> t=[0::10]; >> [y,t]=step(sys,t); >> plot(t,y),grid >> xlabel(‘time(s)’) >> ylabel(‘output’) >> hold on; >> [y1,x1,t]=impulse(num,den,t); >> plot(t,y1,’:’),grid (3) 当系统输入r(t)?sin5t时,运用Simulink搭建系统并仿真,用示波器观察系统的输出,绘出响应曲线。
曲线:二、某单位负反馈系统的开环传递函数为:6s3?26s2?6s?20G(s)?4频率范围??[,100] s?3s3?4s2?2s?2 绘制频率响应曲线,包括Bode图和幅相曲线。
>> num=[6 26 6 20]; >> den=[1 3 4 2 2]; >> sys=tf(num,den); >> bode(sys,{,100}) >> grid on >> clear; >> num=[6 26 6 20]; >> den=[1 3 4 2 2]; >> sys=tf(num,den); >> [z , p , k] = tf2zp(num, den); >> nyquist(sys) 根据Nyquist判据判定系统的稳定性。
控制工程基础实验报告
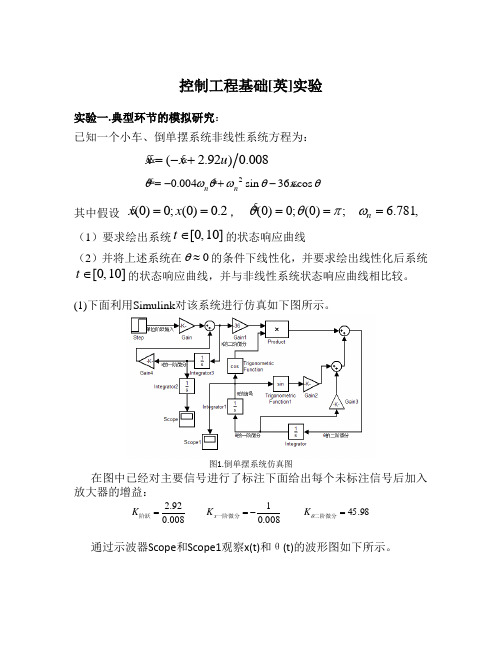
控制工程基础[英]实验实验一.典型环节的模拟研究:已知一个小车、倒单摆系统非线性系统方程为:( 2.92)0.008x x u =-+20.004sin 36cos n n x θωθωθθ=-+-其中假设 (0)0;(0)0.2x x ==,(0)0;(0); 6.781,n θθπω===(1)要求绘出系统[0,10]t ∈的状态响应曲线(2)并将上述系统在0θ≈的条件下线性化,并要求绘出线性化后系统[0,10]t ∈的状态响应曲线,并与非线性系统状态响应曲线相比较。
(1)下面利用Simulink 对该系统进行仿真如下图所示。
图1.倒单摆系统仿真图在图中已经对主要信号进行了标注下面给出每个未标注信号后加入放大器的增益:008.092.2=阶跃K 008.01-=一阶微分x K 98.45=二阶微分θK通过示波器Scope 和Scope1观察x(t)和θ(t)的波形图如下所示。
图2.x(t)波形图3.θ(t)波形(2)将上述系统在0θ≈的条件下线性化,则方程组改写成如下形式:( 2.92)0.008x x u=-+20.004sin36n n xθωθωθ=-+-在Simulink中对系统仿真如下所示。
图4.线性化后仿真系统通过示波器模块可以观察输出信号,图形如下图所示。
图5.x(t)输出波形图6.θ(t )输出波形实验二.典型系统时域响应动、静态性能和稳定性研究; 已知系统的开环传递函数为2()11G s s s =++(1)利用已知的知识判断该开环系统的稳定性(系统的特征方程根、系统零极点表示法)。
(2)判别系统在单位负反馈下的稳定性,并求出闭环系统在[0,10]t ∈内的脉冲响应和单位阶跃响应,分别绘制出相应响应曲线。
(1)该系统的特征方程的根、零极点表示的求解代码如下:输出结果如下图所示。
图7.特征方程求根结果图8.零极点分布图从图中可以看出两个极点在虚轴上,所以该系统处于临界稳定状态。
控制工程基础实验报告

控制工程基础实验报告控制工程基础实验报告引言:控制工程是一门涉及自动化、电子、计算机等多个学科的交叉学科,其实验是培养学生动手能力和实践能力的重要环节。
本篇文章将以控制工程基础实验为主题,探讨实验的目的、过程和结果等方面。
实验目的:控制工程基础实验的目的是让学生通过实践了解控制系统的基本原理和方法,培养其分析和解决问题的能力。
通过实验,学生可以掌握闭环控制系统的设计与调试技巧,加深对控制理论的理解。
实验内容:本次实验的内容是设计一个简单的温度控制系统。
系统由温度传感器、控制器和加热器组成。
温度传感器采集环境温度,控制器根据设定的温度值来控制加热器的工作状态,以维持温度在设定值附近。
实验步骤:1. 搭建实验平台:将温度传感器、控制器和加热器按照实验要求连接起来,确保电路正常工作。
2. 设计控制算法:根据控制系统的要求,设计合适的控制算法。
可以采用比例控制、积分控制或者PID控制等方法。
3. 参数调试:根据实验平台和控制算法的特点,调试控制器的参数,使系统能够快速、稳定地响应设定值的变化。
4. 实验数据采集:通过实验平台上的数据采集器,记录系统的输入和输出数据,以便后续分析和评估。
实验结果:经过实验,我们得到了一组温度控制系统的数据。
通过对这些数据的分析,我们可以评估系统的控制性能和稳定性。
在实验中,我们使用PID控制算法,经过参数调试,得到了较好的控制效果。
系统能够在设定值附近稳定工作,并且对设定值的变化能够快速响应。
实验总结:通过这次实验,我们深入了解了控制工程的基本原理和方法。
实践中遇到的问题和挑战,锻炼了我们的动手能力和解决问题的能力。
实验结果表明,合适的控制算法和参数调试是实现良好控制效果的关键。
控制工程实验的重要性不言而喻,它不仅是理论学习的延伸,更是培养学生实践能力的重要途径。
结语:控制工程基础实验是掌握控制工程理论和方法的重要环节。
通过实践,学生能够更好地理解和应用所学知识,提高解决实际问题的能力。
燕山大学控制工程基础实验报告(带数据)

自动控制理论实验报告实验一典型环节的时域响应院系:班级:学号:姓名:实验一 典型环节的时域响应一、 实验目的1.掌握典型环节模拟电路的构成方法,传递函数及输出时域函数的表达式。
2.熟悉各种典型环节的阶跃响应曲线。
3.了解各项参数变化对典型环节动态特性的影响。
二、 实验设备PC 机一台,TD-ACC+教学实验系统一套。
三、 实验步骤1、按图1-2比例环节的模拟电路图将线接好。
检查无误后开启设备电源。
注:图中运算放大器的正相输入端已经对地接了100k 电阻。
不需再接。
2、将信号源单元的“ST ”端插针与“S ”端插针用“短路块”接好。
将信号形式开关设为“方波”档,分别调节调幅和调频电位器,使得“OUT ”端输出的方波幅值为1V ,周期为10s 左右。
3、将方波信号加至比例环节的输入端R(t), 用示波器的“CH1”和“CH2”表笔分别监测模拟电路的输入R(t)端和输出C(t)端。
记录实验波形及结果。
4、用同样的方法分别得出积分环节、比例积分环节、惯性环节对阶跃信号的实际响应曲线。
5、再将各环节实验数据改为如下:比例环节:;,k R k R 20020010== 积分环节:;,u C k R 22000==比例环节:;,,u C k R k R 220010010=== 惯性环节:。
,u C k R R 220010=== 用同样的步骤方法重复一遍。
四、 实验原理、内容、记录曲线及分析下面列出了各典型环节的结构框图、传递函数、阶跃响应、模拟电路、记录曲线及理论分析。
1.比例环节 (1) 结构框图:图1-1 比例环节的结构框图(2) 传递函数:K S R S C =)()( KR(S)C(S)(3) 阶跃响应:C(t = K ( t ≥0 ) 其中K = R 1 / R 0 (4) 模拟电路:图1-2 比例环节的模拟电路图(5)记录曲线:(6)k R k R 20020010==,时的记录曲线:_R0=200kR1=100k_ 10K10KC(t)反相器 比例环节 R(t)(7)曲线分析:比例放大倍数K 与1R 的阻值成正比。
控制工程基础实验报告

控制工程基础实验报告实验一 典型环节及其阶跃响应实验目的1.学习构成典型环节的模拟电路。
2.熟悉各种典型环节的阶跃响应曲线,了解参数变化对典型环节动态特性的影响。
3.学会由阶跃响应曲线计算典型环节的传递函数。
4.熟悉仿真分析软件。
实验内容各典型环节的模拟电路如下:1. 比例环节 12)(R R s G -=2. 惯性环节 RC T Tss G =-=1)(3. 积分环节 1221)(R R K C R T Ts Ks G ==+-=4. 微分环节 RCs s G -=)(改进微分环节1)(12+-=Cs R Cs R s G 5. 比例微分环节)41()(212s C R R R s G +-=实验步骤1.用Workbench 连接好比例环节的电路图,将阶跃信号接入输入端,此时使用理想运放;2.用示波器观察输出端的阶跃响应曲线,测量有关参数;改变电路参数后,再重新测量,观察曲线的变化。
3. 将运放改为实际元件,如采用“LM741",重复步骤2。
5.仿真其它电路,重复步骤2,3,4。
实验总结通过这次实验,我对典型环节的模拟电路有了更加深刻的了解,也熟悉了各种典型环节的阶跃响应曲线,了解参数变化对典型环节动态特性的影响;熟悉仿真分析软件。
这对以后的控制的学习有很大的帮助。
实验二 二阶系统阶跃响应实验目的1. 研究二阶系统的两个重要参数阻尼比ξ和无阻尼自然频率ωn 对系统动态性能的影响。
2. 学会根据阶跃响应曲线确定传递函数,熟悉二阶系统的阶跃响应曲线。
实验内容二阶系统模拟电路如图: 1)/(1)(12222++-=RCs R R s C R s G 思考:如何用电路参数表示ξ和ωn实验步骤1. 在workbench 下连接电路图;将阶跃信号接入输入端,用示波器观测记录响应信号;2.取ωn=10rad/s,即令R=100K,C=1uf :分别取ξ=0,0.25,0.5,0.7,1,2, 即取R1=100K,考虑R2应分别取何值,分别测量系统阶跃响应,并记录最大超调量δp%和调节时间ts 。
2022年南理工机械院控制工程基础实验报告方案

试验1 模拟控制系统在阶跃响应下特性试验一、试验目根据等效仿真原理,运用线性集成运算放大器及分立元件构成电子模拟器,以干电池作为输入信号,研究控制系统阶跃时间响应。
二、试验内容研究一阶与二阶系统构造参数变化,对系统阶跃时间响应影响。
三、试验成果及理论分析1.一阶系统阶跃响应a.电容值1uF,阶跃响应波形:b.电容值2.2uF,阶跃响应波形:c. 电容值4.4uF ,阶跃响应波形:2. 一阶系统阶跃响应数据表电容值 (uF ) 稳态终值U c (∞)(V ) 时间常数T(s) 理论值 实际值 理论值 实际值 1.0 2.87 2.90 0.51 0.50 2.2 2.87 2.90 1.02 1.07 4.42.872.902.242.06元器件实测参数U r = -2.87VR o =505k ΩR 1=500k ΩR 2=496k Ω其中C R T 2=r c U R R U )/()(21-=∞误差原因分析:①电阻值及电容值测量有误差;②干电池电压测量有误差;③在示波器上读数时产生误差;④元器件引脚或者面包板老化,导致电阻变大;⑤电池内阻影响输入电阻大小。
⑥在C=4.4uF试验中,受硬件限制,读数误差较大。
3.二阶系统阶跃响应a.阻尼比为0.1,阶跃响应波形:b.阻尼比为0.5,阶跃响应波形:c.阻尼比为0.7,阶跃响应波形:d.阻尼比为1.0,阶跃响应波形:4.二阶系统阶跃响应数据表ξR w(Ω)峰值时间t p(s)U o(t p)(V)调整时间t s(s)稳态终值U s(V)超调(%)M p震荡次数N0.1 454k 0.3 4.8 2.8 2.95 62.7 6 0.5 52.9k 0.4 3.3 0.5 2.95 11.9 10.7 24.6k 0.4 3.0 0.3 2.92 2.7 11.02.97k 1.0 2.98 1.0 2.98 0 0四、回答问题1.为何要在二阶模拟系统中设置开关K1和K2,并且必须同步动作?答:K1作用是用来产生阶跃信号,撤除输入信后,K2则是构成了C2放电回路。
控制工程基础实验报告讲解

控制工程基础实验报告北京工业大学机电学院指导教师:初红艳学号:姓名:一.实验目的本实验中,学生使用MATLAB 语言进行控制系统的分析,可以达到以下目的: (1)通过MATLAB 的分析,掌握控制系统的时域瞬态响应、频率特性,根据时域性能指标、频域性能指标评价控制系统的性能,根据系统频率特性进行稳定性分析,了解对系统进行校正的方法,从而进一步巩固、加深对课堂内容的掌握,加强对控制工程基础知识的掌握。
(2)熟悉MATLAB 的控制系统图形输入与仿真工具SIMULINK ,能够对一些框图进行仿真或线性分析,使一个复杂系统的输入变得相当容易且直观。
(3)通过本实验,使学生掌握进行控制系统计算机辅助分析的方法,学会利用MATLAB 语言进行复杂的实际系统的分析、校正与设计,具备解决工程实际问题的能力。
二.实验内容控制系统方块图如图1所式。
这是一个电压—转角位置随动系统,系统的功能是用电压量去控制一个设备的转角,给定值大,输出转角也就成比例地增大。
图1 系统方块图 图中,)(1s G 为前置放大及校正网络传递函数K 2为功率放大器放大倍数,102=K K 3为电动机传递系数,s V rad K ⋅=/83.23 T M 为电动机机电时间常数,s T M 1.0= T a 为电动机电磁时间常数,ms T a 4= K c 为测速传递系数,rad s V K c /15.1⋅=β 为测速反馈分压系数,1=βK a 为主反馈电位计传递系数,rad V K a /7.4= U i 为输入电压U b 为反馈电压 U i 2为速度环输入电压 U c 为测速机电压 U D 为电动机电压n 为电动机转速取1=β三、实验报告1.对于二阶系统:1)(23++=s s G Ts T T KMaM,a M MaM T T T T T 21n ==ζω其阶跃响应和单位脉冲响应分别如图1-1、1-2所示:MATLAB 语言为: >>num=[2.83]num =2.8300>> den=[0.0004,0.1,1]den =0.0004 0.1000 1.0000>> sys=tf(num,den) sys =2.83 ---------------------- 0.0004 s^2 + 0.1 s + 1Continuous -time transfer function.>> step(sys)>> impulse(sys)图1-1图1-2此时阻尼比为2.5,由其阶跃响应可知其稳态值为2.83,为过阻尼状态,瞬态响应指标如上图所示;在无阻尼自振角频率不变时,通过简单计算得出如下的结论:M a M n T T T 25===ζω,0004.0,50调整TM=0.01,Ta=0.04,使得系统处于欠阻尼状态,0.25=ξ,其阶跃响应与单位脉冲响应1-3、1-4;MATLAB 语言如下:>>num=[2.83]num =2.8300>> den=[0.0004,0.01,1]den =0.0004 0.0100 1.0000>> sys=tf(num,den) sys =2.83 -----------------------0.0004 s^2 + 0.01 s + 1Continuous -time transfer function.>> step(sys) >> impulse(sys)其瞬态响应指标在下图中标出;图1-3图1-4调整TM=0.04,Ta=0.01,使得系统处于临界阻尼状态,其阶跃响应与单位脉冲响应如图1-5、1-6所示;MATLAB语言如下:>>num=[2.83]num =2.8300>> den=[0.0004,0.04,1]den =0.0004 0.0400 1.0000>> sys=tf(num,den)sys =2.83-----------------------0.0004 s^2 + 0.04 s + 1Continuous-time transfer function.>> step(sys)>> impulse(sys图1-5图1-6由以上当TM=0.1,Ta=0.0004,系统处于过阻尼状态,其阶跃响应与单位脉冲响应见图1-1、1-2所示:分析:由以上响应曲线和响应指标可知,过阻尼与临界阻尼无超调、无振荡,而欠阻尼有超调和振荡,过阻尼达到平衡状态所需的时间比临界阻尼和过阻尼都要长。
控制工程实验报告

Hefei University of Technology《控制工程基础》实验报告学院机械与汽车工程学院姓名学号专业班级机械设计制造及其自动化13-7班2015年12月15日自动控制原理实验• 1、线性系统的时域分析• 1.1典型环节的模拟研究一、实验要求1、掌握各典型环节模拟电路的构成方法、传递函数表达式及输出时域函数表达式。
2、观察和分析各典型环节的阶跃响应曲线,了解各项电路参数对典型环节动态特性的影响。
二、实验原理(典型环节的方块图及传递函数)三、实验内容及步骤在实验中欲观测实验结果时,可用普通示波器,也可选用本实验机配套的虚拟示波器。
如果选用虚拟示波器,只要运行LABACT 程序,选择自动控制菜单下的线性系统的时域分析下的典型环节的模拟研究实验项目,再选择开始实验,就会弹出虚拟示波器的界面,点击开始即可使用本实验机配套的虚拟示波器(B3)单元的CH1测孔测量波形。
具体用法参见用户手册中的示波器部分。
1) 观察比例环节的阶跃响应曲线典型比例环节模拟电路如图3-1-1所示。
该环节在A1单元中分别选取反馈电阻R1=100K 、200K 来改变比例参数。
图3-1-1 典型比例环节模拟电路实验步骤: 注:“SST ”不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V 作为系统的信号输入(Ui ) (2)安置短路套、联线,构造模拟电路:(a(b(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A6单元信号输出端OUT (Uo )。
注:CH1选“X1”档。
时间量程选“x4”档。
(4)运行、观察、记录:按下信号发生器(B1)阶跃信号按钮时(0→+5V 阶跃),用示波器观测A6输出端(Uo )的实际响应曲线Uo (t ),且将结果记下。
改变比例参数(改变运算模拟单元A1的反馈电阻R1),重新观测结果,其实际阶跃响应曲线见表3-1-1。
2) 观察惯性环节的阶跃响应曲线典型惯性环节模拟电路如图3-1-2所示。
控制工程基础实验三报告 臧孟
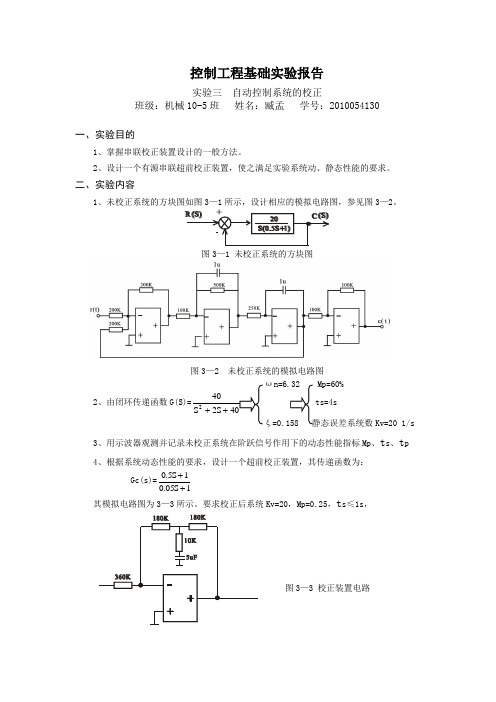
控制工程基础实验报告实验三 自动控制系统的校正班级:机械10-5班 姓名:臧孟 学号:2010054130一、实验目的1、掌握串联校正装置设计的一般方法。
2、设计一个有源串联超前校正装置,使之满足实验系统动、静态性能的要求。
二、实验内容1、未校正系统的方块图如图3—1所示,设计相应的模拟电路图,参见图3—2。
图3—1 未校正系统的方块图图3—2 未校正系统的模拟电路图ωn=6.32 Mp=60%2、由闭环传递函数Kv=20 1/s3、用示波器观测并记录未校正系统在阶跃信号作用下的动态性能指标Mp 、t s 、t p4、根据系统动态性能的要求,设计一个超前校正装置,其传递函数为:Gc(s)=1S 05.01S 5.0++ 其模拟电路图为3—3所示。
要求校正后系统Kv=20,Mp=0.25,t s ≤1s ,图3—3 校正装置电路校正后系统的方块图为图3—4所示由图可知,该系统的开环传递函数为G(S)=)20S (S 400)1S 05.0(S 20+=+ 与二阶系统标准形式的开环传递函数相比较,得ωn=400=20 2ξωn=20 ξ=0.5 Mp=e -215ξ-π=0.163<0.25图3—5 校正后系统的模拟电路图三、实验步骤1、按照图3—2接线,并核对图中各环节的参数是否完全满足图3—1所示系统的要求。
2、加入阶跃输入电压,用示波器观察并记录系统输出响应曲线及其性能指标:超调量Mp 和调节时间t s 。
3、按图3—5的要求接入校正装置。
在输入端引入阶跃控制电压,并用示波器观察和记录校正后系统的超调量Mp 和调节时间t s ,以检验系统是否完全满足预期的设计要求。
4、具体参数及响应曲线请参照表3-1。
四、实验思考题1、阶跃输入信号为什么不能取得太大?答:因为线性系统都有自己的线性范围,如果阶跃信号输入太大,会导致输出失真。
2、为什么图3—3所示的校正装置是超前校正装置?答:因为校正装置是一个微分环节,微分环节可以超前校正。
《控制工程基础》实训报告[合集五篇]
![《控制工程基础》实训报告[合集五篇]](https://img.taocdn.com/s3/m/9b85fa26a31614791711cc7931b765ce05087aa1.png)
《控制工程基础》实训报告[合集五篇]第一篇:《控制工程基础》实训报告《控制工程基础》实训报告实训地点:实训时间:所在院系:电子信息学院自动化系专业年级:学生姓名:学生学号:指导教师:A2-310 2013年12月2日至12月10日12电气3班实验一典型环节的模拟研究一:实验目的1、掌握典型环节仿真结构图的建立方法;2、通过观察典型环节在单位阶跃信号作用下的动态特性,熟悉各种典型环节的响应曲线。
3、定性了解各参数变化对典型环节动态特性的影响。
4、初步了解MATLAB中SIMULINK 的使用方法。
二:实验步骤1.建立各典型环节(比例、积分、微分、惯性、振荡)的仿真模型。
进入MATLAB编程环境,在File菜单的New子命令下,新建一个模块文件(*.model)并保存;进入simulink仿真环境,在模块库中找到所需的模块,用鼠标按住该模块并拖至模块文件中,然后再放开鼠标;根据信号流向,用信号线连接各模块。
2.根据实验要求,对每一个模块,选取合适的模块参数;3.在模块文件的simulation菜单下,单击Simulation/paramater子命令,将仿真时间(Stop Time)设置为10秒;4.在模块文件的simulation菜单下,单击Start子命令,开始仿真过程。
5.利用PrintScreen命令,将仿真模型和仿真图形拷贝到WORD文档中。
三:实验内容①惯性环节(仿真结构图、阶跃响应曲线、分析结果);②积分环节(仿真结构图、阶跃响应曲线、分析结果);③比例环节(仿真结构图、阶跃响应曲线、分析结果);④振荡环节(仿真结构图、阶跃响应曲线、分析结果);⑤实际微分(仿真结构图、阶跃响应曲线、分析结果); 1.比例环节连接系统, 如图所示: 22.参数设置: 用鼠标双击阶跃信号输入模块,设置信号的初值和终值,采样时间sample time 和阶跃时间step time3.在simulation/paramater中将仿真时间(Stop Time)设置为10秒,4.仿真:simulation/start,仿真结果如图1-1所示改变Kd,观察仿真结果如下图所示(2)积分环节——放大倍数K不同时的波形(3):微分环节——改变Td、Kd,观察仿真结果(4):惯性环节--改变其放大倍数K及时间常数T 5(5)振荡环节——改变ξω的值的波形四:实训小结积分环节的传递函数为G=1/Ts(T为积分时间常数),惯性环节的传递函数为G=1/(Ts+1)(T为惯性环节时间常数)。
机械控制工程基础实验报告

机械控制工程基础实验报告一、实验目的机械控制工程基础实验是机械工程及相关专业的重要实践环节,通过实验可以加深对机械控制工程基本理论的理解,掌握控制系统的性能分析和设计方法,提高实际动手能力和解决问题的能力。
本次实验的具体目的包括:1、熟悉典型控制系统的组成和工作原理。
2、掌握控制系统数学模型的建立方法。
3、学会运用实验设备对控制系统的性能进行测试和分析。
4、培养团队合作精神和创新思维。
二、实验设备本次实验所使用的设备主要包括:1、控制实验台:包括电机、传感器、控制器等部件,用于构建控制系统。
2、计算机:安装有相关的实验软件,用于数据采集和处理。
3、示波器:用于观察系统的输入输出信号。
三、实验原理1、控制系统的组成控制系统通常由控制对象、控制器、传感器和执行机构组成。
控制对象是被控制的物理设备或过程,控制器根据传感器采集到的系统状态信息,按照一定的控制算法计算出控制量,通过执行机构作用于控制对象,使系统的输出达到预期的目标。
2、控制系统的数学模型数学模型是描述控制系统动态特性的数学表达式,常用的有传递函数和状态空间方程。
传递函数是在零初始条件下,输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。
状态空间方程则是用一组一阶微分方程来描述系统的动态特性。
3、控制系统的性能指标控制系统的性能指标包括稳定性、准确性和快速性。
稳定性是指系统在受到外界干扰后,能够恢复到平衡状态的能力;准确性是指系统的输出与期望值之间的偏差大小;快速性是指系统从一个状态过渡到另一个状态所需的时间。
四、实验内容1、一阶系统的响应特性实验构建一阶系统,输入阶跃信号,观察系统的输出响应,记录响应曲线。
通过改变系统的参数,如时间常数,分析其对系统响应速度和稳定性的影响。
2、二阶系统的响应特性实验构建二阶系统,输入阶跃信号,观察系统的输出响应。
调整系统的阻尼比和自然频率,研究其对系统的超调量、调节时间等性能指标的影响。
3、系统的频率特性实验给系统输入不同频率的正弦信号,测量系统的输出幅值和相位,绘制系统的幅频特性和相频特性曲线。
控制工程基础实验报告

控制系统的仿真数学模型系别:机电工程系班级:1301班专业:机械设计制造及其自动化姓名:学号:201309011指导教师:刘春艳一、实验目的由系统的结构方框图得到控制系统模型,其传递函数方框图,用SIMULINK 模型结构图化简控制系统模型,分析系统的阶跃响应,并绘制响应曲线。
二、上机内容1、 Matlab 基础2、 Matlab 中系统建模3、 Matlab 分析系统的动态特性三、实验平台Windows 98或2000或XP Matlab 6.1以上版本四、操作过程、源程序和计算结果:3.15二阶系统的闭环传递函数为()2222nn n s s s G ωξωω++=式中二阶系统固有频率n ω=10 rad/s,试求该系统在欠阻尼、临界阻尼、过阻尼、零阻尼及负阻尼状态下的单位阶跃响应。
(1)欠阻尼,当取二阶系统阻尼分别为ξ=0.2、0.4、0.6、0.8时,仿真模型如下图所示(2) 临界阻尼、过阻尼、零阻尼及负阻尼状态下的单位阶跃响应,当取二阶系统阻尼分别为 =1.0、1.5、0.0、-0.2时,仿真模型如下图所示例题3.16 某单位反馈控制系统框图如下图所示。
试分析开环放大系数K对该系统稳定性的影响。
3-18 对于典型二阶系统,()2222nn n s s s G ωξωω++= ,要求: 1.当固有振荡频率=n ω6rad/s ,阻尼比分别为0.1,0.2, ------0.9,1.0,2.0时系统的单位阶跃响应曲线和单位脉冲曲线;2.当阻尼比7.0=ξ时,固有频率分别为2,4,6,8,10,12rad/s 时的单位阶跃响应曲线和单位脉冲响应曲线。
(1)t=[0:0.1:10];num=[36];den1=[1 1.2 36];sys1=tf(num,den1);den2=[1 2.4 36];sys2=tf(num,den2);den3=[1 3.6 36]; sys3=tf(num,den3);den4=[1 4.8 36];sys4=tf(num,den4);den5=[1 6 36];sys5=tf(num,den5);den6=[1 7.2 36];sys6=tf(num,den6);den7=[1 8.4 36];sys7=tf(num,den7);den8=[1 9.6 36];sys8=tf(num,den8);den9=[1 10.8 36];sys9=tf(num,den9);den10=[1 12 36];sys10=tf(num,den10);den11=[1 24 36];sys11=tf(num,den11);step(sys1,sys2, sys3, sys4, sys5, sys6, sys7, sys8, sys9, sys10, sys11, t);grid on;t=[0:0.1:6];num=[36];den1=[1 1.2 36]; sys1=tf(num,den1); den2=[1 2.4 36]; sys2=tf(num,den2); den3=[1 3.6 36]; sys3=tf(num,den3); den4=[1 4.8 36]; sys4=tf(num,den4); den5=[1 6 36];sys5=tf(num,den5); den6=[1 7.2 36]; sys6=tf(num,den6); den7=[1 8.4 36];sys7=tf(num,den7);den8=[1 9.6 36];sys8=tf(num,den8);den9=[1 10.8 36];sys9=tf(num,den9);den10=[1 12 36];sys10=tf(num,den10);den11=[1 24 36];sys11=tf(num,den11);impulse(sys1,sys2, sys3, sys4, sys5, sys6, sys7, sys8, sys9, sys10, sys11, t);grid on;(2)t=[0:0.1:5];den1=[1 2.84];sys1=tf([4],den1);den2=[1 5.616];sys2=tf([16],den2);den3=[1 8.436];sys3=tf([36],den3);den4=[1 11.264];sys4=tf([64],den4);den5=[1 14100];sys5=tf([100],den5);den6=[1 16.8144];sys6=tf([144],den6);step(sys1,sys2, sys3, sys4, sys5, sys6, t); grid on;t=[0:0.1:6];den1=[1 2.84];sys1=tf([4],den1);den2=[1 5.616];sys2=tf([16],den2);den3=[1 8.436];sys3=tf([36],den3);den4=[1 11.264];sys4=tf([64],den4);den5=[1 14100];sys5=tf([100],den5);den6=[1 16.8144];sys6=tf([144],den6);impulse(sys1,sys2, sys3, sys4, sys5, sys6, t); grid on;。
南理工 机械院 控制工程基础实验报告

实验1 模拟控制系统在阶跃响应下的特性实验一、实验目的根据等效仿真原理,利用线性集成运算放大器及分立元件构成电子模拟器,以干电池作为输入信号,研究控制系统的阶跃时间响应。
二、实验内容研究一阶与二阶系统结构参数的改变,对系统阶跃时间响应的影响。
三、实验结果及理论分析1.一阶系统阶跃响应a.电容值1uF,阶跃响应波形:b.电容值2.2uF,阶跃响应波形:c. 电容值4.4uF ,阶跃响应波形:2. 一阶系统阶跃响应数据表电容值 (uF ) 稳态终值U c (∞)(V ) 时间常数T(s) 理论值 实际值 理论值 实际值 1.0 2.87 2.90 0.51 0.50 2.2 2.87 2.90 1.02 1.07 4.42.872.902.242.06元器件实测参数U r = -2.87VR o =505k ΩR 1=500k ΩR 2=496k Ω其中C R T 2=r c U R R U )/()(21-=∞误差原因分析:①电阻值及电容值测量有误差;②干电池电压测量有误差;③在示波器上读数时产生误差;④元器件引脚或者面包板老化,导致电阻变大;⑤电池内阻的影响输入电阻大小。
⑥在C=4.4uF的实验中,受硬件限制,读数误差较大。
3.二阶系统阶跃响应a.阻尼比为0.1,阶跃响应波形:b.阻尼比为0.5,阶跃响应波形:c.阻尼比为0.7,阶跃响应波形:d.阻尼比为1.0,阶跃响应波形:4.二阶系统阶跃响应数据表ξR w(Ω)峰值时间t p(s)U o(t p)(V)调整时间t s(s)稳态终值U s(V)超调(%)M p震荡次数N0.1 454k 0.3 4.8 2.8 2.95 62.7 60.5 52.9k 0.4 3.3 0.5 2.95 11.9 10.7 24.6k 0.4 3.0 0.3 2.92 2.7 11.02.97k 1.0 2.98 1.0 2.98 0 0四、回答问题1.为什么要在二阶模拟系统中设置开关K1和K2,而且必须同时动作?答:K1的作用是用来产生阶跃信号,撤除输入信后,K2则是构成了C2的放电回路。
控制工程基础实验报告1 -示例

《控制工程基础》实验报告一班级·学号1501034148 姓名李富国实验日期2017.11.27 任课教师杨世文实验名称实验一控制系统的建模验证型一、实验目的及要求:1.学习在MATLAB命令窗口建立系统模型的方法;2.学习如何在三种模型之间相互转换;3.学习如何用SIMULINK仿真工具建模。
二、上机内容:1、Matlab基础2、Matlab中系统建模3、Matlab分析系统的动态特性三、实验平台Windows 98或2000或XP Matlab 5.3以上版本1. 给定控制系统的传递函数为:在MA TLAB 中建立系统的传递函数模型、零极点增益模型和状态变量模型。
num=[3]; %G 的分子多项式系数den=[1, 3, 5, 7]; %G1的分母多项式系数G=tf(num, den) % 由分子多项式/分母多项式采用tf()函数创建传递函数[z1,p1,k1]=tf2zp(num,den) %求传递函数的零极点sys1zp=zpk(z1,p1,k1) %构建并显示该系统的零极点形式的传递函数运行结果:7533)(23+++=s s s s G2.在SIMULINK中建立如下图所示的结构图:源程序:五、评阅成绩评阅老师年月日《机械控制工程基础》实验报告二班级·学号1501034148 姓名李富国实验日期2017.11.27任课教师杨世文实验名称实验二控制系统的稳定性分析实验验证型一、实验目的及要求:本实验是用MATLAB得到控制系统的频域特性曲线,绘制给定控制系统Bode 图和Nyquist图,并表示出系统的幅值裕量和相位裕量,-π穿越频率和剪切频率等频域性能指标;用频率法对控制系统进行稳定性判断。
二、上机内容:1、Matlab中的频率响应函数2、Matlab求取稳定性裕量三、实验平台Windows 98或2000或XP Matlab 5.3以上版本四、操作过程、源程序和计算结果:1、题目:绘制系统G(s)=[100(s+4)]/[s(s+0.5)(s+50)²]的Bode图。
控制工程基础实验报告DOC

控制工程基础实验报告姓名:朱泽强班级:11020742学号:322013年11月16日实验一系统时域响应分析1. 实验目的本实验的主要目的是:通过实验使学生进一步理解系统参数对时域响应的影响,理解系统参数与时域性能指标之间的关系,同时了解系统稳定性的充要条件。
2. 实验内容完成一阶、二阶系统在典型输入信号作用下的响应,求取二阶系统的性能指标,记录试验结果并对此进行分析。
3.实验的具体内容及步骤(1)一阶系统(选用不同的时间常数T)在典型输入信号(单位脉冲、单位阶跃、正弦信号)作用下的响应。
单位阶跃for T=1:1:5t=[0:0.01:10];num=[1];den=[T 1];G=tf(num,den)[y1,tt]=step(G,t);plot(tt,y1,'--')legend('不同时间参数T下的单位阶跃响应')xlabel('t(sec)'),ylabel('x(t)');grid on;hold onend单位脉冲for T=1:1:5t=[0:0.01:10];num=[1];den=[T 1];G=tf(num,den);[y1,tt]=impulse(G,t);result(T,:)=y1;plot(tt,y1,'--')legend('不同时间参数T下的单位脉冲响应')xlabel('t(sec)'),ylabel('x(t)');grid on;hold onEnd通过图形,得出结论:1)分析T对输出响应的影响系统达到稳态所需时间和T值有关,T值越大达到稳态所需时间越长。
2)分析不同时间点处输出的大小单位阶跃:单位阶跃t=6s t=7s t=8s t=9s t=10sT=6 0.6321 0.6886 0.7364 0.7769 0.8111T=7 0.5756 0.6321 0.6811 0.7235 0.7603T=8 0.5276 0.5831 0.6321 0.6753 0.7135T=9 0.4866 0.5406 0.5889 0.6321 0.6708T=10 0.4512 0.5034 0.5507 0.5934 0.6321单位脉冲t=5s t=6s t=7s t=8s t=9s t=10sT=5 0.073576 0.060239 0.049319 0.040379 0.03306 0.027067T=6 0.072433 0.061313 0.051901 0.043933 0.037188 0.031479T=7 0.069935 0.060625 0.052554 0.045558 0.039493 0.034236T=8 0.066908 0.059046 0.052108 0.045985 0.040582 0.035813T=9 0.06375 0.057046 0.051047 0.045679 0.040875 0.036577T=10 0.060653 0.054881 0.049659 0.044933 0.040657 0.036788(2)二阶系统(选择不同的阻尼比ξ和无阻尼振荡频率w,阻尼比ξ要有欠n阻、临界阻尼和过阻尼三种情况)在典型输入信号(单位脉冲、单位阶跃)作用下作用下的响应t=[0:0.01:5];i=1for wn=1:2:7;num=[wn^2];znb=0; den=[1 2*znb*wn wn^2]; G1=tf(num,den);znb=0.2; den=[1 2*znb*wn wn^2]; G2=tf(num,den);znb=0.5; den=[1 2*znb*wn wn^2]; G3=tf(num,den);znb=1; den=[1 2*znb*wn wn^2]; G4=tf(num,den);znb=1.5; den=[1 2*znb*wn wn^2]; G5=tf(num,den);%5种不同阻尼比系统[y1,T]=impulse(G1,t);[y1a,T]=step(G1,t);[y2,T]=impulse(G2,t);[y2a,T]=step(G2,t);[y3,T]=impulse(G3,t);[y3a,T]=step(G3,t);[y4,T]=impulse(G4,t);[y4a,T]=step(G4,t);[y5,T]=impulse(G5,t);[y5a,T]=step(G5,t);figure(i)plot(T,y1,'--',T,y2,'-.',T,y3,'-',T,y4,'*' ,T,y5,'o')legend('不同阻尼比下的二阶系统单位脉冲响应')xlabel('t(sec)'),ylabel('x(t)');grid on;figure(i+1)plot(T,y1a,'--',T,y2a,'-.',T,y3a,'-',T,y4a,'*' ,T,y5a,'o')legend('不同阻尼比下的二阶系统单位阶跃响应')grid on;xlabel('t(sec)'),ylabel('x(t)');i=i+2end不同无阻尼振荡频率wnt=[0:0.01:3];i=1for znb=[0,0.2,0.5,1,1.5];num=[wn^2];wn=1; den=[1 2*znb*wn wn^2]; G1=tf(num,den);wn=3; den=[1 2*znb*wn wn^2]; G2=tf(num,den);wn=5; den=[1 2*znb*wn wn^2]; G3=tf(num,den);wn=7; den=[1 2*znb*wn wn^2]; G4=tf(num,den); %4种不同wn系统 [y1,T]=impulse(G1,t);[y1a,T]=step(G1,t);[y2,T]=impulse(G2,t);[y2a,T]=step(G2,t);[y3,T]=impulse(G3,t);[y3a,T]=step(G3,t);[y4,T]=impulse(G4,t);[y4a,T]=step(G4,t);figure(i)plot(T,y1,'--',T,y2,'-.',T,y3,'-',T,y4,'*') legend('不同wn下的二阶系统单位脉冲响应')xlabel('t(sec)'),ylabel('x(t)');grid on;figure(i+1)plot(T,y1a,'--',T,y2a,'-.',T,y3a,'-',T,y4a,'*') legend('不同wn下的二阶系统单位阶跃响应')grid on;xlabel('t(sec)'),ylabel('x(t)');i=i+2end(3)完成欠阻尼二阶系统性能指标的求取t=0:0.001:50;yss=1; %稳态输出值1dta=0.02; %误差范围为2%wn=30;s=0.1:0.05:0.95;num=[wn^2];for i=1:18den=[1 2*s(i)*wn wn^2];G=tf(num,den);y=step(G,t);r=1;while y(r)<yssr=r+1;endtr(i)=(r-1)*0.001;[ymax,p]=max(y);tp(i)=(p-1)*0.001;mp(i)=(ymax-yss)/yss;m=50001;while y(m)>1-dta & y(m)<1+dtam=m-1;endts(i)=(m-1)*0.001;endplot(s,tr)legend('阻尼比与上升时间的关系曲线')xlabel('阻尼比'),ylabel('上升时间');grid on;figure(2)plot(s,tp)legend('阻尼比与峰值时间的关系曲线')xlabel('阻尼比'),ylabel('峰值时间');grid on;figure(3)plot(s,mp)legend('阻尼比与超调量的关系曲线')xlabel('阻尼比'),ylabel('超调量');grid on;figure(4)plot(s,ts)legend('阻尼比与调整时间的关系曲线')xlabel('阻尼比'),ylabel('调整时间');grid on;4.实验分析内容(1)分析时间常数对一阶系统时间响应的影响;时间常数T 越大,一阶系统输出响应达到稳定所需要的时间越长. (2)分析系统稳定性与系统特征值的关系;T 值越大,则wn 越大,sigma 也越大,系统的响应和相对稳定性好。
控制工程基础实验报告资料

控制工程基础实验报告姓名:班级:学号:目录实验三 (1)3.1 实验目的 (1)3.2 实验内容 (1)3.3 实验结果 (2)实验四 (15)4.1实验目的 (15)4.2 实验内容 (15)4.3 实验结果 (15)实验三 控制系统的频域与时域分析一、实验目的:1、掌握控制系统数学模型的基本描述方法和相互转化2、了解控制系统的稳定性分析方法3、掌握控制系统频域与时域分析基本方法二、实验内容1、表示下列传递函数模型,并转化成其他的数学模型(1))523()1()66)(2(4)(23322+++++++=S S S S S S S S S G (2) )52(24)(3++-=S S S S G(3)) )2)(12(1)(++=S S S G(4) []⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛21212110102110x x y u x x x x2、一个单位负反馈开环传递函数为)14)(15.0()(++=S S S kS G试绘出系统闭环的根轨迹图;并在跟轨迹图上任选一点,试计算该点的增益及其所有极点的位置。
3.已知某负反馈系统的前向通路传递函数为 ,反馈通路传递函数为 。
绘制系统的单位阶跃响应曲线,并计算上升时间,峰值时间,超调量,延迟时间。
三、实验结果 11102-s s 3.01+(1)传递函数模型num=4*conv([1,2],conv([1,6,6],[1,6,6]));>> den=conv([1,0],conv([1,1],conv([1,1],conv([1,1],[1,3,2,5])))); >> Gs=tf(num,den)Transfer function:4 s^5 + 56 s^4 + 288 s^3 + 672 s^2 + 720 s + 288-----------------------------------------------------s^7 + 6 s^6 + 14 s^5 + 21 s^4 + 24 s^3 + 17 s^2 + 5 s零极点模型[z,p,k]=tf2zp(num,den)z =-4.7321 + 0.0000i-4.7321 - 0.0000i-2.0000-1.2679-1.2679p =-2.9042-0.0479 + 1.3112i-0.0479 - 1.3112i-1.0000-1.0000 + 0.0000i-1.0000 - 0.0000ik =4>> Gs2=zpk(Gs)Zero/pole/gain:4 (s+4.732)^2 (s+2) (s+1.268)^2--------------------------------------------s (s+2.904) (s+1)^3 (s^2 + 0.09584s + 1.722)状态空间模型>> [A , B ,C ,D]= tf2ss (num , den)A =-6 -14 -21 -24 -17 -5 01 0 0 0 0 0 00 1 0 0 0 0 00 0 1 0 0 0 00 0 0 1 0 0 00 0 0 0 1 0 00 0 0 0 0 1 0B =1C =0 4 56 288 672 720 288D =>> Gs3=ss(Gs)a =x1 x2 x3 x4 x5 x6 x7 x1 -6 -3.5 -2.625 -1.5 -1.063 -0.3125 0x2 4 0 0 0 0 0 0 x3 0 2 0 0 0 0 0 x4 0 0 2 0 0 0 0 x5 0 0 0 1 0 0 0x6 0 0 0 0 1 0 0 x7 0 0 0 0 0 0.5 0 b =u1x1 16x2 0x3 0x4 0x5 0x6 0x7 0c =x1 x2 x3 x4 x5 x6 x7 y1 0 0.0625 0.4375 1.125 2.625 2.813 2.25d =u1y1 0(2)传递函数模型num=[4,-2];den=[1,0,2,5];>> gs=tf(num,den)Transfer function:4 s - 2-------------s^3 + 2 s + 5零极点模型>> [z,p,k]=tf2zp(num,den)z =0.5000p =0.6641 + 1.8230i0.6641 - 1.8230i-1.3283k =4>> gs2=zpk(gs)Zero/pole/gain:4 (s-0.5)--------------------------------(s+1.328) (s^2 - 1.328s + 3.764) 状态空间模型gs3=ss(A,B,C,D)a =x1 x2 x3x1 0 -2 -5x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 4 -2d =u1y1 03零极点模型>> z=[];>> p=[-0.5,-2];>> k=[0.5];>> gs1=zpk(z,p,k)Zero/pole/gain:0.5-------------(s+0.5) (s+2)传递函数模型>> [num,den]=zp2tf(z ,p ,k)num =0 0 0.5000 den =1.00002.5000 1.0000 >> gs=tf(num,den)Transfer function:0.5---------------s^2 + 2.5 s + 1状态空间模型[A , B ,C ,D]=zp2ss(z ,p ,k)A =-2.5000 -1.00001.0000 0B =1C =0 0.5000D =>> gs3=ss(A,B,C,D) a =x1 x2 x1 -2.5 -1x2 1 0 b =u1x1 1x2 0c =x1 x2y1 0 0.5d =u1y1 0(4)状态空间模型A=[0 1;-1 -2];>> B=[0;1];>> C=[0 1];>> D=[0];gs3=ss(A,B,C,D)a =x1 x2x1 0 1x2 -1 -2b =u1x1 0x2 1c =x1 x2y1 0 1d =u1y1 0传递函数模型[num,den]=ss2tf(A,B,C,D)num =0 1.0000 -0.0000 den =1 2 1gs=tf(num,den)Transfer function:s - 1.11e-016-------------s^2 + 2 s + 1零极点模型>> [z, p ,k]=ss2zp(A ,B ,C ,D )z =p =-1-1k =1>> gs2=zpk(z,p,k)Zero/pole/gain:s-------(s+1)^22num=[1];den=conv([1,0],conv([0.5,1],[4,1])); >> rlocus(num,den);>> [K,Poles]=rlocfind(num,den) Select a point in the graphics window selected_point =1.1635 + 3.1522iK =103.6761Poles =-4.59571.1728 + 3.1471i1.1728 - 3.1471i3t=0:0.01:5; num=[10]; den=[1,3,9];G=tf(num,den); >> step(G,t);由图形可知:上升时间tr=0.8,峰值时间tp=1.2,超调量Mp=0.19实验四 Matlab 环境下校正环节的设计一. 实验目的1. 研究校正环节的工作原理以及设计实现方法;2. 研究校正环节对系统稳定性及过渡过程的影响;3. 熟练掌握利用Matlab 实现系统辅助设计及仿真技术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制工程基础实验姓名:专业:机电班级:02 学号:1003120225实验一:比较二阶系统在不同阻尼比下的时间响应一、实验目的1.熟悉MA TLAB软件环境,学会编写matlab文件(***.m)和使用SIMULINK建模,进行时间响应分析。
二、实验要求1.编写m文件,使用命令sys=tf(num,den),建立二阶系统的传递函数模型;2.编写m文件,使用命令impulse(sys),画出二阶系统在不同阻尼比下的脉冲响应曲线簇;3.编写m文件,使用命令step(sys),画出二阶系统在不同阻尼比下的阶跃响应曲线簇;4.根据阶跃响应曲线,记录不同阻尼比下的时域性能指标,列表写出实验报告,并分析阻尼比和无阻尼自然频率对于性能的影响;5.利用SIMULINK建立方框图仿真模型,进行阶跃响应实验,学会使用workspace的数组变量传递,使用命令plot(X,Y)画出阶跃响应图。
三、实验过程1.编写m文件,使用命令sys=tf(num,den),建立二阶系统的传递函数模型M文件如下:clear;clc;num=[1];den=[1 2 1];sys=tf(num,den)运行结果:Transfer function:1-------------s^2 + 2 s + 12.编写m文件,使用命令impulse(sys),画出二阶系统在不同阻尼比下的脉冲响应曲线簇M文件如下:clear;clc;k=1;xi=[0.1 0.4 0.8 1 5 8];wn=1;for i=1:length(xi);sys=tf([k*wn^2],[1 2*xi(i)*wn wn^2]);impulse(sys);hold on;endhold offgrid运行结果:3.编写m文件,使用命令step(sys),画出二阶系统在不同阻尼比下的阶跃响应曲线簇M文件如下:clear;clc;k=1;xi=[0.1 0.4 0.8 1 5 8];wn=1;for i=1:length(xi);sys=tf([k*wn^2],[1 2*xi(i)*wn wn^2]);step(sys);hold on;endhold offgrid运行结果:4.根据阶跃响应曲线,记录不同阻尼比下的时域性能指标,列表写出实验报告,并分析阻尼比和无阻尼自然频率对于性能的影响利用时域响应特性函数function [tr,tp,mp,ts,td]=texing(sys,xi,m,n)求得系统在不同阻尼比xi下阶跃响应的时域特性指标(texing函数见附录)。
峰值时间tp/s,最大超调量mp,上升时间tr/s,调整时间ts/s,延迟时间td/sM文件如下:clear;clc;k=1;xi=[0.1 0.4 0.8 1 5 8];wn=1;for i=1:length(xi);sys=tf([k*wn^2],[1 2*xi(i)*wn wn^2]);step(sys);hold on;[tr(i),tp(i),mp(i),ts(i),td(i)]=texing(sys,xi(i),0.02,1);endhold offgridxi,tr,tp,mp,ts,td运行结果:表一不同阻尼比下的时域性能指标角频率wn下阶跃响应的时域特性指标(xi=0.5)M文件如下:clear;clc;k=1;wn=1:5;xi=0.5;for i=1:length(wn);sys=tf([k*wn(i)^2],[1 2*xi*wn(i) wn(i)^2]);step(sys);hold on;[tr(i),tp(i),mp(i),ts(i),td(i)]=texing(sys,xi,0.02,1);endhold offgridxi,tr,tp,mp,ts,td运行结果:表二不同无阻尼自振角频率wn下阶跃响应的时域特性指标(xi=0.5)5.利用SIMULINK建立方框图仿真模型,进行阶跃响应实验,学会使用workspace的数组变量传递,使用命令plot(X,Y)画出阶跃响应图。
幅值为1的阶跃输入下二阶系统21s2s1++的仿真模型方框图如下:运行结果:Scope输出阶跃响应曲线:plot(tout,yout);四、实验结果与性能分析稳定性分析:由表一可以看出最大超调量mp随着阻尼比的增加而减小,系统趋于稳定。
所以系统的阻尼比越大稳定性也越好。
由表二可以看出无阻自然振荡角频率wn的值并不会影响系统的稳定性。
快速性分析:随着阻尼比xi的增大,上升时间tr,峰值时间tp和延迟时间td也随之增大。
系统的快速性下降。
wn越大,上升时间tr,峰值时间tp,调整时间ts和延迟时间td都减少,快速性越好。
在设计二阶系统时,一般取作为0.707为最佳阻尼比。
这是因为此时ts不仅小,而且mp也并不大。
综上讨论,可以看出,欲使二阶系统具有满意的动态性能指标,必须选择合适的阻尼比和无阻尼自然振荡频率。
wn提高,可以提高二阶系统的响应速度。
xi增大,可以提高系统的平稳性,即降低超调量mp,但会增大上升时间tr和峰值时间rp。
系统的响应速度与平稳性之间往往是存在矛盾的。
因此,既要提高系统的平稳性,又要系统具有一定的响应速度,那就只有选择合适的阻尼比和无阻尼自然振荡频率才能实现。
往往采用的是折衷处理方法。
实验二:比较二阶系统在不同阻尼比下的频率特性一、实验目的1.熟悉MA TLAB软件环境,学会编写matlab文件(***.m)和SIMULINK建模,进行频率响应与频率特性分析。
二、实验要求1.编写m文件,使用命令sys=tf(num,den),建立二阶系统的传递函数模型;2.编写m文件,使用命令bode(sys),画出二阶系统在不同阻尼比下的BODE频率曲线簇;3.编写m文件,使用命令nyquist(sys),画出二阶系统在不同阻尼比下的NYQUIST曲线簇;4.编写m文件,使用[Re,Im,Pa]=bode(sys,w)计算频率特性函数,并用plot(X,Y)画出某个二阶系统的实频、虚频、幅频、相频特性4分图;5.根据频率特性曲线,记录不同阻尼比下的频率性能指标,列表写出实验报告,并分析阻尼比和无阻尼自然频率对于性能的影响;6.利用SIMULINK建立方框图仿真模型,进行频率响应实验,学会workspace的数组变量传递,使用命令plot(X,Y)画出频率响应图。
三、实验过程四、实验结果与性能分析1.编写m文件,使用命令sys=tf(num,den),建立二阶系统的传递函数模型2.编写m文件,使用命令bode(sys),画出二阶系统在不同阻尼比下的BODE频率曲线簇M文件如下:clear;clc;k=10;xi=[0.2,0.7,1,2,7];wn=1;for i=1:5;sys1=tf([k*wn^2],[1 2*xi(i)*wn wn^2]);bode(sys1);hold on;endgrid运行结果:3.编写m文件,使用命令nyquist(sys),画出二阶系统在不同阻尼比下的NYQUIST曲线簇M文件如下:clear;clc;k=10;xi=[0.2,0.7,1,2,7];wn=1;for i=1:5;sys1=tf([k*wn^2],[1 2*xi(i)*wn wn^2]);nyquist(sys1);hold on;endgrid运行结果:4.编写m文件,使用[Re,Im,Pa]=bode(sys,w)计算频率特性函数,并用plot(X,Y)画出某个二阶系统的实频、虚频、幅频、相频特性4分图M文件如下:clear;clc;k=10;xi=[0.2,0.7,1,2,7];wn=1;for i=1:5;sys1=tf([k*wn^2],[1 2*xi(i)*wn wn^2]);[mag,phase,w]=bode(sys1);%求系统的幅频特性hold allsubplot(2,2,1);semilogx(w,20*log10(mag(:)));gridtitle('A-\omega');ylabel('magnitude(dB)');xlabel('\omega(rad/sec)');%求系统的相频特性hold allsubplot(2,2,2);semilogx(w,phase(:))gridtitle('P-\omega');ylabel('phase(deg)');xlabel('\omega(rad/sec)');%求系统的虚部特性hold allsubplot(2,2,3);semilogx(w,20*log10(mag(:)).*sin(phase(:)*pi/180)) gridtitle('V-\omega');ylabel('V(w)');xlabel('\omega(rad/sec)');%求系统的实部特性hold allsubplot(2,2,4);semilogx(w,20*log10(mag(:)).*cos(phase(:)*pi/180)) gridtitle('U-\omega');ylabel('U(w)');xlabel('\omega(rad/sec)');end运行结果:5.根据频率特性曲线,记录不同阻尼比下的频率性能指标,列表写出实验报告,并分析阻尼比和无阻尼自然频率对于性能的影响M文件如下:clear;clc;k=10;xi=[0.2,0.7,1,2,7];wn=1;for i=1:5;sys=tf([k*wn^2],[1 2*xi(i)*wn wn^2]);[gm(i),pm(i),wcg(i),wcp(i)]=margin(sys);endgm,pm,wcg,wcp%幅值裕量gm,相位裕量pm,相位穿越频率wcg,幅值穿越频率wcp运行结果:根据频率特性曲线,记录不同无阻尼自振角频率wn下的频率性能指标(xi=0.7)M文件如下:clear;clc;k=10;wn=1:5;xi=0.7;for i=1:length(wn);sys=tf([k*wn(i)^2],[1 2*xi*wn(i) wn(i)^2]);[gm(i),pm(i),wcg(i),wcp(i)]=margin(sys);endgm,pm,wcg,wcp%幅值裕量gm,相位裕量pm,相位穿越频率wcg,幅值穿越频率wcp运行结果:与实验结果可以看出,阻尼比xi增加二阶系统的相位裕度pm也随之增大,系统的稳定性提高,但系统的快速性却会降低。
