结构力学(龙驭球)第4章 影响线
龙驭球《结构力学Ⅰ》(第3版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)

目 录第一部分 名校考研真题第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第二部分 课后习题第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第三部分 章节题库第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第四部分 模拟试题龙驭球《结构力学Ⅰ》(第3版)配套模拟试题及详解第一部分 名校考研真题第1章 绪 论本章不是考研复习重点,暂未编选名校考研真题,若有最新真题会在下一版中及时更新。
第2章 结构的几何构造分析一、判断题图2-1所示体系的几何组成为几何不变体系,无多余约束。
( )[厦门大学2011研]图2-1二、选择题1.图2-2所示平面体系的几何组成是( )。
[浙江大学2010研]A .几何不变,无多余约束 B .几何不变,有多余约束C .几何常变D.几何瞬变图2-2图2-3错【答案】如图2-1(b ),分别视ABD 和基础为刚片Ⅰ和Ⅱ,两刚片通过链杆AC 、BE 和D 处的支座链杆相连,三根链杆相交于一点O ,故该体系为几何瞬变体系。
【解析】A【答案】如图2-3所示,把大地看成刚片3,刚片1和2形成瞬铰(1,2),刚片1和3形成瞬铰(1,3),刚片2和3形成无穷远处瞬铰(2,3),三个铰不共线,因此是无多余约束的几何不变体系。
【解析】2.图2-4(a )所示体系的几何组成是( )。
[武汉大学2012研、郑州大学2010研、华南理工大学2007研、河海大学2007研]A .无多余约束的几何不变体系B .几何可变体系C .有多余约束的几何不变体系D.瞬变体系图2-4三、填空题1.图2-5所示体系是几何________变体系,有________个多余约束。
[重庆大学2006研]图2-52.如图2-6(a )所示体系的几何组成为________体系。
[南京理工大学2011研]图2-6A【答案】鉴于刚片与构件可以等效互换,所以可将图2-4(a )所示体系替换为图2-4(b )所示体系,然后通过依次去除C 支座链杆与CE 杆、D 支座链杆与DE 杆所组成的二元体,以及二元体A-E-B 后,可知原体系为无多余约束的几何不变体系。
结构力学第四章 影响线

2、影响线的作用
(1) 求得某量值的最大值;
(2) 确定该量值的最不利荷载位臵。
15
3、绘制影响线的规定 (1) 反力向上为正;
(2) 弯矩以梁的下侧受拉为正;
(3) 剪力以使截面所在段顺时针转动为正。
(4) 正值画在基线 ( 梁轴线) 上侧,负值画在下侧。
16
§4-2 静力法作影响线
作影响线的方法有两种:
影响系数 FRA的大小。 y 若梁上
作用有固定 1
y1
y2
FRA影响线
荷载,则根
据叠加原理, A支座的反力 FRA为: A
x
FP1
FP2
B
FRA FP1 y1 FP 2 y2
13
二、 影响线定义
当单位集中移动荷载FP=1在结构上移动时,表 示结构指定截面的某量值 Z 变化规律的曲线,称为
该量值Z的影响线。
组竖向集中力(可包括均布荷载), 各集中力的大
7
小、方向固定,相互间的位臵也固定,作为整体在 结构上移动。
FP1 FP2 FP3 FP4
a1 a2
q a4
a3
b
在移动载荷作用下,结构任意截面的内力( M 、 FQ 、 FN)和位移(△、θ)及支座反力均随移动荷 载在结构上的位臵变化而变化。
8
二、问题的提出 结构在移动荷载作用下,主要讨论下述问题: 1、对于给定截面C,其位移或内力(例如Mc) 当给定的移动荷载在什么位臵时得到最大值? 即:(1) 结构的位移、反力和内力最大值是多少? (2) 最大值发生在哪个截面上? (3) 荷载 ( 轮压 ) 移动到何位臵时上述情况发生? 该问题是求移动荷载的最不利位臵问题。
MC
b
龙驭球《结构力学Ⅰ》(配套题库【课后习题】(影响线)

第4章影响线4-1 试用静力法作图中:(a)F yA、M A、M C及F QC的影响线。
(b)斜梁F yA、M C、F QC、F NC的影响线。
图4-1解:(a)如图4-1(a)所示,求F yA、M A、M C及F QC的影响线。
相关说明:A点为坐标原点,单位荷载距离A点为x;F yA向上为正,M A、M C使梁下侧受拉为正,F QC以绕微段隔离体顺时针转动为正。
①F yA的影响线左端为固端约束,F yA承担F P的作用,所以影响线与x无关,作影响线如图4-2(a)所示。
②M A的影响线,与x为线性关系,则作影响线如图4-2(b)所示。
③M C的影响线当荷载作用在C左边时,由固定端承担弯矩,C不受弯矩作用,为0;当荷载作用在C右边时,,则作影响线如图4-2(c)所示。
④F QC的影响线当荷载作用在C左边时,由固定端承担剪力,C点不受剪力作用;当荷载作用在C右边时,,则作影响线如图4-2(d)所示。
图4-2(b)如图4-1(b)所示,求斜梁F yA、M C、F QC及F NC的影响线。
相关说明:A点为坐标原点,单位荷载距离A点水平距离为x;F yA向上为正,M C使梁下侧受拉为正,F QC以绕微段隔离体顺时针转动为正,F NC以受拉为正。
图4-3①F yA的影响线对右端取矩,,解得;作影响线如图4-3(a)所示。
②M C的影响线与简支梁相似,荷载作用在C左边时考虑C右边的结构,计算C点弯矩;当荷载作用在C右边时考虑C左边的结构,计算C点弯矩;作影响线如图4-3(b)所示。
③F QC的影响线当荷载作用在C左边时,取右边计算:;当荷载作用在C右边时,取左边计算得;作影响线如图4-3(c)所示。
④F NC的影响线当荷载作用在C左边时,;当荷载作用在C右边时,;作影响线如图4-3(d)所示。
4-2 试用静力法作图4-4中F RA、F QB、M E、F QE、F RC、F RD、M F、F QF的影响线。
附属部分(AB)各量的影响线与简支梁相同,且在基本部分(BD)无竖距;基本部分(BD)各量的影响线在BD段与伸臂梁BD相同,在AB段为一直线。
《结构力学》课程规范
章
第3章静定结构受力分析
教学目的
和要求
能运用截面法求任意界面的内力,并用叠加法及荷载与内力的关系作各种结构的内力图
重点和难点
重点:截面法求任意界面的内力,用叠加法及荷载与内力的关系作各种结构的内力图
难点:熟练的运用截面法、叠加法作各种结构的内力图
“三基”分析
基本知识:截面法、叠加法
基本理论:截面法求任意界面的内力,用叠加法及荷载与内力的关系作各种结构的内力图
二、课程知识、能力体系
《结构力学》课程知识(能力)体系
序号
知识单元描述
知识点
对应能力
学时
要求
1
第一章
绪论
结构力学的学科内容和教学要求、结构体系的简化、杆件的分类、荷载的分类、学习方法
掌握学习结构力学的方法
2
掌握
2
第二章
结构的几何构造分析
几何构造分析的几个概念.平面几何不变体系的组成规律.平面杆件体系计算的自由度.
本章思考题
3-1,3-2,3-3(b),3-5,3-8(a),3-9(d)
主要
参考资料
结构力学参考书或网络资源;
教材:龙驭球,包世华.结构力学教程(第三版).高等教育出版2006
备注
章
第4章影响线
教学目的
和要求
移动荷载概念,影响线概念,用静力法作简支梁影响线,机动法作影响线,影响线的应用,简支梁包络图和绝对最大弯矩。
4
掌握
9
第九章
矩阵位移法
矩阵位移法的基本步骤.单元刚度矩阵.整体刚度矩阵.等效节点荷载杆端力.
掌握矩阵位移法的解题思路和步骤.理解单元刚度矩阵、总刚度矩阵中元素的物理意义。重点掌握利用单元定位向量将单元刚度矩阵 和单元等效节点荷载向量集成刚度矩阵和结构荷载向量的方法.
结构力学课件 第四章 影响线

ab F l
MC的变化规律
• 分析:
A
a
D
B b
1. 该图线的含义:每一纵坐标值都是MC的值;不同点的纵坐标值代表FP移
动到不同位置时MC的大小。(举例说明) 2. 每一点的MC与FP均成正比,其比例系数称为MC的影响系数,用 M C 表
示,即 M C
MC 。 若将该影响系数的变化规律用图线来表示,则该图线 F
d 3
5d 12
MD影响线
1 6
5d 6
FQD影响线
2 3
5 6
1 3
x
FP=1
F
d d
1 3 2 3 1 3
d
d
d
FQF影响线
1 2
1 3
1 3
1 2
1 6
1 3
FQF左影响线
2 3
5 6
1 3
FQF右影响线
x
FP=1
2d 3
E
d d d d d
1
FQE影响线
2d 3
ME影响线
§4-4 静力法作桁架的影响线
就称为MC的影响线。
二、 影响线
F P=1
A
a
C
ab ab F ll
b
B
M 的影响线 M 的变化规律 C C • 定义:在单位移动荷载FP=1作用下,表示结构上某量值Z的变化规律的图线, 称为Z的影响线。 • 说明:1. Z可以是反力、弯矩、剪力、轴力 2. 求Z的影响线,就是求在单位移动荷载FP=1作用下Z的大小。 3. 在Z的影响线中,横坐标表示的是FP=1的作用位置; 纵坐标表示 的是影响系数 Z 的大小。 (比较:弯矩图、弯矩影响线) • 计算方法:1.静力法 2.机动法(虚功原理)
朱明zhubob结构力学4-5_1影响线的应用

荷载稍向右移,∑FRitanαi ≥0 荷载稍向左移,∑FRitanαi ≤0
3
x FRi tani 0 i 1
结论:
如果S为极值(极大或极小),则荷载稍向左或稍向右 移动时, ∑FRi tanαi 必须变号。
因此使S 成为极大值的 临界位置判别条件可分 两种情况:
S值为:
y qdx
设AB段影响线的面积为A :
则在AB段均布荷载作用下的 S值为:
B
B
S A y qdx qA ydx q A
q
A
B
aC
x dx
b
B
l
b
l
y
a dA
l FQC 影响线
n
S FPi yi i 1
S qA
例4-9 利用影响线求图示伸
臂梁截面C的剪力。
即:
3
x FRi tani 0
i 1
荷载:
S影响线:
y2 y2 3 0
2 0
y3
因此使S 成为极大值的
y1
临界位置判别条件可分 1 0
y1
y3
两种情况:
x
x
x
当Δx>0时(荷载稍向右移),∑FRitanαi ≤0
当Δx<0时(荷载稍向左移),∑FRitanαi ≥0
1 3 3 28
26kN
n
1 FQC
S FPi yi i 1
S qA
4-5-2 确定最不利荷载位置
使某量S达到最大值时,荷载的位置。 ⑴ 单个移动集中荷载:
⑵ 移动的均布荷载:
FP
《结构力学》_龙驭球_第4章_影响线(2)
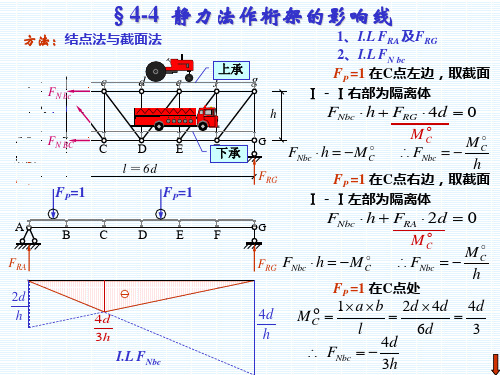
§4-4 静力法作桁架的影响线
方法:结点法与截面法
a
FN bc
bⅠ c
d
e
f
上承
g
h
FP=1
D l = 6d E F 下承
G
1、I.L FRA 及FRG 2、I.L FN bc FP =1 在C点左边,取截面 Ⅰ-Ⅰ右部为隔离体
0 Fy 0 FNcC FQBC
1
上承
2 3
1 2
I.L FN cC
下承
上承
1
I.L FN dD
§4-5 机动法作影响线
理论基础:虚位移原理。 特 点:把作影响线的静力问题化为作位移图的几何问题。
点:不经计算可以得到影响线的形状。 FP=1 x 例:求图示简支梁 支座 B 反力影响线。 解:去掉支杆 B 并代以反力Z (FRB )。 A
1 4
FQB左
A
E
C
3 4
H 1
B
F
D
G
3 4
练习:作I.L FRC , M1 , FQ2 , FQA
A 2m B 2m
FP=1
D E 2m 2m 1m F 4m G 2m H
1 1
C 2m
1m
FRC
C D E F G H
A
B
FRC
1
1.25
I .L FRC
1
A B D C E F G H
M1
1
I .L M 1
如果桁架改为上承,即FP =1 沿上弦移动,有些杆的影响 线局部与下承时不同。
结构力学-第4章影响线

影响线和包络图在该桥设计中的应用
详细阐述影响线和包络图在该桥设计中的应用过程,包括影响线和包络图的绘制、最不利位置的确定、最大内力的计 算等。
设计结果分析与评价
对该桥的设计结果进行分析和评价,包括结构安全性、经济性等方面的评估。同时,可以与其他设计方 案进行对比分析,以进一步验证影响线和包络图在工程设计中的有效性和优越性。
通过绘制建筑结构的包络图,可以找到结构在地震作用下的最大变形和位移,为结构的刚 度设计和稳定性分析提供依据。
影响线和包络图在建筑结构优化设计中的作用
利用影响线和包络图,可以对建筑结构进行优化设计,如调整结构布置、改变构件截面等 ,以提高结构的抗震性能和经济效益。
工程案例分析:某大桥设计过程剖析
工程背景介绍
结构优化设计
根据影响线的形状和分布,对结 构进行优化设计,以改善结构的 受力性能。
80%
工程实例分析
结合具体工程实例,利用影响线 理论进行结构分析和设计,验证 理论的正确性和实用性。
03
超静定结构影响线绘制与应用
超静定梁影响线绘制实例
实例一
实例三
一次超静定梁的影响线绘制。通过选取 基本体系和基本未知量,利用力法方程 求解多余未知力,并绘制影响线。
影响线用于确定桥梁结构在移动荷载作用下的最不利位置
通过绘制桥梁结构的影响线,可以确定移动荷载在桥梁上的最不利位置,从而进行结构分析和设 计。
包络图用于确定桥梁结构的最大内力
通过绘制桥梁结构的包络图,可以找到桥梁在移动荷载作用下的最大内力,为桥梁的强度设计和 稳定性分析提供依据。
影响线和包络图在桥梁优化设计中的作用
影响线在结构优化中的应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 MC 2d FRA h h
FP=1 在 C 左侧作用时,取截 面I-I右侧部分为研究对象: M C 0 , FRG 4d FNbc h 0
FNbc
0 MC 4d FRG h h
结构力学
§4-4 静力法作桁架轴力影响线
A B
2d h
2、上弦杆轴力FNbc的影响线
RB
单位荷载 P=1
1
B
A
单位位移 1
x
1
RB ( x) -y( x)
RB的影响线 和变形图相同
RB的影响线
结构力学
§4-5 机动法作静定内力影响线
影响线
机动法作影响线的步骤:
去除约束结构的变形图
撤除与待求影响线量值S相应的约束使静定变成具有一个自由度的机构.
y
A x
P=1
B x
M
B
0, RAl 1 (l x) 0
lx , (0 x l ) l
RA
RA
l
y
1.0
x
RA的影响线
结构力学
§4-2 静力法作简支梁内力影响线
简支梁的影响线
x A RA a l P=1
0 x a
MC
C b B x RB B
a x l
A
C
结构力学
§4-3 结点承载方式下梁的内力影响线
x
A P=1 B
C
d/2
D
d/2
E
l=4d
F
1
2.5 4
1 2
A
C
1 4 1.5 4
E
B
F QD
1
结构力学
§4-3 结点承载方式下梁的内力影响线
例:求图示结构FYA、FQE的影响线。
F
2m 1m
E
1m
C
B
1m 1m 1m
A
1m
1m
D
1m
1.33
FYA影响线
x A C D P=1
2d x RC d
A C
P=1 B
E
F
l=4d
E
RE xd d
B
C
D E
5 yC d 8
15 d 16
yE
3 d 4
MD影响线
A
C
E
B
M D yc RC yE RE yC (
2d x xd ) yE ( ) d d
结构力学
优点:(1)不需要经过计算就能很快地绘出影响线的轮 廓;(2)用静力法作出的影响线也可用机动法来校核。
结构力学
§4-5 机动法作静定内力影响线
下面以简支梁支座反力影响线为例进行说明求解步骤。 x
A
P=1
B
RB +P ( y x) 0
RB - y ( x) P
RA
虚设位移
y ( x)
d
e
f
g
h
D II FP=1 E F G
A
B
C
5、竖杆轴力FNcC的影响线
0 FNcC FQCD
作截面II-II,利用竖直方向投影方程,求FNcC。 1 3 A 1
1 2
1
B
FNcC的影响线
结构力学
§4-4 静力法作桁架轴力影响线
FP=1 a ( a ) b ( a ) c ( a ) d e f g
x
FQ D 0 M D 0
l l2 d x l l2
F
E
M D (1 x1 ) x1 x (l l2 d )
FQ D 1
D P=1 E d
1 D E
MD
FQD
x1
D E
F QD影响线
静定结构内力的 影响线由一段或 多段直线组成.
§4-3 结点承载方式下梁的内力影响线
x A C P=1 B
D
E
F
l=4d
5 yC d 8
A C
15 d 16
yE
MD影响线
3 d 4
E
B
M D yc RC yE RE yC (
2d x xd ) yE ( ) d d
d x 2d
结论: (1)在结点荷载作用下,结构任何影响线在相邻两结点之间为一直线; (2)先做直接荷载作用下的影响线,用直线连接相邻两结点的竖距, 就得到结点荷载作用下的影响线。
MC
FQC
FQC
b
RB
RA
a
FQC RB
b l
FQC RA
a l
x l
1 B A
A
B
RB的影响线
1
A
1 x l
FQC的影响线
B
RA的影响线
结构力学
§4-2 静力法作简支梁内力影响线
简支梁的影响线
x A RA a l P=1
0 x a
MC
C b B x RB b B
a x l
A
1
1
FQE影响线
1
结构力学
§4-3 结点承载方式下梁的内力影响线
结构力学
§4-3 结点承载方式下梁的内力影响线
结构力学
§4-3 结点承载方式下梁的内力影响线
结构力学
§4-4 静力法作桁架轴力影响线
桁架轴力的影响线在各承载弦的相邻结点间为直线。
(a)
E
F
G
A
C D
B
结构力学
§4-4 静力法作桁架轴力影响线
0 MC 2d FRA h h
0 MC 4d FRG h h
结构力学
§4-4 静力法作桁架轴力影响线
a ( a ) b II ( a ) c ( a )
d
e
f
g
h
D II FP=1 E F G
A
B
C
3、下弦杆轴力FNCD的影响线 作截面II-II,以c为矩心,求FNCD。
h D
FP=1 E F G
A
B
C
6、竖杆轴力FNdD的影响线 荷载作用在下弦时:
FNdD 0
下承荷载
当FP=1在上弦d点时,FNdD=1 当FP=1在其他点时,FNdD=0
A 上承荷载
1
B
FNdD的影响线
结构力学
§4-5 机动法作静定内力影响线
刚体体系的虚功原理 处于受力平衡状态的刚体,当发生符合约束条 件的无限小刚体体系虚位移时,则外力在位移 上所作的虚功总和恒等于零。 机动法是以虚功原理为基础,把作静定内力或支座反 力影响线的静力问题转化为作位移图的几何问题。
RA
b l
RB
a l
)
b A C
B
A
C
B
ab l
MC的影响线
弯矩图
荷载
横坐标x 纵坐标y
移动荷载 荷载位置 截面 C的弯矩值
固定荷载 截面位置 各截面的弯矩值
结构力学
§4-2 静力法作简支梁内力影响线
伸臂梁的影响线 (a) RA的 影响线
F
A
l1
x
P=1
l
B
l2
E
M
B
0, RA
and
x A C
P=1
A
C D E B
P=1 D E l=4d F B
5 yC d 8
15 d 16
3 yE d 4
A
C
E
B
MD的影响线
结构力学
§4-3 结点承载方式下梁的内力影响线
x
A
C
D
E l=4d
F
B
5 d 2
B
0 xd
MD
5 M D RB d 2
RB
5 yC d 8
15 d 16
结构力学
§4-1 移动荷载和影响线的概念
在移动荷载作用下, 结构的内力和支座反力随荷载位置 的变化而变化 .
如何设计?
必须根据最大内力进行设计
确定最不利荷载位置
吊车梁
确定最大内力
结构力学
§4-1 移动荷载和影响线的概念
单位移动荷载作用下,结构内力或支座反力随荷载位置变化规 律的图形称为该量值的影响线
M C RB b
l1 x a
l1 l
b l
B
E
E
M C RA a
a x l l2
b
F A a
C B a
l
ab l
l2 l
l1 F l
b E
a l2 l
A
C B
MC
结构力学
§4-2 静力法作简支梁内力影响线
伸臂梁的影响线
l1 x l l2 d
第四章
影响线
Influence Lines
结构力学
第四章
1、移动荷载和影响线的概念
2、静力法作简支梁内力影响线 3、结点荷载作用下梁的内力影响线
4、静力法作桁架轴力影响线 5、机动法作静定内力影响线
6、影响线的应用
结构力学
§4-1 移动荷载和影响线的概 念
结构承受位置变化的荷载 .
移动荷载
Variable loads
FNCD
M c0 h
B
2d h
A
4d 3h
4d h
FNCD的影响线
结构力学
§4-4 静力法作桁架轴力影响线
I a ( a ) b
( a )
