计算方法复习题及答案
计算方法复习题

《计算方法》复习题一 选 择(每题3分,合计42分)1. x* = 1.732050808,取x =1。
7320,则x 具有 位有效数字。
A 、3 B 、4 C 、5 D 、62. 取73.13≈(三位有效数字),则≤-73.13 。
A 、30.510-⨯B 、20.510-⨯C 、10.510-⨯D 、0。
5 3. 下面 不是数值计算应注意的问题。
A 、注意简化计算步骤,减少运算次数B 、要避免相近两数相减C 、要防止大数吃掉小数D 、要尽量消灭误差 4. 对任意初始向量)0(x 及常向量g ,迭代过程g x B xk k+=+)()1(收敛的充分必要条件是 。
A 、11<B B 、1<∞BC 、1)(<B ρD 、21B <5. 用列主元消去法解线性方程组,消元的第k 步,选列主元)1(-k rka ,使得)1(-k rk a = 。
A 、 )1(1max -≤≤k ikni a B 、 )1(max -≤≤k ikni k a C 、 )1(max -≤≤k kjnj k a D 、 )1(1max -≤≤k kjnj a6. 设ƒ(x)= 5x 3-3x 2+x +6,取x 1=0,x 2=0。
3,x 3=0。
6,x 4=0.8,在这些点上关于ƒ(x )的插值多项式为3()P x ,则ƒ(0.9)—3(0.9)P =__________。
A 、0 B 、0.001 C 、0。
002 D 、0.0037. 用简单迭代法求方程f (x )=0的实根,把方程f (x )=0转化为x =ϕ(x ),则f (x )=0的根是: .A 、y =x 与y =ϕ(x )的交点B 、 y =x 与y =ϕ(x )交点的横坐标C 、y =x 与x 轴的交点的横坐标D 、 y =ϕ(x )与x 轴交点的横坐标8. 已知x 0=2,f (x 0)=46,x 1=4,f (x 1)=88,则一阶差商f [x 0, x 1]为 。
科学和工程计算复习题与答案

科学和工程计算基础复习题一、 填空题:1. :2. 计算机计费的主要依据有两项:一是使用要由算数运算的次数决定;二是占据存储器的空间,3. 用计算机进行数值计算时,4. ,则称该算法是5. 函数求值问题()x f y =的条件数定义为:)()())(()(x f x f x x f cond x C '==6. 单调减且有 下界 的数列一定存在极限; 单调增且有 上界 的数列一定存在极限. 7. 方程实根的存在唯一性定理:设],[)(b a C x f ∈且0)()(<b f a f ,则至少存在一点()b a ,∈ξ使()0=ξf .当()x f '在()b a ,,方程在[]b a ,内有唯一的实根.8. 函数()y x f ,在有界闭区域D 上对y 满足Lipschitz 条件,是指对于D 上的任意一对点()1,y x 和()2,y x 成立不等式:2121),(),(y y L y x f y x f -≤-.其中常数L 只依赖于区域D .9. 设n i R A i n n ,,2,1,, =∈⨯λ为其特征值,则称i ni A λρ≤≤=1max )(为矩阵A 的谱半径.10. 设1-A 存在,则称数A AA cond 1)(-=为矩阵A 的条件数,其中⋅是矩阵的算子范数. 11. 方程组f xB x +=,对于任意的初始向量()0x 和右端项f ,迭代法()()f x B x k k+=+1收敛的充分必要条件是选代矩阵B 的 谱半径1)(<B ρ. 12. 设被插函数()x f 在闭区间[]b a ,上n 阶导数连续,()()x fn 1+在开区间()b a ,上存在.若{}ni i x 0=为[]b a ,上的1+n 个互异插值节点,并记()()∏=+-=ni in x x x 01ω,则插值多项式()()()()()∑=++'-=nk k n k n k n x x x x x f x L 011ωω的余项为)()!1()()()()(1)1(x n f x L x f x R n x n n n +++=-=ωξ,其中),()(b a x x ∈=ξξ.13. 若函数组(){}[]b a C x n k k ,0⊂=ϕ满足⎩⎨⎧=≠≠=l k lk l k ,0,0),(ϕϕ k,l =0,1,2,…,n ,则称(){}nk k x 0=ϕ为正交函数序列. 14. 复化梯形求积公式⎰∑⎥⎦⎤⎢⎣⎡+++=≈-=ban k n b f kh a f a f h f T dx x f 11)()(2)(2)()(,其余项为),(),(12)(2b a f h a b R nT∈''--=ηη15. 复化Simpson 求积公式⎰∑∑⎥⎦⎤⎢⎣⎡++++++=≈-=-=ban k n k n b f kh a f h k a f a f h f S dx x f 1011)()2(2))12((4)(3)()(,其余项为),(),(180)()4(4b a f h a b R nS∈--=ηη16. 选互异节点n x x x ,,,10 为Gauss 点,则Gauss 型求积公式的代数精度为2n+1 .17. 如果给定方法的局部截断误差是()11++=p n h O T ,其中1≥p 为整数,则称该方法是 P 阶的或具有P 阶精度 .18. 微分方程的刚性现象是指快瞬态解严重影响 数值解的稳定性和精度 ,给数值计算造成很大的实质性困难的现象. 19. 迭代序列{}[]b a x k k ,0⊂∞=终止准则通常采用11k k kx x x ε--<+,其中的0>ε为 相对误差20.二、 选择题1. 下述哪个条件不是能使高斯消去法顺利实现求解线性代数方程组(),ijn nAx b A a ⨯==的充分条件? ( D )A. 矩阵A 的各阶顺序主子式均不为零;B. A 对称正定;C. A 严格对角占优;D. A 的行列式不为零.2. 高斯消去法的计算量是以下述哪个数量级的渐近速度增长的? ( B ) A.313n ; B. 323n ; C. 314n ; D. 334n .3. 对于任意的初始向是()0x和右端项f ,求解线性代数方程组的迭代法()()1k kx Bx f +=+收敛的充分必要条件是( A ). A.()1B ρ<; B. 1B <; C. ()det 0B ≠; D. B 严格对角占优.4. 下述哪个条件不是能使求解线性代数方程组(),ijn nAx b A a ⨯==的Gauss-Seidel 迭代法收敛的充分条件? ( C )A. A 为严格对角占优阵;B. A 为不可约弱对角占优阵;C. A 的行列式不为零;D. A 为对称正定阵.5. 设()[]2,f x C a b =,并记()2m a x a xbM f x ≤≤''=,则函数()f x 的过点()()()(),,,a f a b f b 的线性插值余项()1R x ,[],x a b ∀∈满足( A ). A. ()()2218M R x b a ≤-; B. ()()2218M R x b a <-; C. ()()2216M R x b a ≤-; D. ()()2216M R x b a <-.6. 设()n x ϕ是在区间[],a b 上带权()x ρ的首项系数非零的n 次正交多项式()1n ≥,则()n x ϕ的n 个根( A ).A. 都是单实根;B. 都是正根;C. 有非负的根;D. 存在重根7. Legendre 多项式是( )的正交多项式.( B )A. 区间[]1,1-上带权()x ρ=B. 区间[]1,1-上带权()1x ρ=;C. 区间[],-∞∞上带权()2x x e ρ-=; D. 区间[]0,1上带权()1x ρ=8. 离散数据的曲线拟合的线性最小二乘法的Gram 矩阵与( D )无关?A. 基函数(){}n k k x ϕ=; B. 自变量序列{}0mi i x =;C. 权数{}0mi i w =; D. 离散点的函数值{}0mi i y =. 9. Simpson 求积公式的余项是( B ).A. ()()()3,,12h R f f a b ηη''=-∈;B. ()()()()54,,90h R f f a b ηη=-∈; C. ()()()()2,,12h b a R f f a b ηη-''=-∈; D. ()()()()()44,,90h b a R f f a b ηη-=-∈ 10. n 个互异节点的Gauss 型求积公式具有( D )次代数精确度.A. n ;B. 1n +;C. 21n +;D. 21n -.11. 一阶导数的数值计算公式中,中心差商公式的精度为( B ).A. ()O h ;B. ()2O h ;C. ()2o h ; D. ()32O h .12. 对于用插值法建立的数值求导公式,通常导数值的精确度比用插值公式求得的函数值的精度( B ).A. 高; B, 低; C. 相同; D. 不可比.13. 在常微分方程初值问题的数值解法中, 梯形公式是显式Euler 公式和隐式Euler 公式的( A ).A. 算术平均;B. 几何平均;C. 非等权平均;D. 和. 14. 当( B )时,求解(),0y y λλ'=<的显式Euler 方法是绝对稳定的. A. 11h λ-≤≤; B. 20h λ-≤≤; C. 01h λ≤≤; D. 22h λ-≤≤ 15. 求解(),0y y λλ'=<的经典R-K 公式的绝对稳定条件是( C ): A .20h λ-≤≤; B.()2112h h λλ++≤;C.()()()2341123!4!h h h h λλλλ++++≤; D.()()22121211212h h h h λλλλ++≤-+.16. 在非线性方程的数值解法中,只要()()***1,()x x x ϕϕ'≠=,那么不管原迭代法()()1,0,1,2,k k x x k ϕ+==是否收敛,由它构成的Steffensen 迭代法的局部收敛的阶是( D )阶的.A. 1;B. 0;C. 2<;D. 2≥.17. 在非线性方程的数值解法中,Newton 迭代法的局部收敛的阶是( D )阶的. A. 1; B. 0; C. 2<; D. 2≥.18. 在非线性方程的数值解法中,离散Newton 迭代法的局部收敛的阶是( C )阶的.A. 1;B.C.; D. 2. 19. 在求解非线性方程时,迭代终止准则通常采用( A ),其中的0ε>为给定的相对误差容限. A.11k k kx x x ε--<+; B.1k k kx x x ε--<; C. 1k k x x ε--<; D.111k k k x x x ε---<+.20. 在求解非线性方程组时,加进阻尼项的目的,是使线性方程组的( C ).A. 系数矩阵非奇异;B. 系数矩阵的行列式不等于零;C. 系数矩阵非奇异并良态;D. 系数矩阵可逆.三、 判断题1. 在用计算机求数学问题的数值解就是构造算法的构造问题.( × )2. 用计算机进行数值计算时,所有的函数都必须转化成算术运算;在作加减法时,应避免接近的两个数相减;在所乘除法时,计算结果的精度不会比原始数据的高.( √ ) 3. 用计算机作加减法时,交换律和结合律成立.( × ) 4. 单调减且有下界的数列一定存在极限。
计算方法复习题库

计算方法复习题库 一、填空题:1.设某数x *,它的保留三位有效数字的近似值的绝对误差是 。
2.设某数x *,它的精确到10-4的近似值应取小数点后 位。
3.设方程f (x )=x -4+2x=0,在区间[1,2]上满足 ,所以f (x )=0在区间[1,2]内有根。
建立迭代公式xx 2-4=,因为 ,此迭代公式发散。
4.设函数f (x )在区间[a ,b ]内有二阶连续导数,且f (a )f (b )<0,当 时,则用弦截法产生的解数列收敛到方程f (x )=0的根。
5.乘幂法是求实方阵 。
6.二阶阶差()=210,,x x x f7.已知3=n 时,科兹系数()8130=C ,()8331=C ,()8332=C ,则()=33C8.求方程()x f x =根的牛顿迭代格式是9.n 个求积节点插值型求积公式代数精确度至少为 次。
10.数值计算方法中需要考虑误差为 、 。
二、选择题1.用二分法求方程f (x )=0在区间[a ,b ]内的根x n ,已知误差限ε,确定二分的次数n 是使( )。
(A)b -a ≤ε (B)∣f (x )∣≤ε (C)∣x *-x n ∣≤ε (D)∣x *-x n ∣≤b -a2.( )的3位有效数字是0.236×102。
(A)235.54×10-1(B)235.418(C)2354.82×10-2(D)0.0023549×1033.设a *=2.718181828…,取a=2.718,则有( ),称a 有四位有效数字。
(A)(B)(C)(D)4.设某数x *,对其进行四舍五入的近似值是( ),则它有3位有效数字,绝对误差限是。
(A)0.315 (B)0.03150 (C)0.0315 (D)0.00315 5.以下近似值中,( )保留四位有效数字,相对误差限为。
(A)0.01234 (B)–12.34 (C)–2.20 (D)0.22006.牛顿切线法求解方程f (x )=0的近似根,若初始值x 0满足( ),则解的迭代数列一定收敛。
数值计算方法复习题

fuxiti例1证明方程1-x-sin x=0在区间[0,1]内有一个根,使用二分法求误差不超过0.5×10-4的根要迭代多少次?证明令f(x)=1-x-sin x,∵f(0)=1>0,f(1)=-sin1<0∴f(x)=1-x-sin x=0在[0,1]有根.又f'(x)=1-c os x>0(x∈[0.1]),故f(x)=0在区间[0,1]内有唯一实根.给定误差限ε=0.5×10-4,有只要取n=14.例4选择填空题1. 设函数f(x)在区间[a,b]上连续,若满足,则方程f(x)=0在区间[a,b]一定有实根.答案:f(a)f(b)<0解答:因为f(x)在区间[a,b]上连续,在两端点函数值异号,由连续函数的介值定理,必存在c,使得f(c)=0,故f(x)=0一定有根.2. 用简单迭代法求方程f(x)=0的实根,把方程(x)=0表成x=ϕ(x),则f(x)=0的根是( )(A)y=x与y=ϕ(x)的交点(B) y=x与y=ϕ(x)交点的横坐标(C) y=x与x轴的交点的横坐标(D) y=ϕ(x)与x轴交点的横坐标答案:(B)解答:把f(x)=0表成x=ϕ(x), 满足x=ϕ(x)的x是方程的解,它正是y=x与y=ϕ(x)的交点的横坐标.3.为求方程x3―x2―1=0在区间[1.3,1.6]内的一个根,把方程改写成下列形式,并建立相应的迭代公式,迭代公式不收敛的是( )(A)(B)(C)(D)答案:(A)解答:在(A)中故迭代发散.在(B)中,故迭代收敛.在(C)中,,故迭代收敛.在(D)中,类似证明,迭代收敛.例3填空选择题:1. 用高斯列主元消去法解线性方程组作第1次消元后的第2,3个方程分别为。
解答1. 选a21=2为主元,作行互换,第1个方程变为:2x1+2x2+3x3=3,消元得到是应填写的内容。
一、解答下列问题:1) 数值计算中,最基础的五个误差概念(术语)是 , , , , .2) 分别用 2.718281, 2.718282 作数e 的近似值 ,它们的有效位数分别有位, 位; 又取73.13≈ (三位有效数字),则≤-73.13 .3)为减少乘除法运算次数,应将算式32)1(7)1(51318---+-+=x x x y 改写成4)为减少舍入误差的影响,应将算式 9910- 改写成 5)递推公式 ⎪⎩⎪⎨⎧=-==-,2,1,110210n y y y n n如果取41.120≈=y 作计算,则计算到10y 时,误差有这个计算公式数值稳定不稳定 ?1) 绝对误差 , 相对误差 , 有效数字 , 截断误差 , 舍入误差 。
数学五年级上册整数乘法运算定律推广到小数解决问题复习题(含答案)
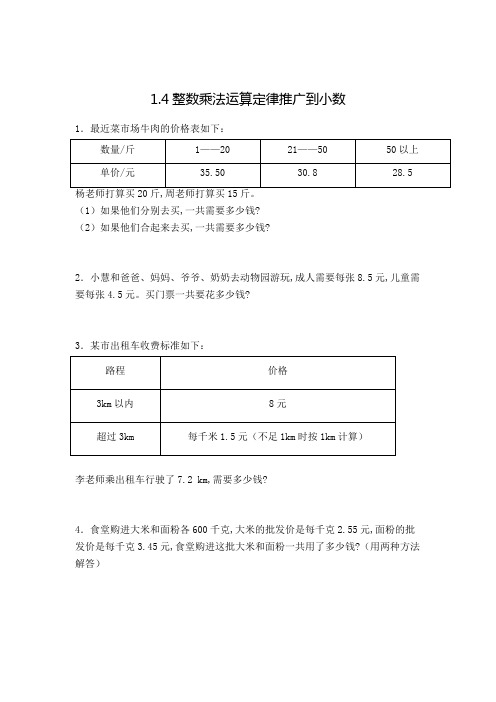
1.4整数乘法运算定律推广到小数1.最近菜市场牛肉的价格表如下:(1)如果他们分别去买,一共需要多少钱?(2)如果他们合起来去买,一共需要多少钱?2.小慧和爸爸、妈妈、爷爷、奶奶去动物园游玩,成人需要每张8.5元,儿童需要每张4.5元。
买门票一共要花多少钱?3.某市出租车收费标准如下:李老师乘出租车行驶了7.2 km,需要多少钱?4.食堂购进大米和面粉各600千克,大米的批发价是每千克2.55元,面粉的批发价是每千克3.45元,食堂购进这批大米和面粉一共用了多少钱?(用两种方法解答)5.邮局邮寄信函的收费标准如表:(1)亮寄给本埠报社编辑一封145g的信函,应付邮费多少钱?(2)刚给外埠的朋友寄一封232g的信函,应付邮费多少钱?6.A、B两辆车同时从甲、乙两地相向而行,A车每小时行65千米,B车每小时行73千米,3.5小时候后相遇,甲乙两地相距多少千米?7.五(1)班42名师生到郊外秋游合影留念。
拍摄一次6寸照片可附送5张照片,费用25. 5元,另外再加印每张2.5元。
每人一张照片,一共需要付多少钱?8.菜站运来1.2吨黄瓜,运来的土豆是黄瓜的1.5倍,运来土豆和黄瓜一共多少吨?9.某商店购进大米和小米各500千克,大米的批发价是每千克2.67元,小米的批发价是每千克3.33元,进这批米共需多少钱?(用两种方法计算)10.五(2)班36名师生照相合影,每人一张照片,一共需付多少钱?11.故事书74.5元一套,科技书85.5元一套。
两种书各买5套,一共需要多少元?12.青椒每千克6.5元,西红柿每千克5.5元,买2千克青椒和1.4千克西红柿共需多少元?13.自来水公司为鼓励节约用水,采取按月分段计费的方法收取水费,9吨以内每吨2.5元,超过9吨的部分,每吨3.8元。
小兵家十月份的用水量为13.5吨,应缴水费多少元?14.某市出租车的起步价为9元(3km以内),超过3km的部分每千米1.5元(不足1km的按1km计算)。
最新科学和工程计算复习题及答案资料

科学和工程计算基础复习题一、 填空题:1. :2. 计算机计费的主要依据有两项:一是使用要由算数运算的次数决定;二是占据存储器的空间,3. 用计算机进行数值计算时,4. ,则称该算法是5. 函数求值问题()x f y =的条件数定义为:)()())(()(x f x f x x f cond x C '==6. 单调减且有 下界 的数列一定存在极限; 单调增且有 上界 的数列一定存在极限. 7. 方程实根的存在唯一性定理:设],[)(b a C x f ∈且0)()(<b f a f ,则至少存在一点()b a ,∈ξ使()0=ξf .当()x f '在()b a ,,方程在[]b a ,内有唯一的实根.8. 函数()y x f ,在有界闭区域D 上对y 满足Lipschitz 条件,是指对于D 上的任意一对点()1,y x 和()2,y x 成立不等式:2121),(),(y y L y x f y x f -≤-.其中常数L 只依赖于区域D . 9. 设n i RA i nn ,,2,1,, =∈⨯λ为其特征值,则称i ni A λρ≤≤=1max )(为矩阵A 的谱半径.10. 设1-A 存在,则称数A AA cond 1)(-=为矩阵A 的条件数,其中⋅是矩阵的算子范数.11. 方程组f x B x +=,对于任意的初始向量()0x 和右端项f ,迭代法()()f x B xk k +=+1收敛的充分必要条件是选代矩阵B 的 谱半径1)(<B ρ. 12. 设被插函数()x f 在闭区间[]b a ,上n 阶导数连续,()()x fn 1+在开区间()b a ,上存在.若{}ni i x 0=为[]b a ,上的1+n 个互异插值节点,并记()()∏=+-=ni in x x x 01ω,则插值多项式()()()()()∑=++'-=nk k n k n k n x x x x x f x L 011ωω的余项为)()!1()()()()(1)1(x n f x L x f x R n x n n n +++=-=ωξ,其中),()(b a x x ∈=ξξ.13. 若函数组(){}[]b a C x n k k ,0⊂=ϕ满足⎩⎨⎧=≠≠=lk lk l k ,0,0),(ϕϕ k,l =0,1,2,…,n ,则称(){}nk k x 0=ϕ为正交函数序列. 14. 复化梯形求积公式⎰∑⎥⎦⎤⎢⎣⎡+++=≈-=ban k n b f kh a f a f h f T dx x f 11)()(2)(2)()(,其余项为),(),(12)(2b a f h a b R nT∈''--=ηη15. 复化Simpson 求积公式⎰∑∑⎥⎦⎤⎢⎣⎡++++++=≈-=-=ban k n k n b f kh a f h k a f a f h f S dx x f 1011)()2(2))12((4)(3)()(,其余项为),(),(180)()4(4b a f h a b R nS∈--=ηη16. 选互异节点n x x x ,,,10 为Gauss 点,则Gauss 型求积公式的代数精度为2n+1 .17. 如果给定方法的局部截断误差是()11++=p n h O T ,其中1≥p 为整数,则称该方法是P 阶的或具有P 阶精度 .18. 微分方程的刚性现象是指快瞬态解严重影响 数值解的稳定性和精度 ,给数值计算造成很大的实质性困难的现象. 19. 迭代序列{}[]b a x k k ,0⊂∞=终止准则通常采用11k k kx x x ε--<+,其中的0>ε为 相对误差20.二、 选择题1. 下述哪个条件不是能使高斯消去法顺利实现求解线性代数方程组(),ijn nAx b A a ⨯==的充分条件? ( D )A. 矩阵A 的各阶顺序主子式均不为零;B. A 对称正定;C. A 严格对角占优;D. A 的行列式不为零.2. 高斯消去法的计算量是以下述哪个数量级的渐近速度增长的? ( B ) A.313n ; B. 323n ; C. 314n ; D. 334n .3. 对于任意的初始向是()0x和右端项f ,求解线性代数方程组的迭代法()()1k kxBx f +=+收敛的充分必要条件是( A ). A.()1B ρ<; B. 1B <; C. ()det 0B ≠; D. B 严格对角占优.4. 下述哪个条件不是能使求解线性代数方程组(),ijn nAx b A a ⨯==的Gauss-Seidel 迭代法收敛的充分条件? ( C )A. A 为严格对角占优阵;B. A 为不可约弱对角占优阵;C. A 的行列式不为零;D. A 为对称正定阵.5. 设()[]2,f x C a b =,并记()2m a x a xbM f x ≤≤''=,则函数()f x 的过点()()()(),,,a f a b f b 的线性插值余项()1R x ,[],x a b ∀∈满足( A ). A. ()()2218M R x b a ≤-; B. ()()2218M R x b a <-; C. ()()2216M R x b a ≤-; D. ()()2216M R x b a <-.6. 设()n x ϕ是在区间[],a b 上带权()x ρ的首项系数非零的n 次正交多项式()1n ≥,则()n x ϕ的n 个根( A ).A. 都是单实根;B. 都是正根;C. 有非负的根;D. 存在重根7. Legendre 多项式是( )的正交多项式.( B )A. 区间[]1,1-上带权()x ρ=B. 区间[]1,1-上带权()1x ρ=;C. 区间[],-∞∞上带权()2x x e ρ-=; D. 区间[]0,1上带权()1x ρ=8. 离散数据的曲线拟合的线性最小二乘法的Gram 矩阵与( D )无关?A. 基函数(){}n k k x ϕ=; B. 自变量序列{}0mi i x =;C. 权数{}0mi i w =; D. 离散点的函数值{}0mi i y =. 9. Simpson 求积公式的余项是( B ).A. ()()()3,,12h R f f a b ηη''=-∈;B. ()()()()54,,90h R f f a b ηη=-∈; C. ()()()()2,,12h b a R f f a b ηη-''=-∈; D. ()()()()()44,,90h b a R f f a b ηη-=-∈ 10. n 个互异节点的Gauss 型求积公式具有( D )次代数精确度.A. n ;B. 1n +;C. 21n +;D. 21n -.11. 一阶导数的数值计算公式中,中心差商公式的精度为( B ). A. ()O h ; B. ()2O h ; C. ()2o h ; D. ()32O h .12. 对于用插值法建立的数值求导公式,通常导数值的精确度比用插值公式求得的函数值的精度( B ).A. 高; B, 低; C. 相同; D. 不可比.13. 在常微分方程初值问题的数值解法中, 梯形公式是显式Euler 公式和隐式Euler 公式的( A ).A. 算术平均;B. 几何平均;C. 非等权平均;D. 和. 14. 当( B )时,求解(),0y y λλ'=<的显式Euler 方法是绝对稳定的. A. 11h λ-≤≤; B. 20h λ-≤≤; C. 01h λ≤≤; D. 22h λ-≤≤ 15. 求解(),0y y λλ'=<的经典R-K 公式的绝对稳定条件是( C ): A .20h λ-≤≤; B.()2112h h λλ++≤;C.()()()2341123!4!h h h h λλλλ++++≤; D.()()22121211212h h h h λλλλ++≤-+.16. 在非线性方程的数值解法中,只要()()***1,()x x x ϕϕ'≠=,那么不管原迭代法()()1,0,1,2,k k x x k ϕ+==是否收敛,由它构成的Steffensen 迭代法的局部收敛的阶是( D )阶的.A. 1;B. 0;C. 2<;D. 2≥.17. 在非线性方程的数值解法中,Newton 迭代法的局部收敛的阶是( D )阶的. A. 1; B. 0; C. 2<; D. 2≥.18. 在非线性方程的数值解法中,离散Newton 迭代法的局部收敛的阶是( C )阶的.A. 1;B.;C.12+; D. 2. 19. 在求解非线性方程时,迭代终止准则通常采用( A ),其中的0ε>为给定的相对误差容限. A.11k k k x x x ε--<+; B. 1k k k x x x ε--<; C. 1k k x x ε--<; D. 111k k k x x x ε---<+.20. 在求解非线性方程组时,加进阻尼项的目的,是使线性方程组的( C ). A. 系数矩阵非奇异; B. 系数矩阵的行列式不等于零; C. 系数矩阵非奇异并良态; D. 系数矩阵可逆.三、 判断题1. 在用计算机求数学问题的数值解就是构造算法的构造问题.( × )2. 用计算机进行数值计算时,所有的函数都必须转化成算术运算;在作加减法时,应避免接近的两个数相减;在所乘除法时,计算结果的精度不会比原始数据的高.( √ ) 3. 用计算机作加减法时,交换律和结合律成立.( × ) 4. 单调减且有下界的数列一定存在极限。
计算方法试题集及答案复习试题精选

复习试题一、填空题:1、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=410141014A ,则A 的LU 分解为A ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦。
答案:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=15561415014115401411A 2、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用辛普生(辛卜生)公式计算求得⎰≈31_________)(dx x f ,用三点式求得≈')1(f 。
答案:2.367,0.253、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L4、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;5、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );答案)(1)(1n n n n n x f x f x x x '---=+6、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );7、计算方法主要研究( 截断 )误差和( 舍入 )误差;8、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n a b );9、求解一阶常微分方程初值问题y '= f (x ,y ),y (x 0)=y 0的改进的欧拉公式为( )],(),([2111+++++=n n n n n n y x f y x f hy y );10、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 );11、 两点式高斯型求积公式⎰10d )(x x f ≈(⎰++-≈1)]3213()3213([21d )(f f x x f ),代数精度为( 5 );12、 解线性方程组A x =b 的高斯顺序消元法满足的充要条件为(A 的各阶顺序主子式均不为零)。
计算方法复习思考题五及答案

计算方法复习思考题五及答案一、选择题(每题2分,共20分)1、解线性方程组的主元素消去法中选择主元的目的是( A )。
A 、控制舍入误差 B 、减小方法误差 C 、防止计算时溢出 D 、简化计算2、舍入误差是( A )产生的误差。
A 、只取有限位数B 、模型准确值与用数值方法求得的准确值C 、观察与测量D 、数学模型准确值与实际值 3、3.141580是π的有( B )位有效数字的近似值。
A 、 6 B 、 5 C 、 4 D 、 74、 用简单迭代法求方程f(x)=0的实根,把方程f(x)=0表示成x=ϕ(x),则f(x)=0的根是( B )。
A 、 y=ϕ(x)与x 轴交点的横坐标B 、 y=x 与y=ϕ(x)交点的横坐标C 、 y=x 与x 轴的交点的横坐标D 、 y=x 与y=ϕ(x)的交点 5、求积公式)2(31)1(34)0(31)(20f f f dx x f ++≈⎰的代数精确度为( C )。
A. 1 B. 2 C. 3 D. 46计算,下列方法中哪种最好?( C )A.7、舍入误差是( A )产生的误差。
A. 只取有限位数B. 模型准确值与用数值方法求得的准确值C. 观察与测量D. 数学模型准确值与实际值 8、解代数线性方程组的松弛法收敛的必要条件是 ( C )A. B. C. D.9、函数表示线性插值( A )点的基函数.A.B.C. D.1732.≈41)x =28-24(-10<<ω10<≤ω20<<ω20≤≤ω101x x x x --0x 0y 1x 1y10、对于次数不超过n 的多项式( C ). A. 任意n 次多项式 B. 任意不超过n 次的多项式 C. 本身 D. 无法确定二、判断题(每题2分,共10分)1、在等距节点的情况下,才能计算函数的差分。
( )√2、向前差分与向后差分不存在等量关系。
( )⨯3、数据拟合的步骤首先是建立正规方程组。
科学和工程计算复习题及答案

科学与工程计算基础复习题一、 填空题:1. 评价一个数值计算方法的好坏主要有两条标准:2. 计算机计费的主要依据有两项:一就是使用中央处理器(CPU)的时间,主要由算数运算的次数决定;二就是占据存储器的空间, 3. 用计算机进行数值计算时,4. 对于某个算法,若输入数据的误差在计算过程中迅速增长而得不到控制,则称该算法就是5. 函数求值问题()x f y =的条件数定义为:)()())(()(x f x f x x f cond x C '==6. 单调减且有 下界 的数列一定存在极限; 单调增且有 上界 的数列一定存在极限、 7. 方程实根的存在唯一性定理:设],[)(b a C x f ∈且0)()(<b f a f ,则至少存在一点()b a ,∈ξ使()0=ξf 、当()x f '在()b a ,,方程在[]b a ,内有唯一的实根、8. 函数()y x f ,在有界闭区域D 上对y 满足Lipschitz 条件,就是指对于D 上的任意一对点()1,y x 与()2,y x 成立不等式:2121),(),(y y L y x f y x f -≤-、其中常数L 只依赖于区域D 、 9. 设n i RA i nn ,,2,1,,Λ=∈⨯λ为其特征值,则称i ni A λρ≤≤=1max )(为矩阵A 的谱半径、10. 设1-A 存在,则称数A A A cond 1)(-=为矩阵A 的条件数,其中⋅就是矩阵的算子范数、11. 方程组f x B x ρρρ+=,对于任意的初始向量()0x ρ与右端项f ρ,迭代法()()f x B xk k ρρρ+=+1收敛的充分必要条件就是选代矩阵B 的 谱半径1)(<B ρ、 12. 设被插函数()x f 在闭区间[]b a ,上n 阶导数连续,()()x fn 1+在开区间()b a ,上存在、若{}ni i x 0=为[]b a ,上的1+n 个互异插值节点,并记()()∏=+-=ni in x x x 01ω,则插值多项式()()()()()∑=++'-=nk k nk n k n x x x x x f x L 011ωω的余项为)()!1()()()()(1)1(x n f x L x f x R n x n n n +++=-=ωξ,其中),()(b a x x ∈=ξξ、13. 若函数组(){}[]b a C x n k k ,0⊂=ϕ满足⎩⎨⎧=≠≠=lk lk l k ,0,0),(ϕϕ k,l =0,1,2,…,n ,则称(){}nk k x 0=ϕ为正交函数序列、 14. 复化梯形求积公式⎰∑⎥⎦⎤⎢⎣⎡+++=≈-=ban k n b f kh a f a f h f T dx x f 11)()(2)(2)()(,其余项为),(),(12)(2b a f h a b R nT∈''--=ηη15. 复化Simpson 求积公式⎰∑∑⎥⎦⎤⎢⎣⎡++++++=≈-=-=ban k n k n b f kh a f h k a f a f h f S dx x f 1011)()2(2))12((4)(3)()(,其余项为),(),(180)()4(4b a f h a b R nS∈--=ηη16. 选互异节点n x x x ,,,10Λ为Gauss 点,则Gauss 型求积公式的代数精度为2n+1 、17. 如果给定方法的局部截断误差就是()11++=p n h O T ,其中1≥p 为整数,则称该方法就是P 阶的或具有P 阶精度 、18. 微分方程的刚性现象就是指快瞬态解严重影响 数值解的稳定性与精度 ,给数值计算造成很大的实质性困难的现象、 19. 迭代序列{}[]b a x k k ,0⊂∞=终止准则通常采用11k k kx x x ε--<+,其中的0>ε为 相对误差20.二、 选择题1、 下述哪个条件不就是能使高斯消去法顺利实现求解线性代数方程组(),ijn nAx b A a ⨯==的充分条件? ( D )A 、 矩阵A 的各阶顺序主子式均不为零;B 、 A 对称正定;C 、 A 严格对角占优;D 、 A 的行列式不为零、2、 高斯消去法的计算量就是以下述哪个数量级的渐近速度增长的? ( B ) A 、313n ; B 、 323n ; C 、 314n ; D 、 334n 、 3、 对于任意的初始向就是()0x 与右端项f ,求解线性代数方程组的迭代法()()1k kxBx f+=+收敛的充分必要条件就是( A )、 A 、()1B ρ<; B 、 1B <; C 、 ()det 0B ≠; D 、 B 严格对角占优、4、 下述哪个条件不就是能使求解线性代数方程组(),ijn nAx b A a ⨯==的Gauss-Seidel 迭代法收敛的充分条件? ( C )A 、 A 为严格对角占优阵;B 、 A 为不可约弱对角占优阵;C 、 A 的行列式不为零;D 、 A 为对称正定阵、5、 设()[]2,f x C a b =,并记()2max a x bM f x ≤≤''=,则函数()f x 的过点()()()(),,,a f a b f b 的线性插值余项()1R x ,[],x a b ∀∈满足( A )、A 、 ()()2218M R x b a ≤-; B 、 ()()2218M R x b a <-; C 、 ()()2216M R x b a ≤-; D 、 ()()2216M R x b a <-、6、 设()n x ϕ就是在区间[],a b 上带权()x ρ的首项系数非零的n 次正交多项式()1n ≥,则()n x ϕ的n 个根( A )、A 、 都就是单实根;B 、 都就是正根;C 、 有非负的根;D 、 存在重根7、 Legendre 多项式就是( )的正交多项式、( B )A 、 区间[]1,1-上带权()x ρ=B 、 区间[]1,1-上带权()1x ρ=;C 、 区间[],-∞∞上带权()2x x e ρ-=; D 、 区间[]0,1上带权()1x ρ=8、 离散数据的曲线拟合的线性最小二乘法的Gram 矩阵与( D )无关?A 、 基函数(){}n k k x ϕ=; B 、 自变量序列{}0mi i x =;C 、 权数{}0mi i w =; D 、 离散点的函数值{}0mi i y =、 9、 Simpson 求积公式的余项就是( B )、A 、 ()()()3,,12h R f f a b ηη''=-∈;B 、 ()()()()54,,90h R f f a b ηη=-∈; C 、 ()()()()2,,12h b a R f f a b ηη-''=-∈; D 、 ()()()()()44,,90h b a R f f a b ηη-=-∈ 10、 n 个互异节点的Gauss 型求积公式具有( D )次代数精确度、A 、 n ;B 、 1n +;C 、 21n +;D 、 21n -、 11、 一阶导数的数值计算公式中,中心差商公式的精度为( B )、 A 、 ()O h ; B 、 ()2O h; C 、 ()2o h ; D 、 ()32O h 、12、 对于用插值法建立的数值求导公式,通常导数值的精确度比用插值公式求得的函数值的精度( B )、A 、 高; B, 低; C 、 相同; D 、 不可比、13、 在常微分方程初值问题的数值解法中, 梯形公式就是显式Euler 公式与隐式Euler 公式的( A )、A 、 算术平均;B 、 几何平均;C 、 非等权平均;D 、 与、 14、 当( B )时,求解(),0y y λλ'=<的显式Euler 方法就是绝对稳定的、 A 、 11h λ-≤≤; B 、 20h λ-≤≤; C 、 01h λ≤≤; D 、 22h λ-≤≤ 15、 求解(),0y y λλ'=<的经典R-K 公式的绝对稳定条件就是( C ): A.20h λ-≤≤; B 、()2112h h λλ++≤;C 、()()()2341123!4!h h h h λλλλ++++≤; D 、()()22121211212h h h h λλλλ++≤-+、16、 在非线性方程的数值解法中,只要()()***1,()x x x ϕϕ'≠=,那么不管原迭代法()()1,0,1,2,k k x x k ϕ+==L 就是否收敛,由它构成的Steffensen 迭代法的局部收敛的阶就是( D )阶的、A 、 1;B 、 0;C 、 2<;D 、 2≥、17、 在非线性方程的数值解法中,Newton 迭代法的局部收敛的阶就是( D )阶的、 A 、 1; B 、 0; C 、 2<; D 、 2≥、18、 在非线性方程的数值解法中,离散Newton 迭代法的局部收敛的阶就是( C )阶的、A 、 1;B 、;C 、12; D 、 2、 19、 在求解非线性方程时,迭代终止准则通常采用( A ),其中的0ε>为给定的相对误差容限、A 、 11k k k x x x ε--<+;B 、 1k k k x x x ε--<;C 、 1k k x x ε--<;D 、 111k k k x x x ε---<+、20、 在求解非线性方程组时,加进阻尼项的目的,就是使线性方程组的( C )、 A 、 系数矩阵非奇异; B 、 系数矩阵的行列式不等于零; C 、 系数矩阵非奇异并良态; D 、 系数矩阵可逆、三、 判断题1. 在用计算机求数学问题的数值解就就是构造算法的构造问题、( × )2. 用计算机进行数值计算时,所有的函数都必须转化成算术运算;在作加减法时,应避免接近的两个数相减;在所乘除法时,计算结果的精度不会比原始数据的高、( √ ) 3. 用计算机作加减法时,交换律与结合律成立、( × ) 4. 单调减且有下界的数列一定存在极限。
(完整版)计算力学复习题答案

计算力学试题答案1. 有限单元法和经典Ritz 法的主要区别是什么?答:经典Ritz 法是在整个区域内假设未知函数,适用于边界几何形状简单的情形;有限单元法是将整个区域离散,分散成若干个单元,在单元上假设未知函数。
有限单元法是单元一级的Ritz 法。
2、单元刚度矩阵和整体刚度矩阵各有什么特征?刚度矩阵[K ]奇异有何物理意义?在求解问题时如何消除奇异性?答:单元刚度矩阵的特征:⑴对称性⑵奇异性⑶主元恒正⑷平面图形相似、弹性矩阵D 、厚度t 相同的单元,相同⑸的分块子矩阵按结点号排列,每一子矩阵代表一个结点,占两行两列,eK eK 其位置与结点位置对应。
整体刚度矩阵的特征:⑴对称性⑵奇异性⑶主元恒正⑷稀疏性⑸非零元素呈带状分布。
的物理意义是任意给定结构的结点位移所得到的结构结点力总体上满足力和力矩的平衡。
[]K 为消除的奇异性,需要引入边界条件,至少需给出能限制刚体位移的约束条件。
[]K 3. 列式说明乘大数法引入给定位移边界条件的原理?答:设:,则将 j j a a =jj jjk k α=j jj jP k a α=即:修改后的第个方程为j 112222j j jj j j n n jj jk a k a k a k a k a αα+++++= 由于得 jj j jj j k a k a αα≈所以 j ja a ≈对于多个给定位移时,则按序将每个给定位移都作上述修正,得到全部进行修正()12,,,l j c c c = 后的K 和P ,然后解方程即可得到包括给定位移在内的全部结点位移值。
4. 何为等参数单元?为什么要引入等参数单元?答:等参变换是对单元的几何形状和单元内的场函数采用相同数目的结点参数及相同的插值函数进行变换,采用等参变换的单元称之为等参数单元。
借助于等参数单元可以对于一般的任意几何形状的工程问题和物理问题方便地进行有限元离散,其优点有:对单元形状的适应性强;单元特性矩阵的积分求解方便(积分限标准化);便于编制通用化程序。
计算方法简明教程复习题

引 论1.基于化归策略的三种基本的算法设计技术为缩减技术、校正技术、松弛技术.缩减技术的设计思想是 ,如;校正技术的设计思想是 ,如 ;松弛技术的设计思想是 ,如 .2.由计算公式32((()))ax bx cx d ax b x c x d +++=+++知,此算法运用了技术.3.设计累乘求积1ni i T a ==∏算法时,可以运用 技术.4.由计算公式322222(((())))x x x = 知:此算法运用了缩减 技术. 5.开方公式是 校正 技术的应用.第一章1.设()i x ϕ为n 次的Lagrange 插值基函数,0~ix i n =()为两两互异的 节点,则()i x ϕ= ;32()x ϕ= 0;0()ni i x ϕ==∑1 ;4(3)njj j xϕ==∑ 81(4)n ≥;若0()()()nn ii i P x x f x ϕ==∑,则()n P x 为次数 n 的插值多项式.2.20ni i y =∆=∑ .3.设()p x 、()N x 是()f x 满足同一插值条件的n 次lagrange 、N ew ton 插值多项式,则()p x =()N x ;若()f x 也是次数不超过n 的代数 多项式,则:()p x =()f x .4.设()3(1)(2)(3)f x x x x x =---,则差商[0,1,2,3]f = 0,[0,1,2,3,4]f = 3,[0,1,2,3,4,5]f = 0.5.已知32()61f x x x =++,则差商23[1,2,2,2]f = 6.6.332,01()1(1)(1)(1)1,132x x s x x a x b x x ⎧ ≤≤⎪=⎨-+-+-+ ≤≤⎪⎩ ,若()s x 是[]0,3上以0,1,3为节点的三次样条函数,则,a b ==3.7.构造插值多项式的三种基本方法是 .第二章1. Romberg 算法设计中,运用了 技术.2.复化C otes 公式与复化Simpson 公式之间存在公式 . 3.五个节点的G auss 求积公式具有阶精度;而五个节点的N ew ton C otes-公式具有阶精度.4.复化梯形求积公式具有 阶代数精度.5.Romberg (龙贝格)算法中,2n n n S T T = - . 6.已知[](1)0()()(),,,nbm ii a i f x dx Af x kfa b kξξ-==+∈∑⎰为常数,则求积公式0()()nbii ai f x dx Af x =≈∑⎰的代数精度为 阶.7.n 个节点的cot N ew ton es -公式的代数精度至少为 . 8.n 个节点的G auss 求积公式具有 阶的代数精度.第三章 1.梯形格式111((,)(,))2n n n n n n h y y f x y f x y +++=++具有阶精度.2.改进的E uler 格式是 阶的方法,其计算公式为.3.E uler 格式是 阶的方法,其计算公式为 . 4.隐式E uler 格式111(,)n n n n y y hf x y +++=+是阶的方法.5.差分格式112(,)n n n n y y hf x y +-=+是步法.第四章1. N ew ton 迭代法求方程的根时,在重根附近是 收敛的. 2.方程()0f x =求根的迭代010()()()k k k k k x x x x f x f x f x +-=--是 迭代公式.3.为求方程23(2)0x -=附近迭代1()3()k k k k f x x x f x +=-'是收敛的,其中23()(2)f x x =-. 4.“设[]1(),0,11x x xϕ=∈+,则(0)1ϕ'=,所以迭代函数不满足压缩性条件,因此[]00,1x ∀∈ ,迭代1()k k x x ϕ+=是发散的.” 此 结论 的.5.方程()0f x =求根的迭代111()()()k k k k k k k x x x x f x f x f x -+--=--是法.6.若*x 是方程()x g x =的根,且**()()0g x g x '''==,而*()0g x '''≠则迭代1()k k x g x +=是阶收敛的.7.N ew ton 迭代法求方程的根时,在单根附近是收敛的.8.设迭代函数()x ϕ在方程()x x ϕ=的根*x 的邻近有连续的二阶导数,且*()1x ϕ'<,则1()k k x x ϕ+=在*x 附近,当*()0x ϕ'≠时,是收敛的;而*()0x ϕ'= ,*()0x ϕ''≠时,是 收敛的. 9.为求方程22()0x a -=的根1()()k k k k f x x x f x +=-'是收敛的,其中22()()f x x a =-.第五、六章1.对角占优线性方程组求解,相应的 迭代法是收敛的.2.求解方程组512121012x xx x-⎧+=⎨+=⎩,使用列主元法时,此方程组变为.3.G S-迭代的迭代矩阵为 ;Jacobi迭代的迭代矩阵为 .4.方程组,其求解的G auss Seidel-迭代总是比其相应的Jacobi迭代收敛得更快.5.矩阵TA LL=,L为对角元为正的下三角矩阵是A为对称正定矩阵的条件.6.若线性方程组 ,则Gauss消去法无需选主元素.7.G auss消去法是 技术的应用.答案:大事化小,小事化了秦九昭算法第五章线性方程组的迭代法1.基本内容:迭代公式的建立及敛散性的判断2.公式:Jacobi迭代、G-S迭代公式的分量及矩阵形式3.定理:1、24.习题:2、4、55.其它:SOR方法第六章线性方程组的直接法1.基本内容:矩阵三角分解法、Gauss消去法2.定理:2、33.习题:1、3、8、104.其它:缩减技术的运用题型:选择题、判断题、计算题、设计题、综合题工具:笔、计算器引论1.基本内容:三种基本的算法设计技术及其设计思想;相关例题及其他各章中三种设计技术的运用。
计算化学期末考试复习题及答案

计算化学期末考试复习题及答案1. 请写出Schrodinger 方程,并说明其在多原子分子的求解过程中的缺点。
ti h H ∂ψ∂-=ψˆ ψψE H =ˆ 答:Schrodinger 方程只能用一种精确的分析方法解决类氢原子、氦离子以及氢负离子等单电子体系,而且数学方法十分复杂,将此方程应用到研究分子行为也没有太大的相关性。
2. 请写出Hartree 方程,并说明其比Schrodinger 方程在求解过程中的优点,并指出其本身在描述多原子分子时的缺点。
答: ()()()()n 00000321ψψψψψ = 优点:对于任何具有多个电子的原子或分子,由于电子与电子之间具有排斥作用,Schrodinger 方程便不可能得到精确解析解。
Hartree 方程考虑了相对论和自选轨道耦合等磁相互作用。
缺点:(1)电子具有自旋的性质,结果中会有两个以下的电子占有一个原子或分子轨道(2)电子是不可辨别的3. 请写出Hartree -Fock 方程,并说明每一项的含义。
()()()()()()()()11ˆ11ˆ11ˆ11ˆ333222111nn n F F F F ψεψψεψψεψψεψ====()()的轨道能是分子轨道为体系的分子轨道算子是11ˆn n n Fock Fψεψ4.写出NH3分子在Gaussian程序中的分子内坐标。
5.请解释什么是Fermi孔,什么是Coulomb孔?答:Fermi孔:由于Pauli不相容原理,自旋平行的两个电子不可能在空间同一点出现,基本上反映出每个电子周围有一个Fermi孔。
Coulomb孔:单电子近似导致独立运动的两个自旋反平行的电子有可能某一瞬间在空间同一点出现,然而由于电子间的库伦排斥作用这种情况便不可能发生,由此形成Coulomb孔。
6.请解释什么是相关能?并说明其在处理化学相关问题中的重要性。
答:(1)指定的一个Hamilton量的某个本征态的电子相关能, 是指该Hamilton 量在该态的精确本征值与它的限制的Hartree-Fock极限期望值之差。
《计算方法》复习题参考答案

《计算方法》练习题一练习题第1套参考答案一、填空题1. 14159.3=π的近似值3.1428,准确数位是( )。
2.满足d b f c a f ==)(,)(的插值余项=)(x R ( )。
3.设)}({x P k 为勒让德多项式,则=))(),((22x P x P ( )。
4.乘幂法是求实方阵( )特征值与特征向量的迭代法。
5.欧拉法的绝对稳定实区间是( )。
二、单选题1.已知近似数,,b a 的误差限)(),(b a εε,则=)(ab ε( )。
A .)()(b a εε B.)()(b a εε+ C.)()(b b a a εε+ D.)()(a b b a εε+ 2.设x x x f +=2)(,则=]3,2,1[f ( )。
A.1 B.2 C.3 D.43.设A=⎥⎦⎤⎢⎣⎡3113,则化A为对角阵的平面旋转=θ( ). A.2πB.3πC.4π D.6π4.若双点弦法收敛,则双点弦法具有( )敛速.A.线性 B.超线性 C.平方 D.三次5.改进欧拉法的局部截断误差阶是( ).A .)(h o B.)(2h o C.)(3h o D.)(4h o三、计算题1.求矛盾方程组:⎪⎩⎪⎨⎧=-=+=+2423212121x x x x x x 的最小二乘解。
2.用4=n 的复化梯形公式计算积分⎰211dx x ,并估计误差。
3.用列主元消元法解方程组:⎪⎩⎪⎨⎧=++=++=++426453426352321321321x x x x x x x x x 。
4.用雅可比迭代法解方程组:(求出)1(x )。
算法复习题目及答案讲解

一、选择题1、二分搜索算法是利用( A )实现的算法。
A、分治策略B、动态规划法C、贪心法D、回溯法2、下列不是动态规划算法基本步骤的是( A )。
A、找出最优解的性质B、构造最优解C、算出最优解D、定义最优解3、最大效益优先是( A )的一搜索方式。
A、分支界限法B、动态规划法C、贪心法D、回溯法4、在下列算法中有时找不到问题解的是( B )。
A、蒙特卡罗算法B、拉斯维加斯算法C、舍伍德算法D、数值概率算法5. 回溯法解旅行售货员问题时的解空间树是( A )。
A、子集树B、排列树C、深度优先生成树D、广度优先生成树6.下列算法中通常以自底向上的方式求解最优解的是( B )。
A、备忘录法B、动态规划法C、贪心法D、回溯法7、衡量一个算法好坏的标准是( C )。
A 运行速度快B 占用空间少C 时间复杂度低D 代码短8、以下不可以使用分治法求解的是( D )。
A 棋盘覆盖问题B 选择问题C 归并排序D 0/1背包问题9. 实现循环赛日程表利用的算法是( A )。
A、分治策略B、动态规划法C、贪心法D、回溯法10、下列随机算法中运行时有时候成功有时候失败的是( C )A 数值概率算法B 舍伍德算法C 拉斯维加斯算法D 蒙特卡罗算法11.下面不是分支界限法搜索方式的是( D )。
A、广度优先B、最小耗费优先C、最大效益优先D、深度优先12.下列算法中通常以深度优先方式系统搜索问题解的是( D )。
A、备忘录法B、动态规划法C、贪心法D、回溯法13.备忘录方法是那种算法的变形。
( B )A、分治法B、动态规划法C、贪心法D、回溯法14.哈弗曼编码的贪心算法所需的计算时间为( B )。
A、O(n2n)B、O(nlogn)C、O(2n)D、O(n)15.分支限界法解最大团问题时,活结点表的组织形式是( B )。
A、最小堆B、最大堆C、栈D、数组16.最长公共子序列算法利用的算法是( B )。
A、分支界限法B、动态规划法C、贪心法D、回溯法17.实现棋盘覆盖算法利用的算法是( A )。
建筑与装饰工程计量与计价复习题计算题及答案

建筑与装饰工程计量与计价复习题计算题及答案 The following text is amended on 12 November 2020.第二章建设工程定额与计价规范1、按劳动定额规定,砌砖工程的小组人数为22人。
根据有关资料统计数据,各种砖墙取定的比重是:双面清水墙占20%,单面清水墙占20%,混水内墙占60%。
劳动定额规定:一面内墙双面清水为工日,单面清水为工日,混水内墙工日。
求小组总产量。
(设一个工人小组配置了一台塔吊和一台砂浆搅拌机,砌砖消耗量定额项目的计量单位为10M3,求机械台班使用量。
)解:小组总产量=22*(22%*+20%*+60%*)=(m3)定额台班使用量=10/=(台班)2、水泥、石灰、砂配合比为1:1:3,砂孔隙率为41%,水泥密度1200Kg/M3,砂损耗率2%,水泥、石灰膏损耗率各为1%,求每M3砂浆各种材料用量。
解:砂消耗量= *(1+)=(m3)水泥消耗量=**(1+)=327(Kg)石灰膏消耗量=**(1+)=(m3)3、计算370mm厚标准砖外墙每1M3砌体砖和砂浆的消耗量。
一直砖的损耗率为2%,砂浆的损耗率为1%。
解:标准砖的净用量==522(块)砖消耗量=522*(1+)=532(块)砂浆的净用量=1-522*=(m3)砂浆的消耗量=*(1+)=(m3)第四章建设工程计价方法1、某工程底层平面图如图所示,墙厚均为240mm,试计算有关基数。
1、解:L中=×3+×2=L内=-+-=L外= L中+×4=+×4=S底=×3+×+-×=㎡S房=-×-×2+-×-=㎡第二篇消耗量定额应用第一章建筑面积1、某单层厂房尺寸如图所示,试计算其建筑面积。
解: S=*(+)+9*(+)*2=(m2)2、某住宅单元标准层平面图如图所示,若该住宅层高均为,共计6层。
试计算该住宅单元的建筑面积。
成人教育《计算方法 提纲》期末考试复习题及参考答案

一、单项选择题1、Jacobi迭代法解方程组Ax = b的必要条件是( C ).A.A的各阶顺序主子式不为零 B.ρ(A)<1C. D.|A|≤12、设,均差( B )A.3B. -3C. 5D.03、设,则ρ(A)为( C ).A. 2B. 5C. 7D. 34、三点的高斯求积公式的代数精度为( B ).A. 2B.5C. 3D. 45、幂法的收敛速度与特征值的分布( A )。
A. 有关B. 不一定C. 无关6、求解线性方程组Ax=b的分解法中,A须满足的条件是( B )。
A. 对称阵B. 正定矩阵C. 任意阵D. 各阶顺序主子式均不为零7、舍入误差是( A )产生的误差。
A.只取有限位数B.模型准确值与用数值方法求得的准确值C. 观察与测量D.数学模型准确值与实际值8、3.141580是π的有( B )位有效数字的近似值。
A.6B.5C. 4D. 79、幂法是用来求矩阵( A )特征值及特征向量的迭代法。
A. 按模最大B. 按模最小C. 所有的D. 任意一个10、用1+x近似表示所产生的误差是( C )误差。
A. 模型B. 观测C.截断D. 舍入11、解线性方程组的主元素消去法中选择主元的目的是( A )。
A.控制舍入误差B. 减小方法误差C.防止计算时溢出D. 简化计算12、解线性方程组Ax=b的迭代格式收敛的充要条件是( D )。
A. |M|<1B. ρ(A)<1C. |ρ(M)|<1D. ρ(M)<113、用近似表示所产生的误差是( D )误差。
A. 舍入B. 观测C.模型D. 截断14、-324.7500是舍入得到的近似值,它有( C )位有效数字。
A. 5B. 6C.7D. 815、反幂法是用来求矩阵( B )特征值及相应特征向量的一种向量迭代法。
A. 按模最大B. 按模最小C.全部D. 任意一个16、用表示自由落体运动距离与时间的关系式( g为重力加速度),是在时间t内的实际距离,则是( C )误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习题与答案复习题一 复习题一答案 复习题二 复习题二答案 复习题三 复习题三答案 复习题四 复习题四答案 自测题复习题(一)一、填空题:1、求方程011015.02=--x x 的根,要求结果至少具有6位有效数字。
已知0099.10110203≈,则两个根为=1x ,=2x .(要有计算过程和结果)2、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=410141014A ,则A 的LU 分解为A ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦。
3、⎥⎦⎤⎢⎣⎡=5321A ,则=)(A ρ ,=∞A . 4、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用抛物线(辛卜生)公式计算求得⎰≈31_________)(dx x f ,用三点式求得≈')1(f .5、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 . 二、单项选择题:1、 Jacobi 迭代法解方程组b x =A 的必要条件是( ). A .A 的各阶顺序主子式不为零 B. 1)(<A ρ C. n i a ii ,,2,1,0 =≠ D. 1≤A2、设753)(99-+-=x x x f ,均差]2,,2,2,1[992 f =( ) .A.3B. -3C. 5D.03、设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=700150322A ,则)(A ρ为( ). A. 2 B. 5 C. 7 D. 3 4、三点的高斯求积公式的代数精度为( ). A. 2 B.5 C. 3 D. 45、幂法的收敛速度与特征值的分布( )。
A. 有关 B. 不一定 C. 无关 三、计算题:1、用高斯-塞德尔方法解方程组 ⎪⎩⎪⎨⎧=++=++=++225218241124321321321x x x x x x x x x ,取T)0,0,0()0(=x ,迭代四次(要求按五位有效数字计算).2、求A 、B 使求积公式⎰-+-++-≈11)]21()21([)]1()1([)(f f B f f A dx x f 的代数精度尽量高,并求其代数精度;利用此公式求⎰=211dxx I (保留四位小数)。
3、已知分别用拉格朗日插值法和牛顿插值法求)(x f 的三次插值多项式)(3x P ,并求)2(f 的近似值(保留四位小数).4、取步长2.0=h ,用预估-校正法解常微分方程初值问题⎩⎨⎧=+='1)0(32y y x y )10(≤≤x5、已知求)(x f 的二次拟合曲线)(2x p ,并求)0(f '的近似值。
6、证明方程24)(3+-=x x x f =0在区间(0,1)内只有一个根,并用迭代法(要求收敛)求根的近似值,五位小数稳定。
复习题(一)参考答案一、一、1、010.204104061021≈+=x ,00980345.0)10406102(22≈+=x2、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=15561415014115401411A 3、103+,84、2.367 0.255、-1, )2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L二、A B C B C 5,4,3,2,1 三、1、迭代格式⎪⎪⎪⎩⎪⎪⎪⎨⎧--=--=--=++++++)222(51)218(41)211(41)1(2)1(1)1(3)(3)1(1)1(2)(3)(2)1(1k k k k k k k k k x x x x x x x x x2、2,,1)(x x x f =是精确成立,即⎪⎩⎪⎨⎧=+=+32212222B A B A 得98,91==B A求积公式为)]21()21([98)]1()1([91)(11f f f f dx x f +-++-=⎰- 当3)(x x f =时,公式显然精确成立;当4)(x x f =时,左=52,右=31。
所以代数精度为3。
69286.014097]321132/11[98]311311[91311113221≈=+++-++++-≈+=⎰⎰--=dt t dx x x t3、)53)(43)(13()5)(4)(1(6)51)(41)(31()5)(4)(3(2)(3------+------=x x x x x x x L)45)(35)(15()4)(3)(1(4)54)(34)(14()5)(3)(1(5------+------+x x x x x x 差商表为)4)(3)(1(41)3)(1()1(22)()(33---+----+==x x x x x x x N x P5.5)2()2(3=≈P f4、解: ⎪⎩⎪⎨⎧+++⨯+=+⨯+=++++)]32()32[(1.0)32(2.0)0(111)0(1n n n n n n n n n n y x y x y y y x y y即 04.078.152.01++=+n n n y x y5正规方程组为 ⎪⎩⎪⎨⎧=+==+4134103101510520120a a a a a1411,103,710210===a a a221411103710)(x x x p ++= x x p 711103)(2+=' 103)0()0(2='≈'p f复习题(二)一、填空题:1、近似值*0.231x =关于真值229.0=x 有( )位有效数字;2*x 的相对误差的( )倍;3、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );4、对1)(3++=x x x f ,差商=]3,2,1,0[f ( ),=]4,3,2,1,0[f ( );5、计算方法主要研究( )误差和( )误差;6、用二分法求非线性方程f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( );7、求解一阶常微分方程初值问题y '= f (x ,y ),y (x 0)=y 0的改进的欧拉公式为( );8、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( );9、两点式高斯型求积公式⎰1d )(xx f ≈( ),代数精度为( );10、解线性方程组A x =b 的高斯顺序消元法满足的充要条件为( )。
二、单项选择题:1、求解线性方程组A x =b 的LL T 分解法中,A 须满足的条件是( )。
A. 对称阵B. 正定矩阵C. 任意阵D. 各阶顺序主子式均不为零 2、舍入误差是( )产生的误差。
A. A. 只取有限位数B.模型准确值与用数值方法求得的准确值C. 观察与测量D.数学模型准确值与实际值 3、3.141580是π的有( )位有效数字的近似值。
A. 6 B. 5 C. 4 D. 74、幂法是用来求矩阵( )特征值及特征向量的迭代法。
A. 按模最大B. 按模最小C. 所有的D. 任意一个 5、用 1+x 近似表示e x 所产生的误差是( )误差。
A. 模型B. 观测C. 截断D. 舍入6、解线性方程组的主元素消去法中选择主元的目的是( )。
A.控制舍入误差B. 减小方法误差C.防止计算时溢出D. 简化计算7、解线性方程组A x =b 的迭代格式x (k +1)=M x (k )+f 收敛的充要条件是( )。
A. 1<MB. 1)(<A ρC. 1)(<M ρD. 1)(<M ρ 三、计算题:1、为了使20的近似值的相对误差限小于0.1%,要取几位有效数字?2、已知x sin 区间[0.4,0.8]的函数表求该近似值。
3、构造求解方程0210=-+x e x的根的迭代格式 ,2,1,0),(1==+n x x n n ϕ,讨论其收敛性,并将根求出来,4110||-+<-n n x x 。
4﹑利用矩阵的LU 分解法解方程组 ⎪⎩⎪⎨⎧=++=++=++2053182521432321321321x x x x x x x x x 。
5﹑对方程组 ⎪⎩⎪⎨⎧=-+=--=++841025410151023321321321x x x x x x x x x(1) 试建立一种收敛的Seidel 迭代公式,说明理由; (2) 取初值T )0,0,0()0(=x,利用(1)中建立的迭代公式求解,要求3)()1(10||||-∞+<-k k x x 。
6﹑用复合梯形求积公式计算xxd e 10⎰,则至少应将[0,1]分为多少等份才能保证所得积分的近似值有5位有效数字?复习题(二)参考答案一、1、2; 2、31倍; 3、)(1)(1n n nn n x f x f x x x '---=+; 4、0]4,3,2,1,0[,1]3,2,1,0[==f f ; 5、截断,舍入;6、12+-n a b ; 7、)],(),([2111+++++=n n n n n n y x f y x f hy y ;8、 0.15; 9、⎰++-≈10)]3213()3213([21d )(f f x x f ; 10、A 的各阶顺序主子式均不为零。
二、1、B 2、A 3、B 4、A 、 5、C 6、A 7、D 三、1、解:设20有n 位有效数字,由 4.420=,知41=a令%1.010811021)20()1()1(1*<⨯=⨯≤----n n r a ε,取 4=n , %1.010125.0)20(3*<⨯≤-r ε故 472.420≈1、 1、解: 应选三个节点,使误差|)(|!3|)(|332x M x R ω≤尽量小,即应使|)(|3x ω尽量小,最靠近插值点的三个节点满足上述要求。
即取节点}7.0,6.0,5.0{最好,实际计算结果596274.063891.0sin ≈,且41055032.0)7.063891.0)(6.0963891.0)(5.063891.0(!31596274.063891.0sin -⨯≤----≤-3、解:令 010)1(,02)0(,210e )(>+=<-=-+=e f f x x f x.且010e )(>+='xx f )(∞+-∞∈∀,对x ,故0)(=x f 在(0,1)内有唯一实根.将方程0)(=x f 变形为)e 2(101x x -=则当)1,0(∈x 时)e 2(101)(x x -=ϕ,110e 10e |)(|<≤-='xx ϕ故迭代格式)e 2(1011n x n x -=+收敛。
取5.00=x ,计算结果列表如下:且满足 6671095000000.0||-<≤-x x .所以008525090.0*≈x .4、解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==2441321153121LU A 令b y =L 得T )72,10,14(--=y ,y x =U 得T)3,2,1(=x .5、解:调整方程组的位置,使系数矩阵严格对角占优⎪⎩⎪⎨⎧=++=-+=--151023841025410321321321x x x x x x x x x故对应的高斯—塞德尔迭代法收敛.迭代格式为⎪⎪⎪⎩⎪⎪⎪⎨⎧+--=++-=++=++++++)1523(101)842(101)54(101)1(2)1(1)1(3)(3)1(1)1(2)(3)(2)1(1k k k k k k k k k x x x x x x x x x取T )0,0,0()0(=x,经7步迭代可得:T )010000.1,326950999.0,459991999.0()7(*=≈x x .6、解:当0<x <1时,='')(x f e x,则 e )(≤''x f ,且x xd e 10⎰有一位整数.要求近似值有5位有效数字,只须误差4)(11021)(-⨯≤f R n .由)(12)()(23)(1ξf n a b f R n ''-≤,只要422)(1102112e 12e )e (-⨯≤≤≤n n R x n ξ即可,解得⋅⋅⋅=⨯≥30877.67106e2n所以 68=n ,因此至少需将 [0,1] 68等份。
