缓和曲线的参数公式-里面可以直接计算
缓和曲线计算公式

缓和曲线计算公式缓和曲线计算公式:缓和曲线参数: 0=A L R ⨯缓和曲线长度R A L ÷=20 缓和曲线半径÷=2A R 0L所谓完整缓和曲线就是某段缓和曲线的一端与直线连接点的曲率半径必须是无穷大(可用10的45次方代替,有时也可用“0”表示,具体情况具体分析),而缓和曲线两端无论在什么情况下与圆曲线相接时,其两端的曲率半径必须与对应连接圆曲线的半径相等。
现在我们来谈谈非完整缓和曲线,从上面的话知道,如果某段缓和曲线的一端与直线连接点曲率半径不是无穷大,而是一个实数,那么这段缓和曲线就是非完整缓和曲线。
设计图中遇到这种情况,一般会告诉这段缓和曲线的长度(我们把这段缓和曲线的长度记作L2,缺少的一段缓和曲线长度记作L1,L1+L2=完整缓和曲线长度L),如果没告诉这段缓和曲线的长度,也可以通过两端的桩号计算出来、设计参数A 及缓和曲线另一端的曲率半径R2(应该是与一个圆曲线相接,也就是说R2等于这个圆曲线的半径)。
我们在输入匝道程序时必须要知道R1(起点曲率半径),怎么办呢?那就通过计算把R1计算出来不就行了,下面就是计算过程: 由公式:R=A2÷L 推出R1= A2÷L1 => A2=R1*L1 ……………………………………………………① R2= A2÷(L1+L2) => A2=R2*(L1+L2) ……………………………………………………②R2= A2÷(L1+L2) => R2= A2÷L => L=A2÷R2 …………………………………………③由公式①②推出R1*L1=R2*(L1+L2) => R1=R2*(L1+L2)÷L1 …………………………………………④L=L1+L2 => L1=L-L2 ……………………………………………⑤由公式③④⑤推出R1=R2*L÷(L-L2) => R1= A2÷(A2÷R2-L2) …………………………………………⑥公式⑥就是我们要找的曲率半径公式,计算得到结果计算完毕。
缓和曲线的计算公式

查看文章高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式2009年06月29日星期一21:57高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式分享给好友高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
公路缓和曲线知识与计算公式

公路缓和曲线知识与计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , l h=s 则 l h=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,a s= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3° ——29° 之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和曲线常用计算公式

一、缓和曲线常数1、 内移距P :3420268824Rl R l P n -= 2、 切垂距m :2302402R l l m -= 3、缓和曲线基本角:Rl R l πβ000902== 3、 缓和曲线偏角: Rl R l πδ000306== 5、缓和曲线反偏角: Rl R l b π000603== 缓和曲线常数既有线元素,又有角元 素,且均 为圆曲线半径R 和缓和曲线长0l 的函数。
线元素要计算到mm ,角元素要计算到秒。
二、缓和曲线综合要素切线长:()m P R T +⎪⎭⎫ ⎝⎛+=2tan α 曲线长:()0022l R L +-=βα外视距:R P R E -⎪⎭⎫ ⎝⎛+=2cos 0α 切曲差:L T q -=2曲线综合要素均为线元素,且均为转向角 α、圆曲线半径R 和缓和曲线长0l 的函数。
曲线综合要素计算到cm 。
三、缓和曲线任意点偏角计算2020202902306Rl l Rl l Rl l Rl l t t t t t t πβπδ====0202603Rl l Rl l b t t t π==实际应用中,缓和曲线长0l 均选用10m 的倍数。
四、偏角法测设缓和曲线遇障碍 ()()T B B T l l l l Rl 2610+-=βδ ()()()()T F T F T F T F F l l l l Rl l l l l Rl 23026100+-=+-=πδ—B l 为靠近ZH(HZ)点的缓和曲线长; —T l 为置镜点的缓和曲线长;—F l 为远离ZH(HZ)点的缓和曲线长。
五、直角坐标法1、缓和曲线参数方程:5202401a a a l l R l x -= 30373033661l R l l Rl y a a a -= 2、圆曲线m R x b b +=αsin()P R y b b +-=αcos 1式中,b α为圆心O 到切线的垂线方向和到B 的半径方向所形成的圆心角,按下式计算:00βα+-=Rl l b b ()()T B B T l l l l Rl 2610+-=βδ ()()T B B T l l l l Rl 2300+-=π。
缓和曲线计算公式

180 i (中桩点里程 HY里程 ) 0 R
X xZH x cos y sin Y xZH x sin y sin
(α为两坐标系旋转角)
4.原始坐标计算 (1)左偏情况: ★ 若该点在缓和曲线上,计算公式:
ZH 里程 =JD里程 -T
xXB yXB
li3 6 Rl0 li5 li 40 R 2l02
li 中桩点里程-ZH 里程
★ 若该点在圆曲线上,计算公式:
xXB R(1 cos i ) P yXB R sin i m
2
m
曲线长度: L R ( 2 0 ) 切曲差: D 2T L
180
2l0 R
180
l0
2
R
HY里程 =ZH 里程 +l0 QZ里程 =HY里程 ( L 2 l0 ) YH里程 =QZ里程 +( L 2 l0 ) HZ里程 =JD里程 +T D
1.曲线常数计算 缓和曲线倾角: 0=
l 0 180 2R
切线外移量(切垂距) : m=
l0 l3 0 2 2 240 R
l02 l04 圆曲线内移值: P= 24 R 2688R 3
2.曲线要素计算 切线长度: T ( R P ) tg 外矢距: E ( R P) sec 3.主点里程推算
i
180 (中桩点里程 HY里程 ) 0 R
(2)右偏情况: ★ 若该点在缓和曲线上,计算公式:
xXB yXB
li5 li 40 R 2l02 l3 i 6 Rl0
公路缓和曲线原理及缓和曲线计算公式

一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
发布日期:2012-01-31 作者:李秋生浏览次数:1494)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
公路缓和曲线段原理及缓和曲线计算公式

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和曲线)计算公式
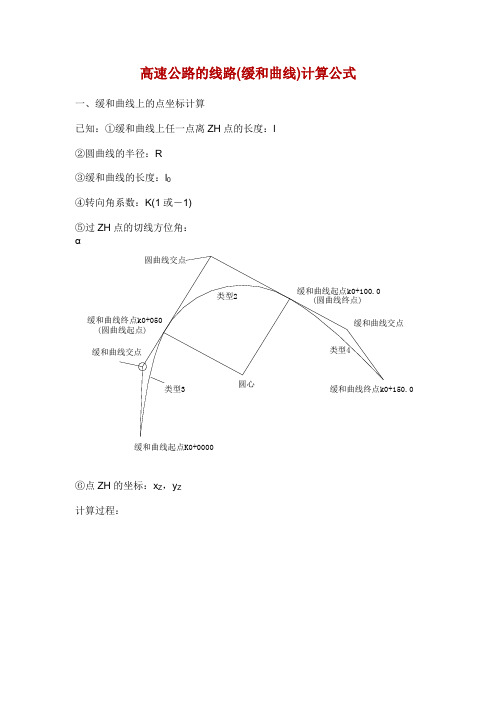
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。
缓和曲线计算公式

缓和曲线、竖曲线、圆曲线、匝道(计算公式)分享作者:下一站'已被分享9次评论(0)复制链接分享转载举报缓和曲线、竖曲线、圆曲线、匝道(计算公式)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
高速公路的线路(缓和曲线)计算公式

一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)——第一缓和曲线长度l1——第二缓和曲线长度l2l——对应的缓和曲线长度R——圆曲线半径R——曲线起点处的半径1R——曲线终点处的半径2——曲线起点处的曲率P1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算(上坡为“+”,下坡为“-”)已知:①第一坡度:i1②第二坡度:i(上坡为“+”,下坡为“-”)2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
缓和曲线知识与计算公式

缓和曲线知识与计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , lh =s 则 lh=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,as= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3° ——29° 之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
公路缓和曲线段原理及缓和曲线计算公式

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
βx=s2/2Rl h(2)缓和曲线的总切线角β=l h2)缓和曲线直角坐标任意一点P处取一微分弧段ds,其所对应的中心角为dβxdx=dscosβxdy=dssinβx3)缓和曲线常数(1)主曲线的内移值p及切线增长值q内移值:p=Y h-R(1-cosβh)=l h2/24R切线增长值:q=X h-Rsinβh=l h/2-lh3/240R2(2)缓和曲线的总偏角及总弦长总偏角:βh=l h/2R总弦长:C h=l h-l h3/90R2O为圆曲线的圆心,圆曲线所对圆心角(等于公路偏角)。
缓和曲线公式(仅供参考)

缓和曲线计算(仅供参考)一、概念曲率半径从某一个值连续匀变为另一个值的曲线称为缓和曲线。
二、缓和曲线的已知参数和特征参数1、已知参数(1) 转角α(2) 圆曲线半径R(3) 缓和曲线长度l s2、缓和曲线特征参数与表达式为了便于说明缓圆曲线特征参数,预先建立直角坐标系ZH点是坐标系原点,ZH至JD点为X轴,过ZH点作X轴的垂直方向为Y轴,形成一个直角坐标系,ZH-HY、HY-ZH是缓圆曲线如图所示。
图、对称缓圆曲线(1) 回旋曲线参数:取图一部分放大如图中,曲线段ZH-HY是缓圆曲线。
回旋曲线是我国应用缓圆曲线的常用线型。
根据一般曲线曲率半径的表达特征,回旋曲线曲率半径表达式为ρ=c/l (3-01)而半径的表达式为 c =Rl s (3-02)(2) 切线角:过缓圆曲线上P 点的切线与缓圆曲线ZH 点切线夹角,称为切线角用β表示。
设P 点附近存在dl 对应的d β为dβ=dl/ρ整理得d β=dl/Rl s积分上式得切线角表达式β=l 2/2Rl s (3-03)角度表达式 β=l 290°/Rl s (3-04)当l=ls 时,有 βs =l s /2R (3-05)角度表达式 βs=l s 90°/R(3-06) (3) 缓圆曲线HY 点的点位坐标:图中,把过ZH 点的切线设为X 轴,过ZH 点作X 轴的垂直方向的直线设为Y 轴,形成缓圆曲线直角坐标系。
在P 点处相对于dl 的变化引起P 点的坐标变化,即dx=dl , dy=dl (3-07)积分处理,舍高次项得缓和曲线上任一点点坐标为x=l-l 5/40R 2l 2s +l 9/3456R 4l 4s -l 13/599040R 6l 6s +l 17/175472640R 8l 8s -l 21/78033715200R 10l10s (3-13) y=l 3/6Rl s -l 7/336R 3l 3s +l 11/42240R 5l 5s -l 15/9676800R 7l 7s +l 19/3530096640R 9l 9s -l 23/1880240947200R 11l11s (3-14)舍去第4项以后各项,有 x=l-l 5/40R 2l 2 s +l 9/3456R 4l 4 sy=l 3/6Rl s -l 7/336R 3l 3s +l 11/42240R 5l 5s (3-15)当l=l s 时,缓圆曲线HY 点的坐标为x s =l s -l 3 s /40R 2+l 5 s /3456R 4,y s =l 2 s /6R-l 4 s /336R 3+l 6 s /42240R 5(3-18) (4) 缓圆曲线内移参数p 与切线增值参数q:图中,在路线中线转弯处如果只设计缓圆曲线,路线中线的F,G 点分别是缓圆曲线(虚线)的ZY,YZ 点.在这种情况 下, 车辆沿AF 直线段运行后在F 处处转入圆曲线,这时的线型必须有相应的变化。
公路缓和曲线段原理及缓和曲线计算公式

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
公路缓和曲线段原理及缓和曲线计算公式Word版

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
