定性数据分析第五章课后答案
定性数据分析第五章课后答案

定性数据分析第五章课后作业1、为了解男性和女性对两种类型的饮料的偏好有没有差异,分别在年青人和老试分析这批数据,关于男性和女性对这两种类型的饮料的偏好有没有差异的问题,你有什么看法?为什么?解:(1)数据压缩分析首先将上表中不同年龄段的数据合并在一起压缩成二维2X 2列联表1.1 ,合起来看,分析男性和女性对这两种类型的饮料的偏好有没有差异?二维22列联表独立检验的似然比检验统计量2ln的值为0.7032,p值为p P( 2(1) 0.7032) 0.4017 0.05,不应拒绝原假设,即认为“偏好类型”与“性别”无关。
(2)数据分层分析其次,按年龄段分层,得到如下三维2X 2X 2列联表1.2,分开来看,男性和女性对这两种类型的饮料的偏好有没有差异?在上述数据中,分别对两个年龄段(即年青人和老年人)进行饮料偏好的调 查,在“年青人”年龄段,男性中偏好饮料A 占58. 73%偏好饮料B 占41.27%; 女性中偏好饮料A 占58. 73%偏好饮料B 占41.27%,我们可以得出在这个年 龄段,男性和女性对这两种类型的饮料的偏好有一定的差异。
同理,在“老年人”年龄段,也有一定的差异。
(3) 条件独立性检验为验证上述得出的结果是否可靠,我们可以做以下的条件独立性检验。
即由题意,可令C 表示年龄段,0表示年青人,C 2表示老年人;D 表示性别,D ! 表示男性,D 2表示女性;E 表示偏好饮料的类型,E !表示偏好饮料A, E 2表示 偏好饮料B 。
欲检验的原假设为:C 给定后D 和E 条件独立 按年龄段分层后得到的两个四格表,以及它们的似然比检验统计量 2ln 的值如下:条件独立性检验问题的似然比检验统计量是这两个似然比检验统计量的和,2ln 6.248 11.822 18.07由于ret 2,所以条件独立性检验的似然比检验统计量的渐近 2分布的自由度为r(e 1)(t 1) 2,也就是上面这2个四格表的渐近 2分布的自由度的和 由于p 值P( 2(2)18.07) 0.000119165很小,所以认为条件独立性不成立,即在年龄段给定的条件下,男性和女性对两种类型的饮料的偏好是有差异的。
第四版统计学课后习题答案

第四版统计学课后习题答案《统计学》第四版统计课后思考题答案第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
大数据概论智慧树知到课后章节答案2023年下上海商学院

大数据概论智慧树知到课后章节答案2023年下上海商学院上海商学院第一章测试1.下列哪个表述是错误的?A:在芯片里运行的程序可以是C语言编写。
B:在芯片里运行的程序可以是面向对象语言编写。
C:在芯片里运行的程序可以是汇编语言编写。
D:在芯片里运行的程序可以是二进制语言编写。
答案:在芯片里运行的程序可以是面向对象语言编写。
2.以下哪一种不是计算机操作系统?A:Linux B:iOS C:Android D:Oracle答案:iOS3.微软对Windows界面的开发主要受到哪家公司的启发?A:3M B:施乐 C:IBM D:苹果答案:苹果4.Windows和Linux或者iOS和Android之间的最大区别在于什么?A:速度:前者快后者慢 B:用户体验:前者优后者差 C:价格:前者贵后者便宜 D:思想:前者封闭后者开源答案:思想:前者封闭后者开源5.医疗领域如何利用大数据?A:用户行为分析 B:社保资金安全 C:个性化医疗 D:临床决策支持答案:用户行为分析;社保资金安全;个性化医疗;临床决策支持6.现在非结构化数据已经占人类数据量的25%。
A:对 B:错答案:错7.大数据与云计算结合起来将给世界带来一场深刻的管理技术革命与社会治理创新。
A:错 B:对答案:对8.Python是一种面向对象、()计算机程序设计语言。
A:编译型 B:解释型答案:解释型9.ASCII码使用一个字节编码。
A:错 B:对答案:对10.GBK是只用来编码汉字的,GBK全称《汉字内码扩展规范》,使用双字节编码。
答案:对第二章测试1.人类科学主要经过了经验科学、理论科学、计算科学、数据科学四个阶段。
A:错 B:对答案:对2.大数据的利用过程是()。
A:采集-清洗-统计-挖掘 B:采集-挖掘-清洗-统计 C:采集-统计-清洗-挖掘 D:采集-清洗-挖掘-统计答案:采集-清洗-统计-挖掘3.信息只有通过反思、启发和学习等过程被每个个体予以有效处理,才能有用。
定性数据统计分析概要课件

通过降维技术,将行变量与列变量在同一低维空间中表示,以便直观揭示行变量 与列变量间的结构关系。
应用场景
适用于有多个分类变量且变量间存在关联性的情况,如市场调研中的品牌与消费 者特征关系分析、生物学中的物种与环境因子关系分析等。
多维尺度分析原理及应用场景
多维尺度分析原理
通过保持原始数据点间的距离关系,在低维空间中重新排列 数据点,以便揭示数据的潜在结构。
适用于研究公众意见、消费行 为、市场需求等领域。
文本分析法
优点
能够深入挖掘文本中的信息,发现其中的 规律和趋势,同时可以进行大规模的分析。
定义
文本分析法是通过对研究对象产生 的文本进行分析,了解其观点、态 度、情感等,收集相关数据和信息
的方法。
A
B
C
D
应用场景
适用于研究社交媒体言论、新闻报道、广 告文案等领域。
相对频率
计算交叉表中各单元格的相对频率, 以百分比形式表示,便于比较。
卡方检验原理及应用场景
卡方检验原理
基于实际观测频数与期望频数之间的差异,判断两个定性变量是否独立。
应用场景
适用于分析两个定性变量之间的关系,如不同性别对某品牌产品的偏好程度。
04
定性数据探索性统计分析 方法
对应分析原理及应用场景
定义:定性数据也称为分类数据 或品质数据,是说明事物性质、 规定事物类别的非数值型数据, 表现为互不相容的类别或属性。
数据的取值是离散的,且一般无 顺序。
数据之间具有独立性,一个数据 的取值不影响另一个数据的取值。
定性数据统计分析意义
了解数据的分布特征
通过统计定性数据的频数分布,可以了解不同类别或属性数据的 分布情况,从而对数据有一个整体的把握。
医学统计学第七版课后答案及解析

医学统计学第七版课后答案第一章绪论一、单项选择题答案 1. D 2. E 3. D 4. B 5. A 6. D 7. A8. C 9. E 10. D二、简答题1答由样本数据获得的结果,需要对其进行统计描述和统计推断,统计描述可以使数据更容易理解,统计推断则可以使用概率的方式给出结论,两者的重要作用在于能够透过偶然现象来探测具有变异性的医学规律,使研究结论具有科学性。
2答医学统计学的基本内容包括统计设计、数据整理、统计描述和统计推断。
统计设计能够提高研究效率,并使结果更加准确和可靠,数据整理主要是对数据进行归类,检查数据质量,以及是否符合特定的统计分析方法要求等。
统计描述用来描述及总结数据的重要特征,统计推断指由样本数据的特征推断总体特征的方法,包括参数估计和假设检验。
3答统计描述结果的表达方式主要是通过统计指标、统计表和统计图,统计推断主要是计算参数估计的可信区间、假设检验的P 值得出相互比较是否有差别的结论。
4答统计量是描述样本特征的指标,由样本数据计算得到,参数是描述总体分布特征的指标可由“全体”数据算出。
5答系统误差、随机测量误差、抽样误差。
系统误差由一些固定因素产生,随机测量误差是生物体的自然变异和各种不可预知因素产生的误差,抽样误差是由于抽样而引起的样本统计量与总体参数间的差异。
6答三个总体一是“心肌梗死患者”所属的总体二是接受尿激酶原治疗患者所属的总体三是接受瑞替普酶治疗患者所在的总体。
第二章定量数据的统计描述一、单项选择题答案 1. A 2. B 3. E 4. B 5. A 6. E 7. E8. D 9. B 10. E二、计算与分析2第三章正态分布与医学参考值范围一、单项选择题答案 1. A 2. B 3. B 4. C 5. D 6. D 7. C8. E 9. B 10. A二、计算与分析12[参考答案] 题中所给资料属于正偏态分布资料,所以宜用百分位数法计算其参考值范围。
王静龙定性数据分析 习题五

王静龙定性数据分析习题五1. 问题描述在定性数据分析中,王静龙遇到了一个问题,他想要了解一份调查问卷中的开放性问题的回答情况。
具体而言,他想要回答以下几个问题:1.开放性问题的回答内容的总体情况如何?2.开放性问题的回答内容中是否存在一些常见的关键词或主题?3.开放性问题的回答内容中是否存在一些特定的意见或情感?为了解决这个问题,王静龙希望能够进行数据分析,并得出一些有用的结论。
2. 数据准备首先,王静龙需要准备调查问卷中开放性问题的回答数据。
这些数据可以以文本文件的形式存储,每一行代表一个回答。
例如,以下是一些示例数据:1. 我觉得工作环境很好,同事们相互合作,给了我很多帮助。
2. 公司的培训计划很好,能够提高员工的技能和知识。
3. 我对公司的管理方式有一些不满意,希望能够改进。
4. 薪资待遇不够优厚,希望能够有所提升。
5. 我觉得公司的发展前景很不错,希望能够有更好的发展空间。
3. 数据分析3.1 总体情况分析为了了解开放性问题的回答内容的总体情况,王静龙可以进行以下分析:•回答的总数•回答的平均长度•回答的最长长度•回答的最短长度为了实现这些分析,可以使用Python编程语言中的文本处理库进行操作。
下面是一个示例代码,可以帮助完成上述分析:```python # 导入所需的库 import pandas as pd 读取文本文件data = pd.read_csv(’responses.txt’, header=None)计算回答的总数total_responses = len(data)计算回答的平均长度average_length = data[0].apply(len).mean()计算回答的最长长度max_length = data[0].apply(len).max()计算回答的最短长度min_length = data[0].apply(len).min()输出结果print(。
定性数据分析课后答案0001
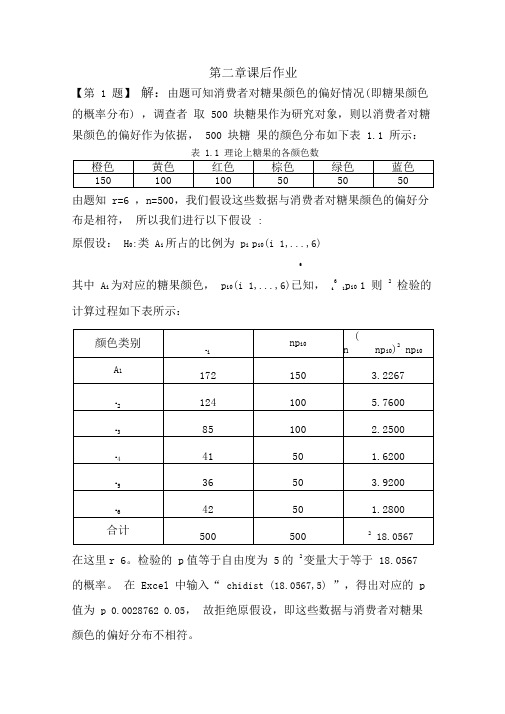
第二章课后作业【第 1 题】解:由题可知消费者对糖果颜色的偏好情况(即糖果颜色的概率分布) ,调查者取500 块糖果作为研究对象,则以消费者对糖果颜色的偏好作为依据,500 块糖果的颜色分布如下表 1.1 所示:表 1.1 理论上糖果的各颜色数由题知r=6 ,n=500,我们假设这些数据与消费者对糖果颜色的偏好分布是相符,所以我们进行以下假设:原假设:H0:类A i所占的比例为p i p i0(i 1, (6)6其中A i为对应的糖果颜色,p i0(i 1,...,6)已知,i61p i0 1 则2检验的计算过程如下表所示:在这里r 6。
检验的p值等于自由度为5的2变量大于等于18.0567 的概率。
在Excel 中输入“ chidist (18.0567,5) ”,得出对应的p 值为p 0.0028762 0.05,故拒绝原假设,即这些数据与消费者对糖果颜色的偏好分布不相符。
【第 2 题】解:由题可知,r=3 ,n=200,假设顾客对这三种肉食的喜好程度相同,即顾客选择这三种肉食的概率是相同的。
所以我们可以进行以下假设:原假设H 0 : p i1(i 1,2,3)0i3则2检验的计算过程如下表所示:在这里r 3。
检验的p值等于自由度为2的2变量大于等于15.72921 的概率。
在Excel 中输入“ chidist (15.72921,2) ”,得出对应的p 值为p 0.0003841 0.05 ,故拒绝原假设,即认为顾客对这三种肉食的喜好程度是不相同的。
【第 3 题】解:由题可知,r=10,n=800,假设学生对这些课程的选择没有倾向性,即选各门课的人数的比例相同, 则十门课程每门课程被选择的概率都相等。
所以我们可以进行以下假设:原假设H 0 : p i 0.1(i 1,2, (10)则2检验的计算过程如下表所示:在这里r 10 。
检验的p值等于自由度为9的2变量大于等于 5.125 的概率。
统计学课后简答题答案

第一章思考题什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论.解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法.推断统计;它是研究如何利用样本数据来推断总体特征的统计方法.统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据.它也是有类别的,但这些类别是有序的.(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值.统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的.实验数据:在实验中控制实验对象而收集到的数据.统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据.时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据.第二章思考题什么是二手资料使用二手资料应注意什么问题与研究内容有关,由别人调查和试验而来已经存在,并会被我们利用的资料为“二手资料”.使用时要进行评估,要考虑到资料的原始收集人,收集目的,收集途径,收集时间使用时要注明数据来源.比较概率抽样和非概率抽样的特点,指出各自适用情况概率抽样:抽样时按一定的概率以随机原则抽取样本.每个单位别抽中的概率已知或可以计算,当用样本对总体目标量进行估计时,要考虑到每个单位样本被抽到的概率.技术含量和成本都比较高.如果调查目的在于掌握和研究对象总体的数量特征,得到总体参数的置信区间,就使用概率抽样.非概率抽样:操作简单,时效快,成本低,而且对于抽样中的统计学专业技术要求不是很高.它适合探索性的研究,调查结果用于发现问题,为更深入的数量分析提供准备.它同样使用市场调查中的概念测试(不需要调查结果投影到总体的情况).除了自填式,面访式和式还有什么搜集数据的办法试验式和观察式等第三章思考题数据预处理内容数据审核(完整性和准确性;适用性和实效性),数据筛选和数据排序.分类数据和顺序数据的整理和图示方法各有哪些分类数据:制作频数分布表,用比例,百分比,比率等进行描述性分析.可用条形图,帕累托图和饼图进行图示分析.顺序数据:制作频数分布表,用比例,百分比,比率.累计频数和累计频率等进行描述性分析.可用条形图,帕累托图和饼图,累计频数分布图和环形图进行图示分析.数据型数据的分组方法和步骤分组方法:单变量值分组和组距分组,组距分组又分为等距分组和异距分组.分组步骤:1确定组数2确定各组组距3根据分组整理成频数分布表第4章数据的概括性度量一组数据的分布特征可以从哪几个方面进行测度数据分布特征可以从三个方面进行测度和描述:一是分布的集中趋势,反映各数据向其中心值靠拢或集中的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的形状,反映数据分布的偏态和峰态.怎样理解平均数在统计学中的地位平均数在统计学中具有重要的地位,是集中趋势的最主要的测度,主要适用于数值型数据,而不适用于分类数据和顺序数据.简述四分位数的计算方法.四分位数是一组数据排序后处于25%和75%位置上的值.根据未分组数据计算四分位数时,首先对数据进行排序,然后确定四分位数所在的位置,该位置上的数值就是四分位数.第七章思考题估计量:用于估计总体参数的随机变量估计值:估计参数时计算出来的统计量的具体值评价估计量的标准:无偏性:估计量抽样分布的数学期望等于被估计的总体参数有效性:对同一总体参数的两个无偏点估计量,有更小标准差的估计量更有效一致性:随着样本容量的增大,估计量的值越来越接近被估计的总体参数置信区间:由样本统计量所构造的总体参数的估计区间第8章思考题假设检验和参数估计有什么相同点和不同点答:参数估计和假设检验是统计推断的两个组成部分,它们都是利用样本对总体进行某种推断,然而推断的角度不同.参数估计讨论的是用样本统计量估计总体参数的方法,总体参数μ在估计前是未知的.而在参数假设检验中,则是先对μ的值提出一个假设,然后利用样本信息去检验这个假设是否成立.什么是假设检验中的显着性水平统计显着是什么意思答:显着性水平是一个统计专有名词,在假设检验中,它的含义是当原假设正确时却被拒绝的概率和风险.统计显着等价拒绝H0,指求出的值落在小概率的区间上,一般是落在或比更小的显着水平上.什么是假设检验中的两类错误答:假设检验的结果可能是错误的,所犯的错误有两种类型,一类错误是原假设H0为真却被我们拒绝了,犯这种错误的概率用α表示,所以也称α错误或弃真错误;另一类错误是原假设为伪我们却没有拒绝,犯这种错误的概论用β表示,所以也称β错误或取伪错误.第10章思考题什么是方差分析它研究的是什么答:方差分析就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显着影响.它所研究的是非类型自变量对数值型因变量的影响.要检验多个总体均值是否相等时,为什么不作两两比较,而用方差分析方法答:作两两比较十分繁琐,进行检验的次数较多,随着增加个体显着性检验的次数,偶然因素导致差别的可能性也会增加.而方差分析方法则是同时考虑所有的样本,因此排除了错误累积的概率,从而避免拒绝一个真实的原假设.方差分析包括哪些类型它们有何区别答:方差分析可分为单因素方差分析和双因素方差分析.区别:单因素方差分析研究的是一个分类型自变量对一个数值型因变量的影响,而双因素涉及两个分类型自变量.第13章思考题简述时间序列的构成要素.时间序列的构成要素:趋势,季节性,周期性,随机性利用增长率分析时间序列时应注意哪些问题.(1)当时间序列中的观察值出现0或负数时,不宜计算增长率;(2)不能单纯就增长率论增长率,要注意增长率与绝对水平的综合分析;大的增长率背后,其隐含的绝对值可能很小,小的增长率背后其隐含的绝对值可能很大.简述平稳序列和非平稳序列的含义.1.平稳序列(stationary series)基本上不存在趋势的序列,各观察值基本上在某个固定的水平上波动或虽有波动,但并不存在某种规律,而其波动可以看成是随机的2.非平稳序列 (non-stationary series)是包含趋势、季节性或周期性的序列,它可能只含有其中的一种成分,也可能是几种成分的组合.因此,非平稳序列又可以分为有趋势的序列、有趋势和季节性的序列、几种成分混合而成的复合型序列.第14章思考题解释指数的含义.答:指数最早起源于测量物价的变动.广义上,是指任何两个数值对比形成的相对数;狭义上,是指用于测定多个项目在不同场合下综合变动的一种特殊相对数.实际应用中使用的主要是狭义的指数.加权综合指数和加权平均指数有何区别与联系加权综合指数:通过加权来测定一组项目的综合变动,有加权数量指数和加权质量指数.使用条件:必须掌握全面数据(数量指数,测定一组项目的数量变动,如产品产量指数,商品销售量指数等)(质量指数,测定一组项目的质量变动,如价格指数、产品成本指数等)拉式公式:将权数的各变量值固定在基期.帕式公式:把作为权数的变量值固定在报告期.加权平均指数:以某一时期的总量为权数对个体指数加权平均.使用条件:可以是全面数据、不完全数据.因权数所属时期的不同,有不同的计算形式.有:算术平均形式、调和平均形解释零售价格指数、消费价格指数、生产价格指数、股票价格指数.答:零售价格指数:反映城乡商品零售价格变动趋势的一种经济指数.消费价格指数:反映一定时期内消费者所购买的生活消费品价格和服务项目价格的变动趋势和程度的一种相对数.生产价格指数: 测量在初级市场上出售的货物(即在非零售市场上首次购买某种商品时) 的价格变动的一种价格指数.股票价格指数:反映某一股票市场上多种股票价格变动趋势的一种相对数,简称股价指数.其单位一般用“点”(point)表示,即将基期指数作为100,每上升或下降一个单位称为“1点”.。
定性分析的误差和分析结果的数据处理

第17章定性分析的误差和分析结果的数据处理【17-1】在以下数值中,各数值包含多少位有效数字? (1) 0.004050 (2)5.6 >10-11 (3)1000(4) 96500(5) 6.20 XI010(6) 23.4082答:(1) 4 位;(2) 2 位;(3) 4 位;(4) 5 位;(5) 3 位;(6) 6 位。
40.0 5.05 104 2.483 0.002120/ 八 0.0432 沃7.5 沃 2.12沢1024(4)1.1 10 ;0.00622(5) 312.46 5.5-0.5868=317.4;(6) 2.136 亠23.05 185.71 2.283 10^-0.00081=0.09267 0.04240 -0.00081 =0.13426 。
【17-3】有一分析天平的称量误差为 ±).2 mg ,如称取试样为0.2000 g ,其相对误差是多少?如 称取试样为2.0000g ,其相对误又是多少?它说明了什么问题?±0 2 汉10解:(1)100% = 0.1% ;0.2000±02^10100% 九。
01%;说明当系统误差相同时,取样越多,相对误差越小。
【17-4】某一操作人员在滴定时,溶液过量了 0.10mL ,假如滴定的总体积为 2.10mL ,其相对误差是多少?如果滴定的总体积为25.80mL ,其相对误差又是多少?它说明了什么问题?3.304.62 10.844.30 20.52 3.90(1)(2)5.68 1040.00105040.0 5.05 1040.0432 7.5 2.12 102(3)(4)2.483 0.0021200.00622(5)321.46 5.5-0.5868(6) _42.136-'23.05 185.71 2.283 10-0.00081【17-2】设下列数值中最后一位是不定值,请用正确的有效数字表示下列各数的答案。
定性数据的分析——卡方检验

2 ) 理论频数计算公式
TRC
nR nC n
T频RC数表;示列联表中第R行第C列交叉格子的理论
nR表示该格子所在的第R行的合计数; nC表示该格子所在的第C列的合计数; n表示总例数。
例10-1 用磁场疗法治疗腰部扭挫伤患者 708人,其中有效673例。用同样疗法治 疗腰肌劳损患者347人,有效312例。观 察结果如表10-6所示。
χ2检验连续性校正公式为
2 ( A T 0.5)2 T
四格表χ2检验连续性校正公式*
2 ( ad bc 0.5n)2 n
(a b)(c d)(a c)(b d )
例10-4 某医生用复合氨基酸胶囊治疗肝硬 化病人,观察其对改善某实验室指标的 效果,见表10-7。
分组 B1
B2
合计
A1
a
b
a+b
A2
c
d
c+d
合计 a+c
b+d
a+b+c+d
案例1 治疗肺炎新药临床试验 用某新药治疗肺 炎病,并选取另一常规药作为对照药,治疗结果 如下:采用新药治100例,有效 60例;采用对照 药治40例,有效 30例。
试问:1) 列表描述临床试验结果;
2)两种药物疗效有无差别?
相应地此时率的标准误估计值按下式计算:
S p ˆ p
p(1 p) n
(10 2)
• 式中,Sp为率的标准误的估计值;p为样本率。
二、率的区间估计
总体率的点估计是计算样本的率,很简单, 但计算得到的样本率不等于总体率,它们 间存在差异。因此,我们还需要知道总体 率大概会在一个什么样的区间范围,即所 谓总体率的可信区间估计。
定性数据分析

在定性数据分析中,保描述
为了保护受访者的隐私,可以采用匿名化处理、去标识化技术等方法来隐藏受访者的身 份信息。此外,分析师应遵守严格的伦理规范和法律法规,确保受访者的隐私权益得到
充分保障。在发布研究结果时,也应避免泄露受访者的个人信息和敏感数据。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
06
定性数据分析案例分享
案例一:社交媒体用户行为分析
总结词
了解用户需求、洞察市场趋势
详细描述
通过分析社交媒体上的用户互动数据, 如评论、点赞和分享等,了解用户对 产品的态度、需求和期望,从而洞察 市场趋势,为产品改进和市场策略提 供依据。
可行性和市场竞争力。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
定性数据分析的挑战与 解决方案
数据解读难度大
总结词
定性数据分析通常基于非结构化数据, 如文本评论、访谈记录等,这些数据往 往难以直接解读,需要经过深入分析和 挖掘。
VS
详细描述
由于定性数据通常缺乏明确的量化指标和 结构,对其解读需要借助一定的主观判断 和分析技巧。这要求分析师具备丰富的专 业知识和经验,能够从大量的非结构化数 据中提取有意义的信息和趋势。
案例二:消费者市场细分研究
要点一
总结词
要点二
详细描述
识别目标市场、制定营销策略
通过定性数据分析方法,如访谈、问卷调查等,了解消费 者的购买动机、需求和行为特征,从而将市场细分为不同 的目标群体,为制定个性化的营销策略提供支持。
案例三:用户访谈在产品改进中的应用
总结词
统计学(贾俊平)第五版课后习题答案(完整版)

亲爱的,一章一章来,肯定能弄完的,你是最棒的!统计学(第五版)贾俊平课后习题答案(完整版)第一章思考题什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
解释分类数据,顺序数据和数值型数据答案同举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
《统计分析与SPSS的应用(第五版)》课后练习答案(第5章)
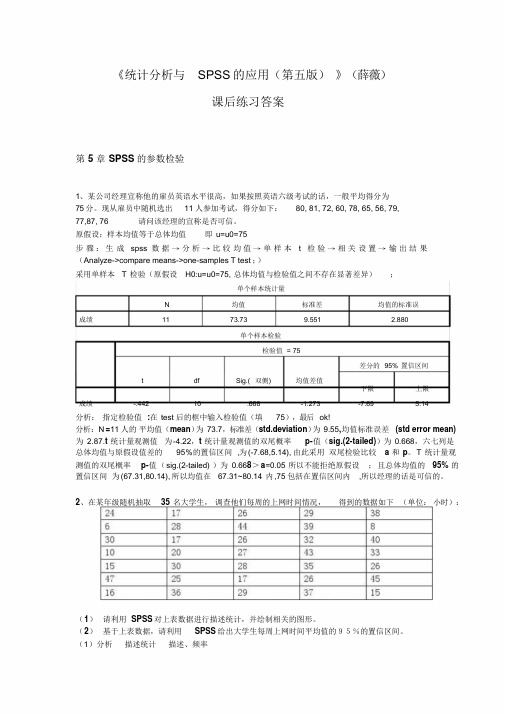
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第5 章SPSS的参数检验1、某公司经理宣称他的雇员英语水平很高,如果按照英语六级考试的话,一般平均得分为75分。
现从雇员中随机选出11人参加考试,得分如下:80, 81, 72, 60, 78, 65, 56, 79,77,87, 76 请问该经理的宣称是否可信。
原假设:样本均值等于总体均值即u=u0=75步骤:生成spss 数据→分析→比较均值→单样本t 检验→相关设置→输出结果(Analyze->compare means->one-samples T test ;)采用单样本T 检验(原假设H0:u=u0=75, 总体均值与检验值之间不存在显著差异);单个样本统计量N 均值标准差均值的标准误成绩11 73.73 9.551 2.880单个样本检验检验值= 75差分的95% 置信区间t df Sig.( 双侧) 均值差值下限上限成绩-.442 10 .668 -1.273 -7.69 5.14分析:指定检验值:在test 后的框中输入检验值(填75),最后ok!分析:N=11 人的平均值(mean)为73.7,标准差(std.deviation)为9.55,均值标准误差(std error mean) 为2.87.t 统计量观测值为-4.22,t 统计量观测值的双尾概率p-值(sig.(2-tailed))为0.668,六七列是总体均值与原假设值差的95%的置信区间,为(-7.68,5.14), 由此采用双尾检验比较 a 和p。
T 统计量观测值的双尾概率p-值(sig.(2-tailed) )为0.668>a=0.05 所以不能拒绝原假设;且总体均值的95% 的置信区间为(67.31,80.14), 所以均值在67.31~80.14 内,75 包括在置信区间内,所以经理的话是可信的。
2、在某年级随机抽取35 名大学生,调查他们每周的上网时间情况,得到的数据如下(单位:小时):(1)请利用SPSS 对上表数据进行描述统计,并绘制相关的图形。
定性数据的统计分析

混合方法研究是一种将定量和定性研究相结合的方法,这种方法可以综
合利用定量和定性的优势,提高研究的全面性和准确性。
感谢您的观看
THANKS
新闻报道内容分析是对新闻
总
报道中的文本内容进行深入
结
分析和解读,以了解新闻事 件的发展趋势和影响。
词
对新闻报道进行分类、
数 据
筛选和整理,确保数据
收
质量。
集
将内容分析结果以图表、 数
报告等形式展示,为企
据 预
业或政府机构提供决策处Fra bibliotek支持。
理
从新闻网站、媒体平台
内 容
等途径收集相关新闻报
分
道。
析
利用文本挖掘技术对新闻报
指非数值型数据,如文字、符号、图片等
分类
按照数据的性质和用途,将定性数据分为类别、顺序、等级和符号等类型
02
定性数据收集方法
访谈法
总结词
通过与研究对象进行面对面的交流,深入了解其观点、态度和经历。
详细描述
访谈法是一种常用的定性数据收集方法,通过与研究对象进行面对面的交流,可以深入了解其观点、态度和经历。 访谈可以采用开放式或半开放式的问题形式,以便获取更具体的信息。访谈过程中应注意建立互信关系,并尊重 被访谈者的隐私和意愿。
03
定性数据分析方法
内容分析法
总结词
内容分析法是一种对文本内容进行客观、系统和定量描述的技术。
详细描述
内容分析法通过对文本内容进行编码、分类和统计,以揭示文本中隐含的意义、 趋势和模式。它广泛应用于新闻媒体、社交媒体、学术文献等领域,帮助研究者 深入了解文本信息的内涵和影响。
主题分析法
市场和社会调查 定性数据分析指南-最新国标

市场和社会调查定性数据分析指南1范围本文件确立了市场和社会调查定性和定量数据的编码、预处理和分析方法等内容。
本文件适用于市场和社会调查中的定性和定量数据预处理和分析活动。
2规范性引用文件下列文件中的内容通过文中的规范性引用而构成本文件必不可少的条款。
其中,注日期的引用文件,仅该日期对应的版本适用于本文件;不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件。
GB/T26315市场、民意和社会调查术语3术语和定义GB/T26315界定的以及下列术语和定义适用于本文件。
3.1定性数据qualitative data指描述性的、非数值的数据,通常用来捕捉现象的本质特征、感受、态度、经验和行为等方面信息。
这种类型的数据通常是文字形式的,但也可能包括图像、视频或音频记录等非文本形式。
3.2定量数据quantitative data指可以通过数字表示的数据,这些数据通常是可测量的,并且可以用数学方法进行分析,分为离散数据和连续数据两类。
3.3定性数据分析qualitative data analysis在数据收集起来以后,在向客户提交最终报告以前所进行的一系列工作,包括对所获得的原始数据进行编码、归类、解释并概括资料所呈现的意义等。
3.4定量数据分析quantitative data analysis指基于数量化数据,使用统计方法和工具进行数据分析和研究的过程。
在数据收集起来以后,在向客户提交最终报告以前所进行的一系列工作,包括对回收的原始资料编码,数据录入和净化、预处理以及统计分析任务书编制等。
3.5资料编码date code给调查问卷中各项问题的每一个可能答案均分配一个代号,该代号通常用数字表示,赋码过程就是调查问卷编码,分为事前编码和事后编码。
3.6访谈记录interview records指座谈会、深度访谈中有关受访者的语言和非语言信息的记录。
4定性和定量数据特点与收集方法4.1定性数据特点定性数据特点包括但不限于:——描述性,定性数据提供了对现象的详细描述,强调的是“为什么”和“怎么样”的问题。
医学统计学定性资料统计描述思考与练习带答案

第五章定性资料的统计描述【思考与练习】一、思考题1.应用相对数时需要注意哪些问题?2。
为什么不能以构成比代替率?3. 标准化率计算的直接法和间接法的应用有何区别?4. 常用动态数列分析指标有哪几种?各有何用途?5。
率的标准化需要注意哪些问题?二、案例辨析题某医生对98例女性生殖器溃疡患者的血清进行检测,发现杜克雷氏链杆菌、梅毒螺旋体和人类单纯疱疹病毒2型病原体感染患者分别是30、51、17例,于是该医生得出结论:女性生殖器溃疡患者3种病原体的感染率分别为30.6%()、52。
0%()和17。
4%()。
该结论是否正确?为什么?三、最佳选择题1。
某地2006年肝炎发病人数占当年传染病发病人数的10.1%,该指标为B A。
率B. 构成比C. 发病率D。
相对比E. 时点患病率2。
标准化死亡比SMR是指AA. 实际死亡数/预期死亡数B. 预期死亡数/实际死亡数C. 实际发病数/预期发病数D。
预期发病数/实际发病数E。
预期发病数/预期死亡数3. 某地人口数:男性13,697,600人,女性13,194,142人;五种心血管疾病的死亡人数:男性16774人,女性23334人;其中肺心病死亡人数:男性13952人,女性19369人.可计算出这样一些相对数:, ,,,,该地男性居民五种心血管疾病的死亡率为DA。
B.C。
D。
E。
4. 根据第3题资料,该地居民五种心血管病的总死亡率为EA。
B。
C.D.E.5。
根据第3题资料,该地男、女性居民肺心病的合计死亡率为DA.B。
C.D。
E。
6。
某地区2000~2005年结核病的发病人数为,则该地区结核病在此期间的平均增长速度是DA.B.C.D。
E。
7. 经调查得知甲、乙两地的恶性肿瘤的粗死亡率均为89。
94/10万,但经过标准化后甲地恶性肿瘤的死亡率为82.74/10万,而乙地为93。
52/10万,发生此现象最有可能的原因是CA。
甲地的诊断技术水平更高B。
乙地的恶性肿瘤防治工作做得比甲地更好C. 甲地的老年人口在总人口中所占比例比乙地多D. 乙地的老年人口在总人口中所占比例比甲地多E。
定性数据统计分析课后练习题含答案

定性数据统计分析课后练习题含答案1. 问题描述一项研究调查了 100 名学生的职业意向,结果发现54人有医生的职业意向,23人希望成为工程师,11人希望成为演员,5人有投行的意向,7人希望成为教师。
请使用适当的统计方法回答以下问题。
2. 题目1.在这100个学生中,有多少人有IT行业的职业意向?2.有多少比例的学生有医生的职业意向?3.有多少比例的学生没有教师和医生的职业意向?4.哪个职业的意向最高?3. 答案1.IT行业的职业意向人数是5人。
解析:根据题目给出的数据,5人有投行的意向,而我们知道投行常常被归类为金融或者IT行业,所以可以推断出这5人中肯定包含有IT行业的职业意向。
2.有医生职业意向的学生比例是 $\\frac{54}{100} = 0.54$。
解析:根据题目给出的数据,有医生职业意向的学生人数为 54,而总样本数为100,所以比例为54/100=0.54。
3.没有教师和医生职业意向的学生比例是 $\\frac{23+11+5}{100} =0.39$,即 $39\\%$。
解析:根据题目给出的数据,有医生职业意向的有54人,有工程师职业意向的有23人,有演员职业意向的有11人,一共这三类职业意向的学生人数为54+23+11=88,而总样本数为100,所以没有这三类职业意向的学生人数为100−88=12,所以比例为12/100=0.12,即 $12\\%$,所以没有教师和医生职业意向的学生比例为1−0.54−0.12=0.34,即$34\\%$。
4.医生职业意向的比例最高,为 $54\\%$。
解析:根据题目给出的数据,有医生职业意向的学生人数为 54,有工程师职业意向的学生人数为 23,有演员职业意向的学生人数为 11,有投行的意向的学生人数为 5,有教师职业意向的学生人数为 7。
因此,医生职业意向的人数最多,比例为 $54\\%$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定性数据分析第五章课后作业
1、为了解男性和女性对两种类型的饮料的偏好有没有差异,分别在年青人和老年人中作调查。
调查数据如下:
偏好饮料A 偏好饮料B
男性37 26
年青人
女性11 23
男性30 43
老年人
女性31 11
试分析这批数据,关于男性和女性对这两种类型的饮料的偏好有没有差异的问题,你有什么看法?为什么?
解:(1)数据压缩分析
首先将上表中不同年龄段的数据合并在一起压缩成二维2×2列联表1.1,合起来看,分析男性和女性对这两种类型的饮料的偏好有没有差异?
表1.1 “性别×偏好饮料”列联表
偏好饮料A 偏好饮料B 合计偏好A比例偏好B比例
男性67 69 136 49.26% 50.74%
女性42 34 76 55.26% 44.74% 二维2×2列联表独立检验的似然比检验统计量
的值为0.7032,
值为
,不应拒绝原假设,即认为“偏好类型”与“性别”无关。
(2)数据分层分析
其次,按年龄段分层,得到如下三维2×2×2列联表1.2,分开来看,男性和女性对这两种类型的饮料的偏好有没有差异?
表1.2 三维2×2×2列联表
偏好饮料A 偏好饮料B 合计偏好A比例偏好B比例男性37 26 63 58.73% 41.27%
年青人
女性11 23 34 32.35% 67.65%
男性30 43 73 41.10% 58.90%
老年人
女性31 11 42 73.81% 26.19%
在上述数据中,分别对两个年龄段(即年青人和老年人)进行饮料偏好的调查,在“年青人”年龄段,男性中偏好饮料A 占58.73%,偏好饮料B占
41.27%;女性中偏好饮料A 占58.73%,偏好饮料B占41.27%,我们可以得出在这个年龄段,男性和女性对这两种类型的饮料的偏好有一定的差异。
同理,在“老年人”年龄段,也有一定的差异。
(3)条件独立性检验
为验证上述得出的结果是否可靠,我们可以做以下的条件独立性检验。
即由题意,可令
表示年龄段,
表示年青人,
表示老年人;
表示性别,
表示男性,
表示女性;
表示偏好饮料的类型,
表示偏好饮料
,
表示偏好饮料。
欲检验的原假设为:
给定后
和
条件独立。
按年龄段分层后得到的两个四格表,以及它们的似然比检验统计量
的值如下:
层
合计
37 26 63
11 23 34
合计48 49 97
层
合计
30 43 73
31 11 42
合计61 54 115
条件独立性检验问题的似然比检验统计量是这两个似然比检验统计量的和,其值为
由于
,所以条件独立性检验的似然比检验统计量的渐近
分布的自由度为
,也就是上面这2个四格表的渐近
分布的自由度的和。
由于
值
很小,所以认为条件独立性不成立,即在年龄段给定的条件下,男性和女性对两种类型的饮料的偏好是有差异的。
(4)产生偏差的原因
a、在(1)中,将不同年龄段的数据压缩在一起合起来后分析发现男性和女性在对两种类型的饮料的偏好上是没有差异的。
但将数据以不同的年龄段分层后并分别分析发现男性和女性在对两种类型的饮料的偏好上是有一定差异的。
合起来看和分开来看的结果不同。
b、由此看来,年龄段在此次调查中属于混杂因素。
由于不同年龄段的人对饮料的选择也会有差异,例如现在的年青人偏好喝一些像可口可乐,美年达等这样的碳酸饮料,而老年人则偏好喝一些红茶,绿茶等这样的非碳酸饮料,在调查中,“老年人”年龄段共有115人,所占比例大,从而使整个结果就倾向于老年人的观点,即使得混杂因素“年龄段”起到一定的干扰作用,从而导致整个调查结果产生了偏差。
2、某工厂有三个车间。
车间主任分别为王、张和李。
过去的一年里,该工厂产品的质量情况总结如下:
王主任将内销和外销产品合并在一起,然后计算各个车间的不合格率。
计算结果如下:
王主任说,我负责的车间生产情况最好,其次是李主任负责的车间,最差的是张主任负责的车间。
这样的比较是不是有偏比较?为什么?
解:不是,有偏比较是指将数据压缩后合起来看与分层后分开来看得出的结果不一致时所产生的偏差,而此题只是将数据压缩起来后相互间比较,因此这样的比较不是有偏比较。
具体分析如下:
由题知,分析车间主任与产品的质量情况之间的关系,则本题是以产品类别为层,以车间主任为行,产品的质量情况为列进行相关分析。
(1)数据压缩分析
首先将上表中不同产品类别的数据合并在一起压缩成二维3×2列联表2.1,合起来看,分析车间主任与产品的质量情况两者之间的关系?
表2.1 “车间主任×产品质量”列联表
合格产品数不合格产品数
王2491 212 7.84%
张1540 258 14.35%
李666 87 11.55%
可计算出该表独立性检验的似然比检验统计量
的值为48.612,
值为。
应该拒绝原假设,即认为车间主任与产品的质量情况两者是有一定相关性的。
(2)数据分层分析
其次,按产品类别分层,得到如下三维2×3×2列联表2.2,分开来看,分析车间主任与产品的质量情况两者之间的关系?
表1.2 三维2×2×2列联表
产品类别车间主任产品的质量情况
不合格率合格产品数不合格产品数
内销王2368 131 5.24% 张293 3 1.01% 李307 12 3.76%
外销王123 81 39.71% 张1247 255 16.98% 李359 75 17.28%
在上述数据中,分别对两个产品类别(即内销和外销)进行分析,在“内销”类别中,王姓主任车间的产品不合格率最高,即车间生产情况最差,张姓主任车间的不合格率最低,即车间生产情况最好;在“外销”类别中,王姓主任车间的产品不合格率最高,即车间生产情况最差,张姓和李姓主任车间生产情况差不多。
(3)条件独立性检验
为验证上述得出的结果是否可靠,我们可以做以下的条件独立性检验。
即由题意,可令
表示产品类别,
表示内销,
表示外销;
表示车间主任,
表示王姓主任,
表示张姓主任,
表示李姓主任;
表示产品的质量情况,
表示合格产品数,
表示不合格产品数。
欲检验的原假设为:
给定后
和
条件独立。
按产品类别分层后得到的两张表格,以及它们的似然比检验统计量
的值如下:
层
合计
2368 131 2499
293 3 296
307 12 319
合计2968 146 3114
层
合计
123 81 204
1247 255 1502
359 75 434
合计1729 411 2140
条件独立性检验问题的似然比检验统计量是这两个似然比检验统计量的和,其值为
由于
,所以条件独立性检验的似然比检验统计量的渐近
分布的自由度为
,也就是上面这2个表格的渐近
分布的自由度的和。
由于
值
很小,所以认为条件独立性不成立,即在产品类别给定的条件下,车间主任与产品的质量情况两者是有一定相关性的。
(4)结论
在(1)中,将不同产品类别的数据压缩在一起合起来后分析发现车间主任与产品的质量情况两者是有一定相关性的;在(2)中,将数据以不同的产品类别分层后分析发现车间主任与产品的质量情况两者也是有一定相关性的。
即合起来看和分开来看的结果相同。
据我们所知,有偏比较是指将数据压缩后合起来看与分层后分开来看得出的结果不一致时所产生的偏差,而此题合起来看和分开来看的结果都是相同的。
因此此题若是分析车间主任与产品的质量情况两者之间的相关关系的话,则该题是无偏的,即不均有有偏性,无法进行有偏比较。
