统计学各种分布表
标准正态分布表使用

标准正态分布表使用标准正态分布表是统计学中常用的一种表格,用于计算和查找标准正态分布的概率值。
标准正态分布是一种特殊的正态分布,其均值为0,标准差为1。
在实际应用中,我们经常需要使用标准正态分布表来进行概率计算和统计分析。
本文将介绍如何使用标准正态分布表进行相关计算,并结合实例进行说明。
首先,我们需要了解标准正态分布表的结构。
标准正态分布表通常包括两部分,一部分是Z值(或称标准正态随机变量),另一部分是对应的累积概率值。
Z值是标准正态分布的随机变量取值,而累积概率值则是对应Z值的累积分布函数值。
在标准正态分布表中,通常以Z值为行标,以小数位数为列标,给出了对应Z值下的累积概率值。
接下来,我们以一个具体的例子来说明如何使用标准正态分布表。
假设我们需要计算标准正态分布随机变量Z小于1.96时的累积概率值。
首先,我们找到Z值为1.9的行,然后找到小数位数为0.06的列,交汇的位置就是对应的累积概率值。
在这个例子中,我们可以得到累积概率值为0.9750。
这意味着标准正态分布随机变量Z小于1.96的概率为0.9750。
除了查找累积概率值,我们还可以使用标准正态分布表进行反查。
也就是给定一个累积概率值,我们需要找到对应的Z值。
例如,如果我们需要找到标准正态分布随机变量Z使得累积概率值为0.95,我们可以在标准正态分布表中查找累积概率值为0.9500的位置,得到对应的Z值为1.64。
这意味着标准正态分布随机变量Z小于1.64的概率为0.95。
在实际应用中,标准正态分布表可以帮助我们进行各种概率计算和统计分析。
例如,在质量控制中,我们可以使用标准正态分布表来计算产品在规定范围内的概率;在市场营销中,我们可以使用标准正态分布表来计算市场需求的概率分布;在金融领域,我们可以使用标准正态分布表来进行风险评估和投资决策。
总之,标准正态分布表是统计学中非常重要的工具,它可以帮助我们进行各种概率计算和统计分析。
通过本文的介绍和实例,相信读者对标准正态分布表的使用有了更深入的理解。
应用统计学第2章统计表统计图

对数图可以直观反映时间序列的环比变化趋势
可以在Office图表类型中选择自定义类型中的“对数图” ,也可通过将一般折线图纵轴“坐标轴格式” 中的“刻度” 设为“对数刻度”来绘制对数图。
例:某公司总成本和劳动成本的增长
该公司总成本和劳动成本每年增加相同的数量 ,因而用绝对数据作图时两条线是平行的,不小心 可能会得出劳动成本占总成本固定比例的误解。实 际上第1年占40%,第6年占60%。使用对数图就可以 清晰反映劳动成本有更高的增长率。
“平滑线”复选框,就将折线图转换为曲线图。
⑵经济管理中几种常见的频数分布曲线
①正态分布曲线 ——这是客观事物数量特征上表现得最为普遍的一
类频数分布曲线。 如人的身高、体重、智商,钢的含碳量、抗拉强度
,某种农作物的产量等等。
正态分布曲线
②偏态曲线
——按其长尾拖向哪一方又可分为右偏(正偏)和 左偏(负偏)两类。
1.频数分布表
频数分布表列出了一系列分类数据的频率、总数 或百分比,可以看出不同类别数据间的区别。
表2-1 1 000美元用途的频数分布表
用钱做什么 购买奢侈品、旅游或礼物 向慈善机构捐款 还贷 储蓄 购买必需品 其他
百分比/% 20 2 24 31 16 7
2.条形图
3.圆饼图
4.帕累托图
L = [ 10 × log 10 n ] 茎叶图类似于横置的直方图,但又有区别
直方图可大体上看出一组数据的分布状况,但没有给出 具体的数值 茎叶图既能给出数据的分布状况,又能给出每一个原始 数值,保留了原始数据的信息
未分组数据—茎叶图(茎叶图的制作)
树茎 树叶
数据个数
10 788
3
11 022347778889
标准正态分布表表含义

标准正态分布表表含义
标准正态分布表是用于计算标准正态分布的累积概率的工具。
标准正态分布表通常由两列数据组成:
第一列是标准正态分布的Z值,即随机变量在标准正态分布
下的标准差单位数。
这些数值可以从-3.9到3.9,以0.1为间隔。
第二列是累积概率,即随机变量小于或等于特定Z值的概率。
这些概率值是标准正态分布曲线下的面积,可以在表中查找。
通过查找Z值,可以在标准正态分布表中找到对应的累积概率。
这对于计算统计学中的各种问题非常有用,比如计算随机变量的概率、计算置信区间等。
例如,如果要计算标准正态分布的随机变量小于等于Z=1.5的
概率,可以在表中查找1.5对应的累积概率,得到0.9332。
这
意味着约有93.32%的随机变量小于或等于1.5。
注意,标准正态分布表通常只包含正值的Z值和累积概率,
因为标准正态分布是对称的。
如果需要计算负值的Z值对应
的累积概率,可以使用对称性质进行推导。
标准正态分布表是统计学中常用的工具,可以方便地查找标准正态分布的累积概率,进而进行各种相关计算。
新教材高中数学第6章统计学初步3统计图表课件湘教版必修第一册

解析 (1)因为总数是100,区间[0.5,1)内的频率为0.08,区间[4,4.5]内的频率为0.02, 所以区间[0.5,1)内的频数为8,区间[4,4.5]内的频数为2,
则x=100-(4+8+15+22+14+6+4+2)=25,y= 6 =0.06.
100
(2)因为从左往右数第4个矩形对应的频率为0.22,且表中的数据组距为0.5, 所以它的高度为0.22÷0.5=0.44.
6.3 统计图表
1 |基本的统计图表
统计图表 条形统计图
扇形统计图 折线统计图
特点 主要用于直观描述不同类别或分组数据的频数 和频率,适用于描述离散型的数据 主要用于直观描述各类数据占总数的比例 主要反映数据的发展变化趋势
2 |频率分布表和频率分布直方图
绘制频率分布表和频率分布直方图的步骤:
1.计算极差.一组数据中① 最大值 与② 最小值 的差.
如果将频率分布直方图中的左边和右边各延长一个分组,取各相邻小矩形⑤ 上底边 的中点,用线段顺次连接各点,就得到频率分布折线图.
判断正误,正确的画“ √” ,错误的画“ ✕” . 1.从频率分布直方图中得不出原始的数据信息. ( √ ) 2.在频率分布直方图中,各个小矩形的面积和为1. ( √ ) 3.频率分布直方图中小矩形的面积表示该组数据的个数.( ✕ ) 提示:频率分布直方图中小矩形的面积表示该组数据的频率. 4.画频率分布直方图时,分组越多越好. ( ✕ ) 5.频率分布折线图反映数据频率分布的规律. ( √ )
|频率分布直方图
1.频率分布直方图的优缺点:频率分布直方图能够直观地表明数据分布的形状,一 般呈中间高、两端低的“峰”状结构.但是从直方图本身得不到具体的数据内
正态分布讲解(含标准表)
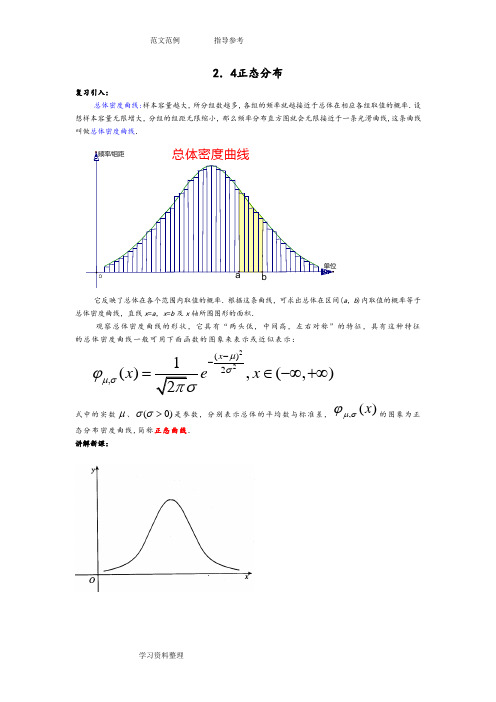
2.4正态分布复习引入:总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线. 总体密度曲线b 单位O 频率/组距a它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,x =b 及x 轴所围图形的面积.观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:22()2,1(),(,)2x x e x μσμσϕπσ--=∈-∞+∞ 式中的实数μ、)0(>σσ是参数,分别表示总体的平均数与标准差,,()x μσϕ的图象为正态分布密度曲线,简称正态曲线.讲解新课:一般地,如果对于任何实数a b <,随机变量X 满足,()()b aP a X B x dx μσϕ<≤=⎰, 则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2σμN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN .经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位.说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.2.正态分布),(2σμN )是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值,讨论均值与标准差对于正态曲线的影响3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图,书中没有做要求,教师也不必补上 讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质4.正态曲线的性质:(1)曲线在x 轴的上方,与x 轴不相交(2)曲线关于直线x=μ对称(3)当x=μ时,曲线位于最高点(4)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数) 并且当曲线向左、右两边无限延伸时,以x 轴为渐近线,向它无限靠近(5)μ一定时,曲线的形状由σ确定σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中:五条性质中前三条学生较易掌握,后两条较难理解,因此在讲授时应运用数形结合的原则,采用对比教学5.标准正态曲线:当μ=0、σ=l 时,正态总体称为标准正态总体,其相应的函数表示式是2221)(x e x f -=π,(-∞<x <+∞)其相应的曲线称为标准正态曲线标准正态总体N (0,1)在正态总体的研究中占有重要的地位 任何正态分布的概率问题均可转化成标准正态分布的概率问题讲解范例:例1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ (1)),(,21)(22+∞-∞∈=-x e x f x π(2)),(,221)(8)1(2+∞-∞∈=--x e x f x π (3)22(1)2(),(,)2x f x e x π-+=∈-∞+∞ 答案:(1)0,1;(2)1,2;(3)-1,0.5例2求标准正态总体在(-1,2)内取值的概率.解:利用等式)()(12x x p Φ-Φ=有)([]}{11)2()1()2(--Φ--Φ=-Φ-Φ=p=1)1()2(-Φ+Φ=0.9772+0.8413-1=0.8151.1.标准正态总体的概率问题: xy对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率,即 )()(00x x P x <=Φ, 其中00>x ,图中阴影部分的面积表示为概率0()P x x < 只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时,)(1)(00x x -Φ-=Φ;而当00=x 时,Φ(0)=0.5 2.标准正态分布表标准正态总体)1,0(N 在正态总体的研究中有非常重要的地位,为此专门制作了“标准正态分布表”.在这个表中,对应于0x 的值)(0x Φ是指总体取值小于0x 的概率,即)()(00x x P x <=Φ,)0(0≥x .若00<x ,则)(1)(00x x -Φ-=Φ.利用标准正态分布表,可以求出标准正态总体在任意区间),(21x x 内取值的概率,即直线1x x =,2x x =与正态曲线、x 轴所围成的曲边梯形的面积1221()()()P x x x x x <<=Φ-Φ. 3.非标准正态总体在某区间内取值的概率:可以通过)()(σμ-Φ=x x F 转化成标准正态总体,然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差,然后进行相应的转化4.小概率事件的含义发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生假设检验方法的基本思想:首先,假设总体应是或近似为正态总体,然后,依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析假设检验方法的操作程序,即“三步曲”一是提出统计假设,教科书中的统计假设总体是正态总体;二是确定一次试验中的a 值是否落入(μ-3σ,μ+3σ);三是作出判断讲解范例:例1. 若x ~N (0,1),求(l)P (-2.32<x <1.2);(2)P (x >2).解:(1)P (-2.32<x <1.2)=Φ(1.2)-Φ(-2.32)=Φ(1.2)-[1-Φ(2.32)]=0.8849-(1-0.9898)=0.8747.(2)P (x >2)=1-P (x <2)=1-Φ(2)=l-0.9772=0.0228.例2.利用标准正态分布表,求标准正态总体在下面区间取值的概率:(1)在N(1,4)下,求)3(F(2)在N (μ,σ2)下,求F(μ-σ,μ+σ);F(μ-1.84σ,μ+1.84σ);F(μ-2σ,μ+2σ);F(μ-3σ,μ+3σ) 解:(1))3(F =)213(-Φ=Φ(1)=0.8413 (2)F(μ+σ)=)(σμσμ-+Φ=Φ(1)=0.8413 F(μ-σ)=)(σμσμ--Φ=Φ(-1)=1-Φ(1)=1-0.8413=0.1587 F(μ-σ,μ+σ)=F(μ+σ)-F(μ-σ)=0.8413-0.1587=0.6826F(μ-1.84σ,μ+1.84σ)=F(μ+1.84σ)-F(μ-1.84σ)=0.9342F(μ-2σ,μ+2σ)=F(μ+2σ)-F(μ-2σ)=0.954F(μ-3σ,μ+3σ)=F(μ+3σ)-F(μ-3σ)=0.997对于正态总体),(2σμN 取值的概率:68.3%2σx 95.4%4σx 99.7%6σx在区间(μ-σ,μ+σ)、(μ-2σ,μ+2σ)、(μ-3σ,μ+3σ)内取值的概率分别为68.3%、95.4%、99.7% 因此我们时常只在区间(μ-3σ,μ+3σ)内研究正态总体分布情况,而忽略其中很小的一部分 例3.某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为π21,求总体落入区间(-1.2,0.2)之间的概率解:正态分布的概率密度函数是),(,21)(222)(+∞-∞∈=--x e x f x σμσπ,它是偶函数,说明μ=0,)(x f 的最大值为)(μf =σπ21,所以σ=1,这个正态分布就是标准正态分布( 1.20.2)(0.2)( 1.2)(0.2)[1(1.2)](0.2)(1.2)1P x -<<=Φ-Φ-=Φ--Φ=Φ+Φ- 教学反思:1.在实际遇到的许多随机现象都服从或近似服从正态分布 在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布 但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口 正态分布在统计学中是最基本、最重要的一种分布 2.正态分布是可以用函数形式来表述的 其密度函数可写成:22()21(),(,)2x f x e x μσπσ--=∈-∞+∞, (σ>0)由此可见,正态分布是由它的平均数μ和标准差σ唯一决定的 常把它记为),(2σμN 3.从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值 从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x 轴,但永不与x 轴相交,因此说曲线在正负两个方向都是以x 轴为渐近线的4.通过三组正态分布的曲线,可知正态曲线具有两头低、中间高、左右对称的基本特征。
统计学原理计算题(公式)复习资料

《统计学原理》复习资料(计算部分)一、 编制分配数列(次数分布表) 统计整理公式a) 组距=上限-下限 b) 组中值=(上限+下限)÷2c) 缺下限开口组组中值=上限-1/2邻组组距 d) 缺上限开口组组中值=下限+1/2邻组组距1.某班40名学生统计学考试成绩分别为:57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 95 76 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61要求:⑴ 根据上述资料按成绩分成以下几组:60分以下,60~70分,70~80分,80~90分,90~100分,整理编制成分配数列。
⑵ 根据整理后的分配数列,计算学生的平均成绩。
解:分配数列成绩(分) 学生人数(人) 频率(%) 60以下 4 10 60—70 6 15 70—80 12 30 80—90 15 37.5 90—100 3 7.5 合计 40 100平均成绩 55465675128515953307076.754040xf x f⨯+⨯+⨯+⨯+⨯====∑∑(分)或 5510%6515%7530%8537.5%957.5%76.75fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑(分)2.某生产车间40名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 37 25 45 29 43 31 36 49 34 47 33 43 38 42 32 25 30 46 29 34 38 46 43 39 35 40 48 33 27 28要求:⑴ 根据以上资料分成如下几组:25~30,30~35,35~40,40~45,45~50,整理编制次数分布表。
⑵ 根据整理后的次数分布表,计算工人的平均日产量。
(作业10P 1) 解:次数分布表日加工零件数(件) 工人数(人)频率(%)25—307 17.5 30—35 8 20 35—40 9 22.5 40—45 10 25 45—50 6 15 合计 40100平均日产量 27.5732.5837.5942.51047.56150037.54040xf x f⨯+⨯+⨯+⨯+⨯====∑∑ 件或 27.517.5%32.520%37.522.5%42.525%47.515%37.5fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑ 件二、 算术平均数和调和平均数的计算 加权算术平均数公式 xfx f=∑∑(常用) fx x f=⋅∑∑(x 代表各组标志值,f 代表各组单位数,ff∑代表各组的比重)加权调和平均数公式 m x m x=∑∑ (x 代表各组标志值,m 代表各组标志总量)分析: m x mx=总产量工人平均劳动生产率(结合题目)总工人人数从公式可以看出,“生产班组”这列资料不参与计算,是多余条件,将其删去。
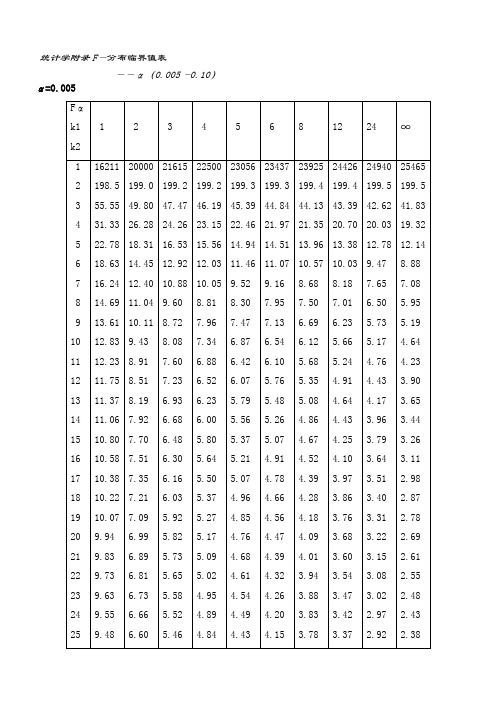
统计学附录_F分布,t分布临界值表_全
14.88
9.36
7.15
5.99
5.29
4.82
4.48
4.24
4.04
3.89
3.77
3.66
3.58
3.50
3.44
3.38
3.33
3.29
3.25
3.22
3.18
3.15
3.13
3.10
3.08
3.06
3.04
3.03
2.90
2.79
2.67
2.57
937.1
39.33
14.73
9.20
7.23
6.93
6.68
6.48
6.30
6.16
6.03
5.92
5.82
5.73
5.65
5.58
5.52
5.46
5.41
5.36
5.32
5.28
5.24
4.98
4.73
4.50
22500
199.2
46.19
23.15
15.56
12.03
10.05
8.81
7.96
7.34
6.88
6.52
6.23
6.00
3.28
3.25
3.21
3.18
2.95
2.74
2.54
24940
199.5
42.62
20.03
12.78
9.47
7.65
6.50
5.73
5.17
4.76
4.43
4.17
3.96
3.79
3.64
标准正态分布分位数表

正态分布的概念在统计学中非常普遍,标准正态分布表在与正态分布有关的计算中经常使用。
如果你知道一个值的标准得分,即z 得分,你可以很方便地在标准正态分布表中找到与标准得分对应的概率值。
任何数值,只要符合正态分布规律,都可以用标准正态分布表来查询其出现概率。
使用时,第一步是计算标准值的标准值,然后将标准值四舍五入到小数点后的第二位,第二步是在标准正态分布表的左侧找到小数点后的第一位直到标准值,然后在相应标准值的小数点后的第二位找到正态分布。
正态分布,也称为“正态分布”,是一个非常重要的概率分布。
它在数学、物理学、工程学以及统计学的许多方面都有很大的影响,它最初是由a. de moivre 在二项分布的渐近公式中得到的。
在研究测量误差时,从另一个角度导出了c。
f。
高斯。
拉普拉斯和高斯研究了它的性质,正常曲线呈钟形,两端低,中间高,对称。
因为它的曲线是钟形的,所以人们通常称之为钟形曲线,如果随机变量x 服从一个带有数学期望和方差2的正态分布,则称为n (,2)。
概率密度函数为正态分布的期望值决定了它的位置,其标准差决定了分布的振幅。
当= 0和= 1时,正态分布是标准正态分布。
正态分布的概念最早是由德国数学家和天文学家莫伊弗尔在1733年提出的,但由于德国数学家高斯率先将其应用于天文学家的研究,它也被称为正态分布分布。
高斯的作品对后世有很大的影响。
他同时给正态分布命名为“正态分布”,后人因此将最小二乘法的发明权归于他。
而今天的德国10马克钞票上印有高斯头像,密度曲线呈正态分布。
这传达了一个观点: 在高斯的所有科学贡献中,对人类文明影响最大的就是这个。
在这个发现的开始,也许人们只能从简单化的理论来评价它的优越性,它的全部影响是不能完全看到的。
这是在20世纪小样本理论得到充分发展之后。
拉普拉斯很快了解到高斯的工作,并立即将其与他发现的中心极限定理联系起来。
基于这个原因,他在一篇即将发表的文章(1810年出版)中增加了一篇补充文章,指出如果按照他的中心极限定理,这个误差可以被看作是多个量的叠加,那么这个误差应该有正态分布。
统计学(第三版)课后答案 袁卫等主编

统计学第一章1.什么是统计学?怎样理解统计学与统计数据的关系?答:统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系,统计学阐述的统计方法来源于对统计数据的研究,目的也在于对统计数据的研究,离开了统计数据,统计方法以致于统计学就失去了其存在意义。
2.简要说明统计数据的来源答:统计数据来源于两个方面:直接的数据:源于直接组织的调查、观察和科学实验,在社会经济管理领域,主要通过统计调查方式来获得,如普查和抽样调查。
间接的数据:从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答:统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的,从理论上看,这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差,它是不可避免的,但可以控制的。
4.答:(1)有两个总体:A品牌所有产品、B品牌所有产品(2)变量:口味(如可用10分制表示)(3)匹配样本:从两品牌产品中各抽取1000瓶,由1000名消费者分别打分,形成匹配样本。
(4)从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答:分二个步骤:(1)按照统计研究的目的,将数据按分组标志进行分组。
按品质标志进行分组时,可将其每个具体的表现作为一个组,或者几个表现合并成一个组,这取决于分组的粗细。
按数量标志进行分组,可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组;组距式分组将变量的取值范围(区间)作为一个组。
统计分组应遵循“不重不漏”原则(2)将数据分配到各个组,统计各组的次数,编制次数分配表。
2.解释洛伦兹曲线及其用途答:洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
3. 一组数据的分布特征可以从哪几个方面进行测度?答:数据分布特征一般可从集中趋势、离散程度、偏态和峰度几方面来测度。
第二节 次数分布表

第二节次数分布表数据是我们了解事物和研究事物的第一手宝贵资料,含有许多有用的信息,有待人们采用特定的方式进行揭示和开发。
从技术上讲,就要采用一些必要的统计手段对数据进行整理与分析,以便揭示数据内部规律性,获取有价值的教育信息。
这一节我们首先介绍次数分布表,它是常用于整理数据的一种方法。
一、次数分布显然,研究一批数据时,我们首先关心的是这批数据中最小的是多小、最大的是多大,以及这批数据从小到大是如何演变的,这就是数据的分布。
例如,我们要研究某班52名学生在一项拼写测验上的分数,最基本、最自然的一种想法是把这52名学生的测验成绩按照分数高低依次排列,见表1-1。
从表1-1中,我们固然可以了解到诸如最高分和最低分是多少,所有的分数分布区间多大,不同的分数各自重复出现的次数多少,大多数学生的分数分布在什么区间等等;但这种单间地把所有数据按照高低顺序一一排列加以整理的方法,难以简要地表达一批数据的次数分布,使人阅读后难以达到印象深刻、一目了然的统计效果。
特别是对于一批为数众多的数据来讲,这种方法更是不能有效地达到整理数据的目的。
为此,我们常从计数角度统计与整理出数据的次数分布。
表1-1 某班52名学生拼写测验分数(从高到低依次排列)所谓次数分布,指的是一批数据中各个不同数值所出现次数多少的情况,或者是这批数据在数轴上各个区间内所出现的次数多少的情况。
由于次数分布是对数据分布最简单、最直接的描述,因此,在许多情形下,我们将把数据分布和次数分布看成同义词。
从次数分布的操作性定义来看,统计一批数据的次数分布有两种方法:第一种方法是按不同的测量值逐点统计次数。
例如表1-2就是根据表1-1的原始数据,从高到低详细地统计不同得分点次数所得到的次数分布表。
在心理测验和教育考试分数转换过程中(如高考的标准分数转换),常使用这种方法统计次数分布。
第二种方法是为了缩简数据,以区间跨度来统计次数,如平时人们常提到的分数段统计,就是这一类。
卫生统计学--集中趋势的统计描述(第一节 频数分布)

脉搏组段
(1) 56~ 59~ 62~ 65~ 68~ 71~ 74~ 77~ 80~ 83~85
合计
组中值(Xi)
(2)
57.5 60.5 63.5 66.5 69.5 72.5 75.5 78.5 81.5 84.5
频数, fi (3)
2 5 12 15 25 26 19 15 10 1
N=∑f 130
料,特别是服从对数正态分布资料
第二节 集中趋势的描述
(三) 中位数 11个大鼠存活天数:
4,10,7,50,3,15,2,9,13,60, 70 平均存活天数? 1、中位数(median)
第二章 集中趋势的 统计描述
第一节 频数分布
第一节 频数分布
一、数值变量的频数分布 1、频数:即变量值的个数 2、频数表:同时列出观察指标的可能取值区间
及其在各区间出现的频数。 3、频数分布通常用频数分布表和频数分布图来
表示。 注意:了解频数分布是分析资料的第一步。 (一)频数分布表(frequency table)
之间,尤以组段的人数71~(次/分)最多。 且上下组段的频数分布基本对称。
3.便于发现一些特大或特小的可疑值
组段
频数 f
(1)
(2)
2.30~
12.60~02.90~03.20~
0
3.50~
17
3.80~
20
4.10~
17
4.40~
12
4.70~
9
5.00~
0
5.30~
0
5.60~5.90
8
合计
图 2-1 130 名 正 常 成 年 男 子脉搏的 频 数 分 布
第一节 频数分布
统计学中的频率分布与概率分布

统计学中的频率分布与概率分布统计学是一门研究数据收集、分析和解释的学科。
在统计学中,频率分布和概率分布是两个重要的概念。
频率分布是指对于一个数据集中各个数值的出现频率进行统计和分析,而概率分布则是通过概率来描述随机变量的分布情况。
本文将详细介绍频率分布和概率分布的概念、计算方法以及它们在统计学中的应用。
一、频率分布频率分布是对数据集中各个数值的出现频率进行统计和展示的方法。
在统计学中,常用的频率分布表格可以将数据划分成一系列的区间,然后记录每个区间内数值的频率。
频率分布表由两列构成,第一列是区间或者数值的范围,第二列则是对应的频数或频率。
在计算频率分布时,首先需要确定数据的范围和区间。
数据的范围是指数据集中最大值和最小值之间的距离;区间是按照一定的范围将数据分组,常用的计算方法是通过数据的范围和期望的组数来决定每个区间的宽度。
然后,统计每个区间内的数据个数(频数),并将频数转化为频率,即频数除以总的数据个数。
最后,将区间和对应的频数或频率记录在频率分布表中。
频率分布的目的是为了更好地了解数据的分布情况,识别数据的中心趋势和离散程度。
通过观察频率分布表,我们可以发现数据的峰值、对称性和偏态等特征。
此外,频率分布还可以用于绘制直方图、箱线图等图表,帮助我们对数据的分布进行可视化分析。
二、概率分布概率分布是用来描述随机变量的出现概率的函数或者规律。
随机变量是指在一个统计实验中可能出现多种结果的变量。
概率分布可以用来计算和预测不同结果出现的概率,并帮助我们更好地理解随机事件的发生规律。
常见的概率分布包括离散概率分布和连续概率分布。
在离散概率分布中,随机变量只能取某些特定的值,其中最常见的概率分布是二项分布、泊松分布和几何分布。
在连续概率分布中,随机变量可以取任意数值,常用的概率分布有正态分布、指数分布和均匀分布等。
计算概率分布的方法取决于不同的概率分布类型。
对于离散概率分布,可以通过列举每个结果的概率来计算整个概率分布。
统计学中的统计分布与概率分布

统计学中的统计分布与概率分布统计学是一门研究收集、分析、解释和展示数据的学科。
在统计学中,统计分布和概率分布是两个重要的概念。
统计分布描述的是一组数据的频数或频率,而概率分布则描述的是随机变量的取值与其对应的概率。
一、统计分布统计分布是指收集到的数据在各个数值上的频数或频率,用于描述数据的分布情况。
统计分布可以通过频数分布表、频率分布表、直方图、饼图等方式进行展示。
频数分布表是一种将数据按照数值的大小进行分类并计算频数的表格。
例如,我们可以将一组考试成绩按照分数段进行分类,并计算各个分数段的频数。
频数分布表可以帮助我们直观地了解数据的分布情况,比如分布是否对称、是否存在峰值等。
频率分布表是在频数分布表的基础上,将频数除以总样本数得到的频率。
频率分布表可以让我们更好地比较不同分类间的数据分布情况,例如在不同分数段的考试成绩分布中,哪个分数段的学生人数占比最高。
直方图是一种常用的统计图表,用于展示数据的分布情况。
直方图的横轴代表数据的范围,纵轴代表频数或频率。
通过直方图,我们可以观察数据分布的形态,比如是否呈现正态分布、偏态分布或者多峰分布等。
饼图是另一种常见的统计图表,用于展示分类数据的分布情况。
饼图的圆形代表整体,每个扇形代表不同分类的比例。
饼图可以帮助我们直观地了解各个分类的占比情况,比如不同民族的人口分布比例。
二、概率分布概率分布是指随机变量的取值与其对应的概率。
随机变量是一个在可能取多个值的随机实验中的变量,而概率分布描述的是随机变量的取值与其对应的概率。
在统计学中,常见的概率分布有离散概率分布和连续概率分布。
离散概率分布描述的是随机变量取离散值的概率情况。
例如,二项分布是一种常见的离散概率分布,描述了在一系列相互独立的伯努利试验中,成功次数的概率分布。
二项分布可以用于模拟投掷硬币、赌博等事件的概率。
连续概率分布描述的是随机变量取连续值的概率情况。
例如,正态分布是一种常见的连续概率分布,也被称为钟形曲线。
标准正态分布表怎么看

标准正态分布表怎么看标准正态分布表是统计学中常用的一种表格,它可以帮助我们计算和查找正态分布的概率值。
在进行统计学分析时,我们经常会遇到需要使用标准正态分布表来进行计算的情况,因此了解和掌握如何使用标准正态分布表是非常重要的。
首先,让我们来了解一下标准正态分布。
标准正态分布是指均值为0,标准差为1的正态分布。
其概率密度函数可以用数学公式表示为:\[f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]其中,\(e\)是自然对数的底,\(x\)代表随机变量的取值,\(f(x)\)代表在该取值处的概率密度。
在实际应用中,我们经常需要计算标准正态分布的累积概率,即随机变量小于某个值的概率。
这时,就需要使用标准正态分布表来进行查找和计算。
标准正态分布表的使用方法如下:1. 首先,我们需要知道要查找的数值对应的标准正态分布的\(\text{Z值}\)。
这个\(\text{Z值}\)可以通过将给定的数值减去均值后再除以标准差来计算得到。
2. 然后,我们可以通过查找标准正态分布表中对应\(\text{Z值}\)的行和列,找到对应的累积概率值。
3. 最后,根据需要进行进一步的计算和分析。
接下来,让我们通过一个例子来演示如何使用标准正态分布表。
假设我们需要计算标准正态分布随机变量小于1.96的概率。
首先,我们计算\(\text{Z值}\):\[\text{Z} = \frac{1.96 0}{1} = 1.96\]然后,我们查找标准正态分布表中\(\text{Z} = 1.96\)对应的累积概率值。
在表中查找到对应的行和列,可以得到累积概率值为0.975。
因此,标准正态分布随机变量小于1.96的概率为0.975。
通过上面的例子,我们可以看到,使用标准正态分布表可以帮助我们快速准确地计算正态分布的累积概率,从而进行统计学分析和推断。
总之,标准正态分布表是统计学中非常重要的工具,它可以帮助我们进行正态分布的概率计算和分析。
正态分布分位数表

正态分布分位数表正态分布分位数表是统计学中一种重要的分位数表,用于计算随机变量的分位值,根据随机变量的概率密度函数得到。
正态分布分位数表的缩写形式常用于统计分析,是计算抽样统计量的非常重要的工具。
正态分布分位数表是由正态分布函数(即钟形曲线)和对应的分位值所组成。
正态分布函数是一个具有很强特征的双峰函数,最大值出现在中间,两边是渐缓收敛由最大值向两边减小。
正态分布分位数表可以用来表示正态分布函数的概率密度函数,用于描述一组随机变量的分布。
正态分布分位数表的使用在统计学中属于一种应用的技术,主要是为了计算一组随机变量的分位值,而不管这一组随机变量是否符合正态分布,其概率值可以从正态分布分位数表得出。
例如,根据正态分布分位数表,如果检测结果的观测值低于第25%分位数,说明这个观测值处于分布的低限,也就是说,这个观测值有着更低几率出现在这个组中。
同样,如果检测结果的观测值高于第75%分位数,说明这个观测值处于分布的高限,也就是说,这个观测值有着更高几率出现在这个组中。
正态分布分位数表是一种应用技术,其中以概率密度函数来表示正态分布函数,可以计算随机变量的分位值,而这些分位值可以用于统计学中的抽样统计分析,从而更好地评估和比较数据分布,推断更多不同组数据之间的差异。
正态分布分位数表广泛应用于各种数据分析,在实验中,可以用它来检验样本是否满足正态分布假定,检验分组的数据分布情况,以及对样本的偏斜进行检验等。
此外,它还可以用于数据预测,计算样本的测试统计量等。
总而言之,正态分布分位数表对于统计数据的分析和预测至关重要。
正态分布分位数表的使用有其显著的优点,首先,它可以实现对一组随机变量的定量分析,例如可以检验数据的分布情况;其次,它可以用于检验一组样本数据满足正态分布假定,以及检验数据的预测能力等;最后,它可以提供对随机变量分位值的定量预测,从而更加有效地评估不同组数据之间的差异。
正态分布分位数表在实际应用中具有重要意义,它可以为统计学究提供重要的参考,帮助我们更好地理解一组样本的分布情况,支持数据分析的结论,提高计量统计学的可信度,从而使得更有效、更准确地把握统计数据的变化趋势,辅助决策分析。
第一节基本统计分析一`频数分布表

以下,我们介绍的主要是SPSS。
SPSS(PASW)基础
软件名称
Statistical Package for Social Science (1975-2000年) Statistical Product and Service Solutions(2000年-2009年4月) Predictive Analytics Software(2009年4月起)
Cumulativ e P erc en t 27.8 44.7 69.5 83.8 92.2 95.8 97.3 98.9 100.0
Statistics:
Dispersion(离差栏):
Std.Deviation 标准差
Variance
方差
Range
全距
Minimum
最小值
Maximum
最大值
Valid Percent 27.8 16.9 24.9 14.2 8.4 3.6 1.6 1.5 1.1 100.0
Cumulative Percent 27.8 44.7 69.5 83.8 92.2 95.8 97.3 98.9 100.0
还可直接作出图形(Charts): Bar charts:条形图 Pie Charts:圆图、饼图 Histograms:直方图,只适用于连续的
4、关于相关系数统计意义的检验:由于抽样误差的存在。 检验的零假设——总体中两个变量间的关系为0。
SPSS只给出给假设成立的概率P值。
(1)Analyze ——Correlations—— Bivariate
计算指定的两个变量之间的相关系数,可选择 Pearson相关、Spearman和
统计学第四章分组和次数分布

● 掌握统计分组的基本理论和方法 ● 掌握分配数列的特性和编制方法
重点、难点
1、统计分组的概念和作用 2、统计分组的原则 3、 分组标志选择及界限的确定(统计分组的
关键)(单选、判断) 4、统计分组的方法(单选、判断) 5、变量数列的编制(计算)(难点)
第一节 统计分组(统计整理的关键)
比率(%) 5 17.5 27.5 30 20 100
二、组距式变量数列(分布表)的编制
2、 注意区分的几组概念 闭口组和开口组 等距变量数列和异距变量数列(书99页表4-8) 同限分组和异限分组(书99页表4-8)
二、组距式变量数列(分布表)的编制
3、 确定组距和组数
全距(R)=最大值-最小值
复合分组体系(p94) 3.按分组标志的性质,可分为品质标志分组和数量标
志分组。
三、统计分组的原则
1、保证组内单位的同质性,组间单位的差异性 2、必须复合完备性原则,即所谓“穷举性”。 3、必须遵循“互斥性”原则
四、分组标志选择及界限的确定
统计整理的关键是统计分组, 统计分组的关键是正确选择 分组标志和划分各组界限。 1、正确选择分组标志应遵循的原则 (1)应根据研究的目的与任务选择分组标志 (2)选择最能体现现象本质特征的标志作为分组标志 (3)结合现象发展的具体历史条件和经济条件选择分 组标志 (补充)
二、组距式变量数列(分布表)的编制
4、 确定组限 确定组限应遵循的原则:分组后,标志值在各组的变动 能反映总体单位的规律性。确定组限应注意特殊的界限点 必须作为组限。 离散型变量的组限:由于变量值之间有 明显的界限,上下限可用明显的数值表 示,组限明确、清楚。 连续型变量的组限:由于变量值之间 可作无限分割,有小数存在,上下限不能用两个确定的数 值表示,前组的上限和本组的下限应同为一个数值。 连续性变量,确定组限应遵循“上组限不在内”原则。 离散变量,对于同限分组也遵循“上组限不在内”原则
