小波分析考试题及答案教学教材
近代数学 小波 简答题+答案

1什么是小波函数?(或小波函数满足什么条件?)答:设)()(2R L t ∈ϕ,且其Fourier 变换)(ωϕ满足可允许性(admissibility )条件+∞<⎰∞+∞-ωωϕd w |||)(|2,则称)(t ϕ为小波函数。
2 Fourier 变换的不足?Fourier 分析的不足,主要表现在以下两点:1) Fourier 分析不能刻画时域信号的局部特性;(只知道信号所含有的频率信息,但不能知道各种不同频率信息在什么时候/位置出现) 2) Fourier 分析对非平稳信号的处理效果不好。
(如音乐、语言、地震、电脉冲等)3 什么是加窗Fourier 变换?用一个时间函数g(t)做窗口函数,该时间函数在有限区间外恒等于零,或很快趋近与零。
用g(t –τ)与待分析函数f(t)相乘,然后对乘积进行Fourier 变换,乘积作用相当与在 t =τ处开了个“窗口”。
即),(τωf G =dt e t g t f Rt i ⎰--ωτ)()(其反演公式为:ττωτωπωd G t g e d t f f R Rti ),()(21)(-=⎰⎰),(τωf G ),(+∞<<-∞+∞<<-∞τω确实包含了f(t)的全部信息。
4.什么是分数傅里叶变换?分数傅里叶变换是傅里叶变换的广义化,傅里叶变换通常指变换整数次,而分数傅里叶变换的变换次数不一定是整数,而是分数,其定义式为 ,当a=1时,分数傅里叶变换就变成了傅里叶变换。
一、写出离散小波、二进小波的表达式 答:(1)离散小波:)2(22,k t j jk j -=--ψψ(2)二进小波:))2(2(2)(2,2τψψτjj j t t j -=--三、二进小波满足什么样的条件时,它的小波变换及其逆变换是存在的? 设小波函数)(2R L t ∈)(ψ,若存在两个常数A,B,满足0<+∞<≤B A ,使得B A j Z≤∑≤∈2j )2(ωψ成立,则称)(,2t j τψ小波是)(2R L 上的二进小波,称上式为二进小波的稳定条件,当A=B 时称为最稳定条件。
小波分析考试题(附答案)

《小波分析》试题适用范围:硕士研究生时 间:2013年6月一、名词解释(30分)1、线性空间与线性子空间解释:线性空间是一个在标量域(实或复)F 上的非空矢量集合V ;设V1是数域K 上的线性空间V 的一个非空子集合,且对V 已有的线性运算满足以下条件 (1) 如果x 、y V1,则x +y V1; (2) 如果x V1,k K ,则kx V1, 则称V1是V 的一个线∈∈∈∈∈性子空间或子空间。
2、基与坐标解释:在 n 维线性空间 V 中,n 个线性无关的向量,称为 V 的一组n 21...εεε,,,基;设是中任一向量,于是 线性相关,因此可以被基αn 21...εεε,,,线性表出:,其中系数 αεεε,,,,n 21...n 21...εεε,,,n 2111an ...a a εεεα+++=是被向量和基唯一确定的,这组数就称为在基下的坐标,an ...a a 11,,,αn 21...εεε,,,记为 ()。
an ...a a 11,,,3、内积解释:内积也称为点积、点乘、数量积、标量积。
,()T n x x x x ,...,,21=,令,称为x 与y 的内积。
()T n y y y y ,...,,21=[]n n y x y x y x y x +++=...,2211[]y x ,4、希尔伯特空间解释:线性 完备的内积空间称为Hilbert 空间。
线性(linearity ):对任意f ,g ∈H ,a ,b ∈R ,a*f+b*g 仍然∈H 。
完备(completeness ):空间中的任何柯西序列都收敛在该空间之内。
内积(innerproduct ):<f ,g>,它满足:,()T n f f f f ,...,,21=时。
()T n g g g g ,...,,21=[]n n y x y x y x y x +++=...,22115、双尺度方程解释:所以都可以用空间的一个1010,V W t V V t ⊂∈⊂∈)()(ψϕ)()和(t t ψϕ1V从图可以明显看出,多分辨分析只是对低频部分进行进一步分解,而高以考虑。
《小波分析及其应用》word版

现代数字信号处理作业小波分析及其应用电研111梁帅小波分析及其应用1.小波分析的概念和特点1.1小波理论的发展概况20世纪80年代逐渐发展和兴起的小波分析(wavelctanalysis)是20世纪数学领域中研究的重要杰出成果之一。
小波分析理论作为数学界中一种比较成熟的理论基础,应用到了各种领域的研究当中,推动了小波分析在各工程应用中的发展。
它作为一种新的现代数字信号处理算法,汲取了现代分析学中诸如样条分析、傅立叶分析、数值分析和泛函分析等众数学多分支的精华部分,替代了工程界中一直应用的傅立叶变换,它是一种纯频域分析方法,不能在时频同时具有局部化特性。
而小波分析中的多尺度分析思想,犹如一台变焦照相机,可以由粗及精逐步观察信号,在局部时频分析中具有很强的灵活性,因此有“数学显微镜”的美称。
它能自动随着频率增加而调节成窄的“时窗”和宽的“频窗”,又随着频率降低而调节成宽的“时窗”和窄的“频窗”以适应实际分析需要。
另外,小波变换在经过适当离散后可以够成标准正交基或正交系,这些在理论和应用上都具有十分重要的意义,因此,小波分析在各个领域得到了高度的重视并取得了许多重要的成果。
小波变换作为一种数学理论和现代数字信号处埋方法在科学技术界引起了越来越多专家学者的关注和重视。
在数学家看来,基于小波变换的小波分析技术是当今数值分析、泛函分析、调和分析等半个多世纪以来发展最完美的结晶,是正在发展中的新的数学分支。
在工程领域,特别是在信号处理、图像处理、机器视觉、模糊识别、语音识别、流体力学、量子物理、地震勘测、电磁学、CT成像、机械故障诊断与监控等领域,它被认为是近年来在工具及方法上的重大突破。
然而,小波分析虽然在众多领域中已经取得了一定的成果,但是,有专家预言小波分析理论的真正高潮并没有到来。
首先,小波分析尚需进一步完善,除一维小波分析理论比较成熟以外,向量小波和多维小波则需要进行更加深入的研究与讨论;其次,针对不同情况选择不同的小波基函数,实现的效果是有差别性的这一问题,对最优小波基函数的选取方法有待进一步研究。
小波分析考试题及答案

一、叙述小波分析理论发展的历史和研究现状答:傅立叶变换能够将信号的时域和特征和频域特征联系起来,能分别从信号的时域和频域观察,但不能把二者有机的结合起来。
这是因为信号的时域波形中不包含任何频域信息,而其傅立叶谱是信号的统计特性,从其表达式中也可以看出,它是整个时间域内的积分,没有局部化分析信号的功能,完全不具备时域信息,也就是说,对于傅立叶谱中的某一频率,不能够知道这个频率是在什么时候产生的。
这样在信号分析中就面临一对最基本的矛盾——时域和频域的局部化矛盾。
在实际的信号处理过程中,尤其是对非常平稳信号的处理中,信号在任一时刻附近的频域特征很重要。
如柴油机缸盖表明的振动信号就是由撞击或冲击产生的,是一瞬变信号,单从时域或频域上来分析是不够的。
这就促使人们去寻找一种新方法,能将时域和频域结合起来描述观察信号的时频联合特征,构成信号的时频谱,这就是所谓的时频分析,亦称为时频局部化方法。
为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并开发了一系列新的信号分析理论:短时傅立叶变换、时频分析、Gabor 变换、小波变换Randon-Wigner变换、分数阶傅立叶变换、线形调频小波变换、循环统计量理论和调幅—调频信号分析等。
其中,短时傅立叶变换和小波变换也是因传统的傅立叶变换不能够满足信号处理的要求而产生的。
短时傅立叶变换分析的基本思想是:假定非平稳信号在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的功率谱。
但从本质上讲,短时傅立叶变换是一种单一分辨率的信号分析方法,因为它使用一个固定的短时窗函数,因而短时傅立叶变换在信号分析上还是存在着不可逾越的缺陷。
小波变换是一种信号的时间—尺度(时间—频率)分析方法,具有多分辨率分析(Multi-resolution)的特点,而且在时频两域都具有表征信号局部特征的能力,使一种窗口大小固定不变,但其形状可改变,时间窗和频率窗都可以改变的时频局部化分析方法。
浙江大学小波分析及其工程应用考试试卷

浙江大学小波分析及其工程应用考试试卷
1、简述傅里叶变换、短时傅里叶变换以及小波变换之间的异同,并
说明小波变换的必要性。
(10分)
2、小波变换堪称数学显微镜,且二维小波变换除了有显微能力之外,还有极化能力,请说明为什么?(10分)
3、说明小波变换的多分辨率分析和时-频局部化能力,请问该变换为
什么能够随着视野的变化自动调整分辨率以及如何调整?(10分)
4、请结合数学推导进行说明:当小波母函数满足正规性条件时,小
波变换能够凸显被分析的细节信息。
(10分)
5、为什么说小波变换的信息是冗余的?为减少其信息冗余度,可采
用离散栅格的方法予以改善,但会带来信息的失真的弊端,请问该如何尽
量避免这种失真?(10分)
6、请问利用函数空间剖分理论说明从第j-1级到j级分辨率的信号
分解过程,并建立同小波变换之间的关系。
(10分)
7、Mallat算法在小波变换中的地位,如同FFT算法在傅里叶变换中
的地位,具有十分重要的应用。
请结合论文说明信号分解时这种算法的基
本过程,以及如何在论文中实施应用,并列举应用时需要注意的事项。
(10分)
8、基于美林变换的算法,基于CZT的算法和Mallat算法分别适合什
么场合下应用?请结合基于CZT的算法和Mallat算法,谈谈任意尺度密
度下快速小波变换的策略。
(10分)
9、列举双通道多采样滤波器的理想重建条件,请问为什么?(10分)
10、小波变换是信号消噪处理的有效手段,请画出基于小波多分辨率
的信号消噪技术方案框图,并列举两类用于该方案的多尺度信噪分离规则。
(10分)。
小波理论期末试题

我个人的理解:小波分析是傅立叶分析思想的发展与延拓,它自产生以来,就一直与傅立叶分析密切相关,他的存在性证明,小波基的构造以及结果分析都依赖于傅立叶分析,二者是相辅相成的,两者主要的不同点:1、傅立叶变换实质是把能量有限信号f(t)分解到以{exp(jωt)}为正交基的空间上去;小 波变换的实质是把能量有限信号f(t)分解到W-j 和V-j 所构成的空间上去的。
2、傅立叶变换用到的基本函数只有sin(ωt),cos(ωt),exp(jωt),具有唯一性;小波分 析用到的函数(即小波函数)则具有多样性,同一个工程问题用不同的小波函数进行分析有时结果相差甚远。
小波函数的选用是小波分析运用到实际中的一个难点问题(也是小波分析研究的一个热点问题),目前往往是通过经验或不断地试验(对结果进行对照分析)来选择小波函数。
3、在频域分析中,傅立叶变换具有良好的局部化能力,特别是对于那些频率成分比较简单的确定性信号,傅立叶变换很容易把信号表示成各频率成分的叠加和的形式,如sin(ω1t)+0.345sin(ω2t)+4.23cos(ω3t),但在时域中傅立叶变换没有局部化能力,即无法从f(t)的傅立叶变换中看出f(t)在任一时间点附近的性态。
事实上,F(w)dw 是关于频率为w 的谐波分量的振幅,在傅立叶展开式中,它是由f(t)的整体性态所决定的。
4、在小波分析中,尺度a 的值越大相当于傅立叶变换中w 的值越小。
5、在短时傅立叶变换中,变换系数S(ω,τ)主要依赖于信号在[τ-δ,τ+δ]片段中的情况,时间宽度是2δ(因为δ是由窗函数g(t)唯一确定的,所以2δ是一个定值)。
在小波变换中,变换系数Wf (a,b )主要依赖于信号在[b-aΔφ,b+aΔφ)片断中的情况,时间宽度是2aΔφ,该时间的宽度是随尺度a 变化而变化的,所以小波变换具有时间局部分析能力。
6、若用信号通过滤波器来解释,小波变换与短时傅立叶变换不容之处在于:对短时傅立叶变换来说,带通滤波器的带宽Δf 与中心频率f 无关;相反小波变换带通滤波器的带宽Δf 则正比于中心频率f 。
小波分析30道题

1. 从Fourier 变换到小波变换的三个阶段: *)信号加窗;**)基加窗;***)小波基;⑴ Fourier 变换是一个强有力的数学工具,它具有重要的物理意义,即信号()f x 的Fourier 变换()()⎰+∞∞-ω-=ωx x f F x d e i表示信号的频谱。
正是Fourier 变换的这种重要的物理意义,决定了Fourier 变换在信号分析和信号处理中的独特地位,特别是作为平稳信号分析的最重要的工具。
但是,在实际应用中,所遇到的信号大多数并不是平稳的。
所以,随着应用范围的逐步扩大和理论分析的不断深入,Fourier 变换的局限性就渐渐展示出来了:首先,从理论上说,为了由Fourier 变换研究一个时域信号()f x 的频谱特性,必须获得信号在时域中的全部信息,以致于包括将来的信息;其次,Fourier 变换对信号的局部畸变没有标定和度量能力。
但是,在许多实际应用中,畸变正是我们所关心的信号在局部范围内的特征;再次,Fourier 变换不能反映信号在局部时间范围内和局部频带上的谱信息分析,或称为局部化时-频分析,而这正是许多实际应用最感兴趣的问题之一;最后,因为一个信号的频率与它的周期长度成反比,因而要给进行分析的一个灵活多变的时间和频率的“窗口”,使其在“中心频率(或称为平均频率、主频)”高的地方,时间窗自动变窄,而在“中心频率”低的地方,时间窗应自动变宽。
⑵ 时间加窗:Gabor 在1946年的论文中,为了提取信号的局部信息,这包括时间和频率两方面的局部信息,引入了一个时间局部化的“窗口函数”()g t b -,其中参数b 用于平行移动窗口,以便于覆盖整个时域。
Gabor 变换继承了Fourier 变换所具有的“信号频谱”这样的物理解释,同时,它克服了Fourier 变换只能反映信号的整体特征而对信号的局部特征没有任何分析能力的缺陷,大大地改进了Fourier 变换的分析能力,为信号处理提供了一种新的分析和处理工具,即信号的时-频分析。
研究生《小波理论及应用》复习题.doc

2005年研究生《小波理论及应用》复习题1.利用正交小波基建立的采样定理适合于:紧支集且有奇性(函数本身或其导数不连续)的函数(频谱无限的函数)。
Shannon采样定理适合于频谱有限的信号o2.信号的突变点在小波变换域常对于小波变换系数模极值点或过零点。
并且信号奇异性大小同小波变换的极值随尺度的变化规律相对立。
只有在适当尺度下各突变点引起的小波变化才能避免交迭干扰,可以用于信号的去噪、奇异性检测、图象也缘提取、数据压缩等。
3.信号在一点的李氏指数表征了该点的奇异性大小,。
越大,该点的光滑性越小,。
越小,该点的奇异性越大。
光滑点(可导)时,它的cr >1 ;如果是脉冲函数,白噪声时« <0 o4.做出三级尺度下正交小波包变换的二进数图,小波包分解过程?说明小波基与小波包基的区别?5.最优小波包基的概念:给定一个序列的代价函数,然后在小波包基中寻找使代价函数最小的基一一最优基。
6・双通道多采样率滤波器组的传递函数为:[人人 1 A ArU) = y.U)+y2U) = - H(Z)H(Z)+G G)G G) H(Z)H(Z)+G(—Z)G(J X(-J请根据此式给出理想重建条件:为了消除映象X(-z)引起的混迭://(-Z)//(Z)+G(-Z)G(Z)=0为了使y(z)成为x(z)的延迟,要求:H(z)育(z) + G(z)G(z)= CZ・k(C,K为任一常数)7・正交镜像对称滤波器/z(77)的)与H(e jw)以“彳为轴左右对称。
如果知道QMF的/2(/7),能否确定gS)=(T)"〃S), 細=-(-1)乜(司g(“)=(-i)w)8・试列出几种常用的连续的小波基函数Morlet 小波,Marr 小波,Difference of Gaussian (DOG),紧支集样条小波9・试简述海森堡测不准原理,说明应用意义?10. 从连续小波变换到离散小波变换到离散小波框架一双正交小波变换一正交变换、紧支集正交小波变换,其最大的特点是追求变换系数的信息冗余小,含有的信息量越集中。
小波分析考试题(附答案)

定义:空间 L2 ( R) 中的多分辨分析是指 L2 ( R) 满足如下性质的一个空间序列Z ∈j j }{V :
(1)单调性: ⊂⊂⊂⊂-101V V V ;(2)逼近性:)(},0{2R L V V j Z
j j Z
j ==∈∈ ;(3)伸缩性:1)2()(+∈⇔∈j j V t f V t f ;(4)平移不变性:j j V t f V t f ∈-⇒∈)1()(,
Z k ∈∀;(5)存在函数0)(V t g ∈,使得Z k k)}-{g(t ∈构成0V 的Riesz 基。
满足上述个条件
的函数空间集合成为一个多分辨分析, 如果)(t g 生成一个多 分辨分析,那么称)(t g 为一个尺度函数。
关于多分辨分析的理解,我们在这里以一个三层的分解进行说明,其小波分解树如图所示。
从图可以明显看出,多分辨分析只是对低频部分进行进一步分解,而高 频部分则不予以考虑。
分解的关系为 112}0{)(+-+++++=j j j V V V R L 。
另外强调一点这 里只是以一个层分解进行说明,如果要进行进一步的分解,则可以把低频部分分解成低频部分和高频部分,以下再分解以此类推。
在理解多分解分析时,我们必须牢牢把握一点:其分解的最终目的是力求构造一个在频率上高度逼近)(2R L 空间的正交小波基,这些频率分辨率不 同的正交小波基相当于带宽各异的带通滤波器。
从上面的多分辨分析树型结 构图可以看出,多分辨分析只对低频空间进行进一步的分解,使频率的分辨率变得越来越高。
Mallat 算法:通过下面公式(1)和(2),可以很快计算出尺度系数和小波系数{cj,k,dj,k},。
小波变换计算题

小波变换计算题
一、以下哪个描述不是小波变换的特点?
A. 多分辨率分析
B. 时间频率局部化
C. 固定的时频分辨率
D. 适用于非平稳信号
(答案)C
二、在小波变换中,以下哪个参数决定了小波函数的伸缩程度?
A. 平移参数
B. 尺度参数
C. 频率参数
D. 相位参数
(答案)B
三、以下哪种小波基函数常用于图像处理?
A. Haar小波
B. Morlet小波
C. Mexican Hat小波
D. Coiflet小波
(答案)A
四、对于一维信号f(t),进行小波变换后得到的小波系数反映了什么信息?
A. 信号的频率成分
B. 信号的时间延迟
C. 信号在特定时间和频率上的能量
D. 信号的相位信息
(答案)C
五、在小波变换中,若尺度参数增大,则对应的小波分析窗口会如何变化?
A. 时间窗口变宽,频率窗口变窄
B. 时间窗口变窄,频率窗口变宽
C. 时间窗口和频率窗口都变宽
D. 时间窗口和频率窗口都变窄
(答案)A
六、以下哪种小波变换常用于信号去噪?
A. 连续小波变换
B. 离散小波变换
C. 小波包变换
D. 多小波变换
(答案)B
七、在进行小波重构时,以下哪个步骤不是必需的?
A. 选择合适的小波基函数
B. 对小波系数进行阈值处理
C. 对小波系数进行逆变换
D. 对原始信号进行预处理
(答案)D
八、对于二维图像,进行小波变换后,通常得到几个子带?
A. 1个
B. 2个
C. 3个
D. 4个
(答案)D。
《水文小波分析原理及其应用》带答案

《水文小波分析原理及其应用》考试试题课程编号:7.637 学分:3.0 任课教师:刘东考试形式:开卷(1)小波分析:wavelet analysis ;(2)小波变换:wavelet transformation ;(3)小波函数:wavelet function ;(4)小波消噪:Wavelet denoising;(5)小波方差:Wavelet varianee ;(6)连续小波变换:Continuous wavelet transform(7)离散小波变换:Discrete wavelet tran sform ;(8)小波人工神经网络模型:Wavelet artificial neural network model;(9)小波随机耦合模型:Wavelet stochastic coupling model(10)快速小波变换算法:Fast wavelet tra nsform algorithm。
答:水文学是研究地球上水分分布、循环、运动等变化规律及水-环境相互作用的一门科学,属于地球科学的一个分支。
水文时间序列在各种因素影响下具有确定性成分、随机成分)。
水文学的一个重要研究途径就是利用现有分析技术对水文时间序列进行描述,探讨水文系统的演变规律。
小波变换克服了Fourier变换的不足,能够反映出水文时间序列在时频域上的总体特征以及时频局部化信息,被誉为数学显微镜”。
利用小波分析的多分辨率功能,可以充分挖掘水文时间序列所包含的信息,展现水文时间序列的精细结构,从而使我们更好地掌握水文时间序列的多时间尺度变化特征及突变特征。
可以说,在水文学领域引入小波分析,为揭示水文时间序列变化规律提供了一条新的研究途径,极大地丰富了水文学的内容。
由此可见,小波分析技术受到了国内外多数学者的青睐。
我们作为农业水土工程专业的研究生,如果能够成功地将小波分析技术与我们的研究内容相结合,必然会使我们的毕业论文增色不少,而且也会发表一批高水平的学术论文。
MATLAB小波分析复习题(第一章)

第一章FOURIER 变换与MATLAB 实现1. 设()f x 为定义在[,](0)T T T ->上的周期函数,则()f x 的Fourier 级数为01()cos sin ,2n n n a f x a nx b nx ∞==++∑ 其中,n n a b ==。
2. 设11,[0,)2()11,[,1]2x f x x ⎧∈⎪⎪=⎨⎪-∈⎪⎩,求()f x 的Fourier 级数。
3. 写出()f x 的傅里叶变换()F w 及逆变换()F w 的定义。
4. 写出2||1()()2x f x e heaviside x -=的傅里叶变换与逆变换2()1w F w w=+逆变换()f x 的MATLAB 程序实现清单。
5. 写出时限信号,带限信号,带宽,采样频率,奈圭斯特采样频率的定义。
6. 写出奈圭斯特采样定理。
7. ()f t 的频谱密度函数是什么?()f t 的振幅频谱是什么?()f t 的相位频谱是什么?8. 用MA TLAB 绘出2||1()()2x f x e heaviside x -=的振幅频谱图(幅频谱图)与相位频谱图。
9. 写出周期序列()x n 的离散Fourier 变换()c k 及其()c k 的离散Fourier 逆变换的定义。
10. 利用定义手工计算(4)(1,2,3,4)x =的离散Fourier 变换()X k 。
再使用MA TLAB 命令DFS 与IDFS 进行验证。
11. 已知信号()0.5sin()sin(/2)f t t t =+,今采样间隔为0.01t ∆=从而得到一个离散 信号()(),099x n f n t n =∆≤≤。
对()x n 使用离散Fourier 变换的MATLAB 命令DFS 得到()x n 的幅频谱图与相位频谱图。
12.证明并验证Fourier 变换的线性性:[()()][()][()]F x n y n F x n F y n αβαβ+=+。
近代数学 小波证明题+答案

一,证明:低通滤波器0h 与高通滤波器1h 的关系: )1()1()(01k h k h k --=证明: 0)()()()(1010=+++πωπωH H w H w H (1) ∴一定存在一个以π2为周期的函数)(ωλ使)()()(01πωωλ+=H w H (2) )()()2()()(001ωπωλπωπωλH H w H +=++= (3) 将(2),(3)带入(1)中有0)]()()[()(00=+++πωλωλπωωH H (4) 若(4)式成立则)()(πωλωλ++=0 有一个特解为:)2()(ωωλωg e i = (5)其中,)(ωg 为周期为π2的函数 将(5)代入(2)中有)()2()(01πωωωω+=H g e H i 取 ωωim eg =)(对所有的ω都成立,则有)()(0)12(1ωω+=+-H e H m i (6) 当 0=m 时,)()(01πωωω+=-H e H i 显然(6)是(1)的解, 由ki ke k h ωω-∑=H )(21)(00ki ke k h ωω-∑=H )(21)(11则 (6) 式左右两边分别为 ki ke k h ωω-∑=H )(21)(11 (7)∑∑-+----==+H kik kkki i i e k h e k h e e ωπωωωπω)1(21)1( )(21)(0)(00 (8)比较(7)(8)两式有)1()1()(01k h k h k --= 证毕一、证明因子a /1的作用是保证不同尺度下,函数)(,t b a ψ与母小波)(t ψ的能量相同。
证明:由)(/1)(,at a t b a τψψ-=,可知其能量为 dt at a dt t E b a 22,|)(/1||)(|⎰⎰+∞∞-+∞∞--==τψψ 令at x τ-=则有adx dt = ⎰⎰⎰+∞∞-+∞∞-+∞∞-===∴dx x dx x a a ax d x a E 222|)(||)(/1|)(|)(/1|ψψψ)(t ψ的能量E dt t E =='⎰+∞∞-2|)(|ψ由此可见因子a /1的作用是保证不同尺度下,函数)(,t b a ψ与母小波)(t ψ的能量相同。
小波变换试题答案

从傅里叶(Fourier)变换到伽柏(Gabor)变换再到小波(Wavelet)变换题目:从傅里叶(Fourier)变换到伽柏(Gabor)变换再到小波(Wavelet)变换本文是边学习边总结和摘抄各参考文献内容而成的,是一篇综述性入门文档,重点在于梳理傅里叶变换到伽柏变换再到小波变换的前因后果,对于一些概念但求多而全,所以可能会有些理解的不准确,后续计划分别再展开学习研究。
通过本文可以了解到:1)傅里叶变换的缺点;2)Gabor变换的概念及优缺点;3)什么是小波;4)小波变换的概念及优点。
一、前言首先,我必须说一下,在此之前,虽然我听说过小波变换(具体是前几年听一位博士毕业答辩里提到了小波降噪)但就再也没什么了,虽然近一年来零零散散地在接触语音信号处理过程中用过短时傅里叶变换(Short Time Fourier Transf orm, STFT),但也就如此了,之于Gabor变换听都没有听过。
这些天看稀疏基,其实也就是看各种变换了,前面看了离散余弦变换(Discret e CosineT ransfo rm, DCT)、离散正弦变换(Discret e Sine Transfo rm, DST)、离散W 变换(Discret eW Transfo rm, DWT)、离散哈特莱变换(Discret e Hartley Transfo rm, DHT),总体来说理解个表皮还是比较容易的,于是打算继续学习,随便挑了一个C urvele t基打算学习一下,搜了一下资料才发现不能从这个开始学习,必须Gabor、Wavelet、Ridgele t、Curvele t、Wedgele t、Bandele t、Beamlet、Contour let等慢慢开始学起,我知道我又陷入了一片沼泽,但或许是一片幸福的沼泽,一个做信号处理的人对这些是应该有一个基本的概念级了解的。
小波分析练习题(做了123456)
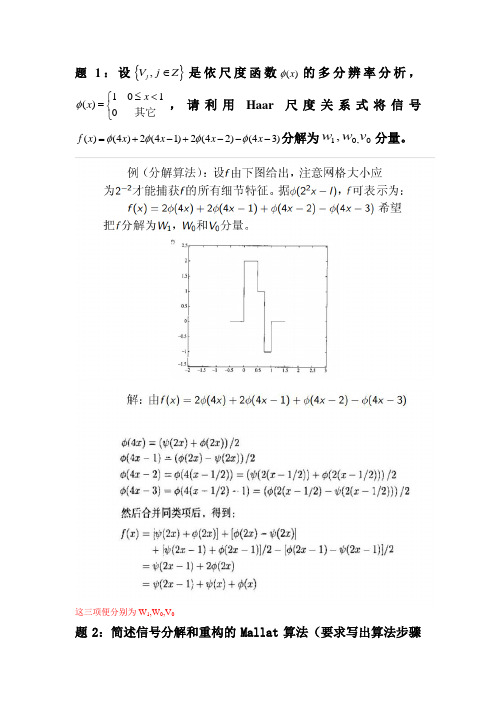
题1:设{},j V j Z ∈是依尺度函数()x φ的多分辨率分析,101()0x x φ≤<⎧=⎨⎩其它,请利用Haar 尺度关系式将信号()(4)2(41)2(42)(43)f x x x x x φφφφ=+-+---分解为10,0,w w v 分量。
这三项便分别为W 1,W 0,V 0题2:简述信号分解和重构的Mallat 算法(要求写出算法步骤并列出分解重构公式。
)分解初始化:选择适当的f j,用来逼近f迭代:由f j分解为f j-1和W j-1,……,以此类推,最后得到f0和W0终止:j=0,并生成下面那两个系数重构:差不多就是倒着说回去。
下面那个系数就是重构出来的f的系数(k(2)j jka x k φ-∑,好像是这个玩意)题3:设{},,,φφψψ构成双正交多分辨分析:(1)写出双正交条件;,,,,,,,,()()()()()()()()()()()(),,l n m n j k j l k nj k j m k nx x x x x x x x x k x k x k x k ϕϕψψϕψϕψϕϕψψϕϕδδψψδδ----<>=<>=⊂⊂⊂⊂⊂-2-1012设存在尺度函数、和小波函数和构成双正交多分辨率分析,则、、、应满足基本条件:(1)平移系{}、{}、{}、{}无关但不正交;(2)满足双正交条件:(3)两种空间嵌套序列:V V V V V ,,,{}{}j j k j j k V span V span ϕ⊂⊂⊂⊂⊂==-2-1012V V V V V 其中,,1111{}{}()(2)()(2)()(2)()(2)j j kj j k j j j j j j j j j j k k k Z k Z k k k Zk ZW span W span V W V W V V W V V W x x k x x k x x k x x k ψφφφφψφψφ----∈∈∈∈==⊥⊥=+=+=-=-=-=-(4)正交补关系:设(5)双尺度方程变为:(2) 写出4个双尺度方程(尺度系数分别为,,,k k k k h h g g );()(2)()2(2)k k k kt h t k t h t k φφφφ⎧=-⎪⎪⎨⎪=-⎪⎩∑ ()(2)()2(2)k k k k t g t k t g t k ψφψφ⎧=-⎪⎪⎨⎪=-⎪⎩∑ (3) 写出尺度系数间的对应关系。
《小波分析与应用》试题

《小波分析与应用》试题学院:信息科学与工程学姓名:钱宏学号:20064249 院1、[10’]小波变化俗称“数字显微镜”,试从尺度因子的变化对时频窗的中心和半径的影响,阐述其时频局部化功能。
尺度因子变大时,相应小波分量表现了某个子频带信号,其频率中心变高且频带变宽,时频窗呈“廋窄”的变化趋势,即时窗变窄,频窗变宽,正好适应于更高频信号时频局部化的需要。
相反,尺度因子变小时,同样相应小波分量表现了某个子频带信号,其频率中心变低且频带变窄,时频窗呈“扁平”的变化趋势,即时窗变宽,频窗变窄,正好适应于低频信号时频局部化的需要。
2、[10’]简述HHT变换的原理和简要实现过程。
HHT 方法包含两个主要步骤:1) 对原始数据进行预处理,即先通过经验模态分解方法, 把数据分解为满足希尔伯特变换要求的n 阶本征模式函数(IMF)和残余函数r n(t)之和;2)对分解出的每一阶IMF 做希尔伯特变换, 得出各自的瞬时频率,做出时频图。
其中经验模态分解(EMD)方法能把非平稳、非线性信号分解成一组稳态和线性的序列集, 即本征模式函数。
且每一阶的IMF 应满足两个条件: 1)数据的极值点和过零点交替出现, 且数目相等或最多相差一个任何点上;2)在任何点上,有局部最大值和局部最小值定义的包络的均值必须是零。
下面以时间序列X(t)介绍经验模态分解的一般过程。
首先, 找出X(t)所有极大和极小值点, 并用三次样条函数对极大值点和极小值点分别进行拟合得到X (t) 的上下包络线;然后将原始数据序列减去上下包络线的均值m1(t) , 就可以得到一个去掉低频的新数据序列:h1(t)=X(t)- m1(t),通常h1(t)不满足IMF 的条件, 还需对h1(t)重复上述处理过程。
经过k次筛分后将产生第1个IMF分量C1(t), 即h1k(t)=h1(k- 1)(t)- m1k(t),C1(t)=h1k(t)。
第1个IMF分量代表原始数据序列中最高频的成分,将原始数据序列X(t)减去第1个分量C1(t)。
小波分析作业(含自编程序)

地球科学学院小波分析课程作业课程名称:小波分析指导老师:学生姓名:学号:几种时频分析方法1 短时傅里叶变换为了研究信号在局部时间范围内的瞬时频率特性,1946年,D.GABOR 引进了短时傅氏变换或窗口傅氏变换的概念,其基本原理是取一个称为(t)g 窗口的函数,使它在有限的区间范围外恒等于零或趋于零。
设任意信号(t)f ,并假设该信号在一个以时间τ为中心,且范围有限的窗口函数)-(t τg 内是稳定的,这样,窗口内函数)-(t)g(t τf 的傅氏变换就定义为短时傅氏变换,表示为dt e T t i STFT ωτωτ--)-f(t)g(t ),(⎰∞∞=STFT 是通过滑动时窗来计算其频谱,因而它的时间分辨率和频率分辨率受Heisenberg 测不准原理约束。
因此利用短窗口有较高的时间分辨率,但是频率分辨率差。
2 小波变换常见的小波变换有连续、二进制以及离散小波变换等。
在连续小波变换中,仅要求小波函数满足容许条件即可,这使得在选择小波函数时具有很大的自由度。
对任意地震信号函数)((t)2R L f ∈,其连续小波变换定义为 )f(t)dt a b -t (a 1(t)f(t)dt b)(a,-*-b a,⎰⎰∞∞∞∞==ϕψw T 式中,a为尺度因子,b为平移参数,函数ψ(t)称为母小波。
小波分析具有可调的时频窗口,被广泛地应用于地震信号处理中,但是也存在着一定的局限性,主要表现在难以选择小波基、固定的基函数、恒定的多分辨率,信号的能量—时间—频率分布也很难定量给出。
3 S 变换为了解决短时傅氏变换只能以一种分辨率进行时频分析及小波变换不能直接与频率对应的缺陷,1996年美国地球物理学家Stockwell 在前人的基础上提出了S 变换。
S 变换中,基本小波是由简谐波与高斯函数的乘积构成的,基本小波中的简谐波在时间域仅作伸缩变换,而高斯函数则进行伸缩和平移。
这一点与连续小波变换不同,在连续小波变换中,简谐波与高斯函数进行同样的伸缩和平移。
近代数学_小波_计算题+答案

2.计算下列分形维数:(1)康托尔集合(the Cantor set)l o g l o g20.631l o g l o g3smDc=-=≈(2)科赫曲线(Koch)log41.262log3sD=-≈(3)谢尔平斯基(Sierpinski)地毯、垫片、海绵地毯:log log81.893log log3fDβκ==≈垫片:log log31.585log log2fDβκ==≈海绵:log log202.763log log3fDβκ==≈(4)阿波罗尼斯垫圆:解:不在此圆内部的点形成一个面积为零的集合,可以说它多于一条线但少于一个面,因此它的分形维数(5)皮亚诺曲线:log ln921ln3log()sNDβ===1.求按下列各图所示方法生成的分形图的分维初始元:生成元:(a)(b)(c)(a)log ln81.51ln4log()sNDβ==≈(b)log ln51.4651ln3log()sNDβ==≈(c)log ln51.4651ln3log()sNDβ==≈2、计算康托尔三分集相似维、Hausdorff 维 解:相似维:log ln 20.63111log()ln3s N D β==≈Hausdorff 维:log log 20.631log log3f D βκ==≈ 3、计算不规则分形盒维数(只计算右下端)ε=1/10 ()N ε=N(1/10)()ln ln 54ln 541.7321ln ln10ln 10B N D εε=-=-=≈二、求下面一维16点离散信号Haar 小波2级分解与重构计算过程及结果,并与Matlab 编程计算结果比较。
x=[ 3 7 8 5 6 5 9 8 3 7 8 5 13 3 9]解: Haar 小波对应的尺度函数为1t 0 1 0{)(≤≤=其它t ϕ低通滤波器系数)(0k h :⎩⎨⎧===⎰--02/1)()()(),()(*,1,10R kk dt t t t t k h ϕϕϕ 其它,==k k 10 )(0k h ={1,1,0,0,…….0}/2)(0k h -={0,0,0,0,……0,1,1}/2={1,1}/2由0h 求高通滤波系数1h⎪⎩⎪⎨⎧-=--=02/12/1)1()1()(01k h k h k其它===k k k 102/}0,.......0,0,1,1{)(1-=k h2/}1,1{2/}1,0,...,0,0{)(1-=-=-k h 1 级尺度系数212,9]/,13,6,4,6,7,11,10,1511,11,14,1[10,15,13, )(*)()(001=-=k c k h k C抽偶 2/]12,4,13,10,17,11,13,10[= 2 级尺度系数2/]16,2823,23[ 6,12]/227,23,17,1[23,24,28, )(*)()(102==-=抽偶k c k h k c 1 级小波系数2]/,-2,0,-6,9,-4,-1,3,41,1,-4,1,5[-4,-1,3,- )(*)()(011=-=k c k h k d抽偶 2/]6,2,3,4,1,1,3,4[----= 2 级小波系数2]/2,-3,9,-8,1[-3,2,-6,7 )(*)()(112=-=k c k h k d抽偶2/]8,3,6,3[ ----= 重构:(逐级重构) 2/]8,3,6,3[)(2----=k d2/]8,0,3,0,6,0,3,0[----=−−→−插值器2/]16,0,23,0,28,0,23,0[2/]16,23,28,23[)(插值器2=−−−−→−=k c2,24]/234,20,26,8[20,26,22, 22/]8,0,3,0,6,0,3,0[*]1,1[2]/2,0,23,0,16[0,23,0,28*[1,1] )(*)()(*)()(21201=-----+=+=k d k h k c k h k c2/]6,0,2,0,3,0,4,0,1,0,1,0,3,0,4,0[2/]6,2,3,4,1,1,3,4[)(1----=−−→−----=插值器k d22/]24,0,8,0,26,0,20,0,34,0,22,0,26,0,20,0[22/]24,8,26,20,34,22,26.20[)(1=−−→−=插值器k c9]3 13 5 8 7 3 8 9 5 6 5 8 7 [3 2,0,-6]/2-4,0,3,0,-0,1,0,1,0,[0,-4,0,3,*[1,-1] /4,0,8,0,24],0,20,0,26,0,22,0,34[0,20,0,26*[1,1] )(*)()(*)()(11100=+=+=k d k h k c k h k c一、已知)(t ϕ(尺度函数)求小波函数)(t ψ⎩⎨⎧=01)(t ϕ其它210≤≤t解:1)⎩⎨⎧=01)(t ϕ其它210≤≤t 易知,{})(n t -ϕ关于n 为一正交归一基.2)求n h()⎰∞--==0,1)2()(2),(dt n t t t t h n n ϕϕϕϕ其中,⎩⎨⎧=-01)2(n t()其它2/2/12/n t n +≤≤当0=n 时,⎩⎨⎧=01)2(t ϕ其它4/10≤≤t当1=n 时,⎩⎨⎧=-01)12(t其它4/32/1≤≤t故当0=n 时,⎩⎨⎧=-01)2().(n t t ϕϕ 其它0=n当0=n 时,⎩⎨⎧=-01)2().(n t t ϕϕ其它4/10≤≤t故⎩⎨⎧=-=⎰022/1)2().(2dt n t t h n ϕϕ 其它0=n3)求n g ⎩⎨⎧=-=022/1)1(n nn h g0=n4)求)()()(0,10,1t g t g t nn--==∑ϕϕψ⎰=⋅=021)2(222/1t ϕ 其它4/10≤≤t1)(t ϕt)(t ψ(ϕ。
小波分析(试卷)及答案

《小波分析与应用》试题及答案学院: 姓名: 学号:1、 [10’] Q 值是滤波器的品质因数,定义为/*Q ωω=∆=带宽/中心频率。
假设小波基函数为1/2,()()a b t a at b ψψ=-,试证明其恒Q 性质。
证:记*ω为频窗中心,ω∆为频窗的半径,则关于窗函数)(t ab ψ,有⎰=*Rab ab d ωωψωωψω22)()(11-121220)()()(1⎪⎪⎭⎫ ⎝⎛-=∆⎰*ωωψωωωψωd R ab ab 1-2 令上1-1、1-2式a=1、b=0可以得出基本量,特别标记为*∧ψω和∧∆ψ(对于给定的小波*∧ψω和∧∆ψ为常数)。
**∧====⎰⎰⎰ψωξξψξωψωωψωωψωωψωωψωa d aa d a a a d Roab R o ab Rab ab 222222)()()()()()()()(1∧∧∆=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=∆⎰⎰**ψψωωωψωωωψωωψωωωψa a d a a d R ab Rab ab 2122021220)()()()(1)()()(1滤波器的品质因数C a a Q =∆=∆=∆=***∧∧∧∧ψψψψωωωω(C 为常数)2、 [10’]假设给定信号的频率范围为(0-4000),使用Mallat 算子H和G 描述提取频率范围分别为(0~250)、(1000~1500)、(3000~4000)分量的分解过程。
图1 信号频率分解图3、 在Matlab 环境下,编写相关程序实现如下功能:加载noissin 信号,对其进行一维连续小波变换,分别绘制a=1.87和a=4.25时的连续小波变换系数曲线(非灰度图)。
clear clcload noissin;%加载信号s=noissin(1:200);%对s 信号进行一维连续小波变换 w1=cwt(s,1.87,'db3'); subplot(211);plot(w1); xlabel('时间'); ylabel('对应尺度a=1.87小波变换系数');w2=cwt(s,4.25,'db3'); subplot(212);plot(w2); xlabel('时间');ylabel('对应尺度a=4.25小波变换系数');图2尺度a=1.87和尺度a=4.25小波变换系数4、[15’] snr=10;init=学号;[xref,x]= wnoise(4,11, snr,init),(1)画出原始信号x的时域波形;(2)使用db3小波进行三层小波分解,设置阈值向量p=[80,87,97]对高频系数进行阈值处理(指令为wthcoef),然后重构,画出重构曲线;(3)使用db3小波进行三层小波分解,对高频系数全部置零,然后重构,画出重构曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、叙述小波分析理论发展的历史和研究现状答:傅立叶变换能够将信号的时域和特征和频域特征联系起来,能分别从信号的时域和频域观察,但不能把二者有机的结合起来。
这是因为信号的时域波形中不包含任何频域信息,而其傅立叶谱是信号的统计特性,从其表达式中也可以看出,它是整个时间域内的积分,没有局部化分析信号的功能,完全不具备时域信息,也就是说,对于傅立叶谱中的某一频率,不能够知道这个频率是在什么时候产生的。
这样在信号分析中就面临一对最基本的矛盾——时域和频域的局部化矛盾。
在实际的信号处理过程中,尤其是对非常平稳信号的处理中,信号在任一时刻附近的频域特征很重要。
如柴油机缸盖表明的振动信号就是由撞击或冲击产生的,是一瞬变信号,单从时域或频域上来分析是不够的。
这就促使人们去寻找一种新方法,能将时域和频域结合起来描述观察信号的时频联合特征,构成信号的时频谱,这就是所谓的时频分析,亦称为时频局部化方法。
为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并开发了一系列新的信号分析理论:短时傅立叶变换、时频分析、Gabor 变换、小波变换Randon-Wigner变换、分数阶傅立叶变换、线形调频小波变换、循环统计量理论和调幅—调频信号分析等。
其中,短时傅立叶变换和小波变换也是因传统的傅立叶变换不能够满足信号处理的要求而产生的。
短时傅立叶变换分析的基本思想是:假定非平稳信号在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的功率谱。
但从本质上讲,短时傅立叶变换是一种单一分辨率的信号分析方法,因为它使用一个固定的短时窗函数,因而短时傅立叶变换在信号分析上还是存在着不可逾越的缺陷。
小波变换是一种信号的时间—尺度(时间—频率)分析方法,具有多分辨率分析(Multi-resolution)的特点,而且在时频两域都具有表征信号局部特征的能力,使一种窗口大小固定不变,但其形状可改变,时间窗和频率窗都可以改变的时频局部化分析方法。
小波变换在低频部分具有较高的频率分辨率和较低的时间分辨率。
在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬态反常现象并展示其成分,所以被誉为分析信号的显微镜。
小波分析最早应用在地震数据压缩中, 以后在图像处理、故障诊断等方面取得了传统方法根本无法达到的效果. 现在小波分析已经渗透到了自然科学、应用科学等方面, 小波分析已成为国际研究热点. 无论是傅里叶分析还是小波分析均以线性变换为基础, 按非线性傅立叶分析提出了非线性小波变换, 这种非线性小波变换处理非线性问题更为有效.二、分析小波的基本定义答:小波(Wavelet)这一术语,顾名思义,“小波”就是小的波形。
所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动性,其振幅正负相间的震荡形式。
与Fourier 变换相比,小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier 变换的困难问题,成为继Fourier 变换以来在科学方法上的重大突破。
有人把小波变换称为“数学显微镜”。
小波分析方法是一种窗口大小(即窗口面积)固定但其形状可改变,时间窗和频率窗都可改变的时频局部化分析方法,即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率。
正是这种特性,是小波变换具有对信号的自适应性。
小波分析被看成调和分析这一数学领域半个世纪以来的工作结晶,已经和必将广泛地应用于信号处理、图像处理、量子场论、地震勘探、语音识别与合成、音乐、雷达、CT 成像、彩色复印、流体湍流、天体识别、机器视觉、机械故障诊断与监控、分形以及数字电视等科技领域。
原则上讲,传统上使用傅立叶分析的地方,都可以用小波分析取代。
小波分析优于傅立叶变换的地方是,它在时域和频域同时具有良好的局部化性质。
设()()R L t 2∈ψ(()R L 2表示平方可积的实数空间,即能量有限的信号空间),其傅立叶变换为()ωψ∧。
()ωψ∧满足允许条件(Admissible Condition ): ()∞<∧=⎰ωωωψψd R C 2时,我们称()t ψ为一个基本小波或母小波(Mother Wavelet )。
将母函数()t ψ经伸缩和平移后,就可以得到一个小波序列。
对于连续的情况,小波序列为⎪⎭⎫ ⎝⎛-=a b t a b a ψψ1, 0;.≠∈a R b a 其中,a 为伸缩因子,b 为平移因子。
对于离散的情况,小波序列为()k t j j k j -=--222/,ψψ Z k j ∈,对于任意的函数()()R L t f 2∈的连续小波变换为()()t d a b t t f af b a W R b a f ⎰⎪⎭⎫ ⎝⎛-==-ψψ2/1,,, 其逆变换为 ()()⎰⎰⎪⎭⎫ ⎝⎛-=+dadb a b t b a W a C t f f R R t ψ,112 小波变换的时频窗口特性与短时傅立叶的时频窗口不一样。
其窗口形状为两个矩形[]⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆+±⎪⎭⎫ ⎝⎛∆-±⨯∆+∆-∧∧a a a b a b /,/,00ψωψωψψ,窗口中心为()a b /,0ω±,时窗宽和频窗宽分别为ψ∆a 和a /∧∆ψ。
其中b 仅仅影响窗口在相平面时间轴上的位置,而a 不仅影响窗口在频率轴上的位置,也影响窗口的形状。
这样小波变换对不同的频率在时域上的取样步长是调节性的:在低频时小波变换的时间分辨率较差,而频率分辨率较高;在高频时小波变换的时间分辨率较高,而频率分辨率较低,这正符合低频信号变化缓慢而高频信号变换迅速的特点。
这便是它优于经典的傅立叶变换与短时傅立叶变换的地方。
从总体上来说,小波变换比短时傅立叶变换具有更好的时频窗口特性。
三、小波分析是傅立叶分析思想方法的发展与延拓,二者相辅相成,试对小波分析和傅立叶变换进行比较答:小波分析是傅立叶分析思想的发展与延拓,它自产生以来,就一直与傅立叶分析密切相关,他的存在性证明,小波基的构造以及结果分析都依赖于傅立叶分析,二者是相辅相成的,两者主要的不同点:1、傅立叶变换实质是把能量有限信号f(t)分解到以{exp(jωt)}为正交基的空间上去;小波变换的实质是把能量有限信号f(t)分解到W-j和V-j所构成的空间上去的。
2、傅立叶变换用到的基本函数只有sin(ωt),cos(ωt),exp(jωt),具有唯一性;小波分析用到的函数(即小波函数)则具有多样性,同一个工程问题用不同的小波函数进行分析有时结果相差甚远。
小波函数的选用是小波分析运用到实际中的一个难点问题(也是小波分析研究的一个热点问题),目前往往是通过经验或不断地试验(对结果进行对照分析)来选择小波函数。
3、在频域分析中,傅立叶变换具有良好的局部化能力,特别是对于那些频率成分比较简单的确定性信号,傅立叶变换很容易把信号表示成各频率成分的叠加和的形式,如sin(ω1t)+0.345sin(ω2t)+4.23cos(ω3t),但在时域中傅立叶变换没有局部化能力,即无法从f(t)的傅立叶变换中看出f(t)在任一时间点附近的性态。
事实上,F(w)dw是关于频率为w的谐波分量的振幅,在傅立叶展开式中,它是由f(t)的整体性态所决定的。
4、在小波分析中,尺度a的值越大相当于傅立叶变换中w的值越小。
5、在短时傅立叶变换中,变换系数S(ω,τ)主要依赖于信号在[τ-δ,τ+δ]片段中的情况,时间宽度是2δ(因为δ是由窗函数g(t)唯一确定的,所以2δ是一个定值)。
在小波变换中,变换系数Wf(a,b)主要依赖于信号在[b-aΔφ,b+aΔφ)片断中的情况,时-间宽度是2aΔφ,该时间的宽度是随尺度a变化而变化的,所以小波变换具有时间局部分析能力。
6、若用信号通过滤波器来解释,小波变换与短时傅立叶变换不容之处在于:对短时傅立叶变换来说,带通滤波器的带宽Δf 与中心频率f 无关;相反小波变换带通滤波器的带宽Δf 则正比于中心频率f 。
四、阐述多分辨分析的思想并给出MALLAT 算法的表达式答:Meyer 于1986年创造性地构造出具有一定衰减性的光滑函数,其二进制伸缩与平移构成()R L 2的规范正交基,才使小波得到真正的发展。
1988年S.Mallat 在构造正交小波基时提出了多分辨分析(Multi-Resolution Analysis )的概念,从空间的概念上形象地说明了小波的多分辨率特性,将此之前的所有正交小波基的构造法统一起来,给出了正交小波的构造方法以及正交小波变化的快速算法,即Mallat 算法。
Mallat 算法在小波分析中的地位相当于快速傅立叶变换算法在经典傅立叶分析中的地位。
定义:空间)(2R L 中的多分辨分析是指)(2R L 满足如下性质的一个空间序列{}Z j j V ∈:(1)调一致性:1+⊂j j V V ,对任意Z j ∈(2)渐进完全性:Φ=∈j Z j V I ,{})(2R L V U close j Z j =∈ (3)伸缩完全性:1)2()(+∈⇔∈j j V t f V t f(4)平移不变性:j j j j j V k t V t Z k ∈-⇒∈∈∀--)2()2(,2/2/φφ(5)Riesz 基存在性:存在0)(V t ∈φ,使得{}Z k k t j j ∈--|)2(2/φ构成j V 的Risez 基。
关于Riesz 的具体说明如下:若)(t φ是0V 的Risez 基,则存在常数A ,B ,且,使得:{}{}222222)(k k k c B k t c c A ≤-≤∑φ 对所有双无限可平方和序列{}k c ,即 {}∞<=∑∈222Zk k k c c 成立。
满足上述个条件的函数空间集合成为一个多分辨分析,如果)(t φ生成一个多分辨分析,那么称)(t φ为一个尺度函数。
关于多分辨分析的理解,我们在这里以一个三层的分解进行说明,其小波分解树如图所示。
从图可以明显看出,多分辨分析只是对低频部分进行进一步分解,而高频部分则不予以考虑。
分解的关系为1231D D D A S +++=。
另外强调一点这里只是以一个层分解进行说明,如果要进行进一步的分解,则可以把低频部分3A 分解成低频部分4A 和高频部分4D ,以下再分解以此类推。
在理解多分解分析时,我们必须牢牢把握一点:其分解的最终目的是力求构造一个在频率上高度逼近()R L 2空间的正交小波基,这些频率分辨率不同的正交小波基相当于带宽各异的带通滤波器。
