第2章部分习题答案讲义.
2019-2020学年人教版生物必修三讲义:第2章 第4节 免疫调节 Word版含答案

第4节 免疫调节学习目 标核 心 素 养1.概述免疫系统的组成2.简述体液免疫和细胞免疫的过程及其关系3.概述免疫系统在维持稳态中的作用4.了解免疫失调引起的疾病1.通过比较非特异性免疫与特异性免疫、体液免疫与细胞免疫的异同,形成辩证统一的观点2.通过分析体液免疫与细胞免疫过程的模式图,培养模型分析能力与建模的思维能力3.通过总结艾滋病的流行与预防等知识,形成健康生活、关爱他人的人生态度一、免疫系统的组成二、免疫系统的防卫功能1.非特异性免疫(1)组成①第一道防线:皮肤、黏膜。
②第二道防线:体液中的杀菌物质(如溶菌酶)和吞噬细胞。
(2)特点:生来就有,不针对某一类特定病原体。
2.特异性免疫(第三道防线)(1)组成:主要由免疫器官和免疫细胞借助血液循环和淋巴循环而组成。
(2)作用:抵抗外来病原体和抑制肿瘤等。
三、特异性免疫的方式1.体液免疫(1)抗原和抗体的概念①抗原:能够引起机体产生特异性免疫反应的物质。
②抗体:机体受抗原刺激后产生的,并且能与该抗原发生特异性结合的具有免疫功能的蛋白质。
(2)体液免疫的过程①参与细胞:吞噬细胞、T细胞、B细胞、记忆细胞、浆细胞。
②结果:抗体可以与病原体结合,抑制病原体的繁殖或对人体细胞的黏附;多数情况下,抗体与抗原结合,形成沉淀或细胞集团,进而被吞噬细胞吞噬消化。
2.细胞免疫(1)阶段Ⅰ:抗原经过吞噬细胞的摄取和处理,再呈递给T细胞。
(2)阶段Ⅱ:T细胞受到抗原刺激后,开始一系列的增殖、分化,大部分形成效应细胞,小部分形成记忆细胞。
(3)阶段Ⅲ:效应T细胞和靶细胞结合,使靶细胞裂解死亡,释放内部的抗原。
四、免疫系统的监控和清除功能及免疫失调疾病1.免疫系统的监控和清除功能:免疫系统可以监控并清除体内已经衰老或因其他因素而被破坏的细胞,以及癌变的细胞。
2.免疫系统的功能异常及疾病(连线)提示:A→③→a→Ⅱ A→②→c→Ⅰ B→①→b→Ⅲ五、免疫学的应用1.接种疫苗可以预防传染病的发生。
2019-2020年人教版化学必修一讲义:第2章+第1节+课时1 简单分类法及其应用及答案

第一节 物质的分类课时1 简单分类法及其应用目标与素养:1.认识物质的分类方法和依据,学会对常见物质分类。
(宏观辨识)2.感受分类在科研和学习中的重要作用。
(社会责任)一、常见的分类方法1.交叉分类法(1)含义:根据不同的分类标准,对同一事物进行多种分类的一种分类方法。
即对事物以不同的标准进行分类。
(2)举例①Na 2CO 3⎩⎨⎧ 按其组成的阳离子来分类,属于钠盐按其组成的阴离子来分类,属于碳酸盐按其溶解性来分类,属于可溶盐②将不同的物质与它所属的类别进行连线。
2.树状分类法(1)含义:对同类事物按照某些属性进行再分类的分类方法,即对同类事物进行再分类。
(2)举例微点拨:交叉分类法是对同一物质以不同的分类标准或角度进行分类,属交叉关系;树状分类法是对同类物质按不同的属性进行逐级分类,各级之间为从属关系,同级之间为并列关系。
二、分类方法的应用分类可以帮助我们更好地认识物质的性质,找出各类物质之间的关系: Ca ――→①CaO ――→②Ca (OH )2――→③CaCO 3 C ――→④CO 2――→⑤H 2CO 3――→⑥CaCO 3――→⑦CaO举例写出有关序号的一种化学方程式并注明反应类型(答案不唯一,合理即可)。
①2Ca +O 2===2CaO ;化合反应。
②CaO +H 2O===Ca(OH)2;化合反应。
③Ca(OH)2+Na 2CO 3===CaCO 3↓+2NaOH ;复分解反应。
④C +O 2=====点燃CO 2;化合反应。
⑤CO 2+H 2O===H 2CO 3;化合反应。
⑥H 2CO 3+Ca(OH)2===CaCO 3↓+2H 2O ;复分解反应。
⑦CaCO 3=====高温CaO +CO 2↑;分解反应。
CO +CuO=====△Cu +CO 2是置换反应吗?提示:不是。
1.判断正误(正确的打“√”,错误的打“×”)(1)交叉分类法是对一种物质的多角度分类法。
中考复习讲义 第2章对称图形 2.4 圆周角定理与圆内接图形(含参考答案)

圆周角定理与圆内接图形圆心角和圆周角1. 圆心角:顶点在圆心的角叫做圆心角.将整个圆分为360等份,每一份的弧对应1︒的圆心角,我们也称这样的弧为1︒的弧.圆心角的度数和它所对的弧的度数相等.2. 圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角.3. 圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧相等. 推论2:半圆(或直径)所对的圆周角是直角,90︒的圆周角所对的弦是直径. 推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.4. 圆心角、弧、弦、弦心距之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.5. 推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等.6. 圆的基本性质有:⑴ 直径所对的圆周角是直角. ⑵ 同弧所对的圆周角相等.⑶ 经过圆心及一弦中点的直线垂直平分该弦. 7. 不在同一直线上的三个点确定一个圆 8. 圆的内接四边形对角互补,外角等于内对角模块一 圆周角定理【例1】 若O e 的一条弧所对的圆周60︒,则这条弧所对的圆心角是( )A .30︒B .60︒ C.120︒D.以上答案都不对【答案】C【例2】 如图,BC 是圆O 的弦,圆周角50ABC ∠=︒,则OCA ∠的度数是_______BCAO【答案】40︒【例3】 如图,O e 正方形ABCD 的外接圆,点P 在O e 上,则APB ∠等于( )自检自查必考点中考必做题OP DCBAA .30︒B .45︒C .55︒D .60︒ 【答案】45︒【例4】 如图,点C 在O e 上,将圆心角AOB ∠绕点O 按逆时针方向旋转到''A OB ∠,旋转角为α,(0α︒<<180︒).若30AOB ∠=︒,'40BCA ∠=︒,则α∠=_______OA'BA【答案】110︒【例5】 如图,AB 是O e 的直径,CD 是O e 的弦。
《优化指导》化学总复习(人教)配套讲义:第二章 基础课2电解质离子反应 含答案

基础课2电解质离子反应考点一从分类依据上突破电解质及其电离(1)分类依据:(2)电解质的强弱与物质类别的关系:今有10种物质:①Al②稀硝酸③乙酸④液氨⑤CO2⑥NaCl⑦BaSO4⑧Na2CO3⑨酒精⑩Al2O3其中属于电解质的是:________;属于非电解质的是________;属于强电解质的是________;属于弱电解质的是________;熔融状态下能导电的电解质是________。
答案:③⑥⑦⑧⑩④⑤⑨⑥⑦⑧⑩③⑥⑦⑧⑩依据元素周期表,突破强、弱电解质的记忆ⅠA:除LiOH外其余都是强碱.ⅡA:除Mg(OH)2、Be(OH)2外其余都是强碱。
ⅢA:Al(OH)3是两性氢氧化物。
ⅣA:H2CO3、H2SiO3均为弱酸。
ⅤA:强酸:HNO3中强(或弱)酸:HNO2、H3PO4。
ⅥA:强酸:H2SO4弱酸:H2SO3、H2S.ⅦA:强酸:HCl、HBr、HI、HClO4等弱酸:HF、HClO等.过渡元素中常见的弱碱:Fe(OH)3、Fe(OH)2、Cu(OH)2、Zn(OH)2等。
注意:盐不论难溶、易溶,绝大多数都是强电解质。
2.电解质的电离(1)概念:电解质在水溶液中或熔融状态下,电离成自由移动的离子的过程。
(2)电离条件:酸的电离条件是溶于水,盐和碱的电离条件是溶于水或熔融,金属氧化物的电离条件是熔融.3.电离方程式的书写(1)强电解质:完全电离,用===表示。
如H2SO4、NaOH、(NH4)2SO4的电离方程式分别为H2SO4===2H++SO2-4;NaOH===Na++OH-;(NH4)SO4===2NH错误!+SO错误!。
2(2)弱电解质:部分电离,用表示。
①多元弱酸分步电离,且电离程度逐步减弱,以第一步电离为主。
如H2S的电离方程式为H2S H++HS-、HS-H++S2-。
②多元弱碱分步电离,但一步写出。
如Cu(OH)2Cu2++2OH-。
③两性氢氧化物双向电离。
如Al(OH)3的电离方程式:H++AlO错误!+H2O错误!Al(OH)3错误!Al3++3OH-.(3)酸式盐:①强酸酸式盐完全电离,一步写出.如NaHSO4在水溶液中的电离方程式为NaHSO4===Na++H++SO错误!,在熔融状态下的电离方程式为NaHSO4===Na++HSO-4。
人教版生物必修二讲义:第2章 第1节 减数分裂和受精作用(Ⅱ)含答案

第1节减数分裂和受精作用(Ⅱ)1.运用模型、装片或视频观察模拟减数分裂过程中染色体的变化。
2.阐明减数分裂产生染色体数量减半的卵细胞,并和精子的形成过程进行比较。
(重点) 3.归纳减数分裂中染色体、染色单体、DNA数目的变化规律。
(重、难点)4.学会辨析细胞分裂的图像。
知识点一卵细胞的形成过程[学生用书P23]阅读教材P19~P201.形成场所:卵巢。
2.细胞的变化写出上图中各种细胞的名称:a.卵原细胞;b.初级卵母细胞;c.第一极体;d.次级卵母细胞;e.第二极体;f.卵细胞。
1.卵细胞形成过程图解(假设体细胞中染色体数为2n)2.精子和卵细胞形成过程的差异项目精子形成过程卵细胞形成过程场所睾丸卵巢细胞质分裂方式均等分裂不均等分裂是否变形变形不变形结果一个精原细胞4个精子一个卵原细胞1个卵细胞、3个极体1.在下图中,不属于精子形成过程的是()[解析]选C。
卵细胞与精子的产生过程基本相同,它们的不同点主要集中在产生部位、分裂后形成的生殖细胞的数量、细胞质的分配特点及其是否变形等。
卵细胞形成过程的两次分裂的后期细胞质不均等分裂。
2.右图是某生物的细胞分裂模式图,以下说法错误的是()A.该细胞处于减数第二次分裂后期B.该细胞不含同源染色体C.该细胞是次级精母细胞或次级卵母细胞D.该细胞分裂形成的子细胞不一定是两个精细胞[解析]选C。
该细胞分裂图中不存在同源染色体,也不存在姐妹染色单体,该细胞处于减数第二次分裂后期,故A、B两项均正确;细胞质进行的是均等分裂,则该细胞可能是次级精母细胞或第一极体,故C项错误,D项正确。
知识点二减数分裂中染色体、DNA等数目的变化规律[学生用书P24]完成表中内容(假设生物正常细胞中染色体数为2N,核DNA数为2C)细胞分裂图像分裂次数分裂时期染色体数核DNA数染色单体数间期2N2C→4C0→4N减数第一次分裂前期2N4C4N中期2N4C4N后期2N4C4N末期2N→N4C→2C4N→2N减数第二次分裂前期N2C2N中期N2C2N后期2N2C0末期2N→N2C→C0细胞减数分裂过程中染色体数目和核DNA含量变化曲线分析1.下图表示细胞分裂过程中染色体、核DNA变化相对值。
《应用光学》第2章课后答案解析

l = 2f′
B F′ B′ A A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平A′ H
H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
第二章 部分习题答案
牛顿公式 一、物像位置关系 二、物像大小关系 1、垂轴放大率 2、轴向放大率 3、角放大率 三、物方像方焦距关系 四、物像空间不变式
f' n' f n
y nl y nl
高斯公式
f' f 1 l' l
nuy n' u' y'
2. 有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反
f' l 2
B
B′ A F′ A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
l=0
B
B′
F′ H A
A′ H′
F
像平面为: 像方主平面
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
考虑物镜组二主面之间的距离)。 解:
9. 已知航空照相机物镜的焦距f′=500mm,飞机飞行高度为
6000m,相机的幅面为300×300mm2,问每幅照片拍摄的地
面面积。 解:
10. 由一个正透镜组和一个负透镜组构成的摄远系统,前组
正透镜的焦距f1′=100,后组负透镜的焦距f2 ′=-50,要 求由第一组透镜到组合系统像方焦点的距离D与系统的组合 焦距之比为1∶1.5,求二透镜组之间的间隔d应为多少?组 合焦距等于多少?
高中数学第2章2.3双曲线2.3.1双曲线的标准方程讲义(含解析)苏教版选修2_1

2.3.1 双曲线的标准方程[对应学生用书P25]在平面直角坐标系中A (-3,0),B (3,0),C (0,-3),D (0,3).问题1:若动点M 满足|MA -MB |=4,设M 的坐标为(x ,y ),则x ,y 满足什么关系? 提示:x 24-y 25=1.问题2:若动点M 满足|MC -MD |=4,设M 的坐标为(x ,y ),则x ,y 满足什么关系? 提示:y 24-x 25=1.双曲线的标准方程焦点在x 轴上 焦点在y 轴上标准方程 x 2a 2-y 2b 2=1(a >0,b >0) y 2a 2-x 2b 2=1(a >0,b >0) 焦点坐标(±c,0)(0,±c )a ,b ,c 的关系c 2=a 2+b 21.双曲线的标准方程与椭圆不同,左边是含x ,y 项的平方差,右边是1. 2.在双曲线中,a >0且b >0,但a 与b 的大小关系不确定. 3.在双曲线中a 、b 、c 满足c 2=a 2+b 2,与椭圆不同.[对应学生用书P26]用待定系数法求双曲线方程[例1] 已知双曲线过点P (-2,-3),Q ⎝⎛⎭⎪⎫153,2两点,求双曲线的标准方程. [思路点拨] 解答本题可分情况设出双曲线的标准方程,再构造关于a 、b 、c 的方程组求解,从而得出双曲线的标准方程.也可以设双曲线方程为mx 2+ny 2=1(mn <0)的形式,将两点代入,简化运算过程.[精解详析] 法一:当双曲线的焦点在x 轴上时,设双曲线方程为x 2a 2-y 2b2=1(a >0,b >0),∵P (-2,-3),Q ⎝⎛⎭⎪⎫153,2两点在双曲线上. ∴⎩⎪⎨⎪⎧(-2)2a 2-(-3)2b2=1,⎝ ⎛⎭⎪⎫1532a 2-(2)2b 2=1,解得⎩⎪⎨⎪⎧1a 2=1,1b 2=13,即a 2=1,b 2=3,∴所求双曲线的标准方程为x 2-y 23=1.当双曲线的焦点在y 轴上时,设双曲线方程为y 2a 2-x 2b 2=1(a >0,b >0), ∵P (-2,-3),Q ⎝⎛⎭⎪⎫153,2两点在双曲线上, ∴⎩⎪⎨⎪⎧(-3)2a 2-(-2)2b2=1,(2)2a 2-⎝ ⎛⎭⎪⎫1532b 2=1.解得⎩⎪⎨⎪⎧1a 2=-13,1b 2=-1,(不符合题意,舍去).综上:所求双曲线的标准方程为x 2-y 23=1.法二:设双曲线的方程为mx 2+ny 2=1(mn <0), 因为双曲线过两点P (-2,-3),Q ⎝⎛⎭⎪⎫153,2,得⎩⎪⎨⎪⎧m (-2)2+n (-3)2=1,m ⎝ ⎛⎭⎪⎫1532+n (2)2=1,解得⎩⎪⎨⎪⎧m =1,n =-13,所以所求双曲线的标准方程为x 2-y 23=1. [一点通] 用待定系数法求双曲线方程的一般步骤为:1.根据下列条件,求双曲线的标准方程.(1)已知双曲线与椭圆x 227+y 236=1有共同的焦点,且过点(15,4),求双曲线的方程;(2)c =6,经过点(-5,2),焦点在x 轴上.解:(1)椭圆x 227+y 236=1的焦点坐标为F 1(0,-3),F 2(0,3),故可设双曲线的方程为y 2a 2-x 2b 2=1. 由题意,知⎩⎪⎨⎪⎧a 2+b 2=9,42a2-(15)2b 2=1,解得⎩⎪⎨⎪⎧a 2=4,b 2=5.故双曲线的方程为y 24-x 25=1.(2)∵焦点在x 轴上,c =6,∴设所求双曲线方程为x 2λ-y 26-λ=1(其中0<λ<6).∵双曲线经过点(-5,2),∴25λ-46-λ=1,∴λ=5或λ=30(舍去). ∴所求双曲线方程是x 25-y 2=1.2.求适合下列条件的双曲线的标准方程:(1)a =4,c =5,焦点在y 轴上;(2)焦点为(0,-6),(0,6),经过点A (-5,6). 解:(1)由题设知,a =4,c =5, 由c 2=a 2+b 2,得b 2=c 2-a 2=52-42=9.因为双曲线的焦点在y 轴上,所以所求双曲线的标准方程为y 216-x 29=1.(2)由已知得c =6,且焦点在y 轴上.因为点A (-5,6)在双曲线上,所以点A 与两焦点的距离的差的绝对值是常数2a ,即2a =|(-5-0)2+(6+6)2-(-5-0)2+(6-6)2|=|13-5|=8,则a =4,b 2=c 2-a 2=62-42=20.因此,所求双曲线的标准方程是y 216-x 220=1.曲线方程的讨论[例2] 若方程x 25-m +y 2m 2-2m -3=1表示焦点在y 轴上的双曲线,求实数m 的取值范围.[思路点拨] 由双曲线的焦点在y 轴上,得关于m 的不等式组,进而解不等式组求m 的范围.[精解详析] 由方程x 25-m +y 2m 2-2m -3=1表示焦点在y 轴上的双曲线,得⎩⎪⎨⎪⎧5-m <0,m 2-2m -3>0.解得m >5.所以实数m 的取值范围是(5,+∞).[一点通] 给出方程x 2m +y 2n =1(mn ≠0),当mn <0时,方程表示双曲线,当⎩⎪⎨⎪⎧m >0,n <0时,表示焦点在x 轴上的双曲线;当⎩⎪⎨⎪⎧m <0,n >0时,表示焦点在y 轴上的双曲线.3.k >9是方程x 29-k +y 2k -4=1表示双曲线的____________条件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”).解析:x 29-k +y 2k -4=1表示双曲线的充要条件是(9-k )·(k -4)<0,即k >9或k <4. 因为k >9是k >9或k <4的充分不必要条件.即k >9是方程x 29-k +y 2k -4=1表示双曲线的充分不必要条件.答案:充分不必要 4.若方程x 22-m+y 2|m |-3=1表示焦点在x 轴上的双曲线,则实数m 的取值范围是________;若该方程表示双曲线,则m 的取值范围是________.解析:①若表示焦点在x 轴上的双曲线,则⎩⎪⎨⎪⎧2-m >0|m |-3<0⇒-3<m <2.②若该方程表示双曲线,则 (2-m )(|m |-3)<0. 解得-3<m <2或m >3.答案:(-3,2) (-3,2)∪(3,+∞)双曲线的定义及其标准方程的应用[例3] 已知F 1,F 2是双曲线x 29-y 216=1的两个焦点,P 是双曲线左支上的点,且PF 1·PF 2=32,试求△F 1PF 2的面积.[思路点拨] 本题是有关双曲线的焦点三角形问题,解答本题的关键是求得∠F 1PF 2的大小.由余弦定理,根据已知条件,结合双曲线的定义即可求得结果.[精解详析] 双曲线的标准方程为x 29-y 216=1,可知a =3,b =4,c =a 2+b 2=5.由双曲线的定义,得|PF 2-PF 1|=2a =6,将此式两边平方,得PF 21+PF 22-2PF 1·PF 2=36, ∴PF 21+PF 22=36+2PF 1·PF 2=36+2×32=100. 在△F 1PF 2中,由余弦定理,得cos ∠F 1PF 2=PF 21+PF 22-F 1F 222PF 1·PF 2=100-1002PF 1·PF 2=0,∴∠F 1PF 2=90°,∴S △F 1PF 2=12PF 1·PF 2=12×32=16.[一点通] 在解决双曲线中与焦点三角形有关的问题时,首先要考虑定义|PF 1-PF 2|=2a ,其次要利用余弦定理(或勾股定理)建立关于PF 1、PF 2、F 1F 2的方程,解方程组可求得PF 1、PF 2或PF 1·PF 2,再解决相关问题.5.已知双曲线x 216-y 225=1的左焦点为F ,点P 为双曲线右支上一点,且PF 与圆x 2+y2=16相切于点N ,M 为线段PF 的中点,O 为坐标原点,则MN -MO =________.解析:如图,设F ′是双曲线的右焦点,连接PF ′,因为M ,O 分别是FP ,FF ′的中点,所以MO =12PF ′,又FN =OF 2-ON 2=5,由双曲线的定义知PF -PF ′=8,故MN -MO =-12PF ′+MF -FN =12(PF-PF ′)-FN =12×8-5=-1.答案:-16.如图所示,已知定圆F 1:x 2+y 2+10x +24=0,定圆F 2:x 2+y 2-10x +9=0,动圆M 与定圆F 1,F 2都外切,求动圆圆心M 的轨迹方程.解:圆F 1:(x +5)2+y 2=1,圆F 2:(x -5)2+y 2=42, ∴F 1(-5,0),半径r 1=1;F 2(5,0),半径r 2=4. 设动圆M 的半径为R ,则MF 1=R +1,MF 2=R +4, ∴MF 2-MF 1=3<F 1F 2=10.∴动圆圆心M 的轨迹是以F 1、F 2为焦点的双曲线左支, 且a =32,c =5.∴b 2=25-94=914.∴动圆圆心M 的轨迹方程为4x 29-4y 291=1(x ≤-32).1.用定义法求双曲线的标准方程时,要注意是一支还是两支.2.用待定系数法求双曲线的标准方程时,要先判断焦点所在的位置,设出标准方程后,由条件列出a ,b ,c 的方程组.[对应课时跟踪训练(十)]1.双曲线x 225-y 224=1上的点P 到一个焦点的距离为11,则它到另一个焦点的距离为________.解析:设双曲线的左、右焦点分别为F 1,F 2,不妨设PF 1=11,根据双曲线的定义知|PF 1-PF 2|=2a =10,∴PF 2=1或PF 2=21,而F 1F 2=14,∴当PF 2=1时,1+11<14(舍去),∴PF 2=21.答案:212.已知点F 1,F 2分别是双曲线x 216-y 29=1的左、右焦点,P 为双曲线右支上一点,I 是△PF 1F 2的内心,且S △IPF2=S △IPF 1-λS △IF 1F 2,则λ=________.解析:设△PF 1F 2内切圆的半径为r ,则由S △IPF 2=S △IPF 1-λS △IF 1F 2⇒12×PF 2×r =12×PF 1×r -12λ×F 1F 2×r ⇒PF 1-PF 2=λF 1F 2,根据双曲线的标准方程知2a =λ·2c ,∴λ=a c =45.答案:453.若方程x 2k -3+y 2k +3=1(k ∈R )表示双曲线,则k 的范围是________.解析:依题意可知:(k -3)(k +3)<0,求得-3<k <3. 答案:-3<k <34.已知椭圆x 24+y 2a 2=1与双曲线x 2a -y 22=1有相同的焦点,则实数a =________.解析:由双曲线x 2a -y 22=1可知a >0,且焦点在x 轴上,根据题意知4-a 2=a +2,即a2+a -2=0,解得a =1或a =-2(舍去).故实数a =1.答案:15.已知双曲线的两个焦点为F 1(-10,0),F 2=(10,0),M 是此双曲线上的一点,且满足1MF u u u u r ·2MF u u u u r =0,|1MF u u u u r |·|2MF u u u u r|=2,则该双曲线的方程是________.解析:∵1MF u u u u r ·2MF u u u u r =0,∴1MF u u u u r ⊥2MF u u u u r.∴|1MF u u u u r |2+|2MF u u u u r |2=40.∴(|1MF u u u u r |-|2MF u u u u r |)2=|1MF u u u u r |2-2|1MF u u u u r |·|2MF u u u u r |+|2MF u u u u r |2=40-2×2=36.∴||1MF u u u u r |-|2MF u u u u r||=6=2a ,a =3.又c =10,∴b 2=c 2-a 2=1, ∴双曲线方程为x 29-y 2=1.答案:x 29-y 2=16.求适合下列条件的双曲线的标准方程:(1)以椭圆x 225+y 29=1的长轴端点为焦点,且经过点P (5,94);(2)过点P 1(3,-4 2),P 2(94,5).解:(1)因为椭圆x 225+y 29=1的长轴端点为A 1(-5,0),A 2(5,0),所以所求双曲线的焦点为F 1(-5,0),F 2(5,0).由双曲线的定义知,|PF 1-PF 2| =|(5+5)2+(94-0)2-(5-5)2+(94-0)2|=| (414)2- (94)2| =8,即2a =8,则a =4.又c =5,所以b 2=c 2-a 2=9.故所求双曲线的标准方程为x 216-y 29=1.(2)设双曲线的方程为Ax 2+By 2=1(AB <0),分别将点P 1(3,-4 2),P 2(94,5)代入,得⎩⎪⎨⎪⎧9A +32B =1,8116A +25B =1,解得⎩⎪⎨⎪⎧A =-19,B =116,故所求双曲线的标准方程为y 216-x 29=1.7.设F 1,F 2为双曲线x 24-y 2=1的两个焦点,点P 在双曲线上,且满足∠F 1PF 2=120°.求△F 1PF 2的面积.解:由已知得a =2,b =1;c = a 2+b 2=5, 由余弦定理得:F 1F 22=PF 21+PF 22-2PF 1·PF 2cos 120°即(2 5)2=(PF 1-PF 2)2+3PF 1·PF 2 ∵|PF 1-PF 2|=4.∴PF 1·PF 2=43.∴S △F 1PF 2=12PF 1·PF 2·sin 120°=12×43×32=33. 8. 如图,在△ABC 中,已知|AB |=4 2,且三内角A ,B ,C 满足2sinA +sin C =2sinB ,建立适当的坐标系,求顶点C 的轨迹方程.解: 以AB 边所在直线为x 轴,AB 的垂直平分线为y 轴,建立平面直角坐标系(如图所示).则A (-2 2,0),B (2 2,0).设边BC 、AC 、AB 的长分别为a 、b 、c ,由正弦定理得sin A =a 2R ,sin B =b 2R ,sin C =c2R (R 为△ABC 外接圆的半径).∵2sin A +sin C =2sin B ,∴2a +c =2b ,即b -a =c2.从而有|CA |-|CB |=12|AB |=2 2<|AB |.由双曲线的定义知,点C 的轨迹为双曲线的右支(除去与x 轴的交点).∵a =2,c =2 2,∴b 2=6.∴顶点C 的轨迹方程为x 22-y 26=1(x >2).。
第2章部分习题答案讲义.

【解】:
阶码采用双符号位, 尾数采用单符号位, 则有
y=11 100, 1.011100
x=00 011, 0.110100 (1) 求阶码和
[Ex]补+ [Ey]补= 00 011+ 11 100= 11 111, 其数值为 -1.
第12页
第二章
习题解答
(2)乘法运算(直接并行补码阵列) ( 0) 1 × ( 1) 0 ( 0) 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0
第13页第二章习题解答2乘法运算直接并行补码阵列第14页第二章习题解答11000101100003规格化当前计算结果不是规格化数向左规格化阶码减1即111101000101100004舍入处理1111010001105溢出判断阶码运算无溢出故结果无溢出
第二章
习题解答
7.若浮点数 x 的IEEE754标准32位存储格式为(8FEFC000 )16, 求其浮点数的十进制值。 【解】: 将x展开成二进制:
(1) 1 1 0 0 1 0 0 1 0 1 1 故 [x×y]补=1. 1001001011 所以 x×y=-0. 0110110101
注意位数对齐
第 8页
第二章
习题解答
22. 已知x和y,用原码阵列除法器计算x÷y。 (1)x=0.10011 y=-0.11011 被除数/余数 【解】: [x]原=0.10011 01001100000 +[-y’]补 100101 [y]原=1.11011 11100000000 商的符号位为: + [y’]补 011011 xf⊕yf=0⊕1=1 令 0010110000 x’=1001100000 y’=11011, +[-y’]补 100101 其中x’和y’分别为[x]原和 [y]原 111011000 + [y’]补 011011 的数值部分: 01000100 [x’]补=01001100000 +[-y’]补 100101 [y’]补=011011 0001110 + [-y’]补 100101 [-y’]补=100101
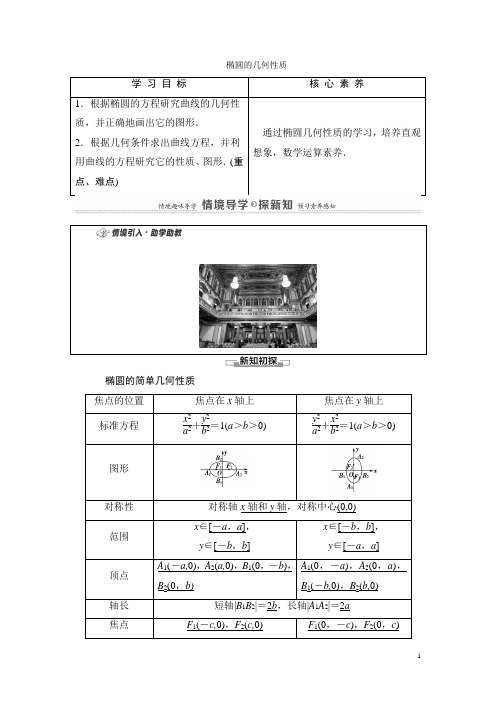
第2章 2.5.2 椭圆的几何性质-人教B版(2021)高中数学选择性必修第一册讲义
椭圆的几何性质学习目标核心素养1.根据椭圆的方程研究曲线的几何性质,并正确地画出它的图形.2.根据几何条件求出曲线方程,并利用曲线的方程研究它的性质、图形.(重点、难点)通过椭圆几何性质的学习,培养直观想象,数学运算素养.椭圆的简单几何性质焦点的位置焦点在x轴上焦点在y轴上标准方程x2a2+y2b2=1(a>b>0)y2a2+x2b2=1(a>b>0)图形对称性对称轴x轴和y轴,对称中心(0,0)范围x∈[-a,a],y∈[-b,b]x∈[-b,b],y∈[-a,a]顶点A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)轴长短轴|B1B2|=2b,长轴|A1A2|=2a焦点F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)焦距 |F 1F 2|=2c 离心率 e =ca (0<e <1)[提示] 最大距离:a +c ;最小距离:a -c .[提示] 在方程x 2a 2+y 2b 2=1(a >b >0)中,a ,b ,c 的几何意义如图所示.即a ,b ,c 正好构成了一个以对称中心,一个焦点、一个短轴顶点构成的直角三角形.1.思考辨析(正确的打“√”,错误的打“×”) (1)椭圆x 2a 2+y 2b 2=1(a >b >0)的长轴长等于a . ( ) (2)椭圆上的点到焦点的距离的最小值a -c . ( ) (3)椭圆上的离心率e 越小,椭圆越圆. ( )[答案] (1)× (2)√ (3)√[提示] (1)× 椭圆x 2a 2+y 2b 2=1(a >b >0)的长轴长等于2a .(2)√ 椭圆上的点到焦点的距离的最大值为a +c ,最小值为a -c . (3)√ 离心率e =ca 越小,c 就越小,这时b 就越接近于a ,椭圆就越圆. 2.椭圆6x 2+y 2=6的长轴端点坐标为( ) A .(-1,0),(1,0) B .(-6,0),(6,0) C .(-6,0),(6,0)D .(0,-6),(0,6)D [x 2+y 26=1焦点在y 轴上,长轴端点坐标为(0,-6),(0,6).] 3.椭圆x 2+4y 2=4的离心率为( )A.32B.34C.22D.23A[化椭圆方程为标准形式得x24+y2=1,所以a2=4,b2=1,所以c2=a2-b2=3.所以e=ca =32.]4.椭圆x29+y216=1的焦点坐标是,顶点坐标是.(0,±7)(±3,0),(0,±4)[由方程x29+y216=1知焦点在y轴上,所以a2=16,b2=9,c2=a2-b2=7.因此焦点坐标为(0,±7),顶点坐标为(±3,0),(0,±4).]椭圆的几何性质【例1】点的坐标.[思路探究]化为标准方程,确定焦点位置及a,b,c的值,再研究相应的几何性质.[解]把已知方程化成标准方程x252+y242=1,可知a=5,b=4,所以c=3.因此,椭圆的长轴和短轴的长分别是2a=10和2b=8,离心率e=ca =35,两个焦点分别是F1(-3,0)和F2(3,0),椭圆的四个顶点是A1(-5,0),A2(5,0),B1(0,-4)和B2(0,4).1.已知椭圆的方程讨论性质时,若不是标准形式的先化成标准形式,再确定焦点的位置,进而确定椭圆的类型.2.焦点位置不确定的要分类讨论,找准a与b,正确利用a2=b2+c2求出焦点坐标,再写出顶点坐标.提醒:长轴长、短轴长、焦距不是a ,b ,c ,而应是a ,b ,c 的两倍.[跟进训练]1.求椭圆4x 2+9y 2=36的长轴长和焦距、焦点坐标、顶点坐标和离心率. [解] 将椭圆方程变形为x 29+y 24=1, ∴a =3,b =2,∴c =a 2-b 2=9-4=5.∴椭圆的长轴长和焦距分别为2a =6,2c =25,焦点坐标为F 1(-5,0),F 2(5,0),顶点坐标为A 1(-3,0),A 2(3,0),B 1(0,-2),B 2(0,2),离心率e =c a =53.利用几何性质求椭圆的标准方程(1)与椭圆4x 2+9y 2=36有相同的焦距,且离心率为55; (2)长轴长是短轴长的2倍,且过点(2,-4). [解] (1)将方程4x 2+9y 2=36化为x 29+y 24=1,可得椭圆焦距为2c =25.又因为离心率e =55, 即55=5a ,所以a =5,从而b 2=a 2-c 2=25-5=20. 若椭圆焦点在x 轴上,则其标准方程为x 225+y 220=1; 若椭圆焦点在y 轴上,则其标准方程为y 225+x 220=1. (2)依题意2a =2×2b ,即a =2b .若椭圆焦点在x 轴上,设其方程为x 2a 2+y 2b 2=1(a >b >0),则有⎩⎨⎧a =2b ,4a 2+16b 2=1.解得⎩⎪⎨⎪⎧a 2=68,b 2=17,所以标准方程为x 268+y 217=1.若椭圆焦点在y 轴上,设其方程为y 2a 2+x 2b 2=1(a >b >0),则有⎩⎨⎧a =2b ,16a 2+4b 2=1,解得⎩⎪⎨⎪⎧a 2=32,b 2=8.所以标准方程为x 28+y 232=1.利用待定系数法求椭圆标准方程的基本步骤及注意事项 (1)用几何性质求椭圆的标准方程通常采用的方法是待定系数法.(2)根据已知条件求椭圆的标准方程的思路是“选标准,定参数”,即先明确焦点的位置或分类讨论.一般步骤是:①求出a 2,b 2的值;②确定焦点所在的坐标轴;③写出标准方程.(3)在求解a 2、b 2时常用方程(组)思想,通常由已知条件与关系式a 2=b 2+c 2,e =ca 等构造方程(组)加以求解.提醒:解答本例时容易忽视焦点的位置而漏解.[跟进训练]2.求适合下列条件的椭圆的标准方程: (1)长轴长是10,离心率是45;(2)在x 轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为6. [解] (1)设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b 2=1(a >b >0). 由已知得2a =10,a =5,e =c a =45,∴c =4. ∴b 2=a 2-c 2=25-16=9.∴椭圆方程为x 225+y 29=1或x 29+y 225=1. (2)依题意可设椭圆方程为 x 2a 2+y 2b 2=1(a >b >0).如图所示,△A 1F A 2为一等腰直角三角形,OF 为斜边A 1A 2的中线(高),且|OF |=c ,|A 1A 2|=2b,2c =6, ∴c =b =3,∴a 2=b 2+c 2=18, 故所求椭圆的方程为x 218+y 29=1.求椭圆的离心率[探究问题[提示] 根据e =ca ,a 2-b 2=c 2,可知要求e ,关键是找出a ,b ,c 的等量关系.[提示]【例3】 已知F 1,F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A ,B 两点,若△ABF 2是正三角形,求该椭圆的离心率.[思路探究] 由题设求得A 、B 点坐标,根据△ABF 2是正三角形得出a ,b ,c 的关系,从而求出离心率.[解] 设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),焦点坐标为F 1(-c,0),F 2(c,0). 依题意设A 点坐标为⎝ ⎛⎭⎪⎫-c ,b 2a ,则B 点坐标为⎝ ⎛⎭⎪⎫-c ,-b 2a ,∴|AB |=2b 2a .由△ABF 2是正三角形得2c =32×2b 2a , 即3b 2=2ac ,又∵b 2=a 2-c 2,∴3a 2-3c 2-2ac =0, 两边同除以a 2得3⎝ ⎛⎭⎪⎫c a 2+2c a -3=0,解得e =c a =33.[解] 设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),焦点坐标为F 1(-c,0),F 2(c,0), 设A 点坐标为(0,y 0)(y 0>0),则B 点坐标为⎝ ⎛⎭⎪⎫-c 2,y 02,∵B 点在椭圆上, ∴c 24a 2+y 204b 2=1, 解得y 20=4b 2-b 2c 2a2,由△AF 1F 2为正三角形得4b 2-b 2c 2a 2=3c 2, 即c 4-8a 2c 2+4a 4=0,两边同除以a 4得e 4-8e 2+4=0, 解得e =3-1.2.(变换条件)“若△ABF 2是正三角形”换成“椭圆的焦点在x 轴上,且A 点的纵坐标等于短半轴长的23”,求椭圆的离心率.[解] 设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),F 1(-c,0),F 2(c,0), 由题意知A ⎝ ⎛⎭⎪⎫-c ,23b 在椭圆上, ∴c 2a 2+49=1,解得e =53.求椭圆离心率的方法(1)直接求出a 和c ,再求e =ca ,也可利用e =1-b 2a 2求解.(2)若a 和c 不能直接求出,则看是否可利用条件得到a 和c 的齐次等式关系,然后整理成ca 的形式,并将其视为整体,就变成了关于离心率e 的方程,进而求解.1.已知椭圆的方程讨论性质时,若不是标准形式要先化成标准形式,再确定焦点的位置,找准a 、b .2.利用椭圆的几何性质求标准方程通常采用待定系数法. 3.求离心率e 时,注意方程思想的运用.1.椭圆x 29+y 216=1的离心率( ) A .74 B .916 C .13D .14A [a 2=16,b 2=9,c 2=7,从而e =c a =74.]2.若中心在原点,焦点在x 轴上的椭圆的长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( )A .x 281+y 272=1 B .x 281+y 29=1 C .x 281+y 245=1D .x 281+y 236=1A [由已知得a =9,2c =13×2a ,∴c =13a =3,b 2=a 2-c 2=72. 又焦点在x 轴上,∴椭圆方程为x 281+y 272=1.]3.椭圆x 2+my 2=1的焦点在y 轴上,长轴长是短轴长的2倍,则m 的值为( )A .12B .2C .14D .4C [椭圆x 2+my 2=1的标准形式为:x 2+y 21m=1.因为焦点在y 轴上,且长轴长是短轴长的2倍,所以1m =4,所以m =14.]4.若一个椭圆长轴的长度,短轴的长度和焦距成等差数列,则该椭圆的离心率是 .35 [由题意有2a +2c =2(2b ),即a +c =2b , 又c 2=a 2-b 2,消去b 整理得5c 2=3a 2-2ac , 即5e 2+2e -3=0,∴e =35或e =-1(舍去).] 5.已知椭圆的标准方程为x 24+y 29=1. (1)求椭圆的长轴长和短轴长; (2)求椭圆的离心率;(3)求以此椭圆的长轴端点为短轴端点,并且经过点P (-4,1)的椭圆方程. [解] (1)椭圆的长轴长为2a =6,短轴长为2b =4. (2)c =a 2-b 2=5,所以椭圆的离心率e =c a =53.(3)若以椭圆的长轴端点为短轴端点,则b ′=3,可设椭圆方程为x 2a ′2+y 29=1,又椭圆过点P (-4,1),将点P (-4,1)代入得16a ′2+19=1, 解得a ′2=18.故所求椭圆方程为x 218+y29=1.。
2019_2020高中物理第二章恒定电流第7节闭合电路的欧姆定律讲义习题(含解析)新人教版选修3_1

第7节闭合电路的欧姆定律1.了解内电路、外电路,知道电动势等于内外电路电势降落之和。
2.掌握闭合电路的欧姆定律并会进行有关计算。
3.会用闭合电路的欧姆定律分析路端电压与负载的关系。
一、闭合电路的欧姆定律1.闭合电路的组成及电流流向2.闭合电路的欧姆定律二、路端电压与负载(外电阻)的关系1.路端电压与电流的关系:U=□01E-Ir。
2.路端电压随外电阻的变化规律(1)外电阻R增大时,电流I□02减小,外电压U□03增大,当R增大到无限大(断路)时,I =□040,U=□05E,即断路时的□06路端电压等于电源□07电动势。
(2)外电阻R减小时,电流I□08增大,路端电压U□09减小,当R减小到零时,即电源短路时I =□10E r,U =□110。
在实验课上,小明同学用电压表去测量1节新干电池的电动势约为1.5 V,1节旧干电池的电动势约为1.45 V ,现在他把这样的两节旧电池串联后接在一个标有“3 V 2 W”的小灯泡两端,结果发现小灯泡不发光,检查电路的连接,各处均无故障。
电池虽然旧了,但电动势并没有减小多少,那么小灯泡为什么不亮呢?提示:电池变旧后,电动势并不明显减小,但内阻明显变大,因而使电路中的电流很小,小灯泡不发光。
(1)电动势就是电源两极间的电压。
( )(2)闭合电路中的电流跟电源电动势成正比,跟整个电路的电阻成反比。
( ) (3)外电路的电阻越大,路端电压就越大。
( ) (4)闭合电路中的短路电流无限大。
( )(5)电源断路时,电流为零,所以路端电压也为零。
( )(6)外电阻变化可以引起内电压的变化,从而引起内电阻的变化。
( ) (7)电源U I 图象上某点纵、横坐标的乘积对应此时的输出功率。
( ) 提示:(1)× (2)√ (3)√ (4)× (5)× (6)× (7)√课堂任务闭合电路的欧姆定律仔细观察下列图片,认真参与“师生互动”。
数学专业英语第2章课后答案上课讲义

数学专业英语第2章课后答案上课讲义2.12.比:ratio 比例:proportion 利率:interest rate 速率:speed 除:divide 除法:division 商:quotient 同类量:like quantity 项:term 线段:line segment 角:angle 长度:length 宽:width高度:height 维数:dimension 单位:unit 分数:fraction 百分数:percentage3.(1)一条线段和一个角的比没有意义,他们不是相同类型的量.(2)比较式通过说明一个量是另一个量的多少倍做出的,并且这两个量必须依据相同的单位.(5)为了解一个方程,我们必须移项,直到未知项独自处在方程的一边,这样就可以使它等于另一边的某量.4.(1)Measuring the length of a desk, is actually comparing the length of the desk to that of a ruler.(3)Ratio is different from the measurement, it has no units. The ratio of the length and the width of the same book does not vary when the measurement unit changes.(5)60 percent of students in a school are female students, which mean that 60 students out of every 100 students are female students.2.22.初等几何:elementary geometry 三角学:trigonometry 余弦定理:Law of cosines 勾股定理/毕达哥拉斯定理:Gou-Gu theorem/Pythagoras theorem 角:angle 锐角:acute angle 直角:right angle 同终边的角:conterminal angles 仰角:angle of elevation 俯角:angle of depression 全等:congruence 夹角:included angle 三角形:triangle 三角函数:trigonometric function直角边:leg 斜边:hypotenuse 对边:opposite side 临边:adjacentside 始边:initial side 解三角形:solve a triangle 互相依赖:mutually dependent 表示成:be denoted as 定义为:be defined as3.(1)Trigonometric function of the acute angle shows the mutually dependent relations between each sides and acute angle of the right triangle.(3)If two sides and the included angle of an oblique triangle areknown, then the unknown sides and angles can be found by using the law of cosines.(5)Knowing the length of two sides and the measure of the included angle can determine the shape and size of the triangle. In other words, the two triangles made by these data are congruent.4.(1)如果一个角的顶点在一个笛卡尔坐标系的原点并且它的始边沿着x轴正方向,这个角被称为处于标准位置.(3)仰角和俯角是以一条以水平线为参考位置来测量的,如果正被观测的物体在观测者的上方,那么由水平线和视线所形成的角叫做仰角.如果正被观测的物体在观测者的下方,那么由水平线和视线所形成的的角叫做俯角.(5)如果我们知道一个三角形的两条边的长度和对着其中一条边的角度,我们如何解这个三角形呢?这个问题有一点困难来回答,因为所给的信息可能确定两个三角形,一个三角形或者一个也确定不了.2.32.素数:prime 合数:composite 质因数:prime factor/prime divisor 公倍数:common multiple 正素因子: positive prime divisor 除法算式:division equation 最大公因数:greatest common divisor(G.C.D) 最小公倍数: lowest common multiple(L.C.M) 整除:divide by 整除性:divisibility 过程:process 证明:proof 分类:classification 剩余:remainder辗转相除法:Euclidean algorithm 有限集:finite set 无限的:infinitely 可数的countable 终止:terminate 与矛盾:contrary to3.(1)We need to study by which integers an integer is divisible, that is , what factor it has. Specially, it is sometime required that an integer is expressed as the product of its prime factors.(3)The number 1 is neither a prime nor a composite number;A composite number in addition to being divisible by 1 and itself, can also be divisible by some prime number.(5)The number of the primes bounded above by any given finite integer N can be found by using the method of the sieve Eratosthenes.4.(1)数论中一个重要的问题是哥德巴赫猜想,它是关于偶数作为两个奇素数和的表示.(3)一个数,形如2p-1的素数被称为梅森素数.求出5个这样的数.(5)任意给定的整数m和素数p,p的仅有的正因子是p和1,因此仅有的可能的p和m的正公因子是p和1.因此,我们有结论:如果p是一个素数,m是任意整数,那么p整除m,要么(p,m)=1.2.42.集:set 子集:subset 真子集:proper subset 全集:universe 补集:complement 抽象集:abstract set 并集:union 交集:intersection 元素:element/member 组成:comprise/constitute包含:contain 术语:terminology 概念:concept 上有界:bounded above 上界:upper bound 最小的上界:least upper bound 完备性公理:completeness axiom3.(1)Set theory has become one of the common theoretical foundation and the important tools in many branches of mathematics.(3)Set S itself is the improper subset of S; if set T is a subset of S but not S, then T is called a proper subset of S.(5)The subset T of set S can often be denoted by {x}, that is, T consists of those elements x for which P(x) holds.(7)This example makes the following question become clear, that is, why may two straight lines in the space neither intersect nor parallel.4.(1)设N是所有自然数的集合,如果S是所有偶数的集合,那么它在N中的补集是所有奇数的集合.(3)一个非空集合S称为由上界的,如果存在一个数c具有属性:x<=c对于所有S中的x.这样一个数字c被称为S的上界.(5)从任意两个对象x和y,我们可以形成序列(x,y),它被称为一个有序对,除非x=y,否则它当然不同于(y,x).如果S和T是任意集合,我们用S*T表示所有有序对(x,y),其中x术语S,y属于T.在R.笛卡尔展示了如何通过实轴和它自己的笛卡尔积来描述平面的点之后,集合S*T 被称为S和T的笛卡尔积.2.52.竖直线:vertical line 水平线:horizontal line 数对:pairs of numbers 有序对:ordered pairs 纵坐标:ordinate 横坐标:abscissas 一一对应:one-to-one 对应点:corresponding points圆锥曲线:conic sections 非空图形:non vacuous graph 直立圆锥:right circular cone 定值角:constant angle 母线:generating line 双曲线:hyperbola 抛物线:parabola 椭圆:ellipse退化的:degenerate 非退化的:nondegenerate 任意的:arbitrarily 相容的:consistent 在几何上:geometrically 二次方程:quadraticequation 判别式:discriminant 行列式:determinant3.(1)In the planar rectangular coordinate system, one can set up aone-to-one correspondence between points and ordered pairs of numbers and also a one-to-one correspondence between conic sections and quadratic equation.(3)The symbol can be used to denote the set of ordered pairs (x,y)such that the ordinate is equal to the cube of the abscissa.(5)According to the values of the discriminate,the non-degenerate graph of Equation (iii)maybe known to be a parabola, a hyperbolaor an ellipse.4.(1)在例1,我们既用了图形,也用了代数的代入法解一个方程组(其中一个方程式二次的,另一个是线性的)。
人教版物理必修一讲义:第2章习题课1 匀变速直线运动规律的应用Word版含答案

习题课1匀变速直线运动规律的应用[学习目标] 1.掌握匀变速直线运动的两个基本公式.2.掌握三个平均速度公式及其适用条件,会应用平均速度公式求解相关问题.3.会推导Δx=aT2,并会用它解决相关问题.1.02.位移公式:x=v0t+12at2.3.应用时注意的问题(1)基本公式中的v0、v、a、x都是矢量,在直线运动中,若规定了正方向,它们都可用带正、负号的代数值表示,把矢量运算转化为代数运算.通常情况下取初速度方向为正方向,凡是与初速度同向的物理量都取正值,凡是与初速度反向的物理量取负值.(2)两个基本公式含有五个物理量,可“知三求二”.(3)逆向思维法的应用:末速度为0的匀减速直线运动,可以倒过来看成是初速度为0的匀加速直线运动.(4)解决运动学问题的基本思路:审题→画过程草图→判断运动性质→选取正方向(或选取坐标轴)→选用公式列方程→求解方程,必要时对结果进行讨论.【例1】在一段限速为50 km/h的平直道路上,一辆汽车遇到紧急情况刹车,刹车后车轮在路面上滑行并留下9.0 m长的笔直的刹车痕.从监控录像中得知该车从刹车到停止的时间为1.5 s.请你根据上述数据计算该车刹车前的速度,并判断该车有没有超速行驶.思路点拨:①若涉及速度、时间问题,应用v=v0+at列式分析.②若涉及位移、时间问题,应用x=v0t+12at2列式分析.[解析]已知汽车刹车的位移为x=9 m,刹车后运动时间t=1.5 s,刹车后的末速度为v=0由于汽车刹车后做匀减速直线运动,根据速度时间关系有:v=v0+at根据匀减速直线运动位移—时间关系有:x=v0t+12at2联立解得汽车刹车时的速度v0=12 m/s=43.2 km/h因为43.2 km/h<50 km/h,所以该汽车没有超速行驶.[答案]12 m/s没有超速1.(多选)一个物体以v0=8 m/s的初速度沿光滑斜面向上滑,加速度的大小为2 m/s2,冲上最高点之后,又以相同的加速度往回运动.则()A.第1 s末的速度大小为6 m/sB.第3 s末的速度为零C.2 s内的位移大小是12 mD.5 s内的位移大小是15 mACD[由t=v-v0a,物体冲上最高点的时间是4 s,又根据v=v0+at,物体1 s末的速度为6 m/s,A对、B错.根据x=v0t+12at2,物体2 s内的位移是12 m,4s内的位移是16 m,第5 s内的位移是沿斜面向下的1 m,所以5 s内的位移是15 m,C、D对.]1.v=xt适用于所有运动.2.v=v0+v2适用于匀变速直线运动.3.v=v t2,即一段时间内的平均速度,等于这段时间内中间时刻的瞬时速度,适用于匀变速直线运动.【例2】一质点做匀变速直线运动,初速度v0=2 m/s,4 s内位移为20 m,求:(1)质点4 s内的平均速度;(2)质点第4 s末的速度;(3)质点第2 s末的速度.[解析](1)利用平均速度公式:4 s内的平均速度v=xt=204m/s=5 m/s.(2)因为v=v0+v2,代入数据解得,第4 s末的速度v4=8 m/s.(3)第2 s末为这段时间的中间时刻,故v2=v=5 m/s.[答案](1)5 m/s(2)8 m/s(3)5 m/s2.某战机起飞前从静止开始做匀加速直线运动,达到起飞速度v所需时间为t,则起飞前的运动距离为()A.v t B.v t 2C.2v t D.不能确定B[因为战机在起飞前做匀加速直线运动,则x=v t=0+v2t=v2t.B正确.]1.Δx =x2-x1=aT2.2.应用(1)判断物体是否做匀变速直线运动如果Δx=x2-x1=x3-x2=…=x n-x n-1=aT2成立,则a为一恒量,说明物体做匀变速直线运动.(2)求加速度利用Δx=aT2,可求得a=Δx T2.【例3】从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球拍下如图所示的照片,测得x AB=15 cm,x BC=20 cm.试问:(1)小球的加速度是多少?(2)拍摄时小球B的速度是多少?(3)拍摄时x CD是多少?思路点拨:①可认为A、B、C、D各点是一个小球在不同时刻的位置.②x AB和x BC为相邻两相等时间内的位移.[解析](1)由推论Δx=aT2可知,小球的加速度为a=ΔxT2=x BC-x ABT2=20×10-2-15×10-20.12m/s2=5 m/s2.(2)由题意知B点对应AC段的中间时刻,可知B点的速度等于AC段上的平均速度,即v B=v AC=x AC 2T=20×10-2+15×10-22×0.1m/s=1.75 m/s.(3)由于连续相等时间内的位移差恒定,所以x CD-x BC=x BC-x AB所以x CD=2x BC-x AB=2×20×10-2 m-15×10-2 m=0.25 m.[答案](1)5 m/s2(2)1.75 m/s(3)0.25 m3.如图所示是每秒拍摄10次的小球沿斜面匀加速滚下的频闪照片,照片中直尺的最小分度值为cm,开始两次小球的照片A、B不清晰,此后C、D、E、F 位置如图所示.试由此确定小球运动的加速度大小.[解析]由题意可知,D是C、E中间时刻的照片,由中间时刻的瞬时速度等于这段时间的平均速度可知v D =x E -x C 2T =(47.0-17.0)×10-20.2 m/s =1.50 m/s同理可求E 处的瞬时速度v E =x F -x D 2T =(67.0-30.0)×10-20.2 m/s =1.85 m/s则a =Δv Δt =v E -v D T =1.85-1.500.1 m/s 2=3.5 m/s 2.[答案] 3.5 m/s 21.一颗子弹以大小为v 的速度射进一墙壁但未穿出,射入深度为x ,如果子弹在墙内穿行时做匀变速直线运动,则子弹在墙内运动的时间为( )A.xv B .2x v C.2x vD .x 2vB [由v =v 2和x =v t 得t =2xv ,B 选项正确.]2.一个向正东方向做匀变速直线运动的物体,在第3 s 内发生的位移为8 m ,在第5 s 内发生的位移为5 m ,则关于物体运动加速度的描述正确的是( )A .大小为3 m/s 2,方向为正东方向B .大小为3 m/s 2,方向为正西方向C .大小为1.5 m/s 2,方向为正东方向D .大小为1.5 m/s 2,方向为正西方向D [设第3 s 内、第5 s 内的位移分别为x 3、x 5,则x 5-x 3=2aT 2,解得a =-1.5 m/s 2,a 的方向为正西方向,D 正确.]3.一物体从斜面顶端由静止开始匀加速滚下,到达斜面中点用时1 s ,速度为2 m/s ,则下列说法正确的是( )A .斜面长度为1 mB .斜面长度为2 mC .物体在斜面上运动的总时间为2 sD .到达斜面底端时的速度为4 m/sB[物体从斜面顶端到斜面中点过程的平均速度v=v中2=1 m/s,L2=v t1=1 m,L=2 m,由12a×(1 s)2=1 m,得a=2 m/s2,故A错,B对;设到达中点时用时为t1,到达底端时用时为t2,则t1∶t2=1∶2得:t2= 2 s,故C错;由v=at知,v底=2 2 m/s,故D错.]4.(多选)物体做匀加速直线运动,在时间T内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则物体()A.在A点的速度大小为x1+x2 2TB.在B点的速度大小为3x2-x1 2TC.运动的加速度为2x1 T2D.运动的加速度为x1+x2 T2AB[匀变速直线运动全程的平均速度等于中间时刻的瞬时速度,则v A=v=x1+x22T,A正确.设物体的加速度为a,则x2-x1=aT2,所以a=x2-x1T2,C、D均错误.物体在B点的速度大小为v B=v A+aT,代入数据得v B=3x2-x12T,B正确.]。
高中数学第2章2.2椭圆2.2.1椭圆的标准方程讲义(含解析)苏教版选修2_1

2.2.1 椭圆的标准方程[对应学生用书P20]在平面直角坐标系中,已知A (-2,0),B (2,0),C (0,2),D (0,-2).问题1:若动点P 满足PA +PB =6,设P 的坐标为(x ,y ),则x ,y 满足的关系式是什么? 提示:由两点间距离公式得 (x +2)2+y 2+(x -2)2+y 2=6, 化简得x 29+y 25=1.问题2:若动点P 满足PC +PD =6,设P 的坐标为(x ,y ),则x 、y 满足什么关系? 提示:由两点间距离公式得x 2+(y -2)2+x 2+(y +2)2=6,化简得y 29+x 25=1.椭圆的标准方程焦点在x 轴上 焦点在y 轴上标准方程 x 2a 2+y 2b 2=1(a >b >0) y 2a 2+x 2b 2=1(a >b >0) 焦点坐标(±c,0)(0,±c )a 、b 、c 的关系c 2=a 2-b 21.标准方程中的两个参数a 和b ,确定了椭圆的形状和大小,是椭圆的定形条件.a ,b ,c 三者之间a 最大,b ,c 大小不确定,且满足a 2=b 2+c 2.2.两种形式的标准方程具有共同的特征:方程右边为1,左边是两个非负分式的和,并且分母为不相等的正值.当椭圆焦点在x 轴上时,含x 项的分母大;当椭圆焦点在y 轴上时,含y 项的分母大,已知椭圆的方程解题时,应特别注意a >b >0这个条件.[对应学生用书P20]待定系数法求椭圆标准方程[例1] 求适合下列条件的椭圆的标准方程: (1)经过两点(2,-2),⎝ ⎛⎭⎪⎫-1,142; (2)过点(3,-5),且与椭圆y 225+x 29=1有相同的焦点.[思路点拨] (1)由于椭圆焦点的位置不确定,故可分焦点在x 轴上和在y 轴上两种情况进行讨论.也可利用椭圆的一般方程Ax 2+By 2=1(其中A >0,B >0,A ≠B ),直接求A ,B .(2)求出焦点,然后设出相应方程,将点(3,-5)代入,即可求出a ,b ,则标准方程易得.[精解详析] (1)法一:若焦点在x 轴上,设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0). 由已知条件得⎩⎪⎨⎪⎧ 4a 2+2b 2=1,1a 2+144b 2=1,解得⎩⎪⎨⎪⎧ 1a 2=18,1b 2=14.所以所求椭圆的标准方程为x 28+y 24=1.若焦点在y 轴上,设椭圆的标准方程为y 2a 2+x 2b2=1(a >b >0).由已知条件得⎩⎪⎨⎪⎧4b 2+2a 2=1,1b 2+144a 2=1,解得⎩⎪⎨⎪⎧1b 2=18,1a 2=14.即a 2=4,b 2=8,则a 2<b 2,与题设中a >b >0矛盾,舍去. 综上,所求椭圆的标准方程为x 28+y 24=1.法二:设椭圆的一般方程为Ax 2+By 2=1(A >0,B >0,A ≠B ).将两点(2,-2),⎝ ⎛⎭⎪⎫-1,142代入,得⎩⎪⎨⎪⎧4A +2B =1,A +144B =1,解得⎩⎪⎨⎪⎧A =18,B =14,所以所求椭圆的标准方程为x 28+y 24=1.(2)因为所求椭圆与椭圆y 225+x 29=1的焦点相同,所以其焦点在y 轴上,且c 2=25-9=16.设它的标准方程为y 2a 2+x 2b2=1(a >b >0).因为c 2=16,且c 2=a 2-b 2,故a 2-b 2=16.① 又点(3,-5)在椭圆上,所以()-52a 2+(3)2b2=1,即5a 2+3b2=1.②由①②得b 2=4,a 2=20, 所以所求椭圆的标准方程为y 220+x 24=1. [一点通] 求椭圆标准方程的一般步骤为:1.求适合下列条件的椭圆的标准方程:(1)两个焦点的坐标分别为(-4,0),(4,0),且椭圆经过点(5,0); (2)经过两点P ⎝ ⎛⎭⎪⎫13,13,Q ⎝ ⎛⎭⎪⎫0,-12. 解:(1)由已知得:c =4,a =5.b 2=a 2-c 2=25-16=9.故所求椭圆方程为x 225+y 29=1.(2)设椭圆方程为Ax 2+By 2=1.(A >0,B >0,A ≠B ) 由已知得,⎩⎪⎨⎪⎧19A +19B =1,14B =1,解得:⎩⎪⎨⎪⎧B =4,A =5,故所求椭圆方程为y 214+x 215=1.2.求适合下列条件的椭圆的方程.(1)焦点在x 轴上,且经过点(2,0)和点(0,1);(2)焦点在y 轴上,与y 轴的一个交点为P (0,-10),P 到它较近的一个焦点的距离等于2.解:(1)因为椭圆的焦点在x 轴上,所以可设它的标准方程为x 2a 2+y 2b2=1(a >b >0).∵椭圆经过点(2,0)和(0,1), ∴⎩⎪⎨⎪⎧22a 2+0b 2=1,0a 2+1b 2=1,∴⎩⎪⎨⎪⎧a 2=4,b 2=1,故所求椭圆的标准方程为x 24+y 2=1. (2)∵椭圆的焦点在y 轴上,所以可设它的标准方程为y 2a 2+x 2b2=1(a >b >0).∵P (0,-10)在椭圆上,∴a =10. 又∵P 到它较近的一个焦点的距离等于2, ∴-c -(-10)=2,故c =8, ∴b 2=a 2-c 2=36, ∴所求椭圆的标准方程是y 2100+x 236=1.椭圆标准方程的讨论[例2] 已知方程x 2·sin α-y 2·c os α=1(0≤α≤2π)表示椭圆. (1)若椭圆的焦点在x 轴上,求α的取值范围. (2)若椭圆的焦点在y 轴上,求α的取值范围.[思路点拨] (1)已知的方程不是椭圆的标准形式,应先化成标准方程.(2)对于椭圆方程x 2m +y 2n=1(m >0,n >0,m ≠n )可由m ,n 的大小确定椭圆焦点的位置,列出三角不等式后求α的范围.[精解详析] 将椭圆方程x 2·sin α-y 2·cos α=1(0≤α≤2π)化为标准形式为x 21sin α+y 21-cos α=1(0≤α≤2π). (1)若方程表示焦点在x 轴上的椭圆, 则1sin α>-1cos α>0,即⎩⎪⎨⎪⎧ α∈⎝ ⎛⎭⎪⎫π2,π,tan α>-1,所以34π<α<π.即α的取值范围是⎝ ⎛⎭⎪⎫3π4,2π.(2)若方程表示焦点在y 轴上的椭圆, 则-1cos α>1sin α>0,即⎩⎪⎨⎪⎧α∈⎝ ⎛⎭⎪⎫π2,π,tan α<-1,所以π2<α<3π4.即α的取值范围是⎝ ⎛⎭⎪⎫π2,3π4.[一点通] 对于讨论椭圆方程中参数的取值范围问题,一般的解题方法是根据题设条件给出的焦点位置,结合对应的标准方程应满足的条件,建立一个含参数的不等式组,通过求解不等式组得到参数的取值范围.3.如果方程x 2a 2+y 2a +6=1表示焦点在x 轴上的椭圆,则实数a 的取值范围是________.解析:由于椭圆的焦点在x 轴上,所以⎩⎪⎨⎪⎧a 2>a +6,a +6>0,即⎩⎪⎨⎪⎧(a +2)(a -3)>0a >-6.解得a >3或-6<a <-2.答案:(3,+∞)∪(-6,-2) 4.已知方程x 2k -5+y 23-k=-1表示椭圆,求k 的取值范围.解:方程x 2k -5+y 23-k=-1可化为x 25-k+y 2k -3=1,由椭圆的标准方程可得⎩⎪⎨⎪⎧5-k >0,k -3>0,5-k ≠k -3,得3<k <5,且k ≠4.所以满足条件的k 的取值范围是{k |3<k <5,且k ≠4}.椭圆的定义及标准方程的应用[例3] 如图所示,已知椭圆的方程为x 24+y 23=1,若点P 在第二象限,且∠PF 1F 2=120°,求△PF 1F 2的面积.[思路点拨] 根据椭圆的标准方程知PF 1+PF 2=4,结合面积公式和余弦定理找到PF 1和PF 2的关系求解.[精解详析] 由已知a =2,b =3, 所以c =a 2-b 2=4-3=1,F 1F 2=2c =2,在△PF 1F 2中,由余弦定理,得PF 22=PF 21+F 1F 22-2PF 1·F 1F 2cos 120°,即PF 22=PF 21+4+2PF 1.① 由椭圆定义,得PF 1+PF 2=4, 即PF 2=4-PF 1.② ②代入①解得PF 1=65.∴S △PF 1F 2=12PF 1·F 1F 2·sin 120°=12×65×2×32=335, 即△PF 1F 2的面积是3 35.[一点通] 在椭圆中,由三条线段PF 1,PF 2,F 1F 2围成的三角形称为椭圆的焦点三角形.涉及椭圆的焦点三角形问题,可结合椭圆的定义列出PF 1+PF 2=2a ,利用这个关系式便可求出结果,因此回归定义是求解椭圆的焦点三角形问题的常用方法.5.已知两定点F 1(-1,0)、F 2(1,0),且F 1F 2是PF 1与PF 2的等差中项,则动点P 的轨迹方程是________.解析:∵F 1(-1,0),F 2(1,0),∴F 1F 2=2. ∵F 1F 2是PF 1与PF 2的等差中项, ∴2F 1F 2=PF 1+PF 2,即PF 1+PF 2=4,∴点P 在以F 1,F 2为焦点的椭圆上, ∵2a =4,a =2,c =1,∴b 2=3. ∴椭圆的方程是x 24+y 23=1.答案:x 24+y 23=16.设F 1,F 2是椭圆x 29+y 24=1的两个焦点,P 是椭圆上的点,且PF 1∶PF 2=2∶1,则△F 1PF 2的面积等于________.解析:由x 29+y 24=1,得a =3,b =2,∴c 2=a 2-b 2=5.∴c = 5.∴F 1F 2=2 5. 由⎩⎪⎨⎪⎧PF 1+PF 2=6,PF 1∶PF 2=2∶1,得⎩⎪⎨⎪⎧PF 1=4,PF 2=2.∴PF 21+PF 22=F 1F 22. ∴△F 1PF 2为直角三角形. ∴S △F 1PF 2=12PF 1·PF 2=4.答案:47.如图,已知F 1,F 2是椭圆x 2100+y 236=1的两个焦点.(1)若椭圆上一点P 到焦点F 1的距离等于15,那么点P 到另一个焦点F 2的距离是多少? (2)过F 1作直线与椭圆交于A ,B 两点,试求△ABF 2的周长. 解:由椭圆的标准方程可知a 2=100,所以a =10.(1)由椭圆的定义得PF 1+PF 2=2a =20,又PF 1=15,所以PF 2=20-15=5,即点P 到焦点F 2的距离为5.(2)△ABF 2的周长为AB +AF 2+BF 2=(AF 1+BF 1)+AF 2+BF 2=(AF 1+AF 2)+(BF 1+BF 2). 由椭圆的定义可知AF 1+AF 2=2a ,BF 1+BF 2=2a ,故AB +AF 2+BF 2=4a =40.用待定系数法求椭圆的标准方程时,若已知焦点的位置,可直接设出标准方程;若焦点位置不确定,可分两种情况求解;也可设Ax 2+By 2=1(A >0,B >0,A ≠B )求解,避免了分类讨论,达到了简化运算的目的.[对应课时跟踪训练(八)]1.若椭圆x 225+y 29=1上一点P 到一个焦点的距离为5,则P 到另一个焦点的距离为________.解析:由椭圆定义知,a =5,P 到两个焦点的距离之和为2a =10,因此,到另一个焦点的距离为5.答案:52.椭圆25x 2+16y 2=1的焦点坐标是________.解析:椭圆的标准方程为x 2125+y 2116=1,故焦点在y 轴上,其中a 2=116,b 2=125,所以c2=a 2-b 2=116-125=9400,故c =320.所以该椭圆的焦点坐标为⎝⎛⎭⎪⎫0,±320.答案:⎝⎛⎭⎪⎫0,±3203.已知方程(k 2-1)x 2+3y 2=1是焦点在y 轴上的椭圆,则k 的取值范围是________. 解析:方程(k 2-1)x 2+3y 2=1可化为x 21k 2-1+y 213=1. 由椭圆焦点在y 轴上,得⎩⎪⎨⎪⎧k 2-1>0,1k 2-1<13.解之得k >2或k <-2.答案:(-∞,-2)∪(2,+∞)4.已知F 1,F 2为椭圆x 225+y 29=1的两个焦点,过F 1的直线交椭圆于A ,B 两点.若|F 2A |+|F 2B |=12,则|AB |=________.解析:由题意,知(|AF 1|+|AF 2|)+(|BF 1|+|BF 2|)=|AB |+|AF 2|+|BF 2|=2a +2a ,又由a =5,可得|AB |+(|BF 2|+|AF 2|)=20,即|AB |=8.答案:85.已知P 为椭圆x 225+4y275=1上一点,F 1,F 2是椭圆的焦点,∠F 1PF 2=60°,则△F 1PF 2的面积为________.解析:在△F 1PF 2中,F 1F 22=PF 21+PF 22-2PF 1·PF 2cos 60°,即25=PF 21+PF 22-PF 1·PF 2.① 由椭圆的定义,得 10=PF 1+PF 2.②由①②,得PF 1·PF 2=25,∴S △F 1PF 2=12PF 1·PF 2sin 60°=25 34.答案:25 346.求适合下列条件的椭圆的标准方程:(1)以(0,5)和(0,-5)为焦点,且椭圆上一点P 到两焦点的距离之和为26; (2)以椭圆9x 2+5y 2=45的焦点为焦点,且经过M (2,6). 解:(1)∵椭圆的焦点在y 轴上,∴设它的标准方程为y 2a 2+x 2b2=1(a >b >0).∵2a =26,2c =10,∴a =13,c =5. ∴b 2=a 2-c 2=144. ∴所求椭圆的标准方程为y 2169+x 2144=1. (2)法一:由9x 2+5y 2=45, 得y 29+x 25=1,c 2=9-5=4, 所以其焦点坐标为F 1(0,2),F 2(0,-2).设所求椭圆的标准方程为y 2a 2+x 2b2=1(a >b >0).由点M (2,6)在椭圆上,所以MF 1+MF 2=2a ,即2a =(2-0)2+(6-2)2+(2-0)2+(6+2)2=43, 所以a =23,又c =2,所以b 2=a 2-c 2=8, 所以所求椭圆的标准方程为y 212+x 28=1. 法二:由法一知,椭圆9x 2+5y 2=45的焦点坐标为F 1(0,2),F 2(0,-2),则设所求椭圆方程为y 2λ+4+x 2λ=1(λ>0),将M (2,6)代入,得6λ+4+4λ=1(λ>0), 解得λ=8或λ=-2(舍去). 所以所求椭圆的标准方程为y 212+x 28=1.7.如图,设点P 是圆x 2+y 2=25上的动点,点D 是点P 在x 轴上的投影,M 为PD 上一点,且MD =45PD ,当P 在圆上运动时,求点M 的轨迹C 的方程.解:设M 点的坐标为(x ,y ),P 点的坐标为(x P ,y P ),由已知易得⎩⎪⎨⎪⎧x P =x ,y P =54y .∵P 在圆上,∴x 2+(54y )2=25.即轨迹C 的方程为x 225+y 216=1.8.已知动圆M 过定点A (-3,0),并且内切于定圆B :(x -3)2+y 2=64,求动圆圆心M 的轨迹方程.解:设动圆M 的半径为r , 则|MA |=r ,|MB |=8-r , ∴|MA |+|MB |=8,且8>|AB |=6,∴动点M 的轨迹是椭圆,且焦点分别是A (-3,0),B (3,0),且2a =8, ∴a =4,c =3, ∴b 2=a 2-c 2=16-9=7.∴所求动圆圆心M 的轨迹方程是x 216+y 27=1.。
原子物理学-杨福家第二章习题答案上课讲义

原子物理学-杨福家第二章习题答案第二章习题2-1 铯的逸出功为1.9eV ,试求: (1)铯的光电效应阈频率及阈值波长;(2)如果要得到能量为1.5eV 的光电子,必须使用多少波长的光照射? 解:(1) ∵ E =hν-W 当hν=W 时,ν为光电效应的最低频率(阈频率),即ν =W /h =1.9×1.6×10-19/6.626×10-34 =4.59×1014 ∵ hc /λ=w λ=hc /w =6.54×10-7(m) (2) ∵ mv 2/2=h ν-W∴ 1.5= h ν-1.9 ν=3.4/h λ=c /ν=hc /3.4(m)=3.65×10-7m 2-2 对于氢原子、一次电离的氦离子He +和两次电离的锂离子Li ++,分别计算它们的:(1)第一、第二玻尔轨道半径及电子在这些轨道上的速度; (2)电子在基态的结合能;(3)由基态到第一激发态所需的激发能量及由第一激发态退激到基态所放光子的波长.n eeZ n a∴H: r 1H =0.053×12/1nm=0.053nm r 2 H =0.053×22/1=0.212nmV 1H =2.19 ×106×1/1=2.19 ×106(m/s) V 2H =2.19 ×106×1/2=1.095 ×106(m/s)∴He+: r 1He+=0.053×12/2nm=0.0265nm r 2He+=0.053×22/2=0.106nmV 1 He+=2.19 ×106×2/1=4.38 ×106(m/s) V 2 He+=2.19 ×106×2/2=2.19 ×106(m/s) Li ++: r 1 Li++=0.053×12/3nm=0.0181nm r 2 Li++=0.053×22/3=0.071nmV 1 Li++=2.19 ×106×3/1=6.57 ×106(m/s) V 2 Li++=2.19 ×106×3/2=3.28 ×106(m/s)(2) 结合能:自由电子和原子核结合成基态时所放出来的能量,它∵基态时n =1H: E 1H =-13.6eVHe+: E 1He+=-13.6×Z 2=-13.6×22=-54.4eV Li ++: E 1Li+=-13.6×22(3) 由里德伯公式Z 2×13.6×3/4=10.2Z 2注意H 、He+、Li++的里德伯常数的近似相等就可以算出如下数值。
组合数学讲义及答案 2章 母函数

x1 x 1 x 3
1 x
6x
4
1 x
ex
-ln(1- a x)
《组合数学》
第二章
母函数
ak ak
k 1 = 2k ! k 1 =
cos x
ak =
2k 1!
1k
1 sin x x
2k 1
1 arctan x x
n
n r r r 2 x r 0
n
n r 即不同的取法共有 a r r 2 种。 n 由于每类元素最多只能出现一次, 故 G(x)= 1 2 x 中不能
有 x 2 项,再由同双的两只鞋子有区别知,x 的系数应为 2。 解法二:用排列组合。先从 n 双鞋中选取 r 双,共有 r 种 r 选法,再从此 r 双中每双抽取一只,有 2 种取法,由乘法原理, 即得结果同上。 解法三: 仍用排列组合。 先取出 k 只左脚的鞋, 再在其余 n k
r 组合数为 x r 之系数 C n 。
r
(2.1.2)
为
推论2 S e1 , e2 ,, en ,则 r 无限可重组合的母函数
j 1 G(x)= x 1 x n j0
3/49
n
(2.1.3)
《组合数学》
第二章
母函数
5 i 6 i 7 i 10 i G1(x)= x x x x i 0 i 0 i 0 i 0 4 28 = 1 4 x 35 x x
与
6/49
《组合数学》
第二章
母函数
0 , 当r n为奇数 ar rn r n , 当r n为偶数 C n 2 1 , 2
2019-2020年人教版生物必修三讲义:第2章+第1节 通过神经系统的调节(二)及答案

第1节 通过神经系统的调节(二)1.兴奋在神经元之间的传递 (1)突触的结构(如图)①突触由图中的b 突触前膜、c 突触间隙以及d 突触后膜组成(填字母及名称)。
②其他结构a .图中a 是指神经元的轴突末梢,形成的膨大部分为突触小体。
b .图中e 、f 、g 分别是指突触小泡、神经递质、受体。
(2)传递过程神经冲动→神经末梢→[b]突触前膜释放神经递质→扩散到[c]突触间隙→然后作用于[d]突触后膜上的[g]受体→引发突触后膜电位变化。
(3)传递特点 ①特点:单向传递。
②原因神经递质只存在于突触前膜的[e]突触小泡中,只能由突触前膜释放,然后作用于突触后膜上,因此神经元之间兴奋的传递只能是单方向的。
(4)常见突触类型从结构上来说,突触主要分为两大类:A.轴突—树突,图示为:。
B.轴突—细胞体,图示为:。
2.神经系统的分级调节3.人脑的高级功能(1)大脑皮层的功能大脑皮层是整个神经系统中最高级的部位。
它除了对外部世界的感知以及控制机体的反射活动外,还具有语言、学习、记忆和思维等方面的高级功能。
(2)大脑皮层言语区①学习是神经系统不断地接受刺激,获得新的行为、习惯和积累经验的过程。
②记忆则是将获得的经验进行贮存和再现。
a.短期记忆主要与神经元的活动和神经元之间的联系有关。
b.长期记忆可能与新突触的建立有关。
判断对错(正确的打“√”,错误的打“×”)1.突触小泡中的神经递质释放到突触间隙的过程属于胞吐。
()2.兴奋在突触小体中的信号转变为:电信号→化学信号。
()3.由于神经递质只能由突触前膜释放,然后作用于后膜上,因此兴奋在神经元间的传递是单向的。
()4.神经递质作用于突触后膜上,就会使下一个神经元兴奋。
()5.上自习课时边看书边记笔记是与人体高级神经中枢直接联系的活动。
() 6.大脑皮层语言H区损伤,导致人不能听懂别人讲话。
()提示:1.√2.√3.√4.×神经递质有兴奋性和抑制性两种,其作用于突触后膜上,就会使下一个神经元兴奋或抑制。
人教版生物必修二讲义:第2章 第1节 减数分裂和受精作用(Ⅰ)含答案

第1节 减数分裂和受精作用(Ⅰ)1.阐明减数分裂的概念。
2.阐述同源染色体、四分体、联会等概念。
(重点) 3.阐明减数分裂产生染色体数量减半的精细胞。
4.描述精子形成过程中各时期染色体的行为变化。
(重、难点)知识点 减数分裂的概念、精子的形成过程[学生用书P20]阅读教材P16~19 1.减数分裂的概念点拨 真核生物的细胞分裂方式一般有三种,精子和卵细胞的形成依靠减数分裂,体细胞的增殖主要依靠有丝分裂,其次依靠无丝分裂。
2.精子的形成过程 (1)形成场所:睾丸。
(2)细胞名称的变化⎭⎪⎬⎪⎫ 精原细胞――→染色体复制 减数第一次分裂前的间期⎭⎪⎬⎪⎫初级精母细胞 ――→分裂减数第一次分裂⎭⎪⎬⎪⎫次级精母细胞――→分裂减数第二次分裂⎭⎬⎫精细胞――→变形 精子变形过程 (3)形成过程1.减数分裂中的相关概念(1)同源染色体与非同源染色体①同源染色体概念:形状和大小一般都相同,一条来自父方,一条来自母方。
上图甲中A 和B ,C 和D 为同源染色体。
②非同源染色体概念:形状和大小一般不相同,来源可能相同,也可能不同。
(2)姐妹染色单体与非姐妹染色单体姐妹染色单体:连在同一个着丝点上的染色单体。
上图乙中1和2、3和4、5和6、7和8为姐妹染色单体;而1和3、4、5、6、7、8为非姐妹染色单体。
(3)联会和四分体①联会:同源染色体两两配对的现象。
②四分体:联会后的每对同源染色体含有4条染色单体。
③相互关系:同源染色体――→复制、联会四分体④数量关系:1个四分体=1对同源染色体=2条染色体=4条染色单体=4个DNA 分子。
2.减数分裂过程中两个分裂阶段的比较项目减数第一次分裂减数第二次分裂 间期DNA 复制与否复制 不复制(无间期)同源染色体 有,分离 无 着丝点变化不分裂分裂染色体主要行为①同源染色体联会;②四分体中非姐妹染色单体交叉互换;③同源染色体分离,非同源染色体自由组合着丝点分裂,姐妹染色单体分开 染色体数目 2N →N (减半) N →2N →N (不减半)DNA 数目 2N →4N →2N 2N →N 染色单体数0→4N →2N2N →01.下列关于同源染色体的叙述,不正确的是()A.一条来自父方、一条来自母方的染色体是同源染色体B.同源染色体上的非姐妹染色单体间能互换对应部分C.在人的正常精子中没有同源染色体D.减数分裂中联会的染色体是同源染色体[解析]选A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 3页
第二章
习题解答
13. 已知[x]补=1.1011000,[y]补=1.0100110,用变形补码计算 2[x]补+1/2[y]补=?,同时指出结果是否发生溢出。 【解】 用变形补码,即双符号位。 2[x]补=11.0110000 1/2[y]补=11.1010011 注意:不管左移还是右移,符号位不变,只对尾数进行 处理。 11.0110000 + 11.1010011 11.0000011 符号位为11,故运算结果未溢出。 2[x]补+1/2[y]补=1.0000011
指数e=阶码-127=00011111-01111111 =(-96)10 包括隐藏位1的尾数:
1.M=1.110 1111 11 于是有 x=(-1)s×1.M×2e
=-(1. 110111111)×2-96= (-959 ×2-105)10
第 1页
第二章
习题解答
8. 将数(-7.28125)10转换成IEEE754的32位浮点数二进制存储格 式。 【解】:首先分别将整数和分数部分转换成二进制数: -7.2812510=-111.010012 然后移动小数点,使其在第1,2位之间 111.01001=1.1101001×22 e=2
第 6页
第二章
习题解答
② 带求补器的补码阵列乘法器 [x]补=0.10111 [y]补=1.01101 乘积的符号位为:xf⊕yf=0⊕1=1 算前求补后输出 |x|=10111,|y|=10011 10111 × 10011 10111 10111 00000 00000 10111 位数 0110110101 算后求补后输出为1001001011 ,加上乘积符号位1,得 [x×y]补=1. 1001001011 所以 x×y=-0. 0110110101
第 4页
第二章
习题解答
17. 已知x和y,用移码运算方法计算x-y,同时指出运算结果 是否发生溢出。 (1) x=1011,y= - 0010 【解】 [x]移=11 1011=01 1011 [-y]补=00 0010 注意:移码最高符号位恒置为0参与运算。 01 1011 + 00 0010 01 1101 符号位为01,故运算结果未溢出。 x-y=1101
第 7页
第二章
习题解答
③ 直接补码阵列乘法器 [x]补=0.10111 [y]补=1.01101 计算过程: (0) 1 0 1 1 1 × (1) 0 1 1 0 1 (0) 1 0 1 1 1 (0) 0 0 0 0 0 (0) 1 0 1 1 1 (0) 1 0 1 1 1 (0) 0 0 0 0 0 0 (1)(0)(1)(1) (1) 0 0 (1) 0 0 1 0 0 1 0 1 1
(1) 1 1 0 0 1 0 0 1 0 1 1 故 [x×y]补=1. 1001001011 所以 x×y=-0. 0110110101
注意位数对齐
第 8页
第二章
习题解答
22. 已知x和y,用原码阵列除法器计算x÷y。 (1)x=0.10011 y=-0.11011 被除数/余数 【解】: [x]原=0.10011 01001100000 +[-y’]补 100101 [y]原=1.11011 11100000000 商的符号位为: + [y’]补 011011 xf⊕yf=0⊕1=1 令 0010110000 x’=1001100000 y’=11011, +[-y’]补 100101 其中x’和y’分别为[x]原和 [y]原 111011000 + [y’]补 011011 的数值部分: 01000100 [x’]补=01001100000 +[-y’]补 100101 [y’]补=011011 0001110 + [-y’]补 100101 [-y’]补=100101
第 5页
第二章
习题解答
20. 已知x和y,分别用带求补器的原码阵列乘法器、带求补器的补码阵 列乘法器和直接补码阵列乘法器计算x×y。 (1) x=0.10111 y=-0.10011 【解】:①带求补器的原码阵列乘法器 [x]原=0.10111 [y]原=1.10011 乘积的符号位为: xf⊕yf=0⊕1=1 因符号位单独考虑,算前求补器的使能控制信号为0,经算前求补 后输出 |x|=10111,|y|=10011 10111 × 10011 10111 10111 10111 位数 0110110101 因算后求补器的使能控制信号为0,经算后求补后输出为 0110110101 ,加上乘积符号位1,得 [x×y]原=1. 0110110101 所以 x×y=-0. 0110110101
【解】 [x]补=00.11011 [y]补=11.01011 [x]补 0 0. 1 1 0 1 1 + [y]补 1 1. 0 1 0 1 1 0 0. 0 0 1 1 0 符号位出现“00”,表示无溢出, x+y=0.00110 12. 已知x和y,用变形补码计算x-y ,同时指出结果是否溢出。 (1) x= 0.10111, y= 0.11011 【解】 [x]补=00. 10111 [-y]补=11.00101 [x]补 0 0. 1 0 1 1 1 + [y]补 1 1. 0 0 1 0 1 1 1. 1 1 1 0 0 符号位出现“11”,表示无溢出,x-y=-0.00100
第二章
习题解答
7.若浮点数 x 的IEEE754标准32位存储格式为(8FEFC000 )16, 求其浮点数的十进制值。 【解】: 将x展开成二进制:
1000 , 1111, 1110 ,1111 ,1100,0000,0000,0000 数符:1 阶码:0001,1111
尾数:110,1111,1100,0000,0000,0000
于是得到: e =E – 127
S=1,E=2+127=129=1000,0001,M=1 最后得到32位浮点数的二进制存储格式为
1100 0000 1110 1001 0000 0000 0000 0000
= (C0E90000)16
第 2页
第二章
习题解答
11. 已知x和y,用变形补码计算x+y ,同时指出结果是否溢出。 (1) x= 0.11011, y= -0.10101
