最新初中数学与角有关的辅助线综合测试卷

合集下载

七年级下册数学之与角有关的辅助线练习题及答案

与角有关的辅助线（讲义）知识过关1. 如图，∠AOB =130°，OC ⊥OB 于点O ，求∠AOC 的度数．解：如图， ∵OC ⊥OB （已知）∴____________（垂直的定义） ∵∠AOB =130°（已知） ∴∠AOC =______-______=______-______=______（等式性质）1. 为了解决几何问题，在原图基础之上另外添加的直线或线段称为辅助线．辅助线通常画成________．2. 辅助线的原则：添加辅助线，构造新图形，形成新关系，建立______和______之间的桥梁，把问题转化成自己已经会解的情况． 3. 辅助线的作用：①________________________________________________； ②________________________________________________． 4. 添加辅助线的注意事项：____________________________．➢ 精讲精练1. 如图，AB ∥CD ，∠E =27°，∠C =52°，则∠EAB 的度数为______________．2. 如图，∠BAF =46°，∠ACE =136°，CD ⊥CE ．求证：AB ∥CD ．3. 已知：如图，直线AB ∥CD ，∠EFG =130°，∠DGH =40°．BOACEDCB AF ABCD E NGHFEDCBA你认为EF ⊥AB 吗？请说明理由．4. 已知：如图，AB ∥CD ，E ，F 分别是AB ，CD 上的点．求证：∠EPF =∠AEP +∠CFP ．5. 如图，l 1∥l 2，∠1=105°，∠2=40°，则∠3=___________．6. 已知：如图，AB ∥EF ，∠B =25°，∠D =30°，∠E =10°，则∠BCD =________．7. 已知：如图，AB ∥ED ，α=∠A +∠E ，β=∠B +∠C +∠D ．求证：β=2α．8. 已知：如图，CD ∥EF ，∠1+∠2=∠ABC ．求证：AB ∥GF ．9. 已知：如图，在四边形ABDC 中．求证：∠BDC =∠A +∠B +∠C ．、321l 2l 1PF E DCBAFEDCBAECDBA 21GFE DC BADCBA【参考答案】➢知识过关1.∠COB=90°∠AOB-∠COB130°-90°40°1.虚线；2.已知，未知3.①把分散的条件转为集中②把复杂的图形转化为基本图形4.明确目的，多次尝试➢精讲精练1.79°2.证明：如图，延长DC到点G．∵CD⊥CE（已知）∴∠ECG=90°（垂直的定义）∵∠ACE=136°（已知）∴∠ACG=∠ACE-∠ECG=136°-90°=46°（等式性质）∵∠BAF=46°（已知）∴∠ACG=∠BAF（等量代换）∴AB∥CD（同位角相等，两直线平行）3.解：EF⊥AB，理由如下：如图，延长EF交CD于点M．∵∠DGH=40°（已知）∠DGH=∠FGM（对顶角相等）∴∠FGM=40°（等量代换）∵∠EFG是△FGM的一个外角（外角的定义）∴∠EFG=∠FGM+∠FMG（三角形的一个外角等于和它不相邻的两个内角的和）∵∠EFG=130°（已知）∴∠FMG=∠EFG-∠FGM=130°-40°=90°（等式性质）∵AB∥CD（已知）∴∠BNE=∠FMG=90°（两直线平行，同位角相等）∴EF⊥AB（垂直的定义）FA BC DEMNGHN M4321PFED CB A4.证明：如图，过点P作MN∥AB．∵CD∥AB（已知）∴AB∥MN∥CD（平行于同一直线的两直线平行）∴∠1=∠2（两直线平行，内错角相等）∠3=∠4（两直线平行，内错角相等）∴∠2+∠4=∠1+∠3（等式的性质）即∠EPF=∠AEP+∠CFP5.115°6.45°7.证明：如图，过点C作MN∥AB．∵AB∥ED（已知）∴MN∥AB∥ED（平行于同一直线的两直线平行）∴∠1+∠D=180°∠2+∠B=180°∠A+∠E=180°（两直线平行，同旁内角互补）∵α=∠A+∠E，β=∠B+∠C+∠D（已知）∴α=180°，β=360°（等式性质）∴β=2α（等式性质）8.证明：如图，延长CB交FG于点M，延长FE交CM于点N．∵CD∥EF（已知）∴∠2=∠FNM（两直线平行，同位角相等）∵∠BMG是△FMN的一个外角（外角的定义）∴∠BMG=∠1+∠FNM=∠1+∠2（三角形的一个外角等于和它不相邻的两个内角的和）∵∠ABC=∠1+∠2（已知）∴∠BMG=∠ABC（等量代换）∴AB∥GF（同位角相等，两直线平行）9.证明：如图，延长BD交AC于点E．∵∠BDC是△CDE的一个外角（外角的定义）∴∠BDC=∠1+∠C（三角形的一个外角等于和它不相邻的两个内角的和）∵∠1是△ABE的一个外角（外角的定义）∴∠1=∠A+∠B（三角形的一个外角等于和它不相邻的两个内角的和）∴∠BDC=∠A+∠B+∠C（等量代换）21E DM C NA BNMABCDEF G121EABCD与角有关的辅助线（随堂测试）2. 已知：如图，AB ⊥EF 于点O ，BD 与MN 相交于点C ，∠1=35°，∠ABC =125°．求证：EF ∥MN ．【参考答案】1. 解：EF ∥MN理由如下：如图，延长AB 交MN 于点G ．∵∠1=35°（已知）∴∠BCG =35°（对顶角相等）∵∠ABC 是△BCG 的一个外角（外角的定义）∴∠ABC =∠BGC +∠BCG （三角形的外角等于和它不相邻的两个内角的和）∵∠ABC =125°（已知） ∴∠BGC =∠ABC -∠BCG =125°-35°=90°（等式的性质）∵AB ⊥EF （已知）∴∠AOF =90°（垂直的定义） ∴∠AOF =∠BGC （等量代换）∴EF ∥MN （同位角相等，两直线平行）与角有关的辅助线（习题）➢ 例题示范例1：已知：如图，∠BED =∠B +∠D ．求证：AB ∥CD ．①读题标注：②梳理思路：要证AB ∥CD ，我们需要找相关的同位角、内错角或同旁内角．观察图形发现，AB ，CD 没有截线，故需要构造截线，然后证明．可尝试延长BE 交CD 于点G ．NM FA BC D E1O EDBA CED BACN MFEGO 1D C B A③过程书写：证明：如图，延长BE交CD于点G．∵∠BED是△DEG的一个外角∴∠BED=∠DGE +∠D∵∠BED=∠B+∠D∴∠DGE=∠B∴AB∥CD➢巩固练习3.已知：如图，a∥b，则∠1+∠2-∠3=_________．4.已知：如图，∠B+∠E+∠D=360°．求证：AB∥CD．5.已知：如图，AB∥CD，∠1=∠2．求证：∠3=∠4．6.已知：如图，AB∥CD．求证：∠1+∠3 ∠2=180°．7.已知：如图，∠3=∠1+∠2．求证：∠A+∠B+∠C+∠D=180°．CA BDEGCA BDE4F123C DEBAba132A BC D123EFGEDCBA321➢ 思考小结已知：如图，在四边形ABDC 中．求证：∠BDC =∠A +∠B +∠C ．（1）请根据图下方的描述在图上作出辅助线，并进行证明（不需要写过程）；延长BD 交AC 于点E 延长CD 交AB 于点E连接AD 并延长AD 到点E 连接BC过点D 作EF ∥AB 交AC 于点E 过点D 作EF ∥AC 交AB 于点E （2）根据上面的证明方法可以总结出辅助线的作用： ①_____________________________________； ②_____________________________________．【参考答案】 ➢ 巩固练习1. 180°2. 证明：如图，过点E 作EF ∥AB ．∴∠B +∠BEF =180°（两直线平行，同旁内角互补）∵∠B +∠BED +∠D =360°（已知） ∴∠FED +∠D =180°（等式性质） ∴EF ∥CD （同旁内角互补，两直线平行）∴AB ∥CD （平行于同一条直线的两条直线互相平行）C DA BC DABC DABCDABC DABC DABF E DBA C5G AB EDC 321F43. 证明：如图，延长BE 交CD 于点G ．∵AB ∥CD （已知）∴∠1=∠5（两直线平行，内错角相等） ∵∠1=∠2（已知） ∴∠2=∠5（等量代换）∴BG ∥CF （同位角相等，两直线平行） ∴∠3=∠4（两直线平行，内错角相等） 4. 证明：如图，延长EA 交CD 于点F ．∵AB ∥CD （已知）∴∠1=∠4（两直线平行，同位角相等） ∵∠4是△CEF 的一个外角（外角的定义）∴∠4=∠2+∠ECF （三角形的一个外角等于和它不相邻的两个内角的和）∵∠ECF =180°-∠3（平角的定义） ∴∠4=∠2+180°-∠3（等量代换） ∴∠4+∠3-∠2=180°（等式性质）∴∠1+∠3-∠2=180°（等量代换）（方法不只一种） 5. 证明：如图，延长EG 交CF 于点H ．∵∠3是△GFH 的一个外角（外角的定义）∴∠3=∠2+∠GHF （三角形的一个外角等于和它不相邻的两个内角的和）∵∠3=∠1+∠2（已知） ∴∠GHF =∠1（等式性质）∴BE ∥CF （内错角相等，两直线平行）∴∠BMD +∠MNC =180°（两直线平行，同旁内角互补） ∵∠BMD 是△ABM 的一个外角（外角的定义）∴∠BMD =∠A +∠B （三角形的一个外角等于和它不相邻的两个内角的和）∵∠MNC 是△CDN 的一个外角（外角的定义）∴∠MNC =∠C +∠D （三角形的一个外角等于和它不相邻的两个内角的和）∴∠A +∠B +∠C +∠D =180°（等量代换）（方法不只一种）➢ 思考小结（1）作辅助线，略；（2）①把分散的条件转为集中；②把复杂的图形转化为基本图形．4F E 321D CBA。

与角有关的辅助线(过程训练一)(人教版)40;含答案41;

与角有关地辅助线（过程训练一）（人教版）
一、单选题(共5道，每道20分)
1.已知：如图，AB∥CD，∠A=60°，∠C=20°，求∠AEC地度数．
横线处应填写地过程最恰当地是( )
文档来自于网络搜索
A.
B.
C.
D.
答案：C
解题思路：
试题难度：三颗星知识点：与角有关地辅助线
2.已知：如图，AB∥CD，∠E=37°，∠D=60°，求∠ABE地度数．
横线处应填写地过程最恰当地是( ) 文档来自于网络搜索
A.
B.
C.
D.
答案：B
解题思路：
试题难度：三颗星知识点：与角有关地辅助线
3.已知：如图，∠AED＝∠A+∠B．求证：DE∥BC．
横线处应填写地过程最恰当地是( ) A.
B.
C.
D.
答案：B
解题思路：
试题难度：三颗星知识点：与角有关地辅助线
4.已知：如图，EF∥MN，∠CBD=125°，∠ACE=90°，求∠MDG地度数．
横线处应填写地过程最恰当地是( ) 文档来自于网络搜索
A.
B.
C.
D.
答案：C
解题思路：
试题难度：三颗星知识点：与角有关地辅助线
5.已知：如图，AB∥CD，若∠A=136°，∠DCE=134°，求∠AEC地度数．
横线处应填写地过程最恰当地是( )
文档来自于网络搜索
A.
B.
C.
D.
答案：A 解题思路：
个人收集整理仅做学习参考试题难度：三颗星知识点：与角有关地辅助线
11 / 11。

初中数学几何辅助线经典100题

初中数学几何辅助线经典100题摘要：初中数学几何辅助线经典100题一、几何辅助线的概念和作用1.几何辅助线的定义2.几何辅助线在解题中的作用二、几何辅助线的常见类型及应用1.角平分线2.线段和差3.中点定理4.倍长中线5.相似三角形6.判定条件7.证明定理三、初中数学几何辅助线经典100题1.题目1-102.题目11-203.题目21-304.题目31-405.题目41-506.题目51-607.题目61-708.题目71-809.题目81-9010.题目91-100正文：初中数学几何辅助线经典100题一、几何辅助线的概念和作用几何辅助线是在解决几何问题时，通过在图形上添加一些特殊的线段，来帮助我们更好地理解和解题的一种工具。

它可以将复杂的几何问题简化为更简单的形式，使问题更容易解决。

几何辅助线在解题中的作用主要体现在以下几个方面：1.揭示图形中隐含的性质：通过添加辅助线，将条件中隐含的有关图形的性质充分揭示出来，以便取得过渡性的推论，达到推导出结论的目的。

2.聚拢集中原则：通过添置适当的辅助线，将图形中分散、远离的元素相对集中、聚拢到有关图形上来，使题设条件与结论建立逻辑关系，从而推导出要求的结论。

3.化繁为简原则：对一类几何命题，其题设条件与结论之间在已知条件所给的图形中，通过添加辅助线，将复杂图形转化为简单图形，从而简化问题，使解题更加顺利。

二、几何辅助线的常见类型及应用几何辅助线有很多种，这里我们列举几种常见的类型及其应用：1.角平分线：角平分线是将一个角平分成两个相等的角的线段。

在解题中，我们常常利用角平分线的性质来证明两个角相等或求解某个角的度数。

2.线段和差：线段和差是指通过两个线段的和与差来求解几何问题。

在解题过程中，我们通常利用线段和差的性质来证明线段相等或求解线段的长度。

3.中点定理：中点定理是指在一个线段上，如果有一个点是线段中点，那么这个点到线段两端的距离相等。

在解题中，我们常常利用中点定理来证明线段相等或求解线段的长度。

与角有关的辅助线辅助线人教版含答案

与角有关的辅助线(辅助线)(人教版)(含答案)与角有关的辅助线(辅助线)(人教版)一、单选题(共10道,每道10分))1.根据下列要求作辅助线:①连接EF;②延长EO交CD于点H,其中符合要求的是(A. B.C. D.答案:B解题思路:根据题目要求:①连接EF,就是作线段EF,排除选项D;②延长EO交CD于点H,就是作射线EO交CD于点H,注意点E是端点,EO是方向,排除选项A和C.故选B.试题难度:三颗星知识点:与角有关的辅助线2.如图,点E为直线AB上一点,点F为直线CD上一点,点G为直线AB和CD 内部的一点,根据几何原理下列作图正确的是( )第1页共7页A.连接 EF，使EF⊥ABB.连接 EF，使EF⊥CDC.过点 G 作直线MN∥ABD.过点 G 作直线MN∥AB∥CD 答案：C 解题思路：作辅助线要根据几何原理，比如两点确定一条直线，过直线外一点有且只有一条直线与已知直线平行，平面内，经过一点有且只有一条直线与已知直线垂直等．还要注意作一条辅助线不能同时满足多个条件．选项 A 中，可以连接 EF，或者过点 E 作EF⊥AB 交 CD 于点 F，但是不能说“连接 EF，使EF⊥AB”，因为连接 EF，不能保证EF⊥AB，需要证明，故选项 A 错误．同理选项 B 错误．选项 C，过点 G 作直线MN∥AB 是正确的，依据的是“过直线外一点有且只有一条直线与已知直线平行”．选项D，过点 G 作直线MN∥AB∥CD 是错误的，只能过点 G 作直线MN∥AB 或作直线MN∥CD，另一个平行需要证明，故选项 D 错误．故选 C．试题难度：三颗星知识点：与角有关的辅助线 3.如图 1，已知AB∥CD，求证：∠A+∠C+∠E=360°．图 2 在图 1 的基础上添加了辅助线用来证明结论，则下列选项中辅助线描述正确的是( )A.延长 CE 交 AB 的延长线于点 FB.延长 CE，延长 BAC.延长 CE 交 BA 于点 FD.延长 CE 交 BA 的延长线于点 F 答案：D 解题思路：从已知出发，由AB∥CD，要找同位角、内错角和同旁内角，因此要找截线，若把 CE 当作截线，可以延长 CE 交 BA 的延长线于点 F．第 2 页共 7 页故选 D．试题难度：三颗星知识点：与角有关的辅助线 4.如图 1，AB∥CD，∠E=∠F，求证：∠B=∠FCD．图 2 在图 1 的基础上添加了辅助线用来证明结论，则下列选项中辅助线描述正确的是( )A.延长 BE 交 CD 于点 GB.过点 E 作EG∥CFC.连接 EGD.作直线 BG 答案：A 解题思路：从已知出发，由AB∥CD，要找同位角、内错角和同旁内角，因此要找截线，若把 BE 当作截线，可以延长 BE 交 CD 于点 G．故选 A．试题难度：三颗星知识点：与角有关的辅助线 5.如图 1，在四边形 ABDC 中，求证：∠BDC=∠A+∠B+∠C．图 2 在图 1 的基础上添加了辅助线用来证明结论，则下列选项中辅助线描述正确的是( )A.连接 ADB.连接 AD 并延长C.作辅助线 ADD.连接 AD 使∠BAD=∠CAD 答案：B 解题思路：第 3 页共 7 页要证明∠BDC=∠A+∠B+∠C，结合图形考虑构造辅助线，把四边形转化为解基本图形（三角形），从而利用三角形内角和定理或三角形外角定理证明．故选 B．试题难度：三颗星知识点：与角有关的辅助线 6.如图 1，已知AB∥CD，CD⊥CE，∠FAB=45°，求∠ACE 的度数．图 2 在图 1 的基础上添加了辅助线用来求∠ACE 的度数，则下列选项中辅助线描述正确的是( )A.作射线 CGB.作辅助线 CG 使得∠ECG=90°，并且 D，C，G 在一条直线上C.延长 DC 到点 GD.作直线DG⊥CE 答案：C 解题思路：从已知出发，由AB∥CD，要找同位角、内错角和同旁内角，因此要找截线，若把 AC 当作截线，证明同位角∠FAB=∠ACG，可以延长 DC 到点 G，利用平行线的性质计算．故选C．试题难度：三颗星知识点：与角有关的辅助线 7.如图 1，MN∥GH，AB⊥MN，∠ABC=134°，求∠HDC 的度数．图 2 在图 1 的基础上添加了辅助线用来求∠HDC 的度数，则下列选项中辅助线描述正确的是( )第 4 页共 7 页A.延长 AB 交 GH 于点 F，使得∠BFH=90° C.连接 BF D.作射线 AFB.延长 AB 交 GH 于点 F答案：B 解题思路：从已知出发，由MN∥GH，要找同位角、内错角和同旁内角，因此要找截线，若把 AB 当作截线，可以延长 AB 交 GH 于点 F，利用平行线的性质计算．故选 B．试题难度：三颗星知识点：与角有关的辅助线 8.如图 1，已知AB∥CD，求证:∠B+∠D+∠E=360°．图 2 在图 1 的基础上添加了辅助线用来证明结论，则下列选项中辅助线描述正确的是( )A.作辅助线 EFB.作射线 EFC.过点 E 作EF∥AB∥CDD.过点 E 作EF∥AB 答案：D 解题思路：从已知出发，由AB∥CD，要证∠B+∠D+∠E=360°，可以通过搭桥的方法过点 E 作EF∥AB．故选 D．试题难度：三颗星知识点：与角有关的辅助线 9.已知：如图，AB∥CD，∠1=135°，∠3=75°，求∠2 的度数．为了求∠2 的度数，某同学添第 5 页共 7 页加辅助线：延长 BA 交 CE 于点 F．请你作出辅助线，并计算∠AFE 的度数为()° ° ° ° 答案：D 解题思路：从已知出发，由AB∥CD，要找同位角、内错角和同旁内角，因此要找截线，若把 EC 当作截线，可以延长 BA 交 EC 于点F．如图，延长 BA 交 CE 于点 F，要求∠2 的度数，可以把∠1 看作△ AEF 的一个外角，利用三角形的外角定理∠2=∠1-∠AFE，因此只需求出∠AFE 的度数即可；根据平行线的性质可以把∠3 往上转，求出∠AFC 的度数，再利用平角的定义可以求出∠AFE 的度数为105°．故选 D．试题难度：三颗星知识点：与角有关的辅助线 10.如图，AB∥CD，那么∠A，∠D，∠E 的关系是( )第 6 页共 7 页A.∠A+∠E+∠D=360° C.∠A-∠E+∠D=180°B.∠A+∠E-∠D=180° D.∠A+∠E+∠D=180°答案：B 解题思路：从已知出发，由AB∥CD，要求∠A，∠D 和∠E 之间的关系，可以通过搭桥的方法过点 E 作EF∥AB．如图，过点 E 作EF∥AB，结合已知AB∥CD，利用平行于同一条直线的两条直线互相平行，可知AB∥EF∥CD，根据平行线的性质可得∠A+∠1=180°，∠2=∠D，两式相加得∠A+∠1+∠2=180°+∠D，而∠1+∠2=∠AED，所以可得∠A+∠AED=180°+∠D，即∠A+∠E-∠D=180°．故选 B．试题难度：三颗星知识点：与角有关的辅助线第 7 页共 7 页相关文档：••••••••••更多相关文档请访问：。

初一初二几何做辅助线练习题

初一初二几何做辅助线练习题几何是数学中的一个重要分支，它研究的是空间和形状的关系。

初一初二阶段是学生接触几何的起始阶段，学生们需要掌握一些基础的几何知识和技巧，以便能够解决一些简单的几何问题。

在解决这些问题的过程中，学生们需要运用辅助线来帮助他们进行推理和证明。

本文将提供一些初一初二学生可以进行练习的几何辅助线题目，并提供相应的解答。

练习题一：三角形内角和问题已知三角形ABC中，∠A=60°，∠B=80°，求∠C的度数。

解答：我们可以利用三角形内角和定理来解决这个问题。

三角形内角和定理指出，三角形的三个内角的度数之和为180°。

因此，我们可以得到如下等式：∠A + ∠B + ∠C = 180°代入已知条件的数值，我们可以得到：60° + 80° + ∠C = 180°化简该等式，我们可以得到：140° + ∠C = 180°接下来，我们通过减法来求解∠C的度数：∠C = 180° - 140°∠C = 40°因此，∠C的度数为40°。

练习题二：平行线的性质问题已知线段AB与线段CD平行，线段AC与线段BD相交于点O。

若∠AOC=65°，求∠BOC的度数。

解答：我们可以利用平行线的性质和相交线的对应角对应角相等的性质来解决这个问题。

根据平行线的性质，我们可以得知∠BOC与∠AOC是对应角，因此它们的度数相等。

也就是说：∠BOC = ∠AOC代入已知条件的数值，我们可以得到：∠BOC = 65°因此，∠BOC的度数为65°。

练习题三：四边形内角和问题已知凸四边形ABCD，∠A=110°，∠B=90°，∠C=80°，求∠D的度数。

解答：我们可以利用凸四边形内角和定理来解决这个问题。

凸四边形内角和定理指出，凸四边形的四个内角的度数之和为360°。

初中数学与角有关的辅助线综合测试卷含答案

初中数学与角有关的辅助线综合测试卷含答案初中数学与角有关的辅助线综合测试卷一、单选题(共6道，每道18分)1.已知:如图,AB∥CD,∠B=60°,∠D=20°,求∠BED的度数.解:如图,延长BE交CD于点F,∵AB∥DC ∴∠B= ∵∠B=60° ∴∠1= ∵∠BED是△EFD的一个外角∴∠BED= + ∵∠D=20° ∴∠BED=60°+20° =80°①∠BED;②∠1;③∠BFC;④60°;⑤120°;⑥∠D;⑦∠FED. 在横线上依次填写正确的顺序为( )A.②④②⑦B.①④②⑥C.②④②⑥D.①④⑥⑦答案：C试题难度：三颗星知识点：与角有关的辅助线2.已知:如图,AB∥CD,∠B=110°,∠E=90°,则∠D的度数( )A.155°B.160°C.165°D.170°答案：B试题难度：三颗星知识点：与角有关的辅助线3.如图,AB∥CD,∠E=27°,∠D=52°,则∠EBA的度数为( )A.79°B.80°C.89°D.75°答案：A试题难度：三颗星知识点：与角有关的辅助线4.已知:如图,AB∥EF,∠A=25°,∠CDE=45°,∠E=15°,则∠ACD的度数为( )A.60°B.50°C.45°D.55°答案：D试题难度：三颗星知识点：与角有关的辅助线5.已知:如图,CD∥AB,∠ACE=135°,CD⊥CE.则∠BAF的度数为( )A.35°B.55°C.45°D.50°答案：C试题难度：三颗星知识点：与角有关的辅助线6.已知:如图,在四边形ABDC 中,∠A=85°,∠B=25°,∠C=35°,求∠BDC的度数.解:如图,延长BD交AC于点E.∵∠1是的外角∴∠1= ∵∠A=85°,∠B=25° ∴∠1 =85°+25°=110° ∵∠BDC是的外角∴∠BDC= ∵∠C=35° ∴∠BDC=110°+35° =145°①△ABE;②∠BEA;③∠A+∠B;④∠A+∠BEA;⑤△EDC;⑥∠EDC;⑦∠1+∠C;⑧∠EDC+∠C. 在横线上依次填写正确的顺序为( )A.②③⑤⑧B.②③⑤⑦C.①③⑤⑦D.①③⑤⑧答案：C试题难度：三颗星知识点：与角有关的辅助线。

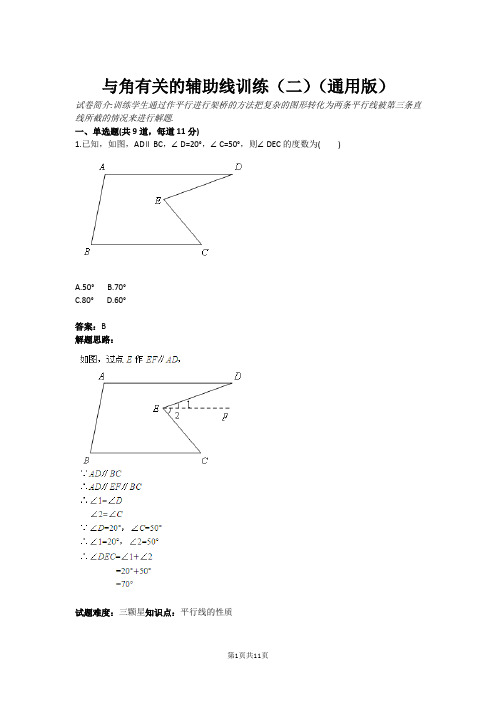
与角有关的辅助线训练(二)(通用版)(含答案)

与角有关的辅助线训练（二）（通用版）试卷简介:训练学生通过作平行进行架桥的方法把复杂的图形转化为两条平行线被第三条直线所截的情况来进行解题.一、单选题(共9道，每道11分)1.已知，如图，AD∥BC，∠D=20°，∠C=50°，则∠DEC的度数为( )A.50°B.70°C.80°D.60°答案：B解题思路：试题难度：三颗星知识点：平行线的性质2.已知，如图，AB∥CD，∠B=40°，∠E=60°，则∠D的度数为( )A.30°B.50°C.20°D.40°答案：C解题思路：试题难度：三颗星知识点：平行线的性质3.已知，如图，AB∥CD，∠B=40°，∠E=100°，则∠C的度数为( )A.100°B.120°C.140°D.130°答案：B解题思路：试题难度：三颗星知识点：平行线的性质4.如图，AB∥EF，∠C=90°，则∠α，∠β，∠γ的关系是( )A.∠β=∠α+∠γB.∠α+∠β+∠γ=180°C.∠α+∠β-∠γ=90°D.∠β+∠γ-∠α=90°答案：C解题思路：试题难度：三颗星知识点：平行线的性质5.已知，如图，AB∥CD，∠B=30°，∠BEF=120°，∠EFD=130°，则∠D的度数为( )A.30°B.50°C.70°D.40°答案：D解题思路：试题难度：三颗星知识点：平行线的性质6.已知，如图，AB∥CD，∠B=50°，∠BEF=20°，∠D=40°，求∠FED的度数.解：如图，过点E作EG∥AB，________________________∵∠B=50°∴∠BEG=50°∵∠1=20°∴∠2=∠BEG-∠1=50°-20°=30°∵∠D=40°∴∠3=40°∴∠FED=∠2+∠3=30°+40°=70°以上空缺处所填正确的是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行线的性质7.已知，如图，AB∥CD，∠B=30°，∠BEF=70°，∠FGC=70°，∠GCD=150°，则∠EFG的度数为( )A.50°B.70°C.80°D.90°答案：C解题思路：试题难度：三颗星知识点：平行线的性质8.如下图所示，AB∥CD，BO与DO相交于点O，从图1中可以得出，∠BOD=∠ABO+∠CDO，那么图2和图3针对三个角关系的结论正确的是( )C.∠BOD+∠ABO+∠CDO=360°；∠BOD=∠ABO+∠CDO；D.∠BOD+∠ABO+∠CDO=360°；∠CDO=∠BOD+∠ABO；答案：D解题思路：试题难度：三颗星知识点：平行线的性质9.已知，如图，AB∥CD，E是AC上一点，∠B=30°，∠D=60°，求证BE⊥ED.证明：如图，____________________∴∠B=∠1，∠D=∠2∵∠B=30°，∠D=60°∴∠1=30°，∠2=60°∴∠BED=∠1+∠2=30°+60°=90°即：BE⊥ED以上空缺处所填正确的是( ) A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：平行线的性质第11页共11页。

初中七年级下册平面几何证明之全等三角形之辅助线习题(含答案发))

初中七年级下册平面几何证明之全等三角形之辅助线习题(含答案发))AB∥CD（已知）___∠ACD（平行线夹角相等）AD∥BC（已知）___∠BCA（平行线夹角相等）ABC∽△CDA（AA）___又因为AC=BD，所以___AB+AD=BD+CDABCD是平行四边形又因为AB∥CD，所以∠ABD=∠CDA在△ABD和△CDA中AB CD（已知）BD AD（证明得出）ABD=∠CDA（证明得出）ABD≌△CDA（SAS）AB=CD，AD=BC（全等三角形对应边相等）3.证明：如图，连接BF、CF在△BFC和△DFC中BC ED（已知）___∠___∠___（已知）BF DF（公共边）BFC≌△DFC（SAS）___∠CFD（全等三角形对应角相等）又因为BC=ED，所以___又因为AB=AE，所以∠AFE=∠BAF在△___和△BAF中AF AF（公共边）AFE=∠BAF（证明得出）AE AB（已知）AFE≌△BAF（SAS）AFB=∠AFE（全等三角形对应角相等）又因为∠___∠CFD，所以∠AFB=∠CFD AFB=∠______⊥BD4.证明：如图，连接BC在△ABC中B=∠C（已知）AB=AC（等角对应边相等）5.证明：如图，连接BD，BE在△ABD和△___中AB EB（共边）ABD=∠___（已知）BD BC（已知）ABD≌△EBC（SAS）BD=BE（全等三角形对应边相等）6.证明：如图，连接BF，CF，AE，DE 在△ABD和△ECD中AE BD（已知）AED=∠ABD（公共角）EC DC（已知）AED≌△ABD（SAS）___∠AFE（全等三角形对应角相等）又因为BF=DF，所以BF+FD=DF+DE 又因为AE=BD，所以AF+FD=BFAF+FD=DF+DEAF-DE=DF-FDAF-DE=DF-FC又因为EC=CD，所以∠ECD=∠CDE在△ECD和△___中EC BC（已知）ECD=∠CDE（证明得出）CD FC（已知）ECD≌△___（SAS）BF=DE（全等三角形对应边相等）又因为BF=DF，所以BF-DE=DF-DEBF-DE=DF-FCBE=CF又因为∠___∠AFE，所以∠BAF+∠___∠AFE+∠CAF ___∠___又因为BE=CF，所以∠___∠CAF___∠CAF___⊥BD7.因为BD，CE是△ABC的高，所以∠ABD=90°，∠ACE=90°又因为BP=AC，CQ=AB，所以___BPC∽△CQA（SAS）又因为∠___∠CQA=90°，所以△BPC和△CQA是直角三角形又因为BP=AC，CQ=AB，所以BP+CQ=AB+AC=BCBP+CQ=BC又因为___，所以BP/BC=AC/(AB+AC)BP/BC=AC/BCBP=AC又因为BP=AC，所以___CQ/BC=AB/ACCQ=AB又因为BP=AC，CQ=AB，所以BP+CQ=AB+AC=BCAP=BQ=BC/2又因为BD，CE是△___的高，所以AP⊥BD，___⊥CE ___⊥BD，___⊥CEAP∥BQ又因为AP=BQ，所以APBQ是平行四边形AP=BQ，AP∥BQ2+∠4=90°又因为AB=AC，所以△ABP≌△ACQ（ASA）AP=AQ又因为AP⊥AQ，所以APQ为等腰直角三角形PAQ=45°8.解：如图。

初二数学全等三角形角平分线辅助练习题及答案

初二数学全等三角形角平分线辅助练习题及答案一、全等三角形角平分线辅助1．（特例感知）（1）如图（1），ABC ∠是O 的圆周角，BC 为直径，BD 平分ABC ∠交O 于点D ，3CD =，4BD =，求点D 到直线AB 的距离．（类比迁移）（2）如图（2），ABC ∠是O 的圆周角，BC 为O 的弦，BD 平分ABC ∠交O 于点D ，过点D 作DE BC ⊥，垂足为点E ，探索线段AB ，BE ，BC 之间的数量关系，并说明理由．（问题解决）（3）如图（3），四边形ABCD 为O 的内接四边形，90ABC ∠=︒，BD 平分ABC ∠，72BD =，6AB =，求ABC 的内心与外心之间的距离．2．在ABC 中，60A ∠=︒，BD ，CE 是ABC 的两条角平分线，且BD ，CE 交于点F ．（1）如图1，用等式表示BE ，BC ，CD 这三条线段之间的数量关系，并证明你的结论；小东通过观察、实验，提出猜想：BE CD BC +=．他发现先在BC 上截取BM ，使BM BE =，连接FM ，再利用三角形全等的判定和性质证明CM CD =即可． ①下面是小东证明该猜想的部分思路，请补充完整： ⅰ）在BC 上截取BM ，使BM BE =，连接FM ，则可以证明BEF 与全等，判定它们全等的依据是； ⅱ）由60A ∠=︒，BD ，CE 是ABC 的两条角平分线，可以得出EFB ∠= °； ②请直接利用ⅰ），ⅱ）已得到的结论，完成证明猜想BE CD BC +=的过程．（2）如图2，若40ABC ∠=︒ ，求证：BF CA =．3．如图，矩形ABCD中，AB=4，AD=3，∠A的角平分线交边CD于点E．点P从点A出发沿射线AE以每秒2个单位长度的速度运动，Q为AP的中点，过点Q作QH⊥AB于点H，在射线AE的下方作平行四边形PQHM（点M在点H的右侧），设P点运动时间为t秒．（1）直接写出AQH的面积（用含t的代数式表示）．（2）当点M落在BC边上时，求t的值．（3）在运动过程中，整个图形中形成的三角形是否存在全等三角形？若存在，请写出所有全等三角形，并求出对应的t的值；若不存在请说明理由（不能添加辅助线）．4．如图，在△ABC中，AB＝AC，∠ABC＝40°，BD是∠ABC的平分线，延长BD至E，使DE＝AD，求证：∠ECA＝40°．5．如图，已知BC是⊙O的弦，A是⊙O外一点，△ABC为正三角形，D为BC的中点，M 为⊙O上一点．（1）若AB 是⊙O 的切线，求∠BMC ；（2）在（1）的条件下，若E ，F 分别是AB ，AC 上的两个动点，且∠EDF =120︒，⊙O 的半径为2，试问BE +CF 的值是否为定值？若是，求出这个定值；若不是，请说明理由． 6．如图所示，在ABC ∆中，=60ACB ∠，,AE BD 是ABC ∆的角平分线，,AE BD 交于点G ，求证：GD GE =．7．已知：ABC ∆中，D 为BC 的中点，AG 平分,BAC CG AG ∠⊥于G ，连结DG ，若6,4AB AC ==，求DG 的长．8．如图，ABC ∆的外角ACD ∠的平分线CP 与内角ABC ∠的平分线BP 交于点P ，若40BPC ∠=︒，求CAP ∠的度数．9．如图，在四边形OACB 中，CE OA ⊥于E ，12∠=∠，CA CB =.求证：34180∠+∠=︒；2OA OB OE +=.10．如图，已知：在△ABC 中，AD 平分∠BAC ，AB=AD ，CE ⊥AD ，交AD 的延长线于E.求证：AB+AC=2AE.【参考答案】***试卷处理标记，请不要删除一、全等三角形角平分线辅助1．（1）125；（2）2AB BC BE +=，理由见解析；（3）5．【分析】（1）如图①中，作DF AB ⊥于F ，DE BC ⊥于E ．理由面积法求出DE ，再利用角平分线的性质定理可得DF DE =解决问题；（2）如图②中，结论：2AB BC BE +=．只要证明()DFA DEC ASA ∆≅∆，推出AF CE =，Rt BDF Rt BDE(HL)∆≅∆，推出AF BE =即可解决问题；（3）如图③，过点D 作DF ⊥BA ，交BA 的延长线于点F ，DE ⊥BC ，交BC 于点E ，连接AC ，作△ABC △ABC 的内切圆，圆心为M ，N 为切点，连接MN ，OM ．由（1）（2）可知，四边形BEDF 是正方形，BD 是对角线．由切线长定理可知：610842AN +-==，推出541ON =-=，由面积法可知内切圆半径为2，在Rt OMN ∆中，理由勾股定理即可解决问题；【详解】解：（1）如图①中，作DF AB ⊥于F ，DE BC ⊥于E ．图①BD 平分ABC ∠，DF AB ⊥，DE BC ⊥，DF DE ∴=，BC 是直径，90BDC ∴∠=︒，2222435BC BD CD ∴=+=+=，1122BC DE BD DC =， 125DE ∴=， 125DF DE =∴=．故答案为125 （2）如图②中，结论：2AB BC BE +=．图②理由：作DF BA ⊥于F ，连接AD ，DC ．BD 平分ABC ∠，DE BC ⊥，DF BA ⊥，DF DE ∴=，90DFB DEB ∠=∠=︒，180ABC ADC ∠+∠=︒，180ABC EDF ∠+∠=︒，ADC EDF ∴∠=∠，FDA CDE ∴∠=∠，90DFA DEC ∠=∠=︒，()DFA DEC ASA ∴∆≅∆，AF CE ∴=，BD BD =，DF DE =，Rt BDF Rt BDE(HL)∴∆≅∆，BF BE ∴=，2AB BC BF AF BE CE BE ∴+=-++=．（3）如图③，过点D 作DF ⊥BA ，交BA 的延长线于点F ，DE ⊥BC ，交BC 于点E ，连接AC ，作△ABC △ABC 的内切圆，圆心为M ，N 为切点，连接MN ，OM ．由（1）（2）可知，四边形BEDF 是正方形，BD 是对角线．图③ 7BD =，∴正方形BEDF 的边长为7，由（2）可知：28BC BE AB =-=，10AC ∴==，由切线长定理可知：610842AN +-==， 541ON ∴=-=，设内切圆的半径为r ，则11111068682222r r r ⨯+⨯⨯+⨯⨯=⨯⨯⨯ 解得2r ，即2MN =，在Rt OMN ∆中，OM ===．【点睛】本题属于圆综合题，考查了角平分线的性质定理，全等三角形的判定和性质，勾股定理，解直角三角形，正方形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．2．（1）①ⅰ）△BMF ，边角边；ⅱ）60；②详见解析；（2）详见解析【分析】（1）先得出结论；①利用三角形内角和求出∠ABC+∠ACB=120°，进而得出∠FBC+∠FCB=60°，得出∠BFC=120°，即可得出结论；②利用角平分线得出∠EBF=∠MBF ，进而得出△BEF ≌△BMF ，求出∠BFM ，即可判断出∠CFM=∠CFD ，即可判断出△FCM ≌△FCD ，即可得出结论；（2）先求出相关角的度数，进而判断出BG=CE ，进而判断出△BGF ≌△CEA ，即可得出结论．【详解】（1）BC CD BE =+①如图1，在BC 上取一点M ，使BM BE =，ⅰ）BD 是ABC ∠的平分线，EBF MBF ∴∠=∠，在BEF ∆和BMF ∆中，BE BM EBF MBF BF BF =⎧⎪∠=∠⎨⎪=⎩，()BEF BMF SAS ∴∆≅∆；ⅱ）BD ，CE 是ABC ∆的两条角平分线， 12FBC ABC ∴∠=∠，12BCF ACB ∠=∠，在ABC ∆中，180A ABC ACB ∠+∠+∠=︒，60A ∠=︒，180120ABC ACB A ∴∠+∠=︒-∠=︒，1180()180()1202BFC CBF BCF ABC ACB ∴∠=︒-∠+∠=︒-∠+∠=︒， 18012060EFB ∴∠=︒-︒=︒；故答案为：ⅰ）ΔBMF ，SAS ；ⅱ）60；②由①知，60BFE ∠=︒，BEF BMF ∆≅∆，60CFD BFE ∴∠=∠=︒，∵BEF BMF ∆≅∆，60BFE BFM ∴∠=∠=︒，60CFM BFC BFM ∴∠=∠-∠=︒，60CFM CFD ∴∠=∠=︒，CE 是ACB ∠的平分线，FCM FCD ∴∠=∠，在FCM ∆和FCD ∆中，CFM CFD CF CF FCM FCD ∠=∠⎧⎪=⎨⎪∠=∠⎩()FCM FCD ASA ∴∆≅∆，CM CD ∴=，BC CM BM CD BE ∴=+=+；（2）如图2，在ABC ∆中，60A ∠=︒，40ABC ∠=︒，80ACB ∴∠=︒，BD ，CE 是ABC ∆的两条角平分线，1202ABD CBD ABC ∴∠=∠=∠=︒，1402BCE ACE ACB ∠=∠=∠=︒， 80AEC ABC BCE ∴∠=∠+∠=︒，ABC BCE ∠=∠，BE CE ∴=，在ABC ∆的边AB 左侧作20ABG ∠=︒，交CE 的延长线于G ，40FBG ABD ABG ACE ∴∠=∠+∠=︒=∠．80AEC ∠=︒，80BEG ∴∠=︒，18080G ABG BEG BEG AEC ∴∠=︒-∠-∠=︒=∠=∠，BG BE ∴=，BG CE ∴=，在BGF ∆和CEA ∆中，4080FBG ACE BG CE BGF AEC ∠=∠=︒⎧⎪=⎨⎪∠=∠=︒⎩，BGF CEA ∴∆≅∆，BF AC ∴=．【点睛】此题是三角形综合题，主要考查了角平分线的定义，三角形内角和定理，全等三角形的判定和性质，解本题的关键是（1）判断出CFM CFD ∠=∠，（2）作出辅助线，判断出BG CE =．3．（1）214t ；（2）22t =3）存在，如图2（见解析），当AHQ HBM ≅时，22t =3（见解析），当ADE AHE ≅时，32t =4（见解析），当EGQ HBF ≅时，722t =【分析】（1）先根据线段中点的定义可得12AQ AP =，再根据矩形的性质、角平分线的定义可得45HAQ ∠=︒，从而可得AQH 是等腰直角三角形，然后根据等腰直角三角形的性质可得AH 的长，最后根据等腰直角三角形的面积公式即可得；（2）先根据平行四边形的性质可得//HQ MP ，从而可得//HQ BP ，再根据三角形中位线定理可得HQ 是ABP △的中位线，从而可得122AH AB ==，然后与（1）所求的22AH =建立等式求解即可得；（3）分①当点H 是AB 的中点时，AHQ HBM ≅；②当点Q 与点E 重合时，ADE AHE ≅；③当EG HB =时，EGQ HBF ≅三种情况，分别求解即可得．【详解】（1）由题意得：2AP t =，点Q 为AP 的中点，12AQ AP t ∴==，四边形ABCD 是矩形，90B D BAD ∴∠=∠=∠=︒，AE ∵是BAD ∠的角平分线，1452HAQ DAE BAD ∴∠=∠=∠=︒， QH AB ⊥，AQH ∴是等腰直角三角形，22AH HQ AQ t ∴===，则AQH 的面积为21124AH HQ t ⋅=；（2）如图1，四边形PQHM 是平行四边形， //HQ MP ∴，点M 在BC 边上，//HQ BP ∴，点Q 为AP 的中点，HQ ∴是ABP △的中位线，122AH BH AB ∴===，由（1）知，2AH =，则22t =，解得t =；（3）由题意，有以下三种情况：①如图2，当点H 是AB 的中点时，则AH HB =，四边形PQHM 是平行四边形， //HM PQ ∴，HAQ BHM ∴∠=∠，在AHQ 和HBM △中，90HAQ BHM AH HB AHQ HBM ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩，()AHQ HBM ASA ∴≅，由（2）可知，此时22t =；②如图3，当点Q 与点E 重合时，在ADE 和AHE 中，9045D AHE DAE HAE AE AE ∠=∠=︒⎧⎪∠=∠=︒⎨⎪=⎩，()ADE AHE AAS ∴≅，3AD AH ∴==， 23=，解得32t =；③如图4，当EG HB =时，四边形ABCD 是矩形，四边形PQHM 是平行四边形，//,//CD AB HM PQ ∴，,90GEQ HAQ BHF EGQ AHQ B ∴∠=∠=∠∠=∠=︒=∠，在EGQ 和HBF 中，GEQ BHF EG HB EGQ B ∠=∠⎧⎪=⎨⎪∠=∠⎩，()EGQ HBF ASA ∴≅， 2,4AH AB ==， 24HB AB AH ∴=-=，在Rt ADE △中，45,3DAE AD ∠=︒=， Rt ADE ∴是等腰直角三角形，232AE ==32EQ AQ AE t ∴=-=-，在Rt GEQ 中，45GEQ HAQ ∠=∠=︒， Rt GEQ ∴是等腰直角三角形，22622t EG EQ -==，则由EG HB =2624t -=-，解得722t =综上，如图2，当AHQ HBM ≅时，22t=；如图3，当ADE AHE ≅时，32t =；如图4，当EGQ HBF ≅时，722t =．【点睛】本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点，较难的是题（3），依据题意，正确分三种情况讨论并画出图形是解题关键．4．见解析【分析】在BC 上截取BF ＝AB ，连DF ，根据SAS 可证明△ABD ≌△FBD ，得出DF ＝DA ＝DE ，证明△DCE ≌△DCF ，故∠ECA ＝∠DCB ＝40°．【详解】证明：在BC 上截取BF ＝AB ，连DF ，∵BD 是∠ABC 的平分线，∴∠ABD ＝∠FBD ，在△ABD 和△ＦBD 中，AB FB ABD FBD BD BD =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△FBD （SAS ），∴DF ＝DA ＝DE ，又∵∠ACB ＝∠ABC ＝40°，∠DFC ＝180°﹣∠A ＝80°，∴∠FDC ＝60°，∴∠EDC ＝∠ADB ＝180°﹣∠ABD ﹣∠A＝180°﹣20°﹣100°＝60°，在△DCE 和△DCF 中，DF DE FDC EDC DC DC =⎧⎪∠=∠⎨⎪=⎩，∴△DCE ≌△DCF （SAS ），∴∠ECA ＝∠DCB ＝40°．【点睛】本题考查了全等三角形的判定与性质，三角形内角和定理，熟练掌握全等三角形的判定与性质是解题的关键．5．（1）60°；（2）BE+CF 的值是定值，BE+CF=3.【分析】（1）连接BO ，由AB 是切线可以得到∠ABO 的度数，由△ABC 为等边三角形，得到∠OBC 的度数，然后得到∠BOC ，根据圆心角与圆周角的关系得到∠BMC 的度数.（2）作DH ⊥AB 于H ，DN ⊥AC 于N ，连结AD ，OD ，如图2，根据等边三角形三角形的性质得AD 平分∠BAC ，∠BAC=60°，则利用角平分线性质得DH=DN ，根据四边形内角和得∠HDN=120°，由于∠EDF=120°，所以∠HDE=∠NDF ，接着证明△DHE ≌△DNF 得到HE=NF ，于是BE+CF=BH+CN ，再计算出BH=12BD ，CN=12DC ，则BE+CF=12BC ，于是可判断BE+CF 的值是定值，为等边△ABC 边长的一半，再计算BC 的长即可．【详解】（1）解：如图，连接BO ，∵AB 是圆的切线，∴∠ABO=90°，∵△ABC 是等边三角形，∴∠ABC=60°，∴∠CBO=90°-60°=30°，∵BO=CO ，∴∠BCO=∠CBO=30°，∴∠BOC=120°，∴∠BMC=1BOC60 2∠=︒（2）解：BE+CF的值是为定值．理由：作DH⊥AB于H，DN⊥AC于N，连结AD，OD，如图2，∵△ABC为正三角形，D为BC的中点，∴AD平分∠BAC，∠BAC=60°，∴DH=DN，∠HDN=120°，∵∠EDF=120°，∴∠HDE=∠NDF，在△DHE和△DNF中，∴DHE DNFDH DNHDE NDF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△DHE≌△DNF，∴HE=NF，∴BE+CF=BH-EH+CN+NF=BH+CN，在Rt△DHB中，∵∠DBH=60°，∴BH=12BD，同理可得CN=12 OC，∴BE+CF=12DB+12DC=12BC，∵3∴BC=23∴3∴BE+CF3【点睛】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．也考查了等边三角形的性质．6．详见解析【解析】【分析】在AB 上截AF AD =，连接FG ，根据角平分线的性质、结合三角形内角和定理可得AGD=120AGB ∠︒∠=︒60，，证明ADG AFG ∆∆≌，得GD=GF ，AGD AGF ∠=∠=60°，可证得BGF BGE ∆∆≌，即可得GF=GE=GD.【详解】证明：在AB 上截AF AD =，连接FG ，∵AE 平分∠BAC ，∴∠EAC=∠EAB ，又∵AG=AG ，∴ADG AFG ∆∆≌，GD GF ∴=，AGD AGF ∠=∠ ，∵60ACB ∠=︒，AE,BD 是ΔABC 的角平分线，∴()111802211802120AGB CAB CBA CAB CBA ∠=︒-∠-∠=︒-∠+∠=︒， ∴60AGD AGF BGF BGE ∠=∠=∠=∠=︒，∵BGF BGE BG BG GBF GBE ∠=∠⎧⎪=⎨⎪∠=∠⎩()BGF BGE ASA ∴∆∆≌，∴GF GE = ，∴GD=GE.【点睛】本题考查角平分线的性质、全等三角形的判定和性质，作辅助线是解题的关键． 7．1DG =【分析】延长CG 交AB 于点E. 根据等腰三角形的判定与性质得CG=EG ，AE=AC,再根据三角形中位线的性质得出DG=12BE=12（AB-AC ），从而得出DG 的长．【详解】解：延长CG 交AB 于点E ．AG 平分BAC ∠，CG AG ⊥于G ，CG EG ∴=，4AE AC ==，2BE AB AC ∴=-=，∵CG EG ，D 为BC 的中点，112DG BE ∴==．故答案为1DG =.【点睛】本题考查等腰三角形的判定与性质，三角形中位线定理，根据题意作出辅助线，利用三角形中位线定理求解是解题的关键．8．50°【解析】【分析】根据外角与内角性质得出∠BAC 的度数，再利用角平分线的性质以及直角三角形全等的判定，得出∠CAP=∠FAP ，即可得出答案．【详解】延长BA ，作PN ⊥BD ，PF ⊥BA ，PM ⊥AC ，设∠PCD=x°，∵CP 平分∠ACD ，∴∠ACP=∠PCD=x°，PM=PN ，∵BP 平分∠ABC ，∴∠ABP=∠PBC ，PF=PN ，∴PF=PM ，∵∠BPC=40°，∴∠ABP=∠PBC=∠PCD-∠BPC=(x-40)°，∴∠BAC=∠ACD-∠ABC=2x°-(x°-40°)-(x°-40°)=80°，∴∠CAF=100°，在Rt △PFA 和Rt △PMA 中，PA PA PM PF =⎧⎨=⎩， ∴Rt △PFA ≌Rt △PMA(HL)，∴∠CAP=∠FAP ，又∵∠CAP+∠PAF=∠CAF ，∴∠CAP =50°．【点睛】本题主要考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识，根据角平分线的性质得出PM=PN=PF 是解决问题的关键．9．详见解析【分析】过点C 向OA 、OB 作垂线，构建全等三角形，继而根据平角定义以及线段的和差即可证得结论.【详解】如图，过点C 作CF OB ⊥与点F ，则∠F=∠CEO=90°，12∠=∠，OC=OC ，FOC EOC ∴∆≅∆，CE CF ∴=，OE OF =，CA CB =，90CEA CFB ∠=∠=︒，()R t t CAE R CBF HL ∴∆≅，4CBF ∴∠=∠，AE BF =，∵3180CBF ∠+∠=︒，34180∴∠+∠=︒，()()2OA OB OE AE OF BF OE OF OE ∴+=++-=+=.【点睛】本题考查了全等三角形的判定与性质，正确添加辅助线构建全等三角形是解题的关键. 10．详见解析【分析】延长AE 到M ，使ME=AE ，连接CM ，求出AC=CM ，求出DM=MC ，即可得出答案．【详解】延长AE 到M ，使ME=AE ，连接CM ，则AM=2AE ，∵CE⊥AE，∴AC=CM，∴∠M=∠CAD=∠DAB，∴AB∥MC，∴∠B=∠MCD，∵AB=AD，∴∠B=∠ADB，∵∠ADB=∠MDC，∴∠MCD=∠MDC，∴MC=MD，∴AM=2AE=AD+MD=AB+AC，即AB+AC=2AE.【点睛】本题考查了平行线的性质和判定，线段垂直平分线性质，等腰三角形的性质和判定的应用，解此题的关键是推出DE=EC，有一定的难度．。

八年级数学上册综合训练与角有关的辅助线随堂测试新人教版(2021年整理)

2017-2018八年级数学上册综合训练与角有关的辅助线随堂测试（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017-2018八年级数学上册综合训练与角有关的辅助线随堂测试（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017-2018八年级数学上册综合训练与角有关的辅助线随堂测试（新版）新人教版的全部内容。

与角有关的辅助线（随堂测试）1。

已知：如图，AB⊥EF 于点O，BD 与MN 相交于点C,∠1=35°，∠B=125°．A求证:EF∥MN．E O FBM NC 1D【参考答案】1. 解：EF∥MN理由如下：如图,延长AB 交MN 于点G．AE O FBM NG C 1D∵∠1=35°（已知）∴∠BCG=35°（对顶角相等）∵∠ABC 是△BCG 的一个外角（外角的定义)∴∠ABC=∠BGC+∠BCG（三角形的外角等于和它不相邻的两个内角的和）∵∠ABC=125°(已知)∴∠BGC=∠ABC∠=125°35°=90°（等式的性质）∵AB⊥EF（已知）∴∠AOF=90°(垂直的定义）∴∠AOF=∠BGC（等量代换）∴EF∥MN(同位角相等，两直线平行）。

辅助线几何练习题初三

辅助线几何练习题初三几何学是数学的一部分，它研究空间和形状之间的关系。

而辅助线是在解决几何问题时常常使用的一种方法。

下面将给出一些辅助线几何练习题，帮助初三学生更好地理解和运用辅助线的概念。

题目一：等腰三角形的性质已知△ABC中，AB=AC，角B=40°。

作辅助线BD ⊥ AC，交BC 于点D，请证明：∠ADC = 70°。

解析：首先，连接AD并延长至E，使得AE=AC。

因为AB=AC，所以△ABD为等腰三角形，角BAD=40°。

又因为BD ⊥ AC，所以角BDA = 90°。

根据△ABD的性质可知角ADB=70°。

又因为AE=AC，所以△AED也为等腰三角形，角AED=70°。

所以∠ADC = 70°。

题目二：平行线的性质已知平行线AB ∥ CD，E是线段AD的中点，交线段BC于点F。

请证明：△AFB为等腰三角形。

解析：连接AE、EF和FB。

因为AB ∥ CD，所以角BAE = 角EFC（同位角）。

又因为AD是线段BC的中点，所以线段AE是线段BF的中点，即AE=EF，所以△AEF为等腰三角形。

根据等腰三角形的性质可知，∠EAF = ∠EFA。

又因为角BAE = 角EFC，所以∠EFA = ∠AFE。

综上所述，△AFB为等腰三角形。

题目三：相似三角形的性质已知△ABC，D是AB的中点，E是AC的中点。

交线段BE和CD 于点F。

请证明：△AFE和△BCF相似。

解析：连接AD和CF。

因为D是AB的中点，所以AD ∥ BC（平行线的性质）。

又因为AC是线段BE的中点，所以AC ∥ EF（平行线的性质）。

所以根据平行线的性质可知，△AFE和△BCF相似。

综上所述，辅助线在解决几何问题中起到了重要的作用。

通过巧妙的运用辅助线，可以简化解题步骤、增加解题的准确性，并帮助初三学生更好地理解和运用几何学中的概念。

希望以上的练习题能帮助到初三的同学们，提升他们在几何学中的表现。

中考数学数学全等三角形角平分线辅助试题及答案

中考数学数学全等三角形角平分线辅助试题及答案一、全等三角形角平分线辅助1．在平面直角坐标系中，点A 的坐标是(0,)a ，点B 的坐标(,0)b 且a ，b 满足212360a a a b -++-=．（1）求A 、B 两点的坐标；（2）如图（1），点C 为x 轴负半轴一动点，OC OB <，BD AC ⊥于D ，交y 轴于点E ，求证：OD 平分CDB ∠．（3）如图（2），点F 为AB 的中点，点G 为x 正半轴点B 右侧的一动点，过点F 作FG 的垂线FH ，交y 轴的负半轴于点H ，那么当点G 的位置不断变化时，AFH FBG S S -△△的值是否发生变化?若变化，请说明理由；若不变化，请求出相应结果．2．问题呈现：下图是小明复习全等三角形时遇到的一个问题并引发的思考，请帮助小明完成以下学习任务．请根据小明的思路，结合图①，写出完整的证明过程．结论应用：（1）如图②，在四边形ABCD 中，AB AD BC =+，DAB ∠的平分线和ABC ∠的平分线交于CD 边上点P ．求证：PC PD =；（2）在（1）的条件下，如图③，若10AB =，1tan 2PAB ∠=．当PBC 有一个内角是45︒时，PAD △的面积是．3．教材呈现：如图是华师版八年级上册数学教材第94页的部分内容.2．线段垂直平分线.我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴，如图，直线MN是线段AB的垂直平分线，P是MN上任一点，连结PA、PB，将线段AB沿直线MN对称，我们发现PA与PB完全重合，由此即有：线段垂直平分线的性质定理线段垂直平分线上的点到线段的距离相等．已知：如图，MN⊥AB，垂足为点C，AC＝BC，点P是直线MN上的任意一点．求证：PA＝PB．分析：图中有两个直角三角形APC和BPC，只要证明这两个三角形全等，便可证明PA＝PB．定理证明：请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程．定理应用：（1）如图②，在△ABC中，直线m、n分别是边BC、AC的垂直平分线，直线m、n的交点为O．过点O作OH⊥AB于点H．求证：AH＝BH．（2）如图③，在△ABC中，AB＝BC，边AB的垂直平分线l交AC于点D，边BC的垂直平分线k交AC于点E．若∠ABC＝120°，AC＝15，则DE的长为．4．∠MON=90°，点A，B分别在OM、ON上运动（不与点O重合）．（1）如图①，AE、BE分别是∠BAO和∠ABO的平分线，随着点A、点B的运动，∠AEB=°（2）如图②，若BC是∠ABN的平分线，BC的反向延长线与∠OAB的平分线交于点D①若∠BAO=60°，则∠D=°．②随着点A，B的运动，∠D的大小会变吗？如果不会，求∠D的度数；如果会，请说明理由．（3）如图③，延长MO至Q，延长BA至G，已知∠BAO，∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F，在△AEF中，如果有一个角是另一个角的3倍，求∠ABO的度数．5．直线MN与直线PQ垂直相交于点O，点A在射线OP上运动（点A不与点O重合），点B在射线OM上运动（点B不与点O重合）．（1）如图1，已知AE、BE分别是∠BAO和∠ABO的角平分线，①当∠ABO＝60°时，求∠AEB的度数；②点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况：若不发生变化，试求出∠AEB的大小；（2）如图2，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，请直接写出∠ABO 的度数．6．已知：等腰直角三角形ABC中，∠ACB=90°；AC=BC；∠1=∠3；BE⊥AD。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初中数学与角有关的辅助线综合测试卷
初中数学与角有关的辅助线综合测试卷
一、单选题(共6道，每道18分)
1.已知:如图,AB∥CD,∠B=60°,∠D=20°,求∠BED的度数.
解:如图,延长BE交CD于点F,
∵AB∥DC ∴∠B= ∵∠B=60°∴∠1=
∵∠BED是△EFD的一个外角∴∠BED= + ∵∠D=20°
∴∠BED=60°+20° =80°
①∠BED;②∠1;③∠BFC;④60°;⑤120°;⑥∠D;⑦∠FED. 在横线上依次填写正确的顺序为( )
A.②④②⑦
B.①④②⑥
C.②④②⑥
D.①④⑥⑦
2.已知:如图,AB∥CD,∠B=110°,∠E=90°,则∠D的度数( )
A.155°
B.160°
C.165°
D.170°
3.如图,AB∥CD,∠E=27°,∠D=52°,则∠EBA的度数为( )
A.79°
B.80°
C.89°
D.75°
4.已知:如图,AB∥EF,∠A=25°,∠CDE=45°,∠E=15°,则∠ACD的度数为( )
A.60°
B.50°
C.45°
D.55°
5.已知:如图,CD∥AB,∠ACE=135°,CD⊥CE.则∠BAF的度数为( )
A.35°
B.55°
C.45°
D.50°
6.已知:如图,在四边形ABDC中,∠A=85°,∠B=25°,∠C=35°,求∠BDC的度数.
解:如图,延长BD交AC于点E.
∵∠1是的外角∴∠1=
∵∠A=85°,∠B=25°∴∠1 =85°+25°=110°∵∠BDC是的外角∴∠BDC=
∵∠C=35°∴∠BDC=110°+35° =145°
①△ABE;②∠BEA;③∠A+∠B;④∠A+∠BEA;⑤△EDC;⑥∠EDC;⑦∠1+∠C;
⑧∠EDC+∠C. 在横线上依次填写正确的顺序为( )
A.②③⑤⑧
B.②③⑤⑦
C.①③⑤⑦
D.①③⑤⑧。