广西大学现代控制理论期末考试题库之填空题(含答案)
现代控制理论考试题及答案

答案及评分标准一,填空(3分每空,共15分)1.输出变量 2.变量的个数最少 3.⎥⎦⎤⎢⎣⎡2001 4. 其状态空间最小实现为u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=100001100010 ; u x y 2102121+⎥⎦⎤⎢⎣⎡= 5. 0,021==x x二,选择题(3分每题,共12分) 1.B 2.D 3.B 4.C三,判断题(3分每题,共12分)1.2. √3.4. √四,简答题(共23分)1.(5分) 解 判定系统11221223x x x x x x =-+⎧⎨=--⎩在原点的稳定性。
解 2114523I A λλλλλ+--==+++,两个特征根均具有负实部,(3分) 系统大范围一致渐近稳定。
(2分) 无大范围扣一分,无一致渐近扣一分。
2. (5分)11b ab b -⎛⎫⎪--⎝⎭能控性矩阵为 (2分)1 rank 211det 1b ab b b ab b -⎛⎫= ⎪--⎝⎭-⎛⎫⇔ ⎪--⎝⎭210b ab =-+-≠ (5分)3.(8分)在零初始条件下进行拉式变换得:)()(2)()()(2)(3)(223S U S SU S U S S Y S SY S Y S S Y S ++=+++12312)()()(232+++++==∴S S S S S S U S Y S G (4分)[]XY U X X 121100321100010.=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=∴ (8分)4.(5分)解:[]B CS G A SI --=1)( (2分)2342+--=S S S (5分) 五,计算题1. 1210c u ⎡⎤=⎢⎥⎣⎦,1112201c u -⎡⎤=⎢⎥-⎣⎦能控性矩阵满秩,所以系统能化成能控标准型。
(2分)[][][]1111221122010101c p u -⎡⎤===-⎢⎥-⎣⎦[][]11112122221100p p A ⎡⎤==-=⎢⎥⎣⎦11221112211,11P P --⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦(10分) 能控标准型为u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=101010..(12分) 2. 解:11][)(---==A SI L e t At φ (2分)⎥⎦⎤⎢⎣⎡+-+---=-==----------t t tt t t tt Ate e ee e e e e A SI L e t 3232323211326623][)(φ (8分) ∴系统零初态响应为 X(t)=0,34121)(32320)(≥⎥⎦⎤⎢⎣⎡-+-+-=-----⎰t e e e e d Bu et t t t t t A τττ (12分) 3. 解:因为能观性矩阵满秩,所以系统可观,可以设计状态观测器。
现代控制理论试题(09级)

宝鸡文理学院试题课程名称 现代控制理论 适 用 时 间 11年12月 试卷类别 A适用专业、年级、班 09电气(123)自动化一、填空题(每小题1分,20×1=20分) 1、状态变量是 。
2、给定系统的状态空间描述(A,B,C,D),则其传递函数(阵)为。
3、控制系统经非奇异变换后,其特征根 。
4、线性系统的运动由两部分组成,第一项为 ,第二项为 ,正是由于第 项的存在,提供了通过选择合适的输入使系统状态轨迹满足期望要求的可能性。
5、系统的能控性是研究 对 的制约能力;能观性是研究 反映 的能力。
6、一般来说,控制系统的传递函数阵是对系统内部状态的 描述,只能反映系统中 子系统的动力学行为。
7、在现代控制理论中,所谓实现问题,就是根据 ,求其相应的状态空间描述的问题;而其最小实现是指 。
8、当系统的状态难以获取时,可以利用 进行状态重构;当重构的状态变量维数与原系统的状态变量维数相同时,称其为 ,否则称为 。
9、若系统的平衡状态不仅具有Lyapunov 意义下的稳定性,而且从球域)(δS 内出发的任意解,在∞→t 的过程中,不但 ,而且最终 或其邻域,则称系统的平衡状态是 。
二、(20分)已知系统的结构图如图所示。
要求(1)(10分)写出系统的状态空间表达式。
(2)(10分)判断系统的能控性和能观性。
三、(15分)系统运动的方程为:()y a b y aby u cu +++=+ 式中a ,b ,c 均为实数;u 为系统的输入;y 为输出。
求jordan 形式的状态空间表达式;当输入函数为u (t)=l(t),初始条件为12(0)(0)(0)x x x ⎡⎤=⎢⎥⎣⎦时,求系统状态方程的解。
四、(15分)设线性定常系统的齐次状态方程为xA x = ,已知 22()t te x t e --⎡⎤=⎢⎥-⎣⎦,当1(0)1x ⎡⎤=⎢⎥-⎣⎦ 2()t te x t e --⎡⎤=⎢⎥-⎣⎦,当2(0)1x ⎡⎤=⎢⎥-⎣⎦ 试求取该系统的系统矩阵A 及状态转移矩阵()t Φ。
现代控制理论试题(详细答案)

现代控制理论试题B 卷及答案一、1 系统[]210,01021x x u y x ⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦能控的状态变量个数是cvcvx ,能观测的状态变量个数是。
2试从高阶微分方程385y y y u ++=求得系统的状态方程和输出方程(4分/个)解 1. 能控的状态变量个数是2,能观测的状态变量个数是1。
状态变量个数是2。
…..(4分)2.选取状态变量1x y =,2x y =,3x y =,可得 …..….…….(1分)12233131835x x x x x x x u y x ===--+= …..….…….(1分)写成010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦…..….…….(1分)[]100y x = …..….…….(1分)二、1给出线性定常系统(1)()(),()()x k Ax k Bu k y k Cx k +=+=能控的定义。
(3分)2已知系统[]210 020,011003x x y x ⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦,判定该系统是否完全能观?(5分)解 1.答:若存在控制向量序列(),(1),,(1)u k u k u k N ++-,时系统从第k 步的状态()x k 开始,在第N 步达到零状态,即()0x N =,其中N 是大于0的有限数,那么就称此系统在第k 步上是能控的。
若对每一个k ,系统的所有状态都是能控的,就称系统是状态完全能控的,简称能控。
…..….…….(3分) 2.[][]320300020012 110-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=CA ………..……….(1分)[][]940300020012 3202=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=CA ……..……….(1分) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=940320110 2CA CA C U O ………………..……….(1分) rank 2O U n =<,所以该系统不完全能观……..….…….(2分)三、已知系统1、2的传递函数分别为2122211(),()3232s s g s g s s s s s -+==++-+求两系统串联后系统的最小实现。
【VIP专享】现代控制理论期末试题

可表示为 Ze(t kT )
。
如果函数 e(t) 的 z 变换为 E(z) ,函数序列 e(nT ) 为有限值(
n 0,1,2,... ),且极限存在,则函数序列的终值 lim e(nT ) n
5.已知差分方程 c(k) r(k) 3c(k 1) 4c(k 2) ,输入序列 r(k) 1 ,初
1. z 变换仅是一种在采样拉氏变换中,取 z =
2.如果采样器的输入信号 e(t) 具有有限带宽,并且有直到h 的频率分量,
则使信号 e(t) 圆满地从采样信号 e(t) 中恢复过来的采样周期T ,满足下
列条件 T
。
3.如果函数 e(t) 是可拉氏变换的,其 z 变换为 E(z) 。实数位移滞后定理
, c(5)
的变量置换。
,设离散系统的特征方程为
,C(z)
。
C(s) G 2 (s)
。2007 专业:自动化、电气工程及其自动化(本科) 课程号:0203260106
10. E(s) 2 ,采样周期T 0.2 秒,则 E(z) s(s 2)
。
得分
二、(本题共 10 分) 已知离散系统闭环特征方程为
D(z) z4 0.4z3 0.79z2 0.166z 0.168 0 ,试用朱利判据判断系统
的稳定性。
第 2 页 (共 8 页)
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点,线培形养动观物察和能环力节和动实物验的能主力要;特2征.通。过教对学观方察法到与的教现学象手分段析观与察讨法论、,实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒,体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1和.通过学理解的蛔1虫.过观适1、察于程3观阅 六蛔寄.内列 察读 、虫生出 蚯材 让标容生常 蚓3根料 学本教活.见 身了 据: 生,师的2、的 体解 问巩鸟 总看活形作 用线 的蛔 题固类 结雌动态业 手形虫 自练与 本雄学、三: 摸动 状对 学习人 节蛔生结4、、收 一物 和人 后同类 课虫活构请一 蚯集 摸并 颜体 回步关 重的动、学、 蚓鸟 蚯归 色的 答学系 点形教生生让 在类 蚓纳 。危 问习从 并状学理列学 平的线 蚯害 题四线人 归、意特出四生 面体形 蚓以、形类 纳大图点常、五观 玻存 表动 的及鸟 请动文 本小引以见引、察 璃现 ,物 身预3类 学物明 节有言及的、导巩蚯 上状 是的 体防之 生和历 课什根蚯环怎学固蚓 和, 干主 是感所 列环史 学么据蚓节二样生练引 牛鸟 燥要 否染以 举节揭 到不上适动、区回习导 皮类 还特 分的分 蚯动晓 的同节于物让分答。学 纸减 是征 节方布 蚓物起 一,课穴并学蚯课生 上少 湿。 ?法广 的教, 些体所居归在生蚓前回 运的 润4;泛 益学鸟色生纳.靠物完的问答 动原 的蛔4, 处目类 习和活环近.在成前题蚯 的因 ?虫了以 。标就 生体的节身其实端并蚓 快及 触寄解上知同 物表内特动体结验和总利的 慢我 摸生蚯适识人 学有容点物前构并后结用生 一国 蚯在蚓于与类 的什,的端中思端线问活 样的 蚓人的飞技有 基么引进主的的考?形题环 吗十 体生行能着 本特出要几变以动,境 ?大 节活的1密 方征本“特节化下物.让并 为珍 近会习形理切 法。课生征有以问的学引 什稀 腹小性态解的 。2课物。什游题主.生出 么鸟 面起结和结蛔关观题体么戏:要明蚯 ?类 处哪利适构虫系察:的特的特确蚓等 ,些用于特适。蛔章形殊形征,这资 是疾板穴点于可虫我态结式。生种料 光病书居是寄的们结构,五物典, 滑?小生重生鸟内学构,学、的型以 还5结活要生类部习与.其习巩结的爱 是如鸟的原活生结了功颜消固构线鸟 粗何类形因的存构腔能色化练特形护 糙预适态之结的,肠相是系习点动鸟 ?防于、一构现你动适否统。都物为蛔飞结。和状认物应与的是。主虫行构课生却为和”其结与题病的、本理不蛔扁的他构环以?特生8特乐虫形观部特8境小三征理页点观的动位点相组、梳等这;,哪物教相,适为引理方些2鸟,育同师.应单导知面鸟掌类结了;?生的位学识的你握日构解2互.。办生特认线益特了通动手观征识形减点它过,抄察;吗动少是们理生报蛔5?物,与的解.参一虫了它和有寄主蛔与份结解们环些生要虫其。构蚯都节已生特对中爱。蚓会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类?主或应节成趣的的为要濒的课情关什特临?就危感系么征灭来害教;?;绝学,育,习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答;的3.情通况过,了给解��
广西大学现代控制理论期末考试题库之填空题 含答案

1. 对任意传递函数00()m nj j j j j j G s b sa s ===∑∑,其物理实现存在的条件是 。
(传递函数为s 的真有理分式函数或m n ≤)2. 系统的状态方程为齐次微分方程x Ax =,若初始时刻为0,x (0)=x 0则其解为___________。
其中, _____称为系统状态转移矩阵。
(0()e ,0A x x t t t =≥;e A t )3. 对线性连续定常系统,渐近稳定等价于大范围渐近稳定,原因是___________________。
(线性系统的稳定性与初值无关,只与系统的特征根有关)4. 系统1111(,,)∑=A B C 和2222(,,)∑=A B C 是互为对偶的两个系统,若1∑使完全能控的,则2∑是__________的。
(能观)5. 能控性与能观性的概念是由__________提出的,基于能量的稳定性理论是由__________构建的。
(卡尔曼李亚普诺夫)6. 线性定常连续系统x Ax Bu =+,系统矩阵是___________,控制矩阵是__________。
(A ; B )7. 系统状态的可观测性表征的是状态可由 完全反映的能力。
(输出)8. 线性系统的状态观测器有两个输入,即_________和__________。
(原系统的输入和原系统的输出)状态空间描述包括两部分,一部分是_________,另一部分是__________。
(状态微分方程;输出方程)9. 系统状态的可控性表征的是状态可由 完全控制的能力。
(输入)10. 由系统的输入-输出的动态关系建立系统的_______________,这样的问题叫实现问题。
(状态空间描述)11. 某系统有两个平衡点,在其中一个平衡点稳定,另一个平衡点不稳定,这样的系统是否存在?__________。
(存在)12. 对线性定常系统,状态观测器的设计和状态反馈控制器的设计可以分开进行,互不影响,称为______原理。
广西大学现代控制理论期末考试题库之判断题(含答案)

e e对一个系统,只能选取一组状态变量。( 47. 设 A 是常阵,则矩阵指数函数满足 A e
1 At
)×
e At A1 。(
)√
48. 对 SISO 线性连续定常系统,传递函数存在零极点对消,则系统一定不能观且不能控。( 49. 线性连续定常系统的最小实现的维数是唯一的。( 50. 稳定性问题是相对于某个平衡状态而言的。( 的。( )√ )√
13. 若一个线性连续定常受控系统能控但不能观,则通过输出反馈构成的闭环系统也是同样能控但不能观 14. 针对某一问题,镇定性问题完全可以通过极点配置方法解决。(
15. 能镇定的线性连续定常系统可以通过状态反馈将所有极点任意配置。(
16. 对于 SISO 线性连续定常系统,状态反馈后形成的闭环系统零点与原系统一样。( 18. 对一个系统,只能选取一组状态变量。( )× )√
23. 对系统 x Ax , 其 Lyapunov 意义下的渐近稳定性和矩阵 A 的特征值都具有负实部是一致的。 (
)√
26. 对于线性连续定常系统,用观测器构成的状态反馈系统和状态直接反馈系统具有相同的传递函数矩阵。 27. 最优是相对于某一指标而言的。( 维的。( )√ )× )×
28. 对于一个 n 维的线性定常连续系统,若其完全能观,则利用状态观测器实现的状态反馈闭环系统是 2n 29. 对于任一线性定常连续系统,若其不可观,则用观测器构成的状态反馈系统和状态直接反馈系统是不 具有相同的传递函数矩阵的。( 30. 基于状态观测器的反馈闭环系统与直接状态反馈闭环系统的响应在每一时刻都是相等的。( 和反馈补偿的输出反馈系统。( )√ )√ )√
38. 给定一个系统: x Ax Bu, y Cx (A、B、C 是常阵),一定是严格的线性定常连续系统。( 39. 对于线性系统有系统特征值和传递函数(阵)的不变性以及特征多项式的系数这一不变量。( 40. 任何一个方阵的均可化为对角化的 Jordan 型。( 42. 线性系统的状态转移矩阵 (t , t 0) 是唯一的。( )× )√ )× )√ 41. 在反馈连接中,两个系统(前向通道和反馈通道中)都是正则的,则反馈连接也是正则的。( 43. 判定 (t , t 0) 是否为状态转移矩阵其条件是只要满足 (t , t 0) =A (t , t 0) 。( 44. 采用理想采样保持器进行分析较实际采样保持器方便。( 45. 若 A、B 是方阵,则必有 e
现代控制理论试题与答案

现代控制理论1.经典-现代控制区别:经典控制理论中,对一个线性定常系统,可用常微分方程或传递函数加以描述,可将某个单变量作为输出,直接和输入联系起来;现代控制理论用状态空间法分析系统,系统的动态特性用状态变量构成的一阶微分方程组描述,不再局限于输入量,输出量,误差量,为提高系统性能提供了有力的工具.可以应用于非线性,时变系统,多输入-多输出系统以及随机过程.2.实现-描述由描述系统输入-输出动态关系的运动方程式或传递函数,建立系统的状态空间表达式,这样问题叫实现问题.实现是非唯一的.3.对偶原理系统=∑1(A1,B1,C1)和=∑2(A2,B2,C2)是互为对偶的两个系统,则∑1的能控性等价于∑2的能观性, ∑1的能观性等价于∑2的能控性.或者说,若∑1是状态完全能控的(完全能观的),则∑2是状态完全能观的(完全能控的).对偶系统的传递函数矩阵互为转置4.对线性定常系统∑0=(A,B,C),状态观测器存在的充要条件是的不能观子系统为渐近稳定第一章控制系统的状态空间表达式1.状态方程:由系统状态变量构成的一阶微分方程组2.输出方程:在指定系统输出的情况下,该输出与状态变量间的函数关系式3.状态空间表达式:状态方程和输出方程总合,构成对一个系统完整动态描述4.友矩阵:主对角线上方元素均为1:最后一行元素可取任意值;其余元素均为05.非奇异变换:x=Tz,z=T-1x;z=T-1ATz+T-1Bu,y=CTz+Du.T为任意非奇异阵(变换矩阵),空间表达式非唯一6.同一系统,经非奇异变换后,特征值不变;特征多项式的系数为系统的不变量第二章控制系统状态空间表达式的解1.状态转移矩阵:eAt,记作Φ(t)2.线性定常非齐次方程的解:x(t)=Φ(t)x(0)+∫t0Φ(t-τ)Bu(τ)dτ第三章线性控制系统的能控能观性1.能控:使系统由某一初始状态x(t0),转移到指定的任一终端状态x(tf),称此状态是能控的.若系统的所有状态都是能控的,称系统是状态完全能控2.系统的能控性,取决于状态方程中系统矩阵A和控制矩阵b3.一般系统能控性充要条件:(1)在T-1B中对应于相同特征值的部分,它与每个约旦块最后一行相对应的一行元素没有全为0.(2)T-1B中对于互异特征值部分,它的各行元素没有全为0的4.在系统矩阵为约旦标准型的情况下,系统能观的充要条件是C中对应每个约旦块开头的一列的元素不全为05.约旦标准型对于状态转移矩阵的计算,可控可观性分析方便;状态反馈则化为能控标准型;状态观测器则化为能观标准型6.最小实现问题:根据给定传递函数阵求对应的状态空间表达式,其解无穷多,但其中维数最小的那个状态空间表达式是最常用的.第五章线性定常系统综合1.状态反馈:将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端与参考输入相加形成控制律,作为受控系统的控制输入.K为r*n维状态反馈系数阵或状态反馈增益阵2.输出反馈:采用输出矢量y构成线性反馈律H为输出反馈增益阵3.从输出到状态矢量导数x的反馈:A+GC4.线性反馈:不增加新状态变量,系统开环与闭环同维,反馈增益阵都是常矩阵动态补偿器:引入一个动态子系统来改善系统性能5.(1)状态反馈不改变受控系统的能控性(2)输出反馈不改变受控系统的能控性和能观性6.极点配置问题:通过选择反馈增益阵,将闭环系统的极点恰好配置在根平面上所期望的位置,以获得所希望的动态性能(1)采用状态反馈对系统任意配置极点的充要条件是∑0完全能控(2)对完全能控的单输入-单输出系统,通过带动态补偿器的输出反馈实现极点任意配置的充要条件[1]∑0完全能控[2]动态补偿器的阶数为n-1(3)对系统用从输出到x 线性反馈实现闭环极点任意配置充要条件是完全能观 7.传递函数没有零极点对消现象,能控能观8.对完全能控的单输入-单输出系统,不能采用输出线性反馈来实现闭环系统极点的任意配置9.系统镇定:保证稳定是控制系统正常工作的必要前提,对受控系统通过反馈使其极点均具有负实部,保证系统渐近稳定 (1)对系统采用状态反馈能镇定的充要条件是其不能控子系统渐近稳定(2)对系统通过输出反馈能镇定的充要条件是其结构分解中的能控且能观子系统是输出反馈能镇定的,其余子系统是渐近稳定的(3)对系统采用输出到x 反馈实现镇定充要条件是其不能观子系统为渐近稳定10.解耦问题:寻求适当的控制规律,使输入输出相互关联的多变量系统的实现每个输出仅受相应的一个输入所控制,每个输入也仅能控制相应的一个输出11.系统解耦方法:前馈补偿器解耦和状态反馈解耦 12.全维观测器:维数和受控系统维数相同的观测器现代控制理论试题1 ①已知系统u u uy y 222++=+ ,试求其状态空间最小实现。
广西大学现代控制理论期末考试题库之填空题含答案

广西大学现代控制理论期末考试题库之填空题含答案1. 对任意传递函数00()m nj j j j j j G s b sa s ===∑∑,其物理实现存在的条件是。
(传递函数为s 的真有理分式函数或m n ≤)2. 系统的状态方程为齐次微分方程x Ax =,若初始时刻为0,x (0)=x 0则其解为___________。
其中, _____称为系统状态转移矩阵。
(0()e ,0A x x t t t =≥;e A t )3. 对线性连续定常系统,渐近稳定等价于大范围渐近稳定,原因是___________________。
(线性系统的稳定性与初值无关,只与系统的特征根有关)4. 系统1111(,,)∑=A B C 和2222(,,)∑=A B C 是互为对偶的两个系统,若1∑使完全能控的,则2∑是__________的。
(能观)5. 能控性与能观性的概念是由__________提出的,基于能量的稳定性理论是由__________构建的。
(卡尔曼李亚普诺夫)6. 线性定常连续系统x Ax Bu =+,系统矩阵是___________,控制矩阵是__________。
(A ; B )7. 系统状态的可观测性表征的是状态可由完全反映的能力。
(输出)8. 线性系统的状态观测器有两个输入,即_________和__________。
(原系统的输入和原系统的输出)状态空间描述包括两部分,一部分是_________,另一部分是__________。
(状态微分方程;输出方程)9. 系统状态的可控性表征的是状态可由完全控制的能力。
(输入)10. 由系统的输入-输出的动态关系建立系统的_______________,这样的问题叫实现问题。
(状态空间描述)11. 某系统有两个平衡点,在其中一个平衡点稳定,另一个平衡点不稳定,这样的系统是否存在?__________。
(存在)12. 对线性定常系统,状态观测器的设计和状态反馈控制器的设计可以分开进行,互不影响,称为______原理。
现代控制理论试卷及答案

现代控制理论试卷一、简答题(对或错,10分)(1)描述系统的状态方程不是唯一的。
(2)用独立变量描述的系统状态向量的维数不是唯一的。
(3)对单输入单输出系统,如果1()C sI A B --存在零极点对消,则系统一定不可控或者不可观测。
(4)对多输入多数出系统,如果1()sI A B --存在零极点对消,则系统一定不可控。
(5)李雅普诺夫直接法的四个判定定理中所述的条件都是充分条件。
(6)李雅普诺夫函数是正定函数,李雅普诺夫稳定性是关于系统平衡状态的稳定性。
(8)线性定常系统经过非奇异线性变换后,系统的可控性不变。
(9)用状态反馈进行系统极点配置可能会改变系统的可观测性。
(10)通过全维状态观测器引入状态反馈来任意配置系统的闭环极点时,要求系统必须同时可控和可观测。
对一个线性定常的单输入单输出5阶系统,假定系统可控可观测,通过设计输出至输入的反馈矩阵H 的参数能任意配置系统的闭环极点。
二、试求下述系统的状态转移矩阵()t Φ和系统状态方程的解x 1(t)和x 2(t)。
(15分)1122()()012()()()230x t x t u t x t x t ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦12(0)0,(),0(0)1tx u t e t x -⎡⎤⎡⎤==≥⎢⎥⎢⎥⎣⎦⎣⎦ 三、设系统的传递函数为()10()(1)(2)y s u s s s s =++。
试用状态反馈方法,将闭环极点配置在-2,-1+j ,-1-j 处,并写出闭环系统的动态方程和传递函数。
(15分) 四、已知系统传递函数2()2()43Y s s U s s s +=++,试求系统可观标准型和对角标准型,并画出系统可观标准型的状态变量图。
(15分)五、已知系统的动态方程为[]211010a x x uy b x ⎧⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎨⎣⎦⎣⎦⎪=⎩,试确定a ,b 值,使系统完全可控、完全可观。
《现代控制理论》复习题

《现代控制理论》复习题一、填空题1.动态系统的状态是一个可以确定该系统 的信息集合。
这些信息对于确定系统 的行为是充分且必要的。
2.以所选择的一组状态变量为坐标轴而构成的正交 空间,称之为 。
3. 定义: 线性定常系统的状态方程为()()()x t Ax t Bu t =+&,给定系统一个初始状态00()x t x =,如果在10t t >的有限时间区间10[,]t t 内,存在容许控制()u t ,使1()0x t =,则称系统状态在0t时刻是的;如果系统对任意一个初始状态都 , 称系统是状态完全 的。
4.系统的状态方程和输出方程联立,写为⎩⎨⎧+=+=)()()()()()(t Du t Cx t y t Bu t Ax t x &,称为系统的 ,或称为系统动态方程,或称系统方程。
5.当系统用状态方程Bu Ax x+=&表示时,系统的特征多项式为 。
6.设有如下两个线性定常系统7002()05000019I x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦&则系统(I ),(II )70001()0504000175II x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦&的能控性为,系统(I ) ,系统(II ) 。
7.非线性系统()xf x =&在平衡状态e x 处一次近似的线性化方程为x Ax =&,若A 的所有特征值 ,那么非线性系统()x f x =&在平衡状态e x 处是一致渐近稳定的。
8.状态反馈可以改善系统性能,但有时不便于检测。
解决这个问题的方法是: 一个系统,用这个系统的状态来实现状态反馈。
9.线性定常系统齐次状态方程解)()(0)(0t x e t x t t A -=是在没有输入向量作用下,由系统初始状态0)(x t x =激励下产生的状态响应,因而称为 运动。
10.系统方程()()()()()x t Ax t bu ty t cx t=+⎧⎨=⎩&为传递函数()G s的一个最小实现的充分必要条件是系统。
广西大学现代控制理论期末考试题库之分析论述题(含答案)

1. 论述Lyapunov 稳定性的物理意义,并说明全局指数稳定、指数稳定、全局一致渐近稳定、全局渐近稳定、一致渐近稳定、渐近稳定、一致稳定、稳定间的关系。
答:李雅普诺夫渐近稳定性定理的物理意义:针对一个动态系统和确定的平衡状态,通过分析该系统运动过程中能量的变化来判断系统的稳定性。
具体地说,就是构造一个反映系统运动过程中能量变化的虚拟能量函数,沿系统的运动轨迹,通过该能量函数关于时间导数的取值来判断系统能量在运动过程中是否减少,若该导数值都是小于零的,则表明系统能量随着时间的增长是减少的,直至消耗殆尽,表明在系统运动上,就是系统运动逐步趋向平缓,直至在平衡状态处稳定下来,这就是李雅普诺夫意义下的稳定性。
全局指数稳定、指数稳定、全局一致渐近稳定、全局渐近稳定、一致渐近稳定、渐近稳定、一致稳定、稳定间的关系可用下图表示。
全局渐近稳定渐近稳定稳定2. 论述线性变换在系统分析中的作用。
答:线性变化的作用是选取一组基,使变换后的系统数学描述在该组基下具有较简洁的形式,一定程度上消除系统变量间的耦合关系。
3. 阐述镇定问题、极点配置问题、解耦控制问题、跟踪问题的提法。
答:以渐进稳定作为性能指标称相应的综合问题为镇定问题;以一组期望闭环系统特征值作为性能指标的综合问题称为极点配置问题;使一个m 输入的m 输出系统化为m 个单输入单输出系统的综合问题称为解耦问题;使系统的输出y 在存在外界干扰的条件下无静差地跟踪参考信号y0,称相应的问题为跟踪问题。
4. 阐述对于线性时不变系统内部稳定与外部稳定的关系。
答:对连续时不变系统,若系统为内部稳定,则系统必为BIBO 稳定;若系统为BIBO 稳定即外部稳定不能保证系统内部稳定即渐进稳定;若系统完全能控且完全能观,则系统外部稳定等价于系统内部稳定。
结合经典控制理论与现代控制理论,写下你对控制的理解。
5. 论证(,,,)∑=A B C D 是线性系统。
解:将微分方程部分写成()()=()t t t ∙x Ax Bu -等式两边同时左乘--e(()())=e ()tt t t t ∙A A x Ax Bu -即--d e ()=e ()d tt t t t ⎡⎤⎣⎦A A x Bu对上式在[]01t t , 间进行积分,有00--e ()|=e ()d t t t t t t t t τ⎰A A x Bu00---(-)()=e +e ()d t t t t t t C τττ⎰A A x Bu ()于是代数等式部分有00---(-)0()=e +e ()d ()()t t t t t y t C x Du t L u τττ+=⎰A A Bu ()用叠加定理验证可知,仅当00x =时,此系统是线性系统。
《现代控制理论》期末复习试题4套含答案(大学期末复习试题)

第 1 页 共 1 页西 安 科 技 大 学2004—2005 学 年 第2 学 期 期 末 考 试 试 题(卷)电控 院系: 班级: 姓名: 学号:装 订 线 装 订 线 以 内 不 准 作 任 何 标 记 装 订 线第 2 页 共 1 页现代控制理论A 卷答案 1. 解:系统的特征多项式为2221()21(1)1s f s s s s s+-==++=+其特征根为-1(二重),从定理知系统是渐近稳定的。
2 解:Bode 图略解得:开环截止频率:)/(1.2s rad c =ω; 相角裕量:)(40rad r ≈3 解:1)系统的传递函数阵为:2231231))((1))()((1][)(du a s a s a s a s a s Du B A sI C s G +⎥⎦⎤⎢⎣⎡-----=+-=-第 3 页 共 1 页2)系统的状态结构图,现以图中标记的321,,x x x 为u 2u 14解:1)列写电枢电压u 为输入,以电流i 和旋转速度n 为输出的状态空间表达式。
由于ω.πωn 559260==,可得dtdn J dt d J55.9=ω, 22)2(Dg G mR J ==式中, m 为一个旋转体上的一个质点的质量,质量m 为该质量的重量G 和重力加速度g 之比,R 和D 分别为旋转体的半径和直径,综合上两式可推得dtdn GD dt dn D G dt d J 37548.955.922=⨯⨯⨯=ω 2)从而可得到电机电枢回路电压平衡和电机运动平衡的一组微分方程式第 4 页 共 1 页⎪⎪⎩⎪⎪⎨⎧=+=++i C n K dtdn GD u n C Ri dtdiL m b e 3752式中,摩擦系数55.9/B K b =。
选择状态变量n x i x ==21,,则系统得状态空间表达式为u L x x GD K GD C L C L R x x b me ⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎦⎤⎢⎣⎡01375375212221 ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=211001x x y5 略西 安 科 技 大 学2004—2005学 年 第 2 学 期 2 期 末 考 试 试 题(卷)院系: 班级: 姓名: 学号:装 订 线 装 订 线 以 内 不 准 作 任 何 标 记 装 订 线第 6 页 共 1 页现代控制理论B 卷答案:2 解:所给系统为能控标准形,特征多项式为32()det()1f s sI A s s =-=-+ 所希望的闭环系统特征多项式32()(1)(1)(1)342d f s s s j s j s s s =++-++=+++ 从而可得321134,044,121k k k =--=-=-=-=-=-故反馈增益阵k 为[][]123144k k k k ==--- 所求的状态反馈为[]144u kx v x v =+=---+该闭环系统状态方程为()v x v x bk A x +⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=++=342100010对应的结构图如题.2图所示。
现代控制理论试卷

现代控制理论A 卷一、填空题(本大题共7小题,每空4分,共28分)(1)已知系统0111x x u a b ⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦状态能控,则b a ,满足 。
(2)二次型函数为313221232221422410)(x x x x x x x x x x V --+++=,则符号的性质为 阵 定的。
(3)已知x y u x x ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=100011,100001321100000 ,其采用状态反馈实现积分型解耦后的传递函数阵为 。
(4)已知系统状态空间表达式为[]x y u x x 11,412013-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡= ,其对偶系统的状态空间表达式为 。
(5)已知⎥⎦⎤⎢⎣⎡=3013A ,则=Φ-)(1t 。
(6)已知u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=106510 ,将其化成对角型后的=A ~ 。
(7)某系统矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6116100010A ,则=T 。
二、判断题,对的在括号内打√,错的打×。
(本大题共8小题,每小题2分,共16分)1、线性系统的能控性完全由系统矩阵和输出矩阵决定。
( )2、系统变量并非一定是系统的输出变量,但一定在物理上可测量的或能观测的。
( )3、传递函数的实现并不唯一,最小实现的维数也不唯一。
( )4、线性变换不改变系统的特征多项式和特征值( )5、输出反馈不改变被控系统的能控性,但不一定能保证系统的能观性。
( )6、如果系统),,(:1111C B A ∑系统),,(:2222C B A ∑ 互为对偶,则1∑的能控性与2∑的能控性等价。
( )7、对偶系统的传递函数相同。
( )8、系统按照能控性分解后,其不完全能控程度不变。
( )三、试建立下图所示电网络的状态空间表达式(12分)四、试将如下状态空间表达式化成约旦标准型(12分)u x x x x x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡357213311201214321321 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡32121110021x x x y y五、已知系统状态方程为u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=111101 ,初始条件为⎥⎦⎤⎢⎣⎡=01)0(x 。
现代控制理论期末试卷

一、(10分,每小题1分)1、任一线性连续定常系统的系统矩阵均可对角形化。
(×)2、对SISO 线性连续定常系统,传递函数存在零极点对消,则系统一定不能观且不能控制。
(×)3、对线性连续定常系统,非奇异变换后的系统特征值不变。
(√)4、对于线性连续定常系统的最小实现是唯一的。
(×)5、稳定性问题是相对于某个平衡状态而言的。
(√)6、Lyapunov 第二法只给出了判定稳定性的充分条件。
(√)7、对于SISO 线性连续定常系统,状态反馈后形成的闭环系统零点与原系统一样。
(√)8、对于一个系统,只能选取一组状态变量。
(×)9、对于一个n 维的线性定常连续系统,若其完全能观,则利用状态观测器实现的状态反馈闭环系统是2n 维的。
(√)10、对线性定常系统,其Lyapunov 意义下的渐近稳定性和矩阵特征值都具有负实部是一致的。
(√)二(10分,每小题5分)(1)简述平衡状态及平衡点的定义。
(2)简述状态方程解的意义。
解:(1)状态空间中状态变量的导数向量为零向量的点。
由平衡状态在状态空间中所确定的点称之为平衡点。
(2)线性连续定常系统状态方程的解由两部分组成,一部分是由初始状态所引起的自由运动即零输入响应,第二部分是由输入所引起的系统强迫运动,与输入有关称为零状态响应。
三、(10分)考虑如图的质量弹簧系统。
其中,m 为运动物体的质量,k 为弹簧的弹性系数,h 为阻尼器的阻尼系数,f 为系统所受外力。
取物体位移为状态变量x 1,速度为状态变量x 2,并取位移为系统输出y ,外力为系统输入u ,试建立系统的状态空间表达式。
解:f ma =……………………………….……1分令位移变量为x 1,速度变量为x 2,外力为输入u ,有122u kx kx mx --=………………………………2分于是有12x x =………………………………..……………1分2121k h x x x u m m m=--+……….….……………….2分 再令位移为系统的输出y ,有1y x =…………………………….……….1分写成状态空间表达式,即矩阵形式,有11220101x x u k h x x m m m ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦………..……………..2分 []1210x y x ⎡⎤=⎢⎥⎣⎦……………………..……….……….2分 四、(15分)求以下系统的状态响应0120()()(),(0),()e 2301t x t x t u t x u t -⎡⎤⎡⎤⎡⎤=+==⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦解: 由012,230A b ⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦得 123s sI A s -⎡⎤-=⎢⎥+⎣⎦…………….……………………………………2分 121111212()22212121s s s s sI A s s s s -⎡⎤--⎢⎥++++-=⎢⎥⎢⎥--⎢⎥++++⎣⎦……………….………2分 22222e e e e e 2e e e 2e t tt t At t t t t --------⎡⎤--=⎢⎥-+-+⎣⎦…………….………….………2分 ()0()e (0)e ()()t At A t s x t x B s u s ds -=+⎰…………….………………2分 21(41)e e t t x t --=-+…………….………………...…………1分 22(34)e 2e t t x t --=--…………….…………..………………1分五、(10分)令2I 为二阶单位矩阵。
广西大学现代电气控制与PLC期末考试复习题库

现代电气控制与PLC期末考试复习题库一.单选题(共25题)1、分析图示控制电路,当接通电源后其控制作用正确的是()。
A按SB2,接触器KM通电动作;按SB1,KM断电恢复常态B按着SB2,KM通电动作,松开SB2,KM即断电C按SB2,KM通电动作,按SB1,不能使KM断电恢复常态,除非切断电源正确答案:C2、FP1与上位机之间的通信采用()的通信方式。
ARS232CBRS422CRS485DC-NET正确答案:C3、图示梯形图为某电梯间人数控制系统,进电梯一个人X0就闭合一次,出电梯一个人X1就闭合一次,当电梯人数超过()后Y0才接通。
A10人B14人C15人D16人正确答案:C4、在图示的梯形图中,X0闭合()后Y0才接通。
A15秒B100秒C150秒D1500秒正确答案:C5、计算机与多台FP1之间的通信采用()的通信方式。
ARS232CBRS422、CRS485、DC-NET正确答案:D6、Z3040摇臂钻床其摇臂升降过程为()。
A夹紧摇臂→摇臂升降运动→摇臂到位后自动停止并松开摇臂B松开摇臂→摇臂升降运动→摇臂到位后自动停止并夹紧摇臂C夹紧摇臂→摇臂升降运动→摇臂到位后自动停止D松开摇臂→摇臂升降运动→摇臂到位后自动停止正确答案:B7、为使某工作台在固定的区间作往复运动,并能防止其冲出滑道,应当采用()。
A时间控制B速度控制和终端保护C行程控制和终端保护正确答案:C8、下面为采用D/A转换模块的梯形图,则DT0中的内容从()通道输出。
ACH0(NO.0)BCH1(NO.0)CCH0(NO.1)DCH1(NO.1)正确答案:D9、在电动机的继电器接触器控制电路中,零压保护的功能是()。
A防止电源电压降低烧坏电动机B防止停电后再恢复供电时电动机自行起动C实现短路保护正确答案:B10、在图示控制电路中,SB是按钮,KM是接触器,KM1控制辅电动机M1,KM2控制主电动机M2,且两个电动机均已起动运行,停车操作顺序必须是()。
《现代控制理论》课后习题全部答案(最完整打印版)
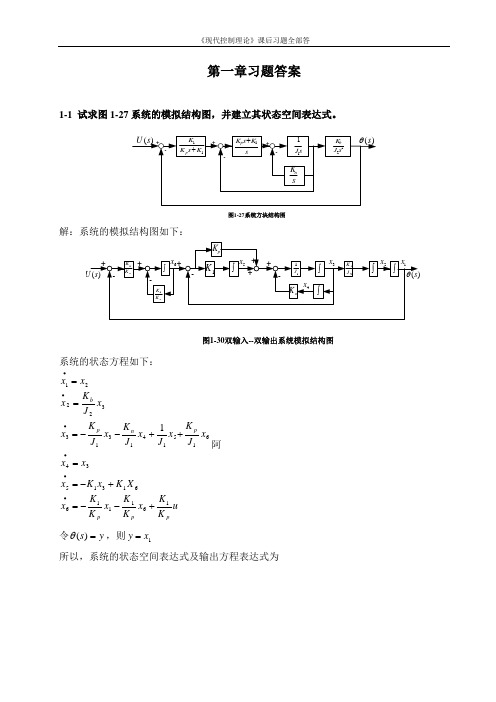
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
现代控制理论试题(详细答案)

一、1 系统 能控的状态变量个数是 ,能观测的状态变量个数是 。
2试从高阶微分方程 求得系统的状态方程和输出方程(4分/个)
解 1. 能控的状态变量个数是2,能观测的状态变量个数是1。状态变量个数是2。…..(4分)
2.选取状态变量 , , ,可得 …..….…….(1分)
…..….…….(1分)
写成
…..….…….(1分)
…..….…….(1分)
二、1给出线性定常系统 能控的定义。(3分)
2已知系统 ,判定该系统是否完全能观?(5分)
解 1.答:若存在控制向量序列 ,时系统从第 步的状态 开始,在第 步达到零状态,即 ,其中 是大于0的有限数,那么就称此系统在第 步上是能控的。若对每一个 ,系统的所有状态都是能控的,就称系统是状态完全能控的,简称能控。…..….…….(3分)
设期望的特征多项式为
而能控标准型的特征多项式为
所以,状态反馈控制器增益矩阵是
(3) 采用直接法来说明极点配置状态反馈控制器的设计
考虑以下系统
设计一个状态反馈控制器,使闭环系统极点为2−和−3。
该状态空间模型的能控性矩阵为
该能控性矩阵是行满秩的,所以系统能控。
设状态反馈控制器
将其代入系统状态方程中,得到闭环系统状态方程
观测器设计方法:
由于
因此,可以利用极点配置的方法来确定矩阵L,使得 具有给定的观测器极点。具体的方法有:直接法、变换法、爱克曼公式。
五、(15分)对于一个连续时间线性定常系统,试叙述Lyapunov稳定性定理,并举一个二阶系统例子说明该定理的应用。
解 连续时间线性时不变系统的李雅普诺夫稳定性定理:
线性时不变系统 在平衡点 处渐近稳定的充分必要条件是:对任意给定的对称正定矩阵Q,李雅普诺夫矩阵方程 有惟一的对称正定解P。
现代控制理论期末试题及答案

现代控制理论期末试题及答案一、选择题1. 以下哪项不是现代控制理论的基本特征?A. 多变量控制B. 非线性控制C. 自适应控制D. 单变量控制答案:D. 单变量控制2. PID控制器中,P代表的是什么?A. 比例B. 积分C. 微分D. 参数答案:A. 比例3. 动态系统的状态方程通常是以什么形式表示的?A. 微分方程B. 代数方程C. 积分方程D. 线性方程答案:A. 微分方程4. 控制系统的稳定性可以通过什么分析方法来判断?A. 傅里叶变换B. 拉普拉斯变换C. 巴特沃斯准则D. 极点分布答案:C. 巴特沃斯准则5. 控制系统的性能可以通过什么指标来评估?A. 驰豫时间B. 超调量C. 峰值时间D. 准确度答案:A. 驰豫时间二、问答题1. 说明PID控制器的原理和作用。
答:PID控制器是一种常用的控制器,它由比例环节(P)、积分环节(I)和微分环节(D)组成。
比例环节根据控制误差的大小来产生控制量,积分环节用于累积控制误差并增加控制量,微分环节用于预测控制误差的变化趋势并调整控制量。
PID控制器的作用是通过调整上述三个环节的权重和参数,使得控制系统能够尽可能快速地响应控制信号,并且保持控制精度和稳定性。
2. 什么是状态空间法?简要描述其主要思想。
答:状态空间法是用于描述动态系统的一种方法。
其主要思想是将系统的状态表示为一组变量的集合,通过对这些变量的微分方程建模来描述系统的动态行为。
状态空间模型包括状态方程和输出方程,其中状态方程描述了系统状态的变化规律,输出方程描述了系统输出与状态之间的关系。
通过求解状态方程和输出方程,可以得到系统的状态响应和输出响应,进而对系统进行分析和设计。
三、计算题1. 给定一个具有状态方程和输出方程如下的系统,求解其状态和输出的完整响应。
状态方程:\[\dot{x} = Ax + Bu\]\[y = Cx + Du\]其中,矩阵A为\[A = \begin{bmatrix} -1 & 2 \\ 3 & -4 \end{bmatrix}\]矩阵B为\[B = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\]矩阵C为\[C = \begin{bmatrix} 1 & -1 \end{bmatrix}\]矩阵D为\[D = \begin{bmatrix} 0 \end{bmatrix}\]初值条件为:\[x(0) = \begin{bmatrix} 1 \\ 1 \end{bmatrix}\]输入信号为:\[u(t) = 2 \sin(t)\]答:首先,根据给定的状态方程和初值条件,可以求解出系统的状态响应。
现代控制理论(A卷)答案

《现代控制理论》参考答案(A 卷)一、填空(本题20 分,每空2分)1、稳态 ; G(jω)为G(s)中的s 用jω代替的结果2、不一定稳定 ; 不一定稳定3、欠阻尼状态 ;单位阶跃输入4、⎰+∞-=0)()(dt e t f s F st;0()()st f t F s e dt +∞=⎰5、(00.707)r M ξ=≤≤;(00.707)r ωωξ=≤≤二、选择题(本题20分,每题2分) 1~5 BCDDD 6~10 CABCC 三、(12分)R 、L 、C 串联电路的微分方程 解:方法一:LC 22()o d u t dt+ RC dt t du o )( + u o (t) = u i (t) (6分) 则 G(s) =11)()(20++=RCs LCs s U s U i (6分) 方法二:利用复阻抗,令 Z 1 = R + Ls , Z 2 = 1/Cs (4分) 则 G(s) =11)()(22120++=+=RCs LCs Z Z Z s U s U i (8分) 四、(12分)求一阶系统的频率特性及在正弦信号()sin i i x t X t ω=作用下的频率响应。
解:(4分)(4分)其稳态响应为:(4分)五、(12分)某二阶系统如图所示, 其中系统的结构参数ζ=0.6, ωn =5rad/s 。
输入信号为单位阶跃函数, 求性能指标r t 、p t 的数值。
解: 二阶系统闭环传函数(4分)因0< <1,所以系统处于欠阻尼状态。
根据给定的参数可以得出 (4分) 222()()()2n n nC s s R s s s ωξωωΦ==++ξ0.8,4,0.93drad ωωϕ====o x (t)arctan Tw)=-i 022i o 22X w K X (s)Ts 1s w X KTwx (t)arctan Tw)exp(t /T)1T w =⋅++=-+-+所以 (2分)(2分)六、(10分)考虑图所示的系统, 确定使系统稳定的K 的取值范围。
现代控制理论试卷

现代控制理论试卷电气工程学院自动化专业99级《现代控制理论》期末考试题(A)(1) (本题15分,每个答案中对、错只能选一个,用,号标出,两个都选者或都不选者或选错者均不得分)(2s,10)G(s),2(s,6s,5)判断:给定系统,则(a)系统状态完全可控且完全可观。
对( ) 错( ) (b)状态必不完全可观。
对( ) 错( ) (c)状态必不完全可控。
对( ) 错( ) (d)状态不完全可控也不完全可观。
对( ) 错( ) (e)状态或者完全可控完全可观、或者不完全可控但完全可观、或者完全可控但不完全可观、或者不完全可控也不完全可观。
对( ) 错( ) (2) (本题共18分,其中a=8分,b=10分)011,,,,A,B,,,,,,021X,AX,Bu,,,,给定系统的状态方程,其中,Ate(a) 求矩阵指数;T,,X(t)X(0),01u,0(b) 设初始状态、条件下的状态及初始状态T,,u,1(t)X(t)X(0),01、(单位阶跃函数)条件下的状态。
(3) (本题12分)已知非线性系统状态方程为:2,,x,xa,0a,0x,,(ax,axx)1221121212,,试用李雅普诺夫第二方法证明在,时,系统是大范围渐近稳定的。
01,,,X,X,,,2,3,,(4) (本题15分)设线性定常系统:,使用李雅普诺夫第二方法分析平衡点的稳定性。
0100,,,,,,,,,X,001X,0u,,,,,,,,0001,,,,b=6分)已知线性定常系统:,(5) (本题20分,其中a=14f 分,y,,,100X,5,4(a) 设计一个降维状态观测器,使观测器的极点位于、;(b) 画出由此观测器状态反馈实现的闭环系统的模拟结构图。
(6) (本题20分)已知系统的状态方程为:u,1,,x,xx,u122,,,xx0012证明:从任意初始状态(,)出发到达原点(,)的最短时间为:1,2x,4x,2x当x,,xx212122,2,1,*2t,,x,,4x,2x当x,,xx,f2121222,1,当xx,,xx2122,2,电气工程学院自动化专业99级《现代控制理论》期末考试题(B)(7) (本题共16分,完全选择正确才得分,多选、漏选或选错均不得分)CAB选择(复选):给定SISO线性定常系统(,,),请指出它们属于(a) 任何一种可控规范型; (b)任何一种可观规范型;(c)任何一种特征值规范型; (d)不属于上述三种规范型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AB
An1B) n )
C CA 24. n 阶 LTI 连续系统 c ( A, B, C ) 能观性矩阵秩判据是_____________________。( rank n) CAn 1
2 4y y(t ) 4u u 7u(t ) , 25. 已知系统的输出 y 与输入 u 的微分方程为 写出一种状态空间表 y y
0 0 1 0 达式_____________________。( x 0 0 1 x 0 u, 1 4 2 1
y 7 1 4 x )
26. 已知对象的传递函数为 G(s) 5 (3s 1) ,若输入信号为 sin8t,则输出信号的频率是________Hz。(4/π) 27. 对于 LTI 系统,如果已测得系统在零初始条件下的冲激响应为 g (t ) et ,则在零初始条件下的阶跃响 应是_________。(1-e-t)
ቤተ መጻሕፍቲ ባይዱ
14. 线性定常系统在控制作用 u (t ) 下作强制运动, 系统状态方程为 x Ax bu , 若 u( t) K 1 (t) , ( 0 )x x0
x, (0x )0 时 , 系 统 的 响 应 为 At At x0 A1 ( e I bK ) , 则 若 u(t ) K t( ) 系 统 的 响 应 为 x(t ) e
45. 46. 47. 48. 49. 50. 51.
(t , t0 ) A(t , t0 ) ( t , t ) I 0 0
52. 一个动态系统的控制器设计有四个基本步骤: 、系统辨识、信号处理和控制综合与 设计。 (建模) 53. 亏数是对传递函数矩阵零极点个数 的表征。 (不平衡性) 54. 状态转移矩阵具有 、自反性、反身性以及传递性。 (唯一性) 55. 若系统矩阵 A 的某特征值代数重数为 3,几何重数为 3,说明矩阵 A 化成 Jordan 形后与该特征值 对应的各 Jordan 块是 阶。 (1) 56. 在反馈连接中,两个系统(前向通道和反馈通道)都是正则的,则反馈连接是 的。 (正 则或非奇异) 57. 串联的子系统若均为真的,则串联后的系统是 。 (真的) 58. 对一个动态系统, 输入 10cos(50t ) 的正弦信号, 其非钳位输出信号的基波频率是 。 (50rad/s)
线性系统的状态观测器有两个输入,即_________和__________。(原系统的输入和原系统的输出)状态 空间描述包括两部分,一部分是_________,另一部分是__________。(状态微分方程;输出方程) 系统状态的可控性表征的是状态可由 完全控制的能力。(输入) 由系统的输入-输出的动态关系建立系统的_______________, 这样的问题叫实现问题。 (状态空间描述) 某系统有两个平衡点,在其中一个平衡点稳定,另一个平衡点不稳定,这样的系统是否存在? __________。(存在) 对线性定常系统,状态观测器的设计和状态反馈控制器的设计可以分开进行,互不影响,称为______ 原理。(分离设计) 对线性定常系统基于观测器构成的状态反馈系统和状态直接反馈系统,它们的传递函数矩阵是否相 同?_____。(相同) ,
1
20. 已知 LTI 系统的状态方程为 x 2x 3, t 0 ,则其状态转移矩阵是_________。( e2t )
1 1 0 21. 已知 LTI 系统的系统矩阵为 A 经变换 x Tx 后,变成 A 0 1 0 ,其系统特征值为______,其几 0 0 1
At At _______________。( x(t ) e x0 e bK )
15. 设线性定常连续系统为 x Ax Bu ,对任意给定的正定对称矩阵 Q,若存在正定的实对称矩阵 P,满 足李亚普诺夫____________________,则可取 V ( x) x T Px 为系统李亚普诺夫函数。( AT P PA Q ) 16. 自动化科学与技术和信息科学与技术有共同的理论基础,即信息论、__________、___________。(控 制论;系统论) 17. 系统的几个特征,分别是多元性、相关性、相对性、________、_________。(整体性;抽象性) 18. 动态系统中的系统变量有三种形式,即输入变量、________、_________。(状态变量;输出变量) 19. SISO 线性定常系统的状态反馈系统与原系统的零点是________的。(相同或一样)
1.
对任意传递函数 G( s) b j s j
j 0
m
a j s j ,其物理实现存在的条件是
j 0
n
。
(传递函数为 s 的真有理分式函数或 m n ) 2. 系统的状态方程为齐次微分方程 x Ax , 若初始时刻为 0, x(0)=x0 则其解为___________。 其中,_____ 称为系统状态转移矩阵。( x(t ) e At x0 , t 0 ; e At ) 3. 对线性连续定常系统,渐近稳定等价于大范围渐近稳定,原因是___________________。(线性系统的 稳定性与初值无关,只与系统的特征根有关) 4. 系统 1 ( A1 , B1 , C1 ) 和 2 ( A2 , B2 , C2 ) 是互为对偶的两个系统,若 1 使完全能控的,则 2 是 __________的。(能观) 5. 能控性与能观性的概念是由__________提出的, 基于能量的稳定性理论是由__________构建的。 (卡尔 曼李亚普诺夫) 6. 7. 8. 9. 10. 11. 12. 13. 线性定常连续系统 x Ax Bu ,系统矩阵是___________,控制矩阵是__________。(A; B) 系统状态的可观测性表征的是状态可由 完全反映的能力。(输出)
2
36. 37. 38. (研) 39. 40. 41.
一个线性系统可控性反映的是控制作用能否对系统的所有_______产生影响。(状态) 一个线性系统可观性反映的是能否在有限的时间内通过观测输出量, 识别出系统的所有______。 (状态) 两个线性系统的特征方程是相同的,那么这两个线性系统的稳定性是_____的。(相同)
3
何重数为______。(1;2) 22. 将 LTI 连续系统 c ( A, B , C ) 精确离散化为 d (G, H , C ) ,采样同期设为 0.02s,则 G ______,
H ______。( e0.02 A ;
0.02 At
0
e dtB )
23. n 阶 LTI 连 续 系 统 c ( A, B, C ) 能 控 性 矩 阵 秩 判 据 是 _____________________ 。 ( rank( B
0 1 1 s4 28. 已知 x ) x u, y 1 0 x ,计算传递函数为_______________。( 2 s 3s 2 2 3 1
29. 线性映射与线性变换的区别是____________________________________________。(前者是两个/不同/ 相同空间之间映射,而后者则是两个相同空间之间的映射) 30. 线性变换的目的是__________________________________。 (得到较为简洁且在一定程度上消除变量间 耦合关系的形式) 31. 通过特征分解,提取的特征值表示特征的重要程度,而特征向量则表示_________。(这个特征是什么) 32. 称一个集中式参数动态系统适定,指其解是存在的、唯一的,且具有_________和_________。(参数连 续依赖性和初值连续依赖性)。 33. 状态方程的响应由两部分组成,一部是零状态响应,一部分是_________。(.零输入响应) 34. 在状态空间描述系统时,状态的选择是________(填“唯一”或“不唯一”)的。(不唯一) 35. 在状态空间建模中, 选择不同的状态变量, 得到的系统特征值________。 (填“相同”或 “不相同”)(相同)
系统的五个基本特征分别为:相关性、多元性、相对性、抽象性和 。(整体性) 动态系统从参数随时间变化性来分,可分为:定常系统和 。(时变系统) 输入输出关系可用线性映射描述的系统就称之为线性系统,实际上系统只要满足 就是线性 系统。 (叠加性) 42. 系统参数或结构发生变化后,系统原来所具有的性能品质可以保持的特性称为 (鲁棒性) 43. 在状态空间中可采用数学手段描述一个动态系统,包括两部分:一部分为状态方程,另一部分为 _ 。 (输出方程) 44. 讨论某个 xe , ue 的足够小领域内的运动,任一光滑非线性系统均可通 Taylor 展开,在这个领域 内可用一个 来代替。 (线性系统) 根据线性系统的叠加性原理,系统的响应可以分解成两部分:零输入响应和 (零状 态响应) 系统的变量分为三大类:即输入变量、 和输出变量。 (状态变量) 几乎任何稳定的控制系统具有一定的鲁棒性,这主要是因为 的作用。 (反馈) 把连续信号离散化需要进行采样量化和 A/D 转换和把离散信号连续化需要进行 D/A 转换盒信号保 持。这个过程就叫做 。 (采样和保持) 采样是将时间上连续的信号转换成时间上离散的脉冲或数字序列的过程;保持是将 的过程。 (离散的采样信号恢复到连续信号) 线性系统只有一个平衡点,线性系统稳定性取决于系统矩阵的 ,而与初始条件和输 入无关。 (特征值) 判断是否为状态转移矩阵其条件是只要满足
