中值定理证明
中值定理证明方法总结
设 f (x) , g(x) , h(x) 都在 (a , b) 上连续 , 且在 [a , b] 内可导, 证明至少存在一点 ξ ∈(a , b) , 使
f (a) f (b) f ′(ξ ) g(a) g(b) g′(ξ ) = 0 h(a) h(b) h′(ξ )
说明 若取 h(x) ≡1, g(x) = x , f (a) = f (b) ,即为罗尔定理; 若取 h(x) ≡1, g(x) = x , 即为拉格朗日中值定理; 若取 h(x) ≡1, g′(x) ≠ 0, 即为柯西中值定理; ( 自己验证 )
柯西 目录 上页 下页 返回 结束
f (b) − f (a) F(x) − f (x) 证: 作辅助函数 ϕ(x) = F(b) − F(a) 则 (x) 在[a,b]上 续, 在(a,b)内 导, 且 ϕ 连 可 f (b)F(a) − f (a)F(b) ϕ(a) = = ϕ(b) F(b) − F(a) 使 由罗尔定理知, 至少存在一点 即 f (b) − f (a) f ′(ξ ) = . F(b) − F(a) F′(ξ ) 思考: 思考 柯西定理的下述证法对吗 ? ∵ f (b) − f (a) = f ′(ξ )(b − a), ξ ∈(a, b) 两个 ξ 不 F(b) − F(a) = F′(ξ )(b − a), ξ ∈(a, b) 一定相同 上面两式相比即得结论. 错!
1 f (n) (x )(x − x )n +⋯+ 0 0 n!
f (b) − f (a) f ′(ξ ) = F(b) − F(a) F′(ξ )
证明中值定理的方法
直观分析 辅助函数法 逆向分析 例如, 证明拉格朗日定理 : f (b) − f (a) = f ′(ξ )(b − a) 要构造满足罗尔定理条件的辅助函数 . y = f (x) 方法1. 方法 直观分析 由图可知 , 设辅助函数
高等数学-中值定理证明
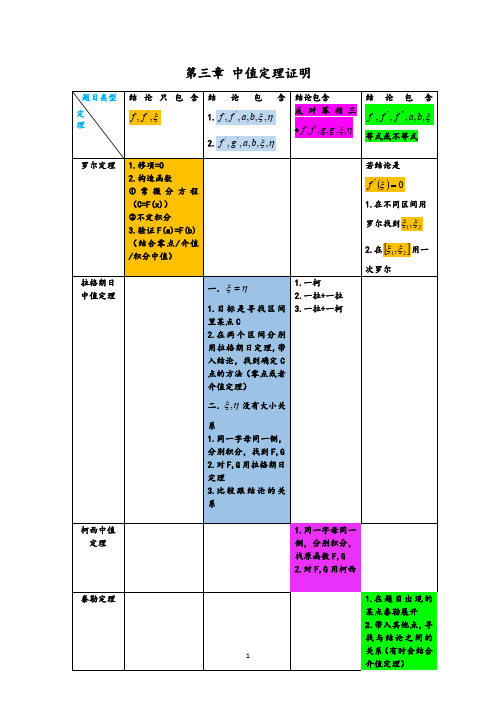
若结论是
f '' 0
1.在不同区间用
罗尔找到 1,2
2.在 1,2 用一
次罗尔
柯西中值 定理
1.同一字母同一 侧，分别积分， 找原函数 F,G 2.对 F,G 用柯西
泰勒定理
1.在 题 目 出 现 的
某点泰勒展开
2.带入其他点，寻
找与结论之间的
1
关系（有时会结合
介值定理）
1.闭区间上连续函数定理 ① ② ③ ④ 2.微分中值定理 ①
（1） 存在（0，1）内两个不同的点 , ，使得 f ' ( ) f ' () 2 .
（2）
存在（0，1）内两个不同的点 , ，使得
1 f ' ( )
1 f ' ()
2 .
（3） 存在（0，1）内两个不同的点 , ，使得 f ' ( ) f ' () 1 .
f ' ( ) （4） 存在（0，1）内两个不同的点 , 及大于零的常数 ，使得 f ' () （5） 对于任意的正整数 n，存在（0，1）内两个不同的点 , 及常数 0 ，
3
5.若 f (x) 在[0,1] 上可导，且当 x [0,1] 时有 0 f (x) 1，且 f (x) 1，证明：在 (0,1) 内有且仅有一个点 使得 f ( )
6.设 f (x) 在[0，1]上连续，在(0，1)内可导，且 f (0) = f (1) =0， f (1 ) =1。试证 2
②
③
④
3.积分中值定理 ① ②
不等式证明思路 构造函数（利用极值） 拉格朗日中值定理 函数凹凸性定义
2
1.若 f (x) 在 [a,b] 上连续，在 (a,b) 上可导， f (a) f (b) 0 ，证明： R ， (a,b) 使得： f ( ) f ( ) 0
中值定理证明方法总结
中值定理证明方法总结中值定理（Intermediate Value Theorem）是微积分中的一项重要定理，它表明如果一个连续函数$f(x)$在闭区间$[a,b]$上取两个不同的值$f(a)$和$f(b)$，那么在开区间$(a,b)$内，函数$f(x)$必然取到介于$f(a)$和$f(b)$之间的所有值。
中值定理的证明是通过构造一个辅助函数$g(x)$，它将闭区间$[a,b]$映射到实数区间$[f(a),f(b)]$上，并利用连续函数的性质来证明中值定理。
证明过程如下：1.首先，我们定义辅助函数$g(x)=f(x)-k$，其中$k$是一个常数。
我们的目标是证明如果$g(a)$和$g(b)$异号，那么在开区间$(a,b)$内，$g(x)$必然等于$0$。
2.根据函数$g(x)$的定义，我们可以得到$g(a)=(f(a)-k)$和$g(b)=(f(b)-k)$。
由于$g(a)$和$g(b)$异号，即$(f(a)-k)$和$(f(b)-k)$异号，所以$g(x)$在$[a,b]$上一定有一个根。
3. 接下来，我们要证明在开区间$(a,b)$内，$g(x)$没有其他根。
假设在$(a,b)$内存在一个根$x=c$，即$g(c)=0$。
根据连续函数的性质，我们有$\lim_{x \to c} g(x) = g(c) = 0$。
又因为$f(x)$是连续函数，所以$\lim_{x \to c} f(x) = f(c)$。
4. 根据极限的性质，我们有$\lim_{x \to c} g(x) = \lim_{x \to c} [f(x)-k] = f(c)-k$。
由于$\lim_{x \to c} g(x) = 0$，所以$f(c)-k=0$，即$f(c)=k$。
这意味着$f(c)-k=0$是$g(x)$的唯一根。
5.综上所述，我们可以得出结论，如果$g(a)$和$g(b)$异号，那么在开区间$(a,b)$内，$g(x)$的根只有$f(c)-k=0$。
拉格朗日中值定理证明及其应用
拉格朗日中值定理证明及其应用拉格朗日中值定理是微积分中的一个重要定理，它在数学分析和物理学等领域具有广泛的应用。
拉格朗日中值定理的证明基于罗尔定理，也是微积分中的一个重要定理。
拉格朗日中值定理可以分为一元函数和多元函数两种形式。
先来看一元函数的形式。
一元函数的拉格朗日中值定理：设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，那么在这个开区间内至少存在一点c，使得f'(c) = (f(b)-f(a))/(b-a)。
证明思路如下：我们定义一个辅助函数F(x)，公式为：F(x)=f(x)-[f(b)-f(a)]/(b-a) * (x-a)。
该函数满足以下条件：F(a) = f(a)，F(b) = f(b)。
接下来，我们看一下多元函数的拉格朗日中值定理的证明。
多元函数的拉格朗日中值定理：设函数f(x1, x2, ..., xn)在闭包区域D上连续，在D的内部可导，那么对于D内部的任意两个点P(x1, x2, ..., xn)和Q(y1, y2, ..., yn)，存在系数α属于(0, 1)，使得f(y1, y2, ..., yn) - f(x1, x2, ..., xn) =(dy1-dx1)∂f/∂x1(P+α(Q-P)) + (dy2-dx2)∂f/∂x2(P+α(Q-P)) + ... +(dyn-dxn)∂f/∂xn(P+α(Q-P))，其中∂f/∂xi表示对xi的偏导数。
证明多元函数的拉格朗日中值定理可以类似地用到辅助函数的方式。
具体证明过程比较复杂，涉及到多元函数的导数和偏导数的概念。
有兴趣的读者可以参考相关的微积分教材或数学分析的资料。
拉格朗日中值定理的应用非常广泛。
它可以用来证明其他定理，如柯西中值定理、洛必达法则等。
在物理学中，拉格朗日中值定理可以用于分析物体运动的速度、加速度等问题。
在经济学中，拉格朗日中值定理可以用于分析边际效应、边际利润等问题。
拉格朗日中值定理是微积分中的一个重要工具，可以帮助我们深入理解函数的性质和解决实际问题。
柯西中值定理的证明
柯西中值定理的证明
柯西中值定理的原理是：如果有一个函数 f(x) 在给定的闭区间[a,b]上具有连续导数并
且在边界处满足f(a)f(b)≤0，那么该函数必定至少存在一个x轴上的极值点。
证明：
设函数f(x)在闭区间[a,b]上连续且具有导数,且f(a)f(b)≤0，首先将区间[a,b]分成左
右两个子区间$[a,c]$和$[c,b]$，且$c$为$[a,b]$的中点，即 $c=(a+b)/2。
$
由于$f(x)$在区间[a,b]上连续且有导数，如果它在区间[a,c]上有极值点，即$f'(c)=0$；
如果不论左区间或右区间，$f$都没有极值点，则可推出：
若$f(a)f(c)>0$，则a与c处的导数是正的，即$f'(a)f'(c)>0$；
根据以上的分析，我们可以得出结论：只要$f(a)f(b)≤0$，函数$f(x)$也就在[a,b]上至
少存在一个极值点。
最后需要说明的是，若f(x)和f`(x)连续，f(a)f(b)≤0，则在[a,b]内至少存在一个极值点，这就是柯西中值定理。
总结：柯西中值定理指出，如果一个函数的导数在一个区间上是连续的，且函数在边界处
满足f(a)f(b)≤0，那么函数至少存在一个极值点。
本文证明了该定理，即极值点存在性
的证明。
中值定理 证明 解微分方程
中值定理证明解微分方程
中值定理是微积分中的一个重要定理，可以用来证明解微分方程的存在和唯一性。
该定理指出，对于一个在闭区间上连续的实函数，存在一个点使得该点的导数等于函数在该区间上的平均变化率。
这个点就是中值定理所述的中间点。
利用中值定理证明解微分方程的存在性，通常先将微分方程化为形如dy/dx=f(x,y)的一阶常微分方程。
然后，将该方程表示为
y'=g(x,y)，其中g(x,y)=f(x,y)/√(1+f(x,y)^2)。
由于g(x,y)在整个平面上的偏导数都是连续的，因此根据偏导数的连续性定理，可以得到g(x,y)在平面上是局部利普希茨连续的。
接下来，对于给定的初始条件y(x0)=y0，可以构造一条以(x0,y0)为起点，斜率为g(x0,y0)的直线。
根据中值定理，该直线与y=f(x)在(x0,x0+1)的某一点处相切。
将该点的横纵坐标记作x1和y1，可以得到y1=y0+g(x0,y0)(x1-x0)。
然后，以(x1,y1)为起点，斜率为g(x1,y1)的直线与y=f(x)在(x1,x1+1)的某一点处相切，构造出新的点(x2,y2)。
如此重复进行下去，可以得到一条光滑的曲线y=y(x)，满足y(x0)=y0，
y'(x)=g(x,y(x))。
由于g(x,y)是局部利普希茨连续的，因此可以证明y(x)在一定范围内是存在且唯一的。
此外，由于y'(x)是连续的，因此y(x)也是连续的。
因此，该曲线就是微分方程的解。
- 1 -。
积分中值定理证明
积分中值定理证明积分中值定理是微积分中的一个重要定理，它是确保一个连续函数区间上存在一个点，其切线与该区间的平均斜率相等的定理。
下面是对积分中值定理的简单证明。
设函数f(x)在闭区间[a,b]上连续且可导，并且它在该区间上非常量。
根据Rolle定理，我们知道如果一个函数在一个区间的两个端点上取相等的值，并且在这个区间的中间至少有一个点处导数为零，那么在这个区间内必然存在至少一个点，该点处导数也为零。
为了应用Rolle定理，我们首先定义一个函数g(x)=f(x)-kx，其中k是常数。
因为k是常数，所以g(x)也是连续且可导的。
现在我们将证明存在至少一个k值，使得g(a)=g(b)。
注意到g(a)=f(a)-ka和g(b)=f(b)-kb。
如果g(a)\neq g(b)，我们可以将区间[a,b]分为两部分：如果在某个点x_1\in(a,b)处，g(x_1)>0，那么必然在x_2\in(a,x_1)处存在g(x_2)<0；反之亦然。
因为g(x)在闭区间[a,b]上连续，根据介值定理，存在一个点x_3\in[a,b]，使得g(x_3)=0。
根据Rolle定理，由g(x)的连续性和可导性，存在至少一个点c\in(a,b)，使得g'(c)=0。
这意味着f'(c)-k=0，即f'(c)=k。
存在至少一个c值，使得f'(c)与k相等。
总结一下，根据Rolle定理的应用，我们证明了对于函数f(x)在闭区间[a,b]上连续且可导的情况，存在至少一个点c\in(a,b)，使得f'(c)与该区间的平均斜率相等。
这就是积分中值定理的证明。
重积分中值定理证明
重积分中值定理证明一、重积分中值定理内容（以二元函数为例）设 f(x,y) 在闭区域 D 上连续，D 的面积为S，则在 D 上至少存在一点(ξ,eta)，使得∬_D f(x,y)dσ = f(ξ,eta)S二、证明过程（一）利用连续函数的性质1. 存在最大值和最小值- 因为 f(x,y) 在闭区域 D 上连续，根据闭区域上连续函数的性质，f(x,y) 在 D 上必能取得最大值 M 和最小值 m。
- 即对于任意(x,y)∈ D，有m≤slant f(x,y)≤slant M。
2. 估计积分值的范围- 由重积分的性质，对于∬_D f(x,y)dσ，有- mS≤slant∬_D f(x,y)dσ≤slant MS，其中S 是区域 D 的面积。
3. 应用介值定理- 因为mS≤slant∬_D f(x,y)dσ≤slant MS，所以(∬_D f(x,y)dσ)/(S)介于 m 和M 之间。
- 又因为 f(x,y) 在 D 上连续，根据连续函数的介值定理，在 D 上至少存在一点(ξ,eta)，使得f(ξ,eta)=(∬_D f(x,y)dσ)/(S)。
- 即∬_D f(x,y)dσ = f(ξ,eta)S。
（二）以一元函数定积分中值定理为基础（拓展思路）1. 将重积分转化为累次积分（以矩形区域D = [a,b]×[c,d]为例）- 根据重积分化为累次积分的定理，∬_D f(x,y)dσ=∫_a^b dx∫_c^d f(x,y)dy。
- 对于固定的x∈[a,b]，令F(x)=∫_c^d f(x,y)dy。
2. 应用一元函数定积分中值定理- 由于F(x) 在[a,b]上连续（因为f(x,y) 连续），根据一元函数定积分中值定理，存在ξ∈[a,b]，使得∫_a^b F(x)dx = F(ξ)(b - a)。
- 即∫_a^b dx∫_c^d f(x,y)dy=∫_c^d f(ξ,y)dy(b - a)。
证明中值定理
证明中值定理
中值定理是微积分基本定理之一，用于说明在某一段区间上连续函数的导数存在一个特定值。
中值定理可以分为罗尔中值定理、拉格朗日中值定理和柯西中值定理三种形式。
1. 罗尔中值定理：
假设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，并且f(a) = f(b)，那么在开区间(a, b)上至少存在一个点c，使得f'(c) = 0。
2. 拉格朗日中值定理：
假设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，那么在开区间(a, b)上至少存在一个点c，使得[f(b) - f(a)] / (b - a) = f'(c)。
3. 柯西中值定理：
假设函数f(x)和g(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，并且g'(x) ≠ 0。
那么在开区间(a, b)上至少存在一个点c，使得[f(b) - f(a)] / [g(b) - g(a)] = f'(c) / g'(c)。
证明中值定理的关键是利用连续函数和导数的性质，将函数的均值和导数联系起来。
具体证明过程根据中值定理的不同类型而有所区别，但关键思路是通过构造辅助函数、使用辅助函数的导数性质或应用罗尔定理来推导出中值点的存在性。
总的来说，中值定理对于数学分析、微积分和实分析等领域的
发展起到了非常重要的作用，也是解决许多数学问题的重要工具。
中值定理证明方法总结
f (a) g (a) h( a )
f (b) g (b) h(b)
f ′(ξ ) g ( a ) g (b ) ′ f (ξ ) g ′(ξ ) = h(a ) h(b) h′(ξ )
f (a) − h( a ) f (b) ′ f (a) g (ξ ) + h(b) g (a) f (b) ′ h (ξ ) g (b)
y
y = f ( x)
o
aξ
b x
在( a , b ) 内至少存在一点 ξ , 使 f ′(ξ ) = 0. 故在[ a , b ]上取得最大值 证: 因 f ( x) 在[ a , b] 上连续，
M 和最小值 m .
若 M = m , 则 f ( x ) ≡ M , x ∈ [ a , b] , 因此 ∀ξ ∈ (a , b) , f ′(ξ ) = 0 .
拉氏 目录 上页 下页 返回 结束
三、柯西(Cauchy)中值定理
f ( x) 及 F ( x) 满足 : (1) 在闭区间 [ a , b ] 上连续 (2) 在开区间 ( a , b ) 内可导 (3)在开区间 ( a , b ) 内 F ′( x) ≠ 0 f (b) − f (a ) f ′(ξ ) = . 至少存在一点 ξ ∈ ( a, b) , 使 F (b) − F (a ) F ′(ξ ) a <η < b 分析: F (b) − F (a ) = F ′(η )(b − a ) ≠ 0 f (b) − f (a ) F ′(ξ ) − f ′(ξ ) = 0 要证 ′(ξ ) ϕ F (b) − F (a ) f (b ) − f ( a ) ϕ ( x) = F ( x) − f ( x) F (b ) − F ( a )
证明中值定理
1利用罗尔定理证明柯西中值定理利用罗尔定理来证明柯西中值定理的关键是如何构造一个辅助函数，并且使其满足罗尔定理的条件.现在我们先来看一下罗尔定理的内容及证明过程.罗尔定理[1] 设函数()f x 在闭区间[],a b 上连续，在开区间(,)a b 内可导，而且在区间的两个端点处函数()f x 的值相等，即()()f a f b =，那么在开区间(,)a b 上至少存在一点ξ,使得函数()f x 在这点的导数为零，即'()0f ξ=. 证明 因为()f x 在[],a b 上连续，所以肯定存在最大值与最小值，分别将它们用M 与m 表示.现在分两种情况来讨论：(1) 如果M m =成立，那么函数()f x 在[],a b 一定为常数，则对于一切的[,]x a b ∈都有'()0f x =.(2) 如果M m ≠，那么不妨假设m M <，又因为()()f a f b =，所以最大值M 与最小值m 至少有一个在(,)a b 内的某一点ξ处取得，从而可知ξ是()f x 的极值点.根据条件可知()f x 在开区间(,)a b 内可导,()f x 在点ξ处可导，所以由费马定理可推知'()0f ξ=.m M >的情况可以用类似的方法证明.罗尔定理的几何意义 在每一点都可导的一段连续曲线上，如果曲线的两端高度相等，则该曲线至少存在一条水平切线.下面证明柯西中值定理：证明 首先作一个辅助函数()()()()()(()())()()f b f a F x f x f ag x g a g b g a -=---- . 这个函数在闭区间[],a b 上显然是连续的，而且在开区间(,)a b 上有导数，此外，()()F a F b =,因此，根据罗尔定理可以找到这样的点(,)a b ξ∈,使得'()0F ξ=,即()()'()'()'()0()()f b f a F fg g b g a ξξξ-=-=-.又因为'()0g ξ≠,因此，可把上式写成'()()()'()()()f f b f a g g b g a ξξ-=-,即得所证. 2 利用复合函数证明柯西中值定理 在柯西中值定理中，我们可以考虑将()g x 看成自变量v ,将x 看成自变量v 的函数，则将()f x 看成中间变量为x ,自变量为v 的复合函数. 达布定理[7] ()f x 在(,)a b 内连续且可导，(1) 有点12,(,)x x a b ∈，12'()'()0f x f x <，则有点12(,)c x x ∈，使得'()0f c =.(2) 设12,(,)x x a b ∈，12'()'()f x f x ≠，则对介于1'()f x 与2'()f x 之间的数m 有点ξ介于1x 和2x 之间，且'()f m ξ=.命题 设函数()f x 在开区间(,)a b 内可导，(,)x a b ∀∈，'()0('()0)f x f x ><， 则()f x 在(,)a b 内严格单调增加（减少）.证明 根据题设可知，对于任意的(,)x a b ∈，'()g x 存在且有'()0g x ≠.根据达布定理[(),()]g a g b 知，'()g x 在开区间(,)a b 内保号，令()v g x =，那么v 就是闭区间[],a b 上的单调连续函数.于是存在单调且连续的反函数1()x g v -=，[(),()]v g a g b ∈. 根据()f x 在闭区间[],a b 上的连续性可知，在闭区间[(),()]g a g b 上存在连续的复合函数1[()]()y f g v h v -==.则由参数方程的求导公式可得 '()'()dydy f x dx dv dv g x dx==，(,)x a b ∈. 所以dy dv在(,)x a b ∈即[(),()]v g a g b ∈内存在.从而()y h v =在闭区间[(),()]g a g b 上满足拉格朗日中值定理的条件，所以至少存在一点()((),())v g g a g b ξξ=∈，使()()||()()v v x dy dy f b f a dv dv g b g a ξξ==-=-，得 '()()()'()()()f f b f a g g b g a ξξ-=-，(,)a b ξ∈.。
积分中值定理的证明过程
积分中值定理的证明过程
积分中值定理的证明：设f(x)在[a，b]上连续，且最大值为m,最小值为m，最大值和最小值可相等。
由估值定理及连续函数的介值定理可证明积分中值定理。
积分中值定理在应用中所起到的重要作用是可以使积分号去掉，或者使复杂的被积函
数化为相对简单的被积函数，从而使问题简化。
因此，对于证明有关题设中含有某个函数
积分的等式或不等式，或者要证的结论中含有定积分，或者所求的极限式中含有定积分时，一般应考虑使用积分中值定理，去掉积分号，或者化简被积函数。
不等式证明
积分不等式是指不等式中含有两个以上积分的不等式,当积分区间相同时,先合并同一
积分区间上的不同积分,根据被积函数所满足的条件,灵灵活运用积分中值定理,以达到证
明不等式成立的目的。
在证明的定分数不等式时, 常常考量运用分数中值定理, 以便换成分数符号, 如果被
内积函数就是两个函数之积时, 可以考量用分数第一或者第二中值定理。
对于某些不等式
的证明, 运用原分数中值定理就可以获得“≥”的结论, 或者不等式显然无法获得证明。
而运用改良了的分数中值定理之后, 则可以获得“\ue”的结论, 或者顺利的解决问题。
积分中值定理(开区间)证明的几种方法
积分中值定理(开区间)的几种证明方法定理：设f 在［a,b ］上连续，则 (a,b)，使得f (x) f ()在［a,b ］上连续，易证(可反证)(这还是书上例2的结论)(a,b)，使得 F( ) f( ) f( ) 0，即 f ( ) f()。
x［证二］:令F(x) f (t)dt ，则F(x)在［a,b ］上满足拉格朗日中值定理的条件，故a(a,b)，使得 F(b) F(a) F ( )(b a)，即结论成立。
(注：书上在后面讲的微积分基本定理 )b［证三］:反证：假设不 (a,b)，使得 f(x)dx f( )(b a)，由积分第一中值定理, a知只能为a 或b ，不妨设为b ，即1bx (a,b), f (x) f (b) - a f(x)dx 。
b a a 由于 f 连续，故 x (a,b), f (x) f(b)(或 f (x) f(b))，(这一点是不是用介值定理来说明 )这样x b(上限 x 改为 b ) f (x)dx f (b)dx f (b)(b a).a a(这个严格不等号不太显然要用书上例 2结论来说明)矛盾。
［证四］:设f 在［a,b ］上的最大值为 M ，最小值为m 。
若m M ，则f c ， 可任取。
b若 m M ，则 x - ［a,b ］，有 M f(x -) 0,故［M f (x)］dx 0,即ab f (x)dx M (b a).f(x)dx f( )(b a)。
［证一］:由积分第一中值定理(P217),b[a,b]，使得 f (x)dx a f( )(b a)。
于是a 【f (X ) f ( )]dx 0.由于函数F(x)同理有m(b ba) & f(x)dx.由连续函数的介质定理知：1 b (a,b)，使得f ( ) f (x)dx.。
b a a主：以上方法有的能推广到定理9.8的证明，有的不能，再思考吧！。
中值定理证明方法总结
在( a, b) 内至少存在一点 ξ, 使 f′(ξ) = 0.
f(a+ ), x= a
证明提示: 设 F(x) =
f(x), f(b− ),
a< x< b x= b
证 F(x) 在 [a, b] 上满足罗尔定理 .
机动 目录 上页 下页 返回 结束
二、拉格朗日中值定理
y
y= f(x)
证毕
拉氏 目录 上页 下页 返回 结束
三、柯西(Cauchy)中值定理
f(x) 及 F(x) 满足 :
(1) 在闭区间 [ a, b] 上连续
(2) 在开区间 ( a, b) 内可导
(3)在开区间 ( a, b) 内F′(x) ≠ 0 至少存在一点 ξ∈(a,b) , 使
f(b) F(b)
− −
f(a) = F(a)
• g(b) − g(a)
•
原函数法
F(x) = f(x)
−
f(b)
−
f(a)
g(
x)
g(b) − g(a)
* 中值定理的条件是充分的, 但非必要. 因此
可适当减弱.
例如, 设 f(x) 在(a,b) 内可导,且 f(a+ 0) = f(b− 0), 则至少存在一点 ξ∈(a,b), 使 f′(ξ) = 0 .
方程两边同时积分
f(b)))) −−−− ff((((aaaa)))) xxxx++++ CCCC ==== ff((((xxxx)))) b− a
解出积分常数 ，则
令辅助 直接积分消不去导数，故变形为 方程两边同时积分
解出积分常数 ，则 令辅助函数
中值定理及其应用
中值定理及其应用中值定理是微积分中的重要定理之一，它是高阶微积分的基础，被广泛应用于物理、经济、工程等领域。
在本文中，我们将介绍中值定理的概念、证明以及其在实际问题中的应用。
一、中值定理的概念中值定理是微积分中的一个基本定理，用来分析函数在某个区间上的平均变化率与瞬时变化率的关系。
它由罗尔定理、拉格朗日中值定理和柯西中值定理组成。
1. 罗尔定理罗尔定理是中值定理的基础，它主要用于研究函数在闭区间上连续且在开区间上可导的情况。
罗尔定理的表述为：设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，并且满足f(a) = f(b)，则存在c∈(a,b)，使得f'(c) = 0。
2. 拉格朗日中值定理拉格朗日中值定理是中值定理的一种形式，它由罗尔定理推导而来。
拉格朗日中值定理的表述为：如果函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导，则存在c∈(a, b)，使得f'(c) = (f(b) - f(a))/(b - a)。
3. 柯西中值定理柯西中值定理是中值定理的另一种形式，它由拉格朗日中值定理推导而来。
柯西中值定理的表述为：如果两个函数f(x)和g(x)在闭区间[a,b]上连续，在开区间(a, b)上可导，并且g'(x)≠0，则存在c∈(a, b)，使得[f(b) - f(a)]/g(b) - g(a) = f'(c)/g'(c)。
二、中值定理的证明中值定理的证明相对复杂，需要运用到微积分中的一些基本概念和定理。
在这里，我们将省略中值定理的详细证明过程。
三、中值定理的应用中值定理在实际问题中具有广泛的应用。
以下是几个常见的应用实例：1. 平均速度与瞬时速度根据拉格朗日中值定理，对于一段时间内的平均速度与某一时刻的瞬时速度，它们之间存在一个相等的关系。
这在物理学中有着重要的意义，可以通过计算平均速度来得到瞬时速度的近似值。
2. 函数求导与图像切线中值定理可以用于求解函数的导数以及函数图像的切线。
广义积分中值定理的证明
广义积分中值定理的证明
广义积分中值定理：若f在[a，b]上连续，则至少存在一点c属于[a，b]，使得在[a，b]上的积分值等于f(c)(b-a)。
推广：若f与g都在[a，b]上连续，且g在[a，b]上不变号，则至少存在一点c属于[a，b]，使得f乘以g在[a，b]上的积分等于f(c)乘以g在[a，b]上的积分。
积分中值定理：设函数f在[a，b]上可积，1：若函数g在[a，b]上递减，且g大于
等于0，则存在一点c属于[a，b]，使得(f乘以g)在[a，b]上的积分等于g(a)乘以（f在[a，c]上的积分）。
2：若函数g在[a，b]上递增，且g大于等于0，则存在一点d属于[a，b]，使得(f乘以g)在[a，b]上的积分等于g(b)乘以（f在[d，b]推论：设函数f在[a，b]上可积。
若g为单调函数，则存在一点c属于[a，b]，使得(f乘以g)的积分等于g(a)乘
以(f在[a，c]上的积分)加上g(b)乘以(f在[c，b]上的积分)。
：若函数g在[a,b]上递增,且g大于等于0,则存在一点d属于[a,b],使得(f乘以g)在[a,b]上的积分等于g(b)乘以
（f在[d,b]上的积分）.推论：设函数f在[a,b]上可积.若g为单调函数,则存在一点c属于[a,b],使得(f乘以g)的积分等于g(a)乘以(f在[a,c]上的积分)加上g(b)乘以(f在
[c,b]上的积分)证明太多。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中值定理首先我们来看看几大定理：1、 介值定理：设函数f(x)在闭区间[a,b]上连续，且在该区间的端点取不同的函数值f(a)=A及f(b)=B ，那么对于A 与B 之间的任意一个数C ，在开区间(a,b)内至少有一点ξ使得f(ξ)=C(a<ξ<b).Ps:c 是介于A 、B 之间的，结论中的ξ取开区间。
介值定理的推论：设函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值M ，最小值m,若m ≤C ≤M,则必存在ξ∈[a,b], 使得f(ξ)=C 。
（闭区间上的连续函数必取得介于最大值M 与最小值m 之间的任何值。
此条推论运用较多）Ps ：当题目中提到某个函数f(x),或者是它的几阶导函数在某个闭区间上连续，那么该函数或者其几阶导函数必可以在该闭区间上取最大值和最小值，那么就对于在最大值和最小值之间的任何一个值，必存在一个变量使得该值等于变量处函数值。
2、 零点定理：设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号，即f(a).f(b)<0,那么在开区间内至少存在一点ξ使得f(ξ)=0.Ps:注意条件是闭区间连续，端点函数值异号，结论是开区间存在点使函数值为0.3、 罗尔定理：如果函数f(x)满足：（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导; （3）、在区间端点处函数值相等，即f(a)=f(b).那么在(a,b)内至少有一点ξ(<a ξ<b),使得f`(x)=0;4、 拉格朗日中值定理：如果函数f(x)满足：（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导;那么在(a,b)内至少有一点ξ(<a ξ<b),使得 f(b)-f(a)=f`(ξ).(b-a).5、 柯西中值定理：如果函数f(x)及g(x)满足（1）、在闭区间[a,b]上连续； （2）、在开区间(a,b)内可导; （3）、对任一x(a<x<b),g`(x)≠0,那么在(a,b)内至少存在一点ξ,使得)`()`()()()()(ξξg f a g b g a f b f =--Ps ：对于罗尔定理、拉格朗日中值定理、柯西中值定理结论都是开开区间内取值。
6、 积分中值定理：若函数f(x)在[a,b]上连续，则至少存在一点],[b a ∈ξ使得)()()(a b f dx x f ba-=⎰ξPs ：该定理课本中给的结论是在闭区间上成立。
但是在开区间上也是满足的，下面我们来证明下其在开区间内也成立，即定理变为：若函数f(x)在[a,b]上连续，则至少存在一点),(b a ∈ξ使得)()()(a b f dx x f ba-=⎰ξ证明：设⎰=xadx x f x F )()(，],[b a x ∈因为)(x f 在闭区间上连续，则)(x F 在闭区间上连续且在开区间上可导（导函数即为)(x f ）。
则对)(x F 由拉格朗日中值定理有：),(b a ∈∃ξ使得ab dx x f ab a F b F F ba-=--=⎰)()()()`(ξ而)()`(ξξf F = 所以),(b a ∈∃ξ使得)()()(a b f dx x f ba-=⎰ξ。
在每次使用积分中值定理的时候，如果想在开区间内使用，我们便构造该函数，运用拉格朗日中值定理来证明下使其在开区间内成立即可。
千万不可直接运用，因为课本给的定理是闭区间。
定理运用：1、设)(x f 在[0,3]上连续，在(0,3)内存在二阶导函数，且⎰+==2)3()2()()0(2f f dx x f f .证明：(1))2,0(∈∃η使)0()(f f =η(2))3,0(∈∃ξ使0)``(=ξf证明：先看第一小问题：如果用积分中指定理似乎一下子就出来了，但有个问题就是积分中值定理是针对闭区间的。
有的人明知这样还硬是这样做，最后只能是0分。
具体证明方法在上面已经说到，如果要在开区间内用积分中指定理，必须来构造函数用拉格朗日中值定理证明其在开区间内符合。
（1）、令]2,0[),()(0∈=⎰x x F dt t f x则由题意可知)2,0(]2,0[)(上连续，在x F 内可导.则对)(x F 由拉格朗日中值定理有：2)0()2()`()2,0(F F F -=∈∃ηη使)2,0(),0(2)()(2∈==∴⎰ηηf dt t f f(2)、对于证明题而言，特别是真题第一问证明出来的结论，往往在第二问中都会有运用，在做第二问的时候我们不要忘记了第一问证明出来的东西，我们要时刻注意下如何将第一问的东西在第二问中进行运用：第二问是要证明存在点使得函数二阶倒数为0，这个很容易想到罗尔定理来证明零点问题，如果有三个函数值相等，运用两次罗尔定理那不就解决问题啦，并且第一问证明出来了一个等式，如果有f(a)=f(b)=f(c)，那么问题就解决了。
第一问中已经在(0,2)内找到一点，那么能否在(2,3)内也找一点满足结论一的形式呢，有了这样想法，就得往下寻找了，)3()2()0(2f f f +=，看到这个很多人会觉得熟悉的，和介值定理很像，下面就来证明：]3,0[)(在x f Θ上连续，则在]3,2[上也连续，由闭区间上连续函数必存在最大值和最小值，分别设为M,m;则.)3(,)2(M f m M f m ≤≤≤≤ 从而，M f f m ≤+≤2)3()2(，那么由介值定理就有：)0(2)3()2()(],3,2[f f f c f c =+=∈∃使]3,2[),2,0(),()()0(∈∈==∴c c f f f ηη则有罗尔定理可知：0)`(),,0(11=∈∃ξηξf ，0)`(),,(22=∈∃ξηξf c 0)``(),3,0(),(21=⊆∈∃ξξξξfPs ：本题记得好像是数三一道真题，考察的知识点蛮多，涉及到积分中值定理，介值定理，最值定理，罗而定理，思路清楚就会很容易做出来。
2、设f(x)在[0,1]上连续，在(0,1)内可导,且f(0)=0,f(1)=1. 证明:ξξξ-=∈∃1)()1,0()1(f 使得、1)`()`(),1,0()2(=⋅∈∃ηξξηf f 使得、两个不同点、 本题第一问较简单，用零点定理证明即可。
（1）、首先构造函数：]1,0[,1)()(∈-+=x x x f x F1)1()1(11)0()0(==-=-=f F f F01)1()0(<-=⋅F F Θ由零点定理知：ξξξξ-==∈∃1)(,0)()1,0(f F 即使得(2)、初看本问貌似无从下手，但是我们始终要注意，对于真题这么严谨的题目，他的设问是一问紧接一问，第一问中的结论或多或少总会在第二问中起到作用。
在想想高数定理中的就这么些定理，第一问用到的零点定理，从第二问的结论来看，也更本不涉及什么积分问题，证明此问题也只可能从三大中值定理出发，具体是哪个定理，得看自己的情况，做题有时候就是慢慢试，一种方法行不通，就换令一种方法，有想法才是最重要的，对于一道题，你没想法，便无从下手。
另外在说一点，在历年证明题中，柯西中值定理考的最少。
本题结论都涉及一阶倒数，乘积之后为常数，很可能是消去了变为1（你题目做多了，肯定就知道事实就是这样）.并且第一问中0与1之间夹了个ξ，如果我们在0与ξ，ξ与1上对)(x f 运用拉格朗日中值定理似乎有些线索。
写一些简单步骤，具体详细步骤就不多写了：将第一问中)(ξf 代入即可。
)1,(,11)()1()`(),0(,1)0()()`(ξζξξξξζξηξξξξη∈-=--=∈-=-=f f f f f f)1,0()1,(),1,0(),0(,1)`()`(⊆∈⊆∈=⋅∴ξζξηηξf fPs ：本题是05年数一的一道真题，第一问是基本问题，送分的，第二问有一定区分度，对定理熟练的会容易想到拉格朗日定理，不熟练的可能难以想到方法。
做任何题，最重要的不是你一下子就能把题目搞出来，而是你得有想法，有想法才是最重要的，有了想法你才能一步步的去做，如果行不通了，在改变思路，寻求新的解法，如果你没想法，你就根本无从下手。
对于这道题的结论比较有意思，比较对称，另外一个就是结论的条件，为何要把ηξ、放在两个范围内，不像上一题中直接来个)1,0(∈ξη、，这个分界点1/2 的作用是干吗的。
很可能也是把1 /2当做某一个点就像上一题中的ξ，是否要用到拉格朗日中值定理呢，这是我们的一个想法。
那具体的函数如何来构造呢，这个得从结论出发，22)`()`(ηξηξ+=+f f我们把等式变一下：0)`()`(22=-+-ηηξξf f ，2)`(ξξ-f 这个不就是331)(ξξ-f 关于ξ的导数（而且题目中f(1)=1/3,貌似这样有点想法了），本题会不会也像上一题那样，运用拉格朗日中值定理后相互消掉变为0呢，有了这些 想法我们就要开始往下走了： 先来构造一个函数：)21(2211)21()1()`()21(221)0()21()`(,0)1(,0)0(,31)()(3F F F F F F F F F F x x f x F -=--==-===-=ηξ0)`()`(=+ξηF F 刚好证明出来。
Ps ：本题是近几年数二的一道真题，只有一问，有比较大区分度的，得从条件结论互相出发，如何构造出函数是关键。
做出来之后我们反过来看这个1/2的作用就知道了，如果只给)1,0(∈ξη、，那就更难了 得自己找这个点，既然题中给了这个点，并且把两个变量分开在两个区间内，我们就对这两个变量在对应区间用相应定理。
说明真题出的还是很有技巧的。
一般设计难一点的中值定理证明，往往得用拉格朗日定理来证明，两个变量，都涉及到导数问题，这是因为拉格朗日中值定理条件要少些，只需连续，可导即可，不像罗尔定理得有式子相等才可进一步运用。
4.设f(x)在区间[-a,a](a>0)上具有二阶连续导数，f(0)=0 (1)、写出f(x)的带拉格朗日余项的一阶麦克劳林公式 (2)、证明在[-a,a]上至少存在一点η使得⎰-=aadx x f f a )(3)``(3η第一问课本上记住了写出来就行，考的很基础 （1）、22!2)``()0`(!2)``(!1)0`()0()(x f x f x f x f f x f ξξ+⋅=++= (2)、第二问先将第一问的式子f(x)代入看看有什么结果出来⎰⎰--⋅=aaaadx x f dx x f 22)``()(ξ，)``(ξf 此处不能直接拿到积分号外面，因为他不是与x 无关的数。
做到这儿，我们想办法把他弄到积分号外面似乎就能出来，有了这样想法就得寻求办法。
题目中说道f(x)有二阶连续导数，为何要这样说呢，我们知道连续函数有最大值，最小值，往往会接着和介值定理一起运用。