抛物线专题练习(含解析)
2023年新高考数学一轮复习9-5 抛物线(真题测试)含详解

专题9.5 抛物线(真题测试)一、单选题1.(2023·全国·高三专题练习)已知抛物线24y x =上一点M 到x 轴的距离是2,则点M 到焦点F 的距离为( )A B .2C .D .32.(2023·全国·高三专题练习)抛物线21:4E y x =的焦点到其准线的距离为( ) A .18B .14C .2D .43.(2022·全国·高考真题(文))设F 为抛物线2:4C y x =的焦点,点A 在C 上,点(3,0)B ,若AF BF =,则AB =( )A .2B .C .3D .4.(2021·全国·高考真题)抛物线22(0)y px p =>的焦点到直线1y x =+,则p =( )A .1B .2C .D .45.(2020·北京·高考真题)设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ l ⊥于Q ,则线段FQ 的垂直平分线( ).A .经过点OB .经过点PC .平行于直线OPD .垂直于直线OP6.(2019·全国·高考真题(文))若抛物线y 2=2px (p >0)的焦点是椭圆2231x y pp+=的一个焦点,则p =( )A .2B .3C .4D .87.(山东·高考真题(文))已知抛物线22(0)y px p =>,过其焦点且斜率为1的直线交抛物线于 ,A B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( ) A .1x = B .1x =- C .2x =D .2x =-8.(2017·全国·高考真题(理))已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,则|AB |+|DE |的最小值为( ) A .16B .14C .12D .10二、多选题9.(2022·全国·高考真题)已知O 为坐标原点,点(1,1)A 在抛物线2:2(0)C x py p =>上,过点(0,1)B -的直线交C 于P ,Q 两点,则( ) A .C 的准线为1y =- B .直线AB 与C 相切 C .2|OP OQ OA ⋅>D .2||||||BP BQ BA ⋅>10.(2022·全国·高考真题)已知O 为坐标原点,过抛物线2:2(0)C y px p =>焦点F 的直线与C 交于A ,B 两点,其中A 在第一象限,点(,0)M p ,若||||AF AM =,则( )A .直线AB 的斜率为B .||||OB OF =C .||4||AB OF >D .180OAM OBM ∠+∠<︒11.(2022·全国·高三专题练习)已知O 为坐标原点,抛物线E 的方程为214y x =,E 的焦点为F ,直线l 与E 交于A ,B 两点,且AB 的中点到x 轴的距离为2,则下列结论正确的是( )A .E 的准线方程为116y =- B .AB 的最大值为6C .若2AF FB =,则直线AB 的方程为1y x =+D .若OA OB ⊥,则AOB 面积的最小值为1612.(2023·全国·高三专题练习)已知抛物线Γ:()220x py p =>,过其准线上的点(),1T t -作的两条切线,切点分别为A ,B ,下列说法正确的是( ) A .2p =B .当1t =时,TA TB ⊥C .当1t =时,直线AB 的斜率为2D .TAB △面积的最小值为4三、填空题13.(2018·北京·高考真题(文))已知直线l 过点(1,0)且垂直于x 轴,若l 被抛物线24y ax =截得的线段长为4,则抛物线的焦点坐标为_________.14.(2023·全国·高三专题练习)已知抛物线C :26y x =的焦点为F ,A 为C 上一点且在第一象限,以F 为圆心,线段FA 的长度为半径的圆交C 的准线于M ,N 两点,且A ,F ,M 三点共线,则AF =______.15.(2020·山东·高考真题)已知抛物线的顶点在坐标原点,焦点F 与双曲线22221(0,0)x y a b a b-=>>的左焦点重合,若两曲线相交于M ,N 两点,且线段MN 的中点是点F ,则该双曲线的离心率等于______.16.(2021·北京·高考真题)已知抛物线24y x =的焦点为F ,点M 在抛物线上,MN 垂直x 轴与于点N .若6MF =,则点M 的横坐标为_______; MNF 的面积为_______.四、解答题17.(2017·北京·高考真题(理))已知抛物线C :y 2=2px 过点P (1,1).过点10,2⎛⎫⎪⎝⎭作直线l 与抛物线C 交于不同的两点M ,N ,过点M 作x 轴的垂线分别与直线OP ,ON 交于点A ,B ,其中O 为原点. (1)求抛物线C 的方程,并求其焦点坐标和准线方程; (2)求证:A 为线段BM 的中点.18.(2019·全国·高考真题(理))已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程; (2)若3AP PB =,求|AB |.19.(2019·北京·高考真题(理))已知抛物线C :x 2=−2py 经过点(2,−1). (Ⅰ)求抛物线C 的方程及其准线方程;(Ⅱ)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线y =−1分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点.20.(2022·全国·高考真题(理))设抛物线2:2(0)C y px p =>的焦点为F ,点(),0D p ,过F 的直线交C 于M ,N 两点.当直线MD 垂直于x 轴时,3MF =. (1)求C 的方程;(2)设直线,MD ND 与C 的另一个交点分别为A ,B ,记直线,MN AB 的倾斜角分别为,αβ.当αβ-取得最大值时,求直线AB 的方程.21.(2020·全国·高考真题(理))已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |.(1)求C 1的离心率;(2)设M 是C 1与C 2的公共点,若|MF |=5,求C 1与C 2的标准方程.22.(2021·全国·高考真题(文))已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为2.(1)求C 的方程;(2)已知O 为坐标原点,点P 在C 上,点Q 满足9PQ QF =,求直线OQ 斜率的最大值.专题9.5 抛物线(真题测试)一、单选题1.(2023·全国·高三专题练习)已知抛物线24y x =上一点M 到x 轴的距离是2,则点M 到焦点F 的距离为( )A B .2C .D .3【答案】B【分析】有题意可知()1,2M ±,由焦点(1,0)F 则可求出点M 到焦点F 的距离. 【详解】M 到x 轴的距离是2,可得()1,2M ±,焦点(1,0)F 则点M 到焦点的距离为2. 故选:B.2.(2023·全国·高三专题练习)抛物线21:4E y x =的焦点到其准线的距离为( ) A .18B .14C .2D .43.(2022·全国·高考真题(文))设F 为抛物线2:4C y x =的焦点,点A 在C 上,点(3,0)B ,若AF BF =,则AB =( )A .2B .C .3D .故选:B4.(2021·全国·高考真题)抛物线22(0)y px p =>的焦点到直线1y x =+,则p =( ) A .1 B .2 C.D .45.(2020·北京·高考真题)设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ l ⊥于Q ,则线段FQ 的垂直平分线( ).A .经过点OB .经过点PC .平行于直线OPD .垂直于直线OP【详解】如图所示:.故选:B.6.(2019·全国·高考真题(文))若抛物线y 2=2px (p >0)的焦点是椭圆2231x y pp+=的一个焦点,则p =( ) A .2B .3C .4D .87.(山东·高考真题(文))已知抛物线22(0)y px p =>,过其焦点且斜率为1的直线交抛物线于 ,A B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( ) A .1x = B .1x =- C .2x = D .2x=-8.(2017·全国·高考真题(理))已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,则|AB |+|DE |的最小值为( ) A .16 B .14C .12D .10二、多选题9.(2022·全国·高考真题)已知O 为坐标原点,点(1,1)A 在抛物线2:2(0)C x py p =>上,过点(0,1)B -的直线交C 于P ,Q 两点,则( ) A .C 的准线为1y =- B .直线AB 与C 相切 C .2|OP OQ OA ⋅> D .2||||||BP BQ BA ⋅>所以2212||||(1)||15BP BQ k x x k ⋅=+=+>,而2||5BA =,故D 正确.故选:BCD10.(2022·全国·高考真题)已知O 为坐标原点,过抛物线2:2(0)Cy px p =>焦点F 的直线与C 交于A ,B 两点,其中A 在第一象限,点(,0)M p ,若||||AF AM =,则( ) A .直线AB 的斜率为B .||||OB OF =C .||4||AB OF >D .180OAM OBM ∠+∠<︒33选项;由0OA OB ⋅<,0MA MB ⋅<求得,易得(,0)2p F ,由AF AM =3(4p OA OB ⋅=又(4p MA MB ⋅=-又360AOB AMB OAM OBM ∠+∠+∠+∠=,则180OAM OBM ∠+∠<,D 正确. 故选:ACD.11.(2022·全国·高三专题练习)已知O 为坐标原点,抛物线E 的方程为214y x =,E 的焦点为F ,直线l 与E 交于A ,B 两点,且AB 的中点到x 轴的距离为2,则下列结论正确的是( )A .E 的准线方程为116y =- B .AB 的最大值为6C .若2AF FB =,则直线AB 的方程为1y x =+D .若OA OB ⊥,则AOB 面积的最小值为16 ,联立抛物线,由2AF FB =解出A 即可求出面积最小值,即可判断D 选项.【详解】由2AF FB =得直线设直线AB 的方程为4A B x x =-.由于2AF FB =,所以22x =±,所以2124A A y x ==,直线AB 的方程为),y OA ⊥所以AOB 面积的是小值为故选:BCD.12.(2023·全国·高三专题练习)已知抛物线Γ:()220x py p =>,过其准线上的点(),1T t -作的两条切线,切点分别为A ,B ,下列说法正确的是( ) A .2p =B .当1t =时,TA TB ⊥C .当1t =时,直线AB 的斜率为2D .TAB △面积的最小值为4220x y ,故AB k C ,切线方程TA :的方程为1xt y -=-三、填空题13.(2018·北京·高考真题(文))已知直线l过点(1,0)且垂直于x轴,若l被抛物线24y ax=截得的线段长为4,则抛物线的焦点坐标为_________.14.(2023·全国·高三专题练习)已知抛物线C:26=的焦点为F,y xA为C上一点且在第一象限,以F为圆心,线段FA的长度为半径的圆交C的准线于M,N两点,且A,F,M三点共线,则AF=______.【答案】6【分析】根据圆的几何性质以及抛物线的定义即可解出.故答案为:6.15.(2020·山东·高考真题)已知抛物线的顶点在坐标原点,焦点F与双曲线22221(0,0)x ya ba b-=>>的左焦点重合,若两曲线相交于M,N两点,且线段MN的中点是点F,则该双曲线的离心率等于______.M在抛物线上,所以M在双曲线上,22cb=-故答案为:16.(2021·北京·高考真题)已知抛物线24y x=的焦点为F,点M在抛物线上,MN垂直x轴与于点N.若6MF=,则点M的横坐标为_______;MNF的面积为_______.FMNS.【FMNS=故答案为:四、解答题17.(2017·北京·高考真题(理))已知抛物线C:y2=2px过点P(1,1).过点10,2⎛⎫⎪⎝⎭作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.(1)求抛物线C的方程,并求其焦点坐标和准线方程;(2)求证:A为线段BM的中点.故A 为线段BM 的中点.18.(2019·全国·高考真题(理))已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程; (2)若3AP PB =,求|AB |. 利用3AP PB =可得y ()22,B x y 1252x x ∴+= 3AP PB = ∴则419AB =+⋅19.(2019·北京·高考真题(理))已知抛物线C :x 2=−2py 经过点(2,−1).(Ⅰ)求抛物线C的方程及其准线方程;(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=−1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.D p,过F的直线交C于20.(2022·全国·高考真题(理))设抛物线2=>的焦点为F,点(),0:2(0)C y px pMF=.M,N两点.当直线MD垂直于x轴时,3(1)求C 的方程;(2)设直线,MD ND 与C 的另一个交点分别为A ,B ,记直线,MN AB 的倾斜角分别为,αβ.当αβ-取得最大值时,求直线AB 的方程.21.(2020·全国·高考真题(理))已知椭圆C 1:22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=43|AB |.(1)求C 1的离心率;(2)设M 是C 1与C 2的公共点,若|MF |=5,求C 1与C 2的标准方程.)(),0F c ,的方程为x =21c=+,解得抛物线2C 的方程为24y cx =,联立24x c y cx=⎧⎨=⎩,43CD =即223c ac +01e <<,解得(2)[方法一由椭圆的第二定义知所以12-a22.(2021·全国·高考真题(文))已知抛物线2=>的焦点F到准线的距离为2.C y px p:2(0)(1)求C的方程;(2)已知O 为坐标原点,点P 在C 上,点Q 满足9PQ QF =,求直线OQ 斜率的最大值. ,则(99PQ QF ==-)09,10y ,由P 在抛物线上可得Q 的轨迹方程为的斜率0025OQ y k x ==(1,0),9=PQ QF ,所以29(1)9x y =-=-,所以的斜率为244=y x t 方法四利用参数法,由题可设()24,4(0),(,)>P t t t Q x y ,求得x,y 关于t 的参数表达式,得到直线OQ 的斜率关于t 的表达式,结合使用基本不等式,求得直线OQ 斜率的最大值.。
高考数学专题《抛物线》习题含答案解析

专题9.5 抛物线1.(2020·全国高考真题(理))已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =( ) A .2 B .3 C .6 D .9【答案】C 【解析】设抛物线的焦点为F ,由抛物线的定义知||122A p AF x =+=,即1292p=+,解得6p.故选:C.2.(2020·北京高三二模)焦点在x 轴的正半轴上,且焦点到准线的距离为4的抛物线的标准方程是( ) A .x 2=4y B .y 2=4x C .x 2=8y D .y 2=8x【答案】D 【解析】根据题意,要求抛物线的焦点在x 轴的正半轴上, 设其标准方程为22(0)y px p =>, 又由焦点到准线的距离为4,即p =4, 故要求抛物线的标准方程为y 2=8x , 故选:D.3.(全国高考真题)设F 为抛物线2:4C y x =的焦点,曲线()0ky k x=>与C 交于点P ,PF x ⊥轴,则k =( )A .12B .1C .32D .2【答案】D 【解析】由抛物线的性质可得(1,2)221kP y k ⇒==⇒=,故选D. 4.(2020·全国高考真题(文))设O 为坐标原点,直线2x =与抛物线C :22(0)y px p =>交于D ,E 两点,若OD OE ⊥,则C 的焦点坐标为( ) A .1,04⎛⎫⎪⎝⎭B .1,02⎛⎫ ⎪⎝⎭C .(1,0)D .(2,0)练基础【答案】B 【解析】因为直线2x =与抛物线22(0)y px p =>交于,E D 两点,且OD OE ⊥, 根据抛物线的对称性可以确定4DOx EOx π∠=∠=,所以()2,2D ,代入抛物线方程44p =,求得1p =,所以其焦点坐标为1(,0)2, 故选:B.5.(2019·四川高三月考(文))若抛物线22y px =的准线为圆2240x y x ++=的一条切线,则抛物线的方程为( ) A.216y x =- B.28y x =-C.216y x =D.24y x =【答案】C 【解析】∵抛物线22y px =的准线方程为x=2p-,垂直于x 轴. 而圆2240x y x ++=垂直于x 轴的一条切线为4x =-, 则42p=,即8p =. 故抛物线的方程为216y x =. 故选:C .6.(2019·北京高考真题(文))设抛物线y 2=4x 的焦点为F ,准线为l .则以F 为圆心,且与l 相切的圆的方程为__________. 【答案】(x -1)2+y 2=4. 【解析】抛物线y 2=4x 中,2p =4,p =2, 焦点F (1,0),准线l 的方程为x =-1, 以F 为圆心,且与l 相切的圆的方程为 (x -1)2+y 2=22,即为(x -1)2+y 2=4.7.(2019·山东高三月考(文))直线l 与抛物线22x y =相交于A ,B 两点,当AB 4=时,则弦AB 中点M 到x 轴距离的最小值为______. 【答案】32【解析】由题意,抛物线22x y =的焦点坐标为(0,12),根据抛物线的定义如图,所求d=111A B AF BF 113M 2222A B AB M ++--==≥= 故答案为:32. 8.(2021·沙湾县第一中学(文))设过抛物线y 2=4x 的焦点F 的直线交抛物线于A ,B 两点,且直线AB 的倾斜角为4π,则线段AB 的长是____,焦点F 到A ,B 两点的距离之积为_________.【答案】8 8 【分析】由题意可得直线AB 的方程为1y x =-,然后将直线方程与抛物线方程联立方程组,消去y 后,利用根与系数的关系,结合抛物线的定义可求得答案 【详解】解:由题意得(1,0)F ,则直线AB 的方程为1y x =-,设1122(,),(,)A x y B x y ,由241y x y x ⎧=⎨=-⎩,得2610x x -+=, 所以12126,1x x x x +==, 所以12628AB x x p =++=+=,因为11221,122=+=+=+=+p pAF x x BF x x , 所以()()1212121116118AF BF x x x x x x ⋅=+⋅+=+++=++=, 故答案为:8,89.(2021·全国高三专题练习)已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点(),3A m -到焦点F 的距离为5,则m 的值为__________;抛物线方程为__________. 【答案】答案见解析 答案见解析 【分析】由于抛物线的开口方向未定,根据点(),3A m -在抛物线上这一条件,抛物线开口向下,向左、向右均有可能,以此分类讨论,利用焦半径公式列方程可得p 的值,根据点(),3A m -在抛物线上可得m 的值. 【详解】根据点(),3A m -在抛物线上,可知抛物线开口向下,向左、向右均有可能, 当抛物线开口向下时,设抛物线方程为22x py =-(0p >), 此时准线方程为2py =,由抛物线定义知(3)52p --=,解得4p =.所以抛物线方程为28x y ,这时将(),3A m -代入方程得m =±当抛物线开口向左或向右时,可设抛物线方程为22y ax (0a ≠),从p a =知准线方程为2ax =-,由题意知()25232am am⎧+=⎪⎨⎪-=⎩,解此方程组得11192a m =⎧⎪⎨=⎪⎩,22192a m =-⎧⎪⎨=-⎪⎩,33912a m =⎧⎪⎨=⎪⎩,44912a m =-⎧⎪⎨=-⎪⎩,综合(1)、(2)得92m =,22y x =; 92m =-,22y x =-;12m =,218y x =; 12m =-,218y x =-;m =±28xy .故答案为:92,92-,12,12-,±22y x =,22y x =-,218y x =,218y x =-,28x y .10.(2019·广东高三月考(理))已知F 为抛物线2:4T x y =的焦点,直线:2l y kx =+与T 相交于,A B 两点.()1若1k =,求FA FB +的值;()2点(3,2)C --,若CFA CFB ∠=∠,求直线l 的方程.【答案】(1)10(2)3240x y +-= 【解析】(1)由题意,可得()0,1F ,设221212,,,44x x A x B x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,联立方程组224y kx x y=+⎧⎨=⎩,整理得2480x kx --=,则124x x k +=,128x x =-,又由22121144x x FA FB +++=+()2121222104x x x x +-=+=.(2)由题意,知211,14x FA x ⎛⎫=- ⎪⎝⎭,222,14x FB x ⎛⎫=- ⎪⎝⎭,()3.3FC =--, 由CFA CFB ∠=∠,可得cos ,cos ,FA FC FB FC =又2114x FA =+,2214x FB =+,则FA FC FB FC FA FC FB FC =, 整理得()1212420x x x x ++-=,解得32k =-, 所以直线l 的方程为3240x y +-=.1.(2021·吉林长春市·高三(理))已知M 是抛物线24y x =上的一点,F 是抛物线的焦点,若以Fx 为始边,FM 为终边的角60xFM ∠=,则FM 等于( ) A .2 B C .D .4【答案】D 【分析】设点200,4y M y ⎛⎫ ⎪⎝⎭,取()1,0a =,可得1cos ,2FM a <>=,求出20y 的值,利用抛物线的定义可求练提升得FM 的值. 【详解】设点()00,M x y ,其中2004y x =,则()1,0F ,2001,4y FM y ⎛⎫=- ⎪⎝⎭,取()1,0a =,则211cos ,2y FM a FM a FM a-⋅<>===⋅⎛,可得4200340480y y -+=,因为20104y ->,可得204y >,解得2012y =,则20034y x ==,因此,014MF x=+=. 故选:D.2.(2017·全国高考真题(文))过抛物线2:4C y x =的焦点F 的直线交C 于点M (在x 轴上方),l 为C 的准线,点N 在l 上且MNl ⊥,则点M 到直线NF 的距离为()A. B. D.【答案】A 【解析】设直线l 与x 轴相交于点P ,与直线MN 相交于点Q ,(1,0)F ,设||||MN MF m ==,因为||2,30PF NQM =∠=,所以||4,||2QF QM m ==, 所以42m m +=,解得:4m =,设00(,)M x y ,由焦半径公式得:014x +=, 所以03x=,0y =,所以sin sin 42NP MNF NFP NF ∠=∠===,所以点M 到直线NF 的距离为||sin 4NM MNF ⋅∠=⋅=3.(2020·广西南宁三中其他(理))已知抛物线28C y x =:的焦点为F ,P 是抛物线C 的准线上的一点,且P 的纵坐标为正数,Q 是直线PF 与抛物线C 的一个交点,若PQ =,则直线PF 的方程为( )A .20x y --=B .20x y +-=C .20x y -+=D .20x y ++=【答案】B 【解析】过Q 点作QH PM ⊥于H ,因为PQ =,由抛物线的定义得PQ =,所以在Rt PQH ∆中,4PQH π∠=,所以4PFM π∠=,所以直线PF 的斜率为1k =-,所以直线PF 的方程为()()012y x -=--, 即20x y +-=, 故选B.4.(2020·浙江高三月考)如图,已知抛物线21:4C y x =和圆222:(1)1C x y -+=,直线l 经过1C 的焦点F ,自上而下依次交1C 和2C 于A ,B ,C ,D 四点,则AB CD ⋅的值为( )A .14B .12C .1D .2【答案】C 【解析】因为抛物线21:4C y x =的焦点为(1,0)F ,又直线l 经过1C 的焦点F ,设直线:(1)l y k x =-,由24(1)y x y k x ⎧=⎨=-⎩得2222(24)0k x k x k -++=, 设1122(,),(,)A x y B x y ,则121=x x由题意可得:1111=-=+-=AB AF BF x x , 同理2=CD x ,所以12cos01︒⋅=⋅⋅==AB CD AB CD x x . 故选C5.【多选题】(2022·全国高三专题练习)已知抛物线21:C y mx =与双曲线222:13y C x -=有相同的焦点,点()02,P y 在抛物线1C 上,则下列结论正确的有( )A .双曲线2C 的离心率为2B .双曲线2C 的渐近线为y x = C .8m =D .点P 到抛物线1C 的焦点的距离为4【答案】ACD 【分析】由双曲线方程写出离心率、渐近线及焦点,即可知A 、B 、C 的正误,根据所得抛物线方程求0y ,即知D 的正误. 【详解】双曲线2C 的离心率为2e ==,故A 正确;双曲线2C 的渐近线为y =,故B 错误; 由12,C C 有相同焦点,即24m=,即8m =,故C 正确; 抛物线28y x =焦点为()2,0,点()02,P y 在1C 上,则04y =±,故()2,4P 或()2,4P -,所以P 到1C 的焦点的距离为4,故D 正确. 故选:ACD .6.【多选题】(2021·海南鑫源高级中学)在下列四个命题中,真命题为( )A .当a 为任意实数时,直线(a -1)x -y +2a +1=0恒过定点P ,则过点P 且焦点在y 轴上的抛物线的标准方程是243x y =B .已知双曲线的右焦点为(5,0),一条渐近线方程为2x -y =0,则双曲线的标准方程为221205x y -= C .抛物线y =ax 2(a ≠0)的准线方程14y a=-D .已知双曲线2214x y m +=,其离心率()1,2e ∈,则m 的取值范围(-12,0)【答案】ACD 【分析】求出直线定点设出抛物方程即可判断A ;根据渐近线方程与焦点坐标求出,a b 即可判断B ;根据抛物线方程的准线方程公式即可判断C ;利用双曲线离心率公式即可判断D . 【详解】对A 选项,直线(a -1)x -y +2a +1=0恒过定点为()2,3P -,则过点P 且焦点在y 轴上的抛物线的标准方程设为22x py =,将点()2,3P -代入可得23p =,所以243x y =,故A 正确;对B 选项,知5,2bc a==,又22225a b c +==,解得225,20a b ==,所以双曲线的标准方程为221520x y -=,故B 错; 对C 选项,得21x y a =,所以准线方程14y a=-,正确;对D 选项,化双曲线方程为2214x y m-=-,所以()1,2e =,解得()12,0m ∈-,故正确.故选:ACD7.(2021·全国高二课时练习)已知点M 为抛物线2:2(0)C y px p =>上一点,若点M 到两定点(,)A p p ,,02p F ⎛⎫⎪⎝⎭的距离之和最小,则点M 的坐标为______.【答案】,2p p ⎛⎫⎪⎝⎭【分析】过点M 作抛物线准线的垂线,垂足为B ,根据抛物线的定义可得||||MF MB =, 易知当A ,B ,M 三点共线时||MB MA +取得最小值且为||AB ,进而可得结果. 【详解】过点M 作抛物线准线的垂线,垂足为B ,由抛物线的定义,知点M 到焦点,02p F ⎛⎫⎪⎝⎭的距离与点M 到准线的距离相等,即||||MF MB =,所以||||||||MF MA MB MA +=+, 易知当A ,B ,M 三点共线时,||MB MA +取得最小值, 所以min 3(||||)||2p MF MA AB +==,此时点M 的坐标为,2p p ⎛⎫⎪⎝⎭. 故答案为:2p p ⎛⎫⎪⎝⎭,8.(2021·全国高二课时练习)抛物线()220y px p =>的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足120AFB ∠=︒,过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N ,则MN AB的最大值为______.【分析】设=AF a ,=BF b ,根据中位线定理以及抛物线定义可得()12MN a b =+,在AFB △中,由余弦定理以及基本不等式可得)AB a b ≥+,即可求得MN AB 的最大值.【详解】设=AF a ,=BF b ,作AQ 垂直抛物线的准线于点Q ,BP 垂直抛物线的准线于点P .由抛物线的定义,知AF AQ =,BF BP =.由余弦定理得()2222222cos120AB a b ab a b ab a b ab =+=︒=++=+-.又22a b ab +⎛⎫≤ ⎪⎝⎭,∴()()()()22221344a b ab a b a b a b +-≥+-+=+,当且仅当a b =时,等号成立,∴)AB a b ≥+,∴()1a b MN AB +≤=MN AB9.(2020·山东济南外国语学校高三月考)抛物线C :22y x =的焦点坐标是________;经过点()4,1P 的直线l 与抛物线C 相交于A ,B 两点,且点P 恰为AB 的中点,F 为抛物线的焦点,则AF BF +=________.【答案】1,02⎛⎫⎪⎝⎭9【解析】抛物线C :22y x =的焦点1,02F ⎛⎫⎪⎝⎭. 过A 作AM ⊥准线交准线于M ,过B 作BN ⊥准线交准线于N ,过P 作PK ⊥准线交准线 于K ,则由抛物线的定义可得AM BN AF BF +=+. 再根据P 为线段AB 的中点,119(||||)||4222AM BN PK +==+=, ∴9AF BF +=,故答案为:焦点坐标是1,02⎛⎫ ⎪⎝⎭,9AF BF +=.10.(2019·四川高考模拟(文))抛物线C :()220x py p =>的焦点为F ,抛物线过点(),1P p .(Ⅰ)求抛物线C 的标准方程与其准线l 的方程;(Ⅱ)过F 点作直线与抛物线C 交于A ,B 两点,过A ,B 分别作抛物线的切线,证明两条切线的交点在抛物线C 的准线l 上.【答案】(Ⅰ)抛物线的标准方程为24x y =,准线l 的方程为1y =-;(Ⅱ)详见解析. 【解析】(Ⅰ)由221p p =⨯,得2p =,所以抛物线的标准方程为24x y =,准线l 的方程为1y =-.(Ⅱ)根据题意直线AB 的斜率一定存在,又焦点()0,1F ,设过F 点的直线方程为1y kx =+,联立241x yy kx ⎧=⎨=+⎩,得,2440x kx --=. 设()11,A x y ,()22,B x y ,则124x x k +=,124x x =-.∴()22221212122168x x x x x x k +=+-=+.由214y x =得,1'2y x =,过A ,B 的抛物线的切线方程分别为 ()()1112221212y y x x x y y x x x ⎧-=-⎪⎪⎨⎪-=-⎪⎩, 即21122211241124y x x x y x x x ⎧=-⎪⎪⎨⎪=-⎪⎩,两式相加,得()()2212121148y x x x x x =+-+,化简,得()221y kx k =-+,即()21y k x k =--, 所以,两条切线交于点()2,1k -,该点显然在抛物线C 的准线l :1y =-上.1.(2021·全国高考真题)抛物线22(0)y px p =>的焦点到直线1y x =+,则p =( ) A .1 B .2 C .D .4【答案】B 【分析】首先确定抛物线的焦点坐标,然后结合点到直线距离公式可得p 的值. 【详解】抛物线的焦点坐标为,02p ⎛⎫ ⎪⎝⎭,其到直线10x y -+=的距离:d == 解得:2p =(6p =-舍去). 故选:B.2.(2021·天津高考真题)已知双曲线22221(0,0)x y a b a b-=>>的右焦点与抛物线22(0)y px p =>的焦点重合,抛物线的准线交双曲线于A ,B 两点,交双曲线的渐近线于C 、D 两点,若|CD AB .则双曲线的离心率为( ) A B C .2D .3练真题【答案】A 【分析】设公共焦点为(),0c ,进而可得准线为x c =-,代入双曲线及渐近线方程,结合线段长度比值可得2212a c =,再由双曲线离心率公式即可得解. 【详解】设双曲线22221(0,0)x y a b a b-=>>与抛物线22(0)y px p =>的公共焦点为(),0c ,则抛物线22(0)y px p =>的准线为x c =-,令x c =-,则22221c ya b-=,解得2b y a =±,所以22b AB a =, 又因为双曲线的渐近线方程为b y x a =±,所以2bcCD a=,所以2bc a c ,所以222212a cbc =-=,所以双曲线的离心率ce a== 故选:A.3.(2020·北京高考真题)设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ l ⊥于Q ,则线段FQ 的垂直平分线( ). A .经过点O B .经过点P C .平行于直线OP D .垂直于直线OP【答案】B 【解析】如图所示:.因为线段FQ 的垂直平分线上的点到,F Q 的距离相等,又点P 在抛物线上,根据定义可知,PQ PF =,所以线段FQ 的垂直平分线经过点P .故选:B.4.(2021·全国高考真题)已知O 为坐标原点,抛物线C :22y px =(0p >)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ OP ⊥,若6FQ =,则C 的准线方程为______. 【答案】32x =-【分析】先用坐标表示P Q ,,再根据向量垂直坐标表示列方程,解得p ,即得结果. 【详解】抛物线C :22y px = (0p >)的焦点,02p F ⎛⎫⎪⎝⎭,∵P 为C 上一点,PF 与x 轴垂直, 所以P 的横坐标为2p,代入抛物线方程求得P 的纵坐标为p ±, 不妨设(,)2pP p ,因为Q 为x 轴上一点,且PQ OP ⊥,所以Q 在F 的右侧, 又||6FQ =, (6,0),(6,)2pQ PQ p ∴+∴=- 因为PQ OP ⊥,所以PQ OP ⋅=2602pp ⨯-=, 0,3p p >∴=,所以C 的准线方程为32x =-故答案为:32x =-.5.的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则AB =________.【答案】163【解析】∵抛物线的方程为24y x =,∴抛物线的焦点F 坐标为(1,0)F ,又∵直线AB 过焦点F AB 的方程为:1)y x =- 代入抛物线方程消去y 并化简得231030x x -+=, 解法一:解得121,33x x ==所以12116||||3|33AB x x =-=-= 解法二:10036640∆=-=> 设1122(,),(,)A x y B x y ,则12103x x +=, 过,A B 分别作准线1x =-的垂线,设垂足分别为,C D 如图所示.12||||||||||11AB AF BF AC BD x x =+=+=+++1216+2=3x x =+故答案为:1636.(2020·浙江省高考真题)如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C 与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于M (B ,M 不同于A ).(Ⅰ)若116=p ,求抛物线2C 的焦点坐标; (Ⅱ)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值.【答案】(Ⅰ)1(,0)32;【解析】 (Ⅰ)当116=p 时,2C 的方程为218y x =,故抛物线2C 的焦点坐标为1(,0)32;(Ⅱ)设()()()112200,,,,,,:A x y B x y M x y I x y m λ=+,由()22222222220x y y my m x y mλλλ⎧+=⇒+++-=⎨=+⎩, 1200022222,,222m m my y y x y m λλλλλλ--∴+===+=+++, 由M 在抛物线上,所以()222222244222m pm mp λλλλλ=⇒=+++, 又22222()220y pxy p y m y p y pm x y mλλλ⎧=⇒=+⇒--=⎨=+⎩, 012y y p λ∴+=,2101022x x y m y m p m λλλ∴+=+++=+,2122222mx p m λλ∴=+-+.由2222142,?22x y x px y px ⎧+=⎪⇒+=⎨⎪=⎩即2420x px +-=12x p ⇒==-222221822228162p p p m p p p λλλλλ+⇒-=+⋅=++≥+,18p ≥,21160p ≤,p ≤ 所以,p,此时A . 法2:设直线:(0,0)l x my t m t =+≠≠,()00,A x y .将直线l 的方程代入椭圆221:12x C y +=得:()2222220m y mty t +++-=,所以点M 的纵坐标为22M mty m =-+.将直线l 的方程代入抛物线22:2C y px =得:2220y pmy pt --=,所以02M y y pt =-,解得()2022p m y m+=,因此()220222p m xm+=,由220012x y +=解得22212242160m m p m m ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,所以当m t ==p .。
抛物线基础练习(有解析)

一、选择题(共 8 小题;共 40 分)
1. 抛物线 A.
68 上一点 的纵坐标为 6,则点 与抛物线焦点的距离为
B.
C. 6
D.
2. 设抛物线 :8 A. 6
3. 若抛物线 8 A.
6 上一点 到 8 轴的距离为 6,则点 到抛物线 的焦点的距离是
B.
C.
D.
的焦点与椭圆 8 t 的右焦点重合,则 的值为
,
则 8 t,将 8 t 代入椭圆 8
t
将 t 代入抛物线方程,t
解得: t.
6
13.
h
t t㌳
t,解得: ,
【解析】抛物线 8 6㌳ ㌳ h 的标准方程为:
所以抛物线的焦点坐标为: h t .
t㌳
14. t
,
t 6㌳
8,
轴,所以 t ,所
第三部分
15. (1) 由题意,抛物线的准线为
抛物线的方程为 8 6 .
所以 t
t
8t
8
8t 8
t 7. C 8. A 第二部分 9. (1) ,(2) ,(3)√,(4) ,(5)√
10. 【解析】依题意,点 为坐标原点,
第 3页(共 4 页)
所以 t,即
.
11.
【解析】由题意知 t h ,又因为曲线 8
t h 与 交于点 ,
以
,解得
.
t
12. t
6
【解析】设 8 t h 8 t h ,由
(2)过 作直线 ,使 与 只ห้องสมุดไป่ตู้一个公共点,求 的方程.
h h t h 到 的距离
16. 已知抛物线 8
的焦点为 ,点 是抛物线上的动点,又有点
初三抛物线试题大全及解析

初三抛物线试题大全及解析一、抛物线的基本概念抛物线是一种重要的几何图形,它在中考数学试题中占有重要地位。
抛物线通常由一条直线和一个二次曲线组成,它可以用来描述一些常见的数学问题,如二次函数、几何问题等。
二、抛物线试题类型1. 已知抛物线解析式求未知量2. 抛物线的性质与应用3. 抛物线的形状与开口方向、对称轴、顶点坐标的关系4. 抛物线与方程的综合题5. 与抛物线有关的实际问题三、抛物线试题解析【例1】(基础题)已知抛物线解析式为y=x²-2x-3,请回答下列问题:(1)求该抛物线的开口方向、对称轴和顶点坐标;(2)当x在什么范围内时,y随x的增大而增大?【解析】(1)因为a=1>0,所以抛物线开口向上。
对称轴为直线x=-b/2a=-(-2)/2=1,顶点坐标为(1,-4)。
(2)因为对称轴为直线x=1,且开口向上,所以当x>1时,y随x的增大而增大。
【例2】(提高题)已知二次函数y=ax²+bx+c的图像经过A(1,0),B(0,-6),C(2,-4)三点,求这个二次函数的解析式。
【解析】由题意可设y=ax²+bx-6,把C(2,-4)代入得4a+2b-6=-4,即b-a=1。
再由点A(1,0)在抛物线上可求c值,即可得到二次函数的解析式。
【答案】解:由题意可设y=ax²+bx-6。
把C(2,-4)代入得4a+2b-6=-4,即b-a=1。
又因为图像经过A(1,0),B(0,-6),所以y=x²+x-6。
【例3】(压轴题)已知二次函数y=ax²+bx+c的图像经过A(0,5),B(1,3),C(-2,7)三点。
求这个二次函数的解析式和图像的对称轴。
【解析】这道题需要用到待定系数法。
首先根据条件确定系数可能取到的值,再代入求出解析式。
然后根据对称性求出对称轴。
【答案】设这个二次函数的解析式为y=a(x-h)²+k,将A(0,5),B(1,3),C(-2,7)三点代入得{c=5a+b+c=39a−2a+k=7解得{a=2k=5∴y=2(x−1)2+3图像的对称轴为直线x=1。
抛物线课件及练习题含详解

为 y k(x p).
2
又因为A,B两点是直线AB与抛物线的交点,则
y k(x y2 2px
p ), 2
x2
(
2p k2
p)x
p2 4
0,
所以x1·x2=p2 .
4
由|AF|·|BF|=
x1
x2
p 2
x1
x
2
p2 4
1. 3
得 p2 p (4 p) 1 ,
2 23
3
即 2p 所1 ,以 p 1 ,
2p y21p2y1y1y1 y2
x
x1
,
= 2p x y1y2 2p (x y1y2 ),
y1 y2 y1 y2 y1 y2
2p
将y1·y2=-4p2代入上式得y 2p x 2p,
y1 y2
故直线AB恒过定点(2p,0).
【方法技巧】利用抛物线的性质可以解决的问题 (1)对称性:解决抛物线的内接三角形问题. (2)焦点、准线:解决与抛物线的定义有关的问题. (3)范围:解决与抛物线有关的最值问题. (4)焦点:解决焦点弦问题.
|AF|=1,|BF|= 1,求抛物线及直线AB的方程.
3
【解题指南】设出A,B两点的坐标,根据抛物线定义可分别表
示出|AF|和|BF|,进而可求得|AF|+|BF|,求得x1+x2的表达
式,表示出|AF|·|BF|,建立等式求得p,则抛物线方程可得.
再由|AB|=
2p sin 2
得4, sin2θ=
(2)y2=2px(p>0)的焦点为( p,0),由题意得
2
( p 2)2 解9 得 5p,=4或p=-12(舍去).
2
2022版新高考数学一轮复习专题限时练习:54 抛物线 (含解析)

2022年新高考数学专题限时练习(五十四) 抛物线建议用时:40分钟一、选择题1.点M (5,3)到抛物线y =ax 2的准线的距离为6,那么抛物线的标准方程是( )A .x 2=112y B .x 2=112y 或x 2=-136y C .x 2=-136yD .x 2=12y 或x 2=-36yD [将y =ax 2化为x 2=1a y .当a >0时,准线y =-14a ,则3+14a =6,∴a =112. 当a <0时,准线y =-14a ,则⎪⎪⎪⎪⎪⎪3+14a =6,∴a =-136.∴抛物线方程为x 2=12y 或x 2=-36y .]2.(2020·泰安模拟)已知抛物线E :y 2=2px (p >0)的焦点为F ,O 为坐标原点,OF 为菱形OBFC 的一条对角线,另一条对角线BC 的长为2,且点B ,C 在抛物线E 上,则p =( )A .1B . 2C .2D .2 2B [由题意,⎝ ⎛⎭⎪⎫p 4,1在抛物线上,代入抛物线方程可得1=p 22,∵p >0,∴p =2,故选B.]3.(2020·北京高考)设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ ⊥l 于Q ,则线段FQ 的垂直平分线( )A .经过点OB .经过点PC.平行于直线OP D.垂直于直线OPB[如图所示:因为线段FQ的垂直平分线上的点到F,Q的距离相等,又点P在抛物线上,根据定义可知,|PQ|=|PF|,所以线段FQ的垂直平分线经过点P.故选B.]4.(多选)(2020·辽宁锦州月考)以下四个命题中,真命题的序号是()①平面内到两定点距离之比等于常数λ(λ≠1)的点的轨迹是圆;②平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹方程为x24-y25=1;③点P是抛物线x2=4y上的动点,点P在x轴上的射影是M,点A的坐标是A(1,0),则|P A|+|PM|的最小值是2+1;④已知点P为抛物线y2=4x上一个动点,点Q为圆x2+(y-4)2=1上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是17-1.A.①B.②C.③D.④AD[对于①,平面内到两定点的距离之比为定值(不等于1)的点的轨迹是圆,这个圆被称为阿波罗尼斯圆,所以①正确;对于②,根据题意,结合双曲线的定义,可知题中点的轨迹是双曲线的一支,所以②错误;对于③,根据题意,结合抛物线的定义,可求得|P A|+|PM|的最小值应为2-1,所以③错误;对于④,根据抛物线的定义,可知抛物线上的点到焦点的距离和到准线的距离是相等的,将其转化为到焦点的距离,结合圆的相关性质可知④是正确的.]5.(多选)(2020·山东胶州一中月考)已知抛物线y2=4x上一点P到准线的距离为d1,到直线l:4x-3y+11=0的距离为d2,则d1+d2的取值可以为()A.3 B.4C. 5 D.10ABD[抛物线上的点P到准线的距离等于到焦点F(1,0)的距离,过焦点F作直线4x-3y+11=0的垂线,则F到直线的距离为d1+d2的最小值,如图所示:所以(d1+d2)min=|4-0+11|42+(-3)2=3,故选ABD.]6.(2020·江西萍乡一模)已知抛物线C:y2=2px(p>0)的焦点为F,准线l:x =-1,点M在抛物线C上,点M在直线l:x=-1上的射影为A,且直线AF的斜率为-3,则△MAF的面积为()A. 3 B.2 3C.4 3 D.8 3C[如图所示,设准线l与x轴交于点N.则|FN|=2.∵直线AF的斜率为-3,∴∠AFN=60°.∴∠MAF=60°,|AF|=4.由抛物线的定义可得|MA|=|MF|,∴△AMF是边长为4的等边三角形.∴S△AMF=34×42=4 3.故选C.]二、填空题7.已知抛物线C:y2=2px(p>0)的焦点为F(2,0),则抛物线C的方程是________;若M是C上一点,FM的延长线交y轴于点N,且M为FN的中点,则|FN|=________.y2=8x6[抛物线C:y2=2px(p>0)的焦点为F(2,0),可得p=4,则抛物线C的方程是y2=8x.由M为FN的中点,得M的横坐标为1,代入抛物线方程得y =±22,则M(1,±22),则点N的坐标为(0,±42),所以|FN|=22+(42)2=6.]8.如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽________米.26[建立平面直角坐标系如图所示,设抛物线方程为x2=-2py(p>0).由题意可知抛物线过点(2,-2),故4=4p,∴p=1,∴x2=-2y.故当y=-3时,x2=6,即x= 6.所以当水位降1米后,水面宽26米.]9.已知抛物线y2=4x的焦点为F,过点F作一条直线交抛物线于A,B两点.若|AF|=3,则|BF|=________.32[法一:由题意可知F(1,0),设A(x A,y A),B(x B,y B),点A在第一象限,则|AF|=x A+1=3,所以x A=2,y A=22,所以直线AB的斜率为k=222-1=2 2.则直线AB的方程为y=22(x-1),与抛物线方程联立整理得2x 2-5x +2=0,x A +x B =52, 所以x B =12,所以|BF |=12+1=32.法二:由1|AF |+1|BF |=2p 可知1|BF |=1-13=23, ∴|BF |=32.] 三、解答题10.如图,抛物线的顶点在原点,圆(x -2)2+y 2=4的圆心恰是抛物线的焦点.(1)求抛物线的方程;(2)一条直线的斜率等于2,且过抛物线焦点,它依次截抛物线和圆于A ,B ,C ,D 四点,求|AB |+|CD |的值.[解] (1)设抛物线方程为y 2=2px (p >0), ∵圆(x -2)2+y 2=22的圆心恰是抛物线的焦点, ∴p =4.∴抛物线的方程为y 2=8x .(2)依题意直线AB 的方程为y =2x -4, 设A (x 1,y 1),D (x 2,y 2),则⎩⎪⎨⎪⎧y =2x -4,y 2=8x ,得x 2-6x +4=0,∴x 1+x 2=6,|AD |=x 1+x 2+p =6+4=10. |AB |+|CD |=|AD |-|CB |=10-4=6.11.如图,已知点F 为抛物线E :y 2=2px (p >0)的焦点,点A (2,m )在抛物线E 上,且|AF |=3.(1)求抛物线E 的方程;(2)已知点G (-1,0),延长AF 交抛物线E 于点B ,证明:GF 为∠AGB 的平分线.[解] (1)由抛物线定义可得|AF |=2+p2=3,解得p =2.∴抛物线E 的方程为y 2=4x .(2)证明:∵点A (2,m )在抛物线E 上,∴m 2=4×2,解得m =±22,由抛物线的对称性,不妨设A (2,22),由A (2,22),F (1,0),∴直线AF 的方程为y =22(x -1),由⎩⎪⎨⎪⎧y =22(x -1),y 2=4x ,得2x 2-5x +2=0,解得x =2或12,∴B ⎝ ⎛⎭⎪⎫12,-2.又G (-1,0),∴k GA =223,k GB =-223, ∴k GA +k GB =0,∴∠AGF =∠BGF . ∴GF 为∠AGB 的平分线.1.已知P 是抛物线y 2=4x 上的一个动点,Q 是圆(x -3)2+(y -1)2=1上的一个动点,N (1,0)是一个定点,则|PQ |+|PN |的最小值为( )A .3B .4C .5D .2+1A [由抛物线方程y 2=4x ,可得抛物线的焦点F (1,0),又N (1,0),所以N 与F 重合.过圆(x -3)2+(y -1)2=1的圆心M 作抛物线准线的垂线MH ,交圆于Q ,交抛物线于P ,则|PQ |+|PN |的最小值等于|MH |-1=3.]2.(2020·济宁三模)已知抛物线C :y 2=4x 的焦点为F ,过点F 的直线与抛物线C 的两个交点分别为A ,B ,且满足AF→=2FB →,E 为AB 的中点,则点E 到抛物线准线的距离为( )A .114B .94C .52D .54B [由题意得抛物线y 2=4x 的焦点坐标为(1,0),准线方程为x =-1,设 A (x 1,y 1),B (x 2,y 2),∵AF →=2FB →,∴|AF |=2|BF |,∴x 1+1=2(x 2+1), ∴x 1=2x 2+1,∵|y 1|=2|y 2|,∴y 21=4y 22,∴x 1=4x 2,∴x 1=2,x 2=12.∴线段AB 的中点到该抛物线准线的距离为12[(x 1+1)+(x 2+1)]=94.故选B.] 3.已知点A (m,4)(m >0)在抛物线x 2=4y 上,过点A 作倾斜角互补的两条直线l 1和l 2,且l 1,l 2与抛物线的另一个交点分别为B ,C .(1)求证:直线BC 的斜率为定值;(2)若抛物线上存在两点关于BC 对称,求|BC |的取值范围. [解] (1)证明:∵点A (m,4)在抛物线上, ∴16=m 2,∴m =±4, 又m >0,∴m =4. 设B (x 1,y 1),C (x 2,y 2),则k AB +k AC =x 1+44+x 2+44=x 1+x 2+84=0,∴x 1+x 2=-8.∴k BC =y 2-y 1x 2-x 1=x 22-x 214(x 2-x 1)=x 1+x 24=-2,∴直线BC 的斜率为定值-2.(2)设直线BC 的方程为y =-2x +b ,P (x 3,y 3),Q (x 4,y 4)关于直线BC 对称,设PQ 的中点为M (x 0,y 0),则k PQ =y 4-y 3x 4-x 3=x 3+x 44=x 02=12,∴x 0=1.∴M (1,-2+b ). 又点M 在抛物线内部, ∴-2+b >14,即b >94.由⎩⎪⎨⎪⎧y =-2x +b ,x 2=4y ,得x 2+8x -4b =0, ∴x 3+x 4=-8,x 3x 4=-4b . ∴|BC |=1+4|x 3-x 4|=5·(x 3+x 4)2-4x 3x 4 =5×64+16b .又b >94,∴|BC |>10 5.∴|BC |的取值范围为(105,+∞).1.(多选)(2020·黑龙江大庆一中月考)如图,过抛物线y 2=8x 的焦点F ,斜率为k 的直线l 与抛物线交于A ,B 两点,与抛物线准线交于C 点,若B 是AC 的中点,则( )A .k =±2 B .k =±2 2 C .|AB |=9D .|AB |=10BC [如图,设A ,B 在准线上的射影分别为D ,E ,连接AD ,BE ,设AB =BC =m ,直线l 的倾斜角为α,则|BE |=m |cos α|,所以|AD |=|AF |=|AB |-|BF |=|AB |-|BE |=m (1-|cos α|),|cos α|=|AD ||AC |=m (1-|cos α|)2m ,解得|cos α|=13,所以|sin α|=1-⎝ ⎛⎭⎪⎫132=223,故|k |=|tan α|=2 2.由抛物线焦点弦的弦长公式|AB |=2p sin 2α可得|AB |=81-19=9.综上,选BC. 或:由|cos α|=13得tan α=±22,可得直线方程.设A (x A ,y A ),B (x B ,y B ),将直线方程与抛物线方程联立,进而可解得x A +x B =5,于是|AB |=x A +x B +4=9.故选BC.]2.(2020·静安区二模)已知抛物线Γ:y 2=4x 的焦点为F ,若△ABC 的三个顶点都在抛物线Γ上,且F A →+FB→+FC →=0,则称该三角形为“核心三角形”. (1)是否存在“核心三角形”,其中两个顶点的坐标分别为(0,0)和(1,2)?请说明理由;(2)设“核心三角形”ABC 的一边AB 所在直线的斜率为4,求直线AB 的方程;(3)已知△ABC 是“核心三角形”,证明:点A 的横坐标小于2. [解] (1)抛物线Г:y 2=4x 的焦点为F (1,0),由F A →+FB →+FC →=0,得1=x A +x B +x C 3,0=y A +y B +y C3,故第三个顶点的坐标为3(1,0)-(0,0)-(1,2)=(2,-2),但点(2,-2)不满足抛物线的方程,即点(2,-2)不在抛物线上,所以这样的“核心三角形”不存在.(2)设直线AB 的方程为y =4x +t ,与y 2=4x 联立,可得y 2-y +t =0, 设A (x 1,y 1),B (x 2,y 2),C (x 3,y 3), y 1+y 2=1,x 1+x 2=14(y 1+y 2-2t )=14-12t , 由(x 1+x 2+x 3,y 1+y 2+y 3)=(3,0), 可得x 3=12t +114,y 3=-1, 代入方程y 2=4x ,可得11+2t =1, 解得t =-5,所以直线AB 的方程为4x -y -5=0.(3)证明:设直线BC 的方程为x =ny +m ,与y 2=4x 联立,可得y 2-4ny -4m =0,因为直线BC 与抛物线相交,故判别式Δ=16(n 2+m )>0,y 1+y 2=4n , 所以x 1+x 2=n (y 1+y 2)+2m =4n 2+2m , 可得点A 的坐标为(-4n 2-2m +3,-4n ), 又因为A 在抛物线上,故16n2=-16n2-8m+12,可得m=-4n2+3,2,因为m>-n2,所以n2<12故A的横坐标为-4n2-2m+3=-4n2+8n2=4n2<2.。
初中抛物线经典练习题(含详细答案)

初中数学抛物线经典试题集锦【编著】黄勇权【第一组题型】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
3、在平面直角坐标系xOy中,已知抛物线的顶点C为(2,4),并在x轴上截得的长度为6。
(1)写出抛物线与x轴交点A、B的坐标(2)求该抛物线的表达式(3)写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4,交x轴于点A,交y轴于点B,若以A 为顶点,,且开口向下作抛物线,交直线AB于点D,交y轴负半轴于点C,(1)若△ABC的面积为20,求此时抛物线的解析式(2)若△BDO的面积为8,求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
解:【第一问】因为函数y=x²+bx+c过点A(2,0),C(0, -8)分别将x=2,y=0代入y=x²+bx+c,得0=4+2b+c-----①将x=0,y=-8代入y=x²+bx+c,得-8=c-------------②将②代入①,解得:b=2--------------------------------------③此时,将②③代入y=x²+bx+c,所以:二次函数的解析式y=x²+ 2x -8【第二问】△ABP的面积= 12│AB│*│y p│----------------------④因为A、B两点在x轴上,令x²+ 2x -8=0(x-2)(x+4)=0解得:x1=2,x2= -4所以:│AB│=│X1- X2│=│2-(- 4)│=6------⑤又△ABP的面积=15-------------------------------------⑥由④⑤⑥,得:12*6*│y p│=15│y p│=5 故有:y p= ±5即:p点的纵坐标为5或-5.把y=5代入y=x²+ 2x -8,即:5=x²+ 2x -8x²+ 2x -13=0解得:x= -1± 14那么,此时p点坐标(-1+ 14,5),(-1- 14,5)-------⑦把y=-5代入y=x²+ 2x -8,即:-5=x²+ 2x -8x²+ 2x -3=0(x-1)(x+3)=0解得:x= 1或x= -3那么,此时p点坐标(1,-5),(-3,-5)------------------⑧由⑦⑧得,使△ABP的面积为15,p点坐标是:(-1+ 14,5),(-1- 14,5),(1,-5),(-3,-5)2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
抛物线的方程及性质(分层练习)

抛物线的方程及性质(分层练习)[基础训练]1.[2020福建厦门一模]若抛物线x 2=ay 的焦点到准线的距离为1,则a =( )A .2B .4C .±2D .±4答案:C 解析:∵x 2=ay =2·a2·y ,∴p =⎪⎪⎪⎪⎪⎪a 2=1,∴a =±2,故选C.2.已知抛物线C: y 2=x 的焦点为F ,A (x 0,y 0)是C 上一点,|AF |=32x 0,则x 0=( )A.14 B .12 C .1D .2答案:B 解析:由题意知,抛物线的准线为x =-14, 因为|AF |=32x 0,根据抛物线的定义可得 x 0+14=|AF |=32x 0,解得x 0=12.3.[2020江西萍乡一模]已知动圆C 经过点A (2,0),且截y 轴所得的弦长为4,则圆心C 的轨迹是( )A .圆B .椭圆C .双曲线D .抛物线答案:D 解析:设圆心C (x ,y ),截y 轴所得弦为BD ,过点C 作CE ⊥y轴,垂足为E ,则|BE |=2,则有|CA |2=|BC |2=|BE |2+|CE |2,∴(x -2)2+y 2=22+x 2,化为y 2=4x ,则圆心C 的轨迹为抛物线.故选D. 4.[2020河南洛阳模拟]已知点M 是抛物线C :y 2=2px (p >0)上一点,F 为C 的焦点,MF 的中点坐标是(2,2),则p 的值为( )A .1B .2C .3D .4答案:D 解析:F ⎝ ⎛⎭⎪⎫p 2,0,那么M ⎝ ⎛⎭⎪⎫4-p 2,4在抛物线上,即16=2p ⎝ ⎛⎭⎪⎫4-p 2,即p 2-8p +16=0,解得p =4.5.过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,O 为坐标原点.若|AF |=3,则△AOB 的面积为( )A.22 B .2 C.322D .22答案:C 解析:焦点F (1,0),设A ,B 分别在第一、四象限,则点A 到准线l :x =-1的距离为3,得A 的横坐标为2,纵坐标为22,AB 的方程为y =22(x -1),与抛物线方程联立可得2x 2-5x +2=0,所以B 的横坐标为12,纵坐标为-2,S △AOB =12×1×(22+2)=322.6.[2020海南海口模拟]过点F (0,3),且和直线y +3=0相切的动圆圆心轨迹方程是( )A .y 2=12xB .y 2=-12xC .x 2=-12yD .x 2=12y答案:D 解析:由已知条件知,动圆圆心到点F 和到直线y +3=0的距离相等,所以动圆圆心轨迹是以点F (0,3)为焦点,直线y =-3为准线的抛物线,故其方程为x 2=12y ,故选D.7.[2020豫南九校联考]已知点P 是抛物线x 2=4y 上的动点,点P 在x 轴上的射影是点Q ,点A 的坐标是(8,7),则|P A |+|PQ |的最小值为( )A .7B .8C .9D .10答案:C 解析:如图,抛物线的焦点为F (0,1),准线方程为y =-1,根据抛物线的定义知,|PF |=|PM |=|PQ |+1.∴|P A |+|PQ |=|P A |+|PM |-1=|P A |+|PF |-1≥|AF |-1=82+(7-1)2-1=10-1=9,当且仅当点P 在线段AF 上时,等号成立, 则|P A |+|PQ |的最小值为9. 故选C.8.已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,|AF |+|BF |=3,则线段AB 的中点到y 轴的距离为( )A.34 B .1 C.54D .74答案:C 解析:如图,过A ,B 及线段AB 的中点C 向抛物线的准线l 作垂线,垂足分别为A 1,B 1,C 1,CC 1交y 轴于C 0.由抛物线定义可知, |AA 1|+|BB 1|=|AF |+|BF |, ∴|CC 0|=|CC 1|-|C 1C 0| =12(|AA 1|+|BB 1|)-|C 1C 0| =32-14=54, 故选C.9.过抛物线y 2=2px (p >0)的焦点F 作直线l 交抛物线于A ,B 两点,交准线于点C ,若CB→=3BF →,则直线l 斜率为________. 答案:±22 解析:如图,过B 作BB 1垂直于准线,垂足为B 1,由抛物线定义可知,|BB 1|=|BF |, ∵CB →=3BF →,∴|BC |=3|BB 1|. 在Rt △B 1BC 中,tan ∠B 1BC =2 2. ∴tan α=22(α为倾斜角). 由对称性可知,斜率还可等于-2 2. ∴斜率为±2 2.10.[2020湖南衡阳联考]已知抛物线C :y 2=2px (p >0)的焦点为F ,过点(-1,0)的直线与C 交于A ,B 两点.若4|F A |+|FB |的最小值为19,则抛物线C 的标准方程为________.答案:y 2=12x 解析:设AB :y =k (x +1),A (x 1,y 1),B (x 2,y 2),联立⎩⎪⎨⎪⎧y =k (x +1),y 2=2px ,得k 2x 2+2(k 2-p )x +k 2=0,则x 1x 2=1,4|F A |+|FB |=4x 1+x 2+52p =4x 1+1x 1+52p ≥4+52p =19⎝ ⎛⎭⎪⎫当x 1=12时等号成立,得p =6,则抛物线C 的标准方程为y 2=12x .11.[2019全国卷Ⅰ]已知点A ,B 关于坐标原点O 对称,|AB |=4,⊙M 过点A ,B 且与直线x +2=0相切.(1)若A 在直线x +y =0上,求⊙M 的半径.(2)是否存在定点P ,使得当A 运动时,|MA |-|MP |为定值?并说明理由. 解:(1)因为⊙M 过点A ,B ,所以圆心M 在AB 的垂直平分线上.由已知A 在直线x +y =0上,且A ,B 关于坐标原点O 对称,所以M 在直线y =x 上,故可设M (a ,a ).因为⊙M 与直线x +2=0相切, 所以⊙M 的半径为r =|a +2|. 由已知得|AO |=2,又MO ⊥AO ,故可得2a 2+4=(a +2)2,解得a =0或a =4. 故⊙M 的半径r =2或r =6.(2)证明:存在定点P (1,0),使得|MA |-|MP |为定值. 理由如下:设M (x ,y ),由已知得⊙M 的半径为r =|x +2|,|AO |=2,由于MO ⊥AO ,故可得x 2+y 2+4=(x +2)2,化简得M 的轨迹方程为y 2=4x . 因为曲线C :y 2=4x 是以点P (1,0)为焦点,以直线x =-1为准线的抛物线, 所以|MP |=x +1.因为|MA |-|MP |=r -|MP |=x +2-(x +1)=1,所以存在满足条件的定点P .[强化训练]1.[2020广东广州一模]已知F 为抛物线C :y 2=6x 的焦点,过点F 的直线l 与C 相交于A ,B 两点,且|AF |=3|BF |,则|AB |=( )A .6B .8C .10D .12答案:B 解析:抛物线y 2=6x 的焦点坐标为F ⎝⎛⎭⎪⎫32,0,准线方程为x =-32,设A (x 1,y 1),B (x 2,y 2),∵|AF |=3|BF |,∴x 1+32=3⎝ ⎛⎭⎪⎫x 2+32, ∴x 1=3x 2+3,∵|y 1|=3|y 2|,∴x 1=9x 2, ∴x 1=92,x 2=12,∴|AB |=⎝ ⎛⎭⎪⎫x 1+32+⎝ ⎛⎭⎪⎫x 2+32=8. 故选B.2.[2020湖北四地七校联考]已知抛物线y 2=2px (p >0),点C (-4,0).过抛物线的焦点作垂直于x 轴的直线,与抛物线交于A ,B 两点,若△CAB 的面积为24.则以直线AB 为准线的抛物线的标准方程是( )A .y 2=4xB .y 2=-4xC .y 2=8xD .y 2=-8x答案:D 解析:因为AB ⊥x 轴,且AB 过点F , 所以AB 是焦点弦,且|AB |=2p ,所以S △CAB =12×2p ×⎝ ⎛⎭⎪⎫p 2+4=24,解得p =4或p =-12(舍), 所以抛物线方程为y 2=8x , 所以直线AB 的方程为x =2,所以以直线AB 为准线的抛物线的标准方程为y 2=-8x , 故选D.3.[2020重庆一中模拟]过抛物线y 2=2px (p >0)的焦点F 作斜率为3的直线,与抛物线在第一象限内交于点A ,若|AF |=4,则p =( )A .4B .2C .1D .3答案:B 解析:设A (x 0,y 0),过A 作x 轴的垂线交x 轴于点M ,在Rt △AMF 中,|AF |=4,由于AF 所在直线的斜率为3, 所以∠AFM =60°,则|FM |=2,故x 0=p 2+2,|AF |=x 0+p 2=4,得x 0=4-p 2,所以p 2+2=4-p2,解得p =2.故选B.4.已知点P 是抛物线y 2=2x 上的动点,点P 到准线的距离为d ,且点P 在y 轴上的射影是M ,点A ⎝⎛⎭⎪⎫72,4,则|P A |+|PM |的最小值是( )A.72 B .4 C.92D .5答案:C 解析:设抛物线y 2=2x 的焦点为F ,则F ⎝⎛⎭⎪⎫12,0.又点A ⎝ ⎛⎭⎪⎫72,4在抛物线的外侧,抛物线的准线方程为x =-12,则|PM |=d -12. 又|P A |+d =|P A |+|PF |≥|AF |=5, 所以|P A |+|PM |≥92.5.设F 为抛物线y 2=6x 的焦点,A ,B ,C 为该抛物线上三点.若F A →+FB →+FC →=0,则|F A →|+|FB→|+|FC →|=( ) A .4 B .6 C .9D .12答案:C 解析:由题意,得抛物线的焦点为F ⎝ ⎛⎭⎪⎫32,0,准线方程为x =-32. 设A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),∵F A →+FB →+FC →=0,∴点F 是△ABC 的重心, ∴x 1+x 2+x 3=92. 由抛物线的定义,可得|F A →|=x 1-⎝⎛⎭⎪⎫-32=x 1+32,|FB →|=x 2-⎝⎛⎭⎪⎫-32=x 2+32,|FC →|=x 3-⎝⎛⎭⎪⎫-32=x 3+32,∴|F A →|+|FB →|+|FC →|=x 1+32+x 2+32+x 3+32=9. 6.[2020安徽合肥一模]已知过抛物线y 2=42x 焦点F 的直线与抛物线交于A ,B 两点,AF→=3FB →,抛物线的准线l 与x 轴交于点C ,AM ⊥l 于点M ,则四边形AMCF 的面积为( )A .123B .12C .83D .63答案:A 解析:由题意得,直线AB 的斜率不为0,设直线AB 的方程为x =my +2,将其与y 2=42x 联立可得y 2-42my -8=0,设A (x A ,y A ),B (x B ,y B ),则y A y B =-8.∵AF →=3FB →,∴y B=-13y A, ∴y 2A =24,则y A =±26,24=42x A , 可得x A =32,|AM |=x A +p2=32+2=42,四边形AMCF 的面积为12(|CF |+|AM |)×|y A |=12×(22+42)×26=12 3. 故选A.7.[2020名校联盟模拟]直线l 与抛物线y 2=2px (p >0)交于A ,B 两点,O 为坐标原点,OA ⊥OB ,若△AOB 的面积的最小值为4,则抛物线的方程为( )A .y 2=xB .y 2=2xC .y 2=4xD .y 2=8x答案:B 解析:设直线l :x =λy +m ,代入抛物线方程,得y 2-2pλy -2pm =0,设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=2pλ,y 1y 2=-2pm .∵OA ⊥OB ,∴OA →·OB →=x 1x 2+y 1y 2=y 21y 222p ·2p +y 1y 2=0,即y 1y 2=-4p 2,∴-2pm =-4p 2,∴m =2p . ∴直线l 恒过点M (2p,0). ∴S △AOB =12|OM ||y 1-y 2| =12×2p (y 1+y 2)2-4y 1y 2 =p (2pλ)2+16p 2 =2p 2λ2+4,当且仅当λ=0时,S △AOB 取最小值4p 2,由4p 2=4得p =1,故抛物线的方程为y 2=2x .故选B.8.[2020河南郑州模拟]已知抛物线C :y 2=2x ,过原点作两条互相垂直的直线分别交C 于A ,B 两点(A ,B 均不与坐标原点重合),则抛物线的焦点F 到直线AB 的距离的最大值为( )A .2B .3 C.32D .4答案:C 解析:设直线AB 的方程为x =my +t ,A (x 1,y 1),B (x 2,y 2).由⎩⎪⎨⎪⎧x =my +t ,y 2=2x⇒y 2-2my -2t =0⇒y 1y 2=-2t , 由OA ⊥OB ⇒x 1x 2+y 1y 2=(y 1y 2)24+y 1y 2=0⇒y 1y 2=-4, ∴t =2,即直线AB 过定点(2,0).∴抛物线的焦点F 到直线AB 的距离的最大值为2-12=32.故选C.9.[2020河南安阳一模]已知抛物线C 1:y =ax 2(a >0)的焦点F 也是椭圆C 2:y 24+x 2b 2=1(b >0)的一个焦点,点M ,P ⎝ ⎛⎭⎪⎫32,1分别为曲线C 1,C 2上的点,则|MP |+|MF |的最小值为________.答案:2 解析:将P ⎝ ⎛⎭⎪⎫32,1代入y 24+x 2b 2=1,可得14+94b 2=1,∴b =3,∴c =1,∴抛物线的焦点F 为(0,1), ∴抛物线C 1的方程为x 2=4y ,准线为直线y =-1. 设点M 在准线上的射影为D , 根据抛物线的定义可知,|MF |=|MD |,∴要求|MP |+|MF |的最小值,即求|MP |+|MD |的最小值,易知当D ,M ,P 三点共线时,|MP |+|MD |最小,最小值为1-(-1)=2.10.[2020湖北武汉一模]设抛物线y 2=2px (p >0)的焦点为F ,准线为l .过焦点的直线分别交抛物线于A ,B 两点,分别过点A ,B 作l 的垂线,垂足分别为点C ,D .若|AF |=2|BF |,且△CDF 的面积为2,则p 的值为________.答案:233 解析:设A (x 1,y 1),B (x 2,y 2).因为直线AB 过焦点F ,所以y 1y 2=-p 2. 不妨设点A 在第一象限,因为|AF |=2|BF |,所以|y 1|=2|y 2|,所以-2y 22=-p 2.解得y 2=-22p ,所以y 1=-2y 2=2p . 所以S △CDF =12|y 1-y 2|×p =12×322p 2=2, 解得p =233.11.[2020北京二中模拟]已知抛物线y 2=2px (p >0)过点A (2,y 0),且点A 到其准线的距离为4.(1)求抛物线的方程;(2)直线l :y =x +m 与抛物线交于两个不同的点P ,Q ,若OP ⊥OQ ,求实数m 的值.解:(1)已知抛物线y 2=2px (p >0)过点A (2,y 0),且点A 到准线的距离为4, ∴2+p2=4,∴p =4, ∴抛物线的方程为y 2=8x .(2)由⎩⎪⎨⎪⎧y =x +m ,y 2=8x ,得x 2+(2m -8)x +m 2=0.设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=8-2m ,x 1x 2=m 2,y 1+y 2=x 1+x 2+2m =8,y 1y 2=(x 1+m )(x 2+m )=x 1x 2+m (x 1+x 2)+m 2=8m . ∵OP ⊥OQ ,∴x 1x 2+y 1y 2=m 2+8m =0, ∴m =0或m =-8.经检验,当m =0时,直线与抛物线交点中有一点与原点O 重合,不符合题意.当m =-8时,Δ=242-4×64>0,符合题意. 综上,实数m 的值为-8.。
(完整版)抛物线练习题(含答案)

抛物线练习题一、选择题1.在直角坐标平面内,到点(1,1)和直线 x+ 2y= 3 距离相等的点的轨迹是 ()A .直线B.抛物线C.圆D.双曲线2.抛物线 y2= x 上一点 P 到焦点的距离是 2,则 P 点坐标为 ()3,± 67,± 79,± 35,± 10A. 22B. 42C. 42D. 223.抛物线 y= ax2的准线方程是y= 2,则 a 的值为 ()11A. 8 B .-8C. 8D.- 84.设抛物线 y2= 8x 上一点 P 到 y 轴的距离是4,则点 P 到该抛物线焦点的距离是 ()A .4B . 6C. 8D. 125.设过抛物线的焦点 F 的弦为 AB,则以 AB 为直径的圆与抛物线的准线的地址关系是()A .订交B .相切C.相离D.以上答案都有可能6.过点 F(0,3)且和直线 y+ 3=0 相切的动圆圆心的轨迹方程为 ()A .y2= 12xB .y2=- 12x C. x2= 12y D .x2=- 12y7.抛物线 y2= 8x 上一点 P 到 x 轴距离为12,则点 P 到抛物线焦点 F 的距离为 ()A .20B .8C. 22D. 248.抛物线的极点在坐标原点,焦点是椭圆4x2+ y2= 1 的一个焦点,则此抛物线的焦点到准线的距离为 ()11A. 2 3 B. 3 C.2 3 D.4 39.设抛物线的极点在原点,其焦点F 在 y 轴上,又抛物线上的点(k,- 2)与 F 点的距离为4,则 k 的值是 ()A. 4 B . 4 或- 4C.- 2 D .2 或- 212的焦点坐标是 ()10.抛物线 y=m x (m<0)A.0,mB. 0,-mC. 0,1D. 0,-1 444m4m11.抛物线的极点在原点,对称轴是x 轴,抛物线上的点(-5,2 5) 到焦点的距离是6,则抛物线的方程为 ()A. y2=- 2x B .y2=- 4x C. y2= 2x D. y2=- 4x 或 y2=- 36x12.已知抛物线y2=2px(p>0) 的准线与圆 (x- 3)2+ y2= 16 相切,则p 的值为 () 1A. 2 B . 1C.2 D .4二、填空题13.过抛物线焦点 F 的直线与抛物线订交于A 、B 两点,若A 、B 在抛物线准线上的射影是A 1、B 1,则∠ A 1FB 1=。
2024届高考数学复习:精选好题专项(抛物线)练习(附答案)

2024届高考数学复习:精选好题专项(抛物线)练习[基础巩固]一、选择题1.抛物线y=14x2的焦点到其准线的距离为()A.1 B.2C.12D.182.已知抛物线y2=2px(p>0)的准线经过点(-1,1),则该抛物线的焦点坐标为() A.(-1,0) B.(1,0)C.(0,-1) D.(0,1)3.动点M到点F(2,1)的距离和到直线l:3x+4y-10=0的距离相等,则动点M的轨迹为()A.抛物线B.直线C.线段D.射线4.若抛物线y2=2px的焦点与双曲线x23-y2=1的右焦点重合,则p的值为()A.-4 B.4C.-2 D.25.[2022ꞏ全国乙卷(文),6] 设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则|AB|=()A.2 B.22C.3 D.326.若抛物线y2=2px(p>0)的焦点是椭圆x23p+y2p=1的一个焦点,则p=()A.2 B.3C.4 D.87.如图,过抛物线y2=2px(p>0)的焦点F的直线依次交抛物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=4,则抛物线的方程为()A.y2=8x B.y2=4xC.y2=2x D.y2=x8.设坐标原点为O ,抛物线y 2=2x 与过焦点的直线交于A ,B 两点,则OA → ꞏOB →等于( )A .34B .-34C .3D .-39.已知抛物线y 2=2px (p >0)的焦点为F ,准线为l ,过点F 的直线交抛物线于A ,B 两点,过点A 作准线l 的垂线,垂足为E ,当A 点坐标为(3,y 0)时,△AEF 为正三角形,则此时△OAB 的面积为( )A .433 B .3C .233D .33二、填空题10.[2021ꞏ新高考Ⅰ卷]已知O 为坐标原点,抛物线C :y 2=2px (p >0)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ ⊥OP ,若|FQ |=6,则C 的准线方程为________.11.[2023ꞏ全国乙卷(理)]已知点A ()1,5 在抛物线C :y 2=2px 上,则A 到C 的准线的距离为________.12.已知直线y =kx +2与抛物线y 2=8x 有且只有一个公共点,则k 的值为________.[强化练习]13.(多选)[2023ꞏ新课标Ⅱ卷]设O 为坐标原点,直线y =-3 (x -1)过抛物线C :y 2=2px (p >0)的焦点,且与C 交于M ,N 两点,l 为C 的准线,则( )A .p =2B .|MN |=83C .以MN 为直径的圆与l 相切D .△OMN 为等腰三角形 14.抛物线有如下光学性质:过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴;反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线y 2=4x 的焦点为F ,一条平行于x 轴的光线从点M (3,1)射出,经过抛物线上的点A 反射后,再经抛物线上的另一点B 射出,则△ABM 的周长为( )A .7112 +26 B .9+26C .9+10D .8312 +2615.已知抛物线C :y 2=2px (p >0)的焦点为F ,准线为l ,抛物线C 有一点P ,过点P 作PM ⊥l ,垂足为M ,若等边△PMF 的面积为43 ,则p =________.16.过抛物线y 2=2px (p >0)的焦点F 作倾斜角为60°的直线,与抛物线分别交于A ,B两点(点A 在x 轴上方),则|AF ||BF | =________.参考答案1.B y =14 x 2可化为x 2=4y ,则焦点到准线的距离为12 ×4=2.2.B ∵y 2=2px 的准线为x =-p 2 ,又准线过点(-1,1),∴-p2 =-1,∴p =2,故其焦点坐标为(1,0).3.B ∵F (2,1)在直线l :3x +4y -10=0上,∴动点M 的轨迹为过点F 且与直线l 垂直的直线.4.B ∵x 23 -y 2=1的右焦点为(2,0),∴p2 =2,p =4.5.B 由已知条件,易知抛物线y 2=4x 的焦点为F (1,0),准线方程为x =-1.又B (3,0),则|AF |=|BF |=2.不妨设点A 在第一象限,则A (x 0,2x 0 ).根据抛物线的定义可知x 0-(-1)=2,所以x 0=1,所以A (1,2),所以|AB |=(1-3)2+(2-0)2 =22 .故选B.6.D 由题意,知抛物线的焦点坐标为⎝⎛⎭⎫p 2,0 ,椭圆的焦点坐标为(±2p ,0),所以p 2 =2p ,解得p =8,故选D.7.B如图,分别过点A ,B 作准线的垂线,交准线于点E ,D ,设准线与x 轴交于点G ,设|BF |=a ,则由已知得|BC |=2a ,由定义得|BD |=a ,故∠BCD =30°,在Rt △ACE 中,∵|AF |=4,|AC |=4+3a ,∴2|AE |=|AC |,∴4+3a =8,从而得a =43 ,∵AE ∥FG ,∴FG AE =CF AC ,即p 4 =48 ,得p =2.∴抛物线方程为y 2=4x .故选B.8.B 当AB 与x 轴垂直时,A ⎝⎛⎭⎫12,1 ,B ⎝⎛⎭⎫12,-1 ,OA → ꞏOB → =12 ×12 +1×(-1)=-34 ;当AB 与x 轴不垂直时,设l :y =k ⎝⎛⎭⎫x -12 , 由⎩⎪⎨⎪⎧y =k ⎝⎛⎭⎫x -12,y 2=2x ,得k 2x 2-(k 2+2)x +k 24 =0 设A (x 1,y 1),B (x 2,y 2)由韦达定理得x 1+x 2=k 2+2k 2 ,x 1x 2=14 ,∴OA → ꞏOB →=x 1x 2+y 1y 2=x 1x 2+k 2⎝⎛⎭⎫x 1-12 ⎝⎛⎭⎫x 2-12 =(1+k 2)x 1x 2-12 k 2(x 1+x 2)+k 24 =-34 . 9.A 不妨设点A 在第一象限,如图所示,过点F 作AE 的垂线,垂足为H ,由题知当A 的坐标为(3,y 0)时△AEF 为正三角形,此时H 为AE 的中点,|AE |=3+p 2 ,|EH |=p ,∴2p =3+p2 ,解得p =2,∴y 2=4x ,A (3,23 ),F (1,0),∴k AF =3 ,直线AF 的方程为y =3 (x -1),代入抛物线方程得3(x -1)2=4x .设A (x 1,y 1),B (x 2,y 2),解得x 1=3,x 2=13 ,此时y 1=23 ,y 2=-233 ,∴S △AOB =S △OFB +S △OF A =12 ×1×⎝⎛⎭⎫233+23 =433 ,故选A. 10.x =-32答案解析:抛物线C :y 2=2px (p >0)的焦点F ⎝⎛⎭⎫p 2,0 ,∵P 为C 上一点,PF 与x 轴垂直,所以P 的横坐标为p2 ,代入抛物线方程求得P 的纵坐标为±p ,不妨设P (p2 ,p ),因为Q 为x 轴上一点,且PQ ⊥OP ,所以Q 在F 的右侧, 又∵|FQ |=6,∴Q (6+p 2 ,0),∴PQ →=(6,-p )因为PQ ⊥OP ,所以PQ → ꞏOP →=p 2 ×6-p 2=0, ∵p >0,∴p =3,所以C 的准线方程为x =-32 . 11.94答案解析:将点A 的坐标代入抛物线方程,得5=2p ,于是y 2=5x ,则抛物线的准线方程为x =-54 ,所以A 到准线的距离为1-⎝⎛⎭⎫-54 =94. 12.0或1答案解析:由⎩⎪⎨⎪⎧y =kx +2,y 2=8x , 得k 2x 2+(4k -8)x +4=0, 若k =0,满足题意;若k ≠0,则Δ=(4k -8)2-4×4k 2=0,得k =1.综上得k =0或k =1.13.AC 由题意,易知直线y =-3 (x -1)过点(1,0).对于A ,因为直线经过抛物线C 的焦点,所以易知焦点坐标为(1,0),所以p2 =1,即p =2,所以A 选项正确.对于B ,不妨设M (x 1,y 1),N (x 2,y 2),x 1<x 2,联立方程得⎩⎨⎧y =-3(x -1)y 2=4x,消去y并整理得3x 2-10x +3=0,解得x 1=13 ,x 2=3.所以M (13 ,233 ),N (3,-23 ),所以由两点间距离公式可得|MN |=(3-13)2-(-23-233)2 =163 ,故B 选项错误.对于C ,由以上分析易知,l 的方程为x =-1,以MN 为直径的圆的圆心坐标为(53 ,-233),半径r =12 |MN |=83 =53 +1,所以以MN 为直径的圆与l 相切,故C 选项正确. 对于D ,由两点间距离公式可得|MN |=163 ,|OM |=133 ,|ON |=21 ,故D 选项错误.综上,选AC.14.B 令y =1,得x =14 ,即A ⎝⎛⎭⎫14,1 . 由抛物线的光学性质可知AB 经过焦点F ,设直线AB 的方程为y =k (x -1),代入y 2=4x .消去y ,得k 2x 2-2(k 2+2)x +k 2=0.则x A x B =1,所以x B =1x A=4.|AB |=x A +x B +p =254 .将x =4代入y 2=4x 得y =±4,故B (4,-4). 故|MB |=(4-3)2+(-4-1)2 =26 .故△ABM 的周长为|MA |+|MB |+|AB |=⎝⎛⎭⎫3-14 +26 +254 =9+26 .故选B. 15.2答案解析:设准线l 和x 轴交于N 点,PM 平行于x 轴,∠PMF =∠MFN =60°,由抛物线的定义得到|NF |=p ,故|MF |=2p ,故34 (2p )2=43 ,∴p =2.16.3答案解析:如图所示,由题意得准线l :x =-p2 .作AC ⊥l 于点C ,BD ⊥l 于点D ,BH ⊥AC 于点H ,则|AF |=|AC |,|BF |=|BD |,|AH |=|AC |-|BD |=|AF |-|BF |,因为在Rt △AHB 中,∠HAB =60°,所以cos 60°=|AH ||AB | =|AF |-|BF ||AF |+|BF |,即12 (|AF |+|BF |)=|AF |-|BF |,得|AF ||BF | =3.。
高中抛物线知识点归纳总结与练习题(含答案)

则 AFK 的面积为
。
7、已知双曲线 x2 y2 1,则以双曲线中心为焦点,以双曲线左焦点为顶点的抛物线方程 45
为
。
8、在平面直角坐标系 xoy 中,有一定点 A(2,1) ,若线段 OA 的垂直平分线过抛物线
y2 2 px( p 0) 焦点,则该抛物线的方程是
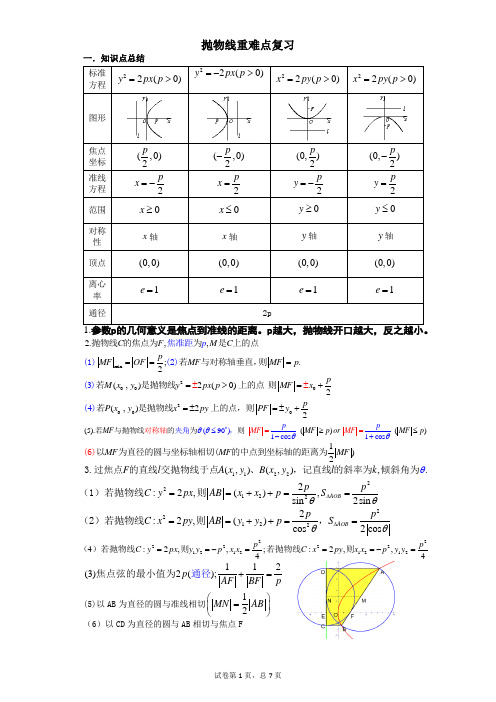
高中抛物线知识点归纳总结与练习题
y 2 2 px ( p 0)
抛
y l
物
线
OF x
y 2 2 px ( p 0)
y l
FO x
x 2 2 py ( p 0)
y
F
O
x
l
x 2 2 py ( p 0)
y l
O x
F
定义 范围
平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹叫做抛物线,点 F 叫 做抛物线的焦点,直线 l 叫做抛物线的准线。
二. 关于直线与抛物线的位置关系问题常用处理方法
直线 l : y kx b 抛物线
1 联立方程法:
y kx b
y
2
2
px
k 2x22源自kbp)x
b2
0
, ( p 0)
设交点坐标为 A(x1, y1) , B(x2, y2 ) ,则有 0 ,以及 x1 x2, x1x2 ,还可进一步求出
距离之和的最小值为
。
3、直线 y x 3 与抛物线 y2 4x 交于 A, B 两点,过 A, B 两点向抛物线的准线作垂线,垂足分
别为 P,Q ,则梯形 APQB 的面积为
。
4、设 O 是坐标原点, F 是抛物线 y2 2 px( p 0) 的焦点, A 是抛物线上的一点, FA 与 x 轴正
(完整版)抛物线练习题(含答案)

抛物线练习题一、选择题1.在直角坐标平面内,到点(1,1)和直线x +2y =3距离相等的点的轨迹是( )A .直线B .抛物线C .圆D .双曲线2.抛物线y 2=x 上一点P 到焦点的距离是2,则P 点坐标为( )A.⎝⎛⎭⎫32,±62B.⎝⎛⎭⎫74,±72C.⎝⎛⎭⎫94,±32D.⎝⎛⎭⎫52,±102 3.抛物线y =ax 2的准线方程是y =2,则a 的值为( )A.18 B .-18C .8D .-8 4.设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是( )A .4B .6C .8D .125.设过抛物线的焦点F 的弦为AB ,则以AB 为直径的圆与抛物线的准线的位置关系是( )A .相交B .相切C .相离D .以上答案都有可能6.过点F (0,3)且和直线y +3=0相切的动圆圆心的轨迹方程为( )A .y 2=12xB .y 2=-12xC .x 2=12yD .x 2=-12y7.抛物线y 2=8x 上一点P 到x 轴距离为12,则点P 到抛物线焦点F 的距离为( )A .20B .8C .22D .248.抛物线的顶点在坐标原点,焦点是椭圆4x 2+y 2=1的一个焦点,则此抛物线的焦点到准线的距离为( )A .2 3 B. 3 C.12 3 D.143 9.设抛物线的顶点在原点,其焦点F 在y 轴上,又抛物线上的点(k ,-2)与F 点的距离为4,则k 的值是( )A .4B .4或-4C .-2D .2或-210.抛物线y =1mx 2(m <0)的焦点坐标是( ) A.⎝⎛⎭⎫0,m 4 B.⎝⎛⎭⎫0,-m 4 C.⎝⎛⎭⎫0,14m D.⎝⎛⎭⎫0,-14m 11.抛物线的顶点在原点,对称轴是x 轴,抛物线上的点(-5,25)到焦点的距离是6,则抛物线的方程为( )A .y 2=-2xB .y 2=-4xC .y 2=2xD .y 2=-4x 或y 2=-36x12.已知抛物线y 2=2px (p >0)的准线与圆(x -3)2+y 2=16相切,则p 的值为( )A.12 B .1 C .2 D .4二、填空题13.过抛物线焦点F的直线与抛物线相交于A、B两点,若A、B在抛物线准线上的射影是A1、B1,则∠A1FB1= 。
2025届高考数学复习:压轴好题专项(抛物线中的切线问题)练习(附答案)

2025届高考数学复习:压轴好题专项(抛物线中的切线问题)练习1.(2023届云南省名校高三上学期月考)已知抛物线()2:20E x py p =>的焦点为F ,斜率为()0k k ≠的直线l 与E 相切于点A .(1)当=2k ,=5AF 时,求E 的方程;(2)若直线l '与l 平行,l '与E 交于B ,C 两点,且2BAC π∠=,设点F 到l '的距离为1d ,到l 的距离为2d ,试问:12d d 是否为定值?若是,求出定值;若不是,说明理由. 2.(2023届河南省北大公学禹州国际学校高三上学期月考)已知抛物线C 的顶点在坐标原点,焦点在y 轴的正半轴上,直线l :10mx y +-=经过抛物线C 的焦点. (1)求抛物线C 的方程;(2)若直线l 与抛物线C 相交于A ,B 两点,过A ,B 两点分别作抛物线C 的切线,两条切线相交于点P ,求△ABP 面积的最小值.3.(2022届浙江省绍兴市高三上学期12月选考)已知抛物线C 的焦点是10,4⎛⎫⎪⎝⎭,如图,过点,(0)2⎫≤⎪⎪⎝⎭D t t 作抛物线C 的两条切线,切点分别是A 和B ,线段AB 的中点为M .(1)求抛物线C 的标准方程; (2)求证:直线//MD y 轴;(3)以线段MD 为直径作圆,交直线AB 于MN ,求||||||||AB MN AB MN -+ 的取值范围.4.(2022届山东省济宁市高三上学期期末)已知抛物线E :22y px =(0p >)上一点()01,C y 到其焦点F 的距离为2. (1)求实数p 的值;(2)若过焦点F 的动直线l 与抛物线交于A 、B 两点,过A 、B 分别作抛物线的切线1l 、2l ,且1l 、2l 的交点为Q ,1l 、2l 与y 轴的交点分别为M 、N .求QMN 面积的取值范围. 5.(2022届百校联盟高三上学期12月联考)已知曲线C 上任意一点到1(1,0)F -,2(1,0)F 距离之和为3,抛物线E :22y px =的焦点是点2F.(1)求曲线C 和抛物线E 的方程;(2)点()()000,0Q x y x <是曲线C 上的任意一点,过点Q 分别作抛物线E 的两条切线,切点分别为M ,N ,求QMN 的面积的取值范围.6.(2022届四川省达州高三上学期诊断)过定点()0,1的动圆始终与直线l :1y =-相切. (1)求动圆圆心的轨迹C 的方程;(2)动点A 在直线l 上,过点A 作曲线C 的两条切线分别交x 轴于B ,D 两点,当ABD △的面积是32时,求点A 坐标. 7.(2022届四川省成都市高三上学期考试)已知抛物线()2:20C x py p =>的焦点为F .且F与圆()22:41M x y ++=上点的距离的最小值为4. (1)求抛物线的方程;(2)若点P 在圆M 上,PA ,PB 是C 的两条切线.A ,B 是切点,求PAB △面积的最大值.8.(2022届山西省怀仁市高三上学期期中)已知抛物线C :()220y px p =>的焦点为F ,准线与x 轴交于D 点,过点F 的直线与抛物线C 交于A ,B 两点,且FA FB FA FB ⋅=+. (1)求抛物线C 的方程;(2)设P ,Q 是抛物线C 上的不同两点,且PF x ⊥轴,直线PQ 与x 轴交于G 点,再在x 轴上截取线段GE GD =,且点G 介于点E 点D 之间,连接PE ,过点Q 作直线PE 的平行线l ,证明l 是抛物线C 的切线.9.已知抛物线2:2C x py =,点()4,4M -在抛物线C 上,过点M 作抛物线C 的切线,交x 轴于点P ,点O 为坐标原点. (1)求P 点的坐标;(2)点E 的坐标为()2,1--,经过点P 的直线交抛物线于A ,B 两点,交线段OM 于点Q ,记EA ,EB ,EQ 的斜率分别为1k ,2k ,3k ,是否存在常数λ使得123k k k λ+=.若存在,求出λ的值,若不存在,请说明理由.10.如图,已知()()1122,,A x y B x y 、为二次函数2(0)y ax a =>的图像上异于顶点的两个点,曲线2y ax =在点()()1122,,A x y B x y 、处的切线相交于点()00,P x y .(1)利用抛物线的定义证明:曲线2y ax =上的每一个点都在一条抛物线上,并指出这条抛物线的焦点坐标和准线方程;(2)求证:102x x x 、、成等差数列,102y y y 、、成等比数列;(3)设抛物线2y ax =焦点为F ,过P 作PH 垂直准线l ,垂足为H ,求证:BPH APF ∠∠=. 11.已知抛物线22(0)x py p =>上的任意一点到(0,1)P 的距离比到x 轴的距离大1. (1)求抛物线的方程;(2)若过点(0,2)的直线l 与抛物线交于A ,B 两点,过A ,B 两点分别作抛物线的切线,两条切线交于点Q ,求QAB 重心G 的轨迹方程.12.已知抛物线()2:20C x py p =>的焦点为F ,点()02,P y -为抛物线上一点,抛物线C 在点P处的切线与y 轴相交于点Q ,且FPQ △的面积为2. (1)求抛物线的方程.(2)若斜率不为0的直线l 过焦点F ,且交抛物线C 于A ,B 两点,线段AB 的中垂线与y 轴交于点M ,证明:MFAB为定值. 13.(2022届新未来4月联考)已知直线:10l x ky k -+-=与抛物线2:2(0)C y px p =>交于A ,B 两点,过A ,B 两点且与抛物线C 相切的两条直线相交于点D ,当直线l x ⊥轴时,||4AB =.(1)求抛物线C 的标准方程; (2)求||OD 的最小值.14.过原点O 的直线与拋物线C :22y px =(0p >)交于点A ,线段OA 的中点为M ,又点()3,0P p ,PM OA ⊥.在下面给出的三个条件中任选一个填在横线处,并解答下列问题:①OA =②PM =;③POM 的面积为(1)______,求拋物线C 的方程;(2)在(1)的条件下,过y 轴上的动点B 作拋物线C 的切线,切点为Q (不与原点O 重合),过点B 作直线l 与OQ 垂直,求证:直线l 过定点. 注:如果选择多个条件分别解答,按第一个解答计分.15.已知抛物线22(0)x py y =>,其焦点为F ,抛物线上有相异两点()11,A x y ,()22,B x y .(1)若//AF x 轴,且经过点A 的抛物线的切线经过点(1,0),求抛物线方程;(2)若2p =,且||||4AF BF +=,线段AB 的中垂线交x 轴于点C ,求ABC 面积的最大值. 16.设抛物线C :22x py =(0p >)的焦点为F ,点(),2P m (0m >)在抛物线C 上,且满足3PF =.(1)求抛物线C 的标准方程;(2)过点()0,4G 的直线l 与抛物线C 交于A ,B 两点,分别以A ,B 为切点的抛物线C 的两条切线交于点Q ,求三角形PQG 周长的最小值.17.已知圆()22:21C x y +-=与定直线:1l y =-,且动圆M 与圆C 外切并与直线l 相切.(1)求动圆圆心M 的轨迹E 的方程;(2)已知点P 是直线1:2l y =-上一个动点,过点P 作轨迹E 的两条切线,切点分别为A 、B .①求证:直线AB 过定点; ②求证:PCA PCB ∠=∠.18.设抛物线C :()220x py p =>,其焦点为 F ,准线为l ,点P 为C 上的一点,过点P 作直线l 的垂线,垂足为M ,且MF FP =,2FM FP ⋅=.(1)求抛物线C 的方程;(2)设点Q 为C 外的一点且Q 点不在坐标轴上,过点Q 作抛物线C 的两条切线,切点分别为A ,B ,过点Q 作y 轴的垂线,垂足为S ,连接 AS ,BS ,证明:直线AS 与直线BS 关于y 轴对称.参考答案1.(2023届云南省名校高三上学期月考)已知抛物线()2:20E x py p =>的焦点为F ,斜率为()0k k ≠的直线l 与E 相切于点A .(1)当=2k ,=5AF 时,求E 的方程;(2)若直线l '与l 平行,l '与E 交于B ,C 两点,且2BAC π∠=,设点F 到l '的距离为1d ,到l 的距离为2d ,试问:12d d 是否为定值?若是,求出定值;若不是,说明理由. 【过程详解】(1)由22x py =得22x y p=,则x y p '=, 令2x p =,则2x p =,即2A x p =,()2222A p y p p== 则252pAF p =+=,所以=2p ,故抛物线E 的方程为24x y =. (2)设()2002,2A pt pt ,()2112,2B pt pt ,()2222,2C pt pt , 则切线l 的斜率0022pt k t p==, 则切线l 的方程为:()2000222y pt t x pt -=-,即20022y t x pt =-,221212122222BCpt pt k t t pt pt -==+-. 直线l '的方程为()()2112122y pt t t x pt -=+-,化简得()12122y t t x pt t =+-,因为l l '∥,所以1202t t t +=,由2BAC π∠=得222210201020222212222pt pt pt pt pt pt pt pt --⋅=---, 则()()10201t t t t +=-+,即012213t t t =--, 即200:2260l t x y p pt '-++=.由0,2p F ⎛⎫⎪⎝⎭,则20136p pt d +=,2022p pt d +==所以20122013223122p t d d p t ⎛⎫+ ⎪⎝⎭==⎛⎫+ ⎪⎝⎭. 故12d d 是定值,定值为3.2.(2023届河南省北大公学禹州国际学校高三上学期月考)已知抛物线C 的顶点在坐标原点,焦点在y 轴的正半轴上,直线l :10mx y +-=经过抛物线C 的焦点.(1)求抛物线C 的方程;(2)若直线l 与抛物线C 相交于A ,B 两点,过A ,B 两点分别作抛物线C 的切线,两条切线相交于点P ,求△ABP 面积的最小值.【过程详解】(1)由题意,设抛物线C 的方程为()220x py p =>,因为直线:10l mx y +-=经过()0,1,即抛物线C 的焦点(0,)2p F ,所以12p=,解得2p =, 所以抛物线C 的方程为24x y =.(2)设()11,A x y 、()22,B x y ,联立方程组2410x ymx y ⎧=⎨+-=⎩,整理得2440x mx +-=, 因为216160m ∆=+>,且124x x m +=-,124x x =-,()222121221212242444x x x x x x y y m +-+=+==+,()2221212414416x x y y -=⨯== 所以()21241AB y y p m =++=+,由24x y =,可得24x y =,则2x y '=, 所以抛物线C 经过点A 的切线方程是()1112x y y x x -=-,将2114x y =代入上式整理得21124x x y x =-,同理可得抛物线C 经过点B 的切线方程为22224x x y x =-,联立方程组2112222424x x y x x xy x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得1212,24x x x x x y +==,所以2,1x m y =-=-, 所以()2,1P m --到直线10mx y +-=的距离d ==所以ABP的面积()()322211414122S AB d m m ==⨯⨯+⨯=+,因为211m +≥,所以4S ≥,即当0m =时,4S =,所以ABP 面积的最小值为4.3.(2022届浙江省绍兴市高三上学期12月选考)已知抛物线C 的焦点是10,4⎛⎫⎪⎝⎭,如图,过点,(0)2⎫≤⎪⎪⎝⎭D t t 作抛物线C 的两条切线,切点分别是A 和B ,线段AB 的中点为M .(1)求抛物线C 的标准方程; (2)求证:直线//MD y 轴;(3)以线段MD 为直径作圆,交直线AB 于MN ,求||||||||AB MN AB MN -+ 的取值范围.【过程详解】(1)设抛物线的方程为()220x py p =>,由题意可得124p =,所以12p =,所以抛物线方程2y x =. (2)由(1)2y x =,因为2y x '=,设1122(,),(,)A x y B x y , 直线AD 的方程为2112y x x x =-,直线BD 的方程为2222y x x x =-,联立上述两直线方程,得D 点坐标1212,2+⎛⎫⎪⎝⎭x x D x x ,又因为M 点为线段AB 的中点,所以M 点坐标1212,12+⎛⎫- ⎪⎝⎭x x M x x ,因为D M x x =,所以直线//MD y 轴:(3)因为点(0)2⎛⎫≤ ⎪ ⎪⎝⎭D t t ,所以12122x x x x t +==,则2⎛⎫- ⎪ ⎪⎝⎭M t ,圆心1,22⎫⎪⎪⎝⎭,直线AB 的斜率为22121212x x k x x x x -==+=-直线AB 方程为y t =-, 2y xy t⎧=⎪⎨-⎪⎩,得20x t +=,24t ∆=-,||AB ==, 圆心到直线AB 的距离为d 半径||1222MD tr -==,||12)3MN t ==-(,1m =≥, ||||361||||33AB MN m AB MN m m --==-++++在m 1≥时单调递减,||||11,||||2-⎛⎤∈- ⎥+⎝⎦AB MN AB MN .4.(2022届山东省济宁市高三上学期期末)已知抛物线E :22y px =(0p >)上一点()01,C y 到其焦点F 的距离为2. (1)求实数p 的值;(2)若过焦点F 的动直线l 与抛物线交于A 、B 两点,过A 、B 分别作抛物线的切线1l 、2l ,且1l 、2l 的交点为Q ,1l 、2l 与y 轴的交点分别为M 、N .求QMN 面积的取值范围. 【过程详解】(1)因为点()01,C y 到其焦点F 的距离为2,由抛物线的定义知122p+= 解得2p =(2)由上问可知,抛物线方程E :24y x =设211,4y A y ⎛⎫ ⎪⎝⎭,222,4y B y ⎛⎫⎪⎝⎭,(10y ≠,20y ≠),设l :1x ty =+,联立241y xx ty ⎧=⎨=+⎩,得2440y ty --=, 判别式2=16160t ∆+>,故t ∈R124y y t +=,124y y =-设1l :2114y y y k x ⎛⎫-=- ⎪⎝⎭联立方程组221144y xy y y k x ⎧=⎪⎛⎫⎨-=- ⎪⎪⎝⎭⎩,消x 得2211440ky y y ky -+-=,所以()()2221111Δ16444440k y ky ky k y =--=-+=所以12k y =则1l :211124y y y x y ⎛⎫-=- ⎪⎝⎭,即1122y y x y =+,令0x =,得10,2y M ⎛⎫⎪⎝⎭,同理2l :2222y y x y =+,20,2y N ⎛⎫⎪⎝⎭, 联立11222222yy x y y y x y ⎧=+⎪⎪⎨⎪=+⎪⎩,得交点Q 的横坐标为1214Q y y x ==-, ∴1211112222QMN Q y y S MN x =⋅=-⨯==≥△∴QMN 面积的取值范围是[)1,+∞.5.(2022届百校联盟高三上学期12月联考)已知曲线C 上任意一点到1(1,0)F -,2(1,0)F 距离抛物线E :22y px =的焦点是点2F . (1)求曲线C 和抛物线E 的方程;(2)点()()000,0Q x y x <是曲线C 上的任意一点,过点Q 分别作抛物线E 的两条切线,切点分别为M ,N ,求QMN 的面积的取值范围.【过程详解】(1)依题意,曲线C 是以1(1,0)F -,2(1,0)F 为左右焦点,,则短半轴长b有222113b =-=,曲线C 的方程为:2214133x y +=,即223314x y +=,在22y px =中,12p =,即2p =, 所以曲线C 的方程为:223314x y +=,抛物线E 的方程为:24y x =.(2)显然,过点Q 的抛物线E 的切线斜率存在且不为0,设切线方程为:00()y y k x x -=-,由002()4y y k x x y x-=-⎧⎨=⎩消去x 并整理得:20004k y y y kx ⋅-+-=,依题意,200001()10k y kx x k y k ∆=--=-+=,设二切线斜率为12,k k ,则0120y k k x +=,1201k k x =,设斜率为1k 的切线所对切点11(,)M x y ,斜率为2k 的切线所对切点22(,)N x y , 因此,112y k =,222y k =,于是得21112(,)M k k ,22212(,)N k k ,2212121122(,)NM k k k k =-- , 直线MN 上任意点(,)P x y ,21112(,)MP x y k k =-- ,由//MP NM得: 222121*********()()(0x y k k k k k k -----=,化简整理得:121212220k k x y k k k k +-+=, 则直线MN 的方程为:00220x y y x -+=,点Q 到直线MN的距离2d =,||MN ====,则QMN的面积322200111||(224)2QMNy x S MN d =⋅==- ,而点()()000,0Q x y x <在曲线C 上,即22001134y x =-,00x ≤<,220000114443y x x x -=--+在0[x ∈上单调递减,当00x =时,200min 1(4)3y x -=,当0x =时,200max(4)y x -=于是有200143y x <-≤则32200(4)93y x <-≤,183QMN S <≤ 所以QMN的面积的取值范围是(,]183.6.(2022届四川省达州高三上学期诊断)过定点()0,1的动圆始终与直线l :1y =-相切. (1)求动圆圆心的轨迹C 的方程;(2)动点A 在直线l 上,过点A 作曲线C 的两条切线分别交x 轴于B ,D 两点,当ABD △的面积是32时,求点A 坐标. 【过程详解】(1)设动圆圆心坐标为(),x y , 因为过定点()0,1的动圆始终与直线l :1y =-相切, 可得1y =+,化简得24x y =, 即动圆圆心的轨迹方程C :24x y =.(2)设动点()0,1A x -,根据题意过点A 作曲线C 的切线斜率存在, 设为()0k k ≠,所以切线方程为()01y k x x =--,联立方程组()204,1x y y k x x ⎧=⎪⎨=--⎪⎩,整理得204440x kx kx -++=,且2010k kx ∆=--=, 因为2010k kx --=有两不等实根,所以有两条切线,斜率分别设为1k ,2k ,所以120k k x +=,121k k =-,切线()101y k x x =--交x 轴于点011,0B x k ⎛⎫+ ⎪⎝⎭,切线()201y k x x =--交x 轴于点021,0D x k ⎛⎫+ ⎪⎝⎭,所以21001212111131222ABDk k S x x k k k k -=+--⨯===△, 32=,解得0x =, 所以点A 坐标为)1-或()1-.7.(2022届四川省成都市高三上学期考试)已知抛物线()2:20C x py p =>的焦点为F .且F与圆()22:41M x y ++=上点的距离的最小值为4. (1)求抛物线的方程;(2)若点P 在圆M 上,PA ,PB 是C 的两条切线.A ,B 是切点,求PAB △面积的最大值. 【过程详解】(1)抛物线C 的焦点为0,2p F ⎛⎫ ⎪⎝⎭,42pFM =+, 所以,F 与圆22:(4)1M x y ++=上点的距离的最小值为4142p+-=,解得2p =; 所以抛物线的方程为24x y =.(2)抛物线C 的方程为24x y =,即24x y =,对该函数求导得2x y '=, 设点()11,A x y ,()22,B x y ,()00,P x y , 直线PA 的方程为()1112x y y x x -=-,即112x xy y =-,即11220x x y y --=, 同理可知,直线PB 的方程为22220x x y y --=,由于点P 为这两条直线的公共点,则10102020220220x x y y x x y y --=⎧⎨--=⎩, 所以,点A 、B 的坐标满足方程00220x x y y --=, 所以,直线AB 的方程为00220x x y y --=,联立0022204x x y y x y --=⎧⎪⎨=⎪⎩,可得200240x x x y -+=, 由韦达定理可得1202x x x +=,1204x x y =,所以AB ===点P 到直线AB的距离为d =所以,()3220011422PABS AB d x y =⋅==-△, ()()2222000000041441215621x y y y y y y -=-+-=---=-++ ,由已知可得053y -≤≤-,所以,当05y =-时,PAB △的面积取最大值321202⨯=8.(2022届山西省怀仁市高三上学期期中)已知抛物线C :()220y px p =>的焦点为F ,准线与x 轴交于D 点,过点F 的直线与抛物线C 交于A ,B 两点,且FA FB FA FB ⋅=+. (1)求抛物线C 的方程;(2)设P ,Q 是抛物线C 上的不同两点,且PF x ⊥轴,直线PQ 与x 轴交于G 点,再在x 轴上截取线段GE GD =,且点G 介于点E 点D 之间,连接PE ,过点Q 作直线PE 的平行线l ,证明l 是抛物线C 的切线.【过程详解】(1)解:设过点F 的直线方程为2p y k x ⎛⎫=- ⎪⎝⎭,()()1122,,,A x y B x y ,联立222p y k x y px⎧⎛⎫=-⎪ ⎪⎝⎭⎨⎪=⎩,得()22222204k p k x pk p x -++=, 则22121222,4pk p p x x x x k ++=⋅=, 所以21222222p p pk pFA FB x x k ++=+++=, ()22212222222p k p p p FA FB x x k +⎛⎫⎛⎫⋅=++=+ ⎪⎪⎝⎭⎝⎭, 因为FA FB FA FB ⋅=+,所以()22222222222p k pk p p kk ++=+, 化简得()221210p p k ⎛⎫-+= ⎪⎝⎭,所以2p =,当过点F 的直线斜率不存在时,则FA FB p ==,故22,FA FB p FA FB p +=⋅=,又因为FA FB FA FB ⋅=+, 则22p p =,所以2p =, 综上所述,2p =, 所以24y x =;(2)证明:不妨设点P 在第一象限, 则()()()1,2,1,0,1,0P D F -,设直线PQ 的方程为()21,0y m x m -=-≠,()33,Q x y ,联立()2214y m x y x ⎧-=-⎨=⎩,消元整理得22204m y y m --+=,则342y m +=,即342m y m -=故()2322m x m -=,即()22242,m m Q m m ⎛⎫-- ⎪ ⎪⎝⎭, 当0y =时,21x m =-+,则21,0G m ⎛⎫-+ ⎪⎝⎭,又因GE GD =,且点G 介于点E 点D 之间,则G 为DE 的中点,所以43,0E m ⎛⎫-+ ⎪⎝⎭,则直线PE 的斜率为2422m m m =--,因为直线PE 平行直线l , 所以直线l 的斜率为2mm-, 故直线l 的方程为()222422m m m y x m m m ⎡⎤---=-⎢⎥-⎢⎥⎣⎦,即22m my x m m -=+-, 联立2224m m y x m m y x-⎧=+⎪-⎨⎪=⎩,消元整理得()22042m m y y m m --+=-, ()214042m mm m-∆=-⨯⋅=-,所以直线l 与抛物线只有一个交点, 有直线l 斜率不为0, 所以l 是抛物线C 的切线.9.已知抛物线2:2C x py =,点()4,4M -在抛物线C 上,过点M 作抛物线C 的切线,交x 轴于点P ,点O 为坐标原点. (1)求P 点的坐标;(2)点E 的坐标为()2,1--,经过点P 的直线交抛物线于A ,B 两点,交线段OM 于点Q ,记EA ,EB ,EQ 的斜率分别为1k ,2k ,3k ,是否存在常数λ使得123k k k λ+=.若存在,求出λ的值,若不存在,请说明理由.【过程详解】(1)因为()4,4M -在抛物线C 上,所以()248p -=,所以2p =所以抛物线C 的方程为24x y =,即214y x =,则12y x '=, 所以切线的斜率为1(4)22⨯-=-,所以过点M 的切线方程为()244y x =-++,即y x =--24联立24y x y =--⎧⎨=⎩,解得P 点的坐标为()2,0- (2)由题意可知过点P 的直线的斜率存在,设为2y kx k =+,线段OM 所在的直线为y x =-,联立2y kx k y x =+⎧⎨=-⎩,解得Q 点坐标为22,11k k k k ⎛⎫- ⎪++⎝⎭, 所以3213112221kk k k k k +++==-++ 设211,4x A x ⎛⎫ ⎪⎝⎭,222,4x B x ⎛⎫ ⎪⎝⎭,联立224y kx k x y =+⎧⎨=⎩,得2480x kx k --=, 所以124x x k +=,128x x k =-.则()()()()22221212121212121212121111444422224x x x x x x x x x x k k x x x x x x +++++++++=+=+++++()22184161641242318844k k k k k k k k -+++++===+-++ 所以1232k k k +=,即存在2λ=满足条件.10.如图,已知()()1122,,A x y B x y 、为二次函数2(0)y ax a =>的图像上异于顶点的两个点,曲线2y ax =在点()()1122,,A x y B x y 、处的切线相交于点()00,P x y .(1)利用抛物线的定义证明:曲线2y ax =上的每一个点都在一条抛物线上,并指出这条抛物线的焦点坐标和准线方程;(2)求证:102x x x 、、成等差数列,102y y y 、、成等比数列;(3)设抛物线2y ax =焦点为F ,过P 作PH 垂直准线l ,垂足为H ,求证:BPH APF ∠∠=. 【过程详解】(1)证明:令10,4F a ⎛⎫ ⎪⎝⎭,直线l :14y a =-,曲线2y ax =上任意一点()200,P x ax ,又0a >,则点()200,P x ax 到直线l 的距离2014d ax a=+,则PF ===22001144ax ax d a a ==+=+=, 即曲线2y ax =上任意一点到点10,4F a ⎛⎫⎪⎝⎭的距离与到直线l :14y a =-的距离相等,且点10,4F a ⎛⎫⎪⎝⎭不在直线l :14y a =-上,所以曲线2y ax =上的每一个点都在一条抛物线上,抛物线的方程即为2y ax =,焦点坐标为10,4F a ⎛⎫⎪⎝⎭,准线方程为14y a =-;(2)解:对于2y ax =,则2y ax '=,所以11|2x x y ax ='=,22|2x x y ax ='=,即过点()11,A x y 、()22,B x y 的切线方程分别为()1112y y ax x x -=-、()2222y y ax x x -=-,又211y ax =,222y ax =,所以2112y ax x ax =-、2222y ax x ax =-,由21122222y ax x ax y ax x ax ⎧=-⎨=-⎩,解得12212x x x y ax x +⎧=⎪⎨⎪=⎩,即1221,2x x P ax x +⎛⎫⎪⎝⎭, 即1202x x x +=,021y ax x =,又222202112y a x x y y ==⋅, 所以1x 、0x 、2x 成等差数列,1y 、0y 、2y 成等比数列;(3)解:由(2)可知22BP k ax =,12AP k ax =,10,4F a ⎛⎫⎪⎝⎭,所以02112011442PF y ax x a a k x x x --==+,如图,设AP ,PF ,PB 与x 轴分别交于点C 、D 、E ,则1tan 2ACx ax ∠=,2tan 2BEx ax ∠=,211214tan 2ax x a FDx x x -∠=+,又()22BPH BEx BEx πππ∠=--∠=∠-,FPA FDx ACx ∠=∠-∠,所以211tan tan 2tan 2BPH BEx BEx ax π⎛⎫∠=∠-=-=- ⎪∠⎝⎭, ()tan tan tan tan 1tan tan FDx ACxFPA FDx ACx FDx ACx∠-∠∠=∠-∠=+∠∠2111221112142214122ax x a axx x ax x a ax x x --+=-+⋅+122111221112421224x x ax x ax a x x ax x ax a +--⋅=+⎛⎫+-⋅ ⎪⎝⎭21221211214222ax a x x x a x x --=++-21222121422ax ax a x x --=+()212221214142ax ax a x x --=+()()221222211412214a x ax ax a x -+==-++, 即tan tan BPH FPA ∠=∠, 所以BPH FPA ∠=∠;11.已知抛物线22(0)x py p =>上的任意一点到(0,1)P 的距离比到x 轴的距离大1. (1)求抛物线的方程;(2)若过点(0,2)的直线l 与抛物线交于A ,B 两点,过A ,B 两点分别作抛物线的切线,两条切线交于点Q ,求QAB 重心G 的轨迹方程.【过程详解】(1)由抛物线的定义可得2p =,∴抛物线的方程为24x y =;(2)由题意可得直线AB 的斜率存在,设其为k ,设()()1122,,,A x y B x y ,则直线AB 的方程为2y kx =+;代入抛物线方程得2480x kx --=,则有12124,8x x k x x +==-,∵24x y =,∴2x y '=,∴()111:2-=-AQ x l y y x x ,即21124x x y x =-①同理可得222:24=-BQ x x l y x ②,①-②有22121224x x x x x ⎛⎫=⎪-⎝⎭-,得1222Q x x x k +==,∴2111124=-=-=-Q x y kx kx y .∴(2,2)Q k - 又()21212444y y k x x k +=++=+,设()G x y ,,则12212234233Q Q x x x x k y y y k y ++⎧==⎪⎪⎨+++⎪==⎪⎩,消k 得223+=x y ,所以G 的轨迹方程为21233=+y x . 12.已知抛物线()2:20C x py p =>的焦点为F ,点()02,P y -为抛物线上一点,抛物线C 在点P处的切线与y 轴相交于点Q ,且FPQ △的面积为2. (1)求抛物线的方程.(2)若斜率不为0的直线l 过焦点F ,且交抛物线C 于A ,B 两点,线段AB 的中垂线与y 轴交于点M ,证明:MFAB为定值. 【过程详解】(1)将()02,P y -代入22x py =得,02y p= 设抛物线的切线方程为2(2)y k x p=++,代入22x py =整理得: 22(44)0x pkx pk --+=由题知224440p k pk ∆=++=,解得2k p=-又22Q y k p =+,所以222p FQ k p =-- 所以222222FPQ p p S k p p=--=+= ,解得2p = 所以抛物线C 的方程为24x y =(2)记AB 中点为N ,112233(,),(,),(,)A x y B x y N x y 设直线AB 方程为1y mx =+,代入24x y =整理得: 2440x mx --=,则12124,4x x m x x +==-所以24(1)AB m =+ 因为N 为AB 中点,所以12322x x x m +==,2321y m =+ 所以直线MN 的方程为21(21)(2)y m x m m-+=-- 则223M y m =+所以222MF m =+所以222214(1)2MF m AB m +==+ 13.(2022届新未来4月联考)已知直线:10l x ky k -+-=与抛物线2:2(0)C y px p =>交于A ,B 两点,过A ,B 两点且与抛物线C 相切的两条直线相交于点D ,当直线l x ⊥轴时,||4AB =. (1)求抛物线C 的标准方程; (2)求||OD 的最小值.【过程详解】(1)当直线l x ⊥轴时,1x =,代入22y px =解得y =∴||4AB ==,得2p =,∴抛物线C 的标准方程为24y x =;(2)设()()(),,,,,A A B B D D A x y B x y D x y .联立210,4,x ky k y x -+-=⎧⎨=⎩得24440y ky k -+-=.∴4,44A B A B y y k y y k +=⋅=-①,∵直线:10l x ky k -+-=恒过点(1,1),且与抛物线有两个交点,点(1,1)在抛物线上,∴0k ≠,当直线AD 和直线BD 斜率存在时,设直线:AD y mx n =+,联立2,4,y mx n y x =+⎧⎨=⎩∴2440my y n -+=,Δ16440m n =-⋅=,∴1⋅=m n ,∴2A y m =,同理,设直线:BD y ax b =+,则21,B ab y a ==,联立,,y mx n y ax b =+⎧⎨=+⎩∴1,11.D D x amy a m ⎧=⎪⎪⎨⎪=+⎪⎩ 由①可知22224,44k k m a m a +=⋅=-,∴1122m a ma+-=,即22D D y x -=,∴点D 在直线220x y -+=上.当直线AD 或直线BD 斜率不存在时,即直线l 过原点时,1k =,过原点的切线方程为0x =,易知另外一点为(4,4),过点(4,4)的切线方程设为4(4)x t y -=-,联立24(4)4x t y y x-=-⎧⎨=⎩,得2416160y ty t -+-=, ()2Δ16416160t t =--=,解得2t =,即切线方程122y x =+.此时交点D 的坐标为(0,2),在直线220x y -+=上,故OD 的最小值为原点到直线220x y -+=的距离,5=. 14.过原点O 的直线与拋物线C :22y px =(0p >)交于点A ,线段OA 的中点为M ,又点()3,0P p ,PM OA ⊥.在下面给出的三个条件中任选一个填在横线处,并解答下列问题:①OA =②PM =;③POM的面积为(1)______,求拋物线C 的方程;(2)在(1)的条件下,过y 轴上的动点B 作拋物线C 的切线,切点为Q (不与原点O 重合),过点B 作直线l 与OQ 垂直,求证:直线l 过定点. 注:如果选择多个条件分别解答,按第一个解答计分.【过程详解】(1)由题意知直线OA 的斜率存在且不为0,设其方程为()0y kx k =≠,由22,y px y kx ⎧=⎨=⎩得0,0x y =⎧⎨=⎩或22,2,p x k p y k ⎧=⎪⎪⎨⎪=⎪⎩即()0,0O ,222,p p A k k ⎛⎫ ⎪⎝⎭所以线段OA 的中点2,p p M k k ⎛⎫⎪⎝⎭.因为PM OA ⊥,所以直线PM 的斜率存在,22133PM p kkk pk p k ==--. 所以2113k k k ⋅=--,解得2k =±, 所以直线OA的方程为0x =,()4,A p ±. 若选①,不妨令()4,A p ,由OA ==解得2p =(舍去2p =-),所以抛物线C 的方程为24y x =. 若选②,因为PM OA ⊥,PM=所以点P 到直线OA 的距离为=,解得2p =(舍去2p =-),所以抛物线C 的方程为24y x=. 若选③,不妨令()4,A p ,因为12OM OA ===,点P 到直线OA的距离PM ==,所以1122POM S OM PM =⋅==△,解得2p =(舍去2p =-), 所以抛物线C 的方程为24y x =.(2)由题意可知切线BQ 的斜率存在且不为0. 设()()0,0B b b ≠,切线BQ 的方程为1y k x b =+, 由12,4y k x b y x=+⎧⎨=⎩得21440k y y b -+=,(*) 所以()214440k b ∆=--⨯⨯=,解得11k b=, 所以方程(*)的根为2y b =,代入24y x =得2x b =,所以切点()2,2b b ,于是222OQ b k b b ==,则2l b k =-, 所以直线l 的方程为2by x b =-+,即()22b y x =--,所以当b 变化时,直线l 恒过定点()2,0.15.已知抛物线22(0)x py y =>,其焦点为F ,抛物线上有相异两点()11,A x y ,()22,B x y .(1)若//AF x 轴,且经过点A 的抛物线的切线经过点(1,0),求抛物线方程;(2)若2p =,且||||4AF BF +=,线段AB 的中垂线交x 轴于点C ,求ABC 面积的最大值. 【过程详解】(1)抛物线22(0)x py y =>,焦点坐标为0,2p ⎛⎫⎪⎝⎭,因为//AF x ,所以2A p y =,所以A x p =,又22x y p =,所以x y p '=,所以过A 点的切线的斜率1k =,所以切线方程为2p y x p -=-,令0y =得12px ==,所以2p =,所以24x y = (2)若2p =,则抛物线为24x y =,焦点为()0,1,准线方程为1y =-,因为||||4AF BF +=,所以114A B y y +++=,所以2A B y y +=,设直线AB 的方程为y kx m =+,联立24x y =得2440x kx m --=,216160k m ∆=+>所以124x x k +=,124x x m =-,所以212122422y y kx kx m k m +=++=+=,即212m k =-,所以()221616120k k ∆=+->,解得11k -<<,当0k =时,直线方程为1y =,则()2,0A ,()2,0B -,所以AB 的中垂线恰为y 轴,则()0,0C ,所以14122ABC S =⨯⨯= , 当11k -<<,且0k ≠时,又AB 的中点坐标为()1212,2,122x x y y k ++⎛⎫= ⎪⎝⎭,所以AB 的中垂线l 的方程为()121y x k k =--+,令0y =得3x k =,所以()3,0C k ,所以C 到AB 的距离d =又AB =所以221312ABC S AB d k m k ==+=+= 令21k t -=,则()0,1t ∈,()()232244f t t t t t t =-=-+,因为()()()2384232f t t t t t '=-+=--,所以当20,3t ⎛⎫∈ ⎪⎝⎭时()0f t '>,()f t 在20,3⎛⎫ ⎪⎝⎭上单调递增,当2,13t ⎛⎫∈ ⎪⎝⎭时()0f t '<,()f t 在2,13⎛⎫ ⎪⎝⎭上单调递减,所以()max 232327f t f ⎛⎫==⎪⎝⎭所以()max 2ABC S =>所以()max ABC S =16.设抛物线C :22x py =(0p >)的焦点为F ,点(),2P m (0m >)在抛物线C 上,且满足3PF =.(1)求抛物线C 的标准方程;(2)过点()0,4G 的直线l 与抛物线C 交于A ,B 两点,分别以A ,B 为切点的抛物线C 的两条切线交于点Q ,求三角形PQG 周长的最小值. 【过程详解】(1)由抛物线定义,得232pPF =+=,得2p =, ∴抛物线C 的标准方程为24xy =;(2)设()11,A x y ,()22,B x y ,直线l 的方程为4y kx =+,∴联立244y kx x y=+⎧⎨=⎩,消掉x ,得24160x kx --=,0∆>,∴124x x k +=,1216x x =-,设A ,B 处的切线斜率分别为1k ,2k ,则112x k =,222x k =, ∴在点A 的切线方程为()1112x y y x x -=-,即21124x x x y =-①,同理,在B 的切线方程为22224x x x y =-②, 由①②得:1222Q x x x k +==,代入①或②中可得:21111444Q x y kx y y ==--=--, ∴()2,4Q k -,即Q 在定直线4y =-上,设点G 关于直线4y =-的对称点为G ',则()0,12G '-,由(1)知()2P ,∵PQ GQ PQ G Q G P ''+=+≥=即,,P Q G '三点共线时等号成立,∴三角形PQG周长最小值为GP G P '+=.17.已知圆()22:21C x y +-=与定直线:1l y =-,且动圆M 与圆C 外切并与直线l 相切. (1)求动圆圆心M 的轨迹E 的方程;(2)已知点P 是直线1:2l y =-上一个动点,过点P 作轨迹E 的两条切线,切点分别为A 、B .①求证:直线AB 过定点; ②求证:PCA PCB ∠=∠.【过程详解】(1)依题意知:M 到()0,2C 的距离等于M 到直线2y =-的距离,∴动点M 的轨迹是以C 为焦点,直线2y =-为准线的抛物线,设抛物线方程为()220x py p =>,则22p=,则4p =,即抛物线的方程为28x y =, 故:动圆圆心M 的轨迹E 的方程为:28x y =;(2)①由28x y =得:218y x =,14y x '∴=,设2111,8A x x ⎛⎫ ⎪⎝⎭、2221,8B x x ⎛⎫⎪⎝⎭,(),2P t -,其中12x x ≠,则切线PA 的方程为()2111184x y x x x -=-,即2111148y x x x =-,同理,切线PB 的方程为2221148y x x x =-, 由21122211481148y x x x y x x x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得121228x x x x x y +⎧=⎪⎪⎨⎪=⎪⎩,1212228x x t x x +⎧=⎪⎪∴⎨⎪-=⎪⎩,即1212216x x t x x +=⎧⎨=-⎩, 2111,8A x x ⎛⎫ ⎪⎝⎭ 、()222121,8B x x x x ⎛⎫≠ ⎪⎝⎭,∴直线AB 的方程为()222121*********x x y x x x x x --=--,化简得121288x x x x y x +=-, 即24ty x =+, 故直线AB 过定点()0,2;②由①知:直线AB 的斜率为4ABt k =, (i )当直线PC 的斜率不存在时,直线AB 的方程为2y =,PC AB ∴⊥,PCA PCB ∴∠=∠; (ii )当直线PC 的斜率存在时,(),2P t - 、()0,2C ,∴直线PC 的斜率2240PC k t t --==--,414AB PC t k k t-∴⋅=⨯=-, PC AB ∴⊥,PCA PCB ∴∠=∠.综上所述:PCA PCB ∠=∠得证.18.设抛物线C :()220x py p =>,其焦点为 F ,准线为l ,点P 为C 上的一点,过点P 作直线l 的垂线,垂足为M ,且MF FP =,2FM FP ⋅=.(1)求抛物线C 的方程;(2)设点Q 为C 外的一点且Q 点不在坐标轴上,过点Q 作抛物线C 的两条切线,切点分别为A ,B ,过点Q 作y 轴的垂线,垂足为S ,连接 AS ,BS ,证明:直线AS 与直线BS 关于y 轴对称.【过程详解】(1)PM PF FM == ,PFM ∴△为等边三角形,60FMP PFM ∴∠=∠=︒,又2cos cos602FM FP FM FP PFM FM ⋅=⋅∠=︒= ,2FM ∴=设直线l 交y 轴于N 点,则在Rt MNF △中30NMF ∠=︒,1NF p ==,C ∴的方程为22x y = (2)设点()(),0,0Q a b a b ≠≠,()11,A x y ,()22,B x y ,又C 的方程为22x y =可化为22x y =,y x '∴=所以过点A 且与C 相切的直线的斜率为1x ,过点B 且与C 相切的直线的斜率为2x ,所以直线QA 的方程为()111y y x x x -=-,直线QB 的方程为()222y y x x x -=-.又直线QA 与QB 均过点Q ,()111b y x a x -=-,()222b y x a x -=-,又2112x y =,2222x y =,11y ax b ∴=-,22y ax b =-,所以直线AB 的方程为y ax b =-,联立方程y ax b =-和22x y =得方程组22,,x y y ax b ⎧=⎨=-⎩消去y 得2220x ax b -+=, 0b ≠ ,10x ∴≠,20x ≠,122x x b = ,又()0,S b ,则直线AS 的斜率111y b k x -=;直线BS 的斜率222y b k x -=,()121212122x x x x b k k x x ⎛⎫+- ⎪⎝⎭∴+=, 1202x x b -=, 120k k ∴+=,所以直线AS 与直线BS 关于y 轴对称.。
抛物线分类题型(含答案)

1练习一 二次函数1、 一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s (米)与时间t (秒)的数据如下表:写出用t 表示s 的函数关系式: 2、 下列函数:① y =()21y x x x =-+;③ ()224y x x x =+-;④ 21y x x =+; ⑤ ()1y x x =-,其中是二次函数的是 ,其中a = ,b = ,c = 3、当m 时,函数()2235y m x x =-+-(m 为常数)是关于x 的二次函数 4、当____m =时,函数()2221mm y m m x --=+是关于x 的二次函数5、当____m =时,函数()2564mm y m x-+=-+3x 是关于x 的二次函数6、若点 A ( 2, m ) 在函数 12-=x y 的图像上,则 A 点的坐标是____.7、在圆的面积公式 S =πr 2 中,s 与 r 的关系是( )A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系8、正方形铁片边长为15cm ,在四个角上各剪去一个边长为x (cm )的小正方形,用余下的部分做成一个无盖的盒子. (1)求盒子的表面积S (cm 2)与小正方形边长x (cm )之间的函数关系式; (2)当小正方形边长为3cm 时,求盒子的表面积.9、如图,矩形的长是 4cm ,宽是 3cm ,如果将长和宽都增加 x cm ,那么面积增加 ycm 2, ① 求 y 与 x 之间的函数关系式. ② 求当边长增加多少时,面积增加 8cm 2.10、已知二次函数),0(2≠+=a c ax y 当x=1时,y= -1;当x=2时,y=2,求该函数解析式.11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料,建造猪舍三间,如图,它们的平面图是一排大小相等的长方形.(1) 如果设猪舍的宽AB 为x 米,则猪舍的总面积S (米2)与x 有怎样的函数关系?(2) 请你帮富根老伯计算一下,如果猪舍的总面积为32米2,应该如何安排猪舍的长BC 和宽AB 的长度?旧墙的长度是否会对猪舍的长度有影响?怎样影响?练习二 函数2ax y =的图象与性质21、填空:(1)抛物线221x y =的对称轴是 (或 ),顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ; (2)抛物线221x y -=的对称轴是 (或 ),顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小,当x= 时,该函数有最 值是 ;2、对于函数22x y =下列说法:①当x 取任何实数时,y 的值总是正的;②x 的值增大,y 的值也增大;③y 随x 的增大而减小;④图象关于y 轴对称.其中正确的是 . 3、抛物线 y =-x 2 不具有的性质是( )A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足 S =12gt 2(g =9.8),则 s 与 t 的函数图像大致是( )A B C D5、函数2ax y =与b ax y +-=的图象可能是( )A .B .C .D .6、已知函数24mm y mx--=的图象是开口向下的抛物线,求m 的值.7、二次函数12-=m mx y 在其图象对称轴的左侧,y 随x 的增大而增大,求m 的值.8、二次函数223x y -=,当x 1>x 2>0时,求y 1与y 2的大小关系. 9、已知函数()422-++=m mx m y 是关于x 的二次函数,求:(1) 满足条件的m 的值;(2) m 为何值时,抛物线有最低点?求出这个最低点,这时x 为何值时,y 随x 的增大而增大; (3) m 为何值时,抛物线有最大值?最大值是多少?当x 为何值时,y 随x 的增大而减小? 10、如果抛物线2y ax =与直线1y x =-交于点(),2b ,求这条抛物线所对应的二次函数的关系式.练习三 函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y随x 的增大而增tttt3大, 当x 时, y 随x 的增大而减小. 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标 、 .3、任给一些不同的实数k ,得到不同的抛物线k x y +=2,当k 取0,1±时,关于这些抛物线有以下判断:①开口方向都相同;②对称轴都相同;③形状相同;④都有最底点.其中判断正确的是 .4、将抛物线122-=x y 向上平移4个单位后,所得的抛物线是 ,当x= 时,该抛物线有最 (填大或小)值,是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称,则m =________;6、二次函数c ax y +=2()0≠a 中,若当x 取x 1、x 2(x 1≠x 2)时,函数值相等,则当x 取x 1+x 2时,函数值等于 .练习四 函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ,顶点坐标是 ,当x 时,y 随x 的增大而减小, 函数有 最 值 .2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标. (1)右移2个单位;(2)左移32个单位;(3)先左移1个单位,再右移4个单位. 3、请你写出函数()21+=x y 和12+=x y 具有的共同性质(至少2个).4、二次函数()2h x a y -=的图象如图:已知21=a ,OA=OC ,试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ,与y 轴交点为B ,求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ,当自变量x 由0增加到2时,函数值增加6.(1)求出此函数关系式.(2)说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上,求k 的值.练习五 ()k h x a y +-=2的图象与性质1、请写出一个二次函数以(2, 3)为顶点,且开口向上.____________.2、二次函数 y =(x -1)2+2,当 x =____时,y 有最小值.3、函数 y =12(x -1)2+3,当 x ____时,函数值y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向 平移3个单位,再向 平移2个单位得到. 5、 已知抛物线的顶点坐标为()2,1,且抛物线过点()3,0,则抛物线的关系式是6、 如图所示,抛物线顶点坐标是P (1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( )A 、x>3B 、x<3C 、x>1D 、x<1 7、已知函数()9232+--=x y .(1) 确定下列抛物线的开口方向、对称轴和顶点坐标; (2) 当x= 时,抛物线有最 值,是 .(3) 当x 时,y 随x 的增大而增大;当x 时,y 随x 的增大而减小. (4) 求出该抛物线与x 轴的交点坐标及两交点间距离; (5) 求出该抛物线与y 轴的交点坐标;(6) 该函数图象可由23x y -=的图象经过怎样的平移得到的? 8、已知函数()412-+=x y .(1) 指出函数图象的开口方向、对称轴和顶点坐标;(2) 若图象与x 轴的交点为A 、B 和与y 轴的交点C ,求△ABC 的面积; (3) 指出该函数的最值和增减性;(4) 若将该抛物线先向右平移2个单位,在向上平移4个单位,求得到的抛物线的解析式; (5) 该抛物线经过怎样的平移能经过原点.(6) 画出该函数图象,并根据图象回答:当x 取何值时,函数值大于0;当x 取何值时,函数值小练习六 c bx ax y ++=2的图象和性质 1、抛物线942++=x x y 2、抛物线251222+-=x x y 的开口方向是 ,顶点坐标是 .3、试写出一个开口方向向上,对称轴为直线x=-2,且与y 轴的交点坐标为(0,3)的抛物线的解析式 .4、将 y =x 2-2x +3 化成 y =a (x -h)2+k 的形式,则 y =____.5 5、把二次函数215322y x x =---的图象向上平移3个单位,再向右平移4个单位,则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________; 7、函数x x y +-=22有最____值,最值为_______;8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位,再沿y 轴向上平移3个单位,得到的图象的函数解析式为122+-=x x y ,则b 与c 分别等于( )A 、6,4B 、-8,14C 、-6,6D 、-8,-149、二次函数122--=x x y 的图象在x 轴上截得的线段长为( ) A 、22 B 、23 C 、32 D 、3310、通过配方,写出下列函数的开口方向、对称轴和顶点坐标: (1)12212+-=x x y ; (2)2832-+-=x x y ; (3)4412-+-=x x y 11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位,再向上平移3个单位,问所得的抛物线有没有最大值,若有,求出该最大值;若没有,说明理由.12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标 13、已知一次函数的图象过抛物线223y x x =++的顶点和坐标原点 1) 求一次函数的关系式;2) 判断点()2,5-是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元,可卖出400台,以每100元为一个价格单位,若将每台提高一个单位价格,则会少卖出50台,那么每台定价为多少元即可获得最大利润?最大利润是多少元?练习七 c bx ax y ++=2的性质1、函数2y x px q =++的图象是以()3,2为顶点的一条抛物线,这个二次函数的表达式为 2、二次函数2224y mx x m m =++-的图象经过原点,则此抛物线的顶点坐标是 3、如果抛物线2y ax bx c =++与y 轴交于点A (0,2),它的对称轴是1x =-,那么acb= 4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点,与y 轴交于点C ,且线段AB 的长为1,△ABC 的面积6 为1,则b 的值为______.5、已知二次函数c bx ax y ++=2的图象如图所示,则a___0,b___0,c___0,ac b 42-____0;6、二次函数c bx ax y ++=2的图象如图,则直线bc ax y +=的图象不经过第 象限. 7、已知二次函数2y ax bx c =++(0≠a )的图象如图所示,则下列结论:1),a b 同号;2)当1x =和3x =时,函数值相同;3)40a b +=;4)当2y =-时,x 的值只能为0;其中正确的是 (第5题)(第6题) (第7题) (第10题) 8、已知二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是-2,则m= 9、二次函数2y x ax b =++中,若0a b +=,则它的图象必经过点( )A ()1,1--B ()1,1-C ()1,1D ()1,1-10、函数b ax y +=与c bx ax y ++=2的图象如上图所示,则下列选项中正确的是( ) A 、0,0>>c ab B 、0,0><c ab C 、0,0<>c ab D 、0,0<<c ab 11、已知函数c bx ax y ++=2的图象如图所示,则函数b ax y +=的图象是( )12、二次函数c bx ax y ++=2的图象如图,那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中,值为正数的有( )A .4个B .3个C .2个D .1个13、抛物线的图角如图,则下列结论: ①>0;②;③>;④<1.其中正确的结论是( ).(A )①② (B )②③ (C )②④ (D )③④14、二次函数2y ax bx c =++的最大值是3a -,且它的图象经过()1,2--,()1,6两点, 求a 、b 、c 的值。
抛物线练习题带答案,知识点总结(基础版)
抛物线重难点复习一.知识点总结2.,,C F p M C 焦抛物线的焦点为为是准距上的点min ;.2pMF OF MF MF p ===(1)(2)若与对称轴垂直,则2000(,)2(0)23p M x y y px p MF x =>=±+±若是抛物线上的点则() 2000(,)224p P x y x py PF y =±=±+若是抛物线上的(点,则) (5).()(90)1cos s ()1co p MF MF pp or MF p MF MF θθθθ≥≤-+==≤ 若与抛物线的为则夹角,对称轴1)2MF MF MF 以为直径的圆与坐标轴相切(的中点到坐标轴的距离为(6)1122(,)(,),.F l A x y B x y l k θ3.过焦点的直线交抛物线于点、,记直线的斜率为倾斜角为221222:2,(),sin 2sin AOB p p C y px AB x x p S θθ∆==++==(1)若抛物线则221222:2,()cos 2cos AOB p p C x py AB y y p S θθ∆==++==(2)若抛物线则, 222222121212124:2,,;:2,,44p p C y px y y p x x C x py x x p y y ==-===-=()若抛物线则若抛物线则112(3)2();p AF BF p+=通焦点弦的最径小值为 (5)以AB 为直径的圆与准线相切12MN AB ⎛⎫=⎪⎝⎭(6)以CD 为直径的圆与AB 相切与焦点F1.已知抛物线22(0)y px p =>上横坐标为 3 的点到其焦点的距离为 4,则p =________. 【答案】2【解析】抛物线y 2=2px (p >0, ∵抛物线y 2=2px (p >04,∴p=2.故答案为2.2.已知F 是抛物线y 2=2x 的焦点,A ,B 是该抛物线上的两点,|AF |+|BF |=11,则线段AB 的中点到y 轴的距离为( ) A. 3 B. 4 C. 5 D. 7 【答案】C 【解析】∵F 是抛物线y 2=2x 的焦点∴F (12,0) ,准线方程x =−12, 设A (x 1,y 1),B (x 2,y 2)∴|AF |+|BF |=x 1+1+x 2+1=11x 1+x 2=10,∴线段AB 的中点横坐标为5∴线段AB 5,所以B 选项是正确的.3.已知抛物线C :的焦点为F ,()00A x y ,是C 上一点,则0x =( )A. 2B. 2±C. 4D. 4± 【答案】D【解析】28x y =,如图,由抛物线的几何意义,可知0022AF Al y y ===+,所以02y =, 所以04x =±,故选D 。
抛物线同步练习题小题含答案

抛物线根底训练题1. 抛物线y 2=8x 的准线方程是〔 A 〕。
〔A 〕x =-2 〔B 〕x =2 〔C 〕x =-4 〔D 〕y =-22. 过抛物线y 2=4x 的焦点F ,作倾斜角为60°的直线,那么直线的方程是〔 B 〕。
〔A 〕y =33(x -1) 〔B 〕y =3 (x -1) 〔C 〕y =33(x -2) 〔D 〕y =3 (x -2)3.抛物线的焦点是F (0,4),那么此抛物线的标准方程是( A )〔A 〕x 2=16y 〔B 〕x 2=8y 〔C 〕y 2=16x 〔D 〕y 2=8x4. 假设抛物线y =x 2与x =-y 2的图象关于直线l 对称,那么l 的方程是〔B 〕。
〔A 〕x -y =0 〔B 〕x +y =0 〔C 〕x =0 〔D 〕y =05.AB 是过抛物线y 2=4x 焦点F 的弦,A ,B 两点的横坐标分别是x 1与x 2,且x 1+x 2=6那么|AB |等于〔 B 〕〔A 〕10 〔B 〕8 〔C 〕7 〔D 〕66.经过〔1,2〕点的抛物线的标准方程是〔C 〕〔A 〕y 2=4x 〔B 〕x 2=21y (C ) y 2=4x 或x 2=21y (D ) y 2=4x 或x 2=4y7. 过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1, y 1)、B (x 2, y 2)两点,如果AB 与x 轴成45°角,那么|AB |等于〔 B 〕。
〔A 〕10 〔B 〕8 〔C 〕6 〔D 〕48.抛物线的焦点在y 轴上,准线与椭圆4x 2+3y 2=1的左准线重合,并且经过椭圆的右焦点,那么它的对称轴方程是C〔A 〕y =24 〔B 〕y =26 或 y =-26〔C 〕y =26 〔D 〕y =22或y =-229. 顶点在原点,焦点是F (6, 0)的抛物线的方程是2y 24x =。
10.抛物线x 2=4y 的焦点为F ,A 是抛物线上一点,|AF |=4+22,那么AF 所在直线方程是111-122y x y x =+=+或。
高中数学抛物线练习题(含答案)

抛物线练习题一、选择题1.在直角坐标平面内,到点(1,1)和直线x +2y =3距离相等的点的轨迹是( )A .直线B .抛物线C .圆D .双曲线2.抛物线y 2=x 上一点P 到焦点的距离是2,则P 点坐标为( )A.⎝⎛⎭⎫32,±62B.⎝⎛⎭⎫74,±72C.⎝⎛⎭⎫94,±32D.⎝⎛⎭⎫52,±102 3.抛物线y =ax 2的准线方程是y =2,则a 的值为( )A.18 B .-18C .8D .-8 4.设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是( )A .4B .6C .8D .125.设过抛物线的焦点F 的弦为AB ,则以AB 为直径的圆与抛物线的准线的位置关系是( )A .相交B .相切C .相离D .以上答案都有可能6.过点F (0,3)且和直线y +3=0相切的动圆圆心的轨迹方程为( )A .y 2=12xB .y 2=-12xC .x 2=12yD .x 2=-12y7.抛物线y 2=8x 上一点P 到x 轴距离为12,则点P 到抛物线焦点F 的距离为( )A .20B .8C .22D .248.抛物线的顶点在坐标原点,焦点是椭圆4x 2+y 2=1的一个焦点,则此抛物线的焦点到准线的距离为( )A .2 3 B. 3 C.12 3 D.143 9.设抛物线的顶点在原点,其焦点F 在y 轴上,又抛物线上的点(k ,-2)与F 点的距离为4,则k 的值是( )A .4B .4或-4C .-2D .2或-210.抛物线y =1mx 2(m <0)的焦点坐标是( ) A.⎝⎛⎭⎫0,m 4 B.⎝⎛⎭⎫0,-m 4 C.⎝⎛⎭⎫0,14m D.⎝⎛⎭⎫0,-14m 11.抛物线的顶点在原点,对称轴是x 轴,抛物线上的点(-5,25)到焦点的距离是6,则抛物线的方程为( )A .y 2=-2xB .y 2=-4xC .y 2=2xD .y 2=-4x 或y 2=-36x12.已知抛物线y 2=2px (p >0)的准线与圆(x -3)2+y 2=16相切,则p 的值为( )A.12 B .1 C .2 D .4二、填空题13.过抛物线焦点F的直线与抛物线相交于A、B两点,若A、B在抛物线准线上的射影是A1、B1,则∠A1FB1= 。
初中抛物线经典练习题(含详细答案)

初中数学抛物线经典试题集锦【编著】黄勇权【第一组题型】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
3、在平面直角坐标系xOy中,已知抛物线的顶点C为(2,4),并在x轴上截得的长度为6。
(1)写出抛物线与x轴交点A、B的坐标(2)求该抛物线的表达式(3)写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4,交x轴于点A,交y轴于点B,若以A 为顶点,,且开口向下作抛物线,交直线AB于点D,交y轴负半轴于点C,(1)若△ABC的面积为20,求此时抛物线的解析式(2)若△BDO的面积为8,求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
解:【第一问】因为函数y=x²+bx+c过点A(2,0),C(0, -8)分别将x=2,y=0代入y=x²+bx+c,得0=4+2b+c-----①将x=0,y=-8代入y=x²+bx+c,得-8=c-------------②将②代入①,解得:b=2--------------------------------------③此时,将②③代入y=x²+bx+c,所以:二次函数的解析式y=x²+ 2x -8【第二问】△ABP的面积= 12│AB│*│y p│----------------------④因为A、B两点在x轴上,令x²+ 2x -8=0(x-2)(x+4)=0解得:x1=2,x2= -4所以:│AB│=│X1- X2│=│2-(- 4)│=6------⑤又△ABP的面积=15-------------------------------------⑥由④⑤⑥,得:12*6*│y p│=15│y p│=5故有:y p= ±5即:p点的纵坐标为5或-5.把y=5代入y=x²+ 2x -8,即:5=x²+ 2x -8x²+ 2x -13=0解得:x= -1± 14那么,此时p点坐标(-1+ 14,5),(-1- 14,5)-------⑦把y=-5代入y=x²+ 2x -8,即:-5=x²+ 2x -8x²+ 2x -3=0(x-1)(x+3)=0解得:x= 1或x= -3那么,此时p点坐标(1,-5),(-3,-5)------------------⑧由⑦⑧得,使△ABP的面积为15,p点坐标是:(-1+ 14,5),(-1- 14,5),(1,-5),(-3,-5)2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
初中抛物线经典练习题(含详细答案)

【编著】 黄勇权【第一组题型】1、已知二次函数y=x ²+bx+c 过点A (2,0),C (0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p 使△ABP 的面积为15,请直接写出p 点的坐标。
2、在平面直角坐标系xOy 中,抛物线y=2x ²+mx+n 经过点A (5,0),B (2,-6).(1)求抛物线的表达式及对称轴(2)设点B 关于原点的对称点为C ,写出过A 、C 两点直线的表达式。
初中数学抛物线 经典试题集锦3、在平面直角坐标系xOy中,已知抛物线的顶点C为(2,4),并在x轴上截得的长度为6。
(1)写出抛物线与x轴交点A、B的坐标(2)求该抛物线的表达式(3)写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4,交x轴于点A,交y轴于点B,若以A为顶点,,且开口向下作抛物线,交直线AB于点D,交y轴负半轴于点C,(1)若△ABC的面积为20,求此时抛物线的解析式(2)若△BDO的面积为8,求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A(2,0),C(0, -8)(1)求此二次函数的解析式,(2)在抛物线上存在一点p使△ABP的面积为15,请直接写出p点的坐标。
解:【第一问】因为函数y=x ²+bx+c 过点A (2,0),C (0, -8)分别将x=2,y=0代入y=x ²+bx+c , 得 0=4+2b+c-----①将x=0,y=-8代入y=x ²+bx+c ,得-8=c-------------②将②代入①,解得:b=2--------------------------------------③此时,将② ③代入y=x ²+bx+c ,所以:二次函数的解析式 y=x ²+ 2x -8【第二问】△ABP 的面积= 12│AB │*│y p │----------------------④ 因为A 、B 两点在x 轴上,令x ²+ 2x -8=0(x-2)(x+4)=0解得:x 1=2,x 2= -4所以:│AB │=│X 1- X 2│=│2-(- 4)│=6------⑤又△ABP 的面积=--------------------------⑥由 ④ ⑤ ⑥,得 : 12*6*│y p │=15│y p│=5故有:y p= ±5即:p点的纵坐标为5或-5.把y=5代入 y=x²+ 2x -8,即:5=x²+ 2x -8x²+ 2x -13=0解得:x= -1± 14那么,此时p点坐标(-1+ 14,5),(-1- 14,5)-------⑦把y=-5代入 y=x²+ 2x -8,即:-5=x²+ 2x -8x²+ 2x -3=0(x-1)(x+3)=0解得:x= 1或x= -3那么,此时p点坐标(1,-5),(-3,-5)------------------⑧由⑦⑧得,使△ABP的面积为15,p点坐标是:(-1+ 14,5),(-1- 14,5),(1,-5),(-3,-5)2、在平面直角坐标系xOy中,抛物线y=2x²+mx+n经过点A(5,0),B(2,-6).(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点为C,写出过A、C两点直线的表达式。
高中数学选择性必修一(人教版)《抛物线练习题1答案》

抛物线11.若抛物线x 2=4y 上的点P (m ,n )到其焦点的距离为5,则n =( ) A .194B .92C .3D .4解析:选D 抛物线x 2=4y 的准线方程为y =-1,根据抛物线定义可知5=n +1,即n =4.2.(2019·全国卷Ⅱ)若抛物线y 2=2px (p >0)的焦点是椭圆x 23p +y 2p=1的一个焦点,则p =( )A .2B .3C .4D .8解析:选D 抛物线y 2=2px (p >0)的焦点坐标为⎝⎛⎭⎫p 2,0,椭圆x 23p +y2p =1的焦点坐标为(±2p ,0).3.已知动点P (x ,y )满足5(x -1)2+(y -2)2=|3x +4y -1|,则点P 的轨迹为( ) A .直线 B .抛物线 C .双曲线 D .椭圆解析:选B 把5(x -1)2+(y -2)2=|3x +4y -1|化为(x -1)2+(y -2)2=|3x +4y -1|5,由于点(1,2)不在直线3x +4y -1=0上,满足抛物线的定义,则点P 的轨迹为抛物线.4.O 为坐标原点,F 为抛物线C :y 2=2x 的焦点,P (x 0,y 0)为C 上一点,若|PF |=32x 0,则△POF 的面积为( )A .1B .2C .22D .24解析:选D 由题意知,F 的坐标为⎝⎛⎭⎫12,0,因为点P (x 0,y 0)为C 上一点,|PF |=32x 0,则12+x 0=32x 0,解得x 0=1,所以P (1,±2),则△POF 的面积为:12×12×2=24. 5.已知A ,B 两点均在焦点为F 的抛物线y 2=2px (p >0)上,若|AF |+|BF |=4,线段AB 的中点到直线x =p2的距离为1,则p 的值为( )A .1B .1或3C .2D .2或6解析:选B |AF |+|BF |=4⇒x A +p 2+x B +p2=4⇒x A +x B =4-p ⇒2x中=4-p ,因为线段AB 的中点到直线x =p2的距离为1,所以⎪⎪⎪⎪x 中-p 2=1,所以|2-p |=1⇒p =1或3. 6.已知A ,B 为抛物线y 2=2x 上两点,且A 与B 的纵坐标之和为4,则直线AB 的斜率为( )A .12B .-12C .-2D .2解析:选A 设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=4,由⎩⎪⎨⎪⎧y 21=2x 1,y 22=2x 2,得(y 1+y 2)(y 1-y 2)x 1-x 2=2,即4k AB =2,k AB =12.7.(2020·福州期末)设抛物线y 2=2px 上的三个点A ⎝⎛⎭⎫23,y 1,B (1,y 2),C ⎝⎛⎭⎫32,y 3到该抛物线的焦点距离分别为d 1,d 2,d 3.若d 1,d 2,d 3中的最大值为3,则p 的值为________.解析:根据抛物线的几何性质可得d 1=p 2+23,d 2=p 2+1,d 3=p 2+32,由题意可得p >0,因此可判断d 3最大,故d 3=p 2+32=3,解得p =3.答案:38.(2018·全国卷Ⅲ)已知点M (-1,1)和抛物线C :y 2=4x ,过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若∠AMB =90°,则k =________.解析:设点A (x 1,y 1),B (x 2,y 2),则⎩⎪⎨⎪⎧y 21=4x 1,y 22=4x 2,∴y 21-y 22=4(x 1-x 2), ∴k =y 1-y 2x 1-x 2=4y 1+y 2.设AB 中点M ′(x 0,y 0),抛物线的焦点为F ,分别过点A ,B 作准线x =-1的垂线,垂足为A ′,B ′,则|MM ′|=12|AB |=12(|AF |+|BF |)=12(|AA ′|+|BB ′|). ∵M ′(x 0,y 0)为AB 的中点,∴M 为A ′B ′的中点,∴MM ′平行于x 轴, ∴y 1+y 2=2,∴k =2. 答案:29.抛物线y =-14x 2上的动点M 到两定点F (0,-1),E (1,-3)的距离之和的最小值为________.解析:抛物线标准方程为x 2=-4y ,其焦点坐标为(0,-1),准线方程为y =1,则|MF |的长度等于点M 到准线y =1的距离,从而点M 到两定点F ,E 的距离之和的最小值为点E (1,-3)到直线y =1的距离.即最小值为4.答案:410.已知抛物线y 2=2px (p >0)上一点M (1,m )到其焦点的距离为5,双曲线x 2-y 2a=1的左顶点为A ,若双曲线的一条渐近线与直线AM 垂直,则实数a =________.解析:根据抛物线的定义得1+p2=5,p =8.不妨取M (1,4),则AM 的斜率为2,由已知得-a ×2=-1,故a =14.答案:1411.如图,已知抛物线y 2=2px (p >0)的焦点为F ,A 是抛物线上横坐标为4,且位于x 轴上方的点,点A 到抛物线准线的距离等于5,过点A 作AB 垂直于y 轴,垂足为点B ,OB 的中点为M .(1)求抛物线的方程;(2)过点M 作MN ⊥FA ,垂足为N ,求点N 的坐标. 解:(1)抛物线y 2=2px 的准线方程为x =-p2,于是4+p2=5,p =2,所以抛物线的方程为y 2=4x .(2)由题意得A (4,4),B (0,4),M (0,2).又F (1,0), 所以k AF =43,则直线FA 的方程为y =43(x -1).因为MN ⊥FA ,所以k MN =-34,则直线MN 的方程为y =-34x +2.解方程组⎩⎨⎧ y =-34x +2,y =43(x -1)得⎩⎨⎧x =85,y =45,所以N ⎝⎛⎭⎫85,45.12.已知AB 是抛物线y 2=2px (p >0)的过焦点F 的一条弦.设A (x 1,y 1),B (x 2,y 2),AB 的中点为M (x 0,y 0).求证:(1)若AB 的倾斜角为θ,则|AB |=2psin 2θ; (2)x 1x 2=p 24,y 1y 2=-p 2;(3)1|AF |+1|BF |为定值2p. 证明:(1)设直线AB 的方程为x =my +p2,代入y 2=2px ,可得y 2-2pmy -p 2=0,则y 1y 2=-p 2,y 1+y 2=2pm ,∴y 21+y 22=2p (x 1+x 2)=(y 1+y 2)2-2y 1y 2=4p 2m 2+2p 2,∴x 1+x 2=2pm 2+p .当θ=90°时,m =0,x 1+x 2=p , ∴|AB |=x 1+x 2+p =2p =2p sin 2θ;当θ≠90°时,m =1tan θ,x 1+x 2=2ptan 2θ+p ,∴|AB |=x 1+x 2+p =2p tan 2θ+2p =2psin 2θ. ∴|AB |=2p sin 2θ. (2)由(1)知,y 1y 2=-p 2,∴x 1x 2=(y 1y 2)24p 2=p 24.(3)1|AF |+1|BF |=1x 1+p 2+1x 2+p2=x 1+x 2+p x 1x 2+p 2(x 1+x 2)+p 24=x 1+x 2+p p 2(x 1+x 2+p )=2p .13.已知抛物线y 2=2x .(1)设点A 的坐标为⎝⎛⎭⎫23,0,求抛物线上距离点A 最近的点P 的坐标及相应的距离|PA |; (2)在抛物线上求一点M ,使M 到直线x -y +3=0的距离最短,并求出距离的最小值. 解:(1)设抛物线上任一点P (x ,y ),则|PA |2=⎝⎛⎭⎫x -232+y 2=⎝⎛⎭⎫x -232+2x =⎝⎛⎭⎫x +132+13, 因为x ≥0,且在此区间上函数单调递增, 所以当x =0时,|PA |min =23,故距点A 最近的点P 的坐标为(0,0).(2)设点M (x 0,y 0)是y 2=2x 上任一点,则M 到直线x -y +3=0的距离为d =|x 0-y 0+3|2=⎪⎪⎪⎪⎪⎪y 20-2y 0+622=|(y 0-1)2+5|22,当y 0=1时,d min =522=524,所以点M 的坐标为⎝ ⎛⎭⎪⎫12,1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛物线专题练习1.(2020·吉林省长春模拟)点M (5,3)到抛物线y =ax 2的准线的距离为6,那么抛物线的标准方程是( )A .x 2=112yB .x 2=112y 或x 2=-136yC .x 2=-136yD .x 2=12y 或x 2=-36y2.(2020·江西省安义中学模拟)已知抛物线y =px 2(其中p 为常数)过点A (1,3),则抛物线的焦点到准线的距离等于( )A.92B.32C.118D.163.(2020·山东省乳山市第一中学模拟)顶点在原点,且过点(-4,4)的抛物线的标准方程是( ) A .y 2=-4xB .x 2=4yC .y 2=-4x 或x 2=4yD .y 2=4x 或x 2=-4y4.(2020·河南省信阳市第一中学模拟)已知AB 是抛物线y 2=8x 的一条焦点弦,|AB |=16,则AB 中点C 的横坐标是( )A .3B .4C .6D .85.(2020·四川省自贡市一中模拟)若直线AB 与抛物线y 2=4x 交于A ,B 两点,且AB ⊥x 轴,|AB |=42,则抛物线的焦点到直线AB 的距离为( )A .1B .2C .3D .56.(2020·四川省资阳模拟)设F 为抛物线y 2=2x 的焦点,A ,B ,C 为抛物线上三点,若F 为⊥ABC 的重心,则|F A →|+|FB →|+|FC →|的值为( )7.A .1 B .2 C .3 D .47.(2020·陕西省延安模拟)已知F 是抛物线C 1:y 2=2px (p >0)的焦点,曲线C 2是以F 为圆心,p2为半径的圆,直线4x -3y -2p =0与曲线C 1,C 2从上到下依次相交于点A ,B ,C ,D ,则|AB ||CD |=( )A .16B .4 C.83 D.538.(2020·广东省惠州市一中模拟)已知抛物线C :y 2=2px (p >0)的焦点为F ,准线方程为x =-2,过点F 的直线与抛物线C 交于M (x 1,y 1),N (x 2,y 2)两点,若|MN |=8,则y 21+y 22=( )A .16B .32C .24D .489.(2020·湖南省邵阳市二中模拟)已知F 是抛物线C :y 2=2px (p >0)的焦点,过点R (2,1)的直线l 与抛物线C 交于A ,B 两点,R 为线段AB 的中点.若|F A |+|FB |=5,则直线l的斜率为( )A .3B .1C .2D.1210.(2020·湖北省汉川市一中模拟)已知直线l :y =k (x +2)(k >0)与抛物线C :y 2=8x 相交于A ,B 两点,F 为C 的焦点.若|F A |=2|FB |,则k =( )A.13B.23C.23D.223 11.(2020·山东省菏泽市一中模拟)已知抛物线y 2=2px (p >0)的焦点F 与双曲线x 23-y 2=1的右焦点重合,若A 为抛物线在第一象限上的一点,且|AF |=3,则直线AF 的斜率为 .12.(2020·江西省任弼时中学模拟)若抛物线x 2=4y 上的点A 到焦点的距离为10,则点A 到x 轴的距离是 .13.(2020·福建省永春一中模拟)已知正三角形AOB (O 为坐标原点)的顶点A ,B 在抛物线y 2=3x 上,则⊥AOB 的边长是 .14.(2020·安徽省池州二中模拟)直线y=k(x-1)与抛物线y2=4x交于A,B两点,若|AB|=163,则k=.15.(2020·江苏省淮北中学模拟)已知抛物线y2=2px(p>0)过点A(2,y0),且点A到其准线的距离为4.(1)求抛物线的方程;(2)直线l:y=x+m与抛物线交于两个不同的点P,Q,若OP⊥OQ,求实数m的值.16.(2020·浙江省丽水中学模拟)如图,已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3.(1)求抛物线E的方程;(2)已知点G(-1,0),延长AF交抛物线E于点B,证明:GF为⊥AGB的平分线.17.(2020·吉林省松原市二中模拟)已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.(1)求抛物线的方程;(2)若过M作MN⊥F A,垂足为N,求点N的坐标.1.(2020·吉林省长春模拟)点M (5,3)到抛物线y =ax 2的准线的距离为6,那么抛物线的标准方程是( )A .x 2=112yB .x 2=112y 或x 2=-136yC .x 2=-136yD .x 2=12y 或x 2=-36y【答案】D【解析】将y =ax 2化为x 2=1a y .当a >0时,准线y =-14a ,则3+14a =6,⊥a =112.当a <0时,准线y =-14a ,则⎪⎪⎪⎪3+14a =6,⊥a =-136. ⊥抛物线方程为x 2=12y 或x 2=-36y2.(2020·江西省安义中学模拟)已知抛物线y =px 2(其中p 为常数)过点A (1,3),则抛物线的焦点到准线的距离等于( )A.92B.32C.118D.16【答案】D【解析】由抛物线y =px 2(其中p 为常数)过点A (1,3),可得p =3,则抛物线的标准方程为x 2=13y ,则抛物线的焦点到准线的距离等于16.故选D.]3.(2020·山东省乳山市第一中学模拟)顶点在原点,且过点(-4,4)的抛物线的标准方程是( ) A .y 2=-4xB .x 2=4yC .y 2=-4x 或x 2=4yD .y 2=4x 或x 2=-4y 【答案】C【解析】设所求抛物线方程为y 2=kx 或x 2=my ,又点(-4,4)在抛物线上,则有-4k =16或4m =16,解得k =-4或m =4,所求抛物线方程为y 2=-4x 或x 2=4y .故选C.]4.(2020·河南省信阳市第一中学模拟)已知AB 是抛物线y 2=8x 的一条焦点弦,|AB |=16,则AB 中点C 的横坐标是( )A .3B .4C .6D .8【答案】C【解析】设A (x 1,y 1),B (x 2,y 2),则|AB |=x 1+x 2+p =16,又p =4,所以x 1+x 2=12,所以点C 的横坐标是x 1+x 22=6.]5.(2020·四川省自贡市一中模拟)若直线AB 与抛物线y 2=4x 交于A ,B 两点,且AB ⊥x 轴,|AB |=42,则抛物线的焦点到直线AB 的距离为( )A .1B .2C .3D .5【答案】A【解析】由|AB |=42及AB ⊥x 轴,不妨设点A 的纵坐标为22,代入y 2=4x 得点A 的横坐标为2,从而直线AB 的方程为x =2.又y 2=4x 的焦点为(1,0),所以抛物线的焦点到直线AB 的距离为2-1=1,故选A.]6.(2020·四川省资阳模拟)设F 为抛物线y 2=2x 的焦点,A ,B ,C 为抛物线上三点,若F 为⊥ABC 的重心,则|F A →|+|FB →|+|FC →|的值为( )A .1B .2C .3D .4 【答案】C【解析】依题意,设点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),又焦点F ⎝⎛⎭⎫12,0,所以x 1+x 2+x 3=3×12=32,则|F A →|+|FB →|+|FC →|=⎝⎛⎭⎫x 1+12+⎝⎛⎭⎫x 2+12+⎝⎛⎭⎫x 3+12=(x 1+x 2+x 3)+32=32+32=3 7.(2020·陕西省延安模拟)已知F 是抛物线C 1:y 2=2px (p >0)的焦点,曲线C 2是以F 为圆心,p2为半径的圆,直线4x -3y -2p =0与曲线C 1,C 2从上到下依次相交于点A ,B ,C ,D ,则|AB ||CD |=( )A .16B .4 C.83 D.53【答案】A【解析】因为直线4x -3y -2p =0过C 1的焦点F (C 2的圆心),故|BF |=|CF |=p 2,所以|AB ||CD |=|AF |-p2|DF |-p2.由抛物线的定义得|AF |-p 2=x A ,|DF |-p2=x D .由⎩⎪⎨⎪⎧4x -3y -2p =0,y 2=2px ,整理得8x 2-17px +2p 2=0,即(8x -p )(x -2p )=0,可得x A =2p ,x D =p 8,故|AB ||CD |=x Ax D =2pp 8=16.故选A 8.(2020·广东省惠州市一中模拟)已知抛物线C :y 2=2px (p >0)的焦点为F ,准线方程为x =-2,过点F 的直线与抛物线C 交于M (x 1,y 1),N (x 2,y 2)两点,若|MN |=8,则y 21+y 22=( )A .16B .32C .24D .48【答案】B【解析】由准线方程为x =-2,可知p =4,则抛物线C 的方程为y 2=8x .由抛物线的定义可知,|MN |=|MF |+|NF |=x 1+x 2+4=8,则x 1+x 2=4,即y 218+y 228=4,故y 21+y 22=32.故选B.] 9.(2020·湖南省邵阳市二中模拟)已知F 是抛物线C :y 2=2px (p >0)的焦点,过点R (2,1)的直线l 与抛物线C 交于A ,B 两点,R 为线段AB 的中点.若|F A |+|FB |=5,则直线l 的斜率为( )A .3B .1C .2 D.12【答案】B【解析】由于R (2,1)为AB 中点,设A (x A ,y A ),B (x B ,y B ).根据抛物线的定义|F A |+|FB |=x A +x B +p =2×2+p =5,解得p =1,抛物线方程为y 2=2x .y 2A =2x A ,y 2B =2x B,两式相减并化简得y B-y A x B -x A =2y A +y B =22×1=1,即直线l 的斜率为1.故选B.]10.(2020·湖北省汉川市一中模拟)已知直线l :y =k (x +2)(k >0)与抛物线C :y 2=8x 相交于A ,B 两点,F 为C 的焦点.若|F A |=2|FB |,则k =( )A.13B.23C.23D.223 【答案】D【解析】由⎩⎪⎨⎪⎧y =k (x +2),y 2=8x ,消去y 得k 2x 2+(4k 2-8)x +4k 2=0.Δ=(4k 2-8)2-16k 4>0,解得-1<k <1.设A (x 1,y 1),B (x 2,y 2).x 1+x 2=8k 2-4.⊥ x 1x 2=4.⊥ 根据抛物线的定义及|F A |=2|FB |,得x 1+2=2(x 2+2),即x 1=2x 2+2,⊥且x 1>0,x 2>0,由⊥⊥解得x 1=4,x 2=1,代入⊥得k 2=89,k >0,⊥k =223.故选D.11.(2020·山东省菏泽市一中模拟)已知抛物线y 2=2px (p >0)的焦点F 与双曲线x 23-y 2=1的右焦点重合,若A 为抛物线在第一象限上的一点,且|AF |=3,则直线AF 的斜率为 .【答案】-22【解析】⊥双曲线x 23-y 2=1的右焦点为(2,0),⊥抛物线方程为y 2=8x .⊥|AF |=3,⊥x A +2=3,得x A =1,代入抛物线方程可得y A =±2 2.⊥点A 在第一象限,⊥A (1,22),⊥直线AF 的斜率为221-2=-2 2.]12.(2020·江西省任弼时中学模拟)若抛物线x 2=4y 上的点A 到焦点的距离为10,则点A 到x 轴的距离是 .【答案】9【解析】根据题意,抛物线x 2=4y 的准线方程为y =-1,点A 到准线的距离为10,故点A 到x 轴的距离是9.]13.(2020·福建省永春一中模拟)已知正三角形AOB (O 为坐标原点)的顶点A ,B 在抛物线y 2=3x 上,则⊥AOB 的边长是 .【答案】63【解析】如图,设⊥AOB 的边长为a ,则A ⎝⎛⎭⎫32a ,12a ,⊥点A 在抛物线y 2=3x 上,⊥14a 2=3×32a ,⊥a =6 3.] 14.(2020·安徽省池州二中模拟)直线y =k (x -1)与抛物线y 2=4x 交于A ,B 两点,若|AB |=163,则k = .【答案】±3【解析】设A (x 1,y 1),B (x 2,y 2),因为直线AB 经过抛物线y 2=4x 的焦点,所以|AB |=x 1+x 2+2=163,所以x 1+x 2=103.联立⎩⎪⎨⎪⎧y 2=4x ,y =k (x -1)得到k 2x 2-(2k 2+4)x +k 2=0,所以x 1+x 2=2k 2+4k 2=103,所以k =± 3.]15.(2020·江苏省淮北中学模拟)已知抛物线y 2=2px (p >0)过点A (2,y 0),且点A 到其准线的距离为4.(1)求抛物线的方程;(2)直线l :y =x +m 与抛物线交于两个不同的点P ,Q ,若OP ⊥OQ ,求实数m 的值. 【解析】(1)已知抛物线y 2=2px (p >0)过点A (2,y 0),且点A 到准线的距离为4, ⊥2+p2=4,⊥p =4,⊥抛物线的方程为y 2=8x .(2)由⎩⎪⎨⎪⎧y =x +m ,y 2=8x 得x 2+(2m -8)x +m 2=0.设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=8-2m ,x 1x 2=m 2,y 1+y 2=x 1+x 2+2m =8,y 1y 2=(x 1+m )(x 2+m )=x 1x 2+m (x 1+x 2)+m 2=8m . ⊥OP ⊥OQ ,⊥x 1x 2+y 1y 2=m 2+8m =0, ⊥m =0或m =-8.经检验,当m =0时,直线与抛物线交点中有一点与原点O 重合,不符合题意. 当m =-8时,Δ=(-24)2-4×64>0,符合题意. 综上,实数m 的值为-8.16.(2020·浙江省丽水中学模拟)如图,已知点F 为抛物线E :y 2=2px (p >0)的焦点,点A (2,m )在抛物线E 上,且|AF |=3.(1)求抛物线E 的方程;(2)已知点G (-1,0),延长AF 交抛物线E 于点B ,证明:GF 为⊥AGB 的平分线. 【解析】(1)由抛物线定义可得|AF |=2+p2=3,解得p =2.⊥抛物线E 的方程为y 2=4x .(2)证明:⊥点A (2,m )在抛物线E 上,⊥m 2=4×2,解得m =±22,由抛物线的对称性,不妨设A (2,22),由A (2,22),F (1,0), ⊥直线AF 的方程为y =22(x -1),由⎩⎨⎧y =22(x -1),y 2=4x ,得2x 2-5x +2=0,解得x =2或12,⊥B ⎝⎛⎭⎫12,-2. 又G (-1,0),⊥k GA =223,k GB =-223,⊥k GA +k GB =0, ⊥⊥AGF =⊥BGF .⊥GF 为⊥AGB 的平分线.17.(2020·吉林省松原市二中模拟)已知抛物线y 2=2px (p >0)的焦点为F ,A 是抛物线上横坐标为4,且位于x 轴上方的点,A 到抛物线准线的距离等于5,过A 作AB 垂直于y 轴,垂足为B ,OB 的中点为M .(1)求抛物线的方程;(2)若过M 作MN ⊥F A ,垂足为N ,求点N 的坐标.【解析】(1)抛物线y 2=2px (p >0)的准线为x =-p 2,于是4+p 2=5,⊥p =2. ⊥抛物线方程为y 2=4x .(2)⊥点A 的坐标是(4,4),由题意得B (0,4),M (0,2).又⊥F (1,0),⊥k F A =43, ⊥MN ⊥F A ,⊥k MN =-34. ⊥F A 的方程为y =43(x -1), ⊥ MN 的方程为y -2=-34x , ⊥联立⊥⊥,解得x =85,y =45, ⊥点N 的坐标为⎝⎛⎭⎫85,45.。
