吉林省辽源市田家炳高级中学复数试题及答案doc
2015-2016年吉林省辽源市田家炳高中高二(下)期中数学试卷(理科)和答案

2015-2016学年吉林省辽源市田家炳高中高二(下)期中数学试卷(理科)一、选择题(本题共12小题,每题5分,共60分)1.(5分)在复平面内,复数i(2﹣i)对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.(5分)用三段论推理:“任何实数的平方大于0,因为a是实数,所以a2>0”,你认为这个推理()A.大前提错误B.小前提错误C.推理形式错误D.是正确的3.(5分)f(x)=x3﹣3x2+2在区间[﹣1,1]上的最大值是()A.﹣2B.0C.2D.44.(5分)用反证法证明命题:“若a、b、c是三连续的整数,那么a、b、c中至少有一个是偶数”时,下列假设正确的是()A.假设a、b、c中至多有一个偶数B.假设a、b、c中至多有两个偶数C.假设a、b、c都是偶数D.假设a、b、c都不是偶数5.(5分)已知函数f(x)的导函数为f′(x),且满足关系式f(x)=x2+3xf′(2),则f′(2)的值等于()A.﹣2B.﹣1C.4D.26.(5分)若a>b>0,则下列不等式中总成立的是()A.a+>b+B.>C.a+>b+D.>7.(5分)已知R上可导函数f(x)的图象如图所示,则不等式(x2﹣2x﹣3)f′(x)>0的解集为()A.(﹣∞,﹣2)∪(1,+∞)B.(﹣∞,﹣2)∪(1,2)C.(﹣∞,﹣1)∪(﹣1,0)∪(2,+∞)D.(﹣∞,﹣1)∪(﹣1,1)∪(3,+∞)8.(5分)若曲线y=x2+ax+b在点(0,b)处的切线方程x﹣y+1=0,则()A.a=1,b=1B.a=﹣1,b=1C.a=1,b=﹣1D.a=﹣1,b=﹣1 9.(5分)若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.B.﹣i C.i D.410.(5分)定积分dx的值为()A.9πB.3πC.D.11.(5分)某厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x小时,原油温度(单位:℃)为,那么,原油温度的瞬时变化率的最小值是()A.8B.C.﹣1D.﹣812.(5分)若f(x)是定义在R上的可导函数,且满足(x﹣1)f′(x)≥0,则必有()A.f(0)+f(2)<2f(1)B.f(0)+f(2)>2f(1)C.f(0)+f(2)≤2f(1)D.f(0)+f(2)≥2f(1)二、填空题(本题共4小题,每道小题5分,共20分)13.(5分)的共轭复数为.14.(5分)已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值范围是.15.(5分)曲线y=lnx上的点到直线2x﹣y+3=0的最短距离是.16.(5分)观察下列式子:,,,…,则可以猜想:.三、解答题(本题共6小题,共70分)17.(10分)已知复数z=1﹣i(i是虚数单位)(1)计算z2;(2)若z2+a,求实数a,b的值.18.(12分)已知函数f(x)=x3﹣ax+a(Ⅰ)若函数f(x)恰好有两个不同的零点,求a的值.(Ⅱ)若函数f(x)的图象与直线y=x﹣1相切,求a的值及相应的切点坐标.19.(12分)设f(x)=e x﹣ax﹣a.(Ⅰ)若a=1,求f(x)的单调区间;(Ⅱ)若f(x)≥0对一切x≥﹣1恒成立,求a的取值范围.20.(12分)已知数列a n的前n项和为S n,且a1=1,S n=n2a n(n∈N),(1)试计算S1,S2,S3,S4,并猜想S n的表达式;(2)证明你的猜想,并求出a n的表达式.21.(12分)求由抛物线y=﹣x2+4x﹣3与它在点A(0,﹣3)和点B(3,0)的切线所围成的区域面积.22.(12分)已知函数f(x)=x3+ax2+bx+c在与x=1时都取得极值;(1)求a,b的值及f(x)的极大值与极小值;(2)若方程x3+ax2+bx+c=1有三个互异的实根,求c的取值范围;(3)若对x∈[1,2],不等式f(x)<c2恒成立,求c的取值范围.2015-2016学年吉林省辽源市田家炳高中高二(下)期中数学试卷(理科)参考答案与试题解析一、选择题(本题共12小题,每题5分,共60分)1.(5分)在复平面内,复数i(2﹣i)对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵复数z=i(2﹣i)=﹣i2+2i=1+2i∴复数对应的点的坐标是(1,2)这个点在第一象限,故选:A.2.(5分)用三段论推理:“任何实数的平方大于0,因为a是实数,所以a2>0”,你认为这个推理()A.大前提错误B.小前提错误C.推理形式错误D.是正确的【解答】解:∵任何实数的平方大于0,因为a是实数,所以a2>0,大前提:任何实数的平方大于0是不正确的,0的平方就不大于0.故选:A.3.(5分)f(x)=x3﹣3x2+2在区间[﹣1,1]上的最大值是()A.﹣2B.0C.2D.4【解答】解:f'(x)=3x2﹣6x=3x(x﹣2),令f'(x)=0可得x=0或2(2舍去),当﹣1<x<0时,f'(x)>0,当0<x<1时,f'(x)<0,∴当x=0时,f(x)取得最大值为f(0)=2.故选:C.4.(5分)用反证法证明命题:“若a、b、c是三连续的整数,那么a、b、c中至少有一个是偶数”时,下列假设正确的是()A.假设a、b、c中至多有一个偶数B.假设a、b、c中至多有两个偶数C.假设a、b、c都是偶数D.假设a、b、c都不是偶数【解答】解:用反证法证明数学命题的方法,应先假设要证命题的否定成立,而命题:“整数a,b,c中至少有一个偶数”的否定为:“a,b,c都不是偶数”,故选:D.5.(5分)已知函数f(x)的导函数为f′(x),且满足关系式f(x)=x2+3xf′(2),则f′(2)的值等于()A.﹣2B.﹣1C.4D.2【解答】解:∵f(x)=x2+3xf'(2),∴f′(x)=2x+3f′(2)令x=2得f′(2)=2×2+3f′(2)∴f′(2)=﹣2.故选:A.6.(5分)若a>b>0,则下列不等式中总成立的是()A.a+>b+B.>C.a+>b+D.>【解答】解:∵a>b>0,∴>.又a>b,∴a+>b+;故选:A.7.(5分)已知R上可导函数f(x)的图象如图所示,则不等式(x2﹣2x﹣3)f′(x)>0的解集为()A.(﹣∞,﹣2)∪(1,+∞)B.(﹣∞,﹣2)∪(1,2)C.(﹣∞,﹣1)∪(﹣1,0)∪(2,+∞)D.(﹣∞,﹣1)∪(﹣1,1)∪(3,+∞)【解答】解:由图象可得:当f′(x)>0时,函数f(x)是增函数,所以f′(x)>0的解集为(﹣∞,﹣1),(1,+∞),当f′(x)<0时,函数f(x)是减函数,所以f′(x)<0的解集为(﹣1,1).所以不等式f′(x)<0即与不等式(x﹣1)(x+1)<0的解集相等.由题意可得:不等式(x2﹣2x﹣3)f′(x)>0等价于不等式(x﹣3)(x+1)(x+1)(x﹣1)>0,所以原不等式的解集为(﹣∞,﹣1)∪(﹣1,1)∪(3,+∞),故选:D.8.(5分)若曲线y=x2+ax+b在点(0,b)处的切线方程x﹣y+1=0,则()A.a=1,b=1B.a=﹣1,b=1C.a=1,b=﹣1D.a=﹣1,b=﹣1【解答】解:y=x2+ax+b的导数为y′=2x+a,可得在点(0,b)处的切线斜率为a,由点(0,b)处的切线方程为x﹣y+1=0,可得a=1,b=1,故选:A.9.(5分)若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.B.﹣i C.i D.4【解答】解:∵|4+3i|==5.∴(3﹣4i)z=|4+3i|,化为===,则z的虚部为.故选:A.10.(5分)定积分dx的值为()A.9πB.3πC.D.【解答】解:由定积分的几何意义知是由曲线,直线x=0,x=3围成的封闭图形的面积,故=,故选:C.11.(5分)某厂将原油精炼为汽油,需对原油进行冷却和加热,如果第x小时,原油温度(单位:℃)为,那么,原油温度的瞬时变化率的最小值是()A.8B.C.﹣1D.﹣8【解答】解:由题意,f′(x)=x2﹣2x=(x﹣1)2﹣1∵0≤x≤5∴x=1时,f′(x)的最小值为﹣1,即原油温度的瞬时变化率的最小值是﹣1故选:C.12.(5分)若f(x)是定义在R上的可导函数,且满足(x﹣1)f′(x)≥0,则必有()A.f(0)+f(2)<2f(1)B.f(0)+f(2)>2f(1)C.f(0)+f(2)≤2f(1)D.f(0)+f(2)≥2f(1)【解答】解:∵(x﹣1)f'(x)≥0∴x>1时,f′(x)≥0;x<1时,f′(x)≤0∴f(x)在(1,+∞)为增函数;在(﹣∞,1)上为减函数∴f(2)≥f(1)f(0)≥f(1)∴f(0)+f(2)≥2f(1)故选:D.二、填空题(本题共4小题,每道小题5分,共20分)13.(5分)的共轭复数为﹣i.【解答】解:∵==+i,∴的共轭复数为﹣i故答案为:﹣i14.(5分)已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值范围是﹣1≤a<7.【解答】解:由题意,f′(x)=3x2+4x﹣a,当f′(﹣1)f′(1)<0时,函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,解得﹣1<a<7,当a=﹣1时,f′(x)=3x2+4x+1=0,在(﹣1,1)上恰有一根x=﹣,当a=7时,f′(x)=3x2+4x﹣7=0在(﹣1,1)上无实根,则a的取值范围是﹣1≤a<7,故答案为﹣1≤a<7.15.(5分)曲线y=lnx上的点到直线2x﹣y+3=0的最短距离是.【解答】解:因为直线2x﹣y+3=0的斜率为2,所以令y′==2,解得:x=,把x=代入曲线方程得:y=﹣ln2,即曲线上过(,﹣ln2)的切线斜率为2,则(,﹣ln2)到直线2x﹣y+3=0的距离d==,即曲线y=lnx上的点到直线2x﹣y+3=0的最短距离是.故答案为:16.(5分)观察下列式子:,,,…,则可以猜想:.【解答】解:由已知中的式子:=,=,=,…,我们可以推断故=故答案为:三、解答题(本题共6小题,共70分)17.(10分)已知复数z=1﹣i(i是虚数单位)(1)计算z2;(2)若z2+a,求实数a,b的值.【解答】解:(1)z2=(1﹣i)2=1﹣2i+i2=1﹣2i﹣1=﹣2i…(4分)(2)…(6分)所以由复数相等的充要条件得:…(8分)所以…(10分)18.(12分)已知函数f(x)=x3﹣ax+a(Ⅰ)若函数f(x)恰好有两个不同的零点,求a的值.(Ⅱ)若函数f(x)的图象与直线y=x﹣1相切,求a的值及相应的切点坐标.【解答】解:(Ⅰ)函数的导数f′(x)=x2﹣a,若a≤0,函数f′(x)=x2﹣a≥0,此时f(x)单调递增,不满足条件,若a>0,由f′(x)=x2﹣a=0的x=±,则x=±,是函数f(x)的两个极值点,若若函数f(x)恰好有两个不同的零点,则f(±)=0,∵f(0)=a>0,∴只能有f()=0,即()3﹣a•+a=0,即﹣+1=0,即=1,=,即a=.(Ⅱ)设切点P(m,n),则f′(m)=m2﹣a,则切线方程为y﹣(m3﹣am+a)=(m2﹣a)(x﹣m),即y=(m2﹣a)x+a﹣m3,∵切线方程为y=x﹣1,∴m2﹣a=1,a﹣m3=﹣1,即m3=0,即m=0,此时n=m﹣1=﹣1,a=﹣1,即若函数f(x)的图象与直线y=x﹣1相切,则a=﹣1,相应的切点坐标P(0,﹣1).19.(12分)设f(x)=e x﹣ax﹣a.(Ⅰ)若a=1,求f(x)的单调区间;(Ⅱ)若f(x)≥0对一切x≥﹣1恒成立,求a的取值范围.【解答】解:(Ⅰ)a=1时,f(x)=e x﹣x﹣1,∴f′(x)=e x﹣1,令f′(x)>0,解得:x>0,令f′(x)<0,解得:x<0,∴f(x)在(﹣∞,0)递减,在(0,+∞)递增;(Ⅱ)由f(x)≥0,得a≤,(x>﹣1),令h(x)=,则h′(x)=,令h′(x)>0,解得:x>0,令h′(x)<0,解得:﹣1<x<0,∴h(x)在(﹣1,0)递减,在(0,+∞)递增,∴h(x)≥h(0)=1,(x>﹣1),∴a≤1,又x=﹣1时,(x+1)a≤e x即为0•a≤e﹣1,此时a取任意值都成立,综上得:a≤1.20.(12分)已知数列a n的前n项和为S n,且a1=1,S n=n2a n(n∈N),(1)试计算S1,S2,S3,S4,并猜想S n的表达式;(2)证明你的猜想,并求出a n的表达式.【解答】解:(1)由a1=1,S n=n2a n(n∈N)得猜想(2)证明:∵S n=n2a n①∴S n﹣1=(n﹣1)2a n﹣1②=n2a n﹣(n﹣1)2a n﹣1①﹣②得S n﹣S n﹣1∴a n=n2a n﹣(n﹣1)2a n﹣1化简得∴把上面各式相乘得∴21.(12分)求由抛物线y=﹣x2+4x﹣3与它在点A(0,﹣3)和点B(3,0)的切线所围成的区域面积.【解答】解:∵y=﹣x2+4x﹣3,∴y′=﹣2x+4,x=0时,y′=4,x=3时,y′=﹣2,∴在点A(0,﹣3)和点B(3,0)的切线方程分别为y=4x﹣3和y=﹣2x+6,两条切线的交点是(1.5,3),如图所示,区域被直线x=1.5分成了两部分,∴所求面积为S=+=+=2.25.22.(12分)已知函数f(x)=x3+ax2+bx+c在与x=1时都取得极值;(1)求a,b的值及f(x)的极大值与极小值;(2)若方程x3+ax2+bx+c=1有三个互异的实根,求c的取值范围;(3)若对x∈[1,2],不等式f(x)<c2恒成立,求c的取值范围.【解答】解:(1)∵f'(x)=3x2+2ax+b由已知有,解得﹣﹣﹣﹣﹣﹣(3分)∴f'(x)=3x2﹣x﹣2,由f'(x)>0得x>1或,由f'(x)<0得﹣﹣﹣(5分)列表如下所以,当时,f(x)有极大值,当x=1时,f(x)有极小值﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)(2)由于方程x3+ax2+bx+c=1有三个互异的实根,故曲线与y=1有三个不同交点﹣﹣﹣﹣﹣﹣﹣﹣(9分)由(1)可知此时有,解得;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)(3)由(1)知,f(x)在x∈[1,2]上递增,此时f(x)max=f(2)=c+2﹣﹣(14分)要满足题意,只须c+2<c2解得c>2或c<﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(16分)。
7.1 复数的概念(精练)(解析版)

7.1 复数的概念(精练)【题组一 实部虚部辨析】1.(2020·江西抚州市)若(2)x i i y i +=+,其中,x y R ∈,i 为虚数单位,则复数z x yi =+的虚部为( ) A .1 B .iC .2-D .2i -【答案】C【解析】由于(2)x i i y i +=+,则1x=且2y =-,所以12z x yi i =+=-,所以复数z 的虚部为2-. 故选:C.2.(2020·江苏宿迁市·宿迁中学高二期中)设i 为虚数单位,则复数55z i =-的实部为( ) A .5- B .5i -C .5D .5i【答案】C【解析】复数55z i =-的实部为5.故选:C.3.(2020·广西桂林市)复数3z i =-的虚部是( ) A .1 B .iC .-1D .i -【答案】C【解析】由复数虚部的定义得复数3z i =-的虚部是1-.故选:C4.(2020·四川省成都市新都一中高二期中)复数24i z =--的虚部是( ) A .2- B .2C .4-D .4【答案】C【解析】因为24i z =--,所以由复数定义可知虚部是4-,故选:C.5.(2020·江苏宿迁市·高二期中)已知复数1z i =-,其中i 是虚数单位,则复数z 的虚部为( ) A .i B .i -C .1-D .1【答案】C【解析】因为1z i =-,则虚部为1-.故选:C. 【题组二 复数的分类】1.(2021·江西景德镇市)已知复数()()1i 1i z m =--+是纯虚数,则实数m =( ) A .-2 B .-1C .0D .1【答案】D【解析】()()()1i 1i 11i z m m m =--+=--+,因为z 为纯虚数且m 为实数,故1010m m -=⎧⎨+≠⎩,故1m =,故选:D2.(2021·甘肃兰州市·兰州一中)i 为虚数单位,已知复数21(1)a a i -+-是纯虚数,则a 等于( ) A .±1 B .1C .1-D .0【答案】C【解析】复数21(1)a a i -+-是纯虚数,所以21010a a ⎧-=⎨-≠⎩,得1a =-.故选:C.3.(2021·江西南昌市)设复数i z a b =+(其中a b R ∈、,i 为虚数单位),则“0a =”是“z 为纯虚数”的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分又非必要条件【答案】B【解析】若复数i z a b =+是纯虚数,则0a =,0b ≠, 则0a =不能证得z 为纯虚数,z 为纯虚数可以证得0a =, 故“0a =”是“z 为纯虚数”的必要非充分条件, 故选:B.4.(2020·贵州毕节市)已知a 为实数,若复数()24(2)z a a i =-++为纯虚数,则复数z 的虚部为( ) A .2 B .4iC .2±D .4【答案】D【解析】2(4)(2)z a a i =-++为纯虚数,∴24020a a ⎧-=⎨+≠⎩,即2a =.∴复数z 的虚部为4. 故选:D .5.(2020·沙坪坝区·重庆南开中学高二期末)已知i 为虚数单位,a R ∈,复数()242a a i -+-是纯虚数,则a =( ) A .2 B .-2 C .4 D .-2或2【答案】B【解析】因为复数()242a a i -+-是纯虚数,所以240,202a a a -=-≠∴=-故选:B6.(2020·北京市八一中学高二期中)若复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则m =______ 【答案】-1【解析】复数(1)(2)z m m i =++-(m ∈R )是纯虚数,则1020m m +=⎧⎨-≠⎩,所以1m =-. 故答案为:-17.(2019·河南洛阳市·高二期中(文))已知复数223(3)z m m m i =--+-为纯虚数,则实数m =_____________ 【答案】1-【解析】由题意,复数223(3)z m m m i =--+-为纯虚数,则满足223030m m m ⎧--=⎨-≠⎩,解得1m =-,即实数m 的值为1-.故答案为:1-.8.(2020·林芝市第二高级中学)实数m 取怎样的值时,复数()22153m m z i m --=-+是: (1)实数? (2)虚数? (3)纯虚数?【答案】(1)5m =或3m =-;(2)5m ≠且3m ≠-;(3)3m =. 【解析】(1)若22150m m --=,则z 为实数,此时3m =-或者5m =. (2)若22150m m --≠,则z 为虚数,此时3m ≠-且5m ≠.(3)若2302150m m m -=⎧⎨--≠⎩ ,则z 为纯虚数,此时3m =.9.(2020·辽源市田家炳高级中学校)已知复数()()11z m m i m R =++-∈. (1)m 取什么值时,z 为实数; (2)m 取什么值时,z 为纯虚数. 【答案】(1)1m =(2)1m =-【解析】(1)复数()()11z m m i m R =++-∈,若z 为实数,则10m -=,即1m =(2)若z 为纯虚数,则1010m m +=⎧⎨-≠⎩,解得1m =-10.(2021·江西上饶市)已知m 为实数,i 为虚数单位,设复数()()2256253z m m m m i =++++-. (1)当复数z 为纯虚数时,求m 的值;(2)当复数z 对应的复点在直线70x y -+=的右下方,求m 的取值范围. 【答案】(1)2-;(2)(4,4)-.【解析】(1)由题意得:225602530m m m m ⎧++=⎨+-≠⎩,解得2m =-;(2)复数z 对应的点的坐标为22(56,253)m m m m +++-, 直线70x y -+=的右下方的点的坐标(),x y 应满足70x y -+>,所以22(56)(253)70m m m m ++-+-+>,解得44m -<<,所以m 的取值范围为(4,4)-. 【题组三 复数的几何意义--复平面】1.(2019·重庆市江津第六中学校高二期中)在复平面内,复数1i -+所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】B【解析】由题,1i -+在复平面内对应的点为()1,1-,在第二象限,故选:B2.(2020·甘肃省岷县第二中学)若,a b ∈R ,则复数()()224526a a b b i -++-+-表示的点在( ) A .在第一象限 B .在第二象限 C .在第三象限 D.在第四象限【答案】D【解析】因为()2245210a a a -+=-+>,()2226150b b b -+-=---<, 所以由复数的几何意义知该复数表示的点在第四象限.故选:D3.(2019·周口市中英文学校高二期中(文))复数()()2lg 2221()x xz x i x R -=-+-+-∈在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【解析】复数()()2lg 2221()x xz x i x R -=-+-+-∈的实部()2lg 2a x -=+、虚部()221x x b -=-+-.因为()22221lg 20x x +≥>⇒+>,所以0a <. 因为21122202x x x x --≥-+⇒≥>+,所以0b <. 所以复数z 在复平面内对应的点位于第三象限.故选:C4.(2020·朔州市朔城区第一中学校)设复数1z ,2z 在复平面内对应的点关于虚轴对称,且12z i =+,则2z =( )A .2i +B .2i -+C .2i -D .2i --【答案】B 【解析】12z i =+,1z ∴在复平面内对应点的坐标为(2,1),由复数1z ,2z 在复平面内对应的点关于虚轴对称,可知2z 在复平面内对应的点的坐标为(2,1)-,22z i ∴=-+,故选:B .5.(2020·重庆高二期中)已知()()214Z m m i =++-在复平面内对应的点在第二象限,则实数m 的取值范围是____. 【答案】(),2-∞-【解析】()()214Z m m i =++-在复平面内对应的点()21,4m m +-在第二象限,所以21040m m +<⎧⎨->⎩,解得2m <-,即实数m 的取值范围是(),2-∞-.故答案为:(),2-∞-6.(2020·浙江台州市·高二期中)已知复数()()22lg 223z m m m m i =-++-若复数z 是实数,则实数m =________;若复数z 对应的点位于复平面的第二象限,则实数的取值范围为________.【答案】3- 21m <<+【解析】z 为实数,则2230m m +-=,解得1m =或3-,又220m m ->,所以3m =-.z对应点在第二象限,则22lg(2)0230m m m m ⎧-<⎨+->⎩,解得21m <<.故答案为:3-;21m <<+7(2021·宁夏长庆高级中学)在复平面内,复数()()222z m m m i =++--对应的点在第一象限,求实数m 的取值范围是________. 【答案】()()2,12,--+∞【解析】根据题意得出22020m m m +>⎧⎨-->⎩,解得21m -<<-或>2m ,所以实数m 的取值范围是()()2,12,--+∞.故答案为:()()2,12,--+∞.【题组四 复数的几何意义--模长】1.(2021·浙江高二期末)已知a R ∈,若有a i -=i 为虚数单位),则a =( ) A .1 B .2-C .2±D .±1【答案】C【解析】因为a R ∈所以a i -==,即215a +=,解得2a =±,故选:C2.(2020·辽宁沈阳市·高二期中)设复数z 满足1z i -=,z 在复平面内对应的点为(),x y 则x ,y 满足的关系式为______. 【答案】22(1)1y x +-=【解析】由题意,设复数(,)z x yi x y R =+∈,因为1z i -=1=,整理得22(1)1y x +-=,即复数z 在复平面内对应的点为(),x y 则,x y 满足的关系式为22(1)1y x +-=.故答案为:22(1)1y x +-=.3.(2021·江苏高二)已知a ,b R ∈,()123ai b a i +=++,则a =______,3a bi +=______.【答案】3- 【解析】∵()123ai b a i +=++∴123ba a =⎧⎨=+⎩,解得31a b =-⎧⎨=⎩,则333a bi i +=-+===故答案为:(1)3-;(2)4.(2020·北京人大附中高二月考)已知i 是虚数单位,若1z i =+,则22z z -=________. 【答案】2【解析】根据复数模的计算公式得:22212+222z z i i i -=+--=.故答案为:25.(2020·上海市通河中学高二期中)若z C ∈且342z i ++≤,则z 的取值范围为__________. 【答案】[]3,7【解析】342z i ++≤的几何意义为复平面内动点Z 到定点()3,4A --的距离小于等于2的点的集合,z 表示复平面内动点Z 到原点的距离,∵||5OA ==,5252z ∴-≤≤+.∴z 的取值范围为[]3,7. 故答案为:[]3,7. 【题组五 复数综合应用】1.(多选)(2020·江苏泰州市·高二期末)已知复数1z i =+(其中i 为虚数单位),则以下说法正确的有( )A .复数z 的虚部为iB .z =C .复数z 的共轭复数1z i =-D .复数z 在复平面内对应的点在第一象限【答案】BCD【解析】因为复数1z i =+, 所以其虚部为1,即A 错误;z ==B 正确;复数z 的共轭复数1z i =-,故C 正确;复数z 在复平面内对应的点为()1,1,显然位于第一象限,故D 正确. 故选:BCD.2.(2020·重庆高二期末)若复数12z i =+(i 为虚数单位),则下列命题正确的是( )A .z 是纯虚数B .z 的实部为2C .z 的共轭复数为12i -+D .z 【答案】D【解析】复数12z i =+(i 为虚数单位)显然不是纯虚数,12z i =+的实部是1,z 的共轭复数为12i -,z =D 正确,故选:D.3.(2020·山东聊城市·高二期末)已知复数z 在复平面上对应的点为()1,1-,则( ) A .z i +是实数(i 为虚数单位) B .z i +是纯虚数(i 为虚数单位) C .1z +是实数 D .1z +是纯虚数 【答案】D【解析】由题意可得,1z i =-+,则1z i +=为纯虚数,12z i i +=-+是虚数,但不是纯虚数, 故选:D .4.(2020·咸阳百灵学校)关于复数3-4i 的说法正确的是( ) ①实部和虚部分别为3和-4;②复数模为5③在复平面内对应的点在第四象限;④共轭复数为3+4i A .①③ B .①②④C .①②③④D .①③④【答案】C【解析】复数3-4i 的实部和虚部分别为3和-4,①正确;复数模为5,②正确;在复平面内对应的点为(3,4)-在第四象限,③正确;复数3-4i 的共轭复数为3+4i ,④正确.故选:C.。
吉林省辽源市田家炳高级中学2021-2022学年高一上学期12月月考英语试题 Word版含答案

田家炳高中2021--2022学年度上学期12月月考高一英语试卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5个小题:每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Where does this conversation take place?A.In a bookstore.B.In the kitchen.C.In a restaurant.2.How does the woman’s daughter usually go to school?A.On foot.B.By bike.C.On her school bus.3.Why does the woman refuse to drink milk today?A.Because she doesn’t feel alright.B.Because the milk has become bad.C.Because she drank to much yesterday.4.What did the man do this afternoon?A.He went swimming.B.He stayed at home.C.He watched a movie.5.What’s the weather like today?A.Sunny.B. RainyC. Snowy.其次节共15小题;(每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
吉林省辽源市田家炳高级中学2021-2022高一英语12月月考试题.doc

吉林省辽源市田家炳高级中学2021-2022高一英语12月月考试题第Ⅰ卷第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)1. Where does the man usually eat?A. At home.B. In his office.C. At a restaurant.2. Who is wanted on the phone?A. Susan.B. LilyC. Tom.3. What will the man do on Sunday?A. Go hiking.B. Write a report.C. Take a holiday.4. What are the two speakers talking about?A. Hobbies.B. MusicC. Musical instruments.5. What does the woman think of the activity?A. She thinks it is dull.B. She thinks it is interesting.C. She thinks it is just so-so.第二节(共15小题;每小题1.5分,满分22.5分)听第6段材料,回答第6至7题。
6. What does the woman think of the man's breakfast he had this morning?A. She thinks it is healthy.B. She thinks it is delicious.C. She thinks it is simple.7. Who usually makes breakfast at the man's home?A. The man's mother.B. The man's father.C. The man.听第7段材料,回答第8至10题。
吉林辽源市田家炳高级中学校高二上学期期中考试英语试题含答案

田家炳高中高二2020-2021第一学期期中英语学科试题高二英语试卷第I卷(选择题)第一部分:听力(共两节,20小题,满分30分)。
第一节(共5小题;每小题1.5分,满分7. 5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What are the speakers mainly talking about?A.Turning off the light.B.Power failure.C.Buying air-conditioning.2.How does the man usually go to work?A.By car.B. On foot.C. By bus.3.What color does the man prefer to paint the bedroom?A.Pink.B. Yellow.C.Light blue.4.Where was the man last night?A. At the concert.B.At home.C. In the library.5.What do we know about the man?A.He used to have a car.B.He likes driving.C.He enjoys traveling by car.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白,每段对话或独白后有几个小题。
从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6.How much should the woman pay for the flat every week if she takes it?A. 17 pounds.B. 70 pounds.C. 30 pounds.7.What does the woman prefer?A.A flat without a kitchen.B.A flat with a big sitting room.C.A room of her own.听第7段材料,回答第8、9题。
吉林省辽源市田家炳高级中学2021-2022高一数学上学期12月月考试题(含解析)

吉林省辽源市田家炳高级中学2021-2022高一数学上学期12月月考试题(含解析)一、选择题 (每题5分 共60分)1.已知集合{}{}10,1,2,21A B x x =-=-<≤,,则A B =( )A. {1}B. {}0,1C. {}101-,,D.{}101,2-,, 【答案】C 【解析】 【分析】利用交集运算即可得到结果.【详解】∵集合{}{}10,1,2,21A B x x =-=-<≤,, ∴AB ={}101-,,故选:C【点睛】本题考查交集概念及运算,属于基础题. 2.函数()f x =的定义域为( )A. [1,2]B. (1,2]C. (1,2)D.(,1)(2,)-∞⋃+∞【答案】D 【解析】 【分析】根据平方根的定义可知负数没有平方根,又其在分式的分母位置,得到被开方数大于0,列出关于x 的不等式,解二次不等式,即为函数的定义域.【详解】解:由已知得2320x x -+>,解得1x <或2x >,故选:D 。
【点睛】此题属于以函数的定义域为平台,考查了一元二次不等式的解法,利用了转化的思想,是高考中的基本题型.3.已知3log 2a =,123b =,21log 3c =,则( ) A. a b c >>B. b c a >>C. c b a >>D.b ac >>【答案】D 【解析】 【分析】利用有理指数幂的运算性质与对数的运算性质分别比较,,a b c 与0和1的大小得答案. 【详解】解:102331b =>=,3330log 1log log 213a =<=<=,2231log log 10c =<=, ∴b a c >>. 故选:D .【点睛】本题考查指对数值的大小比较,考查对数的运算性质,是基础题. 4.若sin cos 0αα⋅>,则角α的终边在( ) A. 第一、二象限 B. 第一、三象限 C. 第一、四象限 D. 第二、四象限【答案】B 【解析】 【分析】结合三角函数在四象限对应的正负号判断即可 【详解】sin cos 0αα⋅>,sin ,cos αα∴同号,所以角α的终边在第一、三象限故选:B【点睛】本题考查根据三角函数正负判断角所在的象限,属于基础题5.若α是第二象限角,且sin 3α=,则tan α=()A. B. C.D. -【答案】D【解析】 【分析】根据角的范围可确定cos 0α<,利用同角三角函数的平方关系和商数关系可求得结果. 【详解】α是第二象限角 cos 0α∴<1cos 3α∴==-sin 3tan 1cos 3ααα∴===--本题正确选项:D【点睛】本题考查同角三角函数值的求解问题,属于基础题.6.()f x 是奇函数,当0x ≥时,2()log (2)1f x x =+-,则()2f -=( ) A. 2 B. 1C. -2D. -1【答案】D 【解析】 【分析】根据奇函数对称性特点进行求解即可 【详解】()f x 是奇函数,()()22f f ∴-=-,当2x =时,2(2)log (22)11f =+-=,()()221f f ∴-=-=-故选:D【点睛】本题考查奇函数具体函数值的求法,奇函数的对称性,属于基础题 7.()cos 2040-= ( )A.12B.2C. D. 12-【答案】D 【解析】 【分析】利用诱导公式即可求出. 【详解】解:()()1cos 2040cos 2040+3606=cos(120)cos(180120)cos602-=-⨯=--=-=-故选:D .【点睛】本题考查利用诱导公式求特殊角的三角函数值,是基础题. 8.已知幂函数()af x x=图象经过点(,则()4f 的值为 ( ) A.12B. 1C. 2D. 8【答案】C 【解析】 【分析】根据幂函数过点可求出幂函数解析式,即可计算求值.【详解】因为幂函数()af x x =的图象经过点(,2a =,解得12a =, 所以()12f x x=,()12442f ==,故选:C【点睛】本题主要考查了幂函数的解析式,属于容易题. 9.2()log 5f x x x =+-的零点所在区间为( ) A. ()1,2 B. ()2,3C. ()3,4D. ()4,5【答案】C 【解析】 【分析】根据零点存在性定理进行判断即可 【详解】201(1)log 154f =+-=-<,202(2)log 252f =+-=-<,22g 3(3)log 35lo 203f =+-=-<,204(4)log 451f =+-=>22(5)log 55log 055f =+-=>,根据零点存在性定理可得()()340f f ⋅<,则2()log 5f x x x =+-的零点所在区间为()3,4故选:C【点睛】本题考查零点存在性定理,属于基础题10.若()f x 是偶函数,且对任意12,x x ∈(0,)+∞且12x x ≠,都有()()21210-f x f x x x -<,则下列关系式中成立的是( )A. 123()()()234f f f >->B. 132()()()243f f f >->C. 312()()()423f f f >->D. 321()()()432f f f ->>【答案】A 【解析】 【分析】由于对任意的x 1,x 2∈(0,+∞),都有()()21210-f x f x x x -<,可得函数f (x )在(0,+∞)上单调递减,即可得出.【详解】∵对任意的x 1,x 2∈(0,+∞),都有()()21210-f x f x x x -<,∴函数f (x )在(0,+∞)上单调递减, 又∵123234<<, ∴123234f f f ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭>>, 又∵f (x )是偶函数,∴f (﹣23)=f (23). ∴123234f f f ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭>>. 故选:A .【点睛】本题考查了函数的奇偶性、单调性的应用,属于基础题. 11.已知角α的终边经过点(,6)P m -,且4cos 5α=-,则m =( ) A. 8B. 8-C. 4D. 4-【答案】B 【解析】【分析】45=-,即可求解,得到答案.【详解】由题意,可得||r OP===根据三角函数的定义,可得4cos5α==-且0m<,解得8m=-.故选B.【点睛】本题主要考查了三角函数的定义的应用,其中解答中熟记三角函数的定义是解答的关键,着重考查了推理与运算能力,属于基础题.12.已知()f x是定义在R上的偶函数,且在区间(),0-∞上单调递增,若实数m满足()()11f m f->-,则m的取值范围是()A. (),0-∞ B. ()(),02,-∞+∞ C. (0,2) D. ()2,+∞【答案】C【解析】【分析】根据函数()f x为R上的偶函数,且在区间(),0-∞上单调递增,可得函数在()0,∞+上的单调性,然后将函数不等式转化为自变量的不等式,即可解得。
吉林省辽源市田家炳高级中学高二数学下学期期中试题 理

田家炳高中2017—2018学年度下学期高二期中考试理科数学试卷本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试时间为120分钟。
一、选择题(本大题共有12个小题。
每小题5分,共60分)1.复数i i z 213--=的共轭复数是( ) A.i -1 B. i +1 C. i -1- D. i +1-2.已知z 是纯虚数,错误!是实数,那么z 等于( ) A .2i B .i C .-i D .-2i3.复数z =2-i 1+i(i 是虚数单位)在复平面内对应的点位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限4.设()f x 在0x x =处可导,'0()2015f x =,则000()()lim x f x f x x x∆→-+∆∆等于( ) A .0 B .2015 C .-2015 D .不存在5.已知函数c bx ax x f ++=23)(,其导函数)(x f '图象如图所示,则函数)(x f 的极小值是( )A .c b a ++B .c b a ++48C .b a 23+D .c6。
若函数32()1f x x x mx =+++是R 上的单调函数,则实数m 的取值范围是【 C 】A 。
1(,)3+∞ B. 1(,)3-∞ C 。
1[,)3+∞ D 。
1(,]3-∞7.在等差数列{}n a 中,有4857a a a a +=+,类比上述性质,在等比数列{}n b 中,有( )A .4857b b b b +=+B .4857b b b b ⋅=⋅C .4578b b b b ⋅=⋅D .4758b b b b ⋅=⋅8.一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●,若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是( B )A .13B .14C .15D .169。
吉林省辽源市田家炳高级中学高二数学上学期期末考试试题理(含解析)

【解析】
【分析】
(1)根据所有长方形面积之和为1,求得未知数 ,计算出区间 长方形的面积之和即为概率,用此数据乘以样本容量即可;
(2)用每个长方形的面积乘以所在区间底边中点值,再求和即可得到结果;
(3)先计算出在 中的车辆数量,再列举出所有的抽取可能性,找出满足题意的可能性,用古典概型的概率计算公式即可求得。
【答案】(1)证明见解析(2)
【解析】
【分析】
(1)建立空间直角坐标系,求出 的坐标,通过计算数量积得出 , ,故 平面 ;
(2)求出平面 的法向量,通过计算两平面的法向量的夹角得出法向量的夹角从而得出二面角 的余弦值。
【详解】
以 为坐标原点,射线 为 轴的正半轴,建立如图所示的空间直角坐标系 。
依题设 .
故选: .
【点睛】本题追要考查是向量共线定理 应用,考查了计算能力,及空间向量的应用,是基础题.
3.执行如图所示的程序框图,输出的k值为
A。 2B. 4
C。 6D。 8
【答案】C
【解析】
【分析】
模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可得到输出的k的值.
【详解】模拟程序的运行,可得 ,
而当 ,时,例如取a=﹣2,b=﹣1,显然不能推出a>b>0.
故 是a>b>0的必要不充分条件.
故选B.
考点:必要条件、充分条件与充要条件的判断.
8.命题 , 的否定 是( )
A。 B。
C. D。
【答案】B
【解析】
【分析】
按存在性命题的否定的规则写出 即可。
【详解】因命题 为“ , ",它是存在性命题,
2021-2022学年吉林省辽源市田家炳高中、东辽二高等五校高二下学期期末考试数学试题(解析版)

2021-2022学年吉林省田家炳高中、东辽二高等五校高二下学期期末考试数学试题一、单选题 1.函数()1f x x=在2x =和3x =处的导数的大小关系是( ) A .()()23f f ''< B .()()23f f ''> C .()()23f f ''= D .不能确定【答案】A【分析】求出函数导数即可比较. 【详解】()1f x x =,()21f x x '∴=-,所以()()112,349f f ''=-=-,即()()23f f ''<. 故选:A.2.在新冠肺炎疫情防控期间,某记者要去武汉4个方舱医院采访,则不同的采访顺序有( ) A .4种 B .12种 C .18种 D .24种【答案】D【分析】由全排列的知识进行计算可得答案.【详解】解:由题意可得不同的采访顺序有4424A =种,故选:D .【点睛】本题主要考查排列组合中的全排列的知识,考查对基础知识的了解,属于基础题.3.对两个变量y 和x 进行回归分析,得到一组样本数据:11(,)x y ,22(,)x y ,…,(,)n n x y ,则下列说法中不正确的是( )A .由样本数据得到的回归方程y bx a =+必过样本中心(),x y B .残差平方和越小的模型,拟合的效果越好C .用相关指数R 2来刻画回归效果,R 2越小,说明模型的拟合效果越好D .若变量y 和x 之间的相关系数为r =-0.9362,则变量y 和x 之间具有线性相关关系 【答案】C【分析】理解回归分析中样本中心、残差、相关指数R 2、相关系数的含义,即可判断各选项的正误.【详解】A :样本中心点在回归直线上,正确;B :残差平方和越小的模型,拟合效果越好,正确,C :R 2越大拟合效果越好,不正确,D :当||r 的值大于0.8时,表示两个变量具有高度线性相关关系,正确. 故选:C.4.设某高山滑雪运动员在一次滑雪训练中滑行路程l (单位:m )与时间t (单位:s )之间的关系为()2322l t t t =+,下列说法正确的是( )A .当3s t =时,运动员的滑雪速度为()3m/s lB .当3s t =时,运动员的滑雪速度为()3m/s l 'C .函数()l t 在[)0,∞+上单调递减D .函数()l t 在[)0,∞+上不是单调函数 【答案】B【分析】由导数的实际意义和导数的正负与函数单调性的关系可得出合适的选项. 【详解】当3s t =时,运动员的滑雪速度为()3m/s l ',A 错B 对; 当0t ≥时,()3402l t t '=+>,故函数()l t 在[)0,∞+上单调递增,CD 均错. 故选:B.5.523x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数是( )A .90B .80C .70D .60【答案】A【解析】根据二项式定理,得到523x x ⎛⎫+ ⎪⎝⎭展开式的第1r +项,再由赋值法,即可求出结果.【详解】因为523x x ⎛⎫+ ⎪⎝⎭展开式的第1r +项为()521031553C C 3rr r r rr r T x xx --+⎛⎫==⋅ ⎪⎝⎭, 令1034r -=,得2r =,则4x 的系数为225C 390⋅=.故选:A.6.某试验每次成功的概率为()01p p <<,现重复进行10次该试验,则恰好有7次试验未成功的概率为( )A .()73310C 1p p -B .()37710C 1p p -C .()67410C 1p p -D .()47610C 1p p -【答案】A【分析】根据二项分布的概率公式即可求解.【详解】由题意可知,重复进行10次试验,7次未成功,说明3次成功,所以所求概率为()73310C 1p p -. 故选:A .7.2022年北京冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”,有着可爱的外表和丰富的寓意,深受各国人民的喜爱.某商店有3个不同造型的“冰墩墩”吉祥物和2个不同造型的“雪容融”吉祥物展示在柜台上,要求“冰墩墩”和“雪容融”彼此间隔排列,则不同的排列方法有多少种?( ) A .24 B .12 C .6 D .2【答案】B【分析】先排2个雪容融,利用插空法排列3个冰墩墩即可.【详解】解:先对2个雪容融排列22A ,将3个冰墩墩插空放在3个空位上排列33A ,由分步乘法计数原理,排列方法有2323A A 12=.故选:B 8.函数3()2ln f x x x x=++的单调递减区间是( ) A .(3,1)- B .(0,1) C .(1,3)- D .(0,3)【答案】B【分析】求出函数的导数,解关于导函数的不等式,求出函数的递减区间即可. 【详解】函数的定义域是(0,+∞), y′=1﹣23x +2x =()()231x x x +- , 令y′(x )<0,解得:0<x <1, 故函数在(0,1)递减, 故选B .【点睛】本题考查了利用导数判断函数的单调性问题,是一道常规题. 二、多选题9.图中的散点图与样本相关系数r 一定不符合的是( ).A .(1)B .(2)C .(3)D .(4)【答案】ACD【分析】利用散点图及样本相关系数r 的概念即得.【详解】对于(1),变量x ,y 的散点图从左向右是下降的,所以样本相关系数0r <,(1)一定不符合;对于(2),变量x ,y 的散点图从左向右是上升的,所以样本相关系数0r >,(2)可能符合;对于(3),变量x ,y 的散点图从左到右是向下的带状分布,所以样本相关系数0r <,(3)一定不符合;对于(4),变量x ,y 的散点图从左向右是上升的带状分布,所以样本相关系数01r <<,(4)一定不符合.综上,散点图与样本相关系数r 一定不符合的是(1)(3)(4). 故选:ACD.10.如图是导函数()y f x '=的图象,则下列说法错误的是( )A .()1,3-为函数()y f x =的单调递增区间B .()0,3为函数()y f x =的单调递减区间C .函数()y f x =在0x =处取得极大值D .函数()y f x =在5x =处取得极小值 【答案】BC【分析】根据导函数函数值的正负与函数单调性的关系,以及函数极值点的定义,对每个选项进行逐一分析,即可判断和选择.【详解】由图可知,当1x <-时,()f x '0<,故()f x 单调递减;当()1,3x ∈-,()f x '0>,故()f x 单调递增;当()3,5x ∈,()f x '0<,故()f x 单调递减;当5x >,()f x '0>,故()f x 单调递增,且()10f '-=,()30f '=,()50f '=,则该函数在1x =-和5x =处取得极小值;在3x =处取得极大值. 故选:BC11.已知随机变量X 的分布列如下,且()2E X =,则下列说法正确的是( )A .12m =,16n =B .13m =,13n =C .()23D X =D .()12D X =【答案】BC【分析】根据期望的公式以及分布列的性质列方程,求得,m n ,计算出()D X ,由此确定正确选项.【详解】依题意()11232123E X m n m n =⋅+⋅+⨯=++=,所以21m n +=,结合113m n ++=,解得13m n ==,所以B 选项正确.()()()()22211121222323333D X =-⋅+-⋅+-⋅=,所以C 选项正确.故选:BC【点睛】本小题主要考查随机变量的分布列、期望和方差的知识,属于基础题. 12.现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是( ) A .从中任选1个球,有15种不同的选法 B .若每种颜色选出1个球,有120种不同的选法C .若要选出不同颜色的2个球,有31种不同的选法D .若要不放回地依次选出2个球,有210种不同的选法 【答案】ABD【分析】利用排列知识计算得到选项ABD 正确;若要选出不同颜色的2个球,有74种不同的选法,所以选项C 错误.【详解】解:A. 从中任选1个球,有456++=15种不同的选法,所以该选项正确; B. 若每种颜色选出1个球,有456=⨯⨯120种不同的选法,所以该选项正确; C. 若要选出不同颜色的2个球,有45+56+46=74⨯⨯⨯种不同的选法,所以该选项错误; D. 若要不放回地依次选出2个球,有1514=⨯210种不同的选法,所以该选项正确. 故选:ABD 三、填空题13.第24届冬季奥运会于2022年2月4日在北京市和河北省张家口市举行.现要安排5名志愿者去四个场馆参加活动,每名志愿者只能去一个场馆.且每个场馆只能安排一名志愿者,则不同的分配方法有___________个.(空格处填写数字) 【答案】120【分析】根据排列的概念和排列数公式,即可求出结果.【详解】解:从5名志愿者中选4人排列45A 120=个.故答案为:120 14.若()310P AB =,()35P A =,则()P B A =______.【答案】120.5【分析】根据条件概率计算公式,计算出所求概率.【详解】()()()3110325P AB P B A P A ===.故答案为:12 15.设随机变量()24,3X N ,且()()01P X P X a <=>-,则实数a 的值为_______.【答案】9 【分析】随机变量()24,3X N 的正态曲线关于4X =对称,即0与1a -关于4X =对称,解出即可.【详解】根据题意有01429a a +-=⨯⇒=故填9【点睛】本题考查正态曲线的特点及曲线所表示的几何意义,属于基础题. 16.函数32123y x x mx =+++是R 上的单调函数,则m 的范围是_________.【答案】[1,)+∞【解析】32123y x x mx =+++是R 上的单调函数,则导函数恒大于等于0或恒小于等于0,而导函数是开口向上的二次函数,只可能是恒大于等于0,则用判别式求解即可. 【详解】32123y x x mx =+++是R 上的单调函数,则导函数恒大于等于02'20y x x m =++≥则440m ∆=-≤,m 1≥ 故答案为:[1,)+∞【点睛】若可导函数f (x )在指定的区间D 上单调递增(减),求参数范围问题,可转化为f ′(x )≥0(或f ′(x )≤0)恒成立问题,从而构建不等式,要注意“=”是否可以取到. 四、解答题17.在生活中,我们出差或旅行时常会乘坐飞机.航空交通的优势在于:快捷、舒适、安全、灵活,航线的开辟不受沿线地面各种天然或人为障碍的限制.若某航空公司要在北京、上海、香港、台北四个民航站之间开设直达航线,则需要准备多少种不同的飞机票?将它们一一列举出来.【答案】12(种),列举答案见解析.【分析】由每两个民航站之间的直达航线有往返两种不同的飞机票,可得答案,再一一列举即可.【详解】解:每两个民航站之间的直达航线有往返两种不同的飞机票,所以四个民航站之间的直达航线,需要准备24A 12=种不同的飞机票. 列举如下:北京→上海,北京→香港,北京→台北, 上海→北京,上海→香港,上海→台北, 香港→北京,香港→上海,香港→台北, 台北→北京,台北→上海,台北→香港.18.为了调查胃病是否与生活规律有关,在某地对60名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共20人,患胃病者生活规律的共10人,未忠胃病者生活不规律的共8人,未忠胃病者生活规律的共22人. (1)补充完整22⨯列联表:(2)依据0.005α=的独立性检验,能否认为40岁以上的人患胃病与否和生活规律有关联. ()()()()()22n ad bc a b c d a c c d χ-=++++,2χ值精确到0.001.附:临界值表:【答案】(1)答案见解析(2)认为40岁以上的人患胃病与否和生活规律有关联 【分析】(1)由已知作出2×2列联表即可; (2)由列联表,结合计算公式,求得2χ,由此判断出两个量之间的关系. 【详解】(1)由已知可列2×2列联表得:(2)由计算公式得2χ的值为:()226022201089.64330303228χ⨯⨯-⨯=≈⨯⨯⨯,∵9.6437.879>∴依据0.005α=的独立性检验,可以认为40岁以上的人患胃病与否和生活规律有关联.19.已知函数31()413f x x x =-+.(1)求曲线()y f x =在点()0,(0)f 处的切线方程; (2)求()y f x =在[]1,1-上的最大值和最小值. 【答案】(1)410x y +-=;(2)最大值14(1)3f -=,最小值3(1)8f =-. 【分析】(1)利用导数的几何意义,求得切线斜率,利用点斜式即可得解; (2)利用导数研究函数的单调性,利用单调性即可求得最值. 【详解】(1)由31()413f x x x =-+得,2()4f x x =-',∴(0)1f =,(0)4f '=-,∴曲线()y f x =在点(0,(0))f 处的切线方程14(0)y x -=--,即410x y +-=; (2)令()0f x '>可得2x >或2x <-,此时函数单调递增, 令()0f x '<可得22x -<<,此时函数单调递减, 故函数()f x 在[]1,1-上单调递减, ∴()f x 的最大值14(1)3f -=,最小值3(1)8f =-. 20.已知()7221314012131412x x a a x a x a x a x +-=+++⋅⋅⋅++. (1)求01214a a a a +++⋅⋅⋅+的值; (2)求13513a a a a +++⋅⋅⋅+的值. 【答案】(1)128 ;(2) 128.【分析】(1)利用赋值法,令1x =求解即可; (2)令1x =-结合(1)作差即可求解.【详解】(1)令1x =,得7012142128a a a a +++⋅⋅⋅+==.(2)令1x =-,得701231314(2)128a a a a a a -+-+⋅⋅⋅-+=-=-.又01214128a a a a +++⋅⋅⋅+=, 所以()13132256a a a ++⋅⋅⋅+=, 所以13513128a a a a +++⋅⋅⋅+=.21.某数学兴趣小组有5名同学,其中3名男生2名女生,现从中选2人去参加一项活动.(1)求选出的2人中,恰有1名男生,1名女生的概率;(2)用X 表示选出的2人中男生的个数,求X 的分布列.【答案】(1)35(2)分布列见解析【分析】(1)根据组合的应用,结合古典概型计算即可;(2)由题知X 可能的取值为0,1,2,进而根据超几何分布求解即可. 【详解】(1)解:某数学兴趣小组有5名同学,其中3名男生2名女生,从中选2人去参加一项活动,有2510C =(种)选法.设“选出的两人中,恰有1名男生,1名女生”为事件A ,则()11323105C C P A == (2)解:根据题意,X 可能的取值为0,1,2.()22101010C P X ===,()113231105C C P X ===,()23321010C P X ===.故X 的分布列为22.已知函数f (x )=x 3+ax 2+bx +c 在x =-23与x =1时都取得极值(1)求a 、b 的值与函数f (x )的单调区间(2)若对[]1,2x ∈-,不等式()2f x c <恒成立,求c 的取值范围.【答案】(1)1,22a b =-=-,单调递增区间为2,3⎛⎫-∞- ⎪⎝⎭和(1,)+∞ ,单调递减区间为2,13⎛⎫- ⎪⎝⎭;(2)1c <-或2>c 【分析】(1)求出函数导数,由题可得203(1)0f f ⎧⎛⎫-=⎪ ⎪⎝⎭⎨⎪='⎩'即可求出,a b ;(2)求出()f x 在[1,2]x ∈-的最大值即可建立关系求解. 【详解】(1)32()f x x ax bx c =+++,∴()232f x x ax b '=++,()f x 在23x =-与1x =时都取得极值,21240393(1)320f a b f a b ⎧⎛⎫-=-+=⎪ ⎪⎝⎭⎨⎪=++=''⎩∴,解得122a b ⎧=-⎪⎨⎪=-⎩,第 11 页 共 11 页 2()32(32)(1)f x x x x x '∴=--=+-,令()0f x '>可解得23x <-或x 1>;令()0f x '<可解得213x -<<, ()f x ∴的单调递增区间为2,3⎛⎫-∞- ⎪⎝⎭和(1,)+∞ ,单调递减区间为2,13⎛⎫- ⎪⎝⎭; (2)[]321()2,1,22f x x x x c x =--+∈-, 由(1)可得当23x =-时,22()27f x c =+为极大值,而(2)2f c =+, 所以()()max 22f x f c ==+,要使2()f x c <对[1,2]x ∈-恒成立,则22c c >+,解得1c <-或2>c .。
吉林省辽源市田家炳高级中学2015-2016学年高二数学下学期期中试题 文
2015-2016学年度第二学期期中考试高二数学(文科)试卷考试时间:120分钟评卷人 得分一、选择题(每题5分) 1.已知i 是虚数单位,则复数5512ii--的共轭复数为( ) A .3i + B .3i -+ C .3i -- D .3i -2.阅读如图所示的程序框图,若要使输入的x 值与输出的y 值相等,则满足条件的x 有( )A .1个B .2个C .3个D .4个 3.复数z 满足(1i)2i Z +=,则复数z 在复平面内对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限4.车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,数据如下: 零件数x (个) 10 20 30 40 50 60 70 80 加工时间(min)y626875818995102108设回归方程为y bx a =+,则点(,)a b 在直线45100x y +-=的( ) A .左上方 B .右上方 C .左下方 D .右下方 5.在复平面内,复数6+5i ,-2+3i 对应的向量分别是和,若复数z 与+的积为实数,且|z|=,则z=( )A.1-2iB.-1+2iC.1-2i,-1+2iD.1+2i,1-2i 6.右图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是( ) A .25 B .66 C .91 D .1207.若通过推理所得到的结论一定是正确的,则这样的推理必定是( ) A .归纳推理 B .类比推理 C .合情推理 D .演绎推理 8.如图,在复平面内,复数z 1和z 2对应的点分别是A 和B ,则=( )A.+i B.+i C.﹣﹣i D.﹣﹣i9.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:认为作业多认为作业不多总数喜欢玩电脑游戏18 9 27 不喜欢玩电脑游戏8 15 23 总数26 24 50根据表中数据得到25018158927232426k()⨯⨯-⨯=≈⨯⨯⨯5.059,因为p(K2≥5.024)=0.025,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为()(A)97.5% (B) 95% (C)90% (D)无充分根据10.如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F 重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是()才A、椭圆B、双曲线C、抛物线D、圆11.如图,PC与圆O相切于点C,直线PO交圆O于BA,两点,弦CD垂直AB于E.则下面结论中,错误..的结论是( ) A .BEC ∆∽△DEA B .∠ACE=∠ACP C .2DE OE EP =⋅ D .2PC PA AB =⋅ 12.如图,⊙O 中,弦AD ∥BC ,DA =DC ,∠BCO =15°,则∠AOC 等于( ).(A )120° (B )130° (C )140° (D )150°填空题(每题5分) 13.观察下列式子:2241+=,313422+=,414533+=,515644+=,……,归纳得出一般规律为.14.已知a b <,则在下列的一段推理过程中,错误的推理步骤有.(填上所有错误步骤的序号)15.已知x 与y 之间的一组数据: a a=+必过点则y与x的线性回归方程为ˆy bx a16.若Z∈C,且|Z+2﹣2i|=1,则|Z﹣2﹣2i|的最小值是.2015-2016学年度第二学期期中考试高二数学(文科)试卷答题卡一选择题(每题5分共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 选项二填空题(每题5分共20分)13. 14.15. 16. 三解答题(共70分) 17. 计算:(12分)(1))23()89()57(i i i -+--+- (2))34)(7()26)(4(i i i i --+-+ (3)iii i -+++112218.(10分)实数m 取怎样的值时,复数i m m m z )152(32--+-=是:(1)实数? (2)虚数? (3)纯虚数?19.(12分)为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本. (1)根据所给样本数据完成下面2×2列联表;(2)请问能有多大把握认为药物有效?不得禽流感得禽流感总计服药不服药总计座号20.(12分)一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,下表是抽样试验结果:若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,求机器的转速应该控制所在的X 围。
吉林省辽源市田家炳高级中学2020学年高二数学6月月考试题 理

田家炳高中2020学年度下学期6月月考试卷高二数学(理科)一、 选择题 (本大题共12小题,每小题5分,共60分)1.若复数z =2i +21+i,其中i 是虚数单位,则复数z 的模为( )A.22B. 2C. 3 D .2 2.=⎰dx 212)1-x -1(( )A .π4B .π2C .πD .2π3.随机变量ξ的概率分布列为P (ξ=k )=k k +1,k =1、2、3、4,其中c 是常数,则P ⎝ ⎛⎭⎪⎫12<ξ<52则值为( )A .23B .34C .45D .564.观察下列各式:a +b =1,a 2+b 2=3,a 3+b 3=4,a 4+b 4=7,a 5+b 5=11,…,则a 10+b 10=( )A .28B .76C .123D .199 5.设(5x -1x)n的展开式中各项系数之和为M ,二项式系数之和为N ,若M -N =240,则展开式中x 的系数为( )A .-150B .150C .300D .-3006.(2020·福建南安市高二期中)将标号为A 、B 、C 、D 、E 、F 的6张卡片放入3个不同的信封中,若每个信封放2张卡片,其中标号为A 、B 的卡片放入同一信封,则不同的放法共有( )A .12种B .18种C .36种D .54种7.摄影师要为5名学生和2位老师拍照,要求排成一排,2位老师相邻且不排在两端,不同的排法共有( )A .1440种B .960种C .720种D .480种A.b<-1或b>2 B.b≤-2或b≥2 C.-1<b<2 D.-1≤b≤211.直线y=a与函数y=x3-3x的图象有相异的三个交点,则a的取值范围是( ) A.-2<a<2 B.-2≤a<2 C.a<-2或a>2 D.a<-2或a≥212.(2020·成都模拟)若函数f(x)在R上可导,且满足f(x)-xf′(x)>0,则( )A.3f(1)<f(3) B.3f(1)>f(3) C.3f(1)=f(3) D.f(1)=f(3)二、填空题(本大题共4小题,每小题5分,共20分)13.已知直线y=kx+b与曲线y=x3+ax+1相切于点(2,3),则b的值为_______.14.若函数f(x)=x3-3x2-9x+k在区间[-4,4]上的最大值为10,则其最小值为_______.15.设函数f(x)=ax3-3x+1(x∈R),若对于任意的x∈(0,1]都有f(x)≥0成立,则实数a的取值范围为________.16.已知函数f(x)=x-1x+1,g(x)=x2-2ax+4,若对任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的最小值是________.三、解答题(本大题共6小题,共70分。
吉林省辽源市田家炳高级中学高一月月考数学试题含答案

田家炳高中2019—2020学年度12月月考试卷高一数学(理科)本试卷考试时间为120分钟,满分150分。
一.选择题 (每题5分 共60分)1.已知集合{}{}10,1,2,21A B x x =-=-<≤,,则A B =I ( ) A .{1} B .{}0,1 C .{}101-,, D .{}101,2-,, 2.函数2()32f x x x =-+的定义域为( )A .[1,2]B .(1,2]C .(1,2)D .(,1)(2,)-∞⋃+∞ 3.已知3log 2a =,123b =,21log 3c =,则( )A .a b c >>B .b c a >>C .c b a >>D .b a c >>4.若sin cos 0αα⋅>,则角α的终边在( ) A .第一、二象限 B .第一、三象限 C .第一、四象限D .第二、四象限5.若α是第二象限角,且22sin 3α=,则tan α=( ) A .5B .6-C .7D .22-6.()f x 是奇函数,当0x ≥时,2()log (2)1f x x =+-,则()2f -=( ) A .2B .1C .-2D .-17.()cos 2040-=o( )A .12B 3C .3D .12-8.已知幂函数()af x x =的图象经过点(2,则()4f 的值为 ( )A .12B .1C .2D .89.2()log 5f x x x =+-的零点所在区间为( ) A .()1,2B .()2,3C .()3,4D .()4,510.若()f x 是偶函数,且对任意12,x x ∈(0,)+∞且12x x ≠,都有()()21210-f x f x x x -<,则下列关系式中成立的是( )A .123()()()234f f f >->B .132()()()243f f f >->C .312()()()423f f f >->D .321()()()432f f f ->>11.已知角α的终边经过点(,6)P m -,且4cos 5α=-,则m =( )A .8B .8-C .4D .4-12.已知()f x 是定义在R 上的偶函数,且在区间(),0-∞上单调递增,若实数m 满足()()11f m f ->-,则m 的取值范围是( )A .(),0-∞B .()(),02,-∞+∞UC .(0,2)D .()2,+∞二、填空题(每题5分,共20分)13.函数log (25)1a y x =--恒过定点的坐标为__________. 14.已知函数()f x 满足()23x f e x =-,则()f x =________. 15.函数()]14212xx f x x +⎡=-∈-⎣,,的值域是________. 16.已知函数()11,123,012xx f x xx ⎧⎛⎫+≥⎪ ⎪⎪⎝⎭=⎨⎪<<⎪⎩,若函数()()g x f x k =-有两个不同的零点,则实数k 的取值范围是__________.三、解答题(共70分)17(10分).设集合{}2|3180A x x x =--≤,{}|84B x m x m =-≤≤+.(1)若3m =,求()R C A B ⋂;(2)当=A B A I 时,求实数m 的取值范围.18(12分).已知二次函数2()3f x x ax =--(a R ∈). (1)若()f x 为偶函数,求a 的值;(2)若()0f x <的解集为{3}x x b -<<,求a ,b 的值;(3)若()f x 在区间[2,)-+∞上单调递增,求a 的取值范围.19(12分).已知tan 3α=,求下列各式的值: (1)4sin cos 3sin 5cos αααα-+(2)2222sin 2sin cos cos 4cos 3sin αααααα--- (3)2231sin cos 42αα+20(12分).已知π3πcos cos(2π)sin 22()3πsin(π)sin 2f αααααα⎛⎫⎛⎫+⋅-⋅- ⎪ ⎪⎝⎭⎝⎭=⎛⎫-⋅+ ⎪⎝⎭.(1)化简()f α;(2)若α是第四象限角,且π1cos 24α⎛⎫+= ⎪⎝⎭,求()f α的值.21(12分).已知函数()()22log 32f x mx mx =-+,m R ∈. (1)若1m =,求函数()f x 的单调递减区间; (2)若函数()f x 的定义域为R ,求实数m 的取值范围.22(12分).已知定义在R 上的函数()f x 满足:① 对任意x ,y ∈R ,有()()()f x y f x f y +=+.②当0x <时,()0f x >且()13f =-.(1)判断()f x 的奇偶性;(2)解不等式()()2212f x f x --≥-.一。
吉林辽源田家炳高级中学高二下学期期中数学(文)含答案

田家炳高中2018-2019学年度下学期期中考试卷高二数学(文)一、选择题(本大题共有12个小题,每小题只有一项是符合题意,请将答案答在答题卡上。
每小题5分,共60分)1.设全集U=R,A={|110}x N x ∈≤≤,B =2{|60}x R x x ∈+-=, 则下图中阴影部分表示的集合为( )A. {}1B. {}2C. {}3,2D. {}2,3- 2.已知集合{}2|230?A x x x =--≥,{}|22B x x =-≤<则A B ⋂= ( ) A. []2,1--B. [)1,2- C. []1,1-D. [)1,23.为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:附:22()()()()()n ad bc K a b c d a c b d -=++++.参照附表,得到的正确结论是( )A.在犯错误的概率不超过1%的前提下,认为"该市居民能否做到'光盘'与性别有关"B.在犯错误的概率不超过1%的前提下,认为"该市居民能否做到'光盘'与性别无关"C.有90%以上的把握认为"该市居民能否做到'光盘'与性别有关"D.有90%以上的把握认为"该市居民能否做到'光盘'与性别无关"4.在一线性回归模型中,计算相关指数20.96R =,下列哪种说法不够妥当?( )A.该线性回归方程的拟合效果较好B.解释变量对于预报变量变化的贡献率约为96%C.随机误差对预报变量的影响约占4%D.有96%的样本点在回归直线上5.已知复数z 的共轭复数12z i =+ (i 为虚数单位),则z 在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限 6.如图,在复平面内,点A 表示复数z ,则图中表示z 的共轭复数的点是( )A. AB. BC. CD. D7.若命题“x R ∃∈,使得()2110x a x +-+<”是假命题,则实数a 的取值范围是( )A. [1,3]-B. (1,3)-C. (][),13,-∞-⋃+∞D. (,1)(3,)-∞-⋃+∞ 8.定义运算||a b ad bc c d =-,则符合条件11||42i z zi-=+的复数z 为( ) A. 3i - B. 13i + C. 3i + D. 13i - 9.复数z 满足 34iz i =-,则z = ( )A. 1B. 25 10.在复平面上的中, 68AC i =+,46BD i =-+.则AD 对应的复数是( )A. 214i +B. 17i +C. 214i -D. 17i -- 11.计算232015i i i i +++⋯+= ( ) A. i B. 1- C. 1 D. 1i -+12.已知集合()(){}221,3156M m m m m i =--+--,{}1,3N =,{}1,3M N ⋂=,则实数m 的为( )A. 4B. 1-C. 4或1-D. 1或6 二、填空题(本大题共有4个小题。
吉林省辽源市田家炳高级中学高中英语阅读理解试题及答案doc

一、高中英语阅读理解1.阅读理解Bright Side did some research on many places throughout the world where you can buy a house for 1 dollar or for free!Roubaix, FranceIf you like France, Roubaix located in the north of France is just for you. The local authorities want it to be populated and attractive. You can buy a small house in the industrial district for just $1. The buyer is supposed to live in this house for 3 years.Buffalo. USABuffalo offers whoever qualifies to buy a house for $1. All you need is to be a lawful citizen of the city and invest amount of money into its decoration. Doing this, the authorities are hoping to make the city beautiful again without spending money.Liverpool, Great BritainIn Liverpool, most of houses were abandoned (遗弃)by the working class during the years of unemployment. The government is trying to sell the houses for just $1. If you want to buy such a house, it has to be your first deal on buying property(房产).Candela, ItalyIf you still have any doubts about spending $1 on a house, you should know: the government will pay you some money, if you move to Candela. In order to be paid, you need to become a permanent(永久的)citizen and have an income of $7500 per year. If moving alone, you will get $800, and if you are going with your family, the pay can be four times as much as only one person. For more information of other cities, please Click Here.(1)Why do the authorities of Buffalo provide a house for people with 1$?A. To improve the lives of poor people.B. To make the city attractive at no cost.C. To solve the problems of employment.D. To attract people to the industrial areas.(2)What is required to buy a house for 1 dollar in Liverpool?A.You need to be an unemployed citizen.B.You should live in the house for 3 years.C.It must be your first house purchase.D.You have to repair and decorate the house.(3)How much money can you get if moving to Candela with a whole family?A.$3200B.$9600C.$800D.$7500【答案】(1)B(2)C(3)A【解析】【分析】本文是一篇应用文,Bright Side在全世界很多地方做了一些研究,介绍了在哪些地方可以用1美元买房子或者免费得到房子。
2015-2016年吉林省辽源市田家炳高中高二(下)期中数学试卷(文科)和答案
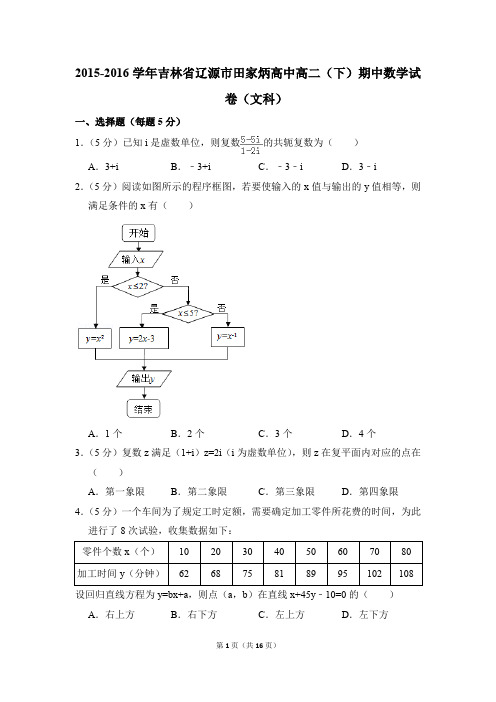
2015-2016学年吉林省辽源市田家炳高中高二(下)期中数学试卷(文科)一、选择题(每题5分)1.(5分)已知i是虚数单位,则复数的共轭复数为()A.3+i B.﹣3+i C.﹣3﹣i D.3﹣i2.(5分)阅读如图所示的程序框图,若要使输入的x值与输出的y值相等,则满足条件的x有()A.1个B.2个C.3个D.4个3.(5分)复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限4.(5分)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:设回归直线方程为y=bx+a,则点(a,b)在直线x+45y﹣10=0的()A.右上方B.右下方C.左上方D.左下方5.(5分)在复平面内,复数6+5i,﹣2+3i对应的向量分别是和,若复数z与+的积为实数,且|z|=,则z=()A.1﹣2i B.﹣1+2i C.1﹣2i,﹣1+2i D.1+2i,1﹣2i 6.(5分)图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第七个叠放的图形中,小正方体木块总数就是()A.25B.66C.91D.1207.(5分)若通过推理所得到的结论一定是正确的,则这样的推理必定是()A.归纳推理B.类比推理C.合情推理D.演绎推理8.(5分)如图,在复平面内,复数z1和z2对应的点分别是A和B,则=()A.+i B.+i C.﹣﹣i D.﹣﹣i 9.(5分)某班主任对全班50名学生进行了作业量多少的调查,数据如表:根据表中数据得到 5.059,因为p(K2≥5.024)=0.025,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为()A.97.5%B.95%C.90%D.无充分根据10.(5分)如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM 交于点P,则点P的轨迹是()A.椭圆B.双曲线C.抛物线D.圆11.(5分)如图,PC与圆O相切于点C,直线PO交圆O于A,B两点,弦CD垂直AB于E.则下面结论中,错误的结论是()A.△BEC∽△DEA B.∠ACE=∠ACP C.DE2=OE•EPD.PC2=PA•AB12.(5分)如图,⊙O中,弦AD∥BC,DA=DC,∠BCO=15°,则∠AOC等于()A.120°B.130°C.140°D.150°二、填空题(每题5分)13.(5分)观察下列式子:,,,,…,归纳得出一般规律为.14.(5分)已知a<b,则在下列的一段推理过程中,错误的推理步骤有.(填上所有错误步骤的序号)15.(5分)已知x与y之间的一组数据:则y与x的线性回归方程=bx+a必过点.16.(5分)若Z∈C,且|Z+2﹣2i|=1,则|Z﹣2﹣2i|的最小值是.三、解答题(共70分)17.(12分)计算:(1)(﹣7i+5)﹣(9﹣8i)+(3﹣2i);(2)(4+i)(6﹣2i)+(7﹣i)(4﹣3i);(3).18.(10分)实数m取怎样的值时,复数z=m﹣3+(m2﹣2m﹣15)i是:(1)实数?(2)虚数?(3)纯虚数?19.(12分)为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.(1)根据所给样本数据画出2×2列联表;(2)请问能有多大把握认为药物有效?20.(12分)一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,如表是抽样试验结果:若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,求机器的转速应该控制所在的范围..21.(12分)(Ⅰ)求证:+<2(Ⅱ)已知a >0,b >0且a+b >2,求证:,中至少有一个小于2.22.(12分)已知A 、B 、C 、D 为圆O 上的四点,直线DE 为圆O 的切线,AC ∥DE ,AC 与BD 相交于H 点. (Ⅰ)求证:BD 平分∠ABC ;(Ⅱ)若AB=4,AD=6,BD=8,求AH 的长.2015-2016学年吉林省辽源市田家炳高中高二(下)期中数学试卷(文科)参考答案与试题解析一、选择题(每题5分)1.(5分)已知i是虚数单位,则复数的共轭复数为()A.3+i B.﹣3+i C.﹣3﹣i D.3﹣i【解答】解:复数==(1﹣i)(1+2i)=3+i.复数的共轭复数为:3﹣i.故选:D.2.(5分)阅读如图所示的程序框图,若要使输入的x值与输出的y值相等,则满足条件的x有()A.1个B.2个C.3个D.4个【解答】解:由程序框图知:程序的功能是求分段函数y=的值,若x≤2,由x2=x得x=0或1;若2<x≤5,由2x﹣3=x得x=3;若x>5,由=x得x=±1(舍去).综上x的值有0,1,3,共计3个.故选:C.3.(5分)复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:(1+i)z=2i(i为虚数单位),∴z===i+1,则z在复平面内对应的点(1,1)在第一象限.故选:A.4.(5分)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:设回归直线方程为y=bx+a,则点(a,b)在直线x+45y﹣10=0的()A.右上方B.右下方C.左上方D.左下方【解答】解:由题意,==45,==85,x i y i=33400,=20400,n 2=16200,n •=30600,∴b==,a=55∵55+45×﹣10=75>0∴(55,)在直线x+45y﹣10=0的右上方.故选:A.5.(5分)在复平面内,复数6+5i,﹣2+3i对应的向量分别是和,若复数z与+的积为实数,且|z|=,则z=()A.1﹣2i B.﹣1+2i C.1﹣2i,﹣1+2i D.1+2i,1﹣2i【解答】解:+=(6+5i)+(﹣2+3i)=4+8i,设z=a+bi(a,b∈R),则|z|==.①∵复数z与+的积为实数,即(a+bi)(4+8i)=(4a﹣8b)+(8a+4b)i为实数,∴2a+b=0.②解①②式得:或.∴z=1﹣2i或z=﹣1+2i.故选:C.6.(5分)图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第七个叠放的图形中,小正方体木块总数就是()A.25B.66C.91D.120【解答】解:分别观察正方体的个数为:1,1+5,1+5+9,…归纳可知,第n个叠放图形中共有n层,构成了以1为首项,以4为公差的等差数列所以∴s7=2•72﹣7=91故选:C.7.(5分)若通过推理所得到的结论一定是正确的,则这样的推理必定是()A.归纳推理B.类比推理C.合情推理D.演绎推理【解答】解:由于归纳推理是由几个特殊事例得出的一般性的结论,故结论不一定正确,故排除A;类比推理是由一类事物的特征来推测另一类失误也有此类似的特征,故得到的结论也不一定正确,故排除B;由合情推理包括归纳推理和类比推理,故排除C;演绎推理一般模式是“三段论”形式,即大前提小前提和结论,在大前提、小前提和推理形式都正确的情况下,得到的结论一定正确,故选:D.8.(5分)如图,在复平面内,复数z1和z2对应的点分别是A和B,则=()A.+i B.+i C.﹣﹣i D.﹣﹣i【解答】解:由图形可得:z1=﹣2﹣i,z2=i.∴====﹣﹣i,故选:C.9.(5分)某班主任对全班50名学生进行了作业量多少的调查,数据如表:根据表中数据得到 5.059,因为p(K2≥5.024)=0.025,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为()A.97.5%B.95%C.90%D.无充分根据【解答】解:∵根据表中数据得到 5.059,因为p(K2≥5.024)=0.025,∴认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为1﹣0.025=97.5%故选:A.10.(5分)如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM 交于点P,则点P的轨迹是()A.椭圆B.双曲线C.抛物线D.圆【解答】解:由题意知,CD是线段MF的垂直平分线.∴|MP|=|PF|,∴|PF|+|PO|=|PM|+|PO|=|MO|(定值),又显然|MO|>|FO|,∴根据椭圆的定义可推断出点P轨迹是以F、O两点为焦点的椭圆.故选:A.11.(5分)如图,PC与圆O相切于点C,直线PO交圆O于A,B两点,弦CD垂直AB于E.则下面结论中,错误的结论是()A.△BEC∽△DEA B.∠ACE=∠ACP C.DE2=OE•EPD.PC2=PA•AB【解答】解:A.∵∠CEB=∠AED,∠BCE=∠DAE,∴△BEC∽△DEA,因此A正确;B.∵PC与圆O相切于点C,∴∠PCA=∠B=∠ACE,因此B正确;C.连接OC,则OC⊥PC,又CD⊥AB,∴CE2=OE•EP,CE=ED,∴ED2=OE•EP,因此C正确;D.由切割线定理可知:PC2=PA•PB≠PA•AB,因此D不正确.故选:D.12.(5分)如图,⊙O中,弦AD∥BC,DA=DC,∠BCO=15°,则∠AOC等于()A.120°B.130°C.140°D.150°【解答】解:连接AC,设∠AOC=2x∵∠B=∠AOC=x∴∠D=180°﹣x∵AD=CD,OA=OC∴∠DAC=∠ACD=x,∠OCA=∠OAC=90°﹣x∵AD∥BC∴∠ACB=∠DAC=x,∴∠BCO=x﹣(90°﹣x)=x﹣90°=15°,∴x=70°,∴∠AOC=140°.故选:C.二、填空题(每题5分)13.(5分)观察下列式子:,,,,…,归纳得出一般规律为.【解答】解:由已知中的式了,我们观察后分析:等式左边的系数分别为与n+1,等式右边为n+1,与的和,根据已知可以推断:第n(n∈N*)个等式为:故答案为:14.(5分)已知a<b,则在下列的一段推理过程中,错误的推理步骤有③④.(填上所有错误步骤的序号)【解答】解:步骤①在不等式两边同时加a,不等式仍成立,故步骤①正确;步骤②在不等式的两边同时减2b,不等式仍成立,故步骤②正确;步骤③在不等式两边同时乘(a﹣b),由于a<b,故a﹣b<0,不等号需改变方向,故步骤③错误;步骤④在不等式两边同时除以(a﹣b)2,由于(a﹣b)2>0,不等号方向不变,故步骤④错误.故答案为:③④.15.(5分)已知x与y之间的一组数据:则y与x的线性回归方程=bx+a必过点(1.5,4).【解答】解:∵,=4,∴本组数据的样本中心点是(1.5,4),∴y与x的线性回归方程为y=bx+a必过点(1.5,4)故答案为:(1.5,4)16.(5分)若Z∈C,且|Z+2﹣2i|=1,则|Z﹣2﹣2i|的最小值是3.【解答】解:|Z+2﹣2i|=1表示复平面上的点到(﹣2,2)的距离为1的圆,|Z﹣2﹣2i|就是圆上的点,到(2,2)的距离的最小值,就是圆心到(2,2)的距离减去半径,即:|2﹣(﹣2)|﹣1=3故答案为:3三、解答题(共70分)17.(12分)计算:(1)(﹣7i+5)﹣(9﹣8i)+(3﹣2i);(2)(4+i)(6﹣2i)+(7﹣i)(4﹣3i);(3).【解答】解:(1)(﹣7i+5)﹣(9﹣8i)+(3﹣2i)=(5﹣9+3)+(﹣7+8﹣2)=﹣1﹣i;(2)(4+i)(6﹣2i)+(7﹣i)(4﹣3i)=24﹣2i2﹣2i+28+3i2﹣25i=51﹣27i;(3)=+=+=2﹣2i+i=2﹣i18.(10分)实数m取怎样的值时,复数z=m﹣3+(m2﹣2m﹣15)i是:(1)实数?(2)虚数?(3)纯虚数?【解答】解:(1)当m2﹣2m﹣15=0,即m=﹣3或m=5时,复数Z为实数;(2)当m2﹣2m﹣15≠0,即m≠﹣3或m≠5时,复数Z为虚数;(3)当m2﹣2m﹣15≠0,且m﹣3=0,即m=3时,复数Z为纯虚数.19.(12分)为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.(1)根据所给样本数据画出2×2列联表;(2)请问能有多大把握认为药物有效?【解答】解:(1)根据服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本,没有服药且没有患病的有20个,得到列联表(2)假设检验问题H0:服药与家禽得禽流感没有关系=由P(K2≥2.706)=0.10∴大概90%认为药物有效.20.(12分)一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,如表是抽样试验结果:若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,求机器的转速应该控制所在的范围..【解答】解:由题意,=12.5,=8.25,∴b=≈0.7286,a=﹣0.8571∴回归直线方程为:y=0.7286x﹣0.8571;∵允许每小时的产品中有缺点的零件数最多为10个,∴0.7286x﹣0.8571≤10,解得x≤14.9013,∴0≤x≤14.9013.21.(12分)(Ⅰ)求证:+<2(Ⅱ)已知a>0,b>0且a+b>2,求证:,中至少有一个小于2.【解答】(Ⅰ)证明:因为和都是正数,所以为了证明+<2,只要证(+)2<(2)2只需证:10<20,即证:2<10,即证:<5,即证:21<25,因为21<25显然成立,所以原不等式成立.(Ⅱ)证明:假设:,都不小于2,则≥2,≥2,∵a>0,b>0,∴1+b≥2a,1+a≥2b,∴1+b+1+a≥2(a+b)即a+b≤2这与已知a+b>2矛盾,故假设不成立,从而原结论成立.22.(12分)已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC ∥DE,AC与BD相交于H点.(Ⅰ)求证:BD平分∠ABC;(Ⅱ)若AB=4,AD=6,BD=8,求AH的长.【解答】解:(Ⅰ)∵AC∥DE,直线DE为圆O的切线,∴D是弧的中点,即又∠ABD,∠DBC与分别是两弧所对的圆周角,故有∠ABD=∠DBC,所以BD平分∠ABC(Ⅱ)∵由图∠CAB=∠CDB且∠ABD=∠DBC∴△ABH∽△DBC,∴又∴AD=DC,∴∵AB=4,AD=6,BD=8∴AH=3。
2020-2021学年吉林省辽源市田家炳高级中学友好学校高二(下)期末数学试卷(理科)(附答案详解)

2020-2021学年吉林省辽源市田家炳高级中学友好学校高二(下)期末数学试卷(理科)一、单选题(本大题共12小题,共60.0分)1.已知复数zi=1+i(i为虚数单位),则|z|等于()A. 1B. 2C. √2D. √32.函数f(x)=x3+x在点x=1处的切线方程为()A. 4x−y+2=0B. 4x−y−2=0C. 4x+y+2=0D. 4x+y−2=03.已知6道试题中有4道语文题和2道数学题,每次从中抽取一道题,抽出的题不再放回,在第一次抽到语文题的条件下,第二次抽到数学题的概率为()A. 14B. 25C. 12D. 354.用反证法证明命题:“设a,b,c为实数,满足a+b+c是无理数,则a,b,c至少有一个是无理数”时,假设正确的是()A. 假设a,b,c都是有理数B. 假设a,b,c至少有一个是有理数C. 假设a,b,c不都是无理数D. 假设a,b,c至少有一个不是无理数5.下列四个命题正确的是()①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;②残差平方和越小的模型,拟合的效果越好;③用相关指数R2来刻画回归效果,R2越接近于1,说明模型的拟合效果越好;④线性回归方程y^=b^x+a^恒过样本点中心(x−,y−).A. ①②③B. ②③④C. ①③④D. ①②④6.∫(1e x+2x)dx=()A. 1B. e−1C. eD. e+17.已知函数f(x)的导函数为f′(x),且满足f(x)=3xf′(e)+lnx,则f′(e)=()A. 2eB. −12e C. 12eD. −2e8.已知随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=P(ξ>6)=0.16,则P(2≤ξ<4)=()A. 0.34B. 0.68C. 0.5D. 0.79. “中国诗词大会”亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.因为前四场播出后反响很好,所以节目组决定将《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另外确定的两首诗词排在后六场,并要求《将进酒》《望岳》相邻,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻,则后六场开场诗词的排法有( )A. 144种B. 48种C. 36种D. 72种10. 已知函数f(x)=−x 3+ax 2−x −1在(−∞,+∞)上是单调递减函数,则实数a 的取值范围是( )A. (−∞,−√3)∪(√3,+∞)B. (−√3,√3)C. (−∞,−√3]∪[√3,+∞)D. [−√3,√3]11. 用数学归纳法证明“1+2+3+⋯+n 3=n 6+n 32,n ∈N ⋅”,则当n =k +1时,应当在n =k 时对应的等式的两边加上( )A. (k 3+1)+(k 3+2)+⋯+(k +1)3B. k 3+1C. (k +1)3D. (k|1)6+(k+1)3212. 对任意x ∈R ,函数y =f(x)的导函数都存在,若f(x)−f′(x)<0恒成立,且a >0,则下列说法正确的是( )A. f(a)<f(0)B. f(a)>f(0)C. f(a)>e a f(0)D. f(a)<e a f(0)二、单空题(本大题共4小题,共20.0分)13. 对大于1的自然数m 的三次幂可用奇数进行以下形式的“分裂”:23{35,33{7911,43{13151719,......以此类推,若m 3的“分裂数”中有一个是67,则m 的值为______.14. 在(2x −1x )6的展开式中1x 2的系数为______ .15. 如图是函数f(x)的导函数f′(x)的图象,现给出如下结论:①f(x)在(−3,−1)是增函数; ②x =4是f(x)的极小值点;③f(x)在(−1,2)上是增函数,在(2,4)上是减函数;④x=−1一定是f(x)的零点.其中正确的结论是______.16.辛丑牛年春晚现场请来了荣获“人民英雄”“时代楷模”“全国道德模范”称号的几位先进人物代表共度新春佳节,他们是“人民英雄”陈薇、“时代楷模”毛相林、张连刚、林占禧,“全国道德模范”张晓艳、周秀芳、张家丰、朱恒银,从中选出两位荣誉称号不同的代表先后给全国人民拜年,则不同的发言情况有______ 种.三、解答题(本大题共6小题,共70.0分)17.已知函数f(x)=x2+ax与g(x)=ln(x+1)在(0,0)处有公共的切线.(1)求a的值;(2)求函数ℎ(x)=f(x)−g(x)(x>−1)的极值.18.在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(Ⅰ)求接受甲种心理暗示的志愿者中包含A1但不包含B1的频率。
吉林省辽源市田家炳高级中学复数试题及答案doc

一、复数选择题1.欧拉是瑞士著名数学家,他首先发现:e cos isin i θθθ=+(e 为自然对数的底数,i 为虚数单位),此结论被称为“欧拉公式”,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系.根据欧拉公式可知,i e π=( ) A .1B .0C .-1D .1+i2.已知复数()123z i i +=- (其中i 是虚数单位),则z 在复平面内对应点在( ) A .第一象限B .第二象限C .第三象限D .第四象限3.已知i 为虚数单位,则复数23ii-+的虚部是( ) A .35 B .35i - C .15-D .15i -4.在复平面内复数Z=i (1﹣2i )对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限5.已知i 是虚数单位,则复数41ii+在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限6.已知i 为虚数单位,若复数()12iz a R a i+=∈+为纯虚数,则z a +=( )A B .3C .5D .7.已知复数512z i=+,则z =( )A .1BCD .58.设2iz i+=,则||z =( )A B C .2D .59.设复数2i1iz =+,则复数z 的共轭复数z 在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限10.复数z 的共轭复数记为z ,则下列运算:①z z +;②z z -;③z z ⋅④zz,其结果一定是实数的是( ) A .①②B .②④C .②③D .①③11.已知复数z 满足202122z i i i+=+-+,则复数z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限12.已知复数z 的共轭复数212iz i-=+,i 是虚数单位,则复数z 的虚部是( ) A .1B .-1C .iD .i -13.复数z 对应的向量OZ 与(3,4)a =共线,对应的点在第三象限,且10z =,则z =( ) A .68i + B .68i - C .68i -- D .68i -+ 14.若复数z 满足213z z i -=+,则z =( )A .1i +B .1i -C .1i -+D .1i --15.复数21ii+的虚部为( ) A .1-B .1C .iD .i -二、多选题16.若复数351iz i-=-,则( )A .z =B .z 的实部与虚部之差为3C .4z i =+D .z 在复平面内对应的点位于第四象限17.已知复数z 满足220z z +=,则z 可能为( ) A .0B .2-C .2iD .2i -18.已知复数(),z x yi x y R =+∈,则( ) A .20zB .z 的虚部是yiC .若12z i =+,则1x =,2y =D .z =19.(多选题)已知集合{},nM m m i n N ==∈,其中i 为虚数单位,则下列元素属于集合M 的是( ) A .()()11i i -+ B .11ii-+ C .11ii+- D .()21i -20.已知复数122z =-+(其中i 为虚数单位,,则以下结论正确的是( ). A .20zB .2z z =C .31z =D .1z =21.已知i 为虚数单位,复数322iz i+=-,则以下真命题的是( ) A .z 的共轭复数为4755i - B .z 的虚部为75i C .3z =D .z 在复平面内对应的点在第一象限22.若复数z 满足(1i)3i z +=+(其中i 是虚数单位),复数z 的共轭复数为z ,则( )A .|z |=B .z 的实部是2C .z 的虚部是1D .复数z 在复平面内对应的点在第一象限23.下列关于复数的说法,其中正确的是( ) A .复数(),z a bi a b R =+∈是实数的充要条件是0b = B .复数(),z a bi a b R =+∈是纯虚数的充要条件是0b ≠ C .若1z ,2z 互为共轭复数,则12z z 是实数D .若1z ,2z 互为共轭复数,则在复平面内它们所对应的点关于y 轴对称 24.下列结论正确的是( )A .已知相关变量(),x y 满足回归方程ˆ9.49.1yx =+,则该方程相应于点(2,29)的残差为1.1B .在两个变量y 与x 的回归模型中,用相关指数2R 刻画回归的效果,2R 的值越大,模型的拟合效果越好C .若复数1z i =+,则2z =D .若命题p :0x R ∃∈,20010x x -+<,则p ⌝:x R ∀∈,210x x -+≥25.已知i 为虚数单位,以下四个说法中正确的是( ). A .234i i i i 0+++= B .3i 1i +>+C .若()2z=12i +,则复平面内z 对应的点位于第四象限D .已知复数z 满足11z z -=+,则z 在复平面内对应的点的轨迹为直线26.已知复数()(()()211z m m m i m R =-+-∈,则下列说法正确的是( )A .若0m =,则共轭复数1z =-B .若复数2z =,则mC .若复数z 为纯虚数,则1m =±D .若0m =,则2420z z ++=27.已知复数z a =+在复平面内对应的点位于第二象限,且2z = 则下列结论正确的是( ).A .38z =B .zC .z 的共轭复数为1D .24z =28.对于复数(,)z a bi a b R =+∈,下列结论错误..的是( ). A .若0a =,则a bi +为纯虚数 B .若32a bi i -=+,则3,2a b == C .若0b =,则a bi +为实数 D .纯虚数z 的共轭复数是z -29.以下命题正确的是( )A .0a =是z a bi =+为纯虚数的必要不充分条件B .满足210x +=的x 有且仅有iC .“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件D .已知()f x =()1878f x x '=30.已知i 为虚数单位,下列命题中正确的是( ) A .若x ,y ∈C ,则1x yi i +=+的充要条件是1x y == B .2(1)()a i a +∈R 是纯虚数C .若22120z z +=,则120z z == D .当4m =时,复数22lg(27)(56)m m m m i --+++是纯虚数【参考答案】***试卷处理标记,请不要删除一、复数选择题 1.C 【分析】利用复数和三角函数的性质,直接代入运算即可 【详解】 由题意可知=, 故选C 解析:C 【分析】利用复数和三角函数的性质,直接代入运算即可 【详解】由题意可知i e π=cos sin 101i ππ+=-+=-, 故选C2.D 【分析】先由复数的运算化简复数z ,再运用复数的几何表示可得选项. 【详解】 由已知得,所以复数z 在复平面上所对应的点为,在第四象限, 故选:D.解析:D 【分析】先由复数的运算化简复数z,再运用复数的几何表示可得选项.【详解】由已知得()()()()312317171+21+212555i ii iz ii i i----====--,所以复数z在复平面上所对应的点为17,55⎛⎫-⎪⎝⎭,在第四象限,故选:D.3.A【分析】先由复数的除法运算化简复数,再由复数的概念,即可得出其虚部. 【详解】因为,所以其虚部是.故选:A.解析:A【分析】先由复数的除法运算化简复数23ii-+,再由复数的概念,即可得出其虚部.【详解】因为22(3)26133(3)(3)1055i i i iii i i-----===--++-,所以其虚部是35.故选:A.4.A【解析】试题分析:根据复数乘法的运算法则,我们可以将复数Z化为a=bi(a,b∈R)的形式,分析实部和虚部的符号,即可得到答案.解:∵复数Z=i(1﹣2i)=2+i∵复数Z的实部2>0,虚解析:A【解析】试题分析:根据复数乘法的运算法则,我们可以将复数Z化为a=bi(a,b∈R)的形式,分析实部和虚部的符号,即可得到答案.解:∵复数Z=i(1﹣2i)=2+i∵复数Z的实部2>0,虚部1>0∴复数Z在复平面内对应的点位于第一象限故选A点评:本题考查的知识是复数的代数表示法及其几何意义,其中根据复数乘法的运算法则,将复数Z化为a=bi(a,b∈R)的形式,是解答本题的关键.5.A【分析】利用复数的乘除运算化简复数的代数形式,得到其对应坐标即知所在象限. 【详解】,所以复数对应的坐标为在第一象限, 故选:A解析:A 【分析】利用复数的乘除运算化简复数的代数形式,得到其对应坐标即知所在象限. 【详解】44(1)2(1)12i i i i i -==++,所以复数对应的坐标为(2,2)在第一象限, 故选:A 6.A 【分析】根据复数运算,化简后由纯虚数的概念可求得,.进而求得复数,再根据模的定义即可求得 【详解】由复数为纯虚数,则,解得 则 ,所以,所以 故选:A解析:A 【分析】根据复数运算,化简后由纯虚数的概念可求得a ,.进而求得复数z ,再根据模的定义即可求得z a + 【详解】()()()()()()2221222121122111i a i a a i a ii a z a i a i a i a a a +-++--++====+++-+++ 由复数()12iz a R a i +=∈+为纯虚数,则222012101a a a a +⎧=⎪⎪+⎨-⎪≠⎪+⎩,解得2a =-则z i =- ,所以2z a i +=--,所以z a += 故选:A7.C 【分析】根据模的运算可得选项. 【详解】 . 故选:C.解析:C 【分析】根据模的运算可得选项. 【详解】512z i ====+故选:C.8.B 【分析】利用复数的除法运算先求出,再求出模即可. 【详解】 , .故选:B .解析:B 【分析】利用复数的除法运算先求出z ,再求出模即可. 【详解】()22212i i i z i i i++===-,∴z ==故选:B .9.D 【分析】先求出,再求出,直接得复数在复平面内对应的点 【详解】因为,所以,在复平面内对应点,位于第四象限. 故选:D解析:D 【分析】先求出z ,再求出z ,直接得复数z 在复平面内对应的点 【详解】因为211i z i i==++,所以1z i -=-,z 在复平面内对应点()1,1-,位于第四象限.故选:D10.D 【分析】设,则,利用复数的运算判断. 【详解】 设,则, 故,, ,. 故选:D.解析:D 【分析】设(),z a bi a b R =+∈,则z a bi =-,利用复数的运算判断. 【详解】设(),z a bi a b R =+∈,则z a bi =-, 故2z z a R +=∈,2z z bi -=,22222z a bi a b abiz a bi a b +-+==-+,22z z a b ⋅=+∈R . 故选:D.11.C 【分析】由已知得到,然后利用复数的乘法运算法则计算,利用复数的周期性算出的值,最后利用复数的几何意义可得结果. 【详解】 由题可得,,所以复数在复平面内对应的点为,在第三象限, 故选:C .解析:C 【分析】由已知得到2021(2)(2)i i iz -++-=,然后利用复数的乘法运算法则计算(2)(2)i i -++,利用复数n i 的周期性算出2021i 的值,最后利用复数的几何意义可得结果. 【详解】由题可得,2021(2)(2)5i z i ii -+=+-=--,所以复数z 在复平面内对应的点为(5,1)--,在第三象限, 故选:C .12.A 【分析】先化简,由此求得,进而求得的虚部. 【详解】 ,所以,则的虚部为. 故选:A解析:A 【分析】先化简z ,由此求得z ,进而求得z 的虚部. 【详解】()()()()212251212125i i i iz i i i i ----====-++-, 所以zi ,则z 的虚部为1.故选:A13.D 【分析】设,根据复数对应的向量与共线,得到,再结合求解. 【详解】 设,则复数对应的向量, 因为向量与共线, 所以, 又, 所以, 解得或,因为复数对应的点在第三象限, 所以, 所以,,解析:D 【分析】设(,)z a bi a R b R =+∈∈,根据复数z 对应的向量OZ 与(3,4)a =共线,得到43a b =,再结合10z =求解.【详解】设(,)z a bi a R b R =+∈∈,则复数z 对应的向量(),OZ a b =, 因为向量OZ 与(3,4)a =共线, 所以43a b =, 又10z =, 所以22100+=a b , 解得68a b =-⎧⎨=-⎩或68a b =⎧⎨=⎩, 因为复数z 对应的点在第三象限,所以68a b =-⎧⎨=-⎩,所以68z i =--,68z i =-+, 故选:D14.A 【分析】采用待定系数法,设,由复数运算和复数相等可求得,从而得到结果. 【详解】 设,则, ,,解得:, . 故选:A.解析:A 【分析】采用待定系数法,设(),z a bi a b R =+∈,由复数运算和复数相等可求得,a b ,从而得到结果. 【详解】设(),z a bi a b R =+∈,则z a bi =-,()()22313z z a bi a bi a bi i ∴-=+--=+=+,133a b =⎧∴⎨=⎩,解得:11a b =⎧⎨=⎩,1z i ∴=+. 故选:A. 15.B 【分析】将分母乘以其共轭复数进行分母实数化,化成的代数形式即得结果. 【详解】 ,故虚部为1.解析:B【分析】将分母乘以其共轭复数进行分母实数化,化成(),a bi a b R +∈的代数形式即得结果.【详解】22(1)11(1)(1)i i i i i i i -==+++-,故虚部为1. 故选:B.二、多选题16.AD【分析】根据复数的运算先求出复数z ,再根据定义、模、几何意义即可求出.【详解】解:,,z 的实部为4,虚部为,则相差5,z 对应的坐标为,故z 在复平面内对应的点位于第四象限,所以AD 正解析:AD【分析】根据复数的运算先求出复数z ,再根据定义、模、几何意义即可求出.【详解】 解:()()()()351358241112i i i i z i i i i -+--====---+,z ∴==z 的实部为4,虚部为1-,则相差5,z 对应的坐标为()41-,,故z 在复平面内对应的点位于第四象限,所以AD 正确, 故选:AD.17.ACD【分析】令代入已知等式,列方程组求解即可知的可能值.【详解】令代入,得:,∴,解得或或∴或或.故选:ACD本题考查了已知等量关系求复数,属于简单题.解析:ACD【分析】令z a bi =+代入已知等式,列方程组求解即可知z 的可能值.【详解】令z a bi =+代入22||0z z +=,得:2220a b abi -+=,∴22020a b ab ⎧⎪-+=⎨=⎪⎩,解得0,0a b =⎧⎨=⎩或0,2a b =⎧⎨=⎩或0,2,a b =⎧⎨=-⎩ ∴0z =或2z i =或2z i =-.故选:ACD【点睛】本题考查了已知等量关系求复数,属于简单题.18.CD【分析】取特殊值可判断A 选项的正误;由复数的概念可判断B 、C 选项的正误;由复数模的概念可判断D 选项的正误.【详解】对于A 选项,取,则,A 选项错误;对于B 选项,复数的虚部为,B 选项错误;解析:CD【分析】取特殊值可判断A 选项的正误;由复数的概念可判断B 、C 选项的正误;由复数模的概念可判断D 选项的正误.【详解】对于A 选项,取z i ,则210z =-<,A 选项错误;对于B 选项,复数z 的虚部为y ,B 选项错误;对于C 选项,若12z i =+,则1x =,2y =,C 选项正确;对于D选项,z =D 选项正确.故选:CD.【点睛】本题考查复数相关命题真假的判断,涉及复数的计算、复数的概念以及复数的模,属于基础题. 19.BC【分析】根据集合求出集合内部的元素,再对四个选项依次化简即可得出选项.根据题意,中,时,;时,;时,;时,,.选项A 中,;选项B 中,;选项C 中,;选项D 中,.解析:BC【分析】根据集合求出集合内部的元素,再对四个选项依次化简即可得出选项.【详解】 根据题意,{},n M m m i n N ==∈中, ()4n k k N =∈时,1n i =;()41n k k N =+∈时,n i i =;()42n k k N =+∈时,1n i =-;()43n k k N =+∈时,n i i =-,{}1,1,,M i i ∴=--.选项A 中,()()112i i M -+=∉;选项B 中,()()()211111i i i i i i M --==-+-∈+; 选项C 中,()()()211111i i i i i i M ++==-+∈-; 选项D 中,()212i i M -=-∉.故选:BC.【点睛】此题考查复数的基本运算,涉及复数的乘方和乘法除法运算,准确计算才能得解. 20.BCD【分析】计算出,即可进行判断.【详解】,,故B 正确,由于复数不能比较大小,故A 错误;,故C 正确;,故D 正确.故选:BCD.【点睛】本题考查复数的相关计算,属于基础题.解析:BCD【分析】 计算出23,,,z z z z ,即可进行判断.【详解】12z =-+, 221313i i=22z z ,故B 正确,由于复数不能比较大小,故A 错误; 33131313i i i 1222222z ,故C 正确; 2213122z,故D 正确.故选:BCD.【点睛】 本题考查复数的相关计算,属于基础题.21.AD【分析】先利用复数的除法、乘法计算出,再逐项判断后可得正确的选项.【详解】,故,故A 正确.的虚部为,故B 错,,故C 错,在复平面内对应的点为,故D 正确.故选:AD.【点睛】本题考解析:AD【分析】先利用复数的除法、乘法计算出z ,再逐项判断后可得正确的选项.【详解】()()32232474725555i i i i i z i ++++====+-,故4755i z =-,故A 正确.z 的虚部为75,故B 错,355z ==≠,故C 错, z 在复平面内对应的点为47,55⎛⎫ ⎪⎝⎭,故D 正确. 故选:AD.【点睛】本题考查复数的概念、复数的运算以及复数的几何意义,注意复数(),z a bi a b R =+∈的虚部为b ,不是bi ,另外复数的除法运算是分子分母同乘以分母的共轭复数.22.ABD【分析】把已知等式变形,然后利用复数代数形式的乘除运算化简,求出复数,根据共轭复数概念得到,即可判断.【详解】,,,故选项正确,的实部是,故选项正确,的虚部是,故选项错误,复解析:ABD【分析】把已知等式变形,然后利用复数代数形式的乘除运算化简,求出复数z ,根据共轭复数概念得到z ,即可判断.【详解】(1i)3i z +=+,()()()()3134221112i i i i z i i i i +-+-∴====-++-,z ∴==,故选项A 正确,z 的实部是2,故选项B 正确,z 的虚部是1-,故选项C 错误, 复数2z i =+在复平面内对应的点为()2,1,在第一象限,故选项D 正确.故选:ABD .【点睛】本题主要考查的是复数代数形式的乘除运算,考查了复数的代数表示及几何意义,是基础题.23.AC【分析】根据复数的有关概念和充分条件和必要条件的定义进行判断即可.【详解】解:对于:复数是实数的充要条件是,显然成立,故正确;对于:若复数是纯虚数则且,故错误;对于:若,互为共轭复数解析:AC【分析】根据复数的有关概念和充分条件和必要条件的定义进行判断即可.【详解】解:对于A :复数(),z a bi a b R =+∈是实数的充要条件是0b =,显然成立,故A 正确;对于B :若复数(),z a bi a b R =+∈是纯虚数则0a =且0b ≠,故B 错误;对于C :若1z ,2z 互为共轭复数,设()1,z a bi a b R =+∈,则()2,z a bi a b R =-∈,所以()()2122222z a bi a bi a b b z i a =+-=-=+是实数,故C 正确; 对于D :若1z ,2z 互为共轭复数,设()1,z a bi a b R =+∈,则()2,z a bi a b R =-∈,所对应的坐标分别为(),a b ,(),a b -,这两点关于x 轴对称,故D 错误;故选:AC【点睛】本题主要考查复数的有关概念的判断,利用充分条件和必要条件的定义是解决本题的关键,属于基础题.24.ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当时,,则该方程相应于点(2,29)的残差为,则A 正确;在两个变量解析:ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.当2x =时,ˆ9.429.127.9y=⨯+=,则该方程相应于点(2,29)的残差为2927.9 1.1-=,则A 正确;在两个变量y 与x 的回归模型中,2R 的值越大,模型的拟合效果越好,则B 正确;1z i =-,z ==C 错误;由否定的定义可知,D 正确;故选:ABD【点睛】本题主要考查了残差的计算,求复数的模,特称命题的否定,属于中档题. 25.AD【分析】根据复数的运算判断A ;由虚数不能比较大小判断B ;由复数的运算以及共轭复数的定义判断C ;由模长公式化简,得出,从而判断D.【详解】,则A 正确;虚数不能比较大小,则B 错误;,则,解析:AD【分析】根据复数的运算判断A ;由虚数不能比较大小判断B ;由复数的运算以及共轭复数的定义判断C ;由模长公式化简11z z -=+,得出0x =,从而判断D.【详解】234110i i i i i i +++=--+=,则A 正确;虚数不能比较大小,则B 错误;()221424341z i i i i =++=+-+=,则34z i =--,其对应复平面的点的坐标为(3,4)--,位于第三象限,则C 错误; 令,,z x yi x y R =+∈,|1||1z z -=+∣,=,解得0x =则z 在复平面内对应的点的轨迹为直线,D 正确;故选:AD【点睛】本题主要考查了判断复数对应的点所在的象限,与复数模相关的轨迹(图形)问题,属于中档题.26.BD【分析】根据每个选项里的条件,求出相应的结果,即可判断选项的正误.对于A ,时,,则,故A 错误;对于B ,若复数,则满足,解得,故B 正确;对于C ,若复数z 为纯虚数,则满足,解得,解析:BD【分析】根据每个选项里的条件,求出相应的结果,即可判断选项的正误.【详解】对于A ,0m =时,1z =-,则1z =-,故A 错误;对于B ,若复数2z =,则满足(()21210m m m ⎧-=⎪⎨-=⎪⎩,解得m ,故B 正确; 对于C ,若复数z为纯虚数,则满足(()21010m m m ⎧-=⎪⎨--≠⎪⎩,解得1m =-,故C 错误; 对于D ,若0m =,则1z =-+,()()221420412z z ++=+--+=+,故D 正确.故选:BD.【点睛】 本题主要考查对复数相关概念的理解,注意不同情形下的取值要求,是一道基础题.27.AB【分析】利用复数的模长运算及在复平面内对应的点位于第二象限求出 ,再验算每个选项得解.【详解】解:,且,复数在复平面内对应的点位于第二象限选项A:选项B: 的虚部是选项C:解析:AB【分析】 利用复数2z =的模长运算及z a =+在复平面内对应的点位于第二象限求出a ,再验算每个选项得解.【详解】解:z a =+,且2z=224a +∴=,=1a ±复数z a =+在复平面内对应的点位于第二象限1a ∴=-选项A : 3323(1)(1)+3(1)+3())8-+=---+=选项B : 1z =-选项C : 1z =-的共轭复数为1z =--选项D : 222(1)(1)+2()2-+=--=--故选:AB .【点睛】本题考查复数的四则运算及共轭复数,考查运算求解能力.求解与复数概念相关问题的技巧:复数的分类、复数的相等、复数的模及共轭复数的概念都与复数的实部、虚部有关,所以解答与复数相关概念有关的问题时,需把所给复数化为代数形式,即()a bi a b R ∈+,的形式,再根据题意求解.28.AB【分析】由复数的代数形式的运算,逐个选项验证可得.【详解】解:因为当且时复数为纯虚数,此时,故A 错误,D 正确;当时,复数为实数,故C 正确;对于B :,则即,故B 错误;故错误的有AB解析:AB【分析】由复数的代数形式的运算,逐个选项验证可得.【详解】解:因为(,)z a bi a b R =+∈当0a =且0b ≠时复数为纯虚数,此时z bi z =-=-,故A 错误,D 正确;当0b =时,复数为实数,故C 正确;对于B :32a bi i -=+,则32a b =⎧⎨-=⎩即32a b =⎧⎨=-⎩,故B 错误; 故错误的有AB ;故选:AB【点睛】本题考查复数的代数形式及几何意义,属于基础题.29.AC【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误;解方程可判断B 选项的正误;利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误;利用基本初等函数的导数公式解析:AC【分析】利用纯虚数的概念以及必要不充分条件的定义可判断A 选项的正误;解方程210x +=可判断B 选项的正误;利用导数与函数单调性的关系结合充分不必要条件的定义可判断C 选项的正误;利用基本初等函数的导数公式可判断D 选项的正误.综合可得出结论.【详解】对于A 选项,若复数z a bi =+为纯虚数,则0a =且0b ≠,所以,0a =是z a bi =+为纯虚数的必要不充分条件,A 选项正确;对于B 选项,解方程210x +=得x i =±,B 选项错误;对于C 选项,当(),x a b ∈时,若()0f x '>,则函数()f x 在区间(),a b 内单调递增, 即“在区间(),a b 内()0f x '>”⇒“()f x 在区间(),a b 内单调递增”.反之,取()3f x x =,()23f x x '=,当()1,1x ∈-时,()0f x '≥, 此时,函数()y f x =在区间()1,1-上单调递增,即“在区间(),a b 内()0f x '>”⇐/“()f x 在区间(),a b 内单调递增”.所以,“在区间(),a b 内()0f x '>”是“()f x 在区间(),a b 内单调递增”的充分不必要条件.C 选项正确;对于D 选项,()11172488f x x x ++===,()1878f x x -'∴=,D 选项错误. 故选:AC.【点睛】本题考查命题真假的判断,涉及充分条件与必要条件的判断、实系数方程的根以及导数的计算,考查推理能力与计算能力,属于中等题. 30.BD【分析】选项A :取,满足方程,所以错误;选项B :,恒成立,所以正确;选项C :取,,,所以错误;选项D :代入,验证结果是纯虚数,所以正确.【详解】取,,则,但不满足,故A 错误;,恒成解析:BD【分析】选项A :取x i =,y i =-满足方程,所以错误;选项B :a ∀∈R ,210a +>恒成立,所以正确;选项C :取1z i =,21z =,22120z z +=,所以错误;选项D :4m =代入 22lg(27)(56)m m m m i --+++,验证结果是纯虚数,所以正确.【详解】取x i =,y i =-,则1x yi i +=+,但不满足1x y ==,故A 错误;a ∀∈R ,210a +>恒成立,所以2(1a i +)是纯虚数,故B 正确;取1z i =,21z =,则22120z z +=,但120z z ==不成立,故C 错误; 4m =时,复数2212756=42g m m m m i i --+++()()是纯虚数,故D 正确.故选:BD .【点睛】本题考查复数有关概念的辨析,特别要注意复数的实部和虚部都是实数,解题时要合理取特殊值,属于中档题.。
吉林省辽源市田家炳高级中学复数试题及答案doc

一、复数选择题1.复数()1z i i =⋅+在复平面上对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.若复数z 满足()13i z i +=+(其中i 是虚数单位),复数z 的共轭复数为z ,则( ) A .z 的实部是1 B .z 的虚部是1C .5z =D .复数z 在复平面内对应的点在第四象限3.若复数1z i i ⋅=-+,则复数z 的虚部为( ) A .-1B .1C .-iD .i4.若复数()()24z i i =--,则z =( ) A .76i --B .76-+iC .76i -D .76i +5.如图所示,在复平面内,网格中的每个小正方形的边长都为1,点A ,B 对应的复数分别是1z ,2z ,则12z z -=( )A 2B .2C .2D .86.已知i 是虚数单位,则复数41ii+在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限7.已知复数202111i z i-=+,则z 的虚部是( )A .1-B .i -C .1D .i8.复数z 的共轭复数记为z ,则下列运算:①z z +;②z z -;③z z ⋅④zz,其结果一定是实数的是( ) A .①② B .②④C .②③D .①③9.复数12iz i=+(i 为虚数单位)在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限10.在复平面内,复数z 对应的点为(,)x y ,若22(2)4x y ++=,则( ) A .22z +=B .22z i +=C .24z +=D .24z i +=11.若复数z 满足213z z i -=+,则z =( ) A .1i +B .1i -C .1i -+D .1i --12.已知()312++=+a i i bi (,a b ∈R ,i 为虚数单位),则实数+a b 的值为( ) A .3B .5C .6D .813.已知i 是虚数单位,设复数22ia bi i-+=+,其中,a b ∈R ,则+a b 的值为( ) A .75B .75-C .15D .15-14.若复数11iz i,i 是虚数单位,则z =( ) A .0 B .12C .1D .215.题目文件丢失!二、多选题16.若复数351iz i-=-,则( )A .z =B .z 的实部与虚部之差为3C .4z i =+D .z 在复平面内对应的点位于第四象限17.已知复数z 满足220z z +=,则z 可能为( ) A .0B .2-C .2iD .2i - 18.已知复数z 满足2724z i =--,在复平面内,复数z 对应的点可能在( ) A .第一象限B .第二象限C .第三象限D .第四象限19.已知复数1cos 2sin 222z i ππθθθ⎛⎫=++-<< ⎪⎝⎭(其中i 为虚数单位),则( )A .复数z 在复平面上对应的点可能落在第二象限B .z 可能为实数C .2cos z θ=D .1z 的实部为12- 20.下列说法正确的是( ) A .若2z =,则4z z ⋅=B .若复数1z ,2z 满足1212z z z z +=-,则120z z =C .若复数z 的平方是纯虚数,则复数z 的实部和虛部相等D .“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件21.已知复数1z =-+(i 为虚数单位),z 为z 的共轭复数,若复数zw z=,则下列结论正确的有( )A .w 在复平面内对应的点位于第二象限B .1w =C .w 的实部为12-D .w22.已知复数12z =-+(其中i 为虚数单位),则以下结论正确的是( )A .20zB .2z z =C .31z =D .1z =23.已知复数z 满足(1﹣i )z =2i ,则下列关于复数z 的结论正确的是( )A .||z =B .复数z 的共轭复数为z =﹣1﹣iC .复平面内表示复数z 的点位于第二象限D .复数z 是方程x 2+2x +2=0的一个根 24.以下为真命题的是( ) A .纯虚数z 的共轭复数等于z -B .若120z z +=,则12z z =C .若12z z +∈R ,则1z 与2z 互为共轭复数D .若120z z -=,则1z 与2z 互为共轭复数25.已知复数z a =+在复平面内对应的点位于第二象限,且2z = 则下列结论正确的是( ).A .38z =B .zC .z 的共轭复数为1D .24z =26.若复数21iz =+,其中i 为虚数单位,则下列结论正确的是( )A .z 的虚部为1-B .||z =C .2z 为纯虚数D .z 的共轭复数为1i --27.对于复数(,)z a bi a b R =+∈,下列结论错误..的是( ). A .若0a =,则a bi +为纯虚数 B .若32a bi i -=+,则3,2a b == C .若0b =,则a bi +为实数 D .纯虚数z 的共轭复数是z -28.复数21iz i+=-,i 是虚数单位,则下列结论正确的是( )A .|z |=B .z 的共轭复数为3122i + C .z 的实部与虚部之和为2D .z 在复平面内的对应点位于第一象限29.(多选)()()321i i +-+表示( ) A .点()3,2与点()1,1之间的距离B .点()3,2与点()1,1--之间的距离C .点()2,1到原点的距离D .坐标为()2,1--的向量的模30.已知复数z ,下列结论正确的是( ) A .“0z z +=”是“z 为纯虚数”的充分不必要条件 B .“0z z +=”是“z 为纯虚数”的必要不充分条件 C .“z z =”是“z 为实数”的充要条件 D .“z z ⋅∈R ”是“z 为实数”的充分不必要条件【参考答案】***试卷处理标记,请不要删除一、复数选择题 1.B 【分析】先利用复数的乘法化简复数z ,再利用复数的几何意义求解. 【详解】 因为复数,所以在复数z 复平面上对应的点位于第二象限 故选:B 解析:B 【分析】先利用复数的乘法化简复数z ,再利用复数的几何意义求解. 【详解】因为复数()11z i i i =⋅+=-+,所以在复数z 复平面上对应的点位于第二象限 故选:B2.C 【分析】利用复数的除法运算求出,即可判断各选项. 【详解】 , ,则的实部为2,故A 错误;的虚部是,故B 错误; ,故C 正;对应的点为在第一象限,故D 错误. 故选:C.解析:C【分析】利用复数的除法运算求出z ,即可判断各选项. 【详解】()13i z i +=+,()()()()3132111i i i z i i i i +-+∴===-++-, 则z 的实部为2,故A 错误;z 的虚部是1-,故B 错误;z ==,故C 正;2z i =+对应的点为()2,1在第一象限,故D 错误.故选:C.3.B 【分析】 ,然后算出即可. 【详解】由题意,则复数的虚部为1 故选:B解析:B 【分析】1iz i -+=,然后算出即可. 【详解】 由题意()11111i i i i z i i i i -+-+--====+⋅-,则复数z 的虚部为1 故选:B4.D 【分析】由复数乘法运算求得,根据共轭复数定义可求得结果. 【详解】 ,. 故选:.解析:D 【分析】由复数乘法运算求得z ,根据共轭复数定义可求得结果. 【详解】()()2248676z i i i i i =--=-+=-,76z i ∴=+.故选:D .5.B 【分析】根据复数的几何意义,求两个复数,再计算复数的模. 【详解】由图象可知,,则, 故. 故选:B.解析:B 【分析】根据复数的几何意义,求两个复数,再计算复数的模. 【详解】由图象可知1z i =,22z i =-,则1222z z i -=-+,故12|22|z z i -=-+== 故选:B .6.A 【分析】利用复数的乘除运算化简复数的代数形式,得到其对应坐标即知所在象限. 【详解】,所以复数对应的坐标为在第一象限, 故选:A解析:A 【分析】利用复数的乘除运算化简复数的代数形式,得到其对应坐标即知所在象限. 【详解】44(1)2(1)12i i i i i -==++,所以复数对应的坐标为(2,2)在第一象限, 故选:A 7.C 【分析】求出,即可得出,求出虚部. 【详解】 ,,其虚部是1. 故选:C.解析:C 【分析】求出z ,即可得出z ,求出虚部. 【详解】()()()220211i 1i i 1i 1i 1i z --===-++-,i z ∴=,其虚部是1.故选:C.8.D 【分析】设,则,利用复数的运算判断. 【详解】 设,则, 故,, ,. 故选:D.解析:D 【分析】设(),z a bi a b R =+∈,则z a bi =-,利用复数的运算判断. 【详解】设(),z a bi a b R =+∈,则z a bi =-, 故2z z a R +=∈,2z z bi -=,22222z a bi a b abiz a bi a b +-+==-+,22z z a b ⋅=+∈R . 故选:D.9.A 【分析】对复数进行分母实数化,根据复数的几何意义可得结果. 【详解】 由,知在复平面内对应的点位于第一象限, 故选:A. 【点睛】本题主要考查了复数除法的运算以及复数的几何意义,属于基础题解析:A 【分析】对复数z 进行分母实数化,根据复数的几何意义可得结果. 【详解】 由()()()122112121255i i i z i i i i -===+++-,知在复平面内对应的点21,55⎛⎫⎪⎝⎭位于第一象限, 故选:A. 【点睛】本题主要考查了复数除法的运算以及复数的几何意义,属于基础题.10.B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数对应的点为,所以 ,满足则 故选:B解析:B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数z 对应的点为(,)x y ,所以z x yi =+x ,y 满足22(2)4x y ++=则22z i +=故选:B11.A 【分析】采用待定系数法,设,由复数运算和复数相等可求得,从而得到结果. 【详解】 设,则, ,,解得:, . 故选:A.解析:A 【分析】采用待定系数法,设(),z a bi a b R =+∈,由复数运算和复数相等可求得,a b ,从而得到结果. 【详解】设(),z a bi a b R =+∈,则z a bi =-,()()22313z z a bi a bi a bi i ∴-=+--=+=+,133a b =⎧∴⎨=⎩,解得:11a b =⎧⎨=⎩,1z i ∴=+.12.D 【分析】利用复数的乘法运算及复数相等求得a,b 值即可求解 【详解】 ,故 则 故选:D解析:D 【分析】利用复数的乘法运算及复数相等求得a,b 值即可求解 【详解】()312++=+a i i bi ,故332a i bi -+=+ 则32,38a b a b -==∴+=故选:D13.D 【分析】先化简,求出的值即得解. 【详解】 , 所以. 故选:D解析:D 【分析】 先化简345ia bi -+=,求出,ab 的值即得解. 【详解】22(2)342(2)(2)5i i ia bi i i i ---+===++-,所以341,,555a b a b ==-∴+=-. 故选:D14.C 【分析】由复数除法求出,再由模计算. 【详解】 由已知, 所以. 故选:C .【分析】由复数除法求出z ,再由模计算. 【详解】由已知21(1)21(1)(1)2i i iz i i i i ---====-++-, 所以1z i =-=. 故选:C .15.无二、多选题 16.AD 【分析】根据复数的运算先求出复数z ,再根据定义、模、几何意义即可求出. 【详解】 解:, ,z 的实部为4,虚部为,则相差5,z 对应的坐标为,故z 在复平面内对应的点位于第四象限,所以AD 正解析:AD 【分析】根据复数的运算先求出复数z ,再根据定义、模、几何意义即可求出. 【详解】 解:()()()()351358241112i i i iz i i i i -+--====---+,z ∴==z 的实部为4,虚部为1-,则相差5,z 对应的坐标为()41-,,故z 在复平面内对应的点位于第四象限,所以AD 正确, 故选:AD.17.ACD 【分析】令代入已知等式,列方程组求解即可知的可能值. 【详解】 令代入,得:,∴,解得或或∴或或.故选:ACD【点睛】本题考查了已知等量关系求复数,属于简单题.解析:ACD【分析】令z a bi =+代入已知等式,列方程组求解即可知z 的可能值.【详解】令z a bi =+代入22||0z z +=,得:2220a b abi -+=,∴22020a b ab ⎧⎪-+=⎨=⎪⎩,解得0,0a b =⎧⎨=⎩或0,2a b =⎧⎨=⎩或0,2,a b =⎧⎨=-⎩ ∴0z =或2z i =或2z i =-.故选:ACD【点睛】本题考查了已知等量关系求复数,属于简单题.18.BD【分析】先设复数,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出,即可确定对应的点所在的象限.【详解】设复数,则,所以,则,解得或,因此或,所以对应的点为或,因此复解析:BD【分析】先设复数(),z a bi a b R =+∈,根据题中条件,由复数的乘法运算,以及复数相等的充要条件求出z ,即可确定对应的点所在的象限.【详解】设复数(),z a bi a b R =+∈,则2222724z a abi b i =+-=--,所以2222724z a abi b i =+-=--,则227224a b ab ⎧-=-⎨=-⎩,解得34a b =⎧⎨=-⎩或34a b =-⎧⎨=⎩, 因此34z i =-或34z i =-+,所以对应的点为()3,4-或()3,4-,因此复数z 对应的点可能在第二或第四象限.故选:BD.【点睛】本题主要考查判定复数对应的点所在的象限,熟记复数的运算法则,以及复数相等的条件即可,属于基础题型.19.BC【分析】由可得,得,可判断A 选项,当虚部,时,可判断B 选项,由复数的模计算和余弦的二倍角公式可判断C 选项,由复数的运算得,的实部是,可判断D 选项.【详解】因为,所以,所以,所以,所以A 选解析:BC【分析】 由22ππθ-<<可得2πθπ-<<,得01cos22θ<+≤,可判断A 选项,当虚部sin 20θ=,,22ππθ⎛⎫∈- ⎪⎝⎭时,可判断B 选项,由复数的模计算和余弦的二倍角公式可判断C 选项,由复数的运算得11cos 2sin 212cos 2i z θθθ+-=+,1z 的实部是1cos 2122cos 22θθ+=+,可判断D 选项.【详解】 因为22ππθ-<<,所以2πθπ-<<,所以1cos21θ-<≤,所以01cos22θ<+≤,所以A 选项错误;当sin 20θ=,,22ππθ⎛⎫∈- ⎪⎝⎭时,复数z 是实数,故B 选项正确;2cos z θ===,故C 选项正确:()()111cos 2sin 21cos 2sin 21cos 2sin 21cos 2sin 21cos 2sin 212cos 2i i z i i i θθθθθθθθθθθ+-+-===+++++-+,1z 的实部是1cos 2122cos 22θθ+=+,故D 不正确. 故选:BC【点睛】本题主要考查复数的概念,复数模的计算,复数的运算,以及三角恒等变换的应用,属于中档题.20.AD【分析】由求得判断A ;设出,,证明在满足时,不一定有判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】若,则,故A 正确;设,由,可得则,而不一定为0,故B 错误;当时解析:AD【分析】 由z 求得z z ⋅判断A ;设出1z ,2z ,证明在满足1212z z z z +=-时,不一定有120z z =判断B ;举例说明C 错误;由充分必要条件的判定说明D 正确.【详解】 若2z =,则24z z z ⋅==,故A 正确;设()11111,z a bi a b R =+∈,()22222,z a b i a b R =+∈ 由1212z z z z +=-,可得()()()()222222121212121212z z a a b b z z a a b b +=+++=-=-+-则12120a a b b +=,而()()121122121212121212122z z a bi a b i a a bb a b i b a i a a a b i b a i =++=-++=++不一定为0,故B 错误;当1z i =-时22z i =-为纯虚数,其实部和虚部不相等,故C 错误;若复数()()()211z a a i a R =-+-∈是虚数,则210a -≠,即1a ≠± 所以“1a ≠”是“复数()()()211z a a i a R =-+-∈是虚数”的必要不充分条件,故D 正确; 故选:AD【点睛】本题考查的是复数的相关知识,考查了学生对基础知识的掌握情况,属于中档题.21.ABC【分析】对选项求出,再判断得解;对选项,求出再判断得解;对选项复数的实部为,判断得解;对选项,的虚部为,判断得解.【详解】对选项由题得.所以复数对应的点为,在第二象限,所以选项正确解析:ABC【分析】对选项,A 求出1=2w -+,再判断得解;对选项B ,求出1w =再判断得解;对选项,C 复数w 的实部为12-,判断得解;对选项D ,w 判断得解. 【详解】对选项,A 由题得1,z =-1=2w ∴===-.所以复数w 对应的点为1(2-,在第二象限,所以选项A 正确;对选项B ,因为1w ==,所以选项B 正确; 对选项,C 复数w 的实部为12-,所以选项C 正确;对选项D ,w 的虚部为2,所以选项D 错误. 故选:ABC【点睛】 本题主要考查复数的运算和共轭复数,考查复数的模的计算,考查复数的几何意义,考查复数的实部和虚部的概念,意在考查学生对这些知识的理解掌握水平.22.BCD【分析】利用复数的运算法则直接求解.【详解】解:复数(其中为虚数单位),,故错误;,故正确;,故正确;.故正确.故选:.【点睛】本题考查命题真假的判断,考查复数的运算法则【分析】利用复数的运算法则直接求解.【详解】解:复数12z =-(其中i 为虚数单位),2131442z ∴=-=--,故A 错误; 2z z ∴=,故B 正确;31113()()12244z =--+=+=,故C 正确;||1z ==.故D 正确. 故选:BCD .【点睛】本题考查命题真假的判断,考查复数的运算法则等基础知识,考查运算求解能力,属于基础题.23.ABCD【分析】利用复数的除法运算求出,再根据复数的模长公式求出,可知正确;根据共轭复数的概念求出,可知正确;根据复数的几何意义可知正确;将代入方程成立,可知正确.【详解】因为(1﹣i )z =解析:ABCD【分析】利用复数的除法运算求出1z i =-+,再根据复数的模长公式求出||z ,可知A 正确;根据共轭复数的概念求出z ,可知B 正确;根据复数的几何意义可知C 正确;将z 代入方程成立,可知D 正确.【详解】因为(1﹣i )z =2i ,所以21i z i =-2(1)221(1)(1)2i i i i i i +-+===-+-+,所以||z ==A 正确; 所以1i z =--,故B 正确;由1z i =-+知,复数z 对应的点为(1,1)-,它在第二象限,故C 正确;因为2(1)2(1)2i i -++-++22220i i =--++=,所以D 正确.故选:ABCD.本题考查了复数的除法运算,考查了复数的模长公式,考查了复数的几何意义,属于基础题.24.AD【分析】根据纯虚数的概念即可判断A 选项;根据实数、复数的运算、以及共轭复数的定义即可判断BCD 选项.【详解】解:对于A ,若为纯虚数,可设,则,即纯虚数的共轭复数等于,故A 正确;对于B解析:AD【分析】根据纯虚数的概念即可判断A 选项;根据实数、复数的运算、以及共轭复数的定义即可判断BCD 选项.【详解】解:对于A ,若z 为纯虚数,可设()0z bi b =≠,则z bi z =-=-,即纯虚数z 的共轭复数等于z -,故A 正确;对于B ,由120z z +=,得出12z z =-,可设11z i =+,则21z i =--, 则21z i =-+,此时12z z ≠,故B 错误;对于C ,设12,z a bi z c di =+=+,则()()12a c b d i R z z =++++∈,则0b d +=, 但,a c 不一定相等,所以1z 与2z 不一定互为共轭复数,故C 错误;对于D ,120z z -=,则12z z =,则1z 与2z 互为共轭复数,故D 正确.故选:AD.【点睛】本题考查与复数有关的命题的真假性,考查复数的基本概念和运算,涉及实数、纯虚数和共轭复数的定义,属于基础题. 25.AB【分析】利用复数的模长运算及在复平面内对应的点位于第二象限求出 ,再验算每个选项得解.【详解】解:,且,复数在复平面内对应的点位于第二象限选项A:选项B: 的虚部是解析:AB【分析】利用复数2z =的模长运算及z a =+在复平面内对应的点位于第二象限求出a ,再验算每个选项得解.【详解】解:z a =+,且2z =224a +∴=,=1a ±复数z a =+在复平面内对应的点位于第二象限1a ∴=-选项A : 3323(1)(1)+3(1)+3())8-+=---+=选项B : 1z =-选项C : 1z =-的共轭复数为1z =--选项D : 222(1)(1)+2()2-+=--=--故选:AB .【点睛】本题考查复数的四则运算及共轭复数,考查运算求解能力.求解与复数概念相关问题的技巧:复数的分类、复数的相等、复数的模及共轭复数的概念都与复数的实部、虚部有关,所以解答与复数相关概念有关的问题时,需把所给复数化为代数形式,即()a bi a b R ∈+,的形式,再根据题意求解.26.ABC【分析】首先利用复数代数形式的乘除运算化简后得:,然后分别按照四个选项的要求逐一求解判断即可.【详解】因为,对于A :的虚部为,正确;对于B :模长,正确;对于C :因为,故为纯虚数,解析:ABC【分析】首先利用复数代数形式的乘除运算化简z 后得:1z i =-,然后分别按照四个选项的要求逐一求解判断即可.【详解】 因为()()()2122211i 1i 12i i z i i --====-++-,对于A :z 的虚部为1-,正确;对于B :模长z =对于C :因为22(1)2z i i =-=-,故2z 为纯虚数,正确;对于D :z 的共轭复数为1i +,错误.故选:ABC .【点睛】本题考查复数代数形式的乘除运算,考查复数的有关概念,考查逻辑思维能力和运算能力,侧重考查对基础知识的理解和掌握,属于常考题.27.AB【分析】由复数的代数形式的运算,逐个选项验证可得.【详解】解:因为当且时复数为纯虚数,此时,故A 错误,D 正确;当时,复数为实数,故C 正确;对于B :,则即,故B 错误;故错误的有AB解析:AB【分析】由复数的代数形式的运算,逐个选项验证可得.【详解】解:因为(,)z a bi a b R =+∈当0a =且0b ≠时复数为纯虚数,此时z bi z =-=-,故A 错误,D 正确;当0b =时,复数为实数,故C 正确;对于B :32a bi i -=+,则32a b =⎧⎨-=⎩即32a b =⎧⎨=-⎩,故B 错误; 故错误的有AB ;故选:AB【点睛】本题考查复数的代数形式及几何意义,属于基础题. 28.CD【分析】根据复数的四则运算,整理复数,再逐一分析选项,即得.【详解】由题得,复数,可得,则A 不正确;的共轭复数为,则B 不正确;的实部与虚部之和为,则C 正确;在复平面内的对应点为,位于第一解析:CD【分析】根据复数的四则运算,整理复数z ,再逐一分析选项,即得.【详解】 由题得,复数22(2)(1)13131(1)(1)122i i i i z i i i i i ++++====+--+-,可得||2z ==,则A 不正确;z 的共轭复数为1322i -,则B 不正确;z 的实部与虚部之和为13222+=,则C 正确;z 在复平面内的对应点为13(,)22,位于第一象限,则D 正确.综上,正确结论是CD.故选:CD【点睛】本题考查复数的定义,共轭复数以及复数的模,考查知识点全面.29.ACD【分析】由复数的模的意义可判断选项A,B ;整理原式等于,也等于,即可判断选项C,D【详解】由复数的几何意义,知复数,分别对应复平面内的点与点,所以表示点与点之间的距离,故A 说法正确,B解析:ACD【分析】由复数的模的意义可判断选项A,B ;整理原式等于2i +,也等于2i --,即可判断选项C,D【详解】由复数的几何意义,知复数32i +,1i +分别对应复平面内的点()3,2与点()1,1,所以()()321i i +-+表示点()3,2与点()1,1之间的距离,故A 说法正确,B 说法错误;()()3212i i i +-+=+,2i +可表示点()2,1到原点的距离,故C 说法正确;()()()()3211322i i i i i +-+=+-+=--,2i --可表示表示点()2,1--到原点的距离,即坐标为()2,1--的向量的模,故D 说法正确,故选:ACD【点睛】本题考查复数的几何意义,考查复数的模30.BC【分析】设,可得出,利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断,从而可得出结论.【详解】设,则,则,若,则,,若,则不为纯虚数,所以,“”是“为纯虚数”必要不充分解析:BC【分析】设(),z a bi a b R =+∈,可得出z a bi =-,利用复数的运算、复数的概念结合充分条件、必要条件的定义进行判断,从而可得出结论.【详解】设(),z a bi a b R =+∈,则z a bi =-, 则2z z a +=,若0z z +=,则0a =,b R ∈,若0b =,则z 不为纯虚数, 所以,“0z z +=”是“z 为纯虚数”必要不充分条件; 若z z =,即a bi a bi +=-,可得0b =,则z 为实数,“z z =”是“z 为实数”的充要条件;22z z a b ⋅=+∈R ,z ∴为虚数或实数,“z z ⋅∈R ”是“z 为实数”的必要不充分条件.故选:BC.【点睛】本题考查充分条件、必要条件的判断,同时也考查了共轭复数、复数的基本概念的应用,考查推理能力,属于基础题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、复数选择题1.欧拉是瑞士著名数学家,他首先发现:e cos isin i θθθ=+(e 为自然对数的底数,i 为虚数单位),此结论被称为“欧拉公式”,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系.根据欧拉公式可知,i e π=( ) A .1B .0C .-1D .1+i2.已知i 是虚数单位,复数2z i =-,则()12z i ⋅+的模长为( )A .6BC .5D 3.若复数1z i i ⋅=-+,则复数z 的虚部为( )A .-1B .1C .-iD .i4.已知,a b ∈R ,若2()2a b a b i -+->(i 为虚数单位),则a 的取值范围是( ) A .2a >或1a <- B .1a >或2a <- C .12a -<< D .21a -<< 5.复数z 满足12i z i ⋅=-,z 是z 的共轭复数,则z z ⋅=( )A B C .3D .56.若复数1211iz i+=--,则z 在复平面内的对应点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限7.设2iz i+=,则||z =( )A B C .2D .58.设复数z 满足方程4z z z z ⋅+⋅=,其中z 为复数z 的共轭复数,若z ,则z 为( )A .1BC .2D .49.在复平面内,复数z 对应的点为(,)x y ,若22(2)4x y ++=,则( ) A .22z += B .22z i +=C .24z +=D .24z i +=10.复数2ii -的实部与虚部之和为( ) A .35 B .15- C .15D .3511.复数112z i =+,21z i =+(i 为虚数单位),则12z z ⋅虚部等于( ). A .1-B .3C .3iD .i -12.在复平面内,已知平行四边形OABC 顶点O ,A ,C 分别表示25-+i ,32i +,则点B 对应的复数的共轭复数为( ) A .17i -B .16i -C .16i --D .17i --13.已知i 是虚数单位,设复数22ia bi i-+=+,其中,a b ∈R ,则+a b 的值为( ) A .75B .75-C .15D .15-14.已知i 为虚数单位,则43ii =-( ) A .2655i + B .2655i - C .2655i -+ D .2655i -- 15.若i 为虚数单位,,a b ∈R ,且2a ib i i+=+,则复数a bi -的模等于( )A BC D二、多选题16.已知复数12z =-,则下列结论正确的有( )A .1z z ⋅=B .2z z =C .31z =-D .2020122z =-+ 17.下列四个命题中,真命题为( ) A .若复数z 满足z R ∈,则z R ∈ B .若复数z 满足1R z∈,则z R ∈ C .若复数z 满足2z ∈R ,则z R ∈D .若复数1z ,2z 满足12z z R ⋅∈,则12z z =18.(多选题)已知集合{},nM m m i n N ==∈,其中i 为虚数单位,则下列元素属于集合M 的是( ) A .()()11i i -+B .11ii-+ C .11ii+- D .()21i -19.已知复数012z i =+(i 为虚数单位)在复平面内对应的点为0P ,复数z 满足|1|||z z i -=-,下列结论正确的是( )A .0P 点的坐标为(1,2)B .复数0z 的共轭复数对应的点与点0P 关于虚轴对称C .复数z 对应的点Z 在一条直线上D .0P 与z 对应的点Z 间的距离的最小值为20.设复数z 满足1z i z+=,则下列说法错误的是( ) A .z 为纯虚数B .z 的虚部为12i -C .在复平面内,z 对应的点位于第三象限D .z =21.若复数z 满足()234z i i +=+(i 为虚数单位),则下列结论正确的有( )A .z 的虚部为3B .z =C .z 的共轭复数为23i +D .z 是第三象限的点22.下面是关于复数21iz =-+(i 为虚数单位)的命题,其中真命题为( ) A .||2z =B .22z i =C .z 的共轭复数为1i +D .z 的虚部为1-23.已知复数1z =-+(i 为虚数单位),z 为z 的共轭复数,若复数zw z=,则下列结论正确的有( )A .w 在复平面内对应的点位于第二象限B .1w =C .w 的实部为12-D .w 的虚部为2i 24.下列结论正确的是( )A .已知相关变量(),x y 满足回归方程ˆ9.49.1yx =+,则该方程相应于点(2,29)的残差为1.1B .在两个变量y 与x 的回归模型中,用相关指数2R 刻画回归的效果,2R 的值越大,模型的拟合效果越好C .若复数1z i =+,则2z =D .若命题p :0x R ∃∈,20010x x -+<,则p ⌝:x R ∀∈,210x x -+≥25.已知复数12ω=-(i 是虚数单位),ω是ω的共轭复数,则下列的结论正确的是( ) A .2ωω=B .31ω=-C .210ωω++=D .ωω>26.设i 为虚数单位,复数()(12)z a i i =++,则下列命题正确的是( ) A .若z 为纯虚数,则实数a 的值为2B .若z 在复平面内对应的点在第三象限,则实数a 的取值范围是(,)122-C .实数12a =-是z z =(z 为z 的共轭复数)的充要条件 D .若||5()z z x i x R +=+∈,则实数a 的值为227.已知复数z 满足(1﹣i )z =2i ,则下列关于复数z 的结论正确的是( )A .||z =B .复数z 的共轭复数为z =﹣1﹣iC .复平面内表示复数z 的点位于第二象限D .复数z 是方程x 2+2x +2=0的一个根 28.下面四个命题,其中错误的命题是( )A .0比i -大B .两个复数当且仅当其和为实数时互为共轭复数C .1x yi i +=+的充要条件为1x y ==D .任何纯虚数的平方都是负实数29.已知复数z 满足23z z iz ai ⋅+=+,a R ∈,则实数a 的值可能是( ) A .1B .4-C .0D .530.对任意1z ,2z ,z C ∈,下列结论成立的是( ) A .当m ,*n N ∈时,有m n m n z z z +=B .当1z ,2zC ∈时,若22120z z +=,则10z =且20z = C .互为共轭复数的两个复数的模相等,且22||||z z z z ==⋅ D .12z z =的充要条件是12=z z【参考答案】***试卷处理标记,请不要删除一、复数选择题 1.C 【分析】利用复数和三角函数的性质,直接代入运算即可 【详解】 由题意可知=, 故选C 解析:C 【分析】利用复数和三角函数的性质,直接代入运算即可 【详解】由题意可知i e π=cos sin 101i ππ+=-+=-, 故选C2.C 【分析】利用复数代数形式的乘除运算化简,再由复数模的公式得答案. 【详解】 , , 所以,, 故选:C.【分析】利用复数代数形式的乘除运算化简,再由复数模的公式得答案. 【详解】2z i =-,(12)(2)(12)43z i i i i ∴⋅+=-+=+,所以,5z =, 故选:C.3.B 【分析】 ,然后算出即可. 【详解】由题意,则复数的虚部为1 故选:B解析:B 【分析】1iz i -+=,然后算出即可. 【详解】 由题意()11111i i i i z i i i i -+-+--====+⋅-,则复数z 的虚部为1 故选:B4.A 【分析】根据虚数不能比较大小可得,再解一元二次不等式可得结果. 【详解】 因为,,所以,, 所以或. 故选:A 【点睛】关键点点睛:根据虚数不能比较大小得是解题关键,属于基础题.解析:A 【分析】根据虚数不能比较大小可得a b =,再解一元二次不等式可得结果. 【详解】因为,a b ∈R ,2()2a b a b i -+->,所以a b =,220a a -->, 所以2a >或1a <-.【点睛】关键点点睛:根据虚数不能比较大小得a b =是解题关键,属于基础题.5.D 【分析】求出复数,然后由乘法法则计算. 【详解】 由题意, . 故选:D .解析:D 【分析】求出复数z ,然后由乘法法则计算z z ⋅. 【详解】 由题意12122i z i i i-==-+=--, 22(2)(2)(2)5z z i i i ⋅=---+=--=.故选:D .6.B 【分析】利用复数的运算法则和复数的几何意义求解即可 【详解】 ,所以,在复平面内的对应点为,则对应点位于第二象限 故选:B解析:B 【分析】利用复数的运算法则和复数的几何意义求解即可 【详解】()()12i 1i 12i33i 33i 111i 2222z +++-+=-=-==-+-, 所以,z 在复平面内的对应点为33,22⎛⎫- ⎪⎝⎭,则对应点位于第二象限 故选:B7.B 【分析】利用复数的除法运算先求出,再求出模即可., . 故选:B .解析:B 【分析】利用复数的除法运算先求出z ,再求出模即可. 【详解】()22212i ii z i i i++===-,∴z ==故选:B .8.B 【分析】由题意,设复数,根据共轭复数的概念,以及题中条件,即可得出结果. 【详解】因为的实部为,所以可设复数, 则其共轭复数为,又, 所以由,可得,即,因此. 故选:B.解析:B 【分析】由题意,设复数(),z yi x R y R =∈∈,根据共轭复数的概念,以及题中条件,即可得出结果. 【详解】因为z ,所以可设复数(),z yi x R y R =∈∈,则其共轭复数为z yi =,又z z =,所以由4z z z z ⋅+⋅=,可得()4z z z ⋅+=,即4z ⋅=,因此z =故选:B.9.B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数对应的点为,所以 ,满足则故选:B解析:B 【分析】利用复数模的计算公式即可判断出结论. 【详解】因为复数z 对应的点为(,)x y ,所以z x yi =+x ,y 满足22(2)4x y ++=则22z i +=故选:B10.C 【分析】利用复数代数形式的乘除运算化简得答案. 【详解】,的实部与虚部之和为. 故选:C 【点睛】易错点睛:复数的虚部是,不是.解析:C 【分析】利用复数代数形式的乘除运算化简得答案. 【详解】()()()2+1212222+555i i i i i i i i -+===-+--,2i i ∴-的实部与虚部之和为121555-+=. 故选:C 【点睛】易错点睛:复数z a bi =+的虚部是b ,不是bi .11.B 【分析】化简,利用定义可得的虚部. 【详解】则的虚部等于 故选:B解析:B 【分析】化简12z z ⋅,利用定义可得12z z ⋅的虚部. 【详解】()()1212113z z i i i ⋅=+⋅+=-+则12z z ⋅的虚部等于3 故选:B12.A 【分析】根据复数的几何意义得出坐标,由平行四边形得点坐标,即得点对应复数,从而到共轭复数. 【详解】 由题意,设,∵是平行四边形,AC 中点和BO 中点相同, ∴,即,∴点对应是,共轭复数为.解析:A 【分析】根据复数的几何意义得出,A C 坐标,由平行四边形得B 点坐标,即得B 点对应复数,从而到共轭复数. 【详解】由题意(2,5),(3,2)A C -,设(,)B x y ,∵OABC 是平行四边形,AC 中点和BO 中点相同, ∴023052x y +=-+⎧⎨+=+⎩,即17x y =⎧⎨=⎩,∴B 点对应是17i +,共轭复数为17i -.故选:A .13.D 【分析】先化简,求出的值即得解. 【详解】 , 所以. 故选:D解析:D 【分析】 先化简345ia bi -+=,求出,ab 的值即得解. 【详解】22(2)342(2)(2)5i i ia bi i i i ---+===++-,所以341,,555a b a b ==-∴+=-. 故选:D14.C 【分析】对的分子分母同乘以,再化简整理即可求解. 【详解】 , 故选:C解析:C 【分析】对43ii -的分子分母同乘以3i +,再化简整理即可求解. 【详解】()()()434412263331055i i i i i i i i +-+===-+--+, 故选:C15.C 【分析】首先根据复数相等得到,,再求的模即可. 【详解】 因为,所以,. 所以. 故选:C解析:C 【分析】首先根据复数相等得到1a =-,2b =,再求a bi -的模即可. 【详解】因为()21a i b i i bi +=+=-+,所以1a =-,2b =.所以12a bi i -=--==故选:C二、多选题 16.ACD 【分析】分别计算各选项的值,然后判断是否正确,计算D 选项的时候注意利用复数乘方的性质. 【详解】因为,所以A 正确;因为,,所以,所以B 错误;因为,所以C 正确;因为,所以,所以D 正确解析:ACD【分析】分别计算各选项的值,然后判断是否正确,计算D 选项的时候注意利用复数乘方的性质.【详解】因为111312244z z ⎛⎫⎛⎫=+= ⎪⎪ ⎪⎪⎝⎭⎭=⎝⋅,所以A 正确;因为22112222z ⎛⎫-=-- ⎪ ⎪⎝⎭=,12z =,所以2z z ≠,所以B 错误;因为321112222z z z i ⎛⎫⎛⎫=⋅=---=- ⎪⎪ ⎪⎪⎝⎭⎝⎭,所以C 正确;因为6331z z z =⋅=,所以()202063364431112222z z z z z ⨯+⎛⎫===⋅=-⋅-=-+ ⎪ ⎪⎝⎭,所以D 正确,故选:ACD.【点睛】本题考查复数乘法与乘方的计算,其中还涉及到了共轭复数的计算,难度较易.17.AB【分析】利用特值法依次判断选项即可得到答案.【详解】对选项A ,若复数满足,设,其中,则,则选项A 正确;对选项B ,若复数满足,设,其中,且,则,则选项B 正确;对选项C ,若复数满足,设解析:AB【分析】利用特值法依次判断选项即可得到答案.【详解】对选项A ,若复数z 满足z R ∈,设z a =,其中a R ∈,则z R ∈,则选项A 正确; 对选项B ,若复数z 满足1R z ∈,设1a z =,其中a R ∈,且0a ≠, 则1z R a=∈,则选项B 正确;对选项C ,若复数z 满足2z ∈R ,设z i ,则21z R =-∈,但z i R =∉,则选项C 错误; 对选项D ,若复数1z ,2z 满足12z z R ⋅∈,设1z i =,2z i =,则121z z ⋅=-∈R , 而21z i z =-≠,则选项D 错误;故答案选:AB【点睛】本题主要考查复数的运算,同时考查复数的定义和共轭复数,特值法为解决本题的关键,属于简单题.18.BC【分析】根据集合求出集合内部的元素,再对四个选项依次化简即可得出选项.【详解】根据题意,中,时,;时,;时,;时,,.选项A 中,;选项B 中,;选项C 中,;选项D 中,.解析:BC【分析】根据集合求出集合内部的元素,再对四个选项依次化简即可得出选项.【详解】 根据题意,{},n M m m i n N ==∈中, ()4n k k N =∈时,1n i =;()41n k k N =+∈时,n i i =;()42n k k N =+∈时,1n i =-;()43n k k N =+∈时,n i i =-,{}1,1,,M i i ∴=--.选项A 中,()()112i i M -+=∉;选项B 中,()()()211111i i i i i i M --==-+-∈+; 选项C 中,()()()211111i i i i i i M ++==-+∈-; 选项D 中,()212i i M -=-∉.故选:BC.【点睛】此题考查复数的基本运算,涉及复数的乘方和乘法除法运算,准确计算才能得解. 19.ACD【分析】根据复数对应的坐标,判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系,判断B 选项的正确性.设出,利用,结合复数模的运算进行化简,由此判断出点的轨迹,由此判读C 选项的正确解析:ACD【分析】根据复数对应的坐标,判断A 选项的正确性.根据互为共轭复数的两个复数坐标的对称关系,判断B 选项的正确性.设出z ,利用|1|||z z i -=-,结合复数模的运算进行化简,由此判断出Z 点的轨迹,由此判读C 选项的正确性.结合C 选项的分析,由点到直线的距离公式判断D 选项的正确性.【详解】复数012z i =+在复平面内对应的点为0(1,2)P ,A 正确;复数0z 的共轭复数对应的点与点0P 关于实轴对称,B 错误;设(,)z x yi x y R =+∈,代入|1|||z z i -=-,得|(1)(1)i|x yi x y -+=+-,即=y x =;即Z 点在直线y x =上,C 正确; 易知点0P 到直线y x =的垂线段的长度即为0P 、Z 之间距离的最小值,结合点到直线的距2=,故D 正确. 故选:ACD【点睛】本小题主要考查复数对应的坐标,考查共轭复数,考查复数模的运算,属于基础题. 20.AB【分析】先由复数除法运算可得,再逐一分析选项,即可得答案.【详解】由题意得:,即,所以z 不是纯虚数,故A 错误;复数z 的虚部为,故B 错误;在复平面内,对应的点为,在第三象限,故C 正确解析:AB【分析】 先由复数除法运算可得1122z i =--,再逐一分析选项,即可得答案. 【详解】 由题意得:1z zi +=,即111122z i i -==---, 所以z 不是纯虚数,故A 错误; 复数z 的虚部为12-,故B 错误; 在复平面内,z 对应的点为11(,)22--,在第三象限,故C 正确;2z ==,故D 正确. 故选:AB【点睛】本题考查复数的除法运算,纯虚数、虚部的概念,复平面内点所在象限、复数求模的运算等知识,考查计算求值的能力,属基础题.21.BC【分析】利用复数的除法求出复数,利用复数的概念与几何意义可判断各选项的正误.【详解】,,所以,复数的虚部为,,共轭复数为,复数在复平面对应的点在第四象限. 故选:BD.【点睛】本题考解析:BC【分析】利用复数的除法求出复数z ,利用复数的概念与几何意义可判断各选项的正误.【详解】()234z i i +=+,34232i z i i+∴=-=-+,所以,复数z 的虚部为3-,z =共轭复数为23i +,复数z 在复平面对应的点在第四象限.故选:BD.【点睛】本题考查复数的四则运算、虚部、模、共轭复数以及几何意义,考查计算能力,属于基础题.22.BD【分析】把分子分母同时乘以,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】解:,,A错误;,B正确;z的共轭复数为,C错误;z的虚部为,D正确.故选:BD.【点解析:BD【分析】把21iz=-+分子分母同时乘以1i--,整理为复数的一般形式,由复数的基本知识进行判断即可.【详解】解:22(1)11(1)(1)iz ii i i--===---+-+--,||z∴=A错误;22iz=,B正确;z的共轭复数为1i-+,C错误;z的虚部为1-,D正确.故选:BD.【点睛】本题主要考查复数除法的基本运算、复数的基本概念,属于基础题.23.ABC【分析】对选项求出,再判断得解;对选项,求出再判断得解;对选项复数的实部为,判断得解;对选项,的虚部为,判断得解.【详解】对选项由题得.所以复数对应的点为,在第二象限,所以选项正确解析:ABC【分析】对选项,A 求出1=2w -+,再判断得解;对选项B ,求出1w =再判断得解;对选项,C 复数w 的实部为12-,判断得解;对选项D ,w 判断得解. 【详解】对选项,A 由题得1,z =-221=422w -+∴===-+.所以复数w 对应的点为1(2-,在第二象限,所以选项A 正确;对选项B ,因为1w ==,所以选项B 正确; 对选项,C 复数w 的实部为12-,所以选项C 正确;对选项D ,w 所以选项D 错误. 故选:ABC【点睛】 本题主要考查复数的运算和共轭复数,考查复数的模的计算,考查复数的几何意义,考查复数的实部和虚部的概念,意在考查学生对这些知识的理解掌握水平.24.ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当时,,则该方程相应于点(2,29)的残差为,则A 正确;在两个变量解析:ABD【分析】根据残差的计算方法判断A ,根据相关指数的性质判断B ,根据复数的模长公式判断C ,根据否定的定义判断D.【详解】当2x =时,ˆ9.429.127.9y=⨯+=,则该方程相应于点(2,29)的残差为2927.9 1.1-=,则A 正确;在两个变量y 与x 的回归模型中,2R 的值越大,模型的拟合效果越好,则B 正确;1z i =-,z ==C 错误;由否定的定义可知,D 正确;故选:ABD【点睛】本题主要考查了残差的计算,求复数的模,特称命题的否定,属于中档题. 25.AC【分析】根据复数的运算进行化简判断即可.【详解】解:∵所以,∴,故A 正确,,故B 错误,,故C 正确,虚数不能比较大小,故D 错误,故选:AC.【点睛】本题主要考查复数的有关概念解析:AC【分析】 根据复数的运算进行化简判断即可.【详解】解:∵12ω=-所以122ω=--,∴213142422ωω=--=--=,故A 正确,32111312244ωωω⎛⎫⎛⎫⎛⎫==---=--= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,故B 错误,2111102222ωω++=---++=,故C 正确, 虚数不能比较大小,故D 错误,故选:AC .【点睛】本题主要考查复数的有关概念和运算,结合复数的运算法则进行判断是解决本题的关键.属于中档题.26.ACD【分析】首先应用复数的乘法得,再根据纯虚数概念、复数所在象限,以及与共轭复数或另一个复数相等,求参数的值或范围,进而可确定选项的正误【详解】∴选项A :为纯虚数,有可得,故正确选项B解析:ACD【分析】首先应用复数的乘法得2(12)z a a i =-++,再根据纯虚数概念、复数所在象限,以及与共轭复数或另一个复数相等,求参数的值或范围,进而可确定选项的正误【详解】()(12)2(12)z a i i a a i =++=-++∴选项A :z 为纯虚数,有20120a a -=⎧⎨+≠⎩可得2a =,故正确 选项B :z 在复平面内对应的点在第三象限,有20120a a -<⎧⎨+<⎩解得12a <-,故错误 选项C :12a =-时,52z z ==-;z z =时,120a +=即12a =-,它们互为充要条件,故正确 选项D :||5()z z x i x R +=+∈时,有125a +=,即2a =,故正确故选:ACD【点睛】本题考查了复数的运算及分类和概念,应用复数乘法运算求得复数,再根据复数的概念及性质、相等关系等确定参数的值或范围27.ABCD【分析】利用复数的除法运算求出,再根据复数的模长公式求出,可知正确;根据共轭复数的概念求出,可知正确;根据复数的几何意义可知正确;将代入方程成立,可知正确.【详解】因为(1﹣i )z =解析:ABCD【分析】利用复数的除法运算求出1z i =-+,再根据复数的模长公式求出||z ,可知A 正确;根据共轭复数的概念求出z ,可知B 正确;根据复数的几何意义可知C 正确;将z 代入方程成立,可知D 正确.因为(1﹣i )z =2i ,所以21i z i =-2(1)221(1)(1)2i i i i i i +-+===-+-+,所以||z ==A 正确; 所以1i z =--,故B 正确;由1z i =-+知,复数z 对应的点为(1,1)-,它在第二象限,故C 正确;因为2(1)2(1)2i i -++-++22220i i =--++=,所以D 正确.故选:ABCD.【点睛】本题考查了复数的除法运算,考查了复数的模长公式,考查了复数的几何意义,属于基础题.28.ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,解析:ABC【分析】根据虚数不能比大小可判断A 选项的正误;利用特殊值法可判断B 选项的正误;利用特殊值法可判断C 选项的正误;利用复数的运算可判断D 选项的正误.【详解】对于A 选项,由于虚数不能比大小,A 选项错误;对于B 选项,()()123i i ++-=,但1i +与2i -不互为共轭复数,B 选项错误; 对于C 选项,由于1x yi i +=+,且x 、y 不一定是实数,若取x i =,y i =-,则1x yi i +=+,C 选项错误;对于D 选项,任取纯虚数()0,ai a a R ≠∈,则()220ai a =-<,D 选项正确. 故选:ABC.【点睛】本题考查复数相关命题真假的判断,涉及共轭复数的概念、复数相等以及复数的计算,属于基础题.29.ABC【分析】设,从而有,利用消元法得到关于的一元二次方程,利用判别式大于等于0,从而求得a 的范围,即可得答案.设,∴,∴,∴,解得:,∴实数的值可能是.故选:ABC.【点解析:ABC【分析】设z x yi =+,从而有222()3x y i x yi ai ++-=+,利用消元法得到关于y 的一元二次方程,利用判别式大于等于0,从而求得a 的范围,即可得答案.【详解】设z x yi =+,∴222()3x y i x yi ai ++-=+, ∴222223,23042,x y y a y y x a ⎧++=⇒++-=⎨=⎩, ∴244(3)04a ∆=--≥,解得:44a -≤≤, ∴实数a 的值可能是1,4,0-.故选:ABC.【点睛】本题考查复数的四则运算、模的运算,考查函数与方程思想,考查逻辑推理能力和运算求解能力.30.AC【分析】根据复数乘法的运算律和复数的模及共轭复数的概念可判断出答案A 和C 正确;C 中可取,进行判断;D 中的必要不充分条件是.【详解】解:由复数乘法的运算律知,A 正确;取,;,满足,但且不解析:AC【分析】根据复数乘法的运算律和复数的模及共轭复数的概念可判断出答案A 和C 正确;C 中可取11z =,2z i =进行判断;D 中12z z =的必要不充分条件是12=z z .【详解】解:由复数乘法的运算律知,A 正确;取11z =,;2z i =,满足22120z z +=,但10z =且20z =不成立,B 错误; 由复数的模及共轭复数的概念知结论成立,C 正确;由12z z =能推出12=z z ,但12||||z z =推不出12z z =,因此12z z =的必要不充分条件是12=z z ,D 错误. 故选:AC【点睛】本题主要考查复数乘法的运算律和复数的基本知识以及共轭复数的概念,属于基础题.。
