基于matlab的凸轮计算
基于Matlab的共轭平行分度凸轮的分析计算

基于Matlab的共轭平行分度凸轮的分析计算高英;王蕊照;钞红晓;王开政【摘要】In the traditional parallel indexing cam design process, selection of the drive angle value was relatively large, which is conducive to the structure of the cam curve. This paper discusses the design of parallel indexing cam in the small drive angle, to solve the problem of parallel indexing cam design in some special occasions, with a high reference value.%针对工程实际应用中的特殊需求,采用全新的曲线轮廓构造方法,利用Matlab仿真计算软件完成了平行分度凸轮的可视化仿真设计.解决了小驱动角平行分度凸轮的参数化设计、分析、计算等一系列问题,大大提高了设计效率。
开发的计算程序同样适用于普通平行分度凸轮的设计计算,具有良好的通用性。
【期刊名称】《电子设计工程》【年(卷),期】2012(020)016【总页数】3页(P28-29,32)【关键词】平行分度凸轮;驱动角;Matlab仿真;分析【作者】高英;王蕊照;钞红晓;王开政【作者单位】西北机电工程研究所,陕西咸阳712000;西北机电工程研究所,陕西咸阳712000;西北机电工程研究所,陕西咸阳712000;西北机电工程研究所,陕西咸阳712000【正文语种】中文【中图分类】TN955平行分度凸轮是用于两平行轴间的一种间歇传动机构,具有传动平稳、承载能力大等优点。
某机构分度凸轮为3分度,传动、结构设计决定了该凸轮驱动角范围为49°~52°,这与以往工程应用中至少90°驱动角的情况有很大不同。
基于MATLAB的配气凸轮优化设计

( o eeo chncl n l t n nier gIs t eo Sohw U vr t,uhu2 5 2 , h a C lg f l Me ai dEe r i E g e n tu f oco n e i S zo 10 1 C i ) aa co c n i ni t i sy n
维普资讯
2O O6年第 1 ( 期 总第 9 期 ) l
山 东 内燃 机
S A D N . . . H N O GIC E
2O 年 2月 O6
【 设计计算 】
基 于 MA L B的 配 气 凸 轮优 化设 计 TA
李 兵, 顾德 裕
( 苏州大学机电工程学院, 江苏 苏州 252) 101
结果表 明, 优化后凸轮的特性参数更佳。
关 键词 : 气凸轮 ; 化设 计 ; T A 配 优 MA L B
中 图分类 号 :K 1 . 文献标 识码 : T 434 A文章 编 号 :6 1 4120 )1 01 3 17 —27(060 —03 —0
Op i iain Dein o eCa fVav y tm a e i M AⅡ 。B t z t s ft m o leS se B sd Ol m o g h A
CA 。 E
收 稿 日期 "05—1 —1 .0 2 2 9
t
维普资讯
山东 内燃 机
2O 年 2月 O6
升 程 h, 如下关 系 : 、 有
+
一
1s ¨譬 + (+ k )
詈 + + + ,般 说丰 + 一 来 ,
摘 要 : 立 了七 次 多项 式动 力凸轮 型线 的优 化设 计数 学模 型 ; 用 MA I 建 利 TAB及其 优化 工具
凸轮的matlab绘制
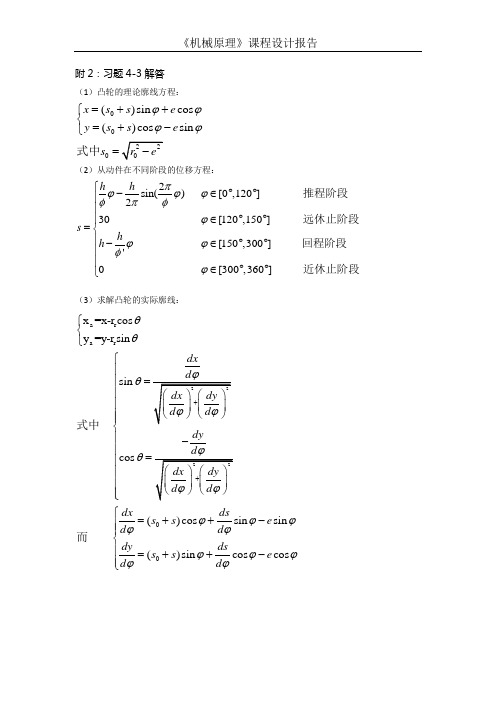
附2:习题4-3解答(1)凸轮的理论廓线方程:000()sin cos ()cos sin x s s e y s s e s ϕϕϕϕ=++⎧⎨=+-⎩=式中 (2)从动件在不同阶段的位移方程:2sin()[0,120]230[120,150][150,300]'0[300,360]h h s h h πϕϕϕφπφϕϕϕφϕ⎧-∈︒︒⎪⎪∈︒︒⎪=⎨⎪-∈︒︒⎪⎪∈︒︒⎩推程阶段远休止阶段回程阶段近休止阶段(3)求解凸轮的实际廓线:a r a r 00x =x-r cos y =y-r sin sin cos ()cos sin sin ()sin cos cos dx dy dxds s s e d d dy ds s s e d d θθθθϕϕϕϕϕϕϕϕϕϕ⎧⎨⎩⎧⎪=⎪⎪⎪⎪⎪⎨⎪-⎪=⎪⎪⎪⎪⎩⎧=++-⎪⎪⎨⎪=++-⎪⎩式中而同样,由于位移s 与从动件所处的运动阶段有关,所以有:2cos()[0,120]0[120,150]s [150,300]'0[300,360]h hd hd πϕϕφφφϕϕϕφϕ⎧-∈︒︒⎪⎪∈︒︒⎪=⎨⎪∈︒︒⎪⎪∈︒︒⎩推程阶段远休止阶段回程阶段近休止阶段(4)代入已知条件,并用Matlab 语言编程求解,编程代码如下: disp ' ******** 偏置直动滚子从动件盘形凸轮设计 ********' disp '已知条件:'disp ' 凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边'disp ' 从动件在推程作摆线运动规律运动,在回程作等速运动规律运动' ro = 50;rr = 10;e = 12;h = 30;ft = 120;fs = 30;fh = 150;fprintf (1,' 基圆半径 ro = %3.4f mm \n',ro) fprintf (1,' 滚子半径 rr = %3.4f mm \n',rr) fprintf (1,' 推杆偏距 e = %3.4f mm \n',e) fprintf (1,' 推程行程 h = %3.4f mm \n',h) fprintf (1,' 推程运动角 ft = %3.4f 度 \n',ft) fprintf (1,' 远休止角 fs = %3.4f 度 \n',fs) fprintf (1,' 回程运动角 fh = %3.4f 度 \n',fh) hd = pi / 180;du = 180 / pi; so = sqrt( ro^2 - e^2 ); d1 = ft + fs;d2 = ft + fs + fh; disp ' 'disp '计算过程和输出结果:'disp ' 1-1 推程(摆线运动规律运动)' s = zeros(ft);ds = zeros(ft);d2s = zeros(ft); for f = 1 : fts(f) = h * f / ft - h * sin(2 * pi * f / ft) / (2 * pi);s = s(f);ds(f) = h / (ft * hd) - h / (ft * hd) * cos(2 * pi * f / ft);ds = ds(f); d2s(f) = 2 * pi * h / (ft * hd) ^ 2 * sin(2 * pi * f / ft);d2s = d2s(f); enddisp ' 1-2 回程(等速运动规律运动)' s = zeros(fh);ds = zeros(fh);d2s = zeros(fh); for f = d1 : d2s(f) = h - h * (f-150) / fh; s = s(f); ds(f) = - h / (fh * hd);ds = ds(f); d2s(f) = 0;d2s = d2s(f); enddisp ' 2- 计算凸轮理论廓线与实际廓线的直角坐标'n = 360;s = zeros(n);ds = zeros(n);r = zeros(n);rp = zeros(n);x = zeros(n);y = zeros(n);dx = zeros(n);dy = zeros(n);xx = zeros(n);yy = zeros(n);xa = zeros(n);ya = zeros(n);xxa = zeros(n);yya = zeros(n);for f = 1 : nif f <= fts(f) = h * f / ft - h * sin(2 * pi * f / ft) / (2 * pi);s = s(f);ds(f) = h /(ft * hd) - h / (ft * hd) * cos(2 * pi * f / ft); ds = ds(f);elseif f > ft & f <= d1s = h;ds = 0;elseif f > d1 & f <= d2s(f) = h - h * (f-150) / fh; s = s(f);ds(f) = - h / (fh * hd);ds = ds(f);elseif f > d2 & f <= ns = 0;ds = 0;endxx(f) = (so + s) * sin(f * hd) + e * cos(f * hd); x = xx(f);yy(f) = (so + s) * cos(f * hd) - e * sin(f * hd); y = yy(f);dx(f) = (ds - e) * sin(f * hd) + (so + s) * cos(f * hd); dx = dx(f);dy(f) = (ds - e) * cos(f * hd) - (so + s) * sin(f * hd); dy = dy(f);xxa(f) = x + rr * dy / sqrt(dx ^ 2 + dy ^ 2);xa = xxa(f);yya(f) = y - rr * dx / sqrt(dx ^ 2 + dy ^ 2);ya = yya(f);r(f) = sqrt (x ^2 + y ^2 );rp(f) = sqrt (xa ^2 + ya ^2 );enddisp ' 2-1 推程(摆线运动规律运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = 10 : 10 :ftnu = [f xx(f) yy(f) xxa(f) yya(f)];disp(nu)enddisp ' 2-2 回程(等速运动规律运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y' for f = d1 : 10 : d2nu = [f xx(f) yy(f) xxa(f) yya(f)];disp(nu)enddisp ' 2-3 凸轮轮廓向径'disp ' 凸轮转角理论r 实际r'for f = 10 : 10 : nnu = [f r(f) rp(f)];disp(nu)enddisp '绘制凸轮的理论轮廓和实际轮廓:'plot(xx,yy,'r-.') % 理论轮廓(红色,点划线)axis ([-(ro+h-10) (ro+h+10) -(ro+h+10) (ro+rr+10)]) % 横轴和纵轴的下限和上限axis equal % 横轴和纵轴的尺度比例相同text(ro+h+3,0,'X') % 标注横轴text(0,ro+rr+3,'Y') % 标注纵轴text(-5,5,'O') % 标注直角坐标系原点title('偏置直动滚子从动件盘形凸轮设计') % 标注图形标题hold on; % 保持图形plot([-(ro+h) (ro+h)],[0 0],'k') % 横轴(黑色)plot([0 0],[-(ro+h) (ro+rr)],'k') % 纵轴(黑色)plot([e e],[0 (ro+rr)],'k--') % 初始偏置位置(黑色,虚线) ct = linspace(0,2*pi); % 画圆的极角变化范围plot(ro*cos(ct),ro*sin(ct),'g') % 基圆(绿色)plot(e*cos(ct),e*sin(ct),'c--') % 偏距圆(蓝绿色,虚线)plot(e + rr*cos(ct),so + rr*sin(ct),'y') % 滚子圆(黄色)plot(xxa,yya,'b') % 实际轮廓(蓝色)(5)求解凸轮理论廓线和实际廓线坐标值如下:******** 偏置直动滚子从动件盘形凸轮设计********已知条件:凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边从动件在推程作摆线运动规律运动,在回程作等速运动规律运动基圆半径ro = 50.0000 mm滚子半径rr = 10.0000 mm推杆偏距 e = 12.0000 mm推程行程h = 30.0000 mm推程运动角ft = 120.0000 度远休止角fs = 30.0000 度回程运动角fh = 150.0000 度计算过程和输出结果:1-1 推程(摆线运动规律运动)1-2 回程(等速运动规律运动)计算凸轮理论廓线与实际廓线的直角坐标2-1 推程(摆线运动规律运动)凸轮转角理论x 理论y 实际x 实际y10.0000 20.2659 45.8284 16.5674 36.537520.0000 28.1734 42.3200 23.8536 33.301230.0000 36.0243 38.3959 31.4216 29.518140.0000 44.1625 33.9622 39.1460 25.311550.0000 52.6430 28.5078 46.7788 20.407760.0000 61.0261 21.3770 53.9159 14.345370.0000 68.4036 12.1267 59.9368 6.8057 80.0000 73.6533 0.8019 64.1128 -2.1946 90.0000 75.8133 -12.0000 65.8180 -12.3064 100.0000 74.4098 -25.3056 64.6887 -22.9602 110.0000 69.5921 -38.0996 60.7079 -33.5092 120.0000 62.0165 -49.6616 54.2107 -43.41102-2 回程(等速运动规律运动)凸轮转角理论x 理论y 实际x 实际y 150.0000 28.8770 -74.0165 25.2424 -64.7004 160.0000 14.9014 -76.0270 14.3851 -66.0404 170.0000 1.1258 -75.4900 2.4259 -65.5749 180.0000 -12.0000 -72.5386 -8.9229 -63.0238 190.0000 -24.0666 -67.3832 -19.3110 -58.5864 200.0000 -34.7179 -60.3010 -28.4390 -52.5180 210.0000 -43.6616 -51.6242 -36.0665 -45.1192 220.0000 -50.6772 -41.7260 -42.0190 -36.7223 230.0000 -55.6208 -31.0065 -46.1908 -27.6786 240.0000 -58.4280 -19.8770 -48.5462 -18.3440 250.0000 -59.1126 -8.7451 -49.1177 -9.0659 260.0000 -57.7635 1.9999 -48.0018 -0.1704 270.0000 -54.5386 12.0000 -45.3524 8.0487 280.0000 -49.6567 20.9409 -41.3723 15.3401 290.0000 -43.3865 28.5615 -36.3031 21.5028 300.0000 -36.0357 34.6616 -30.4141 26.39132-3 凸轮轮廓向径凸轮转角理论r 实际r10.0000 50.1094 40.118220.0000 50.8402 40.962930.0000 52.6498 43.111940.0000 55.7114 46.616350.0000 59.8663 51.036660.0000 64.6619 55.791770.0000 69.4702 60.322080.0000 73.6577 64.150490.0000 76.7571 66.9586100.0000 78.5951 68.6426110.0000 79.3387 69.3420120.0000 79.4501 69.4501130.0000 79.4501 69.4501140.0000 79.4501 69.4501150.0000 79.4501 69.4501160.0000 77.4736 67.5889170.0000 75.4984 65.6197180.0000 73.5245 63.6524190.0000 71.5521 61.6869200.0000 69.5812 59.7237210.0000 67.6121 57.7628220.0000 65.6448 55.8044230.0000 63.6795 53.8489240.0000 61.7165 51.8964250.0000 59.7559 49.9474260.0000 57.7981 48.0021270.0000 55.8432 46.0611280.0000 53.8916 44.1247290.0000 51.9438 42.1935300.0000 50.0000 40.2681310.0000 50.0000 40.0000320 50 40330.0000 50.0000 40.0000340 50 40350.0000 50.0000 40.0000360.0000 50.0000 40.0000(6)由Matlab绘制的实际图轮廓线和理论图轮廓线如下:图例:绿色——基圆;红色点划线——理论廓线;蓝色——实际廓线;黄色——滚子圆;蓝绿色,虚线——偏距圆;黑色,虚线——初始偏置位置;。
凸轮机构matlab程序

凸轮轮廓程序:>> e=20;s0=77.46;a1=0:pi/36:pi/3;s1=50*[3*a1/pi-sin(6*a1)/(2*pi)];x1=(s0+s1).*sin(a1)+e*cos(a1);y1=(s0+s1).*cos(a1)-e*sin(a1);k1=150/pi*[1-cos(6*a1)];>> i1=[(k1-e).*sin(a1)+(s0+s1).*cos(a1)].*[(k1-e).*(k1-e)+(s0+s1).*(s0+s1)].^(-1/2);>> j1=[-(k1-e).*cos(a1)+(s0+s1).*sin(a1)].*[(k1-e).*(k1-e)+(s0+s1).*(s0+s1)].^(-1/2);>> x10=x1-10*j1;>> y10=y1-10*i1;a2=pi/3:pi/36:pi;s2=50;x2=(s0+s2).*sin(a2)+e*cos(a2);y2=(s0+s2).*cos(a2)-e*sin(a2);k2=0;>> i2=[(k2-e).*sin(a2)+(s0+s2).*cos(a2)].*[(k2-e).*(k2-e)+(s0+s2).*(s0+s2)].^(-1/2);j2=[-(k2-e).*cos(a2)+(s0+s2).*sin(a2)].*[(k2-e).*(k2-e)+(s0+s2).*(s0+s2)].^(-1/2);x20=x2-10*j2;y20=y2-10*i2;>> a3=pi:pi/36:4*pi/3;>> s3=50*[1-3*(a3-pi)/pi+sin(6*(a3-pi))/(2*pi)];>> x3=(s0+s3).*sin(a3)+e*cos(a3);>> y3=(s0+s3).*cos(a3)-e*sin(a3);>> k3=50*[-3/pi+3/pi*cos(6*(a3-pi))];>> i3=[(k3-e).*sin(a3)+(s0+s3).*cos(a3)].*[(k3-e).*(k3-e)+(s0+s3).*(s0+s3)].^(-1/2);>> j3=[-(k3-e).*cos(a3)+(s0+s3).*sin(a3)].*[(k3-e).*(k3-e)+(s0+s3).*(s0+s3)].^(-1/2);>> x30=x3-10*j3;>> y30=y3-10*i3;>> a4=4*pi/3:pi/36:2*pi;>> s4=0;>> x4=(s0+s4).*sin(a4)+e*cos(a4);>> y4=(s0+s4).*cos(a4)-e*sin(a4);>> k4=0;>> i4=[(k4-e).*sin(a4)+(s0+s4).*cos(a4)].*[(k4-e).*(k4-e)+(s0+s4).*(s0+s4)].^(-1/2);>> j4=[-(k4-e).*cos(a4)+(s0+s4).*sin(a4)].*[(k4-e).*(k4-e)+(s0+s4).*(s0+s4)].^(-1/2);>> x40=x4-10*j4;>> y40=y4-10*i4;>> plot(x10,y10,'-g*',x20,y20,'-r*',x30,y30,'-b*',x40,y40,'-k*')>>plot(x10,y10,'-g*',x20,y20,'-r*',x30,y30,'-b*',x40,y40,'-k*',x1,y1,'-g*',x2,y2,'-r*',x3,y3,'-b*',x4,y4,'-k*')>>凸轮压力角:>> x=0:0.01:pi/3;>> t=5.76*sin(6*x)+6*x.*sin(6*x)+(2-2*pi/15)*cos(6*x)-2+2*pi/15; >> xx =Columns 1 through 60 0.0100 0.0200 0.0300 0.0400 0.0500Columns 7 through 120.0600 0.0700 0.0800 0.0900 0.1000 0.1100Columns 13 through 180.1200 0.1300 0.1400 0.1500 0.1600 0.1700 Columns 19 through 240.1800 0.1900 0.2000 0.2100 0.2200 0.2300 Columns 25 through 300.2400 0.2500 0.2600 0.2700 0.2800 0.2900 Columns 31 through 360.3000 0.3100 0.3200 0.3300 0.3400 0.3500 Columns 37 through 420.3600 0.3700 0.3800 0.3900 0.4000 0.4100 Columns 43 through 480.4200 0.4300 0.4400 0.4500 0.4600 0.4700 Columns 49 through 540.4800 0.4900 0.5000 0.5100 0.5200 0.5300 Columns 55 through 600.5400 0.5500 0.5600 0.5700 0.5800 0.5900 Columns 61 through 660.6000 0.6100 0.6200 0.6300 0.6400 0.6500 Columns 67 through 720.6600 0.6700 0.6800 0.6900 0.7000 0.7100 Columns 73 through 780.7200 0.7300 0.7400 0.7500 0.7600 0.7700 Columns 79 through 840.7800 0.7900 0.8000 0.8100 0.8200 0.8300 Columns 85 through 900.8400 0.8500 0.8600 0.8700 0.8800 0.8900 Columns 91 through 960.9000 0.9100 0.9200 0.9300 0.9400 0.9500 Columns 97 through 1020.9600 0.9700 0.9800 0.9900 1.0000 1.0100 Columns 103 through 1051.0200 1.0300 1.0400>> tt =Columns 1 through 60.0000 0.3461 0.6925 1.0379 1.3809 1.7202 Columns 7 through 122.0546 2.3825 2.70283.0141 3.3150 3.6042 Columns 13 through 183.88044.1424 4.3889 4.6187 4.83075.0237 Columns 19 through 245.1967 5.3487 5.4788 5.5861 5.6698 5.7292 Columns 25 through 305.7636 5.7725 5.7555 5.7122 5.6422 5.5455 Columns 31 through 365.4219 5.2715 5.0944 4.8908 4.6610 4.4055 Columns 37 through 424.1248 3.8196 3.4906 3.1387 2.7647 2.3699 Columns 43 through 481.9552 1.5219 1.0714 0.6051 0.1243 -0.3692 Columns 49 through 54-0.8740 -1.3882 -1.9102 -2.4381 -2.9701 -3.5044 Columns 55 through 60-4.0388 -4.5716 -5.1008 -5.6243 -6.1401 -6.6464 Columns 61 through 66-7.1410 -7.6221 -8.0877 -8.5359 -8.9648 -9.3727 Columns 67 through 72-9.7578 -10.1184 -10.4528 -10.7596 -11.0372 -11.2843 Columns 73 through 78-11.4996 -11.6820 -11.8304 -11.9439 -12.0215 -12.0627 Columns 79 through 84-12.0668 -12.0335 -11.9623 -11.8531 -11.7059 -11.5207 Columns 85 through 90-11.2979 -11.0378 -10.7410 -10.4081 -10.0399 -9.6374 Columns 91 through 96-9.2016 -8.7339 -8.2356 -7.7081 -7.1530 -6.5722 Columns 97 through 102-5.9674 -5.3405 -4.6937 -4.0291 -3.3489 -2.6554Columns 103 through 105-1.9511 -1.2383 -0.5195>> x=0.46:0.001:0.47;>> t=5.76*sin(6*x)+6*x.*sin(6*x)+(2-2*pi/15)*cos(6*x)-2+2*pi/15; >> xx =Columns 1 through 60.4600 0.4610 0.4620 0.4630 0.4640 0.4650Columns 7 through 110.4660 0.4670 0.4680 0.4690 0.4700>> tt =Columns 1 through 60.1243 0.0755 0.0266 -0.0225 -0.0717 -0.1210Columns 7 through 11-0.1704 -0.2199 -0.2696 -0.3193 -0.3692>> x=0.462:0.0001:0.463;>> t=5.76*sin(6*x)+6*x.*sin(6*x)+(2-2*pi/15)*cos(6*x)-2+2*pi/15; >> xx =Columns 1 through 60.4620 0.4621 0.4622 0.4623 0.4624 0.4625Columns 7 through 110.4626 0.4627 0.4628 0.4629 0.4630>> tt =Columns 1 through 60.0266 0.0217 0.0168 0.0119 0.0070 0.0021Columns 7 through 11-0.0028 -0.0077 -0.0126 -0.0176 -0.0225>> z=[0 0.4625];>> y=[150/pi*(1-cos(6*z))-20].*[45.8+50*(3*z/pi-sin(6*z)/(2*pi))];>> y=[150/pi*(1-cos(6*z))-20]./[45.8+50*(3*z/pi-sin(6*z)/(2*pi))];>> yy =-0.4367 1.1121>> a=atan(y)a =-0.4117 0.8384>> a*180/pians =-23.5900 48.0382>>以上是计算推程压力角的临界值。
基于matlab凸轮轮廓设计

基于matlab凸轮轮廓设计随着科学技术的不断发展,凸轮轮廓设计已经被广泛运用于各种机械和动力学设备中。
MATLAB作为一种强大的技术软件,也被广泛用于凸轮轮廓的设计和分析。
本文将对基于MATLAB的凸轮轮廓设计进行探讨。
凸轮轮廓的设计需要考虑许多因素,如凸轮的形状、材质、运动方式等。
其中,凸轮轮廓的形状对凸轮的运动和性能起着至关重要的作用。
因此,凸轮轮廓的设计需要具有高度的精度和可靠性。
MATLAB作为一种功能强大的数学软件,可以通过编程实现凸轮轮廓的设计和分析。
MATLAB中有许多函数可以用于处理凸轮的相关问题,如curve fitting工具箱、symbolic math工具箱等。
通过这些工具箱和函数,可以实现凸轮轮廓的优化设计和模拟分析。
在凸轮轮廓的设计中,凸轮轨迹的生成是至关重要的一步。
传统的方法是通过手工绘制轮廓图,然后进行图形处理和数值计算等操作。
而在MATLAB中,可以利用数值计算和函数绘图等功能直接生成凸轮轮廓。
具体实现方法如下:首先,我们需要确定凸轮的基本参数,如凸轮的半径、角速度等。
然后,根据凸轮运动的规律,利用MATLAB中的数值计算函数计算出凸轮上各点的位置坐标。
接着,通过MATLAB中的函数绘图功能将各点连接形成凸轮轮廓。
最后,通过调整凸轮参数和轮廓图形,实现凸轮轮廓的优化设计。
除此之外,MATLAB还可以利用符号计算的功能优化凸轮轮廓设计。
通过定义凸轮的基本参数和轮廓方程,利用MATLAB中的符号计算工具求解优化方程,得到凸轮轮廓的最优设计方案。
综上所述,基于MATLAB的凸轮轮廓设计具有快速、精准、可靠等优势。
通过MATLAB的编程和工具箱的使用,可以实现凸轮轮廓的优化设计和模拟分析,为机械和动力学设备的设计和制造提供有力支持。
基于matlab的凸轮计算

基于matlab的凸轮计算>> r=10;>> r0=50;>> e=0;>> delt0=120*pi/180;>> h=50;>> i=100;>> s0=sqrt(r0^2-e^2);>> syms delt1 delt2 delt3;>> s1=h*((delt1/delt0)-sin(2*pi*delt1/delt0)/(2*pi)); >> v1=diff(s1);>> a1=diff(s1,2);>> s2=h*(2+sin(2*pi*delt2/delt0)/(2*pi)-(delt2/delt0)); >> v2=diff(s2);>> a2=diff(s2,2);>> delt1=linspace(0,delt0,i);>> delt2=linspace(delt0,240*pi/180,i);>> delt3=linspace(240*pi/180,2*pi,i);>> s3=0*delt3;>> delt=[delt1 delt2 delt3];>> s11=subs(s1,delt1);>> v11=subs(v1,delt1);>> a11=subs(a1,delt1);>> s22=subs(s2,delt2);>> v22=subs(v2,delt2);>> a22=subs(a2,delt2);>> s=[s11 s22 s3];>> v=[v11 v22 s3];>> a=[a11 a22 s3];>> plot(delt*180/pi,s,delt*180*pi,v,'-.',delt*180/pi,a,'--');>> title('凸轮位移,速度,加速度曲线');>> legend('位移曲线','速度曲线','加速度曲线');>> axis([0 360 -80 80]);>> grid on>> for j=1:3*ixx(j)=(s0+s(j))*sin(delt(j))-e*cos(delt(j));yy(j)=(s0+s(j))*cos(delt(j))+e*sin(delt(j));end>> for m=1:3*isyms deltxyx=(s0+s(m))*sin(deltxy)+e*cos(deltxy);y=(s0+s(m))*cos(deltxy)-e*sin(deltxy);sx=diff(x,deltxy)/(sqrt((diff(x,deltxy))^2+(diff(y,deltxy))^2));cx=diff(y,deltxy)/(sqrt((diff(x,deltxy))^2+(diff(y,deltxy))^2));deltxy=delt(m);ax(m)=subs(sx,deltxy);bx(m)=subs(cx,deltxy);xxx(m)=xx(m)-r*bx(m);yyy(m)=yy(m)-r*ax(m);endfigure>> plot(xxx,yyy)>> grid on>> title('凸轮实际轮廓曲线');>> cave=[xxx;yyy;0*xxx-5];>> fprintf('%10.6f',cave)0.000000 40.000000 -5.000000 1.269243 39.991388 -5.000000 2.538018 39.966909 -5.000000 3.806015 39.928587 -5.000000 5.073092 39.878420 -5.000000 6.339275 39.818364 -5.000000 7.604751 39.750315 -5.000000 8.869863 39.676091 -5.000000 10.135100 39.597420 -5.000000 11.401095 39.515925 -5.000000 12.668608 39.433108 -5.000000 13.938519 39.350338 -5.000000 15.211816 39.268838 -5.000000 16.489581 39.189678 -5.000000 17.772978 39.113760 -5.000000 19.063237 39.041812 -5.000000 20.361640 38.974382 -5.000000 21.669506 38.911829 -5.000000 22.988173 38.854322 -5.000000 24.318985 38.801835 -5.000000 25.663272 38.754145 -5.000000 27.022336 38.710835 -5.000000 28.397436 38.671291 -5.000000 29.789767 38.634708 -5.000000 31.200450 38.600093 -5.000000 32.630511 38.566270 -5.000000 34.080872 38.531891 -5.000000 35.552332 38.495438 -5.000000 37.045557 38.455237 -5.000000 38.561065 38.409469 -5.000000 40.099216 38.356180 -5.000000 41.660201 38.293294 -5.000000 43.244034 38.218627 -5.000000 44.850541 38.129905 -5.000000 46.479357 38.024773 -5.000000 48.129916 37.900818 -5.000000 49.801452 37.755579 -5.000000 51.492993 37.586571 -5.000000 53.203358 37.391297 -5.000000 54.931164 37.167264 -5.000000 56.674820 36.912008 -5.000000 58.432535 36.623105 -5.000000 60.202321 36.298187 -5.000000 61.981998 35.934966 -5.000000 63.769205 35.531242 -5.000000 65.561403 35.084926 -5.000000 67.355891 34.594048 -5.000000 69.149813 34.056777 -5.000000 70.940171 33.471432 -5.000000 72.723841 32.836494 -5.000000 74.497584 32.150618 -5.000000 76.258063 31.412642 -5.000000 78.001860 30.621598 -5.000000 79.725490 29.776719 -5.000000 81.425420 28.877443 -5.000000 83.098087 27.923421 -5.000000 84.739914 26.914517 -5.000000 86.347331 25.850814 -5.000000 87.916791 24.732613 -5.000000 89.444787 23.560431 -5.000000 90.927876 22.334999 -5.000000 92.362689 21.057259 -5.000000 93.745954 19.728360 -5.000000 95.074508 18.349647 -5.000000 96.34531916.922660 -5.000000 97.555495 15.449119 -5.000000 98.702302 13.930915 -5.000000 99.783179 12.370102 -5.000000100.795745 10.768880 -5.000000101.737815 9.129583 -5.000000102.607408 7.454669 -5.000000103.402758 5.746697 -5.000000104.122316 4.008319 -5.000000104.764763 2.242259 -5.000000105.329010 0.451300 -5.000000105.814201 -1.361736 -5.000000106.219718 -3.194005 -5.000000106.545177 -5.042653 -5.000000106.790431 -6.904840 -5.000000106.955562 -8.777752 -5.000000107.040882-10.658618 -5.000000107.046925-12.544727 -5.000000106.974436-14.433446 -5.000000106.824372-16.322227 -5.000000106.597882-18.208630 -5.000000106.296303-20.090331 -5.000000105.921147-21.965134 -5.000000105.474084-23.830985 -5.000000104.956934-25.685979 -5.000000104.371648-27.528371 -5.000000103.720293-29.356583 -5.000000103.005038-31.169209 -5.000000102.228137-32.965021 -5.000000101.391911-34.742971 -5.000000100.498728-36.502197 -5.000000 99.550994-38.242018 -5.000000 98.551128-39.961937 -5.000000 97.501545-41.661638 -5.000000 96.404646-43.340982 -5.000000 95.262794-45.000000 -5.000000 95.262794-45.000000 -5.000000 94.077722-46.638540 -5.000000 92.848837-48.255106 -5.000000 91.575076-49.847744 -5.000000 90.255505-51.414382 -5.000000 88.889338-52.952839 -5.000000 87.475945-54.460840 -5.000000 86.014863-55.936028 -5.000000 84.505807-57.375980 -5.000000 82.948676-58.778223 -5.000000 81.343563-60.140244 -5.000000 79.690755-61.459517 -5.000000 77.990742-62.733508 -5.000000 76.244218-63.959702 -5.000000 74.452080-65.135612 -5.000000 72.615433-66.258803 -5.00000070.735581-67.326904 -5.000000 68.814030-68.337626 -5.000000 66.852480-69.288782 -5.000000 64.852821-70.178297 -5.000000 62.817124-71.004227 -5.000000 60.747632-71.764774 -5.000000 58.646752-72.458299 -5.000000 56.517044-73.083332 -5.000000 54.361205-73.638590 -5.000000 52.182062-74.122982 -5.000000 49.982551-74.535624 -5.000000 47.765709-74.875841 -5.000000 45.534653-75.143179 -5.000000 43.292567-75.337411 -5.000000 41.042683-75.458537 -5.000000 38.788266-75.506791 -5.000000 36.532596-75.482641 -5.000000 34.278950-75.386788 -5.000000 32.030586-75.220167 -5.000000 29.790723-74.983939 -5.000000 27.562529-74.679493 -5.000000 25.349097-74.308435 -5.000000 23.153435-73.872583 -5.000000 20.978450-73.373958 -5.000000 18.826928-72.814773 -5.000000 16.701525-72.197424 -5.000000 14.604753-71.524474 -5.000000 12.538966-70.798644 -5.000000 10.506349-70.022795 -5.000000 8.508912-69.199916 -5.000000 6.548474-68.333103 -5.000000 4.626665-67.425549 -5.000000 2.744911-66.480521 -5.000000 0.904434-65.501344 -5.000000 -0.893750-64.491384 -5.000000 -2.648838-63.454030 -5.000000 -4.360234-62.392674 -5.000000 -6.027553-61.310693 -5.000000 -7.650616-60.211434 -5.000000 -9.229446-59.098191 -5.000000-10.764265-57.974193 -5.000000-12.255484-56.842582 -5.000000-13.703698-55.706402 -5.000000-15.109673-54.568580 -5.000000-16.474341-53.431914 -5.000000-17.798784-52.299057 -5.000000-19.084223-51.172507 -5.000000-20.332006-50.054594 -5.000000-21.543592-48.947468 -5.000000-22.720536-47.853097 -5.000000-23.864474-46.773252 -5.000000-24.977110-45.709505 -5.000000-26.060194-44.663222 -5.000000-27.115508-43.635563 -5.000000-28.144852-42.627476 -5.000000-29.150023-41.639701 -5.000000-30.132800-40.672768 -5.000000-31.094928-39.727000 -5.000000-32.038102-38.802521 -5.000000-32.963951-37.899254 -5.000000-33.874024-37.016935 -5.000000-34.769774-36.155117 -5.000000-35.652545-35.313181 -5.000000-36.523561-34.490347 -5.000000-37.383912-33.685683 -5.000000-38.234547-32.898120 -5.000000-39.076261-32.126466 -5.000000-39.909689-31.369417 -5.000000-40.735297-30.625575 -5.000000-41.553381-29.893465 -5.000000-42.364059-29.171544 -5.000000-43.167267-28.458227 -5.000000-43.962764-27.751896 -5.000000-44.750126-27.050921 -5.000000-45.528751-26.353673 -5.000000-46.297861-25.658546 -5.000000-47.056505-24.963968 -5.000000-47.803568-24.268420 -5.000000-48.537777-23.570450 -5.000000-49.257709-22.868689 -5.000000-49.961799-22.161864 -5.000000-50.648356-21.448813 -5.000000-51.315569-20.728494 -5.000000-51.961524-20.000000 -5.000000-51.961524-20.000000 -5.000000-52.584515-19.262731 -5.000000-53.183972-18.516841 -5.000000-53.759626-17.762665 -5.000000-54.311222-17.000538 -5.000000-54.838511-16.230804 -5.000000-55.341258-15.453805 -5.000000-55.819237-14.669890 -5.000000-56.272235-13.879410 -5.000000-56.700049-13.082719 -5.000000-57.102488-12.280172 -5.000000-57.479371-11.472129 -5.000000-57.830530-10.658953 -5.000000-58.155807 -9.841005 -5.000000-58.455057 -9.018654 -5.000000-58.728147 -8.192267 -5.000000-58.974953 -7.362213 -5.000000-59.195366 -6.528864 -5.000000-59.389287 -5.692594 -5.000000-59.556628 -4.853775 -5.000000-59.697316 -4.012785 -5.000000-59.811287 -3.169998 -5.000000-59.898489 -2.325793 -5.000000-59.958886 -1.480547 -5.000000-59.992448 -0.634639 -5.000000-59.999161 0.211554 -5.000000-59.979022 1.057652 -5.000000-59.932040 1.903277 -5.000000-59.858237 2.748049 -5.000000-59.757644 3.591592 -5.000000-59.630308 4.433528 -5.000000-59.476285 5.273479 -5.000000-59.2956436.111071 -5.000000-59.088465 6.945927 -5.000000-58.8548437.777675 -5.000000-58.594880 8.605942 -5.000000-58.3086949.430357 -5.000000-57.996413 10.250552 -5.000000-57.658176 11.066160 -5.000000-57.294134 11.876815 -5.000000-56.904452 12.682155 -5.000000-56.489302 13.481819 -5.000000-56.048872 14.275449 -5.000000-55.583357 15.062690 -5.000000-55.092966 15.843191 -5.000000-54.577920 16.616601 -5.000000-54.038447 17.382574 -5.000000-53.474791 18.140768 -5.000000-52.887202 18.890843 -5.000000-52.275944 19.632464 -5.000000-51.641291 20.365298 -5.000000-50.983526 21.089019 -5.000000-50.302944 21.803301 -5.000000-49.599849 22.507825 -5.000000-48.874557 23.202276 -5.000000-48.127392 23.886344 -5.000000-47.358687 24.559721 -5.000000-46.568788 25.222107 -5.000000-45.758047 25.873205 -5.000000-44.926828 26.512723 -5.000000-44.075503 27.140376 -5.000000-43.204451 27.755883 -5.000000-42.314065 28.358968 -5.000000-41.404741 28.949362 -5.000000-40.476887 29.526799 -5.000000-39.530917 30.091022 -5.000000-38.567257 30.641778 -5.000000-37.586335 31.178820 -5.000000-36.588593 31.701909 -5.000000-35.574476 32.210810 -5.000000-34.544438 32.705296 -5.000000-33.498939 33.185144 -5.000000-32.438449 33.650141 -5.000000-31.363441 34.100079 -5.000000-30.274397 34.534755 -5.000000-29.171804 34.953975 -5.000000-28.056156 35.357552 -5.000000-26.927951 35.745306 -5.000000-25.787695 36.117062 -5.000000-24.635898 36.472654 -5.000000-23.473075 36.811923 -5.000000-22.299747 37.134717 -5.000000-21.116440 37.440893 -5.000000-19.923681 37.730312 -5.000000-18.722007 38.002845 -5.000000-17.511953 38.258370 -5.000000-16.294062 38.496774 -5.000000-15.068879 38.717948 -5.000000-13.836952 38.921795 -5.000000-12.598833 39.108223 -5.000000-11.355075 39.277148 -5.000000-10.106235 39.428495 -5.000000 -8.852872 39.562197 -5.000000 -7.595547 39.678193 -5.000000 -6.334823 39.776431 -5.000000 -5.071264 39.856868 -5.000000 -3.805435 39.919467 -5.000000 -2.537903 39.964201 -5.000000 -1.269236 39.991049 -5.000000 -0.000000 40.000000 -5.000000>>。
基于MATLAB的高次多项式凸轮型线优化设计

机械装备优化设计三级项目基于MATLAB的高次多项式凸轮型线优化设计班级:12级机械装备-2班设计人员(按贡献大小排序):唐俊杰(12011010093)卫健行(120101010092)王荟博(120101010095)摘要动力凸轮型线的设计十分重要,以高次多项式凸轮型线为例,在基于丰满系数和磨损设计多目标函数情况下,利用MATLAB及其优化工具箱(optimizationtoolbox)对目标函数数学模型进行优化求解。
应用MATLAB的优化函数提供的强大计算功能,确定了凸轮型线高次五项式函数中的系数,并能快速找到目标函数的优化值。
显著提高了型线优化设计的速度和精度,还可根据实际情况灵活地调整权重系数W1和W2的值的大小,计算方便快捷。
在与传统设计方法比较结果表明,经优化设计,提高了动力凸轮的丰满系数,降低了凸轮型线的磨损。
关键词:优化设计; MATLAB; 高次多项式; 凸轮型线前言随着工程技术的发展和最优化技术的广泛应用,科学技术领域中需要求解很多优化问题。
而工程中的最优化问题,绝大多数是有约束的,且多属于非线性规划问题[1]。
内燃机配气系统中凸轮型线的设计就是这一种有约束非线性规划问题。
由于各种限制条件的复杂性,传统凸轮曲线设计方法难以找到合适的曲线参数,本文讨论此类情况下,利用MATLAB优化工具箱(optimizationtoolbox)解决多目标函数情况下凸轮型线优化设计问题。
通过MAT-LAB强大的计算功能,确定了凸轮型线高次五项式函数中的系数,利用其优化工具箱寻找了以丰满系数和磨损设计为数学模型的最优值。
小组分工:唐俊杰负责MATLAB编程和WORD的制作王荟博负责WORD的制作和PPT的制作卫健行负责WORD的制作,查阅资料一、高次五项式凸轮型线凸轮曲线采用高次多项式型线,多项式项位向右影响渐弱,通常高次多项式取五项至七项。
第六项以后对动力性能指标的影响力已很小,随着高次多项式项数的增加,凸轮丰满系数减小,加速度的绝对值变大,凸轮机构工作性能下降。
基于MATLAB汽车发动机配气凸轮的型线设计与接触应力分析

基于MATLAB汽车发动机配气凸轮的型线设计与接触应力分析MATLAB是一款功能强大的工程计算软件,被广泛应用于各个领域。
在汽车工业中,MATLAB可以用来进行发动机配气凸轮的型线设计和接触应力分析。
本文将详细介绍MATLAB在汽车发动机配气凸轮设计中的应用。
汽车发动机配气凸轮是发动机中重要的构件之一,它负责控制气门的开合以调节进出气量,影响整个发动机的性能。
因此,设计一款合理的配气凸轮是非常重要的工作。
在实际设计中,需要考虑凸轮曲线的连续性、尺寸和形状等,并通过模拟和分析来评估其性能和强度。
MATLAB提供了丰富的函数和工具箱,可以用来进行凸轮曲线的设计和分析。
其中,MATLAB的Symbolic Math Toolbox可以用来进行符号计算,求解形式化的数学问题,包括曲线的导数和积分等。
同时,MATLAB的Simscape Multibody可以用来进行动力学仿真和接触分析。
对于配气凸轮的设计,首先需要确定凸轮的基本参数,如凸轮半径、凸轮角度等。
然后,可以根据相应的曲线算法生成凸轮曲线。
接着,可以使用MATLAB的Symbolic Math Toolbox来求解曲线的导数和积分,以计算凸轮曲线的切线和法线。
最后,根据切线和法线的数据,可以绘制出凸轮曲线图像。
接下来是接触应力分析。
在凸轮和气门接触时,会产生接触应力。
为了更好的评估凸轮的强度,需要进行接触应力分析。
可以使用MATLAB的Simscape Multibody进行动力学仿真和接触分析。
首先,需要将凸轮和气门模型导入到模拟环境中,并设置相应的初始参数。
然后,在模拟过程中,MATLAB会计算出接触应力,生成相应的分析报告。
总之,MATLAB在汽车发动机配气凸轮的设计中是非常实用的工具。
通过使用MATLAB的Symbolic Math Toolbox和Simscape Multibody,可以快速、准确地进行凸轮型线设计和接触应力分析,为发动机的性能和强度评估提供有力支持。
matlab凸轮设计

偏置直动尖端推杆盘型凸轮机构一、凸轮参数二、推杆运动规律进程段 余弦加速度运动进程段 S= H-H*(1-cos(pi*i/J1))/2 (00~900) 回程段 余弦加速度运动回程段 S= H*(1-cos(pi*i/J3))/2 (1800~2700) 凸轮廓线方程:)sin(*)()cos(*22J S E R J E X +-+= )sin(*)cos(*)(22J E J S E R Y -+-= 三、程序设计%凸轮机构参数E=10; %偏距H=50; %升程b=0:pi/10:2*pi;R=40; %基圆半径x2=R*cos(b); %基圆轮廓y2=R*sin(b);x1=10*sin(b);%偏心圆轮廓y1=10*cos(b);J1=90; %推程J3=90; %回程s0=sqrt(R^2-E^2);s1=(H/2)*(1-cos(pi*i/J1)); %推程,余弦加速度运动 s2=H*eig(eye(360))'; %停歇,s=Hs3=H-(H/2)*(1-cos(pi*i/J3));%回程,余弦加速度运动 s4(1,360)=0; %停歇,s=0 x(1,360)=0;y(1,360)=0;%凸轮机构循环代码for i=1:360if i>=270s(i)=0;elseif i>=180s(i)=H-H*(1-cos(pi*i/J1))/2;elseif i>=90s(i)=H;elses(i)=H*(1-cos(pi*i/J3))/2;endx(i)=E*cos(pi*i/180)+(s0+s(i))*sin(pi*i/180);y(i)=(s0+s(i))*cos(pi*i/180)-E*sin(pi*i/180); end%凸轮轮廓曲线figure(1)plot(x,y,'-r',x1,y1,'-b',x2,y2,'-g','linewidth',2); title('凸轮轮廓曲线');xlabel('x'),ylabel('y');axis([-80,120,-100,60]);grid on;%位移曲线figure(2)plot(s,'-r','linewidth',2);title('位移曲线');xlabel('转角'),ylabel('位移')axis([0,400,-10,60]);grid on;四、运行结果。
凸轮廓线设计方案MATLAB程序

■2凸轮轮廓及其综合1.凸轮机构从动件的位移凸轮是把一种运动转化为另一种运动的装置。
凸轮的廓线和从动件一起实现运动形式的转换。
凸轮通常是为定轴转动,凸轮旋转运动可被转化成摆动、直线运动或是两者的结合。
凸轮机构设计的内容之一是凸轮廓线的设计。
定义一个凸轮基圆r b 作为最小的圆周半径。
从动件的运动方程如下:L(「)=r b +s(「)a( :) = 0 2 3 w ' w 2n设凸轮的推程运动角和回程运动角均为 3,从动件的运动规律均为正弦加速度运动规律, 则有:s( :) = h(:—sin(2 n / 3 )) Ow w 3s( :) = h — h(心―|31- sin(2 n (「- 3 / 3 ))s( :) = 0 2上式是从动件的位移,h 是从动件的最大位移,并且 o w3w如果假设凸轮的旋转速度 3= d 「/dt 是个常量,则速度 加速度a 和瞬时加速度j(加速度对时间求异)分别如下:速度:h(:)=(1-cos(2 n ■■ / 3 ))0W W加速度:h(;:)=—:(1-cos(2 n (「- 3 )/(;:)=0 2 3 w w 2 na(「)=..厂sin(2 n ■■/ 3 ))a( J =-sin(2 n ( ■- 3 )/ 3 )3w w 23beta=60*pi/180;phi=li nspace(0,beta,40);phi2=[beta+phi]; ph=[phi phi2]*180/pi; arg=2*pi*phi/beta;arg2=2*pi*(phi2-beta)/beta;s=[phi/beta-si n(arg)/2/pi 1-(arg2-si n(arg2))/2/pi]; v=[(1_cos(arg))/beta_(1_cos(arg2))/beta]; a=[2*pi/beta A 2*si n(arg)2*pi/beta A 2*si n(arg2)];j=[4*pi A 2/beta A 3*cos(arg)4*pi A 2/beta A 3*cos(arg2)]:subplot(2,2,1) plot(ph,s, / K x ) xlabel( / Cam angle(degrees) / ) ylabel( / Displacement(S) x ) g=axis; g(2)=120; axis(g) subplot(2,2,2) plot(ph,v, / k x,[0 120],[0 0],/ k-- / ) xlabel( / Cam angle(degrees) / )ylabel(/ Velocity(V)')g=axis; g(2)=120; axis(g) subplot(2,2,3)plot(ph,a, / k x ,[0 120],[0 0], / k--')xlabel( / Cam angle(degrees) / ) ylabel( / Acceleration(A) x ) g=axis; g(2)=120; axis(g) subplot(2,2,4)plot(ph,j, / k ,,[0 120],[0 0],/ k-- j瞬时加速度:j(.)=4-:3 hcos(2 n ■■/ 3 )) j(伫4n ( - 3)/ 3)j(定义无量纲位移S=s/h 、无量纲速度 V=u / 3 h 、无量纲加速度 A=a/h 3 3和无量纲瞬时加速度 J=j/h 3 3。
基于Matlab的共轭平行分度凸轮的分析计算

曲线
d0 2
d 击
丽"d× (+ ) 40 s 手 警 一 (  ̄ i 2 n 等 3 )
理轮 论廓
点 的法 向量
警 i s n 等
1 . 2 分 度 凸轮 轮 廓 计 算
1 . 凸轮 理 论 轮 廓 计 算 .1 2
等 ≤
图 3 实 际 轮 廓 线 和 理 论 轮 廓 线 的关 系
在 高 速 运 转 的情 况 下 很 容 易 造 成 冲 击 变 形 。该 机 构 每 一个 运
动 循 环 凸 轮分 度 机 构 作 一 次 分度 运 动 , 轮 旋 转一 周 , 轮 转 凸 凸
速 很 高 . 平 行 分 度 凸 轮 机构 一 般 是 在 中低 速 情 况 下 工 作 。 而
收 稿 日期 : 0 2 0 — 6 2 1— 7 0
2- 8
正 弦 加速 度 、 进 正 弦 加 速 度 、 进梯 形 加 改 改 转 盘 分度 期 运 动 规 律 转 盘 节 圆半 径 转 盘 和 凸轮 中心 距 滚 子半 径
速度、 改进 等 速 等 运 动 规 律
R
C
r
高 英 ,王蕊 照 , 红晓 ,王 开政 钞
( 北机 电 工程 研 究所 陕 西 成 阳 7 2 0 西 1 0 0)
摘 要 : 对 工 程 实 际应 用 中 的特 殊 需 求 , 用 全 新 的 曲线 轮 廓 构 造 方 法 。 用 Ma a 针 采 利 t b仿 真 计 算 软 件 完成 了平 行 分度 l
F g 2 Di g a o a a lli de i g e n c a im a yi i. a r m fp r l n x n a lme h n s a ltc e n c c lt n l a u ai o
凸轮设计Matlab代码

plot(x1,y1,'b-',x2,y2,'g-',x3,y3,'m-',x4,y4,'c-',...
x6,y6,'b-',x7,y7,'g-',x8,y8,'m-',x9,y9,'c-',...
y6=y1-r*p1; %y' 函数
m2=-(s0+s2).*cos(a2+2*pi/3)+e*sin(a2+2*pi/3); % 中间变量 dx/d$
n2=-(s0+s2).*sin(a2+2*pi/3)-e*cos(a2+2*pi/3); % 中间变量 dy/d$
p2=-m2./sqrt(m2.^2+n2.^2); %sin&
y4=(s0+s4).*cos(a4+7*pi/6)-e*sin(a4+7*pi/6); %y 函数
a0=linspace(0,2*pi); % 基圆自变量
x5=r0*cos(a0); %x 函数
y5=r0*sin(a0); %y 函数
%工作廓线
m1=-(h*3/2/pi*(1-cos(3*a1))-e).*sin(a1)-(s0+s1).*cos(a1); % 中间变量 dx/d$
%凸轮理论廓线与工作廓线的画法
clear %清除变量
r0=50; %定义基圆半径
e=20; %定义偏距
h=50; %推杆上升高度
s0=sqrt(r0^2-e^2);
r=10; %滚子半径
matlab 傅里叶级数 凸轮

傅里叶级数在MATLAB中的应用一、概述1. 傅里叶级数的概念傅里叶级数是一种数学工具,可以将任意周期函数表示成一组正弦和余弦函数的线性组合。
这种表示方法在信号处理、图像处理、通信等领域有广泛的应用,是MATLAB中重要的数学工具之一。
2. MATLAB中傅里叶级数的应用MATLAB作为一种著名的科学计算软件,提供了丰富的工具箱和函数库,使得对傅里叶级数的计算和分析变得轻而易举。
本文将介绍MATLAB中傅里叶级数的基本概念和常见应用,以及其在凸轮设计中的具体应用。
二、MATLAB中的傅里叶级数表示1. 傅里叶级数的计算方法在MATLAB中,可以使用fft函数进行傅里叶级数的计算。
该函数能够将任意输入信号进行傅里叶变换,并返回频域的幅度和相位信息。
2. 傅里叶级数的应用场景傅里叶级数广泛应用于信号处理、图像处理和通信系统中。
在MATLAB中,可以利用傅里叶级数进行信号频谱分析、滤波器设计、频域滤波和频率域图像处理等方面。
三、MATLAB中傅里叶级数的小案例1. 信号频谱分析假设我们有一个周期为T的信号,可以使用MATLAB的fft函数对其进行傅里叶变换,得到其频率分量的幅度和相位信息,从而进行频谱分析。
2. 频域滤波在MATLAB中,可以利用傅里叶级数进行频域图像滤波,例如利用频率域掩膜对图像进行滤波和增强。
四、MATLAB在凸轮设计中的应用1. 凸轮的基本概念凸轮是一种机械传动装置,常见于发动机和机械运动系统中,用于控制阀门、汽缸盖和传动系统的运动。
凸轮的设计需要考虑到其运动曲线和周期性特征。
2. 傅里叶级数在凸轮设计中的应用在凸轮的设计中,可以利用傅里叶级数表示凸轮的运动曲线,从而进行凸轮的分析和设计。
MATLAB提供了丰富的函数和工具,可以对凸轮的运动特性进行傅里叶级数表示和分析,从而优化其运动特性。
五、结论1. MATLAB是一种强大的科学计算软件,提供了丰富的工具箱和函数库,使得对傅里叶级数的计算和分析变得十分便利。
