数字信号处理-MATLAB程序
数字信号处理DFTMATLAB程序

实验三 频域信号处理1. 实验目的(1) 学习信号DFT 变换的matlab 实现; (2) 学习fft 的matlab 实现; (3) 验证DFT 的相关性质。
2. 思考题(1) 若()()()sin 8sin 4x n n n ππ=+是一个128点的有限长序列,求其128点DFT结果; 程序如下:求DFT 变换矩阵A :clc; clear; N=128; A=dftmtx(N) Ai=conj(dftmtx(N)); n=0:(N-1); k=0:(N-1); nk=n'*k;Wn=(sin(pi/8)+sin(pi/4)).^nk Wk=conj(Wn)/N;求128点的DFT (分别用FFT 函数和dftmtx 函数)clc; clear; N=128; n=0:N-1;x=sin(pi/8*n)+sin(pi/4*n); subplot(3,1,1) plot(n,x); grid ontitle('原图') y1=fft(x,N); A=dftmtx(N); y2=x(1:N)*A; subplot(3,1,2) plot(n,y1) grid on title('FFT') subplot(3,1,3) plot(n,y2) grid on title('dftmtx')程序运行结果如图1所示:原图-13FFT-13dftmtx图 1(2) 对模拟信号()()()2sin 45sin 8x t t t ππ=+,以0.01t n =,()0:1n N =-进行采样,求a ) N=40点的FFT 幅度谱,从图中能否观察出两个频谱分量;b ) 提高采样点数值N=128,再求该信号的幅度频谱,此时幅度频谱发生了什么变化?信号的两个模拟频率和数字频率分别为多少?FFT 频谱分析结果和理论上是否一致? 程序如下:clc;clear;N=40;n=0:N-1;t=0.01*nx=2*sin(4*pi*t)+5*sin(8*pi*t);subplot(2,1,1)plot(x(1:N))grid ontitle('原图')y1=fft(x,N);subplot(2,1,2)plot(n,y1(1:N))grid ontitle('40点采样')结果如图2:原图40点采样图2 clc;clear;N=128;n=0:N-1;t=0.01*nx=2*sin(4*pi*t)+5*sin(8*pi*t);subplot(2,1,1)plot(x(1:N))title('原图')y1=fft(x,N);subplot(2,1,2) plot(n,y1(1:N)) title('128点采样')结果如图3:原图128点采样图 3从图2,3中可以看出:N=40和128点的FFT 幅度谱中均出现了两个频谱分量.对于128点采样,11128,128f T f ===,模拟频率分别为124,8ππΩ=Ω=,那么,数字频率分别为1122114,81283212816T T ππωπωπ=Ω=⨯==Ω=⨯=。
Removed_数字信号处理matlab程序

数字信号处理实验报告实验1 常见离散信号的MATLAB 产生和图形显示1.程序(1) 单位抽样序列1()0n δ⎧=⎨⎩00n n =≠如果在时间轴上延迟了k 个单位,得到即:()n δ()n k δ-1()0n k δ⎧-=⎨⎩0n kn =≠程序如下:N=20;k=9;x=zeros(1,N);x(10)=1;n=[k-9:N+k-10];stem(n,x);(2) 单位阶跃序列1()0u n ⎧=⎨⎩00n n ≥<程序如下:N=20;x=ones(1,N);x(1:3)=0;n=[-3:N-4];stem(n,x);title('单位阶跃序列');(3) 正弦序列()sin(2/)x n A fn Fs πϕ=+程序如下:N=50;n=0:N-1;A=1;f=50;Fs=f*N;fai=0.5*pi;x=A*sin(2*pi*f*n/Fs+fai);stem(n,x);(4) 复正弦序列x n eω()j n=程序如下:N=50;n=0:N-1;w=2*pi/N;x=exp(j*w*n);plot(x,'*');复指数序列或,它具有实部与虚部,是复正弦的数字域频率。
0()()j n x n e σω+=0()j n x n e ω=0ω对第一种表示形式,可以写成。
0000()(cos sin )cos sin n n n x n e n j n e n je n σσσωωωω=+=+如果用极坐标表示,则0arg[()]()|()|jw nj x n n x n x n e e e σ==A ,|()|n x n e σ=0arg[()]x n nω=若,则x (n )为衰减的复正弦,其实部和虚部分别为衰减振荡的正弦分量;若实部0n e σ<,则实部和虚部分别为增大的正弦分量;若,则实部和虚部分别为等幅振荡。
0n e σ>0n e σ=本实验中使用的信号为时的情况,即等幅振荡信号。
Matlab中的数字信号处理方法与实例

Matlab中的数字信号处理方法与实例数字信号处理是一门研究数字信号在数字域中分析、处理和改变的学科。
Matlab是一种强大的数值计算工具,被广泛应用于信号处理领域。
本文将介绍一些在Matlab中常用的数字信号处理方法与实例,并通过实例来展示它们的应用。
1. 信号的采样与重构信号采样是指将连续时间信号转化为离散时间信号的过程。
在Matlab中,我们可以使用“sample”函数对信号进行采样,并使用“hold”函数对采样后的信号进行重构。
下面是一个示例:```matlabfs = 100; % 采样频率t = 0:1/fs:1; % 时间序列x = sin(2*pi*5*t); % 原始信号subplot(2,1,1);plot(t,x);title('原始信号');xlabel('时间');ylabel('幅值');subplot(2,1,2);stem(t,x);title('采样和重构后的信号');xlabel('时间');ylabel('幅值');```在这个例子中,我们生成了一个频率为5Hz的正弦信号,然后对该信号进行采样和重构。
从结果可以看出,原始信号和重构后的信号基本上是一致的。
2. 信号的频谱分析频谱分析是指将信号从时域转换到频域的过程,可以用来分析信号的频率成分。
在Matlab中,我们可以使用“fft”函数对信号进行傅里叶变换,并使用“abs”函数获取信号的幅度谱。
下面是一个示例,演示如何对信号进行频谱分析:```matlabfs = 100; % 采样频率t = 0:1/fs:1; % 时间序列x = sin(2*pi*5*t); % 原始信号N = length(x); % 信号长度X = fft(x); % 傅里叶变换f = (0:N-1)*(fs/N); % 频率坐标plot(f,abs(X));title('信号的频谱');xlabel('频率');ylabel('幅度');```在这个示例中,我们同样生成了一个频率为5Hz的正弦信号,然后对该信号进行傅里叶变换,并绘制出信号的频谱图。
数字信号处理MATLAB简介

七、MATLAB的矩阵运算
面向矩阵元素的数学函数 如sin(x)表示将矩阵的每一个元素均取正弦。 表示矩阵i行、j列处的元素可用A(i,j)。 表示矩阵i行用A(i,:)。表示矩阵j列用A(:,j)。 面向矩阵的数学函数:在上述面向矩阵元素的数学函数的函数名后加m。如expm。
八、特殊矩阵的实现
六、MATLAB的矩阵运算
矩阵的常用运算 [L,U]=lu(A):矩阵A的LU分解。也有[L,U,P]=LU(A),置换矩阵P满足PA=LU。 [U,S,V]=svd(A):矩阵A的svd分解。 inv(A):矩阵A的逆。 pinv(A,tol):矩阵A的广义逆。tol为判0误差限,若省略,则默认为eps。
二、MATLAB特点
可靠的数值计算、强大而简易图像与图形显示及处理、图形界面设计风格适合科技人员、智能化程度高、功能化程度高、提供与其它高级语言(如C语言和Fortran语言)的接口。MATLAB提供了一个人机交互的数学环境,可进行演草纸式的数学运算。
01
严格地讲,MATLAB不是一种计算机语言。因为其源程序不能编译成可执行文件(较新版本可以),也不能脱离MATLAB环境运行。但从功能上看,可认为是一种解释性语言(对输入命令翻译并执行,然后返回结果,与解释BASIC语言类似 )。
A=zeros(m, n) 产生m×n的0矩阵赋给A A=zeros(sizes(B)) 产生与B同大的0矩阵赋给A A=zeros(n) 产生n×n的0矩阵赋给A。
零矩阵:
A=eye(n) 产生n×n的单位阵赋给A; A=eye(m, n) 产生m×n大的单位阵赋给A; A=eye(sizes(B)) 产生与B同大的单位阵赋给A
三、MATLAB特性
MATLAB的变量命名 变量名对大小写敏感(Sensitive) fruit、Fruit、FrUit及FRUIT中是不同的变量 每个变量名最多有19个字符 变量名的首字符必须是字母 标点符号不能出现在变量名中
数字信号处理第三版用MATLAB上机实验

实验二:时域采样与频域采样一、时域采样1.用MATLAB编程如下:%1时域采样序列分析fs=1000A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=1000;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,1);stem(n,xn);xlabel('n,fs=1000Hz');ylabel('xn');title('xn');subplot(3,2,2);plot(n,abs(Xk));xlabel('k,fs=1000Hz'); title('|X(k)|');%1时域采样序列分析fs=200A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=200;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs);Xk=fft(xn);subplot(3,2,3);stem(n,xn);xlabel('n,fs=200Hz'); ylabel('xn');title('xn');subplot(3,2,4);plot(n,abs(Xk));xlabel('k,fs=200Hz'); title('|X(k)|');%1时域采样序列分析fs=500A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=500;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,5);stem(n,xn);xlabel('n,fs=500Hz');ylabel('xn');title('xn');subplot(3,2,6);plot(n,abs(Xk));xlabel('k,fs=500Hz'); title('|X(k)|');2.经调试结果如下图:20406080-200200n,fs=1000Hzxnxn2040608005001000k,fs=1000Hz|X (k)|51015-2000200n,fs=200Hzx nxn510150100200k,fs=200Hz |X(k)|10203040-2000200n,fs=500Hzx nxn102030400500k,fs=500Hz|X (k)|实验结果说明:对时域信号采样频率必须大于等于模拟信号频率的两倍以上,才 能使采样信号的频谱不产生混叠.fs=200Hz 时,采样信号的频谱产生了混叠,fs=500Hz 和fs=1000Hz 时,大于模拟信号频率的两倍以上,采样信号的频谱不产生混叠。
如何使用MATLAB进行数字信号处理

如何使用MATLAB进行数字信号处理MATLAB是一种常用的数学软件工具,广泛应用于数字信号处理领域。
本文将介绍如何使用MATLAB进行数字信号处理,并按照以下章节进行详细讨论:第一章: MATLAB中数字信号处理的基础在数字信号处理中,我们首先需要了解信号的基本概念和数学表示。
在MATLAB中,可以使用向量或矩阵来表示信号,其中每个元素对应着一个离散时间点的信号值。
我们可以使用MATLAB 中的向量运算和函数来处理这些信号。
此外,MATLAB还提供了一组强大的工具箱,包括DSP系统工具箱和信号处理工具箱,以便更方便地进行数字信号处理。
第二章: 数字信号的采样和重构在数字信号处理中,采样和重构是两个核心概念。
采样是将连续信号转换为离散信号的过程,而重构则是将离散信号重新转换为连续信号的过程。
在MATLAB中,可以使用"sample"函数对信号进行采样,使用"interp"函数进行信号的重构。
此外,还可以使用FFT(快速傅里叶变换)函数对离散信号进行频率分析和频谱表示。
第三章: 傅里叶变换与频域分析傅里叶变换是一种常用的信号分析工具,可将信号从时域转换到频域。
MATLAB中提供了强大的FFT函数,可以帮助我们进行傅里叶变换和频谱分析。
通过傅里叶变换,可以将信号分解为不同频率的分量,并且可以通过滤波器和滤波器设计来处理这些分量。
MATLAB还提供了许多用于频域分析的函数,如功率谱密度函数、频谱估计函数等。
第四章: 滤波与降噪滤波是数字信号处理中的重要任务之一,旨在去除信号中的噪声或不需要的频率成分。
在MATLAB中,可以使用FIR和IIR滤波器设计工具箱来设计和实现滤波器。
此外,MATLAB还提供了各种滤波器的函数和滤波器分析工具,如lowpass滤波器、highpass滤波器、带通滤波器等。
这些工具和函数可以帮助我们对信号进行滤波,实现信号降噪和频率调整。
第五章: 时域信号分析与特征提取除了频域分析外,时域分析也是数字信号处理的重要内容之一。
数字信号处理,matlab实验报告

Matlab实验报告实验一:1.实验Matlab代码:N=25;Q=0.9+0.3*j;WN=exp(-2*j*pi/N);x=zeros(25,1);format long; %长整型科学计数for k0=1:25x(k0,1)=Q^(k0-1);end;for k1=1:25;X1(k1,1)=(1-Q^N)/(1-Q*WN^(k1-1));end;X1;X2=fft(x,32);subplot(3,1,1);stem(abs(X1),'b.');axis([0,35,0,15]);title('N=25,formular');xlabel('n'); subplot(3,1,2);stem(abs(X2),'g.');axis([0,35,0,15]);title('N=32, FFT');xlabel('n');for(a=1:25)X3(a)=X1(a)-X2(a)end;subplot(3,1,3);stem(abs(X3),'r.');title('difference');xlabel('n');实验结果如图:实验结论:可以看出基2时间抽选的FFT算法与利用公式法所得到的DFT结果稍有偏差,但不大,在工程上可以使用计算机利用FFT处理数据。
2.实验Matlab代码:N = 1000; % Length of DFTn = [0:1:N-1];xn = 0.001*cos(0.45*n*pi)+sin(0.3*n*pi)-cos(0.302*n*pi-pi/4);Xk = fft(xn,N);k=[0:1:N-1];subplot(5,1,1);stem(k,abs(Xk(1:1:N)));title('DFT x(n)');xlabel('k');axis([140,240,0,6])subplot(5,1,2);stem(k, abs(Xk(1:1:N)),'r');%画出sin(0.3npi)-cos(0.302npi-pi/4) axis([140,160,0,6]);title('sin(0.3*pi*n)-cos(0.302*pi*n) ');xlabel('k');subplot(5,1,3);stem(k, 1000*abs(Xk(1:1:N)),'g');%画出0.001*cos(0.45npi)axis([220,230,0,6]);title('cos(0.45*pi*n) ');xlabel('k');subplot(5,1,4);stem(k,0.01*abs(Xk(1:1:N)),'k');%画%sin(0.3npi)-cos(0.302npi-pi/4)axis([140,160,0,6]);title('sin(0.3*pi*n)-cos(0.302*pi*n) ');xlabel('k');subplot(5,1,5);stem(k, 10*abs(Xk(1:1:N)),'m');%画出0.001*cos(0.45npi)axis([220,230,0,6]);title('cos(0.45*pi*n) ');xlabel('k');实验结果如图:实验结论:由上图及过程可知,当DFT变换长度为1000时所得到的谱线非常理想。
数字信号处理 matlab pdf

数字信号处理matlab pdfTornado 是一个Python 的网络框架和异步网络库,起初由FriendFeed 开发。
它使用非阻塞网络I/O,可以处理数以万计的开放连接,非常适合长轮询、WebSockets,以及其他需要长时间实时通信的应用程序。
当使用Tornado 与AJAX 结合时,你通常会有一个Tornado 服务器处理请求并返回一个响应,而这个响应通常是由客户端的JavaScript 通过AJAX 调用来接收的。
以下是一个简单的例子,说明如何使用Tornado 处理AJAX 调用:Tornado 服务器:pythonimport tornado.ioloopimport tornado.webclass MainHandler(tornado.web.RequestHandler):def get(self):self.render("index.html")class AjaxHandler(tornado.web.RequestHandler): async def get(self):data = {"message": "Hello, AJAX!"}self.write(data)def make_app():return tornado.web.Application([(r"/", MainHandler),(r"/ajax", AjaxHandler),])if __name__ == "__main__":app = make_app()app.listen(8888)tornado.ioloop.IOLoop.current().start() HTML 客户端(index.html):html<!DOCTYPE html><html lang="en"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>Tornado AJAX Example</title></head><body><button onclick="fetchData()">Fetch Data</button><script>function fetchData() {fetch('/ajax').then(response => response.json()).then(data => {console.log(data);alert(data.message);}).catch(error => console.error('Error:', error));}</script></body></html>在这个例子中:我们有一个简单的Tornado 服务器,它有两个处理程序:MainHandler 用于呈现主页,AjaxHandler 用于处理AJAX 请求。
学习使用MATLAB进行数字信号处理

学习使用MATLAB进行数字信号处理第一章:MATLAB介绍与基本操作MATLAB是一种强大的数学软件,广泛应用于各个领域的科学计算,包括数字信号处理。
本章将介绍MATLAB的基本操作和数字信号处理领域常用的函数和工具箱。
1.1 MATLAB的安装与配置MATLAB可以在官方网站上下载,并按照安装指南进行安装。
安装完成后,需要进行基本的配置,例如设置工作目录和启用所需的工具箱。
1.2 MATLAB的基本语法和数据类型MATLAB的基本语法与其他编程语言相似,例如定义变量、执行算术运算和函数调用。
MATLAB支持的数据类型也很丰富,包括数值、字符、逻辑和结构等。
1.3 MATLAB的图形用户界面(GUI)MATLAB提供了一个图形用户界面,使用户可以通过可视化的方式进行数据处理和分析。
GUI工具箱可以方便地创建自定义的用户界面,以满足不同的需求。
第二章:数字信号处理基础本章将介绍数字信号处理的基本概念和数学原理,包括采样、量化、频谱分析和滤波等内容。
2.1 采样与重构采样是将连续信号转换为离散信号的过程,重构则是将离散信号还原为连续信号。
MATLAB提供了相应的函数和工具箱,用于进行采样与重构的操作。
2.2 量化与编码量化是将连续信号转换为离散信号的过程,编码则是将离散信号表示为二进制码。
MATLAB提供了多种量化和编码的方法和函数。
2.3 频谱分析频谱分析是分析信号在频域上的特性和分布的过程。
MATLAB 中的FFT函数可以对信号进行快速傅里叶变换,并绘制频谱图。
2.4 数字滤波数字滤波是去除或改变信号中某些频率成分的过程。
MATLAB 提供了多种滤波器设计和滤波器分析的函数和工具箱,方便用户进行数字滤波的操作。
第三章:MATLAB在数字信号处理中的应用本章将介绍MATLAB的数字信号处理工具箱和常用函数,以及应用实例。
3.1 DSP工具箱MATLAB的DSP(Digital Signal Processing)工具箱提供了丰富的函数和工具,用于数字信号的生成、分析和处理。
如何在Matlab中进行数字信号处理

如何在Matlab中进行数字信号处理一、引言数字信号处理是指对模拟信号进行采样、量化和编码,将其转化为离散的数字信号,然后通过一系列信号处理算法和技术对其进行分析、处理和改变的过程。
Matlab作为一种强大的数学计算工具,不仅在科学计算、工程设计等领域广泛应用,也在数字信号处理中发挥着重要的作用。
本文将介绍如何在Matlab中进行数字信号处理。
二、数字信号处理基础在进行数字信号处理之前,首先需要了解一些基础概念。
这些概念包括采样、量化、离散傅里叶变换等。
1. 采样采样是指将连续时间的信号转换为离散时间的信号。
在Matlab中,可以使用采样定理进行采样,即按照一定的时间间隔对信号进行采样。
2. 量化量化是指将连续幅度的信号转换为离散幅度的信号。
在Matlab中,可以使用量化算法将信号的幅度值映射到一组离散的值。
3. 离散傅里叶变换离散傅里叶变换是指将离散时间信号转换为离散频率信号的过程。
在Matlab 中,可以使用fft函数对信号进行离散傅里叶变换,并得到信号的频域表示。
三、Matlab中的数字信号处理函数Matlab提供了丰富的数字信号处理函数,可以方便地进行信号处理和分析。
下面介绍几个常用的函数。
1. 傅里叶变换函数(fft)fft函数可以对信号进行离散傅里叶变换。
使用方法为:Y = fft(X),其中X为输入信号,Y为变换后的频域表示。
2. 逆傅里叶变换函数(ifft)ifft函数可以对频域信号进行逆傅里叶变换。
使用方法为:X = ifft(Y),其中Y为输入频域信号,X为逆变换后的时域表示。
3. 滤波函数(filter)filter函数可以对信号进行滤波处理。
使用方法为:Y = filter(B, A, X),其中B为滤波器的分子系数,A为滤波器的分母系数,X为输入信号,Y为滤波后的信号。
4. 时频分析函数(spectrogram)spectrogram函数可以对信号进行时频分析。
使用方法为:S = spectrogram(X),其中X为输入信号,S为信号的时频图表示。
数字信号处理Matlab实现实例(推荐给学生)

数字信号处理Matlab实现实例第1章离散时间信号与系统例1-1用MATLAB计算序列{-201–13}和序列{120-1}的离散卷积。
解MATLAB程序如下:a=[-201-13];b=[120-1];c=conv(a,b);M=length(c)-1;n=0:1:M;stem(n,c);??????????????xlabel('n');ylabel('幅度');图1.1给出了卷积结果的图形,求得的结果存放在数组c中为:{-2-413151-3}。
例1-2用MATLAB计算差分方程当输入序列为时的输出结果解MATLAB程序如下:N=41;a=[0.8-0.440.360.22];b=[10.7-0.45-0.6];?其DTFT为用MATLAB计算的程序如下:k=256;num=[0.8-0.440.360.02];den=[10.7-0.45-0.6];w=0:pi/k:pi;h=freqz(num,den,w);subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部')xlabel('\omega/\pi');ylabel('幅度')subplot(2,2,2);plot(w/pi,imag(h));gridtitle('虚部')xlabel('\omega/\pi');ylabel('Amplitude')subplot(2,2,3);plot(w/pi,abs(h));gridtitle('幅度谱')xlabel('\omega/\pi');ylabel('幅值')subplot(2,2,4);plot(w/pi,angle(h));gridtitle('相位谱')xlabel('\omega/\pi');ylabel('弧度')第2章离散傅里叶变换及其快速算法例2-1解此时离散序列,即k=8。
数字信号处理Matlab_实现实例(有用)

数字信号处理Matlab_实现实例(有用)数字信号处理Matlab 实现实例离散时间信号与系统例1-1 用MATLAB计算序列 -2 0 1 –1 3 和序列 1 2 0 -1 的离散卷积解 MATLAB程序如下a [-2 0 1 -1 3]b [1 2 0 -1]c conv abM length c -1n 01Mstem ncxlabel n ylabel 幅度图11给出了卷积结果的图形求得的结果存放在数组c中为 -2 -4 1 3 1 5 1 -3例1-2 用MATLAB计算差分方程当输入序列为时的输出结果MATLAB程序如下N 41a [08 -044 036 022]b [1 07 -045 -06]x [1 zeros 1N-1 ]k 01N-1y filter abxstem kyxlabel n ylabel 幅度图 12 给出了该差分方程的前41个样点的输出即该系统的单位脉冲响应1-3 用MATLAB计算例1-2差分方程所对应的系统函数的DTFT1-2差分方程所对应的系统函数为其DTFT为用MATLAB计算的程序如下k 256num [08 -044 036 002]den [1 07 -045 -06]w 0pikpih freqz numdenwsubplot 221plot wpireal h gridtitle 实部xlabel \omega\pi ylabel 幅度subplot 222plot wpiimag h gridtitle 虚部xlabel \omega\pi ylabel Amplitudesubplot 223plot wpiabs h gridtitle 幅度谱xlabel \omega\pi ylabel 幅值subplot 224plot wpiangle h gridtitle 相位谱xlabel \omega\pi ylabel 弧度例2-1 对连续的单一频率周期信号按采样频率采样截取长度N分别选N 20和N 16观察其DFT结果的幅度谱解此时离散序列即k 8用MATLAB计算并作图函数fft用于计算离散傅里叶变换DFT程序如下k 8n1 [0119]xa1 sin 2pin1ksubplot 221plot n1xa1xlabel tT ylabel x nxk1 fft xa1 xk1 abs xk1subplot 222stem n1xk1xlabel k ylabel X kn2 [0115]xa2 sin 2pin2ksubplot 223plot n2xa2xlabel tT ylabel x nxk2 fft xa2 xk2 abs xk2 subplot 224stem n2xk2xlabel k ylabel X k 计算结果示于图21 a 和 b 分别是N 20时的截取信号和DFT结果由于截取了两个半周期频谱出现泄漏 c 和 d 分别是N 16时的截取信号和DFT结果由于截取了两个整周期得到单一谱线的频谱上述频谱的误差主要是由于时域中对信号的非整周期截断产生的频谱泄漏例2-2 用FFT计算两个序列的互相关函数解用MATLAB计算程序如下x [1 3 -1 1 2 3 3 1]y [2 1 -1 1 2 0 -1 3]k length xxk fft x2kyk fft y2krm real ifft conj xk ykrm [rm k22k rm 1k ]m -k1 k-1stem mrmxlabel m ylabel 幅度其计算结果如图22所示2-3计算两个序列的的互相关函数其中x n 2 3 5 2 1 –1 0 0 12 3 5 3 0 –1 –2 0 1 2 y n x n-4 e n e n MATLAB中可以用随机函数rand产生解用MATLAB计算程序如下x [2 3 5 2 1 -1 0 0 12 3 5 3 0 -1 -2 0 1 2]y [0 0 0 0 2 3 5 2 1 -1 0 0 12 3 5 3 0 -1 -2 0 1 2]k length ye rand 1k -05y yexk fft x2kyk fft y2krm real ifft conj xk ykrm [rm k22k rm 1k ]m -k1 k-1stem mrmxlabel m ylabel 幅度计算结果如图23 a 我们看到最大值出现在m 4处正好是y n x n 的延迟2 3 b 是x n 自相关函数他和y n y n 受到噪声的干扰第3章无限长单位脉冲响应 IIR 滤波器的设计方法例3-1 设采样周期T 250μs采样频率fs 4kHz用脉冲响应不变法和双线性变换法设计一个三阶巴特沃兹滤波器其3dB边界频率为fc 1kHz[BA] butter 32pi1000s[num1den1] impinvar BA4000[h1w] freqz num1den1[BA] butter 32000025s[num2den2] bilinear BA4000[h2w] freqz num2den2f wpi2000plot fabs h1 -fabs h2 -gridxlabel 频率Hzylabel 幅值dB程序中第一个butter的边界频率2π×1000为脉冲响应不变法原型低通滤波器的边界频率第二个butter的边界频率2T 2000025为双线性变换法原型低通滤波器的com这两种设计方法所得到的频响虚线为脉冲响应不变法的结果实线为双线性变换法的结果脉冲响应不变法由于混叠效应使得过渡带和阻带的衰减特性变差并且不存在传输零点同时也看到双线性变换法在z -1即ω π或f 2000Hz处有一个三阶传输零点这个三阶零点正是模拟滤波器在Ω ?处的三阶传输零点通过映射形成的例3-2 设计一数字高通滤波器它的通带为400,500Hz通带内容许有05dB的波动阻带内衰减在小于317Hz的频带内至少为19dB采样频率为1000Hz wc 21000tan 2pi400 21000wt 21000tan 2pi317 21000[Nwn] cheb1ord wcwt0519s[BA] cheby1 N05wnhighs[numden] bilinear BA1000[hw] freqz numdenf wpi500plot f20log10 abs haxis [0500-8010]gridxlabelylabel 幅度dB图32给出了MATLAB计算的结果可以看到模拟滤波器在Ω ?处的三阶零点通过高通变换后出现在ω 0z 1处这正是高通滤波器所希望得到的例3-3 设计一巴特沃兹带通滤波器其,dB边界频率分别为f2 110kHz和f190kHz在阻带f3 120kHz处的最小衰减大于,,dB采样频率fs 400kHz w1 2400tan 2pi90 2400w2 2400tan 2pi110 2400wr 2400tan 2pi120 2400[Nwn] buttord [w1 w2][0 wr]310s[BA] butter Nwns[numden] bilinear BA400[hw] freqz numdenf wpi200plot f20log10 abs haxis [40160-3010]gridxlabel 频率kHzylabel 幅度dB图33给出了MATLAB计算的结果可以看出数字滤波器将无穷远点的二阶零点映射为z ?1的二阶零点数字带通滤波器的极点数是模拟低通滤波器的极点数的两倍例3-4 一数字滤波器采样频率fs 1kHz要求滤除100Hz的干扰其,dB的边界频率为95Hz和105Hz原型归一化低通滤波器为w1 95500w2 105500[BA] butter 1[w1 w2]stop[hw] freqz BAf wpi500plot f20log10 abs haxis [50150-3010]gridxlabel 频率Hzylabel 幅度dB图34为MATLAB的计算结果第4章有限长单位脉冲响应 FIR 滤波器的设计方法 2 用凯塞窗设计一FIR 低通滤波器低通边界频率阻带边界频率阻带衰减不小于50dB解首先由过渡带宽和阻带衰减来决定凯塞窗的N和图41给出了以上设计的频率特性 a 为N 30直接截取的频率特性 b 为凯塞窗设计的频率特性凯塞窗设计对应的MATLAB程序为wn kaiser 30455nn [0129]alfa 30-1 2hd sin 04pi nn-alfa pi nn-alfah hdwn[h1w1] freqz h1plot w1pi20log10 abs h1axis [01-8010]gridxlabel 归一化频率ylabel 幅度dB例4-2 利用雷米兹交替算法设计一个线性相位低通FIR数字滤波器其指标为通带边界频率fc 800Hz阻带边界fr 1000Hz通带波动阻带最小衰减At 40dB采样频率fs 4000Hz解在MATLAB中可以用remezord 和remez两个函数设计其结果如图42MATLAB程序如下fedge [800 1000]mval [1 0]dev [00559 001]fs 4000[Nfptsmagwt] remezord fedgemvaldevfsb remez Nfptsmagwt[hw] freqz b1256plot w2000pi20log10 abs hgridxlabel 频率Hzylabel 幅度dB函数remezord中的数组fedge为通带和阻带边界频率数组mval是两个边界处的幅值而数组dev是通带和阻带的波动fs是采样频率单位为Hz 第5章数字信号处理系统的实现例5-1求下列直接型系统函数的零极点并将它转换成二阶节形式解用MATLAB计算程序如下num [1 -01 -03 -03 -02]den [1 01 02 02 05][zpk] tf2zp numdenm abs pdisp disp zdisp 极点 disp pdisp 增益系数 disp ksos zp2sos zpkdisp 二阶节 disp real soszplane numden输入到num和den的分别为分子和分母多项式的系数计算求得零极点增益系数和二阶节的系数零点09615-05730-01443 05850i-01443 - 05850i 极点05276 06997i05276 - 06997i-05776 05635i-05776 - 05635i增益系数1二阶节10000 -03885 -05509 10000 11552 0651110000 02885 03630 10000 -10552 07679系统函数的二阶节形式为极点图见图515-2 分析五阶椭圆低通滤波器的量化效应其截止频率为04 通带纹波为04dB最小的阻带衰减为50dB对滤波器进行截尾处理时使用函数a2dTm 解用以下MATLAB程序分析量化效应clf[ba] ellip 5045004[hw] freqz ba512g 20log10 abs hbq a2dT b5aq a2dT a5[hqw] freqz bqaq512gq 20log10 abs hqplot wpigbwpigqrgridaxis [0 1 -80 5]xlabel \omega\piylabel Gain dBlegend 量化前量化后figure[z1p1k1] tf2zp ba[z2p2k2] tf2zp bqaqzplaneplot [z1z2][p1p2] oxlegend 量化前的零点量化后的零点量化前的极点量化后的极点图51a表示系数是无限精度的理想滤波器的频率响应以实线表示以及当滤波器系数截尾到5位时的频率响应以短线表示由图可知系数量化对频带的边缘影响较大经系数量化后增加了通带的波纹幅度减小了过渡带宽并且减小了最小的阻带衰减图5 1b给出了系数量化以前和系数量化以后的椭圆低通滤波器的零极点位置由图可知系数的量化会使零极点的位置与它们的理想的标称位置相比发生显著的改变在这个例子中靠近虚轴的零点的位置变动最大并且移向靠它最近的极点的位置只要对程序稍作改变就可以分析舍入量化的影响为了研究二进制数量化效应对数字滤波器的影响首先需要将十进制表示的滤波器系数转换成二进制数并进行量化二进制数的量化既可以通过截尾法也可以通过舍入法实现我们提供了如下的两个MATLAB程序com这两段程序分别将向量d中的每一个数按二进制数进行截尾或舍入量化量化的精度是小数点以后保留b位量化后返回的向量为beqfunction beq a2dT dbbeq a2dT db 将十进制数利用截尾法得到b位的二进制数然后将该二进制数再转换为十进制数m 1 d1 abs dwhile fix d1 0d1 abs d 2mm m1endbeq fix d12bbeq sign d beq2 m-b-1 function beq a2dR dbbeq a2dR db 将十进制数利用舍入法得到b位的二进制数然后将该二进制数再转换为十进制数m 1 d1 abs dwhile fix d1 0d1 abs d 2mm m1endbeq fix d12b5beq sign d beq2 m-b-1 第7章多采样率信号处理例7-1在时域上显示一个信号频率为0042 的正弦信号然后以抽取因子3 降采样率并在时域上显示相应的结果比较两者在时域上的特点MATLAB计算程序如下M 3 down-sampling factor 3fo 0042signal frequency 0042generate the input sinusoidal sequencen 0N-1m 0NM-1x sin 2pifomgenerate the down-sampling squencey x [1Mlength x ]subplot 211stem nx 1Ntitle 输入序列xlabel 时间nylabel 幅度subplot 212stem nytitle [输出序列抽取因子为num2str M ]xlabel 时间n ylabel 幅度图71 信号频率为0042例7-2 用汉明窗设计一长度为32的线性相位QMF滤波器组解采用MATLAB设计调用fir2函数设计公共低通滤波器参数缺省即为汉明窗程序如下b1 fir2 31[00405055061][11100600]for k 132 b2 k -1 k-1 b1 kend[H1zw] freqz b11256h1 abs H1z g1 20log10 h1[H2zw] freqz b21256h2 abs H2z g2 20log10 h2figure 1plot wpig1-wpig2--axis [01-10010]gridxlabel \omega\pi ylabel 幅度dBsum h1h1h2h2d 10log10 sumfigure 2plot wpid gridxlabel \omega\pi ylabel 误差dBaxis [01-0303]图72 a 是一个N 32的汉明窗设计结果图中实线表示的低通频响虚线表示它的镜像图72 b 是基于这种设计方法的分析综合滤波器组的整个频响从这个图可见重建误差小于?005dB由于汉明窗设计的频率响应在通带中近乎是平坦的因此最大重建误差发生在这个滤波器的通带边界和过渡带内。
数字信号处理matlab程序

(2) 单位阶跃序列
u(n)
程序如下:
1 0
1 0
n0 n0
nk n0
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料试荷试卷下卷问高总题中体2资2配,料置而试时且卷,可调需保控要障试在各验最类;大管对限路设度习备内题进来到行确位调保。整机在使组管其高路在中敷正资设常料过工试程况卷中下安,与全要过,加度并强工且看作尽护下可关都能于可地管以缩路正小高常故中工障资作高料;中试对资卷于料连继试接电卷管保破口护坏处进范理行围高整,中核或资对者料定对试值某卷,些弯审异扁核常度与高固校中定对资盒图料位纸试置,卷.编保工写护况复层进杂防行设腐自备跨动与接处装地理置线,高弯尤中曲其资半要料径避试标免卷高错调等误试,高方要中案求资,技料编术试写5交、卷重底电保要。气护设管设装备线备置4高敷、调动中设电试作资技气高,料术课中并3试、中件资且卷管包中料拒试路含调试绝验敷线试卷动方设槽技作案技、术,以术管来及架避系等免统多不启项必动方要方式高案,中;为资对解料整决试套高卷启中突动语然过文停程电机中气。高课因中件此资中,料管电试壁力卷薄高电、中气接资设口料备不试进严卷行等保调问护试题装工,置作合调并理试且利技进用术行管,过线要关敷求运设电行技力高术保中。护资线装料缆置试敷做卷设到技原准术则确指:灵导在活。分。对线对于盒于调处差试,动过当保程不护中同装高电置中压高资回中料路资试交料卷叉试技时卷术,调问应试题采技,用术作金是为属指调隔发试板电人进机员行一,隔变需开压要处器在理组事;在前同发掌一生握线内图槽部纸内 故资,障料强时、电,设回需备路要制须进造同行厂时外家切部出断电具习源高题高中电中资源资料,料试线试卷缆卷试敷切验设除报完从告毕而与,采相要用关进高技行中术检资资查料料和试,检卷并测主且处要了理保解。护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
数字信号处理实验全部程序MATLAB

实验一熟悉MATLAB环境一、实验目的(1)熟悉MATLAB的主要操作命令。
(2)学会简单的矩阵输入和数据读写。
(3)掌握简单的绘图命令。
(4)用MATLAB编程并学会创建函数。
(5)观察离散系统的频率响应。
二、实验内容认真阅读本章附录,在MATLAB环境下重新做一遍附录中的例子,体会各条命令的含义。
在熟悉了MATLAB基本命令的基础上,完成以下实验。
上机实验内容:(1)数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4],B=[3 4 5 6],求C=A+B,D=A-B,E=A.*B,F=A./B,G=A.^B并用stem语句画出A、B、C、D、E、F、G。
实验程序:A=[1 2 3 4];B=[3 4 5 6];n=1:4;C=A+B;D=A-B;E=A.*B;F=A./B;G=A.^B;subplot(4,2,1);stem(n,A,'fill');xlabel ('时间序列n');ylabel('A');subplot(4,2,2);stem(n,B,'fill');xlabel ('时间序列n ');ylabel('B'); subplot(4,2,3);stem(n,C,'fill');xlabel ('时间序列n ');ylabel('A+B'); subplot(4,2,4);stem(n,D,'fill');xlabel ('时间序列n ');ylabel('A-B'); subplot(4,2,5);stem(n,E,'fill');xlabel ('时间序列n ');ylabel('A.*B'); subplot(4,2,6);stem(n,F,'fill');xlabel ('时间序列n ');ylabel('A./B'); subplot(4,2,7);stem(n,G,'fill');xlabel ('时间序列n ');ylabel('A.^B');运行结果:(2)用MATLAB实现以下序列。
数字信号处理及matlab实现 pdf

数字信号处理及matlab实现pdf
数字信号处理是一门研究如何对离散的数字信号进行分析、处理和变换的学科。
它在许多领域中都有广泛的应用,包括通信系统、音频处理、图像处理等。
Matlab是一种强大的数值计算和编程环境,可以用于数字信号处理的实现。
在Matlab中,有很多内置的函数和工具箱可以帮助我们进行数字信号的处理。
首先,我们可以使用Matlab读取和存储数字信号。
Matlab 提供了各种函数来读取不同类型的信号文件,比如wav文件、mp3文件等。
我们可以使用这些函数将信号加载到Matlab中进行后续处理。
同样,Matlab也提供了函数来将处理后的信号保存为文件。
其次,Matlab提供了许多常用的数字信号处理函数,例如滤波器设计、频谱分析、时频分析等。
我们可以利用这些函数对信号进行去噪、滤波、频谱分析等操作。
另外,Matlab还提供了许多工具箱,如信号处理工具箱、音频工具箱等,其中包含了更多高级的处理算法和函数。
此外,Matlab还支持自定义函数和算法的开发。
如果我们想要实现特定的数字信号处理算法,可以使用Matlab编写相应的代码。
Matlab具有简单易用的语法和丰富的函数库,可以帮助我们快速实现各种数字信号处理算法。
总之,通过Matlab实现数字信号处理可以获得高效、灵活
和可靠的结果。
无论是对于初学者还是专业人士来说,Matlab 都是一个非常强大和方便的工具。
数字信号处理matlab pdf

数字信号处理matlab数字信号处理(Digital Signal Processing,DSP)是一种处理离散时间信号的方法,这些信号通常通过模拟信号进行数字化获得。
MATLAB是一个广泛使用的科学计算软件,可用于数字信号处理。
在MATLAB中进行数字信号处理的基本步骤通常包括:1.数据导入和预处理:MATLAB中可以方便地导入数字信号,包括音频、图像等。
然后可以对信号进行一些预处理操作,例如滤波、降噪等。
2.信号分析和特征提取:在信号预处理之后,可以进行更深入的分析,如频率分析、功率谱分析、相关性分析等。
此外,还可以提取信号的特征,例如频率、幅值、相位等。
3.信号处理算法实现:在MATLAB中,可以使用各种内置函数和工具箱来实现各种数字信号处理算法,如滤波器设计、频域变换、调制解调等。
4.结果可视化:MATLAB提供了强大的绘图和可视化工具,可以方便地显示信号处理的结果。
以下是一个简单的MATLAB代码示例,展示了如何读取一个音频文件并计算其功率谱:```matlab%读取音频文件[signal,fs]=audioread('filename.wav');%转换为单通道(如果需要)if size(signal,2)==2signal=sum(signal,2);end%计算功率谱[Pxx,F]=periodogram(signal,[],length(signal),fs);%绘制功率谱图figure;plot(F,10log10(Pxx/max(Pxx)));xlabel('Frequency(Hz)');ylabel('Power/Frequency(dB/Hz)');title('Power Spectrum');```请注意,这只是一个非常基础的示例。
实际应用中,数字信号处理可能涉及更复杂的算法和数据处理。
数字信号处理matlab程序实现

1.6.1 离散时间信号的MATLAB 实现1.正弦序列离散正弦序列的MATLAB 表示与连续信号类似,只不过是用stem 函数而不是用plot 函数来画出序列的波形。
下面就是正弦序列k ⎪⎭⎫⎝⎛6sin π的MATLAB 源程序。
程序运行结果如图1.19所示。
%正弦序列实现程序 k=0:39;fk=sin(pi/6*k); stem(k,fk)图1.19 正弦序列波形2.指数序列离散指数序列的一般形式为kca ,可用MATLAB 中的数组幂运算(即点幂运算)c*k a .^来实现。
下面为用MATLAB 编写绘制离散时间实指数序列波形的函数。
function dszsu(c,a,k1,k2) %c :指数序列的幅度 %a :指数序列的底数%k1:绘制序列的起始序号 %k2:绘制序列的终止序号 k=k1:k2; x=c*(a.^k);stem(k,x,'filled') hold onplot([k1,k2],[0,0]) hold off利用上述函数,实现实指数波形MATLAB 程序如下(其中a 值分别为43454345--,,,)。
%离散时间实指数序列实现程序 subplot 221;dszsu(1,5/4,0,20); xlabel('k');title('f1[k]'); subplot 222dszsu(1,3/4,0,20); xlabel('k'); title('f2[k]'); subplot 223;dszsu(1,-5/4,0,20); xlabel('k'); title('f3[k]'); subplot 224;dszsu(1,-3/4,0,20); xlabel('k'); title('f4[k]');程序运行结果如图1.20所示。
Matlab实现数字信号处理(源代码)

1 编制程序产生单位抽样序列δ(n) 及δ(n﹣学号),并绘制出图形。
δ(n) %实现单位抽样序列δ(n)程序k=-30:30;delta=[zeros(1,30),1,zeros(1,30)];stem(k,delta)δ(n﹣学号)%实现单位抽样序列δ(n﹣22)程序k=-30:30;delta=[zeros(1,52),1,zeros(1,8)];stem(k,d2 编制程序产生单位阶跃序列u(n) 及u(n﹣学号)及u(n)﹣u(n﹣学号),并绘制出图形。
%实现单位阶跃序列u(n)程序k=-30:30;delta=[zeros(1,30),1,ones(1,30)]; stem(k,delta)%实现阶跃序列u(n﹣22)程序k=-30:30;delta=[zeros(1,52),1,ones(1,8)];stem(k,delta)%实现阶跃序列u(n)﹣u(n﹣22)程序k=-30:30;(1,52),1,ones(1,8)];stem(k,delta)3 编制程序产生正弦序列x(n)= 学号sin(2πn),x(n)= 学号sin(2πn/学号) 及x(n)= 学号sin(2n),并绘制出图形。
%实现正弦序列x(n)= 22sin(2πn)程序n=0:100;x=22*sin(2*n*pi);stem(n,x)%实现正弦序列x(n)= 22sin(2πn/22)程序Array n=0:100;x=22*sin(2*n*pi/22);stem(n,x)n=0:100;x=22*sin(2*n);stem(n,x)4 编制程序产生复指数序列x(n)= e j学号n,并绘制图形。
%实现复指数序列x(n)= ej22n程序n=0:50;x=exp(i*22).^n;xr=real(x);xi=imag(x);xm=abs(x); xa=angle(x); figure;subplot(221);stem(n,xr);title('实部'); subplot(222);stem(n,xi);title('虚部'); subplot(223);stem(n,xm);title('模'); subplot(224);stem(n,xa);title('相角');实部204060虚部0204060模0204060相角5编制程序产生指数序列x(n)= a n,并绘制出图形。
数字信号处理-MATLAB程序
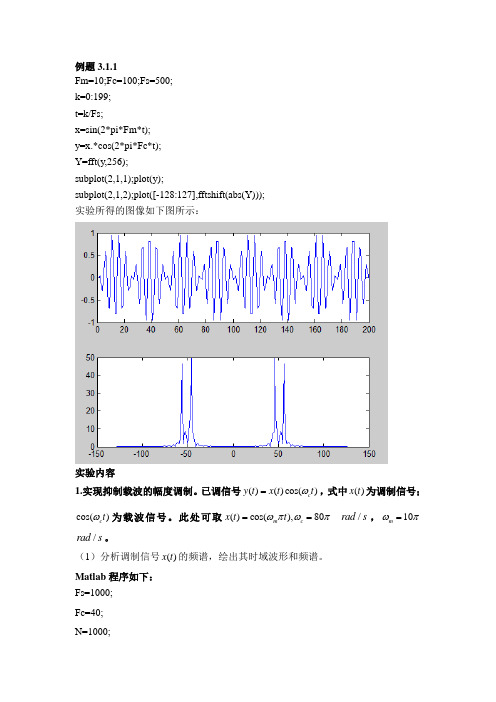
例题3.1.1Fm=10;Fc=100;Fs=500;k=0:199;t=k/Fs;x=sin(2*pi*Fm*t);y=x.*cos(2*pi*Fc*t);Y=fft(y,256);subplot(2,1,1);plot(y);subplot(2,1,2);plot([-128:127],fftshift(abs(Y)));实验所得的图像如下图所示:实验内容1.实现抑制载波的幅度调制。
已调信号()()cos()c y t x t t ω=,式中()x t 为调制信号;cos()c t ω为载波信号。
此处可取()cos(),80m c x t t ωπωπ== /rad s ,10m ωπ= /rad s 。
(1)分析调制信号()x t 的频谱,绘出其时域波形和频谱。
Matlab 程序如下:Fs=1000;Fc=40;N=1000;wc=80*pi;n=0:N-2;t=n/Fs;x=cos(10*pi*pi*t);y=x.*cos(wc*t);z1=fft(x,256);subplot(2,1,1);plot(t,x);legend('x(t)的时域波形');subplot(2,1,2);plot([-128:127],fftshift(abs(z1)));legend('x(t)的频谱'); 实验所得图形如下:(2)分析已调信号()y t的频谱,绘出其时域波形和频谱。
Matlab程序如下:Fs=1000;Fc=40;N=1000;n=0:N-2;t=n/Fs;x=cos(10*pi*pi*t);y=modulate(x,Fc,Fs,'am');z=fft(y,256);subplot(2,1,1);plot(t,y);legend('y(t)的时域波形');subplot(2,1,2);plot([-128:127],fftshift(abs(z)));legend('y(t)的频域波形')(3)设计低通滤波器并应用filter函数,实现信号同步解调设计的低通滤波器为cheby1型低通滤波器,技术参数为:wp=0.2*pi,ws=0.6*pi,Ap=1Db,As=25dB调制:[N,wc]=cheb1ord(0.2*pi,0.6*pi,1,25,’s’);[num,den]=cheby1(N,1,wc,’s’);[b,a]=bilinear(num,den,0.5);x=cos(10*pi*pi*t);y=x.*cos(80*pi*t);w1=filter(b,a,y);plot(w1);Y=fft(w1);plot(w1);axis([0 500 -1 1]);调制后的波形如下图:解调:[N,wc]=cheb1ord(0.2*pi,0.6*pi,1,25,'s'); [num,den]=cheby1(N,1,wc,'s');[b,a]=bilinear(num,den,0.5);x=cos(10*pi*pi*t);y=x.*cos(80*pi*t);w1=filter(b,a,y);plot(w1);Y=fft(w1);Q=demod(Y,Fc,Fs,'am');plot(t,Q);axis([0.3 0.5 -0.1 0.1]);解调后的波形如下图:2.实现含有载波的幅度调制。
如何使用MATLAB进行数字信号处理

如何使用MATLAB进行数字信号处理数字信号处理(Digital Signal Processing,简称DSP)是利用数字技术对连续时间信号进行处理和分析的一种方法。
MATLAB作为一种强大的计算软件,具备丰富的信号处理工具箱,可以方便地进行数字信号处理的相关操作。
本文将介绍如何使用MATLAB进行数字信号处理的基本步骤和常用方法。
一、信号的表示与采样在数字信号处理中,首先需要对连续时间信号进行离散化,即将连续时间信号转换为离散时间信号。
通常采用采样(Sampling)的方式,通过在一段时间内定时获取信号的取样值来进行离散化。
MATLAB提供了信号的表示与采样的函数,如sine、square、sawtooth等,可以生成不同类型的信号。
使用这些函数生成信号,并可以通过设置参数来调整信号的幅度、频率等。
例如,生成正弦信号可以使用sine函数,如:```fs = 1000; % 采样频率t = 0:1/fs:1; % 时间向量f = 10; % 信号频率x = sin(2*pi*f*t); % 生成正弦信号```以上代码生成了频率为10Hz的正弦信号,并将其存储在变量x中。
二、离散信号的分析与处理得到离散信号后,便可以对其进行进一步的分析与处理。
MATLAB提供了众多的函数和工具箱,可以方便地进行信号处理操作。
1. 时域分析通过计算信号的时域特性,我们可以了解信号的幅度、频率、相位等信息。
(1)绘制信号波形可以使用plot函数将离散信号的波形绘制出来。
例如,对于上述生成的正弦信号,可以使用以下代码绘制波形图:```plot(t,x);xlabel('时间');ylabel('幅度');title('正弦信号波形');```(2)计算信号的基本特性通过计算均值、方差、能量、功率等指标,我们可以了解信号的基本特性。
对于上述的正弦信号,可以使用以下代码计算信号的均值和能量:```mean_x = mean(x); % 计算信号的均值energy_x = sum(abs(x).^2)/length(x); % 计算信号的能量```2. 频域分析通过对信号进行傅里叶变换,我们可以将信号在频域上进行分析,了解信号的频率、谱形等信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[N,wc]=cheb1ord(0.2*pi,0.6*pi,1,25,’s’);
[num,den]=cheby1(N,1,wc,’s’);
[b,a]=bilinear(num,den,0.5);
x=cos(10*pi*pi*t);
y=x.*cos(80*pi*t);
w1=filter(b,a,y);
两种调制结果如下:
(3)实现含有载波的幅度调制 ,调制信号为
设 ,载波为 ,取 。
(1)分析调制信号 的频谱,绘出其时域波形和频谱。
(2)分析已调信号 的频谱,绘出其时域波形和频谱。
①Matlab程序为:F来自=1000;Fc=40;
N=1000;
wc=80*pi;
n=0:N-2;
t=0.5/4:0.001:1.5/4;
Matlab程序:
Fm=10;Fc=100;Fs=1000;N=1000;
k=0:N-1;
t=k/Fs;
x=sin(2*pi*Fm*t);
subplot(3,1,1);
plot(t,x);
xlabel('t(s)');
title('Modulate signal');
y=modulate(x,Fc,Fs,'am');
grid on;legend('y(t)的时域波形');
subplot(4,1,4);plot([-128:127],fftshift(abs(z)));
y=x.*cos(wc*t);
z1=fft(x,256);
subplot(2,1,1);plot(t,x);legend('x(t)的时域波形');
subplot(2,1,2);plot([-128:127],fftshift(abs(z1)));legend('x(t)的频谱');
实验所得图形如下:
实验所得的图像如下图所示:
实验内容
1.实现抑制载波的幅度调制。已调信号 ,式中 为调制信号; 为载波信号。此处可取 , 。
(1)分析调制信号 的频谱,绘出其时域波形和频谱。
Matlab程序如下:
Fs=1000;
Fc=40;
N=1000;
wc=80*pi;
n=0:N-2;
t=n/Fs;
x=cos(10*pi*pi*t);
x=t;
z1=fft(x,256);subplot(4,1,1);plot(t,x);
grid on;legend('x(t)= t的时域波形');
subplot(4,1,2);plot([-128:127],fftshift(abs(z1)));
grid on;legend('x(t)= t时的频谱');
subplot(3,1,2);
plot(t,y);
xlabel('t(s)');
title('Modulateed signal(AM)');
y1=(1+0.5*x).*sin(100*pi*t);
subplot(3,1,3);
plot(t,y1);
xlabel('t(s)');
title('Modulateed signal');
plot(w1);
Y=fft(w1);
plot(w1);axis([0 500 -1 1]);
调制后的波形如下图:
解调:
[N,wc]=cheb1ord(0.2*pi,0.6*pi,1,25,'s');
[num,den]=cheby1(N,1,wc,'s');
[b,a]=bilinear(num,den,0.5);
实验图形如下图所示:
②Matlab程序为:
Fs=1000;
Fc=40;
N=1000;
wc=80*pi;
n=0:N-2;
t=0.5/4:0.001:1.5/4;
t0=0.5;
x=-t+t0/4;
z1=fft(x,256);subplot(4,1,1);plot(t,x);
grid on;legend('x(t)= -t+t0/4的时域波形');
(2)分析已调信号 的频谱,绘出其时域波形和频谱。
Matlab程序如下:
Fs=1000;
Fc=40;
N=1000;
n=0:N-2;
t=n/Fs;
x=cos(10*pi*pi*t);
y=modulate(x,Fc,Fs,'am');
z=fft(y,256);
subplot(2,1,1);plot(t,y);legend('y(t)的时域波形');
y=(1+0.8*x).*cos(100*pi*t);
z=fft(y,256);
subplot(4,1,3);plot(t,y);
grid on;legend('y(t)的时域波形');
subplot(4,1,4);plot([-128:127],fftshift(abs(z)));
grid on;legend('y(t)的频域波形');
subplot(4,1,2);plot([-128:127],fftshift(abs(z1)));
grid on;legend('x(t)= -t+t0/4时的频谱');
y=(1+0.8*x).*cos(100*pi*t);
z=fft(y,256);
subplot(4,1,3);plot(t,y);
subplot(2,1,2);plot([-128:127],fftshift(abs(z)));legend('y(t)的频域波形')
(3)设计低通滤波器并应用filter函数,实现信号同步解调
设计的低通滤波器为cheby1型低通滤波器,技术参数为:
wp=0.2*pi,ws=0.6*pi,Ap=1Db,As=25dB
x=cos(10*pi*pi*t);
y=x.*cos(80*pi*t);
w1=filter(b,a,y);
plot(w1);
Y=fft(w1);
Q=demod(Y,Fc,Fs,'am');
plot(t,Q);
axis([0.3 0.5 -0.1 0.1]);
解调后的波形如下图:
2.实现含有载波的幅度调制。已调信号 ,选取 ,观察调制结果,与抑制载波的幅度调制有什么不同?
例题3.1.1
Fm=10;Fc=100;Fs=500;
k=0:199;
t=k/Fs;
x=sin(2*pi*Fm*t);
y=x.*cos(2*pi*Fc*t);
Y=fft(y,256);
subplot(2,1,1);plot(y);
subplot(2,1,2);plot([-128:127],fftshift(abs(Y)));
