山东省历年联考考题汇总
山东卷考试题目及答案

山东卷考试题目及答案一、单项选择题(每题2分,共10题,共20分)1. 下列哪个选项是山东的省会城市?A. 青岛B. 济南C. 烟台D. 潍坊答案:B2. 山东省的简称是什么?A. 鲁B. 齐C. 燕D. 冀答案:A3. 下列哪个名胜古迹位于山东省?A. 故宫B. 泰山C. 长城D. 兵马俑答案:B4. 山东省的海岸线总长度是多少?A. 3000公里B. 2000公里C. 1500公里D. 1000公里答案:B5. 下列哪个节日是山东省的传统民俗节日?A. 春节B. 端午节C. 七夕节D. 潍坊风筝节答案:D6. 山东省的人口数量在全国范围内排名是多少?A. 第一B. 第二C. 第三D. 第四答案:B7. 下列哪个历史人物是山东人?A. 孔子B. 秦始皇C. 汉武帝D. 朱元璋答案:A8. 山东省的主要农作物是什么?A. 小麦B. 水稻C. 玉米D. 棉花答案:A9. 下列哪个城市是山东省的沿海城市?A. 淄博B. 临沂C. 潍坊D. 威海答案:D10. 山东省的省花是什么?A. 牡丹B. 玫瑰C. 菊花D. 荷花答案:A二、多项选择题(每题3分,共5题,共15分)11. 下列哪些是山东省的著名旅游景点?A. 泰山B. 趵突泉C. 蓬莱阁D. 青岛栈桥答案:ABCD12. 山东省有哪些著名的特色美食?A. 鲁菜B. 煎饼卷大葱C. 德州扒鸡D. 东阿阿胶答案:ABCD13. 下列哪些是山东省的主要经济产业?A. 农业B. 工业C. 旅游业D. 服务业答案:ABCD14. 山东省有哪些著名的高等院校?A. 山东大学B. 中国海洋大学C. 青岛大学D. 济南大学答案:ABCD15. 下列哪些是山东省的著名企业?A. 海尔集团B. 青岛啤酒C. 潍柴动力D. 浪潮集团答案:ABCD三、填空题(每题2分,共5题,共10分)16. 山东省位于中国_______部沿海、黄河下游,主要是指太行山以东,故称山东。
山东省考行测历年真题及答案

山东省考行测历年真题及答案(满分100分时间120分钟)第一部分常识判断1.从第四届中国国际消费品博览会组委会获悉,第四届消博会计划于4月13日至18日在()举办。
A.海口B.广州C.珠海D.东莞【答案】:A2.我国首次利用核电商用堆批量生产()同位素,实现供应全面国产化。
A.碳-16B.碳-12C.碳-15D.碳-14【答案】:D3.2024年3月18日市场监管总局等18部门联合印发《贯彻实施〈国家标准化发展纲要〉行动计划(2024—2025年)》,提出在()等关键领域集中攻关,加快研制一批重要技术标准,加大智能产品、功能性产品等新兴消费品标准供给。
A.人工智能、信息融合技术、北斗规模应用B.人工智能、智能网联汽车、北斗规模应用C.人工智能、信息融合技术、现代传感应用D.人工智能、自动控制汽车、现代传感应用【答案】:B4.水利部最新发布,2023年,国家水网主骨架和大动脉加快构建,省级水网先导区建设持续推进,市县级水网先导区接续启动,5处大型灌区开工建设,598处大中型灌区建设与现代化改造加快推进。
农村自来水普及率达到(),规模化供水工程覆盖农村人口比例达到()A.70%80%1/ 14B.60%90%C.90%60%D.80%70%【答案】:C5.2024年5月15日,我国最大规模液化天然气运输船建造项目——中国海油液化天然气运输船项目首制船()在上海交付。
A."国信1号"B."长赐"号C.海洋石油301D."绿能瀛"号【答案】:D6.下列关于古代书法艺术家的表述,正确的一项是:()A.明代著名的草书大家有张旭等B.唐代书法家颜真卿是楷书四大家之一C.宋代“苏,黄,米,蔡”中的“黄”指的是黄公望D.东汉著名书法家王羲之被称为“书圣”【答案】:B7.世界的真正统一性在于它的()A.物质性B.运动性C.存在性D.可知性【答案】:A8.(2017年考题)根据《关于加快推进生态文明建设的意见》,在环境保护和发展中处于优先位罝的是()。
2024济南联考试题及答案

2024济南联考试题及答案一、单项选择题(每题2分,共20分)1. 下列哪个选项是济南的著名景点?A. 故宫B. 泰山C. 大明湖D. 华山答案:C2. 济南因何得名?A. 因泉水众多B. 因地理位置C. 因历史人物D. 因气候特点答案:A3. 济南的市花是什么?A. 荷花B. 牡丹C. 玫瑰D. 菊花答案:A4. 济南的市树是什么?A. 柳树B. 松树C. 槐树D. 银杏5. 济南的著名小吃“煎饼卷大葱”中,煎饼的主要原料是什么?A. 面粉B. 玉米粉C. 米粉D. 豆粉答案:A6. 济南的著名泉水“趵突泉”位于哪个公园内?A. 大明湖公园B. 千佛山公园C. 趵突泉公园D. 五龙潭公园答案:C7. 济南的著名历史人物李清照是哪个朝代的?A. 唐朝B. 宋朝C. 元朝D. 明朝答案:B8. 济南的著名战役“济南战役”发生在哪一年?A. 1937年B. 1948年C. 1950年D. 1960年答案:B9. 济南的著名企业“济南重汽”主要生产什么?B. 摩托车C. 火车D. 飞机答案:A10. 济南的著名文化活动“济南国际泉水节”通常在每年的哪个月份举行?A. 3月B. 6月C. 9月D. 12月答案:C二、多项选择题(每题3分,共15分)11. 下列哪些是济南的著名泉水?A. 珍珠泉B. 黑虎泉C. 五龙潭D. 趵突泉答案:A、B、C、D12. 济南的著名历史遗迹包括哪些?A. 千佛山B. 灵岩寺C. 大明湖D. 济南战役纪念馆答案:A、B、D13. 济南的著名文化活动有哪些?A. 济南国际泉水节B. 济南国际啤酒节C. 济南国际马拉松D. 济南国际书展答案:A、B、C14. 济南的著名小吃还包括哪些?A. 油旋B. 糖火烧C. 九转大肠D. 糖醋鲤鱼答案:A、B、C、D15. 济南的著名企业除了“济南重汽”外,还包括哪些?A. 济南钢铁集团B. 济南轻骑集团C. 济南机床集团D. 济南制药集团答案:A、B、C、D三、填空题(每题2分,共10分)16. 济南因泉水众多而被誉为“泉城”,其中最著名的泉水是________。
山东名校联盟2024年高二下学期6月联考数学试卷+答案

高二质量监测联合调考数学注意事项:1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.4.本试卷主要考试内容:人教A 版选择性必修第二册第五章,选择性必修第三册,必修第一册第一、二章.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知随机变量X 服从正态分布()24,N σ,且()()P X a P X b = ,则a b +=()A.2B.4C.8D.162.已知集合{}220M xx x =<+∣,则M ∩Z 中元素的个数为()A.6B.7C.8D.93.已知曲线ln y x x =在x a =y x b =+,则b =()A.-2B.-1C.2D.14.已知函数()32123f x x x ax =+++,则“()f x 有极值”是“1a <”的( )A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知5对成对样本数据()()()()()1,2,3,3,5,6,7,9,9,10成线性关系,样本相关系数为1r ,去掉1对数据()5,6后,剩下的4对成对样本数据成线性关系,样本相关系数为2r ,则()A.12r r =B.12r r >C.12r r < D.12,r r 的大小无法确定6.某商场有,a b 两种抽奖活动,,a b 两种抽奖活动中奖的概率分别为23,55,每人只能参加其中一种抽奖活动.甲参加,a b 两种抽奖活动的概率分别为23,55,已知甲中奖,则甲参加a 抽奖活动中奖的概率为()A.925 B.425 C.913 D.4137.已知()f x ′是定义域为π0,2的函数()f x 的导函数,且()()sin cos 0f x x f x x +>′,则不等式π1πcos 226f x x f+>的解集为( )A.π,3∞−+B.ππ,23 −−C.π,06 −D.π,03 −8.在空间直角坐标系Oxyz 中,Oxy 平面、Oyz 平面、Ozx 平面把空间分成了八个部分.在空间直角坐标系Oxyz 中,确定若干个点,点的横坐标、纵坐标、竖坐标均取自集合{}2,5,9−,这样的点共有n 个,从这n个点中任选2个,则这2个点在同一个部分的概率为( ) A.50351 B.49351 C.17117 D.16117二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知()f x ′是定义域为[]4,6−的函数()f x 的导函数,()f x ′的图象如图所示,且()f x 有3个零点,则下列结论正确的是( )A.()f x 有2个极小值点B.()f x 有3个极大值点C.()20fD.()()4,6f f −可以同时小于010.在4张奖券中,一、二、三、四等奖各1张,将这4张奖券分给甲、乙、丙、丁四个人,每人至多2张,则下列结论正确的是( )A.若甲、乙、丙、丁均获奖,则共有24种不同的获奖情况B.若甲获得了一等奖和二等奖,则共有6种不同的获奖情况C.若仅有两人获奖,则共有36种不同的获奖情况D.若仅有三人获奖,则共有144种不同的获奖情况 11.已知正数,,a b c 成等差数列,且随机变量X 的分布列为X 1 2 3Pabc下列选项正确的是( )A.14b =B.23a c +=C.()4833E X <<D.()D X 的最大值为23三、填空题:本题共3小题,每小题5分,共15分.12.某图书馆有文化类图书300本,科学类图书400本,若甲从这两类图书中借阅1本,则不同的选法共有__________种.13.若0a b >>,且2a b −=,则1112a b++−的最小值为__________. 14.如图,一个质点在随机外力的作用下,从原点0出发,每次等可能地向左或向右移动一个单位长度,共移动8次,则质点经过-2且最终到达2的位置的概率为__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)某生产企业对原有的生产线进行技术升级,在技术升级前后,分别从其产品中随机抽取样本数据进行统计,制作了如下表格: 合格品 不合格品 合计 升级前 120 80 200 升级后 150 50 200 合计270130400(1)根据上表,依据小概率值0.005α=的2χ独立性检验,能否认为产品的合格率与技术是否升级有关?(2)在抽取的所有合格品中,按升级前后合格品的比例进行分层随机抽样,抽取9件产品,然后从这9件产品中随机抽取4件,记其中属于升级前生产的有X 件,属于升级后生产的有Y 件,求X Y >的概率.附:()()()()22()n ad bc a b c d a c b d χ−=++++,其中n a b c d =+++.α0.1 0.05 0.01 0.005 0.001 x α2.7063.8416.6357.87910.82816.(15分)某考试分为笔试和面试两个部分,每个部分的成绩分为,,A B C 三个等级,其中A 等级得3分、B 等级得2分、C 等级得1分.甲在笔试中获得A 等级、B 等级、C 等级的概率分别为221,,555,在面试中获得A 等级、B 等级、C 等级的概率分别为111,,236,甲笔试的结果和面试的结果相互独立.(1)求甲在笔试和面试中恰有一次获得A 等级的概率;(2)求甲笔试和面试的得分之和X 的分布列与期望. 17.(15分)设函数()f x 的导函数为()(),f x f x ′′的导函数为()(),f x f x ′′′′的导函数为()f x ′′′.若()00f x ′′=,且()00f x ′′′≠,则点()()00,x f x 为曲线()y f x =的拐点.(1)若函数()54116024f x x x =+,判断曲线()y f x =是否有拐点,并说明理由; (2)若函数()21e 2xg x a x ax =−−,且点()()0,0g 为曲线()y g x =的拐点,求()g x 在[1,2]−上的值域.18.(17分)(1)在9(2)x y z +−的展开式中,求形如()2,m nx y zm n ∈N 的所有项的系数之和.(2)证明:()933213311x x x x −+−−展开式中的常数项为918C −.(3x ,比较654321260160240190x x x x x x +++++与1的大小. 19.(17分)已知函数()2exf x ax −=−.(1)讨论()f x 的单调性;(2)当()0,x ∞∈+时,若()2ln f x x x x + 恒成立,求实数a 的最大值.高二质量监测联合调考数学参考答案1.C 由题意得248a b +=×=.2.C (){}4,5,3,2,1,0,1,2,3,4,M M M =−∴∩=−−−∴∩Z Z 中元素的个数为8.3.B 由题意得ln 1y x ′=+,则ln 11a +=,得1a =,所以ln11b =+,得1b =−.4.C ()22f x x x a =++′,若()f x 有极值,则440a −>,解得1a <,所以“()f x 有极值”是“a <1”的充要条件.5.A 由135792369105,655++++++++==,可知5对成对样本数据的样本中心为()5,6,去掉1对数据()5,6后,12r r =.6.D 用事件12,A A 分别表示甲参加,a b 两种抽奖活动,B 表示甲中奖,则()()()()12122323,,,5555P A P A P B A P B A ====∣∣,由全概率公式得()()()()()11221325P B P A P B A P A P B A =+⋅=∣∣,所以()()()()()()1111413P B A P A P A B P A B P B P B ===∣∣. 7.D 设函数()()sin g x f x x =,则()()()sin cos 0g x f x x f x x +′=>′,所以()g x 在π0,2上单调递增. 由π1πcos 226f x x f +>,得ππππsin sin 2266f x x f++>,所以ππ,26ππ0,22x x+> <+<得π03x −<<.8.B 由题意得3327n ==.从这n 个点中任选2个,共有227C 种选法.若这2个点在同一个部分,则这2个点的横坐标、纵坐标、坚坐标的正负均相同,所以八个部分中的点的个数为32,2222,2,2,2,2,2,1.故所求的概率为222842227C 3C 3C 49C 351++=. 9.AC 由图可知,当22,46x x −<<< 时,()0f x ′>,当42,24x x −<−<< 时,()f x ′<0,则()f x 在()(]2,2,4,6−上单调递增,在[)()4,2,2,4−−上单调递减,所以()f x 有2个极小值点,()f x有1个极大值点,A 正确,B 错误.当()20f <时,()()()()220,420f f f f −<<<<,则()f x 至多有2个零点,当()20f 时,()f x 才可能有3个零点,所以()20,C f 正确.当()()4,6f f −同时小于0时,()()()()()240,460,f f f f f x −<−<<<至多有2个零点,D 错误. 10.ACD 若甲、乙、丙、丁均获奖,则共有44A 24=种不同的获奖情况,A 正确.若甲获得了一等奖和二等奖,则其他三人有一人获得2个奖项或者有两人各获得1个奖项,共有1233A A 9+=种不同的获奖情况,B 错误. 若仅有两人获奖,则有两人各获得2个奖项,共有22242422C C A 36A =种不同的获奖情况,C 正确. 若仅有三人获奖,则有一人获得2个奖项,有两人各获得1个奖项,共有2113421422C C C A 144A =种不同的获奖情况,D 正确.11.BCD 由2,1,a c b a b c += ++= 得1,32,3b a c =+=A 错误,B 正确. 由23a c +=,得203c <<,则()448232,333E X a b c c =++=+∈ ,C 正确. ()22244141222323333D X a c c c c=−++−+×+−+2222112522233333c c c c c =−++−+− 228212443933c c c=−++=−−+ ,当13c =时,()D X 取得最大值,且最大值为2,3D 正确.12.700 不同的选法共有300400700+=种.13.45由题意得125a b ++−=,则()111111211412221251251255b a a b a b a b a b −+ +=+++−=+++ +−+−+−,当且仅当2112b a a b −+=+−,即31,22a b ==−时,等号成立.14.132质点从原点0出发,经过-2且最终到达2的位置,需移动8次,其中必然有3次向左,分为两类:第一类,当质点第2次移动到达-2的位置时,质点先向左移动了2次,在后续的6次移动中,只要向左移动1次即可,则所求的概率为25161113C 222128×××=; 第二类,当前3次移动未到达-2,且第4次移动到达-2时,质点前4次的移动顺序为01012,01012→→→−→−→−→→−→−,后续的4次移动中全部向右移动即可,则所求的概率为44111222128 ××=.故所求的概率为31112812832+=. 15.解:(1)零假设为0H :产品的合格率与技术是否升级无关.220.005400(1205015080)400107.87927013020020039x χ××−×==>>=×××,根据小概率值0.005α=的2χ独立性检验,推断0H 不成立,即认为产品的合格率与技术是否升级有关. (2)升级前后合格品的比例为4:5,故抽取的9件中有4件属于升级前生产的,有5件属于升级后生产的.当4,0X Y ==时,44149C 1C 126P ==, 当3,1X Y ==时,3145249C C C P ==, 则X Y >的概率1216P P P =+=. 16.解:(1)甲在笔试和面试中恰有一次获得A 等级的概率为21121115365522×+++×= . (2)由题意得X 的可能取值为2,3,4,5,6,()11125630P X ==×=,()211123565315P X ==×+×=,()2121113456535210P X ==×+×+×=,()21211553523P X ==×+×=,()1216255P X ==×=,则X 的分布列为所以()1231168234563015103515E X =×+×+×+×+×=. 17.解:(1)曲线()y f x =有拐点,理由如下:由题意得()()()433221111,,12632f x x x f x x x f x x x ′′=+=+=′′′+′,由()3211032f x x x ′+′==,得0x =或32−. 因为()3300,024f f ′ =−=≠ ′′′′′, 所以点33,22f−−为曲线()y f x =的拐点. (2)由题意得()()()e ,e 1,e xxxg x a x a g x a g x a =−−=′′′−=′′′, 由()010g a =−′=′,得1a =,且()010g ′=′≠′.()()e 1,e 1x x g x x g x ′′=−−=−′,当0x <时,()()0,g x g x <′′′单调递减,当0x >时,()()0,g x g x >′′′单调递增,则()()00g x g ′′= ,所以()g x 在[]1,2−上单调递增. 因为()()2111,2e 4e 2g g −=+=−,所以()g x 在[]1,2−上的值域为211,e 4e 2+−. 18.(1)解:()2,m nx y zm n ∈N 的项即7279C (2)x y z −展开式中的所有项, 令1x y z ===,得()2,m nx y zm n ∈N 的所有项的系数之和为7299C C 36−=−=−. (2)证明:因为323331(1)x x x x −+−−,所以()99933291113311(1)12x x x x x x x x −+−−=−−=+−9218921(1)x x x x x −+−=, 所以()933213311x x x x −+−−展开式中的常数项为918C −.(3)解:由23=<<2,2x +,所以6(2)65x +=,即061522433344255666666666C 2C 2C 2C 2C 2C 2C x x x x x x ++++++6543212601602401926465x x x x x x =++++++=,所以6543212601602401921x x x x x x +++++=,因为0x >,所以6543212601602401901x x x x x x +++++<.19.解:(1)()2e x f x a −=+′.当0a 时,()0f x ′>恒成立,所以()f x 在R 上单调递增. 当0a <时,()2exf x a −=+′,令()0f x ′>,则()2ln x a <−−,令()0f x ′<,则()2ln x a >−−, 所以()f x 在()(),2ln a ∞−−−上单调递增,在()()2ln ,a ∞−−+上单调递减.(2)由()2ln f x x x x + ,得22e ln x ax x x x −−+ ,即2e ln xa x x x−++ .令()2e ln x g x x x x −++,则()()()()()()2222221e 1e 1e 111x x x x x x x x x g x x x x −−−+−−+′−+++=++==.令()2exh x x −=−,因为()h x 在()0,∞+上单调递增,且()()20e ,21,h h =−= 所以()()020000,2,e0x x h x x −∃∈=−=,所以当()00,x x ∈时,()0g x ′<,当()0,x x ∞∈+时,()0g x ′>, 所以()g x 在()00,x 上单调递减,在()0,x ∞+上单调递增, 所以()02min 0000e ()ln x g x g x x x x −==++.因为020e0x x −−=,所以020e x x −=,所以00022min0002e ()lne 123ex x x g x x x x −−−=++=+−+=, 所以3a ,即a 的最大值为3.。
山东省百所名校2021届高三上学期12月联考数学试卷 Word版含解析

第二次质量监测联考数学一、选择题:本大题共8小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}2340A x x x =+->,{}12B x x =-<,则()RA B =( )A. {}11x x -<≤ B. {}13x x -<< C. {}13x x << D. {}11x x -<<【答案】A 【解析】 【分析】求出集合A 、B ,利用补集和交集的定义可求得集合()A B R.【详解】因为{}{23404A x x x x x =+->=<-或}1x >,所以{}41RA x x =-≤≤.因为{}{}{}1221213B x x x x x x =-<=-<-<=-<<, 因此,(){}R11A B x x ⋂=-<≤.故选:A.2. 已知复数z 满足((2)55i z i +=-,则z =( ) A. 33i - B. 13i -C. 13i +D. 33i +【答案】B 【解析】 【分析】 由条件可得552iz i-=+,根据复数的除法运算可得答案. 【详解】因为()255i z i +=-.所以()()()()()()552551213222i i i z i i i i i i ---===--=-++-. 故选:B3. 已知a ,b 都是实数,则“2211log log a b<”是“22a b >”的( ) A. 充要条件B. 必要不充分条件C. 充分不必要条件D. 既不充分也不必要条件【答案】C 【解析】 【分析】由由2211log log a b <,得110b a>>可推出22a b >,反之不成立,得出答案. 【详解】由2211log log a b <,得110b a>>,则0a b >>,从而22a b >,反之当22a b >时,取3,1a b =-=时,a 为负数,对数无意义,所以2211log log a b<不成立故“2211log <log a b”是“22a b >”的充分不必要条件.故选:C【点睛】结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断: (1)若p 是q 的必要不充分条件,则q 对应集合是p 对应集合的真子集; (2)p 是q 的充分不必要条件, 则p 对应集合是q 对应集合的真子集; (3)p 是q 的充分必要条件,则p 对应集合与q 对应集合相等;(4)p 是q 的既不充分又不必要条件, q 对的集合与p 对应集合互不包含. 4. 函数ln ||()e ex xx f x -=+的部分图象大致为( ) A. B. C.D.【答案】B 【解析】 【分析】先判断函数的奇偶性排除A 、C ,再通过特殊点排除D. 【详解】因为ln ln ()()x xx x x xf x f x e e e e----===++,所以f x ()是偶函数,所以f x ()的图象关于y 轴对称,排除A ,C ;因为10f=(),排除D . 故选:B.5. 点P 为抛物线2:2(0)C y px p =>的准线上一点,直线2x p =交抛物线C 于M ,N 两点,若PMN 的面积为20,则p =( )A. 1B.C. 2D.【答案】C 【解析】 【分析】求得,M N 两点的坐标,根据PMN 的面积列方程,解方程求得p 的值.【详解】由题意不妨设2222M p p N p p -(,),(,),则PMN 的面积为1542022pp ⨯⨯=,解得2p =. 故选:C 6. 已知1sin ,123πθ⎛⎫-= ⎪⎝⎭则sin 23πθ⎛⎫+= ⎪⎝⎭( ) A. 29-B.29C. 79-D. 7 9【答案】D 【解析】 【分析】 设12παθ=-,则1,sin 123πθαα=+=,则sin 2sin 32]23[1πππθα⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭化简,由余弦的二倍角公式可得答案. 【详解】设12παθ=-,则1,sin 123πθαα=+=, 从而2[]7sin 2sin 2sin 2cos 212sin 312329ππππθαααα⎛⎫⎛⎫⎛⎫+=++=+==-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 故选:D【点睛】关键点睛:本题考查三角函数中知值求值的问题,解答本题的关键是设12παθ=-,然后可得sin 2sin 32]23[1πππθα⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭,属于中档题. 7. 已知点P 是边长为2的菱形ABCD 内的一点(包含边界),且120BAD ∠=︒,AP AB ⋅的取值范围是( ) A. [2,4]- B. (2,4)-C. [2,2]-D. (2,2)-【答案】A 【解析】 【分析】如图建系,可求得A,B,C,D 的坐标,设(,)P x y ,则可得AP AB ⋅的表达式,根据x 的范围,即可求得答案.【详解】如图,建立平面直角坐标系,则(00)(20)(13)(13)A B C D -,,,,,,,.设(,)P x y ,则12x -≤≤,故(,)(2[24]20)AP AB x y x ⋅=⋅=∈-,,,即AP AB ⋅的取值范围是[24]-,. 故选:A8. 已知正方体1111ABCD A B C D -的棱长为2,以A 为球心,21111D C B A 的交线长为( )A.2πB.22π C.2πD. π【答案】D 【解析】【分析】根据题意求出交线所在圆弧的圆心和半径,进而求得结论. 【详解】由题意知22112222AB AD ==+=.如图,在平面1111D C B A 内任取一点P ,使12A P =, 则221122AP AA A P =+=故以A 为球心,221111D C B A 的交线是以1A 为圆心,以2为半径的圆弧11B PD ,故该交线长为22ππ⨯=.故选:D.二、选择题:本大题共4小题,在每小题给出的选项中,有多项符合题目要求.9. 已知向量(1,3),(2,1),(3,5),a b c ==-=-则( ) A. (2)//a b c + B. (2)a b c +⊥ C. ||1034a c +=+ D. ||2||a c b +=【答案】AD 【解析】 【分析】利用向量的坐标运算公式直接求解.【详解】由题意可得23542a b a c +=-+=-(,),(,).因为2a b c +=-,所以2//a b c +(),则A 正确,B 错误; 对于C ,D,因为2242a c b +=+==-=(()2a c b +=,则C 错误,D 正确. 故选:AD.10. 已知实数x ,y 满足322,124,x y x y -<+<-<-<则( ) A. x 的取值范围为(1,2)- B. y 的取值范围为(2,1)- C. x y+的取值范围为()3,3-D. x y -的取值范围为(1,3)-【答案】ABD 【解析】 【分析】利用不等式的性质直接求解.【详解】因为124x y -<-<,所以2428x y -<-<.因为322x y -<+<,所以5510x -<<,则12x -<<,故A 正确;因为322x y -<+<,所以6244x y -<+<.因为124x y -<-<,所以421x y -<-+<,所以1055y -<<,所以21y -<<,故B 正确;因为322124x y x y -<+<-<-<,,所以9361142,2555555x y x y -<+<-<-<()(),则22x y -<+<,故C 错误;因为322124x y x y -<+<-<-<,,所以213331222555555x y x y -<-+<-<-<(),(),则13x y -<-<,故D 正确. 故选:ABD.11. 已知函数()2sin()||2,fx x πωϕωϕ+⎛⎫=+∈<⎪⎝⎭N 的图象经过点A ,且()f x 在[0,2]π上有且仅有4个零点,则下列结论正确的是( )A. 2ω=B. 6πϕ=C. ()f x 在,03π⎛-⎫⎪⎝⎭上单调递增 D. ()f x 在(0,2)π上有3个极小值点【答案】AC 【解析】 【分析】先根据函数图象过点(A 得3πϕ=,再根据函数在[0,2]π上有且仅有4个零点得11763ω≤<,进而得2ω=,故()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,再讨论CD 选项即可得答案.【详解】解:因为点(A 在()f x 的图象上,所以2sin ϕ=,所以sin 2ϕ=. 因为2πϕ<,所以3πϕ=,则()()2sin 3f x x N πωω+⎛⎫=+∈ ⎪⎝⎭. 由02x π≤≤,得2333x πππωπω≤+≤+.因为()f x 在[0,2]π上有且仅有4个零点, 所以4253πππωπ≤+<,所以11763ω≤<. 因为N ω+∈,所以2ω=,则()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,故A 正确,B 错误. 令222232k x k k Z πππππ-≤+≤+∈(),解得51212k x k k Z ππππ-≤≤+∈(), 当0k =时,51212x ππ-≤≤.因为5,0,31212πππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭, 所以()f x 在,03π⎛-⎫⎪⎝⎭上单调递增,故C 正确. 由()f x 的图象易知()f x 在()0,2π上有2个极小值点,故D 错误.故选:AC【点睛】本题解题的关键在于根据整体换元思想,由函数()f x 在[0,2]π上有且仅有4个零点进而得4253πππωπ≤+<,进一步得2ω=,则()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,再根据函数解析式求解即可,是中档题.12. 经研究发现:任意一个三次多项式函数32()(0)f x ax bx cx d a =+++≠的图象都只有一个对称中心点()()00,x f x ,其中0x 是()0f x ''=的根,()'f x 是()f x 的导数,()f x ''是()'f x 的导数.若函数32()f x x ax x b =+++图象的对称点为(1,2)-,且不等式(ln 1)x e e mx x -+32()3ef x x x e x ⎡⎤≥--+⎣⎦对任意(1,)x ∈+∞恒成立,则( )A. 3a =B. 1b =C. m 的值可能是e -D. m 的值可能是1e- 【答案】ABC 【解析】 【分析】求导得()62f x x a ''=+,故由题意得()1620f a ''=-+=-,()1112f a b -=-+-+=,即3,1a b ==,故()3231f x x x x =+++.进而将问题转化为()1ln 1e x x e x e m x --++<+,由于1x e x >+,故ln ln 1e e xx xx e ex e x --+=≥-+,进而得()1ln ln 1ln 1e x x e x e e x ee x x --++--≥=-++,即m e ≤-,进而得ABC 满足条件.【详解】由题意可得()1112f a b -=-+-+=, 因为()2321x ax f x =++',所以()62f x x a ''=+,所以()1620f a ''=-+=-,解得3,1a b ==,故()3231f x x x x =+++.因为1x >,所以()()32ln []13xeee mx xf x x x e x -+≥--+等价于()1ln 1e x x e x e m x --++≤+. 设()()10xg x e x x =-->,则()10xg x e '=->,从而()g x 在()0,∞+上单调递增.因为()00g =,所以()0g x >,即1x e x >+, 则ln ln 1ee x xxx e e x e x --+=≥-+(当且仅当x e =时,等号成立), 从而()1ln ln 1ln 1e x x e x e e x ee x x --++--≥=-++,故m e ≤-.故选:ABC.【点睛】本题解题的关键在于根据题意得()3231f x x x x =+++,进而将不等式恒成立问题转化为()1ln 1e x x e x e m x --++≤+恒成立问题,再结合1x e x >+得ln ln 1ee x xxx e e x e x --+=≥-+,进而得m e ≤-.考查运算求解能力与化归转化思想,是难题.三、填空题:本大题共4小题.13. 在等差数列{}n a 中,1242,8a a a =+=-,则数列{}n a 的公差为_________. 【答案】3- 【解析】 【分析】设数列{}n a 的公差为d .,根据等差数列下标和性质得到3a ,再根据n ma a d n m-=-计算可得;【详解】解:设数列{}n a 的公差为d .因为248a a +=-,所以34a =-,则31423312a a d ---===--. 故答案为:3-14. 将一个斜边长为4的等腰直角三角形以其一直角边所在直线为旋转轴旋转一周,所得几何体的表面积为_________.【答案】(8π+ 【解析】 【分析】先求出等腰直角三角形的直角边长,进而求出旋转体圆锥的底面半径和母线,再利用圆锥的表面积公式即可求出结果.【详解】因为等腰直角三角形的斜边长为4,所以直角边长为,由题意可知所得几何体是圆锥,其底面圆的半径r =4l ,则其表面积为(28r rl πππ+=+.故答案为:(8π+.【点睛】关键点点睛:该题考查的是有关圆锥的表面积的问题,正确解题的关键点是: (1)要确定旋转后所得到的几何体是圆锥;(2)要明确圆锥的各个量:底面圆的半径以及母线长; (3)要熟练掌握圆锥的表面积公式.15. 已知双曲线2218:8x y C -=的左焦点为F ,点M 在双曲线C 的右支上,(0,4)A ,当MAF △的周长最小时,MAF △的面积为_________.【答案】12 【解析】 【分析】MAF △的周长为MA MF AF ++,其中AF =为定值,所以即求MA MF +,利用定义可得MF MF '=+,所以周长为MA MF '++A F M 、、三点共线时周长最短,利用面积分割求得面积.【详解】如图,设双曲线C 的右焦点为F '.由题意可得22,4040a F F '=-(,),(,). 因为点M 在右支上,所以242MFMF a '-==,所以42MF MF '=+,则MAF △的周长为8282122MA MF AF MA MF AF ''++=++≥+=,即当M 在M '处时,MAF △的周长最小,此时直线AF '的方程为4y x =-+.联立224188y x x y =-+⎧⎪⎨-=⎪⎩,整理得10y -=,则1M y '=,故MAF △的面积为111'84112222M FF OA FF y ''-=⨯⨯-=(). 故答案为:12【点睛】本题考查双曲线数形结合求最值以及求三角形的面积,属于基础题.方法点睛:(1)双曲线求最值常用定义的方法,把到一个焦点的距离转化为到另一个焦点的距离.(2)圆锥曲线中求三角形的面积经常采用面积分割的方法.16. 已知函数2()1f x x x =--,若关于x 的方程()|1|f x a x =+恰有两个实数根,则实数a 的取值范围是_________. 【答案】{}(1,5)0⋃ 【解析】 【分析】根据题意,能判断出1x =-不是方程的实数根,从而得到1(1)31a x x =++-+,将方程有两个根转化为y a =与1(1)31y x x =++-+的图象恰有两个不同的交点,画出函数图象,观察图象得到结果【详解】由题意可得211x x a x --=+,显然1x =-不是方程的实数根, 则211(1)311x x a x x x --==++-++, 故关于x 的方程()1f x a x =+恰有两个实数根, 等价于y a =与1(1)31y x x =++-+的图象恰有两个不同的交点.画出1(1)31y x x =++-+的大致图象,如图所示,由图象可得(){}1,50a ∈⋃. 故答案为:{}(1,5)0⋃.【点睛】方法点睛:该题考查的是有关根据方程根的个数求参数的取值范围的问题,解题方法如下:(1)观察式子,对其变形;(2)将方程的根的个数转化为图象交点个数来完成; (3)画函数图象,得到结果.四、解答题:本大题共6小题,解答应写出文字说明、证明过程或演算步骤.17. 在ABC 中,角, , A B C 所对的边分别为,,a b c .已知3B π=.(1)若4,3a c ==,求sin A 的值(2)若ABC的面积为ABC 周长的最小值.【答案】(1)13(2)12 【解析】 【分析】(1)由余弦定理得b =sin A =(2)由题知16ac =,进而由余弦定理得222b a c ac =+-,再结合基本不等式得4b ≥,由于()223464a c b ac ac +=+≥=,进而得8a c +≥,故12a b c ++≥,当且仅当a c =是等号成立,进而得周长的最小值.【详解】解:(1)由余弦定理可得22212cos 169243132b ac ac B =+-=+-⨯⨯⨯=,则b =由正弦定理可得sin sin a b A B=,则4sin sin 13a B A b ===. (2)因为ABC的面积为1sin 2ac B ==,则16ac =. 由余弦定理可得222222cos b a c ac B a c ac =+-=+-, 则216b ac ≥=(当且仅当a c =时,等号成立),即4b ≥.因为()22223b a c ac a c ac =+-=+-,所以()223464a c b ac ac +=+≥=,所以8a c +≥(当且仅当a c =时,等号成立), 故12a b c ++≥,即ABC 周长的最小值为12.【点睛】本题第二问解题的关键在于根据余弦定理,结合基本不等式得22216b a c ac ac =+-≥=,()223464a c b ac ac +=+≥=,当且仅当a c =时,等号成立,进而求得答案.18. 在①1120(2)n n n a a a n +--+=≥且151,25a S ==,②235,n a S n tn ==+,③121,3a a ==,且122,,n n n S S S ++-成等差数列这三个条件中任选一个,补充在下面问题中,并作答.问题:设数列{}n a 的前n 项和为n S ,_________.若11n n n b a a +=,求数列{}n b 的前n 项和为n T . 【答案】选择见解析;21nn +. 【解析】 【分析】若选①,由1120n n n a a a +--+=得数列{}n a 是等差数列,进而得21n a n =-,11122121n b n n ⎛⎫=- ⎪-+⎝⎭,再根据裂项相消求和法求和即可;若选②,由33255a S S t =-=+=得0t =,进而根据,n n a S 之间的关系得21n a n =-,再根据裂项相消求和法求和即可;若选③,由122n n n S S S ++-,,成等差数列,得212n n a a ++-=.由于121,3a a ==,故数列{}n a 是首项为1,公差为2的等差数列,故21n a n =-,再根据裂项相消求和法求和即可. 【详解】解:若选①,因为1120n n n a a a +--+=,所以11n n n n a a a a +--=-,即数列{}n a 是等差数列因为15125a S ==,,所以1511545252a S a d =⎧⎪⎨⨯=+=⎪⎩. 解得112a d ==,, 故()1121n a a n d n =+-=-. 因为11n n n b a a +=,所以()()1111212122121n b n n n n ⎛⎫==- ⎪-+-+⎝⎭.则1231111111123355721211n n T b b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫=++++=-+-+-++- ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎛⎫ ⎝⎭⎝⎭⎣⎦⎪⎝⎭11122121n n n ⎛⎫=-=⎪++⎝⎭ 若选②,因为2n S n tn =+,所以223233392224S t t S t t =+=+=+=+,,所以33255a S S t =-=+=,解得0t =, 则()()2211212n n n a S S n n n n -=-=--=-≥. 因为111a S ==满足上式,所以21n a n =-. 因为11n n n b a a +=,所以()()1111212122121n b n n n n ⎛⎫==- ⎪-+-+⎝⎭. 则1231111111123355721211n n T b b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫=++++=-+-+-++- ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎛⎫ ⎝⎭⎝⎭⎣⎦⎪⎝⎭ 11122121n n n ⎛⎫=-= ⎪++⎝⎭ 若选③,因为122n n n S S S ++-,,成等差数列,所以1222n n n S S S ++=-+, 所以()2112n n n n S S S S +++---=,即212n n a a ++-=.因为121,3a a ==,所以212a a -=,则数列{}n a 是首项为1,公差为2的等差数列, 故()1121n a a n d n =+-=-. 因11n n n b a a +=,所以()()1111212122121n b n n n n ⎛⎫==- ⎪-+-+⎝⎭.则1231111111123355721211n n T b b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫=++++=-+-+-++- ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎛⎫ ⎝⎭⎝⎭⎣⎦⎪⎝⎭ 11122121nn n ⎛⎫=-=⎪++⎝⎭. 【点睛】本题解题的关键在于根据递推关系(等差中项,,n n a S 之间的关系等)证明数列{}n a 是首项为1,公差为2的等差数列,进而得21n a n =-.考查运算求解能力,是中档题. 19. 如图,在三棱柱ABC —A 1B 1C 1中,B 1C 1⊥平面AA 1C 1C ,D 是AA 1的中点,ACD ∆是边长为1的等边三角形.(1)求证:CD ⊥B 1D ;(2)若BC 3B —C 1D —B 1的大小. 【答案】(1)证明见解析;(2)6π【解析】 【分析】(1)根据计算,利用勾股定理逆定理得1CD DC ⊥;根据B 1C 1⊥平面AA 1C 1C ,得11CD B C ⊥,最后根据线面垂直判断定理以及性质定理证明结果;(2)建立空间直角坐标系,利用空间向量数量积求二面角大小. 【详解】(1)因为ACD 是边长为1的等边三角形, 所以11111121,1,33CD A D AC DAC C D π===∠=∴=22211112CC CC C D CD CD DC =∴=+∴⊥因为B 1C 1⊥平面AA 1C 1C ,CD ⊂平面AA 1C 1C ,所以11CD B C ⊥ 因为111,DC B C 为平面B 1C 1D 内两相交直线,所以CD ⊥平面B 1C 1D 因为1B D ⊂平面B 1C 1D ,所以CD ⊥B 1D ;(2)以D 为坐标原点,1,,DC DC 过D 平行BC 直线为,,x y z 轴建立如图所示空间直角坐标系,则11(0,0,0),(3,0,0),(3,0,3),(0,13),D C B B设平面BC 1D 的一个法向量为1(,,)n x y z =,平面C 1DB 1的一个法向量为2111(,,)n x y z =由11100n DC n DB ⎧⋅=⎪⎨⋅=⎪⎩得300,30x x y z ⎧=⎪∴=⎨+=⎪⎩令1,3z y =∴=-∴1(0,3,1)n =- 由212100n DC n DB ⎧⋅=⎪⎨⋅=⎪⎩得300,330x x z x z ⎧=⎪∴==⎨+=⎪⎩令1,y =∴2(0,1,0)n = 12121212335cos ,,2126||||n n n n n n n n π⋅-∴<>===-∴<>=⨯因为二面角B —C 1D —B 1为锐二面角,所以二面角B —C 1D —B 1为6π【点睛】本题考查线面垂直判定与性质定理、利用空间向量求二面角,考查综合分析论证与求解能力,属中档题.20. 已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=+>><<的部分图象如图所示.(1)求()f x 的解析式 (2)设()()23216g x f x x π⎛⎫=+-+⎪⎝⎭若关于x 的不等式2()(32)()230g x m g x m -+--≤恒成立,求m 的取值范围.【答案】(1)()2cos(2)3f x x π=+;(2)[11]2-,. 【解析】【分析】(1)由图求出A 、T 、ω和ϕ的值,即可写出()f x 的解析式;(2)由(1)可得()g x 的解析式,设()t g x =,问题等价于()0h t 在[3-,5]上恒成立,列出不等式组求出m 的取值范围. 【详解】解:(1)由图可知2A =,35346124T πππ=-=, 解得T π=,所以22Tπω==,所以()2cos(2)f x x ϕ=+; 因为()f x 的图象过点5(6π,2),所以52cos(2)26πϕ⨯+=,解得523k πϕπ=-,k Z ∈;因为0ϕπ<<,所以3πϕ=,所以()2cos(2)3f x x π=+;(2)由(1)可得()2cos(2)2)136g x x x ππ=++-+2cos(2))133x x ππ=++++4sin(2)136x ππ=+++ 4cos21x =+;设()t g x =,因为1cos21x -,所以3()5g x -; 又因为不等式2()(32)()230g x m g x m -+--恒成立, 即2()(32)230h t t m t m =-+--在[3-,5]上恒成立,则(3)0(5)0h h -⎧⎨⎩,即93(32)230255(32)230m m m m ++--⎧⎨-+--⎩,解得112m -, 所以m 的取值范围是1,12⎡⎤-⎢⎥⎣⎦.【点睛】本题考查了三角函数的图象与性质的应用问题,也考查了不等式恒成立问题,已知f (x )=Asin (ωx +φ)(A >0,ω>0)的部分图象求其解析式时,A 比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:(1)由ω=2Tπ即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x0,则令ωx0+φ=0(或ωx0+φ=π),即可求出φ.(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.21. 已知12,F F分别是椭圆2222:1(0)x yC a ba b+=>>的左,右焦点,过点1F的直线l与椭圆C 交于A,B两点,点(2,1)M在椭圆C上,且当直线l垂直于x轴时,||2AB=.(1)求椭圆C的标准方程;(2)是否存在实数t,使得1111AF BF t AF BF+=恒成立.若存在,求出t的值;若不存在,说明理由【答案】(1)22142x y+=;(2)存在;2t=.【解析】【分析】(1)根据题意得到关于,a b的方程组,求解出22,a b的值,则椭圆方程可求;(2)根据条件可得1111AF BFtAF BF+=,当直线l的斜率不存在时,直接计算即可;当直线l的斜率存在时,设2:l y k x,联立直线l与椭圆方程,根据韦达定理形式表示出t,由此确定出是否存在t满足条件.【详解】解:(1)由题意可得22222211b AB a ab ⎧==⎪⎪⎨⎪+=⎪⎩, 解得224,2a b ==.故椭圆C 的标准方程为22142x y +=.(2)由(1)可知())12F F ,.当直线l 的斜率不存在时,2111b AF BF a===,则11112AF BF t AF BF +==. 当直线l 的斜率存在时,设其斜率为k ,则直线l的方程为(()()1122,,,,y k x A x y B x y =.联立(22142y k x x y ⎧=⎪⎨⎪+=⎩,整理得()222221440k x x k +++-=,则2212122244,2121k x x x x k k +=--=++,从而12221x x k -==+故2111224421k AF BF AB x x k ++==-=+由题意可得1112AF BF ==.则())()221112122211221k AF BF k x x x x k +=++++=+.因为1111AF BF t AF BF +=,所以()22112112442122121k AF BF k t AF BF k k +++===++. 综上,存在实数2t =,使得1111AF BF t AF BF +=恒成立.【点睛】易错点睛:利用直线与圆锥曲线联立求解相关问题的易错点: (1)假设直线方程的时候,要注意分析直线的斜率是否存在;(2)12x x -12y y -不仅可以求解弦长,同时还可以求解两点之间的距离.22. 已知函数121()(1)e (0)2x f x x a x ax x -=---+>. (1)讨论()f x 的单调性.(2)当2a ≤时,若()f x 无最小值,求实数a 的取值范围. 【答案】(1)当0a ≤时,()f x 在0,1上单调递减,在1,上单调递增; 当01a <<时,()f x 在(),1a 上单调递减,在()0,a 和1,上单调递增;当1a =时,()f x 在0,上单调递增;当1a >时,()f x 在()1,a 上单调递减,在(0,1),(,)a +∞上单调递增.(2)1,22e ⎛⎤-⎥⎝⎦. 【解析】 【分析】(1)对()f x 求导,然后对a 分类讨论分别得出f x 所对应的x 的取值范围即为函数的单调增区间,fx 所对应的x 的取值范围即为函数的单调减区间.(2)结合(1)中的单调性结论对函数的最小值进行讨论.对于第四种情况,得出关于a 的不等式后,需要构造新的函数分析求解. 【详解】解:(1)因为121()(1)e (0)2x f x x a x ax x -=---+>,所以()1()(1)(0)x f x x a e x -'=-->. 令0fx ,得x a =或1x =.①当0a ≤时,由0fx,得1x >;由0fx,得01x <<.则()f x 在0,1上单调递减,在1,上单调递增;②当01a <<时,由0fx,得0x a <<或1x >;由0fx ,得1<<a x .则()f x 在(),1a 上单调递减,在()0,a 和1,上单调递增.③当1a =时,0f x 恒成立,则()f x 在0,上单调递增.④当1a >时,由0fx,得01x <<或x a >;由0f x ,得1x a <<.则()f x 在()1,a 上单调递减,在(0,1)和(,)a +∞上单调递增. 综上,当0a ≤时,()f x 在0,1上单调递减,在1,上单调递增;当01a <<时,()f x 在(),1a 上单调递减,在()0,a 和1,上单调递增;当1a =时,()f x 在0,上单调递增;当1a >时,()f x ()1,a 上单调递减,在(0,1)和(,)a +∞上单调递增.(2)①当0a ≤时,由(1)可知()f x 在0,1上单调递减,在1,上单调递增,则()f x 有最小值()112f =-,故0a ≤不符合题意.②当01a <<时,由(1)可知()f x 在(),1a 上单调递减,在()0,a 和1,上单调递增,因为()f x 无最小值,所以()()01f f <,即11<2a e +--,解得112ea -<<; ③当1a =时,由(1)可知()f x 在0,上单调递增,所以()f x 无最小值,所以1a =符合题意;④当12a <≤时,由(1)可知()f x 在()1,a 上单调递减,在()()0,1,,a +∞上单调递增.因为()f x 无最小值,所以()()0f f a <,即2111<2a a a e e -+--,即121102a a e a e-+--<. 设()()1211122x x g x e x x e -+=--<≤,则()()1112x g x e x x e-'=--<≤设()()()1112x h x g x e x x e-'==--<≤,则()110x h x e -'=->在(]1,2上恒成立.故()h x 在(]1,2上单调递增,即()g x '在(]1,2上单调递增. 因为()()1110,220g g e e e''=-<=-->,所以存在唯一的(]01,2x ∈,使得()00g x '=. 故()g x 在()01,x 上单调递减,在(]0,2x 上单调递增.因为()()124310,22022e g g e e e e -=--=<=--<,所以()0g x <在(]1,2上恒成立, 即1211<02a a e a e-+--在(]1,2恒成立,即12a <≤符合题意.综上,实数a 的取值范围为1,22e ⎛⎤- ⎥⎝⎦.【点睛】本题主要考查分类讨论思想,首先利用函数求导公式对函数求导,然后再利用导函数大于0或者小于0讨论函数单调性,分类时一般利用f x 有无解对参数进行分类.常见注意点如下:(1)对二次项系数的符号进行讨论; (2)导函数是否有零点进行讨论; (3)导函数中零点的大小进行讨论;(4)导函数的零点与定义域端点值的关系进行讨论等.。
2023-2024学年山东省日照市校际联考高二(上)期末数学试卷【答案版】

2023-2024学年山东省日照市校际联考高二(上)期末数学试卷一、单项选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数z 满足z (1+i )=1+3i (其中i 是虚数单位),则z =( ) A .2﹣iB .2+iC .﹣2﹣iD .﹣2+i2.已知直线l 的方程为y =x +1,则直线l 的倾斜角为( ) A .30°B .45°C .60°D .135°3.若随机变量ξ∼N (3,σ2),且P (ξ<6)=0.86,则P (3<ξ<6)=( ) A .0.26B .0.34C .0.36D .0.424.若两圆C 1:x 2+y 2+2x =0与C 2:x 2+y 2﹣4x ﹣8y +m =0外离,则实数m 的取值范围为( ) A .m >4B .m <4C .0<m <4D .4<m <205.今年8月份贵州村篮球总决赛期间,在某场比赛的三个地点需要志愿者服务,现有甲、乙、丙、丁四人报名参加,每个地点仅需1名志愿者,每人至多在一个地点服务,若甲不能到第一个地点服务,则不同的安排方法共有( ) A .18B .24C .32D .646.抛物线有一条重要的性质:平行于抛物线的轴的光线,经过抛物线上的一点反射后经过它的焦点.反之,从焦点发出的光线,经过抛物线上的一点反射后,反射光线平行于抛物线的轴.已知抛物线y 2=8x ,从点A (4,y 1)发出一条平行于x 轴的光线,经过抛物线两次反射后,穿过点B (4,y 2),则光线从A 出发到达B 所走过的路程为( ) A .8B .10C .12D .147.在棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中,F 为线段BC 1的中点,则点F 到平面ACD 1的距离为( ) A .√33B .12C .√22 D .18.已知实数x 、y 满足x|x|4+y|y|=1,则|x +2y +2|的取值范围是( )A .(1,√5+√10]B .(2,2+2√2]C .[2,2√2+√5]D .[2√55,2√105+1]二、多项选择题:本大题共4小题,每小题5分,共20分。
2023年山东省美术联考考题及答案

2023年山东省美术联考考题及答案选择题:1. 下列中哪一种颜色不属于三原色?A. 红色B. 绿色C. 黄色D. 蓝色答案:C2. 《清明上河图》的作者是谁?A. 张择端B. 郎世宁C. 吴道子D. 韩干答案:A3. 唐代画家张择端擅长画什么类型的画?A. 山水画B. 花鸟画C. 人物画D. 风俗画答案:D4. 布鲁克林博物馆的藏品中,下列哪一幅画是文化大革命时期的革命画?A. 《罢工潮》B. 《百花齐放》C. 《插队》D. 《大家看动物》答案:D5. 塔利斯·巴特勒是哪个时期的现代艺术家?A. 前现代主义B. 抽象表现主义C. 极简主义D. 波普艺术答案:B填空题:1. 画面上的立体感是由三种画法构成,分别是线描、点描、________。
答案:色彩2. “线是字体,墨是脂肪”这个名言是哪位画家说的?答案:顾恺之3. 唐代诗人王维所画的《鸟还□□,人归□□》两处空缺分别填什么?答案:林、寂寞4. 宋代画家文同曾创作名画《梅犂图》,这幅画描述的是农民在春耕农忙之际休息玩耍的情景,请问这幅画属于什么类型的画?答案:人物画5. 物色画家弗洛伊德·艾伯特的画作《共享便便》是哪种艺术流派的代表作?答案:当代装置艺术判断题:1. 绝色美女是古代中国绘画中一种常见的题材。
答案:正确2. 顾恺之所画的《女史箴图》著名于古代毛笔字。
答案:错误3. 日本浮世绘画是指十六世纪到十九世纪的一种绘画风格。
答案:正确4. 雕塑是将一个具体的物体通过调整材质表面的几何形状而创造出来的。
答案:错误5. 克劳德·莫奈是印象派画家之一,也是首个画出《莲塘香魂》的人。
答案:错误简答题:1. 画家何君墨的作品风格特点是什么?答案:传统水墨画与现代抽象艺术相结合。
2. 五朵金花是中国画史上著名的五个女画家,她们分别是谁?答案:齐白石、潘天寿、张大千、黄宾虹、林风眠。
3. 著名画家范曾思考艺术的本质,提出四个问题,这四个问题是什么?答案:线条的生命力、对比的协调、留白的玄妙、意境的深远。
山东省高三联考试题及答案解析

山东省高三联考试题及答案解析一、单项选择题(每题3分,共30分)1. 下列关于细胞结构的描述中,不正确的是:A. 细胞膜具有选择透过性B. 线粒体是细胞的能量工厂C. 核糖体是蛋白质合成的场所D. 细胞核是细胞内储存遗传物质的唯一场所答案:D2. 光合作用中,光反应和暗反应的联系是:A. 光反应为暗反应提供ATP和[H]B. 暗反应为光反应提供ADP和PiC. 光反应和暗反应相互独立D. 光反应和暗反应在细胞质中同时进行答案:A3. 下列关于遗传信息传递的描述,错误的是:A. DNA复制是半保留复制B. 转录过程中需要RNA聚合酶C. 翻译过程中mRNA上的三个连续碱基决定一个氨基酸D. 遗传密码是通用的答案:C4. 下列关于生态系统的描述,正确的是:A. 生态系统中只有生产者和消费者B. 能量流动是单向的,逐级递减的C. 生物圈是最大的生态系统D. 物质循环是无限制的答案:C5. 下列关于基因突变的描述,正确的是:A. 基因突变是可逆的B. 基因突变一定导致生物性状的改变C. 基因突变是生物进化的原材料D. 基因突变只发生在生殖细胞中答案:C6. 下列关于酶活性的描述,错误的是:A. 酶的活性受温度影响B. 酶的活性受pH值影响C. 酶的活性受底物浓度影响D. 酶的活性不受酶浓度的影响答案:D7. 下列关于细胞周期的描述,错误的是:A. 细胞周期包括间期和有丝分裂期B. 间期是细胞周期中最长的阶段C. 有丝分裂期包括前期、中期、后期和末期D. 细胞周期的长短与细胞类型有关答案:A8. 下列关于减数分裂的描述,正确的是:A. 减数分裂只发生在生殖细胞中B. 减数分裂过程中染色体数目减半C. 减数分裂过程中同源染色体不配对D. 减数分裂过程中没有DNA复制答案:B9. 下列关于基因重组的描述,错误的是:A. 基因重组发生在减数分裂过程中B. 基因重组可以产生新的基因型C. 基因重组是生物进化的重要机制D. 基因重组只发生在有性生殖中答案:D10. 下列关于自然选择的描述,正确的是:A. 自然选择是生物进化的唯一驱动力B. 自然选择是适者生存的过程C. 自然选择可以导致物种灭绝D. 自然选择只能发生在生物种群内部答案:B二、非选择题(每题20分,共70分)11. 描述DNA复制的过程,并解释其生物学意义。
山东省考试题及答案解析

山东省考试题及答案解析一、单项选择题1. 孔子是中国古代伟大的教育家、思想家,其主要思想被收录于《论语》一书中。
孔子提倡的教育理念是()。
A. 因材施教B. 有教无类C. 学而优则仕D. 温故而知新答案:B解析:孔子提倡的教育理念是“有教无类”,意指教育应该面向所有人,不分贵贱、贫富,体现了教育的普及性和平等性。
2. 下列哪项不是中国古代四大发明之一?()A. 造纸术B. 火药C. 指南针D. 望远镜答案:D解析:中国古代四大发明包括造纸术、火药、指南针和印刷术。
望远镜并非中国古代的发明,而是在欧洲文艺复兴时期由伽利略等人发明的。
3. 以下哪位诗人不属于唐代诗人?()A. 李白B. 杜甫C. 白居易D. 辛弃疾答案:D解析:辛弃疾是宋代诗人,而非唐代诗人。
李白、杜甫和白居易都是唐代著名的诗人。
二、多项选择题4. 下列哪些因素会影响人的心理健康?()A. 遗传因素B. 环境因素C. 社会因素D. 个人经历答案:ABCD解析:人的心理健康受多种因素影响,包括遗传因素、环境因素、社会因素和个人经历等。
5. 以下哪些属于中国传统文化中的“四书”?()A. 《大学》B. 《中庸》C. 《论语》D. 《道德经》答案:ABC解析:“四书”是中国传统文化中的经典著作,包括《大学》、《中庸》、《论语》和《孟子》。
《道德经》属于“五经”之一,而非“四书”。
三、判断题6. 中国古代的科举制度是选拔官员的主要方式。
()答案:正确解析:中国古代的科举制度是选拔官员的主要方式,通过考试选拔人才,为国家选拔官员。
7. 黄河是中国的第二长河。
()答案:错误解析:黄河是中国的第二长河,长江是中国的第一长河。
四、简答题8. 简述中国古代的“四大发明”及其对世界文明的影响。
答案:中国古代的“四大发明”包括造纸术、火药、指南针和印刷术。
造纸术的发明极大地促进了文化的传播和保存,火药的发明改变了战争的形态,指南针的发明为航海和地理大发现提供了重要工具,印刷术的发明则极大地推动了知识的普及和传播。
山东省2024届高三12月联考语文试题及答案

山东省2024届高三12月联考语文试题及答案一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
材料一:随着“西学”的强势进入,以儒学为主体的传统文化遇冷,中国学术界对“中国正义论”传统“集体失语”。
殊不知,中国的“正义”学说更加根深叶茂、内涵丰富,是核心价值观念的深厚土壤和牢固根基。
中国尧舜时代已开始思考正义问题。
《尧典》说帝尧的政治具备了这样的原则:“钦明文思安安,允恭克让,光被四表,格于上下。
克明俊德,以亲九族。
九族既睦,平章百姓。
百姓昭明,协和万邦。
黎民于变时雍。
”尧舜之治成为政治治理的样板,在于他们深入思考“天之历数”,思索在“人心”与“道心”之间“允执厥中”。
“礼”是古代中国社会的共同价值基础,它从神圣、德性、程序、器物等不同向度确定着权力的合法性。
古代王朝常借助一定的仪式与典礼表示自己“奉天承运”,这源自政权的天命合法性追求。
儒学大师们通过诸如“王霸”“义利”“人禽”等的系列论辩,为道德、伦理、政治、法律的正义确立内涵和价值标准。
俞荣根先生在《儒家法思想通论》中说:“礼义、仁或仁义、天道、天理便是儒家法哲学中的理想法……儒家法文化的批判精神确具有‘为天地立心,为生民立命’的意义,它包含了良法观念,包含了正义和公道。
”《墨子·天志中》说“义者,正也”。
孔子曰“仁”曰“义”,孟子讲“仁义”,荀子则首提“正义”。
“义”包含人之行为的正当与公正,也包含社会制度评判的合宜与公平。
认真对比分析,不仅西人“正义论”的基本内容尽在其中,且意涵更丰富。
中国早期正义论思索古与今、我与世界、价值观与方法论,是通往中心坐标的最优路径、至佳选择。
儒家十分看重“爱”与“敬”,《论语》说“孝悌也者,其为仁之本与”,孔子说“爱与敬,其政之本与”。
美国的爱默生说:“我们确信,武力会招致另一种武力,只有爱和正义的法则才能实现彻底的革命。
”对于爱与正义,中华传统文明中的信奉全然而彻底。
山东省考行测历年真题

山东省考行测历年真题第一部分常识判断1.为庆祝中法建交()周年,文化和旅游部、法国驻华使馆1月4日共同发布中法文化旅游年系列活动。
A.75B.60C.70D.80【答案】:B2.中国与()两国外长2024年1月24日在北京签署《中华人民共和国和()共和国关于恢复外交关系的联合公报》,两国正式恢复外交关系。
该国成为中国()建交国。
A.汤加、第184个B.瑙鲁、第183个C.斐济、第182个D.秘鲁、第185个【答案】:B3.2024年3月14日,国家九大清洁能源基地之一的()流域水风光一体化基地累计发电量突破1万亿千瓦时,减排二氧化碳约8亿吨。
A.雅砻江B.岷江C.嘉陵江D.金沙江【答案】:A4.日前,我国自主研制的第一架以氢内燃机为动力的()飞机——世界首款四座氢内燃飞机原型机成功首飞。
A.民航B.商航C.通讯1/ 16D.通航【答案】:D5.2023年全年全国粮食总产量69541万吨,比上年增加()吨。
A.888万B.838万C.808万D.818万【答案】:A6.甲,13岁,用春节所得压岁钱5000元在商场买了一部智能手机。
该手机买卖合同的效力属于()。
A.可撤销、可变更B.有效C.无效D.效力待定【答案】:D7.“芳林新叶催陈叶,流水前波让后波”,这一句诗体现的哲理是()。
A.世界处于运动不居的状态B.新事物必然战胜旧事物C.静止是运动的特殊状态D.量的积累达到一定程度必然引起质变【答案】:B8.评价职业生涯的某个阶段是否成功,必须综合考虑()。
因素。
A.个人、家庭B.个人、家庭、企业C.个人、家庭、企业、社会D.企业、社会【答案】:C9.“垄断”一词出自于希腊语,意思是“一个销售者”,也就是指某一个人控制了一个产品的全部市场供给。
因而,完全垄断市场,就是指只有唯一一个供给者的市场类型。
下列选项中不属于完全垄断市场假设前提条件的是()2/ 16A.新企业无法进入市场B.整个市场的物品,劳务或资源都由一个供给者提供C.没有相近的替代品D.整个市场的物品,劳务或资源由少数的几个供给者提供【答案】:D10.子在川上曰:“逝者如斯夫,不舍昼夜。
2024届山东省名校联盟高三下学期5月大联考全真演练物理试题

2024届山东省名校联盟高三下学期5月大联考全真演练物理试题一、单选题:本题共7小题,每小题4分,共28分 (共7题)第(1)题发生α衰变的核反应方程为,某时刻元素钚()和铀()的原子核数之比为,再经历时间后元素钚()和铀()的原子核数之比为,钚()的半衰期为( )A.B.C.D.第(2)题如图所示,理想变压器原、副线圈匝数比为2:1,电源的输出电压,定值电阻,,滑动变阻器的最大阻值为5Ω,a、b为滑动变阻器的两个端点,所有电表均为理想电表。
现将滑动变阻器滑片P置于b端,则( )A.电流表示数为B.电压表示数为10VC.滑片P由b向a缓慢滑动,消耗的功率减小D.滑片P由b向a缓慢滑动,变压器的输出功率减小第(3)题如图所示,abc为等腰直角三角形金属导线框,∠c=90°,def为一与abc全等的三角形区域,其中存在垂直纸面向里的匀强磁场,e点与c点重合,bcd在一条直线上.线框abc以恒定的速度沿垂直df的方向穿过磁场区域,在此过程中,线框中的感应电流i(以刚进磁场时线框中的电流方向为正方向)随时间变化的图像正确的是( )A.B.C.D.第(4)题如图所示,一质量为m、长度为l的均匀柔软细绳PQ竖直悬挂。
用外力将绳的下端Q缓慢地竖直向上拉起至M点,M点与绳的上端P相距l。
重力加速度大小为g。
在此过程中,绳的重力势能增加( )A.mgl B.mglC.mgl D.mgl第(5)题一列简谐横波沿直线由a向b传播,ab相距4m,a、b两质点的振动图像如图甲和乙,则这列波的波长可能是( )A.16m B.10m C.8m D.4m第(6)题如图甲所示,理想变压器原、副线圈的匝数比为1:2,在原线圈回路中接阻值为2Ω的电阻R1,副线圈回路中接电阻R2,原线圈输入端接如图乙所示的交流电源,电表均为理想电表,若开关S闭合时,电流表示数为1A,则( )A.电压表示数为5V B.电阻R2消耗的功率为10WC.通过电阻R2的交流电频率为100Hz D.若断开开关S,电压表示数为20V第(7)题下列关于四幅插图的说法正确的是()A.甲图为方解石的双折射现象,说明方解石是非晶体B.乙图中制作防水衣时用右管材料的防水效果更好C.丙图为粒子的散射实验现象,其中J运动轨迹所占的比例是最多的D.丁图的绝热容器中,抽掉隔板,容器内气体温度降低二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题随着科技的进步,越来越多的人使用蓝牙耳机,手机与基站及耳机的通信如下图所示.若基站与手机、手机与耳机之间通信的电磁波分别为甲波、乙波,则以下说法正确的是( )A.甲、乙波的频率都比可见光的频率小B.真空中甲波的传播速度比乙波慢C.真空中甲波比乙波更容易绕过障碍物D.甲波与乙波有可能发生干涉第(2)题一定质量的理想气体从状态A经过状态B变化到状态C,其V-t图像如图所示,下列说法正确的有( )A.A→B的过程中,气体对外做功B.A→B的过程中,气体放出热量C.B→C的过程中,气体压强变大D.B→C的过程中,气体内能变大第(3)题甲、乙两车从同一地点同时开始运动的x-t图像分别如图中a、b图线所示,其中图线b为开口向下的抛物线,顶点为P,下列说法正确的是( )A.前4s内甲一直向正方向做匀速直线运动B.前4s内乙一直向正方向做匀减速直线运动C.甲、乙两车在2s末相遇D.甲的速度大小为5m/s,乙的加速度大小为10m/s2三、解答题:本题共4小题,每小题8分,共32分 (共4题)第(1)题如图所示,xOy坐标系在y>0空间存在场强为E,方向沿y轴正向的匀强电场,在y<0的空间存在磁感应强度为B,垂直于xoy平面向里的匀强磁场。
山东省聊城市重点中学2024年高三数学试题下学期第二次联考试题

山东省聊城市重点中学2024年高三数学试题下学期第二次联考试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知()f x 是定义在[]2,2-上的奇函数,当(]0,2x ∈时,()21xf x =-,则()()20f f -+=( )A .3-B .2C .3D .2-2.已知双曲线22122:1x y C a b -=与双曲线222:14y C x -=没有公共点,则双曲线1C 的离心率的取值范围是( )A .(1,3⎤⎦B .)3,⎡+∞⎣C .(1,5⎤⎦D .)5,⎡+∞⎣3.下列命题是真命题的是( )A .若平面α,β,γ,满足αγ⊥,βγ⊥,则//αβ;B .命题p :x R ∀∈,211x -≤,则p ⌝:0x R ∃∈,2011x -≤;C .“命题p q ∨为真”是“命题p q ∧为真”的充分不必要条件;D .命题“若()110xx e -+=,则0x =”的逆否命题为:“若0x ≠,则()110xx e -+≠”.4.甲、乙、丙、丁四位同学高考之后计划去、、A B C 三个不同社区进行帮扶活动,每人只能去一个社区,每个社区至少一人.其中甲必须去A 社区,乙不去B 社区,则不同的安排方法种数为 ( ) A .8B .7C .6D .55.已知函数()[]f x x x =-,其中[]x 表示不超过x 的最大正整数,则下列结论正确的是( ) A .()f x 的值域是[]0,1 B .()f x 是奇函数 C .()f x 是周期函数D .()f x 是增函数6.已知复数z 满足i i z z ⋅=+,则z 在复平面上对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限7.若命题:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题:在边长为4的正方形内任取一点,则的概率为,则下列命题是真命题的是( )A .B .C .D .8.若不等式210x ax ++≥对于一切10,2x ⎛⎤∈ ⎥⎝⎦恒成立,则a 的最小值是 ( )A .0B .2-C .52-D .3-9.已知命题p :任意4x ≥,都有2log 2x ≥;命题q :a b >,则有22a b >.则下列命题为真命题的是( ) A .p q ∧B .()p q ∧⌝C .()()p q ⌝∧⌝D .()p q ⌝∨10.已知F 为抛物线24y x =的焦点,点A 在抛物线上,且5AF =,过点F 的动直线l 与抛物线,B C 交于两点,O 为坐标原点,抛物线的准线与x 轴的交点为M .给出下列四个命题: ①在抛物线上满足条件的点A 仅有一个;②若P 是抛物线准线上一动点,则PA PO +的最小值为 ③无论过点F 的直线l 在什么位置,总有OMB OMC ∠=∠;④若点C 在抛物线准线上的射影为D ,则三点B O D 、、在同一条直线上. 其中所有正确命题的个数为( ) A .1B .2C .3D .411.若复数21iz =+,其中i 为虚数单位,则下列结论正确的是( ) A .z 的虚部为i -B .2z =C .z 的共轭复数为1i --D .2z 为纯虚数12.若平面向量,,a b c ,满足||2,||4,4,||3a b a b c a b ==⋅=-+=,则||c b -的最大值为( )A .B .C .D .二、填空题:本题共4小题,每小题5分,共20分。
山东省潍坊市五县市2021届高三10月联考数学试题(含答案和解析)(2020.10)
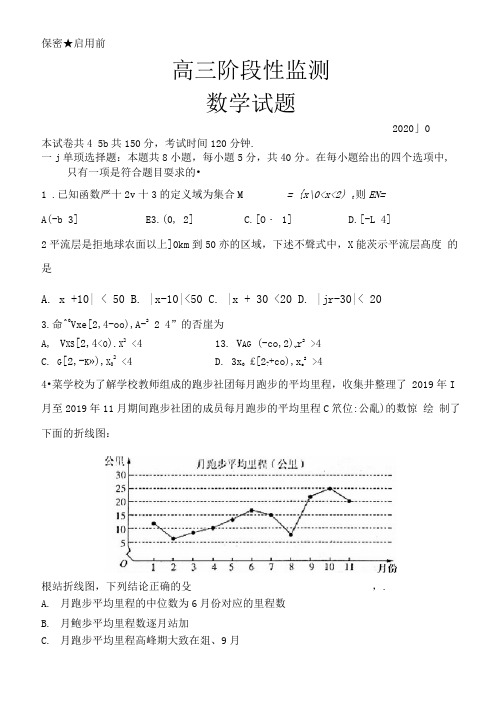
保密★启用前高三阶段性监测数学试题2020」0本试卷共4 5b共150分,考试时间120分钟.一j单顼选择题:本題共8小題,每小題5分,共40分。
在毎小題给出的四个选项中, 只有一项是符合题目耍求的•1 .已知函数严十2v十3的定义域为集合M = {x\0<x<2) t则EN=A(-b 3] E3.(0, 2] C.[O・ 1] D.[-L 4]2平流层是拒地球农面以上]0km到50亦的区域,下述不聲式中,X能茨示平流层髙度的是A. x +10| < 50B. |x-10|<50C. |x + 30 <20D. |jr-30|< 203.命^0Vxe[2,4-oo),A-2 2 4”的否崖为A,V XS[2,4<O).X2 <4 13. V AG (-co,2)v r2 >4C. G[2,-K»),X02 <4D. 3x0£[2?+co),x o2 >44•菜学校为了解学校教师组成的跑步社团每月跑步的平均里程,收集井整理了 2019年I 月至2019年11月期间跑步社团的成员每月跑步的平均里程C笊位:公亂)的数惊绘制了下面的折线图:根站折线图,下列结论正确的殳,.A.月跑步平均里程的中位数为6月份对应的里程数B.月鲍歩平均里程数逐月站加C.月跑步平均里程高峰期大致在爼、9月D・1月至5刀的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳5一已知二次函数/⑴= (x-m)(x-”) + l ,且知工2是方程/(A )-0的两个根,则 知心,恠/的大小关杀可能趾 A,< w < wB. x l <m<x 2<nC.m<n<x, <x 2D.m <x i <x 2<n6•我国古代数学名著燉节九章》屮俨天池盆題:在下雨时,用一个仙台形的天 池盆接雨水.天池往盆口克径为二尺八寸,盆底13径为一尺二寸,盆深一尺八寸•若盆中积 水深九寸,则该处的平地降雨蛍〔盆中积水体积与盆口面枳之比)为F 佑体积公式;二、多项选择题:本題共4小题,每小題5分,共20分。
山东联考高一试题及答案

山东联考高一试题及答案一、选择题(每题2分,共20分)1. 下列关于细胞膜结构的描述,正确的是:A. 细胞膜由脂质双层构成B. 细胞膜是完全不透水的C. 细胞膜上的蛋白质是固定的D. 细胞膜的结构是静态的答案:A2. 光合作用的主要场所是:A. 线粒体B. 叶绿体C. 细胞核D. 细胞质答案:B3. 人体中,负责运输氧气的蛋白质是:A. 血红蛋白B. 肌红蛋白C. 胰岛素D. 甲状腺素答案:A4. 下列关于DNA复制的描述,不正确的是:A. 需要DNA聚合酶B. 需要四种脱氧核苷酸C. 复制过程是双向的D. 复制过程是半保留的答案:C5. 细胞周期中,DNA复制发生在:A. G0期B. G1期C. S期D. G2期答案:C6. 下列关于基因突变的描述,正确的是:A. 基因突变总是有害的B. 基因突变是可遗传的C. 基因突变只发生在生殖细胞中D. 基因突变是不可逆的答案:B7. 人体免疫系统中,负责识别和攻击外来病原体的是:A. 吞噬细胞B. T细胞C. B细胞D. 红细胞答案:B8. 下列关于酶的描述,不正确的是:A. 酶是生物催化剂B. 酶可以加速化学反应C. 酶可以改变反应的平衡状态D. 酶的活性受温度和pH值的影响答案:C9. 人体中,负责合成蛋白质的细胞器是:A. 线粒体B. 核糖体C. 高尔基体D. 内质网答案:B10. 下列关于细胞凋亡的描述,正确的是:A. 细胞凋亡是一种被动的细胞死亡过程B. 细胞凋亡是一种程序化的细胞死亡过程C. 细胞凋亡只发生在衰老的细胞中D. 细胞凋亡对生物体是有害的答案:B二、填空题(每空1分,共20分)1. 细胞膜的主要组成成分是________和蛋白质。
答案:磷脂2. 光合作用中,光能被转化为________能,储存在ATP中。
答案:化学3. 人体血液中,负责运输二氧化碳的分子是________。
答案:碳酸氢盐4. DNA分子的双螺旋结构是由________两条链组成的。
山东省考行测历年真题及答案

山东省考行测历年真题及答案(满分100分时间120分钟)第一部分常识判断1.唯物主义哲学的基石是()。
A.历史范畴B.经济范畴C.阶级范畴D.物质范畴【答案】:D2.马克思主义最重要的理论品质是()A.吐故纳新B.与时俱进C.科学严谨D.博大精深【答案】:B3.血液中的红细胞的主要功能是()。
A.运输养料和氧B.运输废物和二氧化碳C.运输氧和部分二氧化碳D.运输养料和废物【答案】:C4.有关太阳外部结构的正确叙述是()。
A.日冕的高温使高能带电粒子向外运动,速度很高,不断地飞逸到行星际空间,这叫“太阳风”。
B.色球层中,有时会向外猛烈地喷出高达几万至几十万公里的红色火焰,这叫日冕。
C.色球层外包围着一层很薄的、完全电离的气体层,叫耀斑。
D.色球层的某些区域,在短时间内有突然增亮的现象,这叫日珥。
【答案】:A1/ 125.作为规范性公文的正本,其特殊形式不包括()。
A.试行本B.暂行本C.修订本D.抄本【答案】:D6.证券发行和交易的当事人在从事证券买卖的民事活动中应按照市场经济的基本要求进行等价交换’ 这是证券法中的()。
A.公正原则B.有偿原则C.诚实信用原则D.自愿原则【答案】:B7.下列哪些情况不可以采用越级行文的方式?()A.需要检举,控告直接上级机关B.某市人民政府为适应现代化城市建设的需要,拟在原某林场内建一座具有一定规模的某市植物园,为此,决定向上级机关致文请求批准C.国家林业局致文某县林业局要求调查该县某处森林发生重大火灾的原因,该县林业局调查清楚后向国家林业局行文报告D.情况特殊紧急【答案】:B8.实事求是评价毛泽东的历史地位的是()。
A.《解放思想,实事求是,团结一致向前看》B.《中国共产党第十一届中央委员会第三次全体会议决议》C.《中国共产党中央委员会关于建国以来党的若干历史间题的决D.《中国共产党中央委员会关于经济体制改革的决定》【答案】:C9.某老板2016年收入100万,成本支出50万,如果他去做其他工作的工资是10万,则其正常利润和经济利润分别为()万。
山东省2022届高三12月联考历史试题(附参考答案)

山东省2022届高三12月联考历史试题(附参考答案)一、选择题:本题共15小题,每小题3分,共计45分。
在每小题列出的四个选项中,只有一项是最符合题目要求的。
1.《礼记》中有“古之欲明德于天下者,先治其国……心正而后身修,身修而后家齐,家齐而后国治,国治而后天下平。
”《道德经》中有“上善若水,水利万物而不争,处众人之所恶,故几于道。
”《墨子》中有”君臣不相爱,则不惠忠。
父子不相爱,则不慈孝。
兄弟不相爱,则不和调”。
从中看出三者均主张A.关注社会,倡导和谐B.具有民本思想C.关注社会,倡导统一D.推行仁政理念【答案】A【解析】根据材料“古之欲明德于天下者,先治其国”“上善若水,水利万物而不争”“君臣不相爱,则不惠忠”可归纳出当时思想家都关注社会,倡导和谐,故选A2.光武皇帝愠数世之失权,忿强臣之窃命,矫枉过直,政不任下,虽置三公,事归台阁。
自此以来,三公之职,备员而已。
光武帝这一做法旨在A.加强中央集权B.确保决策独断C.提高行政效率D.削弱三公权力【答案】B【解析】材料出自《后汉书∙仲长统列传》,是仲长统对西汉晚期以来皇权旁落、强臣擅权的历史总结。
他认为,刘秀正是针对这一历史教训,矫枉过直,将中枢权力收归尚书台,三公仅仅是个门面而已,没有实际权力。
目的是为了加强皇权,故B项正确。
3.下表所示为唐代文学作品对两税法实施后的社会状况的记述。
这可以用来说明两税法的实施内容出处饶阳因富得州名,不独农桑别有营。
日暖提筐依茗《送张使君赴饶州》树,天阴把酒入银坑。
年年逐利西复东,姓名不在县籍中。
农夫税多长辛《贾客乐》苦,弃业长为贩卖翁。
兖州有民家妇姓贺氏,里人谓之织女,父母以农为《太平广记》业,其丈夫则负担贩卖,往来于郡。
A.促进了商品经济的发展B.减轻了农民的赋税负担C.提高了商人的社会地位D.消弭政府对农民的控制【答案】A【解析】根据材料信息“依茗树”“把酒入银坑”“弃业长为贩卖翁”“丈夫则负担贩卖”可知,两税法以钱代役使政府对农民的人身控制有所放松,它的实施促进了商品经济的发展,故A项正确。
2025届山东省名校联盟新教材数学高三第一学期期末联考试题含解析

2025届山东省名校联盟新教材数学高三第一学期期末联考试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在三角形ABC 中,1a =,sin sin sin sin b c a bA AB C++=+-,求sin b A =( )A .2B .3C .12D .22.抛物线方程为24y x =,一直线与抛物线交于A B 、两点,其弦AB 的中点坐标为(1,1),则直线的方程为( ) A .210x y --=B .210x y +-=C .210x y -+=D .210x y ---=3.已知函数()f x 是奇函数,且22()'()ln(1)ln(1)1f x f x x x x -=+----,若对11[,]62x ∀∈,(1)(1)f ax f x +<-恒成立,则a 的取值范围是( ) A .(3,1)--B .(4,1)--C .(3,0)-D .(4,0)-4.已知直线1l :x my =(0m ≠)与抛物线C :24y x =交于O (坐标原点),A 两点,直线2l :x my m =+与抛物线C 交于B ,D 两点.若||3||BD OA =,则实数m 的值为( ) A .14B .15C .13D .185.已知集合{}{}2|1,|31x A x x B x ==<,则()RAB =( )A .{|0}x x <B .{|01}x xC .{|10}x x -<D .{|1}x x -6.在ABC ∆中,D 为AC 的中点,E 为AB 上靠近点B 的三等分点,且BD ,CE 相交于点P ,则AP =( ) A .2132AB AC + B .1124AB AC + C .1123AB AC + D .2133AB AC + 7.为得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像,只需将函数sin 2y x =的图像( )A .向右平移5π6个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向左平移5π12个长度单位8.如图,在中,点M 是边的中点,将沿着AM 翻折成,且点不在平面内,点是线段上一点.若二面角与二面角的平面角相等,则直线经过的( )A .重心B .垂心C .内心D .外心9.某几何体的三视图如图所示,则该几何体的体积为( )A .23B .13C .43D .5610.空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面α,β,λ两两互相垂直,点A α∈,点A 到β,γ的距离都是3,点P 是α上的动点,满足P 到β的距离与P 到点A 的距离相等,则点P 的轨迹上的点到β的距离的最小值是( ) A .33B .3C 33-D .3211.已知集合{|4},{|2,}A x N y x B x x n n Z =∈=-==∈,则A B =( )A .[0,4]B .{0,2,4}C .{2,4}D .[2,4]12.已知函数f (x )=223,1ln ,1x x x x x ⎧--+≤⎨>⎩,若关于x 的方程f (x )=kx -12恰有4个不相等的实数根,则实数k 的取值范围是( ) A .1e 2⎛⎝ B .12e ⎡⎢⎣C .1,2e e ⎛⎤ ⎥ ⎝⎦D .1,2e e ⎛⎫⎪⎝⎭二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省历年联考考题汇总
如今,美术联考对于美术生发挥着重要作用。
为此,对于美术生而言,只有研究历年的美术联考考题,整理出其规律,才能在后续的美术联考中发挥出好成绩。
下面笔者做了一个历年的山东省历年联考考题汇总的整理,希望可以帮助到您。
一、2018山东美术联考考试题目
1.考试大纲:造型基础(素描)科目一般采用人物头像、石膏像、静物写生或默写等方式进行考查; 色彩基础科目一般采用静物写生、风景默写等方式进行考查。
我省2018年造型基础(素描)和色彩基础的考试内容均为静物。
考试形式以文字命题结合图形素材的方式。
2.造型基础(素描)、色彩基础单科满分为150分,两科总分为300分。
3.素描考题:
4.色彩考题:
二、2017年山东美术联考考试题目
1.素描考题:美术统考于2016年12月18日进行,具体考试时间如下:造型基础(8∶30—11∶30)色彩基础(14∶00—17∶00)。
造型基础(素描)和色彩基础的考试用时均为180分钟。
考试用纸为4开专用素描纸,由考点统一向考生提供。
考试用纸的左上角为考生信息条粘贴处(约10cm×4cm);信息条右侧设有按手印处(约2cm×4cm);左侧上半部分为答卷信息栏,内容包括考试科目、考点名称、考场号、座位号、姓名、考生号等,由考生考试时填写(约4cm×15cm);左侧中间部分为考试要求(约4cm×11cm);左侧底端设有按手印处(约4cm×2cm);上侧的空白区域,供评卷使用(约40cm×4cm);左侧、上侧以外部分为考生答题区域(约46cm×33cm)。
2.素描考题内容:石膏体1个、鸽子标本1个、硬皮书1个、郁金香花2。
