最优化计算方法上机题目2
最优化方法习题答案

最优化方法习题答案最优化方法习题答案最优化方法是数学中一门重要的学科,它研究如何找到使函数取得最大值或最小值的方法。
在实际问题中,最优化方法被广泛应用于经济学、工程学、管理学等领域。
本文将为读者提供一些最优化方法习题的答案,希望能够帮助读者更好地理解和应用这一学科。
一、单变量函数的最优化问题1. 求函数f(x) = x^2 - 2x + 1在区间[0, 3]上的最小值。
解:首先,我们需要找到函数f(x)的驻点。
计算f'(x) = 2x - 2,并令其等于零,得到x = 1。
然后,我们计算f''(x) = 2,发现在x = 1处,f''(x)大于零,说明该点是函数的极小值点。
接下来,我们需要检查区间的端点和驻点,找到函数f(x)在这些点的函数值。
f(0) = 1,f(1) = 0,f(3) = 4。
由于f(1)是最小的函数值,因此函数f(x)在区间[0, 3]上的最小值为0。
2. 求函数f(x) = e^x - 2x在整个实数轴上的最小值。
解:首先,我们计算f'(x) = e^x - 2,并令其等于零,得到x = ln(2)。
然后,我们计算f''(x) = e^x,发现在x = ln(2)处,f''(x)大于零,说明该点是函数的极小值点。
接下来,我们需要检查整个实数轴上的函数值。
由于函数f(x)在x趋近负无穷大时趋于负无穷大,而在x趋近正无穷大时趋于正无穷大,因此函数f(x)在整个实数轴上没有最小值。
二、多变量函数的最优化问题1. 求函数f(x, y) = x^2 + y^2 - 2x - 4y在闭区域D={(x, y)|0≤x≤2, 0≤y≤3}上的最小值。
解:首先,我们需要找到函数f(x, y)的驻点。
计算f_x(x, y) = 2x - 2和f_y(x, y) = 2y - 4,并令它们同时等于零,得到x = 1和y = 2。
最优化方法练习题答案修改建议版本--删减版要点

练习题一1、建立优化模型应考虑哪些要素? 答:决策变量、目标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停止准则。
答:针对一般优化模型()()min ()..0,1,2, 0,1,,i j f x s t g x i m h x j p≥===,讨论解的可行域D ,若存在一点*X D ∈,对于X D ∀∈ 均有*()()f X f X ≤则称*X 为优化模型最优解,最优解存在;迭代算法的收敛性是指迭代所得到的序列(1)(2)(),,,K X X X ,满足(1)()()()K K f X f X +≤,则迭代法收敛;收敛的停止准则有(1)()k k x x ε+-<,(1)()()k k k x x x ε+-<,()()(1)()k k f x f x ε+-<,()()()(1)()()k k k f x f x f x ε+-<,()()k f x ε∇<等等。
练习题二1、某公司看中了例2.1中厂家所拥有的3种资源R 1、R2、和R 3,欲出价收购(可能用于生产附加值更高的产品)。
如果你是该公司的决策者,对这3种资源的收购报价是多少?(该问题称为例2.1的对偶问题)。
解:确定决策变量 对3种资源报价123,,y y y 作为本问题的决策变量。
确定目标函数 问题的目标很清楚——“收购价最小”。
确定约束条件 资源的报价至少应该高于原生产产品的利润,这样原厂家才可能卖。
因此有如下线性规划问题:123min 170100150w y y y =++1231231235210..23518,,0y y y s t y y y y y y ++≥⎧⎪++≥⎨⎪≥⎩ *2、研究线性规划的对偶理论和方法(包括对偶规划模型形式、对偶理论和对偶单纯形法)。
答:略。
3、用单纯形法求解下列线性规划问题:(1)⎪⎪⎩⎪⎪⎨⎧≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ; (2)⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min53243232132 i x x x x x x x x x x t s x x z i 解:(1)引入松弛变量x 4,x 5,x 6123456min 0*0*0*z x x x x x x =-++++12341232 =22 5 =3..1 3 6=41,2,3,4,5,60x x x x x x x x s t x x x x x x x x x +-+⎧⎪+++⎪⎨-++⎪⎪≥⎩因检验数σ2<0,故确定x 2为换入非基变量,以x 2的系数列的正分量对应去除常数列,最小比值所在行对应的基变量x 4作为换出的基变量。
最优化方法习题答案
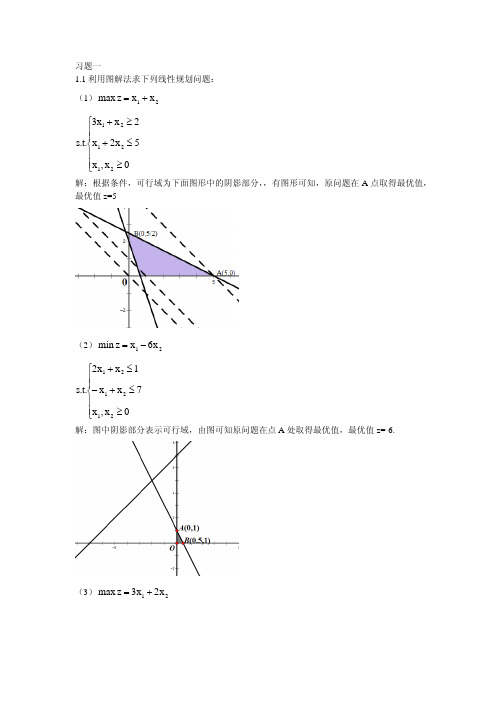
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。
最优化计算方法课后习题答案----高等教育出社。施光燕

习题二包括题目: P36页 5(1)(4)5(4)习题三包括题目:P61页 1(1)(2); 3; 5; 6; 14;15(1) 1(1)(2)的解如下3题的解如下5,6题14题解如下14. 设22121212()(6)(233)f x x x x x x x =+++---, 求点在(4,6)T-处的牛顿方向。
解:已知 (1)(4,6)T x=-,由题意得121212212121212(6)2(233)(3)()2(6)2(233)(3)x x x x x x x f x x x x x x x x +++-----⎛⎫∇= ⎪+++-----⎝⎭∴ (1)1344()56g f x -⎛⎫=∇=⎪⎝⎭21212122211212122(3)22(3)(3)2(233)()22(3)(3)2(233)22(3)x x x x x x x f x x x x x x x x +--+--------⎛⎫∇= ⎪+--------+--⎝⎭∴ (1)2(1)1656()()564G x f x --⎛⎫=∇=⎪-⎝⎭(1)11/8007/400()7/4001/200G x --⎛⎫= ⎪--⎝⎭∴ (1)(1)11141/100()574/100d G x g -⎛⎫=-=⎪-⎝⎭15(1)解如下15. 用DFP 方法求下列问题的极小点(1)22121212min 353x x x x x x ++++解:取 (0)(1,1)T x=,0H I =时,DFP 法的第一步与最速下降法相同2112352()156x x f x x x ++⎛⎫∇= ⎪++⎝⎭, (0)(1,1)T x =,(0)10()12f x ⎛⎫∇= ⎪⎝⎭(1)0.07800.2936x -⎛⎫= ⎪-⎝⎭, (1)1.3760() 1.1516f x ⎛⎫∇= ⎪-⎝⎭以下作第二次迭代(1)(0)1 1.07801.2936x x δ-⎛⎫=-= ⎪-⎝⎭, (1)(0)18.6240()()13.1516f x f x γ-⎛⎫=∇-∇= ⎪-⎝⎭0110111011101T T T TH H H H H γγδδδγγγ=+- 其中,111011126.3096,247.3380T T TH δγγγγγ===111.1621 1.39451.3945 1.6734Tδδ⎛⎫= ⎪⎝⎭ , 01101174.3734113.4194113.4194172.9646T TH H γγγγ⎛⎫== ⎪⎝⎭所以10.74350.40560.40560.3643H -⎛⎫= ⎪-⎝⎭(1)(1)1 1.4901()0.9776dH f x -⎛⎫=-∇= ⎪⎝⎭令 (2)(1)(1)1xx d α=+ , 利用 (1)(1)()0df x d d αα+=,求得 10.5727α=-所以 (2)(1)(1)0.77540.57270.8535xx d⎛⎫=-= ⎪-⎝⎭ , (2)0.2833()0.244f x ⎛⎫∇= ⎪-⎝⎭以下作第三次迭代(2)(1)20.85340.5599x x δ⎛⎫=-= ⎪-⎝⎭ , (2)(1)2 1.0927()()0.9076f x f x γ-⎛⎫=∇-∇= ⎪⎝⎭22 1.4407T δγ=- , 212 1.9922T H γγ=220.72830.47780.47780.3135T δδ-⎛⎫=⎪-⎝⎭1221 1.39360.91350.91350.5988T H H γγ-⎛⎫= ⎪-⎝⎭所以22122121222120.46150.38460.38460.1539T T T TH H H H H δδγγδγγγ-⎛⎫=+-= ⎪-⎝⎭(2)(2)20.2246()0.1465d H f x ⎛⎫=-∇= ⎪-⎝⎭令 (3)(2)(2)2xxdα=+ , 利用(2)(2)()0df x d d αα+=,求得 21α=所以 (3)(2)(2)11x x d ⎛⎫=+=⎪-⎝⎭, 因为 (3)()0f x ∇=,于是停止 (3)(1,1)T x =-即为最优解。
最优化方法试题及答案

最优化方法试题及答案一、选择题1. 下列哪项不是最优化方法的特点?A. 目标性B. 可行性C. 多样性D. 随机性答案:D2. 在最优化问题中,约束条件的作用是什么?A. 限制解的可行性B. 增加问题的复杂性C. 提供额外的信息D. 以上都是答案:A3. 线性规划问题中,目标函数与约束条件之间的关系是什么?A. 无关B. 相等C. 线性D. 非线性答案:C二、简答题1. 简述最优化问题的基本构成要素。
答案:最优化问题的基本构成要素包括目标函数、决策变量、约束条件和解的可行性。
目标函数是衡量最优化问题解的质量的函数,决策变量是问题中需要确定的参数,约束条件是对决策变量的限制,解的可行性是指解必须满足所有约束条件。
2. 什么是局部最优解和全局最优解?请举例说明。
答案:局部最优解是指在问题的邻域内没有其他解比当前解更优的解,而全局最优解是指在整个解空间中最优的解。
例如,在山峰攀登问题中,局部最优解可能是到达了一个小山丘的顶部,而全局最优解是到达了最高峰的顶部。
三、计算题1. 假设一个农民有一块矩形土地,长为100米,宽为80米,他想在这块土地上建一个矩形的养鸡场,但只能沿着土地的长边布置。
如果养鸡场的一边必须靠在土地的长边上,另一边与土地的宽边平行,求养鸡场的最大面积。
答案:为了使养鸡场的面积最大,养鸡场的一边应该靠在土地的宽边上,另一边与土地的长边平行。
这样,养鸡场的长将是80米,宽将是100米,所以最大面积为80米 * 100米 = 8000平方米。
2. 一个工厂需要生产三种产品A、B和C,每种产品都需要使用机器X 和机器Y。
生产一个单位的产品A需要机器X工作2小时和机器Y工作1小时;产品B需要机器X工作3小时和机器Y工作2小时;产品C需要机器X工作1小时和机器Y工作3小时。
工厂每天有机器X总共300小时和机器Y总共200小时的使用时间。
如果工厂每天需要生产至少100单位的产品A,50单位的产品B和20单位的产品C,请问工厂应该如何安排生产以最大化产品的总产量?答案:设生产产品A的单位数为x,产品B的单位数为y,产品C的单位数为z。
最优化计算方法

ymax=subs(y,x,xmax)
Newton 法
求方程F(x)=0的根.
牛顿法: x(n)=x(n-1)-F(x(n-1))/F’(x(n-1))
F = dydx; F1 = diff(F,x); format long N = 10; % number of iterations x0 = 19 % initial guess fprintf(' iteration xvalue\n\n'); for i=1:N x1=x0-subs(F,x,x0)/subs(F1,x,x0); fprintf('%5.0f %1.16f\n', i, x1); x0 = x1; end display('Hence, the critical point (solution of F=0) is (approx)'), x1
xmax figure, ezcontourf(z,[0.1 10 0.1 10]) hold on plot3(xmax(1),xmax(2),zmax, 'mo', 'LineWidth',2,... 'MarkerEdgeColor','k', 'MarkerFaceColor',[.49 1 .63],... 'MarkerSize',12); title('Countour plot and optimal value');
a=0; b=6; c=0; d=6; N=1000; x0 = a+(b-a)*rand(1); y0 = c+(d-c)*rand(1); zmin = subs(z,[x,y],[x0,y0]); fprintf(' Iteration xmin ymin zmin value\n\n'); for n=1:N xnew=a+(b-a)*rand(1); ynew=c+(d-c)*rand(1); znew=subs(z,[x,y],[xnew,ynew]); if znew<zmin xmin=xnew; ymin=ynew; zmin=znew; fprintf('%4.0f %1.6f %1.6f %1.6f\n', n, xmin, ymin, zmin); end end
西电最优化上机报告(大作业)

上机报告一.最速下降法算法简述:1.在本例中,先将最速下降方向变量赋一个值,使其二范数满足大于ε的迭代条件,进入循环。
2.将函数的一阶导数化简,存在一个矩阵,将其hesse矩阵存在另一个矩阵。
依照公式求出α,进而求出下一任迭代的矩阵初值。
循环内设置一个计数功能的变量,统计迭代次数。
3.求其方向导数的二范数,进行判别,若小于ε,则跳出循环,否则将继续迭代。
4.显示最优解,终止条件,最小函数值。
心得体会:最速下降法的精髓,无疑是求梯度,然后利用梯度和hesse矩阵综合计算,求解下一个当前最优解。
但是,要求函数是严格的凸函数,结合严格凸函数的大致图像,这就给初值的选取提供了一点参考。
例如在本例中,由于含有两个变量的二次方之和,结合大致图像,想当然的,初值的选取应当在原点附近;又因为变量的二次方之和后面,还减去了变量的一次形式和一次混合积,所以初值的选取应该再向第一象限倾斜。
综合以上考量,第一次选取(1,1)作为初值,判别精度方面,取到千分位,暂定为0.001。
运行以后,结果显示迭代了25次,最优解为(3.9995,1.9996),终止条件为5.4592e-04,目标函数为-8.0000。
这个结果已经相当接近笔算结果。
整体的运行也比较流畅,运算速度也比较快。
第二次取值,决定保留判别精度不变,将初值再适当向第一象限倾斜,取(2,2)作为初值,运行后,显示只迭代了11次!最优结果显示(3.9996,1.9997),终止条件为3.6204e-04,最优解-8.0000。
可见,最优结果更接近理想值,终止条件也变小了,最关键的是,迭代次数减少至第一次的一半以下!这说明以上初选取的方向是对的!第三次再进行初值细化,判别精度仍然不变,初值取(3,3)。
结果令人兴奋,只迭代了四次!最优解已经显示为(4.0000,2.0000),终止条件为2.4952e-04,目标函数-8.0000。
第四次,判别精度不变,取初值(4,4)。
最优化考试题2.doc

最优化方法定义可行方案:如果一个方案能达到预定目的,则该方案就叫可行方案。
最优方案:可行方案中最好的方案叫最有方案,它能达到最优化效果。
最优化M题:如何从可行方案中找出最优方案就叫最优化M题。
最优化方法:求解最优化闷题的数学方法叫最优化方法。
最优化方法解决实际问题的一般步骤:1提出最优化问题,叙述目标是什么?约束条件是什么?求什么变量?即确定变量,列出目标函数及约束表达式,建立最优化问题的数学模型。
2分析模型,选择合适的求解方法。
3编制计算机程序,上机求最优解。
对算法的收敛性,通用性,简便性,效率及误差等作出评价。
系统:由相互联系的若干部分构成的具有一定功能的整体。
系统的基本特征:1系统巾若干部分组成,每一部分具有其特定的功能。
2系统屮的各个要素之间相互制约,联系和作用。
3系统是具有一定功能的整体,系统的总功能不等于各个部分功能的简单迭加,系统的功能大于各部分的功能之和。
4系统存在于一定的环境之中,系统与环境之间存在相互作川,系统与环境的划分是相对的,对于一个系统是环境,而对于另一个系统而言可能是其中的一部分。
系统分析法:1确定所研宄系统的范M及其所处的环境。
2确定系统的组成部分,结构,功能,目的,各部分的功能和闪部规律。
3明确系统各个部分之间的联系,及整个系统与环境之间的联系。
4在上述分析的基础上,确记问题的决策变量及评价方案优劣的指标。
决策变量:决定方案优劣的变量。
数学模型:用字母,数字,各种符号,图像,逻辑框图描述实际系统的特征和内在联系的模型。
数学模型的组成:1常数,指在所研究的问题中保持相对固定或变化不大的呈。
2参数由具体系统的内外部条件确定的量。
3变量,指在模型中待确定的量。
4函数关系描述模型中常数,参数,变量之间相互关系的方程式或不等式。
独立变量:彼此独立的变量。
相关变量:其值可由独立变量确定的量。
工程优化问题:最优准则包括系统性能准则和经济准则。
系统性能准则是指使系统的某些性能指标达到最大或最小。
最优化计算方法试题

最优化计算方法试题
一、(20分)解释下列概念:
(1)凸集,凸规划;
(2)线性规划的基和基本解;
(3)无约束优化算法的下降搜索方向,举出两种搜索方向;
(4)约束最优化问题的可行解集合或容许解集合;
(5)共轭方向。
二、(10分)解答下列问题
三、(15分)写出下列线性规划的对偶形式,并用单纯形法求解原规划的最优解和最优值。
五、(10分)写出一维搜索0.618法的基本思想和算法步骤或框图。
六、(15分)分别利用外点罚函数法和内点罚函数法求解非线性规划
七、(15分)设A为n阶对称正定矩阵,
(1)写出A共轭向量组的定义;
(2)并证明该向量组必为线性无关向量组;
八、(15分)简述DFP算法的优缺点;并证明矩阵
满足拟牛顿方程。
最优化理论试题及答案

最优化理论试题及答案一、单项选择题1. 以下哪个函数是凸函数?A. f(x) = x^2B. f(x) = -x^2C. f(x) = x^3D. f(x) = e^x答案:A2. 线性规划问题的基本解是:A. 基本可行解B. 可行解C. 基本解D. 基本最优解答案:A3. 单纯形法中,如果目标函数的最优值是无界的,则对应的解是:A. 无解B. 可行解C. 基本可行解D. 基本最优解答案:A4. 在拉格朗日乘数法中,拉格朗日函数是:A. 目标函数和约束条件的乘积B. 目标函数和约束条件的和C. 目标函数和约束条件的差D. 目标函数和约束条件的商答案:B5. 以下哪个算法用于解决非线性规划问题?A. 单纯形法B. 内点法C. 匈牙利法D. 动态规划答案:B二、多项选择题1. 以下哪些条件是凸优化问题的必要条件?A. 目标函数是凸函数B. 所有约束条件是凸集C. 目标函数是凹函数D. 所有约束条件是凹集答案:A, B2. 在线性规划中,以下哪些是可行域的性质?A. 非空B. 凸集C. 闭集D. 有界答案:A, B, C3. 以下哪些方法可以用于解决整数规划问题?A. 分支定界法B. 割平面法C. 单纯形法D. 动态规划答案:A, B, D4. 以下哪些是拉格朗日乘数法的用途?A. 寻找局部最优解B. 寻找全局最优解C. 确定约束条件的活跃性D. 确定目标函数的梯度答案:A, C5. 以下哪些是动态规划的基本要素?A. 状态B. 决策C. 阶段D. 策略答案:A, B, C三、填空题1. 一个函数f(x)是凸函数,当且仅当对于任意的x1, x2和任意的λ∈[0,1],有f(λx1 + (1-λ)x2) ≤ λf(x1) + (1-λ)f(x2)。
2. 线性规划问题的标准形式是:最大化或最小化目标函数z = c^T x,满足约束条件Ax ≤ b和x ≥ 0。
3. 单纯形法的基本思想是通过不断地从一个基本可行解移动到另一个基本可行解,直到找到最优解。
最优化方法试卷及答案5套.docx

最优化⽅法试卷及答案5套.docx《最优化⽅法》1⼀、填空题:1. _______________________________________________________ 最优化问题的数学模型⼀般为:_____________________________________________ ,其中___________ 称为⽬标函数,___________ 称为约束函数,可⾏域D可以表⽰为_______________________________ ,若 ________________________________ ,称/为问题的局部最优解,若为问题的全局最优解。
2.设f(x)= 2⽄+2“2-兀|+5花,则其梯度为__________ ^x = (l,2)r?6/ = (l,0)r,则f(x)在壬处沿⽅向d的⼀阶⽅向导数为___________ ,⼏何意义为_____________________________________ ,⼆阶⽅向导数为____________________ ,⼏何意义为_____________________________3.设严格凸⼆次规划形式为:min /(%) = 2兀]2 + 2x; - 2兀]-x2s.t. 2%! 4- x2 < 1> 0x2 > 0则其对偶规划为_______________________________________________min%(d ) = f (x k +ad k )的最优步长为务=—叫)F.d kT Gd k2. (10分)证明凸规划min/(x ),x G D (其中⼦(兀)为严格凸函数,D 是凸集)的最优解是唯⼀的3. (13分)考虑不等式约束问题min /(x )s.t. c i (x ) < 0, Z G / = {1,2,…,加}其中/(x ),6 (兀)a e /)具有连续的偏导数,设X 是约束问题的可⾏点,若在元处 d 满⾜巧(计<0,VC,(元)(可则d 是元处的可⾏下降⽅向。
最优化方法-习题

( x2 x1) f ( x 2) f ( x2) f ( x1)
三 、 设 f(x)=
2 1
“充分性” 由 则
x ,x
1
2
的任意性取
x = x 时,f( x )>f( x )
1
T 1 T T Qx b x c, Q Q 0 试 证 : 共 轭 梯 度 法 的 线 性 搜 索 中 2x
3
*
T
f ( x)
x
2
1
2 x 2 2 x1 x2 4 x1 , x R
T
1、 给定问题
x
(1)
(1,1)
解:1)DFC 法 取初始对称矩阵
1 0 H1 0 1
第一次迭代:
x x x 2 x 6 x 14 x x x x 2 s.t. x 2 x 3 x 0, x 0, x 0 取初始点 x (1 ,1,0) ,用简约梯度法求其最优解
T
2) 因为 Q=
2 2 2 2 ,所以 |Q|= 2 6 =8>0 即可知 Q 是非奇异的 2 6 2 2 2 6
=8>0 ,所以 Q 是正定的,故 f(x)是正定的
f ( x1) (2,4,5)
3) 因为|2|>0,
2 d f ( x1) =(1,0,-1) 4 = -3<0 5
2 2
2
一、设 f(x)为定义在区间[a,b]上的实值函数,
2) f(x)=ln(
x1 + x x x 2 )
x1 x2 9 x3 , x1 6 x2 x3 2 , 9 x1 x2 )
最优化方法试卷及答案5套

《最优化方法》1一、填空题:1.最优化问题的数学模型一般为:____________________________,其中 ___________称为目标函数,___________称为约束函数,可行域D 可以表示 为_____________________________,若______________________________, 称*x 为问题的局部最优解,若_____________________________________,称*x 为问题的全局最优解。
2.设f(x)= 212121522x x x x x +-+,则其梯度为___________,海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________,几何意义为___________________________________,二阶 方向导数为___________________,几何意义为_________________________ ___________________________________。
3.设严格凸二次规划形式为:则其对偶规划为___________________________________________。
4.求解无约束最优化问题:n R x x f ∈),(min ,设k x 是不满足最优性条件的第k 步迭代点,则:用最速下降法求解时,搜索方向k d =___________ 用Newton 法求解时,搜索方向k d =___________ 用共轭梯度法求解时,搜索方向k d =___________________________________________________________________________。
二.(10分)简答题:试设计求解无约束优化问题的一般下降算法。
最优化方法考试试题

最优化方法考试试题一、选择题(每题2分,共20分)1、下列哪个选项不是最优化方法的常见应用场景?A.生产计划优化B.金融投资组合优化C.图像处理优化D.自然语言处理优化正确答案:D.自然语言处理优化。
2、下列哪个算法不是求解线性规划问题的常用算法?A.单纯形法B.内点法C.外点法D.牛顿法正确答案:D.牛顿法。
3、下列哪个选项不是整数规划问题的特点?A.变量取值必须是整数B.问题复杂度较高,通常需要特殊算法求解C.在实际应用中比线性规划更为广泛D.可以使用与线性规划相同的方法求解正确答案:D.可以使用与线性规划相同的方法求解。
4、下列哪个选项不是梯度下降法的优点?A.简单易行,易于实现B.能较快地收敛到局部最优解C.对初值不敏感,易于找到全局最优解D.对于大规模数据处理效率较高正确答案:C.对初值不敏感,易于找到全局最优解。
5、下列哪个选项不是模拟退火算法的特点?A.基于概率的搜索方法,有一定的随机性B.在解空间内随机搜索,可以跳出局部最优解的陷阱C.可以找到全局最优解,但需要设置退火温度等参数D.对于组合优化问题通常比暴力搜索算法更快找到最优解正确答案:D.对于组合优化问题通常比暴力搜索算法更快找到最优解。
二、填空题(每空2分,共20分)6.最优化方法中,通常使用__________来衡量一个解的好坏。
正确答案:目标函数。
7.在使用单纯形法求解线性规划问题时,__________是算法终止的条件。
正确答案:迭代次数达到预设的上限。
8.整数规划问题中,如果所有变量都有上限和下限的约束,则称为__________规划问题。
正确答案:背包。
9.在使用模拟退火算法求解组合优化问题时,__________是算法终止的条件。
正确答案:达到预定的迭代次数或者解的变化小于某个给定的阈值。
10.最优化方法中,__________是一种启发式搜索方法,通常用于解决组合优化问题。
正确答案:遗传算法。
最优化问题在现实世界中随处可见,从解决日常生活中的最佳路线问题,到企业寻求最大化利润和最小化成本,最优化方法都发挥着至关重要的作用。
最优化计算方法课后习题集答案解析

解:取 , 时,DFP法的第一步与最速下降法相同
, ,
,
以下作第二次迭代
,
其中,
,
所以
令 , 利用 ,求得
所以 ,
以下作第三次迭代
,
,
所以
令 , 利用 ,求得
所以 , 因为 ,于是停止
即为最优解。
习题四
包括题目: P95页 3;4;8;9(1);12选做;13选做
3题解如下
3.考虑问题 ,其中
X1,x2,x3≥0 (3)
求出点(1,1,0)处的一个下降可行方向.
解:首先检查在点(1,1,0)处哪些约束为有效约束。检查易知(1),X3≥0为有效约束。设所求可行方向d=(d1,d2,d3)T。根据可行方向d的定义,应存在a>0,使对∀t∈(0,a)能有
X+td=(1+td1,1+td2,0+td3)T
(1)
s.t.
(2)
s.t.
(1)解:非线性规划的K-T条件如下:
(1)
(2)
(3)
再加上约束条件 (4)
为求出满足(1)~(4)式的解,分情况考虑:
①若(4)式等号不成立,即 ,那么由(2)式得 ,将 代入(1)式解得 , ,所得值不满足 的条件,故舍去。
②若(4)式等号成立,由(1)式可以解得 , ,代入(4)式有:
JBi
1
2
3
4
5
6
7
8
9
di0
1
1
0
-5/6
-1/6
1
10/6
4
0
0
38/6
2
0
1
-9/6
最优化 马昌凤 第二章作业

最优化方法及其Matlab程序设计习题作业暨实验报告学院:数学与信息科学学院班级:12级信计一班姓名:李明学号:1201214049第二章 线搜索技术一、上机问题与求解过程 1、用0.618法求解 .1)(min 2--=x x x f 初始区间]1,1[-,区间精度为50.=0δ. 解:当初始时不限制近似迭代函数值得大小,编写程序运行结果为:从结果可以看出迭代次数为9次,极小点为5016.0,极小点的函数值为2500.1-。
根据人工手算,极小值点应该为500.0,所以在设计程序的时候添加函数值误差范围,并取范围为10101-⨯。
编写的设计函数程序并调试改正如下:function [s,fs,k,G,FX,E]=gold(f,a,b,H,F) %输入:% f:目标函数,a :搜索区间左侧端点;b:搜索区间右侧端点; % H :搜索区间允许范围;F :搜索区间函数值允许范围; %输出:% s:近似极小值点:fa :近似极小点数值;k:迭代次数:% FX :近似迭代函数值;E=[h,fh],h 为近似区间误差,fh 为函数值误差 t=(sqrt(5)-1)/2;h=b-a; p=a+(1-t)*h;q=a+t*h;fa=feval(f,a);fb=feval(f,b); fp=feval(f,p);fq=feval(f,q); k=1;G(k,:)=[a,p,q,b];%初始时错误语句:G(1,:)=[a,p,q,b]; %初始调试的时候没有注意到后面需要开辟k 行空间 FX(k,:)=[fa,fp,fq,fb];while (abs(fa-fb)>F) ((b-a)>H) if (fp<fq)b=q;fb=fq;q=p;fq=fp;h=b-a;p=a+(1-t)*h;fp=feval(f,p); %初始时错误语句:b=q;fb=fq;h=b-a;q=a+t*h;fq=feval(f,q); %初始调试的时候对0.618方法没有充分理解所以出现错误 elsea=p;fa=fp;p=q;fp=fq;h=b-a;q=a+t*h;fq=feval(f,q);%初始时错误语句:a=p;fa=fp;h=b-a;p=a+(1-t)*h;fp=feval(f,p); %初始调试的时候对0.618方法没有充分理解所以出现错误 end极小点(s) 迭代次数搜索区间误差 函数值误差 0.501690.04260.0006k=k+1;G(k,:)=[a,p,q,b];%初始时错误语句:G(1,:)=[a,p,q,b]; %初始调试的时候没有注意到前面已经开辟k 行空间 FX(k,:)=[fa,fp,fq,fb]; end if (fp<fq) s=p;fs=fp; elses=q;fs=fq; endh=b-a;fh=abs(fb-fa);%选取试探点最小的数值为近似点,并且计算出以上为搜索区间的的最后误差以及函数值误差 E=[h,fh];在命令窗口内输入如下命令:[s,fs,k,G,FX,E]=gold(inline('s^2-s-1'),-1,1,0.05,1e-10) 回车之后得到如下数据结果:附:在窗口中输出的结果如下>> [s,fs,k,G,FX,E]=gold(inline('s^2-s-1'),-1,1,0.05,1e-10) s = 0.5000 fs = -1.2500 k = 24 G =-1.0000 -0.2361 0.2361 1.0000 -0.2361 0.2361 0.5279 1.0000 0.2361 0.5279 0.7082 1.0000极小点 极小点数值 迭代次数 搜索区间误差 函数值误差 0.500-1.250024410321.0-⨯0000.00.2361 0.4164 0.5279 0.70820.4164 0.5279 0.5967 0.70820.4164 0.4853 0.5279 0.59670.4164 0.4590 0.4853 0.52790.4590 0.4853 0.5016 0.52790.4853 0.5016 0.5116 0.52790.4853 0.4953 0.5016 0.51160.4953 0.5016 0.5054 0.51160.4953 0.4992 0.5016 0.50540.4953 0.4977 0.4992 0.50160.4977 0.4992 0.5001 0.50160.4992 0.5001 0.5006 0.50160.4992 0.4997 0.5001 0.50060.4997 0.5001 0.5003 0.50060.4997 0.5000 0.5001 0.50030.4997 0.4999 0.5000 0.50010.4999 0.5000 0.5000 0.50010.5000 0.5000 0.5000 0.50010.5000 0.5000 0.5000 0.50000.5000 0.5000 0.5000 0.50000.5000 0.5000 0.5000 0.5000 FX =1.0000 -0.7082 -1.1803 -1.0000 -0.7082 -1.1803 -1.2492 -1.0000 -1.1803 -1.2492 -1.2067 -1.0000 -1.1803 -1.2430 -1.2492 -1.2067 -1.2430 -1.2492 -1.2406 -1.2067 -1.2430 -1.2498 -1.2492 -1.2406 -1.2430 -1.2483 -1.2498 -1.2492 -1.2483 -1.2498 -1.2500 -1.2492 -1.2498 -1.2500 -1.2499 -1.2492 -1.2498 -1.2500 -1.2500 -1.2499 -1.2500 -1.2500 -1.2500 -1.2499 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.25001.0e-04*0.3121 0.00002、用0.618法求解.12)(min 3+-=x x x f的近似最优解,初始搜索区间为]3,0[,区间精度为50.=1δ. 解:当初始时不限制近似迭代函数值得大小,编写程序运行结果为:从结果可以看出迭代次数为8次,极小点为8115.0,极小点的函数值为0886.0-。
最优化上机作业
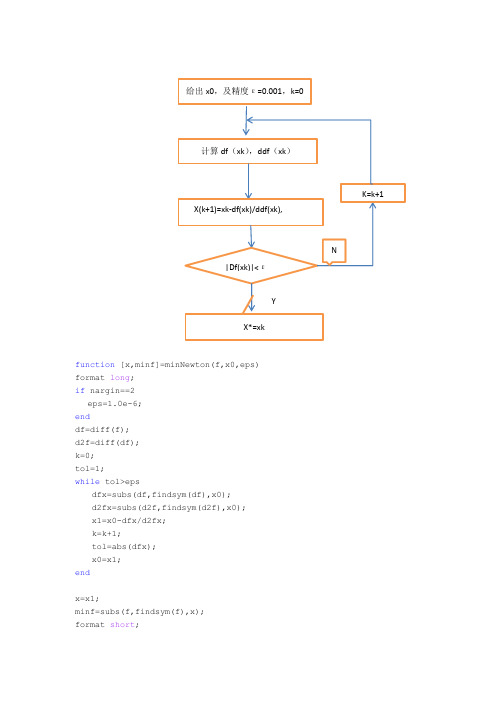
给出x0,及精度ε=0.001,k=0计算df(xk),ddf(xk)K=k+1X(k+1)=xk-df(xk)/ddf(xk),N|Df(xk)|<εYX*=xkfunction [x,minf]=minNewton(f,x0,eps)format long;if nargin==2eps=1.0e-6;enddf=diff(f);d2f=diff(df);k=0;tol=1;while tol>epsdfx=subs(df,findsym(df),x0);d2fx=subs(d2f,findsym(d2f),x0);x1=x0-dfx/d2fx;k=k+1;tol=abs(dfx);x0=x1;endx=x1;minf=subs(f,findsym(f),x);format short;>> f=3*t^4-16*t^3+30*t^2-24*t+8;>> x=minNewton(f,2)x =2抛物线法function[x,minf]=minPWX(f,a,b,eps)format long;if nargin==3eps=1.0e-6;endt0=(a+b)/2;k=0;tol=1;while tol>epsfa=subs(f,findsym(f),a);fb=subs(f,findsym(f),b);ft0=subs(f,findsym(f),t0);tu=fa*(b^2-t0^2)+fb*(t0^2-a^2)+ft0*(a^2-b^2); td=fa*(b-t0)+fb*(t0-a)+ft0*(a-b);t1=tu/2/td;ft1=subs(f,findsym(f),t1);if ft1<=ft0if t1<=t0b=t0;t0=t1;elsea=t0;t0=t1;endk=k+1;elseif t1<=t0a=t1;elseb=t1;k=k+1;endendx=t1;minf=subs(f,findsym(f),x);format short;syms t;f=t^4/4-4*t^3/3+5*t^2/2-2*t; x=minPWX(f,0.5,4)共轭梯度法function f=conjugate_grad_2d(x0,t)x=x0;syms xi yi a;f=xi^2+2*yi^2-4*xi-2*xi*yi;f fx=diff(f,xi);fy=diff(f,yi);fx=subs(fx,{xi,yi},x0);fy=subs(fy,{xi,yi},x0);fi=[fx,fy];count=0; 0while double(sqrt(fx^2+fy^2))>ts=-fi;if count<=0s=-fi;elses=s1;endx=x+a*s;f=subs(f,{xi,yi},x);f1=diff(f);f1=solve(f1);if f1~=0ai=double(f1);elsebreakendx=subs(x,a,ai);f=xi^2+2*yi^2-4*xi-2*xi*yi;fxi=diff(f,xi);fyi=diff(f,yi);fxi=subs(fxi,{xi,yi},x);fyi=subs(fyi,{xi,yi},x);fii=[fxi,fyi];d=(fxi^2+fyi^2)/(fx^2+fy^2);s1=-fii+d*s;count=count+1;fx=fxi;fy=fyi;endx,f=subs(f,{xi,yi},x),count阻尼牛顿法function y=fun(x);y=x(1)^2+x(2)^2+x(1)*x(2);function g=gfun(x);g=2*x(1)+ x(2)+2*x(2)+ x(1);function He=Hess(x); n=length(x);He=zeros(n,n);He=1;function [x,val,k]=dampnm(fun,gfun,Hess,x0); maxk=100;rho=0.55;sigma=0.4;k=0;epsilon=1e-5;while (k<maxk)gk=feval(gfun,x0);Gk=feval(Hess,x0);dk=-Gk\gk;if (norm(dk)<epsilon)break;endm=0;mk=0;while(m<20)if (feval(fun,x0+rho^m*dk)<feval(fun,x0)+sigma*rho^m*gk'*dk) mk=m; break; end m=m+1; endx0=x0+rho^mk*dk; k=k+1; endx=x0;val=feval(fun,x);x0=[1,1]';[x,val,k]=dampnm('fun','gfun','Hess',x0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目5
编写程序实现牛顿法。
牛顿法用来求解一维函数的局部极小值点;
利用Matlab编写函数[x,minf]=Newton(f,x0,eps).
其中f为目标函数,x0为初始点,eps为算法终止的精度。
用牛顿法求解无约束优化问题minf(x)。
算法3
S1 给出x0ÎR精度e>0,令k:=0;
S2 若¢f(x
k
)£e, 停止,极小值点为x k;
S3 令x
k+1=x
k
-
¢f(x
k
)
¢¢f(x
k
)
;
S4 令k:=k+1, 转S2.
题目6
取初始点x0=2,用牛顿法求函数f(t)=t2-ln t-5的任一极小值点。
题目7
编写程序实现全局牛顿法。
利用Matlab编写函数 [x,miny]=GlobalNewton(f,x0,eps).其中f为目标函数,x0为初始点,eps为算法终止的精度。
用全局牛顿法求解无约束优化问题minf(x)。
算法4
S1 给出x0ÎR精度e>0,令k:=0;
S2 计算¢f(x
k
),¢¢f(x k), 若¢f(x k)¹0则转S4;若¢¢f(x k)³0则停止;令初始值d=e;
S3 令d=2d, 如果f(x
k
+d)³f(x k), 则转 S3;
令x
k+1=x
k
+d,k=k+1,转S2;
S4令b
k =¢¢f(x
k
), 如果b k£0, 则令b k=1,置a k=1;
S5 如果
f(x
k -
a
k
¢f(x
k
)
b
k
)£f(x
k
)-
a
k
4b
k
¢f(x
k
)
[]2
则转S6;置a
k
=a k/2;转S5;
S6 令x
k+1=x
k
-
a
k
¢f(x
k
)
b
k
, k=k+1,转S2.
题目8
取初始点x0=5,用全局牛顿法求函数f(t)=t3-3t+2的极小值点。
