北师大版数学高一必修4课时习题24两角和与差的正切函数

合集下载

北师版数学高一-课时作业两角和与差的正切函数

2.3 两角和与差的正切函数一、选择题1．若tan α＝13，tan(α＋β)＝12，则tan β等于( ) A.17 B.16 C.57 D.562.3tan 23°tan 97°－tan 23°－tan 97°的值为( )A ．2B ．2 3 C. 3 D ．03．已知tan(α＋β)＝25，tan ⎝⎛⎭⎫β－π4＝14，则tan ⎝⎛⎭⎫α＋π4的值为( ) A.322 B.2213 C.1318 D.164．A ，B ，C 是△ABC 的三个内角，且tan A ，tan B 是方程3x 2－5x ＋1＝0的两个实数根，则△ABC 是( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．无法确定5．若tan 28°tan 32°＝a ，则tan 28°＋tan 32°等于( ) A.3a B.3(1－a ) C.3(a －1) D.3(a ＋1)6．设向量a ＝(cos α，－1)，b ＝(2，sin α)，若a ⊥b ，则tan ⎝⎛⎭⎫α－π4等于( ) A ．－13 B.13C ．－3D ．3 7．在△ABC 中，tan A ＋tan B ＋tan C ＝33，tan 2B ＝tan A ·tan C ，则B 等于( )A ．30°B ．45°C ．120°D ．60°二、填空题8．(1＋tan 21°)(1＋tan 22°)(1＋tan 23°)(1＋tan 24°)＝________.9.tan 75°－tan 15°1＋tan 75°tan 15°＝________. 10．已知α，β均为锐角，且tan β＝cos α－sin αcos α＋sin α，则tan(α＋β)＝________. 三、解答题11．如果tan α，tan β是方程x 2－3x －3＝0的两根，求sin (α＋β)cos (α－β)的值．12．已知tan(π4＋α)＝12. (1)求tan α的值；(2)求2sin αcos α－cos 2α2cos 2α的值．13.已知tan α，tan β是方程6x 2－5x ＋1＝0的两根，且0<α<π2，π<β<3π2，求tan(α＋β)及α＋β的值．四、探究与拓展14.如图，在△ABC 中，AD ⊥BC ，D 为垂足，AD 在△ABC 的外部，且BD ∶CD ∶AD ＝2∶3∶6，则tan ∠BAC ＝__________.15．如图，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A ，B 两点，已知A ，B 的横坐标分别为210，255.(1)求tan(α＋β)的值；(2)求α＋2β的值．答案精析1．A 2.C 3.A 4.A 5.B 6.B 7.D 8．4 9.3 10.111．解 sin (α＋β)cos (α－β)＝sin αcos β＋cos αsin βcos αcos β＋sin αsin β＝tan α＋tan β1＋tan αtan β＝31＋(－3)＝－32. 12．解 (1)∵tan(π4＋α)＝12， ∴1＋tan α1－tan α＝12， ∴2＋2tan α＝1－tan α，∴tan α＝－13. (2)2sin αcos α－cos 2α2cos 2α＝tan α－12＝－13－12＝－56. 13．解 ∵tan α，tan β是方程6x 2－5x ＋1＝0的两根，∴tan α＋tan β＝56，tan αtan β＝16， ∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝561－16＝1. ∵0<α<π2，π<β<3π2， ∴π<α＋β<2π，∴α＋β＝5π4. 14.1715．解由条件得cos α＝210，cos β＝255. ∵α，β为锐角，∴sin α＝1－cos 2α＝7210，sin β＝1－cos 2β＝55. 因此tan α＝sin αcos α＝7，tan β＝sin βcos β＝12. (1)tan(α＋β)＝tan α＋tan β1－tan αtan β＝7＋121－7×12＝－3.(2)∵tan 2β＝tan(β＋β)＝2tan β1－tan 2β＝2×121－⎝⎛⎭⎫122＝43，∴tan(α＋2β)＝tan α＋tan 2β1－tan αtan 2β＝7＋431－7×43＝－1.又∵α，β为锐角，∴0<α＋2β<3π2，∴α＋2β＝3π4.。

北师大版数学高一必修4练习两角和与差的正切函数

[A 基础达标]1．若tan ⎝⎛⎭⎫π4－α＝3，则tan α的值为( )A ．－2B ．－12C.12D ．2解析：选B.tan α＝tan ⎣⎡⎦⎤π4－⎝⎛⎭⎫π4－α＝1－tan ⎝⎛⎭⎫π4－α1＋tan ⎝⎛⎭⎫π4－α＝1－31＋3＝－12.2．设α、β∈⎝⎛⎭⎫0，π2，且tan α＝17，tan β＝43，则α－β等于( )A.π3B.π4 C.34π D ．－π4解析：选D.tan(α－β)＝tan α－tan β1＋tan αtan β＝17－431＋17×43＝－1.因为tan α<tan β且α，β∈⎝⎛⎭⎫0，π2，所以α<β.所以α－β＝－π4.3．直线l 1：x －2y ＋1＝0，倾斜角为α，直线l 2：x ＋3y －1＝0，倾斜角为β，则β－α＝( )A.π4B.3π4 C ．－π4D ．－3π4解析：选B.由题意可知，tan α＝12，tan β＝－13，所以0<α<π2，π2<β<π.所以0<β－α<π，所以tan(β－α)＝tan β－tan α1＋tan β tan α＝－13－121－13×12＝－1.所以β－α＝3π4.4．在△ABC 中，C ＝120°，tan A ＋tan B ＝233，则tan A tan B ＝( )A.14B.13C.12D.53解析：选B.因为C ＝120°，则A ＋B ＝60°，又tan(A ＋B )＝tan A ＋tan B 1－tan A tan B ，故2331－tan A tan B＝3，所以tan A tan B ＝13.5．在△ABC 中，若sin A －3cos A ＝0，sin 2B －sin B cos B －2cos 2B ＝0，则角C 为( ) A.π3B.π4 C.π6D.3π4解析：选B.由sin A －3cos A ＝0得tan A ＝3.由sin 2B －sin B cos B －2cos 2B ＝0得tan 2B －tan B －2＝0，解得tan B ＝2或tan B ＝－1，当tan B ＝2时，tan C ＝－tan(A ＋B )＝1，由C ∈(0，π)得C ＝π4；当tan B ＝－1时，tan C＝－tan(A ＋B )＝－12，此时B 、C 均为钝角不合题意，舍去，综上所述C ＝π4.6．若A ＝18°，B ＝27°，则(1＋tan A )(1＋tan B )的值是________．解析：原式＝tan A ＋tan B ＋tan A tan B ＋1＝tan(18°＋27°)·(1－tan18°tan27°)＋tan18°·tan27°＋1＝2.答案：2 7.tan 20°tan （－50°）－1tan 20°－tan 50°＝________．解析：原式＝－tan 20°tan 50°＋1tan 20°－tan 50°＝1tan 50°－tan 20°1＋tan 20°tan 50°＝1tan （50°－20°）＝1tan 30°＝ 3.答案： 38．已知tan ⎝⎛⎭⎫π4＋α＝2，则12sin αcos α＋cos 2α＝________．解析：因为tan ⎝⎛⎭⎫π4＋α＝2，所以1＋tan α1－tan α＝2，解得tan α＝13，所以12sin α·cos α＋cos 2α＝sin 2α＋cos 2α2sin α·cos α＋cos 2α＝tan 2α＋12tan α＋1＝19＋123＋1＝23.答案：239．已知cos(α＋β)＝13，cos(α－β)＝15，求tan α·tan β的值．解：cos(α＋β)＝cos αcos β－sin αsin β＝13，①cos(α－β)＝cos αcos β＋sin αsin β＝15，②由①②整理得⎩⎨⎧cos αcos β＝415，sin αsin β＝－115，则tan αtan β＝sin αsin βcos αcos β＝－115415＝－14.10．若tan α，tan β是方程x 2－3x －3＝0的两根，求sin 2(α＋β)－3sin(α＋β)cos(α＋β)－3cos 2(α＋β)的值．解：由根与系数的关系可得， tan α＋tan β＝3，tan αtan β＝－3，所以tan(α＋β)＝tan α＋tan β1－tan αtan β＝31－（－3）＝34.sin 2(α＋β)－3sin(α＋β)cos(α＋β)－3cos 2(α＋β)＝sin 2（α＋β）－3sin （α＋β）cos （α＋β）－3cos 2（α＋β）sin 2（α＋β）＋cos 2（α＋β）＝tan 2（α＋β）－3tan （α＋β）－3tan 2（α＋β）＋1＝⎝⎛⎭⎫342－3×34－3⎝⎛⎭⎫342＋1＝－3. [B 能力提升]1．(1＋tan21°)(1＋tan22°)(1＋tan23°)(1＋tan24°)的值为( ) A ．16 B ．8 C ．4D ．2解析：选C.由于21°＋24°＝45°，23°＋22°＝45°，利用两角和的正切公式及其变形可得(1＋tan21°)(1＋tan24°)＝2，(1＋tan22°)(1＋tan23°)＝2，故(1＋tan21°)(1＋tan22°)(1＋tan23°)(1＋tan24°)＝4.2．已知tan α＝13，cos β＝55且0<α<π2，3π2<β<2π则α＋β的值为________．解析：因为3π2<β<2π且cos β＝55，所以sin β＝－255，所以tan β＝sin βcos β＝－2，所以tan(α＋β)＝tan α＋tan β1－tan αtan β＝13－21＋23＝－1，又因为0<α<π2，所以3π2<α＋β<52π，所以α＋β＝74π.答案：74π3．已知tan ⎝⎛⎭⎫π4＋α＝2，tan β＝12，求sin （α＋β）－2sin αcos β2sin αsin β＋cos （α＋β）的值．解：由tan ⎝⎛⎭⎫α＋π4＝1＋tan α1－tan α＝2，解得tan α＝13.所以sin （α＋β）－2sin αcos β2sin αsin β＋cos （α＋β）＝sin αcos β＋cos αsin β－2sin αcos β2sin αsin β＋cos αcos β－sin αsin β＝cos αsin β－sin αcos βcos αcos β＋sin αsin β＝sin （β－α）cos （β－α）＝tan(β－α)＝tan β－tan α1＋tan βtan α＝12－131＋12×13＝17.4．(选做题)如图所示，在平面直角坐标系xOy 中，以Ox 轴为始边的两个锐角为α，β，它们的终边分别交单位圆于A ，B 两点，已知A ，B 两点的横坐标分别是210和255. (1)求tan(α＋β)的值； (2)求α＋2β的值．解：(1)由单位圆中三角函数的定义，可得cos α＝210，cos β＝255. 由于α，β为锐角，所以sin α＝1－cos 2α＝7210，sin β＝1－cos 2 β＝55.从而tan α＝7，tan β＝12，所以tan(α＋β)＝tan α＋tan β1－tan αtan β＝7＋121－72＝－3.(2)因为tan(α＋2β)＝tan[(α＋β)＋β]＝tan （α＋β）＋tan β1－tan （α＋β）tan β＝－3＋121＋32＝－1，又0＜α＜π2，0＜β＜π2，所以0＜α＋2β＜3π2，从而α＋2β＝3π4.。

高中数学必修四北师大版两角和与差的正切函数课时作业含答案

两角和与差的正切函数课时作业北师大版必修4一、选择题1．若tan α＝3，tan β＝43，则tan(α－β)等于( )A ．－3B ．－13C ．3D ．13[答案] D[解析] tan(α－β)＝tan α－tan β1＋tan αtan β＝3－431＋3×43＝13.2．若tan ⎝ ⎛⎭⎪⎫π4－α＝3，则tan α等于( ) A ．－2 B ．－12C ．12 D ．2[答案] B[解析] tan α＝tan ⎣⎢⎡⎦⎥⎤π4－⎝ ⎛⎭⎪⎫π4－α＝tan π4－tan ⎝ ⎛⎭⎪⎫π4－α1＋tan π4tan ⎝ ⎛⎭⎪⎫π4－α＝－12.3．若tan α＝2，tan β＝3，且α，β∈(0，π2)，则α＋β的值为( )A ．30°B ．45°C ．135°D ．225° [答案] C[解析] ∵tan(α＋β)＝tan α＋tan β1－tan αtan β＝2＋31－2×3＝－1,0<α＋β<π，∴α＋β＝135°.4．若sin α＝45，tan(α＋β)＝1，且α是第二象限角，则tan β的值为( )A ．43B ．－43C ．－7D ．－17[答案] C[解析] 因为sin α＝45，α是第二象限角，所以cos α＝－35.所以tan α＝－43.因为tan(α＋β)＝tan α＋tan β1－tan αtan β，所以1＝－43＋tan β1＋43tan β，解得tan β＝－7.5．若∠A ＝22°，∠B ＝23°，则(1＋tan A )(1＋tan B )的值是( ) A ． 3 B ．2C ．1＋ 2D ．2(tan A ＋tan B )[答案] B[解析] 因为原式＝1＋tan A ＋tan B ＋tan A tan B ＝1＋tan A tan B ＋tan(A ＋B )(1－tan A tan B )＝1＋tan A tan B ＋tan45°(1－tan A tan B )＝2＋tan A tan B －tan A tan B ＝2. 6．若tan28°tan32°＝m ，则tan28°＋tan32°的值为( ) A ．3m B ．3(1－m ) C ．3(m －1) D ．3(m ＋1) [答案] B[解析] ∵tan(28°＋32°)＝tan28°＋tan32°1－tan28°tan32°，∴tan28°＋tan32°＝tan60°(1－tan28°tan32°)＝3(1－m )．二、填空题 7.tan23°＋tan37°1－tan23°tan37°＝________.[答案]3[解析] 原式＝tan(23°＋37°)＝tan60°＝ 3.8．设sin α＝35(π2<α<π)，tan(π－β)＝12，则tan(α－2β)＝________.[答案]724[解析] sin α＝35(π2<α<π)，则tan α＝－34.tan(π－β)＝12，则tan β＝－12，tan(α－β)＝tan α－tan β1＋tan αtan β＝－34＋121＋34×12＝－211，tan(α－2β)＝tan α－β －tan β1＋tan α－β tan β＝－211＋121＋211×12＝724.三、解答题9．计算下列各式的值． (1)tan15°＋tan75°； (2)tan41°＋tan19°1－tan41°tan19°. [分析] 观察各式的特点，设法化为特殊角的和、差正切公式计算．[解析] (1)tan15°＋tan75°＝tan(45°－30°)＋tan(45°＋30°)＝1－tan30°1＋tan30°＋1＋tan30°1－tan30°＝1－331＋33＋1＋331－33＝3－11＋3＋1＋33－1＝4. (2)原式＝tan(41°＋19°)＝tan60°＝ 3.10．如图，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆交于A ，B 两点．已知点A，B 的横坐标分别为210，255.(1)求tan(α＋β)的值； (2)求α＋2β的值．[解析] (1)由已知条件及三角函数的定义，可知cos α＝210，cos β＝255. 因为α为锐角，故sin α>0，从而sin α＝1－cos 2α＝7210. 同理可得sin β＝55.因此tan α＝7，tan β＝12. 所以tan(α＋β)＝tan α＋tan β1－tan αtan β＝7＋121－7×12＝－3.(2)tan(α＋2β)＝tan[(α＋β)＋β]＝tan α＋β ＋tan β1－tan α＋β tan β＝－3＋121－－3 ×12＝－1.又0<α<π2，0<β<π2，故0<α＋2β<3π2，从而由tan(α＋2β)＝－1，得α＋2β＝3π4.一、选择题1．△ABC 中，tan A ·tan B >1，则△ABC 为( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．不能确定[答案] A[解析] ∵tan A ·tan B >1>0.∴tan A >0且tan B >0(否则A 、B 同为钝角，不可能)， ∴tan(A ＋B )＝tan A ＋tan B1－tan A tan B <0，∴90°<A ＋B <180°，∴0°<C <90°.2．已知sin2α＝35⎝ ⎛⎭⎪⎫π2<2α<π，tan(α＋β)＝－2，tan(α－β)的值为( ) A ．12 B ．－12C ．－211D ．211 [答案] A。

高中数学北师大版必修4《第3章22.3两角和与差的正切函数》课件

34
谢谢大家
1_＋__ta_n__α_ta_n_β__
使用条件
α，β，α＋β≠kπ＋π2(k∈Z) 且 tan α·tan β≠1
α，β，α－β≠kπ＋π2(k∈Z) 且 tan α·tan β≠－1
3
(1)变形公式
tan α＋tan β＝tan(α＋β)(1－tan αtan β)；
tan α－tan β＝tan(α－β)(1＋tan αtan β)；
数学北师大版高中数学
2.3 两角和与差的正切函数
学习目标
核心素养
1.能利用两角和(或差)的正弦、
1.通过利用两角和(或差)的正弦、
余弦公式导出两角和(或差)的正
余弦公式导出两角和(或差)的正
切公式．(重点)
切公式，提升逻辑推理素养．
2.掌握公式 T(α±β)及其变形式，并能利用这些公式解决化简、求
A＋tan B A＋ 3tan
＝ B
3 3.
又 0°<C<180°，∴C＝30°，∴B＝30°.
∴△ABC 是顶角为 120°的等腰三角形．
26
将例 3 中的条件变为“△ABC 中，∠C＝120°，tan A＋tan B＝ 23 3”，试求 tan A·tan B 的值．
[解] 因为 A＋B＋C＝180°，∠C＝120°，
第三个．( )
(2)tanπ2＋π3能用公式 tan(αR，使 tan(α＋β)＝tan α＋tan β 成立．( )
(4)公式 T(α±β)对任意 α，β 都成立．( )
[答案] (1)√ (2)× (3)√ (4)×
31
2．已知 A＋B＝45°，则(1＋tan A)(1＋tan B)的值为( )

数学北师大版必修4练习24 两角和与差的正切函数 Word版含解析

两角和与差的正切函数时间：分钟满分：分班级姓名分数一、选择题：(每小题分，共×＝分)．设α＝，β＝，且α、β角为锐角，则α＋β的值是( )或答案：解析：由α＝，β＝，得(α＋β)＝＝＝.又α、β均是锐角，∴α＋β＝.的值是( )．－．－答案：解析：＝＝(°＋°)＝°＝－°＝－.．已知(α＋β)＝，＝，那么＝( )答案：解析：因为α＋＝(α＋β)－，所以＝＝＝，故选.．已知α＝，则的值是( )．．－．－答案：解析：解法一：因为α＝，所以＝＝＝，所以＝＝.故选.解法二：＝＝＝α＝.故选.．在△中，若>，则△是( )．锐角三角形．直角三角形．钝角三角形．无法确定答案：解析：由>得角，均为锐角，然后切化弦，得>，即(＋)<，∴(π－)<，∴－<，∴>，∴角为锐角，∴△是锐角三角形，故选.．设α和β是方程＋(－)＋(－)＝的两根，则(α＋β)的最小值是( )．－．不确定答案：解析：∵α和β是＋(－)＋(－)＝的两根，∴(\\(α＋β＝－(－)，α·β＝(－)，≠，,Δ＝(－(－(－(≥.))∴≤，且≠(α＋β)＝＝＝＝－＋.∴当＝时，(α＋β)的最小值为－.二、填空题：(每小题分，共×＝分)．已知α为第三象限的角，α＝－，则(＋α)＝.答案：－解析：∵α为第三象限的角，则π＋π≤α≤π＋，∴π＋π≤α≤π＋π(∈)，又α＝－，∴α＝，α＝－，∴(＋α)＝＝－.．＋＋·的值为．答案：解析：＋＋·＝＋·＝＋·＝.．若，是非零实数，且＝，则＝.答案：解析：∵＝＝＝(＋)＝，∴＝＝.三、解答题：(共分，＋＋)．在平面直角坐标系中，以为始边作两个锐角α，β，它们的终边分别与单位圆相交于，两点，已知点，的横坐标分别为，.()求(α＋β)的值；()求的值．解析：()由题意，得α＝，β＝.因为α，β为锐角，所以α＝，β＝，因为α＝，β＝.所以(α＋β)＝＝＝－.()＝×＝×[(α＋β)－α]＝×β＝×＝.．已知(α＋β)＝，(α－β)＝，求(π＋α)＋(π＋β)的值．解析：因为(α＋β)＝，(α－β)＝，所以α＝[(α＋β)＋(α－β)]＝＝＝－，β＝[(α＋β)－(α－β)]＝＝＝－，所以(π＋α)＋(π＋β)＝α＋β＝－－＝－.．已知向量＝(θ，)，＝(θ，))，且，共线，其中θ∈.()求的值；()若(θ－φ)＝φ，<φ<，求φ的值．解析：()∵，共线，∴θ－θ＝，即θ＝.∴＝＝＝－.()由()，知θ＝，又θ∈，∴θ＝，θ＝.∵(θ－φ)＝φ，∴(θφ＋θφ)＝φ，即φ＋φ＝φ，∴φ＝φ.又<φ<，∴φ＝，∴φ＝.。

北师大版数学高一-两角和与差的正切公式同步练习(北师大版必修四)

两角和与差的正切函数同步练习一、选择题1.tan20°tan20°tan40°=（）2.若A 、B 为锐角三角形的两个锐角，则tanAtanB 的值是（） A.不大于1 B. 小于1 C. 等于1 D. 大于13.已知tan(+)=2/5,tan(-/5)=1/4,则tan(+/5）=( )A.-1/6B.1/6C.13/12D.3/22 4.在ABC 中，已知tansin 2A BC ,下列四个论断中正确的是（）① tanA cotB=1 ② 0<sinA+sinB③22sin cos 1AB ④ 222cos cos sin A B CA.①③B.②④C.①④D.②③5.已知tan=4,cot=13,则tan(）= ( ) A.711 B. -711 C.713 D.-7136.已知(,),2 sin =35,则tan(4)=( )A .17 B.7 C.-17D. -77.若1tan 21tan，则tan(4）=（）A. 2B. -2C.12 D. -128.51tantan 1245tan tan 124 =（）9.在ABC 中，tanAtanB,则 C=（）A .3B .23 C.6 D.410.若tanA=2,tan(B-A)=3,则tan(B-2A)=（）A. -1B. -15 C .57 D .17二、填空题11.在ABC 中，已知tanA 、tanB 是方程 23810x x 的两个根，则tanC=________12.已知,满足=4，则（1+tan ）(1+tan )=_______13.已知=6，且,tantan+a ）+2 tan+3 tan=0,则tan =_______参考答案1.答案：B解析：原式=tan60°（1-tan20°tan40°）tan20°tan40°=tan60°2.答案：D解析：由题知180°>A+B>90°，tan(A+B)<0,由tan(A+B)=tan tan 1tan tan A BA B,且tanA>0,tanB>0,1-tanAtanB<0,tanAtanB>13.答案：D 解析：tan(+ /5）=tan[(+)-(-/5)]=215421154=3/224.解析：A+B+C=180°tan tan(902A B °-2C ）=cot 2C =cos2sin 2C C =sinC=2sin 2C cos 2Csin2C =2,2C =45°，故C=90°。

2020-2021学年数学北师大版必修4课时作业：3-2-3 两角和与差的正切函数

课时作业24 两角和与差的正切函数时间：45分钟满分：100分——基础巩固类——一、选择题(每小题5分，共40分) 1．求值：1－tan15°1＋tan15°＝( C )A ．12B ． 3C ．33D ．32解析：1－tan15°1＋tan15°＝tan45°－tan15°1＋tan45°tan15°＝tan(45°－15°)＝tan30°＝33.故选C ．2．若tan ⎝ ⎛⎭⎪⎫α－π4＝13，则tan α等于( C )A ．12 B ．－12 C ．2D ．－2解析：∵tan ⎝ ⎛⎭⎪⎫α－π4＝tan α－11＋tan α＝13， ∴tan α＝2.3．若A ＝15°，B ＝30°，则(1＋tan A )(1＋tan B )的值为( B ) A ．1 B ．2 C ．－1D ．－2解析：∵tan(A ＋B )＝tan45°＝1，∴tan A ＋tan B1－tan A tan B ＝1.∴tan A ＋tan B ＝1－tan A tan B ．∴(1＋tan A )(1＋tan B )＝1＋tan A ＋tan B ＋tan A tan B ＝2.4．△ABC 中，tan A ·tan B >1，则△ABC 为( A ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．不能确定解析：∵tan A ·tan B >1>0.∴tan A >0且tan B >0(否则A 、B 同为钝角，不可能)， ∴tan(A ＋B )＝tan A ＋tan B 1－tan A tan B <0，∴90°<A ＋B <180°，∴0°<C <90°.5．若tan(α＋β)＝34，tan(β－π4)＝12，那么tan(α＋π4)的值等于( A ) A ．211 B ．411 C ．12D ．2解析：∵α＋π4＝(α＋β)－(β－π4)， ∴tan(α＋π4)＝tan[(α＋β)－(β－π4)]＝tan (α＋β)－tan (β－π4)1＋tan (α＋β)tan (β－π4)＝34－121＋34×12＝14118＝211. 6．若sin α＝45，tan(α＋β)＝1，且α是第二象限角，则tan β＝( C ) A ．43 B ．－43 C ．－7D ．－17解析：因为sin α＝45，α为第二象限角，所以cos α＝－35，所以tan α＝－43. 因为tan(α＋β)＝tan α＋tan β1－tan αtan β，所以1＝－43＋tan β1＋43tan β，解得tan β＝－7. 7．已知tan α，tan β是关于x 的一元二次方程x 2＋6x ＋2＝0的两个实数根，则sin (α＋β)cos (α－β)＝( C )A ．－1B ．1C ．－2D ．2解析：∵tan α，tan β是关于x 的一元二次方程x 2＋6x ＋2＝0的两个实数根，∴tan α＋tan β＝－6，tan α·tan β＝2.则sin (α＋β)cos (α－β)＝sin αcos β＋cos αsin βcos αcos β＋sin αsin β＝tan α＋tan β1＋tan αtan β＝－61＋2＝－2.8．已知tan110°＝a ，求tan10°的值，那么以下四个★★★★答案★★★★中：①a ＋31－3a ；②a ＋33a －1；③a ＋a 2＋1；④a －a 2＋1正确的是( D )A ．①②B ．③④C ．①④D ．②③解析：tan110°＝－tan70°＝－sin70°cos70°＝－cos20°sin20°＝－1tan20°＝－1tan (10°＋10°)＝－1－tan 210°2tan10°＝a ，则tan 210°－2a tan10°－1＝0， ∴tan10°＝a ±a 2＋1，由于tan110°<0，∴a <0，而tan10°>0， ∴tan10°＝a ＋a 2＋1，故③正确．又tan10°＝－tan170°＝－tan110°＋tan60°1－tan110°tan60°＝－a ＋31－3a ＝a ＋33a －1，故②正确．二、填空题(每小题5分，共15分)9．在△ABC 中，tan A ＋tan B ＋3＝3tan A tan B ，则C ＝π3.解析：由已知得tan A ＋tan B ＝－3(1－tan A tan B )， ∴tan(A ＋B )＝－ 3.∵A ，B 均为△ABC 的内角，∴0<A ＋B <π. ∴A ＋B ＝2π3.∴C ＝π3.10．已知α、β均为锐角，且tan β＝cos α－sin αcos α＋sin α，则tan(α＋β)＝1.解析：tan β＝cos α－sin αcos α＋sin α＝1－tan α1＋tan α＝tan(π4－α)，∵α，β均为锐角，∴β＝π4－α，∴α＋β＝π4， ∴tan(α＋β)＝tan π4＝1.11．已知tan(α＋β＋γ)＝m tan(α－β＋γ)，且sin2(α＋γ)＝5sin2β，则实数m ＝32.解析：设A ＝α＋β＋γ，B ＝α－β＋γ，则2(α＋γ)＝A ＋B,2β＝A －B ．因为sin2(α＋γ)＝5sin2β，所以sin(A ＋B )＝5sin(A －B )，所以sin A cos B ＋cos A sin B ＝5(sin A cos B －cos A sin B )，所以6cos A sin B ＝4sin A cos B ，所以2tan A ＝3tan B ．故m ＝tan A tan B ＝32.三、解答题(共25分，解答应写出必要的文字说明、证明过程或演算步骤)12．(12分)如图，△ABC 中，∠BAC ＝45°，BC 边上的高AD 将BC 分成2 cm 和3 cm 两段，求△ABC 的面积．解：设∠BAD ＝α，∠CAD ＝β，AD ＝x .在Rt △ADB 中，tan α＝BD AD ＝2x . 在Rt △ADC 中，tan β＝DC AD ＝3x . tan45°＝tan α＋tan β1－tan α·tan β＝2x ＋3x 1－2x ·3x ＝1，即5xx 2－6＝1. 解这个方程，得x ＝6或x ＝－1(舍)．故S △ABC ＝12×5×6＝15(cm 2)．13．(13分)在△ABC 中，tan B ＋tan C ＋3tan B tan C ＝3，3tan A ＋3tan B ＋1＝tan A tan B ，试判断△ABC 的形状．解：由tan B ＋tan C ＋3tan B tan C ＝3，得tan B ＋tan C ＝3(1－tan B tan C )．若tan B tan C ＝1，则tan B ＝1tan C . 故在△ABC 中，∠B ＝π2－∠C ， ∴∠B ＋∠C ＝π2，即∠A ＝π2，此时tan A 无意义，与题设矛盾． ∴tan B tan C ≠1， ∴tan B ＋tan C1－tan B tan C＝tan(B ＋C )＝ 3.又∵∠B ＋∠C ∈(0，π)， ∴∠B ＋∠C ＝π3.同理，∵3tan A ＋3tan B ＋1＝tan A tan B ， ∴tan(A ＋B )＝tan A ＋tan B 1－tan A tan B＝－33.∵∠A ＋∠B ∈(0，π)， ∴∠A ＋∠B ＝56π. 又∵∠A ＋∠B ＋∠C ＝π， ∴∠A ＝23π，∠B ＝∠C ＝π6， ∴△ABC 为等腰三角形．——能力提升类——14．(5分)已知△ABC 的三个内角分别为A ，B ，C ，若sin A ＋3cos Acos A －3sin A ＝tan 5π6，则sin(B ＋C )＝( B )A ．32B ．1C ．12D ．22 解析：由sin A ＋3cos A cos A －3sin A＝tan 5π6，得sin (A ＋π3)cos (A ＋π3)＝tan 5π6，所以tan(A ＋π3)＝tan 5π6，所以A ＋π3＝k π＋5π6，k ∈Z ，所以A ＝π2＋k π，k ∈Z .因为角A 为三角形的内角，所以A ＝π2，所以sin(B ＋C )＝1，故选B ．15．(15分)是否存在锐角α和β，使α＋2β＝2π3①，且tan α2tan β＝2－3②，同时成立？若存在，求出α和β的值；若不存在，请说明理由．解：存在．解法一：由①得α2＋β＝π3.∴tan(α2＋β)＝tan α2＋tan β1－tan α2tan β＝ 3. 将②代入得tan α2＋tan β＝3－ 3.∴tan α2，tan β是方程x 2－(3－3)x ＋2－3＝0的两根．解得x 1＝1，x 2＝2－ 3.若tan α2＝1，则与α为锐角矛盾．∴tan β＝1，tan α2＝2－3，∴β＝π4，代入①得α＝π6，满足tan α2＝2－ 3.解法二：由①得α2＝π3－β，代入②得： tan(π3－β)·tan β＝2－ 3 ⇒3－tan β1＋3tan β·tan β＝2－ 3 ⇒tan 2β－(3－3)tan β＋2－3＝0， tan β＝1或2－ 3.若tan β＝1，则β＝π4，α＝π6.若tan β＝2－ 3.代入②得tan α2＝1.不合题意．故存在α＝π6，β＝π4，使①②同时成立．感谢您的下载!快乐分享，知识无限！由Ruize收集整理！。

高中数学 3.2.3两角和与差的正切函数课时作业北师大

两角和与差的正切函数一、选择题(每小题3分,共18分)1.(2014·南昌高一检测)tan10°tan20°+(tan10°+tan20°)等于( )A. B.1 C. D.【解析】选B.原式=1-+(tan10°+tan20°)=1-(tan10°+tan20°)+(tan10°+tan20°)=1.2.已知tan(α-β)=,tan=-,则tan的值为( )A.-B.C.D.-【解题指南】α+可以表示为α-β与β+和的形式.【解析】选B.分析题中角度之间的关系可知,tan=tan===.3.(2014·合肥高一检测)在△ABC中,已知tanA,tanB是方程3x2+8x-1=0的两个根,则tanC等于( )A.2B.-2C.4D.-4【解题指南】根据根与系数的关系求得tanA+tanB与tanAtanB,再求ta n(A+B)=-tanC.【解析】选 A.由于tanA,tanB是方程3x2+8x-1=0的两个根,那么根据根与系数的关系,有tanA+tanB=-,tanA·tanB=-.则tanC=tan[π-(A+B)]=-tan(A+B)=-=-=2.4.在△ABC中,若0<tanBtanC<1,则△ABC是( )A.锐角三角形B.钝角三角形C.直角三角形D.形状不能确定【解析】选B.由条件知,tanB>0,tanC>0,因为0<tanBtanC<1,所以1-tanBtanC>0,根据两角和的正切公式可得tan(B+C)=>0.所以B+C为锐角,从而A为钝角.故选B.【一题多解】选B.因为0<tanBtanC<1,所以B,C均为锐角,所以<1,所以cos(B+C)>0,所以cosA<0,所以A为钝角.故选B.5.已知sinα=且α为锐角,tanβ=-3且β为钝角,则角α+β的值为( )A. B. C. D.【解析】选B.sinα=,且α为锐角,则cosα=,tanα=,所以tan(α+β)===-1,又α+β∈,故α+β=.6.(2014·安庆高一检测)已知tanα和tan是方程ax2+bx+c=0的两个根,则a,b,c的关系是( )A.b=a+cB.2b=a+cC.c=a+bD.c=ab【解析】选C.tanα+tan=-,tanαtan=,所以tan==1.所以-=1-.所以-b=a-c,所以c=a+b.二、填空题(每小题4分,共12分)7.(2014·抚州高一检测)的值为.【解析】原式==tan(105°-60°)=tan 45°=1.答案:1【变式训练】计算:= .【解析】原式==·tan30°=.答案:8.已知tanα=,tan(α-β)=,则tanβ= .【解析】tanβ=tan[α-(α-β)]===-.答案:-9.(2013·宁波高一检测)若tanα+tanβ-tanαtanβ+1=0,α,β∈,则α+β为. 【解析】tanα+tanβ=tan(α+β)(1-tanαtanβ),因为tanα+tanβ-tanαtanβ+1=0,所以1-tanαtanβ=-tan(α+β)(1-tanαtanβ),所以tan(α+β)=-1,又因为α,β∈,所以π<α+β<2π,所以α+β=.答案:三、解答题(每小题10分,共20分)10.(2014·长春高一检测)已知角α的终边经过点P(-3,-4),求tan的值.【解析】由已知得OP==.由三角函数的定义得sinα==-,cosα==-,tanα==.tan===-.11.(2014·西安高一检测)已知tanα与tan是方程x2+px+q=0的两根,且tanα∶tan=3∶2,求p和q的值.【解析】由已知tanα∶tan=3∶2得tanα∶=3∶2,所以2tan2α+5tanα-3=0,解得tanα=或tanα=-3.当tanα=时,tan=,此时tanα+tan=-p,tanαtan=q,所以p=-,q=.当ta nα=-3时,tan=-2,p=-=5,q=tanαtan=6.所以p=-,q=或p=5,q=6.一、选择题(每小题4分,共16分)1.(2014·南昌高一检测)的值为( )A.2+B.C.2-D.【解析】选C.分析角度关系,可知sin6°=sin(15°-9°)=sin15°cos9°-cos15°sin9°,cos6°=cos(15°-9°)=cos15°cos9°+sin15°sin9°,所以原式=tan15°=tan(45°-30°)==2-.2.(2014·合肥高一检测)已知cos=-,且x是第三象限角,则的值为( )A.-B.-C.D.【解题指南】先求tan,再逆用公式Tα+β即得.【解析】选D.由cos=-,且x是第三象限角知sin=-.所以tan==,所以==tan=.3.若tan 28°·tan 32°=m,则tan 28°+tan 32°= ( )A.mB.(1-m)C.(m-1)D.(m+1)【解析】选B.tan(28°+32°)=tan 60°===,所以tan 28°+tan 32°=(1-m).4.(2014·汉中高一检测)已知a=(cosx,2),b=(2sinx,3),且a∥b,则tan=( )A.7B.-7C.D.-【解析】选A.因为a=(cos x,2),b=(2sinx,3),且a∥b,故3cosx=4sinx,即tanx=,所以tan===7.【变式训练】已知α+β=π,则(1-tanα)(1-tanβ)=( )A.2B.-2C.1D.-1【解析】选A.-1=tan(α+β)=,所以tanα+tanβ=-1+tanαtanβ.所以(1-tanα)(1-tanβ)=1-tanα-tanβ+tanαtanβ=2.二、填空题(每小题5分,共10分)5.若锐角α,β满足(1+tanα)(1+tanβ)=4,则α+β= .【解析】因为(1+tanα)(1+tanβ)=4,所以1+(tanα+tanβ)+3tanαtanβ=4,即tanα+tanβ=(1-tanαtanβ).所以tan(α+β)===.又因为0<α+β<π,所以α+β=.答案:6.(2014·宝鸡高一检测)计算:tan(18°-x)tan(12°+x)+[tan(18°-x)+tan(12°+x)]= . 【解析】因为tan[(18°-x)+(12°+x)]==tan30°=,所以tan(18°-x)+tan(12°+x)=[1-tan(18°-x)·tan(12°+x)]于是原式=tan(18°-x)tan(12°+x)+·[1-tan(18°-x)·tan(12°+x)]=1.答案:1【变式训练】计算:= .【解析】由tan60°=tan(18°+42°)==,得到tan18°+tan42°=-tan18°tan42°,则===-1.答案:-1三、解答题(每小题12分,共24分)7.(2014·西安高一检测)一元二次方程mx2+(2m-3)x+(m-2)=0的两根为tanα,tanβ,求tan(α+β)的最小值.【解析】因为mx2+(2m-3)x+(m-2)=0有两根tanα,tanβ,所以解得m≤,且m≠0,由一元二次方程的根与系数的关系得tanα+tanβ=,tanα·tanβ=,所以tan(α+β)====-m≥-=-.故tan(α+β)的最小值为-.【误区警示】解答本题时易忽视Δ≥0且m≠0,即实数m的取值范围求错而致误.8.是否存在锐角α,β,使得(1)α+2β=.(2)tan·tanβ=2-同时成立?若存在,求出锐角α,β的值;若不存在,说明理由.【解析】假设存在锐角α,β,使得(1)α+2β=.(2)tan·tanβ=2-同时成立.由(1)得+β=,所以tan==.又tan tanβ=2-,所以tan+tanβ=3-.因此tan,tanβ可以看成是方程x2-(3-)x+2-=0的两个根. 解得x1=1,x2=2-.若tan=1,则α=,这与α为锐角矛盾.所以tan=2-,tanβ=1,所以α=,β=.所以满足条件的α,β存在,且α=,β=.。

高中数学-3.2.3两角和与差的正切函数课件-北师大必修4

3
(4)原式=tan(22°+23°)=tan 45°=1.
答案：1
【要点探究】
知识点正切的和、差角公式Tα±β 1.公式成立的条件
角α,β以及α±β均不能等于kπ+ (k∈Z)，且tanαtanβ
≠1(或tan αtan β≠-1).
2
2.结构特征公式Tα±β的右侧为分式形式，其中分子为tan α与tan β的和或差，分母为1与tan αtan β的差或和.
【解析】(1)错误，因为tan(α±β)= tan tan . 1 tan tan
(2)错误，因为tan(α+β)= tan tan . (3)错误，tan(40°+50°)中410°+tan50°ta=n90°,不成立.
(4)错误,因为tan 90°不存在. 答案：(1)× (2)× (3)× (4)×
3 3 x+4=0的两根，且＜＜，＜＜，则α+β的值为 2 22 2
()
A. 3
C. 2 或 33
B. 2 3
D.无法确定
(2)(2014·上饶高一检测)已知tan(α-β)= 且α,β∈(0,π),
1 2
,tan
β=
1 7
,
①求tan α;
②求2α-β的值.
【解题探究】
1.一元二次方程ax2+bx+c=0中，根与系数有怎样的关系？
ta反n 映了复角化单角的思想1，即tan要求tanα± β的正 tan
切函数值，只需知道tan α和tan β的值，代入求解便可.
(2)整体意识：公式Tα±β中有两个小团体“tan α±tan β ” 及“tan αtan β ”，求解时可利用整体思想代入求解.

北师大版高中数学必修四24 两角和与差的正切函数.docx

24 两角和与差的正切函数时间：45分钟满分：80分班级________ 姓名________ 分数________一、选择题：(每小题5分，共5×6＝30分)1．设tan α＝12，tan β＝13，且α、β角为锐角，则α＋β的值是( ) A.3π4 B.π4或3π4C.π4D.5π4答案：C解析：由tan α＝12，tan β＝13，得tan(α＋β)＝tan α＋tan β1－tan αtan β＝12＋131－12×13＝1.又α、β均是锐角， ∴α＋β＝π4. 2.1＋tan75°1－tan75°的值是( ) A. 3 B ．－ 3C.33 D ．－33答案：B解析：1＋tan75°1－tan75°＝tan45°＋tan75°1－tan45°tan75°＝tan(45°＋75°)＝tan120°＝－tan60°＝－ 3. 3．已知tan(α＋β)＝25，tan ⎝⎛⎭⎫β－π4＝14，那么tan ⎝⎛⎭⎫α＋π4＝( ) A.1318 B.1322C.322D.518答案：C解析：因为α＋π4＝(α＋β)－⎝⎛⎭⎫β－π4，所以tan ⎝⎛⎭⎫α＋π4＝tan ⎣⎡⎦⎤(α＋β)－⎝⎛⎭⎫β－π4＝tan (α＋β)－tan ⎝⎛⎭⎫β－π41＋tan (α＋β)tan ⎝⎛⎭⎫β－π4＝322，故选C.4．已知tan α＝12，则tan ⎝⎛⎭⎫π4＋α－11＋tan ⎝⎛⎭⎫π4＋α的值是( ) A ．2 B.12C ．－1D ．－3答案：B解析：解法一：因为tan α＝12，所以tan ⎝⎛⎭⎫π4＋α＝tan π4＋tan α1－tan π4·tan α＝1＋tan α1－tan α＝3，所以tan ⎝⎛⎭⎫π4＋α－11＋tan ⎝⎛⎭⎫π4＋α＝3－11＋3＝12.故选B. 解法二：tan ⎝⎛⎭⎫π4＋α－11＋tan ⎝⎛⎭⎫π4＋α＝tan ⎝⎛⎭⎫π4＋α－tan π41＋tan ⎝⎛⎭⎫π4＋α·tan π4＝tan ⎣⎡⎦⎤⎝⎛⎭⎫π4＋α－π4＝tan α＝12.故选B. 5．在△ABC 中，若tan A tan B >1，则△ABC 是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．无法确定答案：A解析：由tan A tan B >1得角A ，B 均为锐角，然后切化弦，得sin A sin B >cos A cos B ，即cos(A＋B )<0，∴cos(π－C )<0，∴－cos C <0，∴cos C >0，∴角C 为锐角，∴△ABC 是锐角三角形，故选A.6．设tan α和tan β是方程mx 2＋(2m －3)x ＋(m －2)＝0的两根，则tan(α＋β)的最小值是( )A.154B.34C ．－34D ．不确定答案：C解析：∵tan α和tan β是mx 2＋(2m －3)x ＋(m －2)＝0的两根， ∴⎩⎪⎨⎪⎧ tan α＋tan β＝－2m －3m ，tan α·tan β＝m －2m，m ≠0，Δ＝(2m －3)2－4m (m －2)≥0.∴m ≤94，且m ≠0.tan(α＋β)＝tan α＋tan β1－tan αtan β＝－2m －3m 1－m －2m＝－2m ＋32＝－m ＋32. ∴当m ＝94时，tan(α＋β)的最小值为－34. 二、填空题：(每小题5分，共5×3＝15分)7．已知α为第三象限的角，cos2α＝－35，则tan(π4＋2α)＝________.答案：－17解析：∵α为第三象限的角，则2k π＋π≤α≤2k π＋3π2，∴4k π＋2π≤2α≤4k π＋3π(k ∈Z )，又cos2α＝－35， ∴sin2α＝45，tan2α＝－43，∴tan(π4＋2α)＝1＋tan2α1－tan2α＝－17. 8．tan π9＋tan 2π9＋3tan π9·tan 2π9的值为________．答案： 3解析：tan π9＋tan 2π9＋3tan π9·tan 2π9＝tan ⎝⎛⎭⎫π9＋2π9⎝⎛⎭⎫1－tan π9·tan 2π9＋3tan π9·tan 2π9＝3⎝⎛⎭⎫1－tan π9·tan 2π9＋3tan π9·tan 2π9＝ 3. 9．若a ，b 是非零实数，且a sin π5＋b cos π5a cos π5－b sin π5＝tan 8π15，则b a ＝________. 答案： 3解析：∵a sin π5＋b cos π5a cos π5－b sin π5＝tan π5＋b a 1－b a tan π5＝tan 8π15＝tan(π5＋π3)＝tan π5＋tan π31－tan π5·tan π3，∴b a ＝tan π3＝ 3. 三、解答题：(共35分，11＋12＋12)10．在平面直角坐标系xOy 中，以Ox 为始边作两个锐角α，β，它们的终边分别与单位圆相交于A ，B 两点，已知点A ，B 的横坐标分别为13，255. (1)求tan(α＋β)的值；(2)求tan (α＋β)－tan α2＋2tan (α＋β)·tan α的值．解析：(1)由题意，得cos α＝13，cos β＝255. 因为α，β为锐角，所以sin α＝223，sin β＝55，因为tan α＝22，tan β＝12. 所以tan(α＋β)＝tan α＋tan β1－tan αtan β＝22＋121－22×12＝－9＋522. (2)tan (α＋β)－tan α2＋2tan (α＋β)·tan α＝12×tan (α＋β)－tan α1＋tan (α＋β)·tan α＝12×tan[(α＋β)－α] ＝12×tan β ＝12×12＝14. 11．已知tan(α＋β)＝2，tan(α－β)＝3，求tan(3π＋2α)＋tan(4π＋2β)的值．解析：因为tan(α＋β)＝2，tan(α－β)＝3，所以tan2α＝tan[(α＋β)＋(α－β)]＝tan (α＋β)＋tan (α－β)1－tan (α＋β)tan (α－β)＝2＋31－2×3＝－1， tan2β＝tan[(α＋β)－(α－β)]＝tan (α＋β)－tan (α－β))1＋tan (α＋β)tan (α－β)＝2－31＋2×3＝－17，所以tan(3π＋2α)＋tan(4π＋2β)＝tan2α＋tan2β＝－1－17＝－87. 12．已知向量a ＝(sin θ，2)，b ＝(cos θ，1))，且a ，b 共线，其中θ∈⎝⎛⎭⎫0，π2. (1)求tan ⎝⎛⎭⎫θ＋π4的值； (2)若5cos(θ－φ)＝35cos φ，0<φ<π2，求φ的值．解析：(1)∵a ，b 共线，∴sin θ－2cos θ＝0，即tan θ＝2.∴tan ⎝⎛⎭⎫θ＋π4＝1＋tan θ1－tan θ＝1＋21－2＝－3.(2)由(1)，知tan θ＝2，又θ∈⎝⎛⎭⎫0，π2，∴sin θ＝255，cos θ＝55. ∵5cos(θ－φ)＝35cos φ，∴5(cos θcos φ＋sin θsin φ)＝35cos φ，即5cos φ＋25sin φ＝35cos φ， ∴cos φ＝sin φ.又0<φ<π2，∴tan φ＝1，∴φ＝π4.。

数学北师大版必修4 3.2两角和与差的正切函数含解析

备课资料备用习题1.已知A 、B 、C 是斜△ABC 的三个内角,求证:(1)tanA+tanB+tanC=tanAtanBtanC; (2)tan2A tan 2B +tan 2B tan 2C +tan 2C tan 2A =1. 2.设关于x 的一元二次方程mx 2+(2m-1)x+(m+1)=0的两个实根为tanα与tanβ,求tan(α+β)的取值范围. 3.求tan70°+tan50°-3tan50°tan70°的值. 4.已知sinβ=m·sin(2α+β),求证:tan(α+β)=m m -+11tanα. 5.化简AB A sin )2sin(+-2cos(A+B). 6.已知5sinβ=sin(2α+β).求证:2tan(α+β)=3tanα.参考答案:1.解:(1)∵A 、B 、C 是斜△ABC 的内角,∴A+B+C=π,即A+B=π-C.由题意可知,A 、B 、C 都不为2π,因此有tan(A+B)=tan(π-C)=-tanC. ∴BA B A tan tan 1tan tan -+=-tanC,去分母,移项,整理可得 tanA+tanB+tanC=tanAtanBtanC.(2)∵2A +2B +2C =2π,∴2A +2B =2π-2C . ∴tan(2A +2B )=tan(2π-2C ). ∴2tan 12tan 2tan 12tan 2tanC B A B A =-+.去分母,移项,整理可得 tan2A tan 2B +tan 2B tan 2C +tan 2C tan 2A =1. 2.解:由题设可知m≠0,且Δ=(2m -1)2-4m(m+1)≥0.① 由①解得m ∈(-∞,0)∪(0,81］. 根据韦达定理可得⎪⎪⎩⎪⎪⎨⎧-=--=++=∙,2112tan tan ,1tan tan m m m m m m βαβα 则tan(α+β)=mm m m1121tan tan 1tan tan +--=-+βαβα=2m-1.∵m ∈(-∞,0)∪(0,81］,∴2m-1≤2×81-1=-43,且2m-1≠-1. ∴tan(α+β)的取值范围为(-∞,-1)∪(-1,-43］. 3.解:原式=tan(70°+50°)(1-tan70°tan50°)-3tan50°tan70° =-3(1-tan70°tan50°)-3tan50°tan70° =-3+3tan70°tan50°-3tan50°tan70°=-3. ∴原式的值为-3.4.证明:由sinβ=ｍsin(2α+β)⇒sin ［(α+β)-α］=ｍsin ［(α+β)+α］⇒sin(α+β)cosα-cos(α+β)sinα=ｍ［sin(α+β)cosα+cos(α+β)sinα］⇒(1-ｍ)·sin(α+β)cosα=(1+ｍ)·cos(α+β)sinα⇒tan(α+β)=mm -+11tanα. 点评:仔细观察已知式与所证式中的角,不要盲目展开,要有的放矢,看到已知式中的2α+β 可化为结论式中的α+β与α的和,不妨将α+β作为一整体来处理.此方法是综合法,利用综合法证明恒等式时,必须有分析的基础,才能顺利完成证明. 5.解:原式=AA B A A B A A A B A A B A sin sin )cos(cos )sin(sin sin )cos(])sin[(+-+=+-++ AB A A B A sin sin sin ])sin[(=-+= 点评:本题中三角函数均为弦函数,所以变形的问题只涉及角.一般来说,三角函数式的化简问题首先考虑角,其次是函数名,再次是代数式的结构特点.6.解:∵β=(α+β)-α,2α+β=(α+β)+α,∴5sin ［(α+β)-α］=sin ［(α+β)+α］,即5sin(α+β)cosα-5cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα.∴2sin(α+β)cosα=3cos(α+β)sinα.∴2tan(α+β)=3tanα.点评:注意到条件式的角是β和2α+β,求证式中的角是α+β和α,显然“不要”的角β和2α+β应由要保留下来的角α+β与α来替代.三角条件等式的证明,一般是将条件中的角(不要的)用结论式中的角(要的)替代,然后选择恰当的公式变形.三角变换中经常要化复角为单角,化未知角为已知角.因此,看准角与角的关系十分重要.哪些角消失了,哪些角变化了,结论中是哪些角,条件中有没有这些角,在审题中必须对此认真观察和分析.常见的变角方式有:α=(α+β)-β;2α=(α+β)+(α-β);2α-β=(α-β)+α.当然变形的方式不唯一,应因题而异,要具体问题具体分析.(设计者:郑吉星)。

2022-2021学年高一数学北师大版必修4学案：3.2.3 两角和与差的正切函数 Word版含答案

2.3 两角和与差的正切函数明目标、知重点 1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.2.能利用两角和与差的正切公式进行化简、求值、证明.3.生疏两角和与差的正切公式的常见变形，并能机敏应用．1．两角和与差的正切公式 (1)T α＋β：tan(α＋β)＝tan α＋tan β1－tan αtan β.(2)T α－β：tan(α－β)＝tan α－tan β1＋tan αtan β.2．两角和与差的正切公式的变形 (1)T α＋β的变形：tan α＋tan β＝tan(α＋β)(1－tan αtan β)． tan α＋tan β＋tan αtan βtan(α＋β)＝tan(α＋β)． tan αtan β＝1－tan α＋tan βtan (α＋β).(2)T α－β的变形：tan α－tan β＝tan(α－β)(1＋tan αtan β)． tan α－tan β－tan αtan βtan(α－β)＝tan(α－β)． tan αtan β＝tan α－tan βtan (α－β)－1.[情境导学] 某城市的电视放射塔建在市郊的一座小山上．小山的高BC 约为30米，在地平面上有一点A ，测得A 、C 两点间距离约为67米，从点A 处观测电视放射塔的视角(∠CAD )约为45°.求这座电视放射塔的高度．解设电视放射塔的高CD ＝x ，∠CAB ＝α，则sin α＝3067.在Rt △ABD 中， tan(45°＋α)＝x ＋3030tan α，于是x ＝30tan (45°＋α)tan α－30.如何能由sin α＝3067求得tan(45°＋α)的值呢？或者说能不能用sin α把tan(45°＋α)表示出来呢？虽然我们已经学习了两角和与差的正弦、余弦公式，但是使用这些公式明显不能直接解决上述问题．我们有必要得到两角和与差的正切公式．探究点一两角和与差的正切公式的推导思考1 你能依据同角三角函数基本关系式tan α＝sin αcos α，从两角和与差的正弦、余弦公式动身，推导出用任意角α，β的正切值表示tan(α＋β)，tan(α－β)的公式吗？试一试．答当cos(α＋β)≠0时，tan(α＋β)＝sin (α＋β)cos (α＋β)＝sin αcos β＋cos αsin βcos αcos β－sin αsin β.当cos αcos β≠0时，分子分母同时除以cos αcos β，得 tan(α＋β)＝tan α＋tan β1－tan αtan β.依据α，β的任意性，在上面式子中，以－β代替β得 tan(α－β)＝tan α＋tan (－β)1－tan αtan (－β)＝tan α－tan β1＋tan αtan β.思考2 在两角和与差的正切公式中，α，β，α±β的取值是任意的吗？答在公式T α＋β，T α－β中α，β，α±β都不能等于k π＋π2(k ∈Z )．探究点二两角和与差的正切公式的变形公式思考两角和与差的正切公式变形形式较多，例如： tan α±tan β＝tan(α±β)(1∓tan αtan β)， tan αtan β＝1－tan α＋tan βtan (α＋β)＝tan α－tan βtan (α－β)－1.这些变形公式在解决某些问题时是格外便利的．请利用两角和与差的正切公式或变形公式完成以下练习．练习直接写出下列式子的结果： (1)tan 12°＋tan 33°1－tan 12°tan 33°＝； (2)tan 75°＝； (3)1－tan 15°1＋tan 15°＝ . 答案 (1)1 (2)2＋3 (3)33例1 求下列各式的值： (1)3＋tan 15°1－3tan 15°； (2)tan 15°＋tan 30°＋tan 15°tan 30°.解 (1)原式＝tan 60°＋tan 15°1－tan 60°tan 15°＝tan(60°＋15°)＝tan 75°＝tan(30°＋45°)＝tan 30°＋tan 45°1－tan 30°tan 45°＝33＋11－33＝2＋ 3.(2)∵tan 45°＝tan 15°＋tan 30°1－tan 15°tan 30°＝1，∴tan 15°＋tan 30°＝1－tan 15°tan 30°∴原式＝(1－tan 15°tan 30°)＋tan 15°tan 30°＝1.反思与感悟公式T α＋β，T α－β是变形较多的两个公式，公式中有tan αtan β，tan α＋tan β(或tan α－tan β)，tan(α＋β)(或tan(α－β))三者知二可表示或求出第三个．跟踪训练1 求下列各式的值： (1)cos 75°－sin 75°cos 75°＋sin 75°； (2)tan 36°＋tan 84°－3tan 36°tan 84°. 解 (1)原式＝1－tan 75°1＋tan 75°＝tan 45°－tan 75°1＋tan 45°tan 75°＝tan(45°－75°)＝tan(－30°)＝－tan 30°＝－33. (2)原式＝tan 120°(1－tan 36°tan 84°)－3tan 36°tan 84° ＝tan 120°－tan 120°tan 36°tan 84°－3tan 36°tan 84° ＝tan 120°＝－ 3.例2 若α，β均为钝角，且(1－tan α)(1－tan β)＝2，求α＋β的值．解 ∵(1－tan α)(1－tan β)＝2， ∴1－(tan α＋tan β)＋tan αtan β＝2，∴tan α＋tan β＝tan αtan β－1， ∴tan α＋tan β1－tan αtan β＝－1.∴tan(α＋β)＝－1.∵α，β∈⎝⎛⎭⎫π2，π，∴α＋β∈(π，2π)． ∴α＋β＝7π4.反思与感悟此类题是给值求角题，解题步骤如下：(1)求所求角的某一个三角函数值，(2)确定所求角的范围．此类题常犯的错误是对角的范围不加争辩，范围争辩的程度过大或过小，会产生增解或者漏解．跟踪训练2 已知tan α，tan β是方程x 2＋33x ＋4＝0的两根，且－π2<α<π2，－π2<β<π2，求角α＋β.解由已知得⎩⎪⎨⎪⎧tan α＋tan β＝－33tan α·tan β＝4，∴tan α、tan β均为负，∴－π2<α<0，－π2<β<0.∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝－331－4＝ 3.∵－π<α＋β<0，∴α＋β＝－2π3. 例3 已知△ABC 中，tan B ＋tan C ＋3tan B tan C ＝3，且3tan A ＋3tan B ＝tan A tan B －1，试推断△ABC 的外形．解 ∵3tan A ＋3tan B ＝tan A tan B －1， ∴3(tan A ＋tan B )＝tan A tan B －1， ∴tan A ＋tan B1－tan A tan B＝－33，∴tan(A ＋B )＝－33. 又∵0<A ＋B <π， ∴A ＋B ＝5π6，∴C ＝π6，∵tan B ＋tan C ＋3tan B tan C ＝3，tan C ＝33，∴tan B ＋33＋tan B ＝3，tan B ＝33， ∴B ＝π6，∴A ＝2π3，∴△ABC 为等腰钝角三角形．反思与感悟三角形中的问题，A ＋B ＋C ＝π确定要用，有时与诱导公式结合，有时利用它查找角之间的关系削减角的个数．跟踪训练3 已知A 、B 、C 为锐角三角形ABC 的内角．求证：tan A ＋tan B ＋tan C ＝tan A tan B tan C . 证明 ∵A ＋B ＋C ＝π，∴A ＋B ＝π－C . ∴tan(A ＋B )＝tan A ＋tan B 1－tan A tan B ＝－tan C .∴tan A ＋tan B ＝－tan C ＋tan A tan B tan C . 即tan A ＋tan B ＋tan C ＝tan A tan B tan C .1．若tan(π4－α)＝3，则tan α的值为( )A ．－2B ．－12C.12 D ．2答案 B解析 tan α＝tan ⎣⎡⎦⎤π4－⎝⎛⎭⎫π4－α＝1－tan ⎝⎛⎭⎫π4－α1＋tan ⎝⎛⎭⎫π4－α＝1－31＋3＝－12.2．已知A ＋B ＝45°，则(1＋tan A )(1＋tan B )的值为( ) A ．1 B ．2 C ．－2 D ．不确定答案 B解析 (1＋tan A )·(1＋tan B )＝1＋(tan A ＋tan B )＋tan A tan B＝1＋tan(A ＋B )(1－tan A tan B )＋tan A tan B ＝1＋1－tan A tan B ＋tan A tan B ＝2.3．已知A ，B 都是锐角，且tan A ＝13，sin B ＝55，则A ＋B ＝ .答案 π4解析 ∵B 为锐角，sin B ＝55， ∴cos B ＝255，∴tan B ＝12，∴tan(A ＋B )＝tan A ＋tan B1－tan A tan B＝13＋121－13×12＝1.∵0<A ＋B <π，∴A ＋B ＝π4.4．已知tan ⎝⎛⎭⎫α－β2＝12，tan ⎝⎛⎭⎫β－α2＝－13，则tan ⎝⎛⎭⎫α＋β2＝ . 答案 17解析 tan ⎝⎛⎭⎪⎫α＋β2＝tan ⎣⎡⎦⎤⎝⎛⎭⎫α－β2＋⎝⎛⎭⎫β－α2 ＝tan ⎝⎛⎭⎫α－β2＋tan ⎝⎛⎭⎫β－α21－tan ⎝⎛⎭⎫α－β2tan ⎝⎛⎭⎫β－α2＝12＋⎝⎛⎭⎫－131－12×⎝⎛⎭⎫－13＝17.[呈重点、现规律]1．公式T α±β的适用范围、结构特征和符号规律(1)由正切函数的定义可知α、β、α＋β(或α－β)的终边不能落在y 轴上，即不为k π＋π2(k ∈Z )．(2)公式T α±β的右侧为分式形式，其中分子为tan α与tan β的和或差，分母为1与tan αtan β的差或和． (3)符号变化规律可简记为“分子同，分母反”． 2．公式T α±β的逆用一方面要熟记公式的结构，另一方面要留意常值代换．如tan π4＝1，tan π6＝33，tan π3＝3等．要特殊留意tan ⎝⎛⎭⎫π4＋α＝1＋tan α1－tan α，tan ⎝⎛⎭⎫π4－α＝1－tan α1＋tan α. 3．公式T α±β的变形应用只要见到tan α±tan β，tan αtan β时，要有机敏应用公式T α±β的意识，就不难想到解题思路．一、基础过关1．已知α∈⎝⎛⎭⎫π2，π，sin α＝35，则tan ⎝⎛⎭⎫α＋π4的值等于( ) A.17 B ．7 C ．－17D ．－7答案 A2．已知tan(α＋β)＝35，tan ⎝⎛⎭⎫β－π4＝14，那么tan ⎝⎛⎭⎫α＋π4等于( ) A.1318 B.1323 C.723 D.16 答案 C解析 tan ⎝⎛⎭⎫α＋π4＝tan ⎣⎡⎦⎤α＋β－⎝⎛⎭⎫β－π4＝35－141＋35×14＝723. 3．已知tan α＝12，tan β＝13，0<α<π2，π<β<3π2，则α＋β的值是( )A.π4 B.3π4 C.5π4 D.7π4答案 C4．A ，B ，C 是△ABC 的三个内角，且tan A ，tan B 是方程3x 2－5x ＋1＝0的两个实数根，则△ABC 是( ) A ．钝角三角形 B ．锐角三角形 C ．直角三角形 D ．无法确定答案 A解析 ∵tan A ＋tan B ＝53，tan A ·tan B ＝13，∴tan(A ＋B )＝52，∴tan C ＝－tan(A ＋B )＝－52，∴C 为钝角． 5.1＋tan 75°1－tan 75°＝ .答案－36．已知tan ⎝⎛⎭⎫π4＋α＝2，则12sin αcos α＋cos 2α的值为．答案 23解析 ∵tan ⎝⎛⎭⎫π4＋α＝2，∴1＋tan α1－tan α＝2，解得tan α＝13. ∴12sin αcos α＋cos 2α＝sin 2α＋cos 2α2sin αcos α＋cos 2α ＝tan 2α＋12tan α＋1＝19＋123＋1＝23. 7．求下列各式的值：(1)sin 7°＋cos 15°sin 8°cos 7°－sin 15°sin 8°；(2)(1－tan 59°)(1－tan 76°)．解 (1)原式＝sin (15°－8°)＋cos 15°sin 8°cos (15°－8°)－sin 15°sin 8°＝sin 15°cos 8°cos 15°cos 8°＝tan 15°＝tan(45°－30°)＝tan 45°－tan 30°1＋tan 45°tan 30°＝1－331＋33＝2－ 3.(2)原式＝1－tan 59°－tan 76°＋tan 59°tan 76° ＝1－(tan 59°＋tan 76°)＋tan 59°tan 76° ＝1－tan 135°(1－tan 59°tan 76°)＋tan 59°tan 76° ＝1＋1－tan 59°tan 76°＋tan 59°tan 76°＝2.二、力气提升8．化简tan 10°tan 20°＋tan 20°tan 60°＋tan 60°tan 10°的值等于( ) A ．1 B ．2 C ．tan 10° D.3tan 20°答案 A解析原式＝tan 10°tan 20°＋3tan 20°＋ 3 tan 10° ＝3(tan 10°＋tan 20°＋33tan 10°tan 20°) ＝3×33＝1. 9．设θ为其次象限角，若tan ⎝⎛⎭⎫θ＋π4＝12，则sin θ＋cos θ＝ . 答案－105解析由于tan ⎝⎛⎭⎫θ＋π4＝tan θ＋11－tan θ＝12，所以tan θ＝－13，由于θ为其次象限角，所以cos θ＝－11＋tan 2θ＝－31010，sin θ＝1－cos 2θ＝1010，则sin θ＋cos θ＝1010－31010＝－105. 10．已知α、β均为锐角，且tan β＝cos α－sin αcos α＋sin α，则tan(α＋β)＝ .答案 1解析 ∵tan β＝cos α－sin αcos α＋sin α＝1－tan α1＋tan α.∴tan β＋tan αtan β＝1－tan α. ∴tan α＋tan β＋tan αtan β＝1. ∴tan α＋tan β＝1－tan αtan β. ∴tan α＋tan β1－tan αtan β＝1，∴tan(α＋β)＝1.11．在△ABC 中，求证：tan A 2tan B 2＋tan B 2tan C 2＋tan C 2tan A 2＝1.证明 ∵A ＋B ＋C ＝180°，∴A 2＋B 2＋C2＝90°.∴A ＋B 2＝90°－C 2.∴tan ⎝⎛⎭⎪⎫A ＋B 2＝tan ⎝⎛⎭⎫90°－C 2＝1tanC 2. ∴tan ⎝⎛⎭⎪⎫A ＋B 2·tan C2＝1. ∴⎝⎛⎭⎫tan A 2＋tan B 2tan C21－tan A 2tanB2＝1，∴tan A 2tan C 2＋tan B 2tan C 2＝1－tan A 2tan B 2.即tan A 2tan B 2＋tan B 2tan C 2＋tan C 2tan A 2＝1.12.如图，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A ，B 两点，已知A ，B 的横坐标分别为210，255. 求：(1)tan(α＋β)的值； (2)α＋2β的大小．解由条件得cos α＝210，cos β＝255.∵α，β为锐角，∴sin α＝1－cos 2α＝7210， sin β＝1－cos 2β＝55. 因此tan α＝sin αcos α＝7，tan β＝sin βcos β＝12.(1)tan(α＋β)＝tan α＋tan β1－tan α·tan β＝7＋121－7×12＝－3.(2)∵tan 2β＝tan(β＋β)＝2tan β1－tan 2β＝2×121－⎝⎛⎭⎫122＝43，∴tan(α＋2β)＝tan α＋tan 2β1－tan α·tan 2β＝7＋431－7×43＝－1.∵α，β为锐角，∴0<α＋2β<3π2，∴α＋2β＝3π4.三、探究与拓展13．已知tan α，tan β是方程x 2－3x －3＝0的两根，试求 sin 2(α＋β)－3sin(α＋β)cos(α＋β)－3cos 2(α＋β)的值．解由已知有⎩⎪⎨⎪⎧tan α＋tan β＝3，tan α·tan β＝－3，∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝31－(－3)＝34.∴sin 2(α＋β)－3sin(α＋β)cos(α＋β)－3cos 2(α＋β) ＝sin 2(α＋β)－3sin (α＋β)cos (α＋β)－3cos 2(α＋β)sin 2(α＋β)＋cos 2(α＋β)＝tan 2(α＋β)－3tan (α＋β)－3tan 2(α＋β)＋1＝(34)2－3×34－3(34)2＋1＝－3.。

高中数学 3.2.3 两角和与差的正切函数课时训练北师大版必修4

【课堂新坐标】（教师用书）2013-2014学年高中数学 3.2.3 两角和与差的正切函数课时训练北师大版必修4一、选择题1．已知α∈(－π2，0)，sin α＝－45，则tan(α＋π4)＝( )A ．－7B ．－17C.17D ．7【解析】 ∵α∈(－π2，0)，sin α＝－45，∴cos α＝35，∴tan α＝－4535＝－43，∴tan(α＋π4)＝1＋tan α1－tan α＝1－431＋43＝－17.【答案】 B2．tan 20°tan 50°＋tan 20°tan 60°－tan 60°tan 50°等于( ) A ．1 B ．－1 C. 3D ．－ 3【解析】原式＝tan 20°(tan 50°＋tan 60°)－tan 60°tan 50°＝tan 20°tan 110°(1－tan 50°tan 60°)－tan 60°tan 50°＝tan 20°(－tan 70°)(1－tan 50°tan 60°)－tan 50°tan 60° ＝－(1－tan 50°tan 60°)－tan 50°tan 60° ＝－1. 【答案】 B3．(1＋tan 17°)(1＋tan 18°)(1＋tan 27°)(1＋tan 28°)的值是( ) A ．2 B ．4 C ．8D ．16【解析】 (1＋tan 17°)(1＋tan 28°)＝1＋tan 17°＋tan 28°＋tan 17°·tan 28°，①又∵tan 45°＝tan(17°＋28°) ＝tan 17°＋tan 28°1－tan 17°tan 28°，∴①式＝1＋(1－tan 17°tan 28°)＋tan 17°tan 28°＝2. 同理(1＋tan 18°)(1＋tan 27°)＝2. ∴原式＝4.故选B. 【答案】 B4．在△ABC 中，tan A ＝13，tan B ＝－2，则角C 的值为( )A.π6B.π4C.π3D.π2【解析】 C ＝π－(A ＋B )，∴tan C ＝tan[π－(A ＋B )]＝－tan(A ＋B ) ＝－tan A ＋tan B1－tan A tan B ＝－13－21＋13×2＝1，∴C ＝π4，故选B.【答案】 B5．设tan θ和tan(π4－θ)是方程x 2＋px ＋q ＝0的两个根，则p 、q 之间的关系是( )A ．p ＋q ＋1＝0B ．p －q ＋1＝0C ．p ＋q －1＝0D ．p －q －1＝0【解析】 ∵tan θ＋tan(π4－θ)＝－p ，tan θ·tan(π4－θ)＝q ，π4＝θ＋(π4－θ)， ∴tan π4＝tan[θ＋(π4－θ)]＝－p 1－q ＝1，∴p －q ＋1＝0. 【答案】 B 二、填空题6．已知α为第三象限的角，cos 2α＝－35，则tan(π4＋2α)＝________.【解析】 ∵α为第三象限的角，则2k π＋π≤α≤2k π＋3π2，∴4k π＋2π≤2α≤4k π＋3π(k ∈Z )．又cos 2α＝－35，∴sin 2α＝45，tan 2α＝－43，∴tan(π4＋2α)＝1＋tan 2α1－tan 2α＝－17.【答案】－177．已知α、β、γ都是锐角，且tan α＝12，tan β＝15，tan γ＝18，则α＋β＋γ＝________.【解析】 ∵tan(α＋β)＝tan α＋tan β1－tan αtan β＝12＋151－12×15＝79，tan(α＋β＋γ)＝tan α＋β＋tan γ1－tan α＋βtan γ＝79＋181－79×18＝1，由于tan α＝12＜33.且α为锐角，∴0＜α＜π6，同理0＜β＜π6，0＜γ＜π6∴0＜α＋β＋γ＜π2，∴α＋β＋γ＝π4.【答案】π48．若a ，b 是非零实数，且a sin π5＋b cosπ5a cos π5－b sinπ5＝tan 8π15，则ba ＝________.【解析】 ∵a sin π5＋b cosπ5a cos π5－b sinπ5＝tan π5＋b a 1－b a tan π5＝tan 8π15＝tan(π5＋π3)＝tan π5＋tanπ31－tan π5·tanπ3，∴b a ＝tan π3＝ 3. 【答案】 3三、解答题9．已知tan α，tan β是方程mx 2＋(2m －3)x ＋(m －2)＝0的两根，求tan(α＋β)的最小值．【解】由题设知，tan α＋tan β＝－2m －3m ，tan α·tan β＝m －2m.∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝3－2mm 1－m －2m＝32－m ，又Δ＝(2m －3)2－4m (m －2)≥0，∴4m 2－12m ＋9－4m 2＋8m ≥0，∴－4m ＋9≥0，即m ≤94，∴－m ≥－94，∴32－m ≥32－94＝－34，即tan(α＋β)≥－34.因此tan(α＋β)的最小值为－34.10．在△ABC 中，tan B ＋tan C ＋3tan B tan C ＝3且3tan A ＋3tan B ＋1＝tan A tanB ，判断△ABC 的形状．【解】由tan A ＝tan[π－(B ＋C )]＝－tan(B ＋C ) ＝tan B ＋tan C tan B tan C －1＝3－3tan B tan Ctan B tan C －1＝－3，而0°<A <180°，∴A ＝120°.由tan C ＝tan[π－(A ＋B )]＝tan A ＋tan B tan A tan B －1＝tan A ＋tan B 3tan A ＋3tan B ＝33，而0°<C <180°，∴C ＝30°，∴B ＝30°，∴△ABC 是顶角为120°的等腰三角形． 11．已知tan α＝－13，cos β＝55，α，β∈(0，π)．(1)求tan(α＋β)的值；(2)求函数f (x )＝2sin(x －α)＋cos(x ＋β)的最大值．【解】 (1)由cos β＝55，β∈(0，π)得sin β＝255，tan β＝2. 于是tan(α＋β)＝tan α＋tan β1－tan αtan β＝－13＋21＋23＝1.(2)因为tan α＝－13，α∈(0，π)，所以sin α＝1010，cos α＝－31010. f (x )＝2(sin x ·cos α－cos x ·sin α)＋cos x ·cos β－sin x ·sin β＝2(－31010·sin x －1010·cos x )＋55cos x －255sin x＝－355sin x －55cos x ＋55cos x －255sin x＝－5sin x ，所以f (x )的最大值为 5.。

数学北师大版高一必修4练习：24_两角和与差的正切函数

答案：A
解析：由tanAtanB>1得角A，B均为锐角，然后切化弦，得sinAsinB>cosAcosB，即cos(A＋B)<0，∴cos(π－C)<0，∴－cosC<0，∴cosC>0，∴角C为锐角，∴△ABC是锐角三角形，故选A.
6．设tanα和tanβ是方程mx2＋(2m－3)x＋(m－2)＝0的两根，则tan(α＋β)的最小值是()
答案：－
解析：∵α为第三象限的角，则2kπ＋π≤α≤2kπ＋，∴4kπ＋2π≤2α≤4kπ＋3π(k∈Z)，又cos2α＝－，
∴sin2α＝，tan2α＝－，∴tan( ＋2α)＝＝－ .
8．tan ＋tan ＋ tan ·tan 的值为________．
答案：
解析：tan ＋tan ＋ tan ·tan
4．已知tanα＝，则的值是()
A．2B.
C．－1D．－3
答案：B
解析：解法一：因为tanα＝，所以tan ＝＝＝3，所以＝＝ .故选B.
解法二：＝＝tan ＝tanα＝ .故选B.
5．在△ABC中，若tanAtanB>1，则△ABC是()
A．锐角三角形B．直角三角形
C．钝角三角形D．无法确定
∴α＋β＝ .
2. 的值是()
A. B．－
C. D．－
答案：B
解析：＝＝tan(45°＋75°)＝tan120°＝－tan60°＝－ .
3．已知tan(α＋β)＝，tan ＝，那么tan ＝()
A. B.
C. D.
答案：C
解析：因为α＋＝(α＋β)－，所以tan ＝tan ＝＝，故选C.
(1)求tan(α＋β)的值；

2017-2018学年高中数学24两角和与差的正切函数练习(含解析)北师大版必修4

224 两角和与差的正切函数时间：45分钟满分：80分— 姓名 _______________ 分数、选择题：（每小题5分，共5X 6= 30分）1 =2， tan 3 n 3 nB. /或 4 4 5 n 4班级1 .设 tan 13，且a 、3角为锐角，则 a + 3的值是（）3n A. 4nC.4答案:D.解析:tan 1 a = 2，tan1 3= 3，得 tan( a + 3 )=3 tan1 —tan1 1—+a + tan 3 2 3 ------- =--------- =1.又 a 、a tan 31 1 1——X-2 33均是锐角, n4 . 1 + tan75 ° ，+2. 的值是( 1 — ta n75 「•a + 3A. .3 B . -3 C「3D .3 3 答案： B解析：1 + tan75 ° — tan45 ° + tan75 ° 1—tan45 ° tan75 ° =tan(45+ 75° )=tan 120 =—tan60 °—\.；3.3.已知tan( a + 3)=5,tan 3 -—141,那么7ttann +n =(13 A.18 3 C.22 答案: B. D. 1322 5 18n3—4tan7ttan a + 3 4 =因为+31 + ［川丨a+ 3trill 3c选故3一-4.已知tan a1 2,tan则一1 + tann 4 + a — 1 的值是( + aA. 2B.C.— 1 D . — 3答案：B1解析：解法一：因为tan a = 2，所以tann4 +antan — + tan a4 1 + tan a=3,n1 — tan — • tan 4 1 — tan aatan 所以一 ,■ n 1 + tan 庁 + a—1 3— 1 1=1 + 3 = 2. 故选 B. tan 解法二：一 1 + ta n —1 tan n+ a — tan — 4 4 n , 4 + a 1 + tan n , n 4 +a• tan 4=tan 右 =tan a12.故选B. 5. A. C. 在厶ABC 中, 锐角三角形钝角三角形若 tan A ta 门91,则厶 ABC 是 ( ) B •直角三角形 D .无法确定答案：A 解析：由tan A tan B >1得角A, B 均为锐角，然后切化弦，得sin A sin B>cos A cosB,即cos( A + B )<0 ,• cos( n — C )<0 , 故选A.6. 设小值是( 15 A 了 3 C •- 4 D 答案：C 解析：■/ tan a 和 tan •••— cos C <0,「. cos O >0,「.角 C 为锐角，•••△ ABC 是锐角三角形, ta n) B. a 和 tan 3 •不确定 ” tan a + tan tan a • tan m^ 0,m —2是方程 mx + (2 m-3)x + (n — 2) = 0的两根，则tan( a + 3 )的最 23 是 mx + (2 m- 3)x + (n — 2) = 0 的两根,2 m- 33=— m ，m- 23= m ，2— 4m n —me 9，且 m. 0.ta n( a+3 )=驚"罗 34 1— tan a tan 32 m- 3m— 2ir + 33m- 2 = 2 =— 21—m93 •••当m=，时，tan( a + 3 )的最小值为一.44二、填空题：(每小题5分，共5X 3= 15分)3・” n5，贝V tan( 4 + 2 a )=7.已知a 为第三象限的角，cos2 a答案：—3 n解析：' ：a 为第二象限的角，贝 U 2k n + nWaW2k n +—?，二 4k n + 2nW2 aW4k nn2 nn2 n/+、『8. tan —--+ tan — v3tan -9 • tan ―—的值为 ___________ 答案：■. 3n2 n— n2 n解析：tan© + tan 寸 + 3ta n-9 • ta n-9-nna sin+ b cos _.5 5 8 n b9. ------------------------------------------------------------ 若 a , b 是非零实数，且 =tan —^，^H_ =n , . n 15 a ----------------------- a cos — b sin55tan a + tan 3所以 tan( a + 3 ) = 1 — tan a tan 3 = tan a + 3 —tan a+ 3 n (k € Z)，又 C0S2 a3 5,/• sin2 a 4 45, tan2 a = — 3,tan(n c \ 1 + tan2 a4 + 2 a )= 1 — tan2 a =答案:解析:nnasln石 + bc0s 石a cos *—b sin -555n b ta n + c 5 a 8 n =tanb n1 — tan 「 n 15 =tan( 5 + 3)=nn tan石+tan ㊁nn '1 — tan 一 • tan —5 3=tan = 3.三、解答题：（共35分，11+ 12+ 12）10. 在平面直角坐标系 xOy 中，以Ox 为始边作两个锐角 a , 位圆相交于A , B 两点，已知点A , B 的横坐标分别为1,纣53，它们的终边分别与单因为因为［日 12 +aa , 3为锐角，所以 sintan a = 2 '2, tan 31 3,2 5cos 3 =~:~.5-tan的值. ⑵求解析：⑴由题意，得cos(1)求 tan( a + 3 )的值;(2)')2 + 2tan a + 3一• tan a1 tan a + 3—tan a =X2 1 + tan_ a + 3• tan a12 x ta n[( a + 1=x tan 3 21 1 =x2 2_ 1= --4'11.已知 tan( a 解析：因为tan(+ 3 ) = 2, tan( a — 3 ) = 3,求 tan(3 n + 2 a ) + tan(4 n + 2 3 )的值. a + 3 ) =2, tan( a — 3 ) = 3, 所以 tan2 a = tan[( a + 3) + ( a — 3 )] 2 + 31 —2X3-1, tan2 3 = tan[( a + 3 ) — ( a — 3 )]= tan a + 3 — tan a — 32 — 31 + tan a + 3 tan a — 3= 1 +2X31 7,所以 tan(3 n+ 2 a ) + tan(4 n + 23 ) = tan21 8a + tan2 3 =— 1—-=—-.12.已知向量a = (sin 0 , 2),b = (cos 0 , 1)) ，且a , b 共线，其中0€ 0, 2 .(1)求 tan i 0 +4的值;〜7t0 , 0<0 < 2,0 — 2cos 0 = 0, 1+ 2• tan i 0 +~ = ------------------ = ------- = — 3.‘ 4 丿 1 — tan 0 1 — 2⑵若 5cos( 0 — 0 ) = 3 , 5cos 解析：(1) T a , b 共线，• sin 1 + tan 0即 tan 0 = 2.(2)由(1)，知 tan 0 = 2,又 0 € 0,专,• sin 0 = ^5, cos 0 =—5<2J5 5■/ 5cos( ••• 5(cos--cos 0—0 ) = 3 5cos 0 , 0 cos 0 +sin 0 sin =sin 0 .7t,7t•- tan 0 = 1, • 0 = "4. 0 ) = 3 .5COS 0，即 V5cos 0 + R5sin 0 = ^5cos 0 , <2，又0<$。

【精品推荐】高中数学北师大版必修四课后训练3.2.3 两角和与差的正切函数 Word版含答案

ቤተ መጻሕፍቲ ባይዱ
3
10．设一元二次方程 mx2＋(2m－1)x＋(m＋1)＝0 的两根为 tan α，tan β，求 tan(α＋β)的取值范围．
参考答案
1 答案：A 2 答案：B 3 答案：B 4 答案：B 5 答案：D 6 答案：
3
2 3
7 答案： 3 8 答案：
9 答案：18 m 10 答案：(－∞，－1)∪ 1, 4
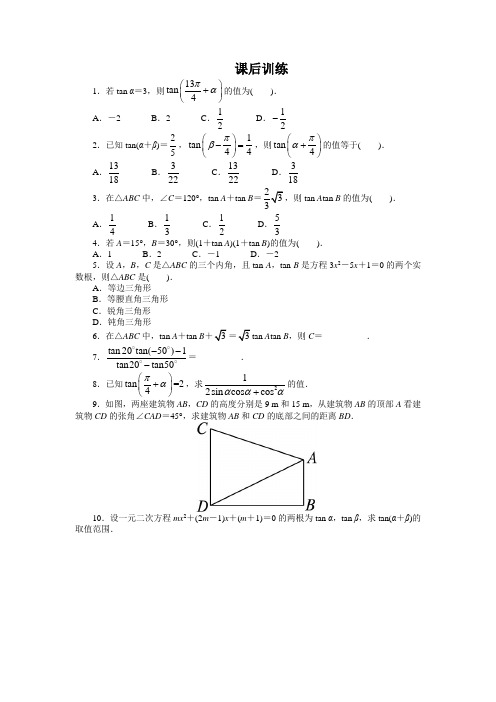
1．若 tan α＝3，则 tan 4．若 A＝15° ，B＝30° ，则(1＋tan A)(1＋tan B)的值为( )． A．1 B．2 C．－1 D．－2 5．设 A，B，C 是△ABC 的三个内角，且 tan A，tan B 是方程 3x2－5x＋1＝0 的两个实数根，则△ABC 是( )． A．等边三角形 B．等腰直角三角形 C．锐角三角形 D．钝角三角形 6．在△ABC 中，tan A＋tan B＋ 3 ＝ 3 tan Atan B，则 C＝__________．
课后训练
13 )．的值为( 4 1 1 A．－2 B．2 C． D． 2 2 2 1 2．已知 tan(α＋β)＝， tan ，则 tan 的值等于( )． 5 4 4 4 13 3 13 3 A． B． C． D． 18 22 22 18 2 3 ，则 tan Atan B 的值为( 3．在△ABC 中，∠C＝120° ，tan A＋tan B＝ )． 3 1 1 1 5 A． B． C． D． 4 3 2 3
tan 20 tan50 1 7．＝__________． tan20 tan50 1 8．已知 tan =2 ，求的值． 2sin cos cos 2 4

高中数学3.2.3两角和与差的正切函数课时分层作业含解析北师大版必修4.doc

课时分层作业(二十四) 两角和与差的正切函数(建议用时：40分钟)一、选择题 1.tan 51°＋tan 9°1－tan 51°tan 9°＝( )A ．tan 42°B ．33C ． 3D ．－ 3C [原式＝tan (51°＋9°)＝tan 60°＝ 3.]2．在△ABC 中，tan A ＋tan B ＋3＝3tan A ·tan B ，则角C ＝( ) A ．π3B ．2π3C ．π6D ．π4A [tan C ＝－tan (A ＋B )＝－tan A ＋tan B1－tan A ·tan B＝－3（tan A ·tan B －1）1－tan A ·tan B＝3，所以C ＝π3.]3．(1＋tan 21°)(1＋tan 22°)(1＋tan 23°)(1＋tan 24°)的值为( ) A ．16 B ．2 C ．4D ．8C [∵(1＋tan 21°)(1＋tan 24°) ＝1＋tan 21°＋tan 24°＋tan 21°tan 24°＝1＋(1－tan 21°tan 24°)tan (21°＋24°)＋tan 21°tan 24° ＝1＋1－tan 21°tan 24°＋tan 21°tan 24° ＝2.同理(1＋tan 22°)(1＋tan 23°)＝2， ∴原式＝2×2＝4.] 4.tan 10°＋tan 50°＋tan 120°tan 10°·tan 50°的值应是( )A ．－1B ．1C ． 3D ．－ 3D [因为tan (10°＋50°)＝tan 10°＋tan 50°1－tan 10° tan 50°，所以tan 10°＋tan 50°＝tan 60°－tan 60°·tan 10°·tan 50°，所以原式＝tan 60°－tan 60°·tan 10°·tan 50°＋tan 120°tan 10°·tan 50°＝－ 3.]5．已知A ，B ，C 是△ABC 的三个内角，且tan A ，tan B 是方程3x 2－5x ＋1＝0的两个实数根，则△ABC 的形状是 ( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．无法确定A [由题意，知tan A ＋tanB ＝53，tan A ·tan B ＝13，所以tan (A ＋B )＝52，所以tan C ＝－tan (A ＋B )＝－52，所以C 为钝角，故选A.] 二、填空题6．若α＋β＝3π4，则(1－tan α)(1－tan β)＝________．2 [(1－tan α)(1－tan β)＝1－(tan α＋tan β)＋tan α·tan β. 又tan (α＋β)＝tan ⎝⎛⎭⎫3π4＝－1＝tan α＋tan β1－tan αtan β，所以tan α＋tan β＝tan αtan β－1，所以(1－tan α)(1－tan β)＝1＋1－tan αtan β＋tan αtan β＝2.] 7．已知tan (α＋β)＝13，tan α＝－2，则tan β＝________．7 [∵β＝(α＋β)－α，∴tan β＝tan （α＋β）－tan α1＋tan （α＋β）tan α＝7.]8．已知α∈⎝⎛⎭⎫π2，3π2，tan ⎝⎛⎭⎫α－π4＝－7，则sin α＝________．35 [由tan ⎝⎛⎭⎫α－π4＝tan α－11＋tan α＝－7，∴tan α＝－34<0，又α∈⎝⎛⎭⎫π2，3π2， ∴α∈⎝⎛⎭⎫π2，π，∴sin α＝35.] 三、解答题9．已知cos (α＋β)＝13，cos (α－β)＝15，求tan α·tan β的值．[解] cos (α＋β)＝cos αcos β－sin αsin β＝13，①cos (α－β)＝cos αcos β＋sin αsin β＝15，②由①②整理得⎩⎨⎧cos αcos β＝415，sin αsin β＝－115，则tan αtan β＝sin αsin βcos αcos β＝－115415＝－14.10．已知tan ⎝⎛⎭⎫π4＋α＝12. (1)求tan α的值；(2)求2sin αcos α－cos 2α2cos 2α的值．[解] (1)∵tan ⎝⎛⎭⎫π4＋α＝12， ∴1＋tan α1－tan α＝12.∴tan α＝－13.(2)原式＝2tan α－12＝2×⎝⎛⎭⎫－13－12＝－56.1．若tan 28°tan 32°＝a ，则tan 28°＋tan 32°等于( ) A ．3a B ．3(1－a ) C ．3(a －1)D ．3(a ＋1)B [∵tan (28°＋32°)＝tan 28°＋tan 32°1－tan 28°tan 32°＝3，∴tan 28°＋tan 32°＝3(1－a ).]2．化简tan 10°tan 20°＋tan 20°tan 60°＋tan 60°tan 10°的值等于( ) A ．1 B ．2 C ．tan 10° D ．3tan 20° A[原式＝tan 10°tan 20°＋3tan 20°＋3tan 10°＝3⎝⎛⎭⎫tan 10°＋tan 20°＋33tan 10°tan 20°＝3×33＝1.]3．如果tan α，tan β是方程x 2－3x －3＝0的两根，则sin （α＋β）cos （α－β）＝________．－32 [sin （α＋β）cos （α－β）＝sin αcos β＋cos αsin βcos αcos β＋sin αsin β ＝tan α＋tan β1＋tan αtan β＝31＋（－3）＝－32.]4．已知α、β均为锐角，且tan β＝cos α－sin αcos α＋sin α，则tan (α＋β)＝________.1 [∵tan β＝cos α－sin αcos α＋sin α＝1－tan α1＋tan α.∴tan β＋tan αtan β＝1－tan α. ∴tan α＋tan β＋tan αtan β＝1. ∴tan α＋tan β＝1－tan αtan β. ∴tan α＋tan β1－tan αtan β＝1，∴tan (α＋β)＝1.] 5.如图，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A ，B 两点．已知A ，B 的横坐标分别为210，255.(1)求tan (α＋β)的值； (2)求α＋2β的值．[解] (1)由已知条件及三角函数的定义，可知cos α＝210，cos β＝255，因为α为锐角，故sin α>0. 从而sin α＝1－cos 2α＝7210. 同理可得sin β＝55. 因此tan α＝7，tan β＝12.所以tan (α＋β)＝tan α＋tan β1－tan αtan β＝7＋121－7×12＝－3.(2)tan (α＋2β)＝tan [(α＋β)＋β]＝－3＋121－（－3）×12＝－1. 又0<α<π2，0<β<π2，故0<α＋2β<3π2.从而由tan (α＋2β)＝－1，得α＋2β＝3π4.。

北师大版高中数学必修四学两角和与差的正切函数课后训练

"【志鸿全优设计】2013-2014学年高中数学 3.2.3 两角和与差的正切函数课后训练北师大版必修4 "1．若tan α＝3，则13tan 4πα⎛⎫+⎪⎝⎭的值为( )． A ．－2 B ．2 C ．12 D ．12- 2．已知tan(α＋β)＝25，1tan 44πβ⎛⎫-= ⎪⎝⎭，则tan 4πα⎛⎫+ ⎪⎝⎭的值等于( )． A ．1318 B ．322 C ．1322 D ．3183．在△ABC 中，∠C ＝120°，tan A ＋tan B tan A tan B 的值为( )． A ．14 B ．13 C ．12 D ．53 4．若A ＝15°，B ＝30°，则(1＋tan A )(1＋tan B )的值为( )．A ．1B ．2C ．－1D ．－25．设A ，B ，C 是△ABC 的三个内角，且tan A ，tan B 是方程3x 2－5x ＋1＝0的两个实数根，则△ABC 是( )．A ．等边三角形B ．等腰直角三角形C ．锐角三角形D ．钝角三角形6．在△ABC 中，tan A ＋tan B tan A tan B ，则C ＝__________．7．tan 20tan 501tan20tan50(-)--o o o o＝__________． 8．已知tan =24πα⎛⎫+ ⎪⎝⎭，求212sin cos cos ααα+的值． 9．如图，两座建筑物AB ，CD 的高度分别是9 m 和15 m ，从建筑物AB 的顶部A 看建筑物CD 的张角∠CAD ＝45°，求建筑物AB 和CD 的底部之间的距离BD ．10．设一元二次方程mx 2＋(2m －1)x ＋(m ＋1)＝0的两根为tan α，tan β，求tan(α＋β)的取值范围．参考答案1答案：A2答案：B3答案：B4答案：B5答案：D6答案：3π78答案：2 39答案：18 m10答案：(－∞，－1)∪31,4⎛⎤--⎥⎝⎦。

高中数学第3章三角恒等变形 2.3 两角和与差的正切函数练习北师大版必修4-北师大版高一必修4

2.3 两角和与差的正切函数课后拔高提能练一、选择题 1．若α∈⎝ ⎛⎭⎪⎫π2，π，tan ⎝ ⎛⎭⎪⎫α＋π4＝17，则sin α＝( )A ．35B ．45 C ．－35D ．－45解析：选A tan α＝tan ⎝ ⎛⎭⎪⎫α＋π4－π4＝tan ⎝ ⎛⎭⎪⎫α＋π4－11＋tan ⎝ ⎛⎭⎪⎫α＋π4＝17－11＋17＝－34，因为α∈⎝ ⎛⎭⎪⎫π2，π，所以sin α＝35，选A ．2．已知tan(α＋β)＝35，tan ⎝ ⎛⎭⎪⎫β－π4＝14，那么tan ⎝ ⎛⎭⎪⎫α＋π4＝( ) A ．1318 B ．1323 C ．723D ．16解析：选C tan ⎝ ⎛⎭⎪⎫α＋π4＝tan ⎣⎢⎡⎦⎥⎤(α＋β)－⎝ ⎛⎭⎪⎫β－π4 ＝tan (α＋β)－tan ⎝⎛⎭⎪⎫β－π41＋tan (α＋β)tan ⎝⎛⎭⎪⎫β－π4＝35－141＋35×14＝723.3．若tan ⎝ ⎛⎭⎪⎫π4＋α＝2，则12sin αcos α＋cos 2α的值为( ) A ．32 B ．－32C ．23D ．－23解析：选C 由tan ⎝ ⎛⎭⎪⎫α＋π4＝2知， tan α＝tan ⎝⎛⎭⎪⎫α＋π4－π4＝2－11＋2＝13.又12sin αcos α＋cos 2α＝sin 2α＋cos 2α2sin αcos α＋cos 2α＝tan 2α＋12tan α＋1＝19＋123＋1＝106＋9＝23. 4．若tan α＝lg 10m ，tan β＝lg m ，且α－β＝π4，则实数m 的值为( )A ．1B ．110C ．1或110D ．1或10解析：选C ∵tan α＝lg 10m ＝1＋lg m ，tan β＝lg m ，又α－β＝π4，∴tan(α－β)＝tan α－tan β1＋tan αtan β＝1＋lg m －lg m1＋(1＋lg m )lg m ＝1，∴lg m (lg m ＋1)＝0，∴lg m ＝0或lg m ＝－1， ∴m ＝1或110.二、填空题5．(2017·某某卷)若tan ⎝ ⎛⎭⎪⎫α－π4＝16，则tan α＝________. 解析：解法一：∵tan ⎝ ⎛⎭⎪⎫α－π4＝tan α－11＋tan α＝16，即6tan α－6＝1＋tan α，∴tan α＝75.解法二：tan α＝tan ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π4＋π4＝ tan ⎝ ⎛⎭⎪⎫α－π4＋tan π41－tan ⎝ ⎛⎭⎪⎫α－π4tan π4＝16＋11－16＝75.答案：756．(2018·全国卷Ⅱ)已知tan ⎝⎛⎭⎪⎫α－5π4＝15，则tan α＝________.解析：tan ⎝⎛⎭⎪⎫α－5π4＝tan α－tan5π41＋tan α·ta n5π4＝tan α－11＋tan α＝15，解方程得tan α＝32.答案：327．已知tan ⎝ ⎛⎭⎪⎫α－β2＝12，tan ⎝ ⎛⎭⎪⎫β－α2＝－13，则tan ⎝ ⎛⎭⎪⎫α＋β2＝________.解析：tan ⎝ ⎛⎭⎪⎫α＋β2＝tan ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫α－β2＋⎝ ⎛⎭⎪⎫β－α2＝12－131＋12·13＝17. 答案：17三、解答题8．已知△ABC 中，tan B ＋tan C ＋3tan B tan C ＝3，且3tan A ＋3tan B ＝tan A tan B －1，试判断△ABC 的形状．解：∵3tan A ＋3tan B ＝tan A tan B －1， ∴tan A ＋tan B 1－tan A tan B ＝－33.∴tan(A ＋B )＝－33. ∵0<A ＋B <π，∴A ＋B ＝5π6，∴C ＝π6.又∵tan B ＋tan C ＋3tan B tan C ＝3， ∴tan B ＋33＋3×33tan B ＝ 3. ∴tan B ＝33，∴B ＝π6，从而A ＝2π3. ∴△ABC 是等腰钝角三角形．9．若tan α，tan β是关于x 的方程mx 2－(2m －3)x ＋m －2＝0的两个实根． (1)求m 的取值X 围；(2)求tan(α＋β)的取值X 围．解：(1)∵tan α，tan β是方程mx 2－(2m －3)x ＋m －2＝0的两实根，且tan α∈R ，tan β∈R ，∴只需⎩⎪⎨⎪⎧m ≠0，Δ≥0，即⎩⎪⎨⎪⎧m ≠0，(2m －3)2－4m (m －2)≥0.得m ≤94且m ≠0.∴m 的取值X 围是(－∞，0)∪⎝ ⎛⎦⎥⎤0，94.(2)∵tan(α＋β)＝tan α＋tan β1－tan αtan β，且tan αtan β＝m －2m ，tan α＋tan β＝2m －3m， ∴tan(α＋β)＝2m －32＝m －32.∵m ≤94且m ≠0，∴tan(α＋β)≤34，且tan(α＋β)≠－32.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(1)求tan 的值；的值．
解析：(1)∵a，b共线，∴sinθ－2cosθ＝0，即tanθ＝2.
∴tan ＝＝＝－3.
(2)由(1)，知tanθ＝2，又θ∈ ，∴sinθ＝，cosθ＝ .
∵5cos(θ－φ)＝3 cosφ，
∴5(cosθcosφ＋sinθsinφ)＝3 cosφ，即 cosφ＋2 sinφ＝3 cosφ，
∴cosφ＝sinφ.
又0<φ< ，∴tanφ＝1，∴φ＝ .
∴α＋β＝ .
2. 的值是()
A. B．－
C. D．－
答案：B
解析：＝＝tan(45°＋75°)＝tan120°＝－tan60°＝－ .
3．已知tan(α＋β)＝，tan ＝，那么tan ＝()
A. B.
C. D.
答案：C
解析：因为α＋＝(α＋β)－，所以tan ＝tan ＝＝，故选C.
答案：－
解析：∵α为第三象限的角，则2kπ＋π≤α≤2kπ＋，∴4kπ＋2π≤2α≤4kπ＋3π(k∈Z)，又cos2α＝－，
∴sin2α＝，tan2α＝－，∴tan( ＋2α)＝＝－ .
8．tan ＋tan ＋ tan ·tan 的值为________．
答案：
解析：tan ＋tan ＋ tan ·tan
24两角和与差的正切函数
时间：45分钟满分：80分
班级________姓名________分数________
一、选择题：(每小题5分，共5×6＝30分)
1．设tanα＝，tanβ＝，且α、β角为锐角，则α＋β的值是()
A. B. 或
C. D.
答案：C
解析：由tanα＝，tanβ＝，得tan(α＋β)＝＝＝1.又α、β均是锐角，
A. B.
C．－ D．不确定
答案：C
解析：∵tanα和tanβ是mx2＋(2m－3)x＋(m－2)＝0的两根，
∴
∴m≤ ，且m≠0.tan(α＋β)＝＝＝＝－m＋ .
∴当m＝时，tan(α＋β)的最小值为－ .
二、填空题：(每小题5分，共5×3＝15分)
7．已知α为第三象限的角，cos2α＝－，则tan( ＋2α)＝________.
答案：A
解析：由tanAtanB>1得角A，B均为锐角，然后切化弦，得sinAsinB>cosAcosB，即cos(A＋B)<0，∴cos(π－C)<0，∴－cosC<0，∴cosC>0，∴角C为锐角，∴△ABC是锐角三角形，故选A.
6．设tanα和tanβ是方程mx2＋(2m－3)x＋(m－2)＝0的两根，则tan(α＋β)的最小值是()
4．已知tanα＝，则的值是()
A．2B.
C．－1D．－3
答案：B
解析：解法一：因为tanα＝，所以tan ＝＝＝3，所以＝＝ .故选B.
解法二：＝＝tan ＝tanα＝ .故选B.
5．在△ABC中，若tanAtanB>1，则△ABC是()
A．锐角三角形B．直角三角形
C．钝角三角形D．无法确定
解析：因为tan(α＋β)＝2，tan(α－β)＝3，
所以tan2α＝tan[(α＋β)＋(α－β)]＝＝＝－1，
tan2β＝tan[(α＋β)－(α－β)]＝＝＝－，
所以tan(3π＋2α)＋tan(4π＋2β)＝tan2α＋tan2β＝－1－＝－ .
12．已知向量a＝(sinθ，2)，b＝(cosθ，1))，且a，b共线，其中θ∈ .
(1)求tan(α＋β)的值；
(2)求的值．
解析：(1)由题意，得cosα＝，cosβ＝ .
因为α，β为锐角，所以sinα＝，sinβ＝，
因为tanα＝2 ，tanβ＝ .
所以tan(α＋β)＝＝＝－ .
(2)
＝ ×
＝ ×tan[(α＋β)－α]
＝ ×tanβ
＝ ×
＝ .
11．已知tan(α＋β)＝2，tan(α－β)＝3，求tan(3π＋2α)＋tan(4π＋2β)的值．
＝tan ＋ tan ·tan
＝＋ tan ·tan ＝ .
9．若a，b是非零实数，且＝tan ，则＝________.
答案：
解析：∵ ＝＝tan ＝tan( ＋ )＝，∴ ＝tan ＝ .
三、解答题：(共35分，11＋12＋12)
10．在平面直角坐标系xOy中，以Ox为始边作两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知点A，B的横坐标分别为， .