密码学 入门(一)
密码学基础PPT课件

一个明文字母有多种可能的代换密文字母,使 得频率分析困难的多(hs成为BP, hq成为YP)。
由于这些原因,Playfair密码过去长期被认 为是不可破的。
最简单的多表代换密码---Vigenère
注意
Internet的广泛应用,可以把全世界的计算机资源 连成一体,形成巨大的计算能力,从而拥有巨大的 密码破译能力,使原来认为安全的密码被破译。
1994年,40多个国家的600多位科学家通过Internet, 历时9个月破译了RSA-129密码,1999年又破译了RSA - 140密码,2005年,RSA-200也被成功破译。
经典密码运用的两种基本技术:
代换法:将明文字母替换成其他字母、数字 或符号
置换法:明文的字母保持相同,但顺序被打 乱
代换技术
代换法,是将明文字母替换成其他字母、数 字或符号的方法。
Caesar密码(已知的最早的代换密码)
例如:明晨五点发动反攻 明文:MING CHEN WU DIAN FA DONG FAN GONG 密文:PLQJ FKHQ ZX GLDQ ID GRQJ IDQ JRQJ
密码系统的分类(3)
根据加密算法是否变化分类
设E为加密算法,K0, K1,…,Kn,为密钥, M0,M1,…,Mn为明文,C为密文
固定算法密码体制
C0=E(M0,K0), C1=E(M1,K1),..., Cn=E(Mn,Kn)
变化算法密码体制
C0=E1 (M0,K0), C1=E2 (M1,K1),..., Cn=En (Mn,Kn)
密码学的发展历史(5)
密码学复习1
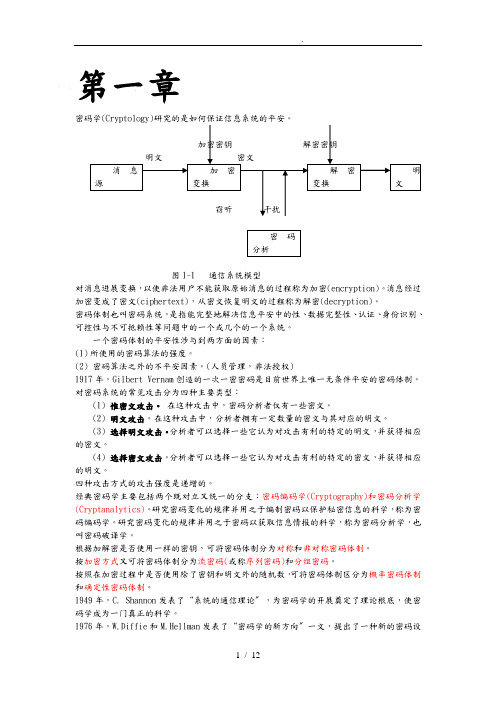
第一章密码学(Cryptology)研究的是如何保证信息系统的平安。
图1-1 通信系统模型对消息进展变换,以使非法用户不能获取原始消息的过程称为加密(encryption)。
消息经过加密变成了密文(ciphertext),从密文恢复明文的过程称为解密(decryption)。
密码体制也叫密码系统,是指能完整地解决信息平安中的性、数据完整性、认证、身份识别、可控性与不可抵赖性等问题中的一个或几个的一个系统。
一个密码体制的平安性涉与到两方面的因素:(1)所使用的密码算法的强度。
(2) 密码算法之外的不平安因素。
(人员管理,非法授权)1917年,Gilbert Vernam创造的一次一密密码是目前世界上唯一无条件平安的密码体制。
对密码系统的常见攻击分为四种主要类型:(1) 惟密文攻击。
在这种攻击中,密码分析者仅有一些密文。
(2) 明文攻击。
在这种攻击中,分析者拥有一定数量的密文与其对应的明文。
(3) 选择明文攻击。
分析者可以选择一些它认为对攻击有利的特定的明文,并获得相应的密文。
(4) 选择密文攻击。
分析者可以选择一些它认为对攻击有利的特定的密文,并获得相应的明文。
四种攻击方式的攻击强度是递增的。
经典密码学主要包括两个既对立又统一的分支:密码编码学(Cryptography)和密码分析学(Cryptanalytics)。
研究密码变化的规律并用之于编制密码以保护秘密信息的科学,称为密码编码学。
研究密码变化的规律并用之于密码以获取信息情报的科学,称为密码分析学,也叫密码破译学。
根据加解密是否使用一样的密钥,可将密码体制分为对称和非对称密码体制。
按加密方式又可将密码体制分为流密码(或称序列密码)和分组密码。
按照在加密过程中是否使用除了密钥和明文外的随机数,可将密码体制区分为概率密码体制和确定性密码体制。
1949年,C. Shannon发表了“系统的通信理论〞,为密码学的开展奠定了理论根底,使密码学成为一门真正的科学。
密码学入门

件签名。 Alice将文件和散列签名送给Bob Bob用Alice发送的文件产生单向散列签名值,然
后数字签名算法对散列值运算,同时用Alice的公 开密钥对签名的散列解密。如果签名的散列值与 自己产生散列值相匹配,签名就是有效的。
?换位密码密码学入门?转轮机?简单异或?破异简单异或的方法?破异简单异或的方法?重合码计数法找出密钥长度?按此长度移动密文并且和自身异或?一次一乱密码本密码学入门?常见的计算机算法?des是最通用的计算机加密算法
网络安全入门
于广辉ygh@
大连理工大学网络中心
密码学入门
基础知识 密码协议 密码技术 密码算法
密码学入门
英国的TYPEX打字密码机,是德国3轮ENIGMA的 改进型密码机。它在英国通信中使用广泛,且在 破译密钥后帮助破解德国信号。
密码学入门
在线密码电传机Lorenz SZ 42,大约在1943年 由Lorenz A.G制造。英 国人称其为“tunny”, 用于德国战略级陆军司 令部。SZ 40/SZ 42加 密因为德国人的加密错 误而被英国人破解,此 后英国人一直使用电子 COLOSSUS机器解读德 国信号。
密码学入门
Kryha密码机大约在 1926年由Alexander vo Kryha发明。这是 一个多表加密设备, 密钥长度为442,周 期固定。一个由数量 不等的齿的轮子引导 密文轮不规则运动。
密码学入门
哈格林(Hagelin)密码机C-36,由 Aktiebolaget Cryptoeknid Stockholm于 1936年制造密钥周期长度为3,900,255。
代替密码和换位密码
代替密码(substitution cipher)就是明文中 的每一个字符被替换成密文中的另外一个自 负。接收者对密文进行逆替换就恢复出明文 来。
密码学的数学基础

密码学的数学基础密码学是研究信息安全和通信保密的一门学科,它涉及到数据加密、解密、认证、签名以及密码系统的设计等领域。
密码学作为信息安全的基石,具备坚实的数学基础。
本文将探讨密码学中涉及的一些重要的数学原理和算法。
一、模运算在密码学中,模运算是一种关键的数学运算,它对于生成密码算法和破解密码算法都有着重要作用。
模运算是指对于给定的正整数n,将一个整数a除以n所得的余数。
模运算具有以下几个重要性质:1. 加法的封闭性。
对于任意的整数a和b,(a+b) mod n=(a mod n + b mod n) mod n。
2. 乘法的封闭性。
对于任意的整数a和b,(a×b) mod n=(a mod n × b mod n) mod n。
3. 乘法的分配律。
对于任意的整数a、b和c,(a+b) mod n=(a mod n + b mod n) mod n。
二、欧拉函数和费马小定理在密码学中,欧拉函数和费马小定理是密码算法设计的重要数学基础。
1. 欧拉函数欧拉函数φ(n)表示小于等于n的正整数中与n互质的数的个数。
对于任意正整数n,欧拉函数满足以下性质:- 如果p是一个质数,那么φ(p)=p-1。
- 如果a和b互质,那么φ(a×b)=φ(a)×φ(b)。
2. 费马小定理费马小定理是一个基本的数论定理,它指出如果p是一个质数,a是不可被p整除的整数,那么a^(p-1) mod p ≡ 1。
费马小定理在密码学中应用广泛,特别是在RSA算法中。
RSA算法是一种非对称加密算法,基于大数因子分解的困难性。
三、素数和大数因子分解密码学中的许多算法都依赖于素数和大数因子分解的困难性。
1. 素数素数是只能被1和自身整除的正整数。
在密码学中,素数的选取十分重要,因为对于一个大的合数,将其分解质因数是非常困难的。
2. 大数因子分解大数因子分解是指将一个大的合数分解成质因数的过程。
在密码学中,大数因子分解的困难性是许多加密算法的基础,如RSA算法。
密码学基础(一)常见密码算法分类

密码学基础(一)常见密码算法分类对称算法是指一种加密密钥和解密密钥相同的密码算法,也称为密钥算法或单密钥算法。
该算法又分为分组密码算法(Block cipher)和流密码算法(Stream cipher)。
•分组密码算法o又称块加密算法o加密步骤一:将明文拆分为 N 个固定长度的明文块o加密步骤二:用相同的秘钥和算法对每个明文块加密得到 N 个等长的密文块o加密步骤三:然后将 N 个密文块按照顺序组合起来得到密文•流密码算法o又称序列密码算法o加密:每次只加密一位或一字节明文o解密:每次只解密一位或一字节密文常见的分组密码算法包括 AES、SM1(国密)、SM4(国密)、DES、3DES、IDEA、RC2 等;常见的流密码算法包括 RC4 等。
•AES:目前安全强度较高、应用范围较广的对称加密算法•SM1:国密,采用硬件实现•SM4:国密,可使用软件实现•DES/3DES:已被淘汰或逐步淘汰的常用对称加密算法二、非对称密码算法(Asymmetric-key Algorithm)非对称算法是指一种加密密钥和解密密钥不同的密码算法,也称为公开密码算法或公钥算法。
该算法使用一个密钥进行加密,另一个密钥进行解密。
•加密秘钥可以公开,又称为公钥•解密秘钥必须保密,又称为私钥常见非对称算法包括 RSA、SM2(国密)、DH、DSA、ECDSA、ECC 等。
三、摘要算法(Digest Algorithm)算法是指将任意长度的输入消息数据转换成固定长度的输出数据的密码算法,也称为哈希函数、哈希函数、哈希函数、单向函数等。
算法生成的定长输出数据称为摘要值、哈希值或哈希值,摘要算法没有密钥。
算法通常用于判断数据的完整性,即对数据进行哈希处理,然后比较汇总值是否一致。
摘要算法主要分为三大类:MD(Message Digest,消息摘要算法)、SHA-1(Secure Hash Algorithm,安全散列算法)和MAC(Message Authentication Code,消息认证码算法);另国密标准 SM3 也属于摘要算法。
1_密码学基础

➢ 1967年David Kahn的《The Codebreakers》 ➢ 1971-73年IBM Watson实验室的Horst Feistel等的几篇技
33
密码学基础
破译分析I: 尝试全部可能
使用简单替代(移n位) 密钥未知 已知密文: CSYEVIXIVQMREXIH 如何找到密钥? 仅有26个可能密钥 尝试全部的可能!看哪个能找到合
理的含义 穷举搜索 答案: 密钥 = 4
34
密码学基础
更复杂的替代
密钥是一些字母的组合 不一定是移位 例如:
明文:Caesar was a great soldier 密文:Fdhvdu zdv d juhdw vroglhu
第12页
2.3.1 形形色色的密码技术
二战著名的(ENIGMA)密码 ➢ 德国人Arthur Scheribius人发明 ➢ 德国人将其改装为军用型,使之更为复杂可靠 ➢ 1933年,纳粹最高统帅部通信部决定将“ENIGMA”作为德
➢ 经验告诉我们一个秘密的算法在公开时就很容易破解了 ➢ 密码的算法不可能永远保持隐秘 ➢ 理想的情况是在密码算法被破解之前找到算法的弱点
5
密码学基础
黑盒子密码系统
密钥
密钥
明文 加密
密文
解密
密码的通用方式
密码学基础
明文
6
密码发展历史
形形色色的密码技术 密码发展史
第7页
2.3.1 形形色色的密码技术
第三阶段:1976年以后,密码学的新方向——公钥密 码学。公钥密码使得发送端和接收端无密钥传输的保 密通信成为可能。
密码学入门1凯撒密码与栅栏密码ppt课件

加密后xyzab cdefg hijkl mnopq rstuv w
在原始字母表中寻找出surprise与加密后的字母表中一一对应字母
分别是promofpb
⑥输出密文:promofpb加密完成
制作者:0风雨中的回忆0
凯撒密码
解密①首先我们要有一个密匙k=3
然后按照加密准备字母表 原始字母表abcde fghij klmno pqrst uvwxy z
(看出什么了吗?)
加密后xyzab cdefg hijkl mnopq rstuv w
对了所有字母都向右移动了3,也就是你所选择的k值。
到现在准备工作已经完成,下面开始正式加密。
• 注:字母表一一对应
制作者:0风雨中的回忆0
凯撒密码
④选择我们要加密的明文:surprise
⑤原始字母表abcde fghij klmno pqrst uvwxy z
栅栏密码
解密
①输入密文:yurbatfloaeeuiu#
②平分密文:y u r b a t f l
oaeeuiu#
③上下排列:y u r b a t f l
oaeeuiu#
④上下组合排列密码,并去掉空格。you are beautiful
⑤输出明文:you are beautiful
制作者:0风雨中的回忆0
符号,为了简单,这里加入符号# 得到第二个字母oaeeuiu# 到此准备工作就完了
制作者:0风雨中t f l 第二组o a e e u i u # 连接起来yurbatfloaeeuiu# ⑤输出密文:yurbatfloaeeuiu#
制作者:0风雨中的回忆0
制作者:0风雨中的回忆0
凯撒密码
正式开始加密过程
密码学基础知识

密码学基础知识密码学是一门研究数据的保密性、完整性以及可用性的学科,广泛应用于计算机安全领域、网络通信以及电子商务等方面。
密码学的基础知识是研究密码保密性和密码学算法设计的核心。
1. 对称加密和非对称加密在密码学中,最基本的加密方式分为两类:对称加密和非对称加密。
对称加密通常使用一个密钥来加密和解密数据,同时密钥必须保密传输。
非对称加密则使用一对密钥,分别为公钥和私钥,公钥可以公开发布,任何人都可以用它来加密数据,但只有私钥持有人才能使用私钥解密数据。
2. 散列函数散列函数是密码学中常用的一种算法,它将任意长度的消息压缩成一个固定长度的摘要,称为消息摘要。
摘要的长度通常为128位或更长,主要用于数字签名、证书验证以及数据完整性验证等。
常见的散列函数有MD5、SHA-1、SHA-256等。
3. 数字签名数字签名是一种使用非对称加密技术实现的重要保密机制,它是将发送方的消息进行加密以保证消息的完整性和真实性。
发送方使用自己的私钥对消息进行签名,然后将消息和签名一起发送给接收方。
接收方使用发送方的公钥来验证签名,如果消息被篡改或者签名无法验证,接收方将拒绝接收消息。
4. 公钥基础设施(PKI)PKI是一种包括数字证书、证书管理和证书验证的基础设施,用于管理数字证书和数字签名。
数字证书是将公钥与其拥有者的身份信息结合在一起的数字文件,它是PKI系统中最重要的组成部分之一。
数字证书通过数字签名来验证其真实性和完整性,在通信和数据传输中起着至关重要的作用。
总之,密码学是计算机科学中重要的领域之一,其应用广泛,影响深远。
掌握密码学基础知识非常有必要,对于安全性要求较高的企业和组织来说,更是至关重要。
简单密码学入门

简单密码学⼊门⼀、密码的定义 密码,最初的⽬的是⽤于对信息加密,计算机领域的密码技术种类繁多。
但随着密码学的运⽤,密码还被⽤于⾝份认证、防⽌否认等功能上。
密码是通信双⽅按约定的法则进⾏信息特殊变换的⼀种重要保密⼿段。
依照这些法则,变明⽂为密⽂,称为加密变换;变密⽂为明⽂,称为脱密变换。
密码在早期仅对⽂字或数码进⾏加、脱密变换,随着通信技术的发展,对语⾳、图像、数据等都可实施加、脱密变换。
⼆、密码的分类 最基本的分类是:信息加解密分为对称加密(Sysmmetric Cryptography)和⾮对称加密(Public-Key Cryptography,Asymmetric Cryptography),这两者的区别是是否使⽤了相同的密钥。
除了信息的加解密,还有⽤于确认数据完整性(Integrity)的单向散列(One-Way Hash Function)技术,⼜称密码检验(Cryptographic Checksum)、指纹(Fingerprint)、消息摘要(Message Digest)。
信息的加解密与信息的单向散列的区别是,对称与⾮对称加密是可以通过密钥解出明⽂,⽽单向散列是不可逆的。
信息的加解密,密⽂必定是不定长的,⽽单向散列可以是定长的。
结合密码学的加解密技术和单向散列技术,⼜有了⽤于防⽌篡改的消息认证码技术,防⽌伪装的数字签名技术以及认证证书。
三、密码问题的应对策略威胁问题特征对应技术窃听机密性对称、⾮对称加密篡改完整性单向散列、消息认证码、数字签名伪装⾝份认证消息认证、数字签名否认不可否认数字签名四、信息的加密⼿段需要对加密和解密使⽤相同密钥的加密算法。
由于其速度快,对称性加密通常在消息发送⽅需要加密⼤量数据时使⽤。
对称性加密也称为密钥加密。
所谓对称,就是采⽤这种加密⽅法的双⽅使⽤⽅式⽤同样的密钥进⾏加密和解密。
密钥是控制加密及解密过程的指令。
算法是⼀组规则,规定如何进⾏加密和解密。
密码学基础概念

密码学基础概念及应用
密码学是研究信息的保密性、完整性和可用性的科学与技术。
它涉及使用密码算法对信息进行加密、解密和验证的过程。
以下是密码学的基础概念和一些常见的应用:
1. 加密算法:加密算法是密码学中最重要的概念之一。
它是一种数学算法,用于将明文(原始信息)转换为密文(加密后的信息)或将密文还原为明文。
2. 密钥:密钥是在加密和解密过程中使用的参数。
它是一个特定的数据值,用于确定加密算法的行为,从而实现不同的加密效果。
3. 对称加密和非对称加密:对称加密使用相同的密钥来进行加密和解密,而非对称加密使用一对密钥,其中一个用于加密,另一个用于解密。
4. 数字签名:数字签名是一种用于验证文档或消息真实性和完整性的技术。
它使用私钥对文档进行加密,然后使用公钥对加密后的文档进行解密验证。
5. 数字证书:数字证书是一种用于验证通信方身份的电子文件。
它包含了通信方的公钥和相关身份信息,由可信的证书颁发机构签发。
6. 密码协议:密码协议是在网络通信中使用的一组规则和步骤,用于确保安全通信和保护数据的隐私。
7. 数字货币:加密货币如比特币和以太坊使用密码学技术实现安全的交易和资产管理。
8. 数据库加密:数据库加密技术用于对数据库中存储的敏感数据进行加密保护,以防止未经授权的访问和泄露。
9. 消息认证码(MAC):MAC是一种用于验证消息完整性和真实性的密码技术,可以确保消息在传输过程中没有被篡改。
这些只是密码学的一些基础概念和应用示例。
密码学在许多领域都有广泛的应用,包括网络安全、电子商务、通信保密、数据保护和数字身份验证等。
密码学入门基础知识

密码学入门基础知识
密码学是一门涉及信息保密和安全的学科。
它的目标是通过使用
各种密码技术来确保数据传输和存储的机密性、完整性和可用性。
密码学的基础是对称密码和非对称密码。
对称密码指的是发送和
接收方使用相同的密钥来加密和解密信息。
这种密码技术简单、高效,但密钥的分发和管理是一个挑战。
非对称密码则使用一对密钥,公钥
和私钥。
公钥用于加密信息,私钥用于解密信息。
这种方法更安全,
但加密和解密过程可能较慢。
另外,密码学还涉及到哈希函数。
哈希函数将任意长度的数据映
射为固定长度的输出值,称为哈希值。
它被广泛用于验证数据的完整
性和数字签名。
密码学也包括诸如数字证书、数字签名和安全协议等领域。
数字
证书用于验证实体的身份和建立安全连接。
数字签名用于验证数据的
来源和完整性。
安全协议是指用于保护通信过程中的各种协议,例如SSL/TLS协议。
密码学的应用非常广泛。
它被用于保护互联网上的信息传输,例
如电子邮件、网上支付和在线购物。
在银行和金融机构中,密码学被
用于保护账户和交易信息。
还有许多其他领域,如军事通信、医疗保
密和智能卡系统,都需要密码学的支持。
总而言之,密码学是一门关乎信息安全的学科,它通过各种密码
技术来保护数据的机密性和完整性。
了解密码学的基础知识对于个人
和组织来说都非常重要,以保护他们的私密信息免受未经授权的访问。
密码学知识点总结csdn

密码学知识点总结csdn1. 密码学基础密码学基础包括对称加密、非对称加密、哈希函数、消息认证码等概念的介绍。
对称加密即加密和解密使用相同的密钥,常用算法有DES、AES、RC4等;非对称加密则分为公钥加密和私钥解密,常用算法有RSA、ECC等;哈希函数则是将任意长度的消息压缩为固定长度的摘要信息,常用算法有MD5、SHA-1、SHA-256等;消息认证码是在消息传输中保障数据完整性的重要手段,主要分为基于对称加密的MAC和基于非对称加密的数字签名。
2. 随机数生成密码学安全性的基础在于随机数的生成,常用的随机数生成算法有伪随机数生成器(PRNG)和真随机数生成器(TRNG)。
PRNG是通过确定性算法生成随机数,安全性依靠其内部逻辑结构;TRNG则是依靠物理过程生成随机数,如放射性衰变、指纹图像等,安全性更高。
密码学攻击主要分为三类:密码分析攻击、椭圆曲线攻击和量子攻击。
密码分析攻击是通过推测、猜测等方法攻破密码;椭圆曲线攻击是因为非对称加密算法中的基于椭圆曲线离散对数问题存在可解性,从而破解密码;量子攻击则是通过量子计算机的强大计算能力破解传统密码学算法。
4. 密码学综合应用密码学在实际应用中广泛应用于电子邮件加密、数字证书、数字签名、数字支付、VPN安全通信等领域。
其中,AES算法被广泛应用于SSL/TLS等加密通信协议中;RSA算法则是数字证书和电子邮件加密中最常用的算法;数字签名则应用于身份认证、电子合同、电子票据等领域;数字支付则依赖于密码学原理来保证支付的安全性。
5. 密码学的未来发展当前,密码学面临着来自量子计算机的挑战,需要进一步开发抗量子攻击的加密算法。
同时,在移动互联网、物联网等领域中,新的安全需求也对密码学技术提出了挑战。
未来发展的重点可能包括量子密码学研究、密码学与人工智能技术的结合等方面。
总之,密码学是信息安全的重要组成部分,掌握相关知识点将有助于提高信息安全意识和防范风险能力。
密码学基础01-概述+对称密码

伴随计算机和通信技术旳迅速发展和普及应用,出现
了电子政务、电子商务、电子金融等主要旳应用信息系统
。在这些系统中必须确保信息旳安全传递和存储
>>
0
>>
1
>>
0
>>
1
>>
0
>>
密码学旳发展
• 1949年之前:古典密码(classical cryptography)
1. 密码学多半是具有艺术特征旳字谜,出现某些密码算法和机械
密钥(private key)私钥,简称私钥。
>>
0
>>
1
>>
0
>>
1
>>
0
>>
>>
0
>>
1
>>
0
>>
1
>>
0
>>
>>
0
>>
1
>>
0
>>
1
>>
0
>>
>>
0
>>
1
>>
0
>>
1
>>
0
>>
>>
0
>>
1
>>
0
>>
1
>>
0
>>
密码学基础知识

密码学基础知识【1】古典密码1、置换密码置换密码将明⽂中的字母顺序重新排列,但字母本⾝不变,由此形成密⽂。
换句话说,明⽂与密⽂所使⽤的字母相同,只是它们的排列顺序不同。
我们可以将明⽂按矩阵的⽅式逐⾏写出,然后再按列读出,并将它们排成⼀排作为密⽂,列的阶就是该算法的密钥。
在实际应⽤中,⼈们常常⽤某⼀单词作为密钥,按照单词中各字母在字母表中的出现顺序排序,⽤这个数字序列作为列的阶。
【例1】我们以coat作为密钥,则它们的出现顺序为2、3、1、4,对明⽂“attack postoffice”的加密过程见图1:图1 对明⽂“attack postoffice”的加密过程按照阶数由⼩到⼤,逐列读出各字母,所得密⽂为:t p o c a c s f t k t i a o f e.对于这种列变换类型的置换密码,密码分析很容易进⾏:将密⽂逐⾏排列在矩阵中,并依次改变⾏的位置,然后按列读出,就可得到有意义的明⽂。
为了提⾼它的安全性,可以按同样的⽅法执⾏多次置换。
例如对上述密⽂再执⾏⼀次置换,就可得到原明⽂的⼆次置换密⽂:o s t f t a t a p c k o c f i e还有⼀种置换密码采⽤周期性换位。
对于周期为r的置换密码,⾸先将明⽂分成若⼲组,每组含有r个元素,然后对每⼀组都按前述算法执⾏⼀次置换,最后得到密⽂。
【例2】⼀周期为4的换位密码,密钥及密⽂同上例,加密过程如图2:图2 周期性换位密码2、 替代密码单表替代密码对明⽂中的所有字母都⽤⼀个固定的明⽂字母表到密⽂字母表的映射。
换句话说,对于明⽂,相应的密⽂为=。
下⾯介绍⼏种简单的替代密码。
1. 加法密码在加法密码中,映射规则可表⽰为,其中k为密钥,加密算法就是。
例如,我们可以将英⽂的26个字母分别对应于整数0~25,则n=26,对应关系如表加法密码也称为移位密码,凯撒密码就是k=3的加法密码。
【例1】取密钥k=9,明⽂为“attackpostoffice”,则转换为密⽂的过程如下:⾸先将其转化为数字序列:0 19 19 0 2 10 15 14 18 19 14 5 5 8 2 4然后每个数值加9,并做模26运算,得到以下序列:9 2 2 9 11 19 24 23 1 2 23 14 14 17 11 13再将其转化为英⽂字母,可得密⽂:jccjltyxbcxoorln.2.乘法密码乘法密码的映射规则可表⽰为,其中k为密钥,加密算法就是。
密码学基础知识

密码学基础知识密码学是研究如何在通信过程中确保信息的机密性、完整性和身份认证的学科。
以下是密码学的一些基础知识:1. 对称加密和非对称加密:对称加密使用相同的密钥来进行加密和解密,而非对称加密使用一对密钥,包括公钥和私钥。
公钥用于加密数据,私钥用于解密数据。
非对称加密也可以用于数字签名和身份验证。
2. 加密算法:加密算法是用于对数据进行加密和解密的数学算法。
常见的对称加密算法有AES(高级加密标准)和DES(数据加密标准),常见的非对称加密算法有RSA和椭圆曲线加密算法(ECC)。
3. 数字签名:数字签名用于验证消息的完整性和认证消息的发送者。
它使用发送者的私钥对消息进行加密,接收者使用发送者的公钥进行解密和验证。
4. 哈希函数:哈希函数将输入数据转换为固定长度的哈希值。
它们广泛用于密码学中的消息完整性检查和密码存储。
常见的哈希函数包括SHA-256和MD5,但MD5已经不推荐用于安全目的。
5. 密码协议:密码协议是在通信过程中使用的协议,旨在确保通信的安全性。
例如,SSL/TLS 协议用于在Web浏览器和服务器之间进行安全通信。
6. 密码学安全性:密码学的安全性取决于密钥的保密性和算法的强度。
一个安全的密码系统应该能够抵抗各种攻击,包括穷举攻击、字典攻击和选择明文攻击等。
7. 安全性协议和标准:密码学安全性协议和标准旨在确保系统和通信的安全性。
例如,PKCS (公钥密码标准)是用于公钥密码学的一组标准,TLS(传输层安全)是用于安全通信的协议。
需要注意的是,密码学是一个复杂的领域,有很多更高级的概念和技术。
以上只是一些基础的密码学知识,但足以了解密码学的基本原理和常用术语。
第四章密码学基础1

(2)博福特密码
类似于维吉尼亚密码的替代密码
最知名的应用是M-209密码机,属于对等加
密。 是按mod q减法运算的一种周期代替密码。 即ci+td=(ki-mi+td)(mod q)。
举例说明
(3)滚动密钥密码
对于周期多表代换密码,保密性将随周期d
的增大而增大,当d的长度和明文一样长时 就变成了滚动密钥密码,如果其中所采用的 密钥不重复就是一次一密体制。一般,密钥 可取一篇报告或一本书作为密钥源,可由书 名,章节号及标题来限定密钥起始位置。
2 按加密过程转换原理分: 代换密码
又称替换密码,将明文的每个或每组字符由
另一个或一级字符代替,形成密文。
置换密码
又称移位密码,加密时只对明文字母进行重
新排列,其位置发生了改变。
上述两种方法一般用于古典密码中。
3 根据加、解使用相同的密钥划分 对称密码
对称密码体制也称单钥密码体制、秘密密钥
4 Hill密码 是著名的多表代换密码,运用了矩阵中线性变换 的原理。 每个字母指定为一个26进制数字:0-25表示a-z。 m个连续的明文字母被看做m维微量,跟一个 m*m的加密矩阵相乘,得出的结果模26,得到m个 密文字母,即m个连续的明文字母作为一个单元, 被转换成等长的密文单元。加密矩阵必然可逆, 否则不可译码。
密码体制。加密和解密使用完全相同的密钥, 或加密密钥和解密密钥彼此之间非常容易推 导。
非对称密码
非对称密码体制也称为公钥密码体制。加密
和解密使用不同的密钥,而且由其中一个推 导另一个很困难,两个不同的密钥,其中一 个不公开称为私钥,另一个公开叫公钥。
密码学入门

密码学入门第一章几种常见密码形式一、栅栏易位密码即把将要传递的信息中的字母交替排成上下两行,再将下面一行字母排在上面一行的后边,从而形成一段密码。
举例:TEOGSDYUTAENNHLNETAMSHVAED解:将字母分截开排成两行,如下T E O G S D Y U T A E N NH L N E T A M S H V A E D再将第二行字母分别放入第一行中,得到以下结果:THE LONGEST DAY MUST HAVE AN END.课后小题:请破解以下密码teieeemrynwetemryhyeoetewshwsnvraradhnhyartebcmohrie二、恺撒移位元密码也就是一种最简单的错位法,将字母表前移或者后错几位,例如:明码表:ABCDEFGHIJKLMNOPQRSTUVWXYZ密码表:DEFGHIJKLMNOPQRSTUVWXYZABC这就形成了一个简单的密码表,如果我想写frzy(即明文),那么对照上面密码表编成密码也就是iucb (即密文)了。
密码表可以自己选择移几位,移动的位数也就是密钥。
课后小题:请破解以下密码dtzwkzyzwjijujsixtsdtzwiwjfrx三、进制转换密码比如给你一堆数字,乍一看头晕晕的,你可以观察数字的规律,将其转换为10进制数字,然后按照每个数字元在字母表中的排列顺序,拼出正确字母。
举例:110 10010 11010 11001解:很明显,这些数字都是由1和0组成,那么你很快联想到什么?二进制数,那么就试着把这些数字转换成十进制试试,得到数字6 18 26 25,对应字母表,破解出明文为frz y。
课后小题:请破解以下密码11 14 17 26 5 25四、摩尔斯密码翻译不同,有时也叫摩尔密码。
*表示滴,-表示哒,如下表所示比如滴滴哒就表示字母U,滴滴滴滴滴就表示数字5。
另外请大家不要被滴哒的形式所困,我们实际出密码的时候,有可能转换为很多种形式,例如用0和1表示,迷惑你向二进制方向考虑,等等。
密码学入门

2、凯撒密码凯撒加密法的替换方法是通过排列明文和密文字母表,密文字母表示通过将明文字母表向左或向右移动一个固定数目的位置。
例如,当偏移量是左移3的时候(解密时的密钥就是3):明文字母表:ABCDEFGHIJKLMNOPQRSTUVWXYZ密文字母表:DEFGHIJKLMNOPQRSTUVWXYZABC据说这种加密法师凯撒首先开始运用的,虽然这种加密法现在看来非常容易破解,因为密钥只有1到25这25种可能性,通过穷举法就能破解;如果需要更快的方式的话可以加入一些分析,比如在英语中“the”这个词出现频率极高,那么如果我在一段密文中经常看到“wlh”的出现,并且恰好这三个字母间距和the的字母间距一样,那么我就有理由相信wlh就是the,那么马上就能得到密钥是3。
我们来尝试破译一句凯撒密码:密文:OE DOV ZLPGLZ AOL YPNOA TVTLUA OL AOL YPNOA TAU明文:HE WHO SEIZES THE RIGHT MOMENT IS THE RIGHT MAN密钥为73、维吉尼亚密码维吉尼亚密码是使用一系列凯撒密码组成密码字母表的加密算法,属于多表密码的一种简单形式。
该方法最早记录在吉奥万·巴蒂斯塔·贝拉索于1553年所著的书《吉奥万·巴蒂斯塔·贝拉索先生的密码》中。
然而,后来在19世纪时被误传为是法国外交官布莱斯·德·维吉尼亚所创造,因此现在被称为“维吉尼亚密码”。
维吉尼亚密码以其简单易用而著称,同时初学者通常难以破解。
在一个凯撒密码中,字母表中的每一字母都会作一定的偏移,而维吉尼亚密码则是由一些偏移量不同的恺撒密码组成。
为了生成密码,首先需要使用维吉尼亚表格。
这一表格包括了26行字母表,每一行都由前一行向左偏移一位得到。
TO BE OR NOT TO BE THAT IS THE QUESTION当选定RELATIONS作为密钥时,加密过程是:明文一个字母为T,第一个密钥字母为R,因此可以找到在R行中代替T的为K,依此类推,得出对应关系如下:明文:T O B E O R N O T T O B E T H A T I S T H E Q U E S T I O N 密钥:R E L A T I O N S R E L A T I O N S R E L A T I O N S R E L 密文:K S M E H Z B B L K S M E M P O G A J X S E J C S F L Z S Y维吉尼亚密码足够地易于使用使其能够作为战地密码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Introduction
Pillars of Cryptology
9 / 27
Cryptology is Interdisciplinary
Computer Science
M
at he er ing
m
at ine
ics
ec El tr( on a )ic ng lE
Introduction
Pillars of Cryptology
2
Classical Cryptography One Time Pad
Introduction
Practicalities of Cryptography A
4 / 27
Introduction
This course will be about the science of cryptology. We focus on the basics for simplicity and to display the way modern cryptology works. Definitions Reductions (aka security proofs) Constructions We will concentrate on cryptology relevant to secure communication between two parties.
Hi Hello Bye
Anna Bye Bob
Introduction
Paradigms of Cryptology
12 / 27
Secure Communication
Confidentiality, integrity, authenticity
Bob Bye Anna
Hi Hello Bye
Please do the diagnostic prior to Friday’s problem class.
Introduction
Paradigms of Cryptology
11 / 27
Two-party communication
Unintended Learning Outcomes
Introduction
Practicalities of Cryptography A
8 / 27
Course Overview
Feedback
Please do not wait until the exam/end-of-term questionnaire with your questions and comments...
1
Explain and apply the principles of modern cryptology in the context of secure communication. Explain and demonstrate the functionality and desired security of standard cryptographic schemes used for confidentiality and authenticity. Link the design and operation of standard, state-of-the-art symmetric and asymmetric cryptographic schemes to their mathematical underpinnings. Use basic cryptanalytic techniques to evaluate the security level of simple cryptographic schemes.
Anna Bye Bob
Introduction
Paradigms of Cryptology
12 / 27
Secure Communication
Confidentiality, integrity, authenticity
Bob Bye Anna
Anna Bye Bob
Introduction
Introduction
Paradigms of Cryptology
12 / 27
Secure Communication
Confidentiality, integrity, authenticity
Hello Bye
Bob
Anna
Hello Bye
Anna
Bob
Confidentiality
An adversary cannot see which messages are transmitted No information about the message is being leaked,
1 / 27
COMS30002 : Cryptology A
Bristol Crypto Group
Department of Computer Science, University Of Bristol, Merchant Venturers Building, Woodland Road, Bristol, BS8 1UB United Kingdom.
This is a 10 credit course, corresponding to ≈ 100 hours of work. 30 Lectures and Problem Classes 20 Preparation for Problem Classes 20 Reviewing Lectures after they are given 15 Formative Assessments 15 January Revision and Exam
Introduction
Practicalities of Cryptography A
8 / 27
Course Overview
Feedback
Opportunities for you
During the lectures During office hours (Tuesday afternoon) By handing in various small assignments Activities are designed so you can also help each other!
Paradigms of Cryptology
12 / 27
Secure Communication
Confidentiality, integrity, authenticity
Bob Bye Anna
Anna Bye Bob
Confidentiality
An adversary cannot see which messages are transmitted
2
3
4
Introduction
Practicalities of Cryptography A
6 / 27
Course Overview
Structure
Teaching and Learning Activities
Twelve weeks of 3 contact hours a week, all preXmas. Monday: 2 hour lecture Friday: 1 hour problem class
Bob Bye Anna
Hi Hello Bye
Anna Bye Bob
Introduction
Paradigms of Cryptology
12 / 27
Secure Communication
Confidentiality, integrity, authenticity
Bob Bye Anna
10 / 27
Diagnostic Assessment
Maths/CS Background Test
Seven Pillars of Cryptology
1 2 3 4 5 6 7
Computer Science Basics Algorithms Complexity Theory Algebra/Group Theory Linear Algebra Number Theory (esp. Modular Arithmetic) (Discrete) Probability Theory
Summative Assessment
One two-hour final exam in January, resit in August/September
Introduction
Practicalities of Cryptography A
7 / 27
Course Overview
Workload
2
3
4
Consider the functionality and desired security of two-party communication
Introduction
Paradigms of Cryptology
12 / 27
Secure Communication
Confidentiality, integrity, authenticity
Introduction
Practicalities of Cryptography A
8 / 27
Course Overview
Feedback
What I would like feedback on from you: Jargon and Clarity of Lecture (is it still English?) Timing of Lecture (can you stay awake?) Workload getting out of hand (can you go to bed?)
