2018全国高考新课标2卷理科数学试题(解析版)
2018全国高考数学二试题及答案(理科)
的素数中,随机选取连个不同的数,其和等于 30 的概率是( )
A. 1 12
【答案】C
B. 1 14
C. 1 15
D. 1 18
9.在长方体 ABCD A1B1C1D1 中, AB BC 1, AA1 3 ,则异面直线 AD1 与 DB1 所成角的余弦值为( )
A. 1 5
【答案】C
为了预测该地区 2018 年的环境基础设施投资额, 建立了 y 与时间变量 t 的两 个线性回归模型.根据 2000 年至 2016 年的数据(时间 变量 t 的值依次为1, 2, ,17 )建立模型①:y 30.4 13.5t ;根据 2010 年至 2016
年的数据(时间变量 t 的值依次为1, 2, ,7 )建立模型②: y 99 17.5t . (1)分别利用这两个模型,求该地区 2018 年的环境基础设施投资额的预测值; (2)你认为用哪个模型得到的预测值更可靠?并说明理由. 【解析】(1)由题意可知,用模型①预测 2018 年投资额为
(2)若 f (x) 在 (0, ) 只有一个零点,求 a .
【解析】(1)当 a 1时,f (x) ex x2 ,则 f x() e x2x .令 h(x) f (x) ex 2x ,
由 h(x) ex 2 知 h(x) 在 (0, ln 2) 上单调递减,在 (ln 2, ) 上单调递增.从而 h(x) f (x) h(ln 2) f (ln 2) 2 2ln 2 0 ,所以 f (x) 在 (0, ) 上单调递增.
S3 3a1 3d 21 3d 15 解得 d 2 .所以 an 7 2(n 1) 2n 9 . (2)由(1)可知 Sn n2 8n (n 4)2 16 .由二次函数性质可知当 n 4 时,Sn 取 得最小值 16 . 18.(12 分)下图是某地区 2000 年至 2016 年环境基础设施投资额 y (单位:亿 元)的折线图.
2018年高考理科数学新课标全国2卷 逐题解析

2018年普通高等学校招生全国统一考试新课标2卷理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.1+2i1-2i=( ) A .- 45 - 35iB .- 45 + 35iC .- 35 - 45iD .- 35 + 45i解析:选D2.已知集合A={(x,y)|x 2+y 2≤3,x ∈Z,y ∈Z },则A 中元素的个数为 ( ) A .9 B .8 C .5 D .4 解析:选A 问题为确定圆面内整点个数 3.函数f(x)= e x-e-xx2的图像大致为 ( )解析:选B f(x)为奇函数,排除A,x>0,f(x)>0,排除D,取x=2,f(2)= e 2-e-24>1,故选B4.已知向量a ,b 满足|a|=1,a ·b=-1,则a ·(2a-b)= ( ) A .4 B .3 C .2D .0解析:选B a ·(2a-b)=2a 2-a ·b=2+1=35.双曲线x 2a 2-y2b 2=1(a >0,b >0)的离心率为3,则其渐近线方程为( )A .y=±2xB .y=±3xC .y=±22x D .y=±32x 解析:选A e= 3 c 2=3a 2b=2a6.在ΔABC 中,cos C 2=55,BC=1,AC=5,则AB= ( )A .4 2B .30C .29D .2 5解析:选A cosC=2cos 2C 2 -1= - 35AB 2=AC 2+BC 2-2AB ·BC ·cosC=32 AB=4 27.为计算S=1- 12 + 13 - 14 +……+ 199 - 1100,设计了右侧的程序框图,则在空白框中应填入( )A .i=i+1B .i=i+2C .i=i+3D .i=i+4 解析:选B 8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( ) A .112B .114C .115D .118解析:选C 不超过30的素数有2,3,5,7,11,13,17,19,23,29共10个,从中选2个其和为30的为7+23,11+19,13+17,共3种情形,所求概率为P=3C 102=1159.在长方体ABCD-A 1B 1C 1D 1中,AB=BC=1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( ) A .15B .56C .55D .22解析:选C 建立空间坐标系,利用向量夹角公式可得。
2018年全国统一高考数学试卷(理科)(新课标ⅱ)(含解析版)
2018年全国统一高考数学试卷(理科)(新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)=()A.i B.C.D.2.(5分)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为()A.9B.8C.5D.43.(5分)函数f(x)=的图象大致为()A.B.C.D.4.(5分)已知向量,满足||=1,=﹣1,则•(2)=()A.4B.3C.2D.05.(5分)双曲线=1(a>0,b>0)的离心率为,则其渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x6.(5分)在△ABC中,cos=,BC=1,AC=5,则AB=()A.4B.C.D.27.(5分)为计算S=1﹣+﹣+…+﹣,设计了如图的程序框图,则在空白框中应填入()A.i=i+1B.i=i+2C.i=i+3D.i=i+48.(5分)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是()A.B.C.D.9.(5分)在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=,则异面直线AD1与DB1所成角的余弦值为()A.B.CD.10.(5分)若f(x)=cosx﹣sinx在[﹣a,a]是减函数,则a的最大值是()A.B.C.D.π11.(5分)已知f(x)是定义域为(﹣∞,+∞)的奇函数,满足f(1﹣x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.﹣50B.0C.2D.5012.(5分)已知F1,F2是椭圆C:=1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A 且斜率为的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。
2018年高考全国二卷(全国卷Ⅱ)理科数学试题及答案

2018年高考全国二卷(全国卷Ⅱ)理科数学试题及答案1.已知复数 $\frac{1+2i}{1-2i}=\frac{-43}{55}$,求其值。
2.已知集合 $A=\{(x,y)|x+y^2\leq 3,x\in Z,y\in Z\}$,求$A$ 中元素的个数。
3.函数 $f(x)=\frac{e^x-e^{-x}}{x^2}$ 的图像大致为什么样子?4.已知向量 $a,b$ 满足 $|a|=1$,$a\cdot b=-1$,求 $a\cdot (2a-b)$ 的值。
5.双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$ 的离心率为 $3$,求其渐近线方程。
6.在$\triangle ABC$ 中,$\cos A=\frac{4}{5}$,$BC=1$,$AC=5$,求 $AB$ 的值。
7.设计一个程序框图来计算 $S=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots-\frac{1}{100}$。
8.XXX猜想是“每个大于 $2$ 的偶数可以表示为两个素数的和”,在不超过 $30$ 的素数中,随机选取两个不同的数,其和等于 $30$ 的概率是多少?9.在长方体 $ABCD-A_1B_1C_1D_1$ 中,$AB=BC=1$,$AA_1=3$,求异面直线$AD_1$ 和$DB_1$ 所成角的余弦值。
10.若 $f(x)=\cos x-\sin x$ 在 $[-a,a]$ 上是减函数,求$a$ 的最大值。
11.已知 $f(x)$ 是定义域为 $(-\infty,+\infty)$ 的奇函数,满足 $f(1-x)=f(1+x)$,且 $f(1)=2$,求$f(1)+f(2)+f(3)+\cdots+f(50)$ 的值。
12.已知 $F_1,F_2$ 是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点,$A$ 是椭圆的左顶点,点 $P$ 在过 $A$ 且斜率为 $3$ 的直线上,$\triangle PF_1F_2$ 是等腰三角形,且 $\angleF_1PF_2=120^\circ$,求椭圆的离心率。
2018年全国普通高等学校招生统一考试理科数学(新课标II卷)-附答案解析

学校:___________姓名:___________班级:___________考号:___________
1.
A. B. C. D.
2.已知集合 ,则 中元素的个数为
A.9B.8C.5D.4
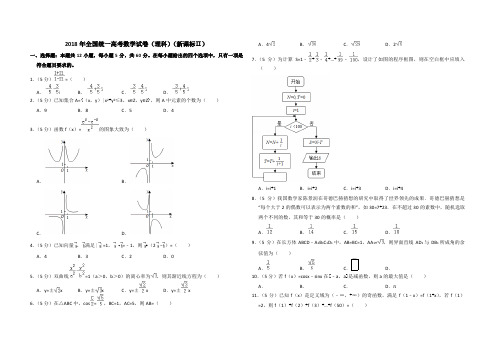
3.函数 的图像大致为()
A. B.
C. D.
8.C
【解析】
分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.
详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有 种方法,因为 ,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为 ,选C.
(1)证明: 平面 ;
(2)若点 在棱 上,且二面角 为 ,求 与平面 所成角的正弦值.
21.已知函数 .
(1)若 ,证明:当 时, ;
(2)若 在 只有一个零点,求 的值.
22.在直角坐标系 中,曲线 的参数方程为 ( 为参数),直线 的参数方程为 ( 为参数).
(1)求 和 的直角坐标方程;
(2)若曲线 截直线 所得线段的中点坐标为 ,求 的斜率.
分析:先根据二倍角余弦公式求cosC,再根据余弦定理求AB.
详解:因为
所以 ,选A.
点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.
7.B
【解析】
分析:根据程序框图可知先对奇数项累加,偶数项累加,最后再相减.因此累加量为隔项.
A. B. C. D.
9.在长方体 中, , ,则异面直线 与 所成角的余弦值为
2018年全国高考理科数学2卷---精美解析版.docx
2018 年普通高等学校招生全国统一考试(新课标II 卷)理科数学2018.6.29本试卷 4 页, 23 小题,满分150 分.考试用时120 分钟.一、选择题:本题共12 小题,每小题 5 分,共60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.12i()12iA . 4 3 i B. 4 3 i C. 3 4 i D. 3 4 i555555551.【解析】12i112i 234i34i,故选 D.12i2i12i5552.已知集合A{( x, y) | x2y 23, x Z , y Z} ,则A中元素的个数为()A .9B . 8C. 5D. 42.【解析】A{(1,1), ( 1,0), (1,1), (0,1), (0,0), (0,1),(1,1), (1,0), (1, 1)} ,元素的个数为9,故选 A .3.函数f (x)e x e x的图像大致为()x 2y yA .1B .1O1x O 1xy yC.1 D .1O1x O 1xe x e xf ( x) ,即 f ( x) 为奇函数,排除 A ;由f (1) e 1D;由3.【解析】 f ( x)20 排除x ef (4)e4 e 41211)(e11f (1)排除 C,故选 B .16(ee2 )(ee)e16e e4.已知向量a, b满足a 1 , a b1,则a(2a b)()A .4B . 3C. 2D. 04.【解析】a(2a b)2a b 2 1 3 ,故选B.2ax2y 21( a0, b0) 的离心率为 3 ,则其渐近线方程为()5.双曲线b2a2A .y2x B.y3x C.y2x D.y3 2x25.【解析】离心率e c3c2 a 2b2b,渐近线方程为y 2 x ,故选A.a a 2a23 ,所以2a6.在ABC 中,cos C5, BC1, AC 5 ,则 AB()25A .4 2B .30C.29D.2 56.【解析】cosC 2 cos2C13,开始25由余弦定理得AB BC 2AC22BC ACcos4 2 ,N0, T0C故选 A .i17.为计算S11111,设计了右侧的是i100否1349921001程序框图,则在空白框中应填入()N Ni S N TA .i i11B .i i2T T输出 Si 1C.i i3结束D .i i47.【解析】依题意可知空白框中应填入i i 2 .第1次循环: N1,T 1,i 3 ;第2次循环:2N 11,T11,i5;;第50 次循环:N111,T111, i101 ,结32439924100束循环得 S11111,所以选 B.1349910028.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于 2 的偶数可以表示为两个素数的和”,如30723,在不超过30 的素数中,随机选取两个不同的数,其和等于30的概率是()1B .1C .11A .1415D .12188.【解析】 不超过 30 的素数有: 2,3,5,7,11,13,17,19,23,29 ,共 10 个.从中选取两个不同的数, 其和等于 30的有: 7 与 23、 11与 19、 13 与 17 ,共 3 对.则所求概率为31,故选 C .C 102159.在长方体 ABCD A 1B 1C 1 D 1 中, AB BC1, AA 13 ,则异面直线 AD 1 与 DB 1 所成角的余弦值为()1B . 5C . 52A .65D .529.【解析】建立如图所示的空间直角坐标系,z则 A(1,1,0) , D 1 (1,0, 3) , D (1,0,0) , B 1 (0,1, 3)C 1,1DA 1 B所以 AD 1(0, 1, 3) , DB 1 ( 1,1, 3) ,1AD 1 DB 12 5DCBy则cosAD 1, DB 1,故选 C .AAD 1 DB 12 55x10.若 f ( x)cos x sin x 在 [a,a] 上是减函数,则 a 的最大值是()A .B .3D .2C .4410.【解析】 因为 f ( x)cos x sin x2 cos( x) 在区间 [ , 3 ,] 上是减函数, 所以 a 的最大值是44 44故选 A .11 . 已 知 f (x) 是 定 义 域 为 ( ,) 的 奇 函 数 , 满 足 f (1 x)f (1 x) . 若 f (1)2 , 则f (1) f ( 2) f (3)f (50)()A .50 B . 0C . 2D . 5011.【解析】因为 f ( x)f ( x) ,所以 f (1 x) f (x 1) ,则 f ( x1) f (x 1) , f ( x) 的最小正周期 为 T4 . 又 f (1) 2 , f (2)f ( 0) 0 , f (3)f (1)2 , f (4) f (0)0 , 所 以f (1)f ( 2)f (3)f (50) 12[ f (1) f (2) f (3)f ( 4)] f (49)f (50)f (1)f (2) 2 ,选 C .x 2y 2 1( a b312.已知 F 1, F 2 是椭圆 C :2b 20) 的左、右焦点, A 是 C 的左顶点, 点 P 在过 A 且斜率为a6的直线上,PF 1F 2 为等腰三角形,F 1F 2 P 120 ,则 C 的离心率为()2B .11 1A .2C .D .33412.【解析】如图,因为PF 1F 2 为等腰三角形, F 1 F 2 P 120 且 F 1F 2 2c ,所以 PF 1 F 2 30 ,则 P的坐标为 (2c,3c) ,故 k PA3c 3,化简得 4c a ,所以离心率e c1,故选 D .2c a6a4yPA F1 O F 2x二、填空题:本题共 4 小题,每小题 5 分,共 20 分.13.曲线y2ln( x1)在点 (0,0)处的切线方程为.13.【解析】y2y|x 0 2 ,则曲线 y2ln( x1)在点 (0,0)处的切线方程为 y2x.x1x 2 y5014.若x, y满足约束条件x 2 y30 ,则z x y 的最大值为.x5014.【解析】可行域为ABC 及其内部,当直线y x z 经过点B(5,4)时,z max9 .yBAC-3O5x15.已知sin cos1, cos sin0 ,则 sin().15.【解析】sin cos2sin 2 2 sin cos cos21,cos sin2cos2 2 cos sin sin 20 ,则 sin 22sin cos cos2cos22cos sin sin 20 1 1 ,即2 2 sin cos2cos sin1sin()1.216.已知圆锥的顶点为S ,母线SA, SB所成角的余弦值为7, SA与圆锥底面所成角为45,若SAB的面8积为 515 ,则该圆锥的侧面积为.16.【解析】如图所示,因为cos ASB 7ASB15S ,所以 sin,88SSAB1SA SB sin ASB15SA2 5 15 ,所以 SA4 5 .216又 SA与圆锥底面所成角为45,即SAO45 ,AO则底面圆的半径 OA210 ,圆锥的侧面积S OA SA40 2 .B三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第17~21 题为必考题,每个试题考生都必须作答.第 22、 23 题为选考题,考生根据要求作答.(一)必考题:共 60 分.17.( 12 分)记 S n 为等差数列 a n 的前 n 项和,已知 a 17 , S 315 .( 1)求 a n 的通项公式;( 2)求 S n ,并求 S n 的最小值.17.【解析】( 1)设等差数列a n 的公差为 d ,则 由 1 7 , S 3 3a 1 3d 15 得 d 2 ,a所以 a n7 (n 1) 22n 9,即 a n 的通项公式为 a n 2n 9 ;( 2)由( 1)知 S nn( 72n9) n 2 8n ,2因为 S n (n 4)2 16 ,所以 n4 时, S n 的最小值为 16 .18.( 12 分)下图是某地区2000 年至 2016 年环境基础设施投资额y (单位:亿元)的折线图.投资额240220220209200184180 171160148140 122 129120 1006053 568035374242 4740192514202000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 年份为了预测该地区2018 年的环境基础设施投资额,建立了y 与时间变量 t 的两个线性回归模型,根据2000 年至 2016年的数据(时间变量 t 的值依次为 1,2, ,17y 30.4 13.5t ;根据 2010年至 2016)建立模型①: ?年的数据(时间变量 t 的值依次为 1,2, ,7 )建立模型②: y 99 17.5t .?( 1)分别利用这两个模型,求该地区2018 年的环境基础设施投资额的预测值;( 2)你认为哪个模型得到的预测值更可靠?并说明理由.18.【解析】( 1)将t19代入模型①:?30.4 13.5 19 226.1(亿元),y所以根据模型①得该地区2018 年的环境基础设施投资额的预测值为226.1亿元;将 t 9 代入模型②:?99 17.59256.5 (亿元),y所以根据模型②得该地区2018 年的环境基础设施投资额的预测值为256.5亿元.( 2)模型②得到的预测值更可靠.理由如下:答案一:从折现图可以看出,2010 年至 2016 年的数据对应的点并没有紧密地均分分布在回归直线y30.413.5t的上下,2009年至2010年的环境基础设施投资额出现了明显的大幅度增加,这说明模型?①不能很好的反应环境基础设施投资额呈线性增长.而2010 年至 2016年的数据对应的点紧密的分布在回归?17.5t 的附近,这说明模型②能更好地反应环境基础设施投资额呈线性增长,所以模型②得到的直线 y 99预测值更可靠.答案二:从计算结果来看,相对于2016 年的环境基础设施投资额为220 亿元,利用模型①得到的该地区2018 年的环境基础设施投资额的预测值为226.1 亿元的增幅明显偏低,而利用模型②得到的该地区2018 年的环境基础设施投资额的预测值为256.5亿元的增幅明显更合理,所以模型②得到的预测值更可靠.19.( 12 分)设抛物线 C : y24x的焦点为F,过F且斜率为k (k0) 的直线l 与 C 交于A, B两点,AB8 .(1)求l的方程;(2)求过点A, B且与C的准线相切的圆的方程.19.【解析】( 1)焦点F为 (1,0),则直线 l :y k( x1) ,联立方程组y k( x1),得22( 224)x 20,yy24x k x k k A令 A( x1 , y1 ), B( x2 , y2 ) ,则 x1x22k 24x1 x21.k2,- 1O F x根据抛物线的定义得AB x1x2 2 8 ,B 即 2k 24 6 ,解得k 1 (舍去 k1),k 2所以 l 的方程为y x1;( 2)设弦AB的中点为M,由( 1)知x1x2 3 ,所以M的坐标为(3,2),2则弦 AB 的垂直平分线为y x5,令所求圆的圆心为(m,5m) ,半径为 r ,2m5m12根据垂径定理得r AB221234 ,22m m由圆与准线相切得m 1221234,解得 m3或 m11 .m m则所求圆的方程为:( x 3) 2( y 2) 216 或 ( x 11) 2( y 6) 214420.( 12 分)如图,在三棱锥P ABC 中,AB BC22 ,PA PB PC AC4, O 为 AC 的中点.( 1)证明:PO平面 ABC ;( 2)若点M在棱BC上,且二面角M PA C 为30,求 PC 与平面 PAM 所成角的正弦值.P20.【解析】( 1)证明:连接OB,PA PC , O 为 AC 的中点,PO AC ,AB BC22, AC 4,AB 2BC 2AC 2,即AB BC ,OB 1AC 2 ,AOC 2又 PO23, PB 4 ,则 OB2PO 2PB 2,即 OP OB ,B MAC OB O ,PO平面 ABC ;( 2)由( 1)知OB,OC , OP两两互相垂直,z以 O 为坐标原点建立如图所示的空间直角坐标系,P则 B(2,0,0) , C (0,2,0) , A(0,2,0) , P(0,0,2 3) ,BC ( 2,2,0), AP(0,2,23), CP(0,2,23)令 BM BC ,[ 0,1] .A OC y 则 OM OB BC(22,2,0) , AM(22,22,0) ,M令平面 PAM 的法向量为 n(x, y, z) ,Bxn AP 2 y 2 3z0,取 x3 1 ,得n ( 3 1 , 3 1 ,1)由n AM(2 2 )x ( 22) y 0易知平面 PAC 的一个法向量为m(1,0,0) ,所以 cos n, mn m3(1)3(1)3,1) 21) 2) 27 2cos302n m3(3((127解得1(舍去3),即n( 43,23,2) ,3333n CP 83因为 cos n, CP333.8,所以PC 与平面 PAM 所成角的正弦值为n CP444 321.( 12 分)已知函数 f ( x)e x ax2.( 1)若a1,证明:当 x0 时,f ( x)1;( 2)若f ( x)在(0,) 只有一个零点,求 a .21.【解析】( 1)方法 1:欲证明当x0 时, f ( x)1,即证明e x1 .x21令 g ( x)e x,则g ( x)e x (x 21)2xe x(x 1) 2 e x0,x 2x 2 1 2x2 1 2 1则 g ( x) 为增函数, g (x)g (0) 1 ,得证.方法 2:a1时, f ( x) e x x2,则 f ( x) e x2x ,令 f (x)g( x) ,则 g ( x)e x 2 ,x[0, ln 2) 时, g (x)0 , g( x) 为减函数, x(ln 2,) 时, g ( x)0 , g( x) 为增函数,所以 g( x) min g(ln 2)22ln 20,即当x0 时, f (x)0, f (x) 为增函数,所以 f ( x) f (0) 1 ,因此 a 1 , x0 时, f (x) 1.( 2)方法 1:若f ( x)在(0,) 只有一个零点,则方程e xa 只有一个实数根.x2令 h(x)e xh( x) 的图像与直线y a 只有一个公共点.x2,等价于函数y又 h ( x)x2e x2xe x x 2 e xx4x3,x(0,2) 时, h ( x)0 , h( x) 为减函数, x (2,) 时, h ( x)0 , h( x) 为增函数,所以 h( x) min h(2)e2, x0 时h(x), x时 h( x).4则 a e2) 只有一个零点.时, f ( x) 在 (0,4方法 2:若f ( x)在(0,) 只有一个零点,则方程e xax 只有一个实数根.x令 h(x)e xh(x) 的图像与直线y ax 只有一个公共点.,等价于函数 yx当直线 y ax 与曲线y h(x) 相切时,设切点为(x0, e x0) ,x0又 h ( x)xe x e x x 1 e x x0 1 e x0e x0x0 2 ,此时a h ( x0)e2 x2x 2,则 h ( x0 )x02x02.4又当 x(0,1) 时, h ( x)0 , h( x) 为减函数,yx (1, ) 时, h ( x) 0 , h(x) 为增函数,所以 h( x) min h(1) e ,且 x 0 时 h(x), x 时 h( x).根据 yh( x) 与 yax 的图像可知,O 1 2xe 2 时,函数 yh(x) 的图像与直线 yax 只有一个公共点,即f ( x) 在 (0,) 只有一个零点.a4(二)选考题:共 10 分.请考生在第 22、 23 题中任选一题作答.如果多做,则按所做的第一题计分.22. [选修 4—4:坐标系与参数方程]( 10 分)在 直 角 坐 标 系 xOy 中 , 曲 线 C 的 参 数 方 程 为x 2 cosy( 为 参 数 ) , 直 线 l 的 参 数 方 程 为4sinx 1 t cos y2 (t 为参数 )t sin( 1)求 C 和 l 的直角坐标方程;( 2)若曲线 C 截直线 l 所得线段的中点坐标为(1,2) ,求 l 的斜率.22.【解析】( 1)消去参数,得 C 的直角坐标方程为x 2 y 2 41;16消去参数 t ,得 l 的直角坐标方程为 sin x cos y sin2 cos0 ;( l 的直角坐标方程也可写成:y tan (x 1)2() 或 x 1 .)2( 2)方法 1:将 l 的参数方程:x 1 t cos x 2 y 2y 2t sin(t 为参数 ) 代入 C :164 4 1 t cos22 t sin216 ,即 1 3 cos2t24 2 cossint由韦达定理得 t 14 2cossint 23 cos 2,1依题意,曲线 C 截直线 l 所得线段的中点对应t 1t 2 0,即 2 cossin2因此 l 的斜率为 2 .方法 2:令曲线 C 与直线 l 的交点为 A( x 1 , y 1 ), B(x 2 , y 2 ) ,x 1 2 y 1 2 1416x 2 x 1x 2y 1y 2 y 1y 2则由x 10 ,其中 x 1x 2 2 y 2 2 得4 1614161得:8 0 ,0 ,得 tan 2 .x 2 2, y 1 y 2 4 .所以x 1x2y 1 y 2y 1 y 2 2 ,即 l 的斜率为 2 .24x 1 x 223. [选修 4—5:不等式选讲 ]( 10 分)设函数f (x)5x ax 2 .( 1)当 a1时,求不等式f (x)0 的解集;( 2)若 f ( x)1 ,求 a 的取值范围.23.【解析】( 1) a1时, f ( x) 5 x 1x 2 ,x 1时, f( x) 5 x1 x2 2x 4 0 ,解得2 x 1 ; 1 x 2 时, f ( x) 5x1 x2 2 0,解得 1 x 2 ; x 2 时, f ( x)5 x 1 x22x6 0 ,解得 2 x3,综上所述,当 a 1 时,不等式 f (x) 0 的解集为 [ 2,3] .( 2) f (x)5 x ax2 1,即 xa x2 4 ,又 x a x 2 x a x 2 a 2 ,所以 a 24 ,等价于 a 2 4 或 a 24 ,解得 a 的取值范围为 { a | a2 或 a6} .。
2018年高考理科数学全国卷2(含答案解析)

绝密★启用前2018年普通高等学校招生全国统一考试理科数学本试卷共23题,共150分,共5页,考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.1212ii+=- 43. 55A i -- 43. 55B i -+ 34. 55C i -- 34. 55D i -+2.已知集合(){}22,3,,A x y x y x Z y Z =+≤∈∈,则A 中元素的个数为. 9A. 8B . 5C . 4D3.函数2()x xe ef x x--=的图象大致为4.已知向量,a b 满足1,1a a b =⋅=-,则()2a a b ⋅-=. 4A . 3B . 2C . 0D5.双曲线()222210,0x y a b a b-=>>的离心率为3,则其渐近线方程为. 2A y x =± . 3B y x =± 2. 2C y x =± 3. 2D y x =±6.在ABC ∆中,5cos ,1,5,25C BC AC ===则AB = . 42A . 30B . 29C. 25D 7.为计算11111123499100S =-+-++-,设计了右侧的程序框图,则在空白框中应填入. 1A i i =+ . 2B i i =+ . 3C i i =+ . 4D i i =+8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23. 在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是1.12A 1. 14B 1. 15C 1. 18D 9.在长方体1111ABCD A B C D -中,11,3,AB BC AA ===则异面直线1AD 与1DB 所成角的余弦值为1. 5A5. 6B 5. 5C 2.2D 10.若()cos sin f x x x =-在[],a a -是减函数,则a 的最大值是.4A π.2B π3.4C π .D π-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________11.已知()f x 是定义域为(),-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=. 50A -. 0B . 2C . 50D12.已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,A 是C 的左顶点,点P 在过A且斜率为6的直线上,12PF F ∆为等腰三角形,12120F F P ∠=,则C 的离心率为2. 3A 1. 2B 1. 3C 1. 4D二、填空题(本题共4小题,每小题5分,共20分)13.曲线2ln(1)y x =+在点()0,0处的切线方程为_____________.14.若,x y 满足约束条件250,230,50,x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩则z x y =+的最大值为________.15.已知sin cos 1,cos sin 0αβαβ+=+=,则()sin αβ+=__________.16.已知圆锥的顶点为S ,母线SA 、SB 所成角的余弦值为78,SA 与圆锥底面所成角为45.若SAB ∆的面积为则该圆锥的侧面积为__________.三、解答题(共70分。
2018年全国高考新课标2卷理科数学试题(解析版)

2018年全国高考新课标2卷理科数学试题(解析版)2018年普通高等学校招生全国统一考试新课标2卷理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知1+2i/(1-2i),则结果为:A。
--iB。
-+iC。
--iD。
-+i解析:选D。
2.已知集合A={(x,y)|x+y≤3,x∈Z,y∈Z },则A中元素的个数为:A。
9B。
8C。
5D。
4解析:选A。
问题为确定圆面内整点个数。
3.函数f(x)=2/x的图像大致为:A。
B。
C。
D。
解析:选B。
f(x)为奇函数,排除A。
当x>0时,f(x)>0,排除D。
取x=2,f(2)=1,故选B。
4.已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=:A。
4B。
3C。
2D。
2-2xy解析:选B。
a·(2a-b)=2a-a·b=2+1=3.5.双曲线a^2(x^2)-b^2(y^2)=1(a>0,b>0)的离心率为3,则其渐近线方程为:A。
y=±2xB。
y=±3xC。
y=±2x/abD。
y=±3x/ab解析:选A。
e=3,c=3ab=2a。
6.在ΔABC中,cosC=1/5,BC=1,AC=5,则AB=:A。
42B。
30C。
29D。
25解析:选A。
cosC=2cos^2(C/2)-1=-1/5,AB=AC+BC-2AB·BC·cosC=32,AB=42.7.为计算S=1-1/3+1/5-1/7+……+(-1)^n-1/(2n-1),设计了右侧的程序框图,则在空白框中应填入:开始N=0,T=1i=1是N=N+1/T=T+(-1)^N-1/(2N-1)i<100否S=N-T输出S结束A。
2018高考全国新课标2卷理科数学版及答案解析

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.12i12i+=- A .43i 55--B .43i 55-+C .34i 55--D .34i 55-+2.已知集合(){}223A x y xy x y =+∈∈Z Z ,≤,,,则A 中元素的个数为 A .9B .8C .5D .43.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.双曲线22221(0,0)x y a b a b-=>>3A .2y x =B .3y x =C .2y x = D .3y x = 6.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .2B 30C 29 D .257.为计算11111123499100S =-+-++-…,设计了右侧的程序框图,则在空白框中应填入 A .1i i =+ B .2i i =+ C .3i i =+ D .4i i =+8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 A .112B .114C .115D .1189.在长方体1111ABCD A B C D -中,1AB BC ==,1AA ,则异面直线1AD 与1DB 所成角的余弦值为 A .15BCD10.若()cos sin f x x x =-在[,]a a -是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=…A .50-B .0C .2D .5012.已知1F ,2F 是椭圆22221(0)x y C a b a b+=>>:的左,右焦点,A 是C 的左顶点,点P 在过A 且斜率的直线上,12PF F △为等腰三角形,12120F F P ∠=︒,则C 的离心率为 A . 23B .12C .13D .14二、填空题:本题共4小题,每小题5分,共20分。
2018年全国高考理科数学2卷-精美解析版

2018 年一般高等学校招生全国一致考试(新课标II 卷)理科数学本试卷 4 页, 23 小题,满分150 分.考试用时120 分钟.一、选择题:此题共12 小题,每题5 分,共 60 分.在每题给出的四个选项中,只有一项为哪一项切合题目要求的.1.12i()12iA .4 3 i B.4 3 i C.3 4 i D.3 4 i555555551.【分析】12i112i234i34i ,应选D.1 2i2i12i5552.已知会合A.9 2.【分析】A{( x, y) | x2y 23, x Z , y Z} ,则A中元素的个数为()B . 8C. 5D. 4A{( 1,1), ( 1,0), (1, 1), (0,1), (0,0), (0, 1),(1,1), (1,0), (1, 1)},元素的个数为9,应选 A .e x e x的图像大概为()3.函数f (x)2xy yA .1B.1O1x O1xy yC.1 D .1O1x O1xe x e xf ( x) ,即 f ( x) 为奇函数,清除A;由f (1) e1D;由3.【分析】 f ( x)20 清除x ef (4)e4 e 4 1 (e21)(e1)(e1)e1 f (1) 清除C,应选B.1616e2e e e4.已知向量a, b知足a 1 , a b1,则a(2a b)()A .4B . 3C. 2D. 04.【分析】a(2a b)2a b 2 13,应选B.2ax2y 21( a0, b0) 的离心率为 3 ,则其渐近线方程为()5.双曲线b2a2A .y2x B.y3x C.y2x D.y3 2x25.【分析】离心率c3c2 a 2b23 ,所以b2,渐近线方程为y 2 x ,应选A.ea 2a2aa6.在ABC 中,cos C5,BC1, AC5,则 AB()25A.4 2B.30C.29D.2 56.【分析】cosC 2 cos2C13,开始25由余弦定理得AB BC 2AC22BC ACcos4 2 ,N0, T0C应选 A.i17.为计算S11111,设计了右边的是i否13499100 21001程序框图,则在空白框中应填入()N Ni S N TA .i i11B .i i2T T输出 Si 1C.i i3结束D .i i47.【分析】依题意可知空白框中应填入i i2.第 1次循环:N1,T 1,i3;第 2次循环:2N 11,T11,i5;;第50 次循环:N111,T111, i101 ,结32439924100束循环得 S11111,所以选 B.1349910028.我国数学家陈景润在哥德巴赫猜想的研究中获得了世界当先的成就.哥德巴赫猜想是“每个大于 2 的偶数能够表示为两个素数的和”,如30723,在不超出30 的素数中,随机选用两个不一样的数,其和等于30的概率是()111D.1A .B.C.181214158.【分析】不超出30的素数有:2,3,5,7,11,13,17,19,23,29 ,共10个.从中选用两个不一样的数,其和等于 30的有: 7 与 23、 11与 19、 13 与 17 ,共3对.则所求概率为31,应选 C.C102159.在长方体ABCD A1B1C1 D1中,AB BC 1,AA1 3 ,则异面直线AD1与 DB1所成角的余弦值为()1552A .B.C.D.56529.【分析】成立以下图的空间直角坐标系,则 A(1,1,0) , D (1,0,3) ,D (1,0,0),B (0,1,3)11所以 AD1(0, 1, 3), DB1( 1,1,3) ,则cos AD1, DB1AD1DB125AD1DB1255C1z,B1D 1A1CByD,应选 C.Ax10.若f ( x)cos x sin x 在 [a,a] 上是减函数,则 a 的最大值是()A .B .3D .C.42410.【分析】由于f ( x)cos x sin x 2 cos( x)在区间 [3] 上是减函数,所以 a 的最大值是,,4444应选 A.11 .已知f (x)是定义域为(,) 的奇函数,满足 f (1x) f (1 x) .若 f (1) 2 ,则f (1) f ( 2) f (3) f (50)()A.50B.0C.2D.5011.【分析】由于 f (x) f ( x) ,所以 f (1 x) f (x1) ,则 f ( x1) f (x1), f ( x) 的最小正周期为T 4.又 f(1)2, f (2) f ( 0)0 , f (3) f (1)2, f (4) f (0) 0,所以f (1) f ( 2) f (3) f (50)12[ f (1) f (2) f (3) f ( 4)] f (49) f (50) f (1) f (2)2,选C.12.已知F1, F2是椭圆C :x2y 21( a b3 a2b20) 的左、右焦点,A是C的左极点,点P在过A且斜率为6的直线上,PF1F2为等腰三角形,F1F2 P 120,则 C 的离心率为()21C.11A .B.3D.32412.【分析】如图,由于PF1F2为等腰三角形,F1F2 P120 且F1F22c ,所以PF1 F2 30 ,则P的坐标为 (2c, 3c) ,故 k PA3c 3,化简得 4c a ,所以离心率 ec 1 ,应选 D .2c a6a 4yPAF 1 O F 2x二、填空题:此题共 4 小题,每题 5 分,共 20 分.13.曲线 y 2ln( x 1) 在点 (0,0) 处的切线方程为 .13.【分析】 y2y |x 02 ,则曲线 y2ln( x 1) 在点 (0,0) 处的切线方程为 y 2x .1xx 2 y 5 014.若 x, y 知足拘束条件x 2 y 3 0 ,则 z x y 的最大值为.x 514.【分析】可行域为 ABC 及其内部,当直线 yxz 经过点 B(5,4) 时, z max9 .15.已知 sin cos 1, cos sin0 ,则y sin().15.【分析】sincos2sin 22 sin cos cos 2 B 1,2cos 2sin2ACcossin2 cos sinO 0 ,5x-3则 sin 22sin coscos 2cos 2 2cos sinsin 2 011,即 2 2 sin cos2cossin1sin()1.216.已知圆锥的极点为 S ,母线 SA, SB 所成角的余弦值为7 ,与圆锥底面所成角为45 ,若SAB 的面8SA积为 5 15 ,则该圆锥的侧面积为.16.【分析】以下图,由于cos ASB 7 ,所以 sinASB15 ,S88SSAB1SA SBsin ASB15 SA 2 5 15 ,所以 SA 4 5 .216又 SA 与圆锥底面所成角为45 ,即SAO 45 ,AO则底面圆的半径 OA 210 ,圆锥的侧面积 SOA SA40 2 .B三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17~21 题为必考题,每个试题考生都一定作答.第22、 23 题为选考题,考生依据要求作答.(一)必考题:共 60 分.17.( 12 分)记 S n 为等差数列 a n 的前 n 项和,已知 a 17, S 315.( 1)求 a n 的通项公式;( 2)求 S n ,并求 S n 的最小值.17.【分析】( 1)设等差数列a n 的公差为 d ,则 由 a 1 7 , S 3 3a 1 3d 15 得 d2 ,所以 a n7 (n 1) 22n 9 ,即 a n 的通项公式为 a n 2n 9 ;( 2)由( 1)知 S nn(7 2n 9) n 2 8n ,2由于 S n (n 4)2 16 ,所以 n4 时, S n 的最小值为 16 .18.( 12 分)下列图是某地域 2000 年至 2016 年环境基础设备投资额 y (单位:亿元)的折线图.投资额240220220209200184180 171160148140 122 129120 1006053 5680353742424740192514202000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016年份为了展望该地域 2018 年的环境基础设备投资额,成立了y 与时间变量 t 的两个线性回归模型,依据 2000年至 2016 年的数据(时间变量 t 的值挨次为1,2, ,17)成立模型①: ?30.4 13.5t;依据 2010 年至 2016y年的数据(时间变量t的值挨次为 1,2,,7)成立模型②:y 99 17.5t.?( 1)分别利用这两个模型,求该地域2018 年的环境基础设备投资额的展望值;( 2)你以为哪个模型获得的展望值更靠谱?并说明原因.181t 19y 30.4 13.5 19 226.1 (亿元),.【分析】( )将代入模型①: ?所以依据模型①得该地域2018 年的环境基础设备投资额的展望值为226.1 亿元;将 t?99 17.5 9256.5 (亿元),9 代入模型②: y所以依据模型②得该地域2018 年的环境基础设备投资额的展望值为256.5 亿元.( 2)模型②获得的展望值更靠谱.原因以下:答案一:从折现图能够看出,2010 年至 2016 年的数据对应的点并无密切地均分散布在回归直线y?30.4 13.5t 的上下,2009年至2010年的环境基础设备投资额出现了显然的大幅度增添,这说明模型①不可以很好的反响环境基础设备投资额呈线性增添.而2010 年至 2016 年的数据对应的点密切的散布在回归直线 y? 99 17.5t 的邻近,这说明模型②能更好地反响环境基础设备投资额呈线性增添,所以模型②获得的展望值更靠谱.答案二:从计算结果来看,相关于2016 年的环境基础设备投资额为220 亿元,利用模型①获得的该地域2018 年的环境基础设备投资额的展望值为226.1亿元的增幅显然偏低,而利用模型②获得的该地域 2018 年的环境基础设备投资额的展望值为 256.5 亿元的增幅显然更合理,所以模型②获得的展望值更靠谱.19.( 12 分)设抛物线 C : y24x 的焦点为F,过F且斜率为 k (k 0) 的直线l与C交于 A, B 两点,AB8 .(1)求l的方程;(2)求过点A, B且与C的准线相切的圆的方程.19.【分析】( 1)焦点F为 (1,0) ,则直线 l :y k( x1) ,联立方程组y k( x1),得k 2x2( 224)x k20,yAy24x k令 A( x1 , y1 ), B( x2 , y2 ) ,则 x1x22k 241.k2,x1 x2- 1O F x依据抛物线的定义得AB x1x2 2 8 ,B 即 2k 24 6 ,解得k 1 (舍去k 1 ),k 2所以 l 的方程为y x1;( 2)设弦AB的中点为M,由( 1)知x1x2 3 ,所以M的坐标为(3,2) ,2则弦 AB 的垂直均分线为y x5,令所求圆的圆心为(m,5m) ,半径为 r ,2m5m12依据垂径定理得AB221234,r22m m由圆与准线相切得1221234 ,解得或.m m m m3m 11则所求圆的方程为:( x3) 2( y2) 216 或 ( x11) 2( y6) 214420.( 12 分)如图,在三棱锥P ABC 中,AB BC22,PA PB PC AC4, O 为 AC 的中点.( 1)证明:PO平面 ABC ;( 2)若点M在棱BC上,且二面角M PA C为30,求 PC 与平面 PAM 所成角的正弦值.20.【分析】( 1)证明:连结OB,PPA PC , O 为 AC 的中点,PO AC ,ABBC 2 2, AC 4,AB 2 BC 2AC 2,即 AB BC , OB1 AC2 ,2又 PO2 3,PB 4,则 OB 2PO 2 PB 2,即 OPOB ,AC OB O , PO 平面 ABC ;( 2)由( 1)知 OB,OC , OP 两两相互垂直, z以 O 为坐标原点成立以下图的空间直角坐标系,P则 B(2,0,0) , C(0,2,0) , A(0, 2,0) , P(0,0,2 3) ,BC ( 2,2,0) , AP(0,2,2 3), CP(0, 2,2 3)令 BMBC ,[ 0,1] .AOCy则 OMOBBC(22 ,2 ,0) , AM (22 ,22,0) ,M令平面 PAM 的法向量为 n(x, y, z) ,BxnAP2 y2 3z 0,取 x 31 ,得 n ( 31 , 31 ,1)由n AM(2 2 )x ( 22) y 0易知平面 PAC 的一个法向量为 m (1,0,0) ,所以 cosn, mn m3(1)3(1)3 ,1) 21) 2) 27 2cos302n m3( 3((1 27解得1 (舍去 3),即 n(43,2 3,2), 33 3 3n CP8 3 3 3由于 cosn, CP3.8,所以 PC 与平面 PAM 所成角的正弦值为n CP4 44321.( 12 分)已知函数 f ( x) e x ax 2 .( 1)若 a1,证明:当 x 0 时, f ( x) 1;( 2)若 f ( x) 在 (0,) 只有一个零点,求 a .21.【分析】( 1)方法 1:欲证明当 x 0 时, f ( x)令 g ( x)e x ,则 g ( x)e x (x 2 1) 2xe x2x22x 111,即证明e x 1 .2x 1(x1) 2 e x0 ,x 221则 g ( x) 为增函数, g (x) g (0) 1 ,得证.方法 2:a 1时,f ( x) e x x2,则 f ( x) e x2x ,令 f (x) g( x) ,则 g ( x)e x x [0, ln 2) 时, g (x)0 , g(所以 g( x) min g(ln 2)22ln 所以 f ( x) f (0) 1 ,2 ,x) 为减函数,x (ln 2, ) 时, g ( x)0 , g( x) 为增函数,2 0,即当x0 时, f (x)0 , f (x) 为增函数,所以 a 1 , x0 时, f (x) 1.( 2)方法1:若f ( x)在(0,) 只有一个零点,则方程e xa 只有一个实数根.x 2令 h(x)e xh( x) 的图像与直线y a 只有一个公共点.x2,等价于函数y又 h ( x)x2e x2xe x x 2 e xx4x3,x (0,2) 时, h ( x)0 , h( x) 为减函数, x (2,) 时, h ( x)0 , h( x) 为增函数,所以 h( x) min h(2)e20 时h(x), x时 h( x), x.4e2) 只有一个零点.则 a时, f ( x) 在 (0,4方法 2:若f ( x)在(0,) 只有一个零点,则方程e xax 只有一个实数根.x令 h(x)e xy h(x) 的图像与直线y ax 只有一个公共点.,等价于函数x当直线 y ax 与曲线y h(x) 相切时,设切点为(x0, e x0) ,x0又 h ( x)xe x e x x 1 e x x0 1 e x0e x0x0 2,此时a h ( x0 )e2 x 2x 2,则 h ( x0 )x02x02.4又当 x(0,1) 时, h ( x)0 , h( x) 为减函数,yx (1,) 时, h ( x)0 , h(x) 为增函数,所以 h( x) min h(1)e,且 x0 时h(x), x时 h( x).依据 y h( x) 与y ax 的图像可知,O 1 2xe2时,函数 y h(x) 的图像与直线y ax只有一个公共点,即 f ( x) 在 (0,) 只有一个零点.a4(二)选考题:共10 分.请考生在第22、 23 题中任选一题作答.假如多做,则按所做的第一题计分.22. [选修 4—4:坐标系与参数方程]( 10 分)在 直 角 坐 标 系 xOy 中 , 曲 线 C 的 参 数 方 程 为x 2 cos y( 为 参 数 ) , 直 线 l 的 参 数 方 程 为4sinx 1 t cos y2 (t 为参数 )t sin( 1)求 C 和 l 的直角坐标方程;( 2)若曲线 C 截直线 l 所得线段的中点坐标为(1,2) ,求 l 的斜率.22.【分析】( 1)消去参数,得 C 的直角坐标方程为x 2 y 2 41;16消去参数 t ,得 l 的直角坐标方程为 sin x cos y sin2 cos0 ;( l 的直角坐标方程也可写成:ytan (x 1)2() 或 x 1 .)2x 1 t cos22( 2)方法 1:将 l 的参数方程:(t 为参数 ) 代入 C : xy y 2 t sin4164 1 t cos22 t sin 216 ,即 1 3 cos2t24 2 cossint由韦达定理得 t 1t 24 2cos sin,13 cos2依题意,曲线 C 截直线 l 所得线段的中点对应t 1t 2 0 ,即 2 cossin2所以 l 的斜率为 2 .方法 2:令曲线 C 与直线 l 的交点为 A( x 1 , y 1 ), B(x 2 , y 2 ) ,x 1 2y 121416x 1 x 2 x 1x 2y 1y 2 y 1y 2则由得0 ,此中 x 1 x 22y 2 24161416所以x1x 2 y 1 y 2 0y 1 y 2 2 ,即 l 的斜率为 2 .24x 1 x 223. [选修 4—5:不等式选讲 ]( 10 分)设函数 f (x)5 x a x 2 .( 1)当 a1时,求不等式 f (x)0 的解集;( 2)若 f ( x) 1 ,求 a 的取值范围.23.【分析】( 1) a1时, f ( x)5 x 1 x 2 ,x1时, f( x) 5 x 1 x 2 2x 4 0 ,解得 2 x 1 ;1 x2 时, f ( x) 5x 1x 22 0 ,解得1 x2 ;1得:8 0 ,0 ,得 tan 2 .x 2 2, y 1 y 24 .x 2 时, f ( x) 5 x1x 22x60 ,解得2x 3,综上所述,当 a1时,不等式 f (x)0 的解集为 [2,3] .( 2)f (x)5x a x 2 1,即 x a x24,又 x a x 2 x a x 2 a 2 ,所以 a 2 4 ,等价于 a2 4 或 a24,解得 a 的取值范围为 { a | a2或 a6} .。
(word完整版)2018年高考全国2卷理科数学带答案解析

绝密★启用前2018年普通高等学校招生全国统一考试理科数学本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.12i 12i +=-A .43i 55--B .43i 55-+C .34i 55--D .34i 55-+2.已知集合22{(,)|3,,A x y x y x y =+≤∈∈Z Z},则A 中元素的个数为A .9B .8C .5D .43.函数2e e ()x xf x x --=的图象大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.双曲线22221(0,0)x y a b a b-=>>3A .2y x =±B .3y x =C .2y = D .3y x = 6.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .42B 30C 29D .257.为计算11111123499100S =-+-++-L ,设计了右侧的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是A .112 B .114 C .115 D .1189.在长方体1111ABCD A B C D -中,1AB BC ==,1AA 1AD 与1DB 所成角的余弦值为A .15BCD10.若()cos sin f x x x =-在[,]a a -是减函数,则a 的最大值是A .π4 B .π2 C .3π4D .π 11.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=L A .50- B .0 C .2 D .5012.已知1F ,2F 是椭圆22221(0)x y C a b a b+=>>:的左,右焦点,A 是C 的左顶点,点P 在过A的直线上,12PF F △为等腰三角形,12120F F P ∠=︒,则C 的离心率为 A .23 B .12 C .13D .14二、填空题:本题共4小题,每小题5分,共20分。
2018高考全国新课标2卷理科数学版及答案解析资料讲解

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.12i12i+=- A .43i 55--B .43i 55-+C .34i 55--D .34i 55-+2.已知集合(){}223A x y xy x y =+∈∈Z Z ,≤,,,则A 中元素的个数为 A .9B .8C .5D .43.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.双曲线22221(0,0)x y a b a b-=>>3A .2y x =B .3y x =C .2y x = D .3y x = 6.在ABC △中,5cos 2C =1BC =,5AC =,则AB = A .2B 30C 29 D .257.为计算11111123499100S =-+-++-…,设计了右侧的程序框图,则在空白框中应填入 A .1i i =+ B .2i i =+ C .3i i =+ D .4i i =+8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 A .112B .114C .115D .1189.在长方体1111ABCD A B C D -中,1AB BC ==,1AA ,则异面直线1AD 与1DB 所成角的余弦值为 A .15BCD10.若()cos sin f x x x =-在[,]a a -是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=…A .50-B .0C .2D .5012.已知1F ,2F 是椭圆22221(0)x y C a b a b+=>>:的左,右焦点,A 是C 的左顶点,点P 在过A 且斜率的直线上,12PF F △为等腰三角形,12120F F P ∠=︒,则C 的离心率为 A . 23B .12C .13D .14二、填空题:本题共4小题,每小题5分,共20分。
2018年高考全国卷2理科数学真题附含答案解析
2018年普通高等学校招生全国统一考试理科数学本试卷共23题,共150分,共5页。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.A. B. C. D.2.已知集合A={(x,y)|x ²+y ²≤3,x∈Z,y∈Z},则A中元素的个数为A.9B.8C.5D.43.函数f(x)=e ²-e-x/x ²的图像大致为A.B.C.D.4.已知向量a,b满足∣a∣=1,a·b=-1,则a·(2a-b)=A.4B.3C.2D.05.双曲线x ²/a ²-y ²/b ²=1(a﹥0,b﹥0)的离心率为,则其渐进线方程为A.y=±xB.y=±xC.y=±D.y=±6.在中,cos=,BC=1,AC=5,则AB=A.4B.C.D.27.为计算s=1-+-+…+-,设计了右侧的程序框图,则在空白框中应填入A.i=i+1B.i=i+2C.i=i+3D.i=i+48.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。
哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23,在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是A. B. C. D.9.在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=则异面直线AD1与DB1所成角的余弦值为A. B.10.若f(x)=cosx-sinx在[-a,a]是减函数,则a的最大值是A. B. C. D. π11.已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x)。
若f(1)=2,则f(1)+ f(2)+ f(3)+…+f(50)=A.-50B.0C.2D.5012.已知F1,F2是椭圆C: =1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A且斜率为的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为A..B.C.D.二、填空题:本题共4小题,每小题5分,共20分。
2018年高考试题真题——理科数学(新课标全国卷(2)II) Word版含详细答案解析

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.A. B. C. D.【答案】D【解析】分析:根据复数除法法则化简复数,即得结果.详解:选D.点睛:本题考查复数除法法则,考查学生基本运算能力.2. 已知集合,则中元素的个数为A. 9B. 8C. 5D. 4【答案】A【解析】分析:根据枚举法,确定圆及其内部整点个数.详解:,当时,;当时,;当时,;所以共有9个,选A.点睛:本题考查集合与元素关系,点与圆位置关系,考查学生对概念理解与识别.3. 函数的图像大致为A. AB. BC. CD. D【答案】B【解析】分析:通过研究函数奇偶性以及单调性,确定函数图像.详解:为奇函数,舍去A,舍去D;,所以舍去C;因此选B.点睛:有关函数图象识别问题的常见题型及解题思路(1)由函数的定义域,判断图象左右的位置,由函数的值域,判断图象的上下位置;②由函数的单调性,判断图象的变化趋势;③由函数的奇偶性,判断图象的对称性;④由函数的周期性,判断图象的循环往复.4. 已知向量,满足,,则A. 4B. 3C. 2D. 0【答案】B【解析】分析:根据向量模的性质以及向量乘法得结果.详解:因为所以选B.点睛:向量加减乘:5. 双曲线的离心率为,则其渐近线方程为A. B. C. D.【答案】A【解析】分析:根据离心率得a,c关系,进而得a,b关系,再根据双曲线方程求渐近线方程,得结果. 详解:因为渐近线方程为,所以渐近线方程为,选A.点睛:已知双曲线方程求渐近线方程:.6. 在中,,,,则A. B. C. D.【答案】A【解析】分析:先根据二倍角余弦公式求cosC,再根据余弦定理求AB.详解:因为所以,选A.点睛:解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.7. 为计算,设计了下面的程序框图,则在空白框中应填入A.B.C.D.【答案】B【解析】分析:根据程序框图可知先对奇数项累加,偶数项累加,最后再相减.因此累加量为隔项.详解:由得程序框图先对奇数项累加,偶数项累加,最后再相减.因此在空白框中应填入,选B.点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.8. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是A. B. C. D.【答案】C【解析】分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有种方法,因为,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.点睛:古典概型中基本事件数的探求方法: (1)列举法. (2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法. (3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化. (4)排列组合法:适用于限制条件较多且元素数目较多的题目.9. 在长方体中,,,则异面直线与所成角的余弦值为A. B. C. D.【答案】C【解析】分析:先建立空间直角坐标系,设立各点坐标,利用向量数量积求向量夹角,再根据向量夹角与线线角相等或互补关系求结果.详解:以D为坐标原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系,则,所以,因为,所以异面直线与所成角的余弦值为,选C.点睛:利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.10. 若在是减函数,则的最大值是A. B. C. D.【答案】A【解析】分析:先确定三角函数单调减区间,再根据集合包含关系确定的最大值详解:因为,所以由得因此,从而的最大值为,选A.点睛:函数的性质:(1). (2)周期 (3)由求对称轴, (4)由求增区间;由求减区间.11. 已知是定义域为的奇函数,满足.若,则A. B. 0 C. 2 D. 50【答案】C【解析】分析:先根据奇函数性质以及对称性确定函数周期,再根据周期以及对应函数值求结果.详解:因为是定义域为的奇函数,且,所以,因此,因为,所以,,从而,选C.点睛:函数的奇偶性与周期性相结合的问题多考查求值问题,常利用奇偶性及周期性进行变换,将所求函数值的自变量转化到已知解析式的函数定义域内求解.12. 已知,是椭圆的左,右焦点,是的左顶点,点在过且斜率为的直线上,为等腰三角形,,则的离心率为A. B. C. D.【答案】D【解析】分析:先根据条件得PF2=2c,再利用正弦定理得a,c关系,即得离心率.详解:因为为等腰三角形,,所以PF2=F1F2=2c,由斜率为得,,由正弦定理得,所以,选D.点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于的方程或不等式,再根据的关系消掉得到的关系式,而建立关于的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年普通高等学校招生全国统一考试新课标2卷理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.1+2i1-2i=( ) A .- 45 - 35iB .- 45 + 35iC .- 35 - 45iD .- 35 + 45i解析:选D2.已知集合A={(x,y)|x 2+y 2≤3,x ∈Z,y ∈Z },则A 中元素的个数为 ( ) A .9 B .8 C .5 D .4解析:选A 问题为确定圆面内整点个数 3.函数f(x)=ex-e-xx2的图像大致为 ( )解析:选B f(x)为奇函数,排除A,x>0,f(x)>0,排除D,取x=2,f(2)= e2-e-24>1,故选B 4.已知向量a ,b 满足|a|=1,a ·b=-1,则a ·(2a-b)= ( ) A .4 B .3C .2D .0解析:选B a ·(2a-b)=2a 2-a ·b=2+1=35.双曲线x2a2-y2b2=1(a >0,b >0)的离心率为3,则其渐近线方程为( )A .y=±2xB .y=±3xC .y=±22x D .y=±32x 解析:选A e= 3 c 2=3a 2b=2a6.在ΔABC 中,cos C 2=55,BC=1,AC=5,则AB= ( )A .4 2B .30C .29D .2 5解析:选A cosC=2cos 2C 2 -1= - 35AB 2=AC 2+BC 2-2AB ·BC ·cosC=32 AB=4 27.为计算S=1- 12 + 13 - 14 +……+ 199 - 1100,设计了右侧的程序框图,则在空白框中应填入( )A .i=i+1B .i=i+2C .i=i+3D .i=i+4 解析:选B8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( ) A .112B .114C .115D .118解析:选C 不超过30的素数有2,3,5,7,11,13,17,19,23,29共10个,从中选2个其和为30的为7+23,11+19,13+17,共3种情形,所求概率为P=3C102=1159.在长方体ABCD-A 1B 1C 1D 1中,AB=BC=1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( ) A .15B .56C .55D .22解析:选C 建立空间坐标系,利用向量夹角公式可得。
10.若f(x)=cosx-sinx 在[-a,a]是减函数,则a 的最大值是( ) A .π4B .π2C .3π4D .π解析:选A f(x)= 2cos(x+π4),依据f(x)=cosx 与f(x)= 2cos(x+π4)的图象关系知a 的最大值为π4。
11.已知f(x)是定义域为(-∞,+ ∞)的奇函数,满足f(1-x)= f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)= ( ) A .-50 B .0 C .2 D .50 解析:选C 由f(1-x)= f(1+x)得f(x+2)=-f(x),所以f(x)是以4为周期的奇函数,且f(-1)=-f(1)=-2,f(0)=0,f(1)=2,f(2)=f(0)=0,f(3)=f(-1)=-2,f(4)=f(0)=0; f(1)+f(2)+f(3)+…+f(50)=f(1)+f(2)=2 12.已知F 1,F 2是椭圆C:x2a2+y2b2=1(a>b>0)的左,右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,ΔP F 1F 2为等腰三角形,∠F 1F 2P=1200,则C 的离心率为( ) A .23B .12C .13D .14解析:选D AP 的方程为y=36(x+a),∵ΔP F 1F 2为等腰三角形 ∴|F 2P|=| F 1F 2|=2c, 过P 作PH ⊥x 轴,则∠PF 2H=600, ∴|F 2H|=c,|PH|=3c, ∴P(2c, 3c),代入AP 方程得4c=a 二、填空题:本题共4小题,每小题5分,共20分。
13.曲线y=2ln(x+1)在点(0,0)处的切线方程为__________. 解析:y=2x14.若x,y 满足约束条件⎩⎪⎨⎪⎧x+2y-5≥0x-2y+3≥0 x-5≤0 ,则z=x+y 的最大值为__________.解析:915.已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)=__________. 解析:- 12两式平方相加可得16.已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若ΔSAB 的面积为515,则该圆锥的侧面积为__________.解析:设圆锥底面圆半径为r,依题SA=2r, 又SA ,SB 所成角的正弦值为158,则12×2r 2×158=515 ∴r 2=40, S=π×r ×2r=40 2三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)记S n 为等差数列{a n }的前n 项和,已知a 1=-7,S 3=-15. (1)求{a n }的通项公式;(2)求S n ,并求S n 的最小值.解:(1)设{a n }的公差为d ,由题意得3 a 1+3d=-15,由a 1=-7得d=2. 所以{a n }的通项公式为a n =2n-9.(2)由(1)得S n =n 2-8n=(n-4)2-16. 所以当n=4时, S n 取得最小值,最小值为−16. 18.(12分)下图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y 与时间变量t 的两个线性回归模型.根据2000年至2016年的数据(时间变量t 的值依次为1,2,…,17)建立模型①:y ^=-30.4+13.5t ;根据2010年至2016年的数据(时间变量t 的值依次为1,2,…,7)建立模型②:y ^=99+17.5t . (1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;(2)你认为用哪个模型得到的预测值更可靠?并说明理由.解:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为y ^=-30.4+13.5×19=226.1 (亿元).利用模型②,该地区2018年的环境基础设施投资额的预测值为y ^=99+17.5×9=256.5 (亿元).(2)利用模型②得到的预测值更可靠. 理由如下:(ⅰ)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y ^=-30.4+13.5t 上下.这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型y ^=99+17.5t 可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.(ⅱ)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理.说明利用模型②得到的预测值更可靠. 以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.19.(12分)设抛物线C:y 2=4x 的焦点为F ,过F 且斜率为k(k>0)的直线l 与C 交于A ,B 两点,|AB|=8. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.解:(1)由题意得F(1,0),l 的方程为y=k(x-1)(k>0).设A(x 1,y 1),B(x 2,y 2),由⎩⎪⎨⎪⎧y=k(x-1)y2=4x 得k 2x 2-(2k 2+4)x+k 2=0.Δ=16k 2+16>0,故x 1+x 2=2k2+4k2. 所以|AB|= x 1+x 2+2=2k2+4k2+2=8 ,解得k=-1(舍去),k=1. 因此l 的方程为y=x-1.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为y-2=-(x-3),即y=-x+5. 设所求圆的圆心坐标为(x 0,y 0),则⎩⎪⎨⎪⎧y0=-x0+5(x0+1)2=(y0-x0+1)22+16解得⎩⎪⎨⎪⎧x0=3y0=2或⎩⎪⎨⎪⎧x0=11y0=-6因此所求圆的方程为(x-3)2+(y-2)2=16或(x-11)2+(y+6)2=144.20.(12分)如图,在三棱锥P-ABC 中,AB=BC=22,PA=PB=PC=AC=4,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M-PA-C 为300,求PC 与平面PAM 所成角的正弦值.PAOCBM解:(1)因为AP=CP=AC=4,O 为AC 的中点,所以OP ⊥AC ,且OP=2 3. 连结OB.因为AB=BC=22AC ,所以ΔABC 为等腰直角三角形, 且OB ⊥AC ,OB=12AC=2.由OP 2+OB 2=PB 2知OP ⊥OB.由OP ⊥OB,OP ⊥AC 知OP ⊥平面ABC.(2)如图,以O 为坐标原点,建立如图空间直角坐标系.由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0,),P(0,0,23),AP → =(0,0,23) 取平面PAC 的法向量OB →=(2,0,0).设M(a,2-a,0)(0<a ≤2),则AM →=(a,4-a,0).设平面PAM 的法向量为n=(x,y,z).则⎩⎨⎧2y+23z=0ax+(4-a)y=0,可取n=(3(a-4), 3a,-a),所以cos<OB→,n>=23(a-4)23(a-4)2+3a2+a2.由已知得|cos<OB→,n>|=32. ∴23|(a-4)|23(a-4)2+3a2+a2==32 解得a=-4(舍去),a=43. 所以n=(-833,433,- 43).又PC →=(0,2,-23),所以cos<PC→,n>=34. 所以PC 与平面PAN 所成角的正弦值为34. 21.(12分)已知函数f(x)=e x -ax 2.(1)若a=1,证明:当x ≥0时,f(x)≥1; (2)若f(x)在(0,+∞)只有一个零点,求a .【解析】(1)当a=1时,f(x)≥1等价于(x 2+1)e -x-1≤0.设函数g(x) (x 2+1)e -x -1,则g ′(x)=-(x-1)2e -x.当x ≠1时,g ′(x)<0,所以g(x)在(0,+∞)单调递减.而g(0)=0,故当x ≥0时,g(x)≤0,即f(x)≥1.(2)设函数h(x)=1-ax 2e -x.f(x)在(0,+∞)只有一个零点当且仅当h(x)在(0,+∞)只有一个零点. (i )当a ≤时,h(x)>0,h(x)没有零点;(ii )当a>0时,h ′(x)=ax(x-2) e -x.当x ∈(0,2)时,h ′(x)<0;当x ∈(2,+∞)时,h ′(x)>0. 所以h(x)在(0,2)单调递减,在(2,+∞)单调递增. 故h(2)=1- 4ae2是h(x)在[0,+∞)的最小值.①若h(2)>0,即a<e24,h(x)在(0,+∞)没有零点; ②若h(2)=0,即a=e24,h(x)在(0,+∞)只有一个零点; ③若h(2)<0,即a>e24,由于h(0)=1,所以h(x)在(0,2)有一个零点, 由(1)知,当x>0时,e x =x 2,所以h(4a)=1-16a3(e2a)2>1-16a3(2a)4=1- 1a >0故h(x)在(2,4a)有一个零点,因此h(x)在(0,+∞)有两个零点. 综上,f(x)在(0,+∞)只有一个零点时,a=e24.(二)选考题:共10分。
