2013南京中考数学试题(含答案)
南京市2013年中考数学试卷及答案
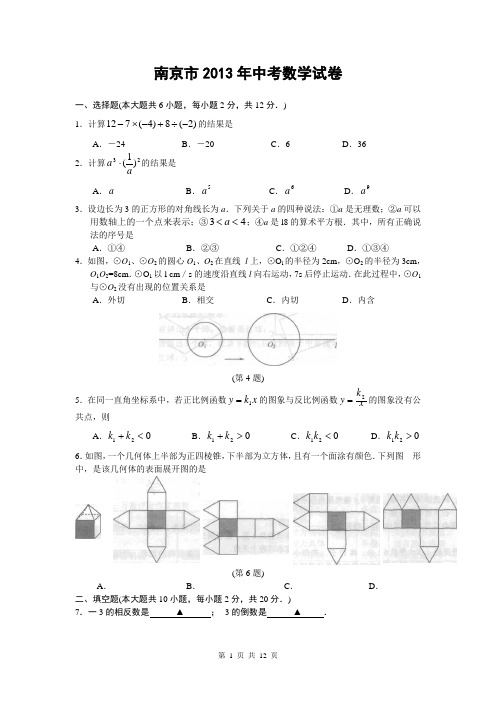
南京市2013年中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分.) 1.计算)2(8)4(712-÷+-⨯-的结果是A .-24B .-20C .6D .36 2.计算23)1(aa ⋅的结果是A .aB .5a C .6a D .9a3.设边长为3的正方形的对角线长为a .下列关于a 的四种说法:①a 是无理数;②a 可以用数轴上的一个点来表示;③43<<a ;④a 是l8的算术平方根.其中,所有正确说法的序号是A .①④B .②③C .①②④D .①③④4.如图,⊙O 1、⊙O 2的圆心O 1、O 2在直线 l 上,⊙O l 的半径为2cm ,⊙O 2的半径为3cm ,O 1O 2=8cm .⊙O 1以l cm /s 的速度沿直线l 向右运动,7s 后停止运动.在此过程中,⊙O 1与⊙O 2没有出现的位置关系是A .外切B .相交C .内切D .内含(第4题)5.在同一直角坐标系中,若正比例函数x k y 1=的图象与反比例函数x ky 2=的图象没有公共点,则A .021<+k kB .021>+k kC .021<k kD .021>k k 6.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图 形中,是该几何体的表面展开图的是(第6题)A .B .C .D . 二、填空题(本大题共10小题,每小题2分,共20分.)7.一3的相反数是 ▲ ;--3的倒数是 ▲ .8.计算2123-的结果是 ▲ . 9.使式子111-+x 有意义的戈的取值范围是▲ . 10.第二届亚洲青年运动会将于2013年8月l6日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务.将13000用科学记数法表示为 ▲ .11.如图,将矩形ABCD 绕点A 顺时针旋转到矩形AB ’C ’D ’的位置,旋转角为α (0°<α< 90°). 若∠l=110°,则∠α = ▲ 。
2013江苏南京中考数学

南京市2013年初中毕业学业考试数 学注意事项:1.本试卷共6页.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合.再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写再答题卡及本试卷上.3.答选择题必须用2B 铅笔将答题卡上对应的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置.在其他位置答题一律无效.4.作图必须用2B 铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共6小题,每小题2分,共12分.在每个小题所给出的四个选项中,恰有一项是符合题目要求的.请将正确选项前的字母代号填涂在答题卡相应位置上) 1. (2013江苏南京,1,2分)计算12-7×(-4)+8÷(-2)的结果是 A.-24 B.-20 C.6 D. 36 【答案】D .2. (2013江苏南京,2,2分)计算a 3·21⎪⎭⎫⎝⎛a 的结果是A.aB.a 5C. a 6D. a 9 【答案】A .3. (2013江苏南京,3,2分)设边长为3的正方形的对角线长为a ,下列关于a 的四种说法:①a 是无理数;②a 可以用数轴上的一个点来表示;③3<a <4;④a 是18的算术平方根.其中,所有正确说法的序号是 A. ①④ B. ②③ C. ①②④ D. ①③④ 【答案】C .4. (2013江苏南京,4,2分)如图,⊙O 1、⊙O 2的圆心O 1、O 2在直线l 上,⊙O 1的半径为2cm ,⊙O 2的半径为3cm ,O 1O 2=8cm. ⊙O 1以1cm/s 的速度沿直线l 向右运动,7s 后停止运动,在此过程中,⊙O 1与⊙O 2没有出现的位置关系是 A. 外切 B.相交 C.内切 D. 内含【答案】D .5. (2013江苏南京,5,2分)在同一直角坐标系中,若正比例函数y =k 1x 的图象与反比例函数y =xk 2的图象没有公共点,则 A. k 1+k 2<0 B. k 1+k 2>0 C. k 1k 2<0 D. k 1k 2>0 【答案】C .6. (2013江苏南京,6,2分)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是A B C D【答案】B.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程.请把答案直接填写在答题卡相应位置上)7.(2013江苏南京,7,2分)-3的相反数是_________;-3的倒数是___________.【答案】3;-31.8.(2013江苏南京,8,2分)计算2123-的结果是___________.【答案】2.9.(2013江苏南京,9,2分)使式子1+11-x有意义的x的取值范围是________.【答案】x≠1.10.(2013江苏南京,10,2分)第二届亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务.将13000用科学记数法表示为_________.【答案】1.3×104.11.(2013江苏南京,11,2分)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则∠α=________°.【答案】20.12.(2013江苏南京,12,2分)如图,将菱形纸片ABCD折叠.使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2cm,∠A=120°,则EF=______cm.第6题ABCDB′C′D′(第11题)1【答案】3.13. (2013江苏南京,13,2分)△OAB 是以正多边形相邻的两个顶点A 、B 与它的中心O 为顶点的三角形,若△OAB 的一个内角为70°,则该正多边形的边数为_________. 【答案】9.14. (2013江苏南京,14,2分)已知如图所示的图形的面积为24.根据图中的条件,可列出方程:______________.【答案】答案不唯一,如(x +1)2=25.15. (2013江苏南京,15,2分)如图,在梯形ABCD 中,AD ∥BC ,AB =DC ,AC 与BD 相交于点P .已知A (2,3),B (1,1),D (4,3).则点P 的坐标为______________.【答案】(3,37). 16. (2013江苏南京,16,2分)计算⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛----6151413121514131211-⎪⎭⎫⎝⎛+++⎪⎭⎫ ⎝⎛-----5141312161514131211的结果为__________. 【答案】61. 三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答.解答时应写出文字说明,证明过程或演算步骤)17. (2013江苏南京,17,6分)化简b a a b a b b a +÷⎪⎭⎫⎝⎛---221. (第15题)ABDEFO (第12题)(第14题)【答案】解:b a a b a b b a +÷⎪⎭⎫⎝⎛---221=()aba b a b a bb a +∙-+-+))((=aba b a b a a +∙-+))(( =ba -1.……………………………………………………6分 18. (2013江苏南京,18,6分)解方程xx x --=-21122. 【答案】解:方程两边同乘(x -2),得2x =x -2+1.解这个方程,得x =-1.检验:x =-1时x -2≠0,x =-1是原方程的解. ………………………………6分19. (2013江苏南京,19,8分)如图,在四边形ABCD 中,AB =BC ,对角线BD 平分∠ABC ,P 是BD 上一点,过点P 作PM ⊥AD ,PN ⊥CD .垂足分别为M 、N . (1)求证:∠ADB =∠CDB ; (2)若∠ADC =90°,求证:四边形MPND 是正方形.【答案】证明:(1)∵BD 平分∠ABC ,∴∠ABD =∠CBD . 又∵BA =BC ,BD =BD , ∴△ABD ≌△CBD . ∴∠ADB =∠CDB . ………………………………4分(2)∵PM ⊥AD ,PN ⊥CD , ∴∠PMD =∠PND =90° 又∵∠ADC =90°, ∴四边形MPND 是矩形. ∵∠ADB =∠CDB ,PM ⊥AD ,PN ⊥CD , ∴PM =PN . ∴四边形MPND 是正方形. ………………………………8分 20. (2013江苏南京,20,8分)(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各一个,这些球除颜色外都相同.求下列事件的概率:①搅匀后从中任意摸出一个球,恰好是红球;②搅匀后从中任意摸出一个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球; (2)某次考试共有6道选择题,每道题所给的4个选项中,恰有一项是正确的.如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部选择正确的概率是( )ABCD PMN(第19题)A.41B.641⎪⎭⎫ ⎝⎛ C.1-641⎪⎭⎫ ⎝⎛D. 1-643⎪⎭⎫ ⎝⎛【答案】(1)解:①搅匀后从中任意摸出1个球,所有可能出现的结果有:红、黄、蓝、白,共有4种,它们出现的可能性相同.所有的结果中,满足“恰好是红球”(记为事件A )的结果只有一种,所以P (A )=41. ②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀.再从中任意摸出1个球,所有可能出现的结果有:(红,红)、(红,黄)、(红,蓝)、(红,白)、(黄,红)、(黄,黄)、(黄,蓝)、(黄,白)、(蓝,红)、(蓝,黄)、(蓝,蓝)、(蓝,白)、(白,红)、(白,黄)、(白,蓝)、(白,白).共有16种,它们出现的可能性相同.所有的结果中,满足“两次都是红球”(记为事件B )的结果只有1种,所以P (B )=161.…………………6分 (2)B …………………8分21. (2013江苏南京,21,9分)某校有2000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:某校150名学生上学方式扇形统计图理由;(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图:(3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议.如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地.请你结合上述统计的全过程,再提出一条合理化建议:___________. 【答案】(1)不合理.因为如果150名学生全部在同一个年级抽取,那么全校每个学生被抽到的机会不相等,样本不具有代表性. …………………2分 (2)人数 0某校2000名学生上学方式条形统计图共交通工具乘私家车其它 上学方式骑车34%乘公共 交通工具 30%乘私家车20% 步行 10% 其它 6%…………………………………………………………………………7分 (3)本答案不惟一,下列解法供参考.乘私家车上学的学生约400人,建议学校与交通部门协商安排停车区域. …………………………………………………………………………9分22. (2013江苏南京,22,8分)已知不等臂跷跷板AB 长4m.如图①,当AB 的一端A 碰到地面时,AB 与地面的夹角为α;如图②,当AB 的另一端B 碰到地面时,AB 与地面的夹角为β.求跷跷板AB 的支撑点O 到地面的高度OH .(用含α、β的式子表示)【答案】解:在Rt △AHO 中,sinα=OAOH ,∴OA =αsin OH.在Rt △BHO 中,sinβ=OB OH ,∴OB =βsin OH. ∵AB =4,∴OA +OB =4.即αsin OH +βsin OH=4 ∴OH =βαβαsin sin sin sin 4+(m )…………………………………………………………………………8分23. (2013江苏南京,23,8分)某商场促销方案规定:商场内所有商品按标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额:OAH B①αO AH B②β (第22题)人数某校2000名学生上学方式条形统计图共交通工具乘私家车其它 上学方式注:.根据上述促销方案,顾客在该商场购物可以获得双重优惠.例如,若购买标价为400元的商品.则消费金额为320元,获得的优惠额为400×(1-80%)+30=110(元).(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?(2)如果顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为多少元?【答案】解:(1)购买一件标价为1000元的商品,消费金额为800元,顾客获得的优惠额为1000×(1-80%)+150=350(元)…………………………………2分 (2)设该商品的标价为x 元. 当80%x ≤500,即x ≤625时, 顾客获得的优惠额不超过625×(1-80%)+60=185<226; 当500<80%x ≤600,即625<x ≤750时, (1-80%)x +100≥226.解得x ≥630. 所以630≤x ≤750.当600<80%x ≤800×80%,即750<x ≤800时, 顾客获得的优惠额大于750×(1-80%)+130=280>226.综上,顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为630元. …………………………………8分24. (2013江苏南京,24,8分)小丽驾车从甲地到乙地.设她出发第x min 时的速度为y km/h ,图中的折线表示她在整个驾车过程中y 与x 之间的函数关系. (1)小丽驾车的最高速度是_______km/h ;(2)当20≤x ≤30时,求y 与x 之间的函数关系式,并求出小丽出发第22min 时的速度; (3)如果汽车每行驶100km 耗油10L ,那么小丽驾车从甲地到乙地共耗油多少升?【答案】解:(1)60;…………………………………1分(2)当20≤x ≤30时,设y 与x 之间的函数关系式为y =kx +b . 根据题意,当x =20时,y =60;当x =30时,y =24.所以⎩⎨⎧+=+=b k b k 30242060解得⎩⎨⎧=-=1326.3b k所以y 与x 之间的函数关系式为y=-3.6x +132 当x =22时,y =-3.6×22+132=52.8.(第24题) y (km/h )所以,小丽出发第22min 时的速度为52.8km/h.…………………………………5分 (3)小丽驾车从甲地到乙地行驶的路程为605204860104860524824601022460601060605260126052120⨯++⨯+⨯++⨯++⨯+⨯++⨯+=33.5(km ).所以,小丽驾车从甲地到乙地共耗油33.5×10010=3.35(L ). ………………8分 25. (2013江苏南京,25,8分)如图,AD 是⊙O 的切线,切点为A ,AB 是⊙O 的弦.过点B 作BC ∥AD ,交⊙O 于点C ,连接AC ,过点C 作CD ∥AB ,交AD 于点D .连接AO 并延长交BC 于点M ,交过点C 的直线于点P ,且∠BCP =∠ACD .(1)判断直线PC 与⊙O 的位置关系,并说明理由; (2)若AB =9,BC =6,求PC 的长.【答案】解法一:(1)直线PC 与⊙O 相切.如图①,连接CO 并延长,交⊙O 于点N ,连接BN . ∵AB ∥CD ,∴∠BAC =∠ACD . ∵∠BAC =∠BNC , ∴∠BNC =∠ACD . ∵∠BCP =∠ACD , ∴∠BNC =∠BCP . ∵CN 是⊙O 的直径, ∴∠CBN =90. ∴∠BNC +∠BCN =90°. ∴∠BCP +∠BCN =90°. ∴∠PCO =90°,即PC ⊥OC .…………………………………4分 (2)∵AD 是⊙O 的切线,∴AD ⊥OA ,即∠OAD =90°. ∵BC ∥AD ,∴∠OMC =180-∠OAD =90°,即OM ⊥BC . ∴MC =MB . ∴AB =AC .在Rt △AMC 中,∠AMC =90°,AC =AB =9,MC =21BC =3. 由勾股定理,得AM =26392222=-=-MC AC .设⊙O 的半径为r ,在Rt △OMC 中,∠OMC =90°,OM =AM -OA =62-r .MC =3,OC =r . 由勾股定理,得OM 2+MC 2=OC 2,即(62-r )2+32=r 2.解得r =8272.在△OMC 和△OCP 中,AB CDO M . (第25题)∵∠OMC =∠OCP ,∠MOC =∠COP ,∴△OMC ∽△OCP ,∴PCCMOC OM =,即PC32827282726=-. ∴PC =727.…………………………………8分解法二:(1)直线PC 与⊙O 相切.如图②,连接OC . ∵AD 是⊙O 的切线,∴AD ⊥OA ,即∠OAD =90°. ∵BC ∥AD ,∴∠OMC =180°-∠OAD =90°,即OM ⊥BC . ∴MC =MB . ∴AB =AC . ∴∠MAB =∠MAC . ∴∠BAC =2∠MAC . 又∵∠MOC =2∠MAC , ∴∠MOC =∠BAC . ∵AB ∥CD ,∴∠BAC =∠ACD . ∴∠MOC =∠ACD . 又∵∠BCP =∠ACD , ∴∠MOC =∠BCP . ∵∠MOC +∠OCM =90°, ∴∠BCP +∠OCM =90°. ∴∠PCO =90°,即PC ⊥OC . 又∵点C 在⊙O 上,∴直线PC 与⊙O 相切.………………4分(2)在Rt △AMC 中,∠AMC =90°,AC =AB =9,MC =21BC =3, 由勾股定理,得AM =26392222=-=-MC AC .设⊙O 的半径为r .在Rt △OMC 中,∠OMC =90°,OM =AM -AO =62-r .MC =3,OC =r. 由勾股定理,得OM 2+MC 2=OC 2,即(62-r )2+32=r 2.解得r =8272.在△OMC 和△OCP 中, ∵∠OMC =∠OCP ,∠MOC =∠COP ,AB C DO M P. ①N∴△OMC ∽△OCP ,∴PCCMOC OM =,即PC32827282726=-. ∴PC =727.…………………………………8分26. (2013江苏南京,26,9分)已知二次函数y =a (x -m )2-a (x -m )(a 、m 为常数,且a ≠0). (1)求证:不论a 与m 为何值,该函数的图象与x 轴总有两个公共点; (2)设该函数的图象的顶点为C .与x 轴交于A 、B 两点,与y 轴交于点D . ①当△ABC 的面积等于1时,求a 的值; ②当△ABC 的面积与△ABD 的面积相等时,求m 的值. 【答案】(1)证明:y =a (x -m )2-a (x -m )=ax 2-(2am +a )x +am 2+am . 因为当a ≠0时,[-(2am +a )]2-4a (am 2+am )=a 2>0.所以,方程ax 2-(2am +a )x +am 2+am =0有两个不相等的实数根.所以,不论a 与m 为何值,该函数的图象与x 轴总有两个公共点. ………3分 (2)解:①y =a (x -m )2-a (x -m )=a (x -212+m )2-4a, 所以,点C 的坐标为(212+m ,-4a). 当y =0时,a (x -m )2-a (x -m )=0.解得x 1=m ,x 2=m +1.所以AB =1. 当△ABC 的面积等于1时,21×1×4a -=1. 所以21×1×(-4a )=1,或21×1×4a=1. 所以a =-8,或a =8. ②当x =0时,y =am 2+am .所以点D 的坐标为(0,am 2+am ). 当△ABC 的面积与△ABD 的面积相等时,21×1×4a -=21×1×am am +2 21×1×(-4a )=21×1×(am 2+am ),或21×1×4a =21×1×(am 2+am ). 所以m =-21,或m =221--,或m =221+-.………9分 27.(2013江苏南京,27,10分)对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图ABC DO M . ②①△ABC ∽△A ′B ′C ′,且沿周界ABCA 与A ′B ′C ′A ′环绕的方向相同,因此△ABC 与△A ′B ′C ′互为顺相似;如图②,△ABC ∽△A ′B ′C ′,且沿周界ABCA 与A ′B ′C ′A ′环绕的方向相反,因此△ABC 与△A ′B ′C ′互为逆相似.(1)根据图Ⅰ、图Ⅱ和图Ⅲ满足的条件,可得下列三对相似三角形:①△ADE 与△ABC ;②△GHO 与△KFO ;③△NQP 与△NMQ .其中,互为顺相似的是________;互为逆相似的是__________.(填写所有符合要求的序号)(2)如图③,在锐角△ABC 中,∠A <∠B <∠C ,点P 在△ABC 的边上(不与点A 、B 、C 重合).过点P 画直线截△ABC ,使截得的一个三角形与△ABC 互为逆相似.请根据点P 的不同位置,探索过点P 的截线的情形,画出图形并说明截线满足的条件,不必说明理由.【答案】(1)①②;③………4分(2)解:根据点P 在△ABC 边上的位置分为以下三种情况 第一种情况:如图①,点P 在BC (不含点B 、C )上,过点P 只能画出2条截线PQ 1、PQ 2,分别使∠CP Q 1=∠A ,∠BP Q 2=∠A .此时,△PQ 1C 、△PBQ 2都与△ABC 互为逆相似. 第二种情况:如图②,点P 在AC (不含点A 、C )上,过点B 作∠CBM =∠A ,BM 交AC 于点M . 当点P 在AM (不含点M )上时,过点P 1只能画出1条截线P 1Q ,使∠AP 1Q =∠ABC ,此时△AP 1Q 与△ABC 互为逆相似;当点P 在CM 上时,过点P 2只能画2条截线P 2Q 1、P 2Q 2,分别使∠AP 2Q 1=∠ABC ,∠CP 2Q 2=∠ABC ,此时,△AP 2Q 1、△Q 2 P 2C 分别都与△ABC 逆相似; 第三种情况:如图③,点P 在AB (不含点A 、B )上,过点C 做∠BCD =∠A ,∠ACE =∠B ,CD 、CE 分别交AC 于点D 、E .当点P 在AD (不含点D )上时,过点P 只能画一条截线P 1Q ,使∠AP 1Q =∠ACB ,此时△AQP 1与△ABC互为逆ABCD E OH GKFN图Ⅰ图Ⅱ图Ⅲ条件:DE ∥BC条件:GH ∥KF条件:∠NQP =∠MCB ′′C B ′C ′①②(第27题)AB③相似;当点P在DE上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使∠AP2Q1=∠ACB,∠BP2Q2=∠BCA,此时,△AQ1P2、△Q2BP2都与△ABC互为逆相似;当点P在BE(不含点E)上时,过点P3只能画出1条截线P3Q′,使∠BP3Q′=∠BCA,此时△Q′BP3与△ABC逆相似.AA②AB③2′。
2013年江苏省南京市中考数学试卷含答案

南京市2013年初中毕业生学业考试数学注意事项:1. 本试卷共6页。
全卷满分120分。
考试时间为120分钟。
考生答题全部答在答题卡上,答在本试卷上无效。
2. 请认真核对监考教师在答题卡上所黏贴条形码的姓名、考试证号是否与本人相符,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上。
3. 答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其他答案。
答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效。
4. 作图必须用2B铅笔作答,并请加黑加粗,描写清楚。
一、选择题(本大题共6小题,每小题2分,共12分。
在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1. 计算12-7⨯(-4)+8÷(-2)的结果是(A) -24 (B) -20 (C) 6 (D) 362. 计算a3.( 1a)2的结果是(A) a(B) a5(C) a6(D) a93. 设边长为3的正方形的对角线长为a,下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③ 3<a<4;④a是18的算术平方根。
其中,所有正确说法的序号是(A) ①④(B) ②③(C) ①②④(D) ①③④4. 如图,圆O1、圆O2的圆心O1、O2在直线l上,圆O1的半径为2 cm,圆O2的半径为3 cm,O1O2=8 cm。
圆O1以1 cm/s的速度沿直线l向右运动,7s后停止运动,在此过程中,圆O1与圆O2没有出现的位置关系是(A) 外切(B) 相交(C) 内切(D) 内含5. 在同一直线坐标系中,若正比例函数y=k1x的图像与反比例函数y=k2x的图像没有公共点,则(A) k1+k2<0 (B) k1+k2>0 (C) k1k2<0 (D) k1k2>06. 如图,一个几何体上半部为正四棱椎,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是(B)(D)二、填空题(本大题共10小题,每小题2分,共20分。
2013年江苏省南京市中考数学试卷-答案

321a a = 【考点】分式的乘除法 【解析】边长为③1618<<a 是18的算术平方根,说法正确.所以说法正确的有①②④.【解析】128cm O O =,此时两圆的半径的差为【提示】根据两圆的半径和移动的速度确定两圆的圆心距的最小值,【解析】正比例函数120k<.【解析】如图,四边形,矩形,12∠=∠4907020∴∠=︒-︒=︒,20α∴∠=︒.110,再根据四边形的内角和为,四边形,120BAD ∠=,BAC ∴∠,AOB ∠=BO DO =,EF AC ⊥,,AC BD ⊥BD ,∴EF 3)322=.,AD BC ∥,AD BC ∥,∴AD BC =23AM x ⊥∴CPF △∽△2CF CP ,2AN =,∴43PF =,∴b ⎫⎪⎭16ab =+,1a b +=123=--1)()()a b a a b a a b a b a a b++==+--.【提示】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除以一个数等于乘以这个数的)PM AD ⊥,ADC ∠=ADB CDB ∠=∠,45ADB ∴∠=︒,∴PM MD =,∴四边形MPND 是正方形.【考点】频数(率)分布表,抽样调查的可靠性,用样本估计总体,扇形统计图,条形统计图sin sin αββ+意有A O =sin BO OH =÷sin m sin αββ+.故跷跷板sin sin αββ+(m )【提示】根据三角函数的知识分别用,函数图象经过点302⨯24)60+8m,∥,如图,CE,AB DC ∠=,BAC)AD,BC AD∥26CM-=2CM OC=E MCP∠=∠44,0a≠,∴0得1x m=,ABC △的面积与214m ++=)m 看作一个整体,令【提示】(1)根据互为顺相似和互为逆相似的定义即可作出判断;△边上的位置分为三种情况,需要分类讨论,逐一分析求解.(2)根据点P在ABC【考点】相似形综合题11 / 11。
13年江苏省南京市中考数学试卷

2013年江苏省南京市中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.计算:12-7×(-4)+8÷(-2)的结果是( )A.-24 B.-20 C.6 D.362.计算的结果是( )A.a B.a3C.a6D.a93.设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是( )A.①④B.②③C.①②④D.①③④4.如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1m/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是( )A.外切B.相交C.内切D.内含5.在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数的图象没有公共点,则( )A.k1+k2<0 B.k1+k2>0 C.k1k2<0 D.k1k2>06.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是( )A.B.C.D.二、填空题(本大题共10小题,每小题2分,共20分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)7.-3的相反数是________;-3的倒数是________.8.计算:的结果是________.9.使式子有意义的x的取值范围是________.10.第二届亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务.将13000用科学记数法表示为________.11.如图,将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=________.12.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=________cm.13.△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为________.14.已知如图所示的图形的面积为24,根据图中的条件,可列出方程:________.15.如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为(________,________).16.计算的结果是________.三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤)17.化简.18.解方程:.19.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.20【1】.一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个.这些球除颜色外都相同.求下列事件的概率:①搅匀后从中任意摸出1个球,恰好是红球;②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球;20【2】.某次考试共有6道选择题,每道题所给出的4个选项中,恰有一个是正确的.如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部正确的概率是________.A.B.C.D.21.某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:(1)理解划线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;(3)该校数学兴趣小组结合调查获取信息,向学校提出了一些建议,如:骑车上学的学生约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化的建议:________.22.已知不等臂跷跷板AB长4m.如图①,当AB的一端A碰到地面上时,AB与地面的夹角为α;如图②,当AB的另一端B碰到地面时,AB与地面的夹角为β.求跷跷板AB的支撑点O到地面的高度OH.(用含α,β的式子表示)23.某商场促销方案规定:商场内所有商品按标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额.消费金额(元) 300-400 400-500 500-600 600-700 700-900 …返还金额(元) 30 60 100 130 150 …根据上述促销方案,顾客在该商场购物可以获得双重优惠,例如:若够买标价为400元的商品,则消费金额为320元,获得的优惠额为400×(1-80%)+30=110(元).(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?(2)如果顾客购买标价不超过800元的商品,要使获得的优惠不少于226元,那么该商品的标记至少为多少元?24.小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.(1)小丽驾车的最高速度是________km/h;(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度;(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?25.如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与⊙O的位置关系,并说明理由;(2)若AB=9,BC=6.求PC的长.26.已知二次函数y=a(x-m)2-a(x-m)(a,m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于点D.①当△ABC的面积等于1时,求a的值;②当△ABC的面积与△ABD的面积相等时,求m的值.27.对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相同,因此△ACB和△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相反,因此△ACB 和△A′B′C′互为逆相似.(1)根据图Ⅰ,图Ⅱ和图Ⅲ满足的条件.可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO;③△NQP与△NMQ;其中,互为顺相似的是________;互为逆相似的是________.(填写所有符合要求的序号).(2)如图③,在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与点A,B,C重合).过点P 画直线截△ABC,使截得的一个三角形与△ABC互为逆相似.请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由.。
2013年江苏省南京市中考数学试卷-答案

江苏省南京市 2013 年中考数学试卷数学答案分析一、选择题1.【答案】 D【分析】原式12 28 4 36.【提示】依据运算次序先计算乘除运算,最后算加减运算,即可获取结果.【考点】有理数的混淆运算2.【答案】 A 【分析】原式 a31a a2【提示】先算出分式的乘方,再约分.【考点】分式的乘除法3.【答案】 C【分析】边长为 3 的正方形的对角线长为a,a3232183 2① a 3 2 是无理数,说法正确;② a 能够用数轴上的一个点来表示,说法正确;③16 18 25,418 5 ,即4 a 5,说法错误;④a 是 18 的算术平方根,说法正确.因此说法正确的有①②④.【提示】先利用勾股定理求出 a 3 2,再依据无理数的定义判断①;依据实数与数轴的关系判断②;利用估量无理数大小的方法判断③;利用算术平方根的定义判断④.【考点】估量无理数的大小,算术平方根,无理数,实数与数轴,正方形的性质4.【答案】 D【分析】O1O2 8cm ,⊙ O1以1cm/s l向右运动,7s后停止运动,7s后两圆的圆心距为的速度沿直线1cm,此时两圆的半径的差为 3 2 1cm,此时内切,挪动过程中没有内含这类地点关系.【提示】依据两圆的半径和挪动的速度确立两圆的圆心距的最小值,从而确立两圆可能出现的地点关系,找到答案.【考点】圆与圆的地点关系5.【答案】 C【分析】正比率函数y k1x 的图象与反比率函数y k2的图象没有公共点,k1与 k2异号,即 k1 k20 .x【提示】依据反比率函数与一次函数的交点问题进行解答即可.【考点】反比率函数与一次函数的交点问题6.【答案】 B【分析】选项 A 和 C 带图案的一个面是底面,不可以折叠成原几何体的形式;选项 B 能折叠成原几何体的形式;选项 D 折叠后下边带三角形的面与原几何体中的地点不一样.【提示】由平面图形的折叠及几何体的睁开图解题,注意带图案的一个面不是底面.【考点】几何体的睁开图二、填空题7.【答案】 3131【分析】3的相反数是3;3的倒数是.3【提示】依据倒数以及相反数的定义即可求解.【考点】倒数,相反数8.【答案】 2【分析】原式3 2 22 2 .2【提示】先进行二次根式的化简,而后归并同类二次根式即可.【考点】二次根式的加减法9.【答案】x 1【分析】由题意知,分母x 1 0 ,即 x 1时,式子11存心义.x 1【提示】分式存心义,分母不等于零.【考点】分式存心义的条件10.【答案】104【分析】 13000 1.3 104【提示】科学记数法的表示形式为 a 10n的形式,此中 1 | a | 10 ,n为整数.确立n 的值时,要看把原数变为 a 时,小数点挪动了多少位,n 的绝对值与小数点挪动的位数同样.当原数绝对值 1 时,n是正数;当原数的绝对值 1 时,n是负数.2/ 11【分析】如图, 四边形 ABCD 为矩形, BD BAD 90 , 矩形 ABCD 绕点 A 顺时针旋转获取 矩形 AB ′C ′D ′D D90,4,12 110,3 360 90 90 110 70 ,,4 90 70 20 ,20 .【提示】依据矩形的性质得 B D BAD 90 ,依据旋转的性质得D D 90 , 4,利用对顶角相等获取 12 110 ,再依据四边形的内角和为360 可计算出3 70 ,而后利用互余即可得到的度数.【考点】旋转的性质,矩形的性质 12. 【答案】 3【分析】连结 BD 、AC , 四边形 ABCD 是菱形, AC BD ,AC 均分 BAD , BAD 120 ,BAC 60 ,ABO 9060 30 ,AOB 90 ,AO1 1 1 ,由勾股定理得: BODO3 ,AB222A 沿 EF 折叠与 O 重合,EF AC ,EF 均分 AO , ACBD , EF ∥BD , EF 为 △ABD 的中位线,EF1BD1 ( 3 3)3 .22【提示】依据菱形性质得出AC BD , AC 均分 BAD ,求出 ABO 30 ,求出 AO 、 BO 、 DO ,依据折叠得出 EFAC ,EF 均分 AO ,推出 EF ∥BD ,推出, EF 为 △ ABD 的中位线,依据三角形中位线定理求出即可.【考点】菱形的性质,翻折变换(折叠问题)13.【答案】 9【分析】当OAB70 时, AOB 40 ,则多边形的边数是 360 409 ;当 AOB70 时, 360 70结果不是整数,故不切合条件.【提示】分OAB 70 和 AOB 70 两种状况进行议论即可求解.【考点】正多边形和圆14.【答案】 ( x 1)2 25【分析】依据题意得( x 1)2 1 24 ,即 ( x 1)2 25 .【提示】此图形的面积等于两个正方形的面积的差,据此能够列出方程.【考点】由实质问题抽象出一元二次方程15.【答案】 3,73【分析】过 A 作 AM x 轴与 M ,交 BC 于 N ,过 P 作 PEx 轴与 E ,交 BC 于 F , AD ∥BC , A(2,3) ,B(1,1),D(4,3) ,AD ∥BC ∥x 轴,AM,,3 1 2,4 2 2 ,2 1 1 ,3 MNEF1ANADBNC 的坐标是 (5,1) ,1 4 ,4 1 3 , AD ∥BC , △ APD ∽△ CPB , ADAP2 1BC 5CNBC PC 4,2CP2 AM x 轴,PEx 轴, AM ∥PE , △CPF ∽△ CAN ,PF CF CP 2AN 2,AC 3ANCNCA,3CN3 , PF4, PE4 1 7,CF2, BF2 , P 的坐标是 73, .3333【提示】过 A 作 AM x 轴与 M ,交 BC 于 N ,过 P 作 PE x 轴与 E ,交 BC 于 F ,依据点的坐标求出各个线段的长,依据 △APD ∽△ CPB 和 △ CPF ∽△ CAN 得出比率式,即可求出答案. 【考点】等腰梯形的性质,两条直线订交或平行问题116.【答案】6【分析】设 a1111 1 , b 11 1 11 a1 ab1a ab1 b,则原式a bb2 3 4 523 4 566661( a b) ,a b 1 11111111 1, 原式 1 .62 3 4 5 2 3 4 56【提示】设 a111 1 1 , b1 1 1 1 ,而后依据整式的乘法与加减混淆运算进行计算即可得2 3 4 5 2 3 4 5解.【考点】整式的混淆运算三、解答题117.【答案】baa b b a b a a b 1.【分析】原式( a b)(a b) a (a b)(a b) a a b【提示】原式括号中两项通分并利用同分母分式的减法法例计算,同时利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可获取结果.【考点】分式的混淆运算18.【答案】x 1【分析】去分母得2x x 2 1 ,移项归并得x 1,经查验 x 1是分式方程的解.【提示】分式方程去分母转变为整式方程,求出整式方程的解获取x 的值,经查验即可获取分式方程的解.【考点】解分式方程AB CB【答案】(1 )∵对角线BD 均分ABC ,ABD CBD ,在△ABD 和△ CBD 中,ABD CBD ,19.BD BD△ ABD≌△ CBD (SAS) ,ADB CDB ;(2)PM AD,PN CD ,PMD PND 90 ,ADC 90 ,四边形MPND 是矩形,ADB CDB ,ADB 45 ,PM MD ,四边形 MPND 是正方形.【提示】( 1)依据角均分线的性质和全等三角形的判断方法证明△ ABD≌△ CBD,由全等三角形的性质即可获取ADB CDB ;( 2)若ADC 90 ,由(1)中的条件可得四边形MPND 是矩形,再依据两边相等的四边形是正方形即可证明四边形MPND 是正方形.【考点】正方形的判断,全等三角形的判断与性质120.【答案】(1)①4②116 (2) B【分析】( 1)①搅匀后从中随意摸出 1 个球,恰巧是红球的概率为1;4②列表以下:红黄红(红,红)(黄,红)黄(红,黄)(黄,黄)蓝(红,蓝)(黄,蓝)绿(红,绿)(黄,绿)蓝绿(蓝,红)(绿,红)(蓝,黄)(绿,黄)(蓝,蓝)(绿,蓝)(蓝,绿)(绿,绿)所有等可能的状况数有16 种,此中两次都为红球的状况数有1种,则P1;161 1 6( 2)每道题所给出的 4 个选项中,恰有一个是正确的概率为.,则他 6 道选择题所有正确的概率是44【提示】( 1)①搅匀后从 4 个球中随意摸出 1 个球,求出恰巧是红球的概率即可;②列表得出所有等可能的状况数,找出两次都是红球的状况数,即可求出所求的概率;(2)求出每一道题选择正确的概率,利用乘法法例即可求出所有正确的概率.【考点】列表法与树状图法,概率公式21.【答案】(1)不合理,由于假如150 名学生所有在同一个年级抽取,这样抽取的学生不拥有随机性,比较片面,因此这样的抽样不合理;( 2)步行人数为2000 10% 200 (人),骑车的人数为2000 34%680 (人),乘公共汽车人数为2000 30% 600(人),乘私人车的人数为 2000 20% 400(人),乘其余交通工具得人数为2000 6% 120,以下图:( 3)为了节俭和保护环境请同学们尽量不要乘坐私人车(答案不独一).【提示】( 1)依据抽样检查一定拥有随机性,剖析得出即可;(2)依据扇形统计图分别求出各样搭车的人数,从而画出条形图即可;(3)利用节能减排的角度剖析得出答案即可.【考点】频数(率)散布表,抽样检查的靠谱性,用样本预计整体,扇形统计图,条形统计图4sin sin22.【答案】sinsin【分析】依题意有AO O H s i n ,BO OH sin , AO BO OH sinOH sin ,即O H si nO H s i n ,4m则OH4sin sinm .故跷跷板AB的支撑点O 到地面的高度OH 是sin sin4sin sinsin sin(m).【提示】依据三角函数的知识分别用OH 表示出 AO、 BO 的长,再依据不等臂跷跷板AB 长 4m,即可列出方程求解即可.【考点】解直角三角形的应用23.【答案】(1) 350( 2) 630【分析】( 1)标价为1000 元的商品按80% 的价钱销售,花费金额为800 元,花费金额800 元在 700~900 之间,返还金额为150 元,顾客获取的优惠额是 1000 (1 80%) 150 350 (元);( 2)设该商品的标价为x 元.①当 80%x 500 ,即 x 625时,顾客获取的优惠额不超出625 (1 80%) 60 185 226 ;②当 500 80%x 600,即 625 x 750时,顾客获取的优惠额(1 80%) x 100 226 ,解得x 630,即630 x 750.③当 600 80%x 700,即 750 x 875时,由于顾客购置标价不超出800 元,因此750 x 800,顾客获取的优惠额 750 (1 80%) x 130 280 226 .综上,顾客购置标价不超出 800 元的商品,要使获取的优惠额许多于226 元,那么该商品的标价起码为 630 元.【提示】( 1)依据标价为1000 元的商品按80%的价钱销售,求出花费金额,再依据花费金额所在的范围,求出优惠额,从而得出顾客获取的优惠额;( 2)先设该商品的标价为x 元,依据购置标价不超出800 元的商品,要使获取的优惠许多于226 元,列出不等式,分类议论,求出x 的取值范围,从而得出答案.【考点】一元一次不等式组的应用24.【答案】(1) 60(2)(3)【分析】( 1)由图可知,第 10min 到 20min 之间的速度最高,为60km/h ;()当20 x 30 时,设 y kx b( k 0) ,函数图象经过点(20,60) , (30,24) ,20k b 60 ,解得230k b 24k 1818 x 185 ,因此, y 与 x 的关系式为y 132 ,当 x 22时,y 22 132 ;b 132 5 5( 3 )行驶的总行程 1 (12 0) 5 1 (12 60) 10 5 60 20 10 1 (60 24) 30 202 60 2 60 60 2 601(24 5 45 35 1(48 0)5 17 3 8 2 ,汽车每行驶2 48) 482 603 1060 60 2100km 耗油 10L ,小丽驾车从甲地到乙地共耗油10升.100【提示】( 1)察看图象可知,第10min 到 20min 之间的速度最高;( 2)设y kx b k( 0) ,利用待定系数法求一次函数分析式解答,再把 x 22 代入函数关系式进行计算即可得解;(3)用各时间段的均匀速度乘以时间,求出行驶的总行程,再乘以每千米耗费的油量即可.【考点】一次函数的应用25.【答案】(1) PC 与圆 O 相切,原由于:过 C 点作直径CE,连结 EB ,如图,CE 为直径,EBC 90 ,即E BCE 90 ,AB∥DC ,ACD BAC ,BAC E,BCP ACD.E BCP,BCP BCE 90,即PCE 90 ,CE PC,PC 与圆 O 相切;( 2) AD 是⊙ O 的切线,切点为 A , OAAD , BC ∥AD , AMBC , BM CM1BC 3 ,2AC AB 9 , 在 Rt △ AMC 中 , AM2CM22 ,设⊙O的半径为 r , 则 OCr ,AC6OMAM r6 2 r ,在 Rt △ OCM 中, OM 2CM 22,即 3 2(6 2 )r 2227 2 ,OCr ,解得 r8CE 2r27 2 , OM 62 27 2 21 2 , BE 2OM 21 2 , EMCP,488 4PC CM PC 3 2727 2 21 2, PCRt △ PCM ∽ Rt △CEB ,EB ,即 7 .CE 4 4【提示】( 1)过 C 点作直径 CE ,连结 EB ,由 CE 为直径得 E BCE 90 ,由 AB ∥DC得 ACD BAC ,而 BAC E , BCPACD ,因此 EBCP ,于是 BCPBCE90 ,而后依据切线的判断获取结论;( 2)依据切线的性质获取 OA AD ,而 BC ∥AD ,则 AM BC ,依据垂径定理有 BMCM1BC 3,2依据等腰三角形性质有AC AB 9,在 Rt △AMC 中依据勾股定理计算出AM 62 ;设⊙ O 的半径为 r , 则 OC r ,OM AM r6 2r ,在 Rt △ OCM 中,依据勾股定理计算出r27 2,则CE r 272 2 ,84OM6 2 27 2 212,利用中位线性质得 BE 2OM21 2,而后判断 Rt △ PCM ∽Rt △CEB ,根88 4据相像比可计算出PC .【考点】切线的判断与性质26.【答案】( 1)令 y0 , a( x m)2 a( x m) 0 ,( a)2 4a 0 a 2 ,a 0 , a20 , 无论 a与 m 为什么值,该函数的图象与x 轴总有两个公共点;( 2 ) ① y 0, 则 a( x2a( x)m( a x ) m( x,m1 )解 得0 x 1m , x 2m 1 , m)21aAB ( m1) m 1 , y a( x m)2 a(xm) ax m 1a, △ABC 的面积1 1,解2424得 a8 ;②x 0 时,y a(0 m)2 a(0 m) am2 am ,因此,点 D 的坐标为(0, am2 am) ,△ABD的面积1 1 | am2 am | ,△ABC 的面积与△ABD的面积相等, 1 1 | am2 am | 1 1 a ,整理得2 2 2 4m2 m 1 0 ,或 m2 m 1 0 ,解得 m 1 2或 m 1 .4 4 2 2【提示】( 1)把(x m)看作一个整体,令y 0 ,利用根的鉴别式进行判断即可;(2)①令y 0 ,利用因式分解法解方程求出点A、 B 的坐标,而后求出 AB ,再把抛物线转变为极点式形式求出极点坐标,再利用三角形的面积公式列式进行计算即可得解;②令 x 0 求出点D的坐标,而后利用三角形的面积列式计算即可得解.【考点】二次函数综合题27.【答案】(1)互为顺相像的是①②;互为逆相像的是③;( 2)依据点P 在△ABC边上的地点分为以下三种状况:第一种状况:如图①,点 P 在 BC(不含点 B、C)上,过点 P 只好画出 2 条截线PQ1、PQ2 ,分别使CPQ1 A ,BPQ2 A ,此时△ PQ1C 、△ PBQ2都与△ ABC 互为逆相像.第二种状况:如图②,点P在AC(不含点A、C)上,过点B作CBM A ,BM交AC于点M.当点 P 在 AM(不含点 M)上时,过点 1 1 1ABC 1P 只好画出 1 条截线PQ,使APQ ,此时△ APQ 与△ ABC 互为逆相像;当点P在CM 上时,过点 P2 只好画出 2 条截线P2Q1、P2Q2,分别使AP2 Q1 ABC ,CP2 Q2 ABC ,此时△AP2 Q1、△Q2 P2C 都与△ ABC 互为逆相像.第三种状况:如图③,点P在AB A B C作BCD A,ACE B ,CD、CE分(不含点、)上,过点别交 AB 于点 D、E.当点 P 在 AD(不含点 D )上时,过点 P 只好画出 1 条截线PQ,使APQ ACB,1 1此时△ AQP1与△ ABC 互为逆相像;当点P 在 DE 上时,过点P2 只好画出 2 条截线P2Q1、P2Q2,分别使AP2 Q1 ACB ,BP2 Q2 BCA ,此时△ AQ1P2、△Q2 BP2 都与△ ABC 互为逆相像;当点P 在 BE(不含点 E)上时,过点P 只好画出1 条截线PQ ,使 BPQ BCA ,此时△Q BP 与△ ABC互为逆相像.3 3 3 310/11【提示】( 1)依据互为顺相像和互为逆相像的定义即可作出判断;(2)依据点 P 在△ABC边上的地点分为三种状况,需要分类议论,逐个剖析求解.【考点】相像形综合题11/11。
2013年江苏省南京市中考数学试卷

2013年江苏省南京市中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(2分)计算:12-7X(-4)+84-(-2)的结果是()A.-24B.-20C.6D.362.(2分)计算a3*1(-)之的结果是(a)A.aB.a3C.a6D.a93.(2分)设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是()A.①④B.②③C.①②④D.①③④4.(2分)如图,OOi,。
2的圆心在直线I上,的半径为2cm,。
2的半径为3cm.OiO2=8cm,O0i以lcm/s的速度沿直线I向右运动,7s后停止运动.在此过程中,和。
2没有出现的位置关系是()A.外切B.相交C.内切D.内含5.(2分)在同一直角坐标系中,若正比例函数y=kix的图象与反比例函数y=也的X 图象没有公共点,则()A.ki+k2<0B.ki+k2>0C.kik2<0D.kik2>06.(2分)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是()二、填空题(本大题共10小题,每小题2分,共20分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)7.(2分)-3的相反数是;-3的倒数是.8.(2分)计算:5一的结果是.9.(2分)使式子1+土有意义的x的取值范围是x-110.(2分)第二届亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务.将13000用科学记数法表示为.11.(2分)如图,将矩形ABCD绕点A顺时针旋转到矩形ABVD7的位置,旋转角为a(0。
2013年江苏省南京市中考数学试卷(学生版)

2013年江苏省南京市中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(2分)计算:12﹣7×(﹣4)+8÷(﹣2)的结果是()A.﹣24B.﹣20C.6D.362.(2分)计算a3•()2的结果是()A.a B.a3C.a6D.a93.(2分)设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是()A.①④B.②③C.①②④D.①③④4.(2分)如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是()A.外切B.相交C.内切D.内含5.(2分)在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数y的图象没有公共点,则()A.k1+k2<0B.k1+k2>0C.k1k2<0D.k1k2>06.(2分)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是()A.B.C.D.二、填空题(本大题共10小题,每小题2分,共20分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)7.(2分)﹣3的相反数是;﹣3的倒数是.8.(2分)计算:的结果是.9.(2分)使式子1有意义的x的取值范围是.10.(2分)第二届亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务.将13000用科学记数法表示为.11.(2分)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=.12.(2分)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=cm.13.(2分)△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为.14.(2分)已知如图所示的图形的面积为24,根据图中的条件,可列出方程:.15.(2分)如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为(,).16.(2分)计算(1)()﹣(1)()的结果是.三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤)17.(6分)化简().18.(6分)解方程:1.19.(8分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.20.(8分)(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、绿的球各1个.这些球除颜色外都相同.求下列事件的概率:①搅匀后从中任意摸出1个球,恰好是红球;②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球;(2)某次考试共有6道选择题,每道题所给出的4个选项中,恰有一个是正确的.如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部正确的概率是.A.B.C.1D.1.21.(9分)某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:(1)理解划线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;(3)该校数学兴趣小组结合调查获取信息,向学校提出了一些建议,如:骑车上学的学生约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化的建议:.22.(8分)已知不等臂跷跷板AB长4m.如图①,当AB的一端A碰到地面上时,AB与地面的夹角为α;如图②,当AB的另一端B碰到地面时,AB与地面的夹角为β.求跷跷板AB的支撑点O到地面的高度OH.(用含α,β的式子表示)23.(8分)某商场促销方案规定:商场内所有商品按标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额.消费金额(元)300﹣400400﹣500500﹣600600﹣700700﹣900…返还金额(元)3060100130150…根据上述促销方案,顾客在该商场购物可以获得双重优惠,例如:若购买标价为400元的商品,则消费金额为320元,获得的优惠额为400×(1﹣80%)+30=110(元).(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?(2)如果顾客购买标价不超过800元的商品,要使获得的优惠不少于226元,那么该商品的标价至少为多少元?24.(8分)小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.(1)小丽驾车的最高速度是km/h;(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度;(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?25.(8分)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与⊙O的位置关系,并说明理由;(2)若AB=9,BC=6.求PC的长.26.(9分)已知二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点.(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于D点.①当△ABC的面积为1时,求a的值.②当△ABC的面积与△ABD的面积相等时,求m的值.27.(10分)对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相同,因此△ACB和△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相反,因此△ACB和△A′B′C′互为逆相似.(1)根据图Ⅰ,图Ⅱ和图Ⅲ满足的条件.可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO;③△NQP与△NMQ;其中,互为顺相似的是;互为逆相似的是.(填写所有符合要求的序号).(2)如图③,在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与点A,B,C重合).过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似.请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由.。
2013年南京市中考数学试卷解析

南京市 2013 年初中毕业生学业考试 数学注意事项: 1. 本试卷共 6 页。
全卷满分 120 分。
考试时间为 120 分钟。
考 生答题全部答在答题卡上,答在本试卷上无效。
2. 请认真核对监考教师在答题卡上所黏贴条形码的姓名、考试 证号是否与本人相符,再将自己的姓名、准考证号用 0.5 毫米黑 色墨水签字笔填写在答题卡及本试卷上。
3. 答选择题必须用 2B 铅笔将答题卡上对应的答案标号涂黑。
如 需改动,请用橡皮擦干净后,再选涂其他答案。
答非选择题必须用 0.5 毫米黑色墨水签字笔 写在答题卡上的指定位置,在其他位置答题一律无效。
4. 作图必须用 2B 铅笔作答,并请加黑加粗,描写清楚。
一、 选择题 (本大题共 6 小题,每小题 2 分,共 12 分。
在每小 题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填 涂在答题卡相应位置上) 1. 计算 12 7 ( 4) 8 ( 2)的结果是(A) 24 (B) 20 (C) 6 (D) 36 答案:D 解析:原式=12+28-4=36,选 D。
2. 计算 a3.(1 a)2 的结果是(A) a (B) a5 (C) a6 (D) a9答案:A解析:原式= a31 a2 a ,选A。
3. 设边长为 3 的正方形的对角线长为 a,下列关于 a 的四种说法: a 是无理数; a 可以用数轴上的一个点来表示; 3<a<4;a 是 18 的算术平方根。
其中,所有正确说法的序号是(A)(B)(C)(D)答案:C解析:由勾股定理,得: a 3 2 4.2,所以,③错误,其它都正确。
4. 如图,圆 O1、圆 O2 的圆心 O1、O2 在直线 l 上,圆 O1 的半径为 2 cm,圆 O2 的半径为 3 cm,O1O2=8cm。
圆 O1 以 1 cm/s 的速度沿直线 lO1O2l向右运动,7s 后停止运动,在此过程中,圆 O1 与圆 O2 没有出现的位置关系是(A) 外切 (B) 相交 (C) 内切 (D) 内含答案:D解析:7s 后两圆刚好内切,所以,外切、相交、内切都有,没有内含,选 D。
2013年江苏省南京中考数学卷

第4题lFEO DBA1D'B'C'DCBA第12题第11题2013年江苏省南京中考数学卷一、选择题(本大题共有6小题,共12分,每小题2分.)1.计算12-7×(-4)+8÷(-2)的结果是A.-24 B.-20 C.6 D.362.计算23)1·aa(的结果是A.a B.5a C.6a D.9a3.设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根。
其中,所有正确说法的序号是A.①④B.②③C.①②④D.①③④4.如图,⊙O1、⊙O2的圆心O1、O2在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm,O1O2=8cm。
⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动。
再此过程中,⊙O1与⊙O2没有出现的位置关系是A.外切B.相交C.内切D.内含函数y=k1x的图像与反比例函数xky2=的图5.在同一直角坐标系中,若正比例像没有公共点,则A.k1+ k2<0 B.k1+ k2>0 C.k1k2<0 D.k1k2>06. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,下2分.)7.-3的相反数是的倒数是.8.计算2123-的结果是.9.使式子111-+x有意义的x的取值范围是.10.第二节亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务,将13000用科学计数法表示为.11.如图将矩形ABCD绕点A顺时针旋转到AB’C’D’的位置,旋转角α(0°<α<90°).若∠1=110°,则∠α= °.12. 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2cm,∠A=120°,则EF= cm .13.△OAB是以正多边形相邻的两个顶点A、B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为.14. 已知如图所示的图形的面积为24,根据图中的条件,可列出方程.15. 如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点P,已知A(2,3),B(1,1),D(4,3),则点P的坐标为(,).第6题B.第14题第15题N P M AB 16.计算⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛------⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛----51413121615141312116151413121514131211的结果是 .三、解答题(本大题共有11小题,共88分.) 17.(6分)化简b a a b a b ba +÷⎪⎭⎫⎝⎛---221. 18.(6分)解方程xx x --=-2112219.(8分)如图,在四边形ABCD 中,AB =BC ,对角线BD 平分∠ABC ,P 是BD 上一点,过点P 作PM ⊥AD ,PN ⊥CD ,垂足分别为M 、N. (1)求证:∠ADB =∠CDB ;(2)若∠ADC =90°,求证:四边形MPND 是正方形.20.(8分)(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个,这些球除颜色外都相同,求下列事件的概率:①搅匀后从中任意摸出1个球,恰好是红球;②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是是红球;(2)某次考试共有6道选择题,每道题所给出的4个选项中,恰有一项是正确的.如果小明从每道题的4个选项中随机的选择一个,那么他6道选择题全部选正确的概率是( ) A .41 B .641⎪⎭⎫ ⎝⎛ C .6411⎪⎭⎫ ⎝⎛-D .6431⎪⎭⎫⎝⎛-21.(9分)某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查,整理样本数据,得到下列图表:(1)理解画线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;步行10%其它6%乘私家车 20%乘公共交通工具 30%骑车34%某校150名学生上学方式 频数分布表 某校150名学生上学方式 扇形统计图(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图: (3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议,如:骑车上学的学生数约占全校的34%,建议学生合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化建议: . 22.(8分)已知不等臂跷跷板AB 长4m ,如图①,当AB 的一端A 碰到地面时,AB 与地面的夹角为α;如图②,当AB 的另一端B 碰到地面时,AB 与地面的夹角为β.求跷跷板AB 的支撑点O 到地面的高度OH .(用含α、β的式子表示) 23.(8分)某商场促销方案规定:商场内所有商品按标价的80%出售,同时,当顾客700~900 根据上述促销方案,顾客在该商场购物可以获得双重优惠,例如,若购买标价为400元的商品,则消费金额为320元,获得的优惠额为400×(1-80%)+30=110(元) (1)购买一件标价为1000元的商品,顾客获得的优惠额是多少? (2)如果顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为多少元?24.(8分)小丽驾车从甲地到乙地,设她出发第x min 时的速度为y km/h ,图中折线表示她在整个驾车过程中第y 与 x 之间的函数关系. (1)小丽驾车的最高速度是 km/h; (2)当20≤x ≤30时,求y 与 x 之间的函数关系式,并求出小丽出发第22min 时的速度; (3)如果汽车每行驶100km 耗油10L ,那么小丽驾车从甲地到乙地共耗油多少升?某校2000名学生上学方式条形统计图 步行 骑车 乘公共 乘私 其它 上学方式 交通工具 家车 人数H ① H②O y 方法指导 如果物体的运动速度随着时间均匀增加(或减少),那么其在某个时间段内的平均速度为该时间段开始时刻的速度与结束时刻的速度的平均数。
2013年南京市中考数学试卷(解析)

2013年江苏省南京市中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)2.(2分)(2013•南京)计算a3•()2的结果是()3.(2分)(2013•南京)设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;②a可以用数,再根据无理数的定义判断①a===3a=3<4.(2分)(2013•南京)如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1m/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是()5.(2分)(2013•南京)在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数y=的图象没有公共点,y=6.(2分)(2013•南京)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是()CD二、填空题(本大题共10小题,每小题2分,共20分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上) 7.(2分)(2013•南京)﹣3的相反数是 3 ;﹣3的倒数是 ﹣ ..,﹣8.(2分)(2013•南京)计算:的结果是 .=故答案为:9.(2分)(2013•南京)使式子1+有意义的x 的取值范围是 x ≠1 .有意义.10.(2分)(2013•南京)第二届亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务.将13000用科学记数法表示为 1.3×104.11.(2分)(2013•南京)如图,将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=20°.12.(2分)(2013•南京)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=cm.AO=AB=×BO=DO=EF=BD=(+=故答案为:13.(2分)(2013•南京)△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为9.14.(2分)(2013•南京)已知如图所示的图形的面积为24,根据图中的条件,可列出方程:(x+1)2=25.15.(2分)(2013•南京)如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为(3,).∴∴==,,PE=+1=,).16.(2分)(2013•南京)计算(1﹣)()﹣(1﹣﹣)()的结果是.﹣﹣﹣,+++﹣﹣﹣b=++,)﹣(﹣a b﹣﹣﹣+++=1.故答案为:三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤)17.(6分)(2013•南京)化简()÷.••=18.(6分)(2013•南京)解方程:=1﹣.19.(8分)(2013•南京)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.(1)求证:∠ADB=∠CDB;(2)若∠ADC=90°,求证:四边形MPND是正方形.20.(8分)(2013•南京)(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个.这些球除颜色外都相同.求下列事件的概率:①搅匀后从中任意摸出1个球,恰好是红球;②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球;(2)某次考试共有6道选择题,每道题所给出的4个选项中,恰有一个是正确的.如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部正确的概率是B.A. B. C.1﹣ D.1﹣.个球,恰好是红球的概率为;;个选项中,恰有一个是正确的概率为,道选择题全部正确的概率是()21.(9分)(2013•南京)某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:(1)理解划线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;(3)该校数学兴趣小组结合调查获取信息,向学校提出了一些建议,如:骑车上学的学生约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化的建议:为了节约和保护环境请同学们尽量不要乘坐私家车(答案不唯一).;22.(8分)(2013•南京)已知不等臂跷跷板AB长4m.如图①,当AB的一端A碰到地面上时,AB与地面的夹角为α;如图②,当AB的另一端B碰到地面时,AB与地面的夹角为β.求跷跷板AB的支撑点O到地面的高度OH.(用含α,β的式子表示)m是23.(8分)(2013•南京)某商场促销方案规定:商场内所有商品按标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额.320元,获得的优惠额为400×(1﹣80%)+30=110(元).(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?(2)如果顾客购买标价不超过800元的商品,要使获得的优惠不少于226元,那么该商品的标记至少为多少元?24.(8分)(2013•南京)小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.(1)小丽驾车的最高速度是60km/h;(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度;(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?∴﹣﹣×××+60×+××+××+××25.(8分)(2013•南京)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与⊙O的位置关系,并说明理由;(2)若AB=9,BC=6.求PC的长.BC=3AM=6r=6r= CE=2r=OM=6﹣BE=2OM=BM=CM=BC=3=6,r=6﹣r=CE=2r=OM=6﹣BE=2OM=,∴,即.26.(9分)(2013•南京)已知二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于点D.①当△ABC的面积等于1时,求a的值;②当△ABC的面积与△ABD的面积相等时,求m的值.),×||=1×∴+am|=×||﹣=0﹣27.(10分)(2013•南京)对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相同,因此△ACB和△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相反,因此△ACB和△A′B′C′互为逆相似.(1)根据图Ⅰ,图Ⅱ和图Ⅲ满足的条件.可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO;③△NQP与△NMQ;其中,互为顺相似的是①;互为逆相似的是②③.(填写所有符合要求的序号).(2)如图③,在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与点A,B,C重合).过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似.请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由.参与本试卷答题和审题的老师有:zhjh;yangwy;lantin;CJX;星期八;HLing;gsls;dbz1018;zjx111;sd2011;ZJX;sks;sjzx;HJJ;caicl(排名不分先后)菁优网2013年8月2日。
2013年江苏省南京市中考数学试卷

2013年江苏省南京市中考数学试卷一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(2分)计算:12﹣7×(﹣4)+8÷(﹣2)的结果是()A.﹣24B.﹣20C.6D.362.(2分)计算a3•(1a)2的结果是()A.a B.a3C.a6D.a93.(2分)设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③3<a<4;④a是18的算术平方根.其中,所有正确说法的序号是()A.①④B.②③C.①②④D.①③④4.(2分)如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是()A.外切B.相交C.内切D.内含5.(2分)在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数y=k2 x的图象没有公共点,则()A.k1+k2<0B.k1+k2>0C.k1k2<0D.k1k2>0 6.(2分)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是()A.B.C.D.二、填空题(本大题共10小题,每小题2分,共20分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)7.(2分)﹣3的相反数是;﹣3的倒数是.8.(2分)计算:√2−√12的结果是.9.(2分)使式子1+1x−1有意义的x的取值范围是.10.(2分)第二届亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13000名青少年志愿者提供服务.将13000用科学记数法表示为.11.(2分)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=.12.(2分)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF ,若菱形ABCD 的边长为2cm ,∠A=120°,则EF= cm .13.(2分)△OAB 是以正多边形相邻的两个顶点A ,B 与它的中心O 为顶点的三角形,若△OAB 的一个内角为70°,则该正多边形的边数为 . 14.(2分)已知如图所示的图形的面积为24,根据图中的条件,可列出方程: .15.(2分)如图,在梯形ABCD 中,AD ∥BC ,AB=DC ,AC 与BD 相交于P .已知A (2,3),B (1,1),D (4,3),则点P 的坐标为( , ).16.(2分)计算(1﹣12−13−14−15)(12+13+14+15+16)﹣(1﹣12−13−14−15﹣16)(12+13+14+15)的结果是 .三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤) 17.(6分)化简(1a−b −ba −b )÷aa+b .18.(6分)解方程:2x x−2=1﹣12−x.19.(8分)如图,在四边形ABCD 中,AB=BC ,对角线BD 平分∠ABC ,P 是BD 上一点,过点P 作PM ⊥AD ,PN ⊥CD ,垂足分别为M ,N .(1)求证:∠ADB=∠CDB ;(2)若∠ADC=90°,求证:四边形MPND 是正方形.20.(8分)(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、绿的球各1个.这些球除颜色外都相同.求下列事件的概率: ①搅匀后从中任意摸出1个球,恰好是红球;②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球;(2)某次考试共有6道选择题,每道题所给出的4个选项中,恰有一个是正确的.如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部正确的概率是 .A.14B.(14)6C.1﹣(14)6D.1﹣(34)6. 21.(9分)某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:(1)理解划线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;(3)该校数学兴趣小组结合调查获取信息,向学校提出了一些建议,如:骑车上学的学生约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化的建议:.22.(8分)已知不等臂跷跷板AB长4m.如图①,当AB的一端A碰到地面上时,AB与地面的夹角为α;如图②,当AB的另一端B碰到地面时,AB与地面的夹角为β.求跷跷板AB的支撑点O到地面的高度OH.(用含α,β的式子表示)23.(8分)某商场促销方案规定:商场内所有商品按标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额.消费金额(元)300﹣400400﹣500500﹣600600﹣700700﹣900…返还金额(元)3060100130150…根据上述促销方案,顾客在该商场购物可以获得双重优惠,例如:若购买标价为400元的商品,则消费金额为320元,获得的优惠额为400×(1﹣80%)+30=110(元).(1)购买一件标价为1000元的商品,顾客获得的优惠额是多少?(2)如果顾客购买标价不超过800元的商品,要使获得的优惠不少于226元,那么该商品的标价至少为多少元?24.(8分)小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.(1)小丽驾车的最高速度是km/h;(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min 时的速度;(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?25.(8分)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC ∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO 并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1)判断直线PC与⊙O的位置关系,并说明理由;(2)若AB=9,BC=6.求PC的长.26.(9分)已知二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点.(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于D点.①当△ABC的面积为1时,求a的值.②当△ABC的面积与△ABD的面积相等时,求m的值.27.(10分)对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相同,因此△ACB和△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相反,因此△ACB和△A′B′C′互为逆相似.(1)根据图Ⅰ,图Ⅱ和图Ⅲ满足的条件.可得下列三对相似三角形:①△ADE 与△ABC;②△GHO与△KFO;③△NQP与△NMQ;其中,互为顺相似的是;互为逆相似的是.(填写所有符合要求的序号).(2)如图③,在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与点A,B,C重合).过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似.请根据点P的不同位置,探索过点P的截线的情形,画出图形并说明截线满足的条件,不必说明理由.2013年江苏省南京市中考数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.【解答】解:原式=12+28﹣4=36.故选:D.2.【解答】解:原式=a3•1a2=a,故选:A.3.【解答】解:∵边长为3的正方形的对角线长为a,∴a=√32+32=√18=3√2.①a=3√2是无理数,说法正确;②a可以用数轴上的一个点来表示,说法正确;③∵16<18<25,4<√18<5,即4<a<5,说法错误;④a是18的算术平方根,说法正确.所以说法正确的有①②④.故选:C.4.【解答】解:∵O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动,∴7s后两圆的圆心距为:1cm,此时两圆的半径的差为:3﹣2=1cm,∴此时内切,∴移动过程中没有内含这种位置关系,故选:D.5.【解答】解:∵正比例函数y=k1x的图象与反比例函数y=k2x的图象没有公共点,∴k1与k2异号,即k1•k2<0.故选:C.6.【解答】解:选项A和C带图案的一个面是底面,不能折叠成原几何体的形式;选项B能折叠成原几何体的形式;选项D折叠后下面带三角形的面与原几何体中的位置不同.故选:B.二、填空题(本大题共10小题,每小题2分,共20分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)7.【解答】解:﹣3的相反数是3;﹣3的倒数是﹣1 3.故答案是:3,﹣1 3.8.【解答】解:原式=3√22﹣√22=√2.故答案为:√2.9.【解答】解:由题意知,分母x﹣1≠0,即x≠1时,式子1+1x−1有意义.故答案为:x≠1.10.【解答】解:13000=1.3×104.故答案是:1.3×104.11.【解答】解:如图,∵四边形ABCD为矩形,∴∠B=∠D=∠BAD=90°,∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,∴∠D′=∠D=90°,∠4=α,∵∠1=∠2=110°,∴∠3=360°﹣90°﹣90°﹣110°=70°,∴∠4=90°﹣70°=20°,∴∠α=20°.故答案为:20°.12.【解答】解:连接BD、AC,∵四边形ABCD是菱形,∴AC⊥BD,AC平分∠BAD,∵∠BAD=120°,∴∠BAC=60°,∴∠ABO=90°﹣60°=30°,∵∠AOB=90°,∴AO=12AB=12×2=1,由勾股定理得:BO=DO=√3,∵A沿EF折叠与O重合,∴EF⊥AC,EF平分AO,∵AC⊥BD,∴EF∥BD,∴EF为△ABD的中位线,∴EF=12BD=12×(√3+√3)=√3,故答案为:√3.13.【解答】解:当∠OAB=70°时,∠AOB=40°,则多边形的边数是:360÷40=9;当∠AOB=70°时,360÷70结果不是整数,故不符合条件.故答案是:9.14.【解答】解:根据题意得:(x+1)2﹣1=24,即:(x+1)2=25.故答案为:(x+1)2=25.15.【解答】解:过A 作AM ⊥x 轴与M ,交BC 于N ,过P 作PE ⊥x 轴与E ,交BC 于F , ∵AD ∥BC ,A (2,3),B (1,1),D (4,3),∴AD ∥BC ∥x 轴,AM=3,MN=EF=1,AN=3﹣1=2,AD=4﹣2=2,BN=2﹣1=1, ∴C 的坐标是(5,1),BC=5﹣1=4,CN=4﹣1=3, ∵AD ∥BC , ∴△APD ∽△CPB ,∴AD BC =AP PC =24=12, ∴CP AC =23∵AM ⊥x 轴,PE ⊥x 轴, ∴AM ∥PE , ∴△CPF ∽△CAN ,∴PF AN =CF CN =CP CA =23, ∵AN=2,CN=3,∴PF=43,PE=43+1=73,CF=2,BF=2,∴P 的坐标是(3,73),故答案为:3,73.16.【解答】解:设a=1﹣12﹣13﹣14﹣15,b=12+13+14+15,则原式=a (b +16)﹣(a ﹣16)•b=ab +16a ﹣ab +16b=16(a +b ), ∵a +b=1﹣12﹣13﹣14﹣15+12+13+14+15=1,∴原式=16.故答案为:16.三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤) 17.【解答】解:原式=a+b−b (a+b)(a−b)•a+b a=a (a+b)(a−b)•a+b a =1a−b.18.【解答】解:去分母得:2x=x ﹣2+1, 移项合并得:x=﹣1,经检验x=﹣1是分式方程的解. 19.【解答】证明:(1)∵对角线BD 平分∠ABC , ∴∠ABD=∠CBD , 在△ABD 和△CBD 中, {AB =CB∠ABD =∠CBD BD =BD, ∴△ABD ≌△CBD (SAS ), ∴∠ADB=∠CDB ;(2)∵PM ⊥AD ,PN ⊥CD , ∴∠PMD=∠PND=90°, ∵∠ADC=90°,∴四边形MPND 是矩形,∵∠ADB=∠CDB,∴∠ADB=45°∴PM=MD,∴四边形MPND是正方形.20.【解答】解:(1)①搅匀后从中任意摸出1个球,恰好是红球的概率为1 4;②列表如下:红黄蓝绿红(红,红)(黄,红)(蓝,红)(绿,红)黄(红,黄)(黄,黄)(蓝,黄)(绿,黄)蓝(红,蓝)(黄,蓝)(蓝,蓝)(绿,蓝)绿(红,绿)(黄,绿)(蓝,绿)(绿,绿)所有等可能的情况数有16种,其中两次都为红球的情况数有1种,则P=116;(2)每道题所给出的4个选项中,恰有一个是正确的概率为1 4,则他6道选择题全部正确的概率是(14)6.故选B.21.【解答】解:(1)不合理,因为如果150名学生全部在同一个年级抽取,这样抽取的学生不具有随机性,比较片面,所以这样的抽样不合理;(2)步行人数为:2000×10%=200(人),骑车的人数为:2000×34%=680(人),乘公共汽车人数为:2000×30%=600(人),乘私家车的人数为:2000×20%=400(人),乘其它交通工具得人数为:2000×6%=120(人),如图所示:;(3)为了节约和保护环境请同学们尽量不要乘坐私家车(答案不唯一).22.【解答】解:依题意有:AO=OH÷sinα,BO=OH÷sinβ,AO+BO=OH÷sinα+OH÷sinβ,即OH÷sinα+OH÷sinβ=4m,则OH=4sinα⋅sinβsinα+sinβm.故跷跷板AB的支撑点O到地面的高度OH是4sinα⋅sinβsinα+sinβ(m).23.【解答】解:(1)标价为1000元的商品按80%的价格出售,消费金额为800元,消费金额800元在700﹣900之间,返还金额为150元,顾客获得的优惠额是:1000×(1﹣80%)+150=350(元); 答:顾客获得的优惠额是350元;(2)设该商品的标价为x 元.①当80%x ≤500,即x ≤625时,顾客获得的优惠额不超过625×(1﹣80%)+60=185<226;②当500<80%x ≤600,即625<x ≤750时, 顾客获得的优惠额:(1﹣80%)x +100≥226, 解得x ≥630. 即:630≤x ≤750.③当600<80%x ≤700,即750<x ≤875时,因为顾客购买标价不超过800元,所以750<x ≤800,顾客获得的优惠额:750×(1﹣80%)+130=280>226.综上,顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为630元. 答:该商品的标价至少为630元. 24.【解答】解:(1)由图可知,第10min 到20min 之间的速度最高,为60km/h ;(2)当20≤x ≤30时,设y=kx +b (k ≠0), ∵函数图象经过点(20,60),(30,24), ∴{20k +b =6030k +b =24,解得{k =−185b =132, 所以,y 与x 的关系式为y=﹣185x +132, 当x=22时,y=﹣185×22+132=52.8km/h ;(3)行驶的总路程=12×(12+0)×560+12×(12+60)×10−560+60×20−1060+12×(60+24)×30−2060+12×(24+48)×560+48×45−3560+12×(48+0)×560,=12+3+10+7+3+8+2, =33.5km ,∵汽车每行驶100km 耗油10L ,∴小丽驾车从甲地到乙地共耗油:33.5×10100=3.35升.25.【解答】解:(1)PC 与圆O 相切,理由为: 过C 点作直径CE ,连接EB ,如图, ∵CE 为直径,∴∠EBC=90°,即∠E +∠BCE=90°, ∵AB ∥DC , ∴∠ACD=∠BAC ,∵∠BAC=∠E ,∠BCP=∠ACD . ∴∠E=∠BCP ,∴∠BCP +∠BCE=90°,即∠PCE=90°, ∴CE ⊥PC , ∴PC 与圆O 相切;(2)∵AD 是⊙O 的切线,切点为A , ∴OA ⊥AD , ∵BC ∥AD , ∴AM ⊥BC ,∴BM=CM=12BC=3,∴AC=AB=9,在Rt △AMC 中,AM=√AC 2−CM 2=6√2,设⊙O 的半径为r ,则OC=r ,OM=AM ﹣r=6√2﹣r , 在Rt △OCM中,OM 2+CM 2=OC 2,即32+(6√2﹣r )2=r 2,解得r=27√28,∴CE=2r=27√24,OM=6√2﹣27√28=21√28,∴BE=2OM=21√24,∵∠E=∠MCP ,∴Rt △PCM ∽Rt △CEB ,∴PC CE =CM EB , 即27√24=21√24,∴PC=277.26.【解答】(1)证明:令y=0,a (x ﹣m )2﹣a (x ﹣m )=0, △=(﹣a )2﹣4a ×0=a 2, ∵a ≠0, ∴a 2>0,∴不论a 与m 为何值,该函数的图象与x 轴总有两个公共点;(2)解:①y=0,则a (x ﹣m )2﹣a (x ﹣m )=a (x ﹣m )(x ﹣m ﹣1)=0, 解得x 1=m ,x 2=m +1, ∴AB=(m +1)﹣m=1,y=a (x ﹣m )2﹣a (x ﹣m )=a (x ﹣m ﹣12)2﹣a 4,△ABC 的面积=12×1×|﹣a4|=1,解得a=±8;②x=0时,y=a (0﹣m )2﹣a (0﹣m )=am 2+am , 所以,点D 的坐标为(0,am 2+am ),△ABD 的面积=12×1×|am 2+am |,∵△ABC 的面积与△ABD 的面积相等,∴12×1×|am 2+am |=12×1×|﹣a 4|, 整理得,m 2+m ﹣14=0或m 2+m +14=0,解得m=−1±√22或m=﹣12.27.【解答】解:(1)互为顺相似的是 ①②;互为逆相似的是 ③;(2)根据点P 在△ABC 边上的位置分为以下三种情况:第一种情况:如图①,点P 在BC (不含点B 、C )上,过点P 只能画出2条截线PQ 1、PQ 2,分别使∠CPQ 1=∠A ,∠BPQ 2=∠A ,此时△PQ 1C 、△PBQ 2都与△ABC 互为逆相似.第二种情况:如图②,点P 在AC (不含点A 、C )上,过点B 作∠CBM=∠A ,BM 交AC 于点M .当点P 在AM (不含点M )上时,过点P 1只能画出1条截线P 1Q ,使∠AP 1Q=∠ABC ,此时△AP 1Q 与△ABC 互为逆相似;当点P 在CM 上时,过点P 2只能画出2条截线P 2Q 1、P 2Q 2,分别使∠AP 2Q 1=∠ABC ,∠CP 2Q 2=∠ABC ,此时△AP 2Q 1、△Q 2P 2C 都与△ABC 互为逆相似. 第三种情况:如图③,点P 在AB (不含点A 、B )上,过点C 作∠BCD=∠A ,∠ACE=∠B ,CD 、CE 分别交AB 于点D 、E .当点P 在AD (不含点D )上时,过点P 只能画出1条截线P 1Q ,使∠AP 1Q=∠ACB ,此时△AQP 1与△ABC 互为逆相似;当点P在DE上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使∠AP2Q1=∠ACB,∠BP2Q2=∠BCA,此时△AQ1P2、△Q2BP2都与△ABC互为逆相似;当点P在BE(不含点E)上时,过点P3只能画出1条截线P3Q′,使∠BP3Q′=∠BCA,此时△Q′BP3与△ABC互为逆相似.。
南京市2013年中考数学试卷

南京市2013年中考数学试卷 (满分:120分 时间:120分钟)一、 选择题(本大题共6小题,每小题2分,共12分) 1. 计算12-7×(-4)+8÷(-2)的结果是( )A. -24B. -20C. 6D. 36 2. 计算a 3·⎝⎛⎭⎫1a 2的结果是( )A. aB. a 5C. a 6D. a 93. 设边长为3的正方形的对角线长为a.下列关于a 的四种说法:① a 是无理数;② a 可以用数轴上的一个点来表示;③ 3<a<4;④ a 是18的算术平方根.其中所有正确说法的序号是 ( )A. ①④B. ②③C. ①②④D. ①③④4. 如图,⊙O 1、⊙O 2的圆心O 1、O 2在直线l 上,⊙O 1的半径为2 cm ,⊙O 2的半径为3 cm ,O 1O 2=8 cm. ⊙O 1以1 cm/s 的速度沿直线l 向右运动,7 s 后停止运动.在此过程中,⊙O 1与⊙O 2没有出现的位置关系是( )A. 外切B. 相交C. 内切D. 内含第4题 第6题5. 在同一直角坐标系中,若正比例函数y =k 1x 的图象与反比例函数 y =k 2x 的图象没有公共点,则( )A. k 1+k 2<0B. k 1+k 2>0C. k 1k 2<0D. k 1k 2>06. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是( )A B C D二、 填空题(本大题共10小题,每小题2分,共20分)7. -3的相反数是________;-3的倒数是________. 8. 计算32-12的结果是________. 9. 使式子1+1x -1有意义的x 的取值范围是________.10. 第二届亚洲青年运动会将于2013年8月16日至24日在南京举办,在此期间约有13 000名青少年志愿者提供服务,将13 000用科学记数法表示为________.11. 如图,将矩形ABCD 绕点A 顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则∠α=________°.第11题 第12题12. 如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF.若菱形ABCD 的边长为2 cm ,∠A =120°,则EF =________cm.13. △OAB 是以正多边形相邻的两个顶点A 、B 与它的中心O 为顶点的三角形.若△OAB 的一个内角为70°,则该正多边形的边数为________.14. 如图所示的图形的面积为24,根据图中的条件,可列出方程:________________.第14题 第15题15. 如图,在梯形ABCD 中,AD ∥BC ,AB =DC ,AC 与BD 相交于点P.已知A(2,3),B(1,1),D(4,3),则点P 的坐标为(____,____).16. 计算⎝⎛⎭⎫1-12-13-14-15⎝⎛⎭⎫12+13+14+15+16-(1-12-13-14-15-16)⎝⎛⎭⎫12+13+14+15的结果是________.三、 解答题(本大题共11小题,共88分) 17. (本小题满分6分)化简⎝⎛⎭⎫1a -b -b a 2-b 2÷aa +b .18. (本小题满分6分)解方程2xx-2=1-12-x.19. (本小题满分8分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.(1) 求证:∠ADB=∠CDB;(2) 若∠ADC=90°,求证:四边形MPND是正方形.第19题20. (本小题满分8分)(1) 一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个,这些球除颜色外都相同.求下面事件的概率:①搅匀后从中任意摸出1个球,恰好是红球;②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球;(2) 某次考试有6道选择题,每道题所给出的4个选项中,恰有一项是正确的.如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部选择正确的概率是()A. 14 B. ⎝⎛⎭⎫146C. 1-⎝⎛⎭⎫146D. 1-⎝⎛⎭⎫34621. (本小题满分9分)某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:正正正正正正正正正正正某校150名学生上学方式频数分布表某校150名学生上学方式扇形统计图第21题①(1) 理解划线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,那么这样的抽样是否合理?请说明理由;(2) 根据抽样调查的结果,将估计出的全校2 000名学生上学方式的情况绘制成条形统计图;某校2 000名学生上学方式条形统计图第21题②(3) 该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议.如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地.请你结合上述统计的全过程,再提出一条合理化建议:____________________.22. (本小题满分8分)已知不等臂跷跷板AB长4 m.如图①,当AB的一端A碰到地面时,AB与地面的夹角为α;如图②,当AB的另一端B碰到地面时,AB与地面的夹角为β.求跷跷板AB的支撑点O到地面的高度OH(用含α、β的式子表示).第22题23. (本小题满分8分)某商场促销方案规定:商场内所有商品按标价的80%出售,同时,当顾客在商场内消费满一定金额后,按下表获得相应的返还金额.注:300~400表示消费金额大于300元且小于或等于400元,其他类同.根据上述促销方案,顾客在该商场购物可以获得双重优惠.例如,若购买标价为400元的商品,则消费金额为320元,获得的优惠额为400×(1-80%)+30=110(元).(1) 购买一件标价为1 000元的商品,顾客获得的优惠额是多少?(2) 如果顾客购买标价不超过800元的商品,要使获得的优惠额不少于226元,那么该商品的标价至少为多少元?24. (本小题满分8分)小丽驾车从甲地到乙地.设她出发第x min 时的速度为y km/h ,图中的折线表示她在整个驾车过程中y 与x 之间的函数关系. (1) 小丽驾车的最高速度是________km/h ; (2) 当20≤x ≤30时,求y 与x 之间的函数关系式,并求出小丽出发第22 min 时的速度; (3) 如果汽车每行驶100 km 耗油10 L ,那么小丽驾车从甲地到乙地共耗油多少升?第24题方法指导如果物体的运动速度随着时间均匀增加(或减少),那么其在某个时间段内的平均速度为该时间段开始时刻的速度与结束时刻的速度的平均数.例如,由图象可知,第 5 min 到第10 min 汽车的速度随着时间均匀增加,因此汽车在该时间段内的平均速度为12+602=36(km/h).该时间段行驶的路程为36×10-560=3(km).25. (本小题满分8分)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.(1) 判断直线PC与⊙O的位置关系,并说明理由;(2) 若AB=9,BC=6,求PC的长.第25题26. (本小题满分9分)已知二次函数y=a(x-m)2-a(x-m)(a、m为常数,且a≠0).(1) 求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;(2) 设该函数的图象的顶点为C,与x轴交于A、B两点,与y轴交于点D.①当△ABC的面积等于1时,求a的值;②当△ABC的面积与△ABD的面积相等时,求m的值.27. (本小题满分10分)对于两个相似三角形,如果沿周界按对应点顺序环绕的方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似.例如,如图①,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相同,因此△ABC 与△A′B′C′互为顺相似;如图②,△ABC∽△A′B′C′,且沿周界ABCA与A′B′C′A′环绕的方向相反,因此△ABC与△A′B′C′互为逆相似.第27题(1) 根据图③、图④和图⑤满足的条件,可得下列三对相似三角形:①△ADE与△ABC;②△GHO与△KFO; ③△NQP与△NMQ.其中,互为顺相似的是________;互为逆相似的是________(填写所有符合要求的序号);第27题(2) 如图⑥,在锐角三角形ABC 中,∠A<∠B<∠C ,点P 在△ABC 的边上(不与点A 、B 、C 重合).过点P 画直线截△ABC ,使截得的一个三角形与△ABC 互为逆相似.请根据点P 的不同位置,探索过点P 的截线的情形,画出图形并说明截线满足的条件,不必说明理由.第27题⑥南京市2013年中考数学试卷1. D [解析]按照有理数混合运算的顺序计算,原式=12-(-28)+(-4)=12+28-4=36.2. A [解析]先将非同底数幂相乘形式化为同底数幂相乘的形式,再利用幂的运算法则进行计算,原式=a 3·a -2=a 3+(-2)=a.3. C [解析]由勾股定理得a =32+32=18=32,根据无理数、算术平方根的概念知①④正确;由实数与数轴上的点之间的关系知②正确;∵ 4=16,18>16,即a>4,∴ ③错误.4. D [解析]从两圆相切入手分析,当时间t =3 s 时,O 1O 2=5,两圆外切;当t =7 s 时,O 1O 2=1,两圆内切;∴ 当0<t<3时,两圆外离,当3<t<7时,两圆相交.5. C [解析]联立y =k 1x 与y =k 2x ,消去y ,整理得x 2=k2k 1,本题中两函数图象没有公共点相当于上述关于x 的方程没有实数解,∴k 2k 1<0,即k 1k 2<0. 6. B [解析]根据涂有颜色的正方形与三角形相接,排除选项A 、C ,考虑到选项D 中的四个小三角形不能折叠成正四棱锥,排除选项D.动手操作是解答这类试题的最佳方案(本题从“平面图形→立体图形”).7. 3 -13[解析]直接根据相反数、倒数的概念解题.8. 2 [解析]先化简二次根式,再合并同类二次根式.原式=322-122=⎝⎛⎭⎫32-122=2.9. x ≠1 [解析]只要满足式子1x -1有意义即可,而分式有意义,必须分母不为0,即x -1≠0,解得x ≠1.10. 1.3×104 [解析]科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.当原数的绝对值大于1时, n 的值等于原数的整数位数减去1.11. 20 [解析]设BC 与C′D′相交于点E ,根据四边形ABED′的内角和为360°及对顶角相等,得∠BAD′=360°-90°×2-110°=70°,∴ 旋转角∠BAB′=90°-70°=20°.12. 3 [解析]连接AC 、BD ,则交点为点O ,根据菱形的性质得,AC 与BD 互相垂直平分,AC 平分∠BAD.∴ 在 Rt △AOB 中,OB =2×sin 60°=3,BD =2OB =2 3.由折叠得EF 为△ABD 的中位线,∴ EF =12BD = 3 cm.13. 9 [解析]根据正多边形的性质得OA =OB.若∠AOB =70°,则正多边形的边数为360°÷70°=367,不合题意,舍去;若∠ABO =∠BAO =70°,则∠AOB =40°,此时正多边形的边数为360°÷40°=9.14. 答案不唯一,如(x +1)2=25 [解析]将图形的右上角补全成一个小正方形,则它的边长为(x +1)-x =1,由题意得(x +1)2-12=24,即(x +1)2=25.15. ⎝⎛⎭⎫3,73 [解析]根据题意得,梯形ABCD 是等腰梯形,分别过A 、D 作AE ⊥BC ,DF ⊥BC ,垂足分别为E 、F ,则BE =CF =2-1=1,EF =AD =4-2=2,∴ 点C 的坐标为(5,1).利用待定系数法得直线AC 、BD 的解析式分别为 y =-23x +133、y =23x +13,联立上述解析式构造二元一次方程组,得P ⎝⎛⎭⎫3,73. 16. 16 [解析]本题采用“字母替代数字”方法简化计算过程.设12+13+14+15=x ,则原式=(1-x)⎝⎛⎭⎫x +16-⎝⎛⎭⎫1-x -16x =x +16-x 2-16x -⎝⎛⎭⎫56x -x 2=16. 17. [解析]先将括号中两项通分后利用同分母分式的减法法则计算,最后利用除以一个数等于乘以这个数的倒数将分式除法运算化为分式乘法运算,约分可得结果.解:原式=(a +b )-b (a +b )(a -b )·a +b a =a (a +b )(a -b )·a +b a =1a -b.18. [解析]去分母将分式方程转化为整式方程,求出整式方程的解,代入去分母时的最简公分母计算,看结果是否等于0,即可检验得到原分式方程的解.解:方程两边同乘x -2,得2x =x -2+1,解这个方程,得x =-1.检验:当x =-1时,x -2≠0,∴ x =-1是原方程的解.19. [解析](1) 利用“SAS”证明△ABD ≌△CBD ;(2) 先说明四边形MPND 是矩形和PM =PN ,再利用“有一组邻边相等的矩形是正方形”证明四边形MPND 是正方形.解:(1) ∵ BD 平分∠ABC ,∴ ∠ABD =∠CBD.又 ∵ BA =BC ,BD =BD ,∴ △ABD ≌△CBD.∴ ∠ADB =∠CDB ;(2) ∵ PM ⊥AD ,PN ⊥CD ,∴ ∠PMD =∠PND =90°.又 ∵ ∠ADC =90°,∴ 四边形MPND 是矩形.∵ ∠ADB =∠CDB ,PM ⊥AD ,PN ⊥CD ,∴ PM =PN.∴ 四边形MPND 是正方形.20. [解析](1) ① 直接利用概率的计算公式计算;② 利用列表法或画树状图法求出两次摸出球颜色的所有可能结果,观察其中“两次都是红球”的结果数;(2) 本小题所求概率与按照(1)摸球规则,连续6次摸红球的概率相同.解:(1) ① 搅匀后从中任意摸出1个球,所有可能出现的结果有:红、黄、蓝、白,共有4种,它们出现的可能性相同.所有的结果中,满足“恰好是红球”(记为事件A)的结果只有1种,∴ P(A)=14;② 搅匀后从中任意摸出1个球,记下颜色后放回袋子中并搅匀,再从中任意摸出1个球,所有可能出现的结果有:(红,红)、(红,黄)、(红,蓝)、(红,白)、(黄,红)、(黄,黄)、(黄,蓝)、(黄,白)、(蓝,红)、(蓝,黄)、(蓝,蓝)、(蓝,白)、(白,红)、(白,黄)、(白,蓝)、(白,白),共有16种,它们出现的可能性相同. 所有的结果中,满足“两次都是红球”(记为事件B)的结果只有1种,∴ P(B)=116;(2) B.21. [解析](1) 抽样调查过程中,样本必须具有代表性,假如在同一个年级抽取150名学生,就不能反映全校学生的上学方式;(2) 根据抽样调查中扇形统计图内各种上学方式的百分比求出全校学生采用各种不同上学方式的人数,再画出条形统计图;(3) 本题答案不唯一,可针对人数比较集中的上学方式提一些建议.解:(1) 不合理.如果150名学生全部在同一个年级抽取,那么全校每个学生被抽到的机会不相等,样本不具有代表性;(2) 如图:某校2 000名学生上学方式条形统计图第21题(3) 答案不唯一,如乘私家车上学的学生约400人,建议学校与交通部门协商安排停车区域.22. [解析]在Rt △AHO 、Rt △BHO 中利用α、β的三角函数值与OH 分别表示OA 、OB 的长度,结合AB =OA +OB =4 m 构造关于OH 的方程,求解上述字母方程即可.解:在Rt △AHO 中,sin α=OH OA ,∴ OA =OH sin α.在Rt △BHO 中,sin β=OH OB ,∴ OB =OHsin β.∵ AB=4 m ,∴ OA +OB =4 m ,即OH sin α+OH sin β=4.∴ OH =4sin αsin βsin α+sin β(m).23. [解析](1) 模仿题目条件中给出的范例计算顾客获得的优惠额;(2) 从销售方案的表格中消费金额的几个极端情况入手,判断优惠额不少于226元时消费金额的大致范围,从而建立满足题意的一元一次不等式解题.解:(1) 购买一件标价为1 000元的商品,消费金额为1 000×80%=800(元),顾客获得的优惠额为1 000×(1-80%)+150=350(元);(2) 设该商品的标价为x 元,当消费金额为400元,即标价x =400÷80%=500(元)时,优惠额为500×(1-80%)+30=130(元);当消费金额为500元,即标价x =500÷80%=625(元)时,优惠额为625×(1-80%)+60=185(元);当消费金额为600元,即标价x =600÷80%=750(元)时,优惠额为750×(1-80%)+100=250(元).∴ x 的范围是625<x ≤750,消费金额在500~600元这一档次,根据题意,得(1-80%)x +100≥226,解得x ≥630,因此满足题意的商品的标价至少为630元.24. [解析](1) 驾车的最高速度指y 与x 之间的函数图象中y 的最大值;(2) 根据点C 、D 的两组y 与x 之间的对应值,利用待定系数法求解,再求当x =22时,y 的值;(3) 根据题中图象可知,甲、乙之间的路程分为7段小路程之和,其中BC 段、EF 段为匀速运动,直接利用“速度×时间”求解,另外5段需要根据阅读材料中“方法指导”先求出平均速度,再乘以时间得出相应的路程,最后由总路程与平均耗油量之积求出小丽驾车从甲地到乙地的总耗油量. 解答本题还需注意单位统一.解:(1) 60;(2) 当20≤x ≤30时,设y 与x 之间的函数关系式为y =kx +b.根据题意,当x =20时,y =60;当x =30时,y =24.∴ ⎩⎪⎨⎪⎧20k +b =60,30k +b =24.解得⎩⎪⎨⎪⎧k =-3.6,b =132.∴ y 与x 之间的函数关系式为y =-3.6x +132.当x =22时,y =-3.6×22+132=52.8.即小丽出发第22 min 时的速度为52.8 km/h ;(3) 小丽驾车从甲地到乙地行驶的路程为0+122×560+12+602×560+60×1060+60+242×1060+24+482×560+48×1060+48+02×560=33.5(km).∴ 小丽驾车从甲地到乙地共耗油33.5×10100=3.35(L). 25. [解析](1) 连接OC ,由AD 是⊙O 的切线得AP ⊥AD ,结合平行线的性质、垂径定理得∠ACD =∠BAC =∠MOC ,因此∠OCM +∠BCP =90°,即OC ⊥PC ,∴ 直线PC 与⊙O 相切;(2) 由垂径定理得MC =12BC =3,在Rt △AMC 中,利用勾股定理求出AM =6 2.设⊙O 半径为r ,在Rt △OMC 中,利用勾股定理构造关于r 的方程求出r 的值,最后证△OMC ∽△OCP 得OM OC =CM PC,进而求出PC 的值.解:(1) 直线PC 与⊙O 相切. 如图,连接OC.∵ AD 是⊙O 的切线,∴ AD ⊥OA ,即∠OAD =90°.∵ BC ∥AD ,∴ ∠OMC =180°-∠OAD =90°,即OM ⊥BC.∴ MC =MB.∴ AB =AC ,∠MAB =∠MAC.∴ ∠BAC =2∠MAC.又∵ ∠MOC =2∠MAC ,∴ ∠MOC =∠BAC.∵ AB ∥CD ,∴ ∠BAC =∠ACD.∴ ∠MOC =∠ACD.又∵ ∠BCP =∠ACD ,∴ ∠MOC =∠BCP.∵ ∠MOC +∠OCM =90°,∴ ∠BCP +∠OCM =90°.∴ ∠PCO =90°,即PC ⊥OC.又∵ 点C 在⊙O 上,∴ 直线PC 与⊙O 相切;(2) 在 Rt △AMC 中,∠AMC =90°,AC =AB =9,MC =12BC =3,由勾股定理,得AM =AC 2-MC 2=92-32=6 2.设⊙O 的半径为r.在Rt △OMC 中,∠OMC =90°,OM =AM -AO =62-r ,MC =3,OC =r ,由勾股定理,得OM 2+MC 2=OC 2,即(62-r)2+32=r 2.解得r =2782.在△OMC 和△OCP 中,∵ ∠OMC =∠OCP ,∠MOC =∠COP ,∴ △OMC ∽△OCP.∴ OM OC =CM PC ,即62-27822782=3PC .∴ PC =277. 第25题26. [解析](1) 令y =0,得关于x 的一元二次方程,证该方程的根的判别式大于0;(2) ① 令y =0,利用因式分解法可以解出该方程的2个根,即可求出线段AB 的长,将二次函数的一般式配方成顶点式,得到顶点C 的坐标,点C 到AB 的距离等于点C 纵坐标的绝对值,再利用S △ABC =1构造关于a 的方程求解;② 令x =0,写出点D 的坐标,点D 到AB 的距离等于点D 纵坐标的绝对值,利用S △ABC =S △ABD 构造关于a 、m 的方程,在注意绝对值的双重符号特征基础上,两边同除以|a|得关于m 的方程,解之即得m 的值.解:(1) y =a(x -m)2-a(x -m)=ax 2-(2am +a)x +am 2+am.∵ 当a ≠0时,[-(2am +a)]2-4a(am 2+am)=a 2>0.∴ 方程ax 2-(2am +a)x +am 2+am =0有两个不相等的实数根.因此不论a 与m 为何值,该函数的图象与x 轴总有两个公共点;(2) ① y =a(x -m)2-a(x -m)=⎝⎛⎭⎫x -2m +122-a 4,∴ 点C 的坐标为⎝⎛⎭⎫2m +12,-a 4.当y =0时,a(x -m)2-a(x -m)=0.解得x 1=m ,x 2=m +1.∴ AB =(m +1)-m =1.当△ABC 的面积等于1时,12×1×⎪⎪⎪⎪-a 4=1.即12×1×⎝⎛⎭⎫-a 4=1或12×1×a 4=1.解得a =-8或a =8;② 当x =0时,y =am 2+am ,∴ 点D 的坐标为(0,am 2+am).当△ABC 的面积与△ABD 的面积相等时,12×1×⎪⎪⎪⎪-a 4=12×1×|am 2+am|.即12×1×⎝⎛⎭⎫-a 4=12×1×(am 2+am)或12×1×a 4=12×1×(am 2+am).解得m =-12或m =-1-22或m =-1+22. 27. [解析](1) 根据“互为顺相似”、“互为逆相似”的定义,模仿条件中例子进行判断,注意环绕方向顺时针、逆时针两种;(2) 首先根据“点P 在△ABC 的边上”分三种情况讨论,其次要关注“在锐角三角形ABC 中,∠A<∠B<∠C ”对过点P 的截线条数的影响.解:(1) ①② ③;(2) 根据点P 在△ABC 边上的位置分为以下三种情况:情况一:如图①,点P 在BC(不含点B 、C)上,过点P 只能画出2条截线PQ 1、PQ 2,分别使∠CPQ 1=∠A ,∠BPQ 2=∠A ,此时△PQ 1C 、△PBQ 2都与△ABC 互为逆相似.情况二:如图②,点P 在AC(不含点A 、C)上,过点B 作∠CBM =∠A ,BM 交AC 于点M.当点P 在AM(不含点M)上时,过点P 1只能画出1条截线P 1Q ,使∠AP 1Q =∠ABC ,此时△AP 1Q 与△ABC 互为逆相似;当点P 在CM 上时,过点P 2只能画出2条截线P 2Q 1、P 2Q 2,分别使∠AP 2Q 1=∠ABC ,∠CP 2Q 2=∠ABC ,此时△AP 2Q 1、△Q 2P 2C 都与△ABC 互为逆相似.情况三:如图③,点P 在AB(不含点A 、B)上,过点C 作∠BCD =∠A ,∠ACE =∠B ,CD 、CE 分别交AB 于点D 、E.当点P 在AD(不含点D)上时,过点P 1只能画出1条截线P 1Q ,使∠AQP 1=∠ABC ,此时△AQP 1与△ABC 互为逆相似;当点P 在DE 上时,过点P 2只能画出2条截线P 2Q 1、P 2Q 2,分别使∠AP 2Q 1=∠ACB ,∠BP 2Q 2=∠BCA ,此时△AQ 1P 2、△Q 2BP 2都与△ABC 互为逆相似;当点P 在BE(不含点E)上时,过点P 3只能画出1条截线P 3Q ′,使∠BP 3Q ′=∠BCA ,此时△Q′BP 3与△ABC 互为逆相似.第27题。
