1-2介质的电磁性质
媒质的电磁性质和边界条件

磁导率
表示物质在磁场中导磁能力的物理量,单位为亨利/米(H/m)。
磁导
表示磁场中物质磁导能力的物理量,单位为亨利(H)。
电容率和电感率
电容率
表示电场中物质储存电荷能力的物理 量,单位为法拉/米(F/m)。
电感率
表示磁场中物质储存磁能能力的物理 量,单位为亨利/米(H/m)。
介电常数和磁导率
要点一
介电常数和磁导率的应用案例
介电常数:表示电介质极化程度的物 理量,单位为法拉(F)。
磁导率:表示磁性材料对磁场的影响 能力的物理量,单位为亨利(H)。
应用案例:在电磁波传播和微波工程 中,介电常数和磁导率的应用十分重 要。介电常数决定了电磁波在介质中 的传播速度和波长,而磁导率则影响 微波器件的性能。例如,在天线设计 和微波传输线中,需要选择具有适当 介电常数和磁导率的材料以确保电磁 波的正常传播和有效辐射。此外,介 电常数和磁导率的变化还可以用于制 造电磁波吸收材料和隐身技术等。
THANKS FOR WATCHING
感谢您的观看
06 结论
研究成果总结
媒质的电磁性质对电磁波的传播和散射具有重 要影响,研究媒质的电磁性质有助于深入理解 电磁波与物质相互作用的过程。
边界条件是描述媒质交界处电磁场行为的条件, 对于电磁波的传播和散射具有关键作用。
不同媒质的电磁性质和边界条件会导致电磁波 传播和散射的差异,这在实际应用中具有重要 的意义。
同一媒质间的边界条件
01
在同一媒质中,由于存在不均匀性或异常情况,电磁波的传播 也会受到限制或影响。
02
同一媒质间的边界条件描述了波在媒质中的传播行为,如吸收、
散射、折射等。
这些边界条件通常由物理定律和数学公式来描述,如波动方程、
介质的极化和介电常数

介质的极化和介电常数介质是指具有一定的电导率、介电常数、介磁常数和磁导率的物质,因此,在电磁学中,介质起着非常重要的作用。
介质的极化和介电常数是介质的两个重要性质,对于了解介质的性质和在电磁学应用中起着非常重要的作用。
一、介质的极化介质的极化是指当电场作用于介质时,介质中的分子或离子会发生定向排列,使得介质不再是电中性的状态。
介质中正负电荷的分离称为极化。
1.取向极化介质中的分子或离子具有磁矩或偶极矩,当外加电场作用时,它们会在外力的作用下发生旋转,并与电场方向调整一致而产生极化。
这种极化称为取向极化,它是介电常数与频率有关的一个主要因素。
2.电子云极化电子具有电荷,它在外电场作用下会产生势能,电子云会向外扩散,然后与电场相反的方向移动,形成极化电荷。
因为电子云的大小不一,电子云极化是介电常数与频率有关的另一个重要影响。
3.离子极化在某些情况下,例如在液态和熔融状态下,介质分子可以发生电离或掉电子,从而产生离子极化。
离子极化主要与介质的物理状态、化学结构和温度有关。
二、介电常数介电常数是介质在外电场作用下对电荷的电场力的响应能力的一种量度。
它反映了介质的电介质性质,是比电常数的函数。
介电常数在多种电磁学应用中都有它的功能,例如极板电容器、电场探测器、能量储存设备等。
它的理论计算通过一些基本理论可以求解,例如连续性方程、功率定理、闭合波导等。
综上所述,介质的极化和介电常数是介质电磁性质中的两个基本分支。
极化是介质对电场响应的一种体现,介电常数则对介质电场作用的响应能力进行定量描述,两种性质在相互联系、相互作用的基础上,共同组成了介质电介质学这个广泛应用的分支。
磁粉检测(1~2)

1 磁粉检测基础知识
2磁粉检测的物理基础
2.1磁现象和磁场
2.1.1 磁的基本现象 通常称磁针指向北的一端为北极(N),指向南的一端为 南极(S) 同性磁极相互排斥,异性磁极相互吸引。 地球的南极是地磁场的北极(N),地球的北极是地磁场 的南极(S) 磁极间相互排斥和相互吸引的力称为磁力。 使原来没有磁性的物体得到磁性的过程叫磁化
磁 粉 检 测
武汉信正检测技术有限公司 刘 平 RT-Ⅲ UT-Ⅲ MT-Ⅲ PT-Ⅲ TOFD-Ⅱ
TSG Z8001-2013
1 磁粉检测基础知识
1.1 漏磁场检测分类 漏磁场检测:是利用铁磁性材料或工件被磁化后,在表面和近表面 如有不连续性(材料的均质状态即致密性受到破坏)存在 则在不连续性处磁力线离开工件和进入工件表面发生局部畸变产生磁 极,并形成可检测的漏磁场进行检测的方法。 漏磁场检测包括:磁粉检测和利用检测元件探测漏磁场。 其区别在于,磁粉检测是利用铁磁性粉末-磁粉,作为磁场的传感器, 即利用漏磁场吸附施加在不连续性处的磁粉聚集形成磁痕,从而显示 出不连续性的位置、形状和大小。 利用检测元件探测漏磁场的磁场传感器有磁带、霍尔元件、磁敏二极 管和感应线圈等。
2.3.3磁化曲线
磁化曲线是表征铁磁性材料磁特性的曲线,用以表示外加磁场强度H与 磁感应强度B的变化关系。
2.3.4磁滞回线 剩余磁感应强度 BR 矫顽力 HC
铁磁性材料的特性:
高导磁性 磁饱和性 磁滞性
根据矫顽力HC大小分为软磁材料(HC<100A/M)和硬磁材 料(HC≥100A/M)。
软磁材料与硬磁材料的特征
2磁粉检测的物理基础
磁感应强度:
将原来不具有磁性的铁磁性材料放入外加磁场内,便得到磁化 ,它除了原来的外加磁场外,在磁化状态下铁磁性材料本身还产 生一个感应磁场,这两个磁场叠加起来的总磁场,称为磁感应强 度B。 单位是T (SI)和Gs (CGS)(1T=10000Gs)。 磁感应强度是矢量,有大小和方向,可用磁感应线来表示,磁 感应强度的大小等于穿过与磁感应线垂直的单位面积上的磁通量 ,所以磁感应强度又称为磁通密度。 磁感应强度不仅与外加磁场有关,还与被磁化的铁磁性材料的性 质有关,B=μH。
第六讲:恒定磁场的基本规律、媒质的电磁性质

区域的磁场,远处的磁场是通过场本身的内部作用传递的;
3) Br 0J r 只对稳恒电流成立。
2、安培环路定理
l Br dl s B r dS 0 S J r dS 0I
对电流分布具有某种对称性的情况下,利用安培环路定理求场较方便。常见的
电流布的对称性有:柱对称,面对称。
例题:在下面一些矢量中,哪些可以表示磁感应强度 B ?如果它能代表,求相应的
B(r) 0
4
J
V
r'
dV ' R3
R
0 4
J
V
r'
1 R
dV
'
由公式 A A A ,有:
J
r
R
'
1 R
J
r
'
1 R
J
r
'
(J r' 0)
所以,
B(r )
0 4
V
J
r
R
'
dV
'
0
4
V
J
r
R
'
dV
'
A
式中 Ar 0
J r' dV ' 称为磁场的矢量位或矢势。这样,容易得到:
P dS
P
lim
V 0
S
V
P
Q S P dS
+q l
dS
+q
+q -q
-q -q
特例: (1)均匀极化: P Const P 0,反过来不一定成立。
(2)介质分界面——面极化电荷
取一薄圆柱体,如图所示:
由于 QP
磁化电流密度

( ) , ( ) 。其次在铁电和铁磁物质或强场
情况下,P与E , M与H 之间将不再是齐次线性关系。 另外,对于各向异性的介质来说,介电常数和导磁
系数都是张量,场强和感应场强之间的关系推广为
Di ij E j ,
Bi ij H j , i, j 1,2,3
称为极化电流密度
P1
h
通过薄层进入介质2的正电荷为P2 ds ,由介质1 通过薄层下侧面进入薄层的正电荷为 因此薄层 P 1 ds 出现的净余电荷为
dQp ( P2 P 1 ) ds
以 p 为极化电荷面密度,则有 ˆ ds p ds ( P2 P ) d s ( P P ) n 1 2 1 得到
S V
即
p P
b) 极化电流密度与极化强度的关系
当电场随时间改变时,极化过程中正负电荷的
由此可见,负电荷为极化源头,正电荷为极化尾闾。
相对位移也将随时间改变,由此产生的电流称为极 化电流。极化电流和极化电荷也满足连续性方程:
p jp 0 t
即
p P jp P t t t
对 jm两边取散度,得
jm M
jm 0
这就说明磁化电流不引起电荷的积累,不存在磁化 电流的源头。
b) 磁化电流面密度与磁化强度的关系 对于均匀介质,磁化后介质内部的 M 为一常矢 量。可见 jm M 0 ,即介质内部 jm 0 。但
的总磁化电流: I m ina dl M dl
L
L
以 jm 表示磁化电流密度,有
介质的电磁性质

介质表面均匀分布着等量异号的极化电荷.
板外:E外 E0
板内:E1 E0 E仍为均匀电场。 A
E1 E1t E1n
利用边值关系 E1t E2t E sin
D1n
D2n
E
cos
E1n
E
cos
E1
E1t2 E2t2
sin2 ( cos )2 E
E1,n的夹角
tg
E1t E1n
些有极分子在电场作用下按一定方向有序排列,从 宏观上来看这两种行为都相当于产生了一个电偶极 矩。在电磁学中,曾引进了极化强度矢量:
pi
P i V
其中 pi是第 i 个分子的电偶极矩,即
求和是对 V体积中所有分子进行的。
pi qili
a) 极化电荷体密度与极化强度的关系
由于极化,正负电荷间发生了相对位移,每处的 正负电荷可能不完全抵消,这样就呈现宏观电荷,
负电荷,即
S
Qp Q P dS S
因为
Qp V pdV
式中V是S所包围的体积,所以
V pdV P dS V PdV S
即
p P
由此可见,负电荷为极化源头,正电荷为极化 尾闾。
b) 极化电流密度与极化强度的关系
当电场随时间改变时,极化过程中正负电荷 的相对位移也将随时间改变,由此产生的电流称
由n D2 D1 得:应用于上下极板界面
D1 f , D2 f .
E1
f 1
,
E2
f 2
,
由于 p n P2 P1 , 对两介质分界面:
p
P2 P1
e2 E2
e1
E1
2
1
f
0
左极板: p1 n
静电场的标势及其微分方程

介质的电磁性质方程:Dv
v E
2
§2.1 静电场的标势及其微分方程
1、静电场的标势
静电场的Maxwell方程为:
v
D
v E 0
自由电荷分布
是电位移
v D
的源
静电场是无旋场
➢静电场的无旋性表明电场沿任意闭合回路L的环量等于零
vv
Ñ L E dl 0
蜒 v v v v
E dl E dl 0
v D
vv
对于各向同性线性均匀介质有: D E
v E
v
E
2
Poisson方程,静电势满足的基本 微分方程
7
讨论: (1) Poisson方程的求解,必须给定边界条件。
2
(2) 若介质为不同类型的均匀介质组成,则对于每种介质,建立 Poisson方程,而在介质分界面上建立合适的边值关系以及边界条件。
➢ 导体内部不带净电荷,净电荷只能分布于导体表面上
由高斯定理
S E dS
q
0
可知,q=0
➢ 导体表面上电场必沿法线方向,导体表面为等势面,整
个导体为等势体
由
v E
可知,
为常量,因而是等势体;如果导体表面上的电场
不沿法线方向,则必有切向分量,因而电荷将沿切线方向移动
11
3)导体表面的边值关系
2 S12 常数
静电场
静电场的基本特点:
电荷静止
v J
vv
0
场量不随时间变化 物理量 =0
t
静电场的基本问题:
给定自由电荷的分布,以及周围空间介质或 导体的分布,运用电磁场理论求解带电体系 的电场。
1
解决静电问题的基本方程:
时变电磁场不同介质分界面上的衔接条件

时变电磁场不同介质分界面上的衔接条件
时变电磁场在不同介质分界面上的衔接条件由两个主要方面决定:电场的切向分量和磁场的法向分量。
以下是在不同介质分界面上衔接条件的简要说明:
1. 电场的切向分量:
●切向电场分量(电场强度的切向分量)在分界面上是连续的。
这意味着两个相邻介质的
切向电场分量的大小和方向必须相等。
●假设在介质1中的电场强度为E1,介质2中的电场强度为E2,当电磁波从介质1传播
到介质2时,有E1⊥= E2⊥,即切向电场分量垂直于分界面。
2. 磁场的法向分量:
●法向磁场分量(磁感应强度的法向分量)在分界面上也是连续的。
这意味着两个相邻介
质的法向磁场分量的大小和方向必须相等。
●假设在介质1中的磁感应强度为B1,介质2中的磁感应强度为B2,当电磁波从介质1
传播到介质2时,有B1⊥= B2⊥,即法向磁场分量垂直于分界面。
这些衔接条件基于麦克斯韦方程组和电磁场的连续性原理,确保了电场和磁场在介质分界面上的平滑衔接。
遵循这些衔接条件可以确保电磁波在介质分界面上的传播正确和连续。
需要注意的是,当介质的性质不同时(例如,电介质到导体的分界面),衔接条件可能会有所不同。
在这种情况下,还需要考虑介质表面上的电荷分布和电流分布,以满足电磁场的连续性。
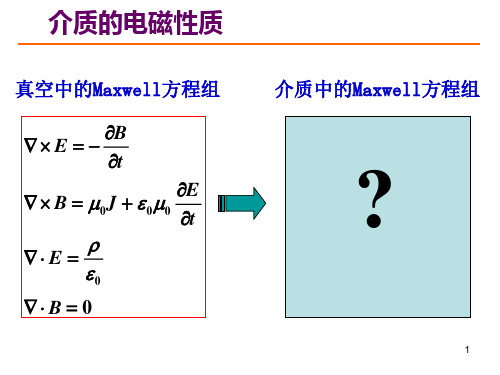
电磁场与电磁波第三章媒质的电磁性质和边界条件

D E B H
4.关于本构矩阵
D B
0
0 E
H
非均匀媒质:C是空间坐标的函数 不稳定媒质:C是时间坐标的函数 时间色散媒质:C是时间导数的函数 空间色散媒质:C是空间坐标导数的函数 非线性媒质: C是场强的函数
四、媒质中的麦克斯韦方程组
2. 极化强度
为了描述介质极化的状态, 引入极化强度 矢量.定义单位体积内的电偶极矩为极化强度 矢量(Polarization Intensity Vector), 即
P lim p
V 0 V
C / m2
式中 p 为体积元 V内电偶极矩的矢量和,
p 的方向从负极化电荷指向正极化电荷。
B
l E dl S t dS
因为
E dl
l
E1tl E2tl
S
B t
dSB tl Nhomakorabeah
0
故:E1t E2t 或 nˆ (E1 E2 ) 0
at
结论:在分界面上 电场强度的切向分 量总是连续的。
若媒质Ⅱ为理想导体时:
E1t 0 理想导体表面没有切向电场。
d eE
式中:
称为电子的迁移率,
e
其单位为 (m。2/V s)
故电流密度为: JC Need 可得: JC NeeeE
如图,单位时间内通过 dS的电量为:
dq Nee ddS 式中:Ne为自由电子密度。
导体材料的物态方程
JC NeeeE
若设: e Nee
令: r 1 m
B 0r H H
磁介质的物态方程
其中 r称为相对磁导率。
第三章 媒质的电磁性质和边界条件

第三章 媒质的电磁性质和边界条件众所周知,物质是由原子核和电子组成的,原子核带正电,电子带负电。
就是说任何物质材料,不论是气体、液体还是固体都含有带电粒子,这些带电粒子的周围一定存在着电场;同时电子一方面绕原子核运动,另一方面也作自旋运动,电荷的运动形成电流,这些电流周围存在磁场。
从微观上看,材料中这些带电粒子是存在电磁效应的,但从宏观上看,由于相邻原子产生的场相互抵消,及大量带电粒子热运动的平均结果,使自然状态下的物质仍呈现电中性。
倘若存在外加电磁场,则由于带电粒子和外加电磁场的相互作用,介质的分子电矩和磁矩将部分或全部取向一致,引起宏观电或磁效应,相当于在材料内部存在附加的场源,这样就需要对真空中的电磁学定律作进一步推广。
在第二章中,我们研究了在真空(或近似真空的空气)中电磁场各场量,如H B D E和,,所遵循的普遍规律,并得到一组麦克斯韦方程组。
麦克斯韦方程组的积分形式描述大尺度(如一个线段、曲面或体积)上的电磁特性,而微分形式描写空间任意一点的电磁场,但归根结底两者描述的仍然是宏观电磁现象。
这一章我们要研究物质的微观模型和性质,把麦克斯韦方程组推广到一般电磁材料中去.本章先研究由材料中带电粒子和电磁场的相互作用而产生的三个基本现象:传导、极化和磁化。
每一种物质在电磁场中均有传导、极化和磁化三种现象,根据某种主要的现象,可将材料分为导体、半导体、电介质和磁介质等。
讨论材料的电磁性质之后,我们可获得三个物态方程和一般媒质中的麦克斯韦方程组。
最后我们研究在不均匀媒质中电磁场所遵循的规律——边界条件。
§3.1 电场中的导体导体是一种含有大量可以自由移动的带电粒子的物质。
导体可分为两种——金属导体和电解质导体。
金属导体的导电靠的是自由电子,由于自由电子的质量比原子核的质量小得多,所以导电过程中没有明显的质量迁移,也不伴随任何化学变化。
而碱、酸、和盐溶液等电解液则属于第二种导体,其导电靠的是带电离子,导电过程中伴随有质量迁移,也要发生化学变化。
§1.1介质的电磁性质

§1.1介质的电磁性质从电学的角度,宏观物质大体可分为导体、绝缘体、半导体。
其中,绝缘体一般又称为“电介质”。
半导体则介于导体与绝缘体之间,根据研究的需要,常常将它纳入导体或电介质模型,或者两种模型都套用。
磁学则认为,一切物质材料都是“磁介质”,依据磁导率的大小,磁介质仅仅有“铁磁质”和“非铁磁质”的区分。
铁磁质的相对导磁率,它相当于磁场的“导体”;而非铁磁质的相对导磁率,它部分地相当于磁场的“绝缘体”。
通过电磁学课程,已对介质的电磁特性作了详尽的研究和讨论,述及的概念和规律正是电动力学起步的基础,因此,我们在这里仅对介质的电磁特性做一个总结性的概述。
1.介质的分类从材料性质分:各向异性、各向同性介质;线性、非线性介质;均匀、非均匀介质;从电磁行为分:电介质、导电介质;铁磁质、顺磁质、抗磁质等。
从场的作用分:磁介质、电介质。
介质是一个带电粒子系统,内部存在规则而迅速变化的微观电磁场。
真空则被看作一种特殊的介质(),现代物理认为,真空是“量子场的基态”,它也具有物质性。
2.介质的极化和磁化规律在电磁场中,介质又可划分为两类情况,即电介质和磁介质。
它们在电场和磁场中分别发生极化和磁化。
下表虽然不能概括介质在场中行为的详尽情况,却反映了它们的主要特点与规律。
从表中罗列的内容我们还可以看出,介质的极化与介质的磁化有着高度的对称性。
不仅介质的极化与“分子电流模型描述的介质磁化”对称,而且介质极化也与“磁荷模型描述的磁极化”对称。
清楚这种对称对我们的学习记忆是在现代电磁理论中,实验和推理都赞成诠释磁场起源的“分子电流观点”,但这并不意味着古典的“磁荷观点”已经失效。
虽然迄今还没有在现实中找到“磁单极子”,或许它根本不存在,但是“磁偶极子”却是真实存在的。
因为一个微小的电流环既可以用“磁矩”表述,同时也可用“磁偶极矩”表述,这就是说,电流环可以等效于磁偶极子,即无论从“环流模型”还是从“磁偶极矩模型”计算研究磁场是等效的,殊途同归的。
电动力学-第一章

解:(1)以距对称轴为r的半径作 一圆周(a<r<b),应用安培
环路定律,由对称性得
2rH I
因而
H
I
2r
导线表面上一般带有电荷,设内导线单位长度的
电荷(电荷线密度)为τ, 由对称性,
可得
2rEr
,因而
Er 2r
能流密度为
S
E
H
Er H
ez
I 4 2r 2
ez
式中 ez为沿导线轴向单位矢量。
介质
坡印亭矢量
§7电磁场的动量和守恒关系 场有动量?
1受力电荷要有动量变化,2场动量,3场动量流
电磁力作用,载荷体动量增加(减少)
若守恒
电磁场动量减少(增加)
场的动量能够流动
电磁场动量—动量密度
场内单位体积的动量
电磁场动量流动—动量流密度
单位时间垂直通过单位横截面的动量 有九个分量 我们取 左边的 i 为动量的
1. 电磁能的传输不是靠电流!
2. 电磁能的传输靠的是电场和磁场
电磁能的传输必须有能量流动,即 S 0 ,所以 E B 0
场能流例题----回路电流的能量流动
场能流例题---同轴电缆的能量流动
例:同轴传输线内导线半径为a,外导线半径为b, 两导线间为均匀绝缘介质(如图)。导线载有电流 I,两导线间的电压为U。 (1) 忽略导线的电阻,计算介质中的能流 S 和传输 功率; (2)计及内导线的有限电 导率,计算通过内导线表 面进入导线内的能流,证 明它等于导线的损耗功 率.
3。介质的磁化
从磁化角度看 a’.有磁矩分子
b’.无磁矩分子 磁化的解释
磁化强度
在外场B条件
各向同性均匀非铁磁物 质
介质基础必学知识点

介质基础必学知识点
介质是指电磁波的传播媒介,包括空气、水、玻璃等。
介质的性质对
于电磁波的传播和反射有着重要的影响。
以下是介质基础必学的知识点:
1. 导电性:介质的导电性决定了其对电磁波的阻抗。
导电性较高的介
质能够吸收和散射电磁波,导致能量损耗。
金属是导电性最高的介质,所以金属可以很好地反射电磁波。
2. 折射率:介质的折射率决定了光在介质中传播的速度。
折射率较高
的介质使光速度减小,折射角度变大。
这就是我们常见的折射现象,
比如光线从空气射入水中时的折射。
3. 透明度:透明度是介质对电磁波的透射能力。
透明度较高的介质能
够让大部分的电磁波穿过,而透明度较低的介质则会吸收或反射大部
分的电磁波。
透明度与介质的导电性和折射率有关。
4. 散射:散射是指光在介质中遇到细小“杂质”时发生的偏折现象。
散射使光传播的方向发生改变,这也是我们能够看到物体的原因。
天
空的蓝色就是因为大气中的气溶胶对太阳光的散射造成的。
5. 反射:反射是指电磁波在介质的界面上发生改变方向的现象。
一部
分反射回来的电磁波会形成反射光线。
反射现象是我们看到物体的基础,通过反射我们能够看到周围的物体。
6. 吸收:吸收是介质对电磁波能量的吸收现象。
吸收使电磁波的能量
被转化为介质内部的能量,导致其温度升高。
吸收现象在微波炉和红
外线加热器中得到了广泛应用。
这些是介质基础必学的知识点,理解这些知识可以帮助我们更好地理解电磁波的传播和相互作用。
介质的电磁性质
在介质中有vvຫໍສະໝຸດ P P0 E f P
v v
0E P f
引入辅助矢量电位移矢量 D 0E P
v
D f
➢
电场强度
v E
描述所有电荷分布激发的场,代表介质内的总宏
观电场,是电场的基本物理量,电位移矢量 Dv只是辅助物理
量,并不代表介质中的场强
12
➢ 实验指出,对于各向同性线性均匀介质,极化强度和电场强度
vv P2 P1
v dS
P
dS
P evn
vv P2 P1
束缚电荷面密度
面束缚电荷不是真正分布在一个几何面上的电荷,而是
在一个含有相当多分子层的薄层内的效应。
10
设介质2为真空,则
v P2
0,有
P
evn
v P
P evn
vv P2 P1
v
P P
4、极化电流
时间当改电变,场因随而时极间化变强化度时,Pv也极发化过生程变中化正,负由电此荷产的生相的对电位流移称也为随极 化电流
电荷可能不完全抵消,内部或表面有可能出现净余的电荷,
即出现宏观的电荷分布,由于这些电荷被束缚在分子内部而
不能在介质内自由运动,故称为束缚电荷
7
➢ 束缚电荷密度与极化强度的关系
若极化时正负电荷拉开的位移为lv, 则必有部分电偶
极子跨过面元dS,当电偶极子的负电荷处于体积
v l
v dS
内时,其对应的正电荷就穿过面元dS,则穿出去的电
6
3、极化强度
1) 极化强度:单位体积内分子电偶极矩的矢量和
v
P
i
pvi
N
pv npv
V V
n 为分子数密度,即单位体积内的分子数
1-4 介质中的麦克斯韦方程分解

B E
0J
B
0 0
t
E
t
B 0
介质中的麦克斯韦方程
D f
H Jf
E
B
D t
t
B 0
E
f
P
0
B 0 J f JP JM
B
0 0
t
E
E
t
B 0
D f
H Jf
E
B
D t
t
B 0
D 0E P
H
B
M
0
从现在起,除特别说明,以后公式中的都是指自 由电荷和自由电流分布。
I、极化强度
定义:
P
i
pi
V
电偶极距:
求和为对 V 体积元中的所有分子求和。
II、简化模型:
pi
P i
V
N
ql nql
V
ql
E
III、极化电荷
E
dS
则因极化而通过 dS 面元跑出去的分子数为 n dS
从 dS 面元跑出去的电量为
nq dS P dS
通过一个封闭的曲面跑出去的总电量为
2)对各向异性的晶体材料 由于存在某些容易电极化的取向,使得电位移矢 量和电场强度一般不在同一方向。它们之间的一 般关系是张量关系:
Dx xxEx xyEy xzEz Dy yxEx yyEy yzEz Dz zx Ex zy Ey zz Ez
Dx
D
y
D ,
E
B
,
t
H
J
D
t
B 0
——(4.23)
4、介质的电磁性质关系
D 0E P
在作用电磁场不是很强,同时外场的变化不是很快 的条件下,介质对外场的响应是线性和同时的。
三种不同的磁介质的b-h关系曲线

一、介绍磁介质及其在电磁学中的作用磁介质是指在外加磁场作用下能够产生磁化的材料。
磁介质在电磁学中起着重要的作用,它们可以用于制造变压器、电感器、磁性存储器等电磁设备,同时也被应用于信息存储、传感器、电磁屏蔽等方面。
二、B-H关系曲线的定义B-H关系曲线也被称为磁滞回线,它表示了磁介质在外加磁场下的磁化特性。
通过测量磁介质在不同外加磁场下的磁化强度和磁场强度的关系,可以得到B-H关系曲线。
B-H关系曲线是研究磁介质特性的重要工具,可以帮助我们了解磁介质的磁化行为、磁滞损耗等性质。
三、磁介质的分类及特性1. 铁磁性材料:铁磁性材料是一类常见的磁介质,其具有明显的磁滞特性和磁饱和现象,通常用于制造变压器、电感器等电磁设备。
铁磁性材料的磁化曲线呈现明显的磁滞现象,磁化强度随着外加磁场的增大呈非线性变化。
2. 铁氧体材料:铁氧体是一类具有特殊磁性和电性能的陶瓷材料,广泛应用于电磁设备中。
其磁化曲线一般以非线性的形式呈现,具有较高的矫顽力和饱和磁感应强度。
3. 铁氧体材料:铁氧体是一类具有特殊磁性和电性能的陶瓷材料,广泛应用于电磁设备中。
其磁化曲线一般以非线性的形式呈现,具有较高的矫顽力和饱和磁感应强度。
四、三种不同磁介质的B-H关系曲线1. 铁磁性材料的B-H关系曲线:铁磁性材料的B-H关系曲线呈现明显的对称性,在磁化过程中存在明显的磁滞现象。
随着外加磁场的增大,磁化曲线逐渐变宽,磁化强度增大,最终趋于饱和。
2. 铁氧体材料的B-H关系曲线:铁氧体材料的B-H关系曲线呈现非线性的特点,表现为磁化曲线不对称,有明显的饱和磁感应强度,并且矫顽力较大。
3. 铁氧体材料的B-H关系曲线:铁氧体材料的B-H关系曲线呈现非线性的特点,表现为磁化曲线不对称,有明显的饱和磁感应强度,并且矫顽力较大。
五、不同磁介质的应用领域及发展趋势1. 铁磁性材料的应用领域主要包括电力电子器件、变压器、电感器等电磁设备,随着现代电子技术的发展,对铁磁性材料磁化特性的要求也越来越高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
✓因此,薄层内净余电荷为(P2
P1)dS ,以P表示束缚电荷面
密度,有
P d S P 2 P 1d S
11
由此,
P n P 2 P 1
n为分界面上由介质1指向介质2的法线。
12
2.介质与场的相互作用 a. 介质与场是相互作用的。介质对宏观
场的作用就是通过束缚电荷激发电场。因 此,在麦氏方程中的电荷密度包括自由电 荷密度和束缚电荷密度,故有
23
1 0 B J fJ M J P0 E t
利用
JMM
JP
P t
D0EP
得
B 0M Jf
D
t
24
引入磁场强度H,定义为
B
H M
0
改写上式为
D
HJf
t
b. B和H之间的实验关系 实验指出,对于各向同性非铁磁物质,磁化
强度M和H之间有简单的线性关系
MMH M称为磁化率。
25
BH, r0, r 1M
称为磁导率, r为相对磁导率。
26
谢谢
介质磁化后,出现宏观磁偶极矩分布,用磁化
强度M,其定义为:
M
m i
V
17
2. 磁化电流密度与磁化强度的关系
若分子电流被边界线L链环着,这分子电流就对IM有贡献。 在其他情形下,或者分子电流根本不通过S,或者从S背面流出来 后再从前面流进,所以对IM没贡献。因此,通过S的总磁化电流 JM 等于边界线L所链环着的分子数目乘上每个分子的电流i。
V
P d
V P d S S
9
这就是极化矢量和束缚电荷之间的积分表达式。 应用矢量分析中的散度定理把面积分化为体积分, 可得微分形式
S P d Sv P d V
P P
10
c. 两介质分界面上的束缚电荷的概念
✓通过薄层右侧面进入介质2的 正电荷为P2dS
✓由介质1通过薄层左侧进入薄 1
层的正电荷为P1dS
1. 磁化电流密度与磁化强度的引入 a. 宏观磁化电流密度JM
在没有外场时,介质不出现宏观电流分 布,在外场作用下,分子电流出现有规则分 布,形成了宏观电流密度JM 。
16
b. 磁化强度M
分子电流可以用磁偶极矩描述,把分子电 流看作载有电流i的小线圈,线圈面积为a.则与 分子电流相应的磁矩为
mia
18
边界线L上的一个线元dl。设分子电流圈的面积 为a. 若分子中心位于体积为adl 的柱体内,则该 分子电流就被dl所穿过。因此,若单位体积分子 数为n,则被边界线L链环着的分子电流数目为
Lnadl
(注意反向电流位于面元内部分积分线元反向)
19
此数目乘上每个分子的电流i即得从S背 面流向前面的总磁化电流
二、介质的极化
1.介质的极化
a. 电极化强度矢量P :在外场作用下, 两种电介质都出现宏观电偶极矩分布。
电极化强度矢量P: 等于单位体积中, 由极化产生的电偶 极矩。
P
pi
V
6
b.束缚电荷密度P和电极化强度P之间的关系 简化模型: 每个分子由 相距为l的一对正负电 荷q构成。
7
当偶极子的负电荷处于体积ldS内 时,同一偶极子的正电荷就穿出界 面dS外边。
I M L n a d l i L n m d l L M d l
以JM表示磁化电流密度,有
SJM dSL M dl
20
把线积分变为M的面积分,由S的任意 性可得微分形式
JMM
21
3. 极化电流JP
a.定义:
当电场变化时,介质的极化强度P
发生变化,这种变化产生另一种电
流,称为极化电流。
0 fP
在实际问题中,束缚电荷不易受实验 条件限制,我们可以将其消去,得
13
0E P f
引入电位移矢量D,定义为
可以得
Df
D0EP
b. D和E之间的实验关系
对于一般各向同性线性介质,极化强 度和之间有简单的线性关系
14
Pe0E
e称为介质的极化率。
于是
DE
r0, r 1e
15
三、介质的磁化
设单位体积内分子数为n,则 穿出dS外面的正电荷为
n ld q S n p d S P d S
8
对包围区域V的闭合界面S积分,则 由V内通过界面S穿出去的正电荷为
SP dS
使体积中留下了多余的负电荷 PdS S
从另一方面看,在体积中的束缚电荷为:V PdV ,这
是同一种事物的两种表达式,应该相等
b.表示式
P
ei xi
P t
V eivi
V
JP
xi是V内每个带电粒子的位置,其电荷为ei 。
22
4. 介质和磁场的相互作用 a.介质与磁场是相互作用、相互制约的。
介质对磁场的作用是通过诱导电流 JP+ JM 激发 磁场。因此,麦氏方程中的J包括自由电流密度 JP 和介质内的诱导电流密度 JP+ JM 在内,则在 介质中的麦氏方程为
