初二数学秋季讲义 第2讲.倍长中线与截长补短 教师版
三角形全等之倍长中线和截长补短讲义
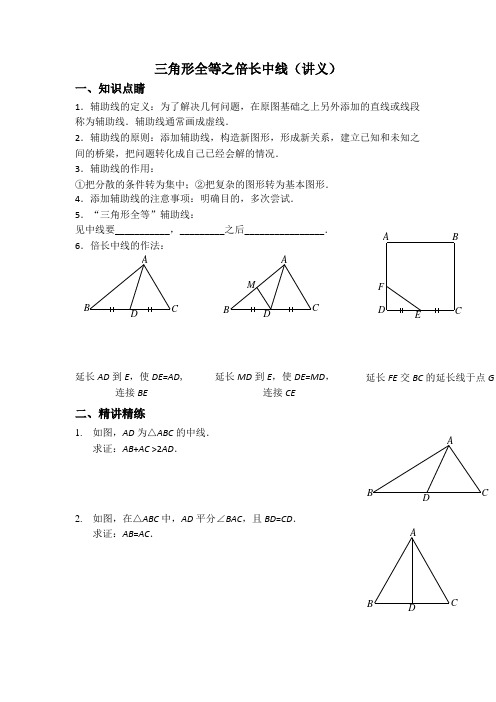
A BCDEF三角形全等之倍长中线(讲义)一、知识点睛1.辅助线的定义:为了解决几何问题,在原图基础之上另外添加的直线或线段称为辅助线.辅助线通常画成虚线.2.辅助线的原则:添加辅助线,构造新图形,形成新关系,建立已知和未知之间的桥梁,把问题转化成自己已经会解的情况. 3.辅助线的作用:①把分散的条件转为集中;②把复杂的图形转为基本图形. 4.添加辅助线的注意事项:明确目的,多次尝试. 5.“三角形全等”辅助线:见中线要___________,_________之后________________. 6.倍长中线的作法:ABCDDCB AM延长AD 到E ,使DE=AD , 延长MD 到E ,使DE=MD ,连接BE 连接CE二、精讲精练1. 如图,AD 为△ABC 的中线.求证:AB +AC >2AD .2. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .BADCABC延长FE 交BC 的延长线于点G3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AC =AB .求证:①CE =2CD ;②CB 平分∠DCE .4. 如图,在△ABC 中,D 是BC 边的中点,E 是AD 上一点,BE =AC ,BE 的延长线交AC 于点F . 求证:∠AEF =∠EAF .5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 中点,EF ∥AD 交CA的延长线于点F ,交AB 于点G ,BG =CF . 求证:AD 为△ABC 的角平分线.A FEBD CAEB DCGE D AF A F EBDCGEDAF6. 如图,在正方形ABCD 中,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,GE ⊥EF .求证:GF =AG +BF .7. 如图,在正方形ABCD 的边CB 的延长线上取一点E ,△FEB 为等腰直角三角形,∠FEB =90°,连接FD ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG .三、回顾与思考________________________________________________________________________________________________________________________________________________________________________________________________【参考答案】DGAEBFCAF EBGCD【知识点睛】见中线要倍长,倍长之后证全等.【精讲精练】1.证明略(提示:延长AD到点E,使DE=AD,连接BE,证明△BED≌△CAD)2.证明略(提示:延长AD到点E,使DE=AD,连接BE,证明△BED≌△CAD)3.证明略(提示:延长CD到点F,使DF=CD,连接BF,证明△BDF≌△ADC,△CBE≌△CBF)4.证明略(提示:延长AD到点M,使DM=AD,连接BM,证明△ADC≌△MDB)5.证明略(提示:延长EF到点M,使EM=EF,连接BM,证明△CFE≌△BME)6.证明略(提示:延长GE交CB延长线于点M,证明△AEG≌△BEM)7.证明略(提示:延长EG交CD延长线于点M,证明△FGE≌△DGM,再证明三角形EGC是等腰直角三角形)三角形全等之倍长中线每日一题1.已知:如图,在梯形ABCD中,AD∥BC,AB=AD+BC,E是CD的中点.求证:AE⊥BE.ADEBC 2.已知:如图,在△ABC中,D为BC边中点,∠BDA=∠BAD,E为BD中点,连接AE.求证:∠C=∠BAE.AE D C3. 已知:如图,△ABC 与△BDE 均为等腰直角三角形,BA ⊥AC ,ED ⊥BD ,垂足分别为点A ,点D ,连接EC ,F 为EC 中点,连接AF ,DF ,猜测AF ,DF 的数量关系和位置关系,并说明理由.FED CA4. 已知:如图,D 为线段AB 的中点,在AB 上任取一点C (不与点A ,B ,D 重合),分别以AC ,BC 为斜边在AB 同侧作等腰Rt △ACE 与等腰Rt △BCF ,∠AEC =∠CFB =90°,连接DE ,DF ,EF . 求证:△DEF 为等腰直角三角形.ABCDE F5. 已知:如图,在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE =∠EAF ,AF 与DC 的延长线相交于点F .试探究线段AB 与AF ,CF 之间的数量关系,并说明理由.EDCBA【参考答案】1. 证明:延长AE 交BC 的延长线于点F .FADEC B∵AD ∥BC∴∠D =∠DCF ,∠DAE =∠F ∵E 是CD 的中点 ∴DE =CE在△ADE 和△FCE 中=⎧⎪∠=∠⎨⎪=⎩∠∠D FCE DAE F DE CE ∴△ADE ≌△FCE (AAS ) ∴AD =FC ,AE =FE ∵AB =AD +BC ∴AB =CF +BC =BF 在△ABE 和△FBE 中=⎧⎪=⎨⎪=⎩AB FB BE BE AE FE ∴△ABE ≌△FBE (SSS ) ∴∠ABE =∠FBE =90° 即AE ⊥BE2. 证明:延长AE 到F ,使得EF =AE ,连接DF .FAB CDE∵E 为BD 中点 ∴BE =ED在△ABE 和△FDE 中=⎧⎪=⎨⎪=⎩∠∠BE DE BEA DEF AE FE ∴△ABE ≌△FDE (SAS )∴AB =FD ,∠BAF =∠F ,∠B =∠FDE ∵∠BDA =∠BAD ∴BD =AB ∵D 为BC 边中点 ∴CD =BD =AB =FD ∵∠BDA =∠BAD∴∠ADF =∠BDA +∠FDE ,∠ADC =∠B +∠BAD 即∠ADF =∠ADC 在△FAD 和△CAD 中=⎧⎪=⎨⎪=⎩∠∠FD CD FDA CDA AD AD ∴△FAD ≌△CAD (SAS ) ∴∠F =∠C ∴∠C =∠BAE3. 解:AF ⊥DF ,AF =DF ,理由如下: 延长DF 交AC 于点P .P AD E FC∵BA ⊥AC ,ED ⊥BD ∴∠BAC =∠EDA=90° ∴DE ∥AC ∴∠DEC =∠ECA ∵F 为EC 中点 ∴EF =FC在△EDF 和△CPF 中DEF PCF EFD CFP EF CF ∠=∠⎧⎪=⎨⎪=⎩∠∠ ∴△EDF ≌△CPF (AAS ) ∴DE =CP ,DF=PF∵△ABC 与△BDE 均为等腰直角三角形 ∴AB =AC ,DE=BD ∴AB -BD=AB -DE=AC -CP 即AD =AP在△DAF 和△PAF 中DF PF AF AF AD AP =⎧⎪=⎨⎪=⎩∴△DAF ≌△PAF (SSS )∴∠DFA =∠PFA =90°,∠DAF =∠PAF =45° ∴AF ⊥DF ,AF =DF4. 证明:延长ED 到点G ,使得DG =DE ,连接BG ,FGDCAE FB∵D 为线段AB 的中点 ∴AD =BD在△EDA 和△GDB 中=⎧⎪=⎨⎪=⎩∠∠ED GD EDA GDB DA DB ∴△EDA ≌△GDB (SAS ) ∴EA =GB ,∠A =∠GBD∵△ACE 与△BCF 是等腰直角三角形∴AE =CE =BG ,CF =FB ,∠A =∠ECA =∠FCB =∠FBC =45° ∴∠ECF =90°,∠FBG =∠FBD +∠GBD =90° 在△ECF 和△GBF 中=⎧⎪=⎨⎪=⎩∠∠EC BG ECF GBF CF BF ∴△ECF ≌△GBF (SAS ) ∴EF =GF ,∠EFC =∠GFB ∵∠CFB =∠CFG +∠GFB =90° ∴∠EFG =∠EFC +∠CFG =90° 在△EFD 和△GFD 中,=⎧⎪=⎨⎪=⎩EF GF FD FD ED GD ∴△EFD ≌△GFD (SSS )∴∠EDF =∠GDF =90°,∠EFD =∠GFD =45° ∴ED =DF∴△DEF 为等腰直角三角形5. 解:AB =AF +CF ,理由如下: 延长AE 交DF 的延长线于点G .CFEBAD∵E 为BC 边的中点 ∴BE =CE ∵AB ∥DC∴∠B =∠BCG ,∠BAG =∠G 在△ABE 和△GCE 中=⎧⎪=⎨⎪=⎩∠∠∠∠B GCE BAE G BE CE ∴△ABE ≌△GCE (AAS ) ∴AB =GC ∵∠BAE =∠EAF ∴∠G =∠EAF ∴AF =GF ∵GC = GF +FC ∴AB =AF +CF三角形全等之倍长中线(随堂测试)1. 在△ABC 中,AC =5,中线AD =4,则边AB 的取值范围是____________________.2. 已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC . 求证:AE 平分∠BAC .FEC A【参考答案】1.3<AB<132.证明略(提示:延长AE 到点M ,使EM =AE ,连接DM , 证明△DME ≌△CAE )三角形全等之倍长中线(作业)3. 已知:如图,在△ABC 中,AB =5,AC =3,则中线AD 的取值范围是________________.A4. 如图,在梯形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,且AF ⊥AB ,若AD =2.7,BE =AE =5,求CE 的长.A B C D EF5. 已知:如图,在△ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边向外作等腰直角三角形.求证:EF =2AD .EAFCB6. 如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G .求证:BF =CG .AC DEFG7. 如图,在正方形ABCD 的边AB 上任取一点E ,作EF ⊥AB 交BD 于点F ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG .BE AFGC D8. 已知:如图,∠ACB =90°,AC =BC ,D 为AB 上一点,连接CD ,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F . 求证:△BCF ≌△CAE .BC D EF9. 多项式9x 2+1加上一个单项式后,能使它成为一个整式的完全平方式,则可以加上的单项式共有________个,分别是______________________________.【参考答案】1.1<AD <42.2.3(提示:延长AF 交BC 于点G ,导角证明AE =EG )3.证明略(提示:延长AD 到点P ,使得AD =PD ,连接CP ,证明△ABD ≌△PCD ,△EAF ≌△PCA )4.证明略(提示:延长FE 到点H ,使得FE =EH ,连接CH ,证明△BFE ≌△CHE ,导角)5.证明略(提示:延长EG 交AD 于点P ,连接CE ,CP ) 6.证明略7.5;-1,-9x 2,-6x ,6x ,814x 4三角形全等之截长补短(讲义)一、知识点睛截长补短:题目中出现__________________________时,考虑截长补短;截长补短的作用是____________________________________________________________________________________.二、精讲精练1. 已知:如图,在△ABC 中,∠1=∠2,∠B =2∠C .求证:AC =AB +BD .2. 已知:如图,在正方形ABCD 中,AD =AB ,∠D =∠ABC =∠BAD =90°,E ,F 分别为DC ,BC 边上的点,且∠EAF =45°,连接EF .求证:EF =BF +DE .3. 已知:如图,在△ABC 中,∠ABC =60º,△ABC 的角平分线AD ,CE 交于点O .求证:AC =AE +CD .F EA B DC21D CA A EBD CO4. 已知:如图,在△ABC 中,∠A =90º,AB =AC ,BD 平分∠ABC ,CE ⊥BD 交BD的延长线于点E .求证:CE =21BD .5. 如图,在梯形ABCD 中,AD ∥BC ,CE ⊥AB 于E ,△BDC 为等腰直角三角形,∠BDC =90°,BD CD ,CE 与BD 交于F ,连接AF .求证:CF =AB +AF .三、回顾与思考________________________________________________________________________________________________________________________________________________________________________【参考答案】【知识点睛】线段间的和差倍分;把几条线段间的数量关系转为两条线段的等量关系. 【精讲精练】 1.证明略 提示:方法一:在AC 上截取AE =AB ,连接DE ,证明△ABD ≌△AED ,然后再证明CE =BD ;ACDEBFCEDA方法二:延长AB到E,使BE=BD,证明△ADE≌△ADC2.证明略提示:延长FB到G,使BG=DE,连接AG,证明△ABG≌△ADE,再证明△AFG≌△AFE)3.证明略提示:在AC上截取AF=AE,连接OF,证明△AEO≌△AFO,∠AOC=120°,再证明△COF≌△COD)4.证明略提示:延长CE交BA的延长线于点F,证明△BEF≌△BEC,得EC=EF,再证明△ACF≌△ABD,得CF=BD)5.证明略提示:方法一:延长BA交CD的延长线交于点H,证明△BDH≌△CDF,得DH=DF,BH=CF,再证明△ADH≌△ADF,得AH=AF;方法二:在CF上截取CH=AB,连接DH,证明△DHC≌△DAB,得DH=DA,CH=BA,∠HDF=∠ADF=45°,再证明△ADF≌△HDF,得AF=HF)三角形全等之截长补短(每日一题) 姓名_________1. 在△ABC 中,AD ⊥BC 于D ,∠B =2∠C .求证:CD =AB +BD .DCBA2. 如图,在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点.求证:AB -AC >PB -PC .PD A 213. 已知:如图,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,∠A +∠C =180°.求证:BD =AB +CD .12A D PN4. 在正方形ABCD 中,点E 在CB 延长线上,点F 在DC 延长线上,∠EAF =45°. 求证:DF =EF +BE .A BCDEF5. 如图,在正方形ABCD 中,E 为BC 边上任意一点,AF 平分∠DAE .求证:AE =BE +DF .FEDCBA【参考答案】1. 证明:如图,在线段DC 上截取DE ,使DE =BD ,连接AE .∵AD ⊥BC∴∠ADB =∠ADE =90° 在△ABD 和△AED 中AD ADADB ADE DB DE =⎧⎪∠=∠⎨⎪=⎩ ∴△ABD ≌△AED (SAS ) ∴∠B =∠1,AB =AE ∵∠B =2∠C ∴∠1=2∠C∵∠1是△AEC 的一个外角 ∴∠1=∠C +∠2 ∴∠C =∠2 ∴AE =CE∵CD =CE +ED ∴CD =AE +BD ∴CD =AB +BD(如果延长DB 到点F ,使BF =AB ,连接AF 也可进行证明)2. 证明:如图,在线段AB 上截取AE =AC ,连接PE .则AB -AC =AB -AE =EB 在△AEP 和△ACP 中12AE AC AP AP =⎧⎪∠=∠⎨⎪=⎩21ABCE12A BCDP∴△AEP ≌△ACP (SAS ) ∴PE =PC在△PEB 中,PB -PE <EB ∴PB -PC <AB -AC 即AB -AC >PB -PC(延长AC 到点F ,使AF =AB ,连接PF ,也可证明结论)3. 证明:如图,在BC 上截取BE =BA ,连接PE .在△ABP 和△EBP 中12BA BE BP BP =⎧⎪∠=∠⎨⎪=⎩∴△ABP ≌△EBP (SAS ) ∴∠A =∠3∵∠A +∠C =180°,∠3+∠4=180° ∴∠4=∠C ∵PD ⊥BC∴∠PDE =∠PDC =90° 在△PDE 和△PDC 中4CPDE PDC PD PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△PDE ≌△PDC (AAS ) ∴DE =DC ∴BD =BE +ED∴BD =AB +CD (过点P 作PF ⊥BA 于F ,也可进行证明)4. 证明:如图,在DF 上截取DG =BE ,连接AG .∵四边形ABCD 为正方形∴∠D =∠BAD =∠ABC =90°,AB =AD ∴∠ABE =∠D =90° 在△ABE 和△ADG 中AB AD ABE D BE DG =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ADG (SAS ) ∴AG =AE ,∠1=∠2 ∵∠EAF =45°,43ENP D CB A 214321GFED CBA∴∠2+∠3=45° ∴∠1+∠3=45° ∴∠GAF =45°=∠EAF 在△EAF 和△GAF 中4AE AG EAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△EAF ≌△GAF (SAS ) ∴EF =GF ∵DF =GF +DG ∴DF =EF +BE5. 证明:如图,延长EB 到点G ,使BG =DF ,连接AG .54321GA BC DEF∵四边形ABCD 为正方形∴AB =AD ,∠D =∠ABC =∠BAD =90° ∴∠ABG =∠D =90° 在△ABG 和△ADF 中AB AD ABG ADF BG DF =⎧⎪∠=∠⎨⎪=⎩∴△ABG ≌△ADF (SAS ) ∴∠1=∠2,∠5=∠G∵AF 平分∠DAE ∴∠1=∠3 ∵∠1+∠5=90°∴∠3+∠G=90°∵∠1+∠3+∠4=90°∴∠2+∠3+∠4=90°∴∠2+∠4=∠G∴AE=EG=BE+BG∴AE =BE+DF三角形全等之截长补短随堂测试题姓名________6.已知:如图,在梯形ABCD中,AD∥BC,∠DAB的平分线AE交CD于E,连接BE,且BE平分∠ABC.求证:AB=AD+BC.【参考答案】证明略提示方法一:在AB上截取AF=AD,连接EF,证明△ADE≌△AFE,再证明△BFE ≌△BCE;方法二:延长AE交BC的延长线于点F,证明△ABE≌△FBE,再证明△ADE ≌△FCE)三角形全等之截长补短(作业)1.如图,在△ABC中,∠BAC=60°,∠ABC=80°,AD是∠BAC的平分线.求证:AC=AB+BD.2.如图,AC平分∠BAD,CE⊥AB,∠B+∠D=180°.求证:AE=AD+BE.EDCBACADC3. 如图,在△ABC 中,∠A =100°,∠ABC =40°,BD 是∠ABC 的平分线,延长BD至E ,使DE =AD .求证:BC =AB +CE .4. 如图,在等边三角形ABC 中,点E ,F 分别在AB ,AC 上,∠EDF =60°,DB =DC ,∠BDC =120°.求证:EF =BE +CF .5. 多项式16x 2+4加上一个单项式后,能使它成为一个整式的完全平方式,则可以加上的单项式共有________个,分别是______________________________.6. 如图,在△ABC 中,AD ⊥BC 于点D ,BE =ED =DC ,∠1=∠2,则:①AD 是△ABC 的边_________上的高,也是________的边BD 上的高,还是△ABE 的边___________上的高;②AD 既是_________的边_______上的中线,又是_______边上的高,还是_________的角平分线.7. 已知:如图,AD ∥EF ,BF ∥DG ,∠A =∠B =∠G =35°.求∠EFG 的度数.CDAEB FCE DABAEBDCFE D CA 218. 计算下列各式:(1)-(3a 3b -2ab 3)÷(-ab )-(-a -2b )(-a +2b )-(-2a )2;(2)01122022111()3(3)3()()(3)233----⨯π---⨯+-÷---.【参考答案】1.证明略 提示:方法一:在AC 上截取AE =AB ,连接DE ,证明△ABD ≌△AED ,再证明CE =BD ; 方法二:延长AB 到E ,使BE =BD ,证明△ADE ≌△ADC 2.证明略提示:在AE 上截取AF =AD ,证明△CDA ≌△CFA ,再证明BE =FE 3.证明略提示:在BC 上截取BF =BA ,连接DF ,证明△ABD ≌△FBD ,再证明△DFC ≌△DEC 4.证明略提示:延长FC 到G ,使CG =BE ,证明△BED ≌△CGD ,得ED =GD ,∠BDE =∠CDG ,再证明△EFD ≌△GFD ,得EF =GF 5.5;16x 4, ±16x ,-4,-16x 2;6.①BC ,△ABD ,BE ; ②△AEC ,EC ,EC ,∠EAC7.略;8.(1。
2020最新人教版数学八年级上册几何证明方法-倍长中线与截长补短-教师版

倍长中线与截长补短模块一倍长中线中线是三角形中的重要线段之一,当题目的条件中有中线时,我们常采用“倍长中线法”添加辅助线,构造一组旋转型的全等,利用全等的结论来解决问题.倍长中线法,就是将三角形的中线延长一倍,以便构造出“8字型”全等.但是给出的条件并不一定要仅限于三角形的中线才可以,有些时候,只要已知条件中有中点就可以运用“倍长中线法”来解决问题.倍长中线(1)如图,AD为△ABC的中线,延长AD至E,使DE=AD,连接CE,求证:AB=CE,且AB//CE.G FEDCBA(2D 是BC 边中点,,求的取值范围.ABCD(3)如图,在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF =EF ,求证:AC =BE .【答案】延长AD 到G ,使DG =AD ,连结BG ∵BD =CD ,BDG CDA ∠=∠,AD =GD ∴ADC GDB ≅∴AC =GB .G EAF ∠=∠又∵AF =EF ,∴EAF AEF ∠=∠ ∴G BED ∠=∠∴BE =BG ,∴BE =AC .倍长类中线如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延长线于点F ,交AB 于点G ,若BG CF =,求证:AD 为ABC ∆的角平分线.BCFEDC BAHAF GBE DC【答案】延长FE 到点H ,使HE FE =,连结BH . 在CEF ∆和BEH ∆中 CE BE CEF BEH FE HE =⎧⎪∠=∠⎨⎪=⎩∴CEF BEH ∆∆≌∴EFC EHB ∠=∠,CF BH BG == ∴EHB BGE ∠=∠,而BGE AGF ∠=∠ ∴AFG AGF ∠=∠ 又∵EF AD ∥∴AFG CAD ∠=∠,AGF BAD ∠=∠ ∴CAD BAD ∠=∠∴AD 为ABC ∆的角平分线.提示:也可延长GE 至H ,使EH GE =,连接CH倍长三角形中线进阶已知,ABC ∆中,AB =AC ,CE 是AB 边上的中线,延长AB 到D ,使BD =AB . 求证:(1)CD =2CE ;(2)D ACE ∠=∠.【答案】(1) 延长CE 到F ,使EF =CE ,连结BF . ∵CE 是AB 的中线,∴AE =EB ,∴EBF EAC ≅ ∴BF =AC =BD ,EBF EAC ∠=∠,∴FBC FBE EBC A ACB DBC ∠=∠+∠=∠+∠=∠,∴FBC DBC ≅ ∴CD =CF =2CE .∠FCB =∠BCD .(2)解法一:又∵AB =AC ∴∠ACB =∠ABC ,∴∠ACB =∠FCB +∠ACE ,F GE DCBAE D CBA FCA EB DFE NABD C∠ABC =∠BCD +∠D ,∴∠D =∠ACE . 解法二:由①中的两个全等,可以得到: F ACE F D ∠=∠∠=∠,,∴D ACE ∠=∠.倍长中线与角平分线综合已知AD 为ABC ∆的中线,ADB ∠,ADC ∠的平分线分别交AB 于E 、交AC 于F . 求证:BE CF EF +>.【答案】延长FD 到N ,使DN DF =,连接BN 、EN . 易证BND ∆≌CFD ∆,∴BN CF =,又∵ADB ∠,ADC ∠的平分线分别交AB 于E 、交AC 于F ,∴90EDF EDN ∠=∠=,利用SAS 证明EDN ∆≌EDF ∆,∴EN EF =, 在EBN ∆中,BE BN EN +>,∴BE CF EF +>.模块二 截长和补短截长补短(1)如图,在ABC △中,2B C ∠=∠,BAC ∠的平分线AD 交BC 与D . 求证:AB +BD =AC .【答案】方法一:在AC 上取一点E ,使得AB =AEFE AB D CDC B AABCDEED C B A FM AB CDE ED CB A连结DE .在ABD △和AED △中 AB =AE ,BAD EAD ∠=∠AD =AD∴ABD AED ≅∴BD =ED ,B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠EDC C ∠=∠,ED =EC ∴AB +BD =AC .方法二:在AB 的延长线上取一点E 使得AC =AE ,连结DE .在AED △和ACD △中,AE =AC EAD CAD ∠=∠,AD =AD∴AED ACD ≅,∴C E ∠=∠又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE =BD ,∴AB +BD =AC .方法三:延长DB 到点E 使得AB =BE ,连结AE 则有EAB E ∠=∠ 2ABC E EAB E ∠=∠+∠=∠又∵2ABC C ∠=∠,∴AE =AC 又∵EAD EAB BAD E DAC C DAC ADE ∠=∠+∠=∠+∠=∠+∠=∠∴AE =DE ,∴AB +BD =EB +BD =ED =AE =AC方法四:如图,作BF 平分ABC ∠交AD 、AC 于E 、F 点 延长BF 到M ,使FM =FA ,连结AM ∴ABF FBC ∠=∠∵2ABC C ∠=∠,∴FBC C ∠=∠.∴FB =FC ∵AF =FM ,∴M FAM ∠=∠ ∵AFE FBC C ∠=∠+∠,又AFE M FAM ∠=∠+∠ 即22AFE M C ∠=∠=∠.∴C M ∠=∠ ∴M ABM DBF C ∠=∠=∠=∠.∴AB =AM ∵ADB C DAC ∠=∠+∠ 且DEB EBA BAE ∠=∠+∠∵BAD DAC ∠=∠,∴ADB DEB ∠=∠.∴BD =BE 同理MA =ME∵AF =FM ,FB =FC ,∴AC =BM .∴AC =AB +BD(2)如图所示,在ABC △中,AD BC ⊥于点D ,2B C ∠=∠.求证:AB BD CD +=.E DCBAABDECMFEDCB A【答案】由AD BC ⊥,2B C ∠=∠知:如果在CD 上截取DE DB =,连接AE ,就可以构造出两个等腰三角形ABE △和AEC △. 如图,在CD 上截取DE DB =,连接AE . 因为AD BC ⊥,DE DB =,所以AE AB =,于是B AEB ∠=∠,又因为AEB C CAE ∠=∠+∠,2B C ∠=∠, 所以CAE C ∠=∠, 于是AE EC =,故AB BD AE ED EC ED CD +=+=+=.(3)如图,AC 平分BAD ∠,CE AB ⊥,且AE AD BE =+, 求证:180B D ∠+∠=︒.【答案】在AE 上截取一点F ,使得AD =AF , 证ACD ≌ACF 即可. (4)已知:如图,四边形ABCD 是正方形,FAD FAE ∠=∠.求证:BE +DF =AE .【答案】延长CB 至M ,使得BM =DF ,连接AM . ∵AB =AD ,AD CD ⊥,AB BM ⊥,BM =DF ,∴,∴AFD AMB ∠=∠,DAF BAM ∠=∠, ∵AB CD ,∴ADF BAF EAF BAE BAE BAM EAM ∠=∠=∠+∠=∠+∠=∠, ∴AMB EAM ∠=∠,∴AE =EM =BE +BM =BE +DF .C D BAFEDCBAABM ADF △≌△FEDCA截长补短进阶如图所示,在ABC △中,100A ∠=,40ABC ∠=,BD 是ABC ∠的平分线,延长BD 至E ,使DE =AD .求证:BC =AB +CE【答案】在BC 上取一点F ,使得BF =BA 易证得ADB FDB ≅ ∴DF =AD , 又∵DA =DE ∴DF =DE∵100A ∠=,AB =AC ∴40ABC ∠= ∵BD 平分ABC ∠, ∴20ABD ∠= ∴60ABD FDB ∠=∠=∵60CDE ADB ∠=∠= ∴ 60FDC EDC ∠=∠= ∴DCF DCE ≅ ∴FC =EC∴BC =BF +FC =AB +CE截长补短应用进阶如图,ABC △中,AB =AC ,108A ∠=,BD 平分ABC ∠交AC 于D 点.求证:BC =AC +CD .【答案】方法一:在BC 上截取E 点使BE =BA ,连结DE . ∵BD 平分ABC ∠,∴ABD EBD ∠=∠.EDCBAAB CDE DCB ADCBAF在ABD △与EBD △中∵AB =EB ,ABD EBD ∠=∠, BD =BD ∴ABD EBD ≅,∴A DEB ∠=∠∵108A ∠=, ∴108DEB ∠=∴72DEC ∠=. 又∵361854ADB ∠=+= ∴72CDE ∠=∴CDE DEC ∠=∠ ∴CD =CE∵BC =BE +EC ,∴BC =AC +CD方法二:如图,延长CA 到F ,使CF =CB ,连结BF . ∵AB =AC ,且108BAC ∠=, ∴36ABC C ∠=∠=. ∵CB =CF ,∴F FBC ∠=∠.∴FAB C ABC ∠=∠+∠. ∴72FAB ∠=.∵12ADB C ABC ∠=∠+∠,∴54ADB ∠=.又∵54FDB ∠= ∴BF =AB =AC =FD .∴AF =CD .∴BC =AC +CD .类型之一 轴对称及轴对称图形1.[2017·盐城]下列图形中,不是轴对称图形的是( C )A B C D【解析】选项A,B,D均可以沿一条直线折叠使图形左右两边的部分重合,故均为轴对称图形,只有C选项不是轴对称图形,故选C.2.[2018·武汉]点A(2,-5)关于x轴对称的点的坐标是( A )A.(2,5) B.(-2,5)C.(-2,-5) D.(-5,2)类型之二线段的垂直平分线3.如图13-1,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( A )图13-1A.115°B.120°C.130°D.140°【解析】由题意知∠B′FC=90°-∠2=50°,由折叠知∠1=12(180°+50°)=115°.4.[2018·黄冈]如图13-2,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( B )图13-2A.50°B.70°C.75°D.80°【解析】∵DE是AC的垂直平分线,∴DA=DC,∴∠DAC=∠C=25°,∵∠B=60°,∴∠BAC=95°,∴∠BAD=∠BAC-∠DAC=70°.5.[2018·南充]如图13-3,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C=__24__°.图13-3【解析】∵DE是AC的垂直平分线,∴EA=EC,∴∠EAC=∠C,∴∠FAC=∠EAC+19°,∵AF平分∠BAC,∴∠FAB=∠EAC+19°,∵∠B+∠BAC+∠C=180°,∴70°+2(∠C+19°)+∠C=180°,解得∠C=24°.6.[2018春·丹东期末改编]如图13-4,在△ABC中,边AB的垂直平分线交AB,BC于点M,E,边AC的垂直平分线交AC,BC于点N,F,△AEF的周长为10.图13-4(1)BC=__10__;(2)若∠B+∠C=45°,则△AEF是什么特殊三角形?解:(1)∵ME是边AB的垂直平分线,∴AE=BE,∵NF是边AC的垂直平分线,∴AF=FC,∵△AEF的周长为10,∴AE+EF+AF=BE+EF+FC=BC=10,则BC=10;(2)由(1)知∠B=∠BAE,∠C=∠FAC,∵∠B+∠C=45°,∴∠B+∠C+∠BAE+∠FAC=90°,∴∠FAE=90°,∴△AEF是直角三角形.7.[2017·连云港]如图13-5,等腰三角形ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接BE,CD,交于点F.图13-5(1)判断∠ABE与∠ACD的数量关系,并说明理由;(2)求证:过点A,F的直线垂直平分线段BC.解:(1)∠ABE=∠ACD.理由:∵AB=AC,∠BAE=∠CAD,AE=AD,∴△ABE≌△∠ACD.∴∠ABE=∠ACD;(2)证明:∵AB=AC,∴∠ABC=∠ACB.由(1)可知,∠ABE=∠ACD,∴∠FBC=∠FCB,∴FB=FC.又∵AB=AC,∴点A,F均在线段BC的垂直平分线上,即直线AF垂直平分线段BC.类型之三等腰三角形的性质与判定8.[2018·邵阳]如图13-6,在等腰三角形ABC中,AB=AC,∠A=36°,将△ABC中的∠A沿DE向下翻折,使点A落在点C处.若AE=3,则BC的长是__3__.图13-6【解析】∵AB=AC,∠A=36°,∴∠B=∠BCD=72°.∵将△ABC 中的∠A 沿DE 向下翻折,使点A 落在点C 处, ∴根据折叠的性质,得△AED ≌△CED , ∴AE =CE ,∠A =∠ECD =36°, ∴∠BCE =∠BCD -∠ECD =36°, ∴∠BEC =180°-∠B -∠BCE =72°, ∴∠BEC =∠B ,∴BC =CE . ∵AE =3,∴BC =CE =AE = 3.9.[2018·镇江]如图13-7,△ABC 中,AB =AC ,点E ,F 在边BC 上,BE =CF ,点D 在AF 的延长线上,AD =AC .图13-7(1)求证:△ABE ≌△ACF ;(2)若∠BAE =30°,则∠ADC 的度数是多少? 解: (1)证明:∵AB =AC , ∴∠B =∠ACF .在△ABE 和△ACF 中,⎩⎪⎨⎪⎧AB =AC ,∠B =∠ACB ,BE =CF ,∴△ABE ≌△ACF ;(2)∵△ABE ≌△ACF ,∠BAE =30°, ∴∠CAF =∠BAE =30°,∵AD =AC ,∴∠ADC =∠ACD , ∴∠ADC =180°-30°2=75°.10.如图13-8,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,AE 平分∠BAC 交CD 于点F ,交BC 于点E ,试说明△CEF 是等腰三角形.图13-8解: 由已知得∠DAF +∠AFD =90°, ∠FAC +∠CEF =90°,又∵∠AFD =∠CFE ,∠FAC =∠DAF , ∴∠CFE =∠CEF ,即△CEF 是等腰三角形.11.如图13-9,△ACB 和△DCE 均为等腰三角形,点A ,D ,E 在同一直线上,连接BE .图13-9(1)若∠CAB =∠CBA =∠CDE =∠CED =50°,求证:AD =BE ; (2)在(1)的条件下,求∠AEB 的度数.解: (1)∵∠CAB =∠CBA =∠CDE =∠CED =50°, ∴∠ACB =∠DCE =180°-2×50°=80°.∵∠ACB =∠ACD +∠DCB , ∠DCE =∠DCB +∠BCE , ∴∠ACD =∠BCE .∵△ACB 和△DCE 均为等腰三角形, ∴AC =BC ,DC =E C.在△ACD 和△BCE 中,⎩⎪⎨⎪⎧AC =BC ,∠ACD =∠BCE ,DC =EC ,∴△ACD ≌△BCE (SAS),∴AD =BE ; (2)∵△ACD ≌△BCE ,∴∠ADC =∠BEC . ∵点A ,D ,E 在同一直线上,且∠CDE =50°, ∴∠ADC =180°-∠CDE =130°,∴∠BEC =130°. ∵∠BEC =∠CED +∠AEB ,且∠CED =50°, ∴∠AEB =∠BEC -∠CED =130°-50°=80°.类型之四 等边三角形的判定与性质12.[2018·福建A 卷]如图13-10,等边三角形ABC 中,AD ⊥BC ,垂足为D ,点E 在线段AD 上,∠EBC =45°,则∠ACE 等于( A )图13-10A.15°B.30°C.45°D.60°【解析】∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵AD⊥BC,∴BD=CD,AD是BC的垂直平分线,∴BE=CE,∴∠EBC=∠ECB=45°,∴∠ACE=60°-45°=15°.类型之五含30°角的直角三角形的性质的运用13.如图13-11,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=__2__.图13-11【解析】∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD平分∠CAB,∴∠CAD=30°,∴BD=AD=2CD=2.14.如图13-12,在△ABC中,BA=BC,∠B=120°,线段AB的垂直平分线MN交AC于点D,且AD=8 cm.求:图13-12 第14题答图(1)∠ADG 的度数; (2)线段DC 的长度.解: (1)∵在△ABC 中,BA =BC , ∴∠A =∠C ,又∵∠B =120°, ∴∠A =12×(180°-120°)=30°,∵MN ⊥AB ,∴∠AGD =90°, ∴∠ADG =90°-30°=60°; (2)如答图,连接BD . ∵MN 是AB 的垂直平分线,∴AD =BD ,∠A =∠ABD =30°,∴∠CBD =90°, 由(1)知∠A =∠C =30°,∴BD =12CD ,∴DC =2BD =2AD ,又∵AD =8 cm ,∴DC =16 cm.类型之六 等腰三角形探究型问题15.[2017·莱芜]已知△ABC 与△DEC 是两个大小不同的等腰直角三角形. (1)如图13-13①,连接AE ,DB .试判断线段AE 和DB 的数量和位置关系,并说明理由;(2)如图②,连接DB ,将线段DB 绕D 点顺时针旋转90°到DF ,连接AF ,试判断线段DE 和AF 的数量和位置关系,并说明理由.图13-13解:(1)AE=DB,AE⊥DB.理由:∵CA=CB,CE=CD,∠ACE=∠BCD=90°,∴Rt△ACE≌Rt△BCD,∴AE=DB.如答图①,延长DB交AE于点M,∵Rt△ACE≌Rt△BCD,∴∠AEC=∠BDC.又∵∠AEC+∠EAC=90°,∴∠BDC+∠EAC=90°,∴在△AMD中,∠AMD=180°-90°=90°,∴AE⊥DB;(2)DE=AF,DE⊥AF.第15题答图理由:如答图②,设ED与AF相交于点N,由题意可知BE=AD. ∵∠EBD=∠C+∠BDC=90°+∠BDC,∠ADF=∠BDF+∠BDC=90°+∠BDC,∴∠EBD=∠ADF,又∵DB=DF,A EF∴△EBD ≌△ADF ,∴DE =AF ,∠E =∠FAD =45°, ∵∠EDC =45°,∴∠AND =90°,∴DE ⊥AF .类型之七 倍长中线与截长补短(选做)16. 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE交AC 于F ,AF 与EF 相等吗?为什么?【答案】延长AD 到G ,使DG AD =,连结BG ∵BD CD =,BDG CDA ∠=∠,AD GD = ∴ADC GDB ∆∆≌.∴AC GB =.G EAF ∠=∠ 又∵BE AC =,∴BE BG =∴G BED ∠=∠,而BED AEF ∠=∠ ∴AEF FAE ∠=∠,故FA FE =.17. 已知,如图,ABC 中,D 是BC 的中点,DE DF ⊥,试判断BE +CF 与EF 的大小关系,并证明你的结论.【答案】BE +CF >EF过点B 作AC 的平行线,交FD 的延长线于点G ∵BG AC ≤(已知)∴1C ∠=∠(两直线平行,内错角相等) ∵D 是BC 中点(已知)FED CBA FEDCBAED CBA∴BD =CD (中点定义) 在BGD 和CFD 中,123CBD CD ∠=∠⎧⎪=⎨⎪∠=∠⎩(已证)(已证)(已知) ∴()BGD CFD ASA ∆∆≌∴BG =CF ,GD =FD 全等三角形对应边相等) ∵DE DF ⊥(已知)∴(垂直定义) 在EDG 和EDF 中,4ED EDEDG GD FD =⎧⎪∠=∠⎨⎪=⎩(公共边)(已证)(已证) ∴()EDG EDF SAS ∆∆≌∴EG =EF (全等三角形对应边相等)∵在BEG 中,BE +BG >EG (三角形中两边之和大于第三边) ∴BE +CF >EF (等量代换)18. 如图,在ABC 中,AB +BD =AC ,BAC ∠的平分线AD 交BC 与D .求证:2B C ∠=∠.【答案】在AC 上取一点E ,使得AB =AE ,连结DE .在ABD 和AED 中, AB =AE ,BAD EAD ∠=∠, AD =AD .∴ABD AED ∆∆≌,∴BD =ED ,B AED ∠=∠又∵AB +BD =AC ,∴EC =BD =ED2AED EDC C C B ∠=∠+∠=∠=∠.其他方法参考例题.490EDG ∠=∠=°D CB A。
学而思初二数学秋季班第2讲.倍长中线与截长补短.提高班.教师版

1初二秋季·第2讲·提高班·教师版三角形9级 全等三角形的经典模型(二)三角形8级全等三角形的经典模型(一) 三角形7级倍长中线与截长补短倍长中线与截长补短满分晋级漫画释义2倍长中线 与截长补短2初二秋季·第2讲·提高班·教师版定 义示例剖析倍长中线:即延长三角形的中线,使得延长后的线段是原中线的两倍.其目的是构造一对对顶的全等三角形; 其本质是转移边和角.EDABC其中BD CD =,延长AD 使得DE AD =,则BDE CDA △≌△.【例1】 已知ABC △中,AD 平分BAC ∠,且BD CD =,求证:AB AC =. 【解析】 延长AD 到E ,使DE AD =,连接CE .则CDE BDA △≌△,∴CE AB =,CED BAD ∠=∠, ∵AD 平分BAC ∠,∴BAD CAD ∠=∠, ∴CED CAD ∠=∠,∴CE AC =, ∴AB AC =.思路导航例题精讲知识互联网题型一:倍长中线EABCDABCD3初二秋季·第2讲·提高班·教师版【教师备选】教师可借用例1对等腰三角形三线合一性质的逆命题进行简单归纳:已知角平分线+中线证等腰三角形,如例1; 已知角平分线+高证等腰三角形,如拓展1; 已知中线+高证等腰三角形,如拓展2.【拓展1】已知△ABC 中,AD 平分∠BAC ,且AD ⊥BC ,求证:AB =AC . 【解析】∵AD 平分∠BAC ,∴∠BAD =∠CAD∵AD ⊥BC ,∴∠ADB =∠ADC =90° ∴△ABD ≌△ACD (SAS) ∴AB =AC .【拓展2】已知△ABC 中,AD ⊥BC ,且BD CD =,求证:AB =AC . 【解析】∵AD ⊥BC ,且BD CD =∴AD 所在直线是线段BC 的垂直平分线 根据垂直平分线上的点到线段两端点距离相等 故AB =AC .【例2】 ⑴如图,已知ABC △中,AB AC =,CE 是AB 边上的中线,延长AB 到D ,使BD AB =.给出下列结论:①AD =2AC ;②CD =2CE ;③∠ACE =∠BCD ;④CB 平分∠DCE ,则以上结论正确的是 . 【解析】 ①正确.∵AB AC =,BD AB =,∴AD =2AC .②、④正确.延长CE 到F ,使EF CE =,连接BF . ∵CE 是AB 的中线,∴AE EB =. 在EBF △和EAC △中 AE BEAEC BEF CE FE =⎧⎪∠=∠⎨⎪=⎩典题精练ABDEDCBA4初二秋季·第2讲·提高班·教师版∴EBF EAC ≌△△∴BF AC AB BD ===,EBF EAC ∠=∠ ∴FBC FBE EBC A ACB DBC ∠=∠+∠=∠+∠=∠ 在FBC △和DBC △中 FB DB FBC DBC BC BC =⎧⎪∠=∠⎨⎪=⎩∴FBC DBC ≌△△∴2CD CF CE ==,∠FCB =∠DCB 即CD =2CE ,CB 平分∠DCE .③错误.∵∠FCB =∠DCB ,而CE 是AB 边上中线而不是∠ACB 的角平分线故∠ACE 和∠BCD 不一定相等.⑵如图,在△ABC 中,点D 、E 为边BC 的三等分点,给出下列结论:①BD =DE =EC ;②AB +AE >2AD ;③AD +AC >2AE ;④AB +AC >AD +AE ,则以上结论正确的是 .NM ED CBAEDCBA【解析】 点D 、E 为边BC 的三等分点,∴BD =DE =CE 延长AD 至点M ,AE 至点N ,使得DM =AD ,EN =AE ,连接EM 、CN ,则可证明△ABD ≌△MED ,进而可得AB +AE >2AD ,再证明△ADE ≌△NCE ,进而可得AD +AC >2AE ,将两式相加可得到AB +AE +AD +AC >2AD +2AE ,即AB +AC >AD +AE . ∴①②③④均正确.【例3】 如图,已知在ABC △中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.FCAEBD5初二秋季·第2讲·提高班·教师版【解析】 延长AD 到G ,使DG AD =,连接BG∵BD CD =,BDG CDA ∠=∠,AD GD = ∴ADC GDB △≌△, ∴AC GB =,G EAF ∠=∠ 又∵AF EF =,∴EAF AEF BED ∠=∠=∠ ∴G BED ∠=∠,∴BE BG =,∴AC BE =.【例4】 在正方形ABCD 中,PQ ⊥BD 于P ,M 为QD 的中点,试探究MP 与MC 的关系.NABCDMPQ Q PMDCBA【解析】 延长PM 至点N ,使PM =MN ,连结CP 、CN 、DN .易证△PMQ ≌△NMD , ∴PB =PQ =DN ,∠PQD =∠NDM ∴PQ ∥DN ,又∵∠BPQ =∠BDN= 90° ∴∠PBQ =∠BDC=∠NDC =45° 再证△BPC ≌△DNC (SAS) 易证△PCN 为等腰直角三角形, 又∵PM =MN ,∴PM ⊥MC ,且PM =CM .GFEDCBA FE D CBA6初二秋季·第2讲·提高班·教师版定 义示例剖析截长:即在一条较长的线段上截取一段较短的线段DCBA在线段AB 上截取AD AC =补短:即在较短的线段上补一段线段使其和较长的线段相等AB C D延长AC ,使得AD AB =【例5】 在ABC △中,A ∠的平分线交BC 于D ,AB AC CD =+,40B ∠=︒,求C ∠的大小.(希望杯培训题)D C B AED CB A【解析】 在AB 上截取AE AC =,连接DE .∵AE AC =,BAD CAD ∠=∠,AD AD =,∴ACD AED △≌△, ∴C AED ∠=∠,CD DE =,∵AB AC CD =+,AE AC =,∴CD BE DE == ∴40EBD EDB ∠=∠=︒,80C AED ∠=∠=︒例题精讲思路导航题型二:截长补短7初二秋季·第2讲·提高班·教师版D CB AEDCB AD CEBAE DCB A【例6】 如图,在ABC △中,2B C ∠=∠,BAC ∠的平分线AD 交BC 于点D .求证:AB BD AC +=. 【解析】方法一:(截长)在AC 上截取AB AE =,连接DE .在ABD △和AED △中AB AE =,BAD EAD ∠=∠,AD AD =∴ABD AED △≌△∴BD ED =,B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠ ∴EDC C ∠=∠,∴ED EC =∴AB BD AC +=. 方法二:(补短)延长AB 到点E 使得AC AE =,连接DE . 在AED △和ACD △中,AE AC =,EAD CAD ∠=∠,AD AD = ∴AED ACD △≌△,∴C E ∠=∠ 又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE BD =,∴AB BD AC +=.方法三:(补短)延长DB 到点E 使得AB BE =,连接AE 则有EAB E ∠=∠,2ABC E EAB E ∠=∠+∠=∠ 又∵2ABC C ∠=∠,∴C E ∠=∠ ∴AE AC = EAD EAB BAD E DAC ∠=∠+∠=∠+∠C DAC ADE =∠+∠=∠∴AE DE =,∴AB BD EB BD ED AE AC +=+=== ∴AB +BD=AC若题目条件或求证结论中含有“a b c =+”的条件,需要添加辅助线时多考虑“截长补短”.建议教师此题把3种解法都讲一下,方便学生更加深刻理解这种辅助线添加方法.【例7】 已知:在ABC △中,AB CD BD =-,AD BC ⊥,求证:2B C ∠=∠.【解析】 方法一:在DC 上取一点E ,使BD DE =,如图1,在ABD △和AED △中,AD BC ⊥,BD ED =,AD AD =.典题精练DC BA8初二秋季·第2讲·提高班·教师版∴ABD AED △≌△. ∴AB AE =,B AED ∠=∠.又∵AE AB CD BD CD DE EC ==-=-= ∴C EAC ∠=∠,∴2C EAC AED C ∠+∠=∠=∠ ∴2B C ∠=∠.图1E AB CD图2EAB CD方法二:延长DB 到点E ,使BE AB =,如图2, ∴E EAB ∠=∠.∵AB CD BD =-,∴ED CD =.在AED △和ACD △中,AD BC ⊥,ED CD =,AD AD =. ∴AED ACD △≌△. ∴E C ∠=∠. ∵2ABD E ∠=∠ ∴2B C ∠=∠.【探究对象】截长补短法是几何证明题中十分重要的方法,通常来证明几条线段的数量关系,常见做辅助线方法有: 截长法:⑴过某一点作长边的垂线;⑵在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
初二数学(几何证明Ⅱ:倍长中线法及截长补短法专题B)学科教师版

精锐教育学科教师辅导讲义 年 级:初二 科 目:数学 课时数:3课 题 几何证明教学目的 能够灵活运用本节课复习的两种解题方法更好的解决证明题.教学内容【例题讲解】题型一:截长补短法【例1】已知:如图,在△ABC 中,2ABC ACB ∠=∠,AD 是BAC ∠的平分线.求证:AB BD AC +=.(根据图中添加的辅助线用两种方法证明)【提示】截长补短,2种方法‘方法一:方法二:【例2】已知:如图,在△ABC 中,2AB BC =,∠B =60°.求证:∠ACB =90°.【提示】截长补短(两种方法)方法一:方法二:【方法总结】当已知(或求证)“一条线段的长度是另一条线段长度的n 倍”或“一条线段的长度等于两条线段长度的和”时,通常用截长补短法.题型二:倍长中线法【例3】已知三角形的两边长分别为7和9,求第三边上中线长的取值范围.【提示】倍长中线【方法总结】当已知“三角形一边中线”通常运用“倍长中线法“解决问题(注:有时倍长的并不一定是中线).可以倍长过中点的任意一条线段.【借题发挥】1. 已知:如图,DA ⊥AC ,FC ⊥AC ,ADB BDF ∠=∠,CFB DFB ∠=∠.求证:DF AD CF =+.【提示】截长补短,2种方法方法一:方法二:2.已知:如图,在正方形ABCD中,M是BC的中点,点P在DC边上,且AP AB CP=+.求证:2BAP BAM∠=∠.AD CBMP【提示】截长补短,2种方法方法一:方法二:=.求证:AC=BF. 3.已知:如图,AD为△ABC的中线,BE交AC于点E,交AD于点F,且AE EF【提示】倍长中线法,2种方法方法一:方法二:+=. 4.已知:如图,△ABC是等边三角形,BD是AC边上的高,作DH⊥BC于点H.求证:DC CH BH【提示】截长补短法,两种方法方法一:方法二:【课堂总结】【课后作业】1.已知D 为EC 的中点,EF ∥AB ,且EF=AC ,求证:AD 平分∠BAC【提示】倍长中线法:延长FD 至G ,使FD=DG ,联结CG2.已知如图,在△ABC 中,AD ⊥BC 于点D ,AB BD DC +=.求证:∠2B =∠C .【提示】截长补短法,两种方法方法一:方法二:二、综合提高训练1.已知:如图,C 是AB 的中点,点E 在CD 上,且AE BD =.求证:AEC BDC ∠=∠.【提示】倍长中线法,2种方法方法一:方法二:2.如图,已知在△ABC 中,∠A=90°,AB=AC, ∠B 的平分线与AC 交于点D ,过点C 作CH ⊥BD ,H 为垂足。
人教版八年级上册 几何证明-常用辅助线专题讲义:中线倍长法和截长补短法(无答案)

几何证明-常用辅助线 (一)中线倍长法:例1 、求证:三角形一边上的中线小于其他两边和的一半。
已知:如图,△ABC 中,AD 是BC 边上的中线,求证:AD ﹤21(AB+AC) 分析:要证明AD ﹤21(AB+AC),就是证明AB+AC>2AD ,也就是证明两条线段之和大于第三条线段,而我们只能用“三角形两边之和大于第三边”,但题中的三条线段共点,没有构成一个三角形,不能用三角形三边关系定理,因此应该进行转化。
待证结论AB+AC>2AD 中,出现了2AD ,即中线AD 应该加倍。
证明:延长AD 至E ,使DE=AD ,连CE ,则AE=2AD 。
在△ADB 和△EDC 中,AD =DE ∠ADB =∠EDCBD =DC∴△ADB ≌△EDC(SAS) ∴AB=CE又 在△ACE 中, AC+CE >AE∴AC+AB >2AD ,即AD ﹤21(AB+AC)小结:(1)涉及三角形中线问题时,常采用延长中线一倍的办法,即中线倍长法。
它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中,以利于问题的获解。
课题练习:ABC ∆中,AD 是BAC ∠的平分线,且BD=CD ,求证AB=ACC例2: 中线一倍辅助线作法△ABC 中方式1: 延长AD 到E ,AD 是BC 边中线使DE=AD ,连接BE 方式2:间接倍长作CF ⊥AD 于F ,延长MD 到N ,作BE ⊥AD 的延长线于使DN=MD , 连接BE 连接CD例3:△ABC 中,AB=5,AC=3,求中线AD 的取值范围例4:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE课堂练习:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例5:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠课堂练习:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE作业:1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
中线倍长法及截长补短经典讲义

几何证明中常用辅助线(一)中线倍长法:例1、求证:三角形一边上的中线小于其他两边和的一半。
已知:如图,△ABC 中,AD 是BC 边上的中线,求证:AD ﹤21(AB+AC)小结:涉及三角形中线问题时,常采用延长中线一倍的办法,即中线倍长法。
它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中,以利于问题的获解。
例2、中线一倍辅助线作法△ABC 中方式1:延长AD 到E , AD 是BC 边中线使连接BE方式2:间接倍长方式3:作CF ⊥AD 于F ,延长MD 到N 作BE ⊥AD 的延长线于E 使DN=MD ,连接BE连接CD例3、△ABC 中,AB=5,AC=3,求中线AD 的取值范围例4、已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE 课堂练习:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线, 求证:∠C=∠BAE 作业:1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论2、已知:如图,?ABC 中,?C=90?,CM ?AB 于M ,AT 平分?BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE. 3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF (二)截长补短法教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例. 例1.已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BDCBCABCD图1-1平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现. 证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中,∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180°.例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的. 证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°, ∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .例3.已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造. 证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD , 在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BP BP PDPE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE .在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PE FE DCBA图1-2ADB CE F1234图2-2ABCDP12N图3-1P12NABCDE 图3-2DCB A 12图4-1∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2 ∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,∴△ABD ≌△AED (AAS ),∴AB =AE . 又AE =AC+CE =AC +DC ,∴AB =AC +DC . 方法二(截长法)在AB 上截取AF =AC ,如图4-3 在△AFD 与△ACD 中,∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD .上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰当选择合适思路进行分析。
倍长中线、截长补短
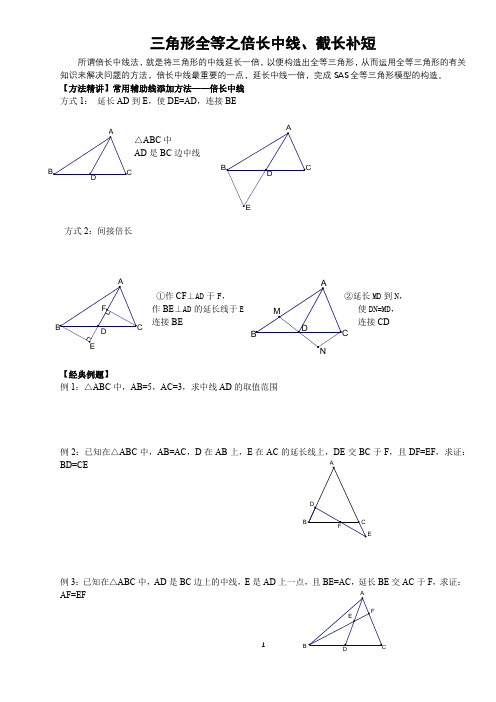
三角形全等之倍长中线、截长补短所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线 方式1: 延长AD 到E ,使DE=AD ,连接BE△ABC 中AD 是BC边中线方式2:间接倍长①作CF ⊥AD 于F ,②延长MD 到N ,作BE ⊥AD 的延长线于使DN=MD , 连接BE 连接CD【经典例题】例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠练习:1、已知:如图,AD 是△ABC 的中线,BE 交AC 于E ,交AD 于F ,且 AE=EF ,求证:AC=BF2、如图,AB=AE ,A B ⊥AE ,AD=AC ,A D ⊥AC ,点M 为BC 的中点,求证:DE=2AM第 1 题图ABFDECC M角平分线中截长补短方法在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗。
例1.已知:如图,在△ABC 中,AB>AC ∠C =2∠B ,∠1=∠2.求证:AB=AC+CD.例2.如图,在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点,连接BP ,CP . 求证:AB -AC >PB -PC .例3.已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.例4.已知:如图,ABCD 是正方形,∠FAD =∠FAE . 求证:BE +DF =AE .DC B A12图4-121PD CB A D OECB AF EDC B A练习:1、已知:△ABC 中,AB=4cm ,BC=6cm ,BD 是AC 边上的中线,求BD 的取值范围。
八年级秋季班第2讲:全等三角形的综合 -教师版

本节课通过推理和专题训练,学会运用全等三角形的判定方法去解决三角形全等的综合问题.通过添加辅助线解决相关的边角证明问题,本节的内容相对综合,难度稍大.全等三角形综合主要是通过全等得出结论,进而求出相应的边和角之间的关系.对于稍复杂的会通过添加平行线,倍长中线或截长补短等方法,解决综合问题.全等三角形的综合内容分析知识结构模块一:全等三角形判定的综合知识精讲【例1】 已知:AE =ED ,BD =AB ,试说明:CA =CD . 【难度】★ 【答案】见解析.【解析】在△ABE 与△DBE 中,AE ED AB BD BE BE =⎧⎪=⎨⎪=⎩, ()ABE DBE SSS ∴∆≅∆,AEB DEB ∴∠=∠, AEC DEC ∴∠=∠.在△ACE 与△DCE 中,AE ED AEC DEC CE CE =⎧⎪∠=∠⎨⎪=⎩, ()AEC DEC SAS ∴∆≅, CA CD ∴=(全等三角形的对应边相等). 【总结】本题主要考查了全等三角形判定定理的应用.【例2】 如图,已知AB =DC ,AC =DB ,BE =CE ,试说明:AE =DE . 【难度】★ 【答案】见解析.【解析】在△ABC 和△DCB 中,AB DCAC DB BC CB =⎧⎪=⎨⎪=⎩, ∴△ABC ≌△DCB (S.S.S ), ∴∠ABC=∠DCB . 在△ABE 和△DCE 中,AB DC ABC DCB BE CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABE ≌△DCE (S.A.S ), ∴AE=DE (全等三角形的对应边相等).【总结】本题主要考查了全等三角形判定定理的应用.例题解析ABECDABCDE【例3】 已知:AB ∥CD ,OE =OF ,试说明:AB =CD . 【难度】★ 【答案】见解析. 【解析】//AB CD ,A D B C ∴∠=∠∠=∠,.(..)A D B CA D AOE DOF AOE DOF OE OF AOE DOF A A S AO DO ∴∠=∠∠=∠∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩∴∆≅∆∴=,在和中,,(..)AO DO AOB DOC A DB C AOB DOC A A S =⎧⎪∆∆∠=∠⎨⎪∠=∠⎩∴∆≅∆在和中, AB CD ∴=(全等三角形的对应边相等). 【总结】本题主要考查了全等三角形判定定理和性质定理的综合应用.【例4】 如图:A 、E 、F 、C 四点在同一条直线上,AE =CF ,过E 、F 分别作BE ⊥AC 、DF ⊥AC ,且AB =CD ,AB ∥CD .试说明:BD 平分EF . 【难度】★★ 【答案】见解析.【解析】∵AB ∥CD ,∴∠A=∠C .在△AGB 和△CGD 中,A CAGB CGD AB CD ∠=∠∠=∠=⎧⎪⎨⎪⎩∴ΔAGB ≌ΔCGD(AAS), ∴BG=DG .∵BE ⊥AC ,DF ⊥AC , ∴∠BEG=∠DFG=90°. 在△BGE 和△DGF 中,BGE DGF BEG DGF BG DG ∠=∠∠=∠=⎧⎪⎨⎪⎩∴ΔBGE ≌ΔDGF (A .A .S ), ∴GE=GF , 即BD 平分EF . 【总结】本题主要考查了全等三角形判定定理和性质定理的应用.ABCDEFOABCDEFG【例5】 如图,已知AD =AE ,AB =AC .试说明:BF =FC . 【难度】★★ 【答案】见解析.【解析】ABE ACD ∆∆在和中,AD AEA A AB AC =⎧⎪∠=∠⎨⎪=⎩,()ABE ACD SAS ∴∆≅∆, B C ∴∠=∠. BD AB AD CE AC AE BD CE =-=-∴=,,.BDF CEF ∆∆在和中,DFB EFCB CBD CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,(..)BDF CEF A A S ∴∆≅∆ , .BF CF ∴= 【总结】本题主要考查了全等三角形判定定理和性质定理的应用.【例6】 如图,在△ABC 中,AC =BC ,∠C =90°,D 是斜边上AB 上任一点,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F ,CH ⊥AB 于H 点,交AE 于G .试说明:BD =CG . 【难度】★★ 【答案】见解析. 【解析】90AC BC ACB =∠=︒,,45CAH CBD ∴∠=∠=︒.CH AB CH AH ACG CAH CBD ⊥∴=∴∠=∠=∠,,.90CH AB BF CD CHD CFB ⊥⊥∴∠=∠=︒,,. CDH BDF HCD DBF ∠=∠∴∠=∠,.ACE ACG HCD CBF CBD DBF ∠=∠+∠∠=∠+∠,,ACE CBF ∴∠=∠. ACE CBF 在和中,ACE CBFAEC CFB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,ACE CBF AAS CAG BCD ∴∴∠=∠≌(),. CAG BCD AGC CDB ACG CBD AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩在和中,,AGC CDB ASA BD CG ∴∴=≌(),.【总结】本题主要考查了全等三角形判定定理和性质定理的综合应用.ABCD EFGHABCDEF【例7】 如图1,△ABD 和△AEC 中,AB =AD =BD ,AE =EC =AC ,连接BE 、CD . (1)请判断:线段BE 与CD 的大小关系是___________;(2)观察图2,当△ABD 和△AEC 分别绕点A 旋转时,BE 、CD 之间的大小关系是 否会改变;(3)观察图3和图4,若四边形ABCD 、DEFG 都是正方形,猜想类似的结论是______, 在图4中证明你的猜想;(4)这些结论可否推广到任意正多边形(不必证明),如图5,BB 1与EE 1的关系 是_________;它们分别在哪两个全等三角形________________;请在图6中标出较小的 正六边形AB 1C 1D 1E 1F 1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三 角形?【难度】★★★【答案】(1)BE CD =;(2)不变;(3)AE CG =,证明见解析;(4)11BB EE =,11ABB AEE ∆∆和,连接FF 1,可证11ABB AFF ∆≅∆. 【解析】(3)如图4,ABCD DEFG 四边形与四边形都是正方形,90AD CD DE DG ADC GDE ∴==∠=∠=︒,,, CDG ADE ∴∠=∠. 在△ADE 和△CDG 中,AD CDADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩()ADE CDG SAS ∴∆∆≌, AE CG ∴=.【总结】本题主要考查了全等三角形判定定理和性质定理的综合应用.ABCD E图1 ABC DE 图2 A B CD E FG ABC D EFG图4图3A BCD E B 1E 1ABCDEF 图6图5【例8】 已知△ABC 中,AB =AC =6cm ,BC =4cm ,B C ∠=∠,点D 为AB 的中点. (1)如果点P 在线段BC 上以1cm /s 的速度由点B 向点C 运动,同时,点Q 在线 段CA 上由点C 向点A 运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,△BPD 与△CQP 是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使 △BPD 与△CQP 全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时 出发,都逆时针沿△ABC 三边运动,求经过多长时间点P 与点Q 第一次在△ABC的哪条边上相遇? 【难度】★★★ 【答案】见解析.【解析】(1)①全等,理由如下: 1111.t BP CQ cm =∴==⨯=秒,63.AB cm D AB BD cm =∴=,点为的中点,4413PC BC BP BC cm PC cm ==∴==又﹣,, ﹣, PC BD ∴=. 在△BPD 和△CQP 中,BD CPB C BP CQ =⎧⎪∠=∠⎨⎪=⎩, (..)BPD CPQ S A S ∴∆≅∆.②P Q V V BP CQ ≠∴≠,. BPD CPQ B C ∆∆∠=∠又和全等,. 23BP CP cm BD CQ cm ∴====,.2s =1.5/Q P Q t V cm s ∴=∴点与点运动的时间,;(2)x P Q 设经过秒后点与点第一次相遇,1.526x x =+⨯由题意得:, 解得:24x =. 此时点P 的运动路程为24厘米. 因为66416ABCC=++=, 所以P Q AC 点、点在边上相遇.即24P Q AC 经过秒点与点第一次在边上相遇.【总结】本题综合性加强,主要考查了动点与全等三角形判定定理和性质定理的结合, 解题时注意分析动点的运动轨迹.ABCDP Q1、 倍长中线法;2、 添加平行线构造全等三角形;3、 截长补短构造全等的三角形;4、 图形的运动构造全等三角形.【例9】 已知三角形的两边分别为5和7,求第三边上的中线长x 的取值范围. 【难度】★★ 【答案】16x <<.【解析】57AB AC ==如图所示,,.AD E AD DE =延长至,使∵AD 是BC 边上中线, ∴BD =CD . 在△BDE 与△CDA 中,AD DE EDB ADC BD CD =⎧⎪∠=∠⎨⎪=⎩∴(..)BDE CDA S A S ∆∆≌, ∴7BE AC ==.在ABE ∆中,∵BE AB AE AB BE -+<<, ∴7575AD -<<+,∴16x <<.【总结】本题主要考查了中线倍长辅助线及三角形三边关系的综合应用.模块二:添加辅助线构造全等三角形知识精讲例题解析【例10】 在△ABC 中,AD 是BC 边上的中线,AE =EF ,试说明:BF =AC . 【难度】★★ 【答案】见解析.【解析】AD G DG AD BG =延长至,使,连接.∵AD 是BC 边上中线, ∴BD =CD . 在△BDG 与△CDA 中,AD DGGDB ADC BD CD =⎧⎪∠=∠⎨⎪=⎩∴(..)BDG CDA S A S ∆∆≌, ∴BG AC G CAD =∠=∠,.AE EF CAD EFA =∴∠=∠, . EFA DFB ∠=∠, DFB G ∴∠=∠,BF BG BF AC ∴=∴=,.【总结】本题中一方面主要考查了辅助线的添加,另一方面考查了等腰三角形的性质的运用,教师可选择性讲解.【例11】 如图所示,AD 是△ABC 的中线,BE 交AC 于E ,交AD 于F ,且AC =BF .试说明:AE =EF . 【难度】★★ 【答案】见解析.【解析】AD M MD FD MC =延长至点,使,连接.∵AD 是BC 边上中线, ∴BD =CD . BD CDBDF CDM BDF CDM DF DM =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,..BDF CDM S A S MC BF M BFD ∴∆∆∴=∠=∠≌(), ,. AC BF AC MC M EAF =∴=∴∠=∠,,. .BFD AFE EAF AFE AE EF ∠=∠∴∠=∠∴=,,【总结】本题中一方面主要考查了辅助线的添加,另一方面考查了等腰三角形的性质的运用,教师可选择性讲解.ABCDEF【例12】 已知:如图所示,△ABC 中,D 为BC 上一点,AB =AC , ED =DF ,试说明:BE =CF . 【难度】★★ 【答案】见解析.【解析】//E EM AC BC M 过点作交于点,则BME ACB ∠=∠.AB AC ABC ACB =∴∠=∠,,ABC BME BE EM ∴∠=∠∴=,.//EM AC EMD FCD ∴∠=∠,.在△EMD 与△FCD 中,EMD FCDED DF EDM FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩(..)EDM FDC A A S EM CF BE CF ∴∆≅∆∴=∴=,,.【总结】本题主要考查了平行线的性质及全等三角形的判定与性质的综合运用.【例13】 △ABC 中,AB =AC ,E 为AC 延长线交于一点,且BD =CE ,连接DE 交底BC于G .试说明:GD =GE .【难度】★★ 【答案】见解析.【解析】//D DF AC BC F 过点作交于,DFG ECG FDG E DFB ACB ∠=∠∠=∠∠=∠则,,. AB AC B ACB B DFB BD DF =∴∠=∠∴∠=∠∴=,,,.BD CE DF CE =∴=,.在△DGF 与△EGC 中,DGF EGCDF EG GDF E ∠=∠⎧⎪=⎨⎪∠=∠⎩()..DFG ECG A SA GD GE ∴∆≅∆∴=,.【总结】 本题主要考查了平行线的性质及全等三角形的判定与性质的综合运用.【例14】 己知,△ABC 中,AB =AC ,CD ⊥AB ,垂足为D ,P 是射线BC 上任一点,PE ⊥AB ,PF ⊥AC 垂足分别为E 、F ,试说明PE 、PF 与CD 的关系. 【难度】★★【答案】当点P 在线段BC 上时,PE PF CD +=; 当点P 在B C 的延长线上时,PE PF CD -=. 【解析】(1)当点P 在线段BC 上时,连接AP ,PE AB PF AC CD AB ⊥⊥⊥,,,111222ABP ACP ABC S AB PE S AC PF S AB CD ∆∆∆∴=⋅⋅=⋅⋅=⋅⋅,,.ABP ACP ABC S S S ∆∆∆+=,111222AB PE AC PF AB CD ∴⋅⋅+⋅⋅=⋅⋅. AB AC =, PE PF CD ∴+=;(2)当点P 在BC 的延长线上时,连接AP , PE AB PF AC CD AB ⊥⊥⊥,,,111222ABP ACP ABC S AB PE S AC PF S AB CD ∆∆∆∴=⋅⋅=⋅⋅=⋅⋅,,.ABP ACP ABC S S S ∆∆∆-=,111222AB PE AC PF AB CD ∴⋅⋅-⋅⋅=⋅⋅. AB AC =, PE PF CD ∴-=.【总结】本题主要考查了利用三角形的面积关系说明线段间的关系.FE D CA BPFEDC A B P【例15】 已知,如图在四边形ABCD 中,BD 平分∠ABC ,BC >AB ,∠A +∠C =180°.试说明:AD =CD . 【难度】★★ 【答案】见解析.【解析】D DE BA BA E ⊥过点作交的延长线于, D DF BC F ⊥过点作,垂足为, 则90E BFD DFC ∠=∠=∠=︒.BD ABC DAE DBF ∠∴∠=∠平分,.E BFDBED BFD ABD FBD BD BD ∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩在和中, , ..ABD EBD A AS ∴∆≅∆(), DE DF ∴=. 180180BAD C BAD EAD ∠+∠=︒∠+∠=︒,, EAD C ∴∠=∠. ..E DFC AED CFD EAD CDE DFAED CFD A A S AD CD∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩∴∆≅∆∴=在和中,(), 【总结】本题主要考查了全等三角形的判定与性质的综合运用,注意辅助线的添加.【例16】 已知,如图,△ABC 中,AB =AC ,∠BAC =90°,D 是AC 的中点,AF ⊥BD于E ,交BC 于F ,连结DF .试说明:∠ADB =∠CDF .【难度】★★ 【答案】见解析.【解析】 A AN BC BC N BD M ⊥过点作交于点,交于点,90 BAC AE BD ABD FAC ∠=︒⊥∴∠=∠,,.45ABC AB AC C BAM DAM ∆∴=∠=∠=∠=︒是等腰直角三角形,,. 在△BAM 与△ACF 中,ABD FACAB ACBAM C ∠=∠=∠=∠⎧⎪⎨⎪⎩, (..)BAM CAF A S A AM CF ∴∆≅∆∴=,. D AC AD CD ∴=为中点,.在△AMD 与△CFD 中,MAD C AD C D M F C A ∠=∠==⎧⎪⎨⎪⎩,(..)AMD CFD S A S ADB CDF ∴∆≅∆∴∠=∠,.【总结】本题考查了等腰直角三角形的性质及全等三角形的判定与性质的综合运用.【例17】 如图,BC ∥AD ,EA 、EB 分别平分∠DAB 、∠CBA ,CD 过点E ,试说明:AB =AD +BC .【难度】★★ 【答案】见解析.【解析】AB AF AD EF =在上截取,连接.EA DAB DAE FAE ∠∴∠=∠平分,. AF ADFAE DAE DAE FAE AE AE =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)FAE DAE S A S AD AF D AFE ∴∆≅∆∴=∠=∠,,.//180BC AD D C ︒∴∠+∠=,,180AFE BFE C BFE ︒∠+∠=∴∠=∠,.EB CBA FBE CBE ∠∴∠=∠平分,. C BFE FBE CBE FBE CBE BE BE ∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)FBE CBE A A S BC BF AB AD BC ∴∆≅∆∴=∴=+,,.【总结】本题主要考查截长补短辅助线的运用.【例18】 如图,在ABC ∆中,AB AC =,108BAC ∠=,BD 平分ABC ∠.试说明:BC AB CD =+. 【难度】★★ 【答案】见解析.【解析】AB CE CD =在上截取,连接DE .108AB AC BAC ︒=∠=,, (180)236C ABC BAC ︒︒∴∠=∠=-∠÷=.(180)272CED CDE C ︒︒∴∠=∠=-∠÷=, 108BED BAD ︒∴∠==∠.BD ABC ABD EBD ∠∴∠=∠平分,.ABD EBDBDA BDE BAD BED BD BD ∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩在和中, , (..)BDA BDE A A S AB BE ∴∆≅∆∴=,.BC BE CE BC AB CD =+∴=+,.【总结】本题主要考查了全等三角形的判定与性质定理及三角形内角和定理的应用.ABCD【例19】 如图,已知ABC ∆中,AD 是BAC ∠的角平分线,2B C ∠=∠.试说明:AB BD AC +=. 【难度】★★ 【答案】见解析.【解析】AC E AE AB DE 在边上取点,使=,连接.AD BAC BAD CAD ∠∴∠∠平分,=.在△AMD 与△CFD 中,AB AEBAD EAD AD AD =∠=∠=⎧⎪⎨⎪⎩(..)ABD AED S A S DE BD AED B ∴∆∆∴=∠=∠≌,,. 22B C AED C ∠=∠∴∠=∠,.AED C CDE C CDE ∠=∠+∠∴∠=∠,,DE CE CE BD ∴=∴=,. AC AE CE AC AB BD =+∴=+,.【总结】本题主要考查了角平分线的性质及全等三角形的判定与性质的综合运用.【例20】 在四边形ABCD 中,AC 平分∠DAB ,若AB >AD ,DC =BC .试说明:180B D ︒∠+∠=. 【难度】★★ 【答案】见解析.【解析】AB AF AD FC =在上截取,连接.AC DAB DAC FAC ∠∴∠=∠平分,. (..)AD AFADC AFC DAC FACAC ACADC AFC S A S D AFC CD CF =⎧⎪∆∆∠=∠⎨⎪=⎩∴∆≅∆∴∠=∠=在与中,,, DC BC FC BC CFB B =∴=∴∠=∠,,,180B D AFC CFB ∴∠+∠=∠+∠=︒.【总结】本题主要考查了角平分线的性质及全等三角形的判定与性质.FABCD【例21】 如图,在△ABC 中,AB =AC ,延长AB 到D ,使BD =AB ,取AB 的中点E ,连接CD 和CE ,试说明:CD =2CE . 【难度】★★ 【答案】见解析.【解析】延长CE 到H ,使EH =CE ,连接BH . ∵E 是AB 的中点, ∴AE = BE . 在△AEC 与△BEH 中, AE BEAEC BEH CE EH =∠=∠=⎧⎪⎨⎪⎩∴AEC BEH ≅, ∴A EBH BH AC AB BD ∠=∠===,.∵AB =AC , ∴13∠=∠.∵13CBD A CBH ABH ∠=∠+∠∠=∠+∠,, ∴CBD CBH ∠=∠. 在△CBD 与△CBH 中, BD BHCBD CBH CB CB =∠=∠=⎧⎪⎨⎪⎩∴CBD CBH ≅, ∴2CD CE =.【总结】本题主要考查了中线倍长辅助线与全等三角形的判定的综合运用.【例22】 已知:正方形ABCD 中,∠BAC 的平分线交BC 于E ,试说明:AB +BE =AC . 【难度】★★ 【答案】见解析.【解析】E EF AC F ⊥过点作于点,则90AFE CFE ∠=∠=︒.9045ABCD B ACB ∴∠=︒∠=︒四边形是正方形, ,,180904545FEC ACB ︒︒︒︒∴∠=--==∠, EF FC ∴=.AE BAC BAE FAE ∠∴∠=∠是的平分线,.BABE AFE BAE FAE AE AE AFE ∠⎧⎪∆∆∠∠=∠=⎨⎪=⎩在和中,(..)ABE AFE A A S ∴∆≅∆, AB AF BE EF FC ∴===,.AF FC AC AB BE AC +=∴+=,.【总结】本题主要考查了正方形的性质及全等三角形的判定与性质的综合运用.231ABCDEFH【例23】 如图:在△ABC 中,∠ABC =2∠C ,AD ⊥BC ,延长AB 到E ,使BD =BE ,延长ED 到F ,交AC 于F ,说明AF =DF =CF 的理由. 【难度】★★ 【答案】见解析.【解析】BD BE =,E BDE ∴∠=∠, 2ABC E BDE BDE ∴∠=∠+∠=∠. 2ABC C BDE C ∠=∠∴∠=∠,.BDE FDC C FDC DF CF ∠=∠∴∠=∠∴=,,.9090AD BC ADF FDC DAF C ︒︒⊥∴∠+∠=∠+∠=,,,ADF DAF AF DF AF DF CF ∴∠=∠∴=∴==,,.【总结】本题综合性较强,主要考查了等腰三角形的性质运用,教师可选择性讲解.【例24】 已知AD 为△ABC 的角平分线,AB >AC ,试说明:AB -AC >BD -DC . 【难度】★★ 【答案】见解析.【解析】AB AE AC DE =在上截取,连接.DAE D A A BC C D A ∴∠=∠∆为的角平分线,. AE ACADE ADC DAE DAC AD AD =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,,(..)ADE ADC S A S DE DC ∴∆∆∴=≌,.BDE BE BD DE BE BD DC ∆>-∴>-,在中,,AB AC BD DC ∴->-.【总结】本题主要考查了全等三角形的判定与性质及三角形三边关系的综合应用.ABCDEF【例25】 已知,如图1正方形ABCD 中,E 是BC 中点,EF ⊥AE 交∠DCE 外角的平分线于F .(1)试说明:AE =EF .(2)如图2,如当E 是BC 上任意一点,而其它条件不变时,AE =EF 是否仍然成 立,试加以分析说明. 【难度】★★★ 【答案】见解析. 【解析】(1)AB H EH 取的中点,连接.90ABCD AB BC B BCD ︒∴=∠=∠=是正方形,,, 90EAH AEB ︒∴∠+∠=.90AE EF FEC AEB EAH FEC ︒⊥∴∠+∠=∴∠=∠,,.H AB E BC AH BH BE BC ∴===为中点,为中点,, 45BHE ︒∴∠=, 18045135AHE ︒︒︒∴∠=-=.45CF DCG FCD ∠∴∠=︒为的角平分线,, 135ECF AHE ECF ︒∴∠=∴∠=∠,. AHE ECFAHE ECF AH EC EAH FEC ∠=∠⎧⎪∆∆=⎨⎪∠=∠⎩在和中,(..)AHE ECF A S A AE EF ∴∆≅∆∴=,;(2)成立.90ABCD AB BC B BCD ︒∴=∠=∠=是正方形,,, 90EAH AEB ︒∴∠+∠=. 90AE EF FEC AEB EAH FEC ︒⊥∴∠+∠=∴∠=∠,,.4518045135AH EC BH BE BHE AHE ︒︒︒︒=∴=∴∠=∴∠=-=,,,.45CF DCG FCD ∠∴∠=︒为的角平分线,, 135ECF AHE ECF ︒∴∠=∴∠=∠,. AHE ECFAHE ECF AH EC EAH FEC ∠=∠⎧⎪∆∆=⎨⎪∠=∠⎩在和中,(..)AHE ECF A S A AE EF ∴∆≅∆∴=,.【总结】本题主要考查了正方形的性质及全等三角形的判定与性质的综合运用.ABCDE FGA BCDE FG图1图2HH【例26】 如图,点D 、E 三等分△ABC 的BC 边.试说明:AB +AC >AD +AE . 【难度】★★★ 【答案】见解析.【解析】AD F DF AD BF =延长至,使,连接,AE G EG AE CG =延长至,使,连接.D E BC BD DE EC ∴==、三等分,. DF ADBDF EDA BDF EDA BD DE =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,..BDF EDA S AS ∴∆≅∆(), BF AE ∴=. 2ABF AB BF AF AB AE AD ∆+>∴+>在中,,. 2AC AD AE +>同理可证:.22AB AE AC AD AD AE ∴+++>+, 即 AB AC AD AE +>+.【总结】本题主要考查了全等三角形的判定与性质及三角形三边关系的应用,注意辅 助线的添加.【例27】 已知:如图,在△ABC 的边上取两点D 、E ,且BD =CE .试说明:AB +AC >AD +AE . 【难度】★★★ 【答案】见解析.【解析】BC M AM N MN AM =取中点,连并延长至,使, BN DN ND AB P 连、,延长交于.BD CE DM EM =∴=,.在△AEM 与△NDM 中,AM MN AME NMD EM DM =⎧⎪∠=∠⎨⎪=⎩()..DMN EMA S A S ∴∆∆≌, DN AE ∴=.BN CA =同理可证:.BN BP PN DP PA AD +>+>,, BN BP DP PA PN AD ∴+++>+. BN AB DN AD AB AC AD AE ∴+>+∴+>+,.【总结】本题主要考查了全等三角形的判定与性质及三角形三边关系的应用.ABCDE M NP【例28】 如图,在△ABC 中,AB =AC ,D 是CB 延长线的一点,且∠D =60°,E 是AD上一点,DE =DB .试说明:AE =BE +BC . 【难度】★★★ 【答案】见解析.【解析】DC F CF BD AF =延长到,使,连接.AB AC ABC ACB ABD ACF =∴∠=∠∴∠=∠,,.在△ABD 与△ACF 中,AB ACABD ACF BD CF =⎧⎪∠=∠⎨⎪=⎩()ABD ACF SAS AD AF ∴∴=≌,.60ADB ADF AD DF ︒∠=∴∆∴=,是等边三角形,.AD AE DE DF DB BC CF =+=++,,AE DE DB BC CF ∴+=++.60DE DB ADB DEB ︒=∠=∴∆,,也是等边三角形, DE BE DB CF AE BE BC ∴===∴=+,.【总结】本题主要考查了全等三角形的判定与性质及等边三角形的判定与性质的综合 运用,综合性较强,注意对学生进行适当的引导.【习题1】 如图△ABC 和△DBC 中,∠ABP =∠DBP ,∠ACP=∠DCP ,P 是BC 上任意一点,试说明:P A =PD .【难度】★ 【答案】见解析.【解析】ABC DBC ∆∆在和中,ABP DBPBC BC ACP DCP ∠=∠⎧⎪=⎨⎪∠=∠⎩,(..)ABC DBC S A S AB BD ∴∆≅∆∴=,.ABP DBP ABP DBP BP BP AB BD ∠=∠⎧⎪∆∆=⎨⎪=⎩在和中,(..)ABP DBP S A S PA PD ∴∆≅∆∴=,.【总结】本题主要考查了全等三角形的判定与性质的运用.随堂检测ABCDPABCDE F【习题2】 已知,△ABC 中,AB =5,AC =3,则中线AD 的取值范围是_________. 【难度】★【答案】14AD <<.【解析】AD E DE AD EC =延长至点,使,连接. 2AD x AE x ==设,则.在△ABD 与△ECD 中,BD CDADB EDC AD ED =⎧⎪∠=∠⎨⎪=⎩(..)5ABD ECD S A S CE AB ∴∆≅∆∴==,. 322814AC x x =∴<<∴<<,,.即14AD <<.【总结】本题主要考查了全等三角形的判定与性质及三角形三边关系的应用.【习题3】 从正方形ABCD 的顶点A 作∠EAF =45°,交DC 于F ,BC 于E ,试说明:DF +BE =EF .【难度】★ 【答案】见解析.【解析】CD G DG BE AG =延长到,使,连接.ABCD 四边形为正方形,90AB AD B ADC ADG ︒∴=∠=∠=∠=,,ADG B ∴∠=∠.(..)B AB AD ABE ADG B ADGABE ADG S A S AE AG BA E E DA D G G=⎧⎪∆∆∠=∠⎨⎪⎩∴∆≅∆∴=∠=∠=在和中, ,, 45EAF ︒∠=,904545GAF DAG DAF BAE DAF BAD EAF ︒︒︒∴∠=∠+∠=∠+∠=∠-∠=-=,即EAF GAF ∠=∠.(..)AE AG AEF AGF EAF GAFAF AFAEF AGF S A S EF GF=⎧⎪∆∆∠=∠⎨⎪=⎩∴∆≅∆∴=在和中, , GF DG DF BE DF BE DF EF =+=+∴+=,.【总结】本题考查了正方形的性质及全等三角形的判定与性质的运用,利用旋转作辅 助线构造全等是解题的关键.ABCD EFGG【习题4】 已知,E 是AB 中点,AF =BD ,BD =5,AC =7,求DC 的长. 【难度】★★ 【答案】2.【解析】FE G EF GE BG =延长至,使,连接.E AB AE BE ∴=是中点,.AE BEAFE BGE AEF BEG FE GE =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)AFE BGE S A S ∴∆≅∆,GB AF G AFG DFC ∴=∠=∠=∠,. AF BD GB BD =∴=,,D G AFG DFC CD CF ∴∠=∠=∠=∠∴=,. 752AC AF DC CF AC AF ==∴==-=,,.【总结】本题主要考查了全等三角形的判定与性质及等腰三角形性质的综合运用,教 师在讲解时注意针对性的引导.【习题5】 如图,△ABC 中,AB <AC ,AD 是中线,试说明:∠DAC <∠DAB . 【难度】★★ 【答案】见解析.【解析】AD E AD DE BE =延长到点,使,连接.AD BD CD ∴=为中线,.BD CDBDE CDA BDE CDA DE AD =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)BDE CDA S A S BE AC DAC E ∴∆≅∆∴=∠=∠,,. AB AC AB BE <∴<,, E DAB DAC DAB ∴∠<∠∴∠<∠,.【总结】本题主要考查了全等三角形的判定与性质及三角形边角关系的综合应用,注 意添加适当的辅助线将问题进行转化.ABCD E【习题6】 △ABC 中,AB >AC ,AD 是∠BAC 的平分线,P 是AD 上任意一点,试说明:AB -AC >PB -PC . 【难度】★★ 【答案】见解析.【解析】AB E AE AC PE =在上取一点,使,连接,则AB AE AB AC BE -=-=.AD BAC EAP CAP ∠∴∠=∠平分,. AEP ACP ∆∆在和中,AE ACEAP CAP AP AP =⎧⎪∠=∠⎨⎪=⎩(S.A.S)AEP ACP PE PC ∴∆≅∆∴=,.BPE ∆在中,BE PB PE AB AC PB PC >-∴->-,.【总结】本题考查了角平分线的性质、全等三角形的判定与性质及三角形三边关系的 综合应用.【习题7】 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 中点,EF ∥AD 交CA 的延长线于点F ,交AB 于点G ,若BG =CF ,试说明:∠BAD=∠CAD .【难度】★★ 【答案】见解析.【解析】GE M EM GE CM =延长到点,使,连接.E BC BE CE ∴=是中点,.BE CEBEG CEM BEG CEM GE EM =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)BEG CEM S A S BG CM BGE M ∴∆≅∆∴=∠=∠,,. BG CF CM CF M F BGE F =∴=∴∠=∠∴∠=∠,,,//EF AD BGE BAD F CAD ∴∠=∠∠=∠,,,BAD CAD ∴∠=∠.【总结】本题主要考查了全等三角形的判定和性质以及平行线的性质的综合运用.MABCD E F G ABCDP E【习题8】 已知:如图,ABCD 是正方形,∠F AD =∠F AE .试说明:BE +DF =AE . 【难度】★★ 【答案】见解析.【解析】CB G BG DF AG =延长到,使,连接.ABCD 四边形为正方形,//90AB AD AB CD D ABC ︒∴=∠=∠=,,. //AB CD AFD BAF EAF BAE ∴∠=∠=∠+∠,.9018090ABC ABG ABC D ︒︒︒∠=∴∠=-∠==∠,. AB ADABG ADG ABG D BG DF =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)ABG ADF S A S G AFD BAG DAF EAF ∴∆≅∆∴∠=∠∠=∠=∠,,.G AFD EAF BAE BAG BAE EAG ∴∠=∠=∠+∠=∠+∠=∠.GE AE ∴=,BE DF BE GB GE AE ∴+=+==.【总结】本题主要考查了在正方形背景下的辅助线的添加及全等三角形的综合运用.【习题9】 如图所示,△ABC 是边长为1的正三角形,∠ BDC = 120°,BD =CD ,以D 为顶点作一个60°的∠MDN ,点M 、N 分别在AB ,AC 上,求△AMN 的周长. 【难度】★★★ 【答案】2【解析】AC E CE BM DE =延长到点,使,连接. 60ABC ABC ACB ︒∆∴∠=∠=为正三角形,.12030BDC BD BC DBC DCB ︒︒∠==∴∠=∠=,,, 9090MBD ACD ECD MBD ︒︒∴∠=∠=∴∠==∠,. BM CEMBD ECD MBD ECD BD BC =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)MBD ECD S A S BDM EDC MD DE ∴∆≅∆∴∠=∠=,,.6060MDN BDM NDC ︒︒∠=∴∠+∠=,,60EDC NDC EDN MDN ︒∴∠+∠==∠=∠. MD DEMDN EDN MDN EDN DN DN =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,,(..)MDN EDN S A S MN EN ∴∆≅∆∴=,.AM MN AN AM EN AN AM NC CE AN ∴++=++=+++ AM BM NC AN AB AC =+++=+,112ABC AM MN AN ∆∴++=+=边长为1,.ABCDEFGABCDMNE【习题10】 如图,已知梯形ABCD 中,AB =CD =10厘米,BC =8厘米,∠B =∠C ,点E为AB 的中点.点P 在线段BC 上由B 点向C 点运动,同时点Q 在线段CD 上由C 点向D 点运动.(1) 若点P 与Q 都以2厘米/秒的速度运动,经过1.5秒后,△BPE 与△CQP 是否全等?请说明理由;(2) 若点P 的速度为3厘米/秒,当点Q 的运动速度为多少时,能够使△PBE 与 △CQP 全等? 【难度】★★★【答案】(1)全等;(2)3/cm s 或15/4cm s . 【解析】(1) 1.533BP CQ ==经过秒后,,,则BP CQ =.105AB E AB BE =∴=,为中点,. 85BC CP BE CP =∴=∴=,,.BE CPBPE CQP B C BP CQ =⎧⎪∆∆∠=∠⎨⎪=⎩在和中, ,(..)BPE CQP S A S ∴∆≅∆;(2)BPE CQP ∆≅∆当时,由(1)可知5BE =,5CP ∴=. 83BC BP CQ =∴==,.3/13/P cm s s Q cm s ∴∴点速度为,运动时间为,点速度为. 45BPE CPQ BP CP CQ ∆≅∆===当时,同理可得:,,4153//34P cm s s Q cm s ∴∴点速度为,运动时间为,点速度为.综上点Q 的运动速度为3/cm s 或15/4cm s . 【总结】本题主要考查了全等三角形的判定与性质,注意分类讨论,综合性较强.A BCDE PQ【作业1】 已知:如图,OD ⊥AD ,OH ⊥AE ,DE 交GH 于O .若∠1=∠2,试说明:OG =OE . 【难度】★ 【答案】见解析.【解析】OD AD OH AE ⊥⊥,,90ADO GDO AHO EHO ∴∠=∠=∠=∠=. 12ADO AHOAOD AOH AO AO ∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)AOD AOH A A S OD OH ∴∆≅∆∴=,.DOG HOE DOG HOE OD OH GDO EHO ∠=∠⎧⎪∆∆=⎨⎪∠=∠⎩在和中,(..)DOG HOE S A S OG OE ∴∆≅∆∆∴=,.【总结】本题主要考查了全等三角形的判定与性质的综合运用.【作业2】 如图,在△ABC 中,AD 为BC 边上的中线.试说明:AD < (AB +AC ). 【难度】★ 【答案】见解析.【解析】延长AD 到点E ,使AD DE =,连接BE ,AD 为BC 边上的中线, BD CD ∴=.BD CDBDE CDA BDE CDA AD DE =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)BDE CDA S A S BE AC ∴∆≅∆∴=,.ABE ∆在中,AB BE AE +>,2AB AC AD ∴+>,1()2AD AB AC ∴<+.【总结】本题主要考查了全等三角形的判定和性质以及三角形三边关系的综合运用.课后作业AGODEH1 2ABCDE【作业3】 已知:AB //ED ,∠EAB =∠BDE ,AF =CD ,EF =BC ,试说明:∠F =∠C . 【难度】★★ 【答案】见解析. 【解析】EB 连接//AB ED ABE DEB ∴∠=∠,.EAB BDEABE DEB ABE DEB BE EB ∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)ABE DEB A A S AE DB ∴∆≅∆∴=,.AF CD AEF DBC EF BC AE DB =⎧⎪∆∆=⎨⎪=⎩在和中,(..)AEF DBC S S S F C ∴∆≅∆∴∠=∠,.【总结】本题主要考查了全等三角形的判定和性质的综合运用.【作业4】 △ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,试说明:∠C =2∠B . 【难度】★★ 【答案】见解析.【解析】AB AE AC DE =在上截取,连接.AD CAB CAD EAD ∠∴∠=∠是的平分线,. AC AECAD EAD CAD EAD AD AD =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)CAD EAD S A S CD DE C AED ∴∆≅∆∴=∠=∠,,.AB AC CD AB AE BE DE BE EDB B =+=+∴=∴∠=∠,,,. 22AED EDB B B C B ∠=∠+∠=∠∴∠=∠,.【总结】本题主要考查了全等三角形的判定和性质及角平分线的性质的综合运用.ABCDE【作业5】 已知:如图,E 是BC 的中点,点A 在DE 上,且∠BAE =∠CDE .试说明:AB =CD . 【难度】★★ 【答案】见解析.【解析】AE F AE EF CF =延长到点,使,连接.E BC BE CE ∴=是的中点,. AE EFABE FCE AEF FEC BE CE =⎧⎪∆∆∠=∠⎨⎪=⎩在和中,(..)ABE FCE S A S AB FC BAE F ∴∆≅∆∴=∠=∠,,,BAE CDE F CDE FC CD AB CD ∠=∠∴∠=∠∴=∴=,,,.【总结】本题主要考查了全等三角形的判定和性质的综合运用.【作业6】 如图所示,已知△ABC 中,AD 平分∠BAC ,E 、F 分别在BD 、AD 上.DE =CD ,EF =AC .试说明:EF ∥AB . 【难度】★★ 【答案】见解析.【解析】AD G AD DG EG =延长到点,使,连接ADC GDE ∆∆在和中, AD DGADC GDE CD DE =⎧⎪∠=∠⎨⎪=⎩(..)ADC GDE S A S CAD G AC EG ∴∆≅∆∴∠=∠=,,.EF AC EF EG EFD G CAD EFD =∴=∴∠=∠∴∠=∠,,,.AD BAC BAD CAD BAD EFD ∠∴∠=∠∴∠=∠平分,,,//EF AB ∴【总结】本题主要考查了全等三角形的判定和性质及平行线的判定定理的综合运用, 注意辅助线的添加.A BCDE FABCD EF G【作业7】 在直角三角形ABC 中,∠BAC =90°,AB =AC ,BD 平分∠ABC ,CE 垂直于BD ,试说明BD =2CE . 【难度】★★ 【答案】见解析.【解析】BA CE F 延、交于点901809090.45.22.567.5.9067.522.5.BAC FAC BAC AB AC ABC ACB BD ABC ABD DBC ADB CE BD BEC BCE ACE ABD ACE ︒︒︒︒︒︒︒︒︒︒∠=∴∠=-==∠=∴∠=∠=∠∴∠=∠=∴∠=⊥∴∠=∴∠=∴∠=∴∠=∠,,平分,,,,,,ABD ACF ∆∆在和中,BAC FAC AB ACABD ACE ∠=∠⎧⎪=⎨⎪∠=∠⎩, (..)ABD ACF S A S ∴∆≅∆, 67.5BD CF ADB F ︒∴=∠=∠=,,F BCE ∴∠=∠.F BCEFBE CBE ABD DBC BE BE ∠=∠⎧⎪∆∆∠=∠⎨⎪=⎩在和中,,(..)FBE CBE A A S ∴∆≅∆.22EF CE CF CE BD CE ∴=∴=∴=,,.【总结】本题主要考查了全等三角形的判定和性质的综合运用.ABCDE F【作业8】 已知:点C 为线段AB 上一点,△ACM 、△CBN 都是等边三角形,且AN 、BM 相交于O .(1) 试说明:AN =BM ; (2)求∠AOB 的度数;(3)若AN 、MC 相交于点P ,BM 、NC 交于点Q ,试说明:PQ ∥AB . 【难度】★★【答案】(1)见解析;(2)120︒;(3)见解析. 【解析】(1),ACM CBN ∆∆是等边三角形,60.(..).AC MC CB CN MCA NCB ACN MCN MCA MCB NCB MCA ACN MCB AC MCACN MCB ACN MCBCN CB MCB ACN S A S AN BM ︒∴==∠=∠=∠=∠+∠∠=∠+∠∴∠=∠=⎧⎪∆∆∠=∠⎨⎪=⎩∴∆≅∆∴=,,,,,在和中,, (2)MCB ACN ∆≅∆,OBA CNA CBM CNA ∴∠=∠∴∠=∠,. 60180120.NOB AOB NOB OAB OBA OAB CNA NCB AOB NOB ︒︒︒∠∆∴∠=∠+∠=∠+∠=∠=∴∠=-∠=是的外角,,(3)PQ 连接18060. (S.A.S)6.0//.MCQ ACM BCN MCQ ACP CAP CMQ AC MC MCQ ACP CAN CMB CAP CMQ MCB AC CP CQ CPQ CPQ CPQ ACM N CMB CA PQ AB N ︒︒︒∆≅∆∴∠∠=-∠-∠=∴∠=∠∆∆=⎧⎪∠=∠⎨⎪∠=∠⎩∴∆≅∆∴=∴∆∴∠=∴∠=∠∠=∴在和中,,为等边三角形,,,,,,【总结】本题主要考查了全等三角形的判定和性质以及三角形外角的性质的综合运用, 解题时注意观察角度间的关系.ABC PQOM N【作业9】 五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,试说明:AD 平分∠CDE . 【难度】★★ 【答案】见解析.【解析】DE F EF BC AF AC =延长至点,使,连接、.180180ABC AED ABC AED AEF ︒︒∠+∠=∴∠=-∠=∠,.在△ABC 与△AEF 中,AB AEABC AEF BC EF =⎧⎪∠=∠⎨⎪=⎩, () ABC AEF SAS AC AF ∴∆≅∆∴=,.在△ADC 与△ADF 中,AC AF CD FD AD AD =⎧⎪=⎨⎪=⎩,(..)ADC ADF S S S ADE ADC ∴∆≅∆∴∠=∠,,AD CDE ∴∠平分.【总结】本题主要考查了全等三角形的判定与性质的综合运用,注意辅助线的添加.【作业10】 如图点M 是△ABD 的边AB 所在直线上的任意一点(点B 除外),其中AB =AD =BD ,作∠DMN =60°,射线MN 与∠DBA 外角的平分线交于点N ,DM 与MN 有怎样的数量关系? 【难度】★★★ 【答案】DM MN =.【解析】AD AF AM FM =在上截取,联接.AB AD BD ABD ==∴∆,为等边三角形, 60A ABD AFM ︒∴∠=∠=∴∆,是等边三角形,()60120606060,11806060.2AFM AMF DFM FDM FMD DMN DMF BMN FDM BMN BN DBE DBN ︒︒︒︒︒︒︒︒∴∠=∠=∴∠=∴∠+∠=∠=∴∠+∠=∴∠=∠∠∴∠=-=,,,,,为的角平分线,120MBN MBD NBD MBN DFM ︒∠=∠+∠=∴∠=∠,. AD AB AF AM DF BM ==∴=,,.在△DFM 与△MBN 中,FDM BMNDFM MBN DF BM ∠=∠⎧⎪∠=∠⎨⎪=⎩,(..)DFM MBN A S A DM MN ∴∆≅∆∴=,.【总结】本题主要考查了等边三角形的性质及全等三角形的判定和性质,作辅助线构 造全等是解题的关键.ABNDEMABC DE F F【作业11】 已知,如图1所示,在△ABC 和△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,且点B 、A 、D 在一条直线上,连接BE 、CD ,M 、N 分别为BE 、 CD 的中点.(1)试说明:①BE =CD ;②AN =AM ;(2)在图1的基础上,将△ADE 绕点A 按顺时针方向旋转180°,其他条件不变, 得到图2所示的图形.请直接写出(1)中的两个结论是否仍然成立. 【难度】★★★【答案】(1)见解析;(2)成立.【解析】BAC DAE ∠=∠①, BAE CAD ∴∠=∠.在△ABE 与△ACD 中, AB ACBAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩(..)ABE ACD S A S ∴∆≅∆,BE CD ∴=; ABE ACD ∆≅∆②,ABE ACD BE CD ∴∠=∠=,.M N BE CD 、分别是、的中点,BM CN ∴=. 在△ACN 与△ABM 中,AB AC ABM ACN BM CN =⎧⎪∠=∠⎨⎪=⎩(..)ABM ACN S A S ∴∆≅∆,AM AN ∴=.(2)成立,证明过程如(1).【总结】本题考查了旋转的性质和三角形全等的判定和性质的综合运用,综合性较强.AB CD EN M 图1ABCDEM N 图2。
初二上学期全等三角形专题之倍长中线与截长补短教案(有答案)

倍长中线与截长补短互动精讲知识点一.倍长中线【知识梳理】∆ABC中AD是BC边中线方式延长AD到E,使DE二AD,连接BE•E方式2:间接倍长,延长MD到N,使DfMD,连接CN作CF丄AD于F,作BE丄AD的延长线于E连接BE【例题精讲】例1、∆ABC 中,AB 二5, AC=3,求中线AD 的取值范围。
.∙. BD= CD I∙.∙ BD = CD t ZADC=ZBDE t AD=DE t :.AADC 9 ΔEDB t:.EB=AC I 根据三角形的三边关系定理:5-3<∕lE<5 + 3 r .•・ 1 < AD < 4.例2、已知:如图,在ΔABC 中,ABHAC, D 、E 在BC 上,且DE 二EC,过D 作DF//BA 交AE 于点F, DF=AC.求证:AE 平分ZBAC≡ΔPEF 和 ZSCEG 中. ED= EC ZDEF = ZCEG , FE=EG・・^DEF 竺ΔCEG. ∖ DF=GC t ZDFE=ZG. ・• DF // AB l ・.ZDFE=乙BAE. :DF = AC l •・ GC=AC.・.厶G =ECAE..ZBAE=ZCA E .即AE 平分上BAC.{证明:如图,延长FE 到G,使EG=EF ,连接CG.E':AD 是厶ABC 的中线,【课堂练习】1、在AABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF = EFOCG-AD是BC边上的中线(已知),•・.DC=DB .在厶ADC和AGDB中,'AD=DG< Z4DC-ZGDB(对顶角相等)DC=DBj.^ADC ^GDB(SAS) I:•厶CAD =厶G ■ BG=ACXv BE=AC e・・.BE=BG ,・・・ZBED ZG ,・.・ ZBED= ZAEF t .∖ΛΛEF^= Z.CAD t 即:/.AEF≈ΔFAE t.・・ AF = EF.2、如图,∆ABC中,E、F分别在AB、AC ±, DE丄DF, D是中点,试比较BE+CF 与EF的大小・BE + CF > FP = EF・延长ED 至P , ^DP = DE t连接FP l CP t•・・D是BC的中点,/. BD= CD I在HBDE和ΔCZ)Pφf(DP=DE< 乙EDB=乙CDP[BD=CD・•・ 5BDE ^^CDP(SAS) f.∙. BE=CP l∖∙ DELDF I DE=DP J.∙. EF = FP,(垂直平分线上的点到线段两端点距离相等) 在厶CFP中.CP + CF = BE+ CF > FP = EF・知识点二.截长补短 【知识梳理】截长补短的方法适用于求证线段的和差倍分关系。
苏科版八年级数学下册 解题模型之截长补短,倍长中线 讲义设计

∵CF平分∠ACE,∴
∴ –,
∴
又
∴∠ECG=∠CGE∴CE=GE=2FO+FE.
例题9、如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.
(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
A.6
B.7
C.8
D.9
【答案】B
【解析】该题考查的是线段的长度计算.
在AC上取点E使得 ,∵AD平分 ,∴ ,
在△BAD和△EAD中,∵
∴△BAD≌△EAD(SAS), , ,
∵ ,∴ ,∴ ,
∵ ,∴ ,所以本题答案的是B.
2、如图所示,在 中, ,延长 到 ,使 , 为 的中点,连接 、 ,求证: .
∴CM=DF=FN=NE﹣FE=NE﹣ME.
例题7、阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
∴ , .∴ .…4分
同理 , ,
∴四边形MDNP为平行四边形.……5分
∴ .
∵ ,
∴
∴ ……6分
∴△EMD≌△DNF
∴ ……7分
例题5、如图,在△ABC中,∠ACB=90°,AC=BC=2,O是BC的中点,P是射线AO上的一个动点,则当∠BPC=90°时,AP的长为________.
学而思初二数学秋季班第2讲.倍长中线与截长补短.提高班.教师版

1初二秋季·第2讲·提高班·教师版三角形9级 全等三角形的经典模型(二)三角形8级全等三角形的经典模型(一) 三角形7级倍长中线与截长补短倍长中线与截长补短满分晋级漫画释义2倍长中线 与截长补短2初二秋季·第2讲·提高班·教师版定 义示例剖析倍长中线:即延长三角形的中线,使得延长后的线段是原中线的两倍.其目的是构造一对对顶的全等三角形; 其本质是转移边和角.EDABC其中BD CD =,延长AD 使得DE AD =,则BDE CDA △≌△.【例1】 已知ABC △中,AD 平分BAC ∠,且BD CD =,求证:AB AC =. 【解析】 延长AD 到E ,使DE AD =,连接CE .则CDE BDA △≌△,∴CE AB =,CED BAD ∠=∠, ∵AD 平分BAC ∠,∴BAD CAD ∠=∠, ∴CED CAD ∠=∠,∴CE AC =, ∴AB AC =.思路导航例题精讲知识互联网题型一:倍长中线EABCDABCD3初二秋季·第2讲·提高班·教师版【教师备选】教师可借用例1对等腰三角形三线合一性质的逆命题进行简单归纳:已知角平分线+中线证等腰三角形,如例1; 已知角平分线+高证等腰三角形,如拓展1; 已知中线+高证等腰三角形,如拓展2.【拓展1】已知△ABC 中,AD 平分∠BAC ,且AD ⊥BC ,求证:AB =AC . 【解析】∵AD 平分∠BAC ,∴∠BAD =∠CAD∵AD ⊥BC ,∴∠ADB =∠ADC =90° ∴△ABD ≌△ACD (SAS) ∴AB =AC .【拓展2】已知△ABC 中,AD ⊥BC ,且BD CD =,求证:AB =AC . 【解析】∵AD ⊥BC ,且BD CD =∴AD 所在直线是线段BC 的垂直平分线 根据垂直平分线上的点到线段两端点距离相等 故AB =AC .【例2】 ⑴如图,已知ABC △中,AB AC =,CE 是AB 边上的中线,延长AB 到D ,使BD AB =.给出下列结论:①AD =2AC ;②CD =2CE ;③∠ACE =∠BCD ;④CB 平分∠DCE ,则以上结论正确的是 . 【解析】 ①正确.∵AB AC =,BD AB =,∴AD =2AC .②、④正确.延长CE 到F ,使EF CE =,连接BF . ∵CE 是AB 的中线,∴AE EB =. 在EBF △和EAC △中 AE BEAEC BEF CE FE =⎧⎪∠=∠⎨⎪=⎩典题精练ABDEDCBA4初二秋季·第2讲·提高班·教师版∴EBF EAC ≌△△∴BF AC AB BD ===,EBF EAC ∠=∠ ∴FBC FBE EBC A ACB DBC ∠=∠+∠=∠+∠=∠ 在FBC △和DBC △中 FB DB FBC DBC BC BC =⎧⎪∠=∠⎨⎪=⎩∴FBC DBC ≌△△∴2CD CF CE ==,∠FCB =∠DCB 即CD =2CE ,CB 平分∠DCE .③错误.∵∠FCB =∠DCB ,而CE 是AB 边上中线而不是∠ACB 的角平分线故∠ACE 和∠BCD 不一定相等.⑵如图,在△ABC 中,点D 、E 为边BC 的三等分点,给出下列结论:①BD =DE =EC ;②AB +AE >2AD ;③AD +AC >2AE ;④AB +AC >AD +AE ,则以上结论正确的是 .NM ED CBAEDCBA【解析】 点D 、E 为边BC 的三等分点,∴BD =DE =CE 延长AD 至点M ,AE 至点N ,使得DM =AD ,EN =AE ,连接EM 、CN ,则可证明△ABD ≌△MED ,进而可得AB +AE >2AD ,再证明△ADE ≌△NCE ,进而可得AD +AC >2AE ,将两式相加可得到AB +AE +AD +AC >2AD +2AE ,即AB +AC >AD +AE . ∴①②③④均正确.【例3】 如图,已知在ABC △中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.FCAEBD5初二秋季·第2讲·提高班·教师版【解析】 延长AD 到G ,使DG AD =,连接BG∵BD CD =,BDG CDA ∠=∠,AD GD = ∴ADC GDB △≌△, ∴AC GB =,G EAF ∠=∠ 又∵AF EF =,∴EAF AEF BED ∠=∠=∠ ∴G BED ∠=∠,∴BE BG =,∴AC BE =.【例4】 在正方形ABCD 中,PQ ⊥BD 于P ,M 为QD 的中点,试探究MP 与MC 的关系.NABCDMPQ Q PMDCBA【解析】 延长PM 至点N ,使PM =MN ,连结CP 、CN 、DN .易证△PMQ ≌△NMD , ∴PB =PQ =DN ,∠PQD =∠NDM ∴PQ ∥DN ,又∵∠BPQ =∠BDN= 90° ∴∠PBQ =∠BDC=∠NDC =45° 再证△BPC ≌△DNC (SAS) 易证△PCN 为等腰直角三角形, 又∵PM =MN ,∴PM ⊥MC ,且PM =CM .GFEDCBA FE D CBA6初二秋季·第2讲·提高班·教师版定 义示例剖析截长:即在一条较长的线段上截取一段较短的线段DCBA在线段AB 上截取AD AC =补短:即在较短的线段上补一段线段使其和较长的线段相等AB C D延长AC ,使得AD AB =【例5】 在ABC △中,A ∠的平分线交BC 于D ,AB AC CD =+,40B ∠=︒,求C ∠的大小.(希望杯培训题)D C B AED CB A【解析】 在AB 上截取AE AC =,连接DE .∵AE AC =,BAD CAD ∠=∠,AD AD =,∴ACD AED △≌△, ∴C AED ∠=∠,CD DE =,∵AB AC CD =+,AE AC =,∴CD BE DE == ∴40EBD EDB ∠=∠=︒,80C AED ∠=∠=︒例题精讲思路导航题型二:截长补短7初二秋季·第2讲·提高班·教师版D CB AEDCB AD CEBAE DCB A【例6】 如图,在ABC △中,2B C ∠=∠,BAC ∠的平分线AD 交BC 于点D .求证:AB BD AC +=. 【解析】方法一:(截长)在AC 上截取AB AE =,连接DE .在ABD △和AED △中AB AE =,BAD EAD ∠=∠,AD AD =∴ABD AED △≌△∴BD ED =,B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠ ∴EDC C ∠=∠,∴ED EC =∴AB BD AC +=. 方法二:(补短)延长AB 到点E 使得AC AE =,连接DE . 在AED △和ACD △中,AE AC =,EAD CAD ∠=∠,AD AD = ∴AED ACD △≌△,∴C E ∠=∠ 又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE BD =,∴AB BD AC +=.方法三:(补短)延长DB 到点E 使得AB BE =,连接AE 则有EAB E ∠=∠,2ABC E EAB E ∠=∠+∠=∠ 又∵2ABC C ∠=∠,∴C E ∠=∠ ∴AE AC = EAD EAB BAD E DAC ∠=∠+∠=∠+∠C DAC ADE =∠+∠=∠∴AE DE =,∴AB BD EB BD ED AE AC +=+=== ∴AB +BD=AC若题目条件或求证结论中含有“a b c =+”的条件,需要添加辅助线时多考虑“截长补短”.建议教师此题把3种解法都讲一下,方便学生更加深刻理解这种辅助线添加方法.【例7】 已知:在ABC △中,AB CD BD =-,AD BC ⊥,求证:2B C ∠=∠.【解析】 方法一:在DC 上取一点E ,使BD DE =,如图1,在ABD △和AED △中,AD BC ⊥,BD ED =,AD AD =.典题精练DC BA8初二秋季·第2讲·提高班·教师版∴ABD AED △≌△. ∴AB AE =,B AED ∠=∠.又∵AE AB CD BD CD DE EC ==-=-= ∴C EAC ∠=∠,∴2C EAC AED C ∠+∠=∠=∠ ∴2B C ∠=∠.图1E AB CD图2EAB CD方法二:延长DB 到点E ,使BE AB =,如图2, ∴E EAB ∠=∠.∵AB CD BD =-,∴ED CD =.在AED △和ACD △中,AD BC ⊥,ED CD =,AD AD =. ∴AED ACD △≌△. ∴E C ∠=∠. ∵2ABD E ∠=∠ ∴2B C ∠=∠.【探究对象】截长补短法是几何证明题中十分重要的方法,通常来证明几条线段的数量关系,常见做辅助线方法有: 截长法:⑴过某一点作长边的垂线;⑵在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形9级 全等三角形的经典模型(二)三角形8级全等三角形的经典模型(一) 三角形7级倍长中线与截长补短倍长中线与截长补短满分晋级漫画释义2倍长中线 与截长补短定 义示例剖析倍长中线:即延长三角形的中线,使得延长后的线段是原中线的两倍.其目的是构造一对对顶的全等三角形; 其本质是转移边和角.EDABC其中BD CD =,延长AD 使得DE AD =,则BDE CDA △≌△.【例1】 已知ABC △中,AD 平分BAC ∠,且BD CD =,求证:AB AC =.【解析】 延长AD 到E ,使DE AD =,连接CE . 则CDE BDA △≌△,∴CE AB =,CED BAD ∠=∠,∵AD 平分BAC ∠,∴BAD CAD ∠=∠,∴CED CAD ∠=∠,∴CE AC =, ∴AB AC =.【教师备选】教师可借用例1对等腰三角形三线合一性质的逆命题进行简单归纳: 思路导航例题精讲知识互联网题型一:倍长中线EAB C DAB CD已知角平分线+中线证等腰三角形,如例1; 已知角平分线+高证等腰三角形,如拓展1; 已知中线+高证等腰三角形,如拓展2.【拓展1】已知△ABC 中,AD 平分∠BAC ,且AD ⊥BC ,求证:AB =AC . 【解析】∵AD 平分∠BAC ,∴∠BAD =∠CAD∵AD ⊥BC ,∴∠ADB =∠ADC =90° ∴△ABD ≌△ACD (SAS) ∴AB =AC . 【拓展2】已知△ABC 中,AD ⊥BC ,且BD CD =,求证:AB =AC . 【解析】∵AD ⊥BC ,且BD CD =∴AD 所在直线是线段BC 的垂直平分线根据垂直平分线上的点到线段两端点距离相等 故AB =AC .【例2】 ⑴如图,已知ABC △中,AB AC =,CE 是AB 边上的中线,延长AB 到D ,使BD AB =.给出下列结论:①AD =2AC ;②CD =2CE ;③∠ACE =∠BCD ;④CB 平分∠DCE ,则以上结论正确的是 .【解析】 ①正确.∵AB AC =,BD AB =,∴AD =2AC .②、④正确.延长CE 到F ,使EF CE =,连接BF . ∵CE 是AB 的中线,∴AE EB =. 在EBF △和EAC △中AE BE AEC BEF CE FE =⎧⎪∠=∠⎨⎪=⎩∴EBF EAC ≌△△∴BF AC AB BD ===,EBF EAC ∠=∠∴FBC FBE EBC A ACB DBC ∠=∠+∠=∠+∠=∠ 在FBC △和DBC △中 FB DB FBC DBC BC BC =⎧⎪∠=∠⎨⎪=⎩∴FBC DBC ≌△△∴2CD CF CE ==,∠FCB =∠DCB 即CD =2CE ,CB 平分∠DCE .③错误.∵∠FCB =∠DCB ,而CE 是AB 边上中线而不是∠ACB 的角平分线故∠ACE 和∠BCD 不一定相等.⑵如图,在△ABC 中,点D 、E 为边BC 的三等分点,给出下列结论:①BD =DE =EC ;②AB +AE >2AD ;③AD +AC >2AE ;④AB +AC >AD +AE ,则以上结论正确的典题精练ABDE DC B A FCA EB D是 .NM ED CBAEDCBA【解析】 点D 、E 为边BC 的三等分点,∴BD =DE =CE 延长AD 至点M ,AE 至点N ,使得DM =AD ,EN =AE ,连接EM 、CN ,则可证明△ABD ≌△MED ,进而可得AB +AE >2AD ,再证明△ADE ≌△NCE ,进而可得AD +AC >2AE ,将两式相加可得到AB +AE +AD +AC >2AD +2AE ,即AB +AC >AD +AE . ∴①②③④均正确.【例3】 如图,已知在ABC △中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.【解析】 延长AD 到G ,使DG AD =,连接BG∵BD CD =,BDG CDA ∠=∠,AD GD =∴ADC GDB △≌△, ∴AC GB =,G EAF ∠=∠ 又∵AF EF =,∴EAF AEF BED ∠=∠=∠ ∴G BED ∠=∠,∴BE BG =,∴AC BE =.【例4】 在正方形ABCD 中,PQ ⊥BD 于P ,M 为QD 的中点,试探究MP 与MC 的关系.GFEDCBA FE D CBANABCDMPQ Q PMDCBA【解析】 延长PM 至点N ,使PM =MN ,连结CP 、CN 、DN .易证△PMQ ≌△NMD ,∴PB =PQ =DN ,∠PQD =∠NDM∴PQ ∥DN ,又∵∠BPQ =∠BDN= 90° ∴∠PBQ =∠BDC=∠NDC =45° 再证△BPC ≌△DNC (SAS)易证△PCN 为等腰直角三角形,又∵PM =MN ,∴PM ⊥MC ,且PM =CM .定 义示例剖析截长:即在一条较长的线段上截取一段较短的线段DCBA在线段AB 上截取AD AC =补短:即在较短的线段上补一段线段使其和较长的线段相等AB C D延长AC ,使得AD AB =例题精讲思路导航题型二:截长补短DCB AED CB A D CE BAEDCBA【例5】 在ABC △中,A ∠的平分线交BC 于D ,AB AC CD =+,40B ∠=︒,求C ∠的大小.(希望杯培训题)D C B AED CB A【解析】 在AB 上截取AE AC =,连接DE .∵AE AC =,BAD CAD ∠=∠,AD AD =, ∴ACD AED △≌△,∴C AED ∠=∠,CD DE =,∵AB AC CD =+,AE AC =,∴CD BE DE == ∴40EBD EDB ∠=∠=︒,80C AED ∠=∠=︒【例6】 如图,在ABC △中,2B C ∠=∠,BAC ∠的平分线AD 交BC 于点D .求证:AB BD AC +=.【解析】方法一:(截长)在AC 上截取AB AE =,连接DE .在ABD △和AED △中AB AE =,BAD EAD ∠=∠,AD AD = ∴ABD AED △≌△∴BD ED =,B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠ ∴EDC C ∠=∠,∴ED EC = ∴AB BD AC +=.方法二:(补短)延长AB 到点E 使得AC AE =,连接DE . 在AED △和ACD △中,AE AC =,EAD CAD ∠=∠,AD AD = ∴AED ACD △≌△,∴C E ∠=∠又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE BD =,∴AB BD AC +=. 方法三:(补短)延长DB 到点E 使得AB BE =,连接AE则有EAB E ∠=∠,2ABC E EAB E ∠=∠+∠=∠ 又∵2ABC C ∠=∠,∴C E ∠=∠∴AE AC =EAD EAB BAD E DAC ∠=∠+∠=∠+∠C DAC ADE =∠+∠=∠ ∴AE DE =,∴AB BD EB BD ED AE AC +=+=== ∴AB +BD=AC若题目条件或求证结论中含有“a b c =+”的条件,需要添加辅助线时多考虑“截长补典题精练短”.建议教师此题把3种解法都讲一下,方便学生更加深刻理解这种辅助线添加方法.【例7】 已知:在ABC △中,AB CD BD =-,AD BC ⊥,求证:2B C ∠=∠.【解析】 方法一:在DC 上取一点E ,使BD DE =,如图1,在ABD △和AED △中,AD BC ⊥,BD ED =,AD AD =. ∴ABD AED △≌△.∴AB AE =,B AED ∠=∠.又∵AE AB CD BD CD DE EC ==-=-= ∴C EAC ∠=∠,∴2C EAC AED C ∠+∠=∠=∠ ∴2B C ∠=∠.图1E AB CD图2EAB CD方法二:延长DB 到点E ,使BE AB =,如图2, ∴E EAB ∠=∠.∵AB CD BD =-,∴ED CD =.在AED △和ACD △中,AD BC ⊥,ED CD =,AD AD =. ∴AED ACD △≌△. ∴E C ∠=∠. ∵2ABD E ∠=∠ ∴2B C ∠=∠.【探究对象】截长补短法是几何证明题中十分重要的方法,通常来证明几条线段的数量关系,常见做辅助线方法有: 截长法:⑴过某一点作长边的垂线;⑵在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短法: ⑴延长短边。
⑵通过旋转等方式使两短边拼合到一起,证与长边相等。
【变式一】正方形ABCD 中,点E 在CD 上,点F 在BC 上,∠EAF =45°,求证:EF =DE +BF .D CBAGAD BCEFFEC BDA【解析】 延长CD 到点G ,使得DG =BF ,连接AG由四边形ABCD 是正方形得:∠ADG =∠ABF =90°,AD =AB 又∵DG =BF∴△ADG ≌△ABF (SAS ) ∴∠GAD =∠F AB ,∴AG =AF 由四边形ABCD 是正方形得∠DAB =90°=∠DAF +∠F AB =∠DAF +∠GAD =∠GAF ∴∠GAE =∠GAF -∠EAF =90°-45°=45° ∴∠GAE =∠F AE =45° 又∵AG =AF ,AE =AE∴△EAG ≌△EAF (SAS ) ∴EF =GE =GD +DE =BF +DE【变式二】正方形ABCD 中,点E 在CD 延长线上,点F 在BC 延长线上,∠EAF =45°,请问现在EF 、DE 、BF 又有什么数量关系?GFECB DAADBCEF【解析】 数量关系为:EF =BF -DE .理由如下:在BC 上截取BG ,使得BG =DF ,连接AG 由四边形ABCD 是正方形得∠ADE =∠ABG =90°,AD =AB 又DE =BG∴△ADE ≌△ABG (SAS ) ∴∠EAD =∠GAB ,AE =AG由四边形ABCD 是正方形得∠DAB =90°=∠DAG +∠GAB =∠DAG +∠EAD =∠GAE ∴∠GAF =∠GAE -∠EAF =90°-45°=45° ∴∠GAF =∠EAF =45° 又∵AG =AE ,AF =AF∴△EAF ≌△GAF (SAS ) ∴EF =GF =BF -BG =BF -DE【变式三】正方形ABCD 中,点E 在DC 延长线上,点F 在CB 延长线上,∠EAF =45°,请问现在EF 、DE 、BF 又有什么数量关系?F EC BDAADBC E FG【解析】 数量关系为:EF =DE -BF .理由如下:在DC 上截取DG ,使得DG =BF ,连接AG 由四边形ABCD 是正方形得∠ADG =∠ABF =90°,AD =AB 又∵DG =BF∴△ADG ≌△ABF (SAS ) ∴∠GAD =∠F AB ,AG =AF 由四边形ABCD 是正方形得∠DAB =90°=∠DAG +∠GAB =∠BAF +∠GAB =∠GAF ∴∠GAE =∠GAF -∠EAF =90°-45°=45° ∴∠GAE =∠F AE =45° 又∵AG =AF ,AE =AE∴△EAG ≌△EAF (SAS ) ∴EF =EG =ED -GD =DE -BF【变式四】正三角形ABC 中,E 在AB 上,F 在AC 上∠EDF =60°,DB =DC ,∠BDC =120°,请问现在EF 、BE 、CF 又有什么数量关系?GABDC EFFE CDBA【解析】 数量关系为:EF =BE +FC ,理由如下延长AC 到点G ,使得CG =BE ,连接DG由△ABC 是正三角形得:∠ABC =∠ACB =60° 又∵DB =DC ,∠BDC =120°,∴∠DBC =∠DCB =30° ∴∠DBE =∠ABC +∠DBC =60°+30°=90°,∠ACD =∠ACB +∠DCB =60°+30°=90°∴∠GCD =180°-∠ACD =90°∴∠DBE =∠DCG =90°又∵DB =DC ,BE =CG ,∴△DBE ≌△DCG (SAS ) ∴∠EDB =∠GDC , DE =DG 又∵∠DBC =120°=∠EDB +∠EDC =∠GDC +∠EDC =∠EDG ∴∠GDF =∠EDG -∠EDF =120-60°=60° ∴∠GDF =∠EDF =60° 又∵DG =DE ,DF =DF∴△GDF ≌△EDF (SAS ) ∴EF =GF =CG +FC =BE +FC【变式五】正方形ABCD 中,点E 在CD 上,点F 在BC 上,∠EAD =15°,∠F AB =30°,求△AEF 的面积.HGAD BCEFFEC BDA【解析】 延长CD 到点G ,使得DG =BF ,连接AG ,过E 作EH ⊥AG前面如变式一所证,△ADG ≌△ABF ,△EAG ≌△EAF∠GAD =∠F AB =30°,S △EAG =S △EAF在Rt△ADG中,∠GAD=30°,AD=3∴∠AGD =60°,AG=2设EH=x在Rt△EGH中和Rt△EHA中∵∠AGD=60°,∠HAE=45°∴HG=33x,AH=xAG=2=HG+AH=33x x+,∴EH=x=33-S△EAG=S△EAF =12EH⨯AG=3-.【例8】已知:正方形ABCD中,∠MAN=45°,绕点A顺时针旋转,它的两边分别交CB、DC (或它们的延长线)于点M、N.⑴如图1,当∠MAN绕点A旋转到BM=DN时,有BM+DN=MN.当∠MAN绕点A旋转到BM DN≠时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;⑵当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间有怎样的等量关系?请写出你的猜想,并证明.(2012密云一模)【解析】⑴图1中的结论仍然成立,即BM DN MN+=.证明:如图2,在MB的延长线上截取BE=DN,连结AE .易证ABE ADN△≌△(SAS).1112∴AE =AN ;∠EAB =∠NAD . 90,45BAD NAM ∠=∠=∴45.BAM NAD ∠+∠= ∴45.EAB BAM ∠+∠=∴EAM NAM ∠=∠.又AM 为公共边, ∴AEM ANM △≌△. ∴ME =MN . ∴MN ME BE BM DN BM ==+=+ 即 DN BM MN +=.⑵猜想:线段BM 、DN 和MN 之间的等量关系为:DN BM MN -= . 证明:如图3,在DN 延长线上截取DE =MB ,连结A E . 易证 ABM ADE △≌△(SAS ). ∴AM =AE ;∠MAB =∠EAD . 易证 AMN AEN △≌△(SAS ). ∴MN EN = .∵DN DE EN -=, ∴DN BM MN -=.13FE N AB D CD C B A EDC BA训练1. 已知AD 为ABC △的中线,ADB ∠、ADC ∠的平分线分别交AB 于E 、交AC 于F .求证:BE CF EF +>.FE AB D C【解析】 延长FD 到N ,使DN DF =,连接BN 、EN .易证BND CFD △≌△,∴BN CF =,又∵ADB ∠、ADC ∠的平分线分别交AB 于E 、交AC 于F , ∴90EDF EDN ∠=∠=︒,利用SAS 证明EDN EDF △≌△,∴EN EF =, 在EBN △中,BE BN EN +>,∴BE CF EF +>.训练2. 如图,在正方形ABCD 中,F 是CD 的中点,E 是BC 边上的一点,且AF 平分DAE ∠,求证:AE EC CD =+【解析】 解一:(截长)作FH AE ⊥于点H分别证明AFH AFD EFH EFC △≌△,△≌△, ∴AH AD HE EC ==,∴AE AH HE CD EC =+=+ 解二:(补短)延长AF BC ,交于点G先证明ADF GCF △≌△,∴CG DA CD ==,G FAD ∠=∠, ∵DAF EAF ∠=∠,∴G EAF ∠=∠∴AE EG =,∴AE EC CG EC CD =+=+.HFEDC BAG FE DCBA训练3. 如图,ABC △中,AB AC =,108A ∠=︒,BD 平分ABC ∠交AC 于D 点.求证:BC AC CD =+.【解析】 方法一:在BC 上截取E 点使BE BA =,连结DE .∵BD 平分ABC ∠,∴ABD EBD ∠=∠.思维拓展训练(选讲)FE DCB A14DCBAF在ABD △与EBD △中∵AB EB =,ABD EBD ∠=∠,BD BD = ∴ABD EBD △≌△,∴A DEB ∠=∠∵108A ∠=︒, ∴108DEB ∠=∠︒∴72DEC ∠=︒. 又∵361854ADB ∠=︒+︒=︒∴72CDE ∠=︒,∴CDE DEC ∠=∠,∴CD CE = ∵BC BE EC =+,∴BC AC CD =+方法二:如图,延长CA 到F ,使CF CB =,连结BF . ∵AB AC =,且108BAC ∠=︒, ∴36ABC C ∠=∠=︒.∵CB CF =,∴F FBC ∠=∠.∴FAB C ABC ∠=∠+∠.∴72FAB ∠=︒.∵12ADB C ABC ∠=∠+∠,∴54ADB ∠=︒.又∵54FBD ∠=︒∴BF AB AC FD ===.∴AF CD =.∴BC AC CD =+.训练4. 五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:AD 平分∠CDE .【解析】 延长DE 至F ,使得EF =BC ,连接AC 、AF .∵∠ABC +∠AED =180°,∠AEF +∠AED =180° ∴∠ABC =∠AEF∵AB =AE ,BC =EF ,∴△ABC ≌△AEF ∴EF =BC ,AC =AF ∵BC +DE =CD ,∴CD =DE +EF =DF∴△ADC ≌△ADF ,∴∠ADC =∠ADF 即AD 平分∠CDE .C EDB AAB DEFC15题型一 倍长中线 课后演练【演练1】 在ABC △中,59AB AC ==,,则BC 边上的中线AD 的长的取值范围是什么? 【解析】中线倍长,27AD <<【演练2】 在Rt ABC △中,F 是斜边AB 的中点,D 、E 分别在边CA 、CB 上,满足90DFE ∠=︒.若3AD =,4BE =,则线段DE 的长度为_________.FEDCBA图 6G E FDBC A【解析】如图,延长DF 至点G ,使得DF FG =,联结GB 、GE . 由AF FB =,有ADF BGF △≌△∴3BG AD ==,ADF BGF ∠=∠,∴AD GB ∥∴180GBE ACB ∠+∠=︒,∴90GBE ∠=︒,∴225GE GB EB =+=. 又DF FG =,EF DG ⊥,∴5DE GE ==.题型二 截长补短 课后演练【演练3】 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?(提示:过点M 作MG BD ∥交AD 于点G )N E B M A DGNEB M A D【解析】 猜测DM MN =.过点M 作MG BD ∥交AD 于点G ,AG AM =,∴GD MB =又∵120ADM DMA +∠=∠,120DMA NMB +=∠∠ ∴ADM NMB =∠∠,而120DGM MBN ==∠∠, ∴DGM MBN △≌△,∴DM MN =. 复习巩固DCBA16【演练4】 如图所示,已知ABC △中,AC BC =,90C ∠=︒,AD 平分BAC ∠,求证:AC CD AB +=.【解析】 解法一:如图,过D 作DE AB ⊥于E .CD AC ⊥∵,12∠=∠, Rt Rt ACD AED ∴△≌△,,CD DE AC AE ==∴.又DE BE ⊥∵,45B ∠=︒,DEB ∴△为等腰直角三角形.有DE BE =,故 BE CD =. AB AE BE AC CD =+=+∴. 解法二:如图,延长AC 到E ,使CE CD =.90ECD ∠=︒∵,45E ∠=︒∴.又12∠=∠∵,45E B ∠=∠=︒,AD 公共,ADE ADB ∴△≌△,有AE AB =.故AB AC CE AC CD =+=+.【演练5】 已知:如图,ABCD 是正方形,∠F AD =∠F AE . 求证:BE +DF =AE .【解析】 延长CB 至M ,使得BM =DF ,连接AM .∵AB =AD ,AD ⊥CD ,AB ⊥BM ,BM =DF ∴ABM ADF △≌△∴∠AFD =∠AMB ,∠DAF =∠BAM ∵AB CD ∥ ∴∠AFD =∠BAF =∠EAF +∠BAE =∠BAE +∠BAM =∠EAM∴∠AMB =∠EAM∴AE =EM =BE +BM =BE +DF .21DC B A EE AB CD 12F E DCB AM F E D C B A17测试1. 如图所示,已知ABC △中,AD 平分BAC ∠,E 、F 分别在BD 、AD 上.DE CD =,EF AC =.求证:EF ∥AB .【解析】 延长AD 到M ,使DM AD =,连结EM ,利用SAS 证明ADC MDE △≌△,∴3M ∠=∠,AC EM =, 又AC EF =,∴EM EF =,∴1M ∠=∠,∴13∠=∠,∵AD 平分BAC ∠,∴23∠=∠,∴12∠=∠,∴EF ∥AB .测试2. 已知ABC △中,60A ∠=,BD 、CE 分别平分ABC ∠和ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.AB CDEO4321O FED CBA【解析】 BE CD BC +=,理由是:在BC 上截取BF BE =,连结OF , 利用SAS 证得BEO △≌BFO △,∴12∠=∠,∵60A ∠=︒,∴1901202BOC A ∠=+∠=,∴120DOE ∠=,∴180A DOE ∠+∠=,∴180AEO ADO ∠+∠=,∴14180∠+∠=, ∵23180∠+∠=,12∠=∠,∴34∠=∠,利用AAS 证得CDO △≌CFO △,∴CD CF =,∴BC BF CF BE CD =+=+.课后测F A C D E B 321M FAC D E B第十五种品格:创新巧问巧答从前,有个有智慧的国王在大臣们的陪同下,来到御花园散步。
