单跨梁等静力计算公式及图表
单跨梁等静力计算公式及图表

MB=1/2 M0Qx=-3/2·M0/ι
Mx=M0-3/2·M0/ιX(X由0→ι)
M最大=M0(在A处)
-M最大=-1/2 M0(在B处)
y最大=-M0ι2/27EI(在X=1/3处)
θA=-M0ι/4EI
两端刚性固定的梁
力作用在跨度间
RA=Pb2/ι3(3α+b)MA=Pαb2/ι2
θA=-M0ι/3EI
θB=M0ι/6EI
力矩作用于跨度间
RA=-RB=-M0/ιQx-M0/ι
Mx=-M0/ιX(AC间)
Mx=M0(1-X/ι)(CB间)
M最大=-M0/ια+M0(C点右一些)
-M最大=-M0/ια(C点左一些)
y=M0/6EI[(6α-3α2/ι-2ι)X-X3/ι](AC间)
两个力作用在外伸端
RA=RB=P
Qx1=-P(CA间)
Qx=0(AB间)
Qx2=P(BD间)
Mx=-Pι1(AB间)
Mx1=-PX1(CA间)
Mx2=-PX2(BD间)
y最大=-Pι2ι1/8EI(在跨中)
θA=-θB=Pιι1/2EI
连续均布载荷
RA=RB=qι/2
Qx=qι/2-qX(X由0→ι)
Mx=-qX2/2(X由0→ι)
MB=-yA=-qι4/8EI
θA=-qι3/6EI
力矩作用在自由端
RB=0
Qx=0
Mx=-M0(X由0→ι)
MB=-M0
M最大=-M0
yA=-M0ι2/2EI
θA=-M0·ι2/EI
两端自由支承梁
一个力作用在跨度间
RA=Pb/ι;RB=Pα/ι
单跨超静定梁的杆端弯矩和杆端剪力

Δ1=δ11X1+δ12X2+δ13X3+Δ1P=0
Δ2=δ21X1+δ22X2+δ23X3+Δ2P=0
b
Δ3=δ31X1+δ32X2+δ33X3+Δ3P=0
式(b)就是由位移条件所建立的求解X1、X2和X3
对于n次超静定结构有n个多余约束,也就是有n 个多余未知力x1,x2,…,xn,且在n个多余约束处 有n个已知的位移条件,故可建立n个方程,例如原 结构在荷载作用下各多余约束处的位移为零时,有
11E 1 I
M 1 2dx1(1ll2l)l3 E I2 3 3E I
1
11q l2 3 q l4
1 P E IM 1 M P d x E I(3 2l l 4 l) 8 E I
单跨静定梁的内力计算

单跨静定梁的内力计算单跨静定梁的内力计算是结构力学中的一个基本问题,通过计算可以得到梁在不同位置处的剪力、弯矩和轴力等内力参数。
这些内力参数是设计和分析梁的性能和安全性的重要依据。
梁的内力计算可以通过多种方法进行,常见的有静力方法、能量方法和受力平衡方法等。
下面将介绍静力方法和能量方法这两种常用的计算方法,并简要说明计算步骤和注意事项。
1. 静力方法:静力方法是一种基于受力平衡的计算方法,通过平衡受力来计算内力。
具体步骤如下:1.1 绘制受力图:根据梁的受力情况,画出受力图,标注各个受力的方向和大小,包括支持力、荷载力、剪力和弯矩等。
1.2 利用受力平衡条件分析:根据受力平衡条件,设置适当的方程组,解方程组得到未知力的大小。
1.3 计算内力:根据受力图和已知力的大小,应用受力平衡和几何关系,计算梁的不同位置处的剪力、弯矩和轴力等内力。
2. 能量方法:能量方法是通过能量原理来计算内力的一种方法,包括弹性势能原理和最小势能原理。
具体步骤如下:2.1 建立适当的变形假设和应变位移关系:对梁的受力状态进行分析,建立适当的变形假设,如小位移假设,然后利用应变位移关系得到各部位的应变和位移。
2.2 建立应变能和位移能的表达式:利用应变能和位移能的定义,建立它们的表达式,一般包括弯曲应变能、剪切应变能和轴向应变能等。
2.3 建立总能量和平衡方程:将总能量表示为应变能和位移能的和,再应用极值原理,建立平衡方程,对系统总能量求导,使其达到极值。
2.4 计算内力:通过求解平衡方程,得到梁在不同位置处的内力。
在进行单跨静定梁的内力计算时,需要注意以下几点:- 细化受力图的绘制,要准确标注各个受力的方向和大小。
- 对于复杂的受力情况,可采用多段剖分的方法,将梁分割为多个小段进行分析,再将结果整合得到整体的内力。
- 静力和能量方法是两种常用的计算方法,其结果应尽可能一致,以确保计算结果的准确性。
- 在应用能量方法计算内力时,应根据实际情况选择适当的应变能和位移能表达式。
钢材知识(十四)工字钢抗弯强度计算方式

钢材知识(十四)-工字钢抗弯强度计算方式工字钢抗弯强度计算方式一、梁的静力计算概况一、单跨梁形式:简支梁二、荷载受力形式:简支梁中间受集中载荷3、计算模型大体参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*+40*=104 KN二、选择受荷截面一、截面类型::I40c二、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3 G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm三、相关参数一、材质:二、x轴塑性进展系数γx:3、梁的挠度操纵[v]:L/250四、内力计算结果一、支座反力 RA = RB =52 KN二、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156五、强度及刚度验算结果一、弯曲正应力σmax = Mmax / (γx * Wx)= N/mm2二、A处剪应力τA = RA * Sx / (Ix * tw)= N/mm23、B处剪应力τB = RB * Sx / (Ix * tw)= N/mm24、最大挠度 fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )=7.33 mm五、相对挠度 v = fmax / L =1/弯曲正应力σmax= N/mm2 < 抗弯设计值 f : 205 N/mm2 ok!支座最大剪应力τmax= N/mm2 < 抗剪设计值 fv : 125 N/mm2 ok!跨中挠度相对值 v=L/ < 挠度操纵值[v]:L/ 250 ok! 验算通过!工字钢抗弯强度计算方式一、梁的静力计算概况1、单跨梁形式:简支梁2、荷载受力形式:简支梁中间受集中载荷3、计算模型大体参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*+40*=104 KN二、选择受荷截面1、截面类型:工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx= 711.2cm3G= 80.1kg/m翼缘厚度 tf= 16.5mm 腹板厚度 tw= 14.5mm三、相关参数1、材质:Q2352、x轴塑性进展系数γx:3、梁的挠度操纵[v]:L/250四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156五、强度及刚度验算结果1、弯曲正应力σmax = Mmax / (γx * Wx)= N/mm22、A处剪应力τA = RA * Sx / (Ix * tw)= N/mm23、B处剪应力τB = RB * Sx / (Ix * tw)= N/mm24、最大挠度 fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )=7.33 mm5、相对挠度 v = fmax / L =1/弯曲正应力σmax= N/mm2 < 抗弯设计值 f : 205 N/mm2 ok!支座最大剪应力τmax= N/mm2 < 抗剪设计值 fv : 125 N/mm2 ok! 跨中挠度相对值 v=L/ < 挠度操纵值[v]:L/ 250 ok! 验算通过!。
静定结构的内力计算图文

30 30
4m
4m
4m
4m
12kN
12kN 12kN
M 图(kN·m)
9kN
9kN
2kN/m
7kN
5kN
9kN
4.5kN
7.5kN
39
第40页/共76页
作业
习题3-5、3-6、3-9 习题3-10、3-12
40
第41页/共76页
§3-3 三铰拱
41
第42页/共76页
一、 概述
1、定义:
通常杆轴线为曲线,在竖向荷载作用下,支座产生水平反力的结构。
AC段受力图:
q
MC
t
C
FNC
FQC
n
x
FAY
FAYSinα
(2)求内力方程:
MC = 0 Ft = 0 Fn= 0
M = 1 qlx 1 qx2 (0 x l) 22
FN
=
q(1 l 2
x) sin
(0 x l)
FQ
=
q(1 2
l
x) cos
(0 x l)
FAYcosα
FAY
M中 =162 / 8 6.23/ 2 =1.385kN.m(下拉)
弯矩图见下图。
1kN/m
6.23 D
C 1.385
6.23 E
1.385kN A
4.5kN
M 图(kN.m)
B 1.385kN
1. 5kN
38
第39页/共76页
例:主从刚架弯矩图。
12kN
2kN/m
36 36
6m
12 42 30
F
F
曲梁
拱
f / l : 高跨比(1~1/10)
结构力学专题十六(单跨梁极限荷载计算)

P
P
A
D
B
C
l/3 l/3 l/3
共有三种可能的破坏机构
Fpu
4 l
Mu
F1
5 l
Mu
F2
4 l
Mu
2.用试算法求解
F3
9 l
Mu
作业:
16—3、 16—4。
补:求图示结构的极限荷载, 材料极限弯矩为Mu。
M
A
C
B
3m
1m
(2)平衡弯矩法
Mmax 1.5FPu M u
FPu
2 3
Mu
2F
F
2m
2m
1m
小结: 静定梁极限荷载计算特点:
静定结构无多余约束,出现一个塑性铰即成为破 坏机构。这时结构上的荷载即为极限荷载。
塑性铰出现的位置应为截面弯矩与极限弯矩之比 的绝对值最大的截面。
求出塑性铰发生的截面后,令该截面的弯矩等于 极限弯矩,利用平衡条件即可求出极限荷载。
(1)可破坏荷载 Fp
对任一破坏机构,由平衡条件求出的荷载称为可破坏 荷载;
(2)可接受荷载 Fp
同时满足屈服条件和平衡条件的荷载称为可接受荷载;
(3)极限荷载 Fpu
同时满足三个条件的荷载称为极限荷载,即极限荷载 既是可破坏荷载,又是可接受荷载。
4、一般定理
(1)基本定理(预备定理)
可破坏荷载恒不小于可接受荷载 Fp Fp
第十六章 梁和刚架的极限荷载
§16-3 单跨梁极限荷载计算
一、静定梁 例2:求图示结构的极限荷载,
材料极限弯矩为Mu。 (1)机动法
2F
F
2m
2m
1m
塑性铰出现在支座处
工字钢抗弯强度计算方法

工字钢抗弯强度计算方法一、梁的静力计算概况1、单跨梁形式:简支梁2、荷载受力形式:简支梁中间受集中载荷3、计算模型基本参数:长 L =6 M4、集中力:标准值Pk=Pg+Pq =40+40=80 KN设计值Pd=Pg*γG+Pq*γQ =40*+40*=104 KN二、选择受荷截面1、截面类型:工字钢:I40c2、截面特性: Ix= 23850cm4 Wx= 1190cm3 Sx=G= m翼缘厚度 tf= 腹板厚度 tw=三、相关参数1、材质:Q2352、x轴塑性发展系数γx:3、梁的挠度控制[v]:L/250四、内力计算结果1、支座反力 RA = RB =52 KN2、支座反力 RB = Pd / 2 =52 KN3、最大弯矩 Mmax = Pd * L / 4 =156五、强度及刚度验算结果1、弯曲正应力σmax = Mmax / (γx * Wx)= N/mm22、A处剪应力τA = RA * Sx / (Ix * t w)= N/mm23、B处剪应力τB = RB * Sx / (Ix * tw)= N/mm24、最大挠度 fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )= mm5、相对挠度 v = fmax / L =1/弯曲正应力σmax= N/mm2 < 抗弯设计值 f : 205 N/mm2 ok!支座最大剪应力τmax= N/mm2 < 抗剪设计值 fv : 125 N/mm2 ok!跨中挠度相对值 v=L/ < 挠度控制值[v]:L/ 250 ok! 验算通过Re: 如何计算角钢的受力---[图,请教]1、? ? ? ? 设每个支点承载力为p=1875N,根据图所示,支点反力R=2p2、? ? ? ? 第一受力点弯矩M1=2p×=,第二受力点弯矩M2=2p×(+)-p×==如弯矩图所示3、? ? ? ? 查东北大学机械设计手册第一册3-157页的50×5的角钢抗弯W==×10-6m34、? ? ? ? 计算弯曲应力σ=M2/w=×10-6=491×106N/m2=491MPa5、? ? ? ? 角钢材料一般为Q235,其屈服应力为235MPa,故判断491>235,角钢将失效Q235钢抗弯强度设计值 = = =mm2 < f=205N/mm2 符合要求。
等截面单跨超静定梁的内力计算

B M图 B
X1=1
M图 11 X1 A
1 1 2 l 11 l 1 EI 2 3 3EI
FQ图
3EI X1 A 3i A ( ) l
2) A l A
i l
B
Δ
A 3i M AB l
B M图
M图
11 X1
l3 11 3EI
l Fl 2 X1 0 3EI 16 EI
X1
3Fl 16
M M1 X 1 M p
3 Fl 16
F
B
5 Fl 32
11 F 16
A
A
+
B
5 F 16
M 图
FQ 图
载常数图:
3l 16
1
B
5l 32 5 16
A
11 16
q
2)
A
B
A
X1
基本体系
B
l
基本方程: A 1
11 X 1 1 p 0
Fl 8
F
A
Fl 8
1 F 2
B
A
+
B
1 F 2
Fl 8
载常数图:
M 图
l 8
FQ 图
1
l 8
A
1 2
B
l 8
1 2
M 图
q
4)
A
B
A
X1
基本体系 A X1=1
X2
B
l
基本方程: 11 X 1 12 X 2 1 p 0
B
21 X 1 22 X 2 2 p 0
Mp图
1 l 1 l ql 2 ql 2 2l ql 3 11 1 l 1 1 p EI EI EI 2 2 8 3 3EI
单跨静定梁的内力计算

单跨静定梁的内力计算单跨静定梁的内力计算是结构工程中重要的计算内容之一。
静定梁是指在受力状态下,其内力可以通过静力学原理直接计算得出的梁结构。
而单跨静定梁是指只有一个支座的静定梁,是静力学中最简单的结构之一。
在计算单跨静定梁的内力时,首先需要明确梁的受力情况。
在单跨静定梁中,通常会受到集中力、均布载荷或者集中力和均布载荷的组合作用。
根据力的平衡条件和梁的几何特性,可以计算出梁的内力,包括弯矩和剪力。
在计算单跨静定梁的内力时,可以采用梁的截面法。
根据力的平衡条件,可以先计算出支座的水平力和垂直力,然后通过力和力矩的平衡条件计算出梁的内力。
在计算弯矩和剪力时,需要根据梁的几何形状和受力情况,采用力的平衡和力矩平衡的原理进行计算。
在计算单跨静定梁的内力时,需要注意以下几点:1. 确定梁的受力情况:包括集中力、均布载荷的大小和作用位置等。
2. 绘制梁的受力图:根据受力情况,绘制出梁的受力图,明确受力的方向和大小。
3. 采用力的平衡和力矩平衡的原理计算内力:根据力的平衡和力矩平衡的原理,计算出梁的内力,包括弯矩和剪力。
4. 考虑梁的内力图:根据计算出的内力,绘制出梁的内力图,明确各处的内力分布情况。
通过以上步骤,可以准确计算出单跨静定梁的内力,为梁的设计和施工提供重要的参考依据。
在实际工程中,计算出的内力可以用来确定梁的截面尺寸和材料的选择,确保梁的受力性能符合设计要求,保证梁的安全性和稳定性。
同时,计算出的内力也可以用来指导梁的施工和监测,确保梁的受力状态符合设计要求,提高梁的使用性能和寿命。
总的来说,单跨静定梁的内力计算是结构工程中的基础计算内容,通过合理的计算方法和步骤,可以准确计算出梁的内力,为梁的设计和施工提供重要的参考依据,确保梁的受力性能符合设计要求,提高梁的使用性能和寿命。
希望以上内容能够对您的工作和学习有所帮助。
单跨静定梁的内力图(1)PPT课件

.
3
单跨静定梁的内力图
❖ 2.剪力图和弯矩图
❖ 为了能直观地观察出梁各截面上的剪力 和弯矩随截面位置变化的规律,可仿照轴力 图的作法绘出剪力图和弯矩图。绘图时以平 行梁轴线的x为横坐标,表示各横截面的位置, 以FQ或M为纵坐标,表示相应横截面上的剪 力和弯矩,规定FQ轴向上为正,M轴向下为 正。
.
.
7
例4.8 试作图示简支梁在集中荷载
a 1 Fb 2
作用下的剪力图和弯矩图。
解:1. 求支座反力 FA=b/l FP FB=a/l FP
A x
C l
B
1 F2
2.用截面法计算x确定的截 面的内力
A FA
x
x
B FB
AC:
FQ(x)
= FA (0<
= X
FPb/l
< a)
M(X) = FAX= FPb/l x
FA
(0< X < l ) 0.5ql
x M(X)
FQ FQ(x)
3.作内力图
(剪力图)
剪力图:一条斜直线
B FB
x 0.5ql
x
弯矩图:二次抛物线
M
ql 2/8 (弯矩图)
.
6
写出梁的内力方程,作内力图。并指出最大内力值以及
q
解
它们所在的截面。
Ax l
B 1.用截面法计算x确定的截面
q MB
Ax
.
10
M
FB
CB
M(X) M
M(X)
FA
FQ(x)
FQ
FQ(x) x
BC: FQ(x) =(L-<FAX+F<B=30/2 l )
M/l
单跨

图10
图11
图12
3.3.2
多跨静定梁的内力计算
由层次图可见,作用于基本部分上的荷载,并不 影响附属部分,而作用于附属部分上的荷载,会以支 座反力的形式影响基本部分,因此在多跨静定梁的内 力计算时,应先计算高层次的附属部分,后计算低层 次的附属部分,然后将附属部分的支座反力反向作用 于基本部分,计算其内力,最后将各单跨梁的内力图 联成一体,即为多跨静定梁的内力图。
解:(1)求支座反力 先假设反力方向如图所示,以 整梁为研究对象: ∑X=0: XA-P=0 XA=P=4kN ∑MB=0: YA*l-q*l*0.5*l=0 YA=0.5ql =0.5×3×4kN=6kN ∑Y=0: YA+YB=ql YB=ql-VA =(3×4-6) kN=6kN
第三章 静 定 梁
本章提要
本章主要介绍了单跨静定梁和多跨静定梁的内力分 析计算及内力图的绘制方法。通过本章的学习,主要应 掌握: (1) 梁的内力及其正负号规定; (2) 单跨静定梁内力计算及内力图绘制方法; (3) 多跨静定梁源自内力分析计算。本 章 内 容
3.1 3.2 单跨静定梁的内力计算; 斜梁的内力计算;
解: 根据叠加法原理,可把该结构分解为如图所示几种 情况。
相应的弯矩图如下图示:
三种情况弯矩图叠加,则最后弯矩如图所示:
三种情况相应的剪力图如下图示:
相叠加,则最后剪力如图所示:
(3) 绘制弯矩图的步骤 ① 求支座反力 ② 求控制截面的弯矩值,控制截面包括杆的两端、 集中力作用处(求剪力时要取两侧各一个截面)、力 偶作用处两侧、均布荷载的起点、终点和中点等; ③ 若二控制截面间无外力作用,则连以直线。若有 外力作用,则连直线(基线)后叠加上简支梁的弯矩 图。
槽钢计算

如图所示,梁跨度9米,两端按不固定计算,中间最大载荷按2吨(20000N)计算。
请问用多大的槽钢合适,真心求教,给出计算过程更好。
谢谢一、梁的静力计算概况1、单跨梁形式:简支梁2、计算模型基本参数:长 L =9 M3、集中力:标准值Pk=Pg+Pq =20+20=40 KN 设计值Pd=Pg*γG+Pq*γQ =20*1.2+20*1.4=52 KN二、选择受荷截面1、截面类型:槽钢:[ 36a2、截面特性: Ix=11870cm4 Wx=660cm3 Sx=389.9 cm3 G=47.8kg/m 翼缘厚度tf= 16mm 腹板厚度tw= 9mm三、相关参数1、材质:Q2352、x轴塑性发展系数γx:1.053、梁的挠度控制[v]:L /250四、内力计算结果1、支座反力 RA = RB =26 KN2、支座反力 RB = Pd / 2 =26 KN3、最大弯矩 Mmax = Pd * L / 4 =117 KN.M五、强度及刚度验算结果1、弯曲正应力σmax = Mmax / (γx * Wx)=168.83 N/mm22、A处剪应力τA = RA * Sx / (Ix * tw)=9.49 N/mm23、B处剪应力τB = RB * Sx / (Ix * tw)=9.4 9 N/mm24、最大挠度 fmax = Pk * L ^ 3 / 48 * 1 / ( E * I )=24.84 mm5、相对挠度 v = fmax / L =1/ 362.3 弯曲正应力σmax= 168.83 N/mm2 < 抗弯设计值 f : 215 N/mm2 ok! 支座最大剪应力τmax= 9.49 N/mm2 < 抗剪设计值fv : 125 N/ mm2 ok! 跨中挠度相对值 v=L/ 362.3 < 挠度控制值[v]:L/ 250 ok! 验算通过!选用槽钢槽钢:[ 36a以上是恒载荷为:20KN,动载荷为:20KN情况下的计算结果首先谢谢楼上各位兄弟学艺不精啊,出校几年,忘光了8楼的朋友应该是软件计算书吧,你又加了2吨的动载荷,本来就是一吨重的东西,设计值现提到2吨,呵呵,够了其实不用这么麻烦的,就是根据力来计算剪力、弯矩,然后校核抗剪强度、抗弯模量,挠度的话,根据允许挠度(按L/400吧),来计算惯性矩,再根据这么多数值,来选一个型号的槽钢。
工字钢受力计算
三、相关参数 1、材质:Q235 2、x轴塑性发展系数 γ x 1.05
3、梁的挠度控制 [v]:L/250 四、单根内力计算结果 1、支座反力RA = RB =Pd/2 2、最大弯矩Mmax =RA×L/2 五、强度及刚度验算结果 1、弯曲正应力σ max = Mmax / (γ x×Wx) 2、A处剪应力 τ A = RA×Iy / (Ix×tw) 3、B处剪应力 τ B = RB×Iy / (Ix×tw)
4、最大挠度fmax =8Pk×l (384 E×I )
3Leabharlann 3.39 KN 8.48 KN.m
164.82 N/mm2 τ A =τ B τ A =τ B 9.11 1/666 f : 205 N/mm2 符合要求 fv : 125 N/mm2 符合要求 [v]:L/ 250 符合要求 5Pk×l^4(384 E×I ) 10.15 N/mm2
2、荷载受力形式: 简支梁
取跨中最不利集中荷载(Pg),单边为1/2 I50c及桥面系自重:
2 根10#工字钢重 12 根横向连接¢28钢筋 合计(Pq)
3、计算模型基本参数:净跨 L
4、荷载: 标准值Pk=Pg+ql 设计值Pd=Pg×γ G+Pq×γ Q
二、选择受荷截面 1、截面类型: 2根工字钢:10# 2、截面特性:
10#工字钢梁受力计算
一、梁的静力计算概况 1、单跨梁形式: 简支梁 中间受集中载荷 计算结果
2 t重车 10 KN 5 m长 22.40 kg/m 0.00 kg/m 0.22 KN/m 0.00 KN/m 0.22 KN/m 5m 11.12 KN γ G=1.2、γ Q=1.4 13.57 KN 宽0.8m 备注
结构静力计算常用公式_secret

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载结构静力计算常用公式_secret地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容结构力学公式结构静力计算目录TOC \o "1-2" \h \z \u HYPERLINK \l "_Toc320439132" 1、常用截面几何与力学特征表 PAGEREF _Toc320439132 \h 1HYPERLINK \l "_Toc320439133" 2、单跨梁的内力及变形表 PAGEREF _Toc320439133 \h 8HYPERLINK \l "_Toc320439134" 2.1 简支梁的反力、剪力、弯矩、挠度 PAGEREF _Toc320439134 \h 8HYPERLINK \l "_Toc320439135" 2.2 悬臂梁的反力、剪力、弯矩和挠度 PAGEREF _Toc320439135 \h 10HYPERLINK \l "_Toc320439136" 2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度 PAGEREF _Toc320439136 \h 12HYPERLINK \l "_Toc320439137" 2.4 两端固定梁的反力、剪力、弯矩和挠度 PAGEREF _Toc320439137 \h 14HYPERLINK \l "_Toc320439138" 2.5 外伸梁的反力、剪力、弯矩和挠度 PAGEREF _Toc320439138 \h 16HYPERLINK \l "_Toc320439139" 3.等截面连续梁的内力及变形表PAGEREF _Toc320439139 \h 19HYPERLINK \l "_Toc320439140" 3.1 二跨等跨梁的内力和挠度系数 PAGEREF _Toc320439140 \h 19HYPERLINK \l "_Toc320439141" 3.2 三跨等跨梁的内力和挠度系数 PAGEREF _Toc320439141 \h 20HYPERLINK \l "_Toc320439142" 3.3 四跨等跨连续梁内力和挠度系数 PAGEREF _Toc320439142 \h 23HYPERLINK \l "_Toc320439143" 3.4 五跨等跨连续梁内力和挠度系数 PAGEREF _Toc320439143 \h 23HYPERLINK \l "_Toc320439144" 3.5 二不等跨梁的内力系数PAGEREF _Toc320439144 \h 24HYPERLINK \l "_Toc320439145" 3.6 三不等跨梁内力系数 PAGEREF _Toc320439145 \h 25HYPERLINK \l "_Toc320439146" 4.双向板在均布荷载作用下的内力及变形系数表 PAGEREF _Toc320439146 \h 26HYPERLINK \l "_Toc320439147" 4.1 四边简支 PAGEREF_Toc320439147 \h 26HYPERLINK \l "_Toc320439148" 4.2 三边简支,一边固定 PAGEREF _Toc320439148 \h 27HYPERLINK \l "_Toc320439149" 4.3 两边简支,两边固定 PAGEREF _Toc320439149 \h 27HYPERLINK \l "_Toc320439150" 4.4 一边简支,三边固定 PAGEREF _Toc320439150 \h 28HYPERLINK \l "_Toc320439151" 4.4 四边固定 PAGEREF_Toc320439151 \h 29HYPERLINK \l "_Toc320439152" 4.5 两边简支,两边固定 PAGEREF _Toc320439152 \h 29HYPERLINK \l "_Toc320439153" 5.拱的内力计算表 PAGEREF_Toc320439153 \h 30HYPERLINK \l "_Toc320439154" 5.1各种荷载作用下双铰抛物线拱计算公式 PAGEREF _Toc320439154 \h 30HYPERLINK \l "_Toc320439155" 6.刚架内力计算表 PAGEREF_Toc320439155 \h 35HYPERLINK \l "_Toc320439156" 6.1 “┌┐”形刚架内力计算表(一) PAGEREF _Toc320439156 \h 35HYPERLINK \l "_Toc320439157" 6.2“┌┐”形刚架内力计算表(二) PAGEREF _Toc320439157 \h 37HYPERLINK \l "_Toc320439158" 6.3“”形刚架的内力计算表PAGEREF _Toc320439158 \h 391、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
荷载与结构静力计算表

2 常用结构计算2-1 荷载与结构静力计算表2—1-1 荷载1.结构上的荷载结构上的荷载分为下列三类:(1)永久荷载如结构自重、土压力、预应力等.(2)可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。
(3)偶然荷载如爆炸力、撞击力等.建筑结构设计时,对不同荷载应采用不同的代表值。
对永久荷载应采用标准值作为代表值。
对可变荷载应根据设计要求,采用标准值、组合值、频遇值或准永久值作为代表值。
对偶然荷载应按建筑结构使用的特点确定其代表值.2.荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载,按承载能力极限状态和正常使用极限状态分别进行荷载(效应)组合,并应取各自的最不利的效应组合进行设计。
对于承载能力极限状态,应按荷载效应的基本组合或偶然组合进行荷载(效应)组合。
γ0S≤R (2—1)式中γ0-—结构重要性系数;S—-荷载效应组合的设计值;R——结构构件抗力的设计值。
对于基本组合,荷载效应组合的设计值S应从下列组合值中取最不利值确定:(1)由可变荷载效应控制的组合(2-2)式中γG-—永久荷载的分项系数;γQi-—第i个可变荷载的分项系数,其中Y Q1为可变荷载Q1的分项系数;S GK——按永久荷载标准值G K计算的荷载效应值;S QiK-—按可变荷载标准值Q ik计算的荷载效应值,其中S Q1K为诸可变荷载效应中起控制作用者;ψci——可变荷载Q i的组合值系数;n—-参与组合的可变荷载数。
(2)由永久荷载效应控制的组合(2-3)(3)基本组合的荷载分项系数1)永久荷载的分项系数当其效应对结构不利时:对由可变荷载效应控制的组合,应取1.2;对由永久荷载效应控制的组合,应取1.35;当其效应对结构有利时:一般情况下应取1.0;对结构的倾覆、滑移或漂浮验算,应取0。
9。
2)可变荷载的分项系数一般情况下应取1。
4;对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。
静力计算公式汇总

静力计算公式汇总————————————————————————————————作者:————————————————————————————————日期:结构力学公式结构静力计算目录1、常用截面几何与力学特征表 (1)2、单跨梁的内力及变形表 (8)2.1 简支梁的反力、剪力、弯矩、挠度 (8)2.2 悬臂梁的反力、剪力、弯矩和挠度 (10)2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度 (12)2.4 两端固定梁的反力、剪力、弯矩和挠度 (14)2.5 外伸梁的反力、剪力、弯矩和挠度 (16)3.等截面连续梁的内力及变形表 (19)3.1 二跨等跨梁的内力和挠度系数 (19)3.2 三跨等跨梁的内力和挠度系数 (20)3.3 四跨等跨连续梁内力和挠度系数 (23)3.4 五跨等跨连续梁内力和挠度系数 (23)3.5 二不等跨梁的内力系数 (24)3.6 三不等跨梁内力系数 (25)4.双向板在均布荷载作用下的内力及变形系数表 (26)4.1 四边简支 (26)4.2 三边简支,一边固定 (27)4.3 两边简支,两边固定 (27)4.4 一边简支,三边固定 (28)4.4 四边固定 (29)4.5 两边简支,两边固定 (29)5.拱的内力计算表 (30)5.1各种荷载作用下双铰抛物线拱计算公式 (30)6.刚架内力计算表 (35)6.1 “┌┐”形刚架内力计算表(一) (35)6.2“┌┐”形刚架内力计算表(二) (37)6.3“”形刚架的内力计算表 (39)1、常用截面几何与力学特征表1234567注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
静定梁的内力—单跨静定梁的内力计算(建筑力学)

MO 0 : M FA x 0
B FB
F
lx
c
FQ FA
M FA x
与横截面相切的内力,称为剪力FQ , 常用单位为N或kN 。
作用在外力作用平面内(纵向对称平面
B
内)的内力偶,其力偶矩称为弯矩M,
FB 常用单位为
N m或 k N m 。
注:不论是左段还是右段隔离体计算出的内力应该是同 一截面上的内力,在大小、性质上应该是相同的结果。
MB 0
FA 4 4 2 21 0 FA 2kN
(2)计算各截面上的剪力
FQ1 FQ2 FQ3 = 2kN FQ4 2+6=4kN FQ4 2 2=4kN
4kN m 2kN/m
12 3
Aபைடு நூலகம்
B4 C
FA
2m
FB
2m
2m
(2)计算各截面上的弯矩
M1 2 2 4kN m(上部受拉) M2 2 2 4 0
M1
qa
a 2
Fa
0
M1
qa
a 2
Fa
4
2
2 2
5
2
18kN
m
(上部受拉)
应用举例
[例2] 如图所示简支梁,已知:F1=F2=30kN, 求1-1横截面上的剪力和弯矩。
F1 1
A
1
FA 1m 1m
2m
F2 B
2m FB
F1 1 M1
1 FA 1m 1m FQ1
M11
F2
1 FS1 2m
2m FB
(2) 代替 留下一部分(脱离体),并以内力代替弃去部分对保留部分的作用。
(3) 平衡 对脱离体建立静力平衡方程,求解未知力。 注意: 取出的梁段上保留作用于该段上的所有外力(包括荷载和支座反力),在截开的 截面上画出未知的剪力和弯矩时,剪力和弯矩均假设为正向。
1、静定结构与超静定结构静力计算公式
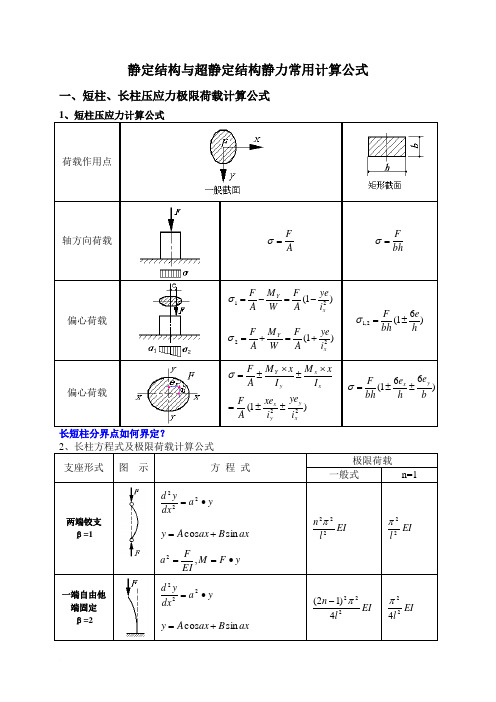
静定结构与超静定结构静力常用计算公式一、短柱、长柱压应力极限荷载计算公式1、短柱压应力计算公式荷载作用点轴方向荷载AF =σ bhF =σ 偏心荷载)1(21x Y i ye A F W M A F -=-=σ )1(22x Y i ye A F W M A F +=+=σ )61(2,1hebh F ±=σ 偏心荷载)1(22xy y x xx y Y i ye i xe A FI x M I x M A F ±±=⨯±⨯±=σ)661(be h e bh Fy x ±±=σ长短柱分界点如何界定?2、长柱方程式及极限荷载计算公式 支座形式图 示方 程 式极限荷载 一般式 n=1两端铰支β=1y a dxy d ∙=222 ax B ax A y sin cos +=y F M EIFa ∙==,2 EI l n 222π EI l 22π一端自由他端固定 β=2y a dxyd ∙=222 ax B ax A y sin cos +=EI l n 2224)12(π-EI l 224πy F M EIFa ∙==,2 两端固定β=0.50)(22=-+F M y a dxyd A FM ax B ax A y A++=sin cos A M y F M EIFa +∙-==,2 EI l 224π EI l 224π 一端铰支他端固定 β=0.75)(222x l EI Q y a dx y d -=∙+)(sin cos x l FQax B ax A y -++=水平荷载-=Q EIFa ,2 ——EI l227778.1π注:压杆稳定临界承载能力计算公式:EI l P cr 22)(βπ=二、单跨梁的反力、剪力、弯矩、挠度计算公式 1、简支梁的反力、剪力、弯矩、挠度计算公式荷载形式M 图V 图反力 2F R R B A == L Fb R A =L Fa R B =2qL R R B A == 4qL R R B A == 剪力V A =R A V B =-R B V A =R A V B =-R B V A =R A V B =-R B V A =R A V B =-R B弯矩4max FL M =LFabM =max 82maxqL M = 122maxqL M = 挠度EIFL 483max=ω 若a >b 时,3)2(932maxab a EIL Fb +=ω(在)2(3b a ax +=处) EIqL 84max=ω EIqL 1204max=ω 注:1、弯矩符号以梁截面下翼缘手拉为正(+),反之为负(—)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续均布载荷
RA=RB=qι/2 MA=MB=1/12 qι2
Qx=qι/2(1-2X/ι)
Mx=qι/2(X-X2/ι-ι/6)(X由0→ι)
M最大=1/24 qι2(X=1/2处)
-M最大=-qι2/12(在A及B处)
y—挠度(m)
θ—截面转角(rad)
ι—梁的跨度(m)
X—截面至坐标原点的距离(m)
E—材料的弹性模量(N/m2)
I—横截面对中性轴的惯性矩(m4)
悬臂梁
集中载荷作用在自由端
RБайду номын сангаас=P
Qx=-P
Mx=-PX
MB=-Pι
M最大=-Pι
yA=-Pι3/3EI
θA=-Pι2/2EI
连续均布载荷
RB=qι
Qx=-qX(X由0→ι)
两个力作用在外伸端
RA=RB=P
Qx1=-P(CA间)
Qx=0(AB间)
Qx2=P(BD间)
Mx=-Pι1(AB间)
Mx1=-PX1(CA间)
Mx2=-PX2(BD间)
y最大=-Pι2ι1/8EI(在跨中)
θA=-θB=Pιι1/2EI
连续均布载荷
RA=RB=qι/2
Qx=qι/2-qX(X由0→ι)
窗体底端
单跨梁等静力计算公式及图表
单跨等截面梁(见表1)
表1单跨等截面梁的支座反力、剪力、弯矩、挠度和转角公式
P—集中载荷(N)
q—均布载荷(N/m)
M0—外加力矩(N·m)
RA,RB—A,B点处的支座反力(N)
MA,MB—A,B点处的反力矩(N·m)
Qx—截面X处的剪力(N)
Mx—截面X处的弯矩(N·m)
RB=Pα2/ι3(3 b+α)MB=Pα2b/ι2
Qx=RA(AC间)
Qx=-RB(CB间)
Mx=-MA+RAX(AC间)
Mx=-MA+RAX-P(X-α)(CB间)
M最大=-MA+RAα=2Pα2b2/ι3(在C处)
-M最大=-MA(当α<b)
-M最大=-MB(当α>b)
y最大=-2/3 Pα3b2/EI(3α+b)2(在X=2αι/3α+b处,当α>b)
Mx=-qX2/2(X由0→ι)
MB=-qι2/2
M最大=-qι2/2
yA=-qι4/8EI
θA=-qι3/6EI
力矩作用在自由端
RB=0
Qx=0
Mx=-M0(X由0→ι)
MB=-M0
M最大=-M0
yA=-M0ι2/2EI
θA=-M0·ι2/EI
两端自由支承梁
一个力作用在跨度间
RA=Pb/ι;RB=Pα/ι
y最大=-qι4384EI(X=1/2处)
力矩作用在跨度间
RA=-RB=-6M0/ι3(αι-α2)
MA=-M0/ι2(4ια-3α2-ι2)
MB=M0/ι2(2ια-3α2)
Qx=RA
Mx=-MA+RAX(AC间)
Mx=-MA+RAX+M0(CB间)
M最大=M0(4α/ι-9α2/ι2+6α3/ι3)(C点右一些)
Q最大=1/2 qι
(X由0→ι)
M最大=1/8 qι2(在X=1/2处)
y最大=-5/384·qι4/EI(在X=ι/2处)
θA=-θB=-qι3/24EI
力矩作用于支承端
RA=-RB=-M0/ι
Qx=-M0/ι
Mx=M0(ι-X/ι)(X由0→ι)
M最大=M0(在A处)
y最大≈-0.0642 M0ι2/EI(在X=0.422ι处)
-M最大=M0(4α/ι-9α2/ι2+6α3/ι3-1)(C点左一些)
y=-1/6EI(3 MAX2-RAX3)(AC间)
y=-1/6EI[(M0+MA)(3 X2-6ιX+3ι2)-RA(3ι2X-X3+2ι3)](CB间)
连续均布载荷
RA=3/8 qι
RB=5/8 qι
MB=1/8 qι2
Qx=3/8 qι-qX
Mx=qX(3/8ι-X/2)
M最大=9/128 qι2(在X=3/8ι处)
-M最大=-1/8 qι2(在B处)
y最大=0.0054 qι4/EI(在X=0.4215ι处)
θA=-qι3/48EI
力矩作用在自由支承端
RA=-3/2·M0/ιRB=3/2·M0/ι
MB=1/2 M0Qx=-3/2·M0/ι
Mx=M0-3/2·M0/ιX(X由0→ι)
M最大=M0(在A处)
-M最大=-1/2 M0(在B处)
y最大=-M0ι2/27EI(在X=1/3处)
θA=-M0ι/4EI
两端刚性固定的梁
力作用在跨度间
RA=Pb2/ι3(3α+b)MA=Pαb2/ι2
Qx=RA(X<α时);Qx=-RB(X>α时)
(X由0→α)
(X由α→ι)
M最大=Pαb/ι(在X=α处)
两个力作用在跨度间
RA=RB=P
Qx=P(AC间)
Qx=0(CD间)
Qx=-P(DB间)
Mx=PX(AC间)
Mx=Pι1(CD间)
M最大=Pι1
θA=-θB=-Pι1(ι-ι1)/2EI
θC=-θD=-Pι1(ι-2ι1)/2EI
y=-M0/6EI[3α2+3 X2-X3/ι-(2ι+3α2/ι)X](CB间)
θA=M0/6EI(2ι-6α+3α2/ι)
θB=M0/6EI(ι-3α2/ι)
θC=M0/EI(α-α2/ι-ι/3)
一端自由支承,一端刚性固定的梁
力在作用在跨度间
RA=P/2(3b2ι-b3/ι3)
RB=P-RA
MB=P/2(b3+2bι2-3b2ι/ι2)
Qx=RA(AC间)
Qx=-RB(CB间)
Mx=RAX(AC间)
Mx=RAX-P(X-ι+b)(CB间)
M最大=RAα
y=1/6EI[RA(X3-3ι2X)+3 P b2X](AC间)
y=1/6EI{RA(X3-3ι2X)+P [3b2X-(X-α)3] }(CB间)
θA=P/4EI(b2/ι-b2)
θA=-M0ι/3EI
θB=M0ι/6EI
力矩作用于跨度间
RA=-RB=-M0/ιQx-M0/ι
Mx=-M0/ιX(AC间)
Mx=M0(1-X/ι)(CB间)
M最大=-M0/ια+M0(C点右一些)
-M最大=-M0/ια(C点左一些)
y=M0/6EI[(6α-3α2/ι-2ι)X-X3/ι](AC间)
