(完整)数值分析学期期末考试试题与答案(A),推荐文档
数值分析2007第二学期期末考试试题与答案(A)

期末考试试卷(A 卷)2007学年第二学期 考试科目: 数值分析 考试时间:120 分钟学号 姓名 年级专业一、判断题(每小题2分,共10分)1. 用计算机求1000100011n n=∑时,应按照n 从小到大的顺序相加。
( )2. 为了减少误差,进行计算。
( )3. 用数值微分公式中求导数值时,步长越小计算就越精确。
( )4. 采用龙格-库塔法求解常微分方程的初值问题时,公式阶数越高,数值解越精确。
( )5. 用迭代法解线性方程组时,迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关,与常数项无关。
( )二、填空题(每空2分,共36分)1. 已知数a 的有效数为0.01,则它的绝对误差限为________,相对误差限为_________.2. 设1010021,5,1301A x -⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦则1A =_____,2x =______,Ax ∞=_____.3. 已知53()245,f x x x x =+-则[1,1,0]f -= ,[3,2,1,1,2,3]f ---= .4. 为使求积公式11231()((0)f x dx A f A f A f -≈++⎰的代数精度尽量高,应使1A = ,2A = ,3A = ,此时公式具有 次的代数精度。
5. n 阶方阵A 的谱半径()A ρ与它的任意一种范数A 的关系是 .6. 用迭代法解线性方程组AX B =时,使迭代公式(1)()(0,1,2,)k k XMX N k +=+= 产生的向量序列{}()k X收敛的充分必要条件是 .7. 使用消元法解线性方程组AX B =时,系数矩阵A 可以分解为下三角矩阵L 和上三角矩阵U 的乘积,即.A LU = 若采用高斯消元法解AX B =,其中4221A -⎡⎤=⎢⎥⎣⎦,则L =_______________,U =______________;若使用克劳特消元法解AX B =,则11u =____;若使用平方根方法解AX B =,则11l 与11u 的大小关系为_____(选填:>,<,=,不一定)。
数值分析期末考试和答案

数值分析期末考试和答案一、单项选择题(每题2分,共20分)1. 在数值分析中,下列哪个方法用于求解线性方程组?A. 插值法B. 迭代法C. 直接法D. 拟合法答案:C2. 以下哪个数值方法是用于求解非线性方程的?A. 高斯消元法B. 牛顿迭代法C. 线性插值法D. 拉格朗日插值法答案:B3. 在数值积分中,梯形法则的误差与下列哪个因素无关?A. 被积函数的二阶导数B. 积分区间的长度C. 积分区间的划分数量D. 被积函数的一阶导数答案:D4. 以下哪个数值方法是用于求解常微分方程的?A. 欧拉方法B. 牛顿迭代法C. 拉格朗日插值法D. 高斯消元法答案:A5. 在数值分析中,下列哪个方法用于求解特征值问题?A. 高斯消元法B. 幂迭代法C. 牛顿迭代法D. 梯形法则答案:B6. 以下哪个数值方法是用于求解线性最小二乘问题的?A. 高斯消元法B. 梯形法则C. 正交分解法D. 牛顿迭代法答案:C7. 在数值分析中,下列哪个方法用于求解非线性方程组?A. 高斯消元法B. 牛顿迭代法C. 线性插值法D. 欧拉方法答案:B8. 在数值分析中,下列哪个方法用于求解偏微分方程?A. 有限差分法B. 牛顿迭代法C. 线性插值法D. 梯形法则答案:A9. 在数值分析中,下列哪个方法用于求解优化问题?A. 高斯消元法B. 梯形法则C. 牛顿迭代法D. 单纯形法答案:D10. 在数值分析中,下列哪个方法用于求解插值问题?A. 高斯消元法B. 梯形法则C. 牛顿迭代法D. 拉格朗日插值法答案:D二、填空题(每题2分,共20分)1. 在数值分析中,求解线性方程组的直接法包括______消元法和______消元法。
答案:高斯;LU2. 牛顿迭代法的收敛速度是______阶的。
答案:二3. 梯形法则的误差与被积函数的______阶导数有关。
答案:二4. 欧拉方法是一种求解______阶常微分方程的数值方法。
答案:一5. 幂迭代法是求解______特征值问题的数值方法。
数值分析期末试卷A卷

数值分析期末试卷A卷第 1 页共 6 页西北农林科技⼤学本科课程考试试题(卷)2015—2016学年第⼆学期《数值分析》课程A 卷专业班级:命题教师:审题教师:学⽣姓名:学号:考试成绩:⼀、填空题(每空2分,共20分)得分:分1. 设x 1=1.216, x 2=3.654均具有3位有效数字,则x 1+ x 2的误差限为 .2. 近似值x *=0.231关于真值x =0.229有位有效数字.3. 误差有多种来源,数值分析主要研究误差和误差.4. 已知f (1)=2,f (2)=3,f (4)=5.9,则2次Newton 插值多项式中x 2项前⾯的系数为 .5. 计算积分?15.0d x x , 计算结果取4位有效数字. ⽤梯形公式计算的近似值为,⽤Simpson 公式计算的近似值为 . 其中,梯形公式的代数精度为,Simpson 公式的代数精度为. ( 1.7321≈≈) 6. 假设n n H R ?∈是Householder 矩阵,n v R ∈是⼀个n 维向量,则Hv = .⼆、选择题(每⼩题 2分,共20分)得分:分1. ⽤13x+所产⽣的误差是误差.A. 舍⼊B. 观测C. 模型D. 截断2.1.732≈,计算)41x =,下列⽅法中最好的是 .A.28-B. (24-C. ()2164+D. ()4161 3. 在Newton-Cotes 求积公式中,当Cotes 系数为负值时,求积公式的稳定性不能保证. 因此在实际应⽤中,当时的Newton-Cotes 求积公式不使⽤.第 2 页共 6 页A. 8n ≥B. 7n ≥C. 5n ≥D. 6n ≥4. 解⽅程组Ax =b 的简单迭代格式(1)()k k x Bx g +=+收敛的充要条件是 .A. ()1A ρ<B. ()1B ρ<C. ()1A ρ>D. ()1B ρ>5. 已知⽅程3250x x --=在x =2附近有根,下列迭代格式中在02x =附近不收敛的是 .A. 1k x +=B.1k x +=C.315k kk x x x +=-- D.3122532k k k x x x ++=- 6. 设--=700150322A ,则)(A ρ为. A . 2 B . 5 C . 7 D . 37. 三点的⾼斯求积公式的代数精度为 .A . 2B .5C . 3D . 48. ⽤列主元消去法解线性⽅程组??-=+--=-+-=+-134092143321321321x x x x x x x x x ,第1次消元时,选择的主元为 .A.-4B. 3C.4D.-99. 假设cond (A )表⽰⾮奇异矩阵A 的条件数,则下列结论中错误的是 .A.()()1cond A cond A -=B.()(),cond A cond A R λλλ=∈C. ()1cond A ≥D.()1cond A A A -=?10. 设)(x f 可微, 求⽅程)(x f x =的⽜顿迭代格式是 .A. 1()1()k k k k k x f x x x f x +-=-'-B. 1()1()k k k k k x f x x x f x ++=+'+C. 1()()k k k k f x x x f x +=-'D. 1()()k k k k f x x x f x +=+'三、简答题(每⼩题5分,共20分)得分:分1. 什么是数值算法的稳定性?如何判断算法是否稳定?为什么不稳定的算法不能使⽤?2. 埃尔⽶特插值与⼀般函数插值有什么不同?3. 简述⼆分法的优缺点.4. 什么是矩阵的条件数?如何判断线性⽅法组是病态的?第 3 页共 6 页第 4 页共 6 页四、计算题(每⼩题8分,共32分)得分:分1. 已知下列函数表(1) 写出相应的3次(2) 作均差表,写出相应的3次Newton 插值多项式,并计算f (1.5)的近似值。
《数值分析》A卷期末考试试题及参考答案

一、单项选择题(每小题3分,共15分) 1、用Simpson 公式求积分1401x dx +⎰的近似值为 ( ).A.2924 B.2429C.65D. 562、已知(1)0.401f =,且用梯形公式计算积分2()f x dx ⎰的近似值10.864T =,若将区间[0,2]二等分,则用递推公式计算近似值2T 等于( ). A.0.824 B.0.401 C.0.864 D. 0.8333、设3()32=+f x x ,则差商0123[,,,]f x x x x 等于( ).A.0B.9C.3D. 64的近似值的绝对误差小于0.01%,要取多少位有效数字( ). A.3 B.4 C.5 D. 25、用二分法求方程()0=f x 在区间[1,2]上的一个实根,若要求准确到小数 点后第四位,则至少二分区间多少次( ).A.12B.13C.14D. 15二、填空题(每小题4分,共40分)1、对于迭代函数2()=(3)ϕ+-x x a x ,要使迭代公式1=()ϕ+k k x x则a 的取值范围为 .2、假设按四舍五入的近似值为2.312,则该近似值的绝对误差限为 .3、迭代公式212(3)=,03++>+k k k k x x a x a x a收敛于α= (0)α>. 4、解方程4()530f x x x =+-=的牛顿迭代公式为 . 5、设()f x 在[1,1]-上具有2阶连续导数,[1,1]x ∀∈-,有1()2f x ''≤,则()f x 在[1,1]-上的线性插值函数1()L x 在点0处的误差限1(0)R ≤______.6、求解微分方程初值问题2(0)1'=-⎧⎨=⎩y xy yy ,0x 1≤≤的向前Euler 格式为 .7、设310131013A -⎛⎫⎪=-- ⎪ ⎪-⎝⎭,则A ∞= .8、用梯形公式计算积分112-⎰dx x 的近似值为 . 9、设12A 21+⎡⎤=⎢⎥⎣⎦a 可作Cholesky 分解,则a 的取值范围为 . 10、设(0)1,(0.5) 1.5,(1)2,(1.5) 2.5,(2) 3.4f f f f f =====,若1=h ,则用三点公式计算(1)'≈f .三、解答题(共45分) 1、给定数据用复化Simpson 公式计算1.381.30()f x dx ⎰的近似值,并估计误差,小数点后保留3位. (8分)2、用直接三角分解法求线性代数方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡432631531321321x x x 的解. (8分) 3、求()λx ,使得迭代公式1()()λ+=+k k k k f x x x x 求方程2()31=+-f x x x 的根的相应迭代序列{}k x 具有平方收敛. (5分)4、已知数据试对数据用最小二乘法求出形如=+y x b的拟合曲线. (8分) 5、已知(2)8f -=,(0)4f =,(2)8=f ,试求二次拉格朗日插值多项式. (8分) 6、设矩阵A 如下,根据谱半径判断用Jacobi 迭代法求解方程组Ax b =的敛散性.(8分)1102111221012A ⎡⎤-⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦一、单项选择题(每小题3分,合计15分) 1、A 2、D 3、C 4、C 5、D 二、填空题(每小题3分,合计30分) 1、0<<a ; 2、31102-⨯; 3;4、4135345++-=-+k k k k k x x x x x ; 5、14; 6、1(2)+=+-n n n n n y y h x y y ; 7、5;8、34-; 9、3>a ;10、1.2;三、计算题(合计55分) 1、给定数据用复化Simpson 公式计算 1.381.30()f x dx ⎰的近似值,并估计误差,小数点后保留3位. (8分)解: 401024S [()4()()]6-=++x x f x f x f x ………… 1分 1.38 1.30(3.624 4.20 5.19)6-=+⨯+ 0.341= ………… 2分20422012234S [()4()()][()4()()]66--=+++++x x x xf x f x f x f x f x f x =0.342 ………… 6分2211[]15-≈-I S S S =-⨯40.6710 ………… 8分 2、用直接三角分解法求线性代数方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡432631531321321x x x 的解. (8分) 解:设111213212223313233u u u 123100135l 100u u 136l l 100u ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=*⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦………… 1分 111=u ,212=u ,313=u ,121=l ,131=l 122=u ,223=u ,132=l133=u ,133=l …………6分所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111011001L ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100210321U …………7分 由b Ly =得Ty )1,1,2(=;由y Ux =得Tx )1,1,1(-=. ………… 8分3、求()λx ,使得迭代公式1()()λ+=+k k k k f x x x x 求方程2()31=+-f x x x 的根的相应迭代序列{}k x 具有平方收敛.(6分)解:要使迭代序列具有平方收敛,则()0ϕ'*=x ………… 2分 而()()()ϕλ=+f x x x x ,即 ………… 3分 2()()()()10()λλλ''**-**+=*f x x x f x x …………4分 而()0*=f x 则有()1()λ'*=-*f x x ………… 5分所以()()23λ'=-=--x f x x ………… 6分4、已知数据试对数据用最小二乘法求出形如=+ay x b的拟合曲线. (8分) 解:因为11=+b x y a a ,令0111,,,====b a a y x x a a y……2分 则有法方程01461061410⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭a a ……5分解出014,1==-a a ,则1,4=-=-a b ……7分 所以1=4-y x……8分5、已知(2)8f -=,(0)4f =,(2)8=f ,试求二次拉格朗日插值多项式. (7分)解:01()(2)8l x x x =- …………2分 211()(4)4l x x =-- …………4分21()(2)8l x x x =+ …………6分 2012()()(2)()(0)()(2)L x l x f l x f l x f =-++24=+x …………7分6、设矩阵A 如下,根据谱半径判断用Jacobi 迭代法求解方程组Ax b =的敛散性.(8分)1102111221012A ⎡⎤-⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦解:100010001D ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,00010021002L ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,10021002000U ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦…………3分1100211()0221002J B D L U -⎡⎤⎢⎥⎢⎥⎢⎥=+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦…………5分 2102111()0222102J E B λλλλλλ⎡⎤-⎢⎥⎢⎥⎢⎥-=--=-=⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦…………6分()2J B ρ=…………7分 所以用Jacobi 迭代法求解方程组Ax b =收敛 …………8分。
数值分析期末试题及答案

数值分析期末试题及答案试题一:1. 简答题(共10分)a) 什么是数值分析?它的主要应用领域是什么?b) 请简要解释迭代法和直接法在数值计算中的区别。
2. 填空题(共10分)a) 欧拉方法是一种______型的数值解法。
b) 二分法是一种______法则。
c) 梯形法则是一种______型的数值积分方法。
3. 计算题(共80分)将以下函数进行数值求解:a) 通过使用二分法求解方程 f(x) = x^3 - 4x - 9 = 0 的近似解。
b) 利用欧拉方法求解微分方程 dy/dx = x^2 + 2x + 1, y(0) = 1 在 x = 1 处的解。
c) 使用梯形法则计算积分∫[0, π/4] sin(x) dx 的近似值。
试题二:1. 简答题(共10分)a) 请解释什么是舍入误差,并描述它在数值计算中的影响。
b) 请解释牛顿插值多项式的概念及其应用。
2. 填空题(共10分)a) 数值稳定性通过______号检查。
b) 龙格-库塔法是一种______计算方法。
c) 零点的迭代法在本质上是将方程______转化为______方程。
3. 计算题(共80分)使用牛顿插值多项式进行以下计算:a) 已知插值节点 (-2, 1), (-1, 1), (0, 2), (1, 4),求在 x = 0.5 处的插值多项式值。
b) 已知插值节点 (0, 1), (1, 2), (3, 7),求插值多项式,并计算在 x = 2 处的值。
c) 使用 4 阶龙格-库塔法求解微分方程 dy/dx = x^2 + 1, y(0) = 1。
答案:试题一:1. a) 数值分析是研究使用数值方法解决数学问题的一门学科。
它的主要应用领域包括数值微积分、数值代数、插值和逼近、求解非线性方程、数值积分和数值解微分方程等。
b) 迭代法和直接法是数值计算中常用的两种方法。
迭代法通过反复迭代逼近解,直到满足所需精度为止;而直接法则通过一系列代数运算直接得到解。
(完整)数值分析试题库与答案解析,推荐文档

模 拟 试 卷(一)一、填空题(每小题3分,共30分)1.有3个不同节点的高斯求积公式的代数精度是 次的.2.设,,则=.,= ______.152210142-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦A 342⎛⎫⎪=- ⎪ ⎪⎝⎭x ∞A1x3.已知y =f (x )的均差(差商),,,01214[,,]3f x x x =12315[,,] 3f x x x =23491[,,]15f x x x =, 那么均差=.0238[,,] 3f x x x =423[,,]f x x x 4.已知n =4时Newton -Cotes 求积公式的系数分别是:则,152,4516,907)4(2)4(1)4(0===C C C = .)4(3C 5.解初始值问题的改进的Euler 方法是阶方法;0(,)()y f x y y x y '=⎧⎨=⎩6.求解线性代数方程组的高斯—塞德尔迭代公式为,123123123530.13260.722 3.51x x x x x x x x x --=⎧⎪-++=⎨⎪++=⎩若取, 则.(0)(1,1,1)=- x(1)=x 7.求方程根的牛顿迭代格式是 .()x f x =8.是以整数点为节点的Lagrange 插值基函数,则01(), (),, ()n x x x 01, ,, ,n x x x =.()nk jk k x x =∑9.解方程组的简单迭代格式收敛的充要条件是.=Ax b (1)()k k +=+x Bx g 10.设,则的三次牛顿插值多项式为(-1)1,(0)0,(1)1,(2)5f f f f ====()f x ,其误差估计式为 .二、综合题(每题10分,共60分)1.求一次数不超过4次的多项式满足:,,()p x (1)15p =(1)20p '=(1)30p ''=,.(2)57p =(2)72p '=2.构造代数精度最高的形式为的求积公式,并求出10101()()(1)2xf x dx A f A f ≈+⎰其代数精度.3.用Newton 法求方程在区间内的根, 要求.2ln =-x x ) ,2(∞8110--<-kk k x x x 4.用最小二乘法求形如的经验公式拟合以下数据:2y a bx=+i x 19253038iy 19.032.349.073.35.用矩阵的直接三角分解法解方程组.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡71735 30103421101002014321x x x x 6 试用数值积分法建立求解初值问题的如下数值求解公式0(,)(0)y f x y y y '=⎧⎨=⎩,1111(4)3n n n n n hy y f f f +-+-=+++其中.(,),1,,1i i i f f x y i n n n ==-+三、证明题(10分)设对任意的,函数的导数都存在且,对于满足x ()f x ()f x '0()m f x M '<≤≤的任意,迭代格式均收敛于的根.20Mλ<<λ1()k k k x x f x λ+=-()0f x =*x 参考答案一、填空题1.5; 2. 8, 9 ; 3.; 4. ; 5. 二; 911516456. , (0.02,0.22,0.1543)(1)()()123(1)(1)()213(1)(1)(1)312(330.1)/5(220.7)/6(12)*2/7k k k k k k k k k x x x x x x x x x ++++++⎧=++⎪=+-⎨⎪=--⎩7. ; 8. ; 9. ;1()1()k k k k k x f x x x f x +-=-'-j x ()1B ρ<10.32(4)11,()(1)(1)(2)/24(1,2)66x x x f x x x x ξξ+-+--∈-二、综合题1.差商表:11122151515575720204272152230781233234()1520(1)15(1)7(1)(1)(2)5432p x x x x x x x x x x =+-+-+-+--=++++其他方法:设233()1520(1)15(1)7(1)(1)()p x x x x x ax b =+-+-+-+-+令,,求出a 和b.(2)57p =(2)72p '=2.取,令公式准确成立,得:()1,f x x =,, , .0112A A +=011123A A +=013A =116A =时,公式左右;时,公式左, 公式右2()f x x =14=3()f x x =15=524=∴ 公式的代数精度.2=3.此方程在区间内只有一个根,而且在区间(2,4)内。
数值分析期末试题及答案

数值分析期末试题及答案一、选择题(每题5分,共20分)1. 在数值分析中,下列哪个算法不是用于求解线性方程组的?A. 高斯消元法B. 牛顿法C. 雅可比法D. 追赶法答案:B2. 插值法中,拉格朗日插值法属于:A. 多项式插值B. 样条插值C. 线性插值D. 非线性插值答案:A3. 以下哪个选项不是数值分析中的误差来源?A. 截断误差B. 舍入误差C. 计算误差D. 测量误差答案:C4. 在数值积分中,梯形法则的误差项是:A. O(h^2)B. O(h^3)C. O(h)D. O(1)答案:A二、填空题(每题5分,共20分)1. 牛顿插值法中,插值多项式的一般形式为:______。
答案:f(x) = a_0 + a_1(x-x_0) + a_2(x-x_0)(x-x_1) + ...2. 牛顿迭代法求解方程的根时,迭代公式为:x_{n+1} = x_n -f(x_n) / __________。
答案:f'(x_n)3. 在数值分析中,______ 用于衡量函数在区间上的近似积分值与真实积分值之间的差异。
答案:误差4. 线性方程组的解法中,______ 法是利用矩阵的LU分解来求解。
答案:克兰特三、解答题(每题10分,共60分)1. 给定函数f(x) = e^(-x),使用拉格朗日插值法,求x = 0.5时的插值值。
解答:首先选取插值节点x_0 = 0, x_1 = 0.5, x_2 = 1,对应的函数值分别为f(0) = 1, f(0.5) = e^(-0.5), f(1) = e^(-1)。
拉格朗日插值多项式为:L(x) = f(0) * (x-0.5)(x-1) / (0-0.5)(0-1) + f(0.5) * (x-0)(x-1) / (0.5-0)(0.5-1) + f(1) * (x-0)(x-0.5) / (1-0)(1-0.5)将x = 0.5代入得:L(0.5) = 1 * (0.5-0.5)(0.5-1) / (0-0.5)(0-1) + e^(-0.5) * (0.5-0)(0.5-1) / (0.5-0)(0.5-1) + e^(-1) * (0.5-0)(0.5-0.5) / (1-0)(1-0.5)计算得L(0.5) = e^(-0.5)。
(完整版)数值分析整理版试题及答案,推荐文档

9
1
xdx T4
h[ 2
f
1
3
2 k 1
f
xk
f
9]
2[ 1 2 3 5 7 9] 2
17.2277
(2)用 n 4 的复合辛普森公式
由于 h 2 , f x
x
,
xk
1
2k k
1, 2,3,
x
k
1
2
2k k
0,1, 2,3,所以,有
2
3
9
1
xdx S4
h[ 6
f
1
若 span1, x,则0 (x) 1 ,1(x) x ,这样,有
2
1
0 ,0 1dx 1
0
1,1
1 0
x2dx
1 3
0
,1
1,0
1
0
xdx
1 2
1
f ,0 exdx 1.7183
0
1
f ,1 xexdx 1
0
所以,法方程为
1
1
1
2 1
a0
a1
1.7183 1
1 0
1
23
2 1
a0
a1
6 1
12
3
再回代解该方程,得到
a1
4
,
a0
11 6
故,所求最佳平方逼近多项式为
S1*
(
x)
11 6
4x
例 3、 设 f (x) ex , x [0,1] ,试求 f (x) 在[0, 1]上关于 (x) 1 , span1, x的最
佳平方逼近多项式。 解:
1
4
x1
1 5
北师大网络教育 数值分析 期末试卷含答案

注:1、教师命题时题目之间不留空白; 2、考生不得在试题纸上答题,教师只批阅答题册正面部分,若考北师大网络教育——数值分析——期末考试卷与答案一.填空题(本大题共4小题,每小题4分,共16分)1.设有节点012,,x x x ,其对应的函数()y f x =的值分别为012,,y y y ,则二次拉格朗日插值基函数0()l x 为 。
2.设()2f x x =,则()f x 关于节点0120,1,3x x x ===的二阶向前差分为 。
3.设110111011A -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦,233x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则1A = ,1x = 。
4. 1n +个节点的高斯求积公式的代数精确度为 。
二.简答题(本大题共3小题,每小题8分,共24分)1. 哪种线性方程组可用平方根法求解?为什么说平方根法计算稳定?2. 什么是不动点迭代法?()x ϕ满足什么条件才能保证不动点存在和不动点迭代序列收敛于()x ϕ的不动点?3. 设n 阶矩阵A 具有n 个特征值且满足123n λλλλ>≥≥≥,请简单说明求解矩阵A 的主特征值和特征向量的算法及流程。
三.求一个次数不高于3的多项式()3P x ,满足下列插值条件:并估计误差。
(10分)四.试用1,2,4n =的牛顿-科特斯求积公式计算定积分1011I dx x=+⎰。
(10分) 五.用Newton 法求()cos 0f x x x =-=的近似解。
(10分) 六.试用Doolittle 分解法求解方程组:注:1、教师命题时题目之间不留空白; 2、考生不得在试题纸上答题,教师只批阅答题册正面部分,若考 12325610413191963630x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦(10分) 七.请写出雅可比迭代法求解线性方程组123123123202324812231530x x x x x x x x x ++=⎧⎪++=⎨⎪-+=⎩ 的迭代格式,并判断其是否收敛?(10分)八.就初值问题0(0)y yy y λ'=⎧⎨=⎩考察欧拉显式格式的收敛性。
2019年数值分析第二学期期末考试试题与答案A

卷)期末考试试卷(A2007学年第二学期考试科目:数值分析分钟考试时间:120年级专业学号姓名题号一2二三0四总分分)分,共10一、判断题(每小题210001?n)( 1. 用计算机求时,应按照从小到大的顺序相加。
1000n1n?219992001?为了减少误差2. ,应将表达式进行计算。
(改写为)19992001?)( 3. 用数值微分公式中求导数值时,步长越小计算就越精确。
) 4. 采用龙格-库塔法求解常微分方程的初值问题时,公式阶数越高,数值解越精确。
(系数矩阵及其演变方式有用迭代法解线性方程组时,5. 迭代能否收敛与初始向量的选择、)(关,与常数项无关。
分)二、填空题(每空2分,共36_________.________,相对误差限为已知数a的有效数为0.01,则它的绝对误差限为1.0?110??????????xA?Ax,0?21,x??5A?_____.则设______,_____,2. ????21?????1?130????53f(x)?2x?4x?5x,f[?1,1,0]?f[?3,?2,?1,1,2,3]? 3. 已知则, .331?)?Af(0)?Af(f(x)dx?Af(?)的代数精度尽量高,应使4. 为使求积公式321331?A?A?A?,此时公式具有,,次的代数精度。
312?nA)(A的关系是 5. A阶方阵的谱半径与它的任意一种范数.(k?1)(k)BAX??N(k?XMX?0,1,2,)产时,使迭代公式用迭代法解线性方程组6.??)k(X .生的向量序列收敛的充分必要条件是AX?BAL和上三角矩7. 使用消元法解线性方程组系数矩阵时,可以分解为下三角矩阵14?2??BAX?.A?LUU?A,则阵若采用高斯消元法解的乘积,即,其中??21??L?U?AX?B,则,______________;若使用克劳特消元法解_______________u?lu BAX?的大小关系为_____(选填:则____;若使用平方根方法解>与,,111111<,=,不一定)。
数值分析期末考试题及答案

数值分析期末考试题及答案一、选择题(每题2分,共20分)1. 在数值分析中,下列哪个算法用于求解线性方程组?A. 牛顿法B. 高斯消元法C. 插值法D. 傅里叶变换答案:B2. 以下哪个选项不是数值分析中的误差类型?A. 舍入误差B. 截断误差C. 测量误差D. 累积误差答案:C3. 多项式插值中,拉格朗日插值法的特点是:A. 插值点必须等距分布B. 插值多项式的次数与插值点的个数相同C. 插值多项式是唯一的D. 插值多项式在插值点处的值都为1答案:B4. 在数值分析中,下列哪个方法用于求解非线性方程?A. 辛普森法则B. 牛顿迭代法C. 欧拉法D. 龙格-库塔法答案:B5. 以下哪个是数值稳定性的指标?A. 收敛性B. 收敛速度C. 条件数D. 误差传播答案:C二、简答题(每题10分,共20分)1. 简述高斯消元法求解线性方程组的基本原理。
答案:高斯消元法是一种直接解法,通过行变换将增广矩阵转换为上三角形式,然后通过回代求解线性方程组。
它包括三个基本操作:行交换、行乘以非零常数、行相加。
2. 解释什么是数值稳定性,并举例说明。
答案:数值稳定性是指数值解对输入数据小的扰动不敏感的性质。
例如,某些数值方法在计算过程中可能会放大舍入误差,导致结果不可靠,这样的方法就被认为是数值不稳定的。
三、计算题(每题15分,共30分)1. 给定线性方程组:\[\begin{align*}x + 2y - z &= 4 \\3x - y + 2z &= 1 \\-x + y + z &= 2\end{align*}\]使用高斯消元法求解该方程组,并给出解。
答案:首先将增广矩阵转换为上三角形式,然后回代求解,得到\( x = 1, y = 2, z = 1 \)。
2. 给定函数 \( f(x) = x^2 - 3x + 2 \),使用拉格朗日插值法在\( x = 0, 1, 2 \) 处插值,并求出插值多项式。
(完整)数值分析学期期末考试试题与答案(A),推荐文档

期末考试试卷( A 卷)2007 学年第二学期 考试科目: 数值分析 考试时间: 120 分钟学号 姓名 年级专业100011. 用计算机求11000时,应按照 n 从小到大的顺序相加。
n1n2. 为了减少误差 ,应将表达式 2001 1999 改写为 2进行计算。
( )2001 19993. 用数值微分公式中求导数值时,步长越小计算就越精确。
( )4. 采用龙格-库塔法求解常微分方程的初值问题时, 公式阶数越高,数值解越精确。
( )5. 用迭代法解线性方程组时, 迭代能否收敛与初始向量的选择、 系数矩阵及其演变方式有关,与常数项无关。
( ) 二、填空每空 2 分,共 36 分)1. 已知数 a 的有效数为 0.01 ,则它的绝对误差限为 _______ ,相对误差限为 _1 0 1 02. 设 A0 2 1 ,x 5 ,则 A 1____________________________ _, x 2 ______ ,Ax1 3 0 13. 已知 f (x) 2x 54x 35x,则 f[ 1,1,0] , f[ 3, 2, 1,1,2,3] .14. 为使求积公式 f (x)dx A 1f ( 3) A 2f (0) A 3f ( 3)的代数精度尽量高,应使13 3A 1 , A 2 , A 3,此时公式具有 次的代数精度。
5. n 阶方阵 A 的谱半径 ( A)与它的任意一种范数 A 的关系是 .6. 用迭代法解线性方程组 AX B 时,使迭代公式 X (k 1)MX (k)N (k 0,1,2,K )产 生的向量序列X (k)收敛的充分必要条件是 .7. 使用消元法解线性方程组AX B时,系数矩阵A可以分解为下三角矩阵L 和上三角矩阵U 的乘积,即A LU. 若采用高斯消元法解AX B,其中A 4 2,则21L ___________ ,U ____________ ;若使用克劳特消元法解AX B ,则u11 _______ ;若使用平方根方法解AX B,则l11与u11的大小关系为(选填:>,<,=,不一定)。
《数值分析》2018-2019学年第二学期期末考试A卷

河海大学2018-2019学年第二学期期末考试《数值分析》试题(A)卷科目:数值分析考试时间:出题教师:集体考生姓名:专业:学号:题号一二三四总分分数一、单项选择题(每小题2分,共10分)1、n 阶方阵A 可作LU 分解的一个充分条件是A 为()。
A.对角占优阵B.正交阵C.非奇异阵D.对称正定阵2、设n 阶方阵A 及单位阵E 满足0|3|=-A E ,则谱半径)(A ρ()。
A.<3B.3≤C.>3D.3≥3、若迭代公式)(1k k x x ϕ=+是p 阶收敛,则=--+∞>-pkk k x x x x )(lim **1()。
A.0B.p!C.)(*)(x p ϕ D.!/)(*)(p x p ϕ4、设)(x Ln 和)(x Nn 是相同的插值条件下关于)(x f 的拉格朗日插值和牛顿插值,则下述式子中正确的是()。
(其中∏=-=nj jxx x w 0)()()A.)(],...,,[)!1()(10)1(x w x x x f n f n n =++ξB.)()!1()()()()1(x w n f x Nn x f n +≠-+ξC.)(],...,,,[)()(10x w x x x x f x Ln x f n ≠-D.)(],...,,,[)()(10x w x x x x f x Ln x f n =-5、称函数)(x ε为[a,b ]上的三次样条函数,是指)(x ε满足条件()。
A.为分段三次多项式且有二阶连续导数B.为分段三次多项式且有三阶连续导数C.为分段函数且有任意阶导数D.为分段三次埃尔米特插值多项式二、填空题(每小题4分,共20分)1、若已知x 的相对误差为%1,则)(x f =10x 的相对误差为。
2、设1)(3-=x x f ,则过节点-1,0,1的二次牛顿插值多项式为。
3、设有求积公式)31()31(10f A f A +-是插值型求积公式,则=0A ,=1A 。
数值分析(计算方法)期末试卷及参考答案
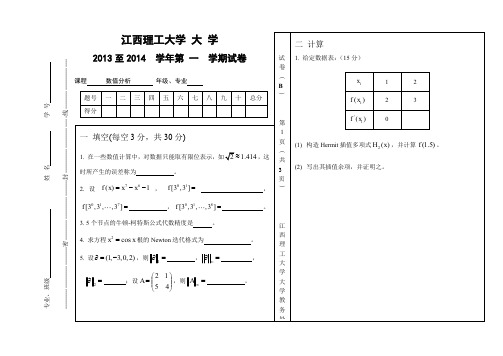
7,,3]= ,,3]=8个节点的牛顿-柯特斯公式代数精度是。
标准答案一. 填空1. 舍入误差2. 729,1,03. 54.21cos 2sin k kk k k kx x x x x x +-=-+ 5. 6,3二. 计算1. 构造重节点的差商表:所以,要求的Hermite 插值为:222()2(1)23H x x x x =+-=-+2(1.5)(1.5) 2.25f H ≈=2.2()()(1)(2)3!f R x x x ξ'''=-- 证明:由题意可知2()()()R x f x H x =-由插值条件知:(1)0,(1)0,(2)0,R R R '===所以,可设:2()()(1)(2)R x k x x x =-- (#) 构造函数:22()()()()(1)(2)t f t H t k x t t ϕ=----易知:,1,2t x =时,()0t ϕ=,且(1)0ϕ'=()0t ϕ'''⇒=至少有一个根ξ,即()0ϕξ'''⇒= 对(#)式求三阶导,并代入得:()()3!f k x ξ'''= 所以,2()()(1)(2)3!f R x x x ξ'''=-- 2. 解:设2()ln 4,f x x x =+-则1()2,f x x x'=+ 牛顿迭代公式为:1()()k k k k f x x x f x +=-'2ln 412k k k k kx x x x x +-=-+325ln 21k k k k k x x x x x +-=+将0 1.5x =代入上式,得1 1.8667x =,2 1.8412x =,3 1.8411x =3230.000110x x --=<所以,方程的近似根为:3 1.8411x =3.解:设()1f x =时,左10()1f x dx ==⎰,右A B C =++,左=右得:1A B C ++=()f x x =时,左101()2f x dx ==⎰,右1Bx C =+,左=右得:112Bx C += 2()f x x =时,左101()3f x dx ==⎰,右21Bx C =+,左=右得:2113Bx C += 3()f x x =时,左101()4f x dx ==⎰,右31Bx C =+,左=右得:3114Bx C += 联立上述四个方程,解得:11211,,,6362A B C x ==== 4()f x x=时,左101()5f x dx ==⎰,右41425Bx C =+=,左≠右 所以,该求积公式的代数精度是3 4.解:Euler 公式是:100(,)()n n n n y y hf x y y x y +=+⎧⎨=⎩ 具体到本题中,求解的Euler 公式是:10.1()0.90.1(0)0n n n n n ny y x y y x y +=+-=+⎧⎨=⎩代入求解得:10y =20.01y = 30.029y =5.解,设A 可以三解分解,即111213212223313233111u u u A LU l u u ll u ⎛⎫⎛⎫⎪⎪== ⎪⎪ ⎪⎪⎝⎭⎝⎭由矩阵的乘法及矩阵相等可得:121351L ⎛⎫⎪= ⎪ ⎪-⎝⎭,1231424U ⎛⎫⎪=- ⎪ ⎪-⎝⎭令,L ,Ux y Ax b y b Ux y ====则可转化为两个等价的三角方程组: 求解三角方程组:Ly b =,得:(14,10,72)y T =-- 求解三角方程组:Ux y =,得:(1,2,3)x T = 所以,原方程组的解为:(1,2,3)x T = 三. 证明证明:分别将1n y -,1n y -',1n y +'在n x 处用Taylor 公式展开得:2331()2!3!nn n n ny y y y y h h h o h -''''''=-+-+ 221()2!n nn n y y y y h h o h -'''''''=-++ 221()2!nn n n y y y y h h o h +'''''''=+++将以上三式代入线性二步法中,得:23315()2!6nn n n ny y y y y h h h o h +''''''=++++ 又方程的真解的Taylor 展式为:2331()()()()()()2!3!n n n n n y x y x y x y x y x h h h o h +''''''=++++ 所以,局部截断误差为:331112()()3n n n n T y x y y h o h +++'''=-=-+ 所以,该方法是二阶的,局部截断误差首项为:323n y h '''-。
数值分析期末考试复习题及其答案

《计篥方法P 实验报告1. 已知X ; =325413, X ; =0.325413都有6位有效数字,求绝对误差限。
(4 分)解:由已知可知,n 二6X : =0.325413x1()6* =6北一n = 0,绝对误差限^ =丄 xl0° =0.522X ; =0・325413xl0°,k=(U—〃 = —6,绝对误差限& =-xl0"62・ -2分心("刃=皿{1,8,32} = 32 1分|H|2 =732=4^23. 设/(x) = (x 2-«)3(6 分)① 写岀f (x)二0解的Newton 迭代格式②当a 为何值时,仏|=卩(忑)(k 二0,1……)产生的序列伉}收敛于、伍【值分析期末考试复习题及其答案1 02.已知4= 02 0 -2解:”州=max{l,4,8} = &分4求IKMJK (6分) 4||^||x =max{l,6,6} = 6,分皿讥如)分_1 0 0 ■ '1A TA = 0 2-20 4 40 0■ 24 二 08 0 -2 4.0 32_w :①Newton 迭代格式为:丿(忑)0(戈)=竺+丄6 6%(屛-°)' _ 5x k a , ・・ , ,6忑(X ;_G )26 6x©⑴三一曲曲以血)卜10—6/~vF<1,即-2<“ <22时迭代收敛 4・给定线性方程组Ax 二b,其中:A =3 -1用迭代公式牙=才「+a(b- Ax (k}) (k=0,1 ........... )求解 Ax 二b, 问取什么实数Q ,可使迭代收敛 (8分)-a 1 一2a.其特征方程为|刀-=八° 一3a}2(X=02分aA-(l -2<z)即,解得=l-a,22 =l-4a2分 要使其满足题意,须使p (B ) < 1,当且仅当0 vav0・52分'12 -2"丁111,b = 6 2 2 1.7.迭代法的收敛性,并建立Gauss-Seidel 迭代格式 (9分)解:A=L+D+UB, =-D~\L + U)= -1-2 -2 0 -22 -1 0|/1/ — By | = A 3= 0,/lj = = Aj = 0即p (B y ) = 0<l,由此可知Jacobi 迭代收敛1一 3a-la所给迭代公式的迭代矩阵为B = I — aA =2分试讨论解此方程的Jacobi5. 设方程Ax 二b,其中A =Gauss-Seidel 迭代格式:X 严=5-2垮)+2宅) <垮+—6-尤严—才 兀严)=7 — 2#申一 2卅Z用Doolittle 分解汁算下列3个线性代数方程组:Ax f =b, (i=l,2,3)其中"2 1 r4' A = 2 3 2 ,s = 7 2 3 4 96. 解: 上2 =兀]上3 =X2 (12分) ① Ax l =b 、x\ =A=由 Ly=bl,由 lxl=y, ②虹=b 2=LU 即y= 4791 10 0 11 12 得xl 二12 0'2 1 rT 2 32 x2= 12 3 4.11 0 o'TT1 1 oy= 1得y= 01 1 11由 Ly=b2=xl,即 (k=0,1,2, 3……)"2 1r丁「OS由Ux2=y,即 02 1 x2= 0得x2二 00 0 2③山3 =仏"2 1r'0.5'2 3 2 x3= 023 4.)0 0"'0.5 '由 Ly=b3=x2,即 1 10 y= 0得y 二 -0.51 110 .0 .'2 1r0.5 ''0.375 -由Ux3二y,即2 1 x3= -0.5得x3二 -0.250 2要求一次数不超过3的H 插值多项式,使 H 3(x /) = y r ,/73(x 1) = y I解:作重点的差分表,如下:H 3(X)= f[x {)] + /[x^x^ ](x-x Q ) + f[x 0,x^x { ](x-x ())(x-x I ) + /[xD ,x p x p x 2](x-x 0)(x-x I )2 二T+(x+l)-x(x+l)+2x. x(x+l)二2x 3 + x 27•已知 函 数 8.有如下函数表:关 数 据(6分)试讣算此列表函数的差分表,并利用Newton前插公式给出它的插值多项式(7分) 解:由已知条件可作差分表,x f = x0 + ih = i (i=0, 1, 2, 3 )为等距插值节点,则Newton向前插值公式为:N3 = f0 + 气評农 + +(—。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
期末考试试卷(A 卷)2007学年第二学期 考试科目: 数值分析 考试时间:120 分钟学号 姓名 年级专业一、判断题(每小题2分,共10分)1. 用计算机求1000100011n n=∑时,应按照n 从小到大的顺序相加。
( )2. 为了减少误差,进行计算。
( )3. 用数值微分公式中求导数值时,步长越小计算就越精确。
( )4. 采用龙格-库塔法求解常微分方程的初值问题时,公式阶数越高,数值解越精确。
( )5. 用迭代法解线性方程组时,迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关,与常数项无关。
( )二、填空题(每空2分,共36分)1. 已知数a 的有效数为0.01,则它的绝对误差限为________,相对误差限为_________.2. 设1010021,5,1301A x -⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦则1A =_____,2x =______,Ax ∞=_____.3. 已知53()245,f x x x x =+-则[1,1,0]f -= ,[3,2,1,1,2,3]f ---= .4. 为使求积公式11231()((0)f x dx A f A f A f -≈++⎰的代数精度尽量高,应使1A = ,2A = ,3A = ,此时公式具有 次的代数精度。
5. n 阶方阵A 的谱半径()A ρ与它的任意一种范数A 的关系是 .6. 用迭代法解线性方程组AX B =时,使迭代公式(1)()(0,1,2,)k k XMX N k +=+=K 产生的向量序列{}()k X收敛的充分必要条件是 .7. 使用消元法解线性方程组AX B =时,系数矩阵A 可以分解为下三角矩阵L 和上三角矩阵U 的乘积,即.A LU = 若采用高斯消元法解AX B =,其中4221A -⎡⎤=⎢⎥⎣⎦,则L =_______________,U =______________;若使用克劳特消元法解AX B =,则11u =____;若使用平方根方法解AX B =,则11l 与11u 的大小关系为_____(选填:>,<,=,不一定)。
8. 以步长为1的二阶泰勒级数法求解初值问题(0)1y x yy '=+⎧⎨=⎩的数值解,其迭代公式为___________________________.三、计算题(第1~3、6小题每题8分,第4、5小题每题7分,共46分)1. 以02x =为初值用牛顿迭代法求方程3()310f x x x =--=在区间(1,2)内的根,要求(1) 证明用牛顿法解此方程是收敛的;(2) 给出用牛顿法解此方程的迭代公式,并求出这个根(只需计算12,,x x 计算结果取到小数点后4位)。
2. 给定线性方程组1231231230.40.410.40.820.40.83x x x x x x x x x ++=⎧⎪++=⎨⎪++=⎩(1) 分别写出用Jacobi 和Gauss-Seidel 迭代法求解上述方程组的迭代公式;(2) 试分析以上两种迭代方法的敛散性。
3. 已知函数()y f x =在如下节点处的函数值(1) (2) 根据后三个节点建立二阶牛顿后插公式2()P x ,并计算(1.1)y 的近似值; (3) 采用事后估计法计算(2)中近似值的截断误差(结果保留四位小数)。
4.5. 已知函数()y f x =在以下节点处的函数值,利用差商表求(3)f '和(3)f ''的近似值。
6. 写出前进欧拉公式、后退欧拉公式,并由这两个公式构造一个预估-校正公式求解下列常微分方程的数值解。
22(01,0.2)(0)0y x y x h y '⎧=+≤≤=⎨=⎩四、(8分)已知n+1个数据点(,)(0,1,2,,)i i x y i n L ,请用多种方法建立这些数据点之间的函数关系,并说明各种函数的适用条件。
期末考试答案及评分标准(A 卷)2007学年第二学期 考试科目: 数值分析一、判断题:(每小题2分,共10分)1. ×2. √3. ×4. ×5. ×二、填空题:(每空2分,共36分) 1. 0.005或20.510-⨯ ,0.5 2.3. 0,24. 1,0,1,35.()A A ρ≤6. ()1M ρ<7. 1042,,1,10212⎡⎤-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦8. 11()(1)2n n n n n n y y x y x y +=+++++或1 1.5 2.50.5,0,1,2,n n n y x y n +=++=L三、解答题(第1~4小题每题8分,第5、6小题每题7分,共46分) 1. (1)证明:3()31f x x x =--,由于a) (1)30,(2)10,f f =-<=> b) 2()330((1,2)),f x x x '=-≠∈c)()60((1,2)),f x x x ''=>∈ 即()f x ''在(1,2)上不变号,d) 对于初值02x =,满足(2)(2)0,f f ''> 所以用牛顿迭代法求解此方程是收敛的。
………………………………………4分(2)解:牛顿迭代法的迭代公式为312()31()33n n n n n n n n f x x x x x x f x x +--=-=-'- ………………………………………2分取初值02x =进行迭代,得1 1.8889,x =………………………………………1分2 1.8795.x =………………………………………1分2. 解:(1)Jacobi 迭代公式为(1)()()123(1)()()213(1)()()3120.40.410.40.820.40.83k k k k k k k k k x x x x x x x x x +++⎧=--+⎪=--+⎨⎪=--+⎩ ……………………………2分 Gauss-Seidel 迭代公式为(1)()()123(1)(1)()213(1)(1)(1)3120.40.410.40.820.40.83k k k k k k k k k x x x x x x x x x ++++++⎧=--+⎪=--+⎨⎪=--+⎩……………………………2分 (2)Jacobi 迭代矩阵的特征方程为0.40.40.40.800.40.8λλλ=,展开得30.960.2560λλ-+=,即(0.8)(0.40.40λλλ-+++-=,从而得 123-1.0928,0.8000,0.2928λλλ===,(或由单调性易判断必有一个大于1的特征根,)因此迭代矩阵的谱半径等于必大于1,所以Jacobi 迭代法发散。
……………………………2分Gauss-Seidel 迭代矩阵的特征方程为0.40.40.40.800.40.8λλλλλλ=,展开得2(0.8320.128)0λλλ-+=,解得1230,0.628,0.204,λλλ=≈≈迭代矩阵的谱半径小于1,所以Gauss-Seidel 迭代法收敛。
……………………………2分3. 解:(1)建立差分表………………………………………2分 (2)建立牛顿后插公式为2232022********()()()()!!()()()P x x x x x x x x =-----=-----=-+ 则所求近似值为211279(.).P =………………………………………3分(3)根据前三个节点建立牛顿后插公式为1221431112312124()()()()!!()()P x x x x x x x x x =----=----=-++ 则 1211268()(.).P =根据事后误差估计法1222209091()()(.)(.)x R x P P x -⎡⎤≈-⎣⎦+ 故截断误差209112792680047121.(.)(..)..R -≈⨯-≈- ………………………………………3分4. 解:设所求二次最小平方逼近多项式为22012().P x a a x a x =++ 根据已知数据,得01211111002,,11151240a M A a Y a -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦……………………………2分则4268268,468186M M M Y ⎡⎤⎡⎤⎢⎥⎢⎥''==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦……………………………1分建立法方程组为0124268268468186a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ ……………………………2分解得0123.5, 1.5, 1.5.a a a ===-……………………………1分从而得所求一次最小平方逼近多项式为21() 3.5 1.5 1.5.P x x x =+-……………………………1分5. 解:设2()P x 为已知节点数据的插值二次多项式。
构造如下差商表:……………………………2分因为二次多项式的二阶差商为常数,又2()P x 是()f x 的插值函数,故有225[4,3,3][3,3,3]2P P ==……………………………2分而22[3,3]75[4,3,3]342P P -==-,因此得29[3,3]2P =, ……………………………1分由于1L 1442443()()![,,,,]k n k f x k P x x x x +≈,从而得293332()[,],f P '==2323335()![,,].f P ''==……………………………2分6. 解:前进欧拉公式:221(,)0.20.2n n n n n n n y y h f x y y x y +=+⋅=++…………1分后退欧拉公式:2211111(,)0.20.2n n n n n n n y y h f x y y x y +++++=+⋅=++ ……1分预估时采用欧拉公式*2210.20.2n n n n y y x y +=++……………………………1分校正时采用后退欧拉公式()22*1110.20.2n n n n y y xy+++=++……………………………1分由初值000002,,.x y h ===知,节点分别为0.2,(1,2,3,4,5)i x i i ==当10.2,x =*2210000.20.20,y y x y =++=()22101102020008*...y y x y=++=,……………………………1分当20.4,x =*2221110.20.20.0160,y y x y =++≈()222122020200401*...y y x y =++≈.……………………………1分当30.6,x =*2232220.20.20.0724,y y x y =++≈()223233020201131*...y y x y =++≈.……………………………1分当40.8,x =*2243330.20.20.1877,y y x y =++≈()224344020202481*...y y x y=++≈.……………………………1分当51.0,x =*2254440.20.20.3884,y y x y =++≈()225455020204783*...y y x y=++≈.四、(8分)答:1、可以建立插值函数: (1)Newton 基本差商公式00100121001110()()()[,]()()[,,]()()()[,,,]L L L n n n P x f x x x f x x x x x x f x x x x x x x x x f x x x -=+-+--++---……………………………1分(2)Lagrange 插值多项式0011()()()()()L L n i i n n L x a f x a f x a f x a f x =+++++其中01101101()()()(),(,,,)()()()()L L L L L i i n i i i i i i i n x x x x x x x x a i n x x x x x x x x -+-+----==----.……………………………1分这两类插值函数的适用条件是:n 不太大;而且要求函数严格通过已知数据点。
