数值分析试题及答案
数值分析试题与答案

一、单项选择题(每小题3分,共15分)1. 和分别作为π(de)近似数具有( )和( )位有效数字. A .4和3 B .3和2 C .3和4 D .4和42. 已知求积公式()()211211()(2)636f x dx f Af f ≈++⎰,则A =( )A . 16B .13C .12D .233. 通过点()()0011,,,x y x y (de)拉格朗日插值基函数()()01,l x l x 满足( )A .()00l x =0,()110l x =B .()00l x =0,()111l x =C .()00l x =1,()111l x = D .()00l x =1,()111l x =4. 设求方程()0f x =(de)根(de)牛顿法收敛,则它具有( )敛速.A .超线性B .平方C .线性D .三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩ 作第一次消元后得到(de)第3个方程( ).A .232x x -+=B .232 1.5 3.5x x -+=C .2323x x -+=D .230.5 1.5x x -=-二、填空题(每小题3分,共15分)1. 设TX )4,3,2(-=, 则=1||||X ,2||||X = .2. 一阶均差()01,f x x =3. 已知3n =时,科茨系数()()()33301213,88C C C ===,那么()33C = 4. 因为方程()420x f x x =-+=在区间[]1,2上满足 ,所以()0f x =在区间内有根.5. 取步长0.1h =,用欧拉法解初值问题()211y y yx y ⎧'=+⎪⎨⎪=⎩(de)计算公式 .0,1,2分 人三、计算题(每题15分,共60分)1. 已知函数211y x =+(de)一组数据:求分段线性插值函数,并计算()1.5f (de)近似值.1. 解 []0,1x ∈,()1010.510.50110x x L x x --=⨯+⨯=---[]1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为()[][]10.50,10.80.31,2x x L x x x ⎧-∈⎪=⎨-∈⎪⎩ ()1.50.80.3 1.50.35L =-⨯=2. 已知线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩(1) 写出雅可比迭代公式、高斯-塞德尔迭代公式;(2) 对于初始值()()00,0,0X =,应用雅可比迭代公式、高斯-塞德尔迭代公式分别计算()1X (保留小数点后五位数字).1.解 原方程组同解变形为1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m =高斯-塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩ (0,1...)m =用雅可比迭代公式得()()10.72000,0.83000,0.84000X =用高斯-塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间(de)近似根(1)请指出为什么初值应取2 (2)请用牛顿法求出近似根,精确到. 3. 解()331f x x x =--,()130f =-<,()210f =>()233f x x '=-,()12f x x ''=,()2240f =>,故取2x =作初始值4. 写出梯形公式和辛卜生公式,并用来分别计算积分111dxx+⎰.四、证明题(本题10分)确定下列求积公式中(de)待定系数,并证明确定后(de)求积公式具有3次代数精确度()()()()1010hhf x dx A f h A f A f h --=-++⎰证明:求积公式中含有三个待定系数,即101,,A A A -,将()21,,f x x x =分别代入求一、 填空(共20分,每题2分)1. 设2.3149541...x *=,取5位有效数字,则所得(de)近似值x= .2.设一阶差商()()()21122114,321f x f x f x x x x --===---,()()()322332615,422f x f x f x x x x --===--则二阶差商 ()123,,______f x x x =3. 设(2,3,1)TX =--, 则2||||X = ,=∞||||X .4.求方程 21.250x x --= (de)近似根,用迭代公式 1.25x x =+,取初始值 01x =, 那么 1______x =。
数值分析试题及答案

数值分析试题及答案一、选择题1. 下列哪个方法不适合用于求解非线性方程的根?A. 二分法B. 牛顿法C. 弦截法D. 正割法2. 当使用二分法求解非线性方程的根时,需要满足的条件是:A. 函数f(x)在区间[a, b]上连续B. 函数f(x)在区间[a, b]上单调递增C. 函数f(x)在区间[a, b]上存在根D. 函数f(x)在区间[a, b]上可导3. 数值积分是通过将定积分转化为求和的方法来近似计算积分值的过程。
下列哪个方法是常用的数值积分方法?A. 矩形法则B. 辛普森规则C. 梯形规则D. 高斯-勒让德法则4. 龙格-库塔法是常用于求解常微分方程的数值解法。
以下哪个选项是描述龙格-库塔法的特点?A. 该方法是一种多步法B. 该方法是一种多项式插值法C. 该方法是一种单步法D. 该方法是一种数值积分法5. 用有限差分法求解偏微分方程时,通常需要进行网格剖分。
以下哪个选项是常用的网格剖分方法?A. 多边形剖分法B. 三角剖分法C. 矩形剖分法D. 圆形剖分法二、解答题1. 将函数f(x) = e^x 在区间[0, 1]上用复化梯形规则进行数值积分,分为6个子区间,求得的近似积分值为多少?解:将区间[0, 1]等分为6个子区间,每个子区间的长度为h = (1-0)/6 = 1/6。
根据复化梯形规则的公式,近似积分值为:I ≈ (1/2) * h * [f(0) + 2f(1/6) + 2f(2/6) + 2f(3/6) + 2f(4/6) + 2f(5/6) +f(1)]≈ (1/2) * (1/6) * [e^0 + 2e^(1/6) + 2e^(2/6) + 2e^(3/6) + 2e^(4/6) +2e^(5/6) + e^1]2. 使用二分法求解方程 x^3 - 3x + 1 = 0 在区间[1, 2]上的根。
要求精确到小数点后三位。
解:首先需要判断方程在区间[1, 2]上是否存在根。
数值分析试题与答案

一. 填空题(本大题共4小题,每小题4分,共16分)1.设有节点012,,x x x ,其对应的函数()y f x =的值分别为012,,y y y ,则二次拉格朗日插值基函数0()l x 为 。
2.设()2f x x =,则()f x 关于节点0120,1,3x x x ===的二阶向前差分为 。
3.设110111011A -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦,233x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则1A = ,1x = 。
4. 1n +个节点的高斯求积公式的代数精确度为 。
二.简答题(本大题共3小题,每小题8分,共24分)1. 哪种线性方程组可用平方根法求解?为什么说平方根法计算稳定?2. 什么是不动点迭代法?()x ϕ满足什么条件才能保证不动点存在和不动点迭代序列收敛于()x ϕ的不动点?3. 设n 阶矩阵A 具有n 个特征值且满足123n λλλλ>≥≥≥,请简单说明求解矩阵A 的主特征值和特征向量的算法及流程。
三.求一个次数不高于3的多项式()3P x ,满足下列插值条件:i x 1 2 3 i y 2 4 12 i y '3并估计误差。
(10分)四.试用1,2,4n =的牛顿-科特斯求积公式计算定积分1011I dx x=+⎰。
(10分) 五.用Newton 法求()cos 0f x x x =-=的近似解。
(10分) 六.试用Doolittle 分解法求解方程组:12325610413191963630x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦ (10分)七.请写出雅可比迭代法求解线性方程组123123123202324812231530x x x x x x x x x ++=⎧⎪++=⎨⎪-+=⎩ 的迭代格式,并判断其是否收敛?(10分)八.就初值问题0(0)y yy y λ'=⎧⎨=⎩考察欧拉显式格式的收敛性。
(10分)《数值分析》(A )卷标准答案(2009-2010-1)一. 填空题(每小题3分,共12分) 1. ()1200102()()()()x x x x l x x x x x --=--; 2.7;3. 3,8;4. 2n+1。
数值分析题库答案(含详细解题步骤)

第 1 页/共 22 页1. 正方形的边长大约为100cm ,应怎样测量才干使面积误差不超过1cm 22. 已测得某场地长l 的值为110=*l m ,宽d 的值为80=*d m ,已知 2.0≤-*l l m,1.0≤-*d d m, 试求面积ld s =的绝对误差限与相对误差限.3.为使π的相对误差小于0.001%,至少应取几位有效数字?4.设x的相对误差界为δ,求n x的相对误差界.5.设有3个近似数a=2.31,b=1.93,c=2.24,它们都有3位有效数字,试计算p=a+bc的误差界和相对误差界,并问p的计算结果能有几位有效数字?第 3 页/共 22 页6. 已知333487.034.0sin ,314567.032.0sin ==,请用线性插值计算3367.0sin 的值,并预计截断误差.7. 已知sin0.32=0.314567, sin0.34=0.333487, sin0.36= 0.352274,用抛物插值计算sin0.3367的值, 并预计误差.8. 已知16243sin ,sin πππ===请用抛物插值求sin50的值,并预计误差9. . .6,8,7,4,1)(,5,4,3,2,1求四次牛顿插值多项式时设当==i i x f x第 5 页/共 22 页10. 已知4)2(,3)1(,0)1(=-=-=f f f , 求函数)(x f 过这3点的2次牛顿插 值多项式.11. 设x x f =)(,并已知483240.1)2.2(,449138.1)1.2(,414214.1)0.2(===f f f ,试用二次牛顿插值多项式计算(2.15)f 的近似值,并研究其误差12. 设],[)(b a x f 在上有四阶延续导数,试求满意条件)2,1,0()()(==i x f x P i i 及)()(11x f x P '='的插值多项式及其余项表达式.13. 给定3201219(),,1,,44f x x x x x ====试求()f x 在1944⎡⎤⎢⎥⎣⎦,上的三次埃尔米特插值多项式()P x ,使它满意11()()(0,1,2),()(),i i P x f x i P x f x ''===并写出余项第 7 页/共 22 页表达式.14. 设],1,0[,23)(2∈++=x x x x f 试求)(x f 在]1,0[上关于,,1{,1)(x span x =Φ=ρ}2x 的最佳平方逼近多项式15.已知实验数据如下:用最小二乘法求形如y=a+bx2的拟合曲线,并计算均方误差.16.已知数据表如下第 9 页/共 22 页x i 1 2 3 4 5 y iωi4 4.56 8 8.5 2 1 3 1 1试用最小二乘法求多项式曲线与此数据组拟合17. .1)(},1{span ,1]41[)(的最佳平方逼近多项式中的关于上的在在求==Φ=x x x x f ρ18. 决定求积公式⎰++≈10110)1()(32)0()(f A x f f A dx x f 中的待定参数110,,A x A , 使其代数精度尽量高,并指出所决定的求积公式的代数精度.19. 用复化辛普森公式计算积分⎰=10dx e I x , 问区间[0,1]应分多少等分才干使截断误差不超过?10215-⨯第 11 页/共 22 页20. 利用下表中给出的数据,分离用复化梯形公式和复化辛甫生公式计算定积分dx x I ln 21⎰=的近似值(要求结果保留到小数点后六位)21. 用复化梯形公式和复化辛甫生公式计算积分⎰=6.28.1)(dx x f I ,函数)(x f 在某些节点上的值如下图:(本题共14分)22. 决定公式⎰+≈101100)()()(x f A x f A dx x f x 的系数1010,,,x x A A ,使其具有最高代数精度23. 决定求积公式⎰++≈1110)1()(32)0()(f A x f f A dx x f 中的待定参数110,,A x A ,使其代数精度尽量高,并指出所决定的求积公式的代数精度第 13 页/共 22 页24.用LU 分解法求解以下方程组 (10分)123123142521831520x x x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭25.用LU 分解法求解以下方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛8892121514131615141321x x x26. 用LU 分解法求解以下方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛542631531321321x x x27. 设方程组b Ax =,其中⎪⎪⎪⎭⎫⎝⎛-=220122101A ,Tb ⎪⎭⎫ ⎝⎛-=32,31,21, 已知它有解Tx ⎪⎭⎫⎝⎛-=0,31,21,若右端有小扰动61021-∞⨯=bδ,试预计由此引起的解的相对误差.第 15 页/共 22 页28. 设方程组b Ax =,其中212 1.0001A -⎛⎫= ⎪-⎝⎭,11.0001b -⎛⎫= ⎪⎝⎭,当右端向量b 有误差00.0001δ⎛⎫= ⎪⎝⎭b 时,试预计由此引起的解的相对误差(用∞范数计算)29. 给定b Ax =,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111a a a a a a A 证实:(1) 当121<<-a 时,A 对称正定,从而GS 法收敛. (2) 惟独当2121<<-a 时,J 法收敛.30. 对于线性方程组⎪⎩⎪⎨⎧-=+-=-+=+1242043 16343232121x x x x x x x ,列出求解此方程组的Jacobi 迭代格式,并判断是否收敛。
数值分析试卷及答案

数值分析试卷及答案数值分析试卷一、选择题(共10题,每题2分,共计20分)1. 数值分析的研究内容主要包括以下哪几个方面?A. 数值计算方法B. 数值误差C. 数值软件D. 数学分析答:A、B、C2. 下列哪种方法不属于数值积分的基本方法?A. 插值法B. 微积分基本公式C. 数值微积分D. 数值积分公式答:A3. 数值积分的目的是求解什么?A. 函数的导数B. 函数的原函数C. 函数的极值D. 函数的积分答:D4. 数值微分的目的是求解什么?A. 函数的导数B. 函数的原函数C. 函数的极值D. 函数的积分答:A5. 数值微分的基本方法有哪几种?A. 前向差分B. 后向差分C. 中心差分D. 插值法答:A、B、C6. 用数值方法求解方程的基本方法有哪几种?A. 迭代法B. 曲线拟合法C. 插值法D. 数值积分法答:A、B、C7. 用迭代法求方程的根时,当迭代结果满足何条件时可停止迭代?A. 当迭代结果开始发散B. 当迭代结果接近真实解C. 当迭代次数超过一定阈值D. 当迭代结果在一定范围内波动答:B8. 下列哪种插值方法能够确保经过所有给定数据点?A. 拉格朗日插值B. 牛顿插值C. 三次样条插值D. 二次插值答:A、B、C9. 数值解线性方程组的基本方法有哪几种?A. 直接法B. 迭代法C. 插值法D. 拟合法答:A、B10. 下列哪种方程求解方法适用于非线性方程?A. 直接法B. 迭代法C. 插值法D. 曲线拟合法答:B二、填空题(共5题,每题4分,共计20分)1. 数值积分的基本公式是_________。
答:牛顿-科特斯公式2. 数值微分的基本公式是_________。
答:中心差分公式3. 数值积分的误差分为_________误差和_________误差。
答:截断、舍入4. 用插值法求解函数值时,通常采用_________插值。
答:拉格朗日5. 数值解线性方程组的常用迭代法有_________方法和_________方法。
数值分析版试题及答案
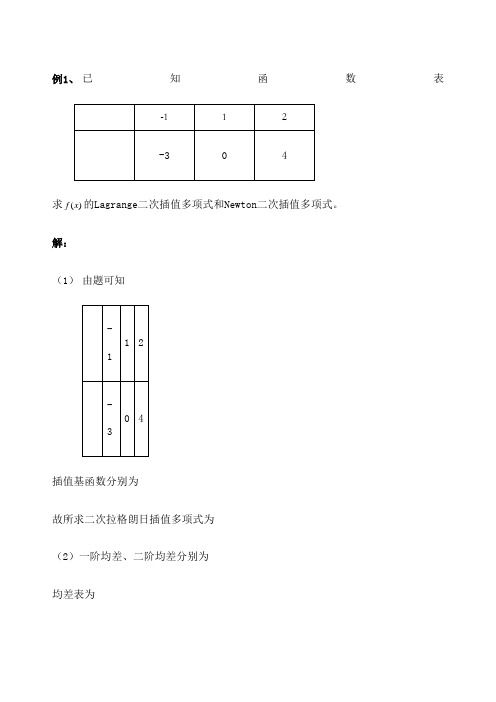
例1、已知函数表求()f x的Lagrange二次插值多项式和Newton二次插值多项式。
解:(1)由题可知插值基函数分别为故所求二次拉格朗日插值多项式为(2)一阶均差、二阶均差分别为均差表为故所求Newton 二次插值多项式为例2、 设2()32f x x x =++,[0,1]x ∈,试求()f x 在[0, 1]上关于()1x ρ=,{}span 1,x Φ=的最佳平方逼近多项式。
解:若{}span 1,x Φ=,则0()1x ϕ=,1()x x ϕ=,且()1x ρ=,这样,有 所以,法方程为01123126119234a a ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦,经过消元得01231162110123a a ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 再回代解该方程,得到14a =,0116a =故,所求最佳平方逼近多项式为*111()46S x x =+例3、 设()x f x e =,[0,1]x ∈,试求()f x 在[0, 1]上关于()1x ρ=,{}span 1,x Φ=的最佳平方逼近多项式。
解:若{}span 1,x Φ=,则0()1x ϕ=,1()x x ϕ=,这样,有 所以,法方程为解法方程,得到00.8732a =,1 1.6902a =, 故,所求最佳平方逼近多项式为例4、 用4n =的复合梯形和复合辛普森公式计算积分1⎰。
解:(1)用4n =的复合梯形公式由于2h =,()f x =,()121,2,3k x k k =+=,所以,有 (2)用4n =的复合辛普森公式由于2h =,()f x =,()121,2,3k x k k =+=,()12220,1,2,3k xk k +=+=,所以,有例5、 用列主元消去法求解下列线性方程组的解。
解:先消元再回代,得到33x =,22x =,11x =所以,线性方程组的解为11x =,22x =,33x = 例6、 用直接三角分解法求下列线性方程组的解。
数值分析习题(含答案)

第一章 绪论姓名 学号 班级习题主要考察点:有效数字的计算、计算方法的比较选择、误差和误差限的计算。
1 若误差限为5105.0-⨯,那么近似数0.003400有几位有效数字?(有效数字的计算) 解:2*103400.0-⨯=x ,325*10211021---⨯=⨯≤-x x 故具有3位有效数字。
2 14159.3=π具有4位有效数字的近似值是多少?(有效数字的计算) 解:10314159.0⨯= π,欲使其近似值*π具有4位有效数字,必需41*1021-⨯≤-ππ,3*310211021--⨯+≤≤⨯-πππ,即14209.314109.3*≤≤π即取(3.14109 , 3.14209)之间的任意数,都具有4位有效数字。
3 已知2031.1=a ,978.0=b 是经过四舍五入后得到的近似值,问b a +,b a ⨯有几位有效数字?(有效数字的计算)解:3*1021-⨯≤-aa ,2*1021-⨯≤-b b ,而1811.2=+b a ,1766.1=⨯b a 2123****102110211021)()(---⨯≤⨯+⨯≤-+-≤+-+b b a a b a b a故b a +至少具有2位有效数字。
2123*****10210065.01022031.1102978.0)()(---⨯≤=⨯+⨯≤-+-≤-b b a a a b b a ab 故b a ⨯至少具有2位有效数字。
4 设0>x ,x 的相对误差为δ,求x ln 的误差和相对误差?(误差的计算) 解:已知δ=-**xx x ,则误差为 δ=-=-***ln ln xx x x x则相对误差为******ln ln 1ln ln ln xxx x xxx x δ=-=-5测得某圆柱体高度h 的值为cm h 20*=,底面半径r 的值为cm r 5*=,已知cm h h 2.0||*≤-,cm r r 1.0||*≤-,求圆柱体体积h r v2π=的绝对误差限与相对误差限。
数值分析期末考试题及答案

数值分析期末考试题及答案一、选择题(每题2分,共20分)1. 在数值分析中,下列哪个算法用于求解线性方程组?A. 牛顿法B. 高斯消元法C. 插值法D. 傅里叶变换答案:B2. 以下哪个选项不是数值分析中的误差类型?A. 舍入误差B. 截断误差C. 测量误差D. 累积误差答案:C3. 多项式插值中,拉格朗日插值法的特点是:A. 插值点必须等距分布B. 插值多项式的次数与插值点的个数相同C. 插值多项式是唯一的D. 插值多项式在插值点处的值都为1答案:B4. 在数值分析中,下列哪个方法用于求解非线性方程?A. 辛普森法则B. 牛顿迭代法C. 欧拉法D. 龙格-库塔法答案:B5. 以下哪个是数值稳定性的指标?A. 收敛性B. 收敛速度C. 条件数D. 误差传播答案:C二、简答题(每题10分,共20分)1. 简述高斯消元法求解线性方程组的基本原理。
答案:高斯消元法是一种直接解法,通过行变换将增广矩阵转换为上三角形式,然后通过回代求解线性方程组。
它包括三个基本操作:行交换、行乘以非零常数、行相加。
2. 解释什么是数值稳定性,并举例说明。
答案:数值稳定性是指数值解对输入数据小的扰动不敏感的性质。
例如,某些数值方法在计算过程中可能会放大舍入误差,导致结果不可靠,这样的方法就被认为是数值不稳定的。
三、计算题(每题15分,共30分)1. 给定线性方程组:\[\begin{align*}x + 2y - z &= 4 \\3x - y + 2z &= 1 \\-x + y + z &= 2\end{align*}\]使用高斯消元法求解该方程组,并给出解。
答案:首先将增广矩阵转换为上三角形式,然后回代求解,得到\( x = 1, y = 2, z = 1 \)。
2. 给定函数 \( f(x) = x^2 - 3x + 2 \),使用拉格朗日插值法在\( x = 0, 1, 2 \) 处插值,并求出插值多项式。
《数值分析》练习题及答案解析

《数值分析》练习题及答案解析一、单选题1. 以下误差公式不正确的是( D )A .()1212x x x x ∆-≈∆-∆B .()1212x x x x ∆+≈∆+∆C .()122112x x x x x x ∆≈∆+∆D .1122()x x x x ∆≈∆-∆ 2. 已知等距节点的插值型求积公式()()352kkk f x dx A f x =≈∑⎰,那么3kk A==∑( C )A .1 B. 2 C.3 D. 4 3.辛卜生公式的余项为( c )A .()()32880b a f η-''-B .()()312b a f η-''-C .()()()542880b a f η--D .()()()452880b a f η--4. 用紧凑格式对矩阵4222222312A -⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦进行的三角分解,则22r =( A ) A .1 B .12C .–1D .–25. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足( D ) A .()00l x =0,()110l x = B . ()00l x =0,()111l x = C .()00l x =1,()111l x = D . ()00l x =1,()111l x =6. 用二分法求方程()0f x =在区间[],a b 上的根,若给定误差限ε,则计算二分次数的公式是n ≥( D )A .ln()ln 1ln 2b a ε-++ B. ln()ln 1ln 2b a ε-+-C.ln()ln 1ln 2b a ε--+ D. ln()ln 1ln 2b a ε--- 7.若用列主元消去法求解下列线性方程组,其主元必定在系数矩阵主对角线上的方程组是( B )A .123123123104025261x x x x x x x x x -+=⎧⎪-+=⎨⎪-+=-⎩ B 。
数值分析试题及答案

数值分析试题及答案一、选择题(每题2分,共20分)1. 以下哪个算法是数值分析中用于求解线性方程组的直接方法?A. 牛顿法B. 高斯消元法C. 梯度下降法D. 蒙特卡洛方法答案:B2. 插值法中,拉格朗日插值法和牛顿插值法的共同点是:A. 都是多项式插值B. 都使用差商C. 都只适用于等距节点D. 都需要预先知道所有数据点答案:A3. 在数值积分中,辛普森(Simpson)公式比梯形公式的误差:A. 更大B. 更小C. 相同D. 无法比较答案:B4. 以下哪个是数值稳定性分析中常用的方法?A. 条件数B. 收敛性C. 收敛速度D. 误差分析答案:A5. 在求解常微分方程的数值解时,欧拉方法属于:A. 单步法B. 多步法C. 隐式方法D. 显式方法答案:A6. 以下哪个是数值分析中求解非线性方程的迭代方法?A. 高斯-约当消元法B. 牛顿-拉弗森方法C. 雅可比迭代法D. 高斯-赛德尔迭代法答案:B7. 线性插值公式中,如果给定两个点\( (x_0, y_0) \)和\( (x_1, y_1) \),插值多项式是:A. \( y = y_0 + \frac{y_1 - y_0}{x_1 - x_0}(x - x_0) \)B. \( y = y_0 + \frac{y_1 - y_0}{x_0 - x_1}(x - x_0) \)C. \( y = y_0 + \frac{x - x_0}{x_1 - x_0}(y_1 - y_0) \)D. \( y = y_1 + \frac{x_1 - x}{x_1 - x_0}(y_0 - y_1) \)答案:C8. 以下哪个是数值分析中用于求解特征值问题的算法?A. 幂法B. 共轭梯度法C. 牛顿法D. 欧拉法答案:A9. 在数值微分中,使用有限差分法来近似导数时,中心差分法的误差:A. 与步长成正比B. 与步长的平方成正比C. 与步长的立方成正比D. 与步长的四次方成正比答案:B10. 以下哪个是数值分析中用于求解线性最小二乘问题的算法?A. 梯度下降法B. 牛顿法C. 奇异值分解法D. 共轭梯度法答案:C二、简答题(每题10分,共30分)1. 简述数值分析中病态问题的特点及其对算法的影响。
数值分析版试题及答案

数值分析版试题及答案 GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-例1、已知函数表求()f x的Lagrange二次插值多项式和Newton二次插值多项式。
解:(1)由题可知插值基函数分别为故所求二次拉格朗日插值多项式为(2)一阶均差、二阶均差分别为均差表为故所求Newton 二次插值多项式为例2、 设2()32f x x x =++,[0,1]x ∈,试求()f x 在[0, 1]上关于()1x ρ=,{}span 1,x Φ=的最佳平方逼近多项式。
解:若{}span 1,x Φ=,则0()1x ϕ=,1()x x ϕ=,且()1x ρ=,这样,有 所以,法方程为01123126119234a a ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦,经过消元得01231162110123a a ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 再回代解该方程,得到14a =,0116a =故,所求最佳平方逼近多项式为*111()46S x x =+ 例3、 设()x f x e =,[0,1]x ∈,试求()f x 在[0, 1]上关于()1x ρ=,{}span 1,x Φ=的最佳平方逼近多项式。
解:若{}span 1,x Φ=,则0()1x ϕ=,1()x x ϕ=,这样,有 所以,法方程为解法方程,得到00.8732a =,1 1.6902a =, 故,所求最佳平方逼近多项式为例4、 用4n =的复合梯形和复合辛普森公式计算积分1⎰。
解:(1)用4n =的复合梯形公式由于2h =,()f x =,()121,2,3k x k k =+=,所以,有 (2)用4n =的复合辛普森公式由于2h =,()f x =,()121,2,3k x k k =+=,()12220,1,2,3k xk k +=+=,所以,有例5、 用列主元消去法求解下列线性方程组的解。
《数值分析》练习题及答案解析

《数值分析》练习题及答案解析第一章 绪论主要考查点:有效数字,相对误差、绝对误差定义及关系;误差分类;误差控制的基本原则;。
1. 3.142和3.141分别作为π的近似数具有( )和( )位有效数字.A .4和3B .3和2C .3和4D .4和4 答案:A2. 设 2.3149541...x *=,取5位有效数字,则所得的近似值x=___________ .答案:2.31503.若近似数2*103400.0-⨯=x 的绝对误差限为5105.0-⨯,那么近似数有几位有效数字 解:2*103400.0-⨯=x ,325*10211021---⨯=⨯≤-x x 故具有3位有效数字。
4 . 14159.3=π具有4位有效数字的近似值是多少?解:10314159.0⨯= π,欲使其近似值*π具有4位有效数字,必需!41*1021-⨯≤-ππ,3*310211021--⨯+≤≤⨯-πππ,即14209.314109.3*≤≤π即取( , )之间的任意数,都具有4位有效数字。
第二章 非线性方程求根 主要考查点:二分法N 步后根所在的区间,及给定精度下二分的次数计算;非线性方程一般迭代格式的构造,(局部)收敛性的判断,迭代次数计算; 牛顿迭代格式构造;求收敛阶;1.用二分法求方程012=--x x 的正根,要求误差小于0.05。
(二分法)解:1)(2--=x x x f ,01)0(<-=f ,01)2(>=f ,)(x f 在[0,2]连续,故[0,2]为函数的有根区间。
"(1)计算01)1(<-=f ,故有根区间为[1,2]。
(2)计算041123)23()23(2<-=--=f ,故有根区间为]2,23[。
(3)计算0165147)47()47(2>=--=f ,故有根区间为]47,23[。
(4)计算06411813)813()813(2>=--=f ,故有根区间为]813,23[。
数值分析练习题附答案

目录一、绪论------------------------------------------------------------------------------------- 2-2二、线性方程组直接解法列主元高斯LU LDL T GG T-------------------- 3-6二、线性方程组迭代法----------------------------------------------------------------- 7-10 三、四、非线性方程组数值解法二分法不动点迭代---------------------- 11-13五、非线性方程组数值解法牛顿迭代下山弦截法----------------- 14-15六、插值线性插值抛物线插值------------------------------------------------ 16-18七、插值Hermite插值分段线性插值-----------------------------------------19-22八、拟合------------------------------------------------------------------------------------ 23-24九、数值积分----------------------------------------------------------------------------- 25-29十、常微分方程数值解法梯形欧拉改进----------------------------------- 30-32 十一、常微分方程数值解法龙格库塔------------------------------------------ 33-35绪论1-1 下列各数都是经过四舍五入得到的近似值 ,试分别指出它们的绝对误差限,相对误差限和有效数字的位数.X 1 =5.420, X 2 =0.5420, X 3 =0.00542, X 4 =6000, X 5 =0.6×105注:将近似值改写为标准形式X 1 =(5*10-1+4*10-2+2*10-3+0*10-4)*101 即n=4,m=1 绝对误差限|△X 1|=|X *1-X 1|≤ 12×10m-n =12×10-3 相对误差限|△r X 1|= |X∗1−X1||X∗1|≤|X∗1−X1||X1|= 12×10-3/5.4201-2 为了使101/2 的相对误差小于0.01%, 试问应取几位有效数字?1-3 求方程x 2 -56x+1=0的两个根, 使它们至少具有4位有效数字( √783≈27.982)注:原方程可改写为(x-28)2=783线性方程组解法(直接法)2-1用列主元Gauss消元法解方程组解:回代得解:X1=0 X2=-1 X3=12-2对矩阵A进行LU分解,并求解方程组Ax=b,其中解:(注:详细分解请看课本P25)A=(211132122)→(211(1/2)5/23/2(1/2)3/23/2)→(2111/25/23/21/2(3/5)3/5)即A=L×U=(11/211/23/51)×(2115/23/23/5)先用前代法解L y=P b 其中P为单位阵(原因是A矩阵未进行行变换)即L y=P b 等价为(11/211/23/51)(y1y2y3)=(111)(465)解得 y 1=4 y 2=4 y 3=35再用回代解Ux =y ,得到结果x即Ux =y 等价为(2115/23/23/5)(x 1x 2x 3)=(y 1y 2y 3)=(443/5) 解得 x 1=1 x 2=1 x 3=1即方程组Ax=b 的解为x =(111)2-3 对矩阵A 进行LDL T 分解和GG T 分解,求解方程组Ax=b,其中A=(164845−48−422) , b =(123)解:(注:课本 P 26 P 27 根平方法)设L=(l i j ),D=diag(d i ),对k=1,2,…,n,其中d k =a kk -∑l kj 2k−1j=1d jl ik =(a ik −∑l ij l kj k−1j=1d j )/ d k 即d 1=a 11-∑l 1j 20j=1d j =16-0=16因为 l 21=(a 21−∑l 2j l 1j 0j=1d j )/ d 1=a 21/ d 1=416=14 所以d 2=a 22-∑l 2j 21j=1d j =5-(14)2d 1=4同理可得d 3=9 即得 D=(1649)同理l 11=(a 11−∑l ij l 1j 0j=1d j )/ d 1=1616=1=l 22=l 33 l 21=(a 21−∑l 2j l 1j 0j=1d j )/ d 1=416=14 l 31=(a 31−∑l 3j l 1j 0j=1d j )/ d 1=816=12 l 32=(a 32−∑l 3j l 2j 1j=1d j )/ d 2=−4−12×14×164=−64=-32即L=(114112−321) L T=(114121−321) 即LDL T分解为A=(114112−321)(1649)(114121−321)解解:A=(164845−48−422)→(41212−32−33)故得GG T分解:A=(4122−33)(4122−33) LDL T分解为A=(114112−321)(1649)(114121−321) 由(114112−321)(y 1y 2y 3)=(123) ,得(y 1y 2y 3)=(0.250.8751.7083)再由(4122−33)(x 1x 2x 3)=(0.250.8751.7083) ,得(x 1x 2x 3)=(−0.54511.29160.5694)2-4 用追赶法求解方程组:解:(4−1−14−1−14−1−14−1−14)→(4−14−1154−415−15615−1556−120956−56209−1780209)由(4−1154−15615−120956−1780209)(y1y2y3y4y5)=(100200),得(y1y2y3y4y5)=(256.66671.785700.4784753.718)再由(1−141−4151−15561−562091)(x1x2x3x4x5)=(256.66671.785700.4784753.718),得(x1x2x3x4x5)=(27.0518.20525.769314.87253.718)线性方程组解法(迭代法)2-1 设线性方程组{4x 1−x 2+2x 3=1−x 1−5x 2+x 3=22x 1+x 2+6x 3=3(1) 写出Jacobi 法和SOR 法的迭代格式(分量形式) (2) 讨论这两种迭代法的收敛性(3) 取初值x (0)=(0,0,0)T ,若用Jacobi 迭代法计算时,预估误差 ||x*-x (10)||∞ (取三位有效数字)解:(1)Jacobi 法和SOR 法的迭代格式分别为Jacobi 法迭代格式SOR(2)因为A 是严格对角占优矩阵,但不是正定矩阵,故Jacobi 法收敛,SOR 法当0<ω≤1时收敛.⎪⎪⎪⎩⎪⎪⎪⎨⎧+--=-+-=+-=+++216131525151412141)(2)(1)1(3)(3)(1)1(2)(3)(2)1(1k k k k k k k k k x x x x x x xx x ⎪⎪⎪⎩⎪⎪⎪⎨⎧-++-=+-+-=+-+-+=++++++)216131()525151()412141()(3)1(2)1(1)(3)1(3)(3)(2)1(1)(2)1(2)(3)(2)(1)(1)1(1k k k k k k k k k k k k k k k x x x x x x x x x x x x x x x ωωω(3)由(1)可见||B ||∞=3/4,且取x (0)=(0,0,0)T ,经计算可得x (1)=(1/4,-2/5,1/2)T ,于是||x (1)-x (0)||∞=1/2,所以有2-2 设方程组为{5x 1+2x 2+x 3=−12−x 1+4x 2+2x 3=202x 1−3x 2+10x 3=3试写出其Jacobi 分量迭代格式以及相应的迭代矩阵,并求解。
数值分析试题及答案

1. 和分别作为π的近似数具有( )和( )位有效数字. A .4和3 B .3和2 C .3和4 D .4和42. 已知求积公式()()211211()(2)636f x dx f Af f ≈++⎰,则A =( )A . 16B .13C .12D .233. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足( )A .()00l x =0,()110l x = B .()00l x =0,()111l x =C .()00l x =1,()111l x = D .()00l x =1,()111l x =4. 设求方程()0f x =的根的牛顿法收敛,则它具有( )敛速。
A .超线性B .平方C .线性D .三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩ 作第一次消元后得到的第3个方程( ).A .232x x -+= B .232 1.5 3.5x x -+=C .2323x x -+= D .230.5 1.5x x -=-单项选择题答案二、填空题(每小题3分,共15分)1. 设TX )4,3,2(-=, 则=1||||X ,2||||X = .2. 一阶均差()01,f x x =3. 已知3n =时,科茨系数()()()33301213,88C C C ===,那么()33C = 4. 因为方程()420x f x x =-+=在区间[]1,2上满足 ,所以()0f x =在区间内有根。
5. 取步长0.1h =,用欧拉法解初值问题()211yy yx y ⎧'=+⎪⎨⎪=⎩的计算公式 .填空题答案1. 9和292.()()0101f x f x x x --3. 18 4. ()()120f f < 5. ()1200.11.1,0,1,210.11k k y y k k y +⎧⎛⎫⎪ ⎪=+⎪ ⎪=+⎨⎝⎭⎪=⎪⎩得 分 评卷人三、计算题(每题15分,共60分)1. 已知函数211y x =+的一组数据:求分段线性插值函数,并计算()1.5f 的近似值.计算题1.答案()101x L x -=-()12x L x -=-()10.8L x ⎧-⎪=⎨⎪⎩()1.50.8L =2. 已知线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩(1) 写出雅可比迭代公式、高斯-塞德尔迭代公式;(2) 对于初始值()()00,0,0X =,应用雅可比迭代公式、高斯-塞德尔迭代公式分别计算()1X(保留小数点后五位数字).计算题2.答案1.解 原方程组同解变形为 1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m =高斯-塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩ (0,1...)m =用雅可比迭代公式得()()10.72000,0.83000,0.84000X =用高斯-塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间的近似根 (1)请指出为什么初值应取2 (2)请用牛顿法求出近似根,精确到.计算题3.答案4. 写出梯形公式和辛卜生公式,并用来分别计算积分1011dx x +⎰.计算题4.答案四、证明题(本题10分)确定下列求积公式中的待定系数,并证明确定后的求积公式具有3次代数精确度()()()()1010hhf x dx A f h A f A f h --=-++⎰证明题答案证明:求积公式中含有三个待定系数,即101,,A A A -,将()21,,f x x x =分别代入求积公式,并令其左右相等,得一、 填空(共20分,每题2分)1. 设2.3149541...x *=,取5位有效数字,则所得的近似值x= .2.设一阶差商()()()21122114,321f x f x f x x x x --===---,()()()322332615,422f x f x f x x x x --===--则二阶差商()123,,______f x x x =3. 设(2,3,1)TX =--, 则2||||X = ,=∞||||X 。
数值分析试题及答案

数值分析试题及答案一、选择题(每题3分,共30分)1. 下列关于数值分析的说法,错误的是()。
A. 数值分析是研究数值方法的科学B. 数值分析是研究数值方法的数学理论C. 数值分析是研究数值方法的误差分析D. 数值分析是研究数值方法的数学理论、误差分析及数值方法的实现答案:B2. 在数值分析中,插值法主要用于()。
A. 求解微分方程B. 求解积分方程C. 求解线性方程组D. 通过已知数据点构造一个多项式答案:D3. 线性方程组的解法中,高斯消元法属于()。
A. 直接方法B. 迭代方法C. 矩阵分解方法D. 特征值方法答案:A4. 牛顿法(Newton's method)是一种()。
A. 插值方法B. 拟合方法C. 迭代方法D. 优化方法答案:C5. 在数值分析中,下列哪种方法用于求解非线性方程的根?A. 高斯消元法B. 牛顿法C. 雅可比方法D. 斯托尔-温格尔方法答案:B6. 下列关于误差的说法,正确的是()。
A. 绝对误差总是大于相对误差B. 相对误差总是小于绝对误差C. 误差是不可避免的D. 误差总是可以消除的答案:C7. 在数值分析中,下列哪个概念与数值稳定性无关?A. 条件数B. 截断误差C. 舍入误差D. 插值多项式的阶数答案:D8. 用泰勒级数展开函数f(x)=e^x,下列哪一项是正确的?A. f(x) = 1 + x + x^2/2! + x^3/3! + ...B. f(x) = 1 - x + x^2/2! - x^3/3! + ...C. f(x) = x + x^2/2 + x^3/6 + ...D. f(x) = x - x^2/2 + x^3/6 - ...答案:A9. 插值多项式的次数最多为()。
A. n-1B. nC. n+1D. 2n答案:B10. 下列关于数值积分的说法,错误的是()。
A. 梯形法则是一种数值积分方法B. 辛普森法则是一种数值积分方法C. 龙格法则是数值积分方法中的一种D. 数值积分方法总是精确的答案:D二、填空题(每题3分,共15分)1. 在数值分析中,条件数是衡量问题的______。
数值分析试题及答案

数值分析试题及答案一、单项选择题(每题3分,共30分)1. 线性代数中,矩阵A的逆矩阵记作()。
A. A^TB. A^-1C. A^+D. A*答案:B2. 插值法中,拉格朗日插值多项式的基函数是()。
A. 多项式B. 指数函数C. 正弦函数D. 余弦函数答案:A3. 在数值积分中,梯形规则的误差是()阶的。
A. O(h^2)B. O(h^3)C. O(h)D. O(1/h)答案:A4. 求解线性方程组时,高斯消元法的基本操作不包括()。
A. 行交换B. 行乘以非零常数C. 行加行D. 行除以非零常数答案:D5. 非线性方程f(x)=0的根的迭代法中,收敛的必要条件是()。
A. f'(x)≠0B. f'(x)=0C. |f'(x)|<1D. |f'(x)|>1答案:C6. 利用牛顿法求解非线性方程的根时,需要计算()。
A. 函数值B. 函数值和导数值C. 函数值和二阶导数值D. 函数值、一阶导数值和二阶导数值答案:B7. 矩阵的特征值和特征向量是()问题中的重要概念。
A. 线性方程组B. 特征值问题C. 线性规划D. 非线性方程组答案:B8. 在数值分析中,条件数是衡量矩阵()的量。
A. 稳定性B. 可逆性C. 正交性D. 稀疏性答案:A9. 利用龙格现象说明,高阶插值多项式在区间端点附近可能产生()。
A. 振荡B. 收敛C. 稳定D. 单调答案:A10. 雅可比迭代法和高斯-塞德尔迭代法都是求解线性方程组的()方法。
A. 直接B. 迭代C. 精确D. 近似答案:B二、填空题(每题4分,共20分)11. 线性代数中,矩阵A的行列式记作________。
答案:det(A) 或 |A|12. 插值法中,牛顿插值多项式的基函数是________。
答案:差商13. 在数值积分中,辛普森规则的误差是________阶的。
答案:O(h^4)14. 求解线性方程组时,迭代法的基本思想是从一个初始近似解出发,通过不断________来逼近精确解。
数值分析试题答案

数值分析试题答案一、选择题1. 以下哪个数值方法用于求解线性方程组?A. 牛顿法B. 高斯消元法C. 欧几里得算法D. 拉格朗日插值法答案:B2. 在数值分析中,舍入误差通常是由什么引起的?A. 人为计算错误B. 计算机表示数字的限制C. 测量误差D. 数据输入错误答案:B3. 插值和拟合的区别在于:A. 插值通过所有数据点,而拟合不通过B. 拟合通过所有数据点,而插值不通过C. 插值是线性的,拟合是非线性的D. 插值是精确的,拟合是近似的答案:A4. 以下哪种方法最适合求解非线性方程?A. 雅可比迭代法B. 牛顿-拉弗森方法C. 托马斯算法D. 布雷尔-史密斯算法答案:B5. 在数值分析中,条件数用于衡量什么?A. 方程组解的存在性B. 方程组解的唯一性C. 方程组解的稳定性D. 方程组解的精确性答案:C二、填空题1. 在数值分析中,__________误差指的是由于计算机舍入而产生的误差,而__________误差指的是由于数据不精确或截断而产生的误差。
答案:截断;舍入2. 线性方程组的矩阵表示为__________,其中A是系数矩阵,x是变量向量,b是常数向量。
答案:Ax = b3. 牛顿法求解非线性方程时,需要计算函数的__________。
答案:导数4. 拉格朗日插值法通过构建一个多项式来近似数据点,该多项式的每一段都与数据点的__________相匹配。
答案:切线5. 为了减少数值分析中的误差,通常采用__________方法来提高计算的精度。
答案:增量三、简答题1. 请简述高斯消元法的基本思想及其在求解线性方程组中的应用。
高斯消元法的基本思想是通过行变换将系数矩阵转化为阶梯形矩阵,进而简化方程组的求解过程。
在求解线性方程组时,首先将增广矩阵进行行变换,使得主元下方的元素为零,然后通过回代过程逐步求解出未知数。
2. 描述牛顿-拉弗森方法求解非线性方程的迭代过程。
牛顿-拉弗森方法是一种迭代求解非线性方程的方法。
数值分析习题与答案

第一章绪论习题一1.设x>0,x*的相对误差为δ,求f(x)=ln x的误差限。
解:求lnx的误差极限就是求f(x)=lnx的误差限,由公式(1.2.4)有已知的相对误差满足,而,故即2.有5位有效数字,其误差限,相对误差限有2位有效数字,有5位有效数字,3.(1)(2)解:要使计算较准确,主要是避免两相近数相减,故应变换所给公式。
(1)(2)4.近似数x*=0.0310,是 3 位有数数字。
5.计算取,利用:式计算误差最小。
1. 给定的数值表解:计(误差限,因误差限,故2. 在-4≤x≤4上给出的等距节点函数表,若用二次插值法求的近似值,要使误差不超过,函数表的步长h应取多少?解:用误差估计式(5.8),令因得3. 若,求和.解:由均差与导数关系于是4. 若互异,求的值,这里解:,由均差对称性可知当有而当P=n+1时于是得5. 求证.解:解:只要按差分定义直接展开得6. 已知由式由此可得f(0.23) N3(0.23)=0.23203由余项表达式(5.15)可得由于7. 给定f(x)=cosx的函数表用Newton等距插值公式计算cos 0.048及cos 0.566的近似值并估计误差解:先构造差分表计算,用误差估计由公式(5.17)得其中计算时用Newton后插公式(5.18)误差估计由公式(5.19)得这里8.使,显然,再令由9. 令称为第二类的表达式,并证明是[]上带权解:因10. 用最小二乘法求一个形如的经验公式,使它拟合下列数据,并计算均方误差.解:本题给出拟合曲线,即,故法方程系数解得最小二乘拟合曲线为11.满足条件的插值多项式(2) ,).设为互异节点,=( ),=( ).(4) 设是区间[0,1]上权函数为ρ(x)=x的最高项系数为1的正交多项式序列,其中,则=( ),=( )答:(1)(2)(3)(4)习题1.解 6.13)对)求出,按式()求得2. 用由(6.8)式估计误差,因,故3. 确定下列求积公式中的待定参数,使其代数精确度尽量高,并指明求积公式所具有的代数精确度.(1)(2)(3)解:本题直接利用求积公式精确度定义,则可突出求积公式的参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题( 每题6分,共30分)
1、辛普生求积公式具有 3 次代数精度,其余项表达式为
4(4)
()(),(,)1802
b a b a f a b ζζ---
∈。
2、2
()1,f x x =+则[1,2,3]1,[1,2,3,4]0f f ==。
3、设()(0,1,2
)j l x j n =是n 次拉格朗日插值多项式的插值基函数,则
()j i l x =1,,0,i j i j
=⎧⎨≠⎩(,0,1,2
)i j n =;0
()n
j j l x ==∑ 1 。
4、设()(0,1,2
)j l x j n =是区间[,]a b 上的一组n 次插值基函数。
则插值
型求积公式的代数精度为 至少是n ;插值型求积公式中求积系数j A =
()b
k
a l x dx ⎰
;且0
n
j j A ==∑ b-a 。
5、按四舍五入原则数2.7182818与8.000033具有五位有效数字的近似值分别为 2.7183 和 8.0000 。
二、计算题(每题10分,共计60分,注意写出详细清晰的步骤) 1、已知函数()y f x =的相关数据
由牛顿插值公式求三次插值多项式3()P x ,并计算1()2
P =的值近似值。
(注:要求给出差商表) 解:差商表
由牛顿插值公式:
323332348
()()21,33
141181
()()2()()
12
232232
p x N x x x x p ==
-++≈=-++=
求它的拟合曲线(直线)。
解:设y a bx =+则可得
530052.90
300220003797a b a b +=⎧⎨
+=⎩
于是 1.235,0.15575a b ==,即 1.2350.15575y x =+。
4、已知012113
,,,424
x x x =
== (1)推导以这三点为求积节点在[0,1]上的插值型求积公式
1
0120
113
()()()()424
f x dx A f A f A f ≈++⎰
;
(2)指明求积公式所具有的代数精度;(3)用所求公式计算1
20
x dx ⎰。
解:(1)所求插值型的求积公式形如:
1
0120
113
()()()()424
f x dx A f A f A f ≈++⎰
11112000000102111
0211000101210122020213()()()()224();
1113()()3()()
424413()()()()144();1113()()3()()
2424
()()()()(x x x x x x A l x dx dx dx x x x x x x x x x x A l x dx dx dx x x x x x x x x A l x dx x x x ----====--------====-------==--⎰⎰⎰⎰⎰⎰⎰1100111()()242;
3131)3()()
4442
x x dx dx x --==--⎰⎰ 故101113()[2()()2()]3424
f x dx f f f ≈-+⎰。
(2)所求的求积公式是插值型,故至少具有2次代数精度,再将
34(),f x x x =代入上述公式,可得
1
3333
144440
11113[2()()2()],43424
11113[2()()2()],53424
x dx x dx =
=-+=≠-+⎰⎰
故代数精度是3次。
(3)由2)可得:
1
2
2220
11131[2()()2()]34243
x dx =-+=⎰。
5、用二分法求方程3
()1f x x x =--在区间[1,1.5]内的根时,若要求精确到小数点后二位,(1) 需要二分几次;(2)给出满足要求的近似根。
解:6次;*
1.32x ≈。
6、用列主元消去法解线性方程组
1231231
232346,3525,433032.
x x x x x x x x x ++=⎧⎪
++=⎨⎪++=⎩ 解:
234643303243303235253525352543303223462346433032433032011/441/219011/441/21903/21110002/114/1143303201182380012⎛⎫⎛⎫⎛⎫
⎪ ⎪ ⎪
→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝
⎭⎛⎫⎛⎫
⎪
⎪
→--→-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭
⎛⎫ ⎪→-- ⎪ ⎪⎝⎭ 即123123233433032,13,118238,8,2.2.x x x x x x x x x ++==⎧⎧⎪⎪
-=-⇒=⎨⎨⎪⎪==⎩⎩。
