2018年全国高考新课标1卷文科数学试题解析版
2018年全国高考新课标1卷文科数学试题解析版

卷12018 年普通高等学校招生全国统一考试新课标文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
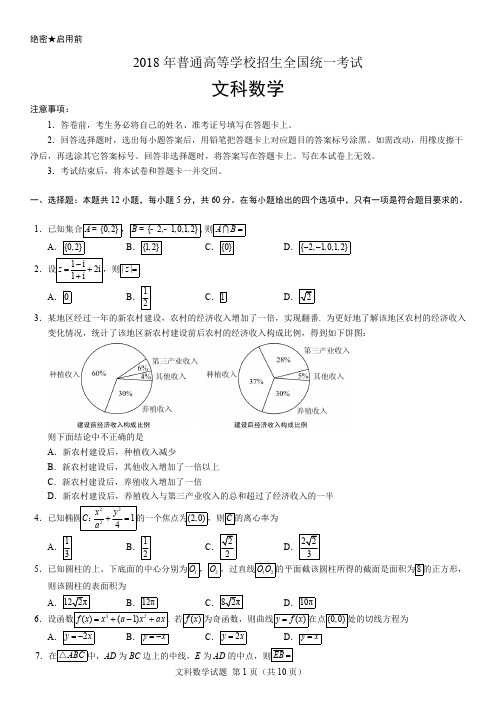
1. 已知集合{0,2}{-21,0,1,2} ,则A HA.{0,2} B .{1,2} C .{0} D .{-21,0,1,2}解析:选A2. 设+2i,贝VA.0 B .C .1 D .解析:选 C +223. 某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设后经济收入构成比例建设前经济收入构成比例则下面结论中不正确的是A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半解析:选A4 .已知椭圆C:+= 1的一个焦点为(2,0),则C的离心率为A. B . C . D .v 2 , 4的平面截该圆柱0O过直线05.已知圆柱2二-4 二2解析:选C的上、下底面的中心分别为O 2121的正方形,则该圆柱的表面积为所得的截面是面积为8 10n D . n C . 8n A . 12n B . 1222 R=12 冗n ,圆柱表面积=2R X 22 n R,解析: 选B 设底面半径为则(2R)=8二23处的切线方(x) +(1)x,若f(x)为奇函数,贝V曲线在点(0,0) 6.设函数f(x)程为.DB. C . 2x 2x A .230)=1 1 二f(x) f ' (x) =3x+1 f ' ( D 解析:选:f(x)为奇函数二故选D=E7.在△中,为边上的中线,为的中点,则+ - C . D . + . - A . B () () - A 解析:选结合图形,22 f(x)=28 .已知函数2,贝V 3 n,最大值为的最小正周期为f(x) . A.B. f(x)的最小正周期为n,最大值为4C. f(x)的最小正周期为2 n,最大值为3D. f(x)的最小正周期为2 n,最大值为4解析:选B f(x)= 2 故选B9.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为A. 2 B . 2 C . 3 D . 2解析:选B所求最短路径即四份之一圆柱侧面展开图对角线的长。
2018全国高考1卷(文科数学)---详细解析(word精美版)

2018年普通高等学校招生全国统一考试(新课标I 卷)文科数学本试卷4页,23小题,满分150分.考试用时120分钟.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合}2,0{=A ,}2,1,0,1,2{--=B ,则=B A ( )A .}2,0{B .}2,1{C .}0{D .}2,1,0,1,2{-- 1.【解析】}2,0{=B A ,选A . 2.设i 2i1i1++-=z ,则=z ( ) A .0 B .21C .1D .2 2.【解析】()()()i i 22i2i 2i 1i 1i 12=+-=+-+-=z ,则1=z,选C .3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面的结论中不正确的是( ) A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半3.【解析】经过一年的新农村建设,农村的经济收入增加了一倍,所以建设前与建设后在比例相同的情况下,建设后的经济收入是原来的2倍,所以建设后种植收入为37%相当于建设前的74%,故选A .4.已知椭圆14:222=+y ax C 的一个焦点为)0,2(,则C 的离心率为( ) 28%5% 30%37%第三产业收入其他收入养殖收入种殖收入建设后经济收入构成比例6%4% 30%60%第三产业收入其他收入养殖收入种殖收入建设前经济收入构成比例A .31 B .21C .22D .3224.【解析】844222=+=+=c b a ,所以离心率22222===a c e ,故选C . 5.已知圆柱的上、下底面的中心分别为21,O O ,过直线21O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A .π212B .π12C .π28D .π105.【解析】易得圆柱的母线长与底面圆的直径均为22,所以圆柱的表面积222⨯⨯=πS 2222⨯+ππ12=,故选B .6.设函数ax x a x x f +-+=23)1()(.若)(x f 为奇函数,则曲线)(x f y =在点)0,0(处的切线方程为( )A .x y 2-=B .x y -=C .x y 2=D .x y =6.【解析】R x ∈,ax x a x ax x a x x f x f +-++--+-=+-2323)1()1()()(2)1(2x a -=0=,则1=a ,则x x x f +=3)(,13)(2+='x x f ,所以1)0(='f ,在点)0,0(处的切线方程为x y =,故选D .7.在ABC ∆中,AD 为BC 边上的中线,E 为AD 的中点,则=EB ( )A .AC AB 4143- B .AC AB 4341- C .AC AB 4143+ D .AC AB 4341+ 7.【解析】AB 4341)(4121)21(21)(21-=-+=+=+=, 则4143-=,故选A . 8.已知函数2sin cos 2)(22+-=x x x f ,则( )A .)(x f 的最小正周期为π,最大值为3B .)(x f 的最小正周期为π,最大值为4C .)(x f 的最小正周期为π2,最大值为3D .)(x f 的最小正周期为π2,最大值为4 8.【解析】252cos 31cos 32)cos 1(cos 2)(222+=+=+--=x x x x x f ,最小正周期为π,最大值为4,故选B .9.某圆柱的高为2,底面周长为16,其三视图如右图. 圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面 上的点N 在左视图上的对应点为B ,则在此圆柱侧面上, 从M 到N 的路径中,最短路径的长度为( )A .172B .52C .3D .29.【解析】将三视图还原成直观图,并沿点A 所在的母线把圆柱侧面展开成如图所示的矩形,从点M 到点N 的运动轨迹在矩形中为直线段时路径最短,长度为52,故选B .A BDE10.在长方体1111D C B A ABCD -中,2==BC AB ,1AC 与平面C C BB 11所成的角为30,则该长方体的体积为( )A .8B .26C .28D .3810.【解析】1AC 与平面C C BB 11所成的角的平面角为301=∠B AC ,因为2==BC AB ,所以3260tan 1== AB B C ,则221=BB ,长方体的体积282222=⨯⨯=V ,故选C .11.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点),2(),,1(b B a A ,且322cos =α,则=-b a ( )A .51B .55C .552D .111.【解析】321cos 22cos 2=-=αα ,65cos 2=∴α,51tan ,61sin 22==∴αα.又角α终边上有两点),2(),,1(b B a A ,则)0(2tan >==ab b a α.555525551422=-=-⇒==∴b a b a ,故选B . 12.已知函数⎩⎨⎧>≤=-0,10,2)(x x x f x ,则满足)2()1(x f x f <+的x 的取值围是( )A .(]1,-∞-B .()+∞,0C .()0,1-D .()0,∞- 12.【解析】方法1:函数)(x f y =的图像如图所示, 则)2()1(x f x f <+即⎩⎨⎧+<<1202x x x ,解得0<x .故选D .方法2:将1-=x 代入)2()1(x f x f <+得)2()0(-<f f ,显然成立,所以排除B 、D ;将21-=x 代入)2()1(x f x f <+得)1()21(-<f f ,显然成立,所以排除A ;故选D .D 1AB C DA 1C 1 B 1M (A二、填空题:本题共4小题,每小题5分,共20分.13.已知函数)(log )(22a x x f +=,若1)3(=f ,则=a .13.【解析】71)9(log )3(2-=⇒=+=a a f .14.若y x ,满足约束条件⎪⎩⎪⎨⎧≤≥+-≤--001022y y x y x ,则y x z 23+=的最大值为 .14.【解析】可行域为ABC ∆及其部,当直线223zx y +-=经过点)0,2(B 时,6max =z .15.直线1+=x y 与圆03222=-++y y x 交于B A ,两点,则=AB . 15.【解析】圆03222=-++y y x 的半径为2=r ,其圆心)1,0(-到直线1+=x y 的距离为222==d ,所以22222=-=dr AB .16.ABC ∆的角C B A ,,的对边分别为c b a ,,.已知C B a B c C b sin sin 4sin sin =+,8222=-+a c b ,则ABC ∆的面积为 .16.【解析】由正弦定理得C B A B C C B sin sin sin 4sin sin sin sin =+,即21sin =A .由根据余弦定理可得8cos 2222==-+A bc a c b ,所以0cos >A ,得23sin 1cos 2=-=A A ,338=bc ,则ABC ∆的面积为3322133821sin 21=⨯⨯==∆A bc S ABC .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)已知数列{}n a 满足11=a ,n n a n na )1(21+=+,设na b nn =. (1)求1b ,2b ,3b ;(2)判断数列{}n b 是否为等比数列,并说明理由; (3)求{}n a 的通项公式.17.【解析】(1)11=a ,4412==∴a a ;1262323=⇒=a a a .11=∴b ,22=b ,43=b .(2)n n a n na )1(21+=+ ,nan a n n 211=+∴+,n n b b 21=∴+,即21=+n n b b .∴数列{}n b 是为等比数列,首项为1,公比为2.(3)由(2)知12-=n n b ,又na b n n =,所以12-⋅=n n n a ,即{}n a 的通项公式为12-⋅=n n n a .18.(12分)如图,在平行四边形ABCM 中,3==AC AB ,90=∠ACM .以AC 为折痕将ACM ∆折起,使点M 达到D 的位置,且DA AB ⊥.(1)证明:平面⊥ACD 平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且DA DQ BP 32==,求三棱锥ABP Q -的体积. 18.【解析】(1)证明: 平行四边形ABCM 中90=∠ACM ,90=∠∴BAC ,即AC AB ⊥.又DA AB ⊥,A DA AC =⊥,⊥∴AB 平面ACD ,⊂AB 平面ABC ,∴平面⊥ACD 平面ABC .(2)DA DQ BP 32== , ∴ABC ABP S S ∆∆=32且点Q 到平面ABC 的距离是点D 到平面ABC 的距离的31. 3==AC AB 且 90=∠ACD ,∴13332127231929292=⨯⨯⨯⨯=⋅⨯===∆---AB S V V V ACD ACD B ABC D ABP Q .19.(12分)某家庭记录了未使用节水龙头50天的日用水量数据(单位:3m )和使用了节水龙头50天的日用水量数据,得到频数分布表如下:未使用节水龙头50天的日用水量频数分布表AP BQMC D使用了节水龙头50天的日用水量频数分布表(2)估计该家庭使用节水龙头后,日用水量小于0.353m 的概率;(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)19.【解析】(1)使用了节水龙头50天的日用水量数据的频数分布直方图:(2)样本中,该家庭使用节水龙头后日用水量小于0.353m 的频率为0.48, 估计该家庭使用节水龙头后,日用水量小于0.353m 的概率为0.48. (3)未使用节水龙头50天的日用水量的平均值约为:频率/组距/3m频率/组距日用水量/3m48.024501]565.02655.0945.0435.0225.0315.0105.0[501=⨯=⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯; 使用了节水龙头50天的日用水量的平均值约为:35.05.17501]555.01645.01035.01325.0515.0105.0[501=⨯=⨯+⨯+⨯+⨯+⨯+⨯⨯, ()45.4735.048.0365=-⨯ ,∴估计该家庭使用节水龙头后,一年能节省47.453m 的水.20.(12分)设抛物线x y C 2:2=,点)0,2(A ,)0,2(-B ,过点A 的直线l 与C 交于N M ,两点. (1)当l 与x 轴垂直时,求直线BM 的方程; (2)证明:ABN ABM ∠=∠.20.【解析】(1)当l 与x 轴垂直时,M 为)2,2(或)2,2(-,则直线BM 的斜率为21或21-,直线BM 的方程为)2(21+=x y 或)2(21+-=x y . (2)方法1:易知直线l 的斜率不为0,不妨设2:+=my x l 且直线BN BM ,的斜率分别为21,k k .由⎩⎨⎧=+=xy my x 222得0422=--my y ,则4,22121-==+y y m y y , 因为21k k +0)4)(4(88)4)(4()(4244222121212122112211=+++-=++++=+++=+++=my my mm my my y y y my my y my y x y x y , 所以直线BN BM ,的倾斜角互补,得ABN ABM ∠=∠. 方法2:设直线BN BM ,的斜率分别为21,k k .①当l 与x 轴垂直时,由(1)知21k k -=,即直线BN BM ,的倾斜角互补,所以ABN ABM ∠=∠; ②当l 不与x 轴垂直时,设),2(:-=x k y l ),(),,(2211y x N y x M .由⎩⎨⎧=-=xy x k y 2)2(2得04)24(2222=++-k x k x k ,则0≠k 且4,24212221=+=+x x k k x x . 因为21k k +0)2)(2()82(2)2(2)2(22212122112211=++-=+-++-=+++=x x x x k x x k x x k x y x y , 所以直线BN BM ,的倾斜角互补,得ABN ABM ∠=∠. 综合①②所述,得ABN ABM ∠=∠.21.(12分)已知函数1ln )(--=x ae x f x.(1)设2=x 是)(x f 的极值点,求a ,并求)(x f 的单调区间; (2)证明:当ea 1≥时,0)(≥x f . 21.【解析】(1))0(1)(>-='x x ae x f x,2221021)2(ea ae f =⇒=-='∴, 又221e a =时,xe e xf x 121)(2-='.由x e e y 221=与xy 1=的图像只有一个交点)21,2(可知0)(='x f 在),0(+∞只有一个解2=x , )2,0(∈x 时,0)(<'x f ,)(x f 为减函数;),2(+∞∈x 时,0)(>'x f ,)(x f 为增函数,即2=x 是)(x f 的极小值点, 则221ea =,)(x f 的减区间为)2,0(,)(x f 的增区间为),2(+∞. (2)方法1:证明:当ea 1≥时,1-≥x x e ae . 令1ln )(1--=-x ex g x ,则xe x g x 1)(1-='-, 令x ex g x h x 1)()(1-='=-,则01)(21>+='-xe x h x ,)(x g y '=为),0(+∞上的增函数. 又01)1()1(0=-='=e g h ,所以)1,0(∈x 时,0)(<'x g ,)(x g 为减函数;),1(+∞∈x 时,0)(>'x g ,)(x g 为增函数,则010)1()(0min =--==e g x g ,即01ln 1≥---x e x .故当ea 1≥时,≥--=1ln )(x ae x f x 01ln 1≥---x e x ,得证. 方法2:证明:当ea 1≥时,1-≥x x e ae . 令x ex g x -=-1)(,则1)(1-='-x e x g ,)1,0(∈x 时,0)(<'x g ,)(x g 为减函数;),1(+∞∈x 时,0)(>'x g ,)(x g 为增函数,则01)1()(0min =-==e g x g ,即x e x ≥-1.又令1ln )(--=x x x h ,则xx x x h 111)(-=-=', )1,0(∈x 时,0)(<'x h ,)(x h 为减函数;),1(+∞∈x 时,0)(>'x h ,)(x h 为增函数,则0101)1()(min =--==h x h ,即1ln +≥x x .综上所述,当ea 1≥时,1ln +≥x ae x,即0)(≥x f . 方法3:证明:令xex x g 1ln )(+=,)0(1ln 1)1(ln )(2>+-=+-='x e x x e x e x e x g x x x x , 令1ln 1)(+-=x x x h ,则22111)(xxx x x h +-=--=', 当0>x 时,0)(<'x h ,)(x h 为减函数.又0101)1(=--=h ,则)1,0(∈x 时,0)(>x h ;),1(+∞∈x 时,0)(<x h .即当)1,0(∈x 时,0)(>'x g ,)(x g 为增函数;当),1(+∞∈x 时,0)(<'x g ,)(x g 为减函数, 所以ex g 1)(max =. 又ea 1≥,即max )(x g a ≥, 所以)(x g a ≥恒成立,即0)(1ln 1ln ≥⇔+≥⇔+≥x f x ae ex a xx,得证.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分. 22.[选修4—4:坐标系与参数方程](10分)在直角坐标系xOy 中,曲线1C 的方程为2||+=x k y .以坐标原点为极点,x 轴正半轴为机轴建立极坐标系,曲线2C 的极坐标方程为03cos 22=-+θρρ.(1)求2C 的直角坐标方程;(2)若1C 与2C 有且仅有三个公共点,求1C 的方程. 22.【解析】(1)θρθρsin ,cos ==y x ,所以2C 的直角坐标方程为03222=-++x y x ; (2)曲线1C :⎩⎨⎧<+-≥+=0,20,2x kx x kx y ,其图像是关于y 轴对称且以)2,0(为端点的两条射线.2C :4)1(22=++y x ,其图像是以)0,1(-为圆心,半径为2的圆.若1C 与2C 有且仅有三个公共点,则0<k 且)0(2≥+=x kx y 与2C 相切(如图). 由2122=++-k k 且0<k ,解得34-=k ,则1C 的方程为:||34+-=x y23.[选修4—5:不等式选讲](10分)已知11)(--+=ax x x f .(1)当1=a 时,求不等式1)(>x f 的解集;(2)若)1,0(∈x 时不等式x x f >)(成立,求a 的取值围. 23.【解析】(1)当1=a 时,11)(--+=x x x f ,则1-≤x 时,2)(-=x f ,则1)(>x f 无解;11<<-x 时,x x f 2)(=,则1)(>x f 的解集为)1,21(;1≥x 时,2)(=x f ,则1)(>x f 的解集为),1[+∞.综上所述,所求解集为),21(+∞.(2))1,0(∈x 时不等式x x f >)(成立,即x ax x >--+11,则11<-ax 成立. 所以xa ax 20111<<⇒<-<-. 因为10<<x 时,有),2(2+∞∈x,所以20≤<a .。
(完整版)2018年高考文科数学(全国I卷)试题及答案,推荐文档
2an n
,即 bn1
2bn
,又 b1
1 ,所以 {bn} 是首项为 1 ,公比为
2
的等比数列.
(3)由(2)可得
an n
2n1 ,所以 an
n 2n1 .
18.解:
(1)由已知可得, BAC 90 , BA AC .
又 BA AD ,所以 AB 平面 ACD .
又 AB 平面 ABC ,
文科数学试题 第 3 页(共 10 页)
19.(12 分)
某家庭记录了未使用节水龙头 50 天的日用水量数据(单位: m3 )和使用了节水龙头 50 天的日用水量数据, 得到频数分布表如下:
未使用节水龙头 50 天的日用水量频数分布表
日用水量 [0,0.1) [0.1,0.2 [0.2,0.3 [0.3,0.4 [0.4,0.5 [0.5,0.6 [0.6,0.7
2
2
(2)当 l 与 x 轴垂直时,AB 为 MN 的垂直平分线,所以 ABM ABN .
当 l 与 x 轴不垂直时,设 l 的方程为 y k(x 2) (k 0) , M (x1, y1) , N (x2 , y2 ) ,则 x1 0, x2 0 .
由
y k(x
y
2
2x
2),
得
ky 2
则 | a b |
1 A.
5
5 B.
5
25 C.
5
D. 1
12.设函数
f
(x)
2x ,
1,
x ≤ 0, 则满足 f (x 1) f (2x) 的 x 的取值范围是 x 0,
A. (, 1]
B. (0,)
C. (1, 0)
最新2018年全国高考新课标1卷文科数学试题(解析版)

2018年普通高等学校招生全国统一考试新课标1卷文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={0,2},B={-2,-1,0,1,2},则A ∩B=A .{0,2}B .{1,2}C .{0}D .{-2,-1,0,1,2} 解析:选A2.设z=1-i1+i+2i ,则|z|=A .0B .12 C .1 D . 2解析:选C z=1-i1+i+2i=-i+2i=i3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例 建设后经济收入构成比例则下面结论中不正确的是A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 解析:选A4.已知椭圆C :x 2a 2+y 24=1的一个焦点为(2,0),则C 的离心率为A .13B .12C .22D .223解析:选C ∵ c=2,4=a 2-4 ∴a=2 2 ∴e=225.已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π解析:选B 设底面半径为R,则(2R)2=8 ∴R=2,圆柱表面积=2πR ×2R+2πR 2=12π 6.设函数f(x)=x 3+(a-1)x 2+ax ,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为 A .y=-2x B .y=-x C .y=2x D .y=x解析:选D ∵f(x)为奇函数 ∴a=1 ∴f(x)=x 3+x f′(x)=3x 2+1 f′(0)=1 故选D 7.在ΔABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →= A .34AB → - 14AC →B . 14AB → - 34AC →C .34AB → + 14AC →D . 14AB → + 34AC →解析:选A 结合图形,EB →=- 12(BA →+BD →)=- 12BA →-14BC →=- 12BA →-14(AC →-AB →)=34AB → - 14AC →8.已知函数f(x)=2cos 2x-sin 2x+2,则A .f(x)的最小正周期为π,最大值为3B .f(x) 的最小正周期为π,最大值为4C .f(x) 的最小正周期为2π,最大值为3D .f(x)的最小正周期为2π,最大值为4 解析:选B f(x)= 32cos2x+52故选B9.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .217B .2 5C .3D .2解析:选B 所求最短路径即四份之一圆柱侧面展开图对角线的长10.在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为300,则该长方体的体积为 A .8B .6 2C .8 2D .8 3解析:选C ∵AC 1与平面BB 1C 1C 所成的角为300,AB=2 ∴AC 1=4 BC 1=2 3 BC=2 ∴CC 1=2 2V=2×2×22=8 211.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=23,则|a-b|=A .15B .55C .255D .1解析:选B ∵cos2α=23 2cos 2α-1=23 cos 2α=56 ∴sin 2α=16 ∴tan 2α=15又|tan α|=|a-b| ∴|a-b|=5512.设函数f(x)= ⎩⎨⎧2-x,x ≤01,x>0,则满足f(x+1)< f(2x)的x 的取值范围是A .(-∞,-1]B .(0,+ ∞)C .(-1,0)D .(-∞,0)解析:选D x ≤-1时,不等式等价于2-x-1<2-2x,解得x<1,此时x ≤-1满足条件 -1<x ≤0时,不等式等价于1<2-2x , 解得x<0, 此时-1<x<0满足条件 x>0时,1<1不成立 故选D二、填空题(本题共4小题,每小题5分,共20分)13.已知函数f(x)=log 2(x 2+a),若f(3)=1,则a=________. 解析:log 2(9+a)=1,即9+a=2,故a=-714.若x ,y 满足约束条件⎩⎪⎨⎪⎧x-2y-2≤0x-y+1≥0 y ≤0,则z=3z+2y 的最大值为_____________.解析:答案为615.直线y=x+1与圆x 2+y 2+2y-3=0交于A,B 两点,则|AB|=________. 解析:圆心为(0,-1),半径R=2,线心距d=2,|AB|=2R 2-d 2=2 216.△ABC 的内角A,B,C 的对边分别为a,b,c ,已知bsinC+csinB=4asinBsinC ,b 2+c 2-a 2=8,则△ABC 的面积为________.解析:由正弦定理及bsinC+csinB=4asinBsinC 得2sinBsinC=4sinAsinBsinC ∴sinA=12由余弦定理及b 2+c 2-a 2=8得2bccosA=8,则A 为锐角,cosA=32, ∴bc=833∴S=12bcsinA=233三、解答题:共70分。
2018全国高考新课标1卷文科数学试题卷解析版

2018年普通高等学校招生全国统一考试新课标1卷文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={0,2},B={-2,-1,0,1,2},则A ∩B= A .{0,2} B .{1,2} C .{0} D .{-2,-1,0,1,2} 解析:选A2.设z=1-i1+i+2i ,则|z|=A .0B .12 C .1 D . 2解析:选C z=1-i1+i+2i=-i+2i=i3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例 建设后经济收入构成比例则下面结论中不正确的是A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 解析:选A4.已知椭圆C :x 2a 2+y 24=1的一个焦点为(2,0),则C 的离心率为A .13B .12C .22D .223解析:选C ∵ c=2,4=a 2-4 ∴a=2 2 ∴e=225.已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π解析:选B 设底面半径为R,则(2R)2=8 ∴R=2,圆柱表面积=2πR ×2R+2πR 2=12π 6.设函数f(x)=x 3+(a-1)x 2+ax ,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为 A .y=-2x B .y=-x C .y=2x D .y=x解析:选D ∵f(x)为奇函数 ∴a=1 ∴f(x)=x 3+x f′(x)=3x 2+1 f′(0)=1 故选D 7.在ΔABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →= A .34AB → - 14AC →B . 14AB → - 34AC →C .34AB → + 14AC →D . 14AB → + 34AC →解析:选A 结合图形,EB→=- 12(BA →+BD →)=- 12BA →-14BC →=- 12BA →-14(AC →-AB →)=34AB → - 14AC → 8.已知函数f(x)=2cos 2x-sin 2x+2,则A .f(x)的最小正周期为π,最大值为3B .f(x) 的最小正周期为π,最大值为4C .f(x) 的最小正周期为2π,最大值为3D .f(x)的最小正周期为2π,最大值为4 解析:选B f(x)= 32cos2x+52故选B9.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .217B .2 5C .3D .2解析:选B 所求最短路径即四份之一圆柱侧面展开图对角线的长10.在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为300,则该长方体的体积为 A .8B .6 2C .8 2D .8 3解析:选C ∵AC 1与平面BB 1C 1C 所成的角为300 ,AB=2 ∴AC 1=4 BC 1=2 3 BC=2 ∴CC 1=2 2 V=2×2×22=8 211.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=23,则|a-b|= A .15B .55C .255D .1解析:选B ∵cos2α=23 2cos 2α-1=23 cos 2α=56 ∴sin 2α=16 ∴tan 2α=15又|tan α|=|a-b| ∴|a-b|=5512.设函数f(x)= ⎩⎨⎧2-x,x ≤01,x>0,则满足f(x+1)< f(2x)的x 的取值范围是A .(-∞,-1]B .(0,+ ∞)C .(-1,0)D .(-∞,0)解析:选D x ≤-1时,不等式等价于2-x-1<2-2x ,解得x<1,此时x ≤-1满足条件 -1<x ≤0时,不等式等价于1<2-2x , 解得x<0, 此时-1<x<0满足条件 x>0时,1<1不成立 故选D二、填空题(本题共4小题,每小题5分,共20分) 13.已知函数f(x)=log 2(x 2+a),若f(3)=1,则a=________. 解析:log 2(9+a)=1,即9+a=2,故a=-714.若x ,y 满足约束条件⎩⎪⎨⎪⎧x-2y-2≤0 x-y+1≥0 y ≤0,则z=3z+2y 的最大值为_____________.解析:答案为615.直线y=x+1与圆x 2+y 2+2y-3=0交于A,B 两点,则|AB|=________. 解析:圆心为(0,-1),半径R=2,线心距d=2,|AB|=2R 2-d 2=2 216.△ABC 的内角A,B,C 的对边分别为a,b,c ,已知bsinC+csinB=4asinBsinC ,b 2+c 2-a 2=8,则△ABC 的面积为________.解析:由正弦定理及bsinC+csinB=4asinBsinC 得2sinBsinC=4sinAsinBsinC ∴sinA=12由余弦定理及b 2+c 2-a 2=8得2bccosA=8,则A 为锐角,cosA=32, ∴bc=833∴S=12bcsinA=233三、解答题:共70分。
2018年普通高等学校招生全国统一考试(全国新课标Ⅰ卷)文科数学试题及详解

2018年普通高等学校招生全国统一考试(全国新课标 1卷)文科数学注意事项:1 •答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2•回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如 需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3 •考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有 项是符合题目要求的。
1 •已知集合 A 」0 ,2 , B-1, 0, 1,2,贝 V A B =()A •〔0 , 2?B .臼,2/C •心D • : -2 , -1 ,0,1, 2; 1. 答案:A解答:A 「B={0,2},故选 A.1 _i.2.设 z2i ,则 z =()1 +i 1 LA • 0B •C . 1D . . 22 2. 答案:C解答:T z = _ +2i=i , — z=1,.••选 C1+i3•某地区经过一年的新农村建设,农村的经济收入增加了一倍•实现翻番•为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比 例•得到如下饼图:建没丽辻济收入构成比例则下面结论中不正确的是()A •新农村建设后,种植收入减少B •新农村建设后,其他收入增加了一倍以上C ・新农村建设后,养殖收入增加了一倍D •新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半3。
答案:A解答:由图可得,A 选项,设建设前经济收入为x ,种植收入为0.6x.建设后经 济收入则为2x ,种植收入则为0.37 2x = 0.74x ,种植收入较之前增加.一八业收入菲殖收入种伙收入其他收入理设后经济牧入构戍比鬪第二产业收入芥怕收入种植收入其他枚入4.已知椭圆2C :笃2的一个焦点 为(2,0),则C 的离心率为 ()a4A . 11 B.-C .迈D 巫322'34、答案: C送解答:知c =2,• a 2 二b 2c 2 =8, a = 2 2 , • 离心率e -25•已知圆柱的上、下底面的中心分别为 O i , O 2,过直线OQ 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为() A • 12 ..2 n B . 12 n C . 8、2n D • 1° n5.答案:B解答:截面面积为8,所以高h =2、、2,底面半径 ^.2,所以表面积为S hM (..2)2 2 2-2 2.2 =12二.6.设函数f xa -1 x 2 ax .若f x 为奇函数,则曲线y = f x 在点0, 0处的切线方程为()A . y - -2xB . y =-xC . y=2xD . y=x6.答案:D解答:••• f (x)为奇函数,•. f (-x) = -f (x),即 a =〔,... f(x) =x ‘ +x ,•. W'1 =, •••切线方程为:y =x ,•选D.' ' ' '1 1[(AB AC)] AB 二 2 22 2& 已知函数 f x =2cos x-sin x 2,则()A . f(x )的最小正周期为 n 最大值为3B . f (x )的最小正周期为 n ,最大值为4C . f(x )的最小正周期为2n ,最大值为3D . f (x )的最小正周期为2 n ,最大值为48、答案:B解答:f (x) =2cos 2 x -(1 - cos 2 x) 2 -3cos 2 x 1 •最小正周期为兀,最大值为4.7.在△ ABC 中,AD 为BC 边上的中线, E 为AD 的中点,贝U EB 二()一一 1 一一- _ A 3AB -- AC '4 41 — _■ 3 — _■B 一 AB - 3 AC C*3 1 一一-1 1 ^3 ——-—13 AB - AC D -AB 3 AC3 AB - 1 AC .4 47.答案:A2AD AB9.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N 的路径中,最短路径的长度为()A . 2.17B . 2.5 C. 3 D . 29. 答案:B解答:三视图还原几何体为一圆柱,如图,将侧面展开,最短路径为M,N连线的距离,所以MN — 42 22=2.5,所以选B.10.在长方体ABCD—ABC I D I中,AB = BC=2,AG与平面BBGC所成的角为30°,则该长方体的体积为()A . 8 B. 6、、2 C. &、2 D. 8 310. 答案:C解答:连接AG和BG,••• AC1与平面BB1GC所成角为30,••• • AC1^30,——二ta 门30弋0=2.3,• CG • V=2 2 ,•选 C.BC111. 已知角?的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点 A 1, a,j 2B (2,b ),且cos2a = 3,则a —b =()31 A.—511. 答案:B2x W 012. 设函数f x ,则满足f x ・1 ::: f 2x 的x 的取值范围是()1,x>0A .」:,-1 1B . 0,::C . -1, 0D . -二,012. 答案:D1 1解答:取x 二匚,贝U 化为f (2^:: f (_1),满足,排除A ,B ; 取x 一1,则化为f (°)” f (一2),满足,排除C ,故选D .二、填空题:本题共 4小题,每小题5分,共20分。
2018年高考新课标卷1文科数学试题解析

2018年普通高等学校招生全国统一考试(新课标卷I)文科数学试题解析一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=A.{0,2} B.{1,2} C.{0} D.{-2,-1,0,1,2}解析:选A2.设z=1-i1+i+2i,则|z|=A.0 B.12C.1 D. 2解析:选C z=1-i1+i+2i=-i+2i=i3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例建设后经济收入构成比例则下面结论中不正确的是A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半解析:选A4.已知椭圆C :x 2a 2+y24=1的一个焦点为(2,0),则C 的离心率为A .13B .12C .22D .223解析:选C ∵ c=2,4=a 2-4 ∴a=2 2 ∴e=225.已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π解析:选 B. 设底面半径为R,则(2R)2=8 ∴R=2,圆柱表面积=2πR ×2R+2πR 2=12π6.设函数f(x)=x 3+(a-1)x 2+ax ,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为 A .y=-2xB .y=-xC .y=2xD .y=x解析:选 D ∵f(x)为奇函数 ∴a=1 ∴f(x)=x 3+x f ′(x)=3x 2+1 f ′(0)=1 故选D7.在ΔABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →=A .34AB → - 14AC →B . 14AB → - 34AC →C .34AB → + 14AC →D . 14AB → + 34AC →解析:选A 结合图形,EB →=- 12(BA →+BD →)=- 12BA →-14BC →=- 12BA →-14(AC →-AB →)=34AB → - 14AC →8.已知函数f(x)=2cos 2x-sin 2x+2,则 A .f(x)的最小正周期为π,最大值为3 B .f(x)的最小正周期为π,最大值为4 C .f(x)的最小正周期为2π,最大值为3 D .f(x)的最小正周期为2π,最大值为4解析:选B f(x)= 32cos2x+52故选B9.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .217B .2 5C .3D .2解析:选B 所求最短路径即四份之一圆柱侧面展开图对角线的长.10.在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为300,则该长方体的体积为 A .8B .6 2C .8 2D .8 3解析:选C ∵AC 1与平面BB 1C 1C 所成的角为300 ,AB=2 ∴AC 1=4 BC 1=2 3 BC=2 ∴CC 1=2 2. V=2×2×22=8 2.11.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=23,则|a-b|=A .15B .55C .255D .1解析:选B ∵cos2α=23 2cos 2α-1=23 cos 2α=56 ∴sin 2α=16 ∴tan 2α=15又|tan α|=|a-b| ∴|a-b|=5512.设函数f(x)= ⎩⎨⎧2-x,x ≤01,x>0,则满足f(x+1)< f(2x)的x 的取值范围是A .(-∞,-1]B .(0,+ ∞)C .(-1,0)D .(-∞,0)解析:选D x ≤-1时,不等式等价于2-x-1<2-2x ,解得x<1,此时x ≤-1满足条件 -1<x ≤0时,不等式等价于1<2-2x , 解得x<0, 此时-1<x<0满足条件x>0时,1<1不成立 故选D.二、填空题(本题共4小题,每小题5分,共20分) 13.已知函数f(x)=log 2(x 2+a),若f(3)=1,则a=________. 解析:log 2(9+a)=1,即9+a=2,故a=-714.若x ,y 满足约束条件⎩⎪⎨⎪⎧x-2y-2≤0x-y+1≥0 y ≤0 ,则z=3z+2y 的最大值为_____________.解析:答案为615.直线y=x+1与圆x 2+y 2+2y-3=0交于A,B 两点,则|AB|=________. 解析:圆心为(0,-1),半径R=2,线心距d=2,|AB|=2R 2-d 2=2 216.△ABC 的内角A,B,C 的对边分别为a,b,c ,已知bsinC+csinB=4asinBsinC ,b 2+c 2-a 2=8,则△ABC 的面积为________.解析:由正弦定理及bsinC+csinB=4asinBsinC 得2sinBsinC=4sinAsinBsinC ∴sinA=12由余弦定理及b 2+c 2-a 2=8得2bccosA=8,则A 为锐角,cosA=32, ∴bc=833∴S=12bcsinA=233三、解答题:共70分。
2018年全国统一高考数学试卷(文科)(新课标ⅰ)(含解析版)

关注公众号”一个高中僧“获取更多高中资料
第 3 页(共 28 页)
18.(12 分)如图,在平行四边形 ABCM 中,AB=AC=3,∠ACM=90°,以 AC 为 折痕将△ACM 折起,使点 M 到达点 D 的位置,且 AB⊥DA.
(1)证明:平面 ACD⊥平面 ABC; (2)Q 为线段 AD 上一点,P 为线段 BC 上一点,且 BP=DQ= DA,求三棱锥
A.12 π
B.12π
C.8 π
D.10π
【考点】LE:棱柱、棱锥、棱台的侧面积和表面积. 菁优网版权所有
【专题】11:计算题;35:转化思想;49:综合法;5F:空间位置关系与距离.
【分析】利用圆柱的截面是面积为 8 的正方形,求出圆柱的底面直径与高,然后
求解圆柱的表面积.
【解答】解:设圆柱的底面直径为 2R,则高为 2R,
(2)估计该家庭使用节水龙头后,日用水量小于 0.35m3 的概率; (3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按 365 天计算,
同一组中的数据以这组数据所在区间中点的值作代表)
20.(12 分)设抛物线 C:y2=2x,点 A(2,0),B(﹣2,0),过点 A 的直线 l 与 C 交于 M,N 两点.
参考答案与试题解析
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选 项中,只有一项是符合题目要求的。
1.(5 分)已知集合 A={0,2},B={﹣2,﹣1,0,1,2},则 A∩B=( )
A.{0,2}
B.{1,2}
C.{0}
D.{﹣2,﹣1,0,1,2}
【考点】1E:交集及其运算. 菁优网版权所有
问题解决问题的能力.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卷2018年普通高等学校招生全国统一考试新课标1 文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净2 后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
分。
在每小题给出的四个选项中,只有一项是符合题目要605分,共一、选择题:本题共12小题,每小题求的。
B=A∩1.已知集合A={0,2},B={-2,-1,0,1,2},则{-2,-1,0,1,2} C.{0} D..A.{0,2} B{1,2}解析:选A1-i|z|= z=2.设,则+2i1+i12A.0 B.C.1 D.21-i+2i=-i+2i=i解析:选C z=1+i为更好地了解该地区农村的经济.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,3 收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例建设后经济收入构成比例则下面结论中不正确的是.新农村建设后,种植收入减少A .新农村建设后,其他收入增加了一倍以上B .新农村建设后,养殖收入增加了一倍C D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半A解析:选22yx C的离心率为1的一个焦点为(2,0),则4.已知椭圆C=:+24a22211 B. D C..A.322322 a=2-4 ∴2 e=∴解析:选C ∵c=2,4=a2的正方形,的平面截该圆柱所得的截面是面积为8,过直线OO5.已知圆柱的上、下底面的中心分别为O,O2211则该圆柱的表面积为.12πC.82 BπD.10π2.A12π22π=12Rπ2R+2×Rπ=2圆柱表面积2,R=∴=8 (2R)则R,设底面半径为B 解析:选.23 (0,0)处的切线方程为f(x)+ax,若为奇函数,则曲线y=f(x)在点6.设函数f(x)=x+(a-1)xy=xy=2x D.B.y=-x C..Ay=-2x23D 0)=1 故选=3x ∴a=1 ∴f(x)=x+x f′(x)+1 f′(为奇函数解析:选D ∵f(x)→= AD为BC边上的中线,E为AD的中点,则EBABC7.在Δ中,31331113→→→→→→→→AC + C..DAB + B..ACABAB --AC AC AB A444444441311111→→→→→→→→→→-ACABBA-解析:选A 结合图形,(BAEB=- +BD)=- (ACBA--ABBC=- )=444224222 x+28.已知函数f(x)=2cosx-sin,则3 A.f(x)的最小正周期为π,最大值为4 B.π,最大值为f(x) 的最小正周期为3 C .f(x) π,最大值为的最小正周期为24 2D .f(x)的最小正周期为π,最大值为53B cos2x+ 故选解析:选B f(x)= 22,圆柱表面在正视图上的对应点为A ,其三视图如图.圆柱表面上的点.某圆柱的高为2,底面周长为16M9 的路径中,最短路径的长度为M 到N 在左视图上的对应点为B ,则在此圆柱侧面上,从N 上的点2 D C ..3 A .217 B .25所求最短路径即四份之一圆柱侧面展开图对角线的长解析:选BC 所成的角为30中,DAB=BC=2,,则该长方体的体积为AC 与平面BB10.在长方体ABCD -ACBC111111138 D8 C .2 A .8 B622 ∴CC=23 BC=2 ,AB=2 ∴AC=4 BC=2BB 解析:选C ∵AC 与平面CC 所成的角为301111112×22=8 V=2×22,cos2α=A(1,a),B(2,b),且已知角α的顶点为坐标原点,11.始边与x 轴的非负半轴重合,终边上有两点3|a -b|= 则55211D . . C . A . B555225112222解析:选B ∵cos2α= 2cos α-1= cos α= ∴sin α= ∴tan α= 336655 |a -b|=α|=|a -b| ∴又|tan5-x02,x ≤??,则满足f(x+1)< f(2x)的x的取值范围是12.设函数f(x)= ?x>0 1,??A .(-∞,-1] B .(0,+ ∞) C .(-1,0) D .(-∞,0)-x -1-2x解析:选D x ≤-1时,不等式等价于2<2,解得x<1,此时x ≤-1满足条件-2x-1<x ≤0时,不等式等价于1<2, 解得x<0, 此时-1<x<0满足条件D故选 不成立1<1时, x>0.4小题,每小题5分,共20分)二、填空题(本题共2+a),若f(3)=1,则a=________.13.已知函数f(x)=log(x 2a=-7解析:9+a=2,故log (9+a)=1,即2x -2y -2≤??? ≥0x -y+1 .若x ,y 满足约束条件_____________.则z=3z+2y 的最大值为, 14??0 ≤ y 6解析:答案为22.A,B 两点,则|AB|=________15.直线y=x+1与圆x+y+2y -3=0交于222-d 2,|AB|=2解析:圆心为(0,-1),半径R=2,线心距Rd==2222的面积=8,则△ABC 的内角A,B,C 的对边分别为a,b,c ,已知bsinC+csinB=4asinBsinC ,b+c -a16.△ABC 为________.1 ∴sinA=2sinBsinC=4sinAsinBsinC 解析:由正弦定理及bsinC+csinB=4asinBsinC 得 2383222bc=为锐角, cosA=∴, 由余弦定理及b+c -a=8得2bccosA=8,则A23321 bcsinA=∴S=32题为必考题,每个试题考生都17~2170分。
解答应写出文字说明、证明过程或演算步骤。
第三、解答题:共 23题为选考题,考生根据要求作答。
必须作答。
第22、 分。
(一)必考题:共60 分)17.(12a n.b=,设{a}满足a=1,na=2(n+1)a 已知数列nn+11nnn ;,b (1)求b,b 321是否为等比数列,并说明理由;(2)判断数列{b}n}(3)求{a 的通项公式.n2(n+1) 1a .)由条件可得a=解:(nn+1n a=4.,而将n=1代入得,a=4aa=1,所以,2211.=3a 将n=2代入得,a ,所以,a=12332从而b=1,b=2.b=4,312的等比数列.是首项为}1,公比为2)(2{b n2aa nn+11,所以{b}是首项为,公比为2的等比数列.b=2b 由条件可得=,即b ,又=1nn1n+1nn+1ann -1n -1.·)可得3()由(2=2,所以an=n2n 18.(分)120的位置,且D 到达点折起,使点为折痕将△∠中,如图,在平行四边形ABCMAB=AC=3,ACM=90,以ACACMM ⊥ABDA . ABC;⊥平面)证明:平面(1ACD2 (上一点,且为线段BCPAD为线段Q2)上一点,,求三棱锥DABP=DQ=Q-ABP 的体积.3..ACBAC=90°,BA⊥.解:18(1)由已知可得,∠.,所以AB⊥平面ACD又BA⊥AD? ABC⊥平面.又AB平面ABC,所以平面ACDDA=32.)由已知可得,DC=CM=AB=3(,22又BP=DQ=DA,所以BP=22.31作QE⊥AC,垂足为E,则QE//DC,且QE=DC.3由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,QE=1.1110因此,三棱锥Q-ABP的体积为V=×QE×S=×1××3×22×sin45=1ABPΔ33219.(12分)3某家庭记录了未使用节水龙头50天的日用水量数据(单位:m)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:未使用节水龙头50天的日用水量频数分布表日用水量[0,0.1)[0.1,0.2) [0.2,0.3) [0.3,0.4) [0.4,0.5) [0.5,0.6) [0.6,0.7)3 频数1 24 9265使用了节水龙头50天的日用水量频数分布表[0.4,0.5)[0.3,0.4)[0.5,0.6)[0.1,0.2)日用水量[0,0.1)[0.2,0.3)5101135频16(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:3 0.35 m)估计该家庭使用节水龙头后,日用水量小于的概率;(2天计算,同一组中的数据以这组数据所3653()估计该家庭使用节水龙头后,一年能节省多少水?(一年按在区间中点的值作代表.))1(解:天日用水量小于0.35m3的频率为(2)根据以上数据,该家庭使用节水龙头后50 ×0.05=0.48,0.2×0.1+1×0.1+2.6×0.1+2 的概率的估计值为0.48.因此该家庭使用节水龙头后日用水量小于0.35m3 )该家庭未使用节水龙头50天日用水量的平均数为(315)=0.48×26+0.65××3+0.25×2+0.354+0.45×x9+0.55=(0.05×1+0.15×150 该家庭使用了节水龙头后50天日用水量的平均数为15)=0.35×10+0.45×16+0.551+0.15×5+0.25×13+0.35×x=(0.05×2503 365=47.45(m).估计使用节水龙头后,一年可节省水(0.48-0.35)×(12分)20.2 N两点.与C交于M,C:y设抛物线=2x,点A(2,0),B(-2,0),过点A的直线l 的方程;l与x轴垂直时,求直线BM(1)当.2)证明:∠ABM=∠ABN(,–2).2解:(1)当l与x轴垂直时,l的方程为x=2,可得M的坐标为(,2)或(211 .x+1或y=- x-1的方程为所以直线BMy=22 ABM=∠ABN.轴垂直时,(2)当l与xAB为MN的垂直平分线,所以∠>0.xy),N(,y),则x>0,x,的方程为当l与x轴不垂直时,设ly=k(x-2)( (k≠0)),M(x212211222.4k=0–,可知y+y,yy=–4=2x代y=k(x-2)入y消去x得ky–2y2211k)yyxy+xy+2(y+y21111222.①+=BN的斜率之和为k+k=直线BM,BNBM+2)+2(xx+2)( x+2x2112yy21的表达式代入①式分子,可得+2及+y,yy=将+2,x=221211kk-8+8y+4k(y)+y2y221 =0y)=+2(y+=+x xy211221kk .ABM=∠ABN=0+k,可知BM,BN的倾斜角互补,所以,∠k所以BNBM分)(1221.x -lnx-1.已知函数f(x)=ae f(x),并求的单调区间;f(x)1()设x=2是的极值点.求a1(2)证明:当a≥时,f(x)≥0.e1x–.′(x)=ae(x)的定义域为(0,+∞),f 解:(1)f x1 .)=0,所以a=由题设知,f ′(222e111xx.)(从而fx)==e- e-lnx-1,f ′(x22x2e2e .′(x)>0x)<0;当x>2时,f 当0<x<2时,f ′(∞)单调递增.)单调递减,在(2,+f(x)在(0,2所以x e1 )≥-lnx-1.)当a≥时,f(x(2ee xx1ee ′(x)= –,则设g(x)= -lnx-1g xee (gx)的最小值点.<0;当x>1时,g′(x)>0.所以x=1是′(当0<x<1时,gx))=0.故当x>0时,g(x)≥g(11 ≥0.因此,当a≥时,f(x)e 23题中任选一题作答。
