摆火柴(几何图形系列题)
一年级数学火柴棒练习题

一年级数学火柴棒练习题火柴棒练习题是一种简单而有趣的数学教学工具,它可以帮助小学一年级的学生学习基本的数学概念和运算。
通过利用火柴棒进行计算和构建图形,学生可以在实践中提高他们的逻辑思维和问题解决能力。
本文将介绍一些适用于一年级学生的数学火柴棒练习题。
一、数的认知1. 使用火柴棒表示数字1-10,并理解每个数字的数值含义。
2. 利用火柴棒完成简单的加法和减法运算,例如:1+1=?、2-1=?等。
二、形状和图形1. 利用火柴棒构建不同的几何形状,如正方形、长方形、三角形等,并给出它们的名称。
2. 利用火柴棒组建一个简单的拼图,让学生根据火柴棒的形状还原图案。
三、数的排列组合1. 给定一些火柴棒,学生通过排列组合的方式尽可能多地制作不同长度的数字。
2. 让学生利用相同数量的火柴棒,尽可能多地组成不同的几何形状。
四、数的比较1. 给出两组火柴棒,让学生判断哪一组更长或更短,并用相应的符号 (<, >, =) 进行比较。
2. 利用火柴棒构建不同长度的线段,让学生判断哪一个线段更长或更短。
五、简单方程1. 使用火柴棒表示简单方程,并让学生解决对应的问题,如:?+1=3,学生需要找到正确的数字,填入问题中的问号处。
2. 让学生通过移动火柴棒的方式使等式成立,如:2+2=4,学生需要移动一个火柴棒,使等式成立。
六、数的倍数1. 利用火柴棒构建一个确定长度的数,让学生找到这个数的不同倍数。
2. 给定一个数,让学生利用火柴棒构建这个数的不同整倍数。
通过以上的火柴棒练习题,一年级的学生可以在锻炼手眼协调能力的同时,巩固数学基本概念,并培养逻辑思维和问题解决能力。
教师可以根据学生掌握情况逐渐增加难度,引导学生逐步提高对数学的理解和运用能力。
总结起来,火柴棒练习题能够帮助一年级学生在数学学习中更好地理解和运用知识,同时提高他们的思维能力和问题解决能力。
教师应根据学生的实际情况和学习进度,设计出合适的火柴棒练习题,让学生在实践中感受到数学的趣味和实用性。
小学奥数题目-二年级-数字敏感度类-火柴棍游戏之进阶

火柴棍游戏之进阶火柴棍除了可以摆成一些数字和运算符号,还可以摆出几何图形如正三角形、正方形、菱形、正多边形和一些物品的形状.通过移动火柴棍,可以用它来做有趣的图形变化游戏。
火柴游戏大体分为两种:一种是摆图形和变换图形;一种是变换算式。
这一讲我们先介绍变换图形的游戏。
题型:摆一个正方形,至少需要4根火柴棍.(1)摆两个大小相同的正方形,至少需要几根火柴棍?(2)摆三个大小相同的正方形,至少需要几根火柴棍?(3)摆五个正方形,最少需要几根火柴棍?1.1.(选择题)你能用10根火柴棒摆成3个相同的正方形吗?A、能B、不能C、A和B都有可能D、以上答案均不对2.2.(单选题)你能用9根火柴棒拼出4个相同的三角形吗?A、不能B、能C、A和B都有可能D、以上答案均不对用四根火柴棍可以拼成1个边长是1根火柴棍的正方形,怎样用12根火柴棍拼出6个边长为1根火柴的正方形呢?1.1.(选择题)你能用7根火柴棒摆成3个相同的三角形吗?A、不能B、能C、A和B都有可能D、以上答案均不对2.2.(选择题)用6根火柴,拼出4个相同的三角形。
问能不能?A、能B、不能C、A和B都有可能D、以上答案均不对移动3根火柴棒,使这条鱼的鱼头朝右,鱼尾朝左。
1.1.(单选题)由10根火柴棒摆成的两个倒扣杯子,如图所示,请你移动4根火柴,把杯口正过来。
问能不能?A、不能B、能C、A和B都有可能D、以上答案均不对2.2.(单选题)用10根火柴棍摆成向上飞的蝙蝠图形,如图所示。
试移动三根火柴,使它变成向下飞的蝙蝠图形。
问能不能?A、能B、不能C、A和B都有可能D、以上答案均不对右图所示为一个倒放着且缺一条腿的椅子,请你移动两根火柴棍把椅子正过来。
1.1.(单选题)水井的计量单位是“口”,人们常说“一口井”、“两口井”等等,图中是用16根火柴排成的一个“井”字。
请移动6根火柴,使它变成两个同样大小的“口”字。
问能不能?A、能B、不能C、A和B都有可能D、以上答案均不对2.2.用火柴棒搭成小猪图,你能移动火柴棒使猪头、猪尾正好换一个方向吗?问你至少移动了____根火柴棒?视频描述请移动左图中的3根火柴棍,使它变成右图的形状。
一年级上册数学试题-奥数几何:小棒游戏(含答案)沪教版(2015秋)

一个五边形、一个六边形、一个八边形。
【考点】小棒游戏
【难度】 1 星
【题型】解答题
【解析】 三 角形最少要三根小棍,还可以用更多的方法。
正方形最少需要四根小棍,还可以是八根,十六根……等等,需要注意摆放的四个角的角度是直
角。
菱形最少需要四根小棍,还可以是八根,十六根……等等。
长方形最少需要六根小棍,可以发散孩子的思维。以及需要注意角度问题。
2 根,用 13 根摆四个,说明需要共用 3 根。
【答案】 【作业 6】 下图是由 12 根火柴组成的三个正方形,你能移动 3 根火柴棒使图中出现 7 个正方形吗?
-7-
【考点】小棒游戏
【难度】 3 星
【解析】 考 虑怎么能移动能多得到正方形。
【题型】解答题
【答案】
【作业 7】 用 10 根火柴棍摆成向上飞的蝙蝠图,请你移动
-1-
平行四边形最少需要四根小棍,可以与正方形、菱形、长方形比较分析。 等腰梯形最少需要 5 根小棍,需要注意上底下底平行。 五边形最少需要 5 根小棍,可以发散孩子的思维,多动手摆一摆。 六边形最少需要 6 根小棍,可以发散孩子的思维,多动手摆一摆。 八边形最少需要 8 根小棍,可以发散孩子的思维,多动手摆一摆。 【答案】答案不唯一。
小棒游戏
知识框架
用火柴棒可以拼搭成各种有趣的图形,这些图形随着火柴棒的移动、增减,会发出意想不到的变化,这类 游戏非常有趣、益智,你也来试试看。
例题精讲
【例 1】 用两根小棍,摆成一个锐角、一个直角、一个钝角。
【考点】小棒游戏
【难度】 1 星
【题型】解答题
【解析】 角 是由从一点引出的两条射线构成的。直角的两边互相垂直,三角板有一个角就是这样的直角。
火柴棒数学趣味题

例5:如图是用10根火柴棍摆成的一座房子。请移动2根火柴,使房子改变方向。
解答:如左下图所示,除虚线表示的2根火柴外,其余火柴是左、右对称的,所以改变房子的方向与这些火柴无关,应移动虚线表示的2根火柴(见右下图)。
例6:“”请你移动三根火柴,
使等成立。
方法点击:在上面的式子中,符号、包括号7里的火柴棒是不可能移动的。而且一个两位数乘以一个一位数积不可能是个四位数。16有可能移动成为15、18、19;122通过移动有可能成为132、133。
解答:
例3:“”请你移去两根火柴,使图形中只剩下两个正方形。
方法点击:解答这个题目时,我们首先应观察清楚图中一共有几个正方形。一共五个,只要破坏其中的三个就形了。这样我们就把问题变成了移去两根火柴减少三个正方形。
解答:
例4:“”请你移动图中的火柴棒,你最多能拼出几个三
角形?你最少只要移动几根火柴棒?
育才小学数学趣味题(火柴棒)题例征集表
姓名:任教班级:
题目
解答Βιβλιοθήκη 例1“”移动图中的三根火柴,使图形从
一个“品”字拼成一个“井”字。
解答:
例2:
请移动“”中的三根火柴,拼出三个角形。
方法点击:解答这个题目时我们还要了解在关三角形的知识,图中一共7根火柴,要拼出三个三角形,一共有9条边,那就必须是有两条边要重叠。
解答:
4年级奥数几何计数问题例题

例1.用3根等长的火柴可以摆成一个等边三角形.如图19-1,用这样的等边三角形拼合成一个更大的等边三角形.如果这个大等边三角形昀每边由20根火柴组成,那么一共要用多少根火柴?[分析与解]把大的等边三角形分为20“层”分别计算火柴的根数:最上一“层”只用了3根火柴;从上向下数第二层用了3×2=6根火柴;从上向下数第三层用了3×3=9根火柴;……从上向下数第20层用了3×20=60根火柴.所以,总共要用火柴3×(1+2+3+…+20)=630根.【巩固提高】1.如下图,一个三角形分成36个小三角形.把每个小三角形涂上红色或蓝色,两个有公共边的小三角形要涂上不同的颜色,已知涂成红色的三角形比涂成蓝色的三角形多,那么多_____个.2.右图是由小立方体码放起来的,其中有一些小方体看不见.图中共有_____个小立方体.3.数一数,下图是由_____个小立方体堆成的.要注意那些看不见的.例2.如图19-2,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?[分析与解]横放需1996×4根,竖放需1997×3根,共需1996×4+1997×3=13975根.【巩固与提高】1.如图下图是一个4×328的长方形,每个小正方形的边长为1厘米,请你计算这个图形中所有线段的长度之和是多少?例3.图19-3是一个跳棋棋盘,请你计算出棋盘上共有多少个棋孔?[分析与解]把棋盘分割成一个平行四边形和四个小三角形,如下图.平行四边形中棋孔数为9×9=81,每个小三角形中有10个棋孔,所以棋孔共有81+10×4=121个.或直接数出有121个.例4.如图19-4,在桌面上,用6个边长为l的正三角形可以拼成一个边长为1的正六边形.如果在桌面上要拼出一个边长为6的正六边形,那么,需要边长为1的正三角形多少个?[分析与解]如图AB=6,组成△AOB需要边长为1的正三角形共:1+3+5+7+9+11=36个,而拼成边长为6的正六边形需要6个△AOB,因此总共需要边长为1的正三角形36×6=216个.【巩固提高】如图一个正六边形,每条边上均与分布着998个点(不包括两个端点),分别连接不相邻的两条边上相互对应的两点,这样就把这个六边形分割成多个等边三角形,请问可以分割出多少个等边三角形?例5.如图19-5,其中的每条线段都是水平的或竖直的,边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4厘米、6厘米、5厘米、1厘米.求图中长方形的个数,以及所有长方形面积的和.[分析与解]确定好长方形的长和宽,长方形就唯一确定,而图中只需确定好横向线段,竖向线段,即可.于是横向线段有(1+2+3+4)=10种选法,竖向线段也有(1+2+3+4)=10种选法,则共有10×10=100个长方形.这些长方形的面积和为:(5+7+9+2+12+16+11+21+18+23)×(4+6+5+1+10+11+6+15+12+16)=124×86=10664(平方厘米).例6.如图19-6,18个边长相等的正方形组成了一个3×6的方格表,其中包含“*”的长方形及正方形共有多少个?[分析与解]我们把所求的长、正方形按占有的行数分为三类,每类的长、正方形的个数相等.其中只占有下面一行的有如下12种情况:于是共有12×3=36个正、长方形包含“*”.【巩固提高】1.下图中长方形(包括正方形)总个数是_____.2.如图19-10,AB,CD,EF,MN互相平行,则图中梯形个数与三角形个数的差是多少?[分析与解]图中共有三角形(1+2+3+4)×4=40个,梯形(1+2+3+4)×(1+2+4)=60个,梯形比三角形多60-40=20个.例7.图19-7是由若干个相同的小正方形组成的.那么,其中共有各种大小的正方形多少个?[分析与解]每个4×4正方形中有:边长为1的正方形4×4个;边长为2的正方形3×3个;边长为3的正方形2×2个,边长为4的正方形1×1个.总共有4×4+3×3+2×2+1×1=30个正方形.现在5个4×4的正方形,它们重叠部分是4个2×2的正方形.因此,图中正方形的个数是30×5-5×4=130.例8.图19-8中共有多少个三角形?[分析与解]边长为1的正三角形,有16个.边长为2的正三角形,尖向上的有3个,尖向下的也有3个.因此共有16+3+3=22个.例9.图19-9是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形.那么,图中包含“*”的各种大小的正三角形一共有多少个?[分析与解]设小正三角形的边长为1,分三类计算计数包含*的三角形中,边长为1的正三角形有1个;边长为2的正三角形有4个,边长为3的正三角形有1个;因此,图中包含“*”的所有大、小正三角形一共有1+4+1=6个.【巩固提高】1.图形中有_____个三角形.2.下图中共有_____个正方形.例10.在图19-1l中,共有多少个不同的三角形?[分析与解]下图中共有35个三角形,两个叠加成题中图形时,又多出5+5×2=15个三角形,共计35×2+15=85个三角形.【巩固提高】在下图中有多少条线段,有多少个三角形?例11.如图19-12,一块木板上有13枚钉子.用橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等等,如图19-13.那么,一共可以构成多少个不同的正方形?[分析与解]按正方形的面积分类,设最小的正方形面积为1,面积为1的正方形有5个,如图a所示;面积为2的正方形有4个,如图b所示;面积为4的正方形有1个,如图c所示;还有1个面积比4大的正方形,如图d所示;于是,一共可以构成5+4+1+1=11个不同的正方形.【巩固提高】1.如下图,方格纸上放了20枚棋子,以棋子为顶点的正方形共有_____个.3.如图19-14,用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵.用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形.在这样得到的三角形中,面积等于1平方厘米的三角形共有多少个?[分析与解]我们分三种情况来找面积为1平方厘米的三角形,这些三角形的底与高分别为1厘米或2厘米,利用正方形的对称性:(1)等腰直角三角形,如下图a所示有△AOC,△COE,△EOG,△GOA,△BOH,△DFB,△FHD,△HBF,共计8个,其中以AC,CF,FG,GA为底的各一个,以BF,DH为底的各两个.(2)直角三角形,如图b所示有△ACH,△CHD,△ACD,△DHA,△BEF,△BCE,△CEF,△CFB,△DEG,△DGH,△EGH,△EHD,△GAB,△GBF,△FAB,△FGA,共计16个,其中以AD、CH、BE、CF、DG、EH、FA、GB为斜边的各两个.(3)钝角三角形,如图c所示有△ABE,△AHE,△ADE,△AFE,△CBG,△CFG,△CDG,△CHG共计8个,其中以AE、CG为边的各四个.于是,综上所述,共有面积为1平方厘米的三角形32个.例12.如图19-15,木板上钉着12枚钉子,排成三行四列的长方阵.那么用橡皮筋共可套出多少个不同的三角形?[分析与解]我们先任意选取三个点,那么第1个点有12个位置可以选择,第2个点有11个位置可以选择,第3个点有10个位置可以选择,但是每6种选法对应的都是同一个图形,如下图,ABC,ACB,BAC,BCA,CAB,CBA 均是同一个图形.所以有12×11×10÷6=220种选法,但是如果这3点在同一条直线上就无法构成三角形,其中每行有4种情况,共3×4;每列有1种情况,共1×4;2个边长为2的正方形的4条对角线,共4种情况.所以,可以套出220-3×4-1×4-4=200个不同的三角形.【巩固提高】1.下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?例13.如图19-16,正方形ACEG的边界上有A,B,C,D,E,F,G这7个点,其中B,D,F分别在边AC,CE,EG上.以这7个点中的4个点为顶点组成的不同四边形的个数等于多少?[分析与解]如果暂时不考虑点之间的排列位置关系,从7个点中任取4个点,则第一个点有7个位置可选,第二个点有6个位置可选,第三个点有5个位置可选,第四个点有4个位置可选,而不考虑先后,那么有4×3×2×1=24种选法的实质是一样的,所有可能的组合数目应该是(7×6×5×4)÷24=35.我们只要从中减去不能构成四边形的情形.对图19-16而言,任取4个点而又不构成四边形的情形只能发生在所取的4个点中有3个来自正方形ACEG的一条边,而另一个则任意选取的时候,例如选定A、B、C3点,第4个点无论如何选取都不能构成四边形.正方形的4条边中有3条都存在这样的情况.而每次这种情况发生时,第4个顶点的选取有4种可能.所取的顶点只有4个,因此不可能出现同时选择了2条有3点共线的边的情况.那么需要排除的情况有4×3=12种.所以,满足题意的四边形个数有35-12=23个.【巩固提高】如下图,在三角形AFJ的边界上有A,B,C,……J,K,L共12个点,以这12个点中的3个点位顶点的三角形共有多少个?。
一年级上册数学试题-奥数几何:小棒游戏

小棒游戏知识框架用火柴棒可以拼搭成各种有趣的图形,这些图形随着火柴棒的移动、增减,会发出意想不到的变化,这类游戏非常有趣、益智,你也来试试看。
例题精讲【例1】用两根小棍,摆成一个锐角、一个直角、一个钝角。
【考点】小棒游戏【难度】1星【题型】解答题【解析】角是由从一点引出的两条射线构成的。
直角的两边互相垂直,三角板有一个角就是这样的直角。
教室里天花板上的角都是直角。
锐角比直角小,钝角比直角大。
【答案】【例2】用四根小棍摆出两条平行直线,再摆出两条相交直线。
【考点】小棒游戏【难度】1星【题型】解答题【解析】两条直线互相平行,没有交点,无论延伸多远都不相交。
两条直线相交,只有一个交点。
【答案】【例3】用小棍摆出一个三角形、一个正方形、一个菱形、一个长方形、一个平行四边形、一个等腰梯形、一个五边形、一个六边形、一个八边形。
【考点】小棒游戏【难度】1星【题型】解答题【解析】三角形最少要三根小棍,还可以用更多的方法。
正方形最少需要四根小棍,还可以是八根,十六根……等等,需要注意摆放的四个角的角度是直角。
菱形最少需要四根小棍,还可以是八根,十六根……等等。
长方形最少需要六根小棍,可以发散孩子的思维。
以及需要注意角度问题。
平行四边形最少需要四根小棍,可以与正方形、菱形、长方形比较分析。
等腰梯形最少需要5根小棍,需要注意上底下底平行。
五边形最少需要5根小棍,可以发散孩子的思维,多动手摆一摆。
六边形最少需要6根小棍,可以发散孩子的思维,多动手摆一摆。
八边形最少需要8根小棍,可以发散孩子的思维,多动手摆一摆。
【答案】答案不唯一。
【例4】用三根小棍可以摆出一个三角形,如图。
(1)再加两根火柴棍,摆出两个三角形。
(2)再加两根,摆出三个三角形来。
(3)再加两根,摆出五个三角形来。
【考点】小棒游戏【难度】2星【题型】解答题【解析】一个三角形必需三根火柴棍,这样计算,摆两个三角形就需要六根。
但是现在只给你增加两根,却要求你用五根摆出两个三角形,可见必有一根火柴棍要供两个三角形公用才行。
五大最难的移动火柴题

五大最难的移动火柴题引言移动火柴题是一种经典的智力游戏,它通过移动和重新排列火柴棍来形成新的图形或等式。
这种游戏既能锻炼我们的逻辑思维能力,又能提高我们的创造力。
在众多的移动火柴题中,有五个被广大玩家认为是最难的。
本文将详细介绍这五个最难的移动火柴题,并给出解题思路和详细步骤。
1. 九宫格题目描述在一个3x3的方格中,使用6根火柴棍构造一个正方形。
要求将这6根火柴棍移动成一个正方形,且不能有任何多余的火柴棍。
解题思路这个题目看似简单,但实际上需要一些技巧和创造力。
我们可以先尝试一些简单的方法,比如将两根火柴棍拼成一条直线,然后再将另外两根火柴棍拼成与之垂直的直线。
但是这样会剩下两根火柴棍,无法构成正方形。
我们需要找到一个更巧妙的方法。
观察3x3的方格,我们可以发现,如果将四个角上的火柴棍移到正方形的对角线上,就可以构成一个正方形,并且没有多余的火柴棍。
解题步骤1.将左上角的火柴棍移到右下角,将右上角的火柴棍移到左下角。
X XX -> XX X2.将左下角的火柴棍移到右下角。
X XX XX X X X3.将右下角的火柴棍移到右上角。
X XX XX X X4.将右上角的火柴棍移到左上角。
X XX X XX X X5.将左上角的火柴棍移到左下角。
X XX X X XX X X6.将左下角的火柴棍移到右下角。
X XX X X X XX X X X7.将右下角的火柴棍移到右上角。
X XX X X X XX X X8.将右上角的火柴棍移到左上角。
X XX X X X XX X X9.将左上角的火柴棍移到左下角。
X XX X X X XX X X X最终,我们成功地将6根火柴棍移动成了一个正方形。
2. 等式变形题目描述给定一个等式,使用移动火柴棍的方式,使等式成立。
每根火柴棍只能移动一次,不能添加或删除火柴棍。
解题思路这个题目的关键在于观察和创造。
我们需要观察等式中的数字和运算符,然后创造出新的等式。
有时,我们需要将火柴棍拼成新的数字,有时,我们需要将数字拆分成更小的数字。
每题移动一根火柴棒
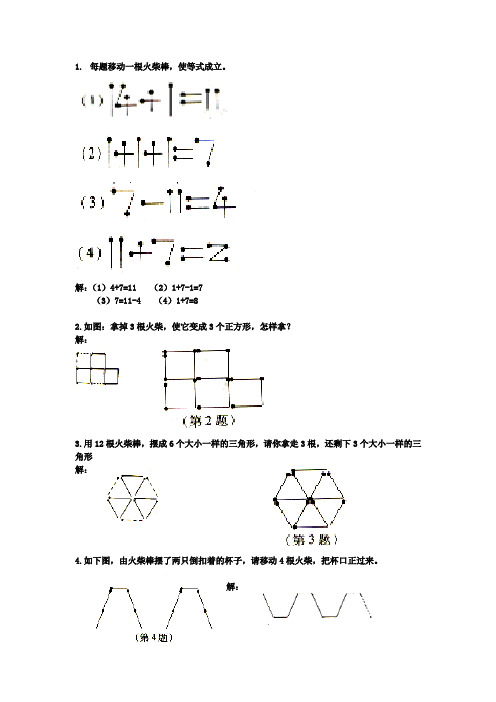
1.每题移动一根火柴棒,使等式成立。
解:(1)4+7=11 (2)1+7-1=7
(3)7=11-4 (4)1+7=8
2.如图:拿掉3根火柴,使它变成3个正方形,怎样拿?
解:
3.用12根火柴棒,摆成6个大小一样的三角形,请你拿走3根,还剩下3个大小一样的三角形
解:
4.如下图,由火柴棒摆了两只倒扣着的杯子,请移动4根火柴,把杯口正过来。
解:
5.由火柴摆成的定风旗如图所示,移动四根火柴,使它成为一座房子。
解:
6.用10根火柴摆成两只高脚杯(如图),移动六根火柴,
使它变成一座房子。
解:
7.用12根火柴,摆成四个大小一样的正方形,怎么摆?
解:
8.先用14根火柴摆成下图的房子,再移动其中的2根火柴,把这座房子改成面向左边的。
解:
9.这个图形是用5根火柴摆成的,请你移动3根火柴的位置,把它倒过来。
解:
10.用火柴棒摆成头朝上的龙虾,移动三根火柴,使它头朝下。
解:
11.用9根火柴摆成的路灯,移动四根,把它变成四个完全相等的三角形。
解:
12.用12根火柴摆成的灯,移动三根火柴,变为五个完全相等的三角形。
解:
13.用10根火柴摆成一个三角阵,请你移动3根火柴,使这个三角阵的尖端向下,把图形倒过来。
解:
14.用火柴摆成四个正方形,如移动其中2根,使图形中减少一个正方形,应怎样移动?
解:
15.你能只移动三根火柴,把这个图形分成四份,而且在每份中都有四种不同的蔬菜图形吗?
16.用10根火柴摆出小鸟向上飞的图形(如图1)。
现在只许你移动其中3根火柴,使小鸟翻个筋斗,即头朝下。
关于火柴的数学题

关于火柴的数学题火柴是一种常见的工具,它可以用于拼图、排列、组合等数学问题。
本文将介绍关于火柴的数学题,包括火柴棒的长度和形状、火柴棒的拼图问题、火柴棒的排列问题、火柴棒的组合问题以及火柴棒的代数问题。
火柴棒的长度和形状火柴棒通常有一定的长度和形状,可以用于构造各种图案和图形。
例如,可以根据火柴棒的长度和形状来拼出一个正方形、三角形或其他多边形。
求解火柴棒的最小长度以及能否用给定长度的火柴棒拼出一个特定形状的问题是常见的数学题。
火柴棒的拼图问题拼图问题是指通过将多个火柴棒拼接在一起,构成一个完整的图案或图形。
常见的拼图问题包括用最少的火柴棒拼出一个特定形状的图形,或者在给定数量的火柴棒下,可以拼出哪些不同的图形。
解决这类问题的关键是要了解图形构成的基本原理,并对图形的边界进行合理的组合。
火柴棒的排列问题排列问题是指将一定数量的火柴棒按照一定的顺序进行排列,构成一个有规律的图案或图形。
常见的排列问题包括如何将火柴棒排列成一圈、一排或一个平面图形,并求解排列的最小长度或最优解。
解决这类问题的关键是要注意图形构成中的规律和周期性,并运用数学中的排列组合知识进行求解。
火柴棒的组合问题组合问题是指将多个火柴棒组合在一起,构成一个新的图形或图案。
常见的组合问题包括求解两个或多个相同或不同形状的火柴棒能够组合成哪些不同的图形或图案,以及如何通过组合得到一个特定的图形或图案。
解决这类问题的关键是要注意图形的组合方式和规律,并运用数学中的组合数学理论进行求解。
火柴棒的代数问题除了上述问题之外,火柴棒还可以涉及到一些代数问题。
例如,可以通过火柴棒的移动和变换来求解代数表达式的结果。
这类问题通常需要运用数学中的代数学和解析几何知识进行求解。
此外,还可以通过火柴棒来构造一些抽象的数学概念或模型,如分形、矩阵等,从而更好地理解数学的原理和应用。
小学一年级奥数题《火柴棒问题大全及答案》题库大全

《火柴棒问题大全及答案》题库大全一、基础篇1. 题目:用4根火柴棒拼出一个正方形。
答案:将4根火柴棒首尾相连,形成一个闭合的四边形,即可得到一个正方形。
2. 题目:用6根火柴棒拼出一个等边三角形。
答案:取3根火柴棒组成一个等边三角形,再用剩余的3根火柴棒分别连接三角形的三个顶点,形成一个更大的等边三角形。
3. 题目:用7根火柴棒拼出一个长方形。
答案:取4根火柴棒组成一个长方形,再用3根火柴棒分别连接长方形的两个对边中点,形成一个更大的长方形。
4. 题目:用8根火柴棒拼出一个正方形和一个等边三角形。
答案:先用4根火柴棒拼出一个正方形,再用剩余的4根火柴棒拼出一个等边三角形。
5. 题目:用10根火柴棒拼出一个梯形。
答案:取6根火柴棒组成一个等边三角形,再用4根火柴棒分别连接三角形的底边两端和顶点,形成一个梯形。
《火柴棒问题大全及答案》题库大全二、进阶篇6. 题目:用5根火柴棒拼出一个星星。
答案:取两根火柴棒交叉放置,形成一个十字形。
然后,将另外三根火柴棒分别放在十字形的三个交叉点上,使它们与十字形的火柴棒相连,形成一个五角星。
答案:取3根火柴棒组成一个等边三角形,再用另外3根火柴棒组成另一个等边三角形,使两个三角形的底边相连。
用剩余的3根火柴棒组成第三个等边三角形,将其底边与前面两个三角形的底边相连。
8. 题目:用12根火柴棒拼出一个六边形。
答案:用6根火柴棒组成一个等边三角形。
接着,将剩余的6根火柴棒分别放在等边三角形的三条边上,使它们与三角形的边平行,形成一个六边形。
9. 题目:用7根火柴棒拼出一个大于号(>)。
答案:取3根火柴棒组成一个等边三角形,然后用4根火柴棒组成一个大于号。
将大于号的尖端与三角形的底边相连,使它们形成一个整体。
10. 题目:用11根火柴棒拼出一个小于号(<)。
答案:先用5根火柴棒组成一个等腰直角三角形,再用6根火柴棒组成一个小于号。
将小于号的尖端与三角形的直角顶点相连,使它们形成一个整体。
小学奥数模块教程火柴上的几何学

广州市小学数学奥林匹克培训学校辅导资料火柴上的几何学(2012,12,2 五)一扎火柴或一些同样长短的小木棒,可以做几何游戏的材料。
做这种游戏,需要有机智的头脑和高度的思考力。
用火柴可以构成各种直线图形,再用搬运火柴的办法,又能使一种图形变成另一种图形。
现在我们用一个题来作例。
例1 24根火柴,一根不折断,全部用上,可以构成几个相等的正方形呢?解:(1)若正方形每边用6根火柴,则只能构成一个正方形。
(2)若正方形每边用3根火柴,则能构成两个相等的正方形。
(3)若正方形每边用2根火柴,则能构成三个相等的正方形。
(4)若正方形每边用1根火柴,则能构成六个,七个,八个,九个相等的正方形。
(5)若正方形每边用二分之一根火柴,则能构成16个相等的正方形。
(6)若正方形每边用三分之一根火柴,则能构成27个相等的正方形。
(7)若正方形每边用五分之一根火柴,则能构成50个相等的正方形。
例2 用10例火柴搭成三个正方形,然后拿掉一根火柴,把其余的火柴搭成一个正方形和两个平行四边形。
解:搭成三个正方形如图(a),搭成一个正方形和两个平行四边形如图(b)。
同学们根据题意完成下面作业:1、如图由8根火柴构成,现在拿掉2根,使变成3个正方形。
2、下面有12根火柴搭成4个相等的正方形,同时还构成1个附加正方形(大的)。
求:(1)拿掉两根火柴,其余火柴不动,要形成2个不相等的正方形;(2)搬动3根火柴,使形成3个相等的正方形;(3)搬动4根火柴,使形成3个相等的正方形;(4)搬动4根火柴,使形成10个正方形。
3、右图是用35根火柴搭成象"螺旋线"样的图形,现在搬动4根火柴,使形成3个正方形。
4、摆一个等边三角形需要3根火柴(不折断火柴的话),但摆6个相等的等边三角形只要12根火柴就够了。
试摆摆看。
再在这个相等的等边三角形上搬动4根火柴,使形成3个等边三角形,其中2个三角形要相等的。
5、如图,摆16个相等的正方形,图中共有多少个正方形呢?至少拿掉几根火柴,可使图上无论大的,小的正方形一个也不剩?*6、取每根火柴为单位长度,现在用这12根火柴作成一个要包含3个平方单位面积的图形,你能组成多少个这样的图形?。
一年级巧移火柴棒数学题

在数学的海洋中,火柴棒数学题犹如一颗颗璀璨的珍珠,闪耀着智慧的光芒。
它们不仅能帮助孩子们开拓思维,培养创造力,还能激发他们对数学的兴趣。
今天,我们就来一起走进一年级巧移火柴棒数学题的世界,领略它们的神奇魅力吧!一、巧妙的数字变换数字变换是火柴棒数学题中最常见的一种题型。
它要求孩子们通过移动或改变火柴棒的数量,使之变成另一个数字。
例如:1. 将数字“5”移动一根火柴棒,变成数字“7”。
2. 将数字“8”改变一根火柴棒的数量,变成数字“3”。
3. 将数字“9”移动一根火柴棒,变成数字“10”。
这些数字变换题看似简单,但实际上却蕴含着丰富的数学知识。
孩子们在解题的过程中,需要观察、思考、比较,才能找到正确的方法。
二、灵动的几何图形火柴棒数学题中,还经常会出现各种各样的几何图形。
这些图形可以是简单的线段、三角形、正方形,也可以是复杂的圆形、五角星、六边形等。
孩子们需要通过移动或改变火柴棒的数量,使之变成这些几何图形。
例如:1. 用火柴棒摆出一个小正方形,然后在它里面再摆出一个小正方形。
2. 用火柴棒摆出一个小三角形,然后在它的旁边再摆出一个小三角形。
3. 用火柴棒摆出一个五角星,然后在它的旁边再摆出一个五角星。
这些几何图形题不仅能锻炼孩子们的动手能力,还能培养他们的空间想象力。
三、神奇的排列组合火柴棒数学题中,还经常会出现排列组合的问题。
这些问题要求孩子们根据给定的条件,排列或组合出各种各样的图形或数字。
例如:1. 用3根火柴棒摆出多少个不同的三角形?2. 用6根火柴棒摆出多少个不同的正方形?3. 用8根火柴棒排列出多少个不同的数字?这些排列组合题不仅能锻炼孩子们的逻辑思维能力,还能培养他们的发散思维能力。
四、巧妙的加减乘除火柴棒数学题中,还经常会出现加减乘除的问题。
这些问题要求孩子们根据给定的数字或图形,进行加减乘除运算。
例如:1. 用火柴棒摆出数字“3”和数字“5”,然后算出它们的和。
2. 用火柴棒摆出数字“6”和数字“8”,然后算出它们的积。
奥数-火柴棍游戏之进阶题库

小学奥数之火柴棍游戏之进阶题型题库火柴棍除了可以摆成一些数字和运算符号,还可以摆出几何图形如正三角形、正方形、菱形、正多边形和一些物品的形状.通过移动火柴棍,可以用它来做有趣的图形变化游戏。
火柴游戏大体分为两种:一种是摆图形和变换图形;一种是变换算式。
这一讲我们先介绍变换图形的游戏。
题型:摆一个正方形,至少需要4根火柴棍.(1)摆两个大小相同的正方形,至少需要几根火柴棍?(2)摆三个大小相同的正方形,至少需要几根火柴棍?(3)摆五个正方形,最少需要几根火柴棍?1.1.(选择题)你能用10根火柴棒摆成3个相同的正方形吗?A、能B、不能C、A和B都有可能D、以上答案均不对2.2.(单选题)你能用9根火柴棒拼出4个相同的三角形吗?A、不能B、能C、A和B都有可能D、以上答案均不对用四根火柴棍可以拼成1个边长是1根火柴棍的正方形,怎样用12根火柴棍拼出6个边长为1根火柴的正方形呢?1.1.(选择题)你能用7根火柴棒摆成3个相同的三角形吗?A、不能B、能C、A和B都有可能D、以上答案均不对2.2.(选择题)用6根火柴,拼出4个相同的三角形。
问能不能?A、能B、不能C、A和B都有可能D、以上答案均不对移动3根火柴棒,使这条鱼的鱼头朝右,鱼尾朝左。
1.1.(单选题)由10根火柴棒摆成的两个倒扣杯子,如图所示,请你移动4根火柴,把杯口正过来。
问能不能?A、不能B、能C、A和B都有可能D、以上答案均不对2.2.(单选题)用10根火柴棍摆成向上飞的蝙蝠图形,如图所示。
试移动三根火柴,使它变成向下飞的蝙蝠图形。
问能不能?A、能B、不能C、A和B都有可能D、以上答案均不对右图所示为一个倒放着且缺一条腿的椅子,请你移动两根火柴棍把椅子正过来。
1.1.(单选题)水井的计量单位是“口”,人们常说“一口井”、“两口井”等等,图中是用16根火柴排成的一个“井”字。
请移动6根火柴,使它变成两个同样大小的“口”字。
问能不能?A、能B、不能C、A和B都有可能D、以上答案均不对2.2.用火柴棒搭成小猪图,你能移动火柴棒使猪头、猪尾正好换一个方向吗?问你至少移动了____根火柴棒?视频描述请移动左图中的3根火柴棍,使它变成右图的形状。
人教版七年级上册数学专题 训练:找规律之图形变化类(一)(含答案)

七年级上册数学专题培优训练:找规律之图形变化类(一)1.如图是由一些火柴棒搭成的图案:(1)摆第1个图案用根火柴棒,摆第2个图案用根火柴棒,摆第3个图案用根火柴棒.(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒(n为正整数)?(3)摆2021根火柴棒时是第几个图案?2.观察图示,解答问题.(1)由上而下第8行,白球有个,黑球有个;(2)若第n(n为正整数)行白球与黑球的总数记作y,求y与n的关系式;(3)求出第2020行白球和黑球的总数.3.如图所示,将一个边长为1的正方形纸片分割成6个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,以此类推.(1)图1的阴影部分的面积是;(2)受此启发,得到++++的值是;(3)若按这个方式继续分割下去,受前面问题的启发,可求得+++…+的值为;(4)请你利用图2,再设计一个能求+++…+的值的几何图形.4.【规律探索】如图所示的是由相同的小正方形组成的图形,每个图形的小正方形个数为S,n是正整数.观察下列图形与等式之间的关系n【规律归纳】(1)S 9﹣S 8= ;S n ﹣S n ﹣1= ; (2)S 9+S 8= ;S n +S n ﹣1= ; 【规律应用】 (3)计算的结果为 .5.“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法. 例如:图1有6个点,图2有12个点,图3有18个点,…,按此规律,求图8、图n 有多少个点?我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个;图3中黑点个数是6×3=18个;…,所以容易求出图8、图n 中黑点的个数分别是 、 .请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题: (1)第6个点阵中有 个圆圈;第n 个点阵中有 个圆圈. (2)小圆圈的个数会等于331吗?请求出是第几个点阵.6.如图是一列用若干根火柴棒摆成的由正方形组成的图案.(1)完成下表的填空:正方形的个数 1 2 3 4 5 6火柴棒的根数 4 7 10 13(2)第n个图形有根火柴棒.(3)小亮用若干根火柴棒按如图所示的方式摆图案,摆完了第1个后,摆第2个,接着摆第3个,第4个,……,当他摆完第n个图案时剩下了20根火柴棒,要刚好摆完第(n+1)个图案还差8根.问最后摆的第(n+1)个图案是第几个图案?7.下列小金鱼图案是用长度相同的小木棒按一定规律拼搭而成,第一条小金鱼图案需8根小木棒,第二条小金鱼图案需14根小木棒,…,按此规律,(1)第n条小金鱼图案需要小木棒根;(2)如果有30000根小木棒,按照如图所示拼搭第1条,第2条……,直到第100条金鱼,请通过计算说明这些木棒是否够用.8.探究题.观察图形,解答下列问题.(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?(2)某一层上有65个圆圈,这是第几层?(3)图中从第一层到第n层一共有多少个圆圈?(4)计算:1+3+5+…+99的和;(5)计算:101+103+105+…+199的和.9.如图是用棋子摆成的“上”字.(1)依照此规律,第4个图形需要黑子、白子各多少枚?(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子、白子各多少枚?(3)请探究第几个“上”字图形白子总数比黑子总数多15枚.10.如图1,给定一个正方形,要通过画线将其分割成若干个互不重叠的正方形.第1次画线分割成4个互不重叠的正方形,得到图2;第2次画线分割成7个互不重叠的正方形,得到图3……以后每次只在上次得到图形的左上角的正方形中画线.尝试:第3次画线后,分割成个互不重叠的正方形;第4次画线后,分割成个互不重叠的正方形.发现:第n次画线后,分割成个互不重叠的正方形;并求第2020次画线后得到互不重叠的正方形的个数.探究:若干次画线后,能否得到1001个互不重叠的正方形?若能,求出是第几次画线后得到的;若不能,请说明理由.参考答案1.解:(1)观察图形的变化可知:摆第1个图案用5+1=6根火柴棒,摆第2个图案用5×2+1=11根火柴棒,摆第3个图案用5×3+1=16根火柴棒;故答案为:6,11,16;(2)结合(1)可知:摆第n个图案用(5n+1)根火柴棒;(3)因为5n+1=2021,解得n=404,所以摆2021根火柴棒时是第404个图案.2.解:(1)第一行1个白球,1个黑球,第二行2个白球,3个黑球,第三行3个白球,5个黑球,…所以可得第n行白球有n个,黑球有2n﹣1个.第8行,白球有8个,黑球有15个;故答案为:8,15;(2)第n(n为正整数)行白球数为n个,黑球数为:(2n﹣1)个,所以总数y与n的关系式为:y=n+2n﹣1=3n﹣1;(3)第2020行白球和黑球的总数为:3×2020﹣1=6059.3.解:(1)∵观察图形发现部分①的面积为:;部分②的面积为=;…∴图1的阴影部分的面积是;故答案为:;(2)++++=1﹣=;故答案为:;(3)+++…+=1﹣;故答案为:1﹣; (4)如图为+++…+的值的几何图形,4.解:(1)根据图形与等式之间的关系可知:S 2﹣S 1=2; S 3﹣S 2=3; S 4﹣S 3=4;… 发现规律:S n ﹣S n ﹣1=n ;∴S 9﹣S 8=9; 故答案为9、n ; (2)S 2+S 1=22;S 3+S 2=32; S 4+S 3=42;… 发现规律:S n +S n ﹣1=n 2;∴S 9+S 8=92=81; 故答案为81、n 2;(3)结合(1)(2)可知:==.故答案为.5.解:图1中黑点个数是6×1=6个; 图2中黑点个数是6×2=12个; 图3中黑点个数是6×3=18个; …,所以图8、图n 中黑点的个数分别是48,6n ; 故答案为:48,6n ;(1)观察点阵可知: 第1个点阵中有1个圆圈;第2个点阵中有7个圆圈;7=2×3×1+1; 第3个点阵中有19个圆圈;19=3×3×2+1; 第4个点阵中有37个圆圈;37=4×3×3+1; 第6个点阵中有圆圈个数为:6×3×5+1=91(个); 发现规律:第n 个点阵中有圆圈个数为:n ×3(n ﹣1)+1=3n 2﹣3n +1. 故答案为:91;n ×3(n ﹣1)+1=3n 2﹣3n +1. (2)会;第11个点阵. 3n 2﹣3n +1=331 整理得,n 2﹣n ﹣110=0解得n 1=11,n 2=﹣10(负值舍去),答:小圆圈的个数会等于331,是第11个点阵.6.解:(1)观察图形的变化可知:第1个图形有3×1+1=4根火柴棒.第2个图形有3×2+1=7根火柴棒.第3个图形有3×3+1=10根火柴棒.…第5个图形有3×5+1=16根火柴棒.第6个图形有3×6+1=19根火柴棒.故答案为:16,19;(2)由(1)可知:第n个图形有(3n+1)根火柴棒.故答案为:(3n+1);(3)因为摆完第n个图案时剩下了20根火柴棒,要刚好摆完第(n+1)个图案还差8根.所以3(n+1)+1=20+8,解得n=8,所以最后摆的第(n+1)个图案是第9个图案.7.解:(1)第一条小金鱼图案需8根小木棒,即8=6×1+2;第二条小金鱼图案需14根小木棒,即14=6×2+2;第三条小金鱼图案需20根小木棒,即20=6×3+2…,发现规律,第n条小金鱼图案需要小木棒(6n+2)根;故答案为:(6n+2);(2)拼搭第1条,第2条……,直到第100条金鱼,所需小木棒:8+14+20+…+602==30500>30000.答:这些木棒不够用.8.解:(1)第八层有15个小圆圈,第n层有(2n﹣1)个小圆圈;(2)令2n﹣1=65,得,n=33.所以,这是第33层;(3)1+3+5+…+(2n﹣1)=n2;(4)1+3+5+…+99=502=2500;(5)101+103+105+...+199=(1+3+5+...+199)﹣(1+3+5+ (99)=1002﹣502=7500.9.解:(1)依照此规律,第4个图形需要黑子5枚,白子14枚;(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子(n+1)枚,白子(3n+2)枚;(3)设第m个“上”字图形白子总数比黑子总数多15枚,则3m+2=m+1+15,解得m=7.所以第7个“上”字图形白子总数比黑子总数多15枚.10.解:尝试:3×3+1=10,3×4+1=13;故答案为:11,13;发现:通过尝试可知:第n次画线后,分割成的正方形为:3n+1;当n=2020时,3n+1=6061,即第2020次画线后得到互不重叠的正方形的个数是6061;故答案为:(3n+1);探究:不能.设每次画线后得到互不重叠的正方形的个数为m,则m=3n+1.若m=1001,则1001=3n+1.解得.这个数不是整数,所以不能.。
小学奥数火柴问题练习题

小学奥数火柴问题练习题一、火柴棒拼数字1. 用火柴棒拼出数字5,至少需要多少根火柴棒?2. 用火柴棒拼出数字8,至少需要多少根火柴棒?3. 用火柴棒拼出数字10,至少需要多少根火柴棒?4. 用火柴棒拼出数字12,至少需要多少根火柴棒?5. 用火柴棒拼出数字15,至少需要多少根火柴棒?二、火柴棒拼图形1. 用火柴棒拼出一个正方形,至少需要多少根火柴棒?2. 用火柴棒拼出一个长方形,至少需要多少根火柴棒?3. 用火柴棒拼出一个等边三角形,至少需要多少根火柴棒?4. 用火柴棒拼出一个直角三角形,至少需要多少根火柴棒?5. 用火柴棒拼出一个梯形,至少需要多少根火柴棒?三、火柴棒移动问题1. 将数字“7”变成数字“9”,至少需要移动几根火柴棒?2. 将数字“5”变成数字“6”,至少需要移动几根火柴棒?3. 将数字“8”变成数字“2”,至少需要移动几根火柴棒?4. 将数字“13”变成数字“15”,至少需要移动几根火柴棒?5. 将数字“18”变成数字“20”,至少需要移动几根火柴棒?四、火柴棒等式问题1. 用火柴棒摆出等式:5 + 5 = 10,至少需要多少根火柴棒?2. 用火柴棒摆出等式:4 + 3 = 7,至少需要多少根火柴棒?3. 用火柴棒摆出等式:8 4 = 4,至少需要多少根火柴棒?4. 用火柴棒摆出等式:9 + 2 = 11,至少需要多少根火柴棒?5. 用火柴棒摆出等式:6 + 6 = 12,至少需要多少根火柴棒?五、火柴棒创意拼图1. 用火柴棒拼出一个房子,至少需要多少根火柴棒?2. 用火柴棒拼出一个船,至少需要多少根火柴棒?3. 用火柴棒拼出一个树,至少需要多少根火柴棒?4. 用火柴棒拼出一个飞机,至少需要多少根火柴棒?5. 用火柴棒拼出一个爱心,至少需要多少根火柴棒?六、火柴棒逻辑推理1. 有三根火柴棒组成的数字“371”,移动两根火柴棒,使其变成一个正确的算式。
2. 有四根火柴棒组成的数字“2345”,移动一根火柴棒,使其变成一个正确的算式。
小学二年级北京版数学下学期几何图形专题练习题

小学二年级北京版数学下学期几何图形专题练习题班级:__________ 姓名:__________1. 动脑筋,移一移。
(1)请你从上面图形中拿走2根火柴,使它有2个正方形。
(2)你能移动3根火柴,使它变成3个正方形吗?2. 再添几个三角形设计一个美丽的图案。
3. 看图,根据角的大小由大到小排序。
A. B. C.__________________4. 在括号内填上合适的数。
(单位:厘米)①______ ②______ ③______ ④______ ⑤______5. 仔细观察并填空。
(填序号)(1)在右面的小棒中,要拼成一个长方形,可选的小棒是______。
(2)要拼成一个正方形,可选的小棒是______6. 在下面的图形中,如果剪去一个角,还剩下几个角?先画一画,再填一填。
画一画:______ 画一画:______ 画一画:______还剩(____)个角还剩(____)个角还剩(____)个角7. 观察下图填空。
①整个图形是______图形,里面分别是______和______图形;②一共有______个______形;③里面有______个______形。
8. 下面的图案分别是由什么图形组成的?由(________)组成由(________)组成9. 在下面的图形中画一条直线,使它分别增加3个直角和4个直角。
10. 看图填一填。
1.下面的图形是什么图形,将名称填在横线上。
____________2.数一数,有______个平行四边形。
11. 至少用你学过的两种图形设计一个图案。
12. 选出正确的图形。
三角形是______。
13. 下面图形中,哪个的平行四边形比较多,(________)填序号。
14. 把下面图形的编号填在合适的圈内。
火柴棒图形游戏习题附答案-幼小衔接小学生数学思维

1.请小朋友用火柴棒拼出下面的图形。
2.用3根火柴棒可以拼出一个三角形,你能用6根火柴棒拼出两个
三角形吗?如果用5根火柴棒,能拼出两个三角形吗?
3.看看右图中有几个正方形?如果再添两根火柴棒,能否搭出5个
正方形?
4.下面的图是用12根火柴棒拼搭成的田字形,能不能拿走两根火柴
棒,把现在的图形变成两个正方形。
5.右图是用12根火柴棒拼搭成的田字形,能不能移动4根火柴棒,
使右图成为3个正方形。
6.请小朋友用4根火柴拼出1个正方形,用7根火柴棒拼出2个正
方形,用10根火柴拼出3个正方形。
7.请小朋友用16根火柴摆出5个同样大小的正方形。
8.请小朋友用9根火柴摆出4个同样大小的三角形。
