学生成绩排名
学生成绩并列名次排名方法

学生成绩并列名次排名方法
嘿,同学们!咱今天来聊聊学生成绩并列名次的排名方法,这可太重要啦!比如说小明和小红,他俩数学考试都考了一样的高分,那怎么给他们排个先后次序呢?
咱先说说按姓氏笔画来排名吧。
就好像班级里有两个同学叫李华和张华,那“李”字笔画多一些,张华就可能排在李华前面。
这是不是挺有意思的呀!可有时候,这方法也不一定完全公平啊,凭什么因为姓氏笔画就决定先后呢?
或者可以看他们其他科目的成绩呀!假如小明和小红数学并列,但是语
文上小明高几分,那是不是小明就该排在前面呢?这就像跑步比赛,虽然一段路大家并驾齐驱,但后面的赛程里有人稍稍领先了呀。
再不然,还可以参考平时的表现呢!比如谁上课更积极发言,谁课后更
认真做作业。
就好比小强和小刚成绩并列,但小强总是积极回答问题,那在老师心里,小强可能就显得更优秀一点咯。
嘿,大家说哪种方法最合理呢?其实呀,我觉得没有一种方法是绝对完
美的。
但无论用哪种,都要尽量做到公平公正呀。
毕竟,这排名可是会影响
到同学们的心情和自信心呢!我们不能因为排名方法不合理就让努力的同学灰心丧气,对吧?成绩并列名次的排名,得综合考虑各种因素,这样才能让大家都心服口服,能更有动力去进步呀!大家觉得我说得对不对呀!。
excel中对学生成绩自动排名
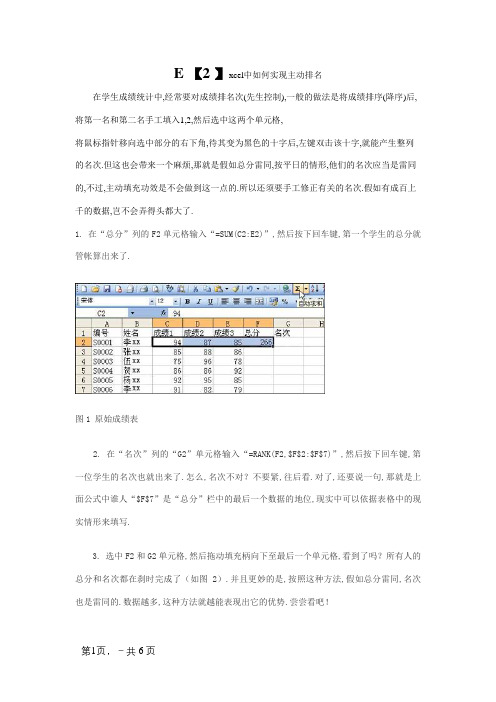
E 【2 】xcel中如何实现主动排名在学生成绩统计中,经常要对成绩排名次(先生控制),一般的做法是将成绩排序(降序)后,将第一名和第二名手工填入1,2,然后选中这两个单元格,将鼠标指针移向选中部分的右下角,待其变为黑色的十字后,左键双击该十字,就能产生整列的名次.但这也会带来一个麻烦,那就是假如总分雷同,按平日的情形,他们的名次应当是雷同的,不过,主动填充功效是不会做到这一点的.所以还须要手工修正有关的名次.假如有成百上千的数据,岂不会弄得头都大了.1. 在“总分”列的F2单元格输入“=SUM(C2:E2)”,然后按下回车键,第一个学生的总分就管帐算出来了.图1 原始成绩表2. 在“名次”列的“G2”单元格输入“=RANK(F2,$F$2:$F$7)”,然后按下回车键,第一位学生的名次也就出来了.怎么,名次不对?不要紧,往后看.对了,还要说一句,那就是上面公式中谁人“$F$7”是“总分”栏中的最后一个数据的地位,现实中可以依据表格中的现实情形来填写.3. 选中F2和G2单元格,然后拖动填充柄向下至最后一个单元格,看到了吗?所有人的总分和名次都在刹时完成了(如图2).并且更妙的是,按照这种方法,假如总分雷同,名次也是雷同的.数据越多,这种方法就越能表现出它的优势.尝尝看吧!图2 排好序的表最后要提示的是,在用于排名次的“=RANK(F2,$F$2:$F$7)”公式中,可万万不要疏忽了符号“$”呀!名次到底能不能排得精确无误,它可是起到很主要的感化呢.如今,我们来看看若何更快.更好地排出一个无纪律的数列.1.在“总分”列的F2单元格输入“=SUM(C2:E2)”,然后按下回车键,第一个学生的总分就管帐算出来了.2.在“名次”列的“G2”单元格输入“=RANK(F2,$F$2:$F$7)”,(意思是盘算F2的数值在F2到F7的名次,留意F7后加逗号,表示将数据按降序排名,逗号后加上1表示,对该列数据按升序排名)然后按下回车键,第一位学生的名次也就出来了.怎么,名次不对?不要紧,往后看.对了,还要说一句,那就是上面公式中谁人“$F$7”是“总分”栏中的最后一个数据的地位,现实中可以依据表格中的现实情形来填写.3.选中F2和G2单元格,双击填充柄(黑色的十字),看到了吗?所有人的总分和名次都在刹时完成了.并且更妙的是,按照这种方法,假如总分雷同,名次也是雷同的.数据越多,这种方法就越能表现出它的优势.尝尝看吧!最后要提示的是,在用于排名次的“=RANK(F2,$F$2:$F$7)”公式中,可万万不要疏忽了符号“$”呀!名次到底能不能排得精确无误,它可是起到很主要的感化呢.若何应用Excel实现名次统计在我们做成绩名次统计的时刻,一般我们会按照成绩总分来做倒序排序,然后再用下来的方法来统计名次,但是如许做会有一个弊端:总分雷同的也被统计成不同的名次,这种统计方法不严谨的,那么我们应当若何来精确的统计名次呢?对象/原料•Excel2010方法/步骤1. 1预备原始数据,并盘算出总分;留意个中红框部分总分雷同2. 2假如我们按照总分排序,在按照下拉的方法来处理,那么则会消失总分雷同而名次不同的情形,如下图!而这不是我们想要的后果!3. 3经由过程RANK函数来实现!具体代码为:=RANK(j2,j$2:j$72,0)RANK函数是则为EXCLE的统计函数,起感化是求某个数值在某一个特定区域内的排名4. 4点击K2单元格在个中输入=RANK(j2,j$2:j$72,0)之后回车即可,之后向下拖动单元格至你所要所要填充的内容区!END留意事项•j$2:j$72为绝对引用,用绝对引用的利益是:当我们在第四部做数据下拉的时刻,其值不会随数据行的转变而转变!若何用函数公式统计各个班各个名次段的人数?做一个统计表用函数统计各班各名次段的人数,就是1~10名1班有若干人,2班有若干人,11~20名,1班有若干人2班有若干人?这个函数公式应当是如何的?感谢学生小我成绩名次分列学号班号姓名语文数学总分班内名次年级名次15 3 黄荣达100 100 200 1 129 2 刘清华99.5 100 199.5 1 241 3 刘艳琼100 99 199 2 317 1 许文成100 98 198 1 427 1 陈弘坤98 100 198 1 425 3 李嘉敏100 98 198 3 420 2 黄慧琳99 98 197 2 743 2 林可欣99 98 197 2 726 3 蔡颖芝100 97 197 4 7比如班号在B3:b9,排名在F3:F9,则1班前10名有=SUMPRODUCT((B3:B9=1)*(F3:F9<=10))2班前10名有=SUMPRODUCT((B3:B9=2)*(F3:F9<=10))1班前11-20名有=SUMPRODUCT((B3:B9=1)*(F3:F9>10)*(F3:F9<=20))2班前11-20名有=SUMPRODUCT((B3:B9=2)*(F3:F9>10)*(F3:F9<=20))假如A1:A100是班级,E1:E100是名次,那么一班在前80名中的人数为=SUMPRODUCT((A1:A100="一班")* (E1:E100<=81))同理,二班的人数为=SUMPRODUCT((A1:A100="二班")* (E1:E100<=81))。
excel中对学生成绩自动排名

e x c e l中对学生成绩自动排名TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-Excel中怎样实现自动排名在学生成绩统计中,经常要对成绩排名次(老师掌握),一般的做法是将成绩排序(降序)后,将第一名和第二名手工填入1,2,然后选中这两个单元格, 将鼠标指针移向选中部分的右下角,待其变为黑色的十字后,左键双击该十字,就能产生整列的名次。
但这也会带来一个麻烦,那就是如果总分相同,按通常的情况,他们的名次应该是相同的,不过,自动填充功能是不会做到这一点的。
所以还需要手工修改有关的名次。
如果有成百上千的数据,岂不会弄得头都大了。
1. 在“总分”列的F2单元格输入“=SUM(C2:E2)”,然后按下回车键,第一个学生的总分就会计算出来了。
图1 原始成绩表2. 在“名次”列的“G2”单元格输入“=RANK(F2,$F$2:$F$7)”,然后按下回车键,第一位学生的名次也就出来了。
怎么,名次不对?不要紧,往后看。
对了,还要说一句,那就是上面公式中那个“$F$7”是“总分”栏中的最后一个数据的位置,实际中可以根据表格中的实际情况来填写。
3. 选中F2和G2单元格,然后拖动填充柄向下至最后一个单元格,看到了吗?所有人的总分和名次都在瞬间完成了(如图2)。
而且更妙的是,按照这种方法,如果总分相同,名次也是相同的。
数据越多,这种方法就越能体现出它的优势。
试试看吧!图2 排好序的表最后要提醒的是,在用于排名次的“=RANK(F2,$F$2:$F$7)”公式中,可千万不要忽略了符号“$”呀!名次到底能不能排得准确无误,它可是起到很重要的作用呢。
现在,我们来看看如何更快、更好地排出一个无规律的数列。
1. 在“总分”列的F2单元格输入“=SUM(C2:E2)”,然后按下回车键,第一个学生的总分就会计算出来了。
2. 在“名次”列的“G2”单元格输入“=RANK(F2,$F$2:$F$7)”,(意思是计算F2的数值在F2到F7的名次,注意F7后加逗号,表示将数据按降序排名,逗号后加上1表示,对该列数据按升序排名)然后按下回车键,第一位学生的名次也就出来了。
Excel中进行数据排序实现学生总成绩排名的操作方法

Excel中进行数据排序实现学生总成绩排名的操作
方法
下面以“在Excel中使用数据排序实现学生总成绩(按学号)的排名”为例子,抛砖引玉,希望对大家有所帮助!
①:如上图,表格数据列有三列,分别为姓名、学号和总分,学号开始的时候是从小到大排序,下面我们实现以总分为参考对象,
先按总分从大到小进行排序!
②:如上图,首先选择总分的第二个单元格,即总分值为400的
C2单元格,之后执行这样的操作:“数据”→“排序”;弹出排序
对话框,之后在“主要关键字”那里选择“总分”并选择“降序”,最后按确定!之后就实现了总分的排名;
③:如上图,按总分排名了之后,下面我们得根据排序出来的总分,写出名次来;如上图,在总分列的右边增加一列,列标题输入
“排名”,之后在其下方的两个单元格分别输入1和2,作为排名
的依据(同时选中输入1和2的单元格,之后使用自动填充的功能进
行填充);
④:如上图,填充结果即显示了排名情况!排名情况有了之后,
这个时候的学号就打乱了,不再是从小到大的顺序,下面我们可再
根据学号进行排序,以符合需要;
⑤:如上图,首先选择学号列的任何一个单元格,之后执行这样的操作:“数据”→“排序”;弹出排序对话框,之后在“主要关键字”那里选择“学号”并选择“升序”,最后按确定!之后就实现了
学号的排名。
3年级数学97分排名第14位

3年级数学97分排名第14位
摘要:
1.描述数学成绩和排名
2.分析成绩和排名的原因
3.提出提高数学成绩的建议
正文:
近日,一名三年级学生参加了数学考试,取得了97 分的优异成绩,在班级中排名第14 位。
这个成绩令人满意,但也有提升的空间。
接下来,我们将对这个成绩和排名进行分析,并提出一些提高数学成绩的建议。
首先,让我们来分析这个成绩和排名。
97 分是一个不错的分数,说明该学生在数学方面有一定的基础和实力。
然而,排名第14 位表明这个成绩在班级中并不算突出。
可能的原因有以下几点:
1.考试时出现了一些失误。
尽管取得了较高的分数,但可能在某些题目上出现了失误,导致失去了一些分数。
2.同学们的整体水平较高。
班级中可能有一些数学高手,导致竞争非常激烈,使得97 分在这个环境中并不突出。
3.学生的数学知识体系还有待完善。
尽管取得了一定的分数,但可能在某些知识点上还存在漏洞,需要加以巩固和提高。
针对以上问题,我们提出以下一些建议,帮助学生提高数学成绩:
1.认真审视自己的失误。
学生可以回顾一下考试过程中的失误,找出原因,并在以后的学习中尽量避免这些问题。
2.加强与同学的交流和学习。
学生可以向班级中的数学高手请教,了解他们的学习方法和经验,取长补短,提高自己的数学水平。
3.系统学习和巩固数学知识。
学生可以利用课余时间,系统地学习数学知识,查漏补缺,确保自己的数学知识体系健全。
总之,这名三年级学生取得了不错的数学成绩,但仍有提升的空间。
高一学生全区成绩排名

6051010218 6051010210 6051010728 6051010234 6051010208 6051010225 6051010207 6051010719 6051010203 6051010366 6051010219 6051010257 6051010774 6051010206 6051010215 6051471044 6051010231 6051010692 6051010738 6051010775 6051010696 6051010711 6051010694 6051010751 6051010262 6051010705 6051010255 6051010229 6051010236 6051010268 6051010272 6051010263 6051010750 6051010216 6051010739 6051010211 6051010239 6051010708 6051010725 6051010042 6051471219 6051010967 6051010726 6051070296
91 87 83 87 89 84 88 85 86 72 82 86 86 88 85 77 89 89 91 87 89 79 86 82 88 77 82 94 79 88 77 83 85 83 84 89 86 88 8 91 93 86 92 94 87 100 83 94 89 80 86 81 85 87 81 95 97 95 88 91 91 80 89 88 86 87 83 81 100 85 97 88 88 83 93 85 84 92
邓茵琳 麦景 莫婧彤 钟煊 李澎生 刘焯莹 雷冠杭 官芷凌 方潮铭 林思颖 傅安琪 叶荣臻 吴芷晴 江泽楷 钟子杰 沈文怀 伍婧尧 黄玉豪 黄康靖 徐逸雪 梁毅强 钟靖阳 李建锋 王诚科 邓楚滢 吴至斌 魏箫 王瑜琳 曾聪 黄紫嫣 邱淑冰 冯隽怡 谭梓骏 程静 李海霖 王思远 陈柱崎 余越 林晓蕾 刘洋 谭伟涛 李晓琳 刘炯余 王梓聪
本科生成绩排名计算方法的研究

本科生成绩排名计算方法的研究摘要:本文通过对本科生学生成绩排名计算方法的研究,探讨了当前常见的几种排名计算方法的优缺点,并提出了一种基于综合评价的新排名计算方法。
本文首先介绍了目前常见的排名计算方法,然后分析了它们在实际应用中的问题和局限性。
接着,针对这些问题,提出了一种新的基于综合评价的排名计算方法,并进行了具体的案例分析和实证研究。
总结了本文的研究成果,并对未来研究方向进行了展望。
关键词:本科生、成绩排名、计算方法、综合评价一、引言在现代社会,教育资源的稀缺性和人才选拔的竞争性导致了学生成绩排名的重要性。
而本科生成绩排名作为学生学业水平的一种评价方式,对学生的学习动力和未来发展至关重要。
本科生成绩排名计算方法的科学性和公平性就显得尤为重要。
目前,国内外对本科生成绩排名计算方法的研究已经取得了一些成果,包括平均绩点法、百分位法、等级法等。
这些方法在实际应用中常常存在一些问题和局限性,如难以反映学生综合能力、不公平性等。
本文旨在通过对这些方法的深入分析,提出一种基于综合评价的本科生成绩排名计算方法,以解决目前方法存在的问题,并提高排名的科学性和公平性。
1. 平均绩点法平均绩点法是目前最常用的本科生成绩排名计算方法之一。
该方法是将学生的各科成绩按照学分加权平均,然后再根据平均绩点进行排名。
这种方法简单直观,易于计算,因此被广泛应用。
平均绩点法存在着明显的问题。
它只反映了学生的学科成绩情况,而没有考虑其他综合因素。
由于学科之间的难易程度不同,学分也不同,导致了平均绩点的公平性问题。
平均绩点法在反映学生真实综合能力方面存在较大局限性。
2. 百分位法百分位法是另一种常见的本科生成绩排名计算方法。
该方法是将学生成绩按照百分位进行排名,即以每门课程的百分位来计算学生在全班的位置,然后将所有课程的排名进行平均。
百分位法也存在着一些问题。
百分位法可能存在分布不均匀的问题,导致了排名的不公平性。
百分位法无法充分反映学生的真实水平,因为百分位法只是一种相对评价方法,不能反映学生在全体学生中的实际位置。
我们班的成绩排名

我们班的成绩排名在学校中,成绩排名一直是学生们关注的焦点。
学生们积极努力,在不同的科目中争取取得好成绩,以期望在班级中获得好的排名。
本文将探讨我们班级的成绩排名情况,并分析其中的原因。
一、排名情况我们班级共有40名学生,每个学期结束时,班主任会公布我们的成绩排名。
在上一学期的排名中,我排在第五名,接下来是李华、王明、张涛和刘娟。
而在这一学期的排名中,情况有所不同。
二、前五名的成绩排名变化在这一学期的成绩排名中,我仍然保持着第五名的位置。
但是,李华成功超越了王明,跃居第二名。
张涛依然排在第三名,而刘娟则掉出了前五名,取而代之的是一个新同学,李雷。
这样一来,前五名的顺序变成了我、李华、张涛、李雷和王明。
三、成绩排名变化的原因1.学习态度与努力程度在我们班级的成绩排名中,学习态度与努力程度是决定因素之一。
第一名的学生在每一次考试中都表现出色,他们充满热情,主动参与课堂讨论,并且每天都会花时间复习和预习。
相比之下,成绩排名下滑的学生可能在学习上投入不够,缺乏耐心和毅力。
2.学习方法和技巧学习方法和技巧在学生成绩中起着至关重要的作用。
一些同学懂得如何有效地整理笔记,制定学习计划,掌握时间管理技巧,而这些因素对于成绩的提升起着重要作用。
有些同学可能尚未找到适合自己的学习方法,导致效率低下,成绩排名下降。
3.家庭环境和学习资源学生的家庭环境和学习资源对于成绩的提高也起着一定的影响。
如果学生有良好的家庭环境和学习资源,如父母的支持、教育资源的丰富等,他们更有可能在学习上取得好成绩。
相反,缺乏这些条件的学生可能在成绩排名中落后。
四、影响成绩排名的因素在班级中,成绩排名受到多个因素的影响。
除了上文提到的原因外,还有其他因素在起作用。
1.外界竞争压力学生们之间的竞争压力是成绩排名的一个重要因素。
在一个竞争激烈的环境中,同学们会更加努力地学习,以争取更高的排名。
竞争压力可以激发出学生们的潜力,但同时也可能给部分同学带来焦虑和压力。
学生成绩排名管理制度

学生成绩排名管理制度随着教育竞争的加剧,学生的学术成绩在升学和就业中起着至关重要的作用。
为了对学生的学术能力进行评估,学生成绩排名管理制度被广泛应用于各级教育机构。
然而,这一制度在实施中也存在一些问题和争议。
本文将从多个角度探讨学生成绩排名管理制度。
一、学生成绩排名管理制度的基本原则学生成绩排名管理制度是衡量学生学术成绩的一种手段,其基本原则是公平、客观、科学和激励。
公平意味着每个学生在同等条件下接受评估;客观意味着通过量化指标进行评估,避免主观因素的干扰;科学意味着评估方法和标准经过科学研究和验证;激励意味着能够鼓励学生主动参与学习并提高学业水平。
二、学生成绩排名管理制度的优点学生成绩排名管理制度有助于促进学生学习的积极性和竞争意识。
通过学生之间的比较,学生们会更加努力地学习和提高成绩,以便在排名中取得更好的名次。
此外,学生成绩排名也为学校和家长提供了一个评估学生学术水平的重要参考指标,便于制定相应的教学和辅导计划,从而提高教学质量和学生综合素养。
三、学生成绩排名管理制度的缺点然而,学生成绩排名管理制度也存在一些缺点。
首先,排名制度容易导致学生间的恶性竞争和压力过大。
学生为了获得更好的排名,可能会采用不正当手段,例如抄袭、舞弊等,这对于学生的道德和品质教育构成了挑战。
其次,学生成绩排名过于强调分数,忽视了学生的个性和全面发展。
排名制度侧重于学术成绩的评估,但学生的成长需要更多的关注和支持,因为他们的潜能可能在其他方面得到展示。
四、学生成绩排名管理制度的改进思路为了克服学生成绩排名管理制度的缺点,可以采取以下措施。
首先,可以引入综合素质评价,将学生的学术成绩与其他方面的表现综合考虑,以更全面地评估学生的能力。
其次,可以采用班级内部排名,鼓励学生积极合作和互助,营造良好的学习氛围。
此外,学校和教师也需要加强对学生综合发展的关注,提供个性化的教学和辅导服务。
五、学生成绩排名管理制度对学生的影响学生成绩排名管理制度对学生的影响是深远的。
高考同分怎么排名

高考同分怎么排名
高考同分的排名方法有很多种,以下是其中几种常见的方法:
1. 根据总分求平均排名:将每个学生的各科成绩相加得到总分,然后按照总分从高到低进行排序,总分相同的学生平分排名。
例如,如果有两名学生总分都是600分,那么他们的排名都是
1名。
2. 根据单科最高分排名:将每个学生各科成绩中的最高分进行比较,按照最高分从高到低进行排序,最高分相同的学生平分排名。
3. 根据学科平均分排名:将每个学生的各科平均分进行比较,按照平均分从高到低进行排序,平均分相同的学生平分排名。
4. 根据各科成绩按权重排名:给予各科成绩不同的权重,例如语文、数学、英语分别占据30%、40%、30%的权重,将每个
学生的加权总分进行比较,按照加权总分从高到低进行排序,加权总分相同的学生平分排名。
需要注意的是,以上排名方法均为常见的排名方式,各高校可能会有不同的排名规则,具体排名方法还需参考当地高校相关规定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):学生成绩排名摘要奖学金制度是国家及各个高校为了鼓励先进,鞭策后进所设立的一种奖励制度,评定奖学金成为每年高校工作的一个重要环节。
本文主要针对某高校某学院某年级95名学生全年20门课程的成绩情况来研究高校的奖学金评定问题(学生成绩排名的问题),建立数学模型,设计出合理、公平的奖学金评定制度。
首先,根据统计学知识,我们运用Excel软件对数据进行了处理。
将基础课、专业课、必选课有低于60分的同学淘汰;留下38名同学。
然后运用加权法给出综合排名前10名的学生学生序号以及成绩。
加权法是利用加权思想对不同性质课程,不同学分课程进行了加权处理得出排名由于每个同学的任选课与人文课的科目不尽相同,这对计算权重造成了很大的麻烦,为了简化计算,我们采用了补偿的方法:将每位同学已修的任选课和人文课的平均分作为这位同学未修课程的得分,因为平均分在一定程度上可以表示此学生的学习能力。
最后通过计算、比较得出成绩最优秀的10%的同学的学生序号是:60 10 12 72 74 54 17 80 13 93 关键字:成绩排名 Excel 加权法权重一、问题的重述学校的每个院系每年都会评定学生奖学金。
设立奖学金的目的是鼓励学生学习期间德智体全面发展。
其中,年度的学习成绩是奖学金评定的主要依据之一,因此,如何根据学生本年度的各门课成绩来合理衡量学生很有必要。
而在实际评优中,由于每个老师的严格程度,每份试卷的难易程度不同,往往会造成相对的不公平出现,所以在评优时应该是尽可能地公平。
附件是某学院某年级95名学生全年20门课程的成绩情况。
请根据该附件中信息,综合考虑各门课程,将成绩最优秀的10%的同学评选出来,作为进一步奖学金评定的候选人。
在论文中,应明确说明是如何考虑课程性质、学时、学分、成绩等因素,给出主要结果及对该问题的建议。
二、问题分析由于每个同学的任选课与人文课的科目不尽相同,这对计算权重造成了很大的麻烦,为了简化计算,我们采用了补偿的方法:将每位同学已修的任选课和人文课的平均分作为这位同学未修课程的得分,因为平均分在一定程度上可以表示此学生的学习能力。
接着我们尝试对加权法进行改进,进一步做无量纲化处理,即对每一学生某门成绩,除以该门成绩最高分,作为其成绩评定办法运用Excel软件对数据进行了处理。
将基础课、专业课、必选课有低于60分的同学淘汰;留下38名同学。
然后运用加权法给出综合排名前10名的学生学生序号以及成绩(加权法是利用加权思想对不同性质课程,不同学分课程进行了加权处理得出排名)。
三、模型的假设与约定1、奖学金候选人的评定仅以本年度课程成绩为依据,除了受题目中所给的因素影响外,不再受其它因素影响;2、学生所取得的成绩均为自己合理方式所取得的,真实;3、题目中所给出的95名同学都参与到了奖学金候选人的评定过程中;4、假设未修的任选课和人文课的成绩为已选该门课程学生的成绩的平均值;5、任选课与人文课参与学生排名,但权重较其它课程较轻;6、基础课、专业课和必修课有不及格的学生淘汰。
四、符合的说明及名词的定义P 课程属性对应值Q 课程学分对应值W i课程I的权重M j学生序列号为J的同学的总成绩S i课程I的成绩S ij学生序列号为J的同学的课程I的成绩S ij*学生序列号为J的同学的课程I的成绩除以课程I的成绩的最大值(SSSiijij Max*)五、模型的建立与求解1、原始数据表格的初始处理首先,我们把基础课、专业课和选修课的成绩有低于60分的同学淘汰,留下38名同学,38名学生的学生序号如下表所示:1 2 4 8 9 10 12 1317 18 20 22 27 29 30 3344 51 53 54 60 62 63 6469 70 71 72 73 74 75 8081 82 86 91 92 93鉴于选修课和人文课评分标准不同于其他科目,且涉及是否选修的问题,我们采用特殊一般化的思路。
将A记为90分,B记为80分,C记为70分,D(不及格)因情节较为严重,记为0分。
对于部分学生未修的选修课和人文课的成绩,采用填充法处理使其统一化。
因考虑到课程属性及学分造成的各门学科权值不同的问题,最终我们采用平均值法填充,即将已选该门课程的学生的成绩平均值,作为未选择该课程学生该门课程的成绩(如下表所示),并利用四舍五入法取整,填充后的表格见附录1。
已选该门课程的学生的成绩平均值课程课程16 课程17 课程18 课程19 课程20 已选该门课程的2029 1690 1270 2010 1780 学生的总成绩已选该门课程的27 23 16 26 23学生的总人数已选该门课程的77 73 79 77 77学生的成绩平均值2、数据分析处理方法及求解:加权法的基本思路是将各学生各门原始成绩乘上该门成绩权重,得到其该门成绩评分,最后将该生各门成绩相加得到该生总评分,通过总评分高低比较进行排名。
其步骤如下:①数据进一步处理:试考虑如下情况。
若某门课程A因考试题目极端困难,导致均分在20分左右,其余课程极端简单,均分在90分左右。
若用传统加权法进行加权分析,课程A对总分的贡献度将难以体现。
因此,我们尝试对加权法进行改进,进一步做无量纲化处理,即对每一学生某门成绩,除以该门成绩最高分,作为其成绩评定办法,如下公式:S SSiijijMax*(i=1,2,3,4,……………,20 ;j=1,2,3,4,…………,38);Sij*的详细结果见附录2数据经此步骤处理,弱化了因考试题目难易程度不同而使各门成绩差异较大对权重造成的影响,使模型更为准确。
②权重矩阵的产生: 每门课程权重由课程属性,学时,学分共同影响。
如下表所示:课程1 课程2 课程3 课程4 课程5 课程6 课程7 课程8 课程9课程10 课程性质 基础课 基础课 基础课 基础课 基础课 基础课 专业课 专业课 专业课 必选课 学时数4 3 3 3 3 2 2 2 33 学分 3.5 3 3 3 3 2 2 2 33课程11 课程12 课程13 课程14 课程15 课程16 课程17 课程18 课程19课程20 课程性质 必选课 必选课 必选课 必选课 必选课 任选课 任选课 任选课 任选课 人文课 学时数3 3 3 3 3 3 3 3 32 学分3 3 3 3 3 2.5 3 3 32经分析,学分与学时成正相关且耦合程度较大,故只将学分计入影响权重因素,足以代表学时与学分的共同影响。
对课程属性因素,为便于计算,将课程属性根据其重要程度进行量化。
课程与属性值p 对应关系如下表所示:得课程属性值矩阵课程属性基础课专业课必修课选修课人文课属性对应值P 1 0.8 0.8 0.25 0.25P= {1,1,1,1,1,1,0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.25,0.25,0.25,0.25,0.25,};又由原始数据表格,得学分矩阵Q={3.5,3,3,3,3,2,2,2,3,3,3,3,3,3,3,2.5,3,3,3,2,} ;权矩阵W 计算公式及结果Q TP W *=={3.5,3,3,3,3,2,1.6,1.6,2.4, 2.4, 2.4, 2.4, 2.4, 2.4, 2.4,0.625,0.75,0.75,0.75,0.5 }得课程权重,结果如下:③模型建立:∑==20**i i ij jW S M(i=1,2,3,4,……………,20 ;j=1,2,3,4,…………,38);④模型求解:利用Excel 求解,结果如下表所示:学生序号60 10 12 72 74 54 17 80 13 93成绩总和 33.7695 33.7475 33.6695 33.662 33.64 33.491 33.4875 33.431 33.419 33.396 学生序号63 62 9 73 44 81 18 69 71 27课程课程1 课程2 课程3 课程4 课程5 课程6 课程7 课程8 课程9 课程10 Wi3.5333321.61.62.42.4课程课程11 课程12 课程13 课程14 课程15 课程16 课程17 课程18 课程19 课程20 Wi2.4 2.4 2.4 2.4 2.4 0.625 0.75 0.75 0.75 0.5成绩总和 33.362 33.2625 33.228 33.2155 33.1095 33.108 33.061 33.0605 32.957 32.8985 学生序号53 92 29 1 4 91 8 22成绩总和 32.8615 32.838 32.8055 32.684 32.4535 32.2995 31.5435 31.0845再利用Excel 筛选出排名前十的同学的学生序号和成绩总和,如下表所示:六、模型的评价(1)模型的优点1.在计算过程采用Excel ,方法简洁易懂,有利于数据的筛选,计算比较精确简便,减少误差;2.合理的假设,使复杂问题简单化,抽象问题具体化;3.在模型分析中,在使用加权法中又使用了平均值法来填充数据使方案更加优化;4.运用了一些表格来进行分析,使模型思路更清晰,更有说服力;5.考虑到不同科目难度不同的问题,利用本课程分数除以本课程最高分作为他们的分数;6.本文用的数学方法都比较简单易懂,方便方案的利用。
7.了正确的数据处理方法,很好的解决了小数取整问题。
8.对附件中的众多表格进行处理,找出了许多变量之间的潜在关系;(2)模型的缺点学生序号 60 10 12 72 74 54 17 80 13 93 成绩总和33.7695 33.7475 33.6695 33.662 33.6433.49133.4875 33.43133.41933.3961.假设A,B,C,D四个等级的时候没有对其进行精确地计算而是在经验的基础上假设了它们的值,太过于理想化了;2.该模型用的软件太少;3.数据比较多,用Excel处理比较繁琐。
