单目相机标定
激光雷达与单目相机联合标定原理

激光雷达与单目相机联合标定原理嘿,朋友们!今天咱来唠唠激光雷达与单目相机联合标定原理这档子事儿。
你说这激光雷达啊,就像是一双超级敏锐的眼睛,能特别精确地感知周围环境的形状和距离。
它那厉害劲儿,就好比是能把周围的一切都看得清清楚楚、明明白白的。
而单目相机呢,也不弱呀!它能捕捉到丰富的色彩和细节,就像一个细心的记录员,把看到的美好都给留下来。
那为啥要把它们联合起来标定呢?这就好比是一场完美的合作!激光雷达能提供精准的距离信息,可在识别具体物体上可能就没那么在行啦。
这时候单目相机就来帮忙啦,它能把那些物体分辨得清清楚楚。
它们俩一联手,那可真是如虎添翼呀!想象一下,激光雷达在前面探路,告诉我们这里有多远那里有多远,单目相机在后面给每个东西都贴上标签,让我们清楚地知道这是啥那是啥。
这配合,多默契呀!联合标定的过程呢,其实也不难理解。
就像是给两个小伙伴制定一套共同的规则,让它们能更好地一起玩耍。
要让它们的信息能够相互匹配、相互补充,这样我们得到的结果才更准确、更有用。
比如说,我们要让激光雷达测量的点和单目相机拍摄的图像中的位置对应起来。
这可不是随随便便就能做到的哦,得经过一番精心的调整和计算。
就跟你调电视画面一样,得把颜色啦、亮度啦都调到最合适的状态。
而且啊,这个标定可不是一锤子买卖,还得经常检查、调整呢。
就像你和好朋友之间的关系,也得时不时维护一下不是?不然时间长了,可能就会出岔子啦。
你说要是没有这个联合标定,那会咋样呢?哎呀,那可能就像两个各说各话的人,谁也听不懂谁,那可不行呀!我们得让它们好好合作,才能发挥出最大的作用。
总之呢,激光雷达与单目相机联合标定原理就是这么重要又有趣。
它让我们能更好地了解周围的世界,让科技为我们的生活带来更多的便利和惊喜。
咱可得好好研究研究,让它们为我们服务得更好呀!这就是我对激光雷达与单目相机联合标定原理的理解,你们觉得呢?原创不易,请尊重原创,谢谢!。
单目相机高精度标定方法

单目相机高精度标定方法摘要:相机标定是计算机视觉中的一个重要环节,对于单目相机来说,其标定过程是获取相机的内部参数和外部参数的过程。
本文介绍了单目相机高精度标定方法的基本原理和具体步骤,并探讨了其中的一些关键技术和注意事项。
一、引言相机标定是计算机视觉中的关键问题之一,它是指通过对相机进行一系列的观测和计算,从而确定相机的内部参数和外部参数。
相机标定是计算机视觉中的基础工作,可以应用于三维重构、目标跟踪、姿态估计等领域。
二、相机标定的基本原理相机标定的基本原理是通过观测特定的标定板上的已知点或特征,利用数学模型将像素坐标与实际世界坐标进行对应。
标定板上的已知点可以是一些特殊的标记点,也可以是一些特征点,例如棋盘格。
通过观测这些已知点在图像中的投影位置,可以通过解方程组的方式求解相机的内部参数和外部参数。
三、单目相机高精度标定方法的步骤1. 准备标定板:选择适当的标定板,例如棋盘格,保证标定板上的特征点清晰可见。
2. 拍摄标定图像:将标定板放置在不同位置和角度下,使用单目相机拍摄一系列标定图像。
要求标定图像的分辨率和图像质量较高。
3. 提取特征点:对于每张标定图像,使用图像处理方法提取出标定板上的特征点,例如角点。
4. 估计初始参数:利用已知的标定板尺寸,结合特征点的像素坐标,通过最小二乘法估计出初始的相机内部参数和外部参数。
5. 优化参数:通过非线性优化算法,对相机内部参数和外部参数进行迭代优化,使标定结果更加精确。
6. 评估标定结果:使用标定结果对标定图像进行重投影,计算重投影误差,评估标定结果的精度。
四、关键技术和注意事项1. 标定图像的质量对标定结果有重要影响,要求标定图像的分辨率较高,图像清晰可见,避免图像模糊或过曝。
2. 标定板的选择也对标定结果有一定影响,一般选择具有规则几何结构的标定板,例如棋盘格。
3. 特征点的提取是标定过程中的关键步骤,可以使用图像处理算法进行特征点的自动提取,或者手动标注特征点。
《基于无穷远信息的单目相机标定方法研究》范文

《基于无穷远信息的单目相机标定方法研究》篇一一、引言在计算机视觉领域,单目相机标定是至关重要的步骤,它决定了相机系统的精确性和可靠性。
然而,传统的标定方法往往受到各种因素的影响,如光照变化、视角变化、畸变等。
因此,如何准确且高效地完成单目相机标定成为了研究的重要课题。
本文提出了一种基于无穷远信息的单目相机标定方法,通过该方法,我们可以有效地提高单目相机的标定精度和稳定性。
二、相关文献综述在过去的几十年里,许多学者对单目相机标定进行了广泛的研究。
传统的标定方法主要依赖于已知的标定物,如棋盘格等。
然而,这些方法往往受到环境因素的影响,如光照变化和视角变化等。
近年来,一些研究者开始尝试使用无穷远信息来进行单目相机标定。
这种方法通过利用无穷远处的点或线作为参考,不受环境和光照等因素的影响,可以有效地提高标定的准确性和稳定性。
三、方法与材料本研究的基于无穷远信息的单目相机标定方法主要分为以下几个步骤:1. 选取合适的标定物:我们选择了一些具有无穷远信息的标定物,如直线和点等。
这些标定物在空间中呈现为理想的几何形状,有利于后续的标定工作。
2. 采集图像数据:通过使用不同的光照条件和不同的视角,我们拍摄了多张含有标定物的图像数据。
这些数据将用于后续的标定过程。
3. 提取特征点:利用图像处理技术,我们从采集的图像数据中提取出特征点。
这些特征点将用于计算相机的内外参数。
4. 计算相机参数:通过使用无穷远信息的约束条件,我们计算出相机的内外参数。
这些参数包括相机的焦距、主点坐标、畸变系数等。
5. 验证与优化:我们使用已知的精确数据对计算出的相机参数进行验证和优化,以确保其准确性和可靠性。
四、实验与结果为了验证本研究的基于无穷远信息的单目相机标定方法的准确性和有效性,我们进行了多组实验。
实验结果表明,该方法可以有效地提高单目相机的标定精度和稳定性。
具体来说,我们的方法在各种光照条件和视角下都能保持较高的标定精度和稳定性,且对畸变等问题的处理效果也较为理想。
单目摄像头标定的原理和方法

单目摄像头标定的原理和方法嘿,咱今儿就来讲讲单目摄像头标定的原理和方法。
你知道吗,这单目摄像头啊,就像是我们的眼睛,但它可没我们的眼睛那么智能,它得经过一番标定,才能更好地看清这个世界呢!想象一下,单目摄像头就像是一个小侦探,它要去观察、去测量周围的一切。
那怎么才能让它更准确呢?这就需要标定啦!标定的原理呢,其实就是建立一个模型,让摄像头知道自己看到的东西在真实世界里的位置和大小。
就好像我们要去一个陌生的地方,得先有张地图一样。
这张地图就是摄像头的标定模型。
通过一系列的操作和计算,让摄像头明白它看到的每个点在实际中的位置关系。
那具体咋标定呢?方法有好几种呢!比如说,可以用一些特制的标定板,上面有很多规则排列的标记点。
摄像头对着这些标定板拍照,然后通过分析这些照片,就能得出很多重要的信息啦。
这就好比是给摄像头出了一套专门的测试题,它通过回答这些问题,来提升自己的能力。
是不是挺有意思的?还有啊,在标定的过程中,可不能马虎。
就像我们做事情一样,得认真仔细,稍有差错,那结果可能就差之千里啦!而且啊,不同的应用场景可能需要不同的标定方法呢。
就像我们穿衣服,不同的场合要穿不同的衣服,总不能穿着睡衣去上班吧!标定好了之后,单目摄像头就能更准确地识别物体、测量距离等等。
它就像是被赋予了超能力一样,可以帮我们做很多事情呢。
比如说在自动驾驶中,单目摄像头可以帮助汽车识别道路、车辆和行人,让汽车更安全地行驶。
这多重要啊,关乎着我们的生命安全呢!在工业生产中,它可以检测产品的质量,确保每个产品都符合标准。
这可不简单,得靠它那精准的“眼光”呢!总之,单目摄像头标定可不是一件小事,它关系到很多领域的发展和应用。
我们得重视它,让它更好地为我们服务。
所以啊,大家可别小看了这小小的单目摄像头标定,它里面的学问大着呢!你说是不是呀?。
单目相机标定原理

单目相机标定原理
单目相机标定是计算机视觉中的一个重要工作,其目的是为了获得相机的内参数矩阵和畸变系数等相关参数,以便在三维空间中还原二维图像的3D信息。
标定的过程主要分为内参数标定和外参数标定两部分。
内参数标定是指计算相机的内部参数,包括焦距、像素间距等,一般采用标定板的方法进行标定。
标定板是一个有特殊图案的平板,其中包含了多个已知大小和位置的角点,通过对这些角点进行识别和匹配,可以得到相机的内参数矩阵和畸变系数等参数。
外参数标定则是指计算相机的外部参数,包括相机的位置和姿态等信息,一般采用多视图几何的方法进行标定。
通过对多张不同角度拍摄的图像进行匹配和反演,可以得到相机的外部参数,进而计算出相机在三维空间中的位置和方向信息。
综上所述,单目相机标定是计算机视觉中的一个非常重要的工作,它不仅可以在3D空间中还原出2D图像的信息,而且在很多实际应用中也具有重要的应用价值。
单目相机标定

单目相机标定展开全文相机标定目的:获取摄像机的内参和外参矩阵,同时也会得到每一副标定图像的旋转和平移矩阵。
内参和外参可以对之后相机拍摄的图像就进行矫正,得到畸变相对很小的图像。
原理:成像模型的坐标系为:世界坐标系 --> 相机坐标系 --> 图像坐标系 --> 像素坐标系先说从相机坐标系到图像坐标系的变换:从针孔成像模型说起:————————————————————————————相机坐标系中实际的点坐标为Q(X, Y, Z)对应的图像(坐标系)平面上的点为 q(x, y , f)理想情况如上所示,但实际上成像芯片的中心通常不在光轴上。
原本的焦距是f,这里把f拆成2个不同的焦距,一个是x轴的焦距,一个是y轴的焦距因此最终计算的结果为:将实际中的点Q(X, Y, Z)映射到投影平面上坐标为(x , y)的点的过程称为投影变换。
这种变换可以使用齐次坐标。
给q(x, y)增加了一个维度w,即为q(x, y, w)下图所示,网上一些资料中也有这种形式:x0、y0为在图像平面上的主点坐标,是Cx,Cy的另一种形式,其中s为坐标轴倾斜参数,理想情况下为0,其他参数都是一样的。
—————————————————————————————————我们已经得到了内参矩阵,能够从相机坐标系转换到图像坐标系上,接下来说如何得到外参矩阵,将其从世界坐标系转换到相机坐标系上从世界坐标系转换到相机坐标系上属于刚体变换,即不会发生形变,也就是说只有旋转和平移。
公式符号说明:带有下标 w 的是世界坐标系带有下标 c 的是相机坐标系设旋转矩阵为 R,平移矩阵为 T再把偏移矩阵T加上即可,偏移矩阵T为 [Tx, Ty, Tz]的转置,是X、Y、Z方向上的平移。
将旋转矩阵R和偏移矩阵T合起来即得外参矩阵即为:——————————————————————————————————图像坐标系和像素坐标系之间的转换:像素坐标系和图像坐标系都在成像平面上,只是各自的原点和度量单位不一样。
单目相机标定matlab

单目相机标定matlab单目相机标定是计算机视觉领域的重要话题,它是将图像坐标系映射到相机坐标系的过程。
Matlab是一个功能强大的工具,可以用来进行单目相机标定。
本文将介绍如何使用Matlab进行单目相机标定。
一、准备工作在开始单目相机标定之前,需要准备以下工作:1.相机。
准备一台拍摄清晰度高的相机,如单反相机或高清摄像头。
2.标定板。
准备一个标定板,标定板是一个由黑白相间的方块组成的平板。
3.计算机。
需要有一台安装了Matlab软件的计算机。
二、安装Matlab工具箱Matlab提供了许多工具箱,包括图像处理工具箱和计算机视觉工具箱。
在进行单目相机标定之前,需要先安装计算机视觉工具箱。
可以通过Matlab的“工具箱浏览器”或Matlab官网下载安装。
三、准备数据在进行单目相机标定之前,需要准备一些数据。
这些数据包括:1.图像。
需要拍摄一组清晰度高的图片,最好是在室内光线较亮的情况下拍摄,拍摄距离和角度可以随意调整。
2.标定板图片。
需要在不同角度下拍摄标定板的图片,拍摄时标定板需要摆放在相机的视野范围内,并将其与相机视野平面垂直。
3.标定板参数。
需要知道标定板的尺寸、方格数、格子尺寸等参数。
四、单目相机标定步骤接下来,我们将通过以下步骤来完成单目相机标定。
1.读取图片。
在Matlab中进行单目相机标定需要读取图片,并将其转换为灰度图像。
2.提取角点。
使用Matlab的“corner”函数来提取标定板上的角点。
这些角点将用于后续计算。
3.计算内参和畸变参数。
使用Matlab的“calibrateCamera”函数来计算相机的内参和畸变参数。
这些参数包括相机的焦点、主点、畸变系数等。
4.计算外参。
使用Matlab的“extrinsics”函数来计算每个标定板图片的相机的外参。
这些参数包括相机的旋转矩阵和平移向量。
5.评估标定结果。
使用Matlab的“showReprojectionErrors”函数来评估标定结果。
单目摄像机标定方法

单目摄像机标定方法《嘿,单目摄像机标定秘籍来啦!》嘿,我的好哥们儿/好姐妹儿!今天我来给你唠唠单目摄像机标定这个神奇的事儿,这可是我的独家秘籍哦!首先啊,咱得准备好工具,就像你出门得带钥匙一样重要。
咱得有个标定板,这玩意儿就像是单目摄像机的好朋友,能帮它找到自己的定位。
然后呢,把这个标定板放好,放得稳稳当当的,可别让它东倒西歪的,不然单目摄像机都不知道该咋对焦啦!这就好比你走路,路要是歪歪扭扭的,你不得摔跟头啊。
接下来,就是让单目摄像机开始工作啦!让它对着标定板一顿猛拍,就像你看到好吃的猛吃一样。
哈哈,别笑,真的很形象好不好!这时候单目摄像机就会把标定板的各种信息都记录下来。
在这过程中啊,你可得注意了,别让什么奇怪的东西挡在摄像机前面,不然它就像被人蒙上了眼睛,啥都看不清啦。
我跟你说,我有一次就不小心把我的臭袜子扔到镜头前面了,哎呀妈呀,那拍出来的都是啥呀!拍完之后呢,就得开始分析这些照片啦。
这就像是你考试完了要改卷子一样。
看看单目摄像机拍得清不清楚,有没有啥问题。
然后根据这些照片和一些专业的软件,算出各种参数。
这可有点像解方程,你得一步一步来,不能着急。
这时候你可能会问啦,“哎呀,这么多参数,我咋记得住啊?”嘿嘿,别担心,你就把它们想象成你喜欢的明星的电话号码,肯定能记住!哈哈,开个玩笑啦。
算完参数之后,可别以为就大功告成了哦!还得检验一下呢。
就像你做好了一道菜,得尝尝味道对不对。
如果检验没问题,那恭喜你,你成功掌握了单目摄像机标定的方法啦!要是有问题,别着急,咱再重新来一遍,就当是复习了。
总之呢,单目摄像机标定就是这么个事儿,听起来好像很复杂,其实只要你按照我说的步骤一步一步来,肯定能学会。
就像走路一样,一步一步走稳了,就能走到目的地。
好啦,我的好哥们儿/好姐妹儿,赶紧去试试吧!祝你成功哦!。
单目相机畸变处理原理

单目相机畸变处理原理
一、相机标定
相机标定是畸变处理的第一步,其目的是为了获取相机的内部参数(如焦距、光心等)和外部参数(如旋转矩阵和平移向量等)。
通过相机标定,可以确定相机的几何模型,为后续的畸变校正提供基础数据。
常用的相机标定方法有传统相机标定和张氏相机标定等。
二、图像采集
图像采集是使用单目相机拍摄图像的过程。
由于单目相机的视角有限,拍摄的图像可能会出现畸变。
因此,在图像采集过程中,需要注意相机的拍摄角度和拍摄距离,以便更好地采集高质量的图像。
三、图像预处理
图像预处理的目的是对采集的图像进行初步处理,以消除噪声、增强图像特征等。
常见的图像预处理方法有灰度化、对比度增强、滤波等。
通过图像预处理,可以改善图像质量,提高后续畸变校正的准确性和稳定性。
四、畸变校正
畸变校正是在获取相机内外参数的基础上,根据相机的几何模型对图像进行畸变校正的过程。
常见的畸变校正方法有直接线性变换、二次曲线变换和径向畸变等。
在实际应用中,需要根据具体的相机和拍摄环境选择合适的畸变校正方法。
五、图像后处理
图像后处理的目的是对校正后的图像进行进一步处理,以改善图
像质量。
常见的图像后处理方法有色彩空间转换、直方图均衡化、边缘检测等。
通过图像后处理,可以提高图像的视觉效果和特征提取的准确性。
总之,单目相机畸变处理原理包括相机标定、图像采集、图像预处理、畸变校正和图像后处理等方面。
在实际应用中,需要根据具体的相机和拍摄环境选择合适的处理方法,以获得高质量的图像。
单目相机标定方法

单目相机标定方法在计算机视觉中,单目相机标定是一项极其重要的技术,它是相机应用的关键基础之一。
单目相机标定指的是根据已知物体的三维坐标和对应的图像坐标,对相机内参、畸变参数等进行精确校准的过程。
以下是单目相机标定的步骤:Step1:制备标定板标定板是这个过程中非常重要的一部分。
它需要是具有不同的特征点以及明确的大小和形状的物体,例如黑白方格板。
标定板中的特征点可以帮助程序识别其在图像中的位置和方位,并通过这些点的位置和方向得出相机内部的参数。
Step2:拍摄标定板将制作好的标定板放置在相机平面上,平行于图像平面拍下多张底片,换取不同的轴角度和物体位置,然后将拍摄到的图像保存下来。
Step3:读取图片信息将标定板拍摄的图像读取到计算机中,并解析出其中的特征点作为后续步骤的输入数据。
Step4:计算角点的位置坐标角点是标定板中一个非常重要的特征点,它们可以根据计算的方式在图像中求得。
从每张图片中提取角点位置信息,以便后续处理。
Step5:校准相机内部参数将标定板的标准定义进行数学建模,并使用标定板中的特征点和相应的图像来确定相机内部参数,例如焦距、畸变、旋转矩阵和平移向量等。
Step6:测试标定效果最后一步是测试标定的效果,通常采用一些标准的度量来计算标定误差。
例如,对于每张图片,使用标定结果进行还原,然后将还原结果与真实值进行比较。
如果误差很小,说明标定效果比较好。
总之,单目相机标定是计算机视觉中的一个关键技术,可以帮助我们准确地校准相机的内部参数,提高图像处理的准确度。
在实际应用中,需要仔细考虑标定板的选择和制备、拍摄条件等多个因素,以确保标定的精度和准确性。
halcon 单目相机 标定例程

HALCON是一个强大的机器视觉软件,它支持各种相机的标定。
单目相机标定的主要目的是完成像素坐标到世界坐标之间的转换。
此外,标定还能帮助我们进行畸变矫正和一维二维图像测量,因为相机成像后往往会产生畸变和缩放。
在HALCON中,你可以使用标定助手来完成单相机的标定。
具体的步骤如下:
1. 打开HALCON并新建一个程序。
2. 在程序编辑中输入算子gen_caltab,然后右击打开算子窗口,输入相关参数,点击确定。
这一步会生成两个文件,一个是后缀为.descr的标定板描述文件,另一个是标定板的图像文件。
3. 打开助手里的标定助手。
4. 进入到标定助手界面,更改描述文件、摄像机模型以及相机相关参数。
5. 点击标定选项卡,然后点击图像采集助手,会立刻弹出图像采集助手对话框(如果之前打开过图像采集助手,在这里就不会弹出),接下里进行相机的连接。
点击自动检测接口,可以选择halcon自带的接口或者是相机的接口。
通过以上步骤,你便可以使用HALCON对单目相机进行标定了。
请注意,这只是一个基本流程,实际操作可能需要根据你的具体需求和设备进行调整。
天津大学精密测试理论实验——视觉图像测量系统——单目摄像机标定
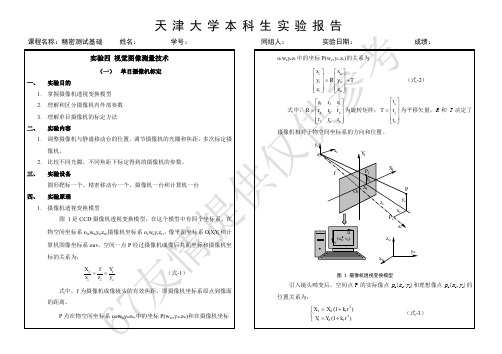
课程名称:精密测试基础 姓名: 学号: 同组人: 实验日期: 成绩: 实验四 视觉图像测量技术
(一) 单目摄像机标定 一、 实验目的 ocwcyczc 中的坐标 P(wc, yc,zc)的关系为
xc xw y R y T c w z c zw r1 式中, R r4 r7 r2 r5 r8
(式-6)
即
xwYd ywYd zwYd Yd xw X d yw X d zw X d L X d T (式-7) 1 1 1 1 1 1 1 L T r s T r s T r s T T s T r T r T r v 1 x v 2 x v 3 x v x x v 4 v 5 v 6
1. 记录的结果中, 摄像机外部参数有哪些?单目摄像机标定得到的这些参数 有什么意义? 答:外部参数有,摄像机坐标系相对于空间坐标系的旋转矩阵 R 和平移矢量 T 其意义在于确定摄像机相对于物空间坐标系的方向和位置。
1. 调整精密移动台的移动方向,使其尽量和标定的摄像机的光轴保持平行,将 标定靶标放在精密移动台上,距离摄像机 250mm-300mm。 2. 点击界面中的“标定试验” ,点击“参数设置” ,设置本次实验的参数。 3. “摄像机选择”选择“Camera1” ,按“采集图像”按钮,采集当前靶标,并 “保存图像” ,点击“图像处理” ,经过椭圆中心提取,可以获得靶标上各圆 孔中心在计算机图像坐标系下的坐标。 4. 旋转精密移动台按钮,将靶标移动一定距离(有“系统参数”中△Z 确定) 。
实验数据有效焦距f12268366mm畸变系数k10000710比例因子sx1010708中心坐标cx66639837mm中心坐标cy369038594mm像元尺寸dx0003797mm像元尺寸dy0003750mm平移矢量tx1740277平移矢量ty12930471平移矢量tz548935885旋转矩阵r10862771旋转矩阵r20008437旋转矩阵r30505524旋转矩阵r40016926旋转矩阵r50998818旋转矩阵r60045556旋转矩阵r70505311旋转矩阵r80047861旋转矩阵r90861609记录的结果中摄像机外部参数有哪些
单目结构光三维成像系统的标定方法

单目结构光三维成像系统的标定方法
单目结构光三维成像系统的标定方法主要包括以下步骤:
1. 获取相机拍摄的标定板图片,保持标定板不动,依序投影结构光编码到标定板上。
2. 找到标定板图片中的特征点坐标。
3. 对相机拍摄到的投影结构光进行解码。
4. 对每个找到的标定板图片中的特征点坐标求局部的单应性矩阵,并使用局部单应性矩阵计算出特征点在投影仪图片上的坐标。
5. 改变标定板位姿,重复步骤1至步骤4。
6. 重复步骤5至少三次,并利用找到的特征点在相机和投影仪中的坐标分别计算出相机内参矩阵和畸变系数,投影仪内参矩阵和畸变系数。
7. 利用找到的特征点在相机和投影仪中的坐标值进行双目标定计算,得到相机和投影仪之间的外参矩阵:旋转矩阵R和平移矩阵T。
通过以上步骤,可以对单目结构光三维成像系统进行准确的标定,提高系统的测量精度和稳定性。
《2024年基于无穷远信息的单目相机标定方法研究》范文

《基于无穷远信息的单目相机标定方法研究》篇一一、引言在计算机视觉领域,单目相机标定是至关重要的步骤,其目的是为了确定相机的内部和外部参数。
相机标定技术的准确性直接影响到后续图像处理和三维重建的精度。
近年来,随着计算机视觉技术的不断发展,基于无穷远信息的单目相机标定方法因其简单、高效和精确的特点,受到了广泛关注。
本文将针对基于无穷远信息的单目相机标定方法进行深入研究,探讨其原理、方法及实施步骤。
二、相关研究回顾在过去的研究中,单目相机标定方法主要包括传统标定方法和自标定方法。
传统标定方法需要使用已知几何形状的标定物,如棋盘格等,通过提取角点信息来计算相机参数。
自标定方法则无需使用标定物,通过拍摄多幅不同场景的图像,利用图像间的对应关系来计算相机参数。
然而,这些方法在处理复杂场景和动态环境时仍存在一定的局限性。
无穷远信息在相机标定中具有重要意义。
由于无穷远处的物体具有特殊的几何特性,基于无穷远信息的标定方法能够提高标定的精度和鲁棒性。
近年来,基于无穷远信息的单目相机标定方法得到了广泛研究,如利用平行线、消失点等特征进行标定。
三、基于无穷远信息的单目相机标定方法1. 方法原理基于无穷远信息的单目相机标定方法主要利用图像中无穷远处的特征信息进行相机参数计算。
这些特征信息包括平行线、消失点等。
通过提取这些特征信息,可以建立相机内外参数的约束关系,从而实现对相机的精确标定。
2. 实施步骤(1)图像预处理:对输入的图像进行去噪、平滑等预处理操作,以提高特征提取的准确性。
(2)特征提取:在预处理后的图像中提取无穷远处的特征信息,如平行线、消失点等。
(3)建立约束关系:根据提取的特征信息,建立相机内外参数的约束关系。
(4)参数计算:通过求解约束关系,计算相机的内外参数。
(5)评估与优化:对计算得到的相机参数进行评估,根据评估结果进行优化,以提高标定的精度。
四、实验与分析为了验证基于无穷远信息的单目相机标定方法的有效性,我们进行了大量实验。
单相机跨视野的标定方法

单相机跨视野的标定方法我折腾了好久单相机跨视野的标定方法,总算找到点门道。
说实话,这事儿一开始我也是瞎摸索。
我最初试着按照普通相机标定的方法来搞这个跨视野标定,想着能有个捷径。
比如说,就按照那些基本的棋盘格标定法,拿着棋盘格在不同视野下拍照,然后就套算法。
但我很快就发现这样不行啊。
普通标定没有考虑到跨视野带来的变化,比如不同视野下的光线、角度啥的很复杂,得到的数据根本不准确。
这就像是你在屋子里量身高和在大太阳下的院子里量身高,不一样的环境有不一样的影响因素,但我一开始忽略了这些。
后来我又想,那我得搞清楚跨视野的时候相机参数的变化规律。
我就开始研究相机视野转换时的对焦距离、光圈等参数的关联。
我做了好多组实验,在不同视野下改变这些参数,然后记录图像变化。
这过程特别繁琐,就像你整理一堆乱麻,一不小心就搞混了。
有一回啊,我没注意把光圈的初始值记错了,结果整个实验的数据都乱套了,那叫一个头疼。
只能重新再来。
然后我发现,在跨视野标定之前,一定要做好相机的预热和稳定性处理。
这就好比运动员比赛前要热身一样重要。
之前没注意这个的时候,相机刚开启拍的那些照片,用来标定时总是存在误差,我还以为是算法的问题,后来才意识到是相机没稳定好。
对于不同视野的图像采集,最好找一个固定的参考点。
就比如说你站在一片树林里要找方向,找到那种特别显眼、固定不会变的大树当参考。
在跨视野标定中,这个参考点能帮助你更好地构建不同视野间的联系。
不确定这个参考点是不是最优解,但我自己实践下来觉得非常有用。
还有啊,在处理数据的时候一定要小心那些异常值。
我之前用算法处理采集到的数据时,查看结果总会有一些不合理的点,后来才发现是数据录入的时候,不小心多输了一个0,导致一个正常的数据变成了异常值,就像把一块好肉不小心混进了变质的肉里,影响了整锅汤的味道。
总之呢,单相机跨视野的标定,你得细心、耐心并且不断从失败中吸取教训。
有些方法可能不是每次都管用,但是慢慢试总能找到合适的套路。
opencv的相机标定方法

opencv的相机标定方法相机标定是计算机视觉中的一个重要步骤,它的目标是通过对相机进行一系列的测量来确定相机的内部参数和外部参数,从而提高图像处理和计算机视觉任务的精确度和稳定性。
OpenCV是一个广泛使用的计算机视觉库,提供了多种相机标定方法。
1.单目相机标定方法:单目相机标定是指使用一个相机拍摄多张不同的棋盘格图像,通过提取图像中的棋盘格角点来确定相机的内部参数和外部参数。
OpenCV中提供了函数`cv::calibrateCamera(`来进行单目相机标定。
该函数需要输入一组棋盘格图像,每幅图像中的棋盘格角点坐标,以及每个角点在现实世界中的坐标。
函数根据这些数据计算相机的内部参数矩阵、畸变系数和每幅图像的旋转矩阵和平移向量。
2.双目相机标定方法:双目相机标定是指使用一对相机拍摄同一场景的图像,并通过识别这些图像中的共享特征点来计算相机的内部参数和外部参数。
OpenCV中提供了函数`cv::stereoCalibrate(`来进行双目相机标定。
该函数需要输入两个相机拍摄的图像,每幅图像中的特征点坐标,以及每个特征点在现实世界中的坐标。
函数根据这些数据计算两个相机的内部参数矩阵、畸变系数和旋转矩阵、平移向量之间的转换关系。
3.深度相机标定方法:深度相机标定是指使用深度相机(如Kinect)拍摄不同的场景,并通过识别图像中的特征点来确定深度相机的内部参数和外部参数。
OpenCV 中提供了函数`cv::rgbd::calibrate(`来进行深度相机标定。
该函数需要输入一系列深度图像和对应的RGB图像,以及特征点的坐标。
函数根据这些数据计算深度相机的内部参数矩阵和旋转矩阵、平移向量之间的转换关系。
4.灰度相机标定方法:灰度相机标定是指使用灰度相机(只能获取灰度图像)进行标定。
与单目相机标定类似,灰度相机标定也是通过拍摄多张棋盘格图像,提取角点坐标进行计算。
OpenCV中提供了函数`cv::calibrateCamera(`来进行灰度相机标定,其使用方式与单目相机标定相似。
单目相机标定

单⽬相机标定(1)从世界坐标系到相机坐标系的变换:可以由⼀个旋转矩阵R和⼀个平移向量t来描述:化为齐次坐标:(2)相机坐标系到图像物理坐标系:其中f是焦距。
化成齐次坐标为:所以可以得到从世界坐标系到图像坐标系的转换:其中是相机的内参数,是外参数。
2、透镜畸变实际的摄像机由于镜头制作⼯艺等原因,使摄像机获取的原始图像存在畸变,畸变有两种,径向畸变和切向畸变。
径向畸变来⾃透镜形状,切向畸变来⾃于整个摄像机的组装过程。
径向畸变可以由三个参数k1,k2,k3确定,切向畸变可由两个参数p1,p2确定。
3、总结相机标定的⽬的就是建⽴摄像机图像像素位置与场景点位置之间的关系,即世界坐标系与图像坐标系之间的关系。
⽅法就是根据摄像机模型,由已知特征点的图像坐标求解摄像机的模型参数,从⽽可以从图像出发恢复出空间点三维坐标,即三维重建。
所以要求解的参数包括4个内参数和5个畸变参数,对于外参数,即旋转矩阵的三个旋转参数和平移向量的三个参数。
内参数直接与期盼所在空间的3D⼏何相关,即外参数。
⽽畸变参数则与点集如何畸变的2D集合相关。
对于外参数,需要知道棋盘的位置,对棋盘的6个不同的视场图像,需要这6个参数,总之,在每个视场中,需要计算4个内参数和6个外参数。
4、opencv中要⽤到的函数Opencv中使⽤的求解焦距和偏移的算法是基于zhang的⽅法,求解畸变参数是基于Brown的⽅法。
Opencv不是使⽤基于3D构造物体的视场,⽽是使⽤平⾯物体的多个视场,使⽤⿊⽩⽅块交替排列的模式能保证在测量上任何⼀边都没有偏移,并且格线⾓点也让亚像素定位函数的使⽤更⾃然。
1、给定⼀个棋盘图像,可以使⽤opencv函数findChessboardCorner()来定位棋盘的⾓点:i n t cvFindChessboardCorners(const void* image, CvSize patternSize, CvPoint2D32f* corners, nt* cornerCount=NULL, int flags=CV_CALIB_CB_ADAPTIVE_THRESH)参数的意义为:image:是⼀个输⼊变量,包含棋盘的单幅图像,必须为8位灰度图像。
《2024年基于无穷远信息的单目相机标定方法研究》范文

《基于无穷远信息的单目相机标定方法研究》篇一一、引言在计算机视觉领域,单目相机标定是一个重要的研究方向。
单目相机标定是获取相机内参和外参的过程,它决定了相机的成像质量和三维重建的准确性。
传统的标定方法主要依赖于已知的标定物和图像之间的对应关系,而基于无穷远信息的标定方法则能够更加有效地解决这一问题。
本文旨在研究基于无穷远信息的单目相机标定方法,提高相机标定的精度和效率。
二、相关工作在单目相机标定领域,目前已有许多方法。
传统的标定方法主要基于已知的标定物和图像之间的对应关系,如张氏标定法等。
然而,这些方法在处理复杂场景时,往往存在精度不高、计算复杂等问题。
近年来,基于无穷远信息的标定方法逐渐成为研究热点。
该方法通过利用无穷远平面的几何特性,可以更加准确地估计相机的内外参数。
三、基于无穷远信息的单目相机标定方法1. 理论基础无穷远信息指的是相机拍摄场景中,处于无穷远处的物体所提供的图像信息。
由于无穷远处的物体在图像上具有特殊的几何特性,因此可以利用这些特性进行相机标定。
本方法基于多视图几何理论,通过构建无穷远平面的约束方程,实现对单目相机的标定。
2. 方法流程(1) 采集数据:利用单目相机在不同角度拍摄同一场景,获取多张图像。
(2) 特征提取:从每张图像中提取出特征点,如角点、边缘点等。
(3) 建立约束方程:根据多视图几何理论,构建无穷远平面的约束方程。
(4) 参数估计:通过优化算法,求解约束方程,得到相机的内外参数。
(5) 标定验证:利用得到的参数对相机进行标定验证,评估标定结果的精度。
四、实验与分析1. 实验设置为验证本方法的有效性,我们在不同场景下进行了实验。
实验中,我们使用单目相机从不同角度拍摄同一场景,获取多张图像。
同时,我们还采用了其他标定方法作为对比,以便进行结果分析。
2. 结果与分析通过实验数据对比分析,我们发现基于无穷远信息的单目相机标定方法在精度和效率上均表现出较好的性能。
与传统的标定方法相比,本方法能够更准确地估计相机的内外参数,从而提高相机的成像质量和三维重建的准确性。
《2024年基于无穷远信息的单目相机标定方法研究》范文

《基于无穷远信息的单目相机标定方法研究》篇一一、引言在计算机视觉领域,单目相机标定是图像处理过程中的关键步骤之一。
这一过程涉及到确定相机的内部参数和外部参数,以便能够准确地将三维世界中的物体投影到二维图像平面上。
传统的标定方法通常依赖于已知的标定物,如棋盘格等,而基于无穷远信息的标定方法则提供了一种新的思路。
本文将研究基于无穷远信息的单目相机标定方法,旨在提高相机标定的准确性和效率。
二、研究背景及意义传统的单目相机标定方法主要依赖于已知的标定物,通过获取标定物的图像信息来计算相机的内部参数和外部参数。
然而,这种方法存在一些局限性,如需要预先准备标定物、标定过程繁琐等。
而基于无穷远信息的标定方法,可以利用场景中的无穷远信息,无需预先准备标定物,具有更高的灵活性和实用性。
因此,研究基于无穷远信息的单目相机标定方法具有重要意义。
三、方法与技术路线基于无穷远信息的单目相机标定方法主要利用场景中的无穷远信息,通过优化算法来计算相机的内部参数和外部参数。
具体步骤如下:1. 选取场景中的无穷远信息作为标定点。
这些标定点可以是已知的三维空间中的点或线,也可以是利用图像处理技术从场景中提取出的特征点或特征线。
2. 建立相机的数学模型。
根据相机的成像原理和几何关系,建立相机的内部参数和外部参数的数学模型。
3. 优化算法。
利用优化算法对相机的内部参数和外部参数进行优化,以使计算结果更加准确。
常用的优化算法包括最小二乘法、非线性最小二乘法等。
4. 实验验证。
通过实验验证所提出的标定方法的准确性和可靠性,包括使用不同场景、不同角度的图像进行测试。
四、实验与分析本文采用多种实验方法来验证所提出的基于无穷远信息的单目相机标定方法的准确性和可靠性。
首先,我们使用已知的三维空间中的点或线作为标定点,通过所提出的标定方法计算相机的内部参数和外部参数,并与实际参数进行比较。
其次,我们使用不同场景、不同角度的图像进行测试,以验证所提出方法的鲁棒性和实用性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,Oc 点为摄像机光心,
Xc 轴和Yc 轴与图像的X 轴与Y 轴平行,Zc 轴为摄像机光轴,它与图像平面垂直。
光轴与图像平面的交点,极为图像坐标系的原点,由点Oc 与Xc 、Yc 、Zc 轴组成的直角坐标系称为摄像机坐标系,OOc 为摄像机焦距:
由于摄像机可以安放在环境中任意位置,所以在环境中选择一个基准坐标系来描述摄像机位置,并用它描述环境中任何物体的位置,该坐标系为世界坐标系。
它有Xw 、Yw 和Zw 轴组成,摄像机坐标系与世界坐标系之间的关系可以用旋转矩阵R 与平移向量t 来描述。
0111C W C W T C W X X Y Y R
t Z Z ⎡⎤⎡⎤⎢⎥⎢⎥⎛⎫⎢⎥⎢⎥= ⎪⎢⎥⎢⎥⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦
总体来说,世界坐标系到图像坐标系的关系可总结如下:
摄像头成像几何关系,其中Oc点称为摄像头(透镜)的光心,Xc轴和Yc轴与图像的x轴和Y轴平行,Zc轴为摄像头的光轴,它与图像平面垂直。
光轴与图像平面的交点O1,即为图像坐标系的原点。
由点Oc与Xc、Yc、Zc轴组成的坐标系称为摄像头坐标系,Oc O1的距离为摄像头焦距,用f表示。
图像坐标系是一个二维平面,又称为像平面,实际上就是摄像头的CCD传感器的表面。
每个CCD传感器都有一定的尺寸,也有一定的分辨率,这个就确定了毫米与像素点之间的转换关系。
举个例子,CCD的尺寸是8mm X 6mm,帧画面的分辨率设置为640X480,那么毫米与像素点之间的转换关系就是80pixel/mm。
”设CCD传感器每个像素点的物理大小为dx*dy,相应地,就有dx=dy=1/80。
二.针孔模型
【针孔模型】
又称为线性摄像机模型,任何空间点M在图像中的投影位置m,为光心Oc与M的连线OcM与图像平面的交点(各种相似三角形有木有,但是要注意像平面和现在讨论的其实是关于Oc对称的哦,所以计算的时候不要忘记了负号,不然出来的图像就是倒着的啦),这种关系也称为重心摄影或者透视投影。
此时有比例关系如下:
将上面的世界坐标到摄像机坐标的转换代入,最后皆可以得到世界坐标系与摄像机坐
标系之间的关系啦:
其中,很容易可以知道
alph=f/dx, beta=f/dy,分别代表了以X轴与Y轴方向上的像素为单位表示的等效焦距。
gamma在较高精度的相机模型中引入,表示图像平面中以像素为单位的坐标轴倾斜程度的量度,gamma=alph a*tan(theta) theta是相机CCD阵列v轴的偏斜角度。
由针孔模型我们可以知道,如果已知摄像机的内外参数,就知道投影矩阵M,这时候对
任何空间点就可以求出其对应图像坐标,但是如果已知空间某点的像点m位置(u,v)即使已经知道摄像机内外参数,Xw也不能唯一确定,因为在投影过程中消去了Zc的信息。
在上面的式子中M是3x4不可逆矩阵,当已知M与(u,v)时,由公式得到的三个方程中消去z,只可以得关于Xw,Yw与Zw的两个线性方程,这个方程组即为射线OP的方程,也就是说,投影点为m的所有点均在该射线上,所以,该空间是不能唯一确定的。
三.相机畸变
摄像头由于光学透镜的特性使得成像存在着径向畸变,可由三个参数k1,k2,k3确定;
由于装配方面的误差,传感器与光学镜头之间并非完全平行,因此成像存在切向畸变,可由两个参数p1,p2确定。
单个摄像头的定标主要是计算出摄像头的内参(焦距f和成像原点cx,cy、五个畸变参数(一般只需要计算出k1,k2,p1,p2,对于鱼眼镜头等径向畸变特别大的才需要计算k3))以及外参(标定物的世界坐标)。
OpenCV 中使用的求解焦距和成像原点的算法
是基于张正友的方法,而求解畸变参数是基于 Brown 的方法
【相机畸变】
1.径向畸变
设(u、v)为理想的图像像素坐标,相对应的,为真实获得的像素坐标。
则(x,y)就为理想的图像物理坐标,为实际获得的图像物理坐标,可以得到如下的关系式:
我们知道,(u0,v0)在求摄像机内参的时候可以知道,在圆心提取排序后也可以知道,(u,v)可以通过OpenCV中cvProjectpoints函数求得反投影残差。
(x,y)可以通过
和求出,于是克得到如下公式:
设Dk=d,所以可以求出畸变系数k1,k2.
在求得了径向畸变的系数以后,就可以如下得到成像仪某点理想的径向位置
其中,r就是当前点的所在透镜半径,k3只有在精度很高的时候才用得到(可以看到其实是将径向畸变做了一个泰勒展开并忽略高阶误差得到的)
2.切向畸变(由于透镜表面曲率不总是严格共线产生)
主要包括离心畸变和薄棱镜畸变,其中,离心畸变是由摄像机的镜头中各个透镜的光轴不能完全重合造成的。
离心畸变其数学模型可以表示为:
薄棱镜畸变是由镜头设计和制造缺陷等误差造成(比如镜头与摄像机像面之间有很小的倾角,其不仅会引起径向偏差,而且会引起切向误差)其数学模型为:
可以看到,薄棱镜畸变的结果就是之前内参矩阵求解时候的那个gamma啦
综合考虑径向畸变和切向畸变,就需要对小孔成像模型进行修正,理想的图像点归一化坐标为p=(x,y)T,有畸变的图像点的归一化坐标为P d=(x d,y d)T之间关系为:
特别说明:在opencv中求出了畸变系数和摄像机内参数以后,就可以用
cvUndistort2( ImageC1, Show1, &intrinsic_matrix, &distortion_coeffs);来进行图像矫正了(建议使用Matlab工具箱来矫正,Opencv自己的函数误差不是一般大,而且对角点提取的精度要求超高(虽然用了亚像素级别),⊙﹏⊙b汗,之前自己按照书上来结果发现矫正以后图像扭曲的不行还以为自己的问题查错查了好久,结果直接标定传入参数进行矫正以后各种准确…….)。
附录:cvUndistort2的函数说明。
