常见数集符号、含义及记忆法
数学中一些常用的数集及其记法

数学中一些常用的数集及其记法大家好!今天咱们来聊聊数学中那些数集的事儿。
听到“数集”这俩字,别以为它们是啥高深的数学术语,其实它们跟我们平常生活中见到的数字关系密切。
你瞧,数学可不是冷冰冰的,它也有它的“小伙伴”,咱们一起来看看吧!1. 自然数(N)1.1 什么是自然数?自然数就是咱们平时最常用的数,从1开始,1, 2, 3,一直到无穷大。
想想你小时候数数,一二三四五就是自然数。
这些数在数学里起着基础性的作用,仿佛是数的“开山祖师”。
1.2 自然数的记法通常用大写字母N来表示自然数。
看起来简单,却是数学的“基石”。
有时我们会用“ℕ”来表示,它和N基本一样,只不过多了点艺术感。
2. 整数(Z)2.1 整数的介绍整数包括了所有的自然数,还加上了它们的负数,比如1, 2, 3,还有0。
这些数就像咱们的生活一样,有起有落,有正有负。
整整齐齐的整数帮我们解决了很多问题,比如负债、温度的变化等。
2.2 整数的记法整数用大写字母Z表示,源于德语中的“Zahlen”,意为“数”。
看到这个字母,你就知道它代表了所有整整齐齐的数,不管是正的还是负的。
3. 有理数(Q)3.1 有理数的定义有理数就是可以表示成两个整数比值的数,比如1/2,3/4,甚至是5(它可以写作5/1)。
简单来说,就是那些可以用分数形式表达的数。
它们就像是数学里的“分割师”,把大数拆成小块,更容易操作。
3.2 有理数的记法有理数用大写字母Q表示,来自于“Rational”的首字母。
Q就像是数学里的万能钥匙,帮我们打开了数的世界。
4. 无理数(I)4.1 无理数的特点无理数是那些不能用简单的分数表示的数,比如π(圆周率)和√2(根号2)。
它们的十进制表示方式是无限不循环的,像是数学里的“小怪兽”。
这些数不易把握,却是数学世界中不可或缺的一部分。
4.2 无理数的记法无理数的记法就比较“神秘”了,通常没有单独的字母来表示,不过我们会用符号来代表它们。
例如π和√2就是直接用符号表达的。
常用数集的记法

常用数集的记法数集是数学中的一个重要概念,用于描述和组织数的集合。
在数学中,我们常常需要对一组数进行分类和表示,以便更好地理解其性质和特点。
常用的数集有自然数集、整数集、有理数集和实数集等。
本文将详细介绍这些常用数集的记法和特点。
自然数集(N)自然数集是由0和比0大的正整数组成的集合,记作N。
自然数集是最早出现的数集,它包含了我们日常生活中常用的计数数字。
自然数集的记法可以表示为:N = {0, 1, 2, 3, …}。
自然数集是一个无限集合,其中的数可以依次递增。
自然数集是整数集、有理数集和实数集的子集,即N ⊂ Z ⊂ Q ⊂ R。
整数集(Z)整数集是由正整数、负整数和0组成的集合,记作Z。
整数集可以表示为:Z = {…, -3, -2, -1, 0, 1, 2, 3, …}。
整数集包含了自然数集,同时还包括了负整数和0。
整数集是一个无限集合,其中的数可以依次递增或递减。
整数集也是有理数集和实数集的子集,即Z ⊂ Q ⊂ R。
有理数集(Q)有理数集是可以表示为两个整数之比的数的集合,记作Q。
有理数集可以表示为:Q = {a/b | a ∈ Z, b ∈ Z, b ≠ 0},其中a和b是整数,且b不等于0。
有理数集包含了整数集和分数。
有理数集是一个无限集合,其中的数可以表示为一个整数除以另一个非零整数的形式。
有理数集是实数集的子集,即Q ⊂ R。
实数集(R)实数集是包含了所有有理数和无理数的集合,记作R。
实数集是数学中最常用的数集,它包含了我们日常生活中遇到的所有实数。
实数集可以表示为:R = {x | x是一个数}。
实数集是一个无限集合,其中的数可以是有理数,也可以是无理数。
有理数是可以表示为两个整数之比的数,而无理数则不能表示为有理数的形式。
实数集是数学中最广泛使用的数集,它包含了所有的实数。
总结常用数集的记法如下:•自然数集:N = {0, 1, 2, 3, …}•整数集:Z = {…, -3, -2, -1, 0, 1, 2, 3, …}•有理数集:Q = {a/b | a ∈ Z, b ∈ Z, b ≠ 0}•实数集:R = {x | x是一个数}这些数集是数学中最基本、最常用的数集,它们在数学的各个分支和应用中起着重要的作用。
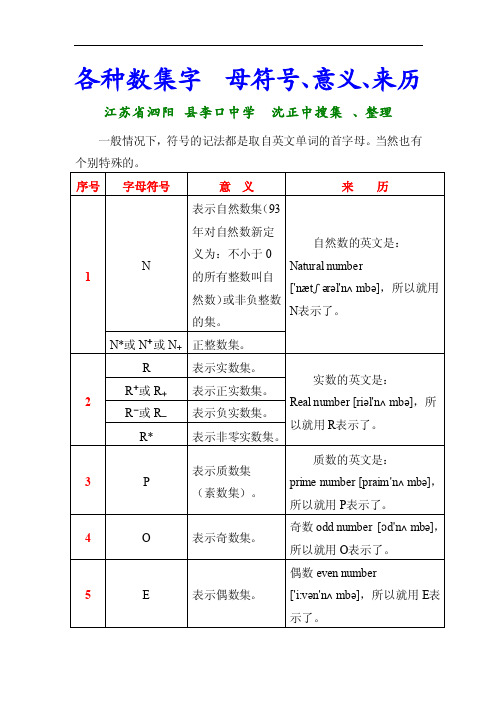
各种数集字母符号、意义、来历
wholenumber [həul'nʌ mbə],
但没能用 W表示。 因为这个涉及到一个德
国女数学家诺特对环理论的
贡献。1921 年她写出的<<整环
的理想理论>>是交换代数发
7
Z
表示整数集。
展的里程碑。其中,诺特在引
入整数环概念的时候(整数集 本身也是一个数环),由于她
各种数集字 母符号、意义、来历
江苏省泗阳 县李口中学 沈正中搜集 、整理
一般情况下,符号的记法都是取自英文单词的首字母。当然也有
个别特殊的。
序号 字母符号
意义
来历
表示自然数集(93
年对自然数新定
自然数的英文是:
义为:不小于 0
N
Natural number
1
的所有整数叫自
示了。
有理数的英文是:
Rational number
['ræʃ ənl'nʌ mbə],但不能再
Q
表示有理数集。
用R 表示了。由于任何一个有
6
理数都是两个整数之比的结
果(商),而商的英文是 quotient
Q+或 Q+ Q-或 Q+
表示正有理数集。 ['kwəuʃ nt],所以就用 Q表示 表示负有理数集。 了。
['nætʃ ərəl'nʌ mbə],所以就用
然数)或非负整数
N表示了。
的集。
N*或 N+或 N+ 正整数集。
R
表示实数集。
实数的英文是:
常用数集及其记法

常用数集及其记法
数学是一门基础而重要的学科,它包含了许多不同的数集。
数集
是指具有特定性质的一组数的集合,如下所述:
1. 自然数集:自然数集是由数1,2,3,4,5,6……组成的集合。
它通常用符号N来表示。
自然数是从1开始,依次向上递增的整数。
2. 整数集:整数集由所有正整数、负整数和0组成。
它通常用符
号Z来表示。
整数是自然数和其相反数的集合。
3. 有理数集:有理数集由所有能表示为两个正整数之比的数组成。
它通常用符号Q来表示。
有理数包括整数和分数。
4. 实数集:实数集由所有实数组成,它通常用符号R来表示。
所
有有理数和无理数都属于实数集。
5. 复数集:复数集由实部和虚部都为实数的数构成。
它通常用符
号C来表示。
以上五种数集都在数学中扮演着非常重要的角色。
它们都有各自
的特点和应用。
自然数集是学习数学的基础,它在数论和代数中经常被使用。
整
数集用于研究整数的性质和应用,如最大公约数和最小公倍数等。
有
理数集适用于测量和几何,它也是高中数学中最为重要的一个数集。
实数集广泛应用于几何和微积分中,对于解决各种实际问题也有重要
意义。
复数集则用于研究电路和波动等现象。
总之,数学中的数集是相互关联、相互作用的。
我们在学习数学的时候,需要理解各种数集的特点和应用,为了逐步地丰富我们的知识和技能。
数学集合符号及含义

数学集合符号及含义数学集合符号及其含义是数学运算中最基础也是最重要的一个环节,是建立数学模型和研究其余各论题的基础。
一般而言,集合是一组有特定关系的元素的总称,它们可以来自有限的自然集或者是无限的自然集,而集合符号(即集合算符号)是用来描述这种集合关系的符号。
按照集合的性质可以分为有限集合和无限集合,而有限集合中的元素个数又可以进一步分为有限集合和无理集合。
因此,可以说,根据集合的特性及其元素,有几种不同形式的集合符号。
下面介绍几种常见的集合符号及其含义:1.合集:用大写字母(A,B,C……)表示,表达的含义是“把所有的集合元素都放在一起”,即取各集合的并集。
2.交集:用字母冒号加括号(A:())表示,表达的含义是“把两个集合中共有的元素都拿出来”,即取各集合的交集。
3.差集:用减号加括号(A-())表示,表达的含义是“从一个集合中减去另一个集合”,即取各集合的差集。
4.补集:用反斜杠加括号(A())表示,表达的含义是“从集合中剔除某些元素”,即取各集合的补集。
5.对偶集:用双下划线(A__)表示,表达的含义是“元素的对偶”,即取各集合的对偶集。
6.空集:用双括号(())表示,表达的含义是“不包含任何元素”,即集合的空集。
另外,还有一些特殊的集合符号,例如:1.子集:用小写字母o表示,表达的含义是“某集合都包括在另一个集合里”,即子集。
2.真子集:用小写字母p表示,表达的含义是“某一集合中的某些元素都包含在另一个集合里”,即真子集。
3.幂集:用大写字母P表示,表达的含义是“某一集合中所有元素的所有可能组合”,即幂集。
4.范围:用椭圆符号表示,表达的含义是“一定数值范围内的所有数值”,即范围。
以上就是有关数学集合符号及其含义的介绍。
通过使用这些常见的集合符号,可以使得数学模型描述及集合研究更加清晰明了,从而更加深入地去理解数学抽象概念。
因此,学习数学集合符号和它们的含义,也是数学学习的基础。
常用数集的符号含义

常用数集的符号含义1. 咱先来说说自然数集,符号是 N!就像咱数数一样,1、2、3、4……这些都是自然数呀。
比如说,你有几个苹果,那肯定得用自然数来表示呀!2. 整数集,符号 Z,这里面可就有正整数、零和负整数啦!这不就像人生的起起落落嘛,有得意的时候,也有失意的时候呀。
就好比你赢了 5 块钱是整数,输了 10 块钱也是整数呀!3. 有理数集,符号 Q,这可包含了好多能写成两数之比的数呢!哎呀,就像各种不同口味的糖果可以混合搭配一样。
比如说,三分之一就是有理数呀!4. 实数集,符号 R,这范围可广啦,有理数和无理数都在里面呢!就像一个超级大的宝库,啥都有。
想想看,你测量的身高、体重,那都是实数呀!5. 正整数集,符号 N+,这就是那些积极向上的数字呀!不就像一群充满活力的小伙伴嘛。
比如说,班级里有几个优秀学生,那就是正整数集里的数呀!6. 负整数集,符号 N-,这些可就是有点“小失落”的数字啦!好比有时候遇到挫折,那就是负整数呀。
像你欠别人 5 块钱,不就是负整数嘛!7. 偶数集,符号 2Z,都是能被 2 整除的数呢!这就像一群有规律排队的小鸭子。
比如说,2、4、6 这些偶数,多整齐呀!8. 奇数集,符号 2Z+1,和偶数不一样,它们不能被 2 整除呢!就像一群特立独行的家伙。
像 3、5、7 这样的奇数,多有个性呀!9. 质数集,符号 P,它们可只有 1 和它本身两个因数哦!这不就像那些很专一的人嘛。
比如说,7 就是质数呀,多纯粹!10. 合数集,符号 H,除了 1 和它本身还有别的因数呢!就像那些丰富多彩的事物。
像 8 就是合数呀,有好多不同的组合呢!我觉得这些数集的符号和含义都好有趣呀,它们让我们能更好地理解和描述这个数字世界呢!。
数集符号记忆口诀

数集符号记忆口诀
嘿,咱就说说数集符号记忆口诀呗。
有一回啊,我上数学课,老师讲到了数集符号。
哎呀,那一堆符号可把我给绕晕了。
什么自然数集N 啦,整数集Z 啦,有理数集Q 啦,实数集R 啦。
我就想,这得咋记住啊?
后来老师教了我们一个口诀,一下子就好记多了。
口诀是“自然牛羊(N)整数猪(Z),有理蜻蜓(Q)实数儿(R)”。
哈哈,是不是很有意思?
我就开始琢磨这个口诀。
自然牛羊(N),就是说自然数集就像一群牛羊一样,都是正整数和零。
我记得有一次,我在操场上数羊,一只、两只、三只……突然就想到了自然数集。
嘿,还真管用,一下子就记住了。
整数猪(Z),就是把整数集想象成一群小猪。
整数包括正整数、负整数和零。
我就想啊,这些小猪有的胖有的瘦,就像整数有大有小一样。
有一次我去动物园看猪,看着那些可爱的小猪,我就想起了整数集。
有理蜻蜓(Q),有理数集就像一群蜻蜓一样,飞来飞去。
有理数包括整数和分数。
我记得有一次,我在公园里看到一群蜻蜓在飞,我就想,这些蜻蜓就像有理数一样,到处都是。
实数儿(R),实数集就像我们的小伙伴一样,无处不在。
实数包括有理数和无理数。
我有一次和小伙伴们一起玩游戏,突然就想到了实数集。
我们就像实数一样,充满了各种可能性。
总之啊,这个数集符号记忆口诀可帮了我大忙了。
以后我再看到这些数集符号,就不会犯迷糊了。
数集符号大全及意义及关系rn

数集符号大全及意义及关系rn数集符号是数学中不可或缺的一部分,它们包括集合符号、关系符号和运算符号。
了解这些符号的意义及作用,对于我们深入理解数学概念和解决实际问题具有重要意义。
一、数集符号的分类1.集合符号:集合符号用于表示数学中的集合,如{x|x>0}表示大于零的实数集合。
常见的集合符号有花括号(表示集合的元素)、竖线(表示集合的边界)、点(表示元素属于集合)。
2.关系符号:关系符号用于表示集合之间的关系,如<表示元素间的大小关系,∈表示元素属于某个集合。
常见的关系符号有小于、大于、等于、不属于等。
3.运算符号:运算符号用于表示集合间的运算,如并集、交集、补集等。
常见的运算符号有并集(∪)、交集(∩)、补集()等。
二、数集符号的意义及作用1.集合符号的意义及作用:集合符号帮助我们表达和描述数学中的各种集合,从而更好地研究数学对象及其性质。
2.关系符号的意义及作用:关系符号帮助我们判断集合中元素之间的大小、属于关系,进而研究集合的性质。
3.运算符号的意义及作用:运算符号帮助我们计算集合间的并集、交集、补集等,从而简化集合运算。
三、数集符号之间的关系1.集合间的包含关系:用符号<表示一个集合包含另一个集合,如A<B表示集合A的所有元素都属于集合B。
2.集合间的相等关系:用符号=表示两个集合相等,如A=B表示集合A和集合B具有相同的元素。
3.集合间的并集、交集、补集关系:- 并集:用符号∪表示两个集合的并集,如A∪B表示集合A和集合B 的所有元素的集合。
- 交集:用符号∩表示两个集合的交集,如A∩B表示集合A和集合B 共有的元素的集合。
- 补集:用符号表示一个集合的补集,如CA表示全集C中不属于集合A的元素的集合。
四、数集符号在数学中的应用1.集合论中的应用:集合论是数学的基础,数集符号在集合论中发挥着重要作用。
2.概率论中的应用:在概率论中,数集符号用于表示样本空间、事件等。
数集符号大全及意义及关系

数集符号大全及意义及关系
嘿,你问数集符号大全及意义及关系啊?这可有点复杂呢,但咱慢慢说。
先说自然数集,符号是 N。
这就是咱平常数的那些 1、2、3 啥的。
就像一群乖宝宝,一个一个排着队。
比如说数苹果,一个苹果、两个苹果,用的就是自然数。
整数集呢,符号是 Z。
这里面不光有自然数,还有负整数和零。
就像一个大家庭,有正数的孩子,负数的孩子,还有零这个中立的小家伙。
比如温度零下几度的时候,就用到负整数了。
有理数集,符号是 Q。
这可就复杂点啦,包括整数和分数。
就像一个大杂烩,啥都有。
比如二分之一、三分之二这些分数都在里面。
要是分蛋糕,几分之一的情况就属于有理数。
实数集,符号是 R。
这个就更广泛啦,有理数和无理数都在里面。
无理数就是像根号 2 这种无限不循环小数。
实数就像一个大宝藏,啥奇怪的数都可能有。
这些数集之间的关系呢,自然数集是整数集的一部分,整数集又是有理数集的一部分,有理数集又是实数集的一部分。
就像俄罗斯套娃一样,一个套一个。
我记得有一次,我做数学作业,就碰到了各种数集的问题。
比如说一个题目要求在有理数集中找一个数,我就得知道有理数包括哪些数才能答对呀。
这就是数集符号的用处啦。
总之呢,数集符号有自然数集 N、整数集 Z、有理数集Q、实数集 R 等。
它们各自有不同的意义,之间也有包含关系。
集合符号大全含义

集合符号大全含义集合符号是数学中常见的一种符号,它们用来表示集合的各种关系和操作。
在集合论和数学分析中,集合符号扮演着非常重要的角色,对于理解和描述集合的性质和运算起着至关重要的作用。
下面我们将对一些常见的集合符号进行介绍,希望能够帮助大家更好地理解和运用这些符号。
1. 相等符号(=)。
相等符号表示两个集合具有相同的元素。
例如,如果集合A={1,2,3},集合B={3,2,1},则A=B。
这说明集合A和集合B包含的元素是相同的。
2. 包含符号(⊆)。
包含符号表示一个集合包含于另一个集合。
如果集合A的所有元素都属于集合B,那么我们说A是B的子集,用符号表示为A⊆B。
例如,如果集合A={1,2},集合B={1,2,3,4},则A⊆B。
3. 真包含符号(⊂)。
真包含符号与包含符号类似,不同之处在于真包含符号表示的是一个集合包含于另一个集合,并且两个集合不相等。
如果集合A是集合B的子集,但A不等于B,那么我们用符号A⊂B表示。
例如,如果集合A={1,2},集合B={1,2,3,4},则A⊂B。
4. 并集符号(∪)。
并集符号表示两个集合的所有元素的集合。
如果A和B是两个集合,它们的并集表示为A∪B。
例如,如果集合A={1,2,3},集合B={3,4,5},则A∪B={1,2,3,4,5}。
5. 交集符号(∩)。
交集符号表示两个集合共有的元素的集合。
如果A和B是两个集合,它们的交集表示为A∩B。
例如,如果集合A={1,2,3},集合B={3,4,5},则A∩B={3}。
6. 补集符号(-)。
补集符号表示一个集合去掉另一个集合后的剩余元素的集合。
如果A和B是两个集合,A-B表示的是属于A但不属于B的元素的集合。
例如,如果集合A={1,2,3,4,5},集合B={3,4,5},则A-B={1,2}。
7. 子集符号(⊂)。
子集符号表示一个集合是另一个集合的子集。
如果A是B的子集,那么我们用符号A⊂B表示。
例如,如果集合A={1,2},集合B={1,2,3,4},则A⊂B。
常见数集符号、含义及记忆法
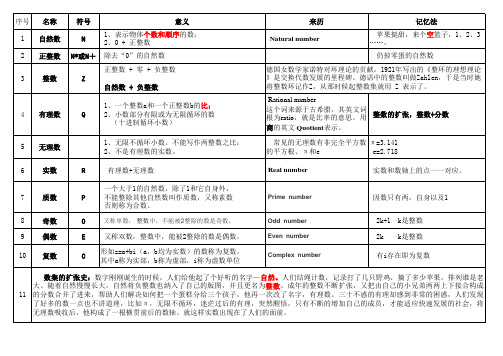
这个词来源于古希腊,其英文词 根为ratio,就是比率的意思。用
整数的扩张,整数+分数
商的英文 Quotient表示。
常见的无理数有非完全平方数 π=3.141
的平方根、π和e
e=2.718
6 实数
R
有理数+无理数
Real number
实数和数轴上的点一一对应。
7 质数
8 奇数 9 偶数 10 复数
序号 名称 1 自然数 2 正整数数和顺序的数; 2、0 + 正整数
N*或N+ 除去“0”的自然数
正整数 + 零 + 负整数 Z
自然数 + 负整数
4 有理数
1、一个整数a和一个正整数b的比;
Q
2、小数部分有限或为无限循环的数
(十进制循环小数)
5 无理数
1、无限不循环小数。不能写作两整数之比; 2、不是有理数的实数。
一个大于1的自然数,除了1和它自身外,
P
不能整除其他自然数叫作质数,又称素数
否则称为合数。
O
又称单数, 整数中,不能被2整除的数是奇数,
E
又称双数,整数中,能被2整除的数是偶数,
C
形如z=a+bi(a,b均为实数)的数称为复数, 其中a称为实部,b称为虚部,i称为虚数单位
Prime number
Odd number Even number Complex number
来历
记忆法
Natural number
苹果挺甜,来个空篮子,1、2、3 ……。
仍掉零蛋的自然数
德国女数学家诺特对环理论的贡献,1921年写出的《整环的理想理论 》是交换代数发展的里程碑。德语中的整数叫做Zahlen,于是当时她 将整数环记作Z,从那时候起整数集就用 Z 表示了。
集合常用的数集符号

集合常用的数集符号正文:在数学中,集合是由一组元素组成的。
为了方便描述和表示集合,人们使用了一些常用的数集符号。
下面是一些常见的数集符号及其含义:1. 自然数集(N):表示由所有正整数组成的集合。
即 N = {1, 2, 3, 4, ...}。
2. 整数集(Z):表示由所有整数(包括正整数、负整数和零)组成的集合。
即 Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}。
3. 有理数集(Q):表示由所有可以表示为两个整数的比值的数构成的集合。
即 Q = {m/n | m ∈ Z, n ∈ Z, n ≠ 0}。
例如,1/2、-3/4、5/1等都属于有理数集。
4. 实数集(R):表示由所有实数组成的集合,包括有理数和无理数。
实数集是数学中最常用的数集符号。
5. 正实数集(R+):表示由所有大于零的实数组成的集合。
即 R+ = {x ∈ R | x > 0}。
6. 非负实数集(R+):表示由所有大于等于零的实数组成的集合。
即R+ = {x ∈ R | x ≥ 0}。
7. 虚数集(I):表示由所有虚数组成的集合,其中虚数定义为平方根为负数的实数。
虚数集通常用于复数的表示和运算。
除了上述常用的数集符号,还有一些集合的特殊符号和运算符号,包括交集 (∩)、并集 (∪)、补集 ()、子集 ()、真子集 ()、空集 () 等。
总之,数集符号是数学中用来表示和描述集合的一种方式,通过这些符号,我们可以更方便地进行集合的运算和推理。
在学习数学的过程中,熟悉并理解这些数集符号是非常重要的。
常见数集符号、含义及记忆法
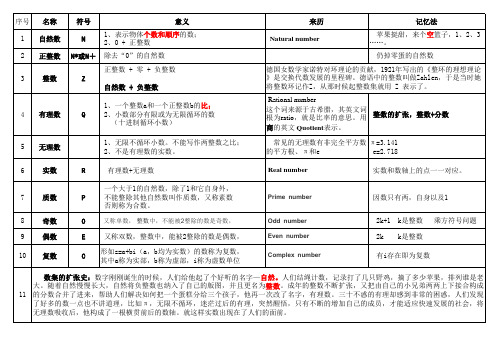
因数只有两,自身以及1
2k+1 k是整数 乘方符号问题 2k k是整数 有i存在即为复数
数集的扩张史:数字刚刚诞生的时候,人们给他起了个好听的名字—自然。人们结绳计数,记录打了几只野鸡,摘了多少苹果,排列谁是老 大。随着自然慢慢长大,自然将负整数也纳入了自己的版图,并且更名为整数。成年的整数不断扩张,又把由自己的小兄弟两两上下接合构成 11 的分数合并了进来,帮助人们解决如何把一个蛋糕分给三个孩子,他再一次改了名字,有理数。三十不惑的有理却感到非常的困惑,人们发现 了好多的数一点也不讲道理,比如π,无限不循环,迷茫过后的有理,突然醒悟,只有不断的增加自己的成员,才能适应快速发展的社会,将 无理数吸收后,他构成了一根横贯前后的数轴。就这样实数出现在了人们的面前。
一个大于1的自然数,除了1和它自身外,
P
不能整除其他自然数叫作质数,又称素数
否则称为合数。
O
又称单数, 整数中,不能被2整除的数是奇数,
E
又称双数,整数中,能被2整除的数是偶数,
C
形如z=a+bi(a,b均为实数)的数称为复数, 其中a称为实部,b称为虚部,i称为虚数单位
Prime number
Odd number Even number Complex number
这个词来源于古希腊,其英文词 根为ratio,就是比率的意思。用
整数的扩张,整数+分数
商的英文 Quotient表示。
常见的无理数有非完全平方数 π=3.141
的平方根、π和e
e=2.718
6 实数
R
有理数+无理数
Real number
实数和数轴上的点一一对应。
7 质数
8 奇数 9 偶数 10 复数
常用数集的记法

常用数集的记法一、自然数集自然数集是由0和所有正整数组成的集合,用符号N表示。
N={0, 1, 2, 3, ...}自然数集是最早出现的数集,它包含了人们最早认识的数,用于计数和表示事物的数量。
自然数集中的数是无限的,每一个数都有其唯一的后继。
二、整数集整数集是由自然数、0和其相反数组成的集合,用符号Z表示。
Z={..., -3, -2, -1, 0, 1, 2, 3, ...}整数集在自然数集的基础上增加了负整数,使得数轴上的每一个点都有对应的整数。
整数集中的数同样是无限的,每一个数都有其相反数和后继。
三、有理数集有理数集是可以表示为两个整数的比值的数的集合,用符号Q表示。
Q={a/b | a∈Z, b∈Z, b≠0}有理数集包括了所有整数和所有可以表示为分数形式的数,可以是正的、负的或零。
有理数可以用两个整数的比值来表示,其中分母不能为零。
四、无理数集无理数集是指不能表示为两个整数的比值的数的集合,用符号I表示。
I={x | x不是有理数}无理数集包括了所有不能用分数形式表示的数,它们是无限不循环的小数。
无理数是不可数的,它们在实数轴上无间断地分布。
五、实数集实数集是由有理数和无理数组成的集合,用符号R表示。
R=Q∪I实数集包括了所有有理数和无理数,是我们通常所说的数。
实数集是连续的,实数轴上的每一点都对应一个实数,实数集是最常用的数集。
六、复数集复数集是由实数和虚数组成的集合,用符号C表示。
C={a+bi | a∈R, b∈R, i^2=-1}复数集包括了实数和虚数,其中虚数是实数乘以虚数单位i得到的数。
复数是二维的,可以用实数部分和虚数部分表示。
七、正整数集正整数集是大于零的整数的集合,用符号N*表示。
N*={1, 2, 3, ...}正整数集是自然数集的子集,它排除了0,只包括大于零的整数。
正整数集用于表示计数和事物的顺序。
八、质数集质数集是只能被1和自身整除的正整数的集合,用符号P表示。
数集符号大全及意义及关系rn

数集集合符号是数学中常见的符号之一,在数学中有着非常重要的作用。
下面将详细介绍数集符号的大全、意义及其关系。
一、数集符号大全1. 包含关系符号:$\in$,表示"属于"的关系,例如$a\in A$表示元素$a$属于集合$A$。
2. 不包含关系符号:$\notin$,表示"不属于"的关系,例如$b\notin B$表示元素$b$不属于集合$B$。
3. 子集关系符号:$\subset$,表示"是集合"的关系,例如$A\subset B$表示集合$A$是集合$B$的子集。
4. 真子集关系符号:$\subsetneq$,表示"真是集合"的关系,例如$A\subsetneq B$表示集合$A$是集合$B$的真子集。
5. 并集符号:$\cup$,表示"并集",例如$A\cup B$表示集合$A$和集合$B$的并集。
6. 交集符号:$\cap$,表示"交集",例如$A\cap B$表示集合$A$和集合$B$的交集。
7. 补集符号:$A^c$,表示集合$A$的补集。
8. 空集符号:$\emptyset$,表示空集。
9. 全集符号:$U$,表示全集。
二、数集符号的意义1. 数集符号可以用来表示元素和集合之间的关系,如属于、包含等关系。
2. 数集符号可以用来表示集合之间的运算关系,如并集、交集等。
三、数集符号的关系1. 包含关系符号$\in$和不包含关系符号$\notin$是互补关系,一个元素要么属于一个集合,要么不属于。
2. 子集关系符号$\subset$和真子集关系符号$\subsetneq$是包含关系的关系,一个集合要么是另一个集合的子集,要么是其真子集。
3. 并集符号$\cup$和交集符号$\cap$是集合之间的运算关系,用来表示两个集合的并集和交集。
4. 补集符号$A^c$表示了集合$A$的补集,即除去集合$A$中所有元素后的集合。
数学自然数集表示

数学自然数集表示
数学自然数集表示:自然数集中自然数的部分和全体都属于自然数集合。
自然数集合就是指自然数的集合,即非负整数全体构成的集合,也叫做自然数集或者非负整数集。
数学上用字母"N"表示自然数集合,自然数集中自然数的部分和全体都属于自然数集合。
数学中一些常用的数集及其记法:
1、所有正整数组成的集合称为正整数集,记作N*,Z+或N+;
2、所有负整数组成的集合称为负整数集,记作Z-;
3、全体非负整数组成的集合称为非负整数集(或自然数集),记作N;
4、全体整数组成的集合称为整数集,记作Z。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Prime?number Odd?number? Even?number? Complex?number
因数只有两,自身以及 1
2k+1 k 是整数 乘方符号问题 2k k 是整数
有 i 存在即为复数
数集的扩张史: 数字刚刚诞生的时候,人们给他起了个好听的名字— 自然。 人们结绳计数,记录打了几只野鸡,摘了多少苹果,排列谁是老
无理数吸收后,他构成了一根横贯前后的数轴。就这样实数出现在了人们的面前。
7
质数
8
奇数
9
偶数
10 复数
一个大于 1的自然数,除了 1和它自身外,
P
不能整除其他自然数叫作质数,又称素数
否则称为合数。
O
又称单数, 整数 中,不能被 2整除的数是奇数,
E
又称双数,整数中,能被 2整除的数是偶数,
C
形如 z=a+bi (a,b均为实数)的数称为复数, 其中 a称为实部, b称为虚部, i 称为虚数单位
Rational number 这个词来源于古希腊,其英文词 根为 ratio,就是比率的意思。用 商的英文 Quotient表示。
整数的扩张,整数 +分数
常见的无理数有非完全平方数 π=3.141
的平方根、 π和e
e=2.718
6
实数
R
有理数 +无理数
Real number
实数和数轴上的点一一对应。
序号 名称 1 自然数 2 正整数
3
整数
符号
意义
N
1 、表示物体 个数和顺序 的数; 2 、0 + 正整数
N*或N+ 除去“ 0”的自然数
正整数 + 零 + 负整数 Z
自然数 + 负整数
4 有理数
1 、一个整数 a和一个正整数 b的 比;
Q
2、小数部分有限或为无限循环的数
(十进制循环小数)
5 无理数
大。随着自然慢慢长大,自然将负整数也纳入了自己的版图,并且更名为
整数 。成年的整数不断扩张,又把由自己的小兄弟两两上下接合构成
11 的分数合并了进来,帮助人们解决如何把一个蛋糕分给三个孩子,他再一次改了名字,有理数。三十不惑的有理却感到非常的困惑,人们发现
了好多的数一点也不讲道理,比如 π ,无限不循环,迷茫过后的有理,突然醒悟,只有不断的增加自己的成员,才能适应快速发展的社会,将
1 、无限不循环小数。不能写作两整数之比; 2 、不是有理数的实数。
来历
记忆法
Natural number
苹果挺甜,来个 空 篮子, 1、2、3 ,, 。
仍掉零蛋的自然数
德国女数学家诺特对环理论的贡献, 1921年写出的《整环的理想理论 》是交换代数发展的里程碑。德语中的整数叫做 Zahlen ,于是当时她 将整数环记作 Z,从那时候起整数集就用 Z 表示了。
