单片机中IIR滤波器的实现
STM32实现IIR低通滤波器

STM32实现IIR低通滤波器matlab的fdatool是好东西,不过很多人不知道该怎么使用它生成的C头文件。
趁着放假有时间,摸索了几天,终于搞定。
希望阿莫给条裤子。
该程序已经用于心电采集实验导联aVF,带宽1-25Hz实验过程中图片(原文件名:DSCF6003.JPG)液晶截图(原文件名:aVF_LCD.jpg)不多说,切入正题这里有个fdatool设计的IIR高通滤波器,采样率400Hz时截止频率1Hz。
设计定型之后,要做些调整。
以下说明中的英文名词有些可能对不上fdatool界面上的原文,请大家意会吧第一步:点击菜单中的Edit->Convert Structure 选择Direct Form I ,SOS,(必须是Direct Form I, II不行)一般情况下,按照默认设置,fdatool设计都是由二阶部分串联组成的。
这种结构的滤波器稳定性比一个section的要好很多,其他方面的性能也好些。
如果不是的话,点击Convert to second order sections。
这时,滤波器的结构(structure)应该显示为 Direct Form I,second order sections第二步:选择quantize filter,精度选择single precision floating point (单精度浮点)之所以不用定点是因为噪声太大,也不容易稳定。
点击菜单中的Targets -> generate c header ,选择export as:single precision floating point (单精度浮点)填写变量名称时,把NUM改成IIR_B,DEN改成IIR_A,其他不用动,保存为iir_coefs.h保存好的文件如下://一大堆注释//然后:/* General type conversion for MATLAB generated C-code */#include "tmwtypes.h"/** Expected path to tmwtypes.h* C:\Program Files\MATLAB\R2010a\extern\include\tmwtyp es.h*//** Warning - Filter coefficients were truncated to fit specified data type.* The resulting response may not match generated theoret ical response.* Use the Filter Design & Analysis T ool to design accurate* single-precision filter coefficients.#define MWSPT_NSEC 9const int NL[MWSPT_NSEC] = { 1,3,1,3,1,3,1,3,1 }; const real32_T IIR_B[MWSPT_NSEC][3] = {{0.8641357422, 0, 0},{1, -2, 1},{0.9949035645, 0, 0},{1, -1.999938965, 1},{0.9985351563, 0, 0},{1, -1.99987793, 1},{0.9996337891, 0, 0},{1, -1.99987793, 1},{1, 0, 0};const int DL[MWSPT_NSEC] = { 1,3,1,3,1,3,1,3,1 }; const real32_T IIR_A[MWSPT_NSEC][3] = {{1, 0, 0},{1, -1.938049316, 0.9401855469},{1, 0, 0},{1, -1.989501953, 0.9900512695},{1, 0, 0},{1, -1.996887207, 0.9971923828},{1, 0, 0},{1, -1.999084473, 0.9993286133},{1, 0, 0};第三步:打开iir_coefs.h把MWSPT_NSEC替换成IIR_NSEC, NL、DL数组删除掉,real32_T改成float ,其中有一个#include "twmtypes.h",不要它了,删掉改完的文件如下:#define IIR_NSEC 9//原来叫做MWSPT_NSECconst float IIR_B[IIR_NSEC][3] = {//为什么改为float很明显了吧{0.8641357422, 0, 0},{1, -2, 1},{0.9949035645, 0, 0},{1, -1.999938965, 1},{0.9985351563, 0, 0},1, -1.99987793, 1},{0.9996337891, 0, 0 },{1, -1.99987793, 1},{1, 0, 0}};const float IIR_A[IIR_NSEC][3] = { {1, 0, 0},{1, -1.938049316, 0.9401855469 },{1, 0, 0},{1, -1.989501953, 0.9900512695 },{1, 0, 0},1, -1.996887207, 0.9971923828},{1, 0, 0},{1, -1.999084473, 0.9993286133},{1, 0, 0}};保存文件,然后使用以下代码进行滤波这段代码是根据Direct Form I 2阶IIR滤波的差分方程编写的a0*y[n] = b0*x[n] + b1*x[n-1] + b2*x[n-2] - a1*y[n-1] -a2*y[n-2];//iir_filter.c#include "datatype.h"#include "iir_filter.h"#include "iir_coefs.h"static float y[IIR_NSEC][3];static float x[IIR_NSEC+1][3];int16 iir_filter(int16 in)uint16 i;x[0][0] = in;for(i=0;i<IIR_NSEC;i++){y[0] =x[0]*IIR_B[0]+x[1]*IIR_B[1]+x[2]*IIR_B[2]-y[1]*IIR_A[1]-y[2]*IIR_A[2];y[0] /= IIR_A[0];y[2]=y[1];y[1]=y[0];x[2]=x[1];x[1]=x[0];x[i+1][0] = y[0];}if( x[IIR_NSEC][0]>32767) x[IIR_NSEC][0]=32767;if( x[IIR_NSEC][0]<-32768) x[IIR_NSEC][0]=-32768;return ((int16)x[IIR_NSEC][0]);}//复位滤波器void iir_reset(void){uint16 i,j;for(i=0;i<IIR_NSEC+1;i++){for(j=0;j<3;j++){x[j]=0;}}for(i=0;i<IIR_NSEC;i++){for(j=0;j<3;j++){y[j]=0;}}}//iir_filter.h#ifndef _IIR_FILTER_H__#define _IIR_FILTER_H__int16 iir_filter(int16 x);void iir_reset(void);#endif使用方法:首先写好iir_coefs.h,然后调用iir_filter.c对数据流进行滤波一个伪代码例子:while(运行中){保存到SD卡(iir_filter(读取ADC采样值()));}这个函数比STM32 DSP库中的函数要好很多,DSP库中的2个IIR滤波函数都不能连续处理数据流。
IIR滤波器的DSP实现
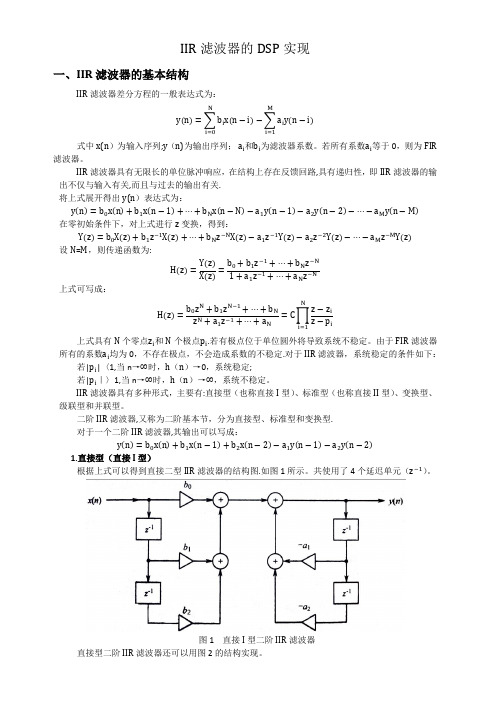
IIR滤波器的DSP实现一、IIR滤波器的基本结构IIR滤波器差分方程的一般表达式为:y(n)=∑b i x(n−i)Ni=0−∑a i y(n−i) Mi=1式中x(n)为输入序列;y(n)为输出序列; a i和b i为滤波器系数。
若所有系数a i等于0,则为FIR 滤波器。
IIR滤波器具有无限长的单位脉冲响应,在结构上存在反馈回路,具有递归性,即IIR滤波器的输出不仅与输入有关,而且与过去的输出有关.将上式展开得出y(n)表达式为:y(n)=b0x(n)+b1x(n−1)+⋯+b N x(n−N)−a1y(n−1)−a2y(n−2)−⋯−a M y(n−M)在零初始条件下,对上式进行z变换,得到:Y(z)=b0X(z)+b1z−1X(z)+⋯+b N z−N X(z)−a1z−1Y(z)−a2z−2Y(z)−⋯−a M z−M Y(z)设N=M,则传递函数为:H(z)=Y(z)X(z)=b0+b1z−1+⋯+b N z−N1+a1z−1+⋯+a N z−N上式可写成:H(z)=b0z N+b1z N−1+⋯+b Nz N+a1z−1+⋯+a N=C∏z−z iz−p iNi=1上式具有N个零点z i和N个极点p i.若有极点位于单位圆外将导致系统不稳定。
由于FIR滤波器所有的系数a i均为0,不存在极点,不会造成系数的不稳定.对于IIR滤波器,系统稳定的条件如下:若|p i|〈1,当n→∞时,h(n)→0,系统稳定;若|p i|〉1,当n→∞时,h(n)→∞,系统不稳定。
IIR滤波器具有多种形式,主要有:直接型(也称直接I型)、标准型(也称直接II型)、变换型、级联型和并联型。
二阶IIR滤波器,又称为二阶基本节,分为直接型、标准型和变换型.对于一个二阶IIR滤波器,其输出可以写成:y(n)=b0x(n)+b1x(n−1)+b2x(n−2)−a1y(n−1)−a2y(n−2)1.直接型(直接I型)根据上式可以得到直接二型IIR滤波器的结构图.如图1所示。
FIR滤波器和IIR滤波器原理及实现

FIR滤波器和IIR滤波器原理及实现FIR和IIR滤波器是数字信号处理中常用的滤波器类型,用于从输入信号中提取或抑制特定频率成分。
它们分别基于有限脉冲响应(FIR)和无限脉冲响应(IIR)的原理设计而成。
下面将分别介绍FIR和IIR滤波器的原理及实现方式。
一、FIR滤波器H(z)=b0+b1•z^(-1)+b2•z^(-2)+...+bM•z^(-M)其中,b0、b1、..、bM是FIR滤波器的系数,M为滤波器的阶数。
1.确定滤波器的设计要求,包括通带和阻带的边界频率、通带和阻带的衰减要求等。
2.根据设计要求,选择合适的滤波器设计方法,如FIR滤波器可以通过窗函数设计、频率采样法设计等。
3.根据设计方法计算得到滤波器的系数,即b0、b1、..、bM。
4.将计算得到的系数应用到差分方程中,实现滤波器。
5.将输入信号通过差分方程进行滤波处理,得到输出信号。
二、IIR滤波器IIR滤波器是一种具有无限长度的单位脉冲响应的滤波器,它具有反馈回路,可以实现对信号频率的持续平滑。
IIR滤波器的离散时间系统函数可以表示为:H(z)=[b0+b1•z^(-1)+b2•z^(-2)+...+bM•z^(-M)]/[1+a1•z^(-1)+a2•z^(-2)+...+aN•z^(-N)]其中,b0、b1、..、bM和a1、a2、..、aN分别为IIR滤波器的前向和反馈系数,M和N分别为前向和反馈滤波器的阶数。
实现IIR滤波器的步骤如下:1.确定滤波器的设计要求,选择合适的滤波器类型(低通、高通、带通、带阻等)。
2.根据设计要求,选择合适的设计方法(脉冲响应不变法、双线性变换法等)。
3.根据设计方法计算得到滤波器的系数,即b0、b1、..、bM和a1、a2、..、aN。
4.将计算得到的系数应用到差分方程中,实现IIR滤波器。
5.将输入信号通过差分方程进行滤波处理,得到输出信号。
IIR滤波器的优点是可以实现较窄的通带和截止频率,具有良好的频率响应特性,但由于反馈回路的存在,容易出现稳定性问题,设计和实现相对较为复杂。
8位单片机低通滤波算法

8位单片机低通滤波算法低通滤波算法是一种常用于信号处理的滤波算法,用于去除高频噪声,保留低频信号。
在8位单片机中实现低通滤波算法,可以采用数字滤波器的方法,其中一种常用的方法是IIR(Infinite Impulse Response)滤波器。
IIR滤波器是一种递归滤波器,其输出是由输入信号和之前的输出信号线性组合而成的。
其结构如下:y[n] = b0 * x[n] + b1 * x[n-1] + ... + bn * x[n-n] - a1 *y[n-1] - a2 * y[n-2] - ... - am * y[n-m]其中,x[n]是当前输入信号,y[n]是当前输出信号,a1, a2, ...,am是滤波器的系数,b0, b1, ..., bn是输入信号的系数。
在单片机中实现低通滤波算法的步骤如下:1. 定义滤波器的系数a1, a2, ..., am和b0, b1, ..., bn,这些系数决定了滤波器的特性。
2.初始化输入和输出缓冲区,用于存储之前的输入和输出信号。
3.循环读取输入信号,并将其存储到输入缓冲区。
4.根据滤波器的结构,计算当前输出信号y[n],并将其存储到输出缓冲区。
5.更新输入和输出缓冲区,将当前输入和输出信号存储到之前的位置。
这样每次循环都可以使用最新的输入和输出信号。
6.将输出信号送入输出端。
需要注意的是,8位单片机的计算能力有限,因此在实现低通滤波算法时,需要考虑计算复杂度和存储空间的限制。
可以通过降低滤波器的阶数或使用简化的计算方法来减少计算量。
例如,如果滤波器的阶数较高,可以使用二阶节拍法(Biquad)结构来实现滤波器,该结构只需要保存两个输入和两个输出缓冲区,大大减少了存储空间的使用。
此外,还可以通过查表的方式来实现低通滤波算法,使用预先计算好的滤波器响应曲线,将输入信号与查表值相乘得到输出信号。
总之,通过合理选择滤波器结构和算法优化技巧,可以在8位单片机上有效实现低通滤波算法。
IIR滤波器实现方波滤波和音乐滤波

实验十一信号滤波1、对周期方波信号进行滤波% 用IIR 滤波器实现clcclearFs=1000; %随实际信号频率适当选择t=0:1/Fs:1;x=square(2*pi*10*t);%产生幅度为[-1,1]的方波% x=sawtooth(2*pi*10*t,0.5); %产生幅度为[-1,1]的三角波plot(t,x)title('矩形波')axis([0,0.4,-1.5,1.5]) %限定输出图形的坐标范围大小%求方波的频谱T=0.1; %取一个周期数据进行采样t1=0:1/Fs:(T-1/Fs);xn=square(2*pi*10*t1); %取样N=Fs*T;Xk=fft(xn,N); %算N点FFT频谱Xk=fftshift(abs(Xk));Xkl=Xk/N;figurestem(Fs/N*[0:1:N-1],Xkl)title('方波信号的频谱')[n,Wn]=buttord(10/500,80/500,3,40);% 确定butterworth滤波器的阶次,% 前两个参数如何设定?[b,a]=butter(n,Wn); %确定滤波器传递函数figurefreqs(b,a); %滤波器频率特性title('滤波器频率特性')y=filter(b,a,x); %滤波figureplot(t,y)title('矩形波通过低通滤波器后的波形')axis([0,0.4,-1.5,1.5]) s=randn(1,1001); %信号叠加噪声为什么是1001点?xs=x+s;figureplot(t,xs)title('信号叠加噪声的波形')%axis([0,0.5,-2,2])N=512; %加噪音信号的频谱fx=fftshift(fft(xs,N));figuref=(-N/2:(N/2-1))*2;f=f*Fs/N;plot(f,abs(fx))title('加噪声的频谱')yl=filter(b,a,xs); %采用filter函数滤波figureplot(t,yl)%滤波后的波形title('滤波后的波形')%axis([0,0.5,-2,2])figurefxs=fftshift(fft(yl,N)); %滤波后波形的频谱f=(-N/2:(N/2-1))*2;f=f*Fs/N;plot(f,abs(fxs))title('滤波后的频谱')2、对混有噪声的音乐信号进行滤波clcclearmusic=wavread('C:\MATLAB7\toolbox\dspblks\ dspdemos\dspafsx_mono.wav');music=music'; % dspafsx_mono.wav文件地址随系统安装位置不同而异a=size(music)%利用media player观察音乐持续时间为3s,信号的采样点数为60000,可知信号的采样频率为20KHzmusic=decimate(music,2);%音乐的采样频率降低为10KHzt=0:0.0001:(3-0.0001);x=sin(2*pi*1000*t)+sin(2*pi*3000*t); %加入两个正弦信号噪声,1kHz和3kHzmx=music+x;sound(music)%用sound函数播放mono.wav音乐文件%sound(mx)figuresubplot(3,1,1),plot(t,music),title('音乐信号')subplot(3,1,2),plot(t,x),title('正弦信号')subplot(3,1,3),plot(t,mx),title('叠加正弦干扰的音乐信号')N=512; %叠加干扰后,信号的频谱Fmx=fftshift(fft(mx,N));f=-N/2:1:(N/2-1);f=f*10000/N;figureplot(f, Fmx)title('叠加干扰后,信号的频谱')[b1,a1]=butter(2,[900/5000,1100/5000],'stop');%直接II型IIR带阻滤波器[b2,a2]=butter(2,[2800/5000,3200/5000],'stop');bt=conv(b1,b2);at=conv(a1,a2);%梳状滤波器传递函数系数bt, atfigurefreqz(bt,at); % 梳状滤波器频率响应title('梳状滤波器频率响应')y2=filter(bt,at,mx);figuresubplot(3,1,1),plot(t,music),title('音乐信号')subplot(3,1,2),plot(t,mx),title('叠加正弦干扰的音乐信号')subplot(3,1,3),plot(t,y2),title('滤波后的信号')%sound(y2)N=512; %滤波后信号的频谱Fmxl=fftshift(fft(y2,N));f=-N/2:1:(N/2-1);f=f*10000/N;figureplot(f,Fmxl)title('滤波后信号的频谱')%用filtfilt函数实现零相位滤波y3=filtfilt(bt,at,mx);figuresubplot(3,1,1),plot(t,music),title('音乐信号')subplot(3,1,2),plot(t,y2),title('非零相位滤波后的信号')subplot(3,1,3),plot(t,y3),title('零相位滤波后的信号') %sound(y3)2014年12月24日(三) -- 12月24日实验内容请完成以下内容1、清楚方波信号的频谱特点;2、掌握IIR和FIR两种滤波器设计方法;3、完成实验指导书上内容后,请改变滤波器参数,使得滤波器可以实现以下各种功能:1)、只保留基波10赫兹成分;(低通)2)、只保留5次谐波即50赫兹信号成分;(带通)3)、保留方波信号中40赫兹以后(含40赫兹)成分;(高通)4)、只滤掉30赫兹信号分量。
iir数字滤波器的设计方法

iir数字滤波器的设计方法IIR数字滤波器的设计方法IIR数字滤波器是一种常用的数字信号处理工具,用于对信号进行滤波和频率域处理。
其设计方法是基于传统的模拟滤波器设计技术,通过将连续时间滤波器转换为离散时间滤波器来实现。
本文将介绍IIR数字滤波器的设计方法和一些常见的实现技巧。
一、IIR数字滤波器的基本原理IIR数字滤波器是一种递归滤波器,其基本原理是将输入信号与滤波器的系数进行加权求和。
其输出信号不仅与当前输入值有关,还与之前的输入和输出值有关,通过不断迭代计算可以得到最终的输出结果。
二、IIR数字滤波器的设计步骤1. 确定滤波器的类型:低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
2. 确定滤波器的阶数:阶数决定了滤波器的陡峭度和性能。
3. 选择滤波器的截止频率或通带范围。
4. 根据所选的滤波器类型和截止频率,设计滤波器的模拟原型。
5. 将模拟原型转换为数字滤波器。
三、IIR数字滤波器的设计方法1. 巴特沃斯滤波器设计方法:- 巴特沃斯滤波器是一种最常用的IIR数字滤波器,具有平坦的通带特性和陡峭的阻带特性。
- 设计方法为先将模拟滤波器转换为数字滤波器,然后通过对模拟滤波器进行归一化来确定截止频率。
2. 阻带衰减设计方法:- 阻带衰减设计方法是一种通过增加滤波器的阶数来提高滤波器阻带衰减特性的方法。
- 通过增加阶数,可以获得更陡峭的阻带特性,但同时也会增加计算复杂度和延迟。
3. 频率变换方法:- 频率变换方法是一种通过对滤波器的频率响应进行变换来设计滤波器的方法。
- 通过对模拟滤波器的频率响应进行变换,可以得到所需的数字滤波器。
四、IIR数字滤波器的实现技巧1. 级联结构:- 将多个一阶或二阶滤波器级联起来,可以得到更高阶的滤波器。
- 级联结构可以灵活地实现各种滤波器类型和阶数的设计。
2. 并联结构:- 将多个滤波器并联起来,可以实现更复杂的频率响应。
- 并联结构可以用于设计带通滤波器和带阻滤波器。
IIR数字滤波器设计及实现

实验三IIR数字滤波器设计及实现一、实验目的(1)熟悉用脉冲响应不变法和双线性变换法设计IIR数字滤波器的原理与方法;(2)学会调用MATLAB信号处理工具箱中滤波器设计函数设计IIR数字滤波器,学会根据滤波需求确定滤波器指标参数。
二、实验原理设计IIR数字滤波器一般采用脉冲响应不变法和双线性变换法。
脉冲响应不变法:根据设计指标求出滤波器确定最小阶数N和截止频率Wc;计算相应的模拟滤波器系统函数;将模拟滤波器系统函数:'转换成数字滤波器系统函数双线性变换法:根据数字低通技术指标得到滤波器的阶数N;取合适的T值,几遍校正计算相应模低通的技术指标--;根据阶数N查表的到归一化低通原型系统函数。
,将"' Q 代入。
‘去归一化得到实际的,/ :' ;用双线性变换法将:’转换成数字滤波器三、实验内容及步骤1、用脉冲响应不变法设计(1)根据设计指标求出滤波器确定最小阶数N和截止频率Wcclear;close all;clc; % 开始准备fp=3400;fs=5000;Fs=22050;Rp=2;Rs=20;T=1/Fs; % T=1s 的模拟滤波器设计指标W1p=fp/Fs*2; W1s=fs/Fs*2; % 求归一化频率[N, Wn] = buttord(W1p, W1s, Rp, Rs, 's'; % 确定 butterworth 的最小阶数 N 和频率参数Wn 得到结果为:N 二7Wn 二 0.3266 即:该设计指标下的模拟滤波器最小阶数为N=7,其截至频率为Wn =0.3266;(2)计算相应的模拟滤波器系统函数打:, clear;close all;clc; % 开始准备fp=3400;fs=5000;Fs=22050;Rp=2;Rs=20;T=1/Fs; % T=1s 的模拟滤波器设计指标W1p=fp/Fs*2; W1s=fs/Fs*2; % 求归一化频率[N, Wn] = buttord(W1p, W1s, Rp, Rs, 's'; % 确定 butterworth 的最小阶数 N 和频率参数 Wn[B,A]=butter(N,1,'s' %计算相应的模拟滤波器系统函数得到结果为: B = 1.0e-003 * 0 00 0 0 0 0 0.3966 A =1.0000 1.4678 1.0773 0.5084 0.1661 0.0375 0.0055 0.0004 >>(3)将模拟滤波器系统函数转换成数字滤波器系统函数 clear;close all;clc; % 开始准备fp=3400;fs=5000;Fs=22050;Rp=2;Rs=20;T=1/Fs; % T=1s 的模拟滤波器设计指标W1p=fp/Fs*2; W1s=fs/Fs*2; % 求归一化频率[N, Wn] = buttord(W1p, W1s, Rp, Rs, 's'; % 确定 butterworth 的最小阶数 N 和频率参数Wn[B,A]=butter(N,1,'s' ; %计算相应的模拟滤波器系统函数 [Bz,Az]=impinvar(B,A %用脉冲相应不变法将模拟滤波器转换成数字滤波器 sys=tf(Bz,Az,T; %得到传输函数‘‘‘‘‘ Bz =1.0e-004 *-0.0000 0.0045 0.2045 0.8747 0.7094 0.1090 0.0016 0Az =1.0000 -5.5415 13.2850 -17.8428 14.4878 -7.1069 1.9491 -0.2304>>>>即:由Bz和Az可以写出数字滤波器系统函数为:Transfer function:-9.992e-015 z~7 + 4.454e-007 z~6 + 2.045e-005 z~5 + 8.747e-005 z~4 + 7.094e-005 z"3 + 1.09e-005 z~2+ 1.561e-007 z z 7 - 5.541 z 6 + 13.28 z 5 - 17.84 z 4 + 14.49 z 3 - 7.107 z 2 + 1.949 z - 0.2304Sampling time: 4.5351e-005>>(4)绘图clear;close all;clc; % 开始准备fp=3400;fs=5000;Fs=22050;Rp=2;Rs=20;T=1/Fs; % T=1s 的模拟滤波器设计指标W1p=fp/Fs*2; W1s=fs/Fs*2; % 求归一化频率[N, Wn] = buttord(W1p, W1s, Rp, Rs, 's'; % 确定butterworth 的最小阶数N 和频率参数Wn[B,A]=butter(N,Wn,'s'; %计算相应的模拟滤波器系统函数[Bz,Az]=impinvar(B,A; %用脉冲响应不变法将模拟滤波器转换成数字滤波器sys=tf(Bz,Az,T;%得到传输函数‘ [H,W]=freqz(Bz,Az,512,Fs; % 生成频率响应参数plot(W,20*log10(abs(H; % 绘制幅频响应grid on; %加坐标网格得到结果为:观察实验结果图可看到:在频率为3402Hz处频率为衰减2.015db,在频率为5017Hz处幅度衰减21.36db。
IIR数字滤波器的设计及软件实现

IIR 数字滤波器的设计及软件实现一.实验目的(1)熟悉用双线性变换法设计IIR 数字滤波器的原理与方法; (2)学会用MATLAB 信号处理工具箱中的滤波器设计函数(或滤波器设计分析工具FDAtool )设计各种滤波器,学会根据滤波需求确定滤波器指标参数; (3)掌握IIR 数字滤波器的MATLAB 实现方法;(4)通过观察滤波器输入、输出信号的时域波形及其频谱,建立数字滤波的概念。
二.实验原理设计IIR 数字滤波器一般采用间接法(脉冲响应不变法和双线性不变法),应用最广泛的是双线性变换法。
基本的设计过程是:①将给定的数字滤波器指标转换成模拟滤波器的指标; ②涉及模拟滤波器;③将模拟滤波器的系统函数转换成数字滤波器的系统函数。
MATLAB 信号处理工具箱中的各种IIR 数字滤波器设计函数都是采用双线性变换法。
本实验的数字滤波器的MATLAB 实验是调用MATLAB 信号处理工具箱的函数filter 对给定的输入信号x(n)进行滤波,得到滤波后的输出信号y(n). 三.实验内容及步骤1.信号处产生函数mstg 产生由三路抑制载波调幅信号相加构成的复合信号st ,该函数还会自动回图显示st 的时域波形和幅频特性曲线,由后图可见,三路信号时域混叠无法在时域分离。
但频域是分离的,所以可通过滤波的方法在频域分离。
2.将st 中三路调幅信号分离,通过观察st 的幅频特性曲线,分别确定可以分离st 中三路抑制载波单频调幅信号的三个滤波器(低通滤波器、带通滤波器、高通滤波器)的通带截止频率和阻带截止频率。
且滤波器的通带最大衰减为0.1dB ,阻带最小衰减为60bB 。
提示:抑制载波单频调幅信号的数学表示式为()()()()()()[]tt t t t s f f f f f f c c c 0002cos 2cos 212cos 2cos )(++-==ππππ 其中,()t fc2cos π称为载波,f c为载波频率,()t f 02cos π称为单频调制信号,f为调制正弦波信号频率,且满足fc>f。
IIR滤波器的设计与实现

IIR滤波器的设计与实现IIR滤波器(Infinite Impulse Response Filter)是一种数字滤波器,其特点是具有无限冲激响应。
与FIR滤波器不同,它的输出不仅与输入信号有关,还与历史输入信号有关。
这使得IIR滤波器在一些应用中具有更高的灵活性和效率。
设计一个IIR滤波器主要包括确定滤波器的传递函数和选择滤波器类型两个步骤。
在确定传递函数时,可以根据不同的要求选择不同的滤波器类型,如低通滤波器、高通滤波器、带通滤波器等。
常见的IIR滤波器设计方法包括脉冲响应不变法、双线性变换法和频率抽样法等。
在实际实现过程中,可以使用各种工具和软件进行设计和仿真。
其中一种常用的设计方法是MATLAB工具包中提供的函数,如butter、cheby、ellip等。
这些函数可以根据用户提供的设计参数生成IIR滤波器的系数。
通过调试和优化这些系数,可以得到满足要求的滤波器。
IIR滤波器的实现通常分为直接形式和间接形式两种。
直接形式实现简单直观,但会引入大量的计算和存储开销;间接形式在计算和存储方面更加高效,但会增加系统的复杂性。
选择哪种实现形式需要根据具体应用场景和性能需求来决定。
在进行IIR滤波器的实际设计和实现时,还需要注意一些常见的问题。
例如,滤波器的阶数和截止频率的选择需要根据信号的特性和要求来确定;如果滤波器存在共振或不稳定的问题,可以通过增加阶数或调整系数来解决;另外,在实际应用中,可能还需要考虑滤波器的滤波延迟、实时性和系统资源消耗等因素。
总之,IIR滤波器的设计和实现是一个综合考虑信号特性、要求和系统约束的过程。
通过选择合适的设计方法、优化滤波器系数和选择合适的实现形式,可以得到满足要求的高性能滤波器。
IIR数字滤波器的设计及软件实现

IIR数字滤波器的设计及软件实现什么是IIR数字滤波器?IIR数字滤波器是一种数字信号处理滤波器,它基于递归的思想,可以对原始信号进行滤波处理。
与FIR数字滤波器相比,IIR数字滤波器具有更高的效率和更灵活的设计。
它的设计基于对滤波器的传递函数进行分析和优化,可以通过不同的传递函数来实现不同的滤波目标。
IIR数字滤波器的设计方法要设计一个IIR数字滤波器,可以采用以下步骤:步骤1:确定滤波器的类型根据滤波的目的和要求,确定滤波器的类型。
常见的滤波器类型有低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
步骤2:计算滤波器的阶数滤波器的阶数是指滤波器中的二阶段数。
阶数越高,滤波器的性能越好,但也意味着计算量和实现难度会增加。
根据滤波的要求和性能要求,计算滤波器的阶数。
步骤3:选择滤波器的截止频率滤波器的截止频率是指滤波器在截止频率附近的频率响应。
对于低通滤波器和高通滤波器,截止频率通常是一个常数。
对于带通滤波器和带阻滤波器,截止频率需要确定两个频率。
步骤4:计算滤波器的传递函数根据滤波器类型、阶数和截止频率,可以通过传递函数的计算得到滤波器的传递函数。
步骤5:采用正则化处理在计算得到传递函数后,需要进行正则化处理。
正则化处理可以消除传递函数中的不稳定性,并确保滤波器的稳定性和可变性。
步骤6:实现反馈环和前馈环根据传递函数,可以实现反馈环和前馈环。
反馈环和前馈环的选择会影响滤波器的性能。
IIR数字滤波器的软件实现要实现IIR数字滤波器,可以使用MATLAB或Python等数学软件。
这里以Python为例进行说明。
步骤1:导入必要的库import numpy as np #用于处理数组和矩阵import scipy.signal as signal #用于信号处理import matplotlib.pyplot as plt #用于绘图步骤2:指定滤波器的类型、截止频率和阶数type ='lowpass'#低通滤波器fc =2000#截止频率order =4#阶数步骤3:计算滤波器的系数b, a = signal.butter(order, fc, type)步骤4:生成信号并进行滤波t = np.linspace(0, 1, 500, endpoint=False)x = np.sin(2* np.pi *5* t) + np.sin(2* np.pi *10* t) + np.sin(2* np.pi *20* t)y = signal.filtfilt(b, a, x)步骤5:绘制原始信号和滤波后的信号plt.plot(t, x, label='original signal')plt.plot(t, y, label='filtered signal')plt.legend(loc='best')plt.show()IIR数字滤波器是数字信号处理中一种重要的滤波器。
基于ARMCortex_M3的IIR滤波器的实现

基于ARM Cortex-M3的IIR滤波器的实现*邹 进 何乐生(云南大学信息学院 昆明 650091)摘 要:基于ARM Cortex-M3芯片设计了IIR滤波器,滤除心电信号混有的50Hz工频干扰。
经MATLAB实验表明所设计的IIR滤波器对50Hz工频干扰具有良好的滤波效果。
将其移植到以ARM Cortex-M3芯片为CPU的系统中,取得了同样良好的滤波效果,验证了ARM Cortex-M3核虽然不是专用的DSP芯片,但其高性能和高时钟频率使其能在数字信号处理应用上获得较好的性能,具有较好的应该用前景。
本文致力于促进ARM Cortex-M3系列在嵌入式系统领域的应用推广。
关键词:ARM Cortex-M3;IIR滤波器;心电信号中图分类号:TP391.9 文献标识码:AIIR filter implementation base on ARM Cortex-M3Zou Jin He Lesheng(School of Information Science &Technology Yunnan University,Kunming 650091,China)Abstract:An IIR filter is designed based on the ARM Cortex-M3chip to filter the 50Hz frequency interference mixed inECG signal.The experiment based on MATLAB shows that the 50Hz frequency interference is effectively filtered fromECG signal by the IIR filter.When it is transplanted to the system in which the ARM Cortex-M3is applied as CPU chip,the IIR filter still works well,that verified better performance can be obtained in digital signal processing as its high per-formance and high clock frequency,although ARM Cortex-M3core is not a dedicated DSP chip and a good prospect in dig-ital signal processing can be expected.This paper is committed to promoting the application and popularization of ARMCortex-M3series in the field of embedded systems.Keywords:ARM Cortex-M3;IIR filter;ECG 收稿日期:2011-6-24*基金项目:云南省科技计划项目(基于嵌入式系统的肌电信号动作识别方法的研究编号:2008CD080)资助。
实验三IIR数字滤波器设计及软件实现

实验三IIR数字滤波器设计及软件实现IIR数字滤波器是一种常见的数字滤波器类型,它可以实现对信号的频率响应进行调整和改变,常用于信号处理和通信系统中。
本实验将介绍IIR数字滤波器的设计方法和软件实现。
设计一个IIR数字滤波器的一般步骤如下:1.确定滤波器的类型:低通滤波器、高通滤波器、带通滤波器或带阻滤波器。
2.确定滤波器的阶数:阶数决定了滤波器的复杂程度和性能。
3.确定滤波器的截止频率:截止频率决定了滤波器对信号的频率响应的影响。
4.根据滤波器类型和截止频率的要求,选择适当的滤波器设计方法:脉冲响应不变法、双线性变换法等。
5.根据滤波器设计方法,计算出滤波器的系数:系数决定了滤波器的频率响应和性能。
6.实现滤波器的差分方程:将滤波器的系数代入差分方程中,得到滤波器的离散时间域表示。
7. 使用合适的软件工具进行滤波器的软件实现和仿真:可以使用MATLAB、Python等编程语言进行滤波器设计和实现。
在软件实现过程中,通常可以通过以下步骤来实现IIR数字滤波器:1.定义滤波器的参数和输入信号:定义滤波器的类型、阶数、截止频率等参数,并读取输入信号。
2.计算滤波器的系数:根据设计方法和参数,计算滤波器的系数。
3.实现滤波器的差分方程:根据滤波器的差分方程,使用循环结构来实现滤波器的运算。
4.输入信号进入滤波器:将输入信号输入滤波器,进行滤波处理。
5.输出滤波后的信号:获取滤波器的输出结果,并进行处理和显示。
需要注意的是,IIR数字滤波器的设计和实现需要对信号处理和数字滤波器的基本原理有一定的了解,并且需要根据实际需求选择合适的设计方法和参数。
参考资料:2. Zhu, Y., & Buck, J. (2024). VLSI signal processing. John Wiley & Sons.。
iir数字滤波器设计及c语言程序

iir数字滤波器设计及c语言程序IIR数字滤波器设计及C语言程序IIR(Infinite Impulse Response)数字滤波器是一种常用的数字信号处理技术,广泛应用于音频处理、图像处理、通信系统等领域。
本文将介绍IIR数字滤波器的设计原理,并给出相应的C语言程序实现。
一、IIR数字滤波器的设计原理IIR数字滤波器的设计基于差分方程,其输入信号和输出信号之间存在一定的差分关系。
相比于FIR(Finite Impulse Response)数字滤波器,IIR数字滤波器具有更窄的转换带宽、更高的滤波器阶数和更好的相位响应等特点。
IIR数字滤波器的设计主要包括两个关键步骤:滤波器规格确定和滤波器参数计算。
首先,根据实际需求确定滤波器的类型(低通、高通、带通或带阻)、截止频率、通带衰减和阻带衰减等规格。
然后,根据这些规格利用数字滤波器设计方法计算出滤波器的系数,从而实现对输入信号的滤波。
二、IIR数字滤波器的设计方法常见的IIR数字滤波器设计方法有脉冲响应不变法、双线性变换法和最小均方误差法等。
下面以最常用的脉冲响应不变法为例介绍设计方法。
脉冲响应不变法的基本思想是将模拟滤波器的脉冲响应与数字滤波器的单位脉冲响应进行匹配。
首先,根据模拟滤波器的传递函数H(s)确定其脉冲响应h(t)。
然后,将连续时间下的脉冲响应离散化,得到离散时间下的单位脉冲响应h[n]。
接下来,根据单位脉冲响应h[n]计算出数字滤波器的差分方程系数,从而得到滤波器的数字表示。
三、IIR数字滤波器的C语言程序实现下面给出一个简单的IIR数字滤波器的C语言程序实现示例,以低通滤波器为例:```c#include <stdio.h>#define N 100 // 输入信号长度#define M 5 // 滤波器阶数// IIR数字滤波器系数float b[M+1] = {0.1, 0.2, 0.3, 0.2, 0.1};float a[M+1] = {1.0, -0.5, 0.3, -0.2, 0.1};// IIR数字滤波器函数float IIR_filter(float *x, float *y, int n) {int i, j;float sum;for (i = 0; i < n; i++) {sum = 0;for (j = 0; j <= M; j++) { if (i - j >= 0) {sum += b[j] * x[i - j]; }}for (j = 1; j <= M; j++) { if (i - j >= 0) {sum -= a[j] * y[i - j]; }}y[i] = sum;}}int main() {float x[N]; // 输入信号float y[N]; // 输出信号int i;// 生成输入信号for (i = 0; i < N; i++) {x[i] = i;}// IIR数字滤波器滤波IIR_filter(x, y, N);// 输出滤波后的信号for (i = 0; i < N; i++) {printf("%f ", y[i]);}return 0;}```以上是一个简单的IIR数字滤波器的C语言程序实现示例。
IIR滤波器的原理与设计方法

IIR滤波器的原理与设计方法IIR(Infinite Impulse Response)滤波器是一种数字滤波器,其具有无限冲激响应的特点。
与FIR(Finite Impulse Response)滤波器相比,IIR滤波器具有更高的效率和更窄的频带特性。
本文将介绍IIR滤波器的原理和设计方法。
一、IIR滤波器的原理IIR滤波器是通过对输入信号和输出信号之间的差异进行递归运算而实现滤波的。
其核心原理是利用差分方程来描述滤波器的行为。
IIR滤波器可以被表达为如下形式:y[n] = b₀x[n] + b₁x[n-1] + ... + bₘx[n-ₘ] - a₁y[n-1] - ... - aₘy[n-ₘ]其中,x[n]表示输入信号的当前采样值,y[n]表示输出信号的当前采样值,a₁,...,aₘ和b₀,...,bₘ是滤波器的系数。
二、IIR滤波器的设计方法设计IIR滤波器需要确定滤波器的阶数、截止频率和系数等参数,以下介绍一种常用的设计方法:巴特沃斯滤波器设计方法。
1. 确定滤波器阶数滤波器的阶数决定了滤波器的复杂度和频率响应的形状。
阶数越高,频率响应越陡峭。
根据需要的滤波效果和计算复杂度,选择适当的滤波器阶数。
2. 确定截止频率截止频率是滤波器在频域上的边界,用于确定滤波器的通带和阻带。
根据信号的频谱分析以及滤波器的应用要求,确定合适的截止频率。
3. 求解滤波器系数根据巴特沃斯滤波器的设计方法,可以采用双线性变换、频率抽样和极点放置等技术求解滤波器的系数。
具体方法比较复杂,需要使用专业的滤波器设计软件或者数字信号处理工具包进行计算。
4. 评估设计结果设计完成后,需要评估滤波器的性能指标,如频率响应、相位响应、群延迟等。
可以通过频域分析和时域仿真等方法来评估滤波器的设计效果。
三、结论IIR滤波器是一种常用的数字滤波器,其具有无限冲激响应的特点。
通过对输入信号和输出信号进行递归运算,可以实现滤波效果。
设计IIR滤波器需要确定滤波器的阶数、截止频率和系数等参数,并通过专业的设计方法进行求解。
IIR滤波器的设计和实现

IIR滤波器的设计和实现摘要目前IIR滤波器的设计方法主要有两种,数模转换法和计算机辅助设计法。
数模转化法就是借助模拟滤波器进行设计。
先按照数字滤波器的设计指标得到模拟滤波器的系统函数,再通过一定的转换方式将其转换为数字滤波器。
而计算机辅助设计法就是将滤波器系数作为要求解的未知数,根据设计指标设联立方程,最终求解得出滤波器系数。
在IIR滤波器的设计当中,使用PSO算法能简化步骤。
种群中每个粒子的位置都是每一组滤波器系数解,而适应函数则是该系数所代表的滤波器幅频响应和理想滤波器之间的均方差之和。
这样适应函数越小,滤波器越接近设计目标。
经过多次迭代,我们求得的全局最佳值即是最好的一组滤波器系数。
关键词:IIR滤波器,双线性转换法,脉冲响应不变法,巴特沃兹滤波器,粒子群优化算法Design and implementation of IIR filterAbstractAt present, there are mainly two methods of IIR filter design, DAC and CAD. The analog to digital conversion method is designed by means of analog filter. First, according to the design index of the digital filter, the system function of the analog filter is obtained, and then converted to digital filter through a certain conversion mode. The computer aided design method is to use the filter coefficient as the unknowns of the required solution, and set up a joint equation according to the design index. Finally, the filter coefficient is obtained.In the design of IIR filter, the PSO algorithm can simplify the steps. The position of each particle in the population is the filter coefficient solution for each group, while the adaptive function is the sum of the amplitude frequency response of the filter and the mean square variance between the ideal filter. The smaller the adaptive function, the closer the filter is to the design target. After many iterations, the best global value is the best set of filter coefficients.Keywords:IIR filter,Bilinear transformation method,impulse invariance,butterworth,PSO目录摘要 (1)Abstract (2)第一章绪论 (4)1.1 研究数字滤波器的背景 (4)1.1.1 数字滤波器 (4)1.1.2 IIR滤波器 (4)1.2 国内外研究现状 (5)1.3 本文的研究内容 (5)第二章采纳数模转换法设计IIR滤波器 (6)2.1 IIR滤波器的简介 (6)2.1.1 IIR滤波器的特性 (6)2.1.2 IIR滤波器的结构 (7)2.1.3 模拟滤波器的特性 (10)2.2 采纳双线性变换法设计IIR滤波器 (11)2.2.1 双线性变换法的基本原理 (11)2.2.2 基于双线性变换法的IIR滤波器设计实例 (13)2.3 采纳脉冲响应不变法设计IIR滤波器 (13)2.3.1 脉冲响应不变法的基本原理 (13)2.3.2 基于脉冲响应不变法的IIR滤波器设计实例 (15)2.4 本章小结 (15)第三章基于PSO算法设计IIR滤波器 (16)3.1 粒子群优化算法 (16)3.1.1 PSO算法的进展 (16)3.1.2 PSO算法的基本原理 (16)3.2 IIR滤波器设计的PSO算法 (18)3.2.1设计原理 (18)3.2.2设计实例 (19)3.3 本章小结 (20)结论 (21)参考文献 (22)致谢 (23)第一章绪论1.1 研究数字滤波器的背景1.1.1 数字滤波器现代社会中,人们的日常生活越来越数字化,越来越多的数字信号需要处理。
STM32F4 DSP库学习笔记9-DSP库函数中IIR滤波器的实现和效果
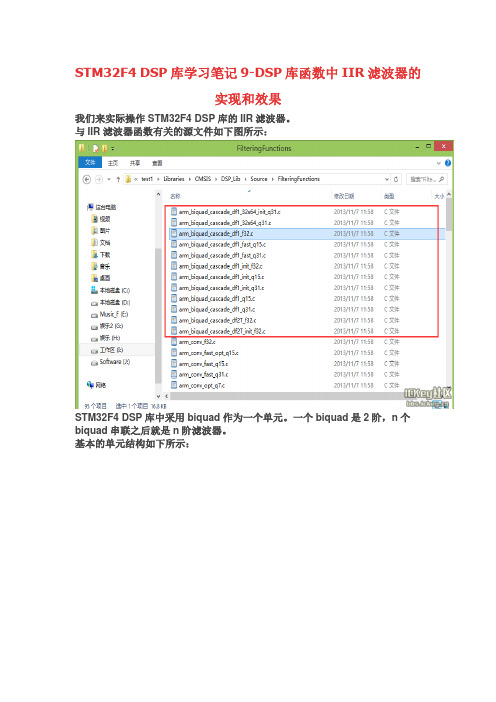
STM32F4 DSP库学习笔记9-DSP库函数中IIR滤波器的实现和效果我们来实际操作STM32F4 DSP库的IIR滤波器。
与IIR滤波器函数有关的源文件如下图所示:STM32F4 DSP库中采用biquad作为一个单元。
一个biquad是2阶,n个biquad串联之后就是n阶滤波器。
基本的单元结构如下所示:我们可以求出一个biquad的差分函数形式是:y[n] = b0 * x[n] + b1 * x[n-1] + b2 * x[n-2] - a1 * y[n-1] - a2 * y[n-2]Matlab里的计算就是按照上面的式子计算的,但是STM32F4 DSP库里的系数a1,a2是取反的。
下面就介绍如何使用MATLAB设计IIR滤波器。
举个例子,我们要设计一个采样率为1kHz,4阶,截止频率100Hz的巴特沃斯滤波器。
首先和设计FIR滤波器一样,首先在MATLAB命令窗口输入fdatool,调出滤波器设计窗口按照方框所示设置好参数:点击Design Filter:注意红框里面是直接II型,我们要把他改为直接I型。
点击Edit->Convert Structure,选择I型:转化好后,点击File-Export,第一项选择Coefficient File(ASCII):第一项选择好以后,第二项选择Decimal:点击Export,保存后生成如下文件:系数对应如下:1 2 1 1 -1.3209134308194264 0.63273879288527657b0 b1 b2 a0 a1 a21 2 1 1 -1.0485995763626117 0.29614035756166951b0 b1 b2 a0 a1 a2实际使用ARM官方的IIR函数调用的时候要将a1和a2取反。
把a0去掉Scale Values表示每个biquad的增益系数。
所以最后用STM32计算后,要乘以这两个系数。
第8章FIR滤波器和IIR滤波器原理及实现

给定的普通巴特沃斯特特性滤波器,其传递函数表示为:
H (s)
1
s2 2s 1
可产生该模拟电路的数字近似为:
H (z)
H
(
s)
|
s
1
(1
z
1
)
T
1 T2
(1
z 1 )2
1 2
1 T
(1
z1) 1
T2
(1 2z1 z2 ))z1 (1 2 T 2 )
FIR数字滤波器的冲激响应特性
❖ 分析: (2)如果将序列的频率增加至2000Hz,则冲激将变得更加尖锐。如图8.12 所示。 (3)减少谐波之间的频率间隔,将频率变为1Hz,2Hz,3Hz,4Hz,…,2000Hz, 也减少了脉冲周期。如图8.13所示。因此在极限状态下,当频率间隔趋于0 时,最后的结果只是一个冲激脉冲。
FIR滤波器和IIR滤波器原理及实现
主要内容
模拟到数字滤波器的转换 数字滤波器的分类及应用 FIR数字滤波器的原理和结构 IIR数字滤波器的原理和结构
DA FIR滤波器的设计 MAC FIR滤波器的设计 FIR Compiler滤波器的设计 HLS FIR滤波器的设计
模拟到数字滤波器的转换
离散域:y(k) 1 x(k) x(k 1) z变换
Ts
连续域:y(t) x(t)dt 拉普拉斯变换
离散域:y(k) Ts x(k) y(k 1) z变换
Y (z)
1 Ts
1
z1
X (z)
Y(s) X (s)
z
变s
换
Y (z)
1 Ts
1
z1
X (z)
模拟到数字滤波器的转换 ——微分方程近似法
STM32F4 DSP库学习笔记9-DSP库函数中IIR滤波器的实现和效果

STM32F4 DSP库学习笔记9-DSP库函数中IIR滤波器的实现和效果我们来实际操作STM32F4 DSP库的IIR滤波器。
与IIR滤波器函数有关的源文件如下图所示:STM32F4 DSP库中采用biquad作为一个单元。
一个biquad是2阶,n个biquad串联之后就是n阶滤波器。
基本的单元结构如下所示:我们可以求出一个biquad的差分函数形式是:y[n] = b0 * x[n] + b1 * x[n-1] + b2 * x[n-2] - a1 * y[n-1] - a2 * y[n-2]Matlab里的计算就是按照上面的式子计算的,但是STM32F4 DSP库里的系数a1,a2是取反的。
下面就介绍如何使用MATLAB设计IIR滤波器。
举个例子,我们要设计一个采样率为1kHz,4阶,截止频率100Hz的巴特沃斯滤波器。
首先和设计FIR滤波器一样,首先在MATLAB命令窗口输入fdatool,调出滤波器设计窗口按照方框所示设置好参数:点击Design Filter:注意红框里面是直接II型,我们要把他改为直接I型。
点击Edit->Convert Structure,选择I型:转化好后,点击File-Export,第一项选择Coefficient File(ASCII):第一项选择好以后,第二项选择Decimal:点击Export,保存后生成如下文件:系数对应如下:1 2 1 1 -1.3209134308194264 0.63273879288527657b0 b1 b2 a0 a1 a21 2 1 1 -1.0485995763626117 0.29614035756166951b0 b1 b2 a0 a1 a2实际使用ARM官方的IIR函数调用的时候要将a1和a2取反。
把a0去掉Scale Values表示每个biquad的增益系数。
所以最后用STM32计算后,要乘以这两个系数。
IIR数字滤波器的原理及设计课件

n
n k1
Ts N Ak e z skTs 1 n k1 n0
Ts
N
Ak
k11eskTs
z1
(6.66)
上式中的幂级数收敛应该满足条件:| eskTs z1 |1即
| z || eskTs |
实际上,只要将模拟滤波器的系统函数 Ha(s)分解为 (6.63)式所示的部分分式之和的形式,立即就可以写出相 应的数字滤波器的系统函数H(z)。
谱Xa ()的周期延拓,即
X a()T 1n Xa(ns)
而
X a( )X(ej)X(ej Ts)
(6.67) (6.68)
其中 Ts ,和 分别为数字角频率和模拟角频
率。也就是说,离散信号的频谱既可表示为数字频率的函
数也可表示为模拟频率的函数。又知道,对于离散信号的
傅里叶变换,有:
e e
Ha(jΩ))就是模拟滤波器的频率响应。如果对ha(t)抽样,
则由(6.70)式可知,有:
e T sha(ns)Tjn T s H a( n s)
n
n
(6.71)
令h(n) = Tsha(nTs),并以表示h(n)的频谱,也就是以h(n) 为冲激响应的数字滤波器的频率响应,于是由(6.71)式可
6.4.1 冲激响应不变法的变换方法
模拟滤波器的系统函数通常可以表示为:
M
M
ai si
(ssi )
Ha(s)
i0 N
A i1 N
bksk
(s sk )
k0
k1
(6.62)
而且一般都满足M<N,因此,可以将上式化为部分分式之
和的形式,即:
Ha(s)
N k1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单片机中(C语言)IIR滤波器的实现
转载原文参见https:///qq_21905401/article/details/53894517 IIR是无限长单位脉冲响应数字滤波器,其系统对应函数有如下形式:
在知道滤波器相应的系数b[],a[]后可根据相应的差分方程,完成对数据的滤波,而滤波器的系数可以通过Matlab滤波器设计和分析工具箱Filter Design&Analysis Tool求得,下面以一个IIR三阶低通滤波器为例,介绍C语言IIR滤波器的实现方法:
1、计算滤波器的系数
根据信号的采样频率以及低通滤波器的截止频率,通过Matlab工具箱求得滤波器的系数b和a。
如信号采样率为f=400Hz,低通滤波器的截止频率fc=60Hz:
Matlab中Start→ToolBoxes→Filter Design→Filter Design & Analysis Tool(fdatool)
在Filter Design & Analysis Tool,输入滤波器的相应指标,点击“Design Filter”设计滤波器。
如下图所示:
通过Analysis→Filter coefficients查看所设计滤波器系数:
响应函数:
2、差分方程C语言实现
根据相应函数得到差分方程:
a[0]*y[i]=Gain*(b[0]*x[i]+b[1]*x[i-1]+b[2]*x[i-2])-a[1]*y[i-1]-a[2]*y(n-2)
其中Gain=0.146747,b[]={1,2,1},a[]={1,-0.837000,0.42398},x[i]为输入信号,y[i]为滤波后信号。
C语言实现代码如下:
B[0]=1;B[1]=2;B[2]=1;
A[0]=1;A[1]=-0.837000;A[2]=0.42398;
Gain=0.146747;
w_x[0]=w_x[1]=w_x[2]=0;
w_y[0]=w_y[1]=w_y[2]=0;
for(int i=0;i<len;i++)
{
w_x[0]=x[i];
w_y[0]=(B[0]*w_x[0]+B[1]*w_x[1]+B[2]*w_x[2])*Gain-w_y[1]*A[1]-w_y[2]*A[2];
y[i]=w_y[0]/A[0];
w_x[2]=w_x[1];w_x[1]=w_x[0];
w_y[2]=w_y[1];w_y[1]=w_y[0];
}
也可以使用如下代码:
w[0]=w[1]=w[2]=0;
for(int i=0;i<len;i++)
{
w[0]=A[0]*x[i]-A[1]*w[2]-A[2]*w[2];
y[i]=(B[0]*w[0]+B[1]*w[1]+B[2]*w[2])*Gain;
w[2]=w[1];w[1]=w[0];
}
注意:在滤波之前,需要将系数w_x[]、w_y[]、w置零。
滤波前
滤波后
运用如上的方法可以设计50Hz陷波器,高通滤波器,只需要改变滤波器系数B、A即可。
50Hz 陷波器,Matlab工具箱设计如下:
50Hz陷波matlab陷波程序如下:
clear all;
clc;
f0=50;
Ts=0.0025;%采样率1khz
len=500;
n=0:len-1;
x=sin(2*pi*30*n*Ts)+sin(2*pi*50*n*Ts);%30,50Hz混合信号y=zeros(1,len);
B=[0.93721 -1.32542 0.93721];%50Hz陷波系数
A=[1 -1.3254 0.87443];
Gain=1;
w0=[0 0 0];
w1=[0 0 0];
for i=1:len
w0(1)=x(i);
c=B(1)*w0(1)+B(2)*w0(2)+B(3)*w0(3);
y(i)=c*Gain-A(2)*w1(2)-A(3)*w1(3);
w1(1)=y(i);
w0(3)=w0(2);w0(2)=w0(1);
w1(3)=w1(2);w1(2)=w1(1);
end
%或者下面的代码
% for i=1:len
% w0(1)=A(1)*x(i)-A(2)*w0(2)-A(3)*w0(3);
% y(i)=(B(1)*w0(1)+B(2)*w0(2)+B(3)*w0(3))*Gain;
% w0(3)=w0(2);w0(2)=w0(1);
% end
figure(1);
subplot(221);
plot(x);
subplot(222);
plot(y);
subplot(223);
hua_fft(x,1/Ts,1);
subplot(224);
hua_fft(y,1/Ts,1);。
