第 04 章 搜索策略 人工智能课件
人工智能之搜索策略介绍课件

实现搜索策略的优化
2
步骤:初始化种群、计算适应 度、选择、交叉、变异、迭代
3
优点:全局搜索能力强,能够 找到最优解
4
缺点:计算复杂度高,收敛速 度慢,容易陷入局部最优解
搜索策略的优化
优化目标
01 提高搜索效率:减少搜索 时间,提高搜索结果的准 确性
01
02
03
信息检索:搜索引擎、 路径规划:地图导航、 问题求解:数学问题、
学术论文检索等
物流配送等
逻辑问题等
04
05
06
游戏AI:棋类游戏、 电子游戏等
机器人控制:自主导 航、路径规划等
优化问题:生产调度、 资源分配等
搜索策略的实现
启发式搜索
概念:根据问题特点,选择 合适的搜索策略,提高搜索
效率
01
03
02
剪枝策略:提前 终止无效或低效 的搜索路径,提 高搜索效率
04
自适应搜索:根 据搜索过程中的 反馈信息,动态 调整搜索策略, 提高搜索效果
优化效果评估
准确率:衡量搜索 结果的准确性
召回率:衡量搜索 结果中相关结果的
比例
速度:衡量搜索算 法的执行效率
稳定性:衡量搜索 算法在不同数据集
上的表现一致性
演讲人
人工智能之搜索策略介 绍课件
目录
01. 搜索策略概述 02. 搜索策略的实现 03. 搜索策略的优化 04. 搜索策略的应用案例
搜索策略概述
搜索策略的定义
搜索策略是指在解
1 决一个问题时,如 何找到最优解或近 似最优解的方法。
搜索策略可以分
2 为两类:无信息 搜索和有信息搜 索。
人工智能搜索技术(PPT 79张)

7 283 714 65 15 2 8 3 714 6 5 24 2 8 3 7 4 615
16 1 2 3 84 765 26 25 2 8 3 1 2 3 1 2 3 714 8 4 784 65 765 65
234 234 28 248 1 8 185 143 1 3 765 76 765 765
3.1 盲目搜索
3.1.2 宽度优先搜索
定义3.1 如果搜索是以接近起始节点的程度依次扩展节点的, 那么这种搜索就叫做宽度优先搜索(breadth-first search)
3.1 盲目搜索
3.1.2 宽度优先搜索
宽度优先搜索算法 (1) 把起始节点放到OPEN表中(如果该起始节点为一目标节点, 则求得一个解答)。 (2) 如果OPEN是个空表,则没有解,失败退出;否则继续。 (3) 把第一个节点(节点n)从OPEN表移出,并把它放入 CLOSED的扩展节点表中。 (4) 扩展节点n。如果没有后继节点,则转向上述第(2)步。 (5) 把n的所有后继节点放到OPEN表的末端,并提供从这些后 继节点回到n的指针。 (6) 如果n的任一个后继节点是个目标节点,则找到一个解答, 成功退出;否则转向第(2)步。
9
2 5 1 4 6 7 3 8 2 5 1 4 6 7 3 8 2 4 5 1 6 7 3 8 2 4 5 1 6 7 3 8 2 4 5 1 3 6 7 8 2 4 5 1 6 7 3 8 2 4 5 1 3 6 7 8 2 4 5 1 3 6 72 8 3 1 6 4 7 5 2 8 3 1 4 7 6 5 2 3
4.图搜索方法分析:
图搜索过程的第8步对OPEN表上的节点进行排序,以便能够 从中选出一个“最好”的节点作为第4步扩展用。这种排序可 以是任意的即盲目的(属于盲目搜索),也可以用以后要讨论的 各种启发思想或其它准则为依据(属于启发式搜索)。每当被选 作扩展的节点为目标节点时,这一过程就宣告成功结束。这时, 能够重现从起始节点到目标节点的这条成功路径,其办法是从 目标节点按指针向S返回追溯。当搜索树不再剩有未被扩展的 端节点时,过程就以失败告终(某些节点最终可能没有后继节 点,所以OPEN表可能最后变成空表)。在失败终止的情况下, 从起始节点出发,一定达不到目标节点。
第四讲-知识搜索.

21
第四章 搜索策略
无信息图搜索属于盲目搜索,这里给两种常用的无信息图搜 索方法:广度优先搜索和深度优先搜索。 4.3.1 广度优先搜索(Breadth-First Search)
韩璐
第四章 搜索策略
搜索是人工智能研究的核心课题之一。人类的思维过程,可 以看作是一个搜索的过程。从小学到现在,你一定遇到过很多种 的智力游戏问题,比方说在第一章中介绍的传教士和野人问题。 如果你来做这个智力游戏的话,在每一次渡河之后,都会有几种 渡河方案供你选择,究竟哪种方案才有利于在满足题目所规定的 约束条件下顺利过河呢?经过反复努力和试探,你终于找到了一 种解决办法。在高兴之余,你马上可能又会想到,这个方案所用 的步骤是否最少?也就是说它是最优的吗?如果不是,如何才能 找到最优的方案?在计算机上又如何实现这样的搜索?这些问题 实际上就是本章我们要介绍的搜索问题。
搜索策略的主要任务是确定如何选取规则的方式。 盲目搜索的方法是不考虑给定问题所具有的特定知识,系统 根据事先确定好的某种固定排序,依次或随机调用规则。 启发式搜索策略是考虑问题领域可应用的知识,动态地确定 规则的排序,优先调用较合适的规则使用。
6
第四章 搜索策略
目前,人工智能领域中已提出许多具体的搜索方法:
(1)求任一解路的搜索策略
回溯法(Backtracking)
爬山法(Hill Climbing)
宽度优先法(Breadth-first)
人工智能搜索策略

通过强化学习技术,让搜索引擎在与用户互动中不断优化自身的搜 索策略,提升用户体验。
知识图谱驱动的搜索策略
借助知识图谱技术,理解实体之间的关系,为用户提供更精准的搜 索结果和推荐。
多智能体协同搜索技术探讨
多智能体系统架构
设计高效的多智能体系统架构,实现智能体之间的协同和信息共 享,提高搜索效率。
IDA*算法优化技巧
迭代加深
01
通过限制搜索深度,逐步增加深度限制,以实现迭代加深搜索,
提高搜索效率。
启发式函数优化
02
针对具体问题领域,设计更为有效的启发式函数,以提供更准
确的搜索指导。
剪枝策略
03
在搜索过程中,根据问题特性采用剪枝策略,如可行性剪枝、
最优性剪枝等,以减少无效搜索。
性能评估与对比分析
目的
搜索策略的主要目的是在给定的问题 空间内,通过智能地选择和探索可能 的解决方案,以最高效的方式找到问 题的最优解或近似最优解。
常见搜索策略类型
盲目搜索
包括深度优先搜索、广度优先搜 索等,这类策略在搜索过程中不 依赖任何问题特定的信息,而是 按照某种固定的模式进行搜索。
启发式搜索
如A*搜索、模拟退火算法等,这 类策略在搜索过程中会利用一些 与问题相关的启发式信息来指导 搜索方向,从而加速搜索过程并
04 遗传算法在搜索中应用
遗传算法基本原理介绍
遗传算法是一种模拟生物进化过 程的优化算法,通过模拟自然选 择和遗传学原理来搜索问题的最
优解。
遗传算法从一组随机生成的初始 解开始,通过不断迭代进化,逐
步逼近问题的最优解。
遗传算法采用适应度函数来评价 每个解的优劣,并根据适应度大 小进行选择、交叉和变异等操作,
人工智能课件-搜索技术

根据上述9种可能的状态和12种操作,可构成二阶梵塔问 题的状态空间图,如下图所示。
Searching: 18
(1,1)
A(1,2)
(2,1) B(1,3) (2,3) A(2,3)
A(1,3) (3,1) B(1,2) (3,2) A(3,2)(3,3)Fra bibliotek(1,3)
(1,2)
(2,2)
二阶梵塔的状态空间图
Searching: 8
状态空间法
• 状态(State): 是表示问题求解过程中每一步问题状况的数据结构,它可 形式地表示为: Sk={Sk0, Sk1, …} 当对每一个分量都给以确定的值时,就得到了一个具体的 状态。 • 操作(Operator) 也称为算符,它是把问题从一种状态变换为另一种状态的 手段。操作可以是一个机械步骤,一个运算,一条规则或一 个过程。操作可理解为状态集合上的一个函数,它描述了状 态之间的关系。
三是操作应保证不产生非法状态。
Searching: 23
操作的表示: 用符号Pij表示从左岸到右岸的运人操作 用符号Qij表示从右岸到左岸的操作 其中:
i表示船上的修道士人数
j表示船上的野人数 操作集 本问题有10种操作可供选择: F={P01, P10, P11, P02, P20,Q01, Q10, Q11, Q02, Q20}
– 初始状态集合:定义了agent所处的环境; – 操作符集合:把一个问题从一个状态变换为另一个状态 的动作; – 目标检测函数:agent用来确定一个状态是不是目标; – 路径费用函数:对每条路径赋予一定费用的函数。
初始状态集合和操作符集合定义了问题的搜索空间
Searching: 12
状态空间法求解问题的基本过程:
人工智能第三版课件第4章 图搜索策略

4.1 图搜索策略
(2)若p∈M且在closed表中,这说明: a. p在n之前已是某一节点m的后继,所以需 要作如(1)同样的处理,如下图右部。 b.p在closed表中,说明p的后继也在n之前 已生成,我们称为Ps,那么对Ps同样可能由 于n→p这一路径的加入又必须比较多条路径 代价后而取代价小的一条,如下图左部。
但由命题3可知:A*终止前,open表上必 存在一点n’,满足
f(n’)≤f*(S0) 即open表不会空,所以,不会终止于第3步。
推论2 凡open表中任一点n,若f(n)< f*(S0), 最终都将被A*算法挑选出来求后继,也 即被挑选出来进行扩充。
证:用反证法,设f(n)< 来作后继
f*(S0)且n没有被选出
证明: 在证明之前需要说明,在图搜索过程中, 若 某一点有几个先辈节点,则只保留最小费用的那 条路,所以A1 和A2搜索的结果是树而不是图。
下面以A2搜索树中节点的深度来归纳证明。
归纳基础 设A2扩充的点n的深度d=0,即n=S0, 显然A1也扩充点n,因为A1 、A2都要从S0开始。
归纳假设 假设A1扩充了A2搜索树中一切深度 d≤k的节点。
4.1.2 A算法与A*算法
1.A算法与A*算法定义
或图通用算法在采用如下形式的估计函数时, 称 为A算法。
f(n)=g(n)+h(n)
其中g(n)表示从S0到n点费用的估计,因为n为当 前节点,搜索已达到n点,所以g(n)可计算出。 h(n)表示从n到Sg接近程度的估计,因为尚未 找到解路径,所以h(n)仅仅是估计值。
命题3 若问题有解,在A* 终止前,open表上
人工智能课件-搜索技术

基于内容的推荐方法
内容推荐原理
通过分析用户历史行为数据和物品内容信息,提取用户和物品的特 征向量,计算用户和物品之间的相似度,从而推荐相似度高的物品。
内容推荐优点
能够推荐新物品,不受冷启动问题影响;可解释性强,用户能够理 解推荐结果的原因。
内容推荐缺点
需要提取用户和物品的特征向量,对特征工程要求较高;无法处理用 户兴趣变化的情况。
出结果。
反向传播
根据输出结果与真实结 果的误差,反向调整神
经网络的权重参数。
卷积神经网络(CNN)在图像搜索中的应用
01
02
03
04
卷积层
通过卷积核提取图像局部特征 ,实现参数共享和稀疏连接。
池化层
降低数据维度,提高计算效率 ,同时增强特征鲁棒性。
全连接层
将卷积层和池化层提取的特征 进行整合,输出图像的全局特
发展历程
随着互联网和大数据技术的快速发展 ,搜索技术经历了从基于关键词的搜 索到基于语义理解的搜索,再到基于 深度学习的搜索等多个阶段的发展。
搜索技术的重要性
01
02
03
信息获取效率
搜索技术能够快速定位到 用户所需的信息,提高信 息获取的效率。
信息质量
通过搜索技术,用户可以 获取到更加准确、全面的 信息,提高信息的质量。
隐马尔可夫模型(HMM)
HMM基本概念
隐马尔可夫模型是一种统计模型,用于描述隐藏的马尔可 夫链生成观测序列的过程。HMM由初始状态概率、状态 转移概率和观测概率确定。
HMM的三个基本问题
评估问题(计算观测序列的概率)、解码问题(找到最可 能的隐藏状态序列)和学习问题(估计HMM的参数)。
HMM应用
精品课件-《人工智能》搜索技术

6 5 76 5
图 八数码难题的宽度优先搜索树
宽度优先搜索(Breadth-First Strategy)
新的节点被插入到栈OPEN的后部
1
CLOSED=( )
2 4
OPEN= (1) 5
10
3
11
6
78
9
12
13
14 15
宽度优先搜索(Breadth-First Stra
17 5 75 4
28 3
5 14
76 5
12
13
28
28 3
14 3 14 5
76 5 76
20
21
28 14 3 76 5
28 3 14 5
76
22
23 24
25 26
27
8 3 8 1 3 2 8 3 2 8 3 12 3 12 3 21 4 2 4 7 4 7 1 4 7 8 4 8 4
76 5 76 5 61 5 6 5
《人工智能》搜索技术
How to find the best path in game ?
迷宫问题
S0 s-----s s s s s s-----s-----s-----s s-----s-----s-----s s ss s ss s-----s-----s-----s-----s Sg
搜索的挑战—组合爆炸
中, 并标以顺序号n; Step4: 若目标节点Sg=N, 则搜索成功,结束. Step5: 若N不可扩展, 则转Step2; Step6: 扩展N, 将生成的一组子节点配上指向N的指针后,
放入OPEN表尾部, 转 Step2;
例子 八数码难题(8-puzzle problem)
人工智能导论

与/或树深度优先搜索
将扩展节点的子节点放在Open表的首部。 子节点中是否有终止节点?若有,执行 可解标记过程;若根节点标记为可解, 结束;否则,删去Open表中的可解节点。 对不可扩展节点,执行不可解标记过程; 若根节点标记为不可解,结束;否则, 删去Open表中的不可解节点。 例4-12解或等价变换为一
系列较简单的问题予以处理。 问题的分解:如果一个问题P可以归约为一组 子问题P1、 P2、…、 Pn,并且只有当所有子问 题Pi(i=1、2、 …、n)都有解时原问题P才有解, 则称子问题P1、 P2、…、 Pn是问题P的分解。 逻辑关系是P= P1∧ P2∧ …∧ Pn
P
…
P1 P2 Pn
本原问题:可直接给出答案的问题。 在解决实际问题时,问题的分解和等价变换可
能被同时使用。
与/或树
P
P2
P1
P3
P21
P22
端节点:没有子节点的节点。 终止节点:若端节点对应的问题可以解决,就称 该端节点为终止节点。 可解节点:终止节点;“或”节点的子节点中有 一个可解;“与”节点的所有子节点可解。 不可解节点:非终止节点;“或”节点的所有子 节点不可解;“与”节点的子节点中有一个不 可解。 解树:导致根节点可解的子树。
P
t t
t
解树
P
t t
t
问题归约求解过程就是生成解树的过程。 例4-4
4-2 状态空间的盲目搜索
由于问题的状态空间可用一个有向图表示,因
此,状态空间搜索就是对有向图的搜索。 基本思想(p.109):节点扩展和检查
4-2-1一般图搜索过程
一般图搜索过程
S0:问题的初始状态。 G:搜索过程所得到的搜索图。 M:当前扩展节点新生成的且不为自己先辈的 子节点集 Open表(未扩展节点表):存放刚生成节点。 Closed表(已扩展节点表):存放已经扩展或 将要扩展的节点。
人工智能之搜索策略介绍课件

游戏AI:启发式搜 索策略在游戏中用
3 于寻找最优策略, 如国际象棋、围棋 等棋类游戏的AI算 法。
任务调度:启发式 搜索策略在任务调
2 度中用于优化任务 分配,如最小化任 务完成时间和资源 消耗。
机器人控制:启发 式搜索策略在机器
4 人控制中用于规划 机器人运动路径, 如自主导航和避障。
务调度、资源分配等。
启发式搜索策略的分类
局部搜索策略:只考虑当前状态
01
附近的解空间 全局搜索策略:考虑整个解空间
02
的所有状态 启发式搜索策略:根据问题特点, 03 选择合适的搜索策略 自适应搜索策略:根据搜索过程
04
中的信息,动态调整搜索策略
启发式搜索策略的应用实例
路径规划:启发式 搜索策略在路径规
强化学习搜索 策略:将强化 学习和搜索策 略相结合,以 实现更优的决 策和行动
强化学习搜索策略的分类
01 基于模型的搜索策略:使
用模型来预测状态和动作 的价值,如Q-learning 和Deep Q-Networks。
02 基于策略的搜索策略:直
接优化策略,如Policy Gradients和ActorCritic方法。
游戏AI:游戏策略、游戏 角色行为等
机器人控制:机器人路径 规划、机器人行为控制等
启发式搜索策略的定义
1
启发式搜索策略是一种基于 启发式信息的搜索策略。
2
它通过使用启发式信息来指 导搜索过程,以减少搜索空
间,提高搜索效率。
3
启发式信息可以是问题领域 的知识、经验或启发式函数。
4
启发式搜索策略广泛应用于 各种问题,如路径规划、任
第 04 章 搜索策略 人工智能课件.pps

第四章搜索策略4.1问题求解的形式化表示4.2状态空间的盲目搜索策略4.2.1广度优先搜索4.2.2深度优先搜索4.2.3有界深度优先搜索4.2.4代价树的广度优先搜索4.2.5代价树的深度优先搜索4.3状态空间的启发式搜索策略4.3.1局部择优搜索4.3.2全局择优搜索4.3.3图的有序搜索4.3.4A*算法4.4与或树搜索4.4.1与或树4.4.2与或树搜索4.5博弈树搜索作业第四章搜索策略2.状态空间与状态空间搜索。
状态空间:三元组〈S,F,G〉①S:初始状态集合。
②F:一组合法的状态转换操作③G:目标状态集合。
状态空间搜索●状态:可用任何数据结构或知识表示法表示,常用一组变量的有序集表示:s k = ( sk1, sk2, ……, skn)●状态空间搜索:从某个初始状态S o开始,按一定的策略选用操作,进行状态变换,直到产生任一目标状态SG例2.分水问题:给定两个水杯,一个容量为4升,另一个为3升,两者均无刻度,另外有一个水管可用来给水杯加水。
假设可随时将水杯中的水倒掉,可将一个杯中的水倒入另一个杯子。
问:如何在4升水杯中恰好装2升水?●状态描述:二元组(x,y)x=0,1,2,3,4,(4升水杯中当前水量)y=0,1,2,3●初态:(0,0)●目标态:(2,y)状态转换规则:①、将4升水杯装满水②、将3升水杯装满水③、将4升水杯中的水全部倒掉④、将3升水杯中的水全部倒掉⑤、将3升水杯中的水倒入4升水杯中,直到加满为止⑥、将4升水杯中的水倒入3升水杯中,直到加满为止⑦、将3升水杯中水全部倒入4升水杯中⑧、将4升水杯中水全部倒入3升水杯中规则描述:①、将4升水杯装满水:IF x<4 THEN x=4 R1②、将3升水杯装满水:R2③、将4升水杯中的水全部倒掉:IF x>0 THEN x=0 R3④、将3升水杯中的水全部倒掉:R4规则描述:⑤、将3升水杯中的水倒入4升水杯中,直到加满为止:IF x<4 ∧y>0 ∧x+y≥4 THEN y=y -(4-x),R5x=4⑥、将4升水杯中的水倒入3升水杯中,直到加满为止:R6⑦、将3升水杯中水全部倒入4升水杯中:IF x<4 ∧y>0 ∧x+y≤4 THEN x=x+y,R7y=0⑧、将4升水杯中水全部倒入3升水杯中:R8广度优先搜索示例深度优先搜索令:到结点x的代价。
人工智能导论课件-4 搜索策略

m=0且0≤c ≤N(左岸没有传道士)
m=1,c=1;m=2,c=2 m=0,c=0,1,2,3 m=3,c=0,1,2,3
N-m=0且0≤N-c≤N(右岸没有传道士)
不可能到达的合法状态:
(0,0,1),(0,3,0),(3,0,1),(3,3,0)
19
可能到达的合法状态共16个
2013-8-19
第3章 搜索策略
问题求解系统划分为两大类
知识贫乏系统
依靠搜索技术解决问题 知识贫乏、缺乏针对性 效率低
知识丰富系统
依靠推理技术解决问题 基于丰富知识的推理技术,直截了当 效率高
1
2013-8-19
3.1 引言
对于给定的问题,智能系统的行为一般是找 到能够达到所希望目标的动作序列,并使其所 付出的代价最小、性能最好。
g5a6c6i6k6j7m7o72019627107循环7成功结束4586427301s??????????6586427031a??????????4586407321b??????????6586427310c??????????5506487321e??????????5586470321d??????????6586047321i??????????5560487321l??????????7056487321m??????????5567480321n????????????????????5674813207o5567408321g??????????7586471320j??????????6580476321k??????????2019627108??????????586427031??????????586407321??????????586427310??????????506487321??????????586470321??????????586047321??????????560487321??????????056487321??????????567480321??????????567481320??????????567408321??????????586427301最理想搜索图g2019627109判断失误4586427301s??????????6586427031a??????????4586407321b??????????6586427310c??????????5506487321e??????????5586470321d??????????6586047321i??????????5560487321l??????????7056487321m??????????5567480321n????????????????????5674813207o5567408321g??????????7586471320j??????????6580476321k??????????2019627110343实现启发式搜索的关键因素和a算法?实现启发式搜索应考虑的关键因素
人工智能搜索策略 优质课件

CLOSED表:CLOSED表则是用来存放将要扩展或已经扩展 的节点,所以它被称为已扩展节点表。
4.状态空间的一般搜索过程描述如下:
1) 把为初G;始节点S0放入OPEN表,并建立目前只包含S0的图,记
2) 检查OPEN表是否为空,若为空则问题无解,退出。
3) 把 OPEN 表的第一个节点取出并放入 CLOSED 表,并记该 节点为节点 n;
3.2.1状态空间的一般搜索过程
5.搜索过程举例:
S0
1
62
3
4
5
实心黑点代表已扩展了节点,它 们位于CLOSED表上;空心圆圈 代表未扩展的节点,它们位于 OPEN表上;有向边旁边的箭头 是指向父节点的指针,它们是在 第 6) 步形成的。
假设现在要扩展节点 1,并且 只生成单一的后继节点 2 。但 是目前节点 2 已有父节点 3, 即节点 2 在先前扩节点 3 时已 被生成了,现在又作为节点 1 的后继节点被再次生成。
3.1.1 什么是搜索 (What’s search)
问题求解系统可在两种基本情况下运用启发式策略:
1. 一个问题由于在问题陈述和数据获取方面固有的模糊性,可 能会使它没有一个确定的解,即它是一个模糊系统。
2. 虽然一个问题可能有确定解,但是求解过程中的搜索代价将 令人难以接受,在很多问题中,其状态空间特别大,搜索中 生成扩展的状态数会随着搜索的深度呈指数级增长。在这种 情况下,穷尽式搜索策略如宽度优先和深度优先搜索,在一 个给定的较实际的时空内很可能得不到最终的解,而启发式 策略则通过引导搜索向最有希望的方向进行来降低搜索复杂 度。通过仔细考虑,删除某些状态及其后裔,启发式策略可 以消除组合爆炸,并得到令人能接受的解。
如果有,则说明搜索成功,从初始状态到目标状 态的一系列算符即是问题的解;
人工智能入门课件第4章博弈与搜索
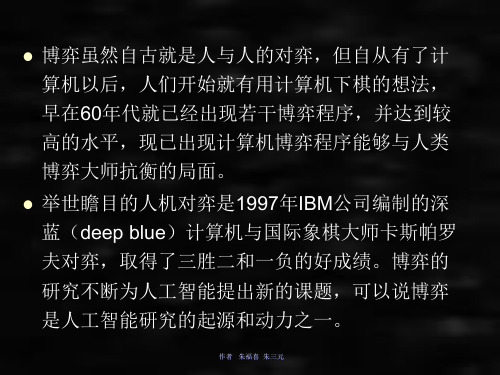
该算法分三个阶段进行。 第一阶段为步骤2-4,使用宽度优先法生成规定深度的全部博弈树,然后对其所有端节点计算其静态估计函数值。 第二阶段为步骤5-7是从底向上逐级求非终结点的倒推估计值,直到求出初始节点的倒推值f(s)为止。f(s)的值应为max min…. {f(ni1i2i3…ik)},其中nik表示深度为k的端节点。 第三阶段,根据f(s)可选的相对好的走步,由Mark (Move, T )标记走步。
4.4.1 围棋博弈程序的发展
4.4.1 围棋博弈程序的发展
图4.8 围棋博弈程序的分类
4.4.2 AlphaGo博弈树搜索算法的改进
MCTS算法大致思想可类比MinMax算法:对于给定的当前根节点(某一棋局),通过计算机模拟推演以当前根节点出发的各种可能的走法,配合高效的“剪枝”算法来控制搜索空间大小,并用演算到最后一步的结果来反过来影响当前节点下一步棋的选择。 针对围棋相对于传统棋类AI的设计难点: 1)可能的走法太多(即Branching Factor较大)导致搜索空间非常大 ; 2)没有一个好的估值函数对进行中的围棋棋局计算一个静态得分。
要达到上述目的有效途径是使用启发式方法引导搜索过程,使其只生成可能赢的走步。而这样的博弈程序应具备: 一个好的(即只产生可能赢棋步骤的)生成过程。 一个好的静态估计函数。 下面介绍博弈中两种最基本的搜索方法。
4.2 极小极大搜索过程
4.2.1 极小极大搜索的思想 极小极大搜索策略是考虑双方对弈若干步之后,从可能的步中选一步相对好的走法来走,即在有限的搜索深度范围内进行求解。 为此要定义一个静态估计函数f,以便对棋局的势态作出优劣估计。这个函数可根据棋局优劣势态的特征来定义。
4.2.2 极小极大搜索算法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章搜索策略4.1问题求解的形式化表示4.2状态空间的盲目搜索策略4.2.1广度优先搜索4.2.2深度优先搜索4.2.3有界深度优先搜索4.2.4代价树的广度优先搜索4.2.5代价树的深度优先搜索4.3状态空间的启发式搜索策略4.3.1局部择优搜索4.3.2全局择优搜索4.3.3图的有序搜索4.3.4A*算法4.4与或树搜索4.4.1与或树4.4.2与或树搜索4.5博弈树搜索作业第四章搜索策略2.状态空间与状态空间搜索。
状态空间:三元组〈S,F,G〉①S:初始状态集合。
②F:一组合法的状态转换操作③G:目标状态集合。
状态空间搜索●状态:可用任何数据结构或知识表示法表示,常用一组变量的有序集表示:s k = ( sk1, sk2, ……, skn)●状态空间搜索:从某个初始状态S o开始,按一定的策略选用操作,进行状态变换,直到产生任一目标状态SG例2.分水问题:给定两个水杯,一个容量为4升,另一个为3升,两者均无刻度,另外有一个水管可用来给水杯加水。
假设可随时将水杯中的水倒掉,可将一个杯中的水倒入另一个杯子。
问:如何在4升水杯中恰好装2升水?●状态描述:二元组(x,y)x=0,1,2,3,4,(4升水杯中当前水量)y=0,1,2,3●初态:(0,0)●目标态:(2,y)状态转换规则:①、将4升水杯装满水②、将3升水杯装满水③、将4升水杯中的水全部倒掉④、将3升水杯中的水全部倒掉⑤、将3升水杯中的水倒入4升水杯中,直到加满为止⑥、将4升水杯中的水倒入3升水杯中,直到加满为止⑦、将3升水杯中水全部倒入4升水杯中⑧、将4升水杯中水全部倒入3升水杯中规则描述:①、将4升水杯装满水:IF x<4 THEN x=4 R1②、将3升水杯装满水:R2③、将4升水杯中的水全部倒掉:IF x>0 THEN x=0 R3④、将3升水杯中的水全部倒掉:R4规则描述:⑤、将3升水杯中的水倒入4升水杯中,直到加满为止:IF x<4 ∧y>0 ∧x+y≥4 THEN y=y -(4-x),R5x=4⑥、将4升水杯中的水倒入3升水杯中,直到加满为止:R6⑦、将3升水杯中水全部倒入4升水杯中:IF x<4 ∧y>0 ∧x+y≤4 THEN x=x+y,R7y=0⑧、将4升水杯中水全部倒入3升水杯中:R8广度优先搜索示例深度优先搜索令:到结点x的代价。
g(x):表示从Sc(x,y):表示从父结点x,到子结点y的代价。
则有:g(y)=g(x)+c(x,y)(1)OPEN = { S0}; g(S)=0; CLOSED = { };(2)If null ( OPEN ) then return fail;(3)n = first(OPEN); 将n加入CLOSED表;(4)if goal(n) then return success;(5)若结点n不可扩展,转(2);(6)扩展结点n,将所有非祖先子结点放到OPEN 表的尾部,并给每个子结点置上父指针;对任一子结点m,计算g(m)=g(n)+c(n,m);将OPEN表中结点按g值排序,然后转(2);代价树的广度优先搜索●与OPEN、CLOSED中结点相同的(非祖先)重复子结点,对应通向同一个结点的多条路径●发现重复结点,意味着找到一条到达该节点的新路径,如果边的代价是单位代价,则新路径一定比老路径长,所以直接舍弃。
●现在由于边的代价不再是单位代价,重复子结点一般对应长度不同的路径,所以不再直接舍弃。
发现重复结点,意味着找到一条到达该节点的新路径A NB B1A NB B1S0代价树的广度优先搜索代价树的深度优先搜索(1)OPEN={S};CLOSED={};(2)if null(OPEN)then return fail;(3)n=first(OPEN);将n加入CLOSED表;(4)if goal(n)then return success;(5)若结点n不可扩展,转(2);(6)扩展结点n,将其非祖先子结点按生成代价从小到大的顺序,放在OPEN表的首部,并给每个子结点置上父指针,然后转(2)4.3.2 全局择优搜索基本思想:据有关知识、经验,对当前所有可能的搜索路径的端结点进行评估,判断其通向最佳解的可能性,然后找出最有希望的端结点进一步扩展。
4.3.2 全局择优搜索(1)OPEN = { S0}; CLOSED = { }; 计算f(S);(2)if null(OPEN)then return fail;(3)n=first(OPEN);将n加入CLOSED表;(4)if goal(n)then return success;(5)若结点n不可扩展,转(2);(6)扩展结点n,用估价函数f(x)计算每个非祖先子结点的估值,并给每个子结点置上父指针,放到OPEN表中,然后对OPEN表中全部结点按估价值从小到大的顺序排序。
(7)转(2)4.3.3 图的有序搜索改进方法:●在搜索过程中,每当产生一个新结点newN时,需要将结点newN与已经产生的所有结点进行比较,如果存在一个结点oldN,与newN完全相同,则说明找到了一条通向oldN的新路径。
●若新路径更短,则修改oldN的父指针,指向新的父结点,否则维持原状。
●最后将newN舍弃。
4.3.3 图的有序搜索结点n中内容:n状态描述状态估值父指针后继结点表图的有序搜索(1)OPEN={S};CLOSED={};计算f(S);(2)if null(OPEN)then return fail;(3)n=first(OPEN);将n加入CLOSED表;(4)if goal(n)then return success;(5)若结点n不可扩展,转(2);(6)扩展结点n,生成其全部子结点。
对每个子结点i,计算估值f(i)。
考察结点i是否已经存在。
①如果结点i既不在OPEN表中,也不在CLOSED表中,则结点i是一个新结点。
给结点i置上父指针,放到OPEN表中,然后对OPEN表中全部结点按估价值从小到大的顺序排序。
②如果结点i在OPEN表中,或在CLOSED表中,则结点i已经存在,说明发现了通向结点i的新路径。
比较结点i的新、旧估值f(i),若新估值较小,则说明新路径更短:(a)更新表中原结点i的估值f(i)和父指针。
(b)若结点i在CLOSED表中,则把结点i移回OPEN表,通过重新扩展结点i,将其新估值向子孙传播。
(7)转(2)4.3.4 A* 算法对有序搜索的评估函数加以限制,即可得到A* 算法评估函数●如何评估端结点n通向最佳解的可能性?●对应每一个端结点n,可能有几条解路径,其中有一条最短,令其长度等于f*(n),且有:f*(n) = g*(n) + h*(n)理想化评估函数图示S oS g n …………g* ( n )h* ( n )f*(n) = g*(n) + h*(n)●g*(n): 从S o到n的最佳路径代价●h*(n):从n到目标的最佳路径代价●f*(n):是从S o到n,再到目标的最佳路径的代价。
(即:n 可能通向的最佳解的代价)注:如果用f*(n)指导搜索,则可直接找到最佳解,因为最佳解路径上任意结点的f*(n)相等且最小,每次从OPEN表中选出的结点一定在最佳解路径上。
启发式评估函数图示S oS g n …………g ( n )h ( n )启发式评估函数f(n) = g(n) + h(n)●g(n):从S o到n的当前最佳路径代价(对g*(n) 的估计)g(n)≥g*(n)(逐步修正、逼近)●h(n):对h*(n)的估计,与具体问题有关●f(n):是对经过n的最佳解代价的估计。
f(n)越小,n越有希望通向最佳解。
A* 算法●当限定评估函数为:f(n)=g(n)+h(n)时,有序搜索又称为A算法。
●当限定:h(n)≤h*(n)时,A算法又称为A*算法。
传播示例A bestN oldN SNS0D E F G C H●传播方式:对oldN的所有后继进行一次深度优先遍历(或广度优先遍历),在遍历的同时执行传播操作。
●每个分支的终止条件是:(1)遇到一个无后继的结点;或(2)遇到这样一个后继结点:其原g值比新g值还小●传播操作:在遍历的过程中,尝试利用当前父结点的g值,修正当前子结点的g值和父指针。
●具体情况可能有:(1)g值、父指针都不变。
(2)只修正g值,父指针不变。
(3)二者都变。
传播示例A bestN oldN SNS0D E F G C H利用A*算法求解九宫题:S O S G2 83 104 7 6 51 2 38 0 47 6 5?●令:g(n)=d(n)=结点n的深度。
h(n)=w(n)=结点n中没有到位的数码个数。
●则:f(n)=d(n)+w(n)●显然:h(n)≤h*(n)2831047653S 02830147654S 12031847654S 22831407655S 32831647055S 4283 104 7653S0283 014 7654S12031847654S22831407655S32831647055S4083 214 7655S52837140656S6283 104 7653S0283 014 7654S12031847654S22831407655S32831647055S4083 214 7655S52837140656S60231847654S75301847656S8A* 算法示例2831047653S 028*******4S 12031847654S 22831407655S 32831647055S 41230847654S 90832147655S 52837140656S 60231847654S 75301847656S 8A* 算法示例2831047653S 028*******4S 12031847654S 22831407655S 32831647055S 41230847654S 90832147655S 52837140656S 60231847654S 75301847656S 81238047654S g 1237840656S 10A* 算法的可采纳性●结论(1):对于有限图,A*算法一定会在有限步内终止。
–要么找到目标,要么open表变为空,所以一定会在有限步内终止。
●结论(2):对于无限图,只要从初始结点到目标结点有路径存在,则A*算法也一定会在有限步内终止。
–首先,假设永远不会结束,open表永远取不空。
–设d*(x)表示从初始结点到open表中任意结点x的最短路径的长度(即最短路径上的分支数目),又设e是图中所有边的最小代价,则有:f(x) ≥ g(x) ≥ g*(x) ≥ d*(x)×e–显然,如果算法永远不结束,则open表中最小的f(x)也将趋于无穷,因为d*(x)会趋于无穷。
