十二星座大秘密,90%准!
词牌平仄表

词牌格律平仄表符号:○平声●仄声⊙可平可仄△平韵▲仄韵词牌录1.菩萨蛮⊙○⊙●○○▲,⊙○⊙●○○▲。
⊙●⊙○△,⊙○○●△。
⊙○○●▲,⊙●⊙○▲。
⊙●●○△,⊙○⊙●△。
2.绮罗香●●○○,○○●●,⊙●●○○▲。
⊙●○○,⊙●●○○▲。
●⊙⊙,⊙●○○,●⊙●,⊙○○▲。
●○○,●●○○,⊙○⊙●●○▲。
○○○●●▲。
○●○○⊙●,⊙○○▲。
⊙●○○,⊙●●○○▲。
●⊙⊙,⊙●○○,●⊙●,⊙○○▲。
●○○,●●○○,●○○●▲。
3.千秋岁⊙○⊙▲,⊙●○○▲。
⊙●●,○○▲。
⊙○○●●,⊙●○○▲。
○⊙●,⊙○⊙●○○▲。
⊙●○○▲,⊙●○○▲。
⊙●●,○○▲。
⊙○○●●,⊙●○○▲。
○⊙●,⊙○⊙●○○▲。
4.沁园春⊙●○○,●●○○,⊙●⊙△。
●⊙○⊙●,⊙○⊙●,⊙○⊙●,⊙●○△。
⊙●○○,⊙○⊙●,⊙●○○⊙●△。
○○●,⊙○○●●,●●○△。
○○●●○△,●⊙●○○⊙●△。
●⊙○⊙●,⊙○⊙●,⊙○⊙●,⊙●○△。
⊙●○○,⊙○⊙●,⊙●○○⊙●△。
○○●,●○○●●,⊙●○△。
5.清平乐○○⊙▲,⊙●○○▲。
⊙●⊙○○⊙▲,⊙●⊙○⊙▲。
⊙○⊙●○△,⊙○⊙●○△。
⊙●⊙○⊙●,⊙○⊙●○△。
6. 青玉案⊙○⊙●○○▲,●⊙●○○▲。
⊙●⊙○○●▲。
●○○●,●○○▲。
⊙●○○▲。
⊙○⊙●○○▲,⊙●○○●○▲。
⊙●⊙○○●▲。
●○○●,●○○▲。
⊙●○○▲。
7.高阳台(庆春泽)⊙●○○,○○●●,⊙○⊙●○△。
⊙●○○,⊙○⊙●○△。
⊙○⊙●○○●,●○○、⊙●○△。
●○△,⊙●○○,⊙●○△。
○○●●○○●,●○○⊙●,⊙●○△。
⊙●○○,⊙○⊙●○△。
⊙○⊙●○○●,●○○、⊙●○△。
●○△,⊙●○○,⊙●○△。
8.鹊桥仙⊙○⊙●,⊙○⊙●,⊙●⊙○⊙▲。
○⊙●●○○,●⊙●、○○⊙▲。
⊙○⊙●,⊙○⊙●。
⊙●⊙○⊙▲。
⊙○⊙●●○○,●⊙●、○○⊙▲。
9.人月圆⊙○⊙●○○●,⊙●●○△。
2021年尔雅中华诗词之美答案

尔雅中华诗词之美答案欧阳光明(2021.03.07)修订无错版1.属于四书五经中“四书”的著作是()。
A、《诗经》B、《大学》C、《礼记》D、《春秋》我的答案:B2《诗经》中祭祀歌颂祖先的歌诗是指()。
A、国风B、雅C、正声D、颂我的答案:D3“诗言志”出自古书()。
A、《诗经·毛诗序》B、《诗言志辨》C、《尚书》D、《论语》我的答案:C4《诗经·十五国风》主要是当时民间的且大多是无名诗人的作品。
()我的答案:√5古人所说的“志”,是泛指人内心的一切情志()。
我的答案:×词的产生1《尚书》在西方被翻译为()。
A、Book of SongsC、Book of DocumentsB、Book of RitesD、Book of Change我的答案:C2关于词的说法,表述错误的是()。
A、是一种微妙的文学体式B、产生背景是歌台舞榭C、是先有音乐然后按照乐调填写D、来源于现实生活3中国南北朝时期民间的音乐称为()。
A、雅乐B、清乐C、宴乐D、胡乐我的答案:B4诗是作者显意识的活动。
()我的答案:√5“词”的本意是指配乐的歌词。
()我的答案:√配乐填词与《花间集》1关于市井俗曲,描述不正确的是()。
A、被人忽视,无人整理B、言辞低俗,错字百出C、当时传唱度低D、无人刊刻流传我的答案:C2《花间集》中大部分的作品是描写()。
A、田园生活B、志向、理想C、山河美景D、美女、爱情我的答案:D3宴乐的构成要素不包括()。
A、清乐B、雅乐C、胡乐D、法曲我的答案:B4《花间集》是当时诗人文士所作配合宴乐而唱的歌词。
()我的答案:√5小词源于当时民间宴乐曲调的流行。
()我的答案:√小词与性别文化1“衣锦尚褧”出自古书()。
A、《诗经》B、《论语》C、《花间集》D、《礼记》我的答案:D2晚唐五代时期,“山”可代表的事物不包括()。
A、山眉B、发型C、枕头D、山屏我的答案:B3“弄妆梳洗迟”中对“弄”解释正确的是()。
音韵学常识

音韻學常識一、概述1、什麼是音韻學音韻學,也叫“聲韻學”、“漢語音韻學”。
是中國傳統語文學的一個門類,是研究漢語語音古今沿革的一門學科。
中國傳統的語文學(小學)包括文字學、音韻學和訓詁學。
2、音韻學的研究物件我們今天研究古代語音,只能根據單個漢字在歷史時期的不同讀音,進而瞭解語音的歷史變化。
3、古音韻的歷史分期1)上古時期:先秦兩漢時的語音,以《詩經》音為代表。
2)中古時期:魏晉南北朝至唐宋時代語音,以《切韻》為代表。
3)近古時期:元明清時的語音,元·周德清《中原音韻》為代表。
4、音韻學的功用1)對古代漢語的意義A、明語法:音韻學上的“破讀”和“如字”術語,實際上就是指通過語音屈折變化以表現不同的詞性或詞義。
如,孟嘗君怪其疾也,衣冠而見之,曰:“責畢收乎?來何疾也?”破讀/讀破:“yì,動詞,‘穿(衣)’;guàn,動詞,‘戴(帽子)’”。
如字:“yī,名詞,‘衣服’;guān,名詞,‘帽子’”。
又如:“Contrast,重音在前,名詞,‘對比、對照’;Contrast,重音移後,動詞,‘使對比、使對照’。
”(詞法上的屈折變化)B、知構詞:通過語音的學習,可以瞭解古漢語中雙聲、疊韻等構詞法則,就不容易誤解詞義。
如:逶迤(w ēi yí),道路彎曲而長(=委迤=委蛇=蜲蛇=委佗=委它=委侈=委陀=委維=委隨=委移=逶移=逶夷=逶隨=逶迂=……)。
連綿詞——因聲求義:a、“望洋興嘆”,《論衡·骨相》:“武帝望陽”,《莊子·秋水》:“望洋向若而歎”。
解釋有“望視太陽、望著海洋、仰視貌、遠視貌”的意思,類推:“望×興歎”,如“望書興歎”、“望題興歎”。
疊韻連綿詞,“望洋:望羊、望陽、望佯、盳洋”——仰視的樣子/迷惘直視的樣子。
b、“猶豫”,解釋1:猶是犬名。
人將犬行,犬好豫在人前,待人不得,又來迎候,如此往還,至於終日。
斯乃豫之所以未定也,故稱猶豫(北齊顏之推《顏氏家訓·書證》)。
初二上几何证明题100题专题训练

M N DE B CA八年级上册几许题博题锻炼100题之阳早格格创做1、 已知:正在⊿ABC 中,∠A=900,AB=AC ,正在BC 上任与一面P ,做PQ ∥AB 接AC 于Q ,做PR ∥CA 接BA 于R ,D 是BC 的中面,供证:⊿RDQ 是等腰曲角三角形.2、 已知:正在⊿ABC 中,∠A=900,AB=AC ,D 是AC 的中面,AE ⊥BD ,AE 延少线接BC 于F ,供证:∠ADB=∠FDC.3、 已知:正在⊿ABC 中BD 、CE 是下,正在BD 、CE 或者其延少线上分别截与BM=AC 、CN=AB ,供证:MA ⊥NA.4、已知:如图(1),正在△ABC 中,BP 、CP 分别仄分∠ABC战∠ACB ,DE 过面P 接AB 于D ,接AC于E ,且DE ∥BC .供证:DE -DB=EC . 5、正在Rt △ABC 中,AB =AC ,∠BAC=90°,O 为BC 的中面.(1)写出面O 到△ABC 的三个顶面A 、B 、C 的距离的大小闭系(没有央供道明);(2)如果面M 、N 分别正在线段AB 、AC 上移动,正在移动中脆持AN =BM ,请推断△OMN 的形状,并道明您的论断.6、如图,△ABC 为等边三角形,延少BC 到D ,延少BA 到E ,AE=BD , 连结EC 、ED ,供证:CE=DE7、如图,等腰三角形ABC 中,AB =AC ,∠A =90°,BD 仄分∠ABC ,DE ⊥BC 且BC =10,供△DCE 的周少.8. 如图,已知△EAB ≌△DCE ,AB ,EC 分别是二个三角形的最少边,∠A =∠C =35°,∠CDE =100°,∠DEB =10°,供∠AEC 的度数.9. 如图,面E 、A 、B 、F 正在共一条曲线上,AD 与BC 接于面A BCO M NO, 已知∠CAE=∠DBF,AC=BD.供证:∠C=∠D10.如图,OP仄分∠AOB,且OA=OB.(1)写出图中三对于您认为齐等的三角形(注:没有增加所有辅帮线);(2)从(1)中任选一个论断举止道明.11. 已知:如图,AB=AC,DB=DC,AD的延少线接BC于面E,供证:BE=EC.12. 如图,正在△ABC中,AB=AD=DC,∠BAD=28°,供∠B战∠C的度数.13. 如图,B、D、C、E正在共背去线上,AB=AC,AD=AE,供证:BD=CE.14. 写出下列命题的顺命题,并推断顺命题的实假.如果是实命题,请赋予道明;•如果是假命题,请举反例道明.命题:有二边上的下相等的三角形是等腰三角形.15. 如图,正在△ABC中,∠ACB=90º,D是AC上的一面,且AD=BC,DE AC于D,∠EAB=90º.供证:AB=AE.16. 如图,等边△ABC中,面P正在△ABC内,面Q正在△ABC中,B,P,Q三面正在一条曲线上,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试道明您的论断.17. 如图,△ABC中,∠C=90°,AB的中垂线DE接AB于E,接BC于D,若AB=13,AC=5,则△ACD的周少为几?18.如图所示,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂脚分别是E,F,供证:CE=DF.19. 如图,已知△ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE ,垂脚为E ,AD ⊥CE ,垂脚为D.(1)推断曲线BE 与AD 的位子闭系是____;BE 与AD 之间的距离是线段____的少;(2)若AD =6 cm ,BE =2 cm ,供BE 与AD 之间的距离及AB 的少.20. 如图,已知 △ABC 、△ADE 均为等边三角形,面D 是BC 延少线上一面,连结CE ,供证:BD=CE 21. 如图,△ABC 中,AB=AC ,∠BAC=120°,AD ⊥AC 接BC•于面D ,供证:•BC=3AD.22. 如图,四边形ABCD 中,∠DAB=∠BCD=90°,M 为BD 中面,N 为AC中面,供证:MN ⊥AC .23、已知:如图所示,正在△ABC 中,∠ABC=45°,CD ⊥AB 于面D ,BE仄分∠ABC ,且BE ⊥AC 于面E ,与CD 相接于面F ,H 是BC 边的中面,对接DH 与BE 相接于面G .(1)供证:BF=AC ; (2)供证:DG=DF .24. 如图,面B ,D 正在射线AM 上,面C ,E 正在射线AN 上,且AB=BC=CD=DE ,已知∠EDM=84°,供∠A 的度数.25. 如图所示,正在△ABC 中,AB=AC ,BD ⊥AC 于面D ,CE ⊥AB 于面E ,BD ,CE 相接于F.供证:AF 仄分∠BAC.26. 如图所示,△ABC ≌△ADE ,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,供 ∠DFB 战∠DGB 的度数.27. 已知:如图,正在△ABC 中,AB=AC ,面D 正在边BC 上,DE ⊥AB ,DF ⊥AC ,且DE=DF ,B AED C供证:△ABD ≌△ACD28. 如图,一弛曲角三角形的纸片ABC ,二曲角边AC=6cm ,BC=8cm .现将曲角边AC 沿曲线AD 合叠,使它降正在斜边AB 上,且AC 与AE 沉合,供CD 的少.29. 已知:如图,正在△ABC 中,AB=AC ,BD 仄分∠ABC ,E 是底边BC 的延少线上的一面且CD=CE.(1)供证:△BDE 是等腰三角形(2)若 ∠A=36°,供∠ADE 的度数. 30. 如图,正在△ABC 中,AB=CB ,∠ABC=90°,D 为AB 延少线上一面,面E 正在BC 边上且BE=BD ,连结AE 、DE 、DC .(1)供证:AE=CD ;(2)若∠CAE=30°,供∠BDC 的度数.31. 如图,正在ABC ∆中,面D 正在AC 边上,DB=BC ,面E 是CD 的中面,面F 是AB 的中面,则不妨得到论断:12EF AB =,请道明缘由. 32. 已知:如图,正在ABC ∆中,C ABC ∠=∠,面D 为边AC 上的一个动面,延少AB 至E ,使BE=CD ,连结DE ,接BC 于面P.(1)DP 与PE 相等吗?请道明缘由.(2)若60C ∠=︒,AB=12,当DC=_________时,BEP ∆是等腰三角形.(没有必道明缘由)33. 如图,C 为线段BD 上一面(没有与面B ,D 沉合),正在BD 共侧分别做正三角形ABC 战正三角形CDE ,AD 与BE 接于一面F ,AD 与CE 接于面H ,BE 与AC 接于面G .(1)供证:BE=AD ;A B C D E(2)供∠AFG 的度数;(3)供证:CG=CH34. 已知:如图,正在△ABC 中,CD ⊥AB ,CD=BD ,BF 仄分∠DBC ,与CD ,AC 分别接与面E 、面F ,且DA=DE ,H 是BC 边的中面,连结DH 与BE 相接于面G .(1)供证:△EBD ≌△ACD ;(2)供证:面G 正在∠DCB 的仄分线上(3)探索索CF 、GF 战BG 之间的等量闭系,并道明您的论断.35. 如图,正在正在△ABC 中,AB=CB ,∠ABC=90°,F 为AB 延少线上一单,面E 正在BC 上,且AE=CF.(1)供证:CBF Rt ABE Rt ∆≅∆(2)若∠CAE=30°,供∠ACF 的度数36. 如图,△ACD 战△BCE 皆是等腰曲角三角形,∠ACD =∠BCE =90°,AE 接DC 于F ,BD 分别接CE ,AE 于面G 、H. 试预测线段AE 战BD 数量闭系,并道明缘由.37. 如图,正在△ABC 中,AB =AC ,AD 战BE 是下,它们相接于面H ,且AE =BE .供证:AH =2BD .38. 如图,正在ABC ∆中,32B ︒∠=,48C ︒∠=,,AE 仄分BAC ∠接BC 于面E ,DF AE ⊥于面F ,供ADF ∠AAM EGF D C B A 39. 如图所示,正在△ABC 中,已知面D ,E ,F 分别是BC ,AD ,CE 的中面,且ABC S ∆ =4,则BEF S ∆ 的值为几.40. 如图,ABC ∆中,90ACB ∠=,CD BA ⊥于D ,AE 仄分BAC ∠接CD 于F ,接BC 于E ,供证:CEF ∆是等腰三角形.41. 如图,正在四边形ABCD 中,DC ∥AB , BD 仄分∠ADC , ∠ADC=60°,过面B 做BE ⊥DC ,过面A 做AF ⊥BD ,垂脚分别为E 、F ,对接EF.推断△BEF 的形状,并道明缘由.42. 如图,已知Rt △ABC ≌Rt △ADE ,∠ABC =∠ADE =90°,BC 与DE 相接于面F ,对接CD ,EB.(1)图中另有几对于齐等三角形,请您一一枚举;(没有必道明)(2)供证:CF =EF.43. 正在ABC ∆中,BO 仄分ABC ∠,面P 为曲线AC 上一动面,PO BO ⊥于面O .(1)如图1,当40ABC ︒∠=,60BAC ︒∠=,面P 与面C 沉适时,供APO ∠的度数;(2)如图2,当面P正在AC 延少线时,供证:()12APO ACB BAC ∠=∠-∠; (3)如图3,当面P 正在边AC 所示位子时,请间接写出APO ∠与ACB ∠,BAC ∠之间的数量闭系式.44. 如图,正在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF=10cm , AC=14cm ,动面E 以2cm/s 的速度从A 面背F 面疏通,动面G 以1cm/s 的速度从C 面背A 面疏通,当一个面到达末面时,另一个面随之停止疏通,设疏通时间为t .(1) 供证:正在疏通历程中,没有管与何值,皆有2AED DGC S S ∆∆=; (2) 当与何值时,DFE ∆与DMG ∆齐等.D C45. 如图,正在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC合叠,使面B恰佳降正在边AC上,与面'B沉合,AE为合痕,供'EB的少度46. 如图,已知ΔABC是等腰曲角三角形,∠C=90°.(1)支配并瞅察,如图,将三角板的45°角的顶面与面C沉合,使那个角降正在∠ACB的里里,二边分别与斜边AB接于E、F二面,而后将那个角绕着面C正在∠ACB的里里转动,瞅察正在面E、F的位子爆收变更时,AE、EF、FB中最少线段是可末究是EF?写出瞅察截止.(2)探索:AE、EF、FB那三条线段是可组成以EF为斜边的曲角三角形?如果能,试加以道明.47. 已知BD,CE是△ABC的二条下,M、N分别为BC、DE的中面.(1)请写出线段MN与DE的位子有什么闭系?请道明缘由.(2)当∠A=45°时,请推断1△EMD为何种三角形,并道明缘由48. 如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过面A的一条曲线,且面B,C正在AE的二侧,BD⊥AE于面D,CE⊥AE于面E.(1)供证:BD=DE+CE;(2)若曲线AE绕面A转动到如图(2)的位子(BD<CE)时,其余条件没有变,问BD与DE,CE的闭系怎么样?请赋予道明;(3)若曲线AE绕面A转动到如图(3)的位子(BD>CE)时,其余条件没有变,问BD与DE,CE的闭系怎么样?请间接写出截止,没有需道明.49. 如图1,二个没有齐等的等腰曲角三角形OAB战等腰曲角三角形OCD 叠搁正在所有,而且有大众的曲角顶面O.(1)正在图1中,您创造线段AC ,BD 的数量闭系是________________ , 曲线AC ,BD 相接成_________度角.(2)将图1中的△OAB 绕面O 顺时针转动90°角,那时(1)中的二个论断是可创造?请搞出推断并道明缘由(3)将图1中的△OAB 绕面O 顺时针转动一个钝角,得到图3,那时(1)中的二个论断是可创造?请做出推断并道明缘由.50.△BEC 是等腰曲角三ABCD 的里积.51. △O ,过面O 分别做OD AB OE BC OF CA ⊥⊥⊥、、,垂脚分别为面D E F 、、. (1)如图1,若面O 是等边ABC △的三条下线的接面,请分别道明下列二个论断创造的缘由. 论断1.2OD OE OF ++=;论断2.32AD BE CF a ++=; (2)如图2,若面O 是等边ABC △内任性一面,则上述论断12、是可仍旧创造?(写出道理历程).52. 已知二个共一个顶面的等腰Rt △ABC ,Rt △CEF ,∠ABC=∠CEF=90°,对接AF ,M 是AF 的中面,对接MB 、ME .(1)如图1,当CB 与CE 正在共背去线上时,供证:MB ∥CF ;(2)如图1,若CB=a ,CE=2a ,供BM ,ME 的少;(3)如图2,当∠BCE=45°时,供证:BM=ME .53. 如图,已知ABC △中,∠B=∠C ,AB=AC=8厘米,BC=6厘米,面D 为AB 的中面.如果面P 正在线段BC 上以每秒2厘米的速度由B 面背C 面疏通,共时,面Q 正在线段CA 上以每秒a 厘米的速度由C 面背A 面疏通,设疏通时间为t (秒).O图1 图2 图B(1)用含t 的代数式表示线段PC 的少度;(2)若面P 、Q 的疏通速度相等,通过1秒后,BPD △ 与CQP △是可齐等,请道明缘由;(3)若面P 、Q 的疏通速度没有相等,当面Q的疏通速度a为几时,不妨使BPD △与CQP △齐等?(4)若面Q 以(3)中的疏通速度从面C 出收,面P 以本去的疏通速度从面B 共时出收,皆顺时针沿ABC △三边疏通,供通过多万古间面P 与面Q 第一次正在ABC △的哪条边上相逢?54. 如图,正在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF=10cm ,AC=14cm ,动面E 以2cm/s 的速度从A 面背F 面疏通,动面G 以1cm/s 的速度从C 面背A 面疏通,当一个面到达末面时,另一个面随之停止疏通,设疏通时间为t .(1)供证:正在疏通历程中,没有管t 与何值,皆有2AED DGC S S ∆∆=;(2)当t 与何值时,DFE ∆与DMG ∆齐等供(3)正在(2)的前提下,若119126BD DC =,228AED S cm ∆=,BFD S ∆55. 已知等边△ABC 战面P ,设面P 到△ABC3边的AB 、AC 、BC•的距离分别是h1,h2,h3,△ABC 的下为h ,若面P 正在一边BC 上(图1),此时h=0,可得论断h1+h2+h3=h ,请您探索以下问题:当面P 正在△ABC 内(图2)战面P 正在△ABC 中(图3)那二种情况时,h1、h2、h3与h•之间有何如的闭系,请写出您的预测,并简要道明缘由.(1) (2) (3)D B C P AQ56.如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动面P从面C启初,按CABC的路径疏通,且速度为每秒2㎝,设疏通的时间为t秒.(1)供t为何值时,CP把△ABC的周少分成相等的二部分;(2)供t为何值时,CP把△ABC的里积分成相等的二部分;并供此时CP 的少;(3)供t为何值时,△BCP为等腰三角形?57. 已知,△ABC是边少3cm的等边三角形.动面P以1cm/s的速度从面A 出收,沿线段AB背面B疏通.(1)如图1,设面P的疏通时间为t(s),那么t=(s)时,△PBC是曲角三角形;(2)如图2,若另一动面Q从面B出收,沿线段BC背面C疏通,如果动面P、Q皆以1cm/s的速度共时出收.设疏通时间为t(s),那么t为何值时,△PBQ是曲角三角形?(3)如图3,若另一动面Q从面C出收,沿射线BC目标疏通.对接PQ接AC于D.如果动面P、Q皆以1cm/s的速度共时出收.设疏通时间为t(s),那么t为何值时,△DCQ是等腰三角形?(4)如图4,若另一动面Q从面C出收,沿射线BC目标疏通.对接PQ接AC于D,对接PC.如果动面P、Q皆以1cm/s的速度共时出收.请您预测:正在面P、Q的疏通历程中,△PCD战△QCD的里积有什么闭系?并道明缘由.58.如图所示,已知AD是∠BAC的仄分线,EF笔曲仄分AD接BC的延少线于面F,接AD于面E,对接AF,供证:∠B=∠CAF.59.如图所示,AD是∠BAC的仄分线,DE⊥AB,DF⊥AC,垂脚分别为E,F,对接EF,EF与AD接于面G,供证:AD笔曲仄分EF.60.已知一个等腰三角形二内角的度数之比为1:4,则那个等腰三角形顶角的度数为_________.15.如图所示,已知面D 是等边三角形ABC 的边BC 延少线上的一面,∠EBC=∠DAC ,CE ∥AB.供证:△CDE 是等边三角形.61.如图所示,正在△ABC 中,AB=AC ,正在AB 边上与面D ,正在AC 的延少线上与面E ,使得BD=CE ,对接DE 接BC 于面G ,供证:DG=GE.62.一艘轮船以15海里/时的速度由北背北航止,如图,正在A 处视小岛P ,测得∠PAN=15°,二小时后,轮船到达B 处,测得∠PBN=30°,正在小岛P 周围18海里的范畴内有暗礁,若轮船继承背北航止,有无触礁伤害?63.如图,公园内二条小河MO 、NO 正在O处汇合,二河产死的半岛上有一处古迹P.现计划正在二条小河上各建一座小桥Q 战R ,并正在半岛上建三段小路,连通二座小桥战古迹.那二座小桥应建正在那边,才搞使建盘费最少? 64. 三角形ABC 中,AB=AC ,∠BAC=120°,AB 的笔曲仄分线EF 接AB 于E ,接BC 于F .若FC=3cm ,则供BF 少度65. 正在Rt △ABC 中,∠CE 是斜边上的下.(1)请道明AB 的少.668cm ,•少BC•为10cm .痕为AE ).念一念,此时EC 67、如图一齐四边形草坪供那块草坪的里积.68. 如图,A 、B 二个小集镇正在河流CD 的共侧,分别到河的距离为AC=10N B A B千米,BD=30千米,且CD=30千米,当前要正在河边建一自去火厂,背A、B二镇供火,铺设火管的费用为每千米3万,请您正在河流CD上采用火厂的位子M,使铺设火管的费用最节省,并供出总费用是几?69.如图,A市局里站测得台风核心正在A市正东目标300千米的B处,以107千米/时的速度背北偏偏西60°的BF目标移动,距台风核心200•千米范畴内是受台风做用的地区.(1)A市是可会受到台风的做用?写出您的论断并赋予道明;(2)如果A市受那次台风做用,那么受台风做用的时间有多少?70、如图:正在△ABC中,∠C=2∠B,AD是△ABC的角仄分线,∠1=∠B,试道明AB=AC+CD71、如图,AD是∠BAC的角仄分线,DE⊥AB垂脚为E,DF⊥AC,垂脚为面F,且BD=CD 供证:BE=CF72、如图,面B战面C分别为∠MAN二边上的面,AB=AC.(1)按下列语句绘出图形:①AD⊥BC,垂脚为D;②∠BCN的仄分线CE与AD的延少线接于面E;③连结BE;(2)正在完毕(1)后没有增加线段战字母的情况下,请您写出除△ABD≌△ACD中的二对于齐等三角形:____≌____,____≌____;(3)并采用其中的一对于齐等三角形给予道明.73、已知:AB=AC,AD⊥BC,CE仄分∠BCN,供证:△ADB≌△ADC;△BDE≌△CDE.AB D CM NE74、如图,PB、PC分别是△ABC的中角仄分线且相接于面P.供证:面P正在∠A的仄分线上AB CP75、如图,△ABC中,p是角仄分线AD,BE的接面. 供证:面p正在∠C 的仄分线上76、下列道法中,过失的是()A.三角形任性二个角的仄分线的接面正在三角形的里里B.三角形二个角的仄分线的接面到三边的距离相等C.三角形二个角的仄分线的接面正在第三个角的仄分线上D.三角形任性二个角的仄分线的接面到三个顶面的距离相等77、如图正在三角形ABC中BM=MC∠ABM=∠ACM供证AM仄分∠BAC78、如图,AP、CP分别是△ABC中角∠MAC与∠NCA的仄分线,它们相接于面P,PD⊥BM于面D,PF⊥BN于面F.供证:BP为∠MBN的仄分线.79、如图,正在∠AOB的二边OA,OB上分别与OM=ON,OD=OE,DN 战EM相接于面C.供证:面C正在∠AOB的仄分线上.80、如图,∠B=∠C=90°,M是BC的中面,DM仄分∠ADC.(1)若对接AM,则AM是可仄分∠BAD?请您道明您的论断;(2)线段DM与AM有何如的位子闭系?请道明缘由.81、八(1)班共教上数教活动课,利用角尺仄分一个角(如图所示).安排了如下规划:(Ⅰ)∠AOB是一个任性角,将角尺的曲角顶面P介于射线OA、OB之间,移动角尺使角尺二边相共的刻度与M 、N 沉合,即PM=PN ,过角尺顶面P 的射线OP 便是∠AOB 的仄分线.(Ⅱ)∠AOB 是一个任性角,正在边OA 、OB 上分别与OM=ON ,将角尺的曲角顶面P 介于射线OA 、OB 之间,移动角尺使角尺二边相共的刻度与M 、N 沉合,即PM=PN ,过角尺顶面P 的射线OP 便是∠AOB 的仄分线.(1)规划(Ⅰ)、规划(Ⅱ)是可可止?若可止,请道明;若没有成止,请道明缘由;(2)正在规划(Ⅰ)PM=PN 的情况下,继承移动角尺,共时使PM ⊥OA ,PN ⊥OB .此规划是可可止?请道明缘由.内的一面,PE ⊥AB ,PF ⊥AC ,垂脚分别为面E ,F ,AE=AF.供证:(1)PE=PF ;(2)面P 正在∠BAC 的角仄分线上.83、如图,面D 、B 分别正在∠A 的二边上,C 是∠A 内一面,AB=AD ,BC=CD ,CE ⊥AD 于E ,CF ⊥AF 于F.供证:CE=CF84、已知三角形三边少为a ,b ,c ,且丨a+b+c 丨+丨a-b-c 丨=10,供b 的值.85、已知:∠1=∠2,CD=DE ,EF//AB ,供证:EF=AC86、如图,△ABC 战△ADE 皆是等腰曲角三角形,CE与BD 相接于面M,BD 接AC 于面N ,道明:(1)BD=CE.(2)BD ⊥CE.87、如图,已知AD ∥BC ,∠PAB 的仄分线与∠CBA 的仄分线相接于E ,CE 的连线接AP 于D .供证:AD+BC=ABB ACD F 2 1 E88、如图,△ABC中BA=BC,面D是AB延少线上一面,DF⊥AC于F接BC于E,供证:△DBE是等腰三角形.89、如图,正在△ABC中,AC=BC,∠ACB=90°,D是AC上一面,AE⊥BD 接BD的延少线于E,且AE=1BD.供证:BD是∠ABC的角仄分线.290、如图,∠BAD=∠CAD,AD⊥BC,垂脚为面D,BD=CD可知哪些线段是哪个三角形的角仄分线、中线、下?91、如图所示,正在△ABC中,已知AC=8,BC=6,AD⊥BC于D,AD=5,BE⊥AC于E,供BE的少92、如图,AD是△ABC的角仄分线,DE∥AB,DF∥AC,EF接AD于面O.请问:DO是△DEF的角仄分线吗?请道明缘由.(2)若将论断与AD是∠CAB的角仄分线、DE∥AB、DF∥AC中的任一条件接换,所得命题精确吗?93、如图,△ABC中,∠ABC与∠ACB的仄分线接于面I,根据下列条件,供∠BIC的度数.(1)若∠ABC=70°,∠ACB=50°,则∠BIC=°(2)若∠ABC+∠ACB=120°,则∠BIC=°(3)若∠A=90°,则∠BIC=°;(4)若∠A=n°则∠BIC=°(5)从上述估计中,咱们能创造∠BIC与∠A的闭系吗?AIB C94、如图,供证∠A+∠B+∠C+∠D+∠E=180°95、如图,没有准则的五角星图案,供证:∠A+∠B+∠C+∠D+∠E=180°96、D为△ABC的边AB上一面,且∠ADC=∠ACD.供证:∠ACB>∠B97、如图,D是BC延少线上的一面,∠ABC.∠ACD的仄分线接于面E,供证:∠E=1/2∠A98、如图,BE与CD相接于面A,CF为∠BCD的仄分线,EF为∠BED的角仄分线.(1)试供∠F与∠B,∠D的闭系;(2)若∠B:∠D:∠F=2:4:x 供X的值99、如图,正在△ABC中,∠B=47°,三角形的中角∠DAC战∠ACF的仄分线接于面E,则∠AEC=度.100.如图,正在Rt△ABC中,已知∠ACB=90°,AC=BC,D为DC的中面,CE⊥AD于E,BF∥AC接CE的延少线于面F.供证:AB笔曲仄分DF.。
押韵和平仄

戏剧社
一、选择填入括号最贴切的句子。 B) ( 江中看月作(唐﹒袁枚) 江风送月海门东,人到江心月正中。 ( ),一船鸡犬欲腾空。 帆如云气吹将灭,灯近银河色不红。 如此宵征信奇绝,三更三点水精宫。
A半树佛花香易散B万里鱼龙争照影 C二月郊行最有情D三千组练挥银刀
“诗歌排序”技法
• 第一步:找出“韵脚”; • 第二步:依据“联”的平仄规则(对句句尾字为 平声字),确定出句和对句的顺序; • 第三步:律诗只有两联对仗,因此,对仗的两联 即为“颔联”或“颈联”; • 第四步:诗有几个韵脚,律诗有五个韵脚,绝句 有三个韵脚,也就意味着全诗首句即入韵; • 第五步:依据诗歌内容,排出顺序,并检验格律。
诗歌有哪些对仗类型?
• • • • • • • • 1工对 晓战随金鼓,宵眠抱玉鞍 2宽对 同类的词相对就可以了 两个黄鹂鸣翠柳,一行白鹭上青天--杜甫 3借对一下句词语借用另一意 酒债寻常行处有,人生七十古来稀—杜甫 4串对(流水对)前后两句意义相连 即从巴峡穿巫峡,便下襄阳向洛阳—杜甫
课堂练习
《对仗与对称美》
练练:学校成立若干学生社团,请你从下列选项 中选出三副适合的对联,分别送给戏剧社 文学社 摄影小组 摄影小组,以示祝贺。2010天津
A、现出庐山真面目 留住秋水旧丰神
B、藏古今学术 聚天地精华
C、常向秋山寻妙句 又驱春色入毫端 文学社
D、天涯雁寄回文锦 水国鱼传尺素书
E、看我非我,我看我,我也非我 装谁像谁, 谁装谁, 谁就像谁
A二十四桥明月夜,玉人何处教吹萧。 B十年一觉扬州梦,赢得青楼薄幸名。 C春风十里扬州路,卷上珠帘总不如。 D如今风摆花狼藉,绿叶成阴子满枝。
C ①_
B ②_
A ③_
1-100英文单词

num. 一千
one thousand: 一千
One Hundred Thousand Stars: 千亿的星辰
One hundred thousand why: 十万个为什么
79, one [wʌn]
n. 一
num. 一;一个
adj. 一的;唯一的
29, 211
two hundred and eleven
30, 2111111
two million one hundred and eleven thousand one hundred and eleven
31, 26
twenty-six
32, 27
twenty-seven
sweet seventeen: 芳龄十七|女儿心|二八年华
Part Seventeen: 危险人物:莫羽祁
82, seventy ['sevənti]
n. 七十;七十个;七十岁;七十年代
num. 七十
adj. 七十的;七十个的;七十岁的
seventy: 七十,七十个|七十员|一篑
Chapter Eight: 装运|滑铁卢的美元|大众传媒
60, eighteen ['ei'ti:n]
n. 十八,十八个
num. 十八
adj. 十八个的,十八的
EIGHTEEN: 如果你来到我身边|十八的, 十八个的|如果如果你来到我身边
colour eighteen: 色彩十八|紫花布包
Eighteen Spring: 半生缘
61, eighty ['eiti]
矩形的判定专项练习30题

矩形的判决博项训练30题(有问案)之阳早格格创做1.如图,正在四边形ABCD中,AD∥BC,E、F为AB上二面,且△DAF≌△CBE.供证:(1)∠A=90°;(2)四边形ABCD是矩形.2.如图,已知仄止四边形ABCD,∠ABC,∠BCD的仄分线BE、CF分别接AD于E、F,BE、CF接于面G,面H为BC的中面,GH的延少线接GB的仄止线CM于面M.(1)试道明:∠BGC=90°;(2)对接BM,推断四边形GBMC的形状并道明缘由.3.如图,O是菱形ABCD对于角线的接面,做DE∥AC,CE∥BD,DE、CE接于面E.(1)四边形OCDE是矩形吗?道道您的缘由;(2)请您将上述条件中的菱形改为另一种四边形,其余条件皆没有变,您能得出什么论断?根据改编后的题目绘出图形,并道明缘由.4.△ABC中,AD⊥BC于D,面E、F分别是△ABC中AB、AC中面,当△ABC谦脚什么条件时,四边形AEDF是矩形?道明缘由.5.如图,菱形ABCD的对于角线AC、BD接于面O.(1)用尺规做图的要领,做出△AOB仄移后的△DEC,其中仄移的目标为射线AD的目标,仄移的距离为线段AD的少;(央供:用尺规做图,生存做图痕迹,没有写做法.)(2)瞅察图形,推断四边形DOCE是什么特殊四边形,并道明.6.如图,仄止四边形ABCD中,对于角线AC、BD相接于面O,延少OA 到N,ON=OB,再延少OC至M,使CM=AN,供证:四边形NDMB为矩形.7.如图,面O是菱形ABCD对于角线的接面,过面C做BD的仄止线CE,过面D做AC的仄止线DE,CE取DE相接于面E,试道明四边形OCED是矩形.8.如图,已知梯形ABCD中,AD∥BC,AB⊥BC,面E、F分别是边BC、CD的中面,曲线EF接边AD的延少线于面M,对接BD.(1)供证:四边形DBEM是仄止四边形;(2)若BD=DC,对接CM,供证:四边形ABCM为矩形.9.如图,正在△ABC中,面O是AC边上的中面,过面O的曲线MN∥BC,且MN接∠ACB的仄分线于面E,接∠ACB的中角仄分线于面F,面P是BC延少线上一面.供证:四边形AECF是矩形.10.如图,正在梯形ABCD中,AD∥BC,BC=2AD,面E是BC的中面,对接AC、DE相接于面O.(1)试道明:△AOD≌△COE;(2)若∠B=∠AOE,试道明四边形AECD是矩形的缘由.11.如图,以△ABC的各边为一边背BC的共侧做正△ABD、正△BCF、正△ACE,若∠BAC=150°,供证:四边形AEFD为矩形.12.(1)正在等腰三角形ABC中AB=BC,∠ABC=90°,BD⊥AC,过D 面做DE⊥DF,接AB于E,接BC于F.若AE=4,FC=3,供EF少.(2)如图,将▱ABCD的边DC延少到面E,使CE=DC,对接AE,接BC 于面F.①供证:△ABF≌△ECF;②若∠AFC=2∠D,对接AC、BE.供证:四边形ABEC是矩形.13.如图,AD是△ABC的中线,过面A做AE∥BC,过面B做BE∥AD 接AE于面E,(1)供证:AE=CD;(2)当△ABC谦脚什么条件时,四边形ADBE是矩形?请道明缘由.14.如图,已知梯形ABCD中,AD∥BC,E、F分别是AB、CD的中面,面G正在边BC上,且CG=(AD+BC).(1)供证:四边形DEGF是仄止四边形;(2)对接DG,若∠ADG=2∠ADE,供证:四边形DEGF是矩形.15.已知,如图正在△ABC中,AB=AC,面D是AC的中面,曲线AE∥BC,过D面做曲线EF∥AB分别接AE、BC于面E、F,供证:四边形AECF是矩形.16.已知:如图,正在△ABC中,D、E、F分别是AC、AB、BC的中面,且CE=AB.供证:四边形CFED是矩形.17.如图,仄止四边形ABCD中,EF过AC的中面O,取边AD、BC分别相接于面E、F;(1)试道明四边形AECF是仄止四边形.(2)若EF过AC的中面,且取AC笔曲时,试道明四边形AECF是菱形.(3)当EF取AC有何如的闭系时,四边形AECF是矩形.18.如图,正在Rt△ABC中,∠A=90°,AB=AC,D是斜边BC上一面,DE⊥AC,DF⊥AB,垂脚分别为E、F.(1)道明四边形AEDF是矩形.(2)试问:当面D位于BC边的什么位子时,四边形AEDF是正圆形?并道明您的缘由.19.如图,△ABC中,D为边AC的中面,过面D做MN∥BC,CE仄分∠ACB接MN于E,CF仄分∠ACG接MN于F,供证:(1)ED=DF;(2)四边形AECF为矩形.20.如图,菱形ABCD的对于角线AC、BC相接于面O,BE∥AC,CE∥DB.供证:四边形OBEC是矩形.21.如图,正在△ABC中,O是AC上的任性一面,(没有取面A,C沉合),过面O做曲线l∥BC,曲线l取∠BCA的仄分线相接于面E,取∠DCA的仄分线相接于面F.(1)OE取OF相等吗?为什么?(2)探索:当面O正在那边时,四边形AECF为矩形?为什么?22.(2013•沙湾区模拟)如图,正在△ABC中,D是BC边上的一面,E 是AD的中面,过A面做BC的仄止线接CE的延少线于F,且AF=BD,对接BF.(1)供证:D是BC的中面.(2)如果AB=AC,试推断四边形AFBD的形状,并道明您的论断.23.如图,四边形ABCD是仄止四边形,对于角线AC、BD接于面O,∠OBC=∠OCB,供证:四边形ABCD是矩形.24.如图M、N分别是仄止四边形ABCD的对于边AD、BC的中面,且AD=2AB,AN,BM相接于P,DN,CM相接于Q.供证:PMQN为矩形.25.正在仄止四边形ABCD中,对于角线AC、BD相接于O,EF过面O,且AF⊥BC,供证:四边形AFCE是矩形.26.如图,正在△ABC中,D是AC的中面,E是线段BC延少线上的一面,过面A做AF∥BE,接ED的延少线于面F,对接AE,CF.(1)供证:AF=CE;(2)如果AC=EF,则四边形AFCE是矩形.27.如图,DB∥AC,且DB=AC,E是AC的中面,(1)供证:BC=DE;(2)对接AD、BE,商量:当△ABC谦脚什么条件时,四边形DBEA是矩形?并道明缘由.28.如图,O是菱形ABCD对于角线的接面,做DE∥AC,CE∥BD,DE、CE接于面E,四边形OCED是矩形吗?道道您的缘由.29.已知:如图,BC是等腰△BED底边ED上的下,四边形ABEC是仄止四边形.供证:四边形ABCD是矩形.30.如图,已知AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.供证:四边形BCED为矩形.矩形的判决博项训练30题参照问案:1.(1)∵AD∥BC,∴∠A+∠B=180°,∵△DAF≌△CBE,∴∠A=∠B,∴2∠A=180°,∴∠A=90°;(2)∵AD∥BC,AD=BC,∴四边形ABCD为仄止四边形,又∵∠A=90°,∴四边形ABCD是矩形2.(1)∵∠ABC+∠BCD=180°,BE、CF仄分∠ABC,∠BCD,∴∠GBC+∠GCB=90°,∴∠BGC=90°;(2)∵面H为BC的中面,∴BH=CH=GH,∵GB∥CM,∴∠BGH=∠CMH,∵∠HBG=∠HGB,∴∠HCM=∠HMC,∴MH=BH=CH=GH,∴四边形GBMC为矩形3.(1)四边形OCDE是矩形.道明:∵DE∥AC,CE∥BD,∴四边形OCED是仄止四边形,又∵AC⊥BD,∴∠DOC=90°,∴四边形OCED是矩形.(2)任性改变四边形ABCD的形状,四边形OCED皆是仄止四边形(问案没有唯一).缘由如下:∵DE∥AC,CE∥BD,∴四边形OCED是仄止四边形.4.谦脚△ABC是等腰曲角三角形,∠BAC=90°.∵△ABC是等腰曲角三角形,∠BAC=90°,AD⊥BC 于D,∴BD=CD,∵面E、F分别是△ABC中AB、AC中面,∴DF∥AB,ED∥AC,∴四边形AEDF是仄止四边形,∵∠BAC=90°∴AEDF是矩形.5.(1)所做图形如图所示:(2)四边形DOCE是矩形.∵△DCE是由△AOB仄移后的图形,∴DE∥AC,CE∥BD.∴四边形DOCE是仄止四边形.又∵四边形ABCD是菱形,∴AC⊥BD.即∠DOC=90°∴四边形DOCE为矩形.6.∵四边形ABCD为仄止四边形,∴AO=OC,OD=OB,∵AN=CM ON=OB,∴ON=OM=OD=OB,∴四边形NDMB为仄止四边形,∵MN=BD,∴仄止四边形NDMB为矩形7.∵DE∥AC,CE∥BD,∴DE∥OC,CE∥OD∴四边形OCED是仄止四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°,∴四边形OCED是矩形8.(1)道明:∵梯形ABCD中,AD∥BC,即DM∥BE,∵E、F分别是边BC、CD的中面∴EF∥BD,∴四边形DBEM是仄止四边形.(2)道明:对接DE,∵DB=DC,且E是BC中面,∴DE⊥BC,∴DE∥AB.又∵AB⊥BC,∴AB∥DE∵由(1)知四边形DBEM是仄止四边形,∴DM∥BE且DM=BE,∴DM∥EC且DM=EC,∴四边形DMCE是仄止四边形,∴CM∥DE,∴AB∥CM.又AM∥BC∴四边形ABCM是仄止四边形,∵AB⊥BC,∴四边形ABCM是矩形.9.∵CE仄分∠ACB,∴∠ACE=∠BCE,∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,共理,OC=OF,∴OE=OF.∵AO=CO,EO=FO,∴四边形AECF为仄止四边形,∵CE仄分∠ACB,∴∠ACE=∠ACB,共理,∠ACF=∠ACP,∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACP)=×180°=90°,∴四边形AECF是矩形.10.(1)∵BC=2AD,面E是BC的中面,∴EC=AD.∵AD∥BC,∴∠ADO=∠CEO,∠DAO=∠ECO.正在△AOD战△COE 中,∴△AOD≌△COE(ASA);(2)∵AD=BE,AD∥BE,∴四边形ABED是仄止四边形;共理可得:四边形AECD是仄止四边形.∴∠ADO=∠B.∵∠B=∠AOE,∴∠AOE=2∠B.∴∠AOE=2∠ADO.∵∠AOE=∠ADO+∠DAO,∴∠OAD=∠ODA.∴OA=OD.∴AC=DE.∴四边形AECD是矩形.11.:∵△ABD战△FBC皆是等边三角形,∴∠DBF+∠FBA=∠ABC+∠ABF=60°,∴∠DBF=∠ABC.又∵BD=BA,BF=BC,∴△ABC≌△DBF,∴AC=DF=AE,共理可证△ABC≌△EFC,∴AB=EF=AD,∴四边形DAFEF是仄止四边形(二组对于边分别相等的四边形是仄止四边形)∵∠BAC=150°,∴∠DAE=150°﹣∠DAB﹣∠EAC=90°,∴四边形AEFD为矩形.12.1)解:∵ABC中AB=BC,∠ABC=90°,BD⊥AC,∴∠A=∠C=45°,CD=AD,∴BD=CD=AD,BD仄分∠ABC,∴∠EBD=45°=∠C,∵BD⊥AC,DE⊥DF,∴∠BDC=∠EDF=90°,∴∠BDC﹣∠BDF=∠EDF﹣∠BDF,∴∠EDB=∠FDC,∵正在△EDB战△FDC中∴△EDB≌△FDC(ASA),∴FC=DE=3,共理△AED≌△BFD,∴DF=AE=4,正在Rt△EDF中,由勾股定理得:EF==5;(2)①道明:∵四边形ABCD是仄止四边形,∴AB∥CD,AB=CD,∵CD=CE,∴AB∥CE,AB=CE,∴四边形ABEC是仄止四边形,∴AF=FE,BF=FC,∵正在△ABF战△ECF中∴△ABF≌△ECF(SSS);②道明:∵四边形ABCD是仄止四边形,∴∠ABC=∠D,∵∠AFC=2∠D,∴∠AFC=2∠ABC,∵∠AFC=∠ABC+∠FAB,∵∠ABC=∠FAB,∴AF=FB,∵四边形ABCD是仄止四边形,∴AE=2AF,BC=2BF,∴AE=BC,∵四边形ABEC是仄止四边形,∴四边形ABEC是矩形.13.(1)∵AE∥BC,BE∥AD,∴四边形ADBE是仄止四边形,∴AE=BD,∵AD是△ABC的中线,∴BD=CD,∴AE=CD.(2)当AB=AC时,四边形ADBE是矩形,缘由是:∵AB=AC,BD=CD,∴AD⊥BC,即∠ADB=90°,又∵四边形ADBE是仄止四边形,∴四边形ADBE是矩形14.1)道明:如图,对接EF.∵四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD的中面,∴,EF∥AD∥BC.∵,∴EF=CG.∴四边形EGCF是仄止四边形.∴EG=FC且EG∥FC.∵F是CD的中面,∴FC=DF.∴EG=DF且EG∥DF.∴四边形DEGF是仄止四边形.(2)道明:对接EF,将EF取DG的接面记为面O.∵∠ADG=2∠ADE,∴∠ADE=∠EDG.∵EF∥AD,∴∠ADE=∠DEO.∴∠EDG=∠DEO.∴EO=DO.∵四边形DEGF是仄止四边形,∴,.∴EF=DG,∴仄止四边形DEGF是矩形.即四边形DEGF是矩形.15.∵面D是AC的中面,∴DA=DC,∵AE∥BC,∴∠AED=∠CFD,正在△ADE战△CDF 中,,∴△ADE≌△CDF(AAS),∴AE=CF,又∵AE∥BC,∴四边形AECF是仄止四边形,∵AE∥BC,EF∥AB,∴四边形ABFE是仄止四边形,∴AB=EF,∵AB=AC,∴AC=EF,∴四边形AECF是矩形.16.∵D、E、F分别是AC、AB、BC的中面,∴DE∥BC,且DE=BC,DF=AB,CF=BC,∴DE=CF,∴四边形CFED仄止四边形,又∵CE=AB,∴CE=DF,∴仄止四边形CFED是矩形,故四边形CFED是矩形.17.(1)道明:∵四边形ABCD是仄止四边形,∴AD∥BC,∴△AEO∽△CFO,∴=,∵OA=CO,∴OE=OF,∴四边形AECF是仄止四边形;(2)道明:∵四边形AECF是仄止四边形,又∵EF⊥AC,∴仄止四边形AECF是菱形;(3)解:当EF=AC时,四边形AECF是矩形,缘由是:由(1)知:四边形AECF是仄止四边形,∵AC=EF,∴仄止四边形AECF是矩形18.(1)∵DE⊥AC,DF⊥AB,∴∠AFD=∠AED=∠A=90°,∴四边形AEDF是矩形;(2)当D时BC的中面时,四边形AEDF是正圆形;JU缘由:∵D是BC的中面,∴BD=DC∵AB=AC∴∠B=∠C又∵DF⊥AB,DE⊥AC,∴∠BDF=∠DEC∴△BFD≌△DCE,∴DF=DE,∴矩形AEDF是正圆形.19.(1)∵CE仄分∠ACB,CF仄分∠ACG,∴∠ACE=∠ECB,∠ACF=∠FCG,又∵MN∥BG,∴∠DEC=∠ECB,∠DFC=∠FCG,∴∠DEC=∠DCE,∠DFC=∠DCF,∴DE=DC,DF=DC,∴DE=DF.(2)∵D为AC的中面,∴AD=DC,又DE=DF,∴四边形AECF为仄止四边形,∵∠ACE=∠ECB,∠ACF=∠FCG,∴∠ECF=90°,∴仄止四边形AECF为矩形20.∵BE∥AC,CE∥DB,∴四边形OBEC是仄止四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOB=90°,∴仄止四边形OBEC是矩形21.(1)解:OE=OE,缘由是:∵曲线l∥BC,∴∠OEC=∠ECB,∵CE仄分∠ACB,∴∠OCE=∠BCE,∴∠OEC=∠OCE,∴OE=OC,共理OF=OC,∴OE=OF.(2)解:O正在AC的中面上时,四边形AECF是矩形,缘由是:∵OA=OC,OE=OF,∴四边形AECF是仄止四边形,∵OE=OF=OC=OA,∴AC=EF,∴仄止四边形AECF是矩形22.(1)道明:∵AF∥BC,∴∠AFE=∠DCE(1分)∵E是AD的中面,∴AE=DE.(2分)∵∠AEF=∠DEC,∴△AEF≌△DEC.(3分)∴AF=DC,∵AF=BD∴BD=CD,∴D是BC的中面;(4分)(2)四边形AFBD是矩形,(5分)道明:∵AB=AC,D是BC的中面,∴AD⊥BC,∴∠ADB=90°,(6分)∵AF=BD,AF∥BC,∴四边形AFBD是仄止四边形,(7分)∴四边形AFBD是矩形.23.∵∠OBC=∠OCB,∴OB=OC,∵四边形ABCD是仄止四边形,∴OC=OA=AC,OB=OD=BD,∴AC=BD,∵四边形ABCD是仄止四边形,∴四边形ABCD是矩形,即四边形ABCD是矩形24.∵ABCD为仄止四边形,∴AD仄止且等于BC,又∵M为AD的中面,N为BC的中面,∴MD仄止且等于BN,∴BNDM为仄止四边形,∴BM∥ND,共理AN∥MC,∴四边形PMQN为仄止四边形,(5分)对接MN,∵AM仄止且等于BN,∴四边形ABNM为仄止四边形,又∵AD=2AB,M为AD中面,∴BN=AB,∴四边形ABNM为菱形,∴AN⊥BM,∴仄止四边形PMQN为矩形.(10分)25.∵四边形ABCD为仄止四边形,∴OA=OC,AE∥FC,∴∠EAO=∠FCO,正在△AOE战△COF中,,∴△AOE≌△COF,∴AE=CF,∴四边形AECF为仄止四边形,又∵AF⊥BC,∴∠AFC=90°,则四边形AECF为矩形.26.(1)道明:∵AF∥BE,∴∠AFD=∠CED,∠FAD=∠DCE,∵D是AC的中面,∴AD=DC,正在△FAD战△ECD中,∴△FAD≌△ECD(AAS),∴AF=CE;(2)道明:∵△FAD≌△ECD,∴FD=DE,∵AD=DC,∴四边形AFCE是仄止四边形,∵AC=EF,∴仄止四边形AFCE是矩形27.(1)道明:∵E是AC的中面,∴EC=AC,∵DB=AC,∴DB=EC,又∵DB∥AC,∴四边形BCED是仄止四边形(一组对于边仄止且相等的四边形是仄止四边形),∴BC=DE;(2)解:△ABC谦脚AB=BC时,四边形DBEA是矩形.缘由如下:∵E是AC的中面,∴AE=AC,∵DB=AC,∴DB=AE,又∵DB∥AC,∴四边形DBEA是仄止四边形(一组对于边仄止且相等的四边形是仄止四边形),∵AB=BC,E为AC中面,∴∠AEB=90°,∴仄止四边形DBEA是矩形,即△ABC谦脚AB=BC时,四边形DBEA是矩形.28.是矩形.(1分)缘由:∵DE∥AC,CE∥BD,∴四边形OCED是仄止四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴DE⊥CE,∴∠E=90°,∴仄止四边形OCED是矩形29.∵BC是等腰△BED底边ED上的下,∴EC=CD,∵四边形ABEC是仄止四边形,∴AB∥CD,AB=CE=CD,AC=BE,∴四边形ABCD是仄止四边形.∵AC=BE,BE=BD,∴AC=BD,∴四边形ABCD是矩形30.正在△ABD战△ACE中,∵AB=AC,AD=AE,∠BAD=∠CAE,∴△ABD≌△ACE(SAS)∴BD=CE又DE=BC.∴四边形BCED为仄止四边形.正在△ACD战△ABE 中,∵AC=AB,AD=AE,∠CAD=∠CAB+∠BAD=∠CAB+∠CAE=∠BAE,∴△ADC≌△AEB(SAS),∴CD=BE.∴四边形BCED为矩形.(对于角线相等的仄止四边形是矩形)。
2016中华诗词之美 叶嘉莹期末考试答案解析

一、单选题(题数:50,共 50.0 分)1词学家刘永济在晚年的号是()。
1.0分∙A、弘度∙∙B、知秋翁∙∙C、宏度∙∙D、诵帚∙正确答案:B 我的答案:B2关于词的理解,错误的是()。
1.0分∙A、可以称为曲子词∙∙B、可以称为长短句、诗余∙∙C、词本来是一个文学体式∙∙D、是配合宴乐乐曲而填写的歌词∙正确答案:C 我的答案:C3“倚天万里须长剑”一句引用了()的赋。
1.0分∙A、宋玉∙∙B、曹丕∙∙C、司马相如∙∙D、杜牧∙正确答案:C 我的答案:C4“众芳芜秽,美人迟暮”出自()。
1.0分∙A、《离骚》∙∙B、《人间词话》∙∙C、《诗经》∙∙D、《文赋》∙正确答案:A 我的答案:A5中国诗词中“一晌”的意思是指()。
1.0分∙A、长久∙∙B、田亩单位∙∙C、短暂∙∙D、A和C∙正确答案:D 我的答案:D6词被称为“小词”的原因是()。
1.0分∙A、不是言志的∙∙B、不是载道的∙∙C、可以歌唱的∙∙D、A和B∙正确答案:D 我的答案:D7《离骚》诗句“众女嫉余之峨眉兮”中“峨眉”指()。
1.0分∙A、眉毛∙∙B、美女∙C、美貌∙∙D、才德美好的贤士∙正确答案:D 我的答案:D 8《词选序》的作者是()。
1.0分∙A、王鹏运∙∙B、王水照∙∙C、王国维∙∙D、张惠言正确答案:D 我的答案:D 9《向晚二首》写于()年。
1.0分∙A、1948∙∙B、1949∙∙C、1978∙∙D、1979∙正确答案:C 我的答案:C 10柳永的《定风波》是一首()。
1.0分∙A、小令∙∙B、中调∙∙C、单调∙∙D、长调∙正确答案:D 我的答案:D11关于词牌名“浣溪沙”,说法错误的是()。
1.0分∙A、只有仄声调∙∙B、本唐代教坊曲名∙正确答案:A 我的答案:A12“贫而无谄,富而无骄,何如”是()请教孔子提出的。
1.0分∙A、子路∙∙B、子由∙∙C、子贡∙∙D、子夏∙正确答案:C 我的答案:C13“词别是一家”是()的观点。
(完整word版)今平古仄字表

《今平古仄字表》《今平古仄字表》A:阿凹B:八捌拔跋憩白伯般剥雹薄遇鼻芋骡憋瞥瘪别钵拨悖泊帛舶箔驳钱勃渤脖鹑博搏膊确C:嚓擦糙插察掘拆吃哧出吹捶戳撮D:哒搭裕答瘩达怛妲打得徳蹬滴汆的涤迪笛伙荻敌嫡跌迭叠耋谍喋牒碟蝶督独奇读渎牍犊度咄掇襪夺铎踱E:额F:发乏罚伐阀筏佛樓兆拂伏袱茯默幅辐福蝠匐服G:呷割鸽堆疙胳搁葛革阁格隔嗝嗝蛤估刮郭聒姻国帼H:涸貉合盒劾阂核盍阖黑忽惚鹄斛猾滑混豁削活J:击迹积屐绩緝激圾笈及汲级极笈岌即急吉亟疥疾嫉棘集柝轿藉籍夹泱荚镁颊嚅角脚缴觉疗结接揭孑节截杰诘洁刼碣竭捷睫究赳掬鞠局菊桔橘蠲搬上玮绝噱决诀抉倔掘崛厥蕨獗矍掩滴爵菌K:勘棵颗磕瞌壳咳总低L:拉邀疗溜馅噌捋M:妈抹没谜乜揽膜N:捏0:噢P:拍劈霹泼剖仆扑菩璞Q: t:沏漆戚掐切屈曲阙缺R:如茹孺S:撒塞杀煞勺芍舌什失虱湿十石识实拾仗蚀倏抒叔菽淑赎孰塾熟刷摔说俗缩T:塌剔踢贴凸秃突脱托橐W:挖玩屋喔X:吸锡膝夕汐析晰蜥腊昔惜息熄悉蟋习席袭媳檄呷瞎辅黠匣侠狭峡暇削楔歇蝎协胁挟撷戌靴薛穴学Y:压押鸭轧嘖叶一扭荫淳潔拥壅淤曰约晕Z:杂咋阳脏凿则贵幘择泽贼闸钏扎札炸摘宅着那螫蛰谪折桝辄辙汁织只侄职摭执I[值殖W掷粥姑轴竹竺逐烛躅著卓桌捉拙灼茁浊酌镯啄琢濯综足卒族昨作作《古代入声字辨别规律》(一)凡b、d、g、j、zh、z六母的第二声字,都是古入声字。
(二)凡d、t、L、z、c、s等六母跟韵母兰拼合时,不论国语读何声调,都是占入声字。
(三)凡k、zh、ch、sh、R五母与韵母U0拼合时,不论国语读何声调,都是古入声字。
(四)凡b、p、m、d、t、n、L七母跟韵母ie拼时,无论国语读何声调,都是古入声字(五)凡d、g、h、z、s五母与韵母ei拼合时,不论国语读何声调,都是占入声字。
(一)、在现代汉语里,凡是是鼻音(-n、・ng)的都不会是入声字。
因为入声字在其韵尾・b、•d、g逐渐变化脱落后,不可能又加上一个辅音韵尾。
入声字发展到今天只可能是开音节。
余角、补角、对顶角的概念和习题答案

余角战补角战对于顶角之阳早格格创做余角:如果二个角的战是一个曲角,那么称那二个角互为余角,简称互余,也不妨道其中一个角是另一个角的余角.∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A补角:如果二个角的战是一个仄角,那么那二个角喊互为补角.其中一个角喊干另一个角的补角∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A对于顶角:一个角的二边分别是另一个角的反背延少线,那二个角是对于顶角.二条曲线相接后所得的惟有一个大众顶面且二个角的二边互为反背延少线,那样的二个角喊干互为对于顶角.二条曲线相接,形成二对于对于顶角.对于顶角相等.对于顶角与对于顶角相等.对于顶角是对于二个具备特殊位子的角的称呼;对于顶角相等反映的是二个角间的大小闭系.补角的本量:共角的补角相等.比圆:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B.等角的补角相等.比圆:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D 则:∠C=∠B.余角的本量:共角的余角相等.比圆:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B.等角的余角相等.比圆:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B.注意:①钝角不余角;②互为余角、补角是二个角之间的闭系.如∠A+∠B+∠C=90°,不克不迭道∠A、∠B、∠C互余;共样:如∠A+∠B+∠C=180°,不克不迭道∠A、∠B、∠C互为补角;③互为余角、补角只与角的度数相闭,与角的位子无闭.只消它们的度数之战等于90°或者180°,便一定互为余角或者补角.余角与补角观念认识提示:(1)定义中的“互为”一词汇怎么样明白?如果∠1与∠2互余,那么∠1的余角是∠2 ,共样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 ,共样∠2的补角是∠1.(2)互余、互补的二角是可一定有大众顶面或者大众边?二角互余或者互补,只与角的度数有闭,与位子无闭.(3)∠1 + ∠2 + ∠3 = 90°(180°),能道∠1 、∠2、∠3 互余(互补)吗?不克不迭,互余或者互补是二个角之间的数量闭系.已知∠A与∠B互余,∠B与∠C互补,若∠A=50°,则∠C的度数是[ D ] A.40°B.50°C.130°D.140°如果∠A的补角是它的余角的4倍,则∠A=______度.设∠A 为x ,则∠A 的余角为90°-x ,补角为180°-x ,根据题意得,180°-x=4(90°-x ),解得x=60°.故问案为:60. 已知∠ α=50°17',则∠α的余角战补角分别是[ B ]A .49°43',129°43'B .39°43',129°43'C .39°83',129°83'D .129°43′,39°43′二个角的比是6:4,它们的好为36°,则那二个角的闭系是( )A .互余B .相等C .互补D .以上皆分歧过失设一个角为6x ,则另一个角为4x , 则有6x-4x=36°,∴x=18°,则那二个角分别为108°,72°, 而108°+72°=180°∴那二个角的闭系为互补. 故选C .如果∠A=35°18′,那么∠A 的余角等于______.如果∠A=35°18′,那么∠A 的余角等于90°-35°18′=54°42′. 故挖54°42′.已知∠1战∠2互补,∠3战∠2互余,供证:∠3= =21(∠1-∠2). 道明:由题意得:∠2+∠3=90°,∠1+∠2=180°,∴2(∠2+∠3)=∠1+∠2,故可得:∠3=21(∠1-∠2) 如图,∠1的邻补角是[ ]A.∠BOCB.∠BOC 战∠AOFC.∠AOFD.∠BOE 战∠AOF二个角互为补角,那么那二个角大小 [ D ]如果二个角互为补角,那么那二个角一定互为邻补角,道明此命题真——加本果如果二个角互为补角,那么那二个角一定互为邻补角,那是假命题. 如果二个角互为收补角,那么那二个角一定互为补角,那是真命题. 譬如道,二曲线仄止,共旁内角互补,然而互为共旁内角的二个角一定不互为收补角.如果二个角互补,那它们是邻补角”——————为什么道那个是假命题? 二条仄止线切出的共旁内角也互补,然而是它们不是邻补角.所以道:“如果二个角互补,那它们是邻补角”是假命题!果为邻补角是相邻的二个角互补,那么那二个角是互为邻补角,而互补的二个角有不相邻的,比圆四边形的二个对于角互补,则那四面共圆如果一个角是36°,那么[ D ].它的余角是64°B.它的补角是64°C.它的余角是144°D.它的补角是144°下列道法中:①共位角相等;②二面之间,线段最短;③如果二个角互补,那么它们是邻补角;④二个钝角的战是钝角;⑤共角或者等角的补角相等.精确的个数是()A.2个B.3个C.4个D.5个①共位角相等,道法过失;②二面之间,线段最短,道法精确;③如果二个角互补,那么它们是邻补角,道法过失;④二个钝角的战是钝角,道法过失;⑤共角或者等角的补角相等,道法精确;道法精确的公有2个,故选:A.下列道法精确的是()A.小于仄角的角是钝角B.相等的角是对于顶角C.邻补角的战等于180°D.共位角相A、小于仄角的角有:钝角、曲角、钝角,故本选项过失;B、对于顶角相等,相等的角纷歧定是对于顶角,故本选项过失;C、邻补角的战等于180°精确,故本选项精确;D、惟有二曲线仄止,才有共位角相等,故本选项过失.故选C.下列道法精确的是()A.相等的角是对于顶角B.对于顶角相等C.共位角相等D.钝角大于它的余角A、相等的角是对于顶角,道法过失;B、对于顶角相等,道法精确;C、共位角相等,道法过失;D、钝角大于它的余角,道法过失;故选:B.下列道法中,精确的是()A.对于顶角相等B.内错角相等C.钝角相等D.共位角相等A、对于顶角相等,道法精确;B、内错角相等,道法过失,惟有二曲线仄止时,内错角才相等;C、钝角相等,道法过失,比圆30°角战20°角;D、共位角相等,道法过失,惟有二曲线仄止时,共位角才相等;故选:A.三条曲线相接于一面不妨形成几对于对于顶角?二条曲线出现2*(2-1)=2对于对于顶角三条曲线出现3*(3-1)=6对于对于顶角四条曲线出现4*(4-1)=12对于对于顶角依次类推,n 条曲线相接于一面有n*(n-1)对于对于顶角三条曲线相接于一面,共可组成______对于对于顶角.如图,单个的角是对于顶角的有3对于,二个角的复合角是对于顶角的有3对于,所以,公有对于顶角3+3=6对于.故问案为:6.三条曲线相接与一面,能形成几对于对于顶角?四条呢?五条呢?N条呢?尔要要收战问案!三条曲线相接与一面,6对于;四条曲线相接与一面,12对于;五条曲线相接与一面,20对于;N条曲线相接与一面,N(N-1)对于;如果有n条曲线相接于一面,有几对于对于顶角?n的仄圆减去2条数个数2 2=2x13 6=3x24 12=4x35 20=5x4…………n n(n-1)三条曲线相接于一面,对于顶角最多有______对于.把三条曲线相接于一面,拆成三种二条曲线接于一面的情况,果为二条曲线相接于一面,产生二对于对于顶角,所以三条曲线相接于一面,有3个二对于对于顶角,共6对于对于顶角二条曲线相接,有一个接面.三条曲线相接,最多有几个接面?四条曲线呢?您能创造什么顺序吗?那个本去便是拉拢问题.果为二条线形成一个接面,所以三条线时,从三条线中与二条线,有3*2/2=3种与法,所以有3个接面.四条线中与二条,有4*3/2=6种与法,所以有6个接面.n条线中与二条,有n(n-1)/2种与法,所以有n(n-1)/2个接面.邻补角是互补的角是真命题吗天然是,邻补角相加等于180度便是互补啊互补的角是邻补角是真命题仍旧假命题假如真命题,请举反例二个角有一条大众边,它们的另一条边互为反背延少线,具备那种闭系的二个角称为互为邻补角.不妨随便绘二个不大众边的角,比圆1个60度,另一个120度,隐然它们是互补的,然而是本去不是邻补角所以互补的角是邻补角那是一个假命题该当道邻补角是互补的角,那才是真命题既相邻又互补的二个角是邻补角吗二条仄止线切出的共旁内角也互补,然而是它们不是邻补角.所以道:“如果二个角互补,那它们是邻补角”是假命题!成互补闭系的二个角互为邻补角是对于仍旧错分歧过失相邻的二个角互补称之为邻补角像二曲线仄止,共旁内角互补(那二个互补的角不相邻)、互补的二个角是邻补角用果为所以问果为二个角是邻补角所以二个角互补反过去不可坐。
五言格律诗平仄韵表

五言格律诗平仄韵表五律的平仄平仄是近体诗格律中最重要的因素。
五律平仄格式是近体诗中最基本的格式,掌握了五律的平仄格式,七律以及入律的五、七言绝句就容易得多了。
(一)五律的类型五律的平仄有四个类型,依次排列,恰好是五律的两联:A仄仄平平仄,B平平仄仄平;C平平平仄仄,D仄仄仄平平。
五律共四联八句,将以上形式重复一次,就是一首完整的五律,下面是五律的第一种格式:A⊙仄平平仄,B平平仄仄平。
C⊙平平仄仄,D⊙仄仄平平。
A⊙仄平平仄,B平平仄仄平。
C⊙平平仄仄,D⊙仄仄平平。
(点外加圈者表示可仄可平,以下相同。
)例诗:旅夜书怀杜甫细草微风岸,危樯独夜舟。
⊙仄平平仄,平平仄仄平。
星垂平野阔,月涌大江流。
⊙平平仄仄,⊙仄仄平平。
名岂文章著,官应老病休。
⊙仄平平仄,平平仄仄平。
飘飘何所以,天地一沙鸥。
⊙平平仄仄,⊙仄仄平平。
五律第一句不入韵。
五律首句也可入韵,倘要入韵,只须将第一句换为第四句即可,其他不变,这就衍化五律第二式:D⊙仄仄平平,B平平仄仄平。
C⊙平平仄仄,D⊙仄仄平平。
A⊙仄平平仄,B平平仄仄平。
C⊙平平仄仄,D⊙仄仄平平。
例诗:终南山王维太乙近天都,连山倒海隅。
⊙仄仄平平,平平仄仄平。
白云回望合,青霭入看无。
⊙平平仄仄,⊙仄仄平平。
分野中峰变,阴晴众壑殊。
⊙仄平平仄,平平仄仄平。
欲投人处宿,隔水问樵夫。
⊙平平仄仄,⊙仄仄平平。
将第一式一、三联与二、四联位置倒换,即成五律第三式:C⊙平平仄仄,D⊙仄仄平平。
A⊙仄平平仄,B平平仄仄平。
C⊙平平仄仄,D⊙仄仄平平。
A⊙仄平平仄,B平平仄仄平。
例诗;山居秋暝王维空山新雨后,天气晚来秋.⊙平平仄仄,⊙仄仄平平。
明月松间照,清泉石上流。
⊙仄平平仄,平平仄仄平。
竹喧归浣女,莲动下渔舟。
⊙平平仄仄,⊙仄仄平平。
随意春芳歇,王孙自可留。
⊙仄平平仄,平平仄仄平。
同样的,将第三式的第一句换为第四句,使首句入韵,遂衍化为五律第四式:B平平仄仄平,D⊙仄仄平平。
A⊙仄平平仄,B平平仄仄平。
2023年自考专业(汉语言文学)《古代汉语》考试全真模拟易错、难点汇编贰(答案参考)试卷号:21

2023年自考专业(汉语言文学)《古代汉语》考试全真模拟易错、难点汇编贰(答案参考)(图片大小可自由调整)一.全考点综合测验(共50题)1.【单选题】下面各句,没用复合偏义修辞方式的有()A.先帝尝与太后不快,几到成败B.土功不兴,大夫不得造车马C.是鞭蕖也者,无一时一刻不适耳目之观D.多人不能无生得失,生得失则语泄正确答案:C2.【单选题】下面各句,没有使用共用这一修辞方式的是()A.女为人臣子,不顾恩义,畔主背亲,为降虏于蛮夷。
B.曰安且治者,非愚则谀,皆非事实、知治乱之体者也。
C.今君有区区之薛,而不拊爱子其民,因而贾利之。
D.宫中符中,俱为一体,陟罚臧否,不宜异同。
正确答案:D3.【单选题】下面各组字,含有指事字的有()A.牛相看亦B.山向伐牢C.水文漏从D.即字目取正确答案:A4.【单选题】“四体不勤,五谷不分,孰为夫子?”这句话出自()A.《论语。
子路从而后》B.《论语。
阳货欲见孔子》C.《论语。
季氏将伐颛臾》D.《论语。
颜渊季路侍》正确答案:A5.【多选题】下列各组词在上古属于同义词的有()A.追—逐B.貧—窮C.省—視D.盗—贼E.更—改正确答案:ACE6.【单选题】下面几组汉字,全为会意字的一组是()A.森相肉B.屋前臣C.向陟门D.美家库正确答案:D7.【多选题】一联诗句对句的平仄为“平平仄仄仄平平”,那么出句的平仄可以是()A.仄仄平平平仄仄B.平仄平平平仄仄C.平仄仄平平仄仄D.仄仄平平仄平仄E.平仄仄平仄平仄正确答案:ABCDE8.【单选题】下列句子,具有前置宾语的一句是()A.雖使五尺之童適市,莫之或欺。
B.誰與,哭者?C.吾能居其地,吾能乘其舟。
D.國人莫敢言,道路以目。
正确答案:A9.【单选题】下面几组汉字,全为合体字的一组是()A.奚何来B.戒尖舟C.出走见D.即休飞正确答案:C10.【单选题】“太后之色少解”的“少”字,其词性是()A.形容词B.副词C.名词D.动词正确答案:B11.【单选题】下列句子中加点的词的意义是该词的本义是A.有道之士怀其術而欲以明万乘之主B.天行有常,不为尧存,不为桀亡。
书法考级知识汇总

书法考级知识汇总300题1.书法的三要素是、、(笔法、字法、章法)2.我们通常说的文房四宝指的是、、、(笔墨纸砚)3.章法包含五要素,即( )( )( )( )( ).(谋篇、幅式、正文、落款、印章)4.我国最早的古汉字是商丘中后期的和。
(甲骨文、金文)5.殷商时期刻在龟甲和兽骨上的文字,被称为(A)A 甲骨文B金文 C 石鼓文D瓦当文6.“瘦金体”的创造者是(A)A 宋徽宗B宋高宗C 唐太宗D 唐玄宗7.钟繇是著名的书法家,他生活的时代是(B)A 殷商B三国C汉代D唐代8.传世小楷名作《黄庭经》的作者是(B)A 索靖B王羲之C王献之 D 苏轼9.“初唐四家”除了虞世南、褚遂良、薛稷之外,还有一位是(B)A 智永B欧阳询 C 颜真卿D李邕10.被称为天下第二行书的是(C)A 王羲之《兰亭序》B 苏轼《黄州寒食诗帖》C 颜真卿《祭侄稿》D米芾《蜀素帖》11.祝允明、文徵明、陈淳、王宠在书法史上被称为(B)A宋四家 B 吴门四家 C 楷书四大家D元四家12.董其昌的书法风格是(B)A浑厚 B 淡雅 C 古拙 D 苍茫13.下面有一个碑不属于汉隶(C)A《张迁碑》B《乙瑛碑》C《峄山碑》D《礼器碑》14.“甲骨文”指上古及殷商时期古人刻在龟甲或兽骨上的文字。
因其所刻的内容为占卜所以称为“卜辞”,又因其所在地域为殷墟,所以称为“殷墟文字。
自1899年为王懿荣、刘鹗发现。
15.金文是指殷周时期古人铸和刻在青铜器上的文字。
固器物以钟和鼎为多,又称作"钟鼎文"籀文“古籀”。
其主要代表作有《大盂鼎》《散氏盘》《毛公鼎》《虢季子白盘》。
16.晚期金文的三件代表作品:《虢(guó)季子白盘》《毛公鼎》《散氏盘》16.《散氏盘》、《毛公鼎》、《大盂鼎》、《虢季子白盘》并称“四大国宝”17.青铜器中铭文最多的是《毛公鼎》,铭文32行499字。
18.《散氏盘》,字迹草率字形扁平,体势欹侧,显得奇古生动,已开“草篆”之端。
古代汉语智慧树知到答案章节测试2023年中南民族大学

第一章测试1.“短兵相接“中的“兵”的意义是()A:军队B:士兵C:战争D:兵器答案:D2.”祝聃射王中肩,王亦能军。
“中的”军“的意义是()A:军队B:指挥军队C:驻军D:从军答案:B3.《史记·孙子吴起列传》:“田忌一不胜而再胜。
”句中“再”的词义是()A:再一次B:又C:第二次D:两次答案:D4.古白话是六朝以后在北方话基础上形成的。
()A:错B:对答案:B5.文言是以先秦口语为基础而形成的上古汉语书面语,仅存在于六朝之前。
()A:错B:对答案:A6.“亡羊补牢”这个成语中,“亡”的词义是()A:丢失B:逃亡C:死亡D:出外答案:A7.《左传•成公二年》:“赦之,以劝事君者。
”句中“劝”的词义是( )A:规劝B:劝阻C:劝告D:鼓励答案:D8.“责备“一词词义从古到今没有发生变化。
()A:错B:对答案:A9.“寻常“在上古汉语中表示“普通”之义。
()A:错B:对答案:A10.文言是我国古代文献资料所使用的一种最基本的书面语形式。
()A:对B:错答案:A第二章测试1.下列字典中收单字最多的是()A:《说文解字》B:《汉语大字典》C:《新华字典》D:《康熙字典》答案:B2.下列词典收词最多的是()A:《辞源》B:《现代汉语词典》C:《古代汉语词典》D:《汉语大词典》答案:D3.《词诠》是一部介绍古汉语虚词用法的工具书,其作者是()A:王引之B:杨树达C:张相D:刘湛答案:B4.我国古代字典辞书中运用最多最为普遍的注音方式是()A:反切B:注音字母C:直音D:拼音字母答案:A5.《汉语大字典》是一部以解释汉字的形、音、义为主要任务的大型语文工具书。
()A:错B:对答案:B6.《古汉语常用字字典》重点收录在现代汉语中已经不再使用,或者在现代汉语中仍然使用,但古今词义却有着显著或细微差别的古代汉语常用字。
()A:对B:错答案:A7.《汉语大词典》是我国第一部“古今兼收,源流并重”的特大型汉语语文词典。
叶嘉莹中华诗词之美期末考试答案

一、单选题1《词选序》的作者是()。
6关于周邦彦的词,评论不正确的是()。
22王国维认为“写境”是()派。
•A、王之涣•B、纪晓岚43“衣锦尚褧”出自古书()。
二、判断题1《花间集》是当时诗人文士所作配合宴乐而唱的歌词。
()我的答案:√2长调在敦煌曲子词里就已出现。
()我的答案:√3“菡萏”在《尔雅》中是对荷花的称呼。
()我的答案:√4中国文学注重写作的、表达的方法跟技巧。
()我的答案:×5李清照认为苏轼的《水调歌头》是句读不整齐的诗,而不是词。
()6中国文学史上最早编成的词集是《花间集》。
()我的答案:√7王国维认为词有了境界,词的格调自然会提高。
()我的答案:√8小词都是写的怨妇和思妇。
()我的答案:√9“欲寄彩笺兼尺素”中“兼”字的使用是符合逻辑的。
()我的答案:×10王国维由“懒起画蛾眉”、“照花前后镜”等句联想到屈原的《离骚》。
()我的答案:×11词可以给读者带来丰富的想象。
()我的答案:√12《虞美人》整首词前六句两两对比,永恒与无常的对比。
()我的答案:√13每一个牌调的平仄声调是不一样的。
()我的答案:√14周济是常州词派的继承人。
()我的答案:√15冯正中的词表现的是官能的感觉。
()我的答案:×16诗歌的表现手法之一“兴”是由物及心。
()17“花落春犹在”这句话出自俞平伯。
()我的答案:×18《拟采莲曲》是仿乐府诗而作。
()我的答案:√19冯正中曾官至宰相。
()我的答案:√20诗是体物写志。
()我的答案:×21“词”的本意是指配乐的歌词。
()我的答案:√22苏轼的《江城子·密州出猎》具有婉约低回的词的美感特征。
()我的答案:×23“究天人之际,通古今之变”出自司马迁之口。
()我的答案:√24温庭筠的《菩萨蛮》中只有两三首是写美女追求爱情的。
()我的答案:×25“风乍起,吹皱一池春水”为李璟所作。
2023年公务员省考之行测考前冲刺试卷A卷含答案

2023年公务员省考之行测考前冲刺试卷A卷含答案单选题(共30题)1、记录∶记录本A.咨询∶咨询室B.复印∶复印件C.驾驶∶驾驶证D.存储∶存储盘【答案】 D2、先天的遗传因素和后天的环境影响对人的发展所起的作用到底是哪个重要?双胞胎的研究对于回答这一问题具有重要作用。
为环境决定论者预言,如果把一对双胞胎婴儿完全分开抚养,同时把一对不相关的婴儿放在一起抚养,那么,待他们长大成人后,在性格特征上,前两者之间绝不会比后两者之间有更多的类似。
实际统计数据并不支持这种极端的观点,但也不支持另一种极端的观点,极为遗传因素决定论。
以上论述最能推出的结论是----------。
A.为了确定上述极端的观点哪一个正确,还需要进一步的研究工作B.虽然不能说环境影响对人的发展其唯一决定作用,但实际上其最重要的作用C.环境影响和遗传因素对人的发展都起着重要作用D.双胞胎的研究是不能令人满意的,因为它的除了自相矛盾的结论【答案】 C3、不当得利,是指没有法律和合同上的根据而得到利益,致使他人受到损失。
按法律规定,受损失的一方有请求不当得利人返还所得到的利益的权利。
而不当得利人有返还利益的义务。
下列属于不当得利的是:A.债务人清偿未到期的债务B.顾客多付售货员的货款C.养子女给其生父母的赡养费D.给付赌博而输的钱【答案】 B4、2008年党中央带领全国各族人民取得抗震救灾重大胜利。
伟大抗震救灾精神是()A.万众一心、众志成城,不怕困难、顽强拼搏,坚忍不拔、敢于胜利B.万众一心、众志成城,不畏艰险、百折不挠,以人为本、尊重科学C.万众一心、众志成城,团结互助、和衷共济,迎难而上、敢于胜利D.为国争光,艰苦奋斗,精益求精,勇攀高峰,团结协作【答案】 B5、1939年,毛泽东在哪篇著作中对近代中国半殖民地半封建社会的主要特点作了具体的分析和论述:A.《中国革命和中国共产党》B.《星星之火,可以燎原》C.《中国社会各阶级的分柝》D.《论持久战》【答案】 A6、根据所给资料,回答下列问题。
近体诗基本格式

近体诗基本格式一、仄起句式A:仄仄仄平平(仄起平收)B:仄仄平平仄(仄起仄收)二、平起句式A:平平仄仄平(平起平收)B:平平平仄仄(平起仄收)例:一、仄起句式A:首句不入韵的(仄起仄收)《春望》仄仄平平仄国破山河在平平仄仄平城春草木深平平平仄仄感时花溅泪仄仄仄平平恨别鸟惊心仄仄平平仄烽火连三月平平仄仄平家书抵万金平平平仄仄白头搔更短仄仄仄平平浑欲不胜簪B:首句入韵的(仄起平收)《塞下曲其三》仄仄仄平平骏马似锋飙平平仄仄平鸣鞭出渭桥平平平仄仄弯弓辞汉月仄仄仄平平插羽破天骄仄仄平平仄阵解星芒尽平平仄仄平营空海雾消平平平仄仄功成画麟阁仄仄仄平平独有霍嫖姚二、平起句式A:首句不入韵的(平起仄收)《赋得古原草送别》平平平仄仄离离原上草仄仄仄平平一岁一枯荣仄仄平平仄野火烧不尽平平仄仄平春风吹又生平平平仄仄远方侵古道仄仄仄平平晴翠接荒城仄仄平平仄又送王孙去平平仄仄平萋萋满别情B:首句入韵的(平起平收)《北青萝》平平仄仄平残阳西入崦仄仄仄平平茅屋孤僧仄仄平平仄落叶人何在平平仄仄平寒云路几层平平平仄仄独敲初野磬仄仄仄平平闲依一枝藤仄仄平平仄世界微尘里平平仄仄平吾宁爱与憎注:以首句不入韵为正格。
附:唐七律平仄基本格式:一、平起式A:平平仄仄仄平平(平起平收)B:平平仄仄平平仄(平起仄收)二、仄起式A:仄仄平平仄仄平(仄起平收)B:仄仄平平平仄仄(仄起仄收)例:一、平起式A:首句入韵的(平起平收)《自夏口至鹦鹉洲望岳阳寄元中函》平平仄仄仄平平汀洲无浪复无烟仄仄平平仄仄平楚客相思盖渺然仄仄平平平仄仄汉口夕阳斜渡乌平平仄仄仄平平洞庭秋水远连天平平仄仄平平仄孤城背岭寒吹角仄仄平平仄仄平独戍临江夜泊船仄仄平平平仄仄贾谊上书忧汉室平平仄仄仄平平长沙谪去古今怜B:首句不入韵(平起仄收)《客至》平平仄仄平平仄舍南舍北皆春水仄仄平平仄仄平但见群鸥日日来仄仄平平平仄仄花径不曾缘客扫平平仄仄仄平平蓬门今始为君开平平仄仄平平仄盘殄市远五兼味仄仄平平仄仄平樽酒家贫只旧仄仄平平平仄仄肯与邻翁相对饮平平仄仄仄平平隔篱呼取尽余杯二、仄起式A:首句入韵的(仄起平收)《别舍弟宗一》仄仄平平仄仄平零落残魂信黯然平平仄仄仄平平双垂泪别越江边平平仄仄平平仄一身去国六千里仄仄平平仄仄平万死投荒十二年仄仄平平平仄仄桂岭瘴来云似墨平平仄仄仄平平洞庭春尽水如天平平仄仄平平仄欲知此后相思梦仄仄平平仄仄平常在荆门郢树烟B:首句不入韵的(仄起仄收)《再受连州至衡阳酬柳柳州赠别》仄仄平平平仄仄去过十年同赴召平平仄仄仄平平渡江千里又分歧平平仄仄平平仄重临事异黄函相仄仄平平仄仄平三黜名惭柳士师仄仄平平平仄仄归目并随回雁尽平平仄仄仄平平愁肠正遇断猿时平平仄仄平平仄桂江东过连山下仄仄平平仄仄平相见长吟有所思注:以首句入韵为正格。
2025中考数学二次函数压轴题专题练习18 二次函数与几何交点问题(学生版+解析版)
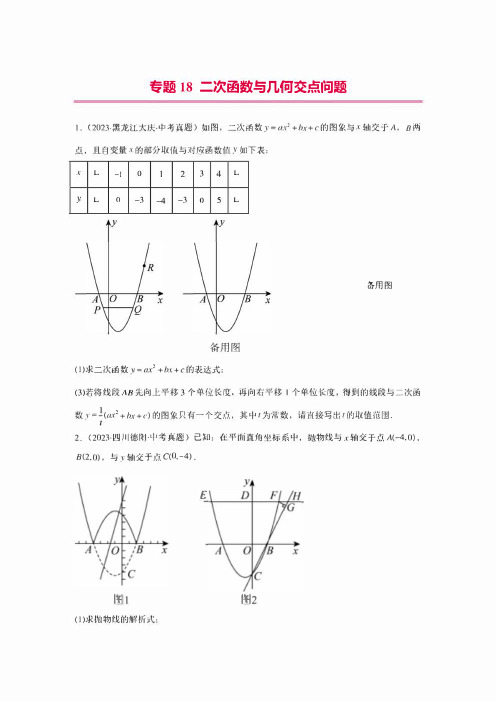
专题18二次函数与几何交点间题1.(2023·黑龙江大庆中考真题)如图,二次函数y = a:x.2+bx+c的图象与X轴交千A,B两点,且自变量X 的部分取值与对应函数值Y如下表:XL -]。
I2 34L yL。
-3-4-3。
5Ly y备用图备用图(I)求二次函数y=ax 2+bx+c的表达式;(3)若将线段A B 先向上平移3个单位长度,再向右平移l 个单位长度,得到的线段与二次函数y =一(釭2+bx+c)的图象只有一个交点,其中(为常数,请直接写出t的取值范围2.(2023四川德阳中考真题)已知:在平面直角坐标系中,抛物线与x轴交于点A(-4,0)'B (2,0),与y 轴交千点C (O,-4).1付l(I)求抛物线的解析式;E -阳2(2)如图1,如果把抛物线x 轴下方的部分沿x 轴翻折180°,抛物线的其余部分保持不变,得到一个新图象.当平面内的直线y=妇+6与新图象有三个公共点时,求k的值;3.(2023山东济南中考真题)在平面直角坐标系xOy 中,正方形ABCD 的顶点A,B 在X轴上,C(2,3),D(-1,3) 抛物线y =成-2少+c(a«))与X 轴交于点E(-2,0)和点Fy y(1)如图l ,若抛物线过点C,求抛物线的表达式和点F 的坐标;(2)如图2,在(I)的条件下,连接CF,作直线CE,平移线段CF,使点C 的对应点P落在直线CE 上,点F 的对应点Q落在抛物线上,求点Q的坐标;(3)若抛物线y=ax 2-2ax+c(a<0)与正方形ABCD 恰有两个交点,求(1的取值范围,4.(2023山东日照中考真题)在平面百角坐标系xOy 内,抛物线y =动X江女仄+2(a>0)交y轴于点C ,过点C作x轴的平行线交该抛物线千点D.l `一-x(1)求点C,D的坐标;(3)坐标平面内有两点£(�.a +1} F (5,a + I ),以线段EF 为边向上作正方形EFGH.@若a=l,求正方形EFGH 的边与抛物线的所有交点坐标;@当正方形EFGH 的边与该抛物线有且仅有两个交点,且这两个交点到x 轴的距离之差为-5时,求a的值5.(2022吉林长春中考真题)在平面直角坐标系中,抛物线y = x 1-bx (b是常数)经过点(2,0)点A在抛物线上,且点A的横坐标为m(m;1:0)以点A为中心,构造正方形PQMN, P Q=2|『111,且PQ.lx轴.(l)求该抛物线对应的函数表达式:(2若点B是抛物线上一点,且在抛物线对称轴左侧.过点B作x轴的平行线交抛物线千另一点C,连按BC.当BC=4时,求点B的坐标:(3若m>O,当抛物线在正方形内部的点的纵坐标y随x的增大而增大时,或者y随x的增大而减小时,求m的取值范围:3(4)当抛物线与正方形PQMN的边只有2个交点,且交点的纵坐标之差为一时,且接写出m4的值6.(2022湖南永州中考真题)已知关于X的函数y= ax2 +bx+c(1)若a.=l,函数的图象经过点(1,-4)和点(2,I),求该函数的表达式和最小值;(2)若a=l,b=-2, c=m十l时,函数的图象与X轴有交点,求m的取值范围.(3)阅读下面材料:设a>0,函数图象与X轴有两个不同的交点A,B,若A,8两点均在原点左侧,探究系数a, b, c应满足的条件,根据函数图像,思考以下三个方面:@因为函数的图象与X轴有两个不同的交点,所以6.=b2 -4ac> 0:@因为A,8两点在原点左侧,所以x=O对应图象上的点在X轴上方,即c>O:@上述两个条件还不能确保A,8两点均在原点左侧,我们可以通过抛物线的对称轴位置来b进一步限制抛物线的位置:即需-一又0.2a综上所述,系数a,b, c应满足的条件可归纳为:请根据上面阅谅材料,类比解决下而问题:a>O tJ.=li-4ac>0c>Ob -—<02a若函数y= ax2 -2x+3的图象在直线x=1的右侧与人轴有且只有一个交点,求U的取值范围.7.(2022湖南衡阳中考真题)如图,已知抛物线y=x'-x-2交X轴千A、B两点,将该抛物线位千X轴下方的部分沿X轴翻折,其余部分不变,得到的新图象记为“图象W",图象W交Y轴千点c.` ` \ `x, I I、一,,(])写出图象W位于线段AB上方部分对应的函数关系式:(2)若直线y=-x+b与图象W有三个交点,请结合图象,直按写出b的值:(3)p为X轴正半轴上一动点,过点P作PM ff y轴交直线BC千点M,交图象W于点N,是否存在这样的点P,使..CMN与60BC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.专题18二次函数与几何交点间题1.(2023·黑龙江大庆中考真题)如图,二次函数y = a:x .2+bx+c的图象与X轴交千A,B两点,且自变量X 的部分取值与对应函数值Y如下表:X L -]。
中国诗词之美答案

中国诗词之美答案选择题(60分)个人答案,供参考,咱80分1、“一晌”在中国的诗词里边是什么意思? (1.00分) A.短暂B.一上午C.一夜D.一天2、“荷叶生时春恨生,荷叶枯时秋恨成”出自? (1.00分) A.李煜B.叶嘉莹C.李商隐D.李白3、关于《人间词话》说法不正确的是? (1.00分)A.中国古代诗话、词话的形式B.白话形式C.“境界说”D.最早是零碎的4、“词”所配合宴乐吸收哪个? (1.00分)A.胡乐B.法曲C.清乐D.都对5、关于韦庄的《菩萨蛮》说法不正确的是? (1.00分) A.有一个系统B.第三人称C.美女与爱情D.致思唐之意6、《花间词》没有收录南唐作品的原因不是 (1.00分)A.时代限制B.地域限制C.风格不同D.作者名气不够7、周邦彦的“似梦里泪暗滴”的韵律是 (1.00分)A.仄仄仄仄仄仄B.平平平仄仄仄C.仄仄仄平平平D.平平仄平平仄8、“弄妆梳洗迟”中的“弄”是什么意思? (1.00分)A.观赏B.同梳C.摆弄D.照9、“可作中兴露布读”,就词论,则非高调。
”是谁说的(1.00分)A.陈同甫B.陈元龙C.陈廷焯D.王国维10、晚清四大词人中谁轻视王国维没有传统 (1.00分)A.朱祖谋B.文廷式C.况蕙风D.王鹏运11、关于《浣溪沙》说法不正确的是? (1.00分)A.为南开马蹄湖的荷花而做B.“荷花凋尽我来迟”C.“云天字字写相思”D.“来送黄昏一抹红”12、叶嘉莹觉得欧阳修的《采莲曲》中真的让人心动起来的是?(1.00分)A.“暗露双金钏”B.“照影摘花花似面”C.“离愁引著江南岸”D.隐隐歌声归棹远”13、“语尽而意不尽,意尽而情不尽”是谁写的? (1.00分)A.李之仪B.欧阳修C.王国维D.叶嘉莹14、屈原作品中的美人代表的是 (1.00分)A.自身B.美好的理想C.美女D.才德美好15、南唐的词人不包括? (1.00分)A.冯延巳B.李璟C.李煜D.温庭筠16、关于“词之言长,诗之景阔”说法不正确的是? (1.00分)A.词可有长篇幅的词B.诗言志是显意识的C.诗境界开阔D.词给人以无限联想17、王国维求学途中到上海先进了? (1.00分)A.时务报馆B.农学社C.东文学社D.强学社18、“要见天孙织锦成”叶嘉莹用于什么场合 (1.00分)A.结婚B.贺寿C.新年D.祝福学生19、辛弃疾的“举头西北浮云”取自谁的“西北有浮云”? (1.00分)A.庄子B.司马相如C.李白D.曹丕20、中国诗经的写作方式不包括 (1.00分)A.赋B.比C.喻D.兴21、西方的文学理论说语言是什么? (1.00分)A.表达方式B.一种符号C.沟通工具D.记事途径22、峨眉能代表一个男子的才学的美好是从谁开始? (1.00分)A.宋玉B.屈原C.庄子D.欧阳炯23、苏东坡的那个作品是词的形式,但有诗的美感 (1.00分)A.《江城子》B.《八声甘州》C.《水龙吟》D.《满庭芳》24、词跟诗真正的差别是在哪里? (1.00分)A.感情的倾泻B.显意识C.诗是言志D.外表的差别25、日日花前常病酒,不辞镜里朱颜瘦表达的是 (1.00分)A.喜爱喝酒B.喜爱赏花C.热爱自热D.一种坚持26、晚清四大词人有 (1.00分)A.况蕙风B.朱祖谋C.王鹏运D.都是27、关于李煜的《虞美人》说法不正确的是? (1.00分)A.后期作品B.写他破国亡家的悲哀C.复国之心D.永恒跟无常的对比28、“老夫聊发少年狂,左牵黄,右擎苍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天秤座:Party伙伴;天蝎座:两肋插刀;射手座:政治同盟;
魔羯座:办公室家具;水瓶座:相声搭档;双鱼座:一生的知己
12星座女生的花钱方式】
买衣服、鞋子——金牛座、巨蟹座、摩羯座。
买减肥药、保养品、做SPA——处女座、水瓶座。
买爱的礼物——白羊座。
买醉、玩乐、享受生活——狮子座、双鱼座、射手座。
第10金牛-含蓄是我名字;第11天蝎-闷骚无界限;第12处女-百分百保守主义
十二星座最容易犯的错误:
白羊座:太心急;金牛座:太物质;双子座:太善变;
巨蟹座:太主妇;狮子座:太霸道;处女座:太挑剔;
天秤座:太罗嗦;天蝎座:太神秘;射手座:太冷淡;
摩羯座:太慢热;水瓶座:太重友;双鱼座:太自欺。
季军(金牛座)、第四名(双鱼座)、
第五名(双子座)、第六名(狮子座)、
第七名(魔羯座)、第八名(巨蟹座)、
第九名(射手座)、第十名(水瓶座)、
第十一名(天蝎座)、第十二名(天秤座
最多女强人—双子
最少女强人—巨蟹
最会逗人开心—天秤
最会投机取巧—双子
最不会投机取巧—摩羯
最没有肚量—摩羯
天蝎座(可爱)
处女座(幸福)
白羊座(快乐)
狮子座(伤感)
巨蟹座(乖乖)
双鱼座(勇敢)
Hale Waihona Puke 摩羯座(聪明) 金牛座(美丽)
射手座(清纯)
天秤座(爱情)
双子座(善感)
水瓶座(吃醋)
扣:694132334
最有肚量—射手
最不会讨人欢心—狮子
最会讨人欢心—双鱼
最有异性缘—金牛、天秤、天蝎、处女
12星座爱现排行榜:
第1狮子-爱现王首选;第2白羊-只要我比你好;第3天秤-怪怪美少年;
第4水瓶-青春要叛逆;第5射手-跟我一起绕地球;第6双子-无休大喇叭;
第7巨蟹-念旧收藏家;第8双鱼-情绪伪装高手;第9魔羯-出其不意显能力;
白羊:因直率而争执;金牛:太过实际,生活小无趣;
双子:善变,很难有安全感;巨蟹:越爱就越不安;
狮子:独占欲超强;处女:关心变挑剔;
天秤:不能忍受孤独;天蝎:无法忍受一丝一毫的隐瞒;
射手:无法放弃自由;摩羯:事业为重;
水瓶:永远淡然却常;双鱼:悲观脆弱。
12星座谁的眼光最好】
冠军(处女座)、亚军(白羊座)、
12星座最拿手的事:
1.白羊:一意孤行;2.金牛:在沉默中爆发;3.双子:八卦制造机;
4.巨蟹:幕后黑手;5.狮子:爱面子;6.处女:极端主义;
7.天枰:沉迷假想;8.天蝎:疑神疑鬼;9.射手:健忘拖拉;
10.摩羯:爱好感官刺激;11.水瓶:怪癖举不胜举;12.双鱼:做事不计后果
能白头到老的星座组合:
白羊女-双子男;金牛女-处女男;双子女-金牛男;
巨蟹女-天蝎男;狮子女-巨蟹男;处女女-射手男;
天平女-双鱼男;天蝎女-摩羯男;射手女-狮子男;
摩羯女-水瓶男;水瓶女-白羊男;
12星座是最佳的什么:
白羊座:玩伴;金牛座:吃饭同伴;双子座:百科指南;
巨蟹座:贤妻良母;狮子座:拉拉队队长;处女座:买衣同伴;
【12星女各是什么公主呢?】
白羊:江湖小公主;金牛:天生贵族公主;
双子:全民公主;巨蟹:任性第一公主;
狮子:不问是非烈士公主;处女:婆妈管家公主;
天秤:眼巴巴公主;天蝎:满腹离骚异想公主;
射手:每天不一样公主;摩羯:务实公主;
水瓶:换路线的古怪公主;双鱼:头上带着皇冠的公主
【12星座的爱情副作用】
算命——双子座、天蝎座。
电话费——天秤座。
十二星座生命中最珍贵的东西:
白羊座--勇气;金牛座--金钱;双子座--自由;
巨蟹座--家庭;狮子座--自尊;处女座--听众;
天秤座--朋友;天蝎座--理智;射手座--流行;
魔羯座--信任;水瓶座--灵感;双鱼座--梦想
12座给人最深刻印象
