初等几何研究试卷4
初等几何研究试题答案(李长明版)

初等几何研究试题答案(I)、线段与角的相等1. O O、O Q相交于A B, O O的弦BC交O Q于E, O 02的弦BD交O0于F,求证:(1)若2 DBA2 CBA贝卩若DF二CE则 / DBA M CBA.证明:⑴连接AC AE AF、AD在O 0 中,由/ CBA W DBA得AC=AF在O O 中,由/ CBA W DBA得AE=AD由A C、B、E四点共圆得/仁/2由A D B、E四点共圆得/ 3二/4所以△ ACE^A AFD••• DF=CE(2) 由(1)得/ 仁/ 2, / 3=2 4v DF=CE• △ACE^A AFD••• AD=AE在O Q 中,由AD=AE^得/ DBA M CBA2. 在厶ABC中,AC=BC,Z ACB=90,D是AC上的一点,AE丄BD的延长线于E,又AE=1BD,2求证:BD平分/ ABC.证明:延长AE,BC交于点F7 AED "BCA =90 ADE "BDC•CBD =/CAF又7 ACF BCA = 90 AC 二BC•ACF 三BCD . AF = BD1 1又、:AE BD . AE AF2 2又ABEE _ BE■ BE平分ABF即BD平分.ABC3. 已知在凸五边形ABCDE中, / BAE=3 ,BC=CD=DE M/ BCD玄CDE=180-求证:/ BAC 2 CAD h DAE.证明:过点B 作BDL BC,交圆周于点D,连结CD ©D•••/ DBC=90, • CD 是直径,则/CAD=90证明:连接BD,得△ CBD 是等腰三角形且底角是/ CDB=[18(0-(180o — 2 - )] -2=.:丄 BDE=(180° — 2G )-O (=180O — 3«••• A B 、D E 共圆同理A C D E 共圆• h BAC h CAD h DAE4. 设H 为锐角△ ABC 的垂心,若AH 等于外接圆的半径由题,可得AH L BC, BH丄AC••• BD// AH, AD// BH二四边形ADBH是□••• AH=BD又;AH等于外接圆的半径(R)• BD=R M CD=2R•••在Rt △ BCD中,CD=2BD即/ BCD=30• / BDC=60又;/ BAC K BDC BAC M BDC=605. 在厶ABC中, / C=90,BE是/B的平分线,CD是斜边上的高,过BE CD之交点0且平行于AB的直线分别交AC BC于F、G,求证AF=CE.证明:如图;/ 1 = 2 3, / 仁/2. 2二/ 3, • GB = GO,;2 5=2 4=2 6, • CO =CE,;FG// AB,「. AF/CF二B$CG二G0CG,又;△ FCO^COG/. CO7CF=G/CG=A/CF,• CO=AF;CO=CE,\ AF=CE.6. 在厶ABC中,先作角A B的平分线,再从点C作上二角的平分线值平行线,并连结它们的交点 D E,若DE// BA,求证:△ ABC等腰.证:如图所示设AG ED的交点为Fv AD是/ A的平分线•••/仁/2T DE// AB 仁/ 3v CE// AD :丄 3二/ 5, / 4二/ 2•/仁/2二/3=Z 4=2 5则厶FAD ffi^ FCE是等腰三角形•A F=DF,EF=CF•A C=DE同理可证BC=DE•A C=BC• △ ABC是等腰三角形7. 三条中线把△ ABC分成6个三角形,若这六个三角形的内切圆中有4个相等.求证:△ ABC是正三角形.AB D C证明:•/△ AOF △ AOE △ COD △ COE △ BOF △ BOD面积都相等--S A OFE=S A OEC即: 11111 1BF X 叶一FOX 叶BO X r= CEX 叶一OE< 叶一OC X r 2 2 2 2 2 21 12 (BF+FO+BO X r= - (CE+OE+OC X r••• BF+FO+BO二CCE+OE+OC••• CE+OE+OC-OG-OI二CE+OE+OC-OL-OJ• 2DH+2BH=2FK+2CK• 2BF=2CE又F、E分别为AB AC之中点••• AB=AC同理:AB=BC故厶ABC是正三角形.8. 平行四边形被对角线分成四个三角形中,若有三个的内切圆相等证明:该四边形为菱形.C证明:又•••△ AOBA BOC、△ CODA DOA四个三角形的面积相等1 1OD DC OC r OB BC OC r2 2CD OC OD 二BC OB OCOD OC DC - OE - OG = OB OC BC - Ol - OG二2DF +2CF =2BH +2CH二2DC =2BC=DC =BC•四边形为菱形9. 凸四边形被对角线分成4个三角形,皆有相等的内切圆,求证:该四边形是菱形证明:连结O i 、O 2,分别作O i 、O 2到AC 的垂线,垂足分别为P 、M•••在厶ABC 中 ,BO 是。
精品《初等几何研究》练习题

《初等几何研究》作业一、填空题1、对直线a上任意两点A、B,把B以及a上与B在A同侧的点的集合称作,并记作。
2、在绝对几何中,外角定理的内容是:。
3、第四组公理由条公理组成,它们的名称分别是。
4、欧氏平行公理是:。
5、罗氏几何公理系统与欧氏几何公理系统的共同之处是,不同之处是。
6、几何证明的基本方法,从推理形式上分为法与归纳法;从思维方向上分为法与分析法;从命题结构上分为证法与间接证法,其中间接证法包括法与法。
7、过反演中心的圆,其反演图形是(过或不过)反演中心的。
8、锐角三角形的所有内接三角形中,周长最短的是三角形。
9、锡瓦定理:设⊿ABC的三边(所在直线)BC、CA、AB上分别有点X、Y、Z,则AX、BY、CZ三线共点(包括平行)的充要条件是。
10、解作图问题的常用方法有:、、、等。
11、数学公理系统的三个基本问题是性、性和性.12、对于共面的直线a和a外两点A、B,若a与(AB)相交,则称A、B在a的,否则称A、B在a的 .13、命题:“过直线外一点,至少有一条直线与已知直线共面但不相交”是定理的推论.14、证明直线和圆的连续性时,主要依据了原理.15、罗氏平行公理是: .16、在罗氏几何中,共面的两条直线有种关系,它们分别是17、几何证明的通用方法一般有法、法、法、法、法、法等.18、等边三角形外接圆周上任一点到三顶点的连线段中,最长线段与另两条线段之和具有的关系.19、尺规可作图的充要条件是 .20.由公理可以证明,线段的合同关系具有性、性、性和性.21.如果线段与角对应,那么线段的中点与角的对应.22.命题:“线段小于任意一条连接其两个端点的折线”是定理的推论.23.绝对几何包括有组公理,它们分别是 .24.写出一条与欧氏平行公理等价的命题: .25.在罗氏几何中,两条直线为分散线的充要条件是 .26、.常用的几何变换有等27.托勒密定理:四边形ABCD是圆内接四边形,则 .28.请写出两条作图公法: .29.在希尔伯特给出的欧几里得公理系统中,三角形的定义是:。
初等几何研究答案

《初等几何研究》作业一、填空题1、对直线a 上任意两点A 、B ,把B 以及a 上与B 在A 同侧的点的集合称作 射线(或半直线),; ,并记作 AB 。
2、在绝对几何中,外角定理的内容是: 三角形的外角大于任一不相邻的内角 。
3、第四组公理由 两 条公理组成,它们的名称分别是 度量公理(或阿基米德公理)和康托儿公理 。
4、欧氏平行公理是:对任意直线a 及其外一点A ,在a 和A 决定的平面上,至多有一条过A 与a 不相交的直线 。
5、罗氏几何公理系统与欧氏几何公理系统的共同之处是 前4组公理(或绝对几何) ,不同之处是 平行公理 。
6、几何证明的基本方法,从推理形式上分为 演绎 法与归纳法;从思维方向上分为 综合 法与分析法;从命题结构上分为 直接 证法与间接证法,其中间接证法包括 反证 法与 同一 法。
7、过反演中心的圆,其反演图形是 不过 (过或不过)反演中心的 直线 。
8、锐角三角形的所有内接三角形中,周长最短的是 垂足三角形。
9、锡瓦定理:设⊿ABC 的三边(所在直线)BC 、CA 、AB 上分别有点X 、Y 、Z ,则AX 、BY 、CZ 三线共点(包括平行)的充要条件是1=⋅⋅ZBAZYA CY XC BX 。
10、解作图问题的常用方法有: 交轨法 、三角奠基法、 代数法 、 变换法 等。
11、数学公理系统的三个基本问题是 相容性、 独立性和 完备 性.33.①答案不惟一.34.①(0,+∞),②,(0,π/2),③连续,④单调递减. 35.①平移,②旋转,③轴对称.36. ①1=⋅⋅ZB AZYA CY XC BX (或-1)37.①写出已知与求作,②分析,③作法,④证明,⑤讨论.12、对于共面的直线a和a外两点A、B,若a与(AB)相交,则称A、B在a的异侧,否则称A、B在a的同侧.13、命题:“过直线外一点,至少有一条直线与已知直线共面但不相交”是外角定理的推论.14、证明直线和圆的连续性时,主要依据了戴德金分割原理.15、罗氏平行公理是:对任意直线a及其外一点A,在a和A决定的平面上,至多有一条过A与a不相交的直线.,16、在罗氏几何中,共面的两条直线有3种关系,它们分别是平行,相交,分散.17、几何证明的通用方法一般有化归法、类比法、构造法、数形结合法、变换法、模型法等.18、等边三角形外接圆周上任一点到三顶点的连线段中,最长线段与另两条线段之和具有相等的关系.19、尺规可作图的充要条件是所求的量可用已知量的有理式或只含平方根的无理式表出.20.由公理可以证明,线段的合同关系具有反身性、对称性、传递性和可加性.21.如果线段与角对应,那么线段的中点与角的角平分线对应.22.命题:“线段小于任意一条连接其两个端点的折线”是外角定理的推论.23.绝对几何包括有四组公理,它们分别是结合公理、顺序公理、合同公理、连续公理. 24.写出一条与欧氏平行公理等价的命题:.25.在罗氏几何中,两条直线为分散线的充要条件是.26、.常用的几何变换有合同变换、相似变换、射影变换、反演变换等27.托勒密定理:四边形ABCD是圆内接四边形,则1=⋅⋅ZBAZYACYXCBX(或-1).28.请写出两条作图公法:过两点可作一条直线(或其部分)。
初等几何试题(李长明版)
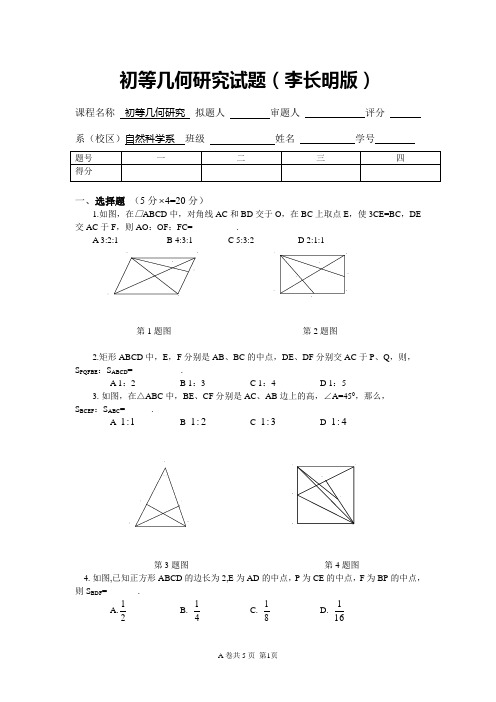
初等几何研究试题(李长明版)课程名称 初等几何研究 拟题人 审题人 评分 系(校区)自然科学系 班级 姓名 学号题号 一 二 三 四 得分一、选择题 (5分⨯4=20分)1.如图,在□ABCD 中,对角线AC 和BD 交于O ,在BC 上取点E ,使3CE=BC ,DE 交AC 于F ,则AO :OF :FC=__________.A 3:2:1B 4:3:1C 5:3:2D 2:1:1第1题图 第2题图2.矩形ABCD 中,E ,F 分别是AB 、BC 的中点,DE 、DF 分别交AC 于P 、Q ,则, S PQFBE :S ABCD =___________.A 1:2B 1:3C 1:4D 1:53. 如图,在△ABC 中,BE 、CF 分别是AC 、AB 边上的高,∠A=450,那么, S BCEF :S ABC =______.A 1:1B 2:1C 3:1D 4:1第3题图 第4题图4. 如图,已知正方形ABCD 的边长为2,E 为AD 的中点,P 为CE 的中点,F 为BP 的中点,则S BDF =_______.A.21 B.41 C.81 D.161二、填空题 (5分⨯4=20分)1. 如图,ABCD 是边长为a 的正方形,△PBC 是正三角形,则△PBD 的面积为_____.第1题图第2题图2.如图,正方形ABCD的边长为2,E,F分别是CD,BC的中点,AE,DF相交于点P,则BP的长度为_____.3. 如图,在△ABC中,DE∥BC,S ADE:S CDE=1:3,且S CDE=1则S BCD=_________.第3题图第4题图4. 如图,AB是⊙O的直径,AB=4,BC=3,BD平分∠ABC,AD、BC的延长线交于E,是S BDE:S ABCD=________.三、证明题(10分 5=50分)(画图并证明)1. 在△ABC中,∠C=900,BE是∠B的平分线,CD是斜边上的高,过BE、CD的交点O,且平行AB的直线分别交AC、BC于F、G。
初等几何研究试题答案(4)

。
D B
C
L1
A
E'
E
证明:A.B.C 为 L1 上顺次取的三点,D、E 为 L2 上异于 L1 的两点 。 。 又∵∠AEC=90 , ∠ADB=90 ∴⊿ADB 的外接圆为以 AB 为直径所做的圆,记为⊙O1, ⊿AEC 的外接圆为以 AC 为直径所做的圆, 记为⊙O2. ∴作图可知⊙O1 是⊙O2 中,以 A 为切点的内切圆。 当 L2 向左移动时, 假设 L2 移动后交⊙O1、⊙O2 于点 D’,E’. 过⊙1 的圆心作线段垂直 AB 交⊙O1 于 F,交⊙O2 于 G. (1) 当 D 移至 F 时,AF﹤AD,AG﹤AE. ∵⊙O2 的半径大于⊙O2 的半径 ∴移动相同单位的距离,其所截线段 GF﹤DE ∴⊿ADE 的外接圆半径变小了。 (2) 当 L2 移过 AB 的中点时, 可知 AD﹥AD’,AE﹥AE’, 又∵D’O﹤OD, OE’ 6 证明:棱形 ABCD 两邻边 AB、BC 被其内切圆之任一切线所截的 线段 AM 和 CN 之积为定值。
A E M B F O N G C D
证明:连接 OM、ON(如图) 令∠AOE=∠1,∠EOM=∠2,∠MOF=∠2´,∠FON=∠3,∠NOG=∠3´,∠ GOC=∠1´ ∵A、C 关于点 O 对称 ∴∠1=∠1´ ∵AM、MN 都是⊙O 的切线 ∴∠2=∠2´ ∵NM、NC 都是⊙O 的切线 ∴∠3=∠3´ ∵∠1+∠2+∠2´+∠3+∠3´+∠1´=180° ∴∠1+∠2+∠3=∠1´+∠2´+∠3´=90° ∵∠NOM=∠2´+∠3=90°-∠1,且∠OAM=90°-∠1 ∴∠OAM=∠NOM ∵∠AMO=∠OMN ∠OAM=∠NOM
初等几何研究期末试卷

试卷
秋季学期 考试时间: 120 分钟
课程名称 初等几何研究 A 卷□ B
一、证明题(每题10 分,共50分)
1 证明:有七条棱的多面体不存在。
2.rh
R
r
h R r 211,2
2
=
-
,证明:
高为底半径为的球作一外切圆锥,其
半径为
3.已知空间四边形OABC ,OA=OB ,CA=CB ,E ,F ,H ,G 分别为线段OA ,OB ,CA ,CB 的中点,证明:四边形EFHG 为矩形。
4.证明:除四面体外,不存在任何一个凸多面体它每个顶点和其余各顶点都有边相连.
5.证明四面体中,一个二面角的平分面将对棱所分成两线段的比等于夹这二面角的两个面的面积之比。
青岛大学师范学院_______课试卷
………………………………………………装………………订………………线………………………………………………
系:班级_____ 姓名______ 学号_______
密 封 线 ———————————————————————————————————————————————————
二、计算题(每题10 分,共50分)
1 设一线段在互垂三平面上的射影分别为r1,r2,r3,求这线段的长。
2.利用“分割,近似,求和,取极限”的方法求球的表面积公式。
3.一平面截球面所得二部分的面积之差等于截面面积,求平面与球心的距离。
4.设四面体的三侧面积相等为S,求从底面上任意一点到三侧面的距离之和。
5.在定三角形ABC的边BC上求一点,从这点引其余二边的平行线,使与余二边交成的平行四边形的周长为定长。
初等几何研究试题

初等几何研究试题一、选择题 (5分⨯4=20分)1. 如图,CD EF AB ||||,已知20=AB ,,80=CD 100=BC 那么,EF 的值是____. A. 10, B.12, C.16, D.20第1题图 第2题图 2. 如图,在ABC ∆中,P 是AC 上的点,取BP 的中点Q ,连结CQ 并延长与AB 交于D ,则ABP S ∆与ACD S ∆的关系是_____.A. ABP ACD S S ∆∆<B. ABP ACD S S ∆∆=C. ABP ACD S S ∆∆>D. 不能确定.3. 如图,在ABC ∆中,BE 、CF 分别是AC 、AB 边上的高,o A 45=∠,那么,FBCE AEF S S :=______.A 1:1B 2:1C 3:1D 4:1第3题图 第4题图4. 如图,ABCD 是面积为1的正方形,PCB ∆是正三角形,PBD ∆的面积为_____.A.213- B. 8132- C. 43D. 413-二、填空题 (5分⨯4=20分)1.如图,已知正方形ABCD 的边长为1,E 为AD 的中点,P 为CE 的中点,F 为BP 的中点,则BFD S =_____.第1题图 第2题图 2.如图,AB 是圆O 直径,4=AB ,弦3=BC ,ABC ∠的平分线交半圆于D ,BC AD ,的延长线交于E ,DCE ABCD S S :=______.3.已知圆O 是ABC ∆的外接圆,半径为r ,CO BO AO ,,分别交对边于F E D ,,, 则:CF BE AD 111++=______.(用r 表示)4.ABC ∆的三条高分别为c b a h h h ,,,又ABC ∆内任一点P 到三边距离分别为c b a p p p ,,,则=++c c b b a a h p h p h p ______.三、证明题(12分⨯5=60分)1. 在ABC ∆中,过点A 作直线BC l ||,B ∠的平分线交AC 于D ,交直线l 于E ,C ∠的平分线交AB 于F ,交直线l 于G ,且FG DE =,求证: ABC ∆是等腰三角形.2.M是以AB为直径的上不同于BA、的任一点,C是直径AB上的定点,过M作CM 垂直的直线交过处BD、,求证:A、的切线于E(1)ED,成等比数列;BM,EC(2)BEAD⋅是定值.3.三条中线把ABC∆分成6个三角形,若这6个三角开的内切圆中有4个相等,求ABC∆是正三角形.4.从等腰ABC ∆的底边AC 上的中点M 作BC 边的垂线MH ,点P 为线段MH 的中点,求证:BP AH ⊥.5.已知: ABC ∆内接于圆O ,N M L ,,分别是弧AB CA BC ,,的中点,连结LM NM ,分别交BC AB ,于E D ,;I 是ABC ∆的内心,求证: (1)BC DE ||;(2)IE DI DE +=.。
初等几何研究综合测试题(三)

初等几何研究综合测试题(三)《初等几何研究》综合测试题(三)适用专业:数学教育专业考试时间:120分钟一、选择题(本题共8小题,每小题3分,共24分)1.两个三角形有两边和一角对应相等,则两个三角形__________。
A.一定全等;B.一定不全等;C.可能全等,可能不全等;D.以上都不是。
2.在在正三角形、等腰梯形、矩形和圆这四种图__________。
第3题图A.1种;B.2种;C.3种;D.4种。
3.如图,在等腰梯形ABCD中,AD//BC,AC与BD 相交于点O,则图中面积相等的三角形共有___________。
A.1对;B.2对;C.3对;D.4对。
4. 在正三角形、等腰梯形、矩形和圆这四种图形中是轴对称图形,又是中心对称图形的有__________。
A.1种;B.2种;C.3种;D.4种。
5.如图,在V ABC中,DE//BC,如果AE:EC=3:2, 那么DE:BC等于________。
A.3:5;B.3:2; C.2:3;D.2:5。
6.⊙O中,AB、CD是两条平行弦,位于圆心的两侧,AB=40cm,CD=48cm,AB、CD的距离为22cm,则⊙O的半径是__________。
A.15cm;B.20cm;C.25cm;D.30cm。
7.在平移过程中,对应线段A.互相平行且相等;B.互相垂直且相等;C.互相平行(或在同一条直线上)且相等;D.以上都不对。
8.下列关于平移的说法中正确的是___________。
A.原图形中两个顶点连成的线段长是平移的距离;B.平移后的两个图形中两个顶点连成的线段长是平移的距离;C.以对应点中的一点为端点的射线是平移的方向。
D.以原图形中的一点为端点,且经过它的对应点的射线的方向是平移的方向;二、判断题(本题共5小题,每小题2分,共10分)1.角的大小与边的长短有关。
()2.一个钝角减去一个直角,其差必为一个锐角。
()3.两直线被第三条直线所截,同位角相等,内错角不相等。
初等几何研究第二版朱德祥朱维宗答案

初等几何研究第二版朱德祥朱维宗答案期中考试题1. P18 T5四边形有一双对角互补,则必为圆内接四边形2. P26 T3 两圆O与O’相交于点P,M是OO’的中点,过P任做直线交两圆与A及A’,Q是AA’的中点。
证明MP=MQ。
3. P27 T10 在中,证明BC边的中垂线和角A的平分线相交在外接圆周上;他们的,ABC交点距B、C两点,距内切圆心,距角A的旁切圆心都等远 4. P30 例4 蝴蝶定理5. 证明勾股定理(毕达哥拉斯)6. P39 T11 证明欧拉线7. P41 例3 三角形中,大边上的平分角线较小P18 T5四边形有一双对角互补,则必为圆内接四边形首先证?A+?C=180如图所示,连接DO, BO. 设优角BOD为θ?圆周角等于所对的圆心角的一半??C=1/2?BOD,同理,?A=1/2θ??A+?C=1/2*360=180,即两角互补。
同理可证?ABC+?ADC=180.所以对角互补。
T6 证明:等腰三角形底边延长线上任意一点到两腰的距离之差等于一腰上的高。
S,S,S ,ABP,ACP,ABC111AB*PF--AC*PE=AC*CH AB=AC 222PF--PE=CH圆内接偶数边凸多边形相间诸角之和等于其余各角之和 Tp5226、从圆上一点到其内接四边形一双对边的距离之积,等于从该点到两条对角线的距离之积设圆内接四边形ABCD,P是其外接圆上任一点,过P分别作对角线AC,BD;边,BC,,DA的垂线,垂足依次为E,F;G,H,。
根据简单几何定理:三角形两边之积等于第三边上的高与外接圆直径之积R中 PA*PC=R*PE (1) ,PAC,PDB,PD*PB=R*PF (2),PAD PA*PD=R*PG (3)PB*PC=R*PH (4) ,PBC(1)*(2)=(3)*(4)=所以得证P27 T9 在三角形ABC中,分别以AB和AC为一边向外做等边三角形ABD和ACE,求证CD=BEAE=AC,AB=AD, ?,DAB,,EAC ?,DAC,,EAB ?,AEB,,ACD ?CD,BEP31 4.四边形ABCD中,设AD=BC。
初等几何研究综合测试题(十四)

《初等几何研究》综合测试题(十四)适用专业:数学教育专业 考试时间:120分钟一、选择题(本题共8小题,每小题3分,共24分)1.等腰三角形的两条边的长为___________。
A.B. ;C.D.或 2.等腰三角形底边长为5cm ,一腰上的中线把其周长分为两部分之差为3cm ,则腰长为__________。
A.2cm ;B.8cm ;C.2cm 或8cm ;D.以上结论都不对。
3.下列四组图形中,是相似形的一组是_________。
A.各有一个角是30°的两个等腰三角形;B.底角为40°的两个等腰三角形;C.各有一个角是120°的两个等腰三角形;D.邻边之比都等于2的两个平行四边形。
4.三条线段长度分别是3,4,6,则以此三条线段为边___________。
A.能构成锐角三角形;B.能构成钝角三角形;C.能构成直角三角形;D.不能构成三角形。
5.扇形的面积为S ,弧长为l ,则扇形中心角的度数为________。
A.2180()l S π ;B. 2180()S l π ;C. 290()l Sπ;D. 290()S l π 。
6.下列命题中能用来判断一条线段是半径的命题是__________。
A.过圆心且垂直于切线的直线必经过切点;B.过切点且垂直于切线的直线必经过圆心;C.圆的切线垂直于过切点的半径;D.过半径的外端且垂直于这条半径的直线是圆的切线。
7下列图形中,轴对称图形有__________。
①角 ② 三角形 ③ 圆 ④线段 ⑤正方形 ⑥扇形 ⑦平行四边形 ⑧等腰梯形 A.3个;B.4个;C.5个;D.6个。
8.如图,有A 、B 、C 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在_________。
A.在AC 、BC 两边高线的交点处; B.在AC 、BC 两边中线的交点处;C.在AC 、BC 两边垂直平分线的交点处;D.在∠A 、∠B 两内角平分线的交点处。
初等几何研究作业参考答案

《初等几何研究》作业参考答案一.填空题1.①射线(或半直线),②。
2. ①两,②度量公理(或阿基米德公理)和康托儿公理。
3.①前4组公理(或绝对几何),②平行公理。
4.①平移,②旋转,③轴对称. 5.1=⋅⋅ZBAZYA CY XC BX 。
6.①交轨法,②三角奠基法,③代数法,④变换法。
7.①反身性、②对称性、③传递性、④可加性. 8.外角. 9.答案不惟一.10.①演绎,②综合,③直接,④反证,⑤同一; 11.1=⋅⋅ZBAZYA CY XC BX .(答-1也对) 12. ①过两点可作一条直线(或其部分),②已知圆心和半径可作一圆(或其部分). 13.①不共线的三点A 、B 、C 及(AB)、(BC)、(CA)构成的点的集合。
14.连续. 15.答案不惟一. 16.①不过,②圆.17.1=⋅⋅ZB AZYA CY XC BX (或-1).18.①写出已知与求作,②分析,③作法,④证明,⑤讨论. 19.①相容,②独立,③完备.20.合同变换、相似变换、射影变换、反演变换等21.对任意直线a 及其外一点A ,在a 和A 决定的平面上,至少有两条过A 与a 不相交的直线. 22.①代数,②解析,③三角,④面积,⑤复数,⑥向量. 23.相等。
24.所求的量可用已知量的有理式或只含平方根的无理式表出. 二.问答题1.对于公理系统∑,若有一组具体事物M ,其性质是已知的,在规定∑中每一个基本概念指M 中某一具体事物后,可验证∑中每个公理在M 中都成立,则称M 为公理系统∑的一个模型;2.①若AB ≡B A '',则d(AB)=d(B A '');②当C BA ˆ时,有d(AB)+d(BC)=d(AC).3.命题“三角形的内角和不大于两个直角” 与欧氏平行公理不等价。
4.结合,介于,合同;结合——即有公共点,介于——即在…之间,合同——相等或完全相等. 5.长度、角度、相等、全等、运动、移置、叠合、重合等.6.由第五公设引出了该公理独立性的问题,对该问题的研究导致了非欧几何等结果的产生. 7.通常用“在……上”、“属于”、“通过”等语句来表述。
初等几何研究期末试题及答案

初等几何研究期末试题及答案第一题:已知四边形ABCD中,AB = 6cm,BC = 8cm,∠ABC = 90°,角ADC的度数为60°。
求四边形ABCD的面积。
解析:由题意可知,四边形ABCD为一个平行四边形,且∠ABC = 90°,∠ADC = 60°。
首先,我们可以使用正弦定理求得∠BAC的度数。
根据正弦定理可以得到:sin∠BAC/AB = sin∠ABC/ACsin∠BAC/6 = sin90°/ACsin∠BAC/6 = 1/ACAC = 6/sin∠BAC接下来,我们可以使用余弦定理求得AC的长度。
根据余弦定理可以得到:AC² = AB² + BC² - 2AB·BC·cos∠ABCAC² = 6² + 8² - 2·6·8·cos90°AC² = 100AC = √100AC = 10再次,我们可以使用正弦定理求得AD的长度。
根据正弦定理可以得到:sin∠ADC/AC = sin∠CAD/ADsin60°/10 = sin∠CAD/AD√3/10 = sin∠CAD/ADAD = 10sin∠CAD/√3最后,我们可以计算四边形ABCD的面积。
四边形ABCD可以分成两个三角形,即△ABC和△ACD。
面积公式为:四边形ABCD的面积 = △ABC的面积 + △ACD的面积= (1/2)·AB·AC + (1/2)·AC·AD= (1/2)·6·10 + (1/2)·10·10sin∠CAD/√3= 30 + 50sin∠CAD/√3综上所述,四边形ABCD的面积为30 + 50sin∠CAD/√3。
第二题:已知直角三角形ABC,其中∠B = 90°,AB = 5cm,AC = 12cm。
试卷4答案
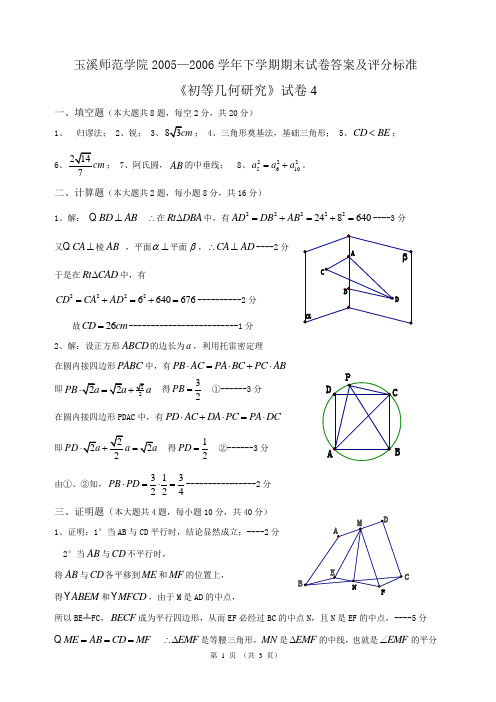
第 1 页 (共 3 页)玉溪师范学院2005—2006学年下学期期末试卷答案及评分标准《初等几何研究》试卷4一、填空题(本大题共8题,每空2分,共20分)1、 归谬法;2、锐; 3、; 4、三角形奠基法,基础三角形; 5、CD BE <;6、7; 7、阿氏圆,AB 的中垂线; 8、2225610a a a =+。
二、计算题(本大题共2题,每小题8分,共16分)1、解: BD AB ⊥ ∴在Rt DBA ∆中,有22222248640AD DB AB =+=+=----3分又CA ⊥棱AB ,平面α⊥平面β,CA AD ∴⊥----2分于是在Rt CAD ∆中,有22226640676CD CA AD =+=+=----------2分故26CD cm =-------------------------1分 2、解:设正方形ABCD 的边长为a ,利用托雷密定理 在圆内接四边形PABC 中,有PB AC PA BC PC AB ⋅=⋅+⋅即PB = 得32PB = ①------3分在圆内接四边形PDAC 中,有PD AC DA PC PA DC ⋅+⋅=⋅即2PD a += 得12PD = ②------3分由①、②知,313224PB PD ⋅=⋅=----------------2分 三、证明题(本大题共4题,每小题10分,共40分)1、证明:1°当AB 与CD 平行时,结论显然成立;----2分 2°当AB 与CD 不平行时,将AB 与CD 各平移到ME 和MF 的位置上, 得ABEM 和MFCD ,由于M 是AD 的中点,所以BE ╩FC ,BECF 成为平行四边形,从而EF 必经过BC 的中点N ,且N 是EF 的中点,----5分ME AB CD MF === EMF ∴∆是等腰三角形,MN 是EMF ∆的中线,也就是EMF ∠的平分C第 2 页 (共 3 页)线,说明直线MN 与ME 、MF 所成的角相等,即直线MN 与AB 、CD 所成的交角相等。
初等几何研究模拟卷4答案

华东师大网络学院考卷《初等几何研究》模拟考卷4答案课程名称:__初等几何研究_______ 学生姓名:___________________ 学号:___________________ 专业:___________________…………………………………………………………………………………………一、(10分)叙述非欧几何的Poincare上半平面模型,并说明在Poincare上半平面模型中欧氏几何的平行公理不成立。
答:见讲义第一章第三节Poincare上半平面模型的介绍.,,ABCD AB CD AD BC ABCD+=+二、(10分)凸四边形中已知则四边形一定有内切圆.C E C图1 图2 图3 (),2.AD AB BCCD D BC E AB DE AD BE AB CD AD BCDC CE DECDE DC CE DECD D BC--证间接证法穷举法假设结论不成立作一圆与、、相切。
第一种情形,此圆与相交,如图,过作圆之切线与的延长线交于,由切线性质知+=+,而已知条件为+=+则+=这和三角形的两边之和+大于第三边矛盾.第二种情形,此圆与相离,如图3,过作圆之切线与的交于EAB CD AD BC DE EC CDCDE DE EC CD,由切线性质及已知条件+=+,得+=这和三角形的两边之和+大于第三边矛盾. 证毕.B,,,ABC AB AC BD CE B C BD CE>∠∠> 三、(10分)如图所示,在中,分别是的平分线,求证:,..,,.,,,,: //BD CE O AB AC C B OCB OBC OB OC OD OE BD CE OD OE OE OF OD OB OH OC HF OCD OHFH HK CE >⇒∠>∠⇒∠>∠⇒>≥><==≅ 证明 设交于由如果显然有结论证得如果则在上截取在上截取连接则有再过作,//.1122.AB K H HG BA CE G GHO B C FHOG OF ∠=∠<∠=∠∴ 交于过点作交于点必在线段上 111,222,, ,.BKH BEC A C A B B BH HK HK GE FE BH HO OD EF OF OC BD CE ∠=∠=∠+∠>∠+∠>∠∴>=>∴++>++> 即四、(10分)证明斯蒂瓦特(Stewart)定理 在,,PAB C AB 中设是边上任意一点则222PA BC PB CA PC AB BC CA AB ⋅+⋅=⋅+⋅⋅.证明 如图所示, 在,,PAB PD AB D D C ⊥ 中作于若点与点不重合, 则PCA ∠与PCB ∠必有一个为钝角, 一个为锐角. 不妨设PCA ∠为钝角, PCB ∠为锐角, 则由广勾股定理, 得2222,PA PC AC AC CD =++⋅ ①2222PB PC BC CB CD =+-⋅ ②①BC ⨯+②AC ⨯,得2222222=PA BC PB CA PC BC AC BC PC CA CB CA PC AB BC CA AB⋅+⋅=⋅+⋅+⋅+⋅⋅+⋅⋅若点D 与点C 重合, 则结论显然成立.五、(10分)求证三角形三边中点,三高线的垂足,垂心与定点连线的中点九点共圆.,(0,2),(2,0),(2,0),'(,0)'(,1),'(,1),(0,2),(0,1),(,),(,).1:(2),:(2),A B b C c A b c B c C b H bc P bc Q b bc R c bc AC y x c cBE y c x b +----⎧=--⎪⎨⎪=-⎩ 证明 如图所示选取直角坐标系设则 由 ()()()()2222212,.11212,.',',':11c bc c c b E cc b bc b b c F A B C b b +-⎛⎫⎪++⎝⎭+-⎛⎫⎪++⎝⎭得 由对称性,得又设过的圆方程为22222222 0.()0()00,10,10,(),1,0.,',',': ()(1)0.,(0,0),(0,1).,x y dx ey f b c d b c e f c d c e f b d c e f d b c e bc f A B C x y b c x bc y D P bc ++++=⎧++++++=⎪++++=⎨⎪++++=⎩=-+=-=+-++-=- 则由 解得 因此过的圆方程为 显然在该圆上 同理由对称性,,,,',',',,,,,,E F R S A B C D E F P Q R ,也在该圆上故九点共圆.,(),,,1,,,,,5//O R AB BX C D E BC CD DE R A AY L M AL R AM CL M MN LE AX N AN ===== 六、(10分)如图所示在的直径的延长线上取三点使得在点的切线上取两点使过点作,交于,求证近似于该圆周长.XA222222//,::111,,2,55121146 2525LE MN AM AN AL AE AM CL AL R AC R R R CL AL AC R R R CL R ∴====+==+=+=∴= 解 由又13522 3.14159192AE RAM AE AN R R R AL π===≈⨯≈ 故,,,,.ABCDEF AC CE M NAM CNr B M N r AC CE=七、(10分)设正六边形的对角线分别被内点分成比为=的两段,如果三点共线,求 F(,120)(,120)(,120),,,,,.,,,120. ,,,,R O R O R O O AM CN BD ND AC CE r M N AC CEMBC NDE B M N BND BD DBG N B G DCN CB C CN CB r CE CE −−−−→=−−−−→−−−−→∠====解 令正六边形的外接圆的圆心为,连接因为=所以所以因为三点共线所以以为边作正则四点共圆,显然是此圆的圆心, 从而.所以=() ''''',,,, '''''(,).A B C D E ABCDE k H A B C D E H O k ABCDE =八、(15分)如果两个多边形和相似相似比为并且对应边平行则存在一个位似变换使得证明:见讲义第四章第三节位似变换的定理9。
初等几何研究综合测试题(一)

《初等几何研究》综合测试题(一)适用专业:数学教育专业 考试时间:120分钟一、 选择题(本题共8小题,每小题3分,共24分)1.在 ABC 中,AB=AC ,高BF 、CE 交于高AD 上一点O ,图中全等三角形的对数是_____。
A.4;B.5;C.6;D.7.2.已知:如图, ABC 中,∠BAC=90°,AD ⊥BC 于D, 若AB=2,BC=3,则DC 的长度是________。
A.83; B.23; C.43; D.53。
3.下面4个图形中,不是轴对称图形的是_________。
A.有两个内角相等的三角形;B.有一个内角是45°的直角三角形;C.有一个内角是30°的直角三角形;D.有一个内角是30°,一个内角是120°的三角形。
4.下列条件中,不能判别四边形是平行四边形的是_________。
A.一组对边平行,另一组对边相等;B.两组对边分别平行;C.对角线互相平分;D.一组对边平行且相等。
5.若一个四边形既是轴对称图形,又是中心对称图形,则这个四边形是_________。
A.直角梯形;B.等腰梯形;C.平行四边形;D.矩形。
6.下列语句正确的是________。
A.圆可以看作是到圆心的距离等于半径的点的集合。
B.圆的内部可以看作是到定点的距离小于定长的点的集合。
C.圆的一部分叫做弧。
D.能够互相重合的弧叫做等弧。
7.在平移过程中,对应线段A.互相平行且相等;B.互相垂直且相等;C.互相平行(或在同一条直线上)且相等;D.以上都不对。
8.下列关于平移的说法中正确的是___________。
A.以原图形中的一点为端点,且经过它的对应点的射线的方向是平移的方向;B.平移后的两个图形中两个顶点连成的线段长是平移的距离;C.原图形中两个顶点连成的线段长是平移的距离;D.以对应点中的一点为端点的射线是平移的方向。
二、 判断题:(本题共5小题,每小题2分,共10分)1.如图1,直线a ,b ,c 在同一平面内,a//b ,a 与c 相交于P ,则b 与c 也一定相交。
初等几何研究试题答案

初等几何研究试题答案题目:在平面直角坐标系中,已知点A(2, 3),点B(-3, 1),点C在x轴上,且三角形ABC是等腰直角三角形,求点C 的坐标。
【解题过程】一、已知条件1. 点A的坐标为(2, 3);2. 点B的坐标为(-3, 1);3. 点C在x轴上,即点C的坐标形式为(x, 0);4. 三角形ABC是等腰直角三角形。
二、分析1. 由于三角形ABC是等腰直角三角形,所以AC=BC;2. 利用两点间的距离公式计算AC和BC的长度;3. 根据AC=BC,列出方程求解x的值;4. 得到点C的坐标。
三、解题步骤1. 计算AC的长度:由两点间的距离公式,AC的长度为:AC = √[(x - 2)² + (0 - 3)²]= √[(x - 2)² + 9]2. 计算BC的长度:由两点间的距离公式,BC的长度为:BC = √[(-3 - x)² + (1 - 0)²]= √[(x + 3)² + 1]3. 列出方程求解x的值:由于AC=BC,所以:√[(x - 2)² + 9] = √[(x + 3)² + 1]两边平方,得:(x - 2)² + 9 = (x + 3)² + 1展开方程,得:x² - 4x + 4 + 9 = x² + 6x + 9 + 1化简方程,得:-10x = -5解得:x = 0.54. 得到点C的坐标:由题意知,点C在x轴上,所以点C的坐标为(0.5, 0)。
四、结论通过以上解题过程,我们得到了点C的坐标为(0.5, 0)。
此时,三角形ABC为等腰直角三角形,满足题目条件。
五、拓展1. 如果将点C的位置限定在y轴上,求点C的坐标;2. 如果将三角形ABC限定为等边三角形,求点C的坐标;3. 如果给定三角形ABC的面积为某个数值,求点C的坐标。
通过以上拓展,我们可以进一步探讨平面几何中的各种问题,提高解题能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 (共 2 页)
4
一、填空题(本大题共 8 题,每空 2 分,共 20分)
1、当结论的反面只有一款时,否定了这一款便完成证明,这种较单纯的反证法叫做
; 2、设CM 是ABC ∆的中线,则当1
2
CM AB >
时,C ∠是 角; 3、两个平行平面的距离等于12cm ,一条直线和它们相交成60,则这条直线夹在两平面间的线段长为 ;
4、一些作图题中,往往可先作成图形的一个三角形,其余部分可由此三角形陆续作出,这种作图方法称为 ,此三角形称为 ;
5、在ABC ∆中,若AB AC >,CD BE 、分别是C ∠和B ∠的平分线,则CD 与BE 的大小关系是 ;
6、已知ABC ∆的三边分别为3cm ,5cm ,6cm ,则ABC ∆的内切圆半径r= ;
7、到两定点A 、B 的距离之比为定比k 的点的轨迹是 和 ;
8、设圆内接正五、六、十边形的边长分别为5a 、6a 、10a ,则它们之间的关系为 。
二、计算题(本大题共 2 题,每题8 分,共 16 分)
1、在直二面角的棱上有两点A 、B ,AC 和BD 各在这个二面角的一个面内,并且都垂直于棱
AB ,设8,6,24AB cm AC cm BD cm ===,求CD 的长。
2、设正方形ABCD 内接于O ,P 为DC 上一点,2
PA PC =
=
,求P B P D ⋅的值。
三、证明题(本大题共 4 题,每小题10 分,共40 分)
1、四边形ABCD 中,设AB CD =,M ,N 分别是AD 、BC
的中点,证明直线MN 与AB 、CD 所成的交角相等。
2、证明:梯形两腰的中点,两对角线的中点,四点共线。
C
第 2 页 (共 2 页)
3、设BE 、CF 是ABC ∆的高,在射线BE 上截取BP AC =,在射线CF 上截取CQ AB =,证明AP 与AQ 相等且垂直。
4、在圆内接四边形ABCD 中,BC CD =,求证:22AB AD BC =AC ⋅+
四、轨迹(本大题共 1 题, 12 分)
1、设定圆中互相垂直的两弦的平方和是常数,则此两弦所在直线交点的轨迹是一圆。
五、作图(本大题共 1 题,每题分,共12分)
1、求作一直线,使平行于三角形一边并平分其面积。
B。
